1

PRZEPŁYW  WODY  W  GRUNCIE

PRZEPŁYW  WODY  W  GRUNCIE

MECHANIKA GRUNTÓW I 

MECHANIKA GRUNTÓW I 

FUNDAMENTOWANIE

FUNDAMENTOWANIE

Budownictwo              semestr 4

Budownictwo              semestr 4

Wykład 9

Wykład 9

2

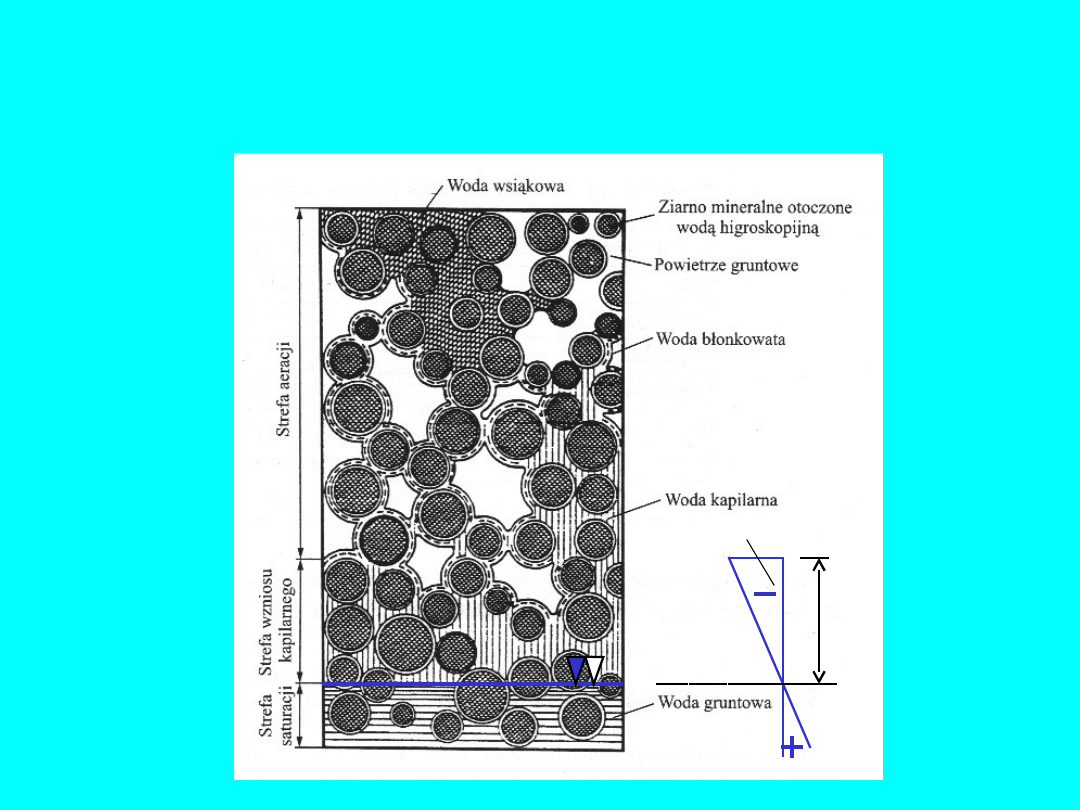
Rodzaje wody w gruncie

Woda  w  gruncie  może  występować  w  trzech  podstawowych 
stanach skupienia: 

gazowym

  

ciekłym

, oraz w stanie 

stałym

.

W  nawiązaniu  do  tego  można  stwierdzić,  że  woda  w  podłożu 
występuje jako:

- 

para wodna,

-  woda  związana  w  postaci:  wody  higroskopijnej  i  błonkowatej 
(silnie i słabo związanej),

- kapilarna (włoskowata),
- krystalizacyjna i chemicznie związana,
- lód.

Wpływ wody na zachowanie się gruntu pod obciążeniem oraz na 
zmiany  właś-ciwości  fizycznych  i  mechanicznych  gruntów  jest 
bardzo  duży.  Niektóre  z  zależności  już  poznaliśmy,  np.  wpływ 
wyporu  wody  na  ciężar  objętościowy,  zjawisko  konsolidacji  czy 
zasadę naprężeń efektywnych. Inne zagadnienia będą poruszone 
tutaj.

3

Woda  związana

    tworzy  na  powierzchni  cząstek  gruntowych  tzw. 

warstwę  pod-wójną,  na  którą  składa  się  woda 

higroskopijna

 

bardzo 

silnie 

przyciągana 

siłami 

elektrostatycznymi 

i 

międzycząsteczkowymi bezpośrednio do powierzchni cząstek oraz 
woda 

błonkowata

. Woda higroskopijna nie podlega grawitacji, zaś 

jej gęstość jest zbliżona do gęstości ciała stałego (1,2 – 2,4 g/cm

3

). 

Woda błonkowata jest już słabiej związana z cząstką i im dalej od 
powierzchni  cząstki,  tym  bardziej  jej  właściwości  są  zbliżone  do 
„zwykłej”  wody.  Łączna  grubość  warstwy  podwójnej  jest  rzędu 
kilku średnic cząstki H

2

O. 

Woda  kapilarna

  wypełnia  kanaliki  w  gruncie,  utworzone  z 

połączonych  porów.  Na  skutek  oddziaływania  sił  napięcia 
powierzchniowego na granicy fazy stałej i ciekłej woda kapilarna 
podnosi  się  ponad  poziom  zwierciadła  wody.  Wysokość  wzniosu 
kapilarnego zależy od wielkości średnicy kapilar gruntowych, a w 
związku  z  tym  również  rozmiarów  ziaren  gruntowych.  Im 
mniejszy  wymiar  cząstek,  tym  wyższe  podciąganie  kapilarne. 
Przybliżoną wysokość podciągania można wyznaczyć ze wzoru:

d

30

,

0

H

kc



d – średnica zastępcza ziarn (cząstek) gruntu w cm

4

Woda krystalizacyjna i chemicznie związana

 nie ma znaczenia w 

praktyce inżynierskiej.

Woda w postaci lodu

 występuje w gruncie w okresach ujemnych 

temperatur.  Głębokość  przemarzania  podłoża  w  naszych 
warunkach  sięga  do  1,5  m.  Lód  ma  znaczny  wpływ  na 
przemieszczanie się wody w gruncie i na właściwości gruntu (np. 
tworzenie się wysadzin, czy powstawanie przełomów wiosennych 
na drogach).

5

Woda  wolna

  swobodnie  wypełnia  pory  w  gruncie,  podlega 

działaniu  grawitacji  i  wywołuje  ciśnienie  hydrostatyczne  w 
gruncie.  Woda  wolna  jako 

woda  podziemna

  ma  zasadnicze 

znaczenie w działalności inżynierskiej.

Rys. 

1

lw
g

h

k

Ciśnienie 
wody

6

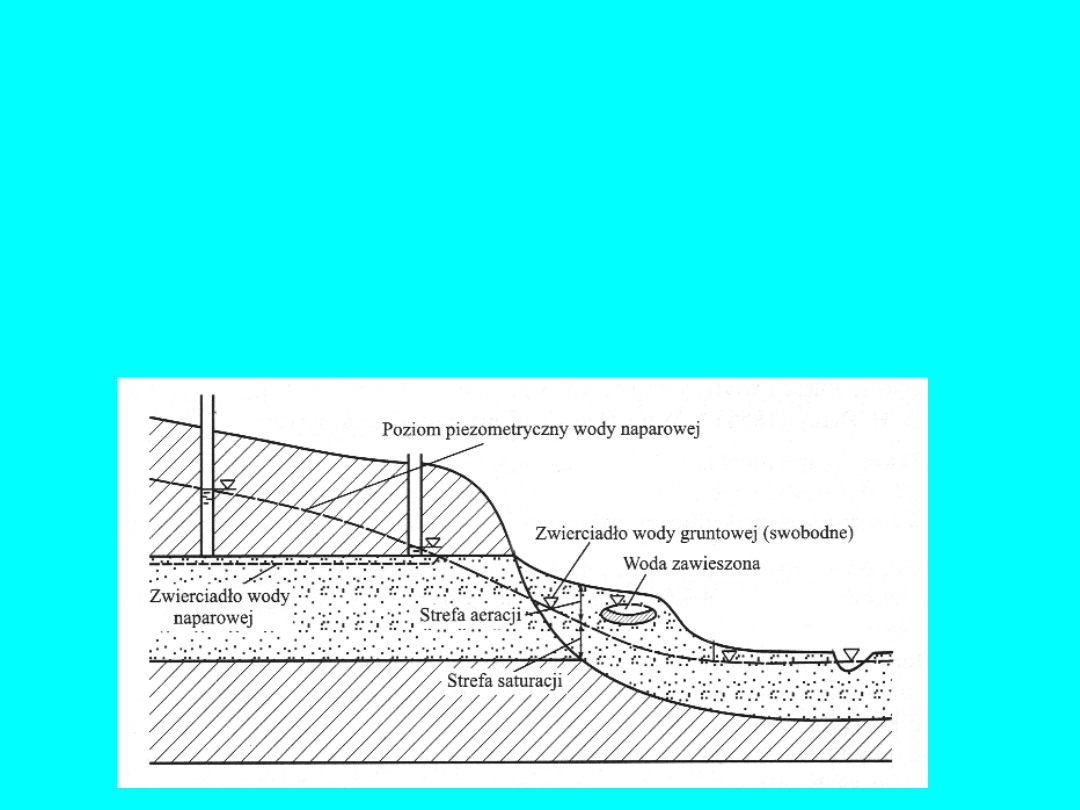
Woda podziemna

 w gruncie występuje w 

warstwach wodonośnych

, 

czyli w utwo-rach przepuszczalnych (piaski i żwiry) podścielonych 
utworami  trudno-przepuszczalnymi  (gliny  i  iły).  Zasoby  wód 
podziemnych  są  zasilane  z  powierzchni  terenu  przez 

infiltrację

 

wód opadowych lub wód powierzchniowych oraz kondensację pary 
wodnej w porach gruntu.

W  obrębie  warstwy  wodonośnej  wyróżnia  się  dwie  strefy 
występowania  wody:  strefę 

aeracji

  (napowietrzenia)  oraz  strefę 

saturacji

  (nasycenia).  Granicą  pomiędzy  nimi  jest 

zwierciadło 

(lustro)  wody  gruntowej

.  Podstawową  terminologię  związaną  z 

wodą podziemną przedstawia poniższy rysunek

Rys. 2

7

Przepływ wody w gruncie

Przepływ  wody  w  gruncie,  czyli 

filtracja

,  jest  wynikiem  działania 

ziemskiej  grawitacji.  Zgodnie  z  zasadami  hydrauliki  ruch  wody 
odbywa się z miejsc o wyższym ciśnieniu do miejsc, gdzie ciśnienie 
jest niższe. 

Opory filtracji zależą od takich czynników jak: rodzaj, uziarnienie i 
porowatość  gruntu  oraz  lepkość  i  temperatura  przepływającej 
wody. Im  drobniejsze są cząstki  gruntu, tym te opory są większe. 
Przepływ  wody  w  gruncie  ma  najczęściej  charakter  ruchu 

laminarnego

, to znaczy, że tory przepływu poszczególnych cząstek 

wody są do siebie równoległe, nie krzyżują się. 

Rys. 

3

8

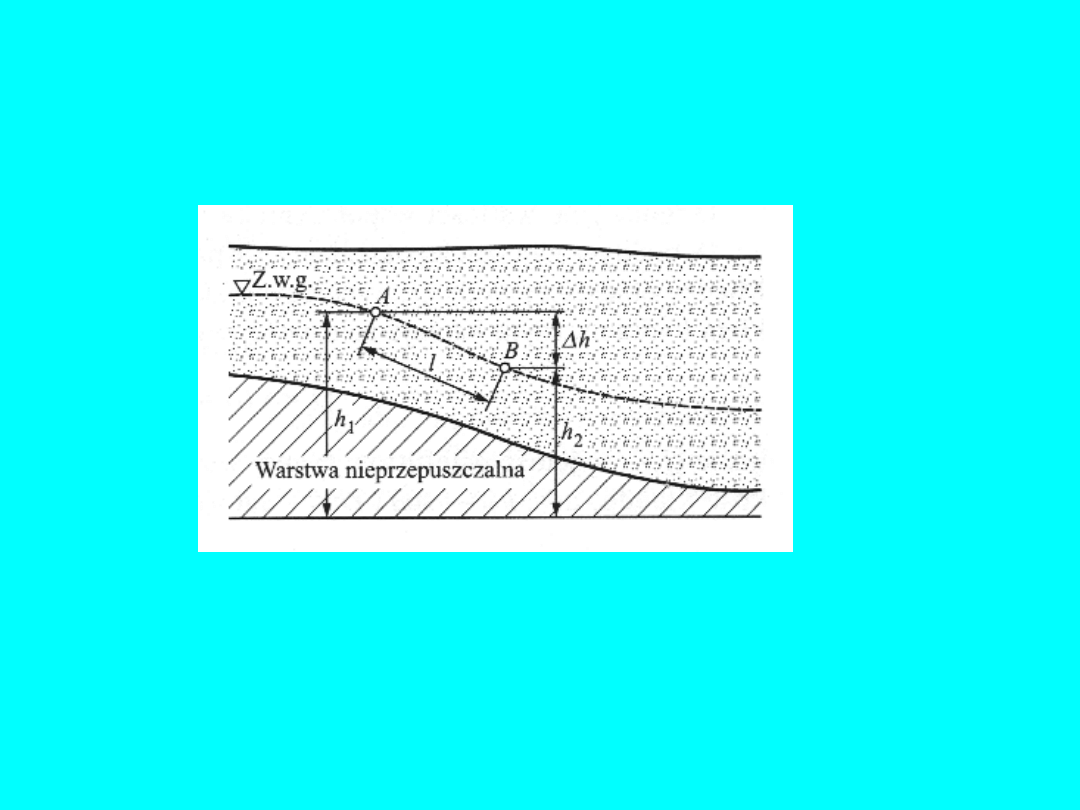
Prędkość  przepływu  wody  w  gruncie,  czyli  prędkość  filtracji 
określił 

H.  Darcy

  (1856  r.).  Stwierdził  on,  że  prędkość  ta  jest 

zależna  liniowo  od  spadku  (gradientu)  ciśnienia  wzdłuż  drogi 
filtracji, czyli od 

spadku hydraulicznego i

:

V  i

Wzór Darcy w pełnej formie ma postać:

V = k · i,

[m/s]

gdzie 

k

  jest  to  współczynnik  proporcjonalności  w  tym  wzorze, 

noszący nazwę 

współczynnika filtracji.

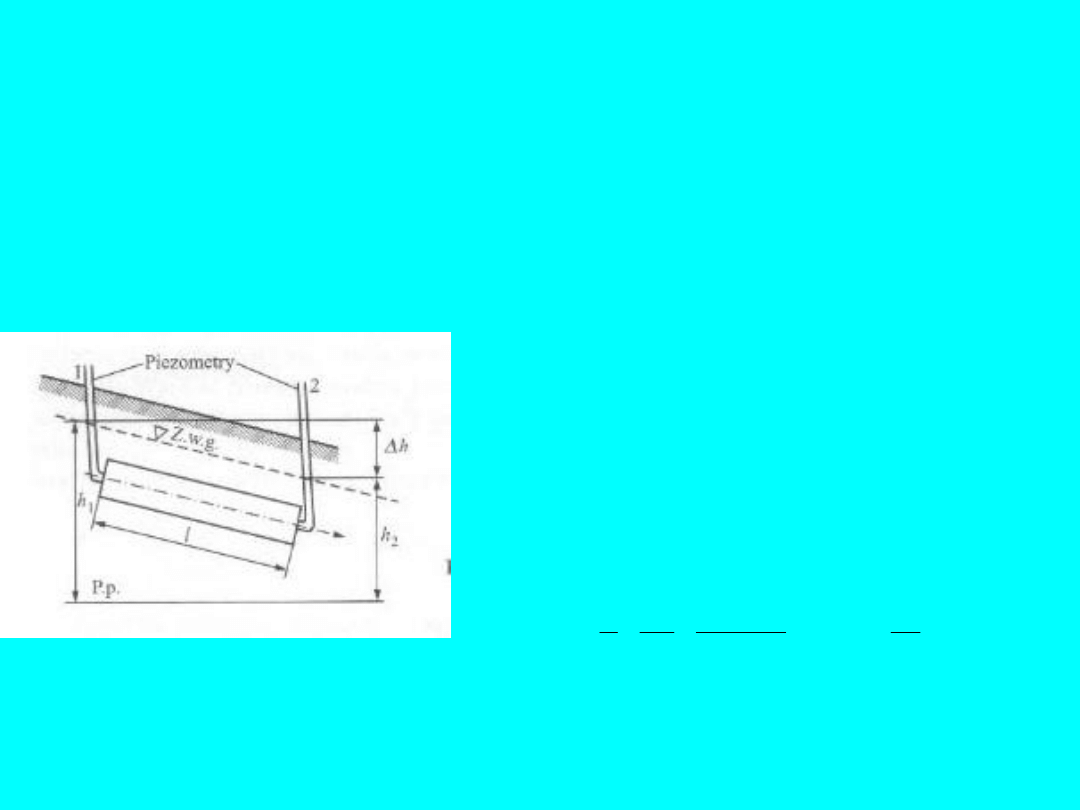
Spadek hydrauliczny wyraża się zależnością  (rys. 3):

l

h

l

h

h

i

2

1









Jeżeli  we  wzorze  Darcy  przyjmiemy 

i  = 1

,  to  otrzymamy 

V  = k

. 

Stąd  wynika  określenie  współczynnika  filtracji,  że  jest  to 

prędkość  filtracji  przy  spadku  hydraulicznym  równym  jedności

. 

Ma on zatem miano prędkości i jest wielkością charakterystyczną 
dla  gruntu  w  określonym  stanie  i  temperaturze.  Po  zmianie 
porowatości  gruntu  lub  temperatury  wody,  zmienia  się  jego 
wartość liczbowa.  

9

Zwykle  dokonujemy  porównania  wartości 

k

  dla  temperatury  10° 

C.  Współczynnik  filtracji 

k

T

  określony  dla  temperatury 

T

  można 

sprowadzić  do  temperatury  10°  C  przy  pomocy  zależności 
empirycznej:

T

03

,

0

7

,

0

k

k

T

10







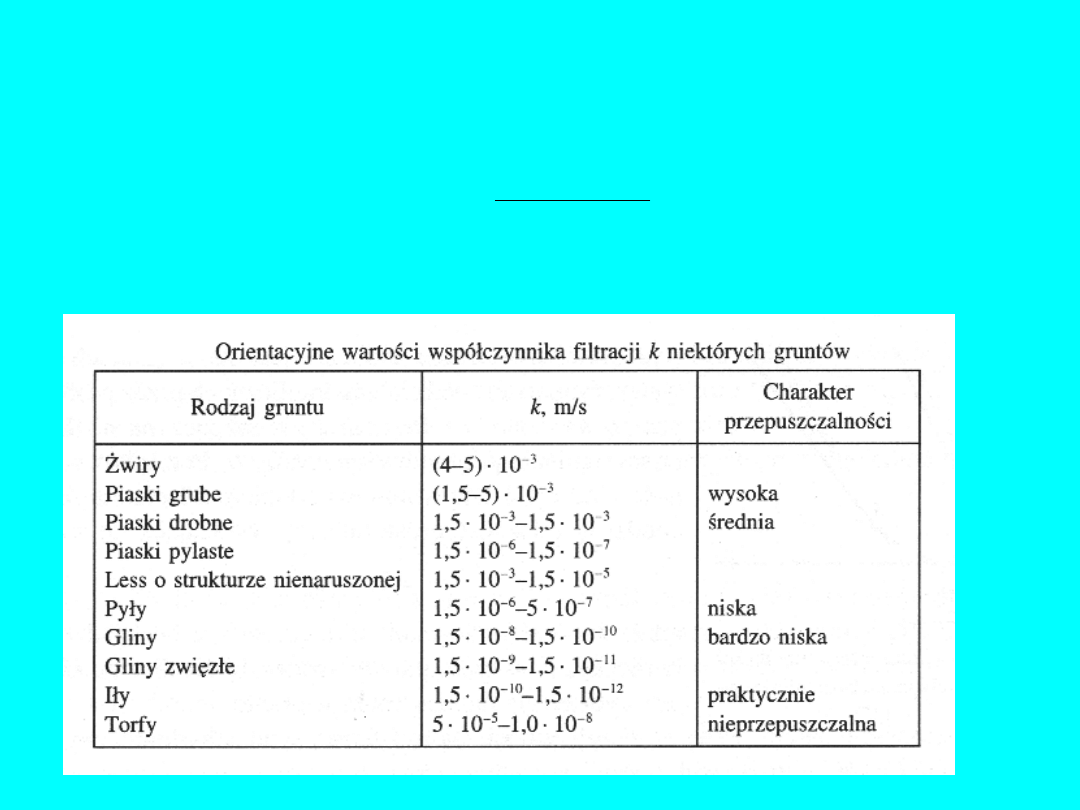
Wartości współczynników filtracji dla różnych gruntów są bardzo 
zróżnicowane:

10

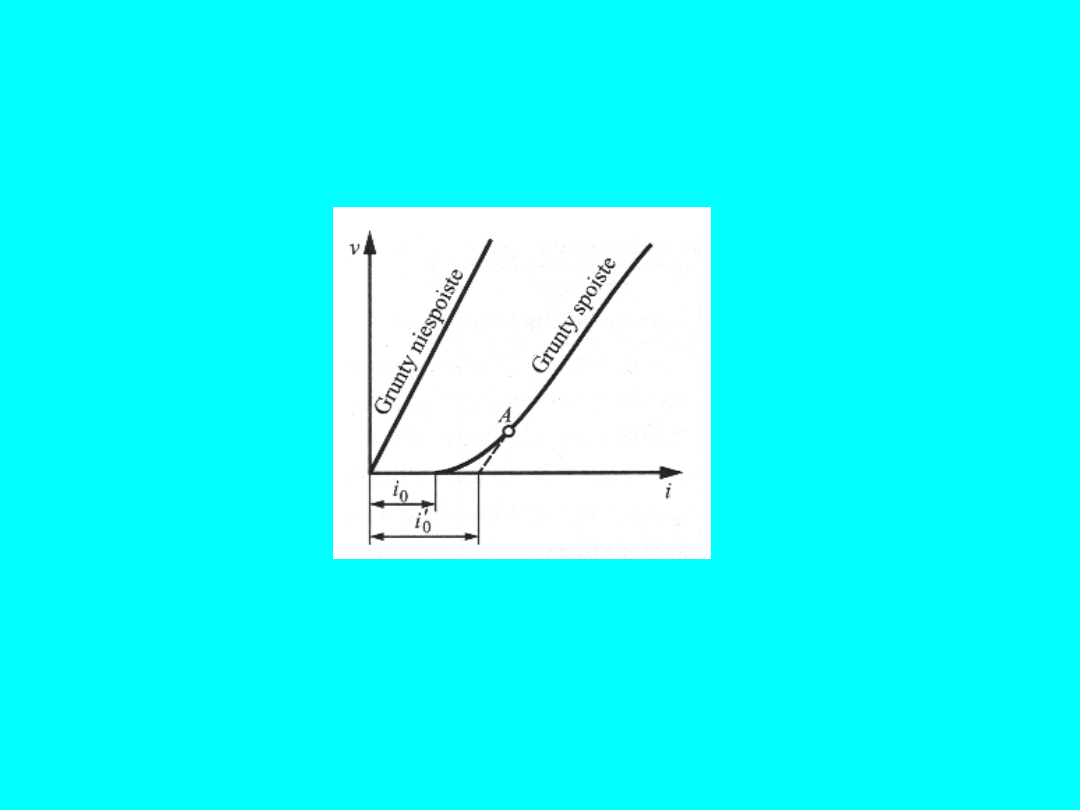
Stwierdzono,  że  filtracja  w  gruntach  spoistych  przebiega  nieco 
odmiennie  niż  w  gruntach  sypkich.  Dla  zainicjowania  przepływu 
niezbędne  jest  pokonanie  wstęp-nych  oporów  i  przepływ 
następuje  dopiero  po  przekroczeniu  pewnego 

począt-kowego 

spadku hydraulicznego i

0

. Dalszy ruch jest już zasadniczo zgodny 

z prawem Darcy:

Dla gruntów spoistych można zapisać prawo Darcy w formie:

V = k(i – i

0

’)

Wartość początkowego spadku i

0

 jest zwykle większa niż 10, zaś 

dla iłów osiąga nawet wartości zbliżone do 30.

Rys. 

4

11

Prędkość wyznaczona ze wzoru Darcy dotyczy przepływu całym 
przekrojem prowadzącym wodę. Ponieważ grunt jest ośrodkiem 
porowatym  i  przepływ  odbywa  się  siecią  połączonych  porów, 
rzeczywista 

prędkość 

przepływu 

jest 

uzależniona 

od 

porowatości gruntu

 n

:

n

V

V

rz



Należy  pamiętać,  że  po  przekroczeniu  pewnej  wartości 
prędkości  przepływu,  zwanej  prędkością 

krytyczną

,  zmienia  się 

charakter ruchu wody z laminarnego na 

turbulentny

 (burzliwy). 

Ruch  taki  może  odbywać  się  w  “przewodach”  gruntowych  o 
dużych  rozmiarach  –  nadkapilarnych.  Wzór  na  prędkość 
krytyczną przedstawia się następująco:





Re

d

,

n

,

V

e

kr









23

0

75

0

gdzie:  n  –  porowatość  (jako  ułamek  dziesiętny),  d

e

  –  średnica  miarodajna  ziarn 

gruntowych,  mm,  Re  –  stała,  zwana  liczbą  Reynoldsa;  Re  =  7,5  –  9,0  (w 
zależności  od  wielkości  ziaren),  ν  –  współczynnik  lepkości  kinematycznej  (w 
przybliżeniu równy współczynnikowi lepkości dynamicznej).

Otrzymana z tego wzoru prędkość krytyczna dla piasków wynosi 
około  300  –  1000  m/dobę.  Rzeczywista  prędkość  przepływu  nie 
przekracza jednak zwykle 250 m/dobę. Można więc przyjąć, że w 
praktycznych  zastosowaniach  w  odniesieniu  do  gruntów 
obowiązuje liniowe prawo filtracji Darcy.

12

Wyznaczanie współczynnika filtracji

Znajomość  wartości  współczynnika  filtracji  gruntu  jest 
niezbędna 

przy 

wielu 

problemach 

związanych 

z 

fundamentowaniem,  takich  jak:  projektowanie  odwod-nienia 
wykopu  fundamentowego  na  czas  budowy  lub  drenażu 
eksploatacyjnego  zabezpieczającego  piwnice  budynku  przed 
napływem wody, analiza konsolidacji podłoża itp. 
Stosuje  się  trzy  grupy  metod  pozwalających  na  wyznaczenie 
współczynnika

 k

:

-  wzory 

empiryczne

  (doświadczalne)  –  ustalone  dla  gruntów  o 

określonych właściwościach (głównie uziarnieniu i porowatości) 
i tylko dla nich ważne,
-  badania 

laboratoryjne

 na próbkach gruntu,

-  badania 

polowe

 (próbne pompowania).

Metody  te  różnią  się  stopniem  dokładności.  Wzory  empiryczne 
pozwalają 

na 

wyznaczenie 

orientacyjnych 

wartości 

współczynnika  k  tanim  kosztem.  W  badaniach  laboratoryjnych 
uzyskujemy wartości współczynnika k bliższe rzeczywistości, ale 
trzeba  pamiętać,  że  dysponujemy  próbką  o  niewielkich 
rozmiarach 

i 

zawsze 

w 

pewien 

sposób 

naruszoną. 

Najdokładniejsze  wyniki,  ale  za  najwyższą  cenę,  uzyskujemy  w 
drodze badań polowych, wykonywanych bezpośrednio w miejscu 
zalegania  warstw  gruntu.  Każdorazowo  zatem  projektant  musi 
ocenić,  czy  przy  danym  problemie  geotechnicznym  wystarczą 
mu wartości przybliżone, czy muszą to być wartości dokładne.

13

Wzory empiryczne

Do  wyznaczenia  współczynnika  filtracji  gruntów  za  pomocą 
wzorów  empirycznych  niezbędne  jest  uprzednie  wykonanie 
analizy  granulometrycznej  (uziarnienia)  gruntu  oraz  niekiedy 
również oznaczenie porowatości.
Jako  przykład  wzorów  empirycznych  podaje  się 

wzór  Hazena

, 

stosowany do gruntów sypkich, dla których średnica d

10

 = 0,1 – 

3,0 mm  oraz  wskaźnik różnoziarnistości  U   5

k

10

 = C·d

10

2

[m/s]  lub  [m/doba]

k

10

  –  współczynnik  filtracji  dla  T  =  10º  C,  w  m/s  lub  w  m/dobę 

(zależnie od przyjętego współczynnika C,·
C – współczynnik ustalony doświadczalnie, zależny od U:

  U

 C [m/s]

C [m/doba]

1

0,0139

1200

2 - 4

0,00925

800

5

0,00463

400

d

10

  –  średnica  miarodajna,  mm,  ustalona  z  krzywej  uziarnienia 

gruntu.

14

Metody laboratoryjne

1. 

Aparat ze stałym spadkiem hydraulicznym

 - grunty sypkie

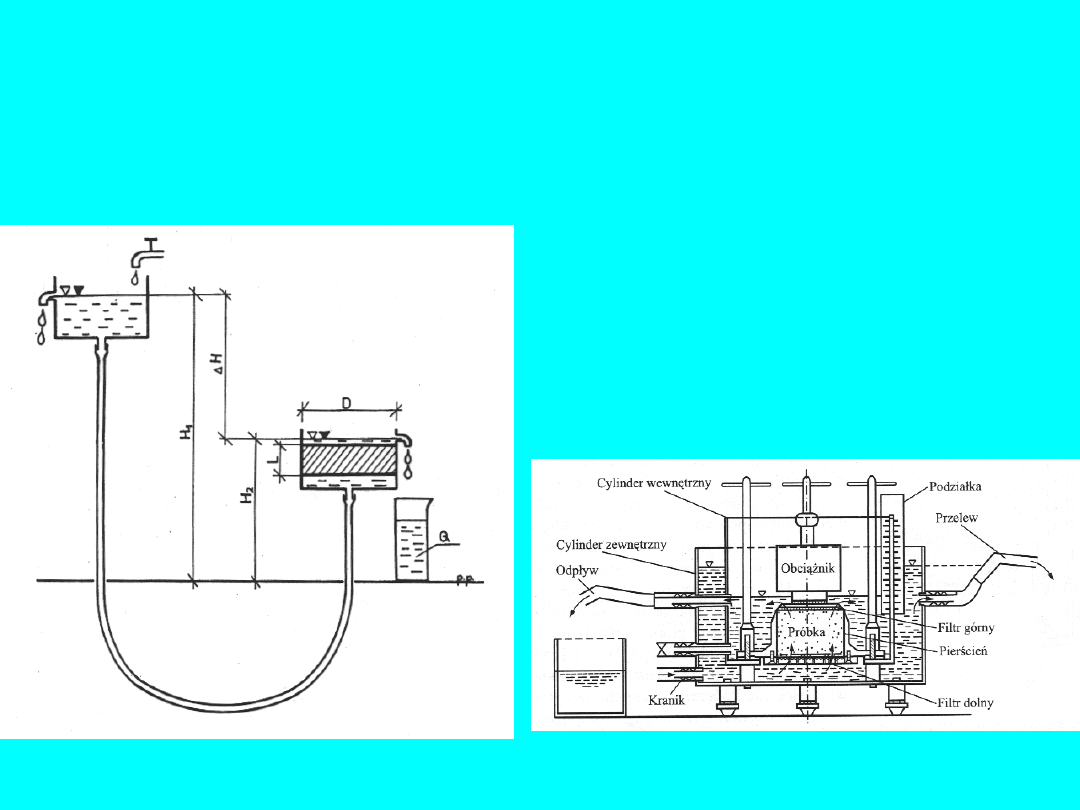
Rys. 5

a) schemat działania aparatu o 
stałym spadku hydraulicznym,

b) aparat ZWK - 2

a
)

b)

15

Ustawiając  odpowiednio  wysokość  górnego  naczynia  można 
regulować wielkość spadku hydraulicznego w granicach 

i = 0,3 

- 0,8

. Woda przepływa od dołu próbki wypierając powietrze z jej 

porów.  Po  ustaleniu  się  zwierciadła  wody  w  obu  naczyniach 
(komorach)  wykonujemy  pomiar  wydatku 

Q

  (ilość  wody,  która 

przesączyła  się  przez  próbkę  o  powierzchni  przekroju 

A 

i 

wysokości

  L

)  w  czasie  badania 

t

.  Badanie  dla  jednej  próbki 

powtarza  się  pięciokrotnie,  a  następnie  zmieniając  wysokości 
naczyń  (przelewów  z  komór)  prowadzimy  pomiary  przy 
przepływie z góry do dołu. Wyniki uśredniamy. 

Ilość  wody,  która  przefiltrowała  przez  próbkę  w  czasie 

t

 

(wydatek) jest równa:

]

cm

[

     

A

t

i

k

A

t

V

Q

T

3















Stąd współczynnik filtracji 

k

T

 (w temperaturze badania 

T

) będzie 

równy:

]

s

/

cm

[

     

A

t

)

H

H

(

L

Q

A

t

i

Q

k

T

















2

1

Zwykle dla danego gruntu przeprowadza się badania dla kilku wartości stopnia 
zagęszczenia  gruntu  -  od  stanu  luźnego  do  zagęszczonego  -  a  następnie 
sporządza  się  wykres  zależności  k  od  I

D

.  Dysponując  takim  wykresem  można 

określić wartość współczynnika filtracji dla dowolnego stopnia zagęszczenia.

16

2. 

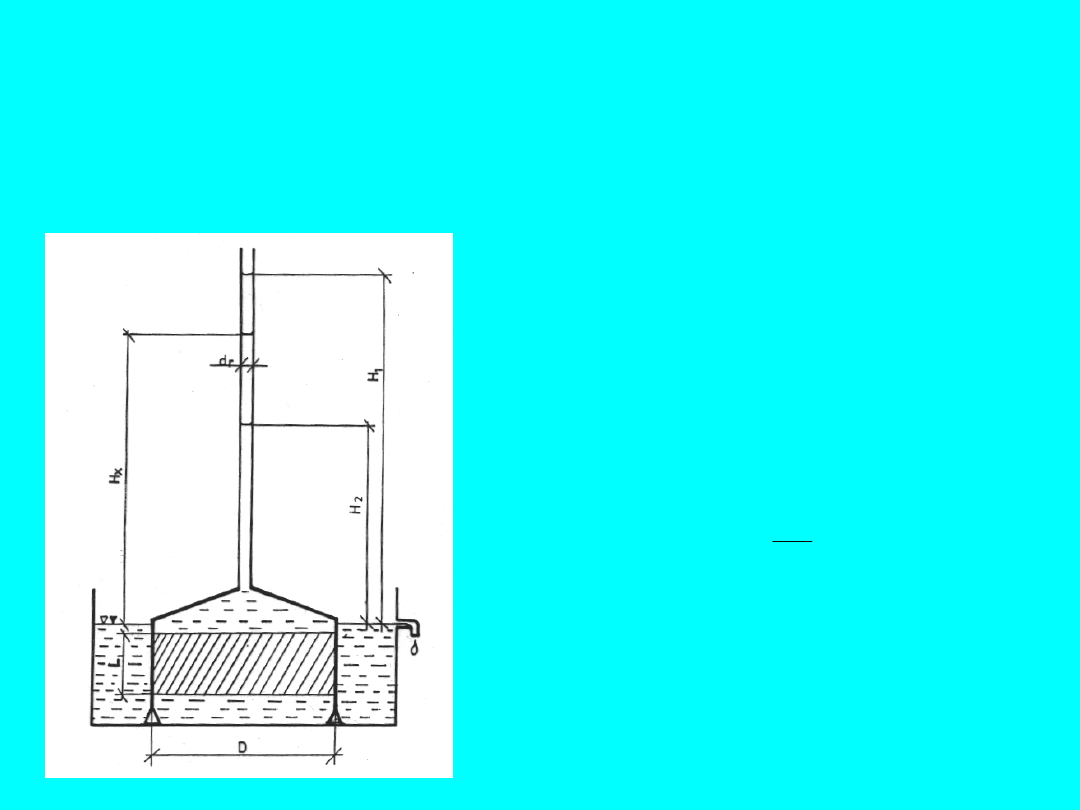
Aparat ze zmiennym spadkiem hydraulicznym

 - grunty spoiste

Jak stwierdzono wcześniej dla zainicjowania przepływu w próbce 
gruntu 

spois-tego 

niezbędny 

jest 

początkowy 

spadek 

hydrauliczny  i

0

  >  10.  Dla  uzyskania  takiego  spadku  stosuje  się 

aparaty o odmiennej konstrukcji niż dla gruntów sypkich

Walcowa  próbka  o  polu  przekroju 

A

 

oraz  wysokości 

L

  znajduje  się  w 

naczyniu  do  którego  podłączona  jest 
wąska  rurka  o  przekroju 

a

.  Rurka 

wypełniona  jest  wodą.  Pod  ciśnieniem 
słupa  wody  o  wysokości  zmieniającej 
się  od 

H

1

  do 

H

2

  następuje  przepływ 

wody  przez  próbkę  w  czasie

  t

.  Spadek 

hydrauliczny  w  danym  momencie 
badania jest równy:

L

H

i

x

t



gdzie Hx jest wysokością  słupa wody w 
rurce  w  danym  momencie.  Spadek 
zmienia  się  więc  w  trakcie  badania  - 
stąd nazwa aparatu.

Rys. 6

17

Objętość wody, jaka ubyła z rurki w czasie 

dt

 jest równa:

dh

a

dQ







znak „-”, gdyż nastąpił ubytek wody w rurce.

Taka sama ilość wody musiała przefiltrować przez próbkę:

A

dt

L

H

k

A

dt

i

k

A

dt

V

dQ

x

T

T























Porównując oba wyrażenia otrzymamy:

A

dt

L

H

k

dh

a

x

T













Po uporządkowaniu równania - rozdzieleniu zmiennych, mamy:

dt

L

a

A

k

H

dh

T

x









Uwzględniając, że w chwili t = 0, H

x

 = H

1

, zaś dla t = t jest H

x

 

=  H

2

,  i  po  obustronnym  scałkowaniu  wyrażenia,  otrzymujemy 

ostatecznie:

2

1

H

H

ln

t

A

L

a

k

T









18

Metody polowe

 - próbne pompowanie

Próbne  pompowanie  polega  na  tym,  że  wykonuje  się 

studnię

, 

czyli metodą wiertniczą zapuszcza się rurę stalową, zaopatrzoną 
w  dolnej  części  w 

filtr

.  Filtr  jest  to  odcinek  rury  perforowanej, 

owiniętej specjalną siatką filtracyjną, przez którą woda z gruntu 
przedostaje  się  do  wnętrza  studni,  skąd  jest  pompowana.  W 
pewnej  odległości  od  studni  wykonuje  się  jeden  lub  dwa  dwa 
dodatkowe  otwory  obserwacyjne,  czyli 

piezometry

,  które  służą 

do pomiaru zmian poziomu lustra wody w trakcie pompowania. 
Omówimy  tutaj  najpierw  przypadek  tzw. 

studni  zupełnej

  ze 

swobodnym lustrem wody, czyli studni, która jest doprowadzona 
do  stropu  warstwy  nieprzepuszczalnej  (np.  iłu),  podścielającej 
warstwę 

wodonośną

 (np. piasku lub żwiru) w której znajduje się 

woda.  Dodatkowo  wymagane  jest,  aby  filtr  obejmował  całą 
miąższość  warstwy  wodonośnej.  Dopływ  wody  do  takiej  studni 
odbywa  się  wyłącznie  radialnie  poprzez  powierzchnię  boczną 
filtra.
Do  wnętrza  studni  wprowadza  się  pompę  głębinową  i 
rozpoczyna  pompowanie  wody.  Na  skutek  tego  lustro  wody 
wokół  studni  zaczyna  się  obniżać,  tworząc  tzw. 

lej  depresyjny

. 

Po pewnym czasie ruch wody w studni ustali się, czyli warunki 
przepływu będą niezmienne. 

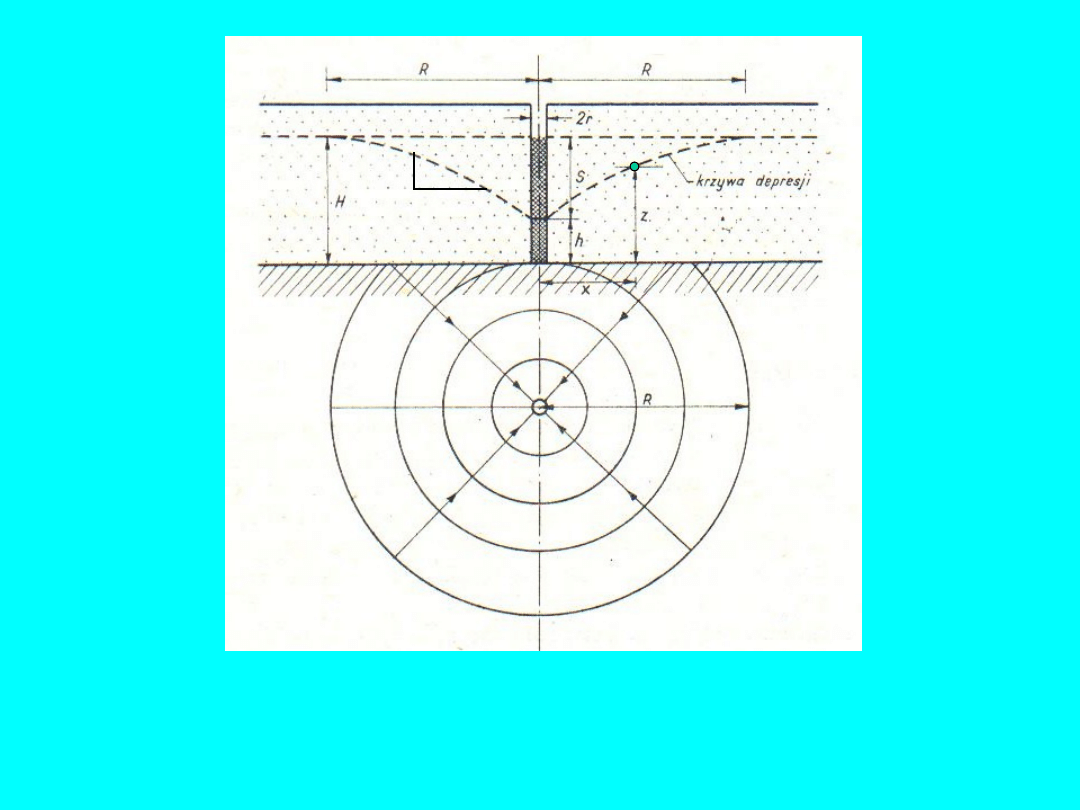
19

Rys. 7. Schemat studni zupełnej w warunkach swobodnego 

zwierciadła wody

dz

dx

dl

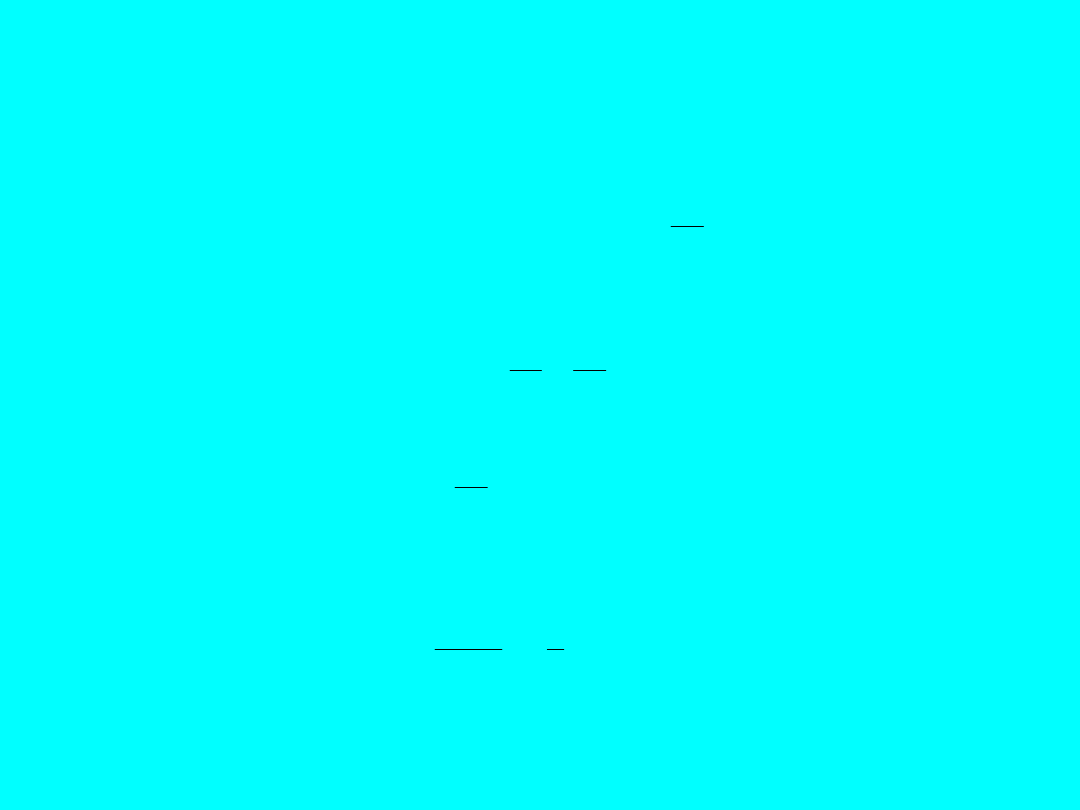
20

Korzystając  z  powyższego  rysunku  wyprowadzimy  równanie 
krzywej  depresji  (śladu  przecięcia  leja  depresji  płaszczyzną 
pionową, przechodzącą przez oś studni).
Ilość wody przepływającej w jednostce czasu przez powierzchnię 
walca  o  promieniu 

x

  i  wysokości 

z

  (równa  ilości  wody 

wypompowywanej ze studni) wynosi: 

dx

dz

k

z

x

i

k

A

Q

T

T



















2

Przyjęto  tutaj,  że  spadek  hydrauliczny  wzdłuż  krzywej  depresji 
jest równy w przybliżeniu:

dx

dz

dl

dz

i





Po uporządkowaniu (rozdzieleniu zmiennych):

dz

z

k

x

dx

Q

T













2

zaś po obustronnym scałkowaniu i uwzględnieniu, że rzędna 

z

 na 

brzegu  studni  (czyli  dla 

x  =  r

)  przyjmuje  wartość 

z  =  h

 

(wysokość słupa wody w studni) otrzymamy:

2

2

h

z

r

x

ln

k

Q

T











Jest to poszukiwane równanie krzywej depresji.

21

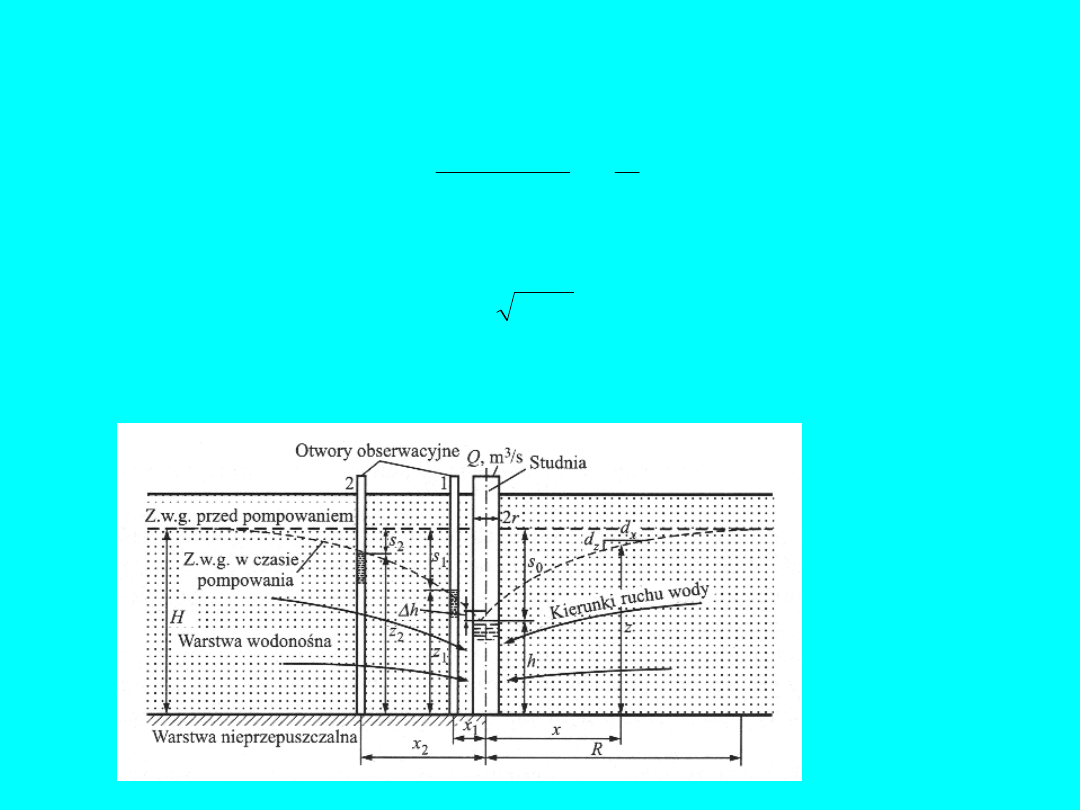
Jeżeli  znamy 

promień  leja  depresji

 

R

  (czyli  punktu,  w  którym

 

depresja

 

s  =  0

,  zaś 

z  =  H

,  gdzie  H  –  miąższość  warstwy 

wodonośnej), to współczynnik filtracji wyznaczymy ze wzoru:

r

R

ln

)

h

H

(

Q

k

T







2

2



Promień leja depresji można oszacować na podstawie wzorów 
empirycznych, np. wzoru Kusakina:

]

m

[

     

,

H

k

s

R







0

575

Bardzo  często  wykonuje  się  pompowanie  w  układzie 

węzła 

hydrogeologicznego

  składającego  się  ze  studni  i  dwu  otworów 

obserwacyjnych - 

piezometrów

:

Rys. 
8

22

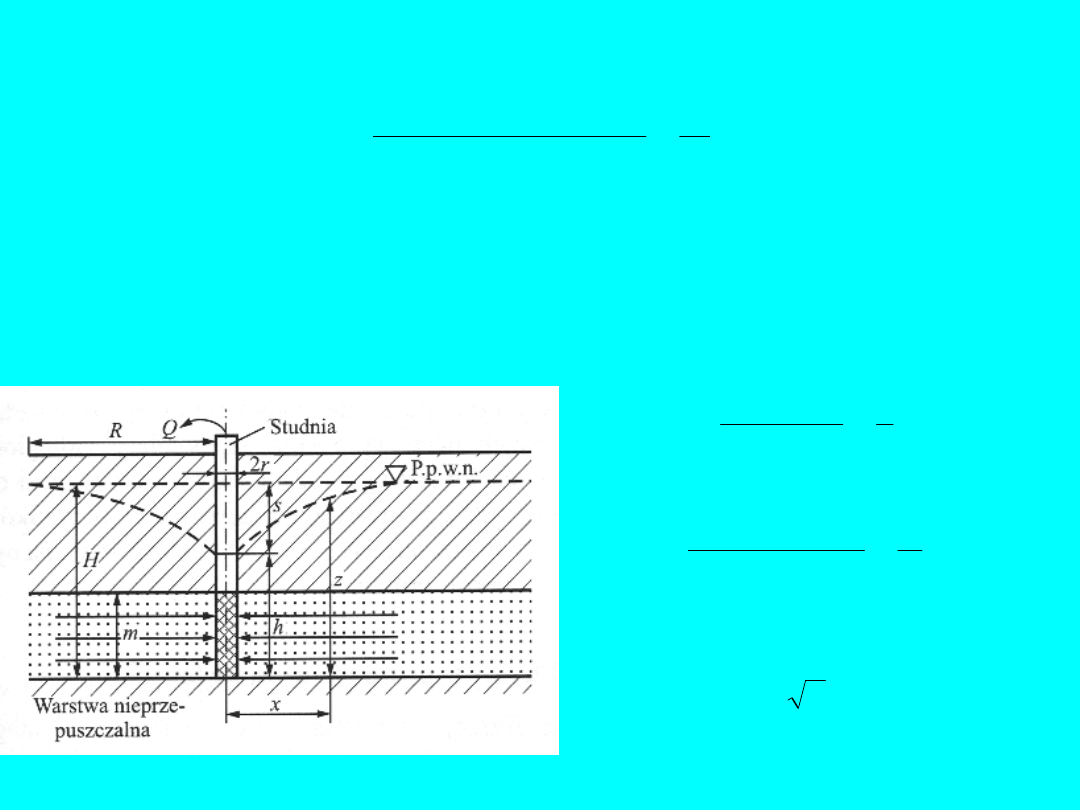
Współczynnik filtracji w takim układzie wyznacza się z 
następującego wzoru:

1

2

2

1

2

1

2

x

x

ln

)

s

s

H

)(

s

s

(

Q

k

T











W analogiczny sposób wyznacza się równanie krzywej depresji 
i  współczynnik  filtracji  dla  studni  zupełnej  przy 

napiętym 

zwierciadle  wody  gruntowej

,  gdzie  woda  znajduje  się  w 

warstwie  wodonośnej  o  miąższości 

m

  pomiędzy  dwoma 

warstwami nieprzepuszczalnymi:

krzywa depresji:

r

x

ln

k

m

Q

h

z

T











2

współczynnik filtracji:

r

R

ln

)

h

H

(

m

Q

k

T











2

zasięg leja depresji – Sichardt:

]

m

[

     

,

k

s

3000

R







Rys. 9

23

Zjawiska w gruncie spowodowane filtracją

Ciśnienie  spływowe

  –  Woda  przepływająca  przez  grunt 

napotyka  na  opory  związane  z  tarciem  wody  o  ziarna  i  cząstki 
szkieletu.  Opór  tarcia  (parcie)  wody  w  odniesieniu  do 
jednostkowej 

objętości 

gruntu 

nosi 

nazwę 

ciśnienia 

spływowego

.  Jest  ono  zawsze  skierowane  zgodnie  z  kierunkiem 

filtracji  (stycznie  do  linii  prądu).  Wartość  ciśnienia  spływowego 
można ustalić w następujący sposób.

Wydzielamy  myślowo  w  gruncie  walec, 
skierowany 

zgodnie 

z 

kierunkiem 

filtracji,  o  przekroju 

F

  i  długości 

l

.  Na 

walec  ten  działa  wy-padkowe  parcie 
hydrostatyczne równe:

F

h

P

w











Siła P (równa oporom filtracji w obrębie 
walca) 

przeliczona 

na 

jednostkę 

objętości 

walca 

jest 

ciśnieniem 

spływowym 

j

:

]

,

i

l

F

F

h

l

F

P

V

P

j

w

w

3

m

N

[

     

























Jak  widać  ciśnienie  spływowe  zależy  wyłącznie  od  wielkości 
spadku hydrau-licznego

Rys. 
10

24

Przepływ  wody  przez  grunt,  a  w  związku  z  tym  ciśnienie 
spływowe,  ma  wpływ  na  wartość  wypadkowego  ciężaru 
objętościowego szkieletu gruntowego pod wodą:

v

j

'

'

'









gdzie:  

γ’

 - ciężar objętościowy gruntu pod wodą, 

j

v

 – składowa pionowa 

ciśnienia spływowego. Znak „

+

” stosuje się przy przepływie wody w dół, 

zaś „

-

” do góry.

Jak  widać  ze  wzoru,  w  przypadku  przepływu  wody  ku  górze 
może  dojść,  przy  odpowiedniej  wartości  ciśnienia  spływowego, 
gdy  

j

v 

= γ’,

 do sytuacji, w której wypadkowy ciężar objętościowy 

gruntu 

’’

  będzie  równy  zero.  Taka  wartość  ciśnienia 

spływowego  nosi  nazwę 

krytycznego  ciśnienia  spływowego

,  a 

odpowiadająca  mu  wartość  spadku  – 

krytycznego  spadku 

hydraulicznego:

w

kr

w

kr

v

'

i

'

i

'

j





















Przy krytycznym spadku hydraulicznym, następuje upłynnienie sypkich 
gruntów takich jak Pd i P oraz gruntów pylastych małospoistych (p, 

).  Ich  wytrzymałość  na  ścinanie  maleje  do  zera.  Grunt  przechodzi  w 

stan  płynny  i  zachowuje  się  jak  ciecz.  Takie  zjawisko  nosi  nazwę 

kurzawki

.  Przy  wykonywaniu  wykopów  w  tego  typu  gruntach,  dla 

uniknięcia upłynnienia, musi być w dnie wykopu spełniony warunek:

j

v

  0,5 ’

25

Wyparcie  gruntu

  jest  to  zjawisko  polegające  na  przesunięciu  pewnej 

objętości gruntu pod wpływem działania wody. Wyparta masa gruntowa 
zwiększa  swoją  objętość,  a  więc  i  porowatość.  Zjawisko  wyparcia 
występuje  najczęściej  przy  przepływie  do  góry  -  rys.  11,  lecz  może 
wystąpić również w kierunku poziomym, a niekiedy w dół.

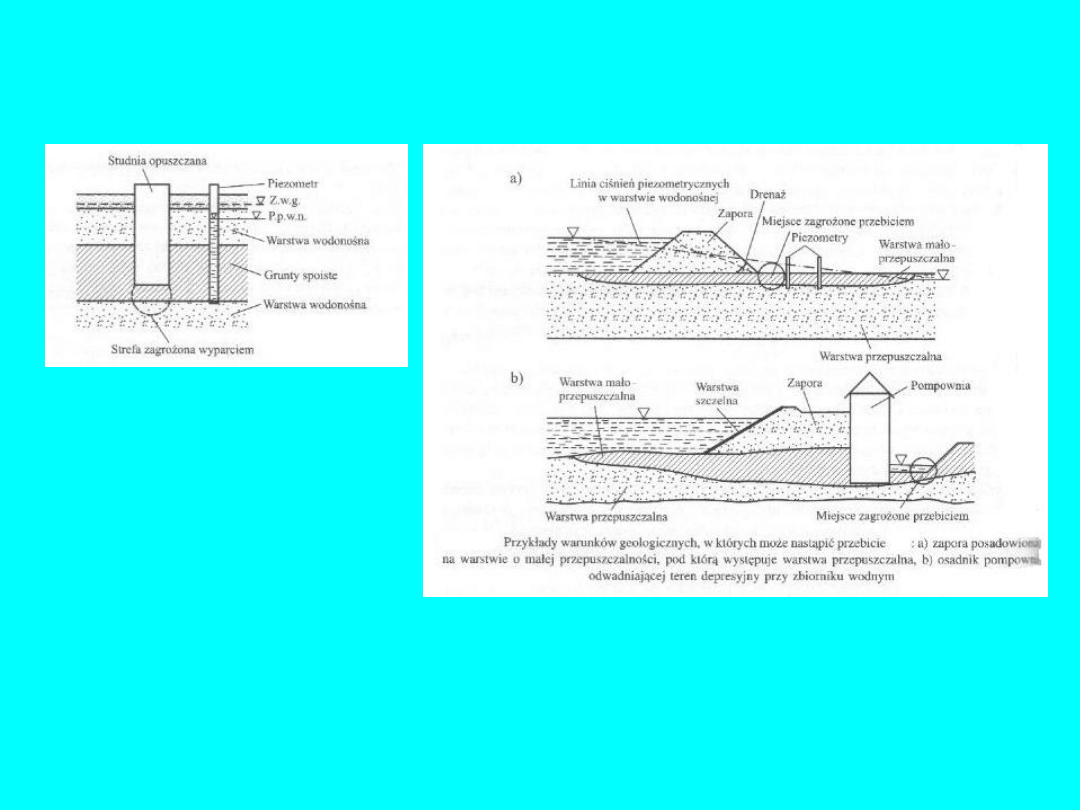
Przebicie  hydrauliczne

 

jest  to  zjawisko  tworzenia 
się  kanału  (przewodu)  w 
masie 

gruntowej, 

wypełnionego  gruntem  o 
naru-szonej 

strukturze, 

łączącego 

miejsca 

o 

wyższym 

i 

niższym 

ciśnieniu  wody  w  porach– 

rys. 12.

Sufozja

 jest to zjawisko polegające na wynoszeniu przez filtrującą wodę 

drobnych cząstek gruntu. Mogą być one przemieszczone w inne miejsce 
lub  wyniesione  poza  obręb  gruntu.  W  wyniku  tego  tworzą  się  kawerny 
lub  kanały  w  masie  gruntowej  i  zjawisko  nabiera  cech  przebicia 
hydraulicznego. Sufozja pojawia się, gdy przekroczony zostaje 

krytyczny 

spadek hydrauliczny

 lub 

krytyczna prędkość filtracji.

Rys. 
11

Rys. 

12

26

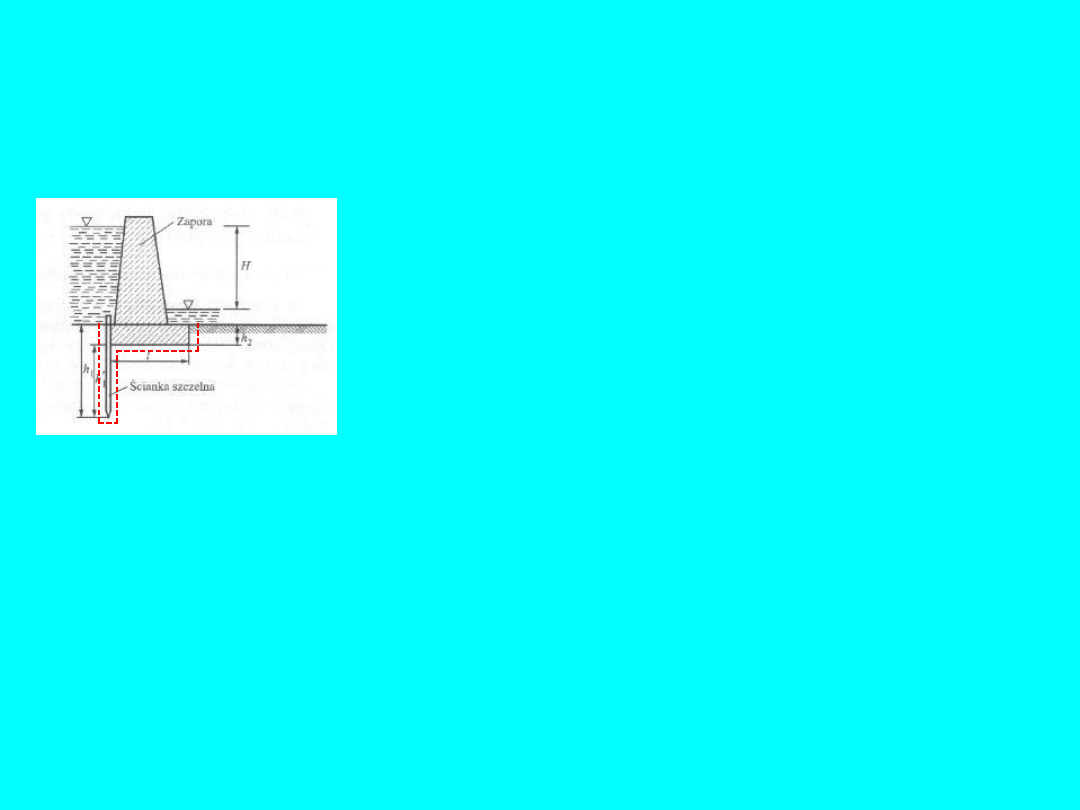
Dla  zabezpieczenia  się  przed  szkodliwym  działaniem  filtracji 
należy,  jak  wynika  z  poprzednich  rozważań,  przede  wszystkim 
zmniejszyć  spadek  hydrauliczny,  który  wpływa  na  prędkość 
filtracji  oraz  ciśnienie  spływowe.  Można  to  uzyskać  wydłużając   
drogę filtracji, np. przez stosowanie ścianek szczelnych:

Bez 

ścianki 

szczelnej 

woda 

przepływa 

bezpośrednio  pod  fundamentem  zapory.  Po  jej 
wykonaniu 

woda 

ma 

wydłużoną 

drogę 

przepływu,  gdyż  musi  dodatkowo  opłynąć 
ściankę.  Dobierając  odpowiednio  głębokość 
wbicia 

ścianki 

h

1

 

mo-żemy 

uzyskać 

zmniejszenie  spadku  hydraulicznego  poniżej 
wartości krytycznej 

i

kr

.

Przy  wykonawstwie  robót  ziemnych  (wykopów)  w  gruntach 
wrażliwych na upłyn-nienie (piaskach i pyłach) ważny jest sposób 
odwodnienia  wykopów  przy  obecności  wody  gruntowej.  Należy 
unikać  bezpośredniego  pompowania  wody  z  wnętrza  wykopu, 
gdyż wówczas kierunek filtracji jest skierowany ku górze i może 
dojść  do  upłynnienia  podłoża.  W  takich  przypadkach  należy 
stosować  odwodnienie  wgłębne  przy  wykorzystaniu 

studni

  lub 

igłofiltrów

  usytuowanych  poza  wykopem,  na  jego  obwodzie. 

Uzyskuje  się  wówczas  całkowicie  bezpieczny  kierunek  filtracji 
skierowany w dół.

Rys. 
13

27

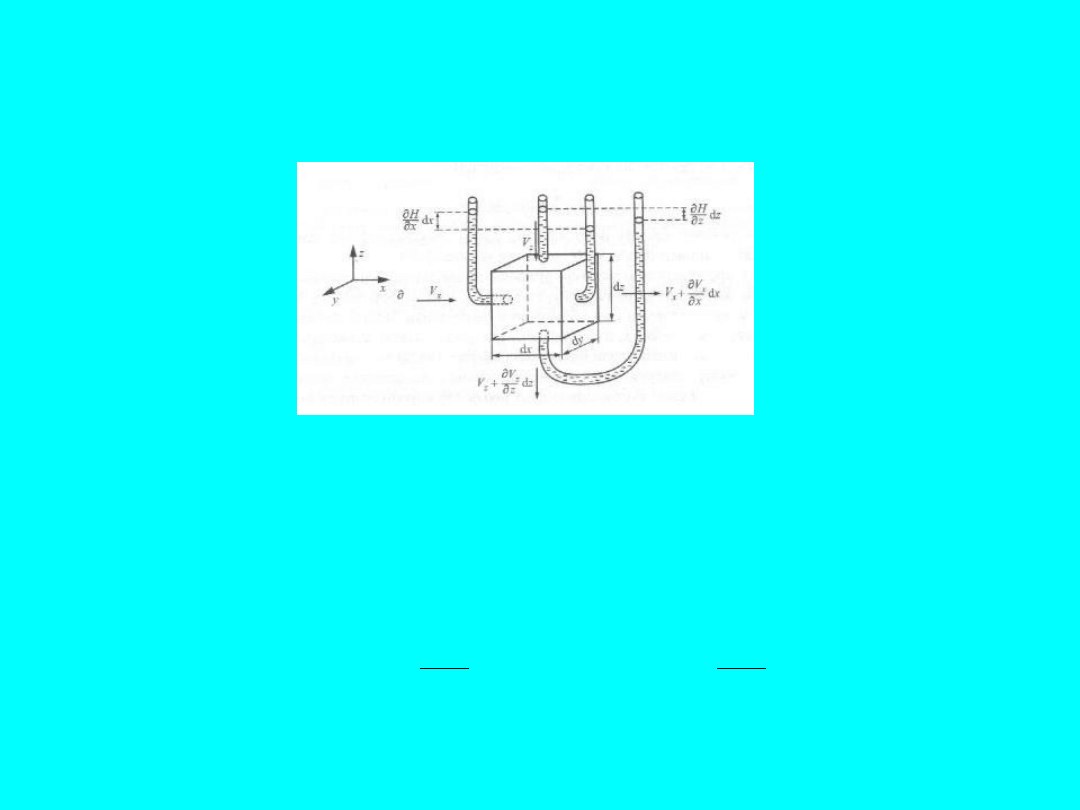
Równania ruchu wody gruntowej

Rozpatrzmy  przepływ  ustalony  wody  przez  myślowo  wydzielony 
elementarny sześcian gruntu o wymiarach dx, dy, dz:

Rys. 
14

Zajmiemy  się  przepływem  płaskim  tzn.  odbywającym  się  w 
kierunkach x i z:

- ilość wody dopływającej do elementu w jednostce czasu:

dxdy

V

dzdy

V

V

z

x

d





- ilość wody odpływającej z elementu:

dxdzdy

z

V

dxdy

V

dxdzdy

x

V

dzdy

V

V

z

z

x

x

o

















28

-  zgodnie  z  zasadą  ciągłości  przepływu,  ilość  wody  dopływającej 
do elementu i odpływającej z niego są sobie równe, czyli:

V

d

 = V

o

Stąd 
otrzymamy:

0

z

V

x

V

z

x













Ponieważ z prawa 
Darcy :

z

H

k

V

     

oraz

     

x

H

k

V

z

z

x

x













mamy:

0

z

H

k

x

H

k

2

2

z

2

2

x













Uwzględniając, że dla gruntu izotropowego k

x

 = k

z

 = k, 

otrzymamy:

0

z

H

x

H

2

2

2

2













Uzyskane    równanie  różniczkowe  nosi  nazwę  równania  ciągłości 
przepływu  (filtra-cji).  Jest  to  równanie  typu  Laplace’a.  Jego 
rozwiązanie polega na znalezieniu wysokości ciśnienia H będącej 
funkcją  współrzędnych  x  i  z,  która  spełnia  warunki  określone 
równaniem wewnątrz rozpatrywanego obszaru, dla którego znane 
są warunki brzegowe.

29

W  rozwiązaniu  równania  ciągłości  przepływu  dla  zadania 
płaskiego dogodnie jest skorzystać z pojęcia dwóch dodatkowych 
funkcji: 

(x,  z)

  – 

funkcji  potencjału  pola  prędkości

  (potencjał 

przepływu 

  =  kH

)  oraz 

(x,z)

  - 

funkcji  prądu

.  Funkcje  te  dla 

przypadku gruntu izotropowego są określone następująco:

Z

H

k

z

V

     

,

x

H

k

x

V

,

z

H

k

z

V

     

,

x

H

k

x

V

z

x

z

x

































































Z porównania tych równań wynika, że:

.

x

z

,

z

x































Równania  powyższe  noszą  nazwę 

równań  Cauchy’ego  – 

Riemanna

.  Rozwiąza-niem  tego  układu  równań  są  dwie  rodziny 

wzajemnie ortogonalnych linii krzywych: 

linii ekwipotencjalnych

 

(jednakowego potencjału) oraz 

linii prądu

 (przepływu). 

Linie te tworzą 

siatkę przepływu (siatkę hydrodynamiczną).

30

Siatka  przepływu  pozwala  w  stosunkowo  prosty  sposób  uzyskać 
rozwiązanie  nawet  skomplikowanych  zagadnień  związanych  z 
filtracją  wody  gruntowej.  W  rozwiązaniach  praktycznych  siatkę 
konstruuje  się  dla  prostych  przypadków  odręcznie  korzystając  z 
warunków  brzegowych  zadania.  „Oczka”  siatki  stanowią 
krzywoliniowe kwadraty wynikające z wzajemnego przecięcia 

linii 

przepływu

  (równoległych  do  kierunku  przepływu  wody)  i 

linii 

ekwipotencjalnych

 

(linii 

o 

jednakowym 

poziomie 

piezometrycznym).  Granicznymi  liniami  przepływu  są:  od  góry  – 
zwierciadło wody gruntowej, zaś od dołu – strop warstwy nieprze-
puszczalnej.  Jednocześnie  musi  być  spełniony  warunek,  aby 
różnice  poziomów  piezometrycznych  między  sąsiednimi  liniami 
ekwipotencjalnymi  były  jednakowe  (

H’  =  H/m  =  const

). 

Liczbę  linii  ekwipotencjalnych,  które  dzielą  strugę  na 

m

 

elementów,  przyjmuje  się  zależnie  od  wymaganej  dokładności. 
Średni spadek hydrauliczny w dowolnym oczku o długości boku 

a

 

wynosi i = H’/a, a prędkość przepływu:

a

'

H

k

i

k

V









Objętość  wody  przepływającej  przez  cały  przekrój  (

n

  strug)  w 

jednostce czasu wyznaczyć można ze wzoru:

m

n

H

k

q









Siatka  przepływu  umożliwia  również  wyznaczenie  wartości  spadku 
hydraulicznego  i  ciśnienia  spływowego  w  każdym  punkcie  ośrodka 
gruntowego.

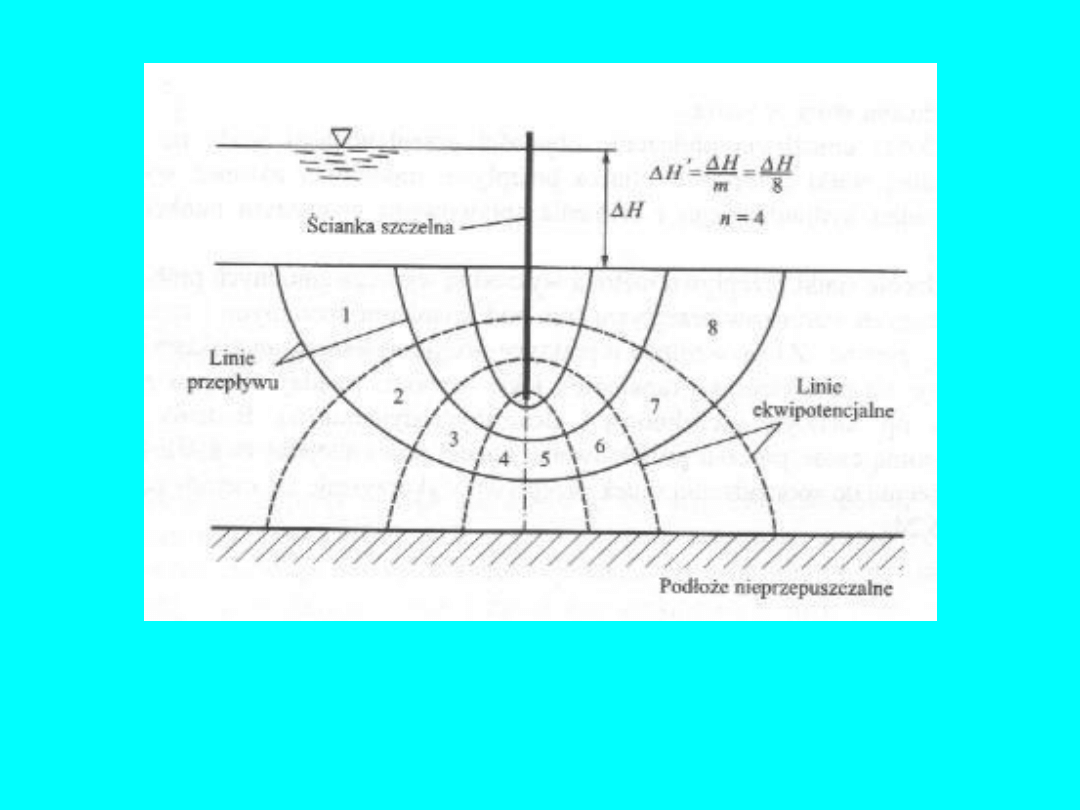
31

Rys.15.  Przepływ pod ścianką szczelną

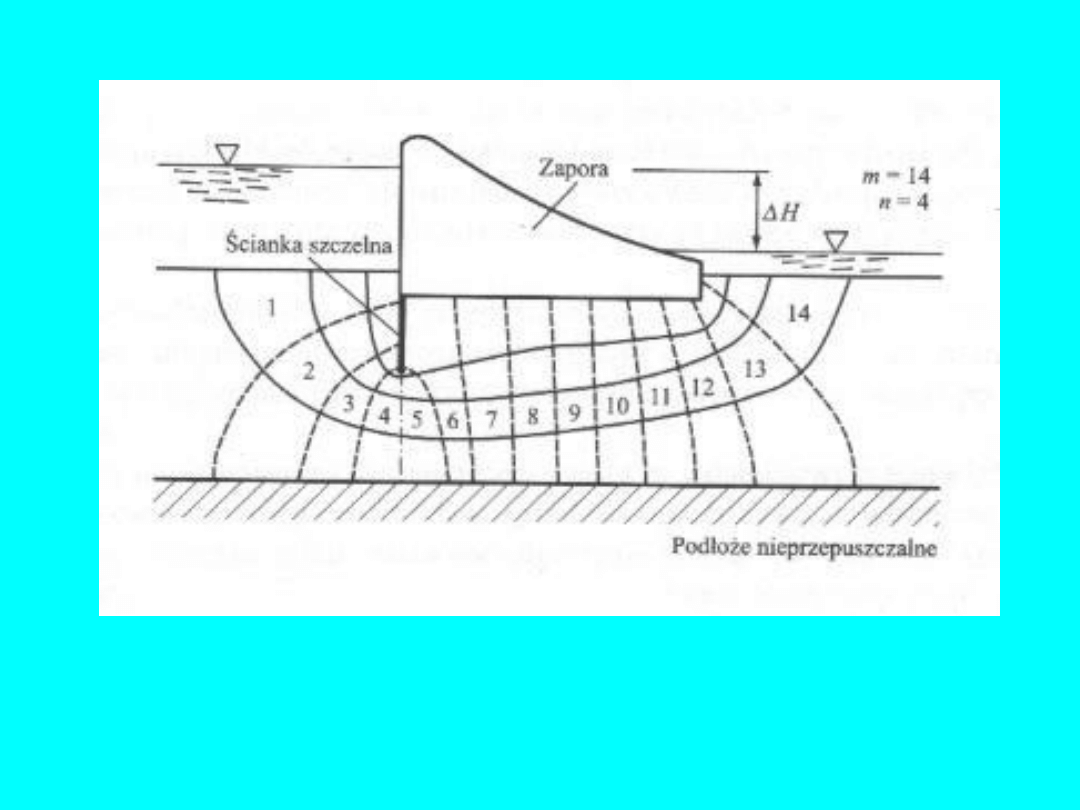
32

Rys. 16. Przepływ pod zaporą