1

Druga zasada

termodynamiki

Wprowadzenie do termodynamiki

chemicznej

Wykład 3

L.
Boltzmann

S.
Carnot

2

4.1. Fakty

doświadczalne i

sformułowanie drugiej

zasady termodynamiki

Wykład 4

3

Wszystkie przemiany zachodzące w
przyrodzie przebiegają w określonym
kierunku...

• Wymiana energii na sposób ciepła.

T

A

T

B

<

T

A

Q

T

B

=

T

A

W wyniku wymiany energii na sposób
ciepła podukłady A i B dążą do stanu
równowagi termicznej, w którym
mają taką samą temperaturę.

4

Wszystkie przemiany zachodzące w
przyrodzie przebiegają w określonym
kierunku...

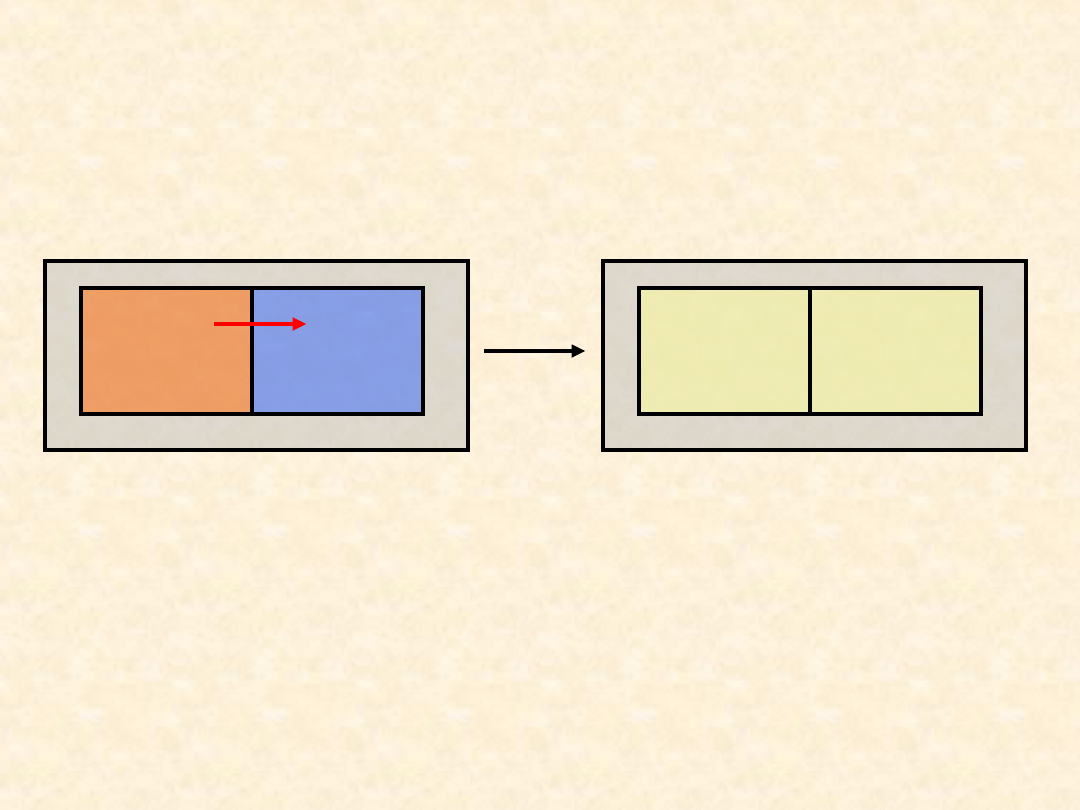
• Dyfuzja w roztworach

W wyniku dyfuzji następuje ujednolicenie
składu roztworu - powstaje faza wieloskładni
- kowa wewnętrznie zrównoważona.

5

Wszystkie przemiany zachodzące w
przyrodzie przebiegają w określonym
kierunku...

• Przemiany fazowe

Stan skupienia substancji czystej zależy
od na- rzuconych układowi wartości
temperatury i ciśnienia. Zmiana wartości
np. temperatury może spowodować
spontaniczny przebieg prze- miany
fazowej - narzucenie, po ciśnieniem at-
mosferycznym, wodzie w stałym stanie
skupie- nia temperatury wyższej niż 0

o

C

spowoduje jej stopienie.

6

Wszystkie przemiany zachodzące w
przyrodzie przebiegają w określonym
kierunku...

• Reakcje chemiczne

W każdej kompletnej bilansowo mieszaninie
reagentów kierunek reakcji jest określony
przez skład początkowy mieszaniny oraz
narzucone więzy - temperaturę i ciśnienie.

7

Wszystkie przemiany zachodzące w
przyrodzie przebiegają w określonym
kierunku...

• Wykonywanie pracy mechanicznej

przeciwko siłom tarcia.

Wykonywanie pracy mechanicznej
przeciwko siłom tarcia na układzie
izolowanym adiabatycznie powoduje
wzrost jego energii wewnętrznej.

8

Wszystkie przemiany zachodzące w
przyrodzie przebiegają w określonym
kierunku...

Betty Davies -
gwiazda
Hollywoodu.

9

Wszystkie przemiany zachodzące w
przyrodzie przebiegają w określonym
kierunku...

10

Wnioski
ogólne...

• Spontaniczny przebieg jakiegokolwiek

procesu pociąga za sobą trwałe -
nieodwracalne zmiany w przyrodzie; z tego
powodu procesy przebie-gające
rzeczywiście nazywa się nieodwracal- nymi.

• Przebieg każdego procesu

nieodwracalnego wy- maga niezerowego
bodźca (gradientu tempera- tury,
stężenia...)

• ....

11

Wnioski
ogólne

• W procesie nieodwracalnym zachodzącym

ze skończoną szybkością uczestniczą fazy
wewnęt- rznie nie zrównoważone -
występują w nich różnice temperatur,
ciśnień lub stężeń.

12

Przemiana
odwracalna

• Wyobrazić sobie serię przemian

zachodzących przy coraz mniejszych
wartościach bodźców; ich granicą jest

przemiana odwracalna

- hipote- tyczny

proces przebiegający nieskończenie powoli
przy zerowych wartościach bodźców
termodynamicznych.

• uczestniczą w niej fazy wewnętrznie

zrównowa-żone, a układ i otoczenie są w
stanie równowagi

• jest to ciąg przemian elementarnych

zachodzą- cych w stanie równowagi.

13

Cel i forma uogólnienia
wniosków

• Sformułować ilościowe kryterium, na

podsta- wie którego można by
przewidywać kierunek przemian i
ewentualnie położenie stanu równo- wagi
układów.

• Rozwiązanie polega na zdefiniowaniu

kolejnej funkcji stanu -

entropii

i ujęciu

w formie pos-tulatu jej właściwości.

14

Sformułowanie II zasady
termodynamiki...

• Każdej wewnętrznie zrównoważonej fazie

przypisuje się entropię S - ekstensywną
funkcję parametrów stanu fazy





k

i

i

x

x

x

S

S



,

,

2

1



•

entropia układu jest sumą entropii faz





i

i

S

S

15

Sformułowanie II zasady
termodynamiki...

• Różniczka zupełna entropii układu jest

równa stosunkowi elementarnej ilości
ciepła wymie- nionego przez układ w
wyniku elementarnej przemiany
odwracalnej do temperatury układu

T

dQ

dS

odwr



• Zmiana entropii układu w wyniku

elementar- nego procesu spontanicznego
musi spełniać nierówność

T

dQ

dS

16

Sformułowanie II zasady
termodynamiki

•

Nierówność Clausiusa

0







T

dQ

dS

S

d

i

d

i

S - entropia wytworzona w układzie

w wyniku przebiegu elementarnej
przemiany nieodwracal- nej

• Różniczka entropii układu jest sumą udziałów

S

d

S

d

dS

i

e





T

dQ

S

d

e



Entropia przeniesiona

17

Podsumowanie II zasady
termodynamiki...

• W wyniku procesu elementarnego

entropia układu może się zmieniać z
dwóch powodów: transportu entropii
między układem i otocze- niem (d

e

S)

oraz produkcji entropii w układzie
(d

i

S).

• Produkcja entropii w wyniku przebiegu

w układzie procesu spontanicznego jest
zawsze dodatnia; proces odwracalny
nie wytwarza entropii.

• ....

18

Podsumowanie II zasady
termodynamiki...

• W przypadku układu izolowanego adiabatycz-

nie entropia przeniesiona (d

e

S) jest równa

zeru; otrzymuje się więc nierówność

0



adiab

dS

W układzie adiabatycznym możliwy jest
wyłącz- nie przebieg procesu, w wyniku
którego nastąpi wzrost jego entropii.

19

Podsumowanie II zasady
termodynamiki

• Jeżeli układ i otoczenie, określane umownie

jako "świat" uznać łącznie za izolowane adia-
batycznie, to ich sumaryczna zmiana entropii

Przebieg każdego procesu w
przyrodzie zwiększa entropię "świata".

0







otoczenie

uklad

total

dS

dS

dS

20

4.2. Molekularna

interpretacja entropii

Wykład 4

21

Energia wewnętrzna gazu

doskonałego

- suma energii
drobin





i

i

U



jadr

i

elektron

i

oscyl

i

rot

i

trans

i

i























- suma
udziałów

Każda z wymienionych form
energii drobiny jest kwantowana,
tzn. energia drobiny może mieć
jedynie wartości określane jako
kwanto- wo dozwolone poziomy
energetyczne określo- ne przez
rozwiązanie równania
Schrődingera.

22

Energia
translacji:

n

x

, n

y

, n

z

= 1,2,3, ...N - liczby kwantowe

translacji

Typowa
wartość:

Wniose
k:





2

2

2

3

2

2

8

z

y

x

trans

n

n

n

mV

h









J

10

03

1

8

40

3

2

2





 ,

mV

h

Typowa
wartość:

K)

(300

J

10

1

4

21





 ,

T

k

B

T

k

B

ij







23

Zasada ekwipartycji
energii

Jeżeli dla wszystkich, sąsiednich
poziomów energetycznych i oraz j,
spełniona jest nierów-ność



ij

<< k

B

T

to obowiązuje

zasada

ekwipartycji energii

, zgod- nie z

którą

każda składowa energii, którą

można wyrazić jako kwadratową
funkcję składowej pędu lub
położenia, wnosi do wartości
średniej energii udział równy k

B

T/2.

24

Średnia energia
translacji:

Wniose
k:

Suma trzech
składowych pędu.

T

k

B

ij























m

p

z

y

x

z

y

x

2

2

,

,

,

,



T

k

B

trans

2

3





RT

E

trans

2

3



25

Energia
rotacji:

I - moment bezwładności;
j = 1,2,3, ...N - liczba
kwantowa rotacji

Wniose
k:

Typowa
wartość:









1

1

8

2

2









j

Bj

j

j

I

h

rot





K)

(300

J

10

10

3

23









B

T

k

B

ij







Wniosek: średnia energia rotacji drobin
o budowie...

;

T

k

B

rot





RT

E

rot



liniowej
:

nieliniow
ej:

;

T

k

B

rot

2

3





RT

E

rot

2

3



26

Energia oscylacji drobiny
dwuatomowej ...

 - masa zredukowana;

k - stała siłowa wiązania;
v = 0, 1, ...N - liczba kwantowa
oscylacji

Wniose
k:

Typowa
wartość:





2

1

2





v

k

h

oscyl







J

10

10

19

20











ij







K

T

T

k

B

ij

300













K

T

T

k

B

ij

2000









27

Energia oscylacji drobiny
dwuatomowej

Ponieważ energia oscylatora
harmonicznego składa się energii
kinetycznej i potencjalnej, to zgodnie z
zasadą ekwipartycji energii,

średnia

nadwyżka ener- gii oscylacji ponad
energię stanu podstawowego w
dostatecznie wysokich temperaturach
osiąga wartość

;

T

k

B

oscyl





0





RT

E

E

oscyl





0

Jeżeli

spełniona jest

nierówność

T

k

B

ij







to niemal wszystkie drobiny pozostają
w podstawo- wym stanie kwantowym
(v=0) gromadząc najmniej- szą
dozwoloną ilość energii.

28

Energia oscylacji drobiny
wieloatomowej

Jądra drobin wieloatomowych wykonują
oscylacje zmieniające zarówno długości
wiązań, jak kąty między nimi; oscylacje
drobiny n - atomowej są równoważne:

3n-5 (drobiny o budowie
liniowej)

3n-6 (drobiny o budowie
nieliniowej)

oscylacjom harmonicznym (nazywa się
je

oscylacja- mi normalnymi

). Sumuje

się udziały energetyczne wszystkich
oscylacji normalnych.

29

Energia elektronowa
drobiny

Energia elektronowa drobin jest
skwantowana za pomocą kilku liczb
kwantowych, a typowe odstępy między
sąsiednimi poziomami są rzędu 10

-19

J

(1 eV). Nawet w dosyć wysokiej
temperaturze speł- niona jest na ogół
nierówność

wskutek czego

drobiny pozostają w

podstawowym stanie elektronowym.

T

k

B

ij







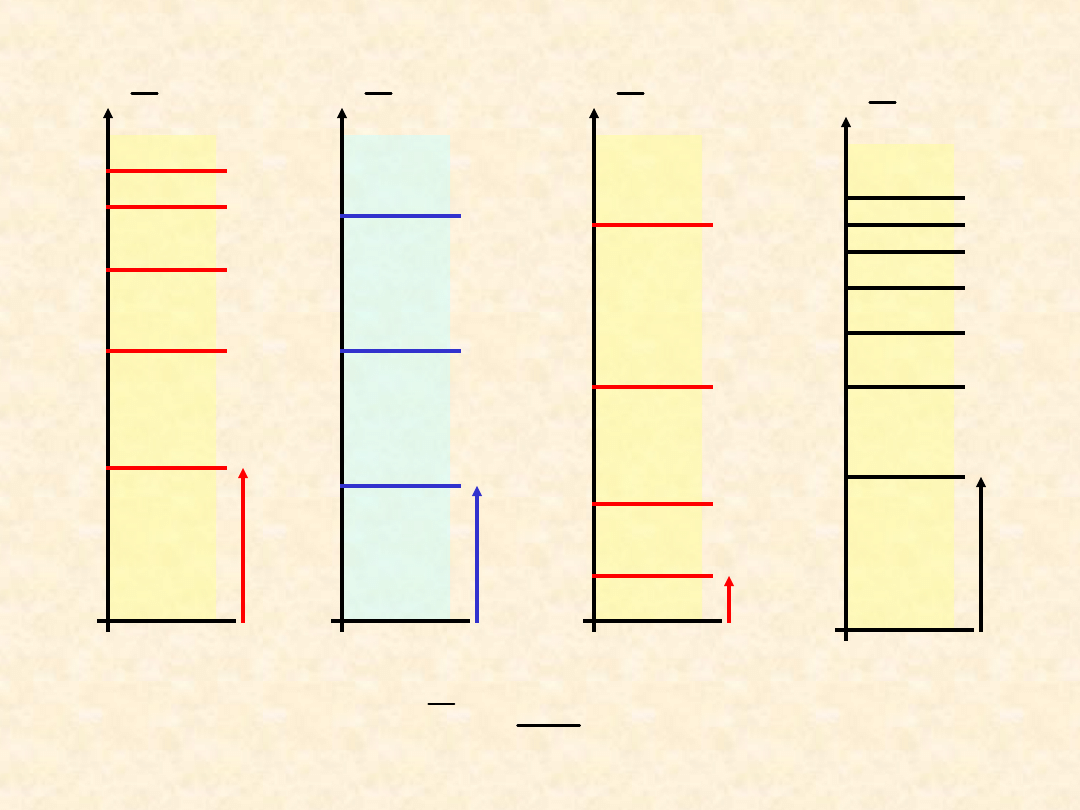
30

Schemat poziomów energetycznych drobiny dwuatomowej

~

5

0

0

0

c

m

-1

elektrono
wa



~

5

0

0

c

m

-1

oscylacyj
na



~

1

c

m

-1

rotacyjna



~

1

0

-1

7

c

m

-1

translacy
jna



hc







31

Model statystyczny
gazu

Stan kwantowy każdej drobiny jest
opisany zbiorem aktualnych wartości
liczb kwantowych (translacji, rotacji,
oscylacji i stanów elektronowych), który
ok- reśla również jej chwilowy zasób
energii. Podczas zderzeń drobiny
przekazują sobie energię; bezustan- nie
zmienia się więc stan kwantowy każdej
drobiny.

Specyfikacja chwilowych stanów
kwantowych wszy- stkich drobin
tworzących układ makroskopowy ok-
reśla chwilowy

mikrostan układu.

W

wyniku wy- miany energii między
drobinami zmienia się

również

mikrostan układu.

32

Model statystyczny gazu -
podstawowy postulat

Stan układu makroskopowego,
określony aktualny- mi wartościami
parametrów i funkcji stanu nazywa się
jego

makrostanem

. Można wykazać, że

każdy makrostan układu jest
realizowany przez wiele róż- nych
mikrostanów

Układ w stanie równowagi termicznej
może się zna- leźć z identycznym
prawdopodobieństwem w każ- dym z
dozwolonych mikrostanów.

Liczbę mikrostanów realizujących
określony makro- stan nazywa się jego

prawdopodobieństwem termo-
dynamicznym

(P) .

33

Postulat L. Boltzmanna (M. Plancka)

- związek między entropią i

prawdopodobieństwem

termodynamicznym

Entropia ma sens statystyczny - jest
miarą liczby rozróżnialnych kwantowo
sposobów podziału ener- gii między
drobinami, odpowiadających określone-
mu stanowi układu makroskopowego.

Układ izolowany dąży do stanu o
maksymalnym prawdopodobieństwie
termodynamicznym, jest on stanem
równowagi tego układu.

P

k

S

B

ln



34

4.3. Potencjały

termodynamiczne

Wykład 4

35

Procesy cykliczne

izotermiczne - problem do

rozwiązania

Dowolny układ mogący wymieniać z
otoczeniem o stałej temperaturze ciepło
(Q) oraz pracę objętościo- wą (W

obj

) i

nieobjętościową (praktycznie
elektryczną (W

elektr

) ulega wieloetapowej

przemianie cyklicznej (powraca do
stanu początkowego).

Zbadać warunki jakie muszą spełniać
sumaryczna praca i sumaryczne ciepło
wymienione między ukła- dem i
otoczeniem w wyniku izotermicznej
przemiany cyklicznej.

36

Podstawowe równanie

termodynamiczne

Połączenie nierówności Clausiusa z
bilansem energii wewnętrznej układu
daje nierówność

będącą ogólnym warunkiem który musi
spełniać każdy proces w przyrodzie
(znak równości odnosi się do
hipotetycznego procesu
odwracalnego).

0







T

dQ

dS

S

d

i

dW

dQ

dU





0







T

dW

dU

dS



(1)

37

Przekształcamy
(1)...

const

T 



(5

a)

0







dW

dU

TdS





dW

TS

U

d





(2

)

Zdefiniować funkcję
stanu:

(3

)

TS

U

F





(4

)

F - energia Helmholtza; energia
swobodna

(3) + (4)



dW

dF

W

dF

F

F

F

B

A

A

B













(5b)

38

A

B

W

odwr

=

F

AB

W >
F

AB

A

C

W

2

>

F

2

B

W

3

>

F

3

W

1

>



F

1

T=con
st

Praca W przemiany
rzeczywistej...

odwr

W

W 

Sumarycznie w przemianie
cyklicznej...

0











cykl

i

cykl

F

F

0







cykl

i

cykl

W

W

0









cykl

cykl

cykl

W

Q

U

0







cykl

i

cykl

Q

Q

39

Wniose
k:

W wyniku każdej rzeczywistej
izotermicznej przemiany cyklicznej
układ musi pobrać wypadko- wo
energię na sposób pracy i oddać
równoważną ilość energii na sposób
ciepła; nie jest natomiast możliwy
odwrotny kierunek przekazywania
energii.

W wyniku każdej rzeczywistej
izotermicznej cyklicznej przemiany
izotermicznej energia pobrana przez
układ na sposób pracy zostaje
nieodwracalnie przekazana otoczeniu
na sposób ciepła - zjawisko to nazywa
się obrazowo

degradacją pracy

.

40

Kryteria spontaniczności przemian -

problem do rozwiązania

Dany jest układ nie elektrochemiczny (W =
W

obj

) na który narzucono określone więzy.

Sformułować kryterium pozwalające
określić:

•Czy pomyślana przemiana od stanu A do
stanu B jest spontaniczna ?
•Jakie będą wartości parametrów w stanie
równo- wagi układu ?

Rozwiązanie polega na odpowiednim
przekształce- niu nierówności
Clausiusa (1) - ogólnego kryterium
spontaniczności przemian.

41

Przemiany izotermiczno-izochoryczne

(T,V = const)

Energia swobodna układu nie
elektrochemicznego maleje w wyniku
każdej przemiany spontanicznej
zachodzącej w warunkach T,V = const;
w stanie równowagi osiąga więc kres
dolny dostępny z zada- nych warunków
początkowych.

PdV

dW

dW

obj







dW

dF

(5a
)



PdV

dF 



(6
)

const

V 



0



dF

(7
)

42

Przemiany izotermiczno-izobaryczne

(T,P = const) ...

(6
)



VdP

dG

(8
)

const

P 



0



dG

(9
)

Zdefiniować funkcję
stanu:

TS

H

G





G - energia Gibbsa; entalpia
swobodna

PV

F

TS

PV

U

G











VdP

PdV

dG

dF







PdV

dF 



(10
)

43

Przemiany izotermiczno-izobaryczne

(T,P = const) ...

Entalpia swobodna układu nie
elektrochemicznego maleje w wyniku
każdej przemiany spontanicznej
zachodzącej w warunkach T,P = const;
w stanie równowagi osiąga więc kres
dolny dostępny z zada- nych warunków
początkowych.

Analogiczni
e:

S,V =
const.
S,P =
const.





0



dH

0



dU

44

W ięz y

P o ten cjał term o d y n am i c zn y

( fu n k c ja ch arak tery sty c z n a)

W aru n ek

sp o n tan ic z n ośc i

T , V = c o n st.

F = U - T S

d F < 0

T , P = c o n st.

G = H - T S

d G < 0

S , V = co n st.

U

d U < 0

S , P = c o n st.

H

d H < 0

Funkcje których wartość maleje w wyniku
spontanicz- nej przemiany układu przy
narzuconych mu więzach (x,y = const) i w
stanie równowagi osiąga kres dolny
nazywa się

potencjałami

termodynamicznymi

lub

funkcjami

charakterystycznymi zmiennych x, y.

45

Zastosowanie potencjałów

termodynamicznych jako kryterium

spontaniczności przemiany

Np. więzy T,P =
const.

Hipotetyczna

przemiana

odwracalna w

stanie równowagi

G=G

B

- G

A

< 0

A

B

G

B

G

A

G

A

>

G

B

G=G

B

- G

A

= 0

A

B

G

B

G

A

G

A

=

G

B

Przemiana

spontanicz

na

46

4.4. Związki między

funkcjami

termodynamicznymi

Wykład 4

47

Elementarna przemiana odwracalna

fazy o stałym składzie (substancja

czysta lub roztwór)

Zadanie:

Znaleźć ogólne relacje matematyczne wiążące
zdefiniowane funkcje stanu (U, H, S, G, F)
oraz ich pierwsze i drugie pochodne
cząstkowe)

pdV

dW 



TdS

dQ





Y

X

f

Z

,



patrz W_01 (reguła Duhema)

48

U = U(S,V)





dV

V

U

dS

S

U

V

S

dU

S

V





































,





PdV

TdS

dW

dQ

V

S

dU









,



V

S

S

V

V

U

S

S

U

V





































































P

V

U

S





















T

S

U

V



















V

S

S

P

V

T





































(13)

(12
)

(1
1)

49

H = H(S,P)





dP

P

H

dS

S

H

P

S

dH

S

P





































,





 

VdP

TdS

PV

d

dU

P

S

dH









,



P

S

S

P

P

H

S

S

H

P





































































V

P

H

S



















T

S

H

P



















P

S

S

V

P

T



































(16)

(15)

(14)

50

F = F(T,V)





dV

V

F

dT

T

F

V

T

dF

T

V





































,





 

PdV

SdT

TS

d

dU

V

T

dF











,



V

T

T

V

V

F

T

T

F

V





































































P

V

F

T





















S

T

F

V





















V

T

T

P

V

S



































(19)

(18)

(17)

51

G = G(T,P)





dP

P

G

dT

T

G

P

T

dG

T

P





































,





 

VdP

SdT

PV

d

dF

P

T

dG











,



P

T

T

P

P

G

T

T

G

P





































































V

P

G

T



















S

T

G

P





















P

T

T

V

P

S





































(22)

(21)

(20)

52

F

T

V

S

P

H

G

U

Kwadrat
termodynamiczny

53

Relacje Maxwella -

zestawienie

S

V

T

V

P

S





































V

T

T

P

V

S



































S

P

T

P

V

S



































P

T

T

V

P

S





































54

Równania Gibbsa -

Helmholtza

(23
)

V

T

F

T

U

F





















TS

U

F







TS

H

G





P

T

G

T

H

G























(24
)

55

Termodynamiczne równania

stanu (I/II)

(26
)

TS

U

F







T

T

T

V

S

T

V

F

V

U





















































V

T

T

P

T

P

V

U







































(25
)



TS

H

G





T

T

T

P

S

T

P

G

P

H





















































P

T

T

V

T

V

P

H





































56

Entropia

V

V

V

T

U

U

S

T

S



















































P

P

P

T

H

H

S

T

S



















































T

C

T

S

V

V



















T

C

T

S

P

P





















(27
)

(28
)



57

Pojemność cieplna



(29
)

(30
)



P

T

T

P

T

P

P

H

T

T

H

P

P

C





















































































P

P

P

T

P

T

V

T

T

V

T

V

T

P

C







































































2

2

















V

T

T

V

T

V

V

U

T

T

UH

V

V

C





















































































V

V

V

T

V

T

P

T

T

P

T

P

T

V

C







































































2

2

















58

P

P

H

A

C

B

P

V

B’

B

A

V

B’

V

A/B

P

B

P

A



H

V

H

p

H

T

Równanie Mayera (C

P

- C

V

)...

59

Równanie Mayera...



(31
)



T

P

V

dH

dH

dH





VdP

dT

C

VdP

dU

dH

V

V

V









dT

C

dH

P

P



dP

T

V

T

V

dP

P

H

dH

P

T

T























































dP

T

V

T

dT

C

C

P

V

P





















V

P

V

P

T

P

T

V

T

C

C







































60

Druga zasada termodynamiki –

pierwsze prawo wszystkich

Nauk.

A. Einstein, (1879 –1955),

fizyk niemiecki