
Theory of Heat Machines
2l.+1cl.
Theory of Heat Machines
2l.+1cl.
Paweł Skowroński Ph.D.,
P.Eng.
pskowr@itc.pw.edu.pl
Tel +22 243 52 13
p. 404

Formalities
Formalities

Scope of the Subject
• Processes in heat machines and
thermal devices
• Thermodynamical cycles – thermal
engines
• Heat machines and systems analysis
and synthesis

Bibliography
• Notes !!!
• Staniszewski B. – „Termodynamika”
• Other handbooks on thermodynamics,
technical thermodynamics, theory of
heat machines, …
• No textbook dedicated to this
lecture!!!!

How to get credit? Three colloquies
• Conditions
– positive (≥ 3=) marks from at least two from
three colloquies
– sum of marks bigger than 8 (bigger – not
equal!) (+: +0,25; –: -0,25; =: -0,33)
– at least a partial answer on theoretical question
and a partial solution of the exercise is
necessary to get a positive mark of a colloquy
(it is necessary but not enough)
– the 1st and the 2nd colloquies can be repeated
during a „marathon”; mark obtained at the
„marathon” replaces the colloquy mark; the 3rd
colloquy will not be repeated

How to get credit? The exam
– there is a written and oral part of the exam
– written examination consists with a complex
exercise and a theoretical topic
– oral examination covers knowledge of the theory
– to take an oral exam one must pass the written
part of the exam; passing the written part with a
mark 3- allows for single approach to the oral part;
– an average of colloquies marks equal or bigger
then 4 releases from the written examination
– an exam mark is given if a sum of colloquies marks
is higher then 8,
– if the sum of colloquies marks is less than 8, the
written part of the exam can be accepted with a
mark at least 4

Energy Conversion
Energy Conversion
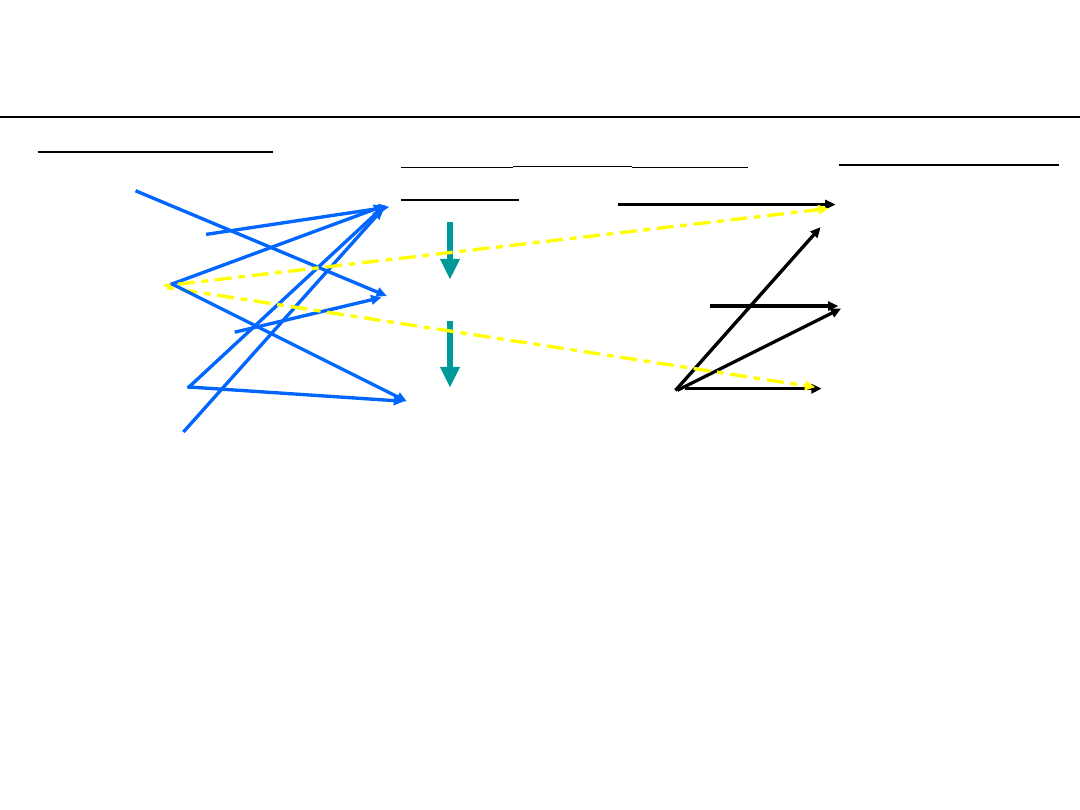
energy conversion
Usable
(possible for use)
energy
carriers
-heat carrier
-mechanical energy
-electricity
use-ful energy
– delivered in
form of heat
–delivered in
form of work
–light
–information
processing
Primary Energy
-of wind
-geothermal
-solar
-water flows
-chemical
-nuclear

energy conversion
Energy conversion is always accompanied with losses:
•
during conversion of heat to work (thermal engine cycles)
– results
from thermodynamic rules
•
resulted from irreversibility of thermodynamic processes
(irreversible entropy growth)
•
imperfectness of conversion of chemical energy into
internal
energy (not-full use of fuels)
•
mechanical fraction between machines elements, and
resistance
in fluid flow
•
electric and magnetic – „at cuprum and in iron”
•
others

Chosen and basic
information on heat
transfer process and heat
exchangers
Chosen and basic
information on heat
transfer process and heat
exchangers

heat transfer mechanisms
• conduction
• convection
– natural
– forced
• radiation
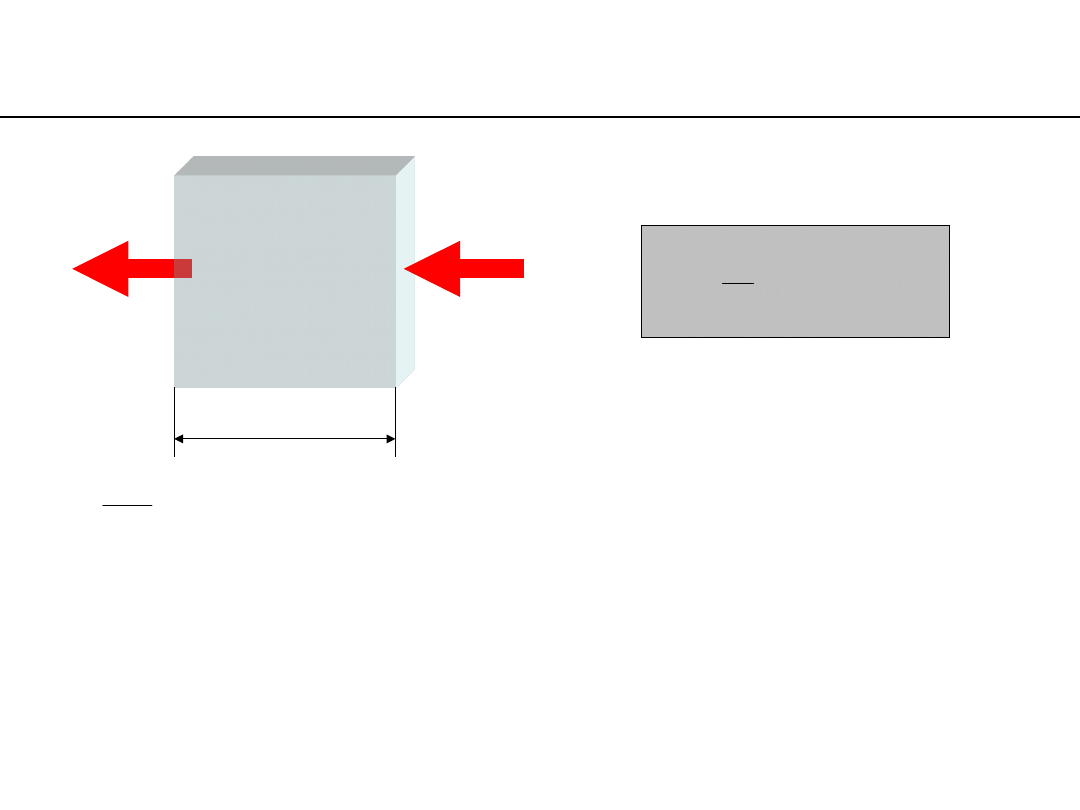
δ
Q
S
t
1
t
2
λ
)
(
2
1
t
t
S
Q
λ
– heat conduction coefficient
K
m
W
t
1
, t
2
[K] – temperatures at surfaces of the heat conducting material
δ [m] – thickness of the wall
S [m
2
] – heat transfer area
heat conduction at a flat wall

values of a heat conduction coefficient λ at 100°C
duralumin
181,4
increases with temperature
brass 70Cu/30Zn:
109,3
increases with temperature
carbon steel
52,3
decreases with temperature
chrome-nickel steel
ok. 11-13
change with temperature depends
on
the steel composition
brick
0,3÷1,2
mineral wool
0,035÷0,05
K
m
W
K
m
W
K
m
W
K
m
W
K
m
W
K
m
W
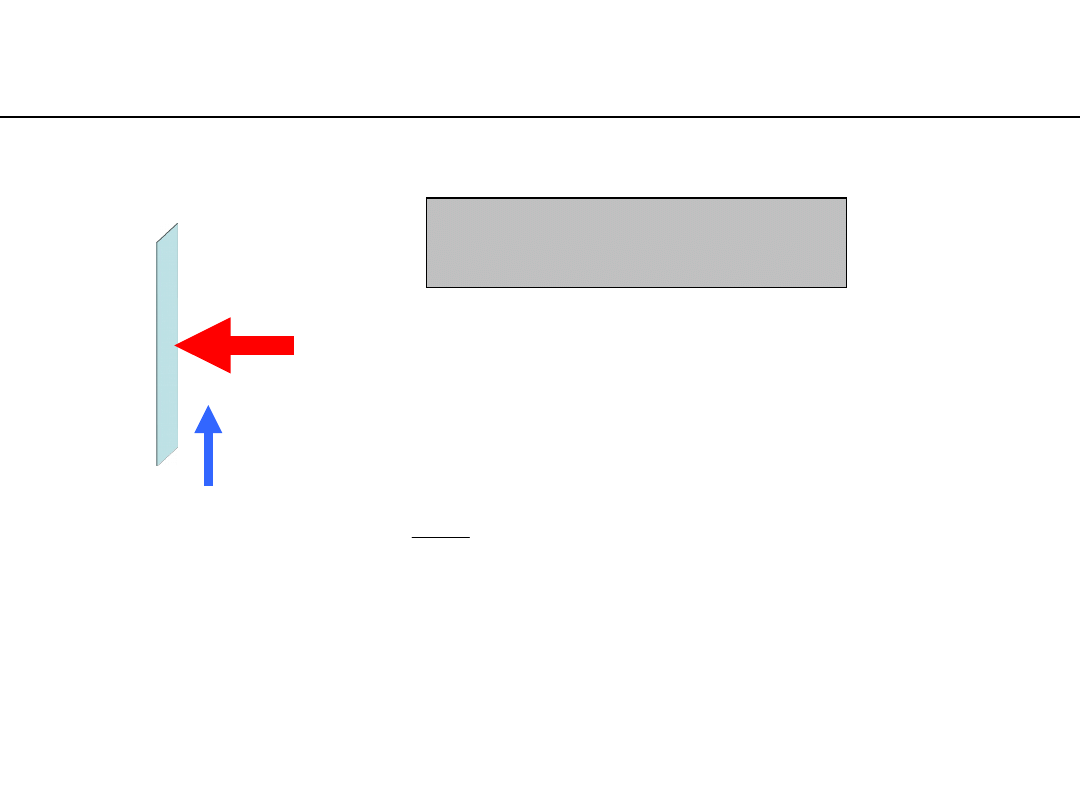
)
(
2
1
t
t
S
Q
Q
S
t
1
t
2
α
heat infiltration coefficient α
fluid – wall surface or wall surface –
fluid depends on:
• velocity, density, viscosity, specific heat, heat conductivity of the fluid
• the fluid phase (gas, liquid, boiling liquid, condensing steam)
• the surface shape and roughness
K
m
W
2
heat infiltration
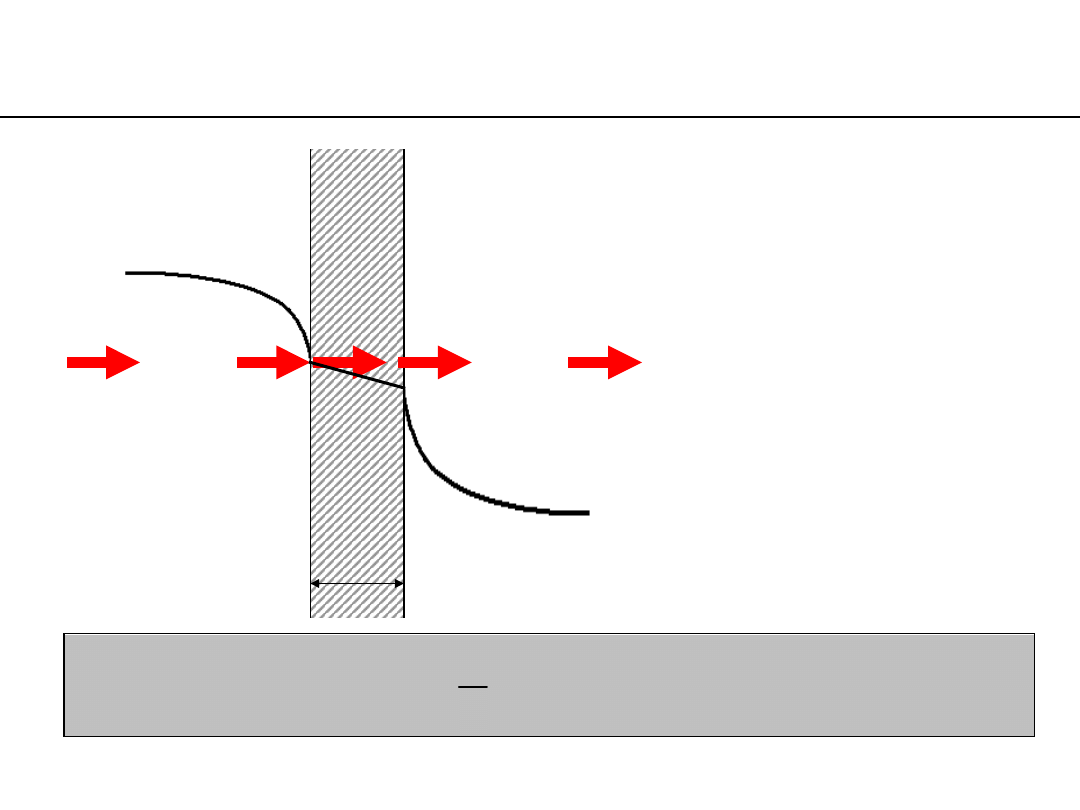
heat transfer through a flat wall
)
(
)
(
)
(
2
2
2
2
1
1
1
1
f
w
w
w
w
f
t
t
dS
t
t
dS
t
t
dS
Q
d
Q
Q
Q
Q
Q
t
f1
t
w1
t
w2
t
f2
λ
δ
α
1
α
2
dS – elementary area
δ – partition thickness
t
w
– partition surface
temperature
t
f
– fluid temperature (far
away from a boundary
layer)
heat transfer through a flat wall,
cont.
)
(
)
(
)
(
2
2
2
2
1
1
1
1
f
w
w
w
w
f
t
t
dS
t
t
dS
t
t
dS
Q
d
dS
Q
d
t
t
w
f
1
1
1
)
(
dS
Q
d
t
t
w
w
)
(
2
1
dS
Q
d
t
t
f
w
2
2
2
)
(

2
1
2
1
1
1
)
(
dS
Q
d
t
t
f
f
dS
Q
d
dS
Q
d
dS
Q
d
t
t
t
t
t
t
f
w
w
w
w
f
2
1
2
2
2
1
1
1
)
(
)
(
)
(
)
(
1
1
1
2
1
2
1
f
f
t
t
dS
Q
d
heat transfer through a flat wall,
cont.
)
(
2
1
f
f
t
t
dS
k
Q
d
2
1
1
1
1
k
coefficient of a heat transfer through a flat wall :
heat transfer through a flat wall,
cont.
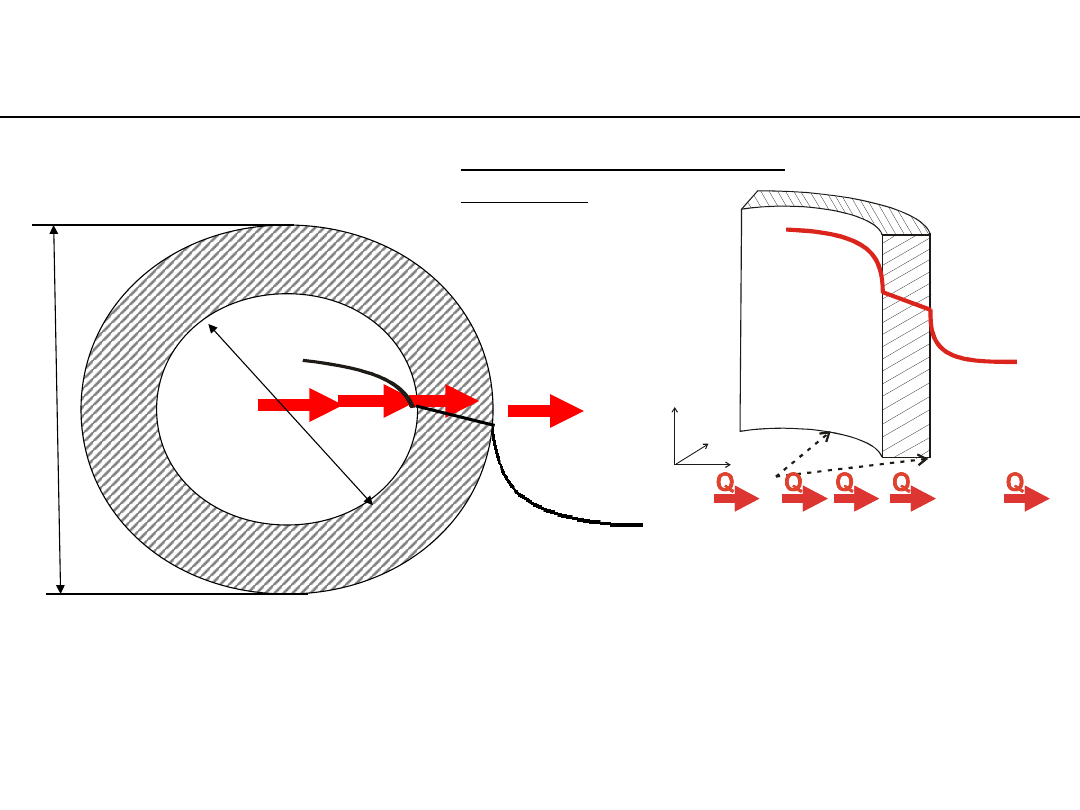
heat transfer through a pipe wall
)
(
)
(
2
1
ext
w
ext
ext
w
in
in
in
t
t
dL
D
t
t
dL
d
Q
d
infiltration
of heat on both sides of the
partition:
a pipe of an elementary
length dL
Q
Q
t
i
n
t
w1
t
w2
t
ext
λ
α
ext
Q
Q
α
in
d
in
D
e
x
t
w
z
T
w 1
T
w 2
T
z
T
w
x
y
z
r
w
r
z
in
ext
ext
in

dr
dt
dL
r
Q
d
2
Heat
conduction
through a pipe wall,
(an area of a heat conduction changes with a radius):
heat transfer through a pipe wall,
cont.
Q
Q
Q
t
in
t
w
1
t
w
2
t
ext
λ
α
ext
Q
Q
α
in
r
dr
dt
dL
r
Q
d
2
r
dr
dL
Q
d
dt
2
in
ext
r
r
w
w
r
r
dL
Q
d
r
dr
dL
Q
d
t
t
ext
in
ln
2
2
2
1
2
1
ln
2
w
w
d
D
t
t
dL
Q
d
in
ext
heat transfer through a pipe wall,
cont.

)
(
)
(
2
1
ext
w
ext
ext
w
in
in
in
t
t
dL
D
t
t
dL
d
Q
d
)
(
)
(
)
(
)
(
2
2
1
1
ext
w
w
w
w
in
ext
in
t
t
t
t
t
t
t
t
dL
D
Q
d
d
D
dL
Q
d
dL
d
Q
d
ext
ext
in
ext
in
in
ln
2
heat infiltration by the pipe surface:
temperature drops composition – infiltration and conduction
ext
ext
in
ext
in
in
D
d
D
d
dL
Q
d
1
ln
2
1
1
heat transfer through a pipe wall,
cont.

)
(
1
ln
2
1
1
1
ext
in
ext
ext
in
ext
in
in
t
t
dL
D
d
D
d
Q
d
K
m
W
D
d
D
d
k
ext
ext
in
ext
in
in
L
1
ln
2
1
1
1
)
(
ext
in
L
t
t
dL
k
Q
d
a coefficient of heat transfer related to a pipe length:
heat transfer through a pipe wall,
cont.

K
m
W
D
d
d
D
d
k
ext
ext
in
in
ext
in
in
in
2
ln
2
1
1
)
(
)
(
)
(
out
in
in
in
out
in
in
in
L
out
in
L
t
t
dS
k
t
t
dL
d
d
k
t
t
dL
k
Q
d
heat transfer through a pipe wall
related to an
internal
surface of a pipe

K
m
W
d
D
D
d
D
k
ext
in
ext
ext
in
in
ext
ext
2
1
ln
2
1
)
(
)
(
ext
in
ext
ext
ext
in
ext
ext
t
t
dS
k
t
t
dL
D
k
Q
d
heat transfer through a pipe wall
related to an
external
surface of a pipe

Assuming that value of the heat transfer coefficient k does not
change along the heat transfer partition (length, area)
or accepting an average value of the k for the whole heat
exchanger,
then taking into account that a difference of the both fluids
temperatures does change along the heat surface
for a flat wall
for a pipe, relating e.g. to the internal surface of the heat exchange:
where
Δt
av
- is an average temperature difference between fluids
in
the heat exchanger.
av
w
w
ext
in
in
in
t
S
k
dL
L
t
L
t
d
k
Q
d
Q
))
(
)
(
(
av
f
f
t
S
k
dS
S
t
S
t
k
Q
d
Q
))
(
)
(
(
2
1
t
11
t
12
t
21
t
22
L
t
22
< t
12
t
t
11
t
21
t
12
)
(
)
(
ln
)
(
)
(
22
12
21
11
22
12
21
11
ln
t
t
t
t
t
t
t
t
t
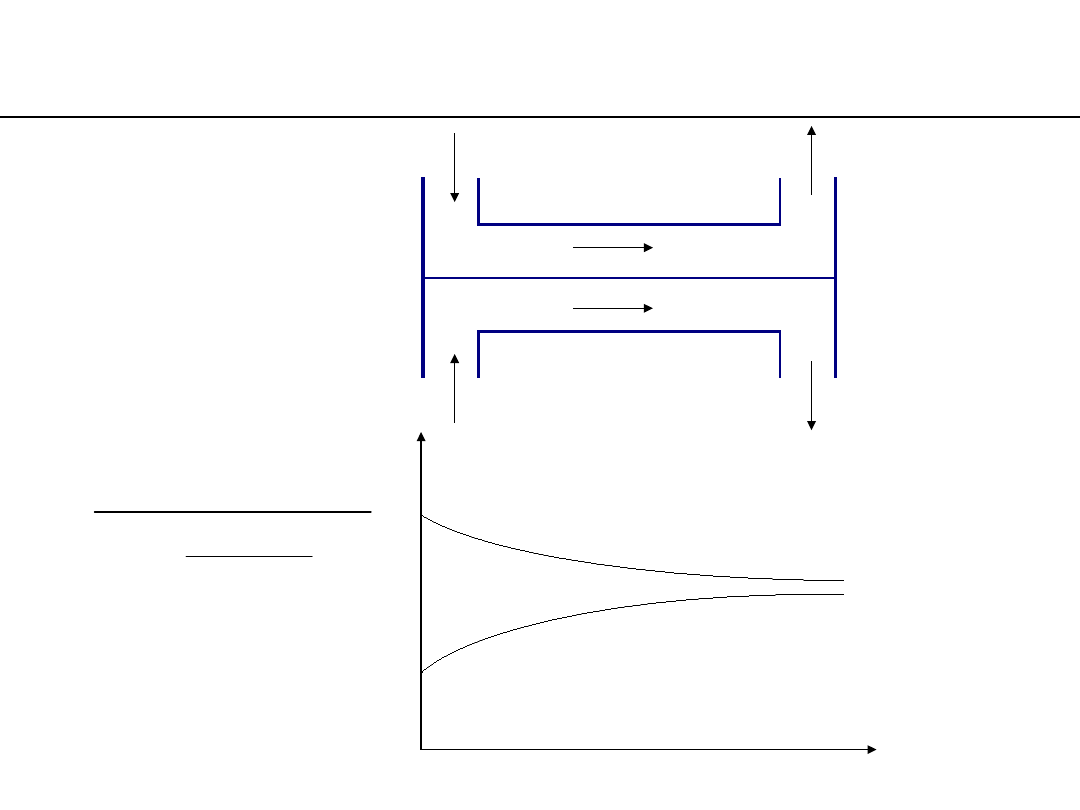
common-flow heat exchanger
temperatures changes along the heat exchange
surface
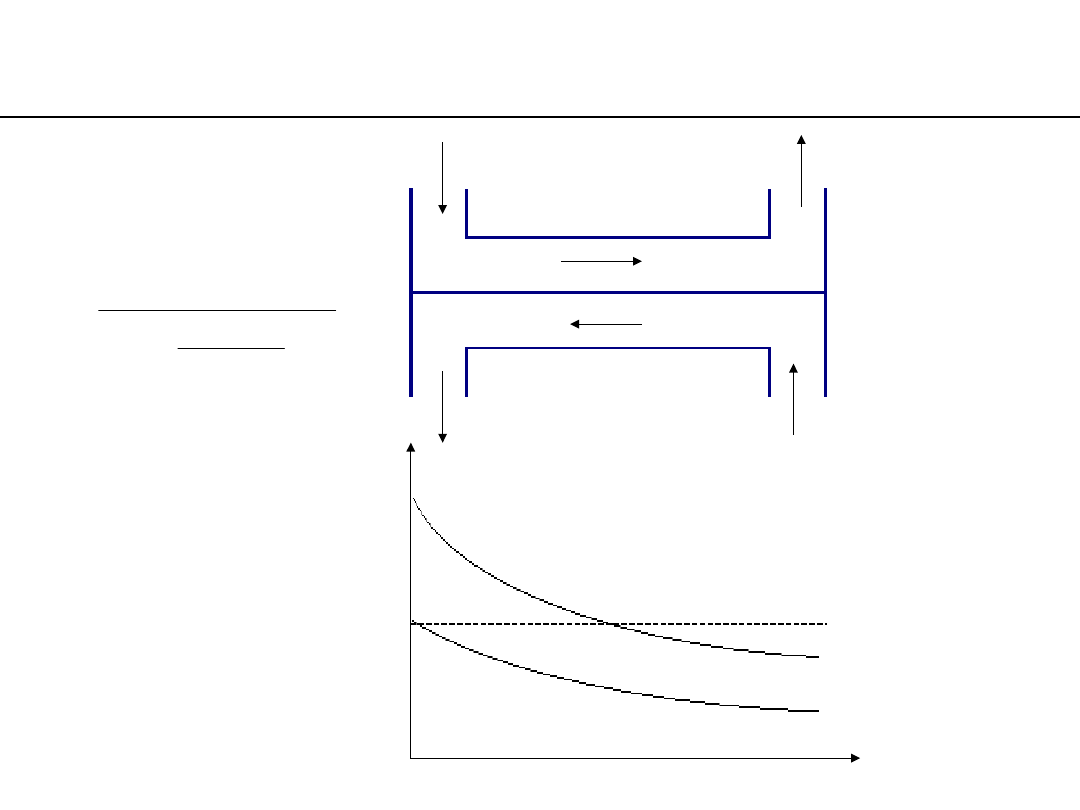
contrary-flow heat exchanger
temperatures changes along the heat exchange
surface
L
t
11
t
12
t
21
t
22
t
t
11
t
22
>
t
12
t
21
t
12
< t
22
)
(
)
(
ln
)
(
)
(
21
12
22
11
21
12
22
11
ln
t
t
t
t
t
t
t
t
t
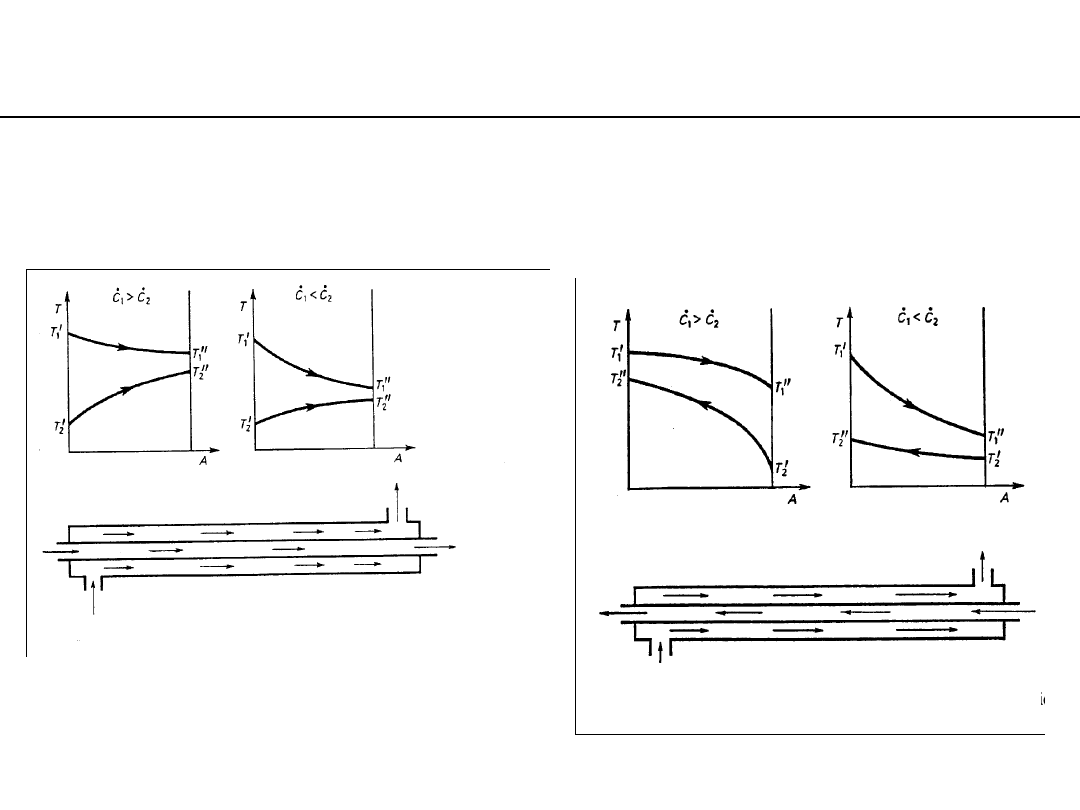
fluids temperature distribution in a heat
exchanger
volume
heat
C
c
m
C
p
After: - Wymiana ciepła, S. Wiśniewski, T.S.
Wiśniewski
fluids temperature distribution
in common-flow heat exchanger
fluids temperature distribution
in contrary-flow heat exchanger

If a temperature difference between fluids along the
heat surface is a linear function of the both fluids
temperatures then an average difference between
fluids temperatures in a heat exchanger is an
logarithmic temperature difference
The condition for the linear dependence between the
fluids temperatures and the difference between these
temperatures is fulfilled if fluids do not change phases
and their heat volumes are constant (m·c = const.).
an average logarithmic difference of
temperatures in a heat exchanger

)
(
2
2
2
1
1
1
t
dS
k
Q
d
dt
c
m
Q
d
dt
c
m
Q
d
f
f
L
t
t
11
t
21
t
22
< t
12
t
12
t
1
t
2
Δt=t
1
-
t
2
an average logarithmic difference of
temperatures in a heat exchanger
cont.
heat exchanged
(transferred)
through an
elementary area dS:

t
dS
k
Q
d
av
t
k
S
Q
t
k
dt
c
m
t
k
Q
d
dS
f
1
1
1
outlet
inlet
f
t
k
dt
c
m
S
1
1
1
ale:
c
f1
, k, Δt change along the heat exchanger and so are a
functions of t
1
(and of t
2
)
an average logarithmic difference of
temperatures in a heat exchanger
cont.

outlet
inlet
f
av
av
t
k
dt
c
t
k
m
t
k
S
Q
)
(
)
(
)
(
1
1
1
outlet
inlet
f
dt
c
m
Q
1
1
1
and also:
so:
outlet
inlet
f
outlet
inlet
f
av
dt
c
t
k
dt
c
t
k
1
1
1
1
)
(
)
(
an average logarithmic difference of
temperatures in a heat exchanger
cont.

outlet
inlet
f
outlet
inlet
f
av
t
k
dt
c
dt
c
t
k
)
(
)
(
1
1
1
1
outlet
inlet
f
outlet
inlet
f
av
dt
c
t
k
dt
c
t
k
1
1
1
1
)
(
)
(
then:
if c
f
and k are const.:
if:
outlet
inlet
outlet
inlet
outlet
inlet
av
t
dt
t
t
t
dt
dt
t
1
11
12
1
1
an average logarithmic difference of
temperatures in a heat exchanger
cont.

by analogy:
outlet
inlet
outlet
inlet
outlet
inlet
av
t
dt
t
t
t
dt
dt
t
2
21
22
2
2
an average logarithmic difference of
temperatures in a heat exchanger
cont.

)
(
)
(
21
2
2
2
1
11
1
1
t
t
c
m
t
t
c
m
f
f
2
2
2
1
1
1
dt
c
m
dt
c
m
f
f
)
(
1
11
2
2
1
1
21
2
t
t
c
m
c
m
t
t
f
f
11
2
2
1
1
21
1
2
2
1
1
2
t
c
m
c
m
t
t
c
m
c
m
t
f
f
f
f
an average logarithmic difference of
temperatures in a heat exchanger
cont.

b
t
a
t
t
c
m
c
m
t
c
m
c
m
t
f
f
f
f
1
21
11
2
2
1
1
1
2
2
1
1
1
2
1
t
t
t
an average logarithmic difference of
temperatures in a heat exchanger
cont.

1
2
1
2
11
12
11
12
11
12
11
12
11
12
11
12
1
1
11
12
1
11
12
ln
ln
)
(
)
(
ln
ln
1
t
t
t
t
b
t
a
b
t
a
b
t
a
b
t
a
b
t
a
b
t
a
t
a
t
a
b
t
a
b
t
a
a
t
t
b
at
dt
t
t
t
dt
t
t
t
outlet
inlet
outlet
inlet
av
an average logarithmic difference of
temperatures in a heat exchanger
cont.

outlet
inlet
outlet
inlet
śr
b
at
dt
t
t
t
dt
t
t
t
1
1
11
12
1
11
12
b
t
a
b
t
a
a
t
t
b
t
a
a
b
t
a
a
t
t
t
av
11
12
11
12
11
12
11
12
ln
1
)
ln(
1
)
ln(
1
1
2
1
2
11
12
11
12
11
12
11
12
ln
ln
)
(
)
(
ln
t
t
t
t
b
t
a
b
t
a
b
t
a
b
t
a
b
t
a
b
t
a
t
a
t
a
t
av
an average logarithmic difference of
temperatures in a heat exchanger
cont.

t
22
t
11
t
12
t
21
)
(
)
(
ln
)
(
)
(
21
12
22
11
21
12
22
11
_
ln_
t
t
t
t
t
t
t
t
t
t
flow
contrary
for
av
ε<1 – a correction related to the heat exchanger
configuration, fluids temperatures drops, temperatures
at the heat exchangers inlet and outlet
cross-kind heat exchanger

„Shell-tubular” heat exchanger of a
mixed flow structure
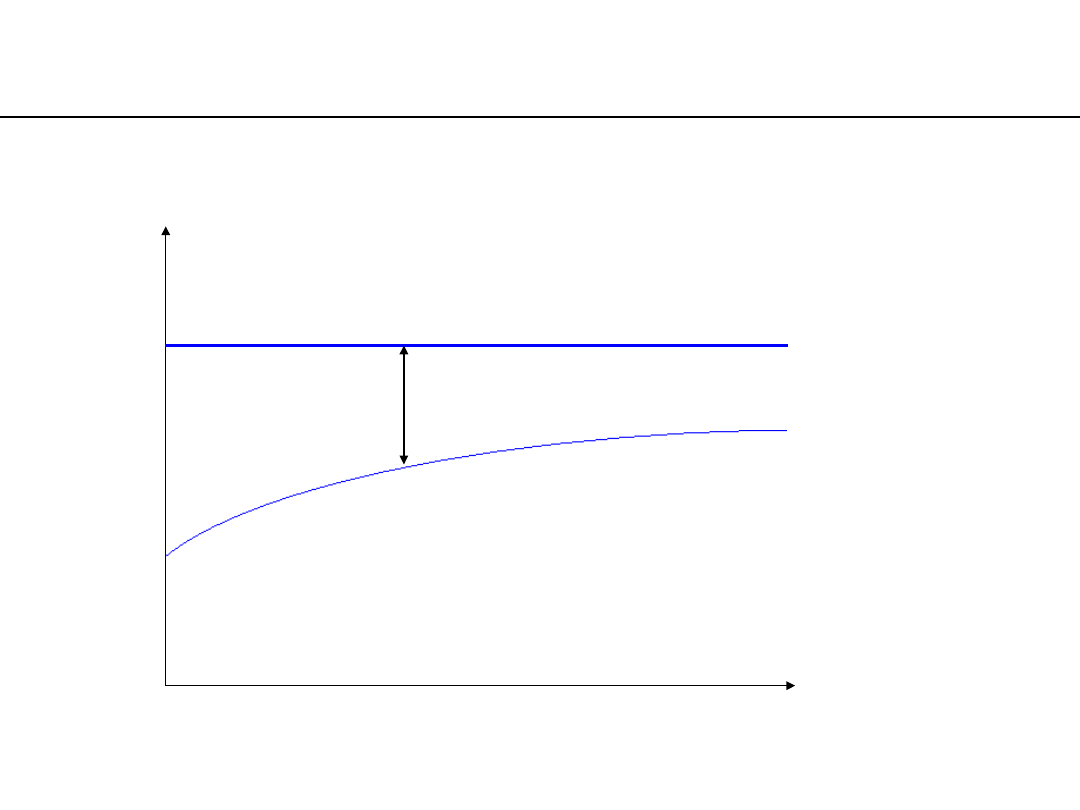
isobaric condensing
p
1
= const. t
1
= const.
t
L
t
2
2
t
21
Δt=t
1
-
t
2
Condenser

As in the case of heat exchange between fluids without a change of
phase, also for an isobaric condensation:
outlet
inlet
outlet
inlet
outlet
inlett
av
t
dt
t
t
t
dt
dt
t
2
21
22
2
2
Δt is linearly related to t
2
(condensing temperature t
1
=
const.):
b
t
a
t
t
t
2
1
2
1
Condenser

1
2
1
2
21
22
21
22
21
22
21
22
21
22
21
22
2
2
21
22
2
21
22
ln
ln
)
(
)
(
ln
ln
1
t
t
t
t
b
t
a
b
t
a
b
t
a
b
t
a
b
t
a
b
t
a
t
a
t
a
b
t
a
b
t
a
a
t
t
b
at
dt
t
t
t
dt
t
t
t
outlet
inlet
outlet
inlet
av
Condenser
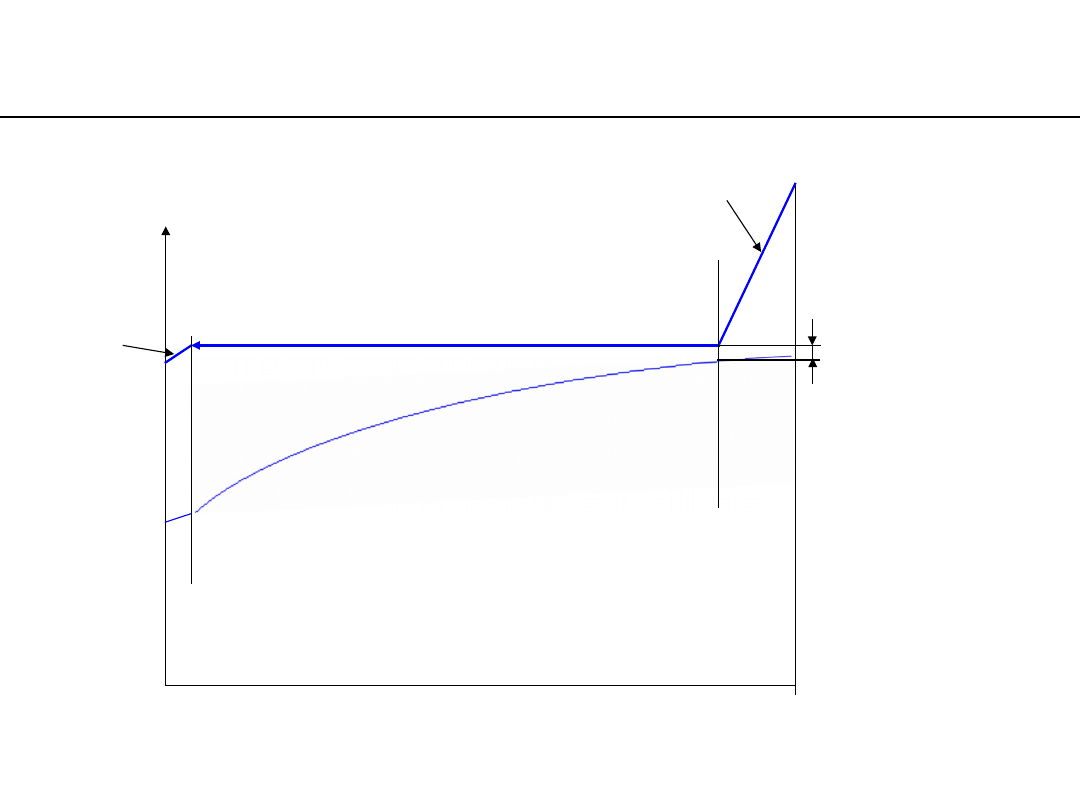
isobaric condensing
p = const. t = const.
t
L
steam cooling
condensate
cooling
Δt
min
- „pinch
point”
steam cooling, steam condensing,
condensate cooling
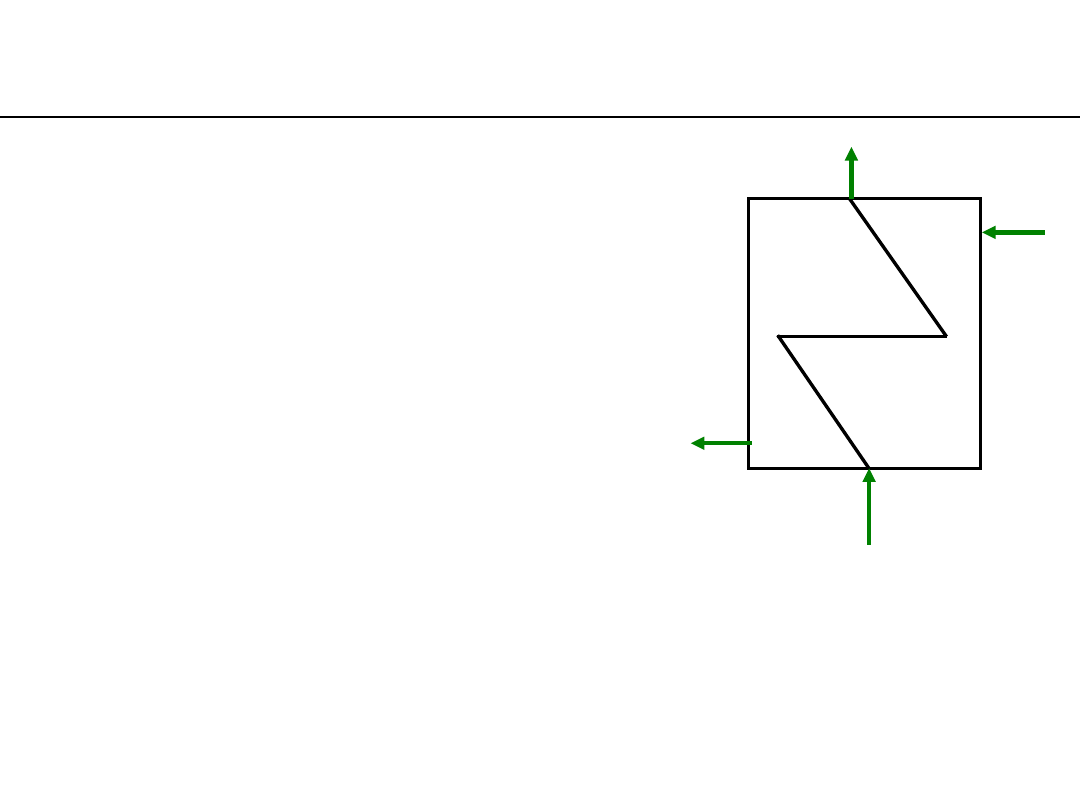
mass balances for a diaphragm-kind heat exchange:
0
22
22
21
21
12
12
11
11
22
22
21
21
12
12
11
11
i
m
i
m
i
m
i
m
Q
i
m
i
m
Q
i
m
i
m
energy balance for a diaphragm-kind heat exchange:
0
0
22
21
12
11
m
m
m
m
or:
balances for a diaphragm-kind heat exchanger
m
12
m
11
m
21
m
22
)
(
)
(
21
22
2
21
12
11
1
11
t
t
c
m
t
t
c
m
Q
p
p
Energy balance for a diaphragm-kind heat exchange and one-
phase flows with c
p
=const.:
balances for a diaphragm-kind heat exchange
L
t
t
11
t
21
t
22
< t
12
t
12
t
1
t
2
Δt=t
1
-
t
2
)
(
2
2
2
1
1
1
t
dS
k
Q
d
dt
c
m
Q
d
dt
c
m
Q
d
w
w

examples of a diaphragm-kind heat
exchangers
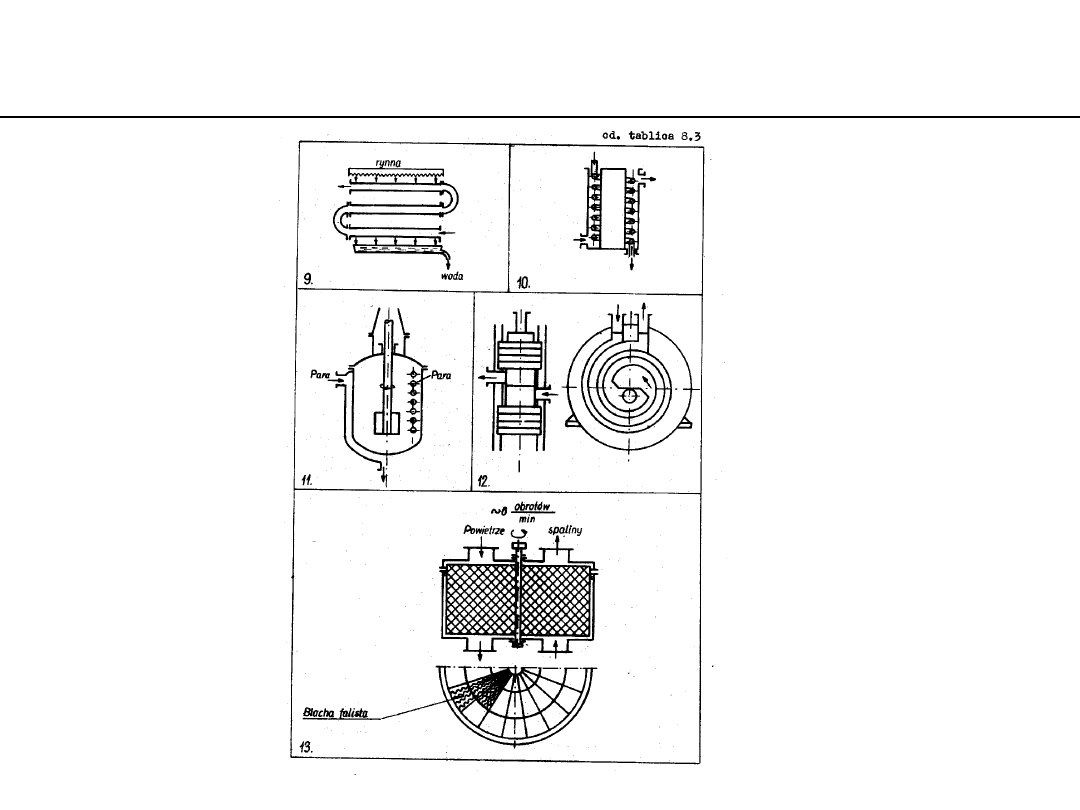
examples of a diaphragm-kind heat
exchangers

approximates values of the heat
infiltration coefficients at recuperates
heat inflitration coefficient [W/m
2
K]
heating or cooling
air
160
superheated steam
20120
oils
601800
liquid water
23012000
water boiling
60052000
film condensation of water
steam
46001800
0
drop-kind condensation of water
steam
46000140
000
condensation of organic
compounds steams
6002300

marginal values of the heat transfer
coefficients k [W/m2K]
gas – gas
30
gas – liquid water
60
light oil – liquid water
350
liquid water – liquid water
1200
condensing water steam – liquid water 3000
condensing water steam – oils
350
condensing water steam – boiling oils
600
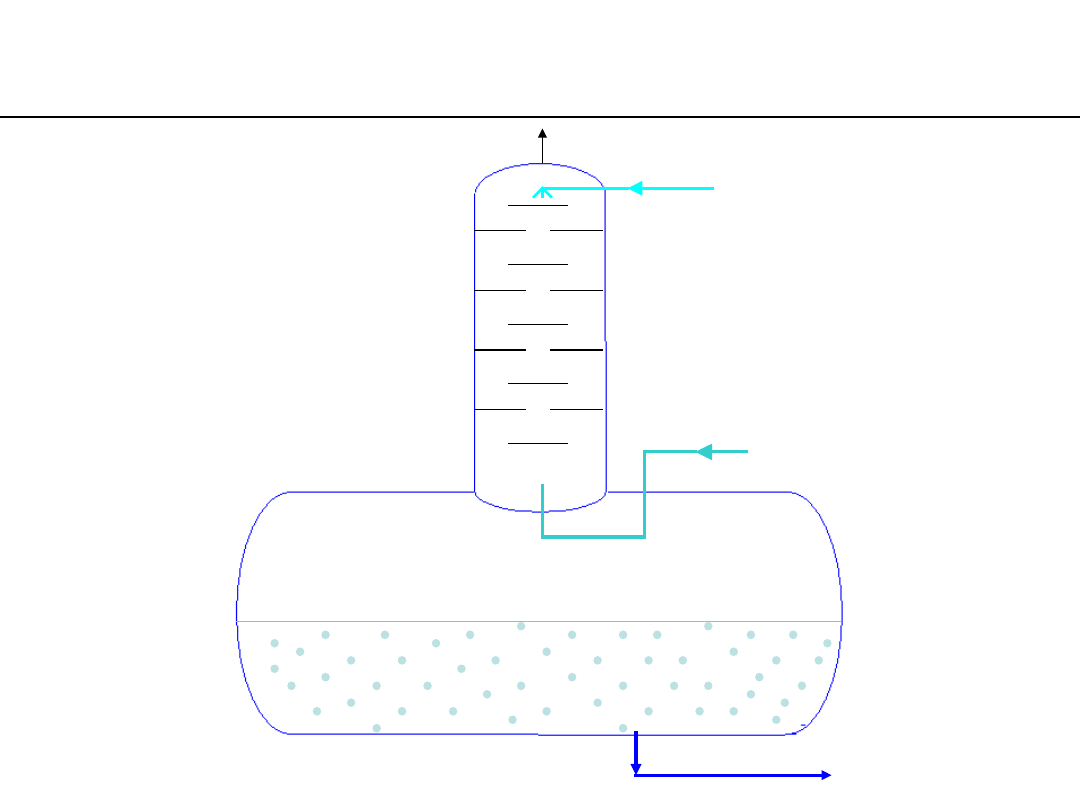
liquid
(1)
heating steam
(2)
gases - vapors (4)
no-diaphragm kind
heat exchanger
thermal deairater
degasified
water (3)
no-diaphragm kind heat exchanger
– deairater (dearating heater)

)
(
"
)
(
'
0
3
4
3
3
4
1
p
i
i
p
i
i
m
m
0
4
3
2
1
m
m
m
m
0
4
4
3
3
2
2
1
1
i
m
i
m
i
m
i
m
mass balance of a deairater
energy balance of a deairater
additional relations – approximated relation between mass of
vapors and supplying water
no-diaphragm kind heat exchanger
– deairater (dearating heater) cont.

Exercise 1
• A fluid „2” is heated from T’
2
=293 K
to T”
2
=343 K. Heating agent „1”
cools down from T’
1
=453 K to
T”
1
=353 K. Compare heat exchange
area for common-flow and contrary-
flow heat exchangers of 1 MW
capacity, if heat transfer coefficient
is k=100 W/(m2K) in the both cases.

Exercise 2
• Two fluids (1) & (2) of temperatures t
1
& t
2
(t
1
>t
2
) are
separated with a partition and exchange a heat. Heat
infiltration coefficient from the fluid (1) to a surface of
the partition α
1
is 300 W/m
2
K, and heat infiltration
coefficient from a surface of the partition to the fluid
(2) α
2
is 900 W/m
2
K. The partition is made of a
homogenous material of heat conduction factor λ
equal to 45 W/mK. Estimate a heat transfer coefficient
k if the partition is:
1. a flat plate 4 mm thick,
2. a pipe ø211x4,
3. a pipe ø32x4,
Formulate conclusions basing on the results.

Exercise 3
• Estimate an area of heat exchanger
water – water, where one fluid is
cooled down form 80°C to 40°C. An
cooling agent is a water supplied
with temperature 30°C. Accept
additional assumptions, chose a
proper kind of a heat exchanger, and
estimate area of its surface.

Exercise 4
• 100 kg/s of a wet steam of an enthalpy 2776
kJ/kg is condensing. Saturated condensate
outflows from the heat exchanger with an
enthalpy 763 kJ/kg. Saturation temperature is
180°C (saturation pressure 10 bar). An cooling
agent is a water supplied with temperature
90°C.
• Accept necessary additional assumptions (e.g.
heat exchanger configuration, k value, …) and
calculate area of heat exchange surface.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
Wyszukiwarka
Podobne podstrony:
6 ZŁOŻONA WYMIANA CIEPŁA W WYMIENNIKACH
Plan Wymiana ciepła i wymienniki m2002
Zestaw 7 Podstawy konwekcyjnej wymiany ciepła
6 ZŁOŻONA WYMIANA CIEPŁA W WYMIENNIKACH
wymiana ciepla i masy, wymienniki ciepła, ZAKRES WYMAGANYCH WIADOMOŚCI
termodynamika Wzory do teorii z wymiany ciepla dla USM, Wzory do teorii z podstaw termodynamiki
Podstawy wymiany ciepla
Wymiana Ciepla
podstawowe wiadomosci (1)
Podstawowe wiadomosci o programie SciLab wykresy
akademia cisco ccna semestr 2 podstawowe wiadomosci o routerach i routingu
PROCESY NIESTACJONARNEJ WYMIANA CIEPŁA, Uczelnia, Metalurgia
Materialy szkoleniowe podstawowe wiadomosci o zagroze
genetyka podstawowe wiadomości, Nauka, biologia, genetyka
więcej podobnych podstron