Wnioskowanie
statystyczne c. d.
Wykład 7
Wnioskowanie
statystyczne c. d.
Wykład 7
Skala nominalna – jeden z rodzajów
.
są na
skali nominalnej, gdy przyjmują
wartości (etykiety), dla których nie
istnieje wynikające z natury danego
zjawiska uporządkowanie.
Skala nominalna
(
)
Nawet jeśli wartości zmiennej nominalnej
są wyrażane liczbowo, to liczby te są
tylko umownymi identyfikatorami, nie
można więc wykonywać na nich działań
arytmetycznych, ani ich porównywać.
Przykłady zmiennych nie
będących nominalnymi:
prędkość samochodu, wiek
Przykłady zmiennych
nominalnych:
stan zdrowia, m - ce
zamieszkania, płeć.
Szczególnym przypadkiem skali
nominalnej jest
, w przypadku
której istnieją tylko dwie możliwe
wartości zmiennej (np. płeć,
odpowiedzi na pytania typu: tak/nie .
-zliczanie,
-obliczanie frakcji (procent
całości),
-modalna,
-binaryzacja (zamiana zmiennej
nominalnej x na szereg
zmiennych dychotomicznych xi,
przyjmujących np. wartość 1, gdy
x = i i 0 w przeciwnym wypadku).
Dopuszczalne operacje
statystyczne
Skala dychotomiczna – jeden
z rodzajów
,
szczególny przypadek
skali nominalnej.
są na
skali dychotomicznej, gdy
przyjmują tylko dwie wartości.
Przykłady zmiennych
dychotomicznych: płeć,
odpowiedzi na pytania tak/nie.
Zmienną nominalną można
przekształcić w ciąg zmiennych
dychotomicznych za pomocą
Skala dychotomiczna
Czułość testu
diagnostycznego
• Czułość – w badaniach naukowych, na
przykład testach diagnostycznych
stosowanych w medycynie, jest
stosunkiem wyników prawdziwie
dodatnich do sumy prawdziwie dodatnich
i fałszywie ujemnych. Czułość 100%
oznaczałaby, że wszystkie osoby chore lub
ogólnie z konkretnymi poszukiwanymi
zaburzeniami zostają rozpoznane. Pojęcie
interpretuje się jako zdolność testu do
prawidłowego rozpoznania choroby tam,
gdzie ona występuje.
Ocena cech przyjmujących
wartości w skali
dychotomicznej
zestawionych w tabelce
2x2
Stan (np. choroba)
Określona jako "złoty" standard.
Prawdziwy
Fałszywy
Wynik
testu
Dodatni
Prawdziwie dodatni
Fałszywie dodatni
→ Wartość predykcyjna dodatnia
Ujemny
Fałszywie ujemny
Prawdziwie ujemny
→ Wartość predykcyjna ujemna
↓
Czułość
↓
Swoistość
Występowanie choroby
Tak
(Cukrzyca)
nie
Wyni
k
testu
Dodat
ni
Prawdziwie
dodatni
(a=74)
Fałszywie
dodatni
(b=21)
→ Wartość
predykcyjna
(a+b=95)
dodatniej
wynosi
a/(a+b)
Ujem
ny
Fałszywie
ujemny
(c=10)
Prawdziwie
ujemny
(d=303)
→ Wartość
predykcyjna
(c+d=313)
ujemna
wynosi c/
(c+d)
↓ (a+c=84)
Czułość
=a/(a+c)
↓(b+d=324)
Swoistość
=d/(b+d
OR- iloraz szansz
OR= (a/(a+b))/ (c/
(c+d))
Przykład
Powstało też wiele metod
przewidujących wartości
zmiennych na tej skali, np.
.
W odróżnieniu od innych
zmiennych na skali nominalnej, do
zmiennych dychotomicznych po
ich zakodowaniu jako 0 i 1 można
też stosować niektóre metody
dostosowane do skali ilorazowej.
Istnieją specjalne metody
statystyczne dostosowane do skali
dychotomicznej, np.
Skala ilorazowa
• Skala ilorazowa (także: skala stosunkowa) – jeden
z rodzajów
.
jest na skali
ilorazowej, gdy
miedzy dwiema jej
wartościami mają interpretację w świecie
rzeczywistym.
• Przykłady zmiennych ilorazowych: temperatura w
(temperatura w
jest na
),
,
,
• Skala ilorazowa, w odróżnieniu od uboższych skal, nie
nakłada ograniczeń w stosowaniu operacji
matematycznych i metod statystycznych. W
odróżnieniu jednak od
z natury
, jaką
należy zastosować.
Zastosowania skali
stosunkowej w
pedagogicznych
•
Skala stosunkowa nie wnosi żadnych ograniczeń w
stosowaniu operacji arytmetycznych do wyników
pomiaru. Oprócz obliczeń uprawnionych dla
, dopuszcza ona przekształcenia
zmienności.
•
Przykładem skali stosunkowej w dziedzinie
może być czas rozwiązywania
szybkości. Początek testowania jest tu
naturalnym punktem zerowym, a
(lub
) pracy badanego —
. Dzięki tym dwu
potrafimy ustalać stosunki między
osiągnięciami
, np. stwierdzić, że dany
rozwiązuje pewnego typu tekst dwa razy
szybciej od innego ucznia
Skala interwałowa
• Skala interwałowa (przedziałowa) – jeden z
rodzajów
.
jest na
skali interwałowej, gdy
miedzy dwiema
jej wartościami dają się obliczyć i mają
interpretację w świecie rzeczywistym, jednak
nie ma sensu dzielenie dwóch wartości
zmiennej przez siebie. Innymi słowy określona
jest
, jednak punkt zero jest
wybrany umownie.
• Przykłady zmiennych interwałowych: daty,
np. data urodzenia, temperatura w
,
,
Dopuszczalne operacje
statystyczne
•
jednej lub
większej liczby zmiennych interwałowych
daje także wielkość na skali interwałowej.
• Różnica dwóch wielkości na skali
interwałowej jest na
.
• Rangowanie zmienia skalę interwałową
na
Obliczanie:
,
,
Pearsona,
,
i
Niedopuszczalne są:
• wyliczanie zmian względnych
(procentowych) w szeregu czasowym
• mnożenie i dzielenie dwóch wielkości
interwałowych
• logarytmowanie
• potęgowanie
•
oprócz arytmetycznej,
takie jak
,
,
Skala porządkowa
• Skala porządkowa – jeden z rodzajów
.
są na skali
porządkowej, gdy przyjmują wartości, dla
których dane jest
(kolejność),
jednak nie da się w sensowny sposób określić
miedzy dwiema
wartościami.
• Przykłady zmiennych porządkowych:
wykształcenie, kolejność zawodników na
podium.
• Przykłady zmiennych nie będących
porządkowymi: płeć, wiek, temperatura
Dopuszczalne operacje
statystyczne:
• porównywanie, która wartość jest mniejsza, a
która większa (ale bez określania o ile)
• zliczanie,
• obliczanie
(procent całości),
•
(zamiana zmiennej nominalnej x na
szereg zmiennych dychotomicznych xi,
przyjmujących np. wartość 1, gdy x = i i 0 w
przeciwnym wypadku).
•
,
•
i
, w szczególności:
–
– obliczanie
, w tym
– wyliczanie
Nie są jednak
dopuszczalne takie operacje,
jak
,
,
,
klasyczna
,
• Dowolną zmienną na skali
interwałowej bądź ilorazowej można
przekształcić w porządkową za
pomocą
Skala absolutna
• Skala absolutna – najbogatszy rodzaj skal
pomiarowych, w którym z natury danego
zjawiska wynika zarówno umiejscowienie
zera na skali, jak i jednostka miary. Skala
absolutna łączy cechy skali interwałowej i
ilorazowej. Dla zmiennych na skali
absolutnej interpretację mają zarówno
iloraz, jak i różnica dwóch pomiarów.
• Przykład zmiennej na skali absolutnej:
liczba jabłek, liczba pacjentów.
Prawdopodobieństwo
subiektywistyczne
• P(X) jest więc obserwowanym
prawdopodobieństwem X, zaś P(X | T) to
prawdopodobieństwo, że X nastąpi według teorii T.
Z kolei P(T) to prawdopodobieństwo, że teoria T
jest prawdziwa, P(T | X) to prawdopodobieństwo,
że teoria T jest prawdziwa, jeśli zaobserwowano X.
• Zdania typu "prawdopodobieństwo, że teoria T jest
prawdziwa" są z punktu widzenia interpretacji
obiektywistycznej nie do przyjęcia – teoria jest
prawdziwa (prawdopodobieństwo równe jedności)
lub też nie (prawdopodobieństwo równe zeru), czyli
prawdziwość teorii nie jest zdarzeniem losowym.
Przykład użycia
• Twierdzenia Bayesa można użyć do
interpretacji rezultatów badania przy użyciu
testów wykrywających narkotyki. Załóżmy, że
przy badaniu narkomana test wypada
pozytywnie w 99% przypadków, zaś przy
badaniu osoby nie zażywającej narkotyków
wypada negatywnie w 99% przypadków.
Pewna firma postanowiła przebadać swoich
pracowników takim testem wiedząc, że 0,5%
z nich to narkomani. Chcemy obliczyć
prawdopodobieństwo, że osoba u której test
wypadł pozytywnie rzeczywiście zażywa
narkotyki. Oznaczmy następujące zdarzenia:
D - dana osoba jest narkomanem
N - dana osoba nie jest narkomanem
+ - u danej osoby test dał wynik pozytywny
− - u danej osoby test dał wynik
negatywny
Wiemy, że:
P(D) = 0,005, gdyż 0,5% pracowników to
narkomani
P(N) = 1 − P(D) = 0,995
P( + | D) = 0,99, gdyż taką skuteczność ma
test przy badaniu narkomana
P( − | N) = 0,99, gdyż taką skuteczność
ma test przy badaniu osoby nie będacej
narkomanem
P( + | N) = 1 − P( − | N) = 0,01
Mając te dane chcemy obliczyć
prawdopodobieństwo,
że osoba u której test wypadł pozytywnie,
rzeczywiście jest narkomanem. Tak więc:
Mimo potencjalnie wysokiej skuteczności
testu, prawdopodobieństwo, że narkomanem jest
badany pracownik u którego test dał wynik
pozytywny, jest równe około 33%, więc jest
nawet bardziej prawdopodobnym, ze taka osoba
nie zażywa narkotyków. Ten przykład pokazuje,
dlaczego ważne jest, aby nie polegać na
wynikach tylko pojedynczego testu.
Wnioskowanie statystyczne - polega na uogólnianiu
wyników otrzymanych na podstawie próby losowej
na całą populację generalną, z której próba została
pobrana
Wnioskowanie statystyczne dzieli się na:
1.
Estymację
–
szacowanie
wartości
parametrów lub postaci rozkładu zmiennej na
podstawie próby – na podstawie wyników próby
formułujemy wnioski dla całej populacji
2. Weryfikację hipotez statystycznych –
sprawdzanie określonych założeń sformułowanych
dla
parametrów
populacji
generalnej
na
podstawie wyników z próby – najpierw wysuwamy
założenie, które weryfikujemy na podstawie
wyników próby
Estymator – wielkość (charakterystyka, miara),
obliczona na podstawie próby, służąca do oceny
wartości nieznanych parametrów populacji
generalnej.
Najlepszym z pośród wszystkich estymatorów
parametru w populacji generalnej jest ten, który
spełnia wszystkie właściwości estymatorów
(jest
równocześnie
nieobciążony,
zgodny,
efektywny, dostateczny).
Przedział ufności jest podstawowym
narzędziem estymacji przedziałowej.
Pojęcie to zostało wprowadzone do
statystyki przez amerykańskiego
matematyka polskiego pochodzenia
Jerzego Spławę-Neymana
• Niech cecha X ma rozkład w populacji z nieznanym
parametrem θ. Z populacji wybieramy próbę losową
(X1, X2, ..., Xn). Przedziałem ufności (θ - θ1, θ +
θ2) o współczynniku ufności 1 - α nazywamy taki
przedział (θ - θ1, θ + θ2), który spełnia warunek:
• P(θ1 < θ < θ2) = 1 − α
• gdzie θ1 i θ2 są funkcjami wyznaczonymi na
podstawie próby losowej.
Podobnie jak w przypadku
estymatorów definicja pozwala
na dowolność wyboru funkcji z
próby, jednak tutaj kryterium
wyboru najlepszych funkcji
narzuca się automatycznie -
zazwyczaj będziemy
poszukiwać przedziałów
najkrótszych
Współczynnik ufności 1 - α jest
wielkością, którą można interpretować w
następujący sposób: jest to
prawdopodobieństwo, że rzeczywista wartość
parametru θ w populacji znajduje się w
wyznaczonym przez nas przedziale ufności.
Im większa wartość tego współczynnika, tym
szerszy przedział ufności, a więc mniejsza
dokładność estymacji parametru. Im
mniejsza wartość 1 - α, tym większa
dokładność estymacji, ale jednocześnie tym
większe prawdopodobieństwo popełnienia
błędu. Wybór odpowiedniego współczynnika
jest więc kompromisem pomiędzy
dokładnością estymacji a ryzykiem błędu. W
praktyce przyjmuje się zazwyczaj wartości:
0,99; 0,95 lub 0,90, zależnie od parametru.
Przykłady przedziałów
ufności
Ponieważ szukamy jak najkrótszych przedziałów
ufności, dlatego przy wyznaczaniu przedziału
staramy się wykorzystać jak najwięcej dostępnych
informacji o rozkładzie cechy w populacji. Jeśli np.
cecha ma rozkład normalny z odchyleniem
standardowym σ, to zastosowanie wzoru na przedział
ufności dla nieznanego σ również da poprawny
wynik, jednak przedział otrzymany tą metodą będzie
szerszy, czyli mniej dokładny. Z kolei wzory
ogólniejsze, np. dla nieznanego rozkładu, często
korzystają z rozkładów granicznych estymatorów i
dlatego wymagają dużej liczebności próby.
Estymacja przedziałowa
polega na budowie przedziału zwanego przedziałem
ufności, który z określonym prawdopodobieństwem
będzie zawierał nieznaną wartość szacowanego
parametru
1
)}
(
)
(
{
2
1
n
n
Z
g
Q
Z
g
P
gdzie:
Q – nieznany parametr populacji generalnej,
końce przedziałów (dolna i górna
granica przedziału), będące funkcją
wylosowanej próby
)
(
1
n
Z
g
)
(
2
n
Z
g
1–α współczynnik ufności – prawdopodobieństwo
tego, że wyznaczając na podstawie n-elementowych
prób wartość funkcji g
1
i g
2
(dolną i górną granicę
przedziału) średnio w (1-α)·100% przypadkach
otrzymamy przedziały pokrywające nieznaną
wartość parametru Q – z prawdopodobieństwem (1-
α) przedział ufności pokrywa nieznaną wartość
szacowanego parametru
Im krótszy przedział (różnica między górną i dolną
granicą przedziału),
tym bardziej precyzyjna jest estymacja
przedziałowa.
Im wyższa jest wartość współczynnika ufności,
tym większa jest długość przedziału.
Przedział ufności dla średniej w populacji o
rozkładzie normalnym ze znanym
odchyleniem standardowym
Estymatorem średniej w populacji jest średnia
arytmetyczna z próby , która ma rozkład
.
X
)
,
(
n
m
N
Przedział ufności dla średniej w populacji ma
postać:
1
}
{
n
n
u
X
u
X
P
- wartość odczytana z tablic rozkładu
normalnego dla danego poziomu istotności
α
- odchylenie standardowe w populacji
generalnej
u
Względna miara precyzji oszacowania
jako miara dokładności dopasowania
określona jest wzorem:
%
100
)
(
n
X
u
X
B
Jeżeli:
- oszacowanie charakteryzuje się dużą
precyzją
- uogólnienia wyników na populację
generalną
należy dokonywać ostrożnie
- nie należy dokonywać żadnych uogólnień
na
populację generalną
%
5
)
(
X
B
%
10
)
(
%
5
X
B
%
10
)
(
X
B
Zadanie 1.
Firma telefoniczna oszacowała przeciętną długość
rozmów lokalnych w czasie weekendu, których czas ma
rozkład normalny z odchyleniem standardowym 5,5
minuty. Z losowej próby 50 rozmów otrzymano średnią
14,5 minuty. Wyznacz z prawdopodobieństwem 1- α
=0,9 przedział ufności dla średniej długości rozmów
lokalnych.
Skorzystaj z funkcji w MS Excel „Ufność”
Zadanie 2.
Wyznacz granice liczbowe krańców przedziału ufności
pomiaru odległości między dwoma wierzchołkami gór
(w metrach) przy poziomie ufności 1- =0.95 , jeśli
wykonano 80 pomiarów ze średnią równą 3000 m.
Rozkład odległości jest rozkładem normalnym z
odchyleniem standardowym równym 10 m.
Skorzystaj z funkcji w MS Excel „Ufność”
Przedział ufności dla średniej w populacji o
rozkładzie normalnym z nieznanym
odchyleniem standardowym
n < 30
Jeżeli próba jest mało liczna - stosujemy statystykę
t o rozkładzie t–Studenta dla n-1 stopni swobody
1
}
{
1
1
,
1
1
,
n
S
n
n
S
n
t
X
m
t
X
P
gdzie:
- odchylenie standardowe z próby
- wartość odczytana z tablic rozkładu
Studenta dla
poziomu istotności α oraz n–1 stopni
swobody
n
i
i
n
x
x
S
1
2
1
)
(
1
,
n
t
Gdy n > 30, wartość odczytaną z tablic
rozkładu Studenta możemy zastąpić wartością ,
odczytaną z tablic rozkładu normalnego oraz
.
1
}
{
n
S
n
S
u
X
m
u
X
P
1
,
n
t
u
S
- wartość odczytana z tablic rozkładu
normalnego dla danego poziomu istotności
α
- odchylenie standardowe w próbie
u
S
Względną precyzję oszacowania oceniamy
następująco:
dla n < 30
%
100
)
(
1
1
,
n
X
S
t
n
X
B
dla n > 30
%
100
)
(
n
X
S
u
X
B
1. W pewnej klasie wybrano losowo grupę 8 osobową,
która miała za zadanie rozwiązać zadanie z
matematyki. Zmierzono czas rozwiązania zadania
przez każdego z uczniów: 25, 16, 12, 10, 12, 21, 25,
20.
Oszacuj
metodą
przedziałową
dla
współczynnika ufności średni czas niezbędny do
rozwiązania zadania w całej zbiorowości uczniów.
Przyjmując poziom istotności = 0,05.
2. W grupie losowo wybranych 625 pracowników w
dużym
koncernie
produkującym
samochody
osobowe, średnia liczba dni nieobecności w pracy
w badanym roku wynosiła 18, natomiast odchylenie
standardowe 3. Przyjmując poziom ufności na
poziomie
0,90
oszacować
średni
poziom
nieobecności
pracowników
w
całym
przedsiębiorstwie
oraz
ocenić
precyzję
oszacowania.
Problem minimalnej liczebność
próby
Minimalna liczebność próby - taka liczebność
próby, która zapewni wymaganą dokładność
(precyzję oszacowania) przy danym poziomie
wiarygodności (prawdopodobieństwa).
Przykład. Chcemy oszacować procent (frakcję)
mieszkańców
pewnego miasta, mających grupę „0”. Ilu należy
wylosować mieszkańców do próby, aby szacowanie
dokonać z błędem maksymalnym 5% przy
współczynniku 0,95.
Rozwiązanie
• Korzystamy ze wzoru: n* ^2/4d^2
Ztablicy rozkładu normalnego N(0,1) dla
wsp. ufności 0,95 odczytujemy wartość
1,96.
Podstawiając do wzoru, mamy:
n= !,96^2/4*0,05^2= 384
u
u
Dla estymacji przedziałowej średniej m w
populacji przy znanym odchyleniu
standardowym σ w populacji
Poszukujemy takiej liczebność próby n, dla której
przy danym współczynniku ufności (1-α) połowa
długości przedziału ufności d – maksymalny błąd
szacunku – nie przekroczy ustalonej z góry
wartości.
2
2
2
d
u
n
2
2
2
d
u
n
stąd
Dla estymacji przedziałowej średniej m w
populacji przy nieznanym odchyleniu
standardowym σ w populacji
Losujemy próbę wstępną n
0
, obliczamy średnią i
wariancję z próby i na jej podstawie wyznaczamy
właściwą liczebność próby:
2
2
2
1
,
ˆ
0
d
S
t
n
n
t
α,n0-1
– wartość odczytana z tablic rozkładu Studenta
dla α i n
0
-1
n
i
i
n
X
X
S
1
1
1
2
)
(
ˆ
Jeżeli n ≤ n
0
to próbę wstępną traktujemy
jako właściwą. Jeżeli zaś n > n
0
to musimy
próbę powiększyć o n – n
0
.
1.
Firma
zajmująca
się
wyszukiwaniem
stanowisk
dla
personelu
kierowniczego
chce
oszacować średnią pensję, jaką może uzyskać
pracownik
pełniący
funkcję
kierowniczą,
z
dokładnością do 2000 $, przy poziomie ufności 95%.
Wiadomo, że rozkład pensji kierowniczych jest
rozkładem normalnym o wariancji 40 mln. Jak liczna
powinna być próba do oszacowania średniej pensji
kierowników?
2. W celu wyznaczenia przeciętnej długości
drogi
hamowania
samochodu
na
asfalcie,
przeprowadzono przy prędkości 40 km/h 12 prób i
otrzymano wyniki w metrach: 17,0; 19,0; 22,0; 20,5;
20,0; 21,0; 20,5; 20,0; 21,0; 18,0; 20,0; 21,0. Czy
liczba prób jest wystarczająca do wyznaczenia
przedziału ufności średniej o długości 0,5 m i dla 1- α
= 0,95. Ewentualnie, jaką liczbę prób należy jeszcze
przeprowadzić?
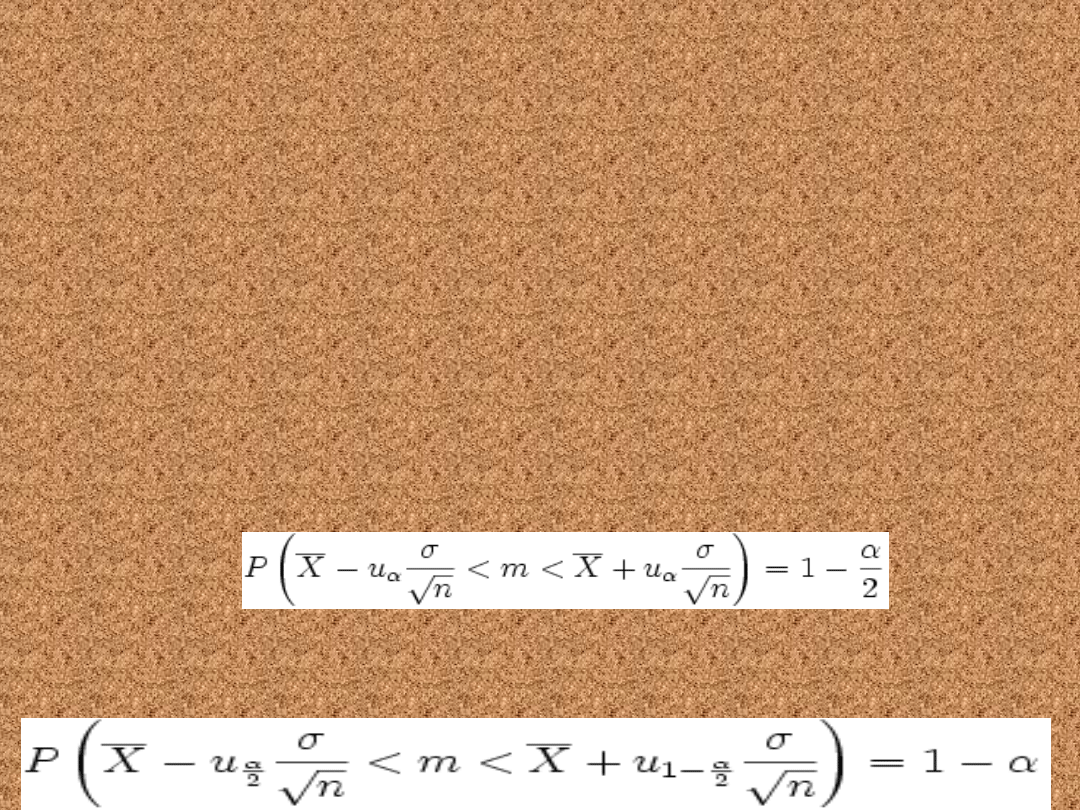
Przedział ufności dla
średniej.
Znane odchylenie
standardowe
• Cecha ma w populacji rozkład normalny
N(m, σ), przy czym odchylenie
standardowe σ jest znane. Przedział
ufności dla parametru m tego rozkładu
ma postać:
• lub równoznacznie:
lub
równoznacznie
gdzie:
n to liczebność próby losowej
oznacza średnią z próby
losowej
σ to odchylenie
standardowe populacji
u
α
jest statystyką,
spełniającą warunek:
P( − u
α
< U < u
α
) = 1 −
α, gdzie U jest zmienną
P( − uα < U < uα) = 1 − α, gdzie U
jest zmienną losową o rozkładzie
normalnym N(0,1).
ora
z
i
rozkładu N(0,1).
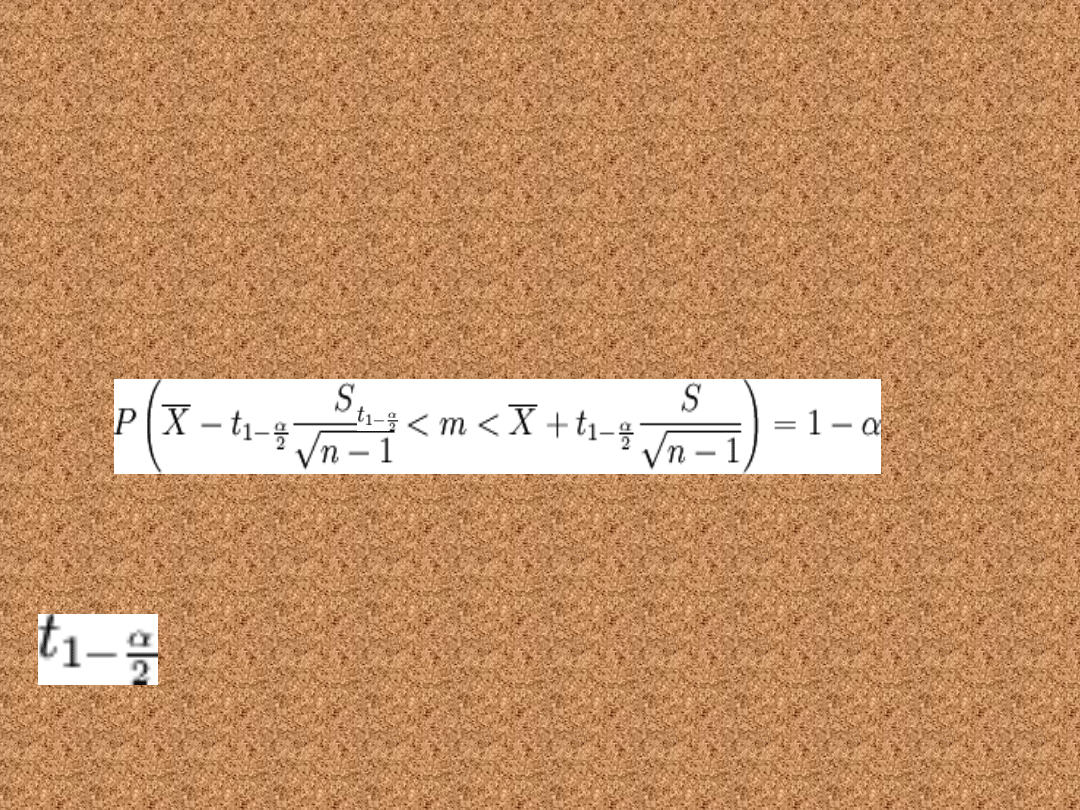
Nieznane odchylenie
standardowe
• Cecha ma w populacji rozkład normalny
N(m, σ), przy czym odchylenie standardowe
σ jest nieznane. Przedział ufności dla
parametru m tego rozkładu ma postać:
• gdzie:
• n to liczebność próby losowej
• oznacza średnią z próby losowej
• S to odchylenie standardowe z próby
ma rozkład Studenta z n - 1 stopniami
swobody
Zwykle stosuje się ten wzór
dla małej próby (n<30). Tak
naprawdę działa on dla każdej
wielkości próby, jednak dla
dużych prób można przybliżyć
rozkład t Studenta rozkładem
normalnym, co jest łatwiejsze
do wyliczenia a dające niemal
takie same wartości (patrz
niżej
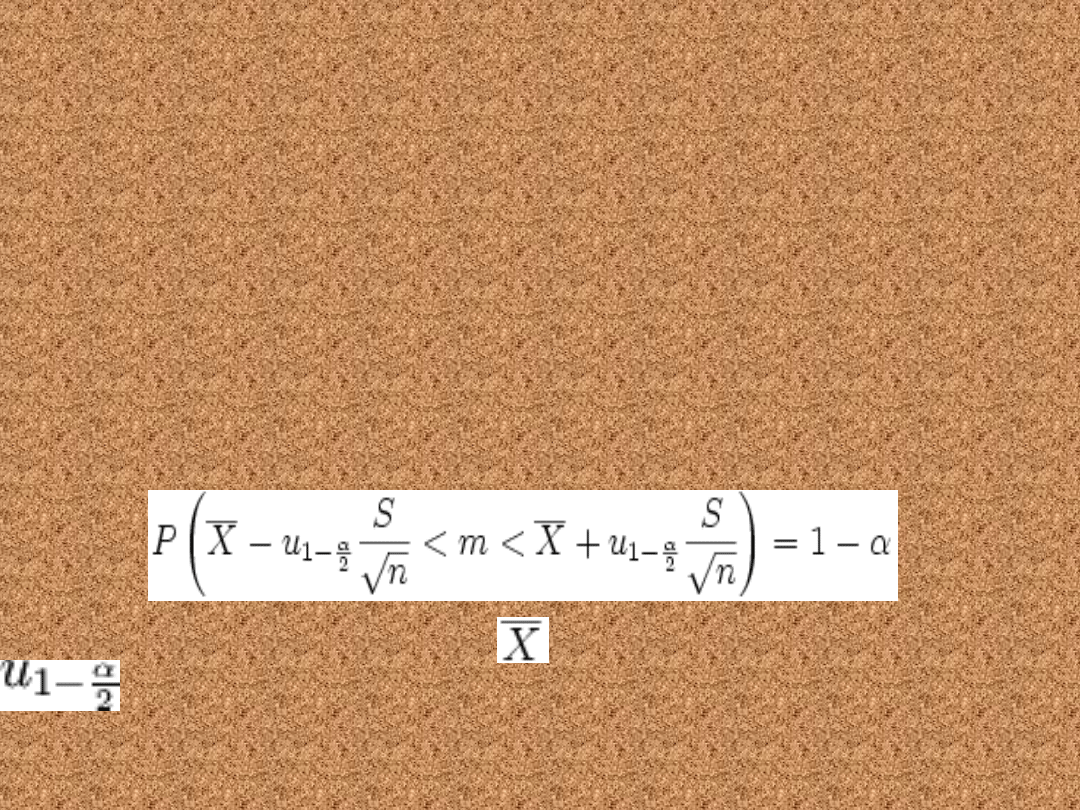
Nieznane odchylenie
standardowe – Duża próba
(n>30
• Cecha ma w populacji rozkład normalny N(m,
σ), przy czym odchylenie standardowe σ jest
nieznane, a próba jest duża (n>30). Granica
30 jest czysto umowna, im n jest większe, tym
wzór dokładniejszy. Przedział ufności dla
parametru m tego rozkładu ma postać:
gdzie:
n to liczebność próby losowej
oznacza średnią z próby losowej
S to odchylenie standardowe z próby
jest statystyką ze zmienną
losową o rozkładzie normalnym N(0, 1
).
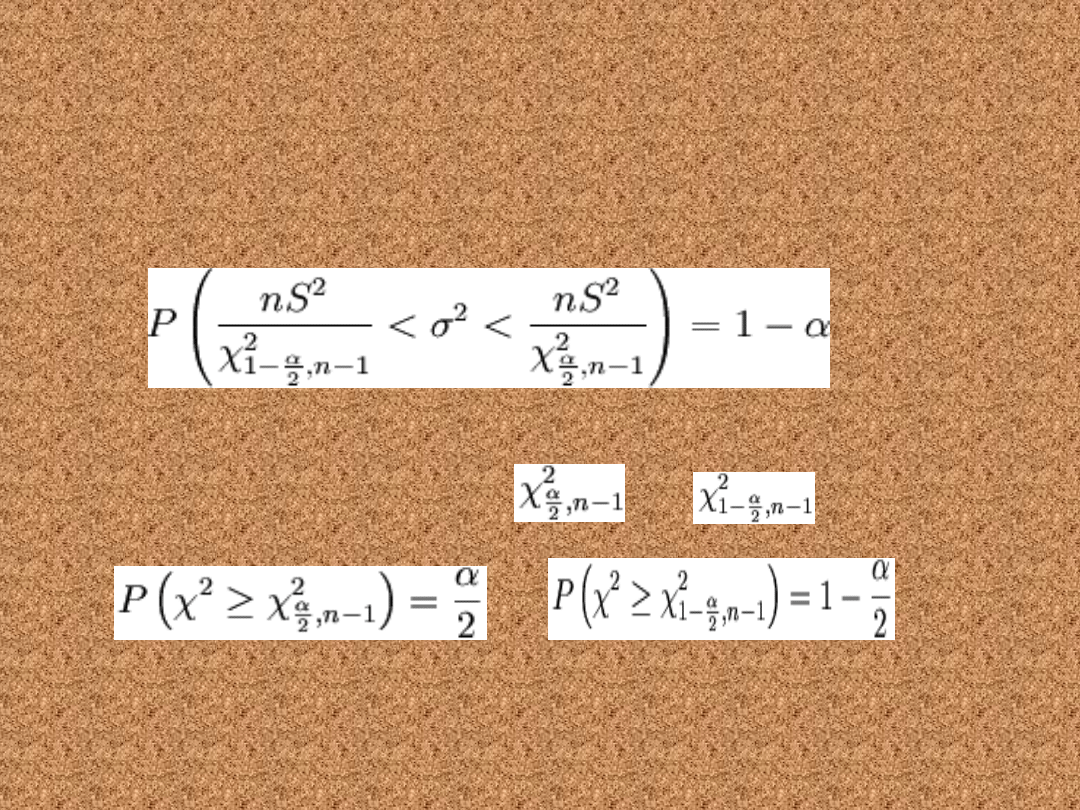
Przedział ufności dla
wariancji
• Poniższy wzór pozwala wyznaczyć
przedział ufności dla wariancji w
populacji o rozkładzie normalnym N(m,
σ)
gdzie: n to liczebność próby losowej, S to
odchylenie standardowe z próby,
i
i
to statystyki spełniające odpowiednio równości:
gdzie χ2 ma rozkład chi-kwadrat z n - 1 stopniami
swobody
Podobnie jak poprzednio zwykle stosuje się ten wzór dla
małej próby (n<30), choć również działa on dla każdej
wielkości próby.
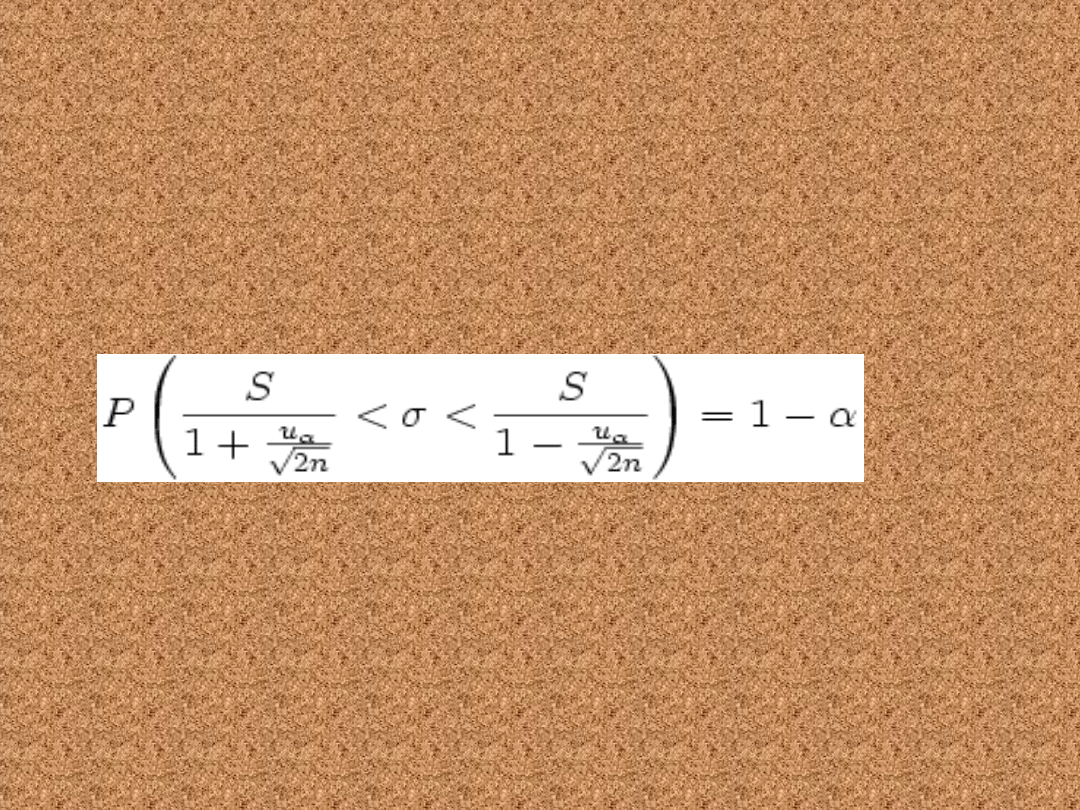
Duża próba (n>30)
• Poniższy wzór pozwala wyznaczyć
przedział ufności dla wariancji w
populacji o rozkładzie normalnym N(m,
σ) dla dużej próby, czyli umownie dla
n>30.
gdzie: n to liczebność próby losowej, S to odchylenie
standardowe z próby, uα jest statystyką, spełniającą
warunek:
gdzie U jest zmienną losową o rozkładzie normalnym N(0, 1).
P( − uα < U < uα) =
1 − α
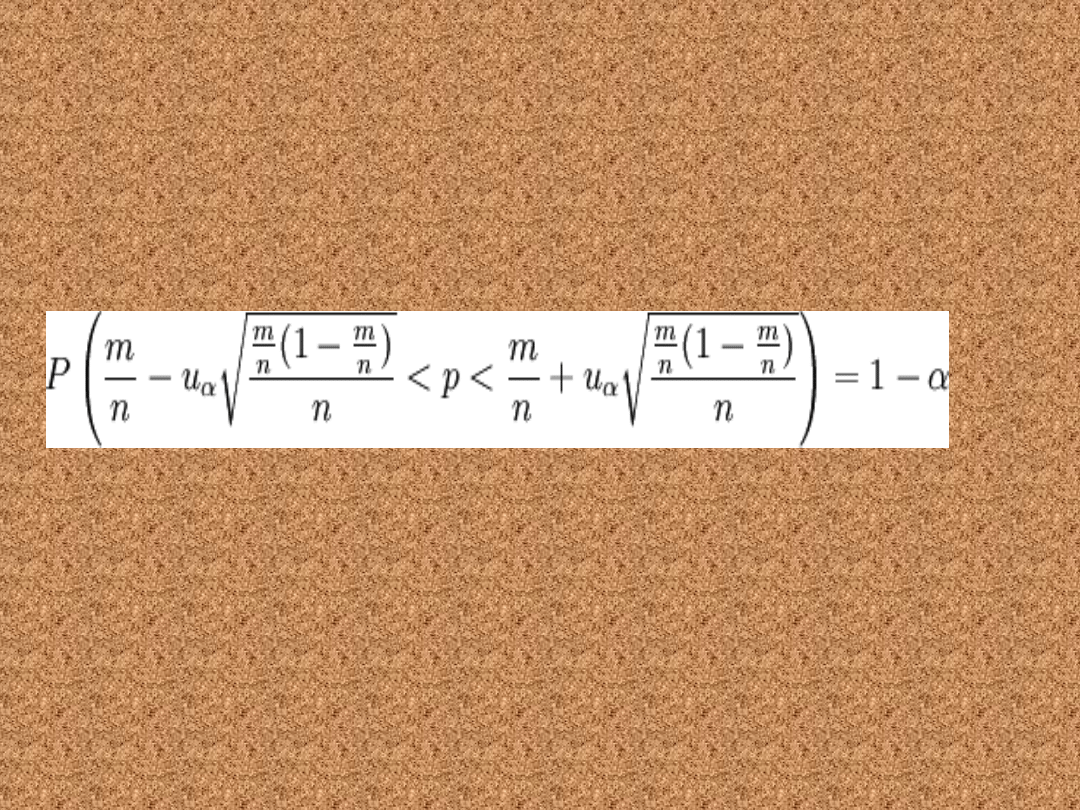
Przedział ufności dla odsetka
(wskaźnik struktury)
• Poniższy wzór pozwala wyznaczyć
przedział ufności dla odsetka w
populacji o rozkładzie normalnym N(m,
σ).
gdzie:
n to liczebność próby losowej
m to liczebność wybranej grupy z próby
uα jest statystyką, spełniającą warunek:
P( − uα < U < uα) = 1 − α gdzie U jest zmienną
losową o rozkładzie normalnym N(0, 1).
Przedział ufności dla
współczynnika korelacji
• Poniższy wzór pozwala wyznaczyć
przedział ufności dla współczynnika
korelacji w populacji o rozkładzie
normalnym N(m, σ). Tak jak poprzednio
działa on dla dowolnej próby choć jest
zwykle stosowany tylko dla prób małych,
n<30.
gdzie: n to liczebność próby losowej, uα jest statystyką,
spełniającą warunek:
P( − uα < U < uα) = 1 − α gdzie U jest
zmienną losową o rozkładzie normalnym
N(0, 1).
r to wspólczynnik korelacji
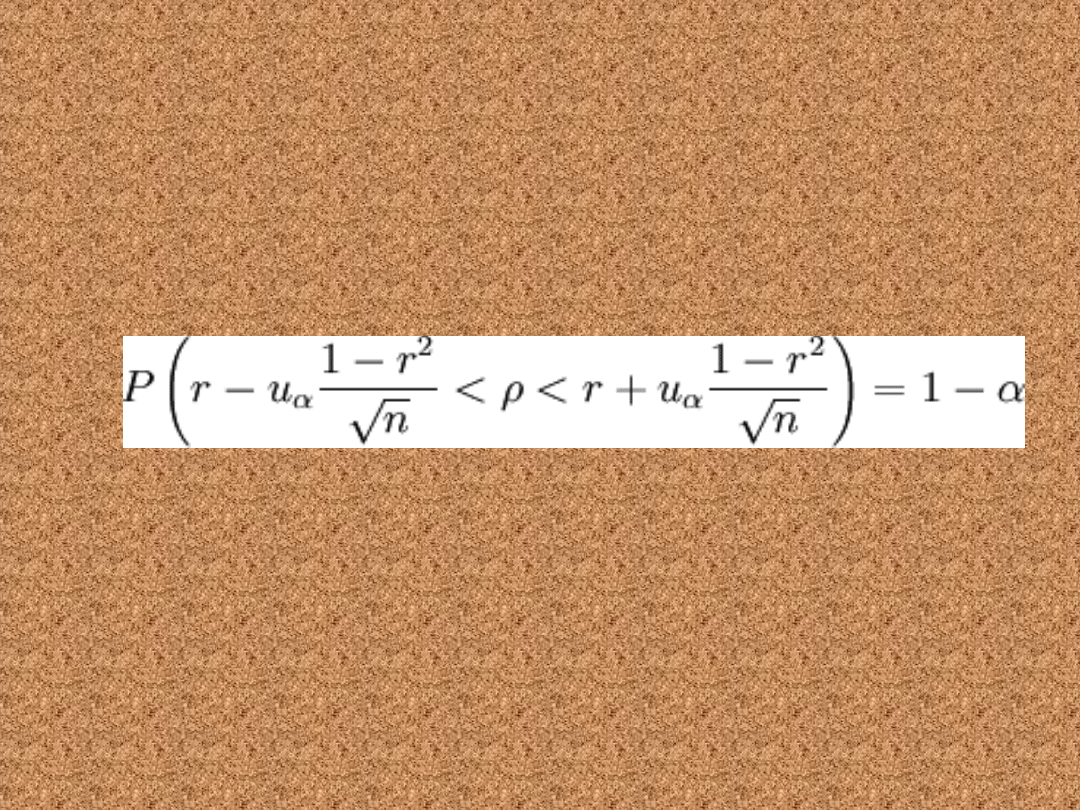
Duża próba (n>30)
• Poniższy wzór pozwala wyznaczyć
przedział ufności dla współczynnika
korelacji w populacji o rozkładzie
normalnym N(m, σ)
gdzie: n to liczebność próby losowej, uα jest statystyką,
spełniającą warunek: P( − uα < U < uα) = 1 − α gdzie U
jest zmienną losową o rozkładzie normalnym N(0, 1),
r to wspólczynnik
korelacji
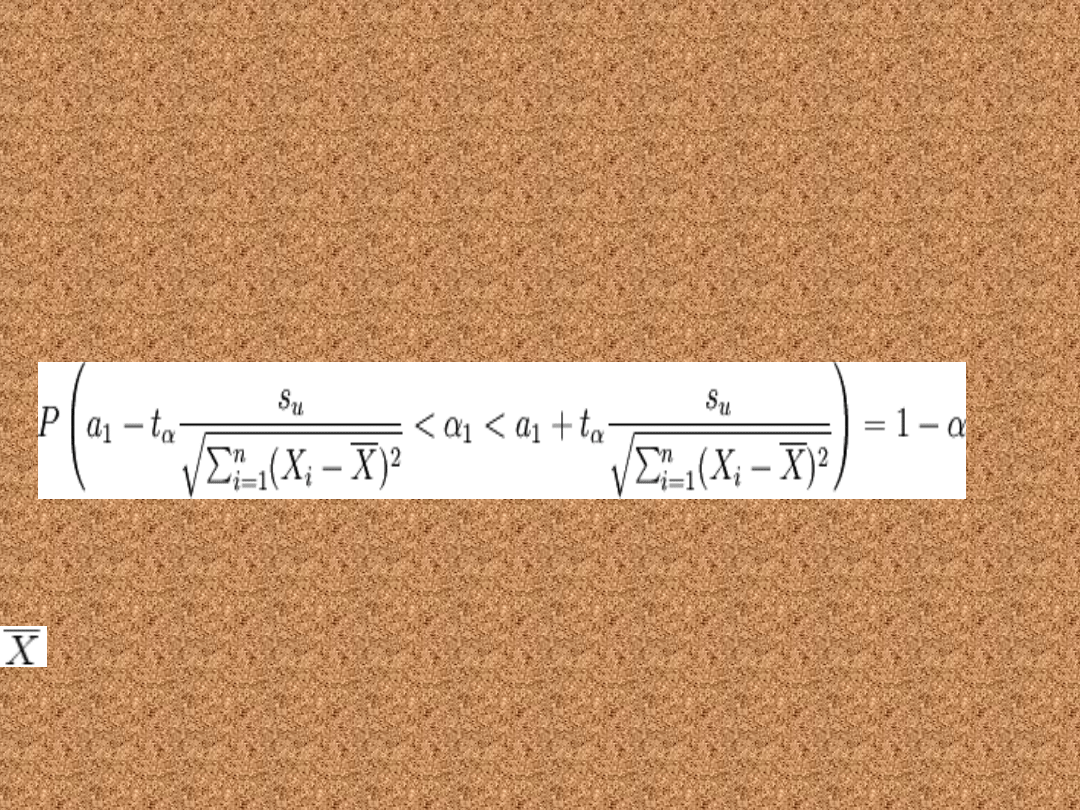
Przedział ufności dla
współczynnika α1
• Poniższy wzór pozwala wyznaczyć
przedział ufności dla współczynnika α1
w populacji o rozkładzie normalnym
N(m, σ)
gdzie: X to wartość z próby
losowej
oznacza średnią z próby losowej, t
α
ma rozkład
Studenta z n - 2 stopniami swobody