Wojciech Gawlik – Struktury Atomowe i Molekularne,
2005/06 , Wykład 1

1/20

Struktury

Struktury

atomowe i molekularne (cząsteczkowe)

atomowe i molekularne (cząsteczkowe)

• Podstawowy składnik materiałów - atom, jon, cząsteczka
(pojedyncze atomy/cząsteczki, gazy, kryształy, ciecze, materiały amorficzne...)

• Opis i zrozumienie możliwe dzięki:

- fizyce a) kwantowej

b) atomowej
c) molekularnej
d) fazy skondensowanej

- chemii [ a), b), c), ...]

• Plan wykładu:

I.

Struktura atomów i cząsteczek

II.

Oddziaływanie atomów (molekuł) z promieniowaniem EM

III.

Główne metody badania struktur atom.-mol.

• Materiały do wykładu (prezentacje + zadania) w internecie:

IF UJ www.if.uj.edu.pl



Zakład Fotoniki

http://fotonika.if.uj.edu.pl/qnog/index_pl.htm

• Kwantowa fizyka - podstawa inżynierii stanów kwantowych

(komputery kwantowe, kryptografia kwantowa)

• Optyka i elektronika kwantowa + „material science” – podstawa fotoniki

(zastosowanie światła do przekazu i PRZETWARZANIA informacji)

Wojciech Gawlik – Struktury Atomowe i Molekularne,
2005/06 , Wykład 1

2/20

Zalecane podręczniki:

 H. Haken, H. Ch. Wolf „Atomy i kwanty”, PWN, 2002 (2

wyd.)

 H. Haken, H. Ch. Wolf „Fizyka molekularna z elementami

chemii kwantowej”, PWN, 1998.

 Paweł Kowalczyk „Fizyka cząsteczek. Energie i widma”,

PWN,2000.

 I.W. Sawieliew „Kurs Fizyki, t.3”, PWN, 1989.

 R. Eisberg, R. Resnick „Fizyka kwantowa”, PWN, 1983.

+ wybrane artykuły w czasopismach „Postępy Fizyki”, „Świat Nauki”,
strony internetowe, itp..

 W. Demtröder „Spektroskopia laserowa”, PWN, 1993.

 Bernard Ziętek, „OPTOELEKTRONIKA”, Wyd.UMK, Toruń
2004

Wojciech Gawlik – Struktury Atomowe i Molekularne,
2005/06 , Wykład 1

3/20

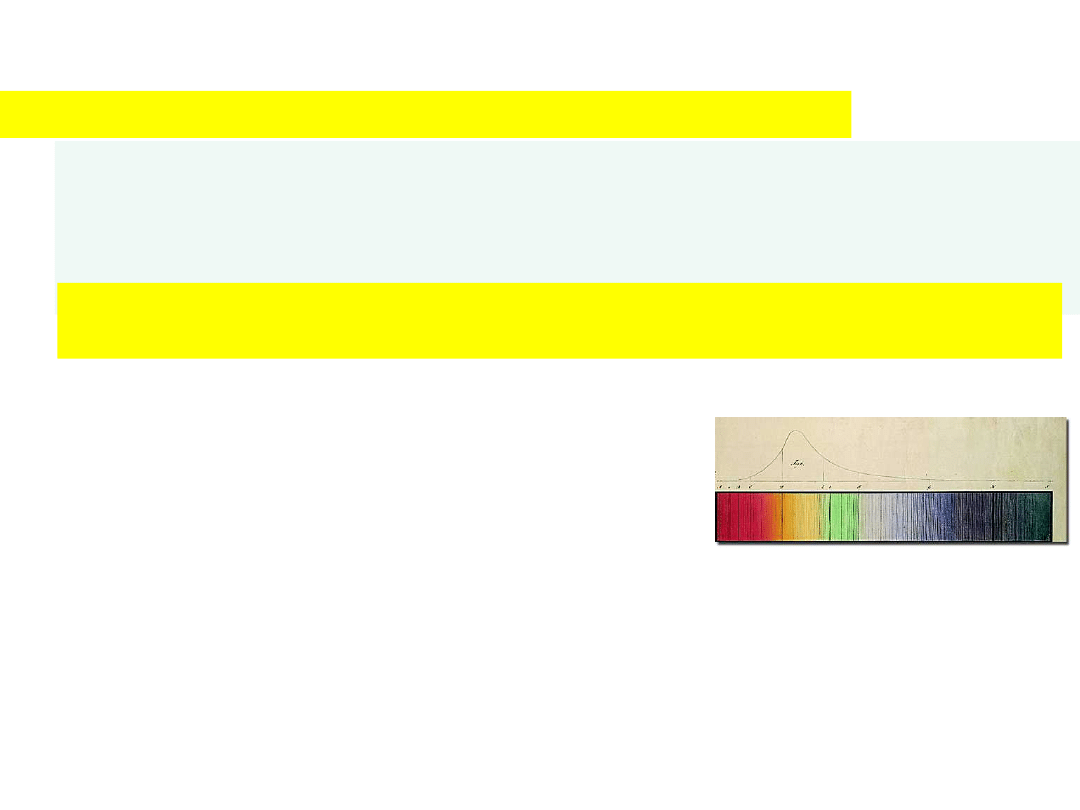
W

W

idmo wod

idmo wod

oru

oru

obserwacje:

1802 Wollaston, 1814 Fraunhofer – widmo słoneczne
1884 Balmer – 4 linie z widma Fraunhofera;



= (9/5)k, (4/3)k, (25/21)k, (9/8)k,

gdzie

k=364,56 nm



serie widmowe



= 1/  = (1/4 – 1/n

2

)

1889 Rydberg



= C(1/n

2

– 1/m

2

)

Geneza

Geneza

rozwoju f

rozwoju f

izyki

izyki

atomowej

atomowej

- poszukiwanie wytłumaczenia danych doświadczalnych

(analiza widmowa: 1817 - linie Fraunhofera w widmie słonecznym,

dyskretne widma źródeł światła laboratoryjne i

astronomiczne)

- rozwój techniki pomiarowej (nowe dane):

pryzmat (Newton), spektrometry: pryzmat., siatkowe (1817 -
Fraunhofer), interferometry, lasery, ...

Wojciech Gawlik – Struktury Atomowe i Molekularne,
2005/06 , Wykład 1

4/20

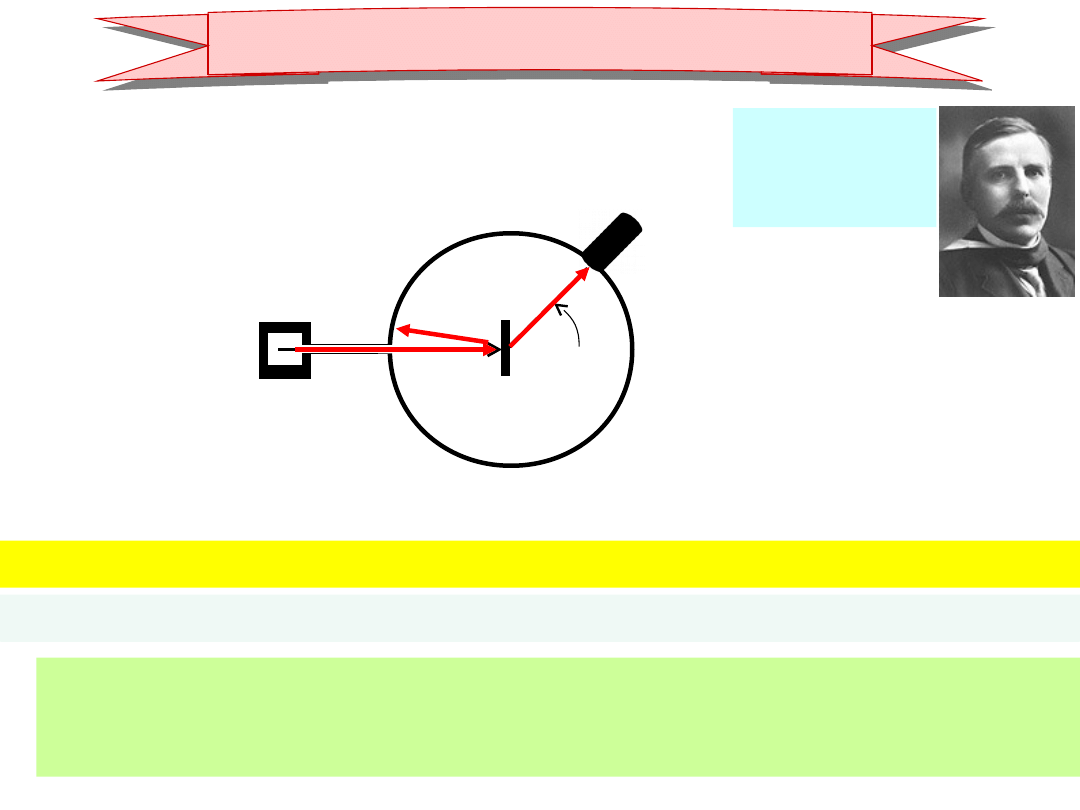
dośw. Ernsta Rutherforda
(~1910)

1871-1937
Nobel 1908
(Chemia)

źródło cząstek 

(jądra He)



detektor cząstek 

Folia metal.

• rozproszenie:
cząstka naładowana  odpychające oddziaływanie kulombowskie

• silne wsteczne rozprosz.  silne oddz. silne polaładunek ~ punktowy

• brak odrzutu atomów folii  ładunki rozpraszające w ciężkich „obiektach”





~ cała materia folii skupiona w ciężkim jądrze
atomy = ciężkie jądra naładowane dodatnio o b. małych rozmiarach

(~ 10

-14

m << rozmiar atomu ~ 10

-10

m )

Pocz

Pocz

ą

ą

tek

tek

„

„

nowo

nowo

ż

ż

ytnej

ytnej

”

”

f. atomowej

f. atomowej

Wojciech Gawlik – Struktury Atomowe i Molekularne,
2005/06 , Wykład 1

5/20

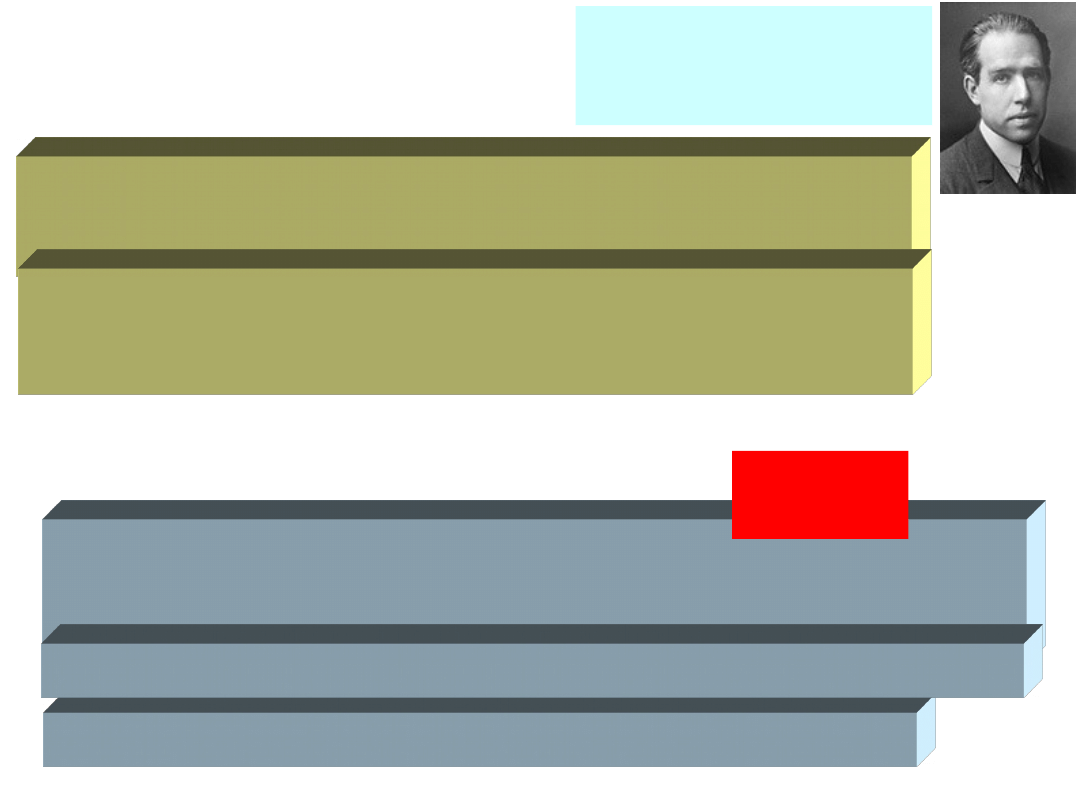
model

model

Bohra:

Bohra:

1913

1913

-

-

.

1  stacjonarne stany elektronu w atomie, w

których elektron nie promieniuje; mr=nħ

(ħ=h/2)

2. zmiana stanu zachodzi skokowo przez

absorpcję (emisję) promieniowania o częstości
=(E

1

-E

2

)/h

konsekwencje:

 





n

n

= Z





0

0

/n

n





0

0

= e

2

/ħ

 

E

E

n

n

= - (Z

2

/n

n

2

2

K

K

2

2

)E

I

E

I

=

K

Kme

4

/2ħ

2

= en. jonizacji = 13,6

eV

stała Rydberga:

R

R =

K

K

2

2

me

4

/2ħ

2

r

r

n

n

= n

n

2

2

a

a

0

0

/Z

a

a

0

0

= ħ

2

/me

2

= 0,052 nm (0,52 Å)

Niels Bohr (1885-

1967)

Nobel 1922

K

K 1/

(4

0

)

Postulaty:

Wojciech Gawlik – Struktury Atomowe i Molekularne,
2005/06 , Wykład 1

6/20

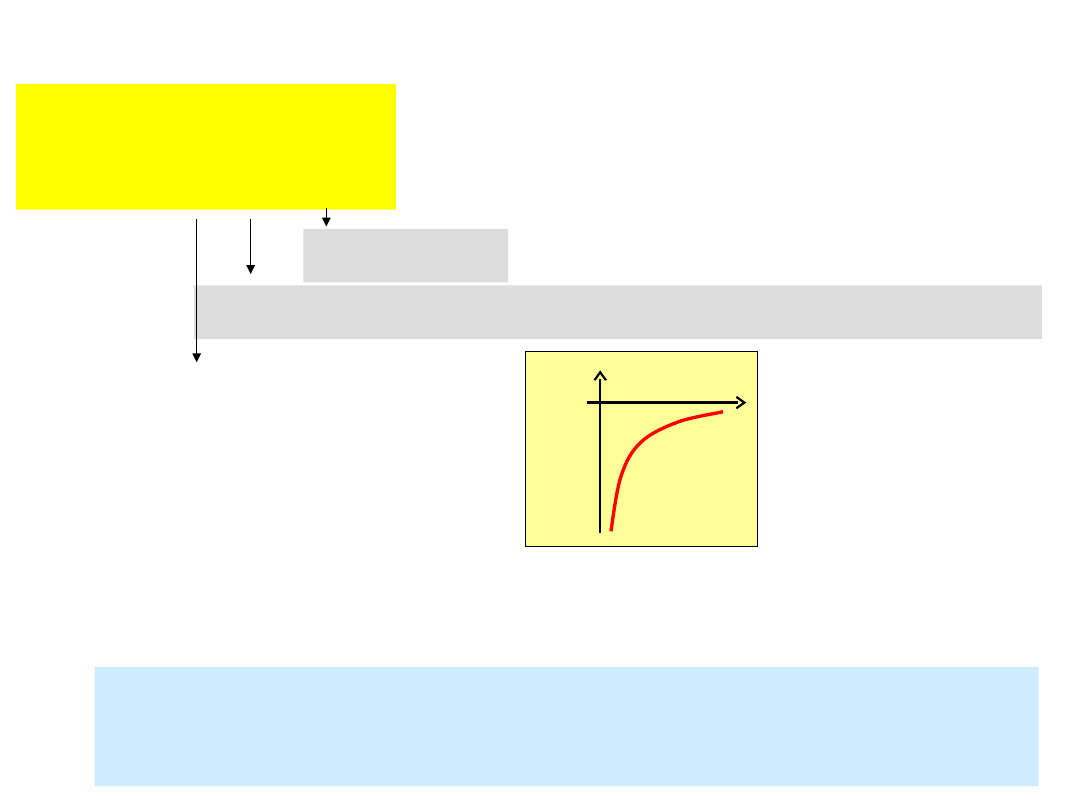
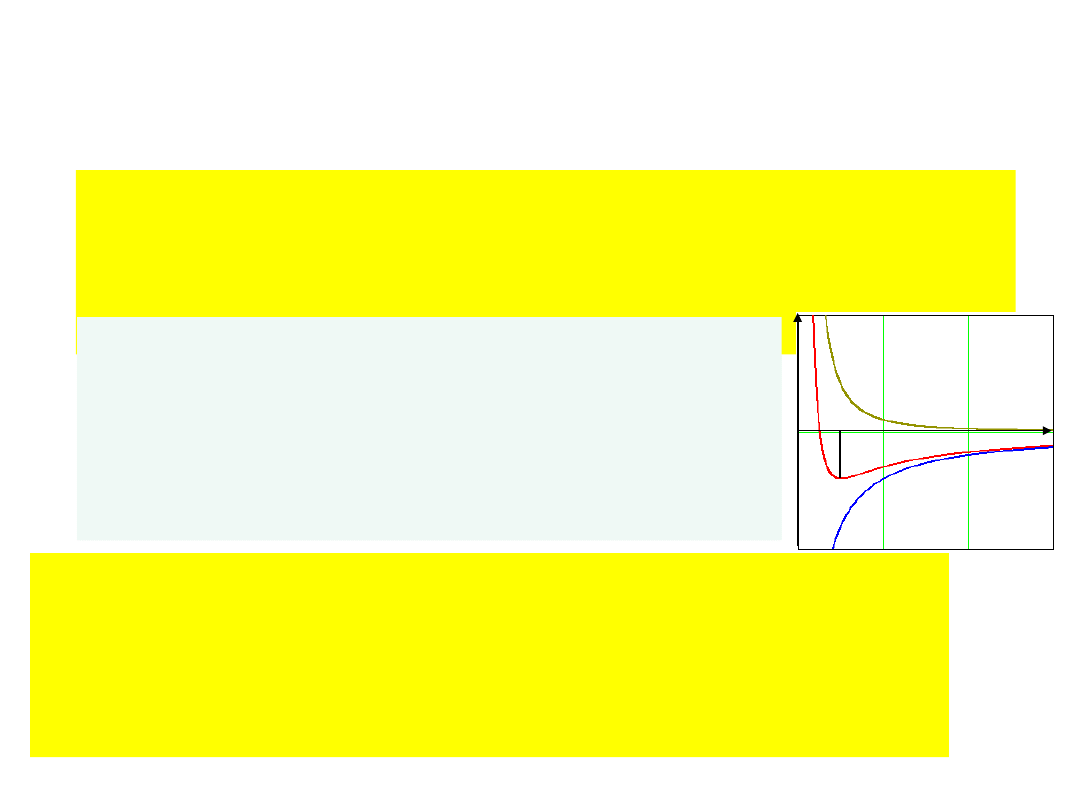
sens poziomów

Bohra





postulat Bohra nie tłumaczy stabilności

atomów

jako stanów stacjonarnych

(odpowiadających minimum
energii)

klasycznie
całkowita
energia E = T

klas

+ V

klas

T

klas

= ½ m

2

=

|

równowaga sił:

m

2

/r

0

= e

2

/r

0

| = ½ e

2

/r

0

E = - ½ e

2

/r

0

V

klas

= - e

2

/r

0

E(r

0

)

0

.

 głęboki dół potencjał
– elektron spada na jądro!

Wojciech Gawlik – Struktury Atomowe i Molekularne,
2005/06 , Wykład 1

7/20

V= -e

2

/r

najkorzystniej gdy r  0 ,

Stabilność atomu wg. mechaniki
kwantowej:

 ale relacja nieokreśloności wymaga, że gdy el.
zlokalizowany w
obszarze o promieniu r

0

, r  r

0

, p  ħ/r

0

(niezerowy

pęd)

 gdy pęd niezerowy, niezerowa en.
kinetyczna

T  T

min

= (p)

2

/2m =

ħ

2

/2mr

0

2



E = T + V

minimum E

min

= T

min

+ V występuje dla r

0

= ħ

2

/me

2

= a

0

stabilny atom



T

min

V

r

0

a

0

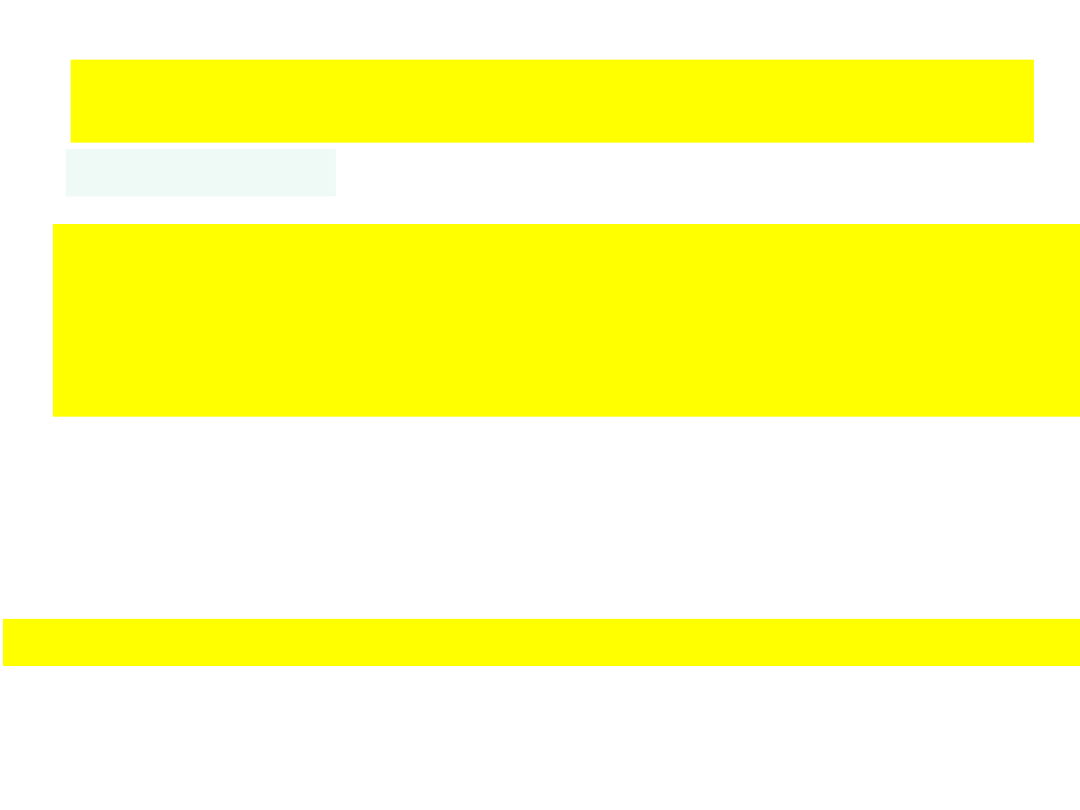
Wojciech Gawlik – Struktury Atomowe i Molekularne,
2005/06 , Wykład 1

8/20

 z mechaniki kwantowej wiemy, że r p  ħ

aby klasyczne orbity i kręt miały sens trzeba p << p, r << r,

czyli (r/r)(p/p)

<< 1

postulaty Bohra
sprzeczne

z dotychczasową fizyką

elektron krążący emituje (przyspieszane ładunki promieniują

)

i powinien spaść na jądro

sprzeczność









ale r p  ħ  (r p)/rp  ħ/rp

mvr = pr = nħ

, czyli (r p)/rp  1/n

 nie można mówić o zlokalizowanych orbitach (w sensie klas.)

(chyba że n>>1 – stany
rydbergowskie)

- pojęcie orbity

?

?

Wojciech Gawlik – Struktury Atomowe i Molekularne,
2005/06 , Wykład 1

9/20

Mechanika kwantowa o poziomach energetycznych
atomu

atomy z Z elektronami w mechanice kwantowej

H

CM

=p

2

/2 - K Ze

2

/r

 m

e

M/(m

e

+M), K 1/(4

0

)

C/r

C/r potencjał kulombowski i centralny

+ 2/ħ(E-C/r)

0

• z założenia centralności
możliwość faktoryzacji na część radialną i kątową

r,R(r)Y()

• warunki rozwiązalności  3 liczby kwantowe:

n

= 1, 2, ...

l = 0, 1, 2, ..., n-1

-l  m l

równ. Schrödingera:

Wojciech Gawlik – Struktury Atomowe i Molekularne,
2005/06 , Wykład 1

10/20

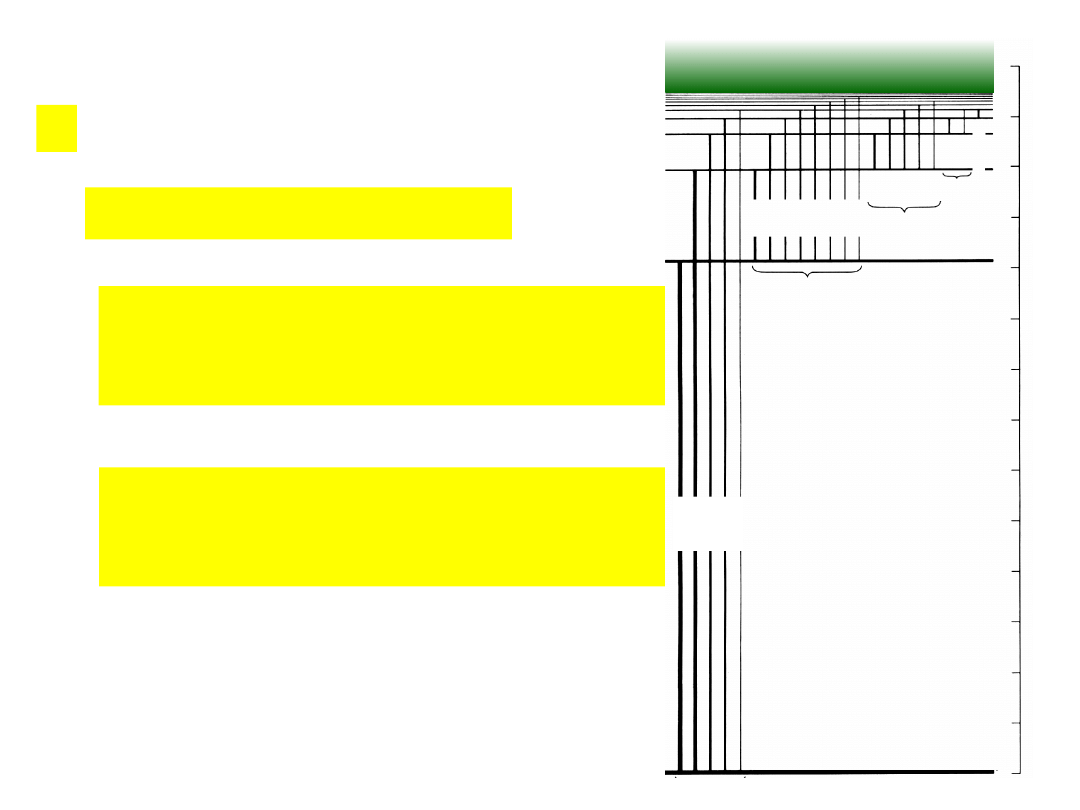
n rozwiązanie części radialnej:

E

n

=-C

2

/2 ħ

2

n

2

=-Z

2

/n

2

Rhc

R =

K

2

me

4

/2ħ

2

- stała Rydberga

(najdokładniej wyznaczona stała
fundamentalna)

Rhc = 13,6 eV - energia jonizacji
atomu wodoru w stanie
podstawowym

14 eV

10

5

0

1

2

1

,

5

1

0

2

,

6

9

7

3

9

5

0

9

3

8

6

5

6

,3

4

8

6

4

3

4

4

1

0

3

9

7

3

8

9

3

8

3

,5

3

8

0

1

8

7

5

1

2

8

2

1

0

9

4

1

0

0

5

9

5

4

,6 4

0

5

0

2

6

3

0

7

4

0

0

seria

Balmer

a

seria Lymana

s.

Paschen

a

B

ra

c

k

e

tt

a

P

fu

n

d

a

n=

2

n=

1

n=

3

n=

4

n=

5

n=

Fizyczna interpretacja liczb kwantowych

Wojciech Gawlik – Struktury Atomowe i Molekularne,
2005/06 , Wykład 1

11/20

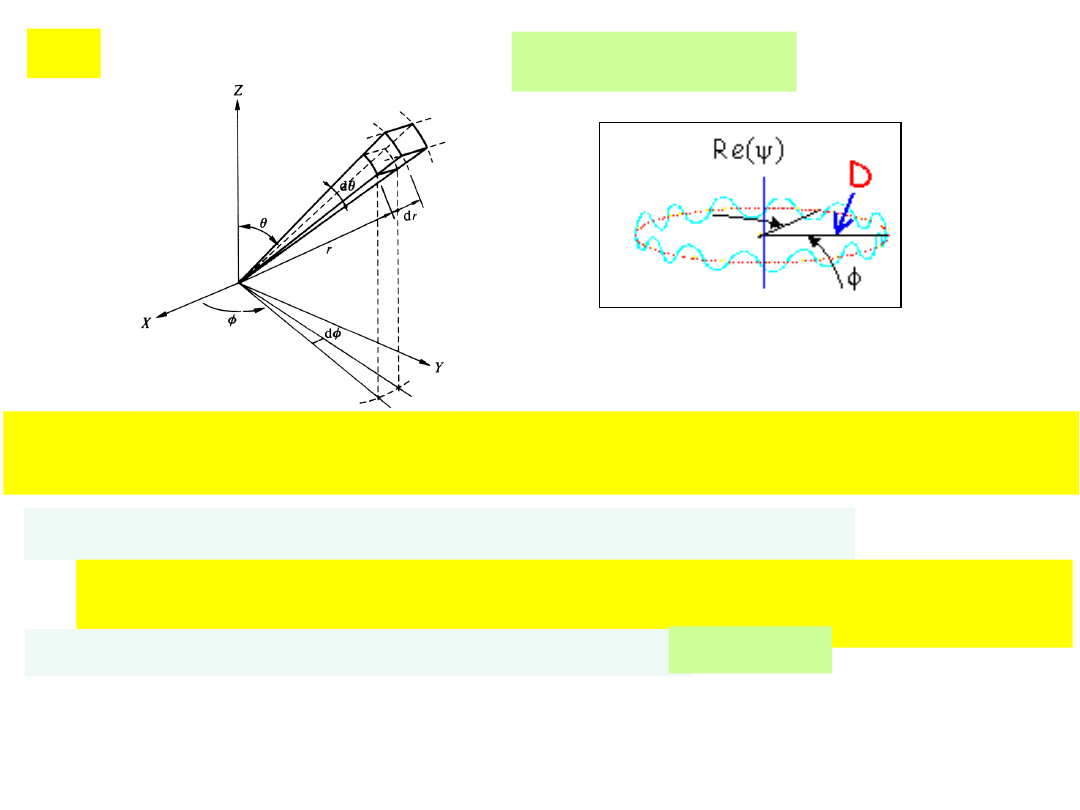
l,

m

rozwiązanie cz. kątowej:

Y

l, m

(,  )



e

im

 ciągłość f. fal. wymaga by całkowita wielokrotność 

zmieściła się na obwodzie orbity (prom. D) kwantyzacja: 2D=m

 dł. fal materii (de Broglie) =h/p

t

(p

t

- skł. styczna p)p

t

D = L

z

= mħ

skł. krętu może mieć tylko wartości skwant.: L

z

=0, ħ, 2ħ,

3ħ, ...

 skwantowana też długość L (wartość L

2

): l(l +1) ħ

2

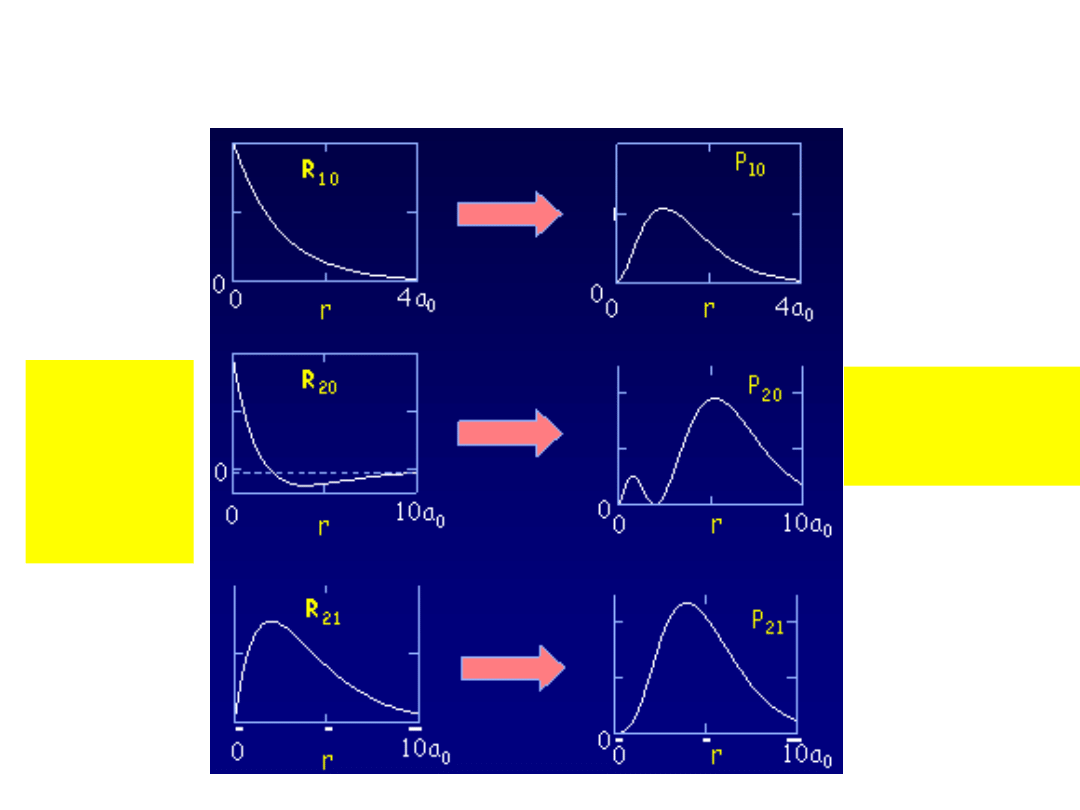
Wojciech Gawlik – Struktury Atomowe i Molekularne,
2005/06 , Wykład 1

12/20

Funkcje falowe

liczba
przejść
R

nl

przez

zero=n-

l

-

1

prawdopod.
radialne
P(r)dr=|R|

2

r

2

dr

a) radialne

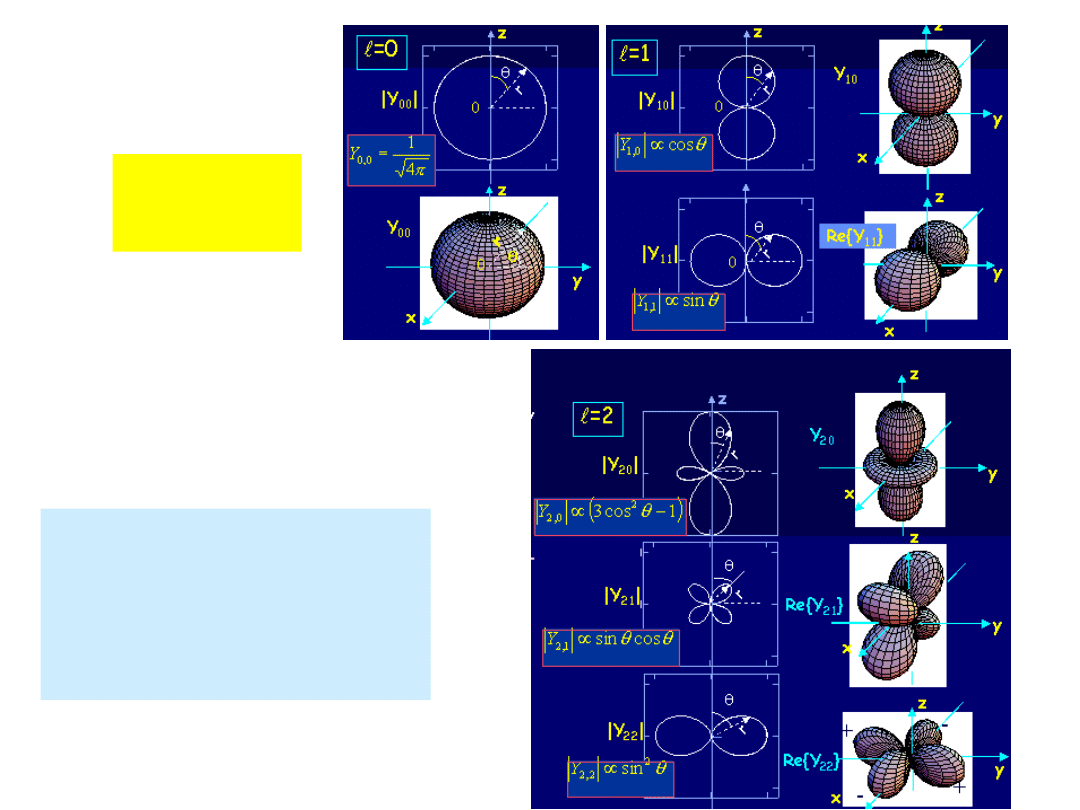
Wojciech Gawlik – Struktury Atomowe i Molekularne,
2005/06 , Wykład 1

13/20

Funkcje falowe

P()=|

Y()|

ważne dla zachowania
się atomów w
zewnętrznych polach i
dla zrozumienia
symetrii cząsteczek

b) kątowe

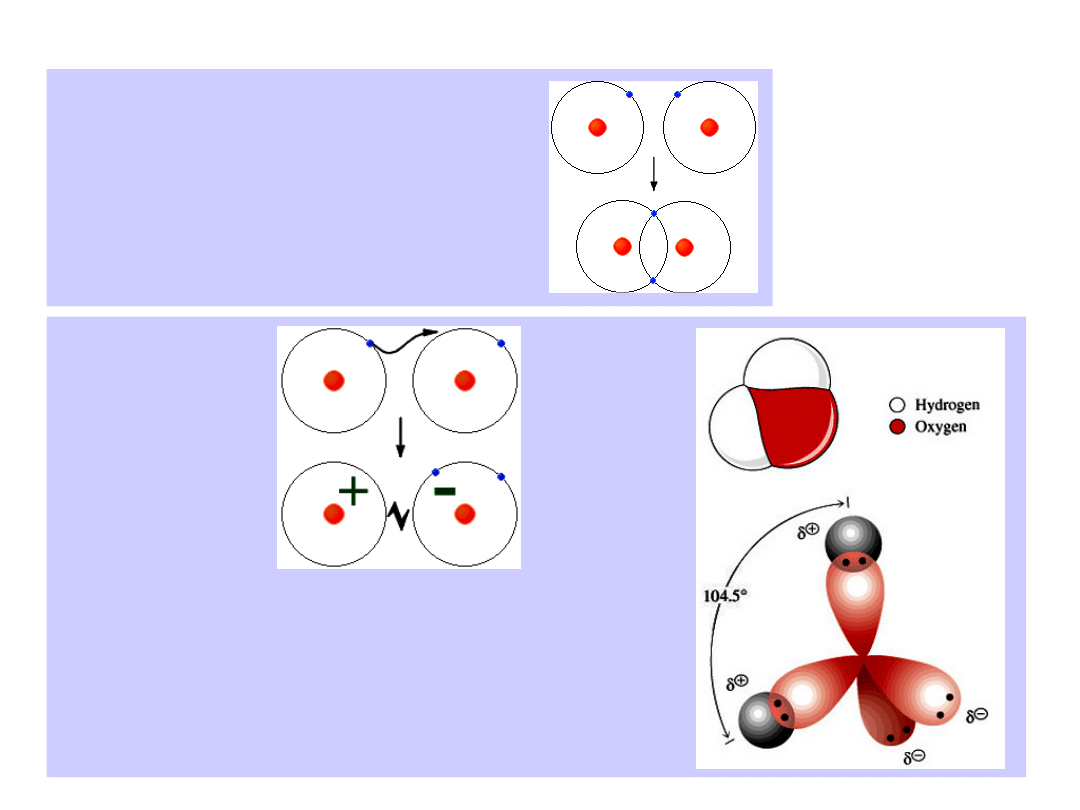
Wojciech Gawlik – Struktury Atomowe i Molekularne,
2005/06 , Wykład 1

14/20

Wiązania chemiczne

a) kowalencyjne (np. H

2

+

, H

2

)

b) jonowe

przykład: H

2

O