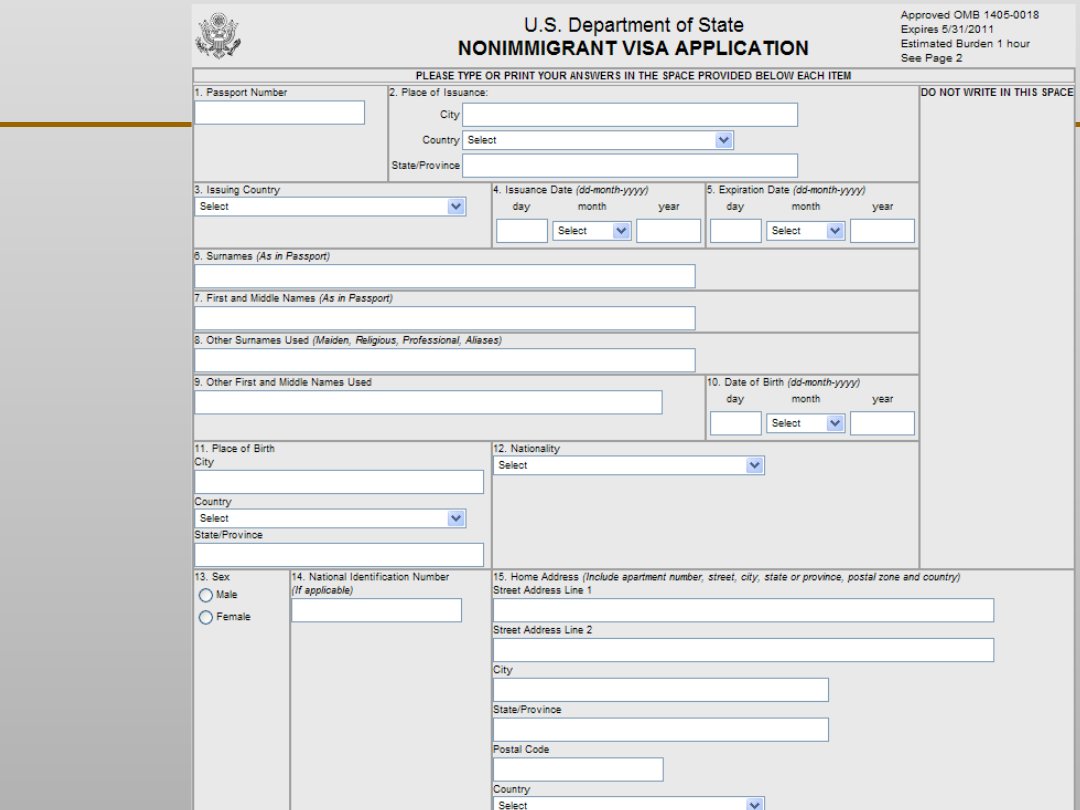
VII EKSPLORACJA DANYCH

Drzewa decyzyjne …

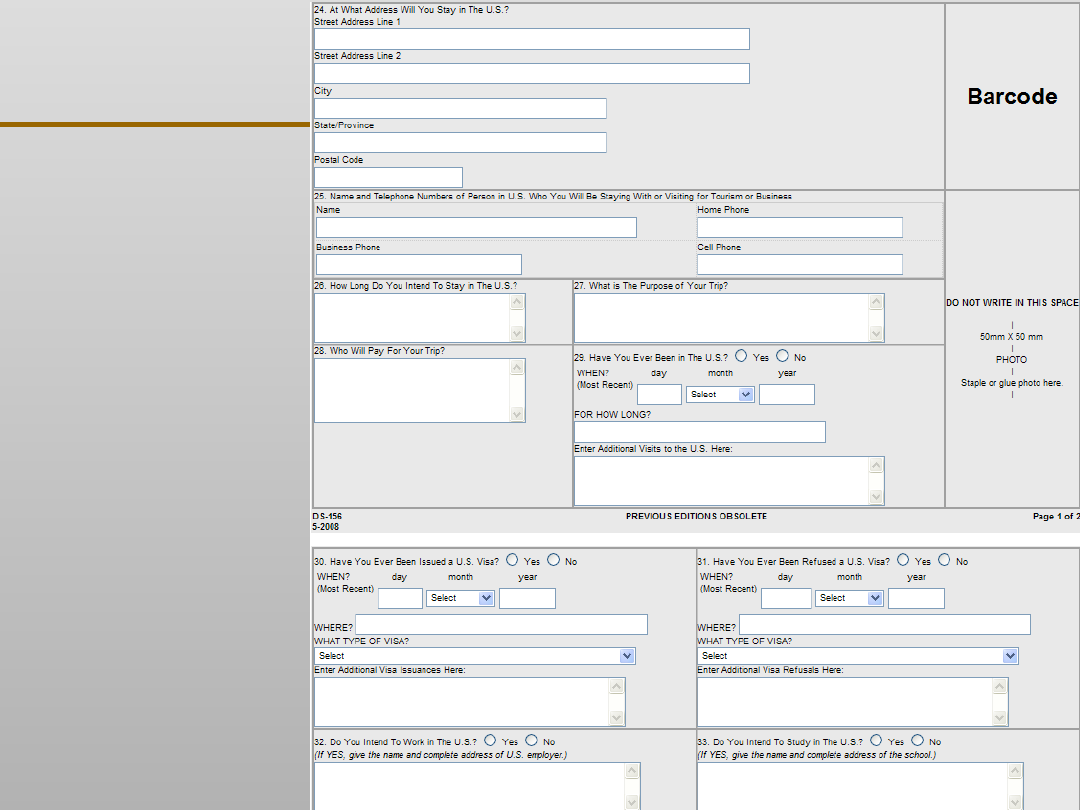
VII EKSPLORACJA DANYCH

Drzewa decyzyjne …

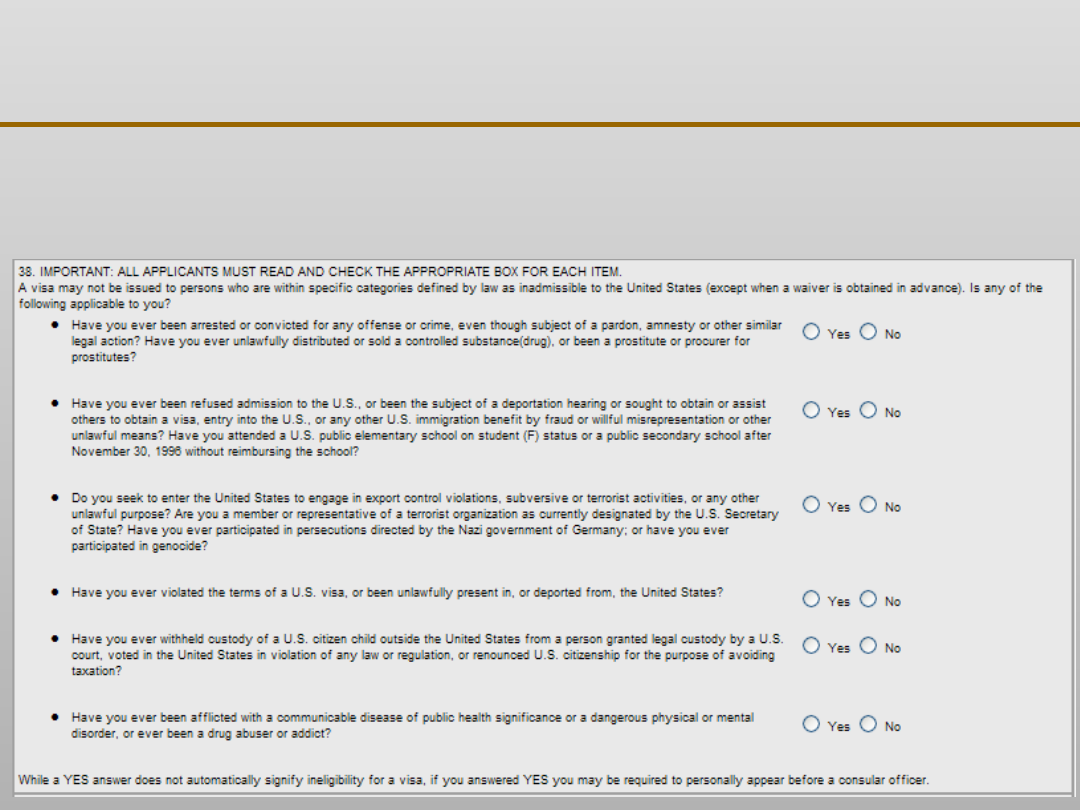
VII EKSPLORACJA DANYCH

Drzewa decyzyjne …

VII EKSPLORACJA DANYCH

Drzewa decyzyjne …

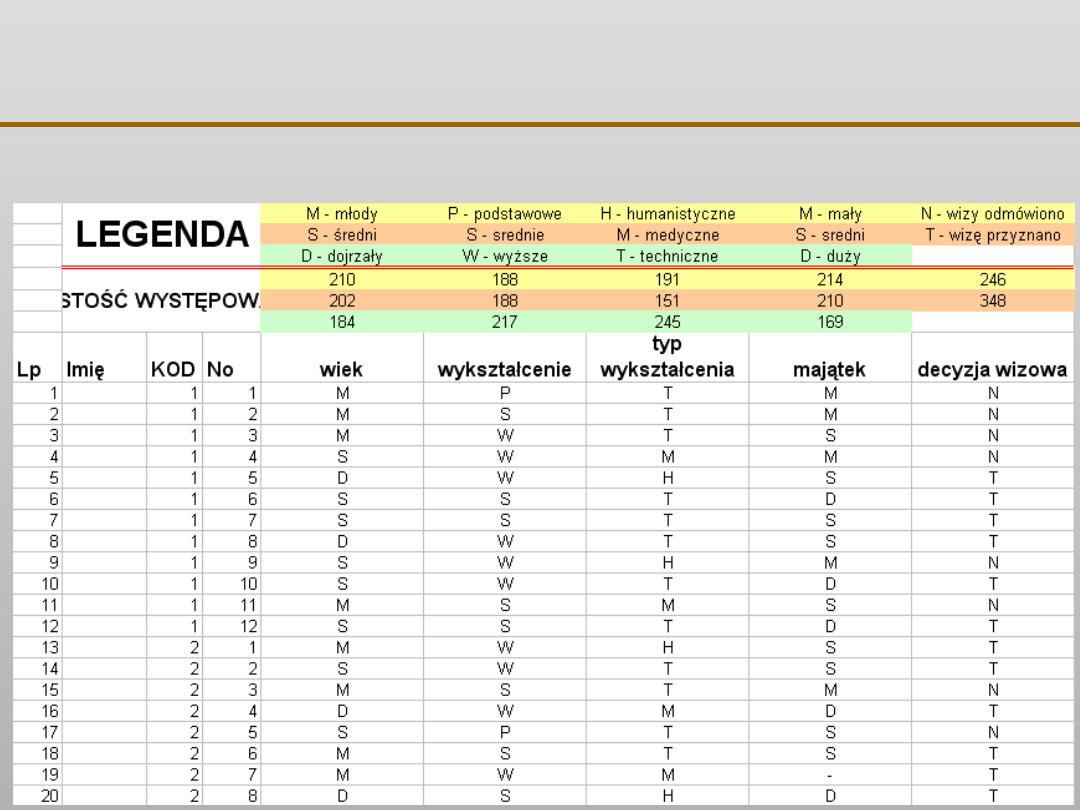
VII EKSPLORACJA DANYCH

Drzewa decyzyjne …

VII EKSPLORACJA DANYCH

Jak drzewa decyzyjne wybierają atrybut
dzielący:

Drzewa decyzyjne starają się stworzyć zbiór liści,
które są najczystsze, tzn. takie które zawierają
jak najwięcej rekordów należących do tej samej
klasy. W ten sposób drzewa decyzyjne
zapewniają przypisanie do klasy z największą
miarą ufności.

Metod określania jednorodności będącej miarą
czystości liści jest wiele, a dwie
najpopularniejsze to:

Algorytm drzew klasyfikacyjnych i regresyjnych

CART

Algorytm C4.5

VII EKSPLORACJA DANYCH

Algorytm drzew klasyfikacyjnych CART

Φ

(s│t) = 2 P

L

P

P



(s│t)

gdzie:



(s│t) =

Σ

│

P(j│t

L

) – P(j│t

P

)

│

VII EKSPLORACJA DANYCH

Algorytm drzew klasyfikacyjnych CART

P

L

=

liczba rekordów w t

L

liczba rekordów w zbiorze uczącym

P

P

=

liczba rekordów w t

P

liczba rekordów w zbiorze uczącym

Φ

(s│t) = 2 P

L

P

P



(s│t)

VII EKSPLORACJA DANYCH

Algorytm drzew klasyfikacyjnych CART



(s│t) =

Σ

│

P(j│t

L

) – P(j│t

P

)

│

P(j│t

L

) =

liczba rekordów należących do klasy j w t

L

liczba rekordów w t

P(j│t

P

) =

liczba rekordów należących do klasy j w t

P

liczba rekordów w t

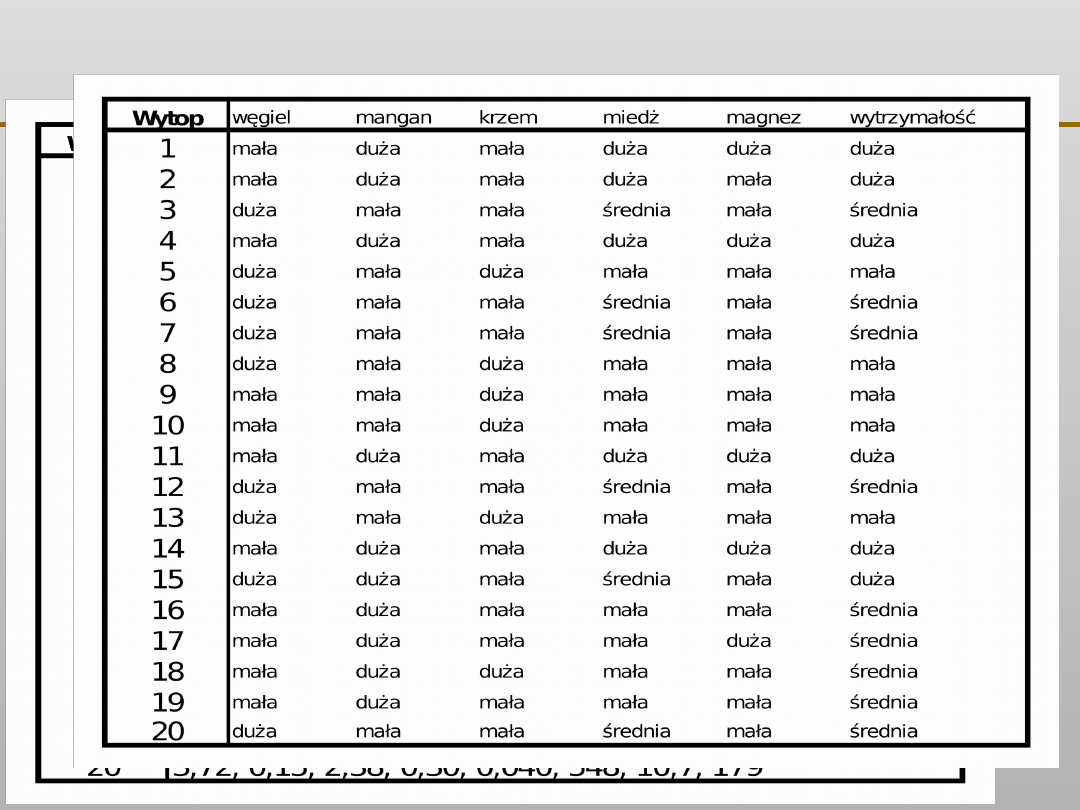
VII EKSPLORACJA DANYCH

Algorytm drzew klasyfikacyjnych CART

VII EKSPLORACJA DANYCH

Algorytm drzew klasyfikacyjnych CART

Podział Lewe poddrzewo

Prawe poddrzewo

1

zawartość węgla = mała

zawartość węgla = duża

2

zawartość manganu = mała zawartość manganu = duża

3

zawartość krzemu = mała

zawartość krzemu = duża

4

zawartość miedzi = mała

zawartość miedzi  {średnia, duża}

5

zawartość miedzi = średnia zawartość miedzi  {mała, duża}

6

zawartość miedzi = duża

zawartość miedzi  {mała, średnia}

7

zawartość magnezu = mała zawartość magnezu = duża

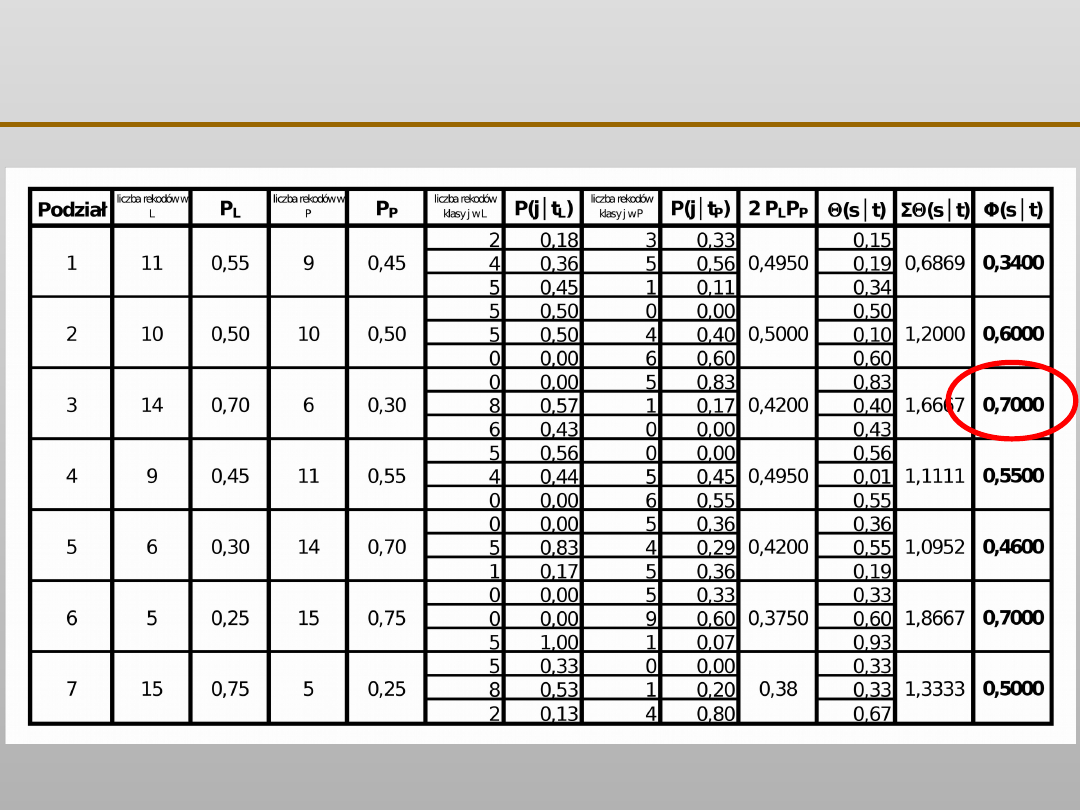
VII EKSPLORACJA DANYCH

Algorytm drzew klasyfikacyjnych CART

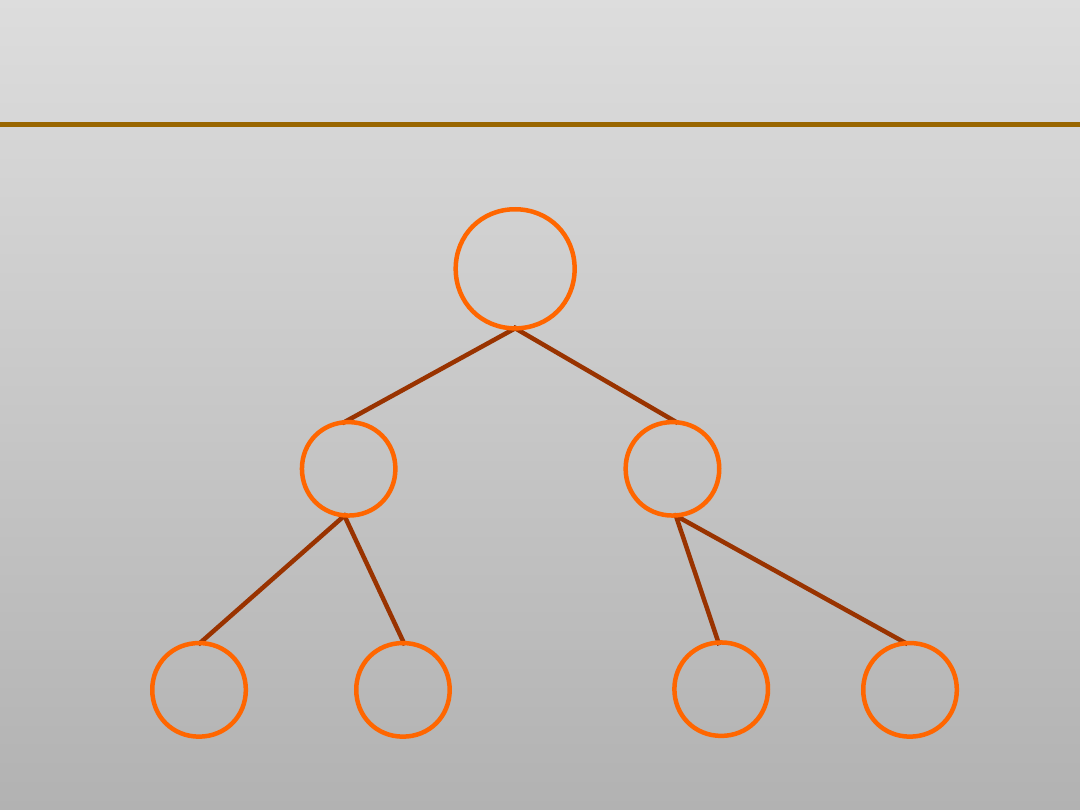
VII EKSPLORACJA DANYCH

Algorytm drzew klasyfikacyjnych CART

R

N

N

L

L

N

L

zawartość Si

5 mała, 1 średnia
zawartość Mn

duża 6

mała 14

8 średnia, 6 duża
zawartość Mn

duża 9

mała 5

5 średnia3 średnia, 6 duża

duża 1

mała 5

5 mała

1 średnia

VII EKSPLORACJA DANYCH

Algorytm C 4.5

Algorytm ID3 jest jednym z algorytmów

operujących

na

drzewach

decyzyjnych,

opracowanym w 1986 roku przez Rossa Quinlana.
Cechą charakterystyczną algorytmu jest wybór
atrybutów, dla których kolejno przeprowadzane są
testy pozwalające, by końcowe drzewo było jak
najprostsze i jak najefektywniejsze. Wybór atrybutu
bazuje na liczeniu entropii. Algorytm C4.5 jest
rozwinięciem algorytmu ID3 opracowanym w 1993
roku również przez Quinlana.

VII EKSPLORACJA DANYCH

Algorytm C 4.5

•

Algorytmy C4.5 nie jest ograniczony do

binarnych podziałów. Podczas, gdy CART tworzy
drzewo binarne, C4.5 tworzy drzewo o bardziej
zróżnicowanym kształcie.

•

Dla zmiennych jakościowych algorytm C4.5 z

definicji tworzy osobne gałęzie dla każdej wartości
atrybutu jakościowego. Może to powodować
nadmierne rozgałęzienie.

•

Metoda mierzenia jednorodności w

algorytmie C4.5 jest zupełnie inna niż w
algorytmie CART i używa pojęcia zysk informacji
lub redukcja entropii.

VII EKSPLORACJA DANYCH

Algorytm C 4.5

H(X) = –Σ p

j

log

2

(p

j

)

Dla zmiennej X przyjmującej k możliwych
wartości z prawdopodobieństwem p
odpowiednio p

1

, p

2

, …p

i

, można zdefiniować

wielkość nazwaną entropią X określoną
wzorem:

VII EKSPLORACJA DANYCH

Algorytm C 4.5

Dla założenia, że możliwy jest podział S,
dzielący zbiór T na kilka podzbiorów T

1

, T

2

, …

T

k

, wówczas ważona suma entropii dla

pojedynczych podzbiorów określona jest
wzorem:

H

S

(T) = Σ P

i

H

S

(T

i

)

i=1

k

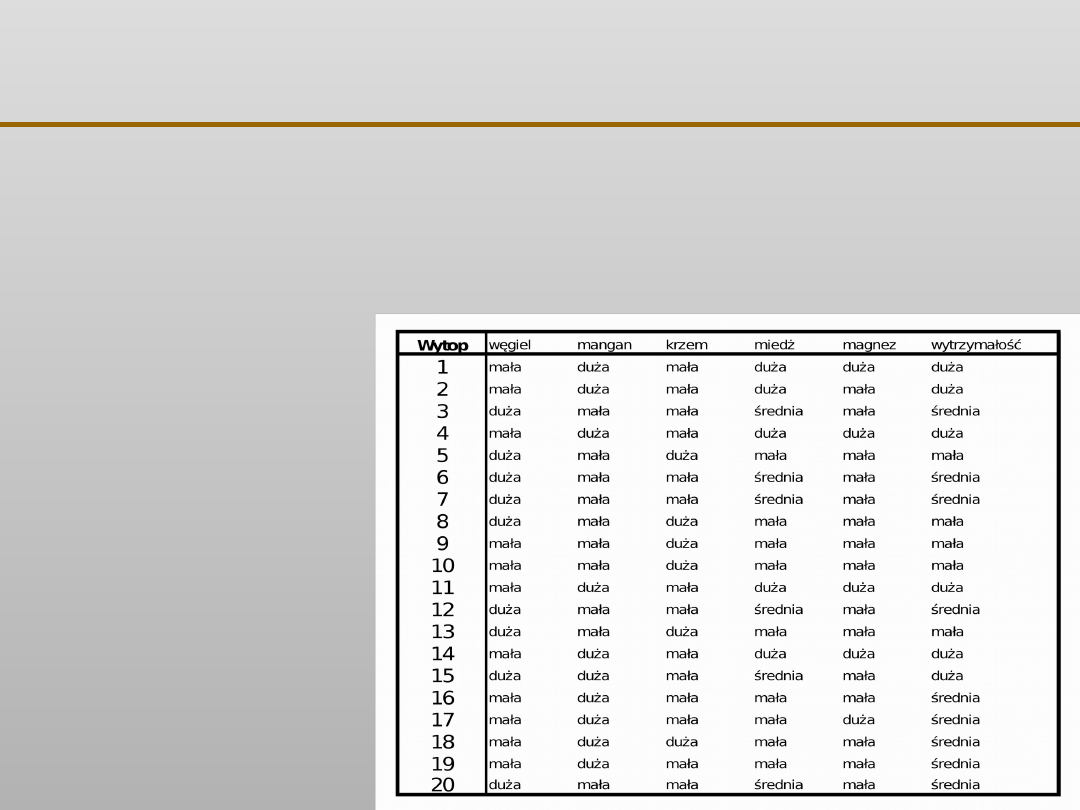
VII EKSPLORACJA DANYCH

H(X) = –Σ p

j

log

2

(p

j

)

H

S

(T) = Σ P

i

H

S

(T

i

)

i=1

k

VII EKSPLORACJA DANYCH

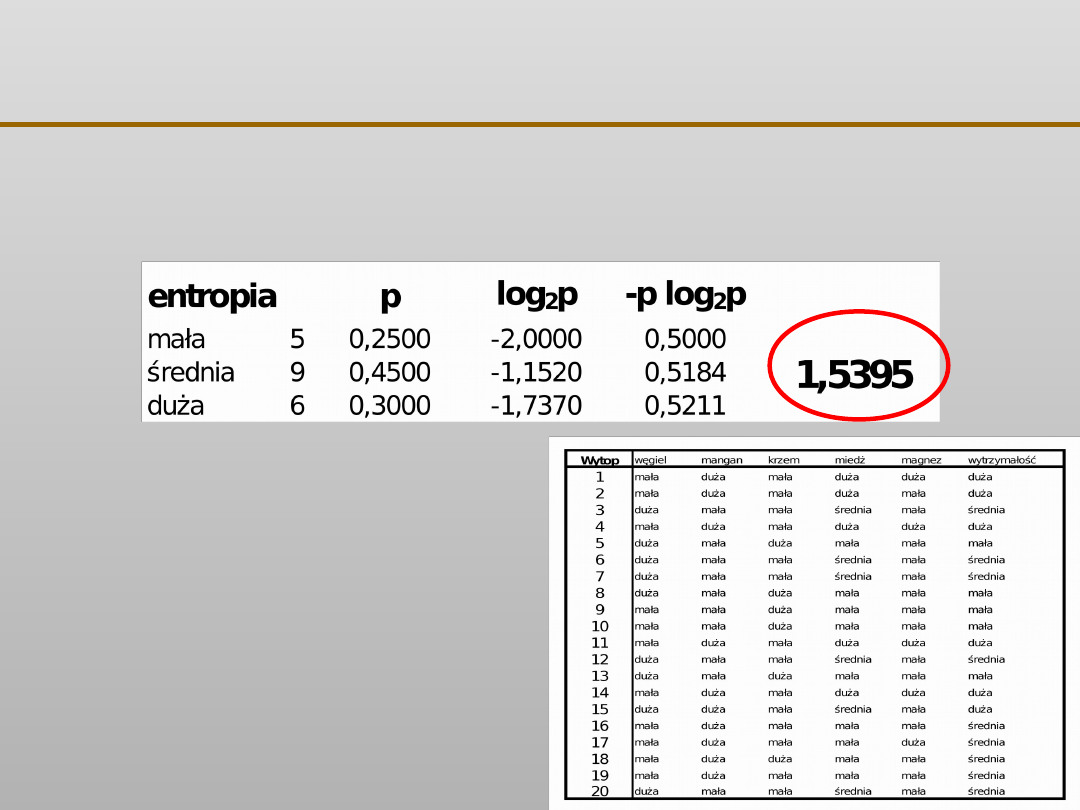
H(X) = –Σ p

j

log

2

(p

j

)

Wytrzymałość:
mała – 5
średnia – 9
duża – 6

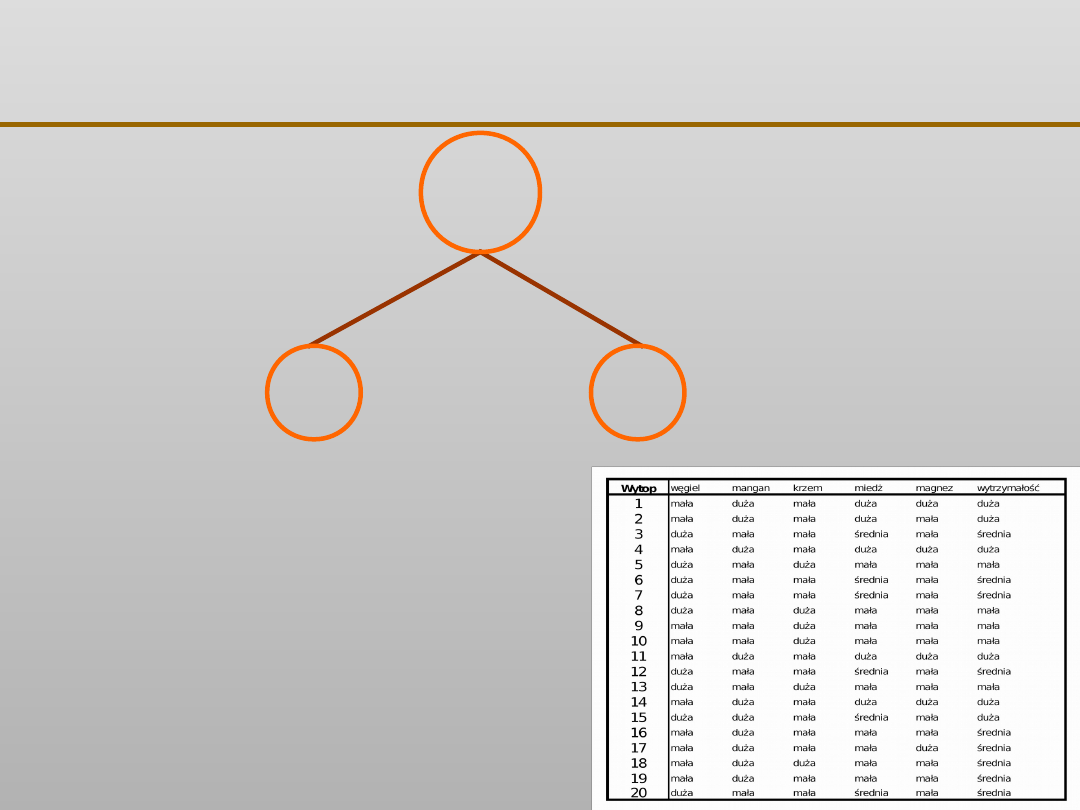
VII EKSPLORACJA DANYCH

R

N

N

zawartość C

3 mała,
5 średnia,
1 duża

duża 9

mała 11

2 mała,
4 średnia,
5 duża

VII EKSPLORACJA DANYCH

R

N

N

zawartość C

3 mała,
5 średnia,
1 duża

duża 9

mała 11

2 mała,
4 średnia,
5 duża

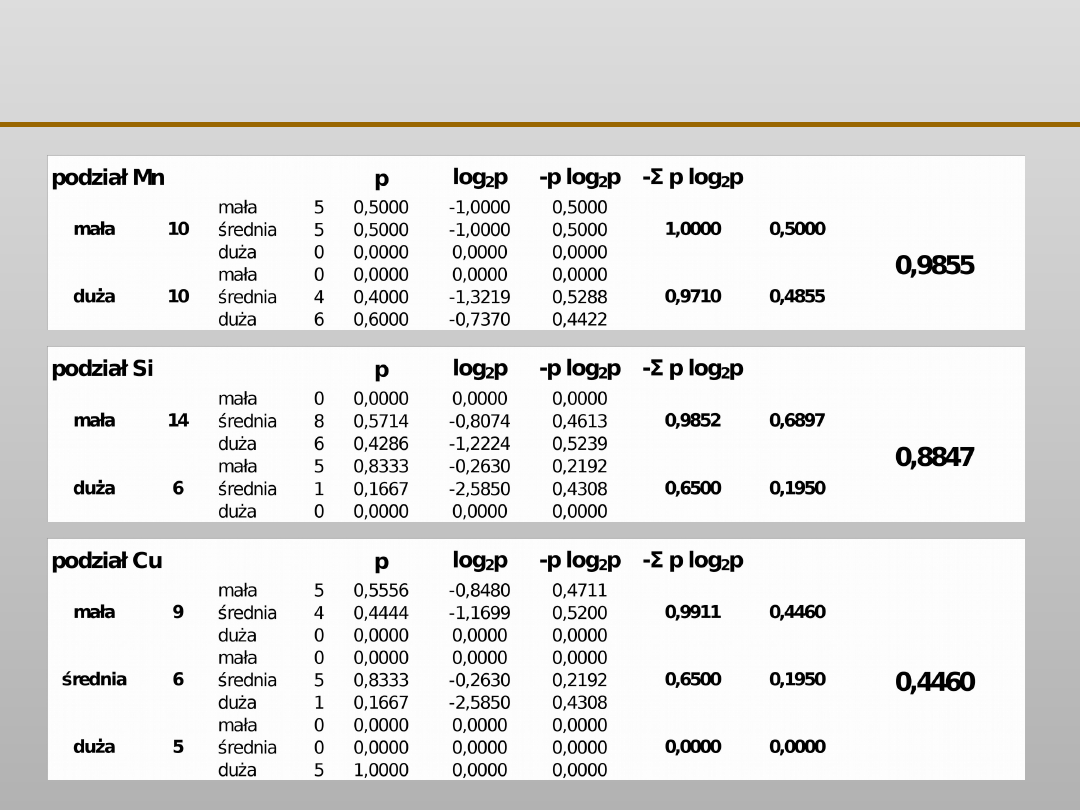
VII EKSPLORACJA DANYCH

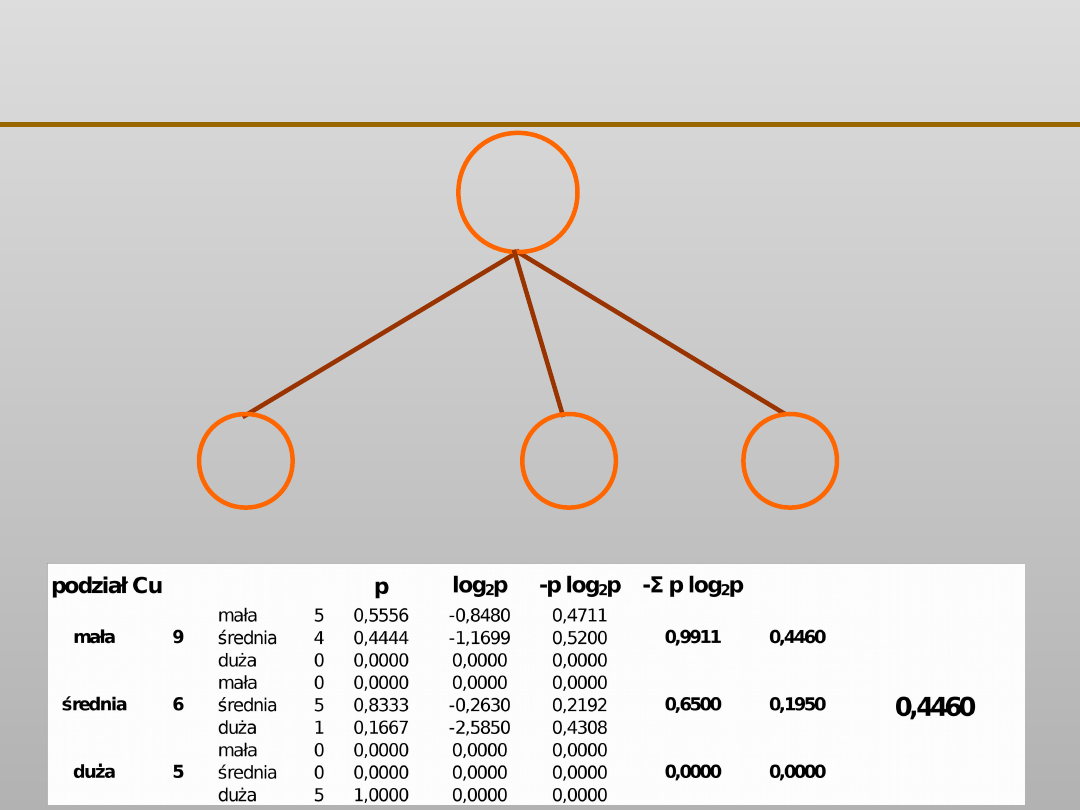
VII EKSPLORACJA DANYCH

R

N

N

zawartość Cu

0 mała,
0 średnia,
5 duża

duża 5

mała 9

5 mała,
4 średnia,
0 duża

N

0 mała,
5 średnia,
1 duża

średnia 6

VII EKSPLORACJA DANYCH

Wady drzew decyzyjnych

•

im więcej klas oraz im bardziej się one

nakładają,

tym większe drzewo decyzyjne

•

trudno zapewnić jednocześnie wysoką

jakość

klasyfikacji i małe rozmiary drzewa

•

w węzłach testowany jeden

atrybut

VII EKSPLORACJA DANYCH

Wady drzew decyzyjnych nadmierne
dopasowanie

•

nadmierne uczenie prowadzi do

dopasowania także do zaszumionych danych

•

zbudowane drzewo dobrze radzi sobie z

danymi ze zbioru uczącego i źle z danymi ze
zbioru testującego

•

drzewo ma niską zdolność do generalizacji

dla nowych danych

VII EKSPLORACJA DANYCH

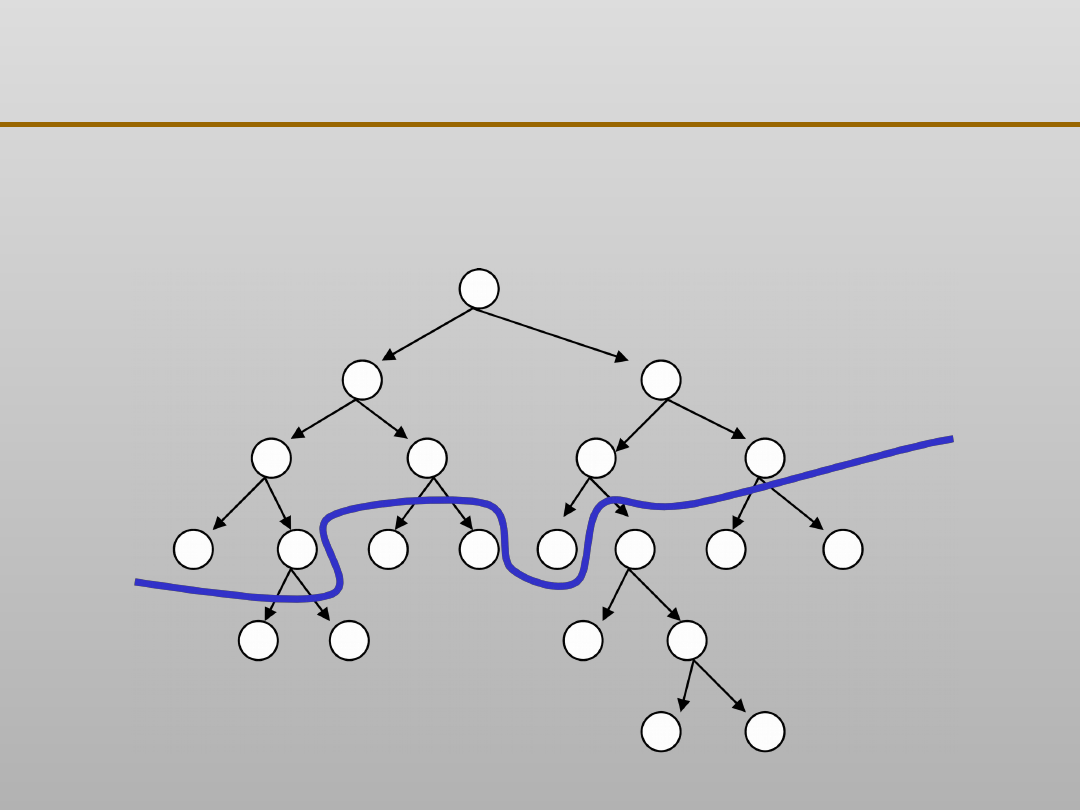
Unikanie nadmiernego dopasowania: dlaczego ?

VII EKSPLORACJA DANYCH

Unikanie nadmiernego dopasowania: przycinanie

dead
branc
h

codominant
stems

included
bark

dead
branch

water
sprouts

broken
branch

decay

sucke
r

Źródło:
Vancouver Urban Forestry
www.cityofvancouver.us/urbanforestry

VII EKSPLORACJA DANYCH

Unikanie nadmiernego dopasowania: przycinanie

VII EKSPLORACJA DANYCH

Unikanie nadmiernego dopasowania: dlaczego ?

Czy przycinanie poprawia dokładność:

•

w większości przypadków TAK,

•

ale efekty zależą od obszaru

zastosowania

VII EKSPLORACJA DANYCH

Unikanie nadmiernego dopasowania: metody

Przycinanie drzew może być

prowadzone na dwa sposoby:

•

pre – pruning (fw) polegający na

zatrzymaniu rozrostu drzewa jeśli prowadzi
to do tworzenia węzłów i liści grupujących
nieliczne przypadki

•

post – pruning, w którym prowadzimy do

wzrostu pełnego drzewa i dopiero wówczas
dokonujemy cięć

VII EKSPLORACJA DANYCH

Unikanie nadmiernego dopasowania: metody

Pre-pruning

Post-pruning

•

pre – pruning (fw) jest uważany za rozwiązanie gorsze

•

post – pruning, wykorzystuje poddrzewa (potomków)

VII EKSPLORACJA DANYCH

Unikanie nadmiernego dopasowania: metody

Przycinanie drzew metodami post:

•

zbuduj pełne drzewo decyzyjne,

pozwalając nawet na nadmierne
dopasowanie

•

przekształć drzewo w zbiór reguł

decyzyjnych

•

przycinaj każdą regułę niezależnie od

innych

•

uporządkuj pozostałe reguły w

sekwencję zdań gotową do użycia

VII EKSPLORACJA DANYCH

Unikanie nadmiernego dopasowania: metody

Przycinanie drzew metodami post:

•

reduced error pruning REP

•

minimum error pruning

MEP

•

pessimistic error pruning

PEP

•

error - based pruning

EBP

•

cost - complexity pruning

CCP

VII EKSPLORACJA DANYCH

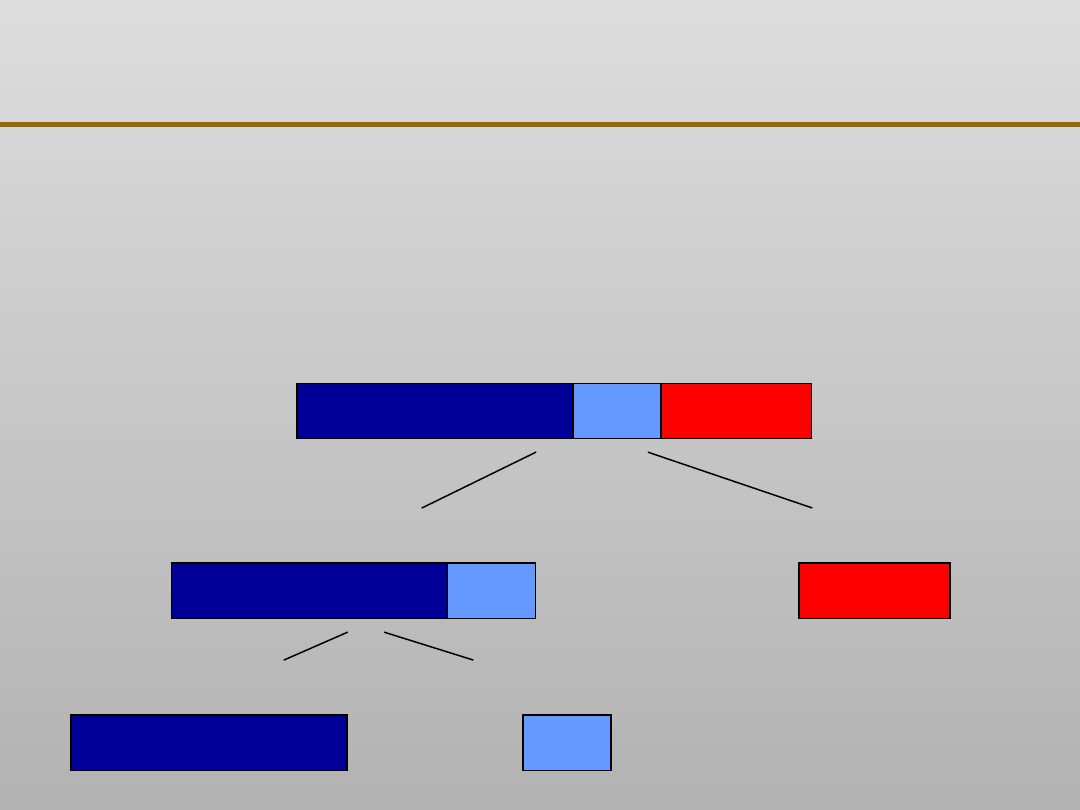
Unikanie nadmiernego dopasowania: metody

Zbiór danych

Zbiór uczący

Zbiór do wzrostu drzewa

Zbiór do przycinania drzewa

Zbiór testujący

70 %

30 %

70 %

30 %

Typowy (powszechnie stosowany) podział danych na zbiory:

VII EKSPLORACJA DANYCH

Unikanie nadmiernego dopasowania:

REP

Algorytm postępowania w metodzie

REP:

•

zbuduj drzewo korzystając z całego zbioru

uczącego

•

losowo wybierz i usuń węzeł

•

zamień węzeł w jego większościową

reprezentację

•

jeśli zmodyfikowane drzewo sprawdzane na

zbiorze testującym jest tak samo dobre lub
lepsze od drzewa podstawowego zastosuj je

•

powróć do punktu 2

VII EKSPLORACJA DANYCH

Unikanie nadmiernego dopasowania: REP,MEP,PEP

Większość algorytmów przycinania (reduced error
pruning, pessimistic error pruning, minimum error
pruning) opiera się na następującym schemacie:

repeat

przeglądaj węzły wewnętrzne drzewa T
if błąd dla poddrzewa T

t

> błąd dla liścia t

then

zastąp poddrzewo T

t

liściem

przypisz do liścia t etykietę

odpowiedniej

klasy

end if
until przycinanie zmniejsza błąd

Poszczególne metody różnią się sposobem szacowania błędu oraz
kolejnością przeglądania węzłów drzewa.