Grupowanie danych: definicja i cel

Grupowanie

oznacza

grupowanie

rekordów,

obserwacji lub przypadków w klasy podobnych
obiektów. Grupa jest zbiorem rekordów, które są
podobne do siebie nawzajem i niepodobne do
rekordów z innych grup.
Grupowanie różni się od klasyfikacji tym, że w
przypadku grupowania nie ma zmiennej celu. Zadanie
grupowania nie próbuje klasyfikować, szacować lub
przewidywać wartości zmiennej celu. Zamiast tego,
algorytm grupowania próbuje podzielić cały zbiór
danych w stosunkowo zgodne podgrupy lub grupy,
przy czym podobieństwo rekordów wewnątrz grup jest
maksymalizowane, a podobieństwo do rekordów
spoza grupy minimalizowane.

VIII EKSPLORACJA DANYCH

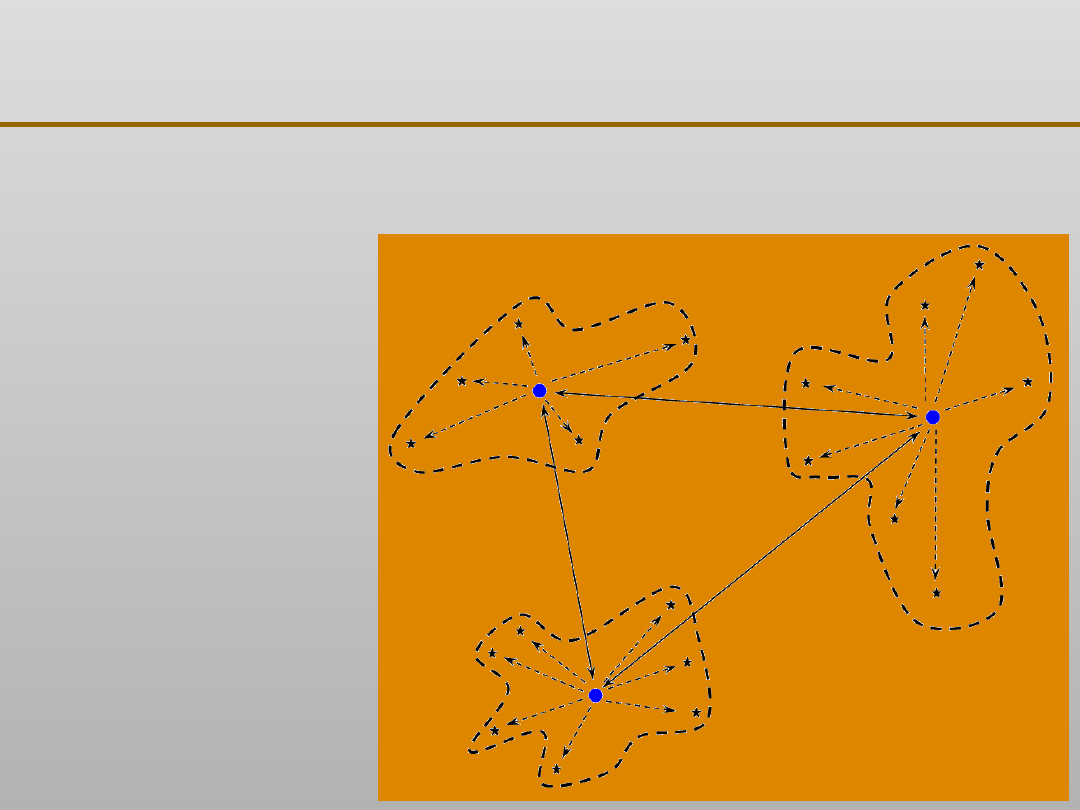
Grupowanie jest często wykorzystywane jako krok
wstępny do procesu eksploracji danych, z wynikowymi
grupami użytymi jako dane wejściowe do innej
techniki, takiej jak sieci neuronowe. Z powodu dużego
rozmiaru wielu baz danych, często jest korzystnie
najpierw

przeprowadzić

analizę

skupień,

aby

zredukować przestrzeń przeszukiwań dla algorytmów.

Grupowanie danych: definicja i cel

VIII EKSPLORACJA DANYCH

Grupowanie danych: definicja i cel

Cel grupowania:

•

znajdowanie naturalnego podziału danych na

istotne

podgrupy

•

dekompozycja danych na części, które są

łatwiejsze do

opisania – bardziej jednolite

•

poznanie rozkładu przykładów (danych)

•

wyróżnienie przypadków, tych, które można

uznać za

typowe i tych, które za wyjątki

VIII EKSPLORACJA DANYCH

•

uzupełnianie brakującej informacji

Grupowanie danych: definicja i cel

Przykłady zadań grupowania w badaniach:

Przykłady zadań grupowania w biznesie:

•

namierzenie grupy potencjalnych klientów

pewnego produktu z niszy rynkowej
wyprodukowanego przez

małą firmę z małym

budżetem reklamowym

•

podział zachowań finansowych na korzystne i

niepewne w celu kontroli obliczeń

•

redukcję wymiarów, gdy zbiór ma setki atrybutów

•

grupowanie ekspresji genów, gdzie bardzo dużo

genów może wykazywać podobne zachowanie

VIII EKSPLORACJA DANYCH

Grupowanie danych: definicja i cel

Przykłady zadań grupowania w marketingu:

Przykłady zadań grupowania w geodezji i kartografii:

•

identyfikacja obszarów o podobnych glebach na

podstawie zdjęć z obserwacji Ziemi

•

lokalizacje epicentrów trzęsień Ziemi, na

podstawie zaobserwowanych defektów
kontynentów

•

identyfikacja grup ubezpieczonych w

towarzystwach

ubezpieczeniowych generujących

wysokie koszty

napraw

•

rozpoznanie potrzeb rozwojowych miasta, na

podstawie grupowania domów o określonej wartości,
lokalizacji, itp.

VIII EKSPLORACJA DANYCH

Grupowanie danych:

metody

•

metody hierarchiczne, polegają na łączeniu

pojedynczych elementów, wg założonego kryterium
odległości (elementy podobne)

•

metody niehierarchiczne, polegają na wstępnym

podzieleniu zbioru na określoną liczbę klas, a następnie
modyfikowaniu podziału (przez przenoszenie elementów
z grupy do grupy) prowadzącym do poprawy tego
podziału

Metody grupowania:

VIII EKSPLORACJA DANYCH

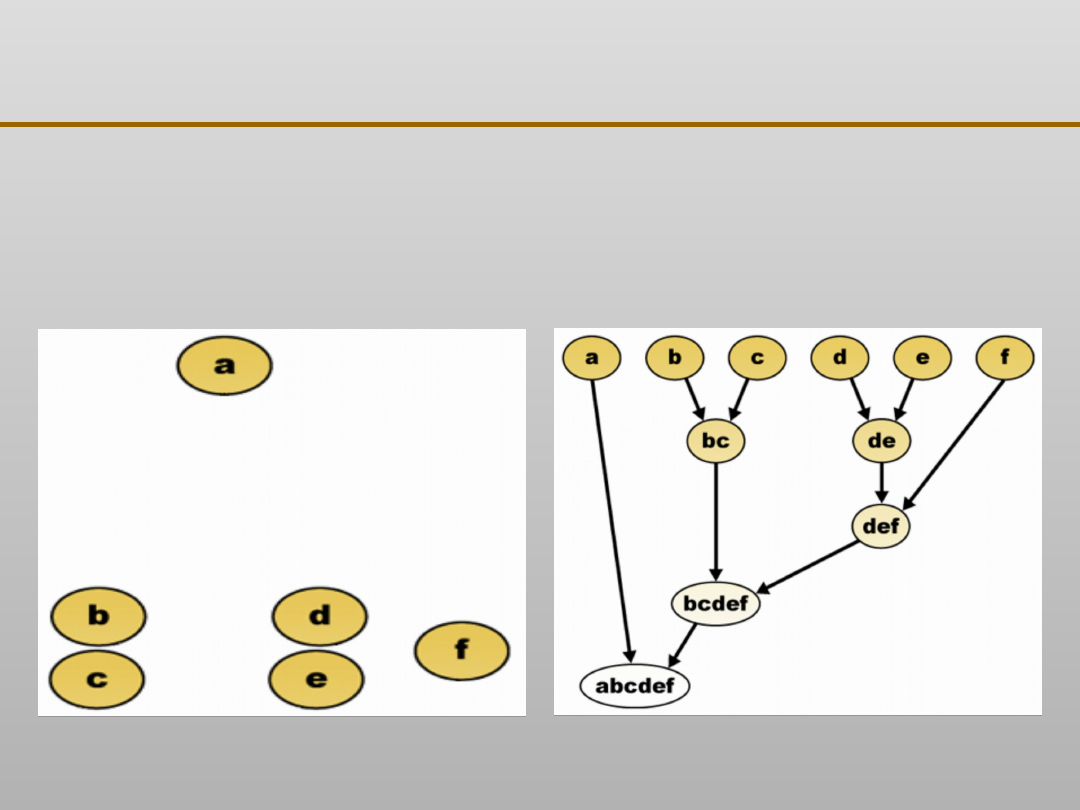
Grupowanie danych:

metody hierarchiczne

•

początkowo każda obserwacja traktowana jest jako

osobne

skupienie

•

wyniki przedstawiane są za pomocą drzewka połączeń

Uogólniony algorytm metod hierarchicznych:

•

następnie tworzona jest macierz odległości pomiędzy

kolejnymi obserwacjami

•

określa się odległości pomiędzy poszczególnymi

skupieniami

i na ich podstawie tworzy się nowe

skupienia obiektów

VIII EKSPLORACJA DANYCH

Grupowanie danych:

metody hierarchiczne

•

metoda najbliższego sąsiada

•

metoda środka ciężkości

Wybór metody aglomeracji:

•

metoda najdalszego sąsiada

•

metoda średniej grupowej

•

metoda mediany (ważonych środków

ciężkości)

VIII EKSPLORACJA DANYCH

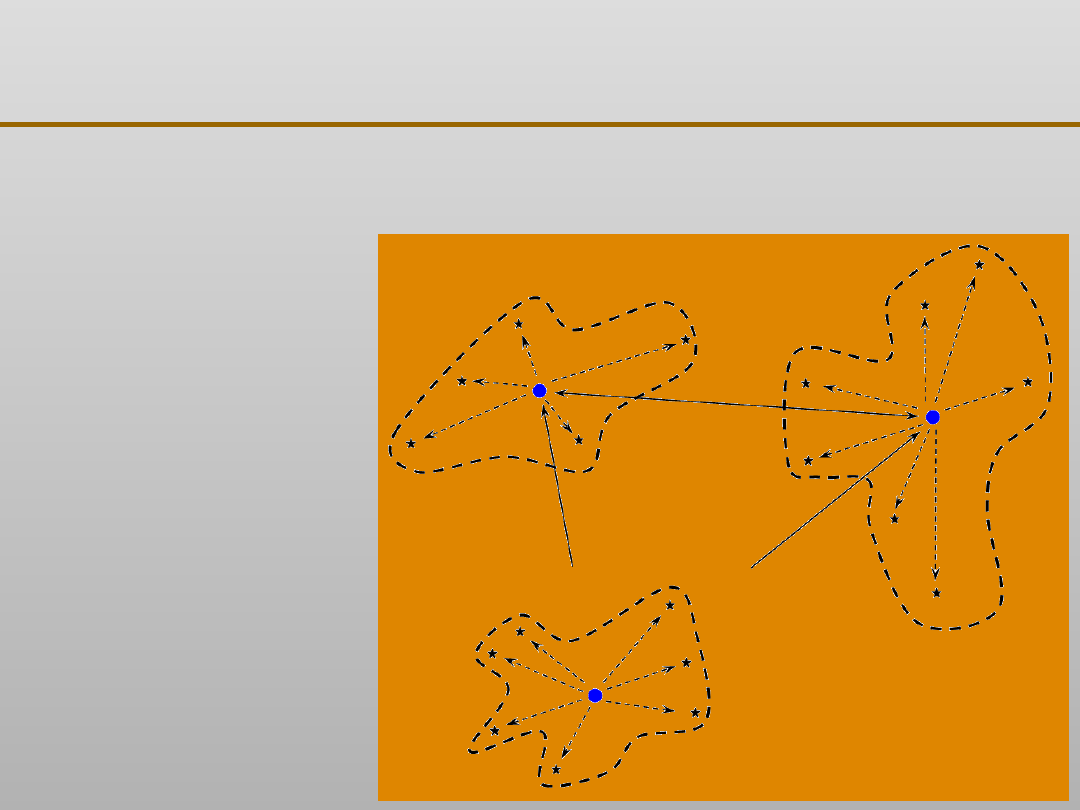
Grupowanie danych:

metody hierarchiczne

•

metoda najbliższego sąsiada

VIII EKSPLORACJA DANYCH

Grupowanie danych:

metody hierarchiczne

•

metoda najbliższego

sąsiada

VIII EKSPLORACJA DANYCH

•

metoda najdalszego sąsiada

Grupowanie danych: metody hierarchiczne

Wady metod hierarchicznych

•

brak oczywistego kryterium stopu dla

uzyskania względnie jednorodnych skupień

•

otrzymane raz skupienie nie może być

rozłączone, czyli ewentualny wcześniejszy błąd
nie może być skorygowany

•

w metodach aglomeracyjnych nie jest znana z

góry ani liczba grup (skupień) ani liczba
obiektów w poszczególnych grupach

VIII EKSPLORACJA DANYCH

Grupowanie danych: algorytm k - średnich

Algorytm k – średnich:

procedura

postępowania

• wybieramy losowo tyle punktów w przestrzeni, na ile
grup dzielimy zbiór danych

• obliczamy odległości wszystkich elementów zbioru od

wylosowanych punktów

• grupujemy zgodnie z bliskością elementów zbioru od

punktów początkowych

• obliczamy centroidy grup jako średnie elementów
grupy

• powtarzamy punkty 2 i 3 aż do osiągnięcia
stabilności

VIII EKSPLORACJA DANYCH

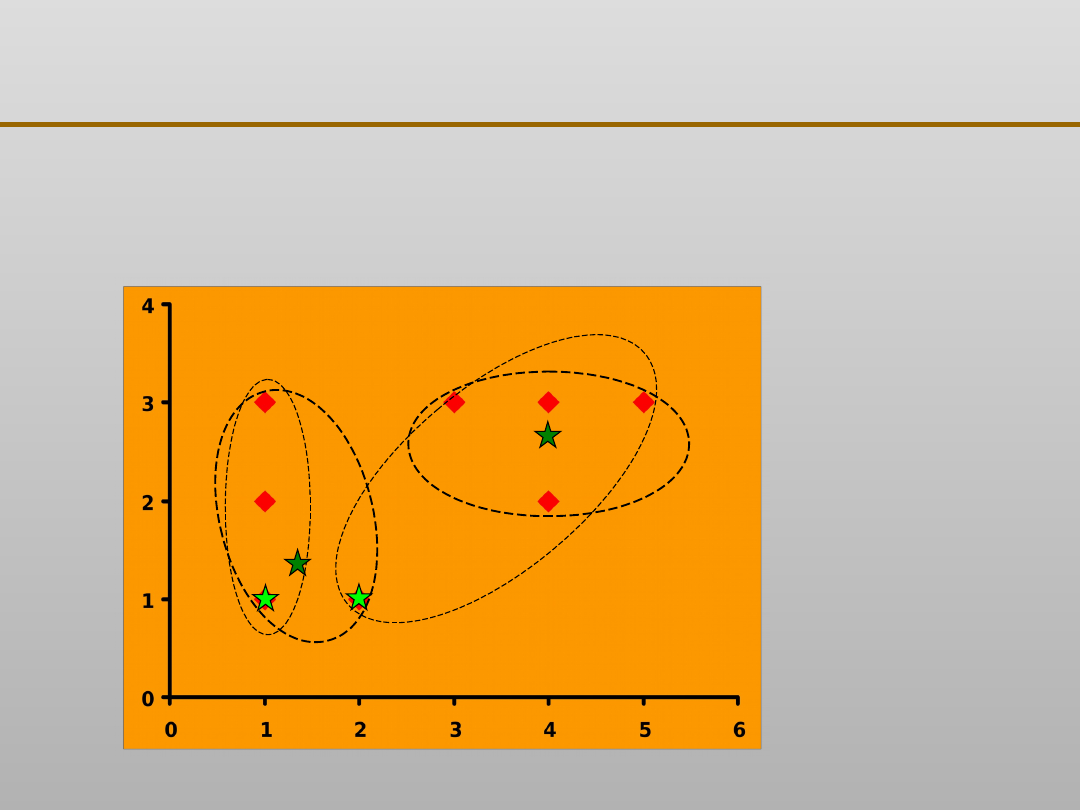
Grupowanie danych: algorytm k - średnich

X

Y

1

1

1

2

1

3

2

1

3

3

4

3

4

2

5

3

VIII EKSPLORACJA DANYCH

Grupowanie danych: algorytm k - średnich

Wskaźnik jakości algorytmu k - średnich

•

ZPG – zmienność pomiędzy grupami

•

ZWG – zmienność wewnątrz grupy

W =

ZPG

ZWG

VIII EKSPLORACJA DANYCH

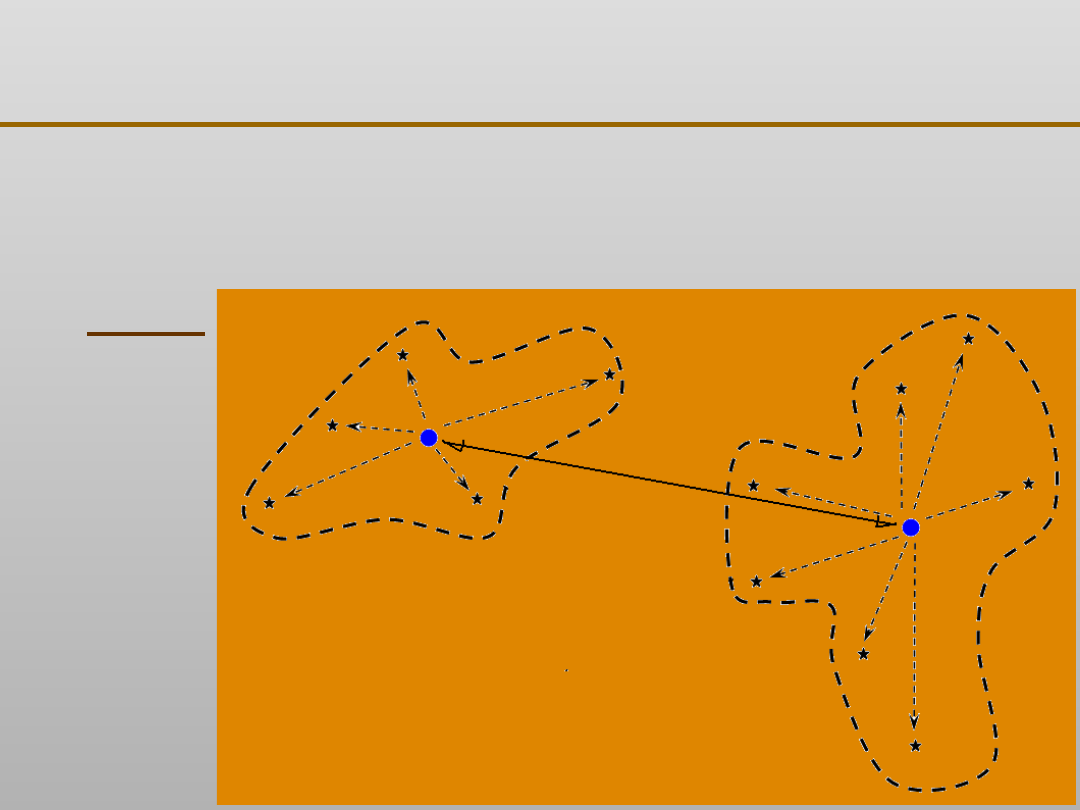
Grupowanie danych: algorytm k - średnich

Wskaźnik jakości algorytmu k - średnich

W =

ZPG

ZWG

c

1

c

2

ZPG = d (c

1

, c

2

)

ZWG =

Σ

Σ d(m

ij

, c

i

)

i=1 j

k

m

15

m

14

m

13

m

12

m

11

m

21

m

26

VIII EKSPLORACJA DANYCH

Grupowanie danych: algorytm k - średnich

Zalety algorytmu k - średnich

•

sprawny – η(nkt), gdzie n jest liczbą

obserwacji, k jest liczbą klasterów, a t jest
liczbą iteracji, zazwyczaj k, t << n

•

obliczenia kończą się po osiągnięciu

minimum lokalnego

•

łatwy w zaprogramowaniu

VIII EKSPLORACJA DANYCH

Grupowanie danych: algorytm k - średnich

Wady algorytmu k - średnich

•

możliwość stosowania jedynie do danych,

dla których możliwe jest obliczenie średnich;

wyłącza to zbiory z danymi

kategorycznymi

•

konieczność wstępnego określenia liczby k

(liczby

grup) przed rozpoczęciem

modelowania

•

niezdolność do radzenia sobie z danymi

zaszumionymi i z danymi odstającymi

VIII EKSPLORACJA DANYCH

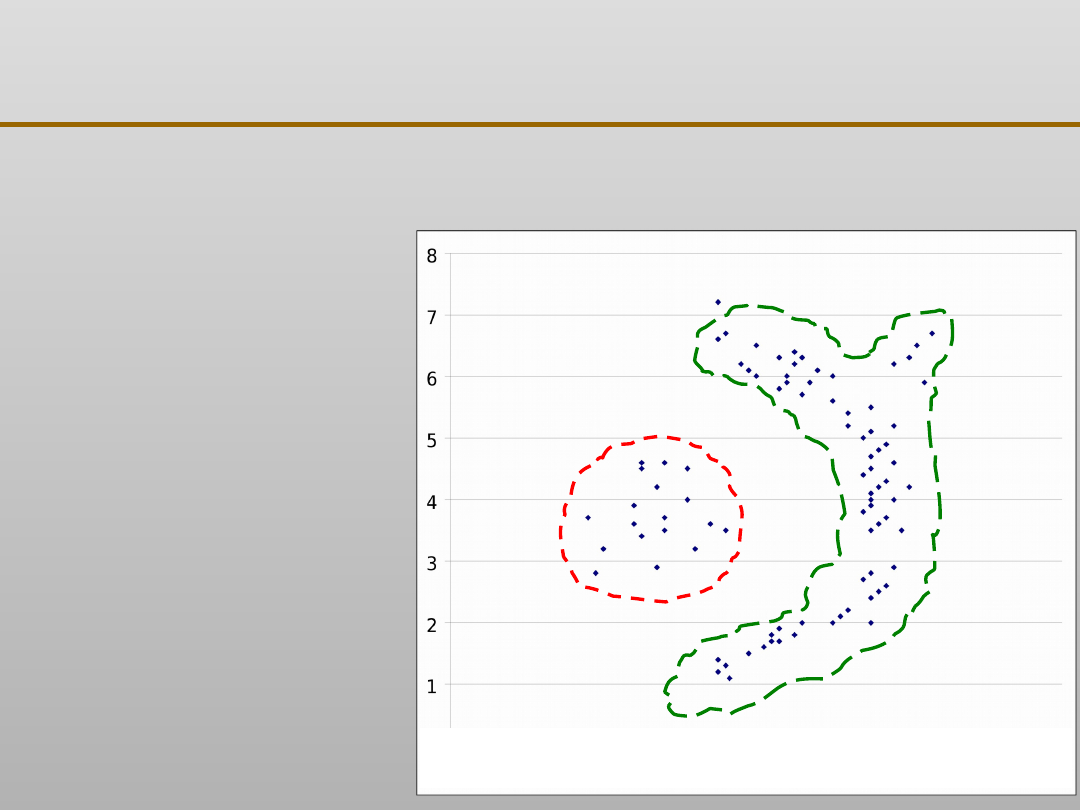
Wady algorytmu k - średnich

Grupowanie danych: algorytm k - średnich

•

nie do zastosowania w przypadku, gdy modelowana

grupa ma kształt wklęsły

VIII EKSPLORACJA DANYCH

Grupowanie danych: definicja i cel

VIII EKSPLORACJA DANYCH

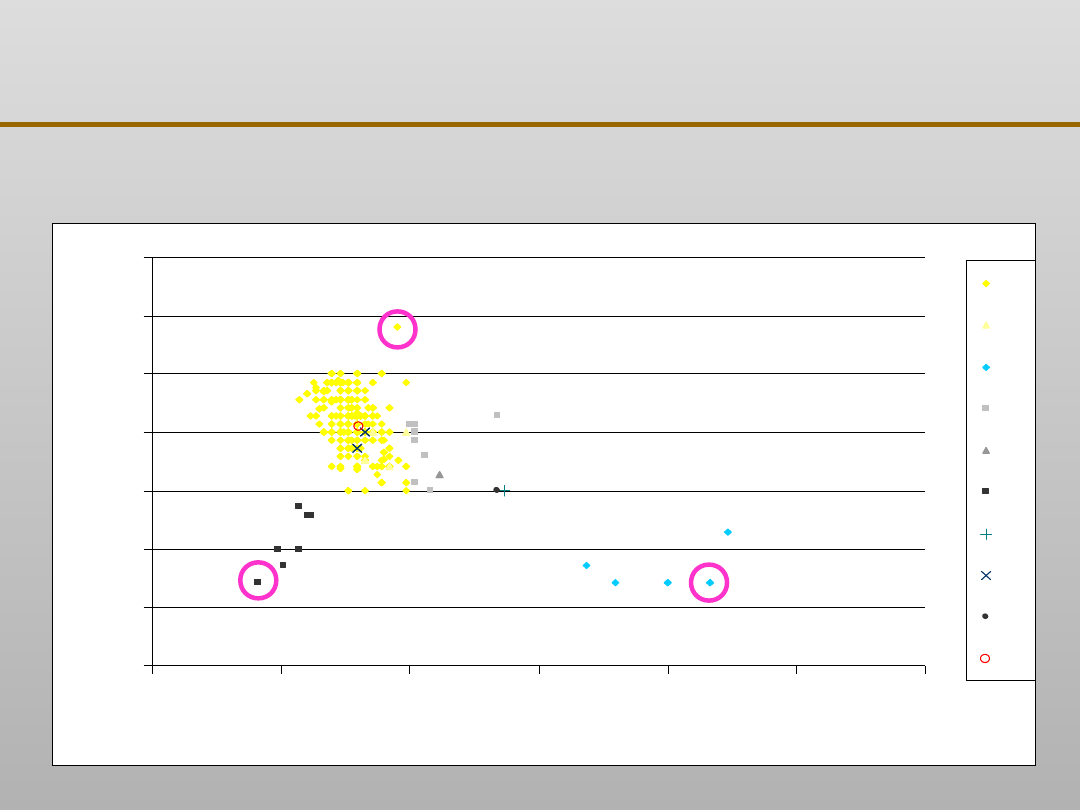
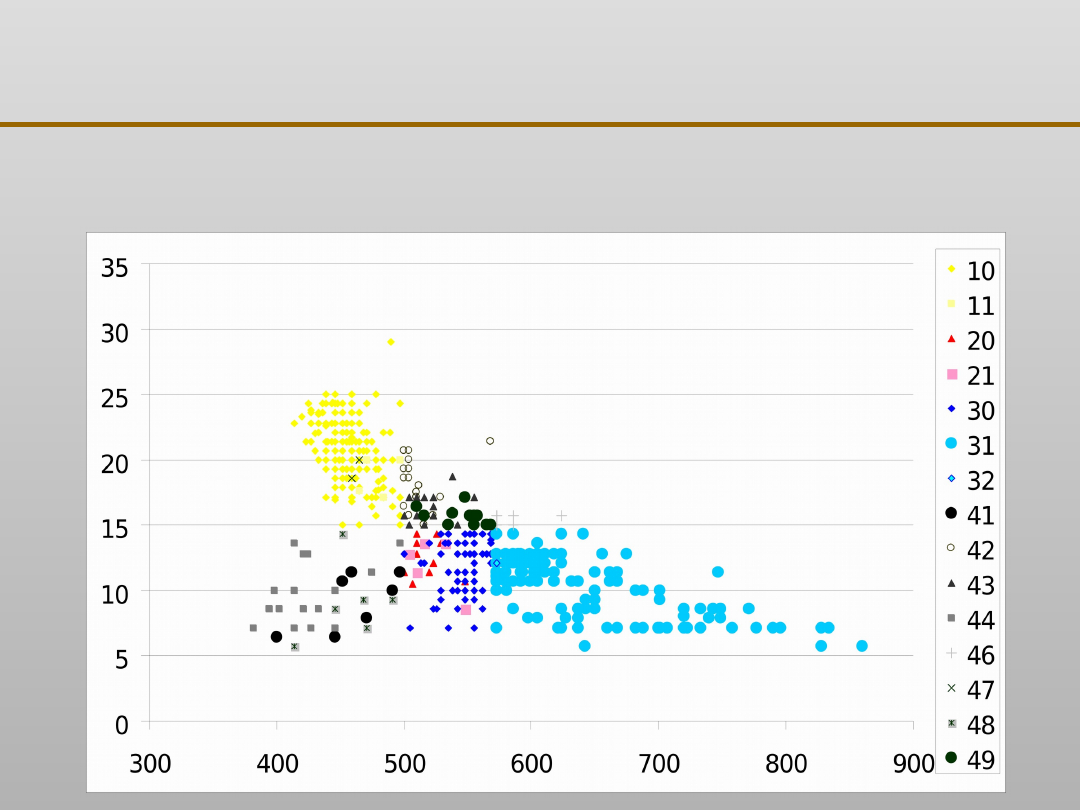
Grupowanie danych: zastosowanie

0

5

10

15

20

25

30

35

300

400

500

600

700

800

900

wytrzymałość [MPa]

w

yd

łu

że

ni

e

[%

]

10
11

31
42
43
44

46
47
49

sc

VIII EKSPLORACJA DANYCH

VIII EKSPLORACJA DANYCH

Grupowanie danych: zastosowanie

0

5

10

15

20

25

30

35

300

400

500

600

700

800

900

wytrzymałość [MPa]

w

yd

łu

że

ni

e

[%

]

10
11
31
42
43
44
46
47
49
sc

Nr

wyt

C %

Mn

%

Si %

P %

S %

Cr %

Ni %

Cu %

Mg

%

Rm

A5

HB

1279,

1

3,84 0,17

2,50

0,05

0,01

0,04

0,02

0,06

0,03

6

747

11,4

248

2039,

1

3,82 0,09

2,50

0,05

7

0,00

8

0,02

0,00

0,03

0,03

7

382

7,1

156

2036,

1

3,76 0,11

2,54

0,05

7

0,01

1

0,03

0,00

0,04

0,04

0

490

29,0

159

2036,

2

3,81 0,12

2,58

0,05

9

0,01

4

0,03

0,01

0,04

0,04

1

490

29,0

159

średn

i

3,78 0,15

2,53

0,05

0,01

0,03

0,01

0,06

0,03

6

460,

9

20,4

163,

7

0114,

1

3,71 0,15

2,43

0,07

0,01

0,02

0,01

0,11

0,03

6

459

20,7

163

1063,

1

3,87 0,14

2,54

0,05

0,01

0,02

0,01

0,04

0,03

5

459

20,7

156

1063,

2

3,86 0,12

2,49

0,05

0,01

0,02

0,01

0,04

0,03

9

459

20,7

156

1232,

1

3,76 0,18

2,55

0,04

0,01

0,04

0,02

0,17

0,03

2

459

20,7

156

1232,

2

3,79 0,18

2,56

0,04

0,01

0,04

0,02

0,17

0,03

4

459

20,7

156

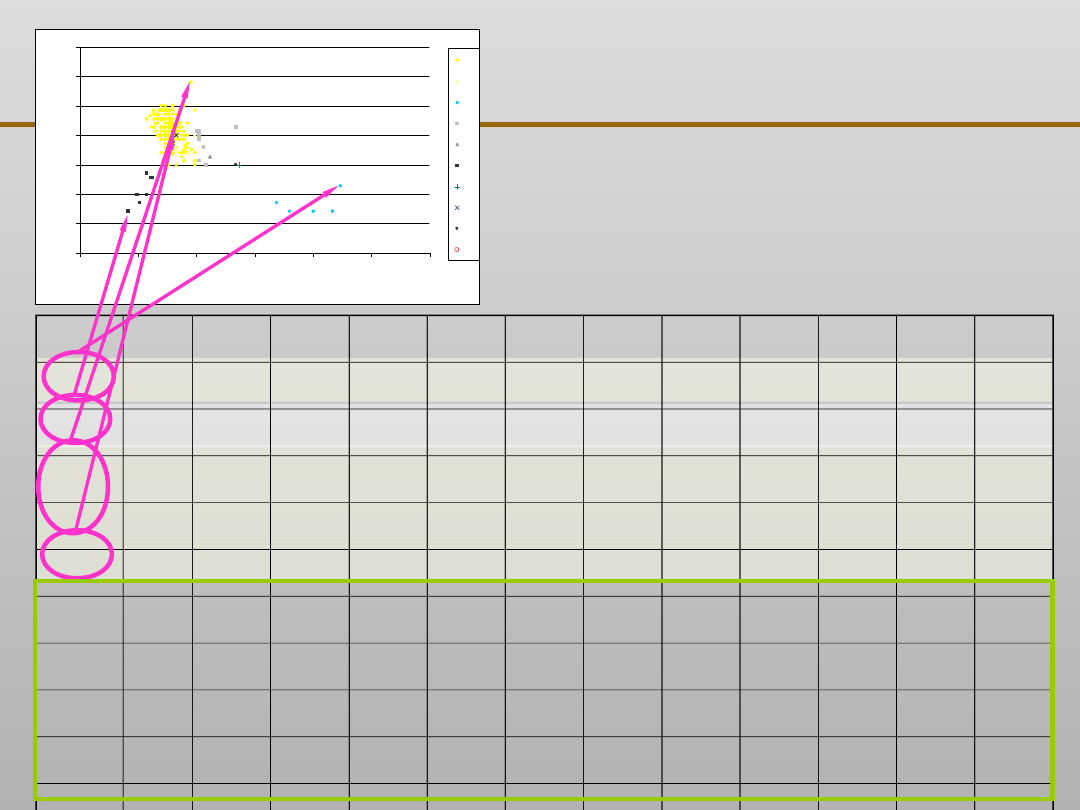
Grupowanie danych:

podsumowanie

Uwaga: niezależnie od zastosowanej metody
wszystkie podziały będą się mieścić pomiędzy
dwoma skrajnymi przypadkami:

• skrajny przypadek: wszystkie obiekty rozkładają się
tak, że uzyskujemy skupienia jednoelementowe (zbiór
n elementów dzielony jest na n skupień
jednoelementowych)

• skrajny przypadek: zbiór elementów jest tak
jednorodny, że nie możliwe jest rozłożenie jego na
podzbiory, tzn. otrzymujemy jedno skupienie n-
elementowe

VIII EKSPLORACJA DANYCH

Grupowanie danych:

podsumowanie

VIII EKSPLORACJA DANYCH

Grupowanie danych:

podsumowanie

VIII EKSPLORACJA DANYCH

Grupowanie danych:

podsumowanie

VIII EKSPLORACJA DANYCH