Statystyka 

- Opisowa analiza zjawisk 
masowych

Opracowanie na podstawie :
„Statystyka” Mieczysław Sobczyk”

Magdalena Kaźmierczak
Anna Dobraś
Aneta Kaptur
Magda Przybył
Ewa Janowska
Andrzej Wowk

Opisowa analiza struktury zjawisk 
masowych

1.Typy rozkładów empirycznych jednej zmiennej.



Rozkładem  empirycznym zmiennej nazywamy 
przyporządkowanie kolejnym wartościom zmiennej (x

1

), 

odpowiadających im liczebności (n

1

). Rozkład odzwierciedla więc 

strukturę badanej zbiorowości z punktu widzenia określonej 
cechy.



Rozkłady empiryczne są ustalane na podstawie konkretnych 
obserwacji, a umiejętność odróżniania różnych ich typów jest 
nieodzownym warunkiem prawidłowej analizy statystycznej. Od 
ich rodzaju zależy bowiem dobór odpowiednich charakterystyk 
służących do opisu zbiorowości. 

Opisowa analiza struktury zjawisk 
masowych



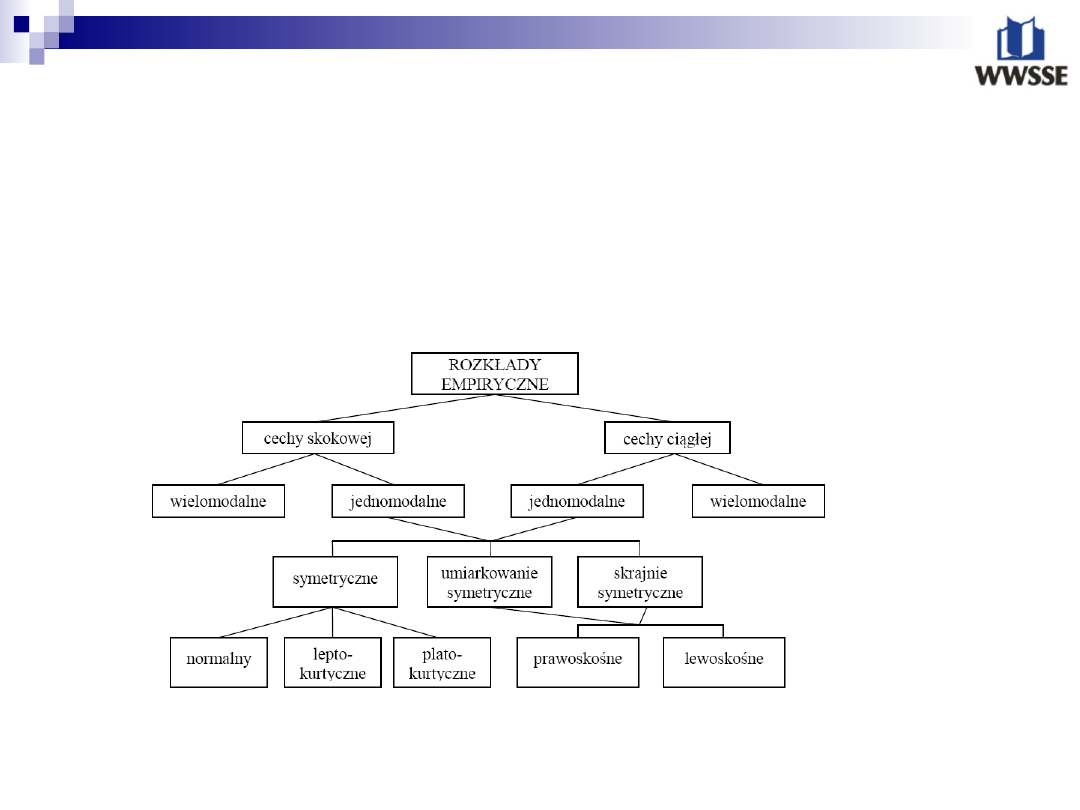
Najczęściej spotykane rodzaje rozkładów empirycznych 
przedstawia następujący rysunek:



Rozkład, którego krzywa liczebności (dla cechy ciągłej) lub 
diagram (dla cechy skokowej) ma jedno maksimum, nazywa się 
rozkładem jednomodalnym. Wśród rozkładów jednomodalnych 
można wyróżnić rozkłady symetryczne, umiarkowanie asymetryczne 
i skrajnej asymetryczne. W rozkładzie symetrycznym 
jednomodalnym liczebności odpowiadające wartościom zmiennej 
rozkładają się symetrycznie w wokół liczebności największej. 



 Rozkładem symetrycznym o jednym maksimum jest rozkład 
normalny. Rozkład ten ma szczególnie duże znaczenie w statystyce 
matematycznej, gdyż wiele cech różnych zbiorowości charakteryzuje 
się takim właśnie rozkładem (np. wzrost lub długość stopy). Należy 
podkreślić, że rozkład normalny jest rozkładem symetrycznym o 
ściśle określonej kurtozie, tzn. koncentracji  wartości zmiennej 
wokół średniej arytmetycznej. Każdy rozkład normalny jest więc 
rozkładem symetrycznym, ale nie każdy rozkład symetryczny jest 
rozkładem normalnym. Na przykład rozkłady: platokurtyczny 
(spłaszczony) i leptokurtyczny (wysmukły) są rozkładami 
symetrycznymi, ale nie normalnymi.



Rozkłady empiryczne o charakterze symetrycznym występują 
rzadko. Często spotykamy się z rozkładami zbliżonymi do 
rozkładu symetrycznego (asymetrycznymi). Rozkłady 
asymetryczne mogą być umiarkowanie asymetryczne i skrajnie 
asymetryczne, a te z kolei prawoskośne i lewoskośne. 



W rozkładach asymetrycznych liczebności mogą skupiać się 
wokół niskich bądź wysokich wartości cechy. W pierwszym 
przypadku mamy do czynienia z rozkładem asymetrii 
prawostronnej (prawoskośnym), a w drugim zaś o 
asymetrii lewostronnej (lewoskośnym). Tak więc w 
rozkładach prawoskośnych dużo jednostek posiada stosunkowo 
niskie wartości cechy, a niewiele jednostek ma wysokie 
wartości. W rozkładach lewoskośnych stosunkowo niewiele jest 
jednostek posiadających niskie wartości cechy, natomiast 
licznie reprezentowane są jednostki o wysokich wartościach 
cechy.



Rozkłady, w których prawie wszystkie jednostki mają niskie 
bądź wysokie wartości cechy, nazywamy rozkładami skrajnie 
asymetrycznymi. Są one rozkładami jednostronnymi 
względem wartości cechy o maksymalnej liczebności. Niektóre 
cechy statystyczne mogą mieć rozkład będący niejako 
kompozycją dwóch rozkładów asymetrycznych. Określa się je 
mianem rozkładów U lub rozkładów siodłowych. 
Występują również rozkłady o wyraźnie zarysowanych dwóch 
punktach skupienia obserwacji. Noszą one nazwę rozkładów 
bimodalnych. Rozkłady mające więcej niż dwa maksima 
lokalne nazywamy wielomodalnymi.



Rozkłady symetryczne i umiarkowanie asymetryczne 
charakteryzują zbiorowości jednorodne ze względu na 
badaną cechę. Natomiast rozkłady skrajnie asymetryczne, 
wielomodalne i siodłowe dotyczą zbiorowości, w których 
wartości cechy są znacznie zróżnicowane. 



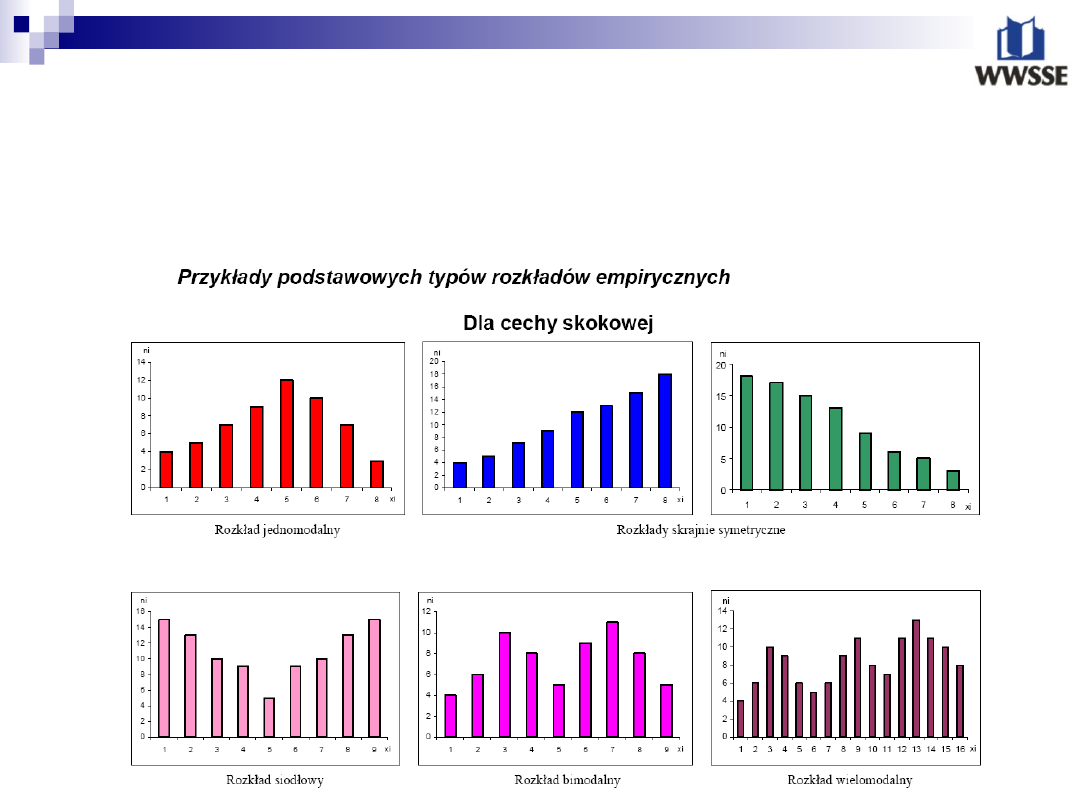
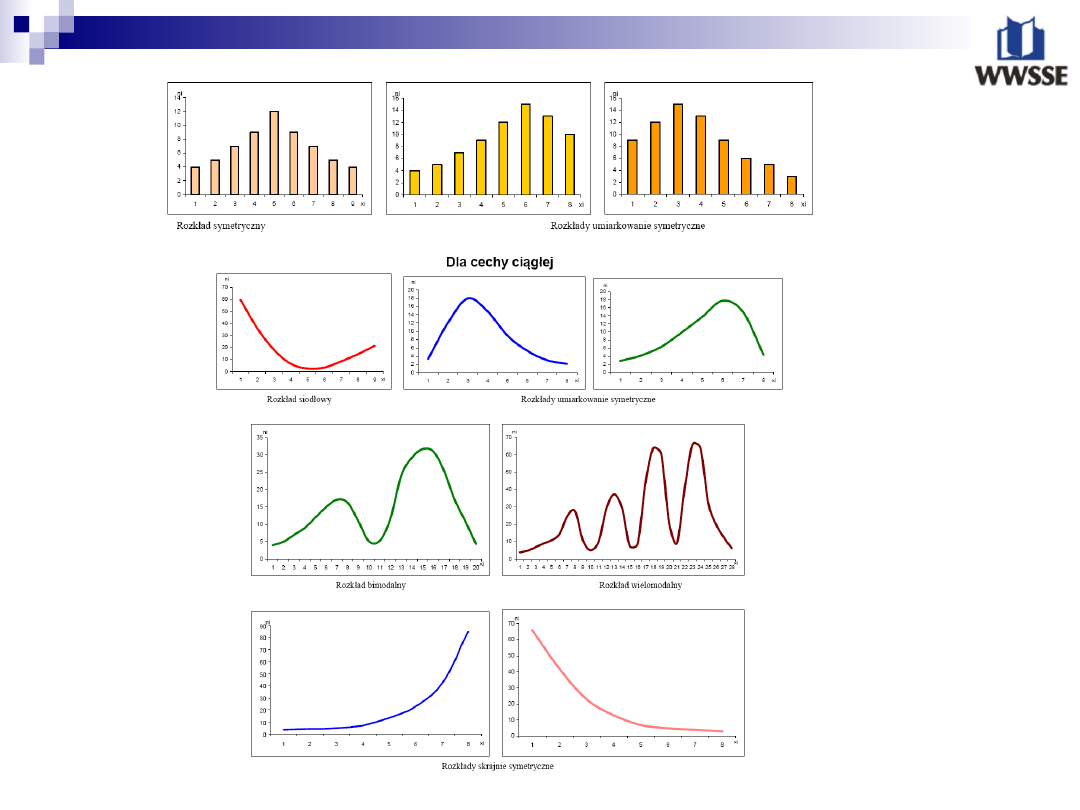
Przykłady podstawowych typów rozkładów empirycznych 
dla cech ciągłych i skokowych przedstawia rysunek. Na osi 
odciętych dokładne są wartości badanej zmiennej, a na osi 
rzędnych – odpowiadające im liczebności lub części 
względne.



 Częstość względna jest stosunkiem liczebności jednostek 
posiadających określony wariant cechy do ogólnej 
liczebności.

Opisowe charakterystyki 
rozkładów

     W teorii statystyki wypracowano wiele charakterystyk opisowych, 

za pomocą których można przeprowadzić analizę struktury zjawisk 
masowych, czyli analizę właściwości różnych rozkładów. Do 
charakterystyk najczęściej wykorzystywanych przy opisie struktury 
zbiorowości należą:



1) miary średnie (zwane też miarami poziomu wartości 
zmiennej, miarami położenia lub przeciętnymi) służące do 
określenia tej wartości zmiennej opisanej przez rozkład, wokół 
której skupiają się wszystkie pozostałe wartości zmiennej,



2) miary rozproszenia (zmienności, zróżnicowania, dyspersji) 
służące do badania stopnia zróżnicowania wartości zmiennej,



3) miary asymetrii (skośności) służące do badania kierunku 
zróżnicowania wartości zmiennej,

Opisowa charakterystyki 
rozkładów



4) miary koncentracji służące do badania stopnia 
nierównomierności rozkładu ogólnej sumy wartości zmiennej 
pomiędzy poszczególne jednostki zbiorowości lub do analizy 
stopnia skupienia poszczególnych jednostek wokół średniej.



Charakterystyki opisowe są bardziej syntetycznymi formami 
opisu rozkładów niż forma graficzna czy tabelaryczna. 
Pozwalają one w sposób syntetyczny określić właściwości 
badanych rozkładów i dokonać porównania różnych 
zbiorowości. Można wyróżnić dwa typy porównań: 



1) porównanie dwóch różnych zbiorowości, ale pod 
względem tej samej cechy badania (np. ocena z egzaminu 
studentów i studentek); 



2) porównanie dotyczące jednej zbiorowości, ale pod 
względem dwóch różnych cech (np. struktura zarobków osób 
względem wieku).

Miary średnie



Miary średnie dzieli się na dwie grupy: średnie klasyczne i 
pozycyjne. Do średnich klasycznych należą: średnia 
arytmetyczna, średnia harmoniczna oraz średnia geometryczna. 
Najczęściej wykorzystywanymi średnimi pozycyjnymi są: 
dominanta (modalna, wartość najczęstsza) o raz 
kwantyle. Wśród kwantyli wyróżniamy z kolei kwartyle 
(dzielące zbiorowość na cztery części), kwintyle (na pięć 
części), decyle (na dziesięć części) oraz centyle, zwane też 
percentylami (na sto części). 



Średnie klasyczne są obliczane na podstawie wszystkich 
wartości szeregu. Średnie pozycyjne są wartościami 
konkretnych wyrazów  szeregu (pozycji) wyróżniających się pod 
pewnym względem.  Obie grupy średnich nawzajem się 
uzupełniają. Każda z nich opisuje bowiem poziom wartości 
zmiennej z innego punktu widzenia. Są jednak sytuacje, w 
których układ informacji liczbowych nie pozwala na obliczanie 
danej średniej.

Miary średnie



Średnia arytmetyczna, jest sumą wartości zmiennej 
wszystkich jednostek badanej zbiorowości podzieloną przez 
liczbę  tych jednostek. 
Wzór: 



gdzie:

 



Średnia ta nazywa się średnią arytmetyczną nieważoną 
(prostą, zwykłą).

N

x

N

x

x

x

x

n

i

i

n















1

2

1

...

Miary średnie



Jeżeli warianty zmiennej występują z różną częstotliwością, to 
oblicza się średnią arytmetyczną ważoną. Wagami są liczebności 
odpowiadające poszczególnym wariantom. Z tego rodzaju sytuacją 
mamy do czynienia w szeregach rozdzielczych punktowych i 
przedziałowych. Wzór na obliczenie średniej arytmetycznej z 
szeregów rozdzielczych punktowych ma następującą postać:



gdzie n

i

 (i=1,2,...k) oznacza liczebność jednostek odpowiadającą 

poszczególnym wariantom zmiennej, a jest sumą tych liczebności.

N

n

x

N

n

x

n

x

n

x

x

k

i

i

i

k

k















1

2

2

1

1

...

Miary średnie



W szeregach rozdzielczych przedziałowych wartości 
zmiennej w każdej klasie nie są jednoznacznie określone, 
ale mieszczą się w pewnym przedziale. W celu obliczenia 
średniej arytmetycznej w przypadku tego rodzaju szeregów 
należy uprzednio wyznaczyć środki przedziałów. Środki 
przedziałów otrzymuje się jako średnią arytmetyczną 
dolnej i górnej granicy każdej klasy. Wzór na średnią 
arytmetyczną z szeregu rozdzielczego przedziałowego 
jest następujący:

N

n

x

N

n

x

n

x

n

x

x

k

i

i

i

o

k

k

o

o

o















1

2

2

1

1

...

Miary średnie



Jeżeli zamiast liczebności absolutnych wykorzystywane są w 
obliczeniach  procentowe wskaźniki struktury, to wzór na 
średnią arytmetyczną przyjmuje postać:

100

1







k

i

i

i

o

w

x

x

Miary średnie



Zdarzają się sytuacje, że znamy średnie arytmetyczne dla 
pewnych grup na tej podstawie chcemy obliczyć średnią 
arytmetyczną dla wszystkich grup łącznie. 
Wykorzystujemy wówczas następujący wzór:



Gdzie x jest średnią ze średnich;  x

i

 - średnia arytmetyczną 

i-tej grupy; n

i 

- liczebnością i-tej grupy;  N - sumą 

liczebności grup.

N

n

x

x

k

i

i

i

o







1

1

x