Statystyka

- Opisowa analiza zjawisk
masowych

Opracowanie na podstawie :
„Statystyka” Mieczysław Sobczyk”

Magdalena Kaźmierczak
Anna Dobras
Aneta Kaptur
Magda Przybył
Ewa Szulc
Andrzej Wowk

Wariacja



Wariacja jako suma kwadratów dzielona przez liczbę

dodatnią, jest zawsze wielkością nieujemną i mianowaną.
Mianem wariacji jest kwadrat jednostki fizycznej. Im zbiorowość
jest bardziej zróżnicowana tym wyższa jest wartość wariacji.



Podamy konkretny przykład wykorzystania równości
wariacyjnej.



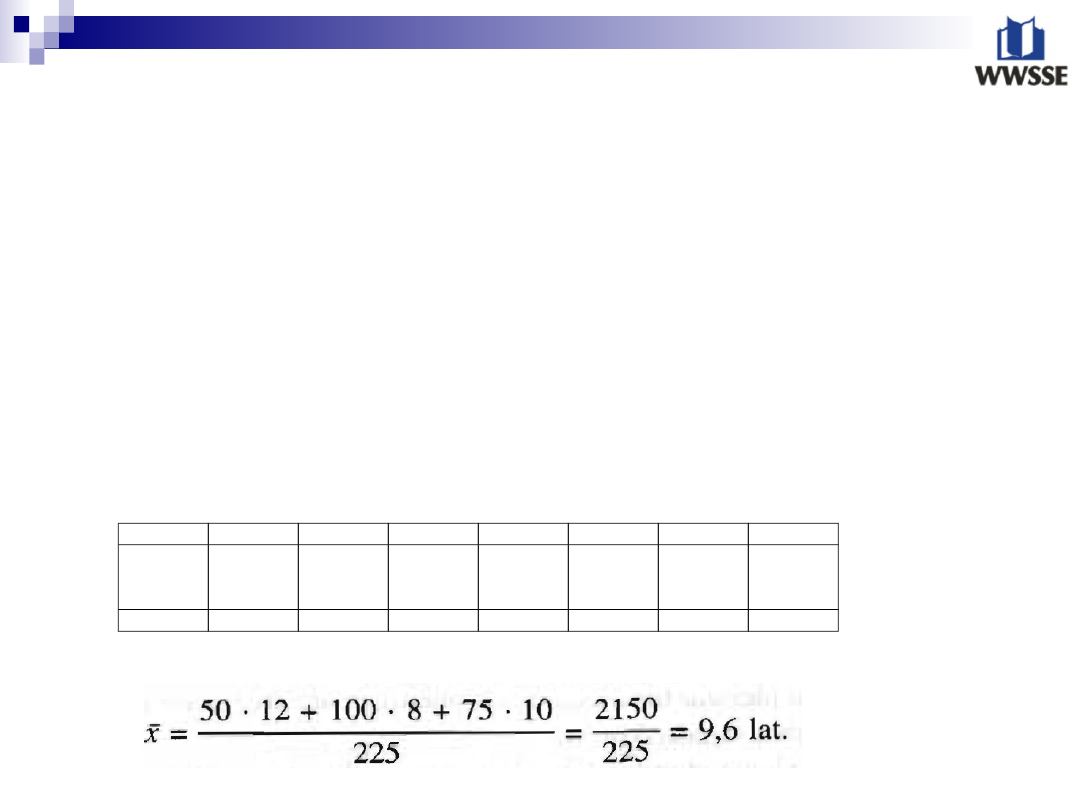
Obliczanie zróżnicowani stażu pracy w przedsiębiorstwie



Średni starz pracy w przedsiębiorstwa obliczymy następująco:

2

Zakłady
I
II
III

50
100
75

12
8
10

600
800
750

3
2
4

2,4
-1,6
0,4

5,46
2,56
0,16

288
256
12

Razem

225

X

2150

X

X

X

556



Wewnątrz grupowe zróżnicowanie stażu pracy jest równe:

Między grupowe zróżnicowanie stażu wynosi:

Wariacja ogólna jest sumą wariacji wewnątrz grupowej i między grupowej:

3

Zakłady
I
II
III

50
100
75

12
8
10

600
800
750

3
2
4

2,4
-1,6
0,4

5,46
2,56
0,16

288
256
12

Razem

225

X

2150

X

X

X

556

Odchylenie standardowe



Odchylenie standardowe określa, o ile wszystkie
jednostki danej zbiorowości różnią się średnio od średniej
arytmetycznej badanej zmiennej. Odchylenie standardowe
można wykorzystać do konstrukcji typowego obszaru
zmienności badanej cechy.



Typowy obszar zmienności określa wzór:



Odchylenie standardowe ma następujące właściwości:



-jest wielkością obliczaną na podstawie wszystkich
obserwacji danym szeregu,

4

Odchylenie standardowe



jego wartość zmieni się, jeśli liczebność szeregu wyrazimy
w liczbach względnych (procentach) dokładnie ustalonych,



wartość odchylenia standardowego nie zmienia się, jeśli do
wszystkich wartości zmiennej w szeregu oddamy pewną
stałą liczbę,



jeżeli wszystkie wartości szeregu pomnożymy przez pewną
stałą liczbę większą od zera, to odchylenie standardowe
będzie również trzykrotnie większe.

5

Odchylenie standardowe



jego wartość zmieni się, jeśli liczebność szeregu wyrazimy
w liczbach względnych (procentach) dokładnie ustalonych,



wartość odchylenia standardowego nie zmienia się, jeśli do
wszystkich wartości zmiennej w szeregu oddamy pewną
stałą liczbę,



jeżeli wszystkie wartości szeregu pomnożymy przez pewną
stałą liczbę większą od zera, to odchylenie standardowe
będzie również trzykrotnie większe.

6

Współczynnik zmienności



jest ilorazem bezwzględnej miary dyspersji i odpowiednich wartości
średnich. Jest on wyrażony w procentach..



Współczynnik zmienności można obliczyć kilkoma metodami:



Dwa pierwsze współczynniki noszą nazwę klasycznych a pozostałe
dwa pozycyjnych.

7



Przykład praktycznego zastosowania współczynnika zmienności dla celów
porównawczych:



Średnie miesięczne wpływy za Świadczenie usług noclegowych losowo
wybranych hotelach A, B i C były równe: X

A

=600tys.zł, X

B

=300tys.zł,

X

C

=500tys.zł. Odchylenia standardowe wartości sprzedanych usług wynosiły:

S

A

=100tys.zł, A

B

=90tys.zł, S

C

.=120tys.zł. W którym hotelu występuje

największa dyspersja miesięcznych wpływów za świadczenie usług
noclegowych? Podstawiając odpowiednie wartości liczbowe otrzymujemy:



Dla hotelu A:V

1

=110/160*100=18,3% brak ułamka



Dla hotelu B:V

2

=90/300*100=30,0%



Dla hotelu C:V

3

=120/500*100=24,0%



Największe zróżnicowanie miesięcznych wpływów za świadczenie usług
noclegowych miało miejsce w hotelu B, najmniejsze w hotelu A.

8



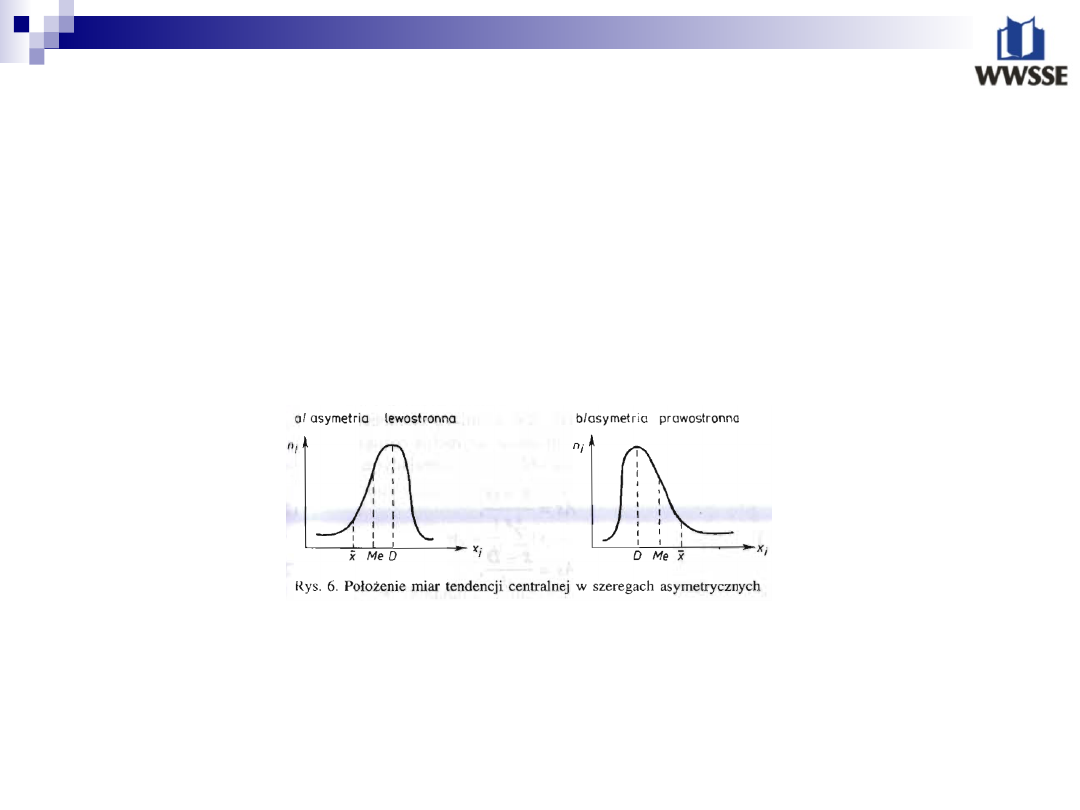
Miary asymetrii



W rozkładach asymetrycznych wszystkie średnie (X, D, Me) są równe. W
rozkładach asymetrycznych wymienione średnie kształtują się na różnych
poziomach. Jeśli spełniona jest nie równość: X> Me> D, to rozkład charakteryzuje
się asymetrią prawostronną; jeżeli zaś zachodzi nierówność: X< Me< D, to
mówimy o asymetrii lewostronnej.



Rozkład jednej zmiennej różniący się między sobą kierunkiem i siłą asymetrii.
Najprostszą miarą asymetrii jest wskaźnik asymetrii skośności określany wzorem:



W

X

= X – D

9