Digital Image

Processing

Lecture 3:

Contrast Transformation &

Image Binarization

Profesor

Valery Starovoitov

2

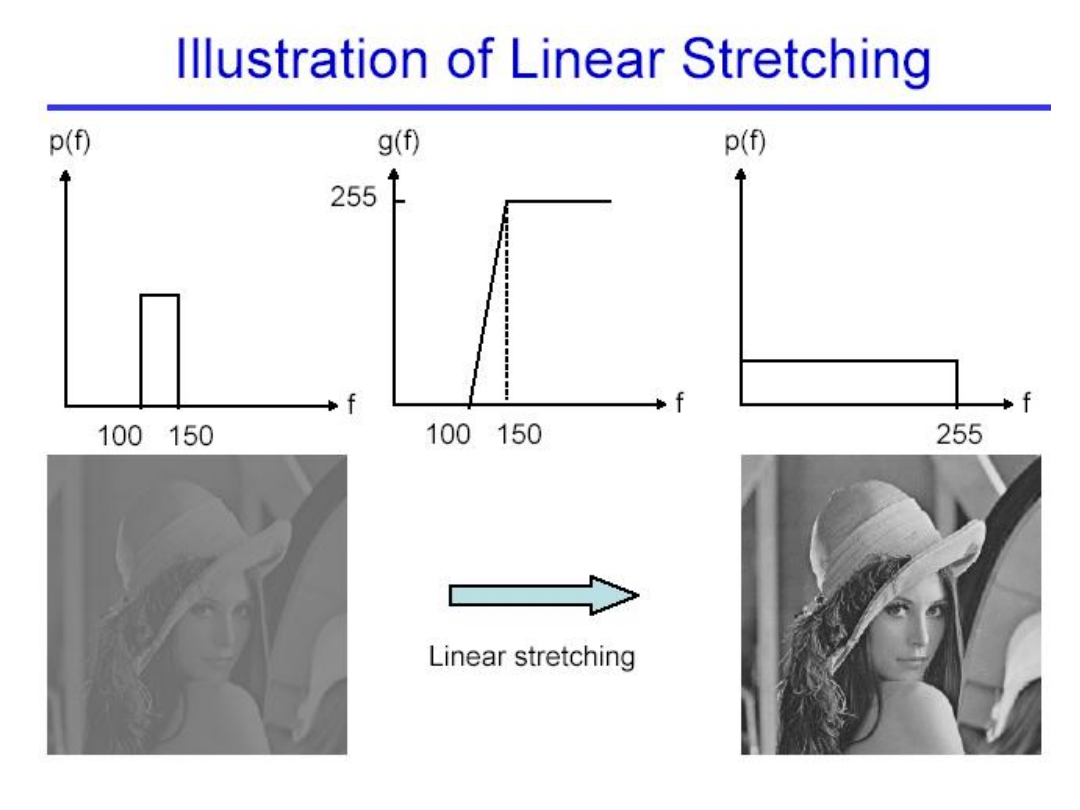
Rozszerzanie zakresu jasności

(Contrast stretching)

W obrazach, których zakres jasności nie zajmuje całej skali
dostępnej dla obrazu, można przez odpowiednią transformację
skorygować i równocześnie zwiększyć kontrast. Rozszerzenie
zakresu jasności omówimy jako przykład operacji liniowej
opisanej wzorem (2.4). Niech zakres jasności wykorzystywany
przez obraz zawiera się pomiędzy Jmin i Jmax. Wtedy operacja
liniowego rozszerzania jasności na cały zakres jasności [0, 255]
wyraża się wzorem:

dla J

min

< J(x, y) <J

max

(2.15)

)

)

,

(

(

255

)

,

(

min

min

max

J

y

x

J

J

J

y

x

J

w







3

4

Obraz po operacji wyrównywania histogramu

Obraz po operacji
liniowego rozszerzania
jasności

5

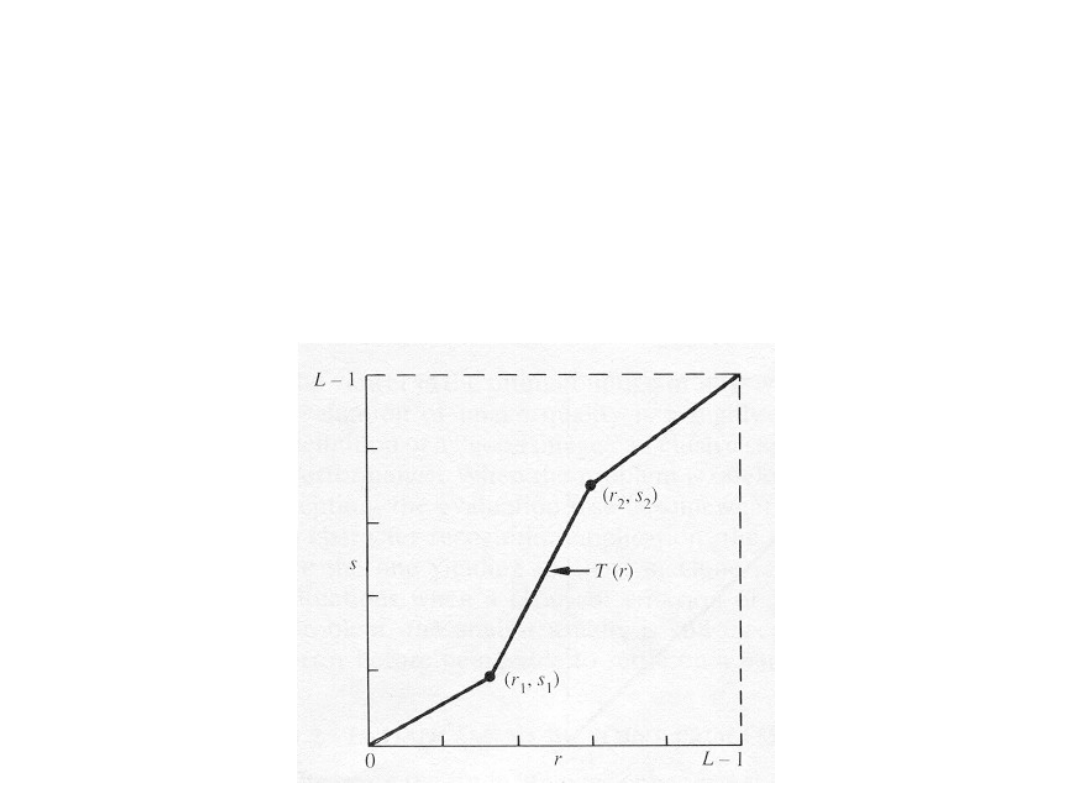
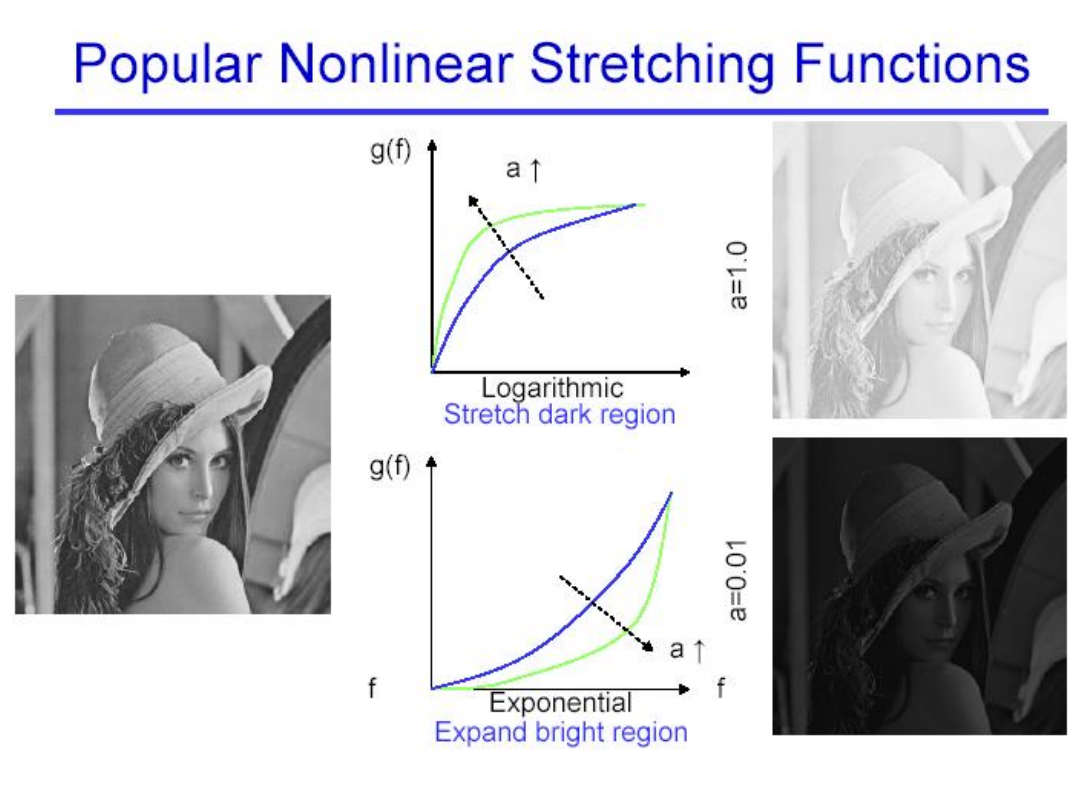
Piecewise-Linear Contrast

Stretching

To increase the dynamic range of the gray

levels in the image being processed.

6

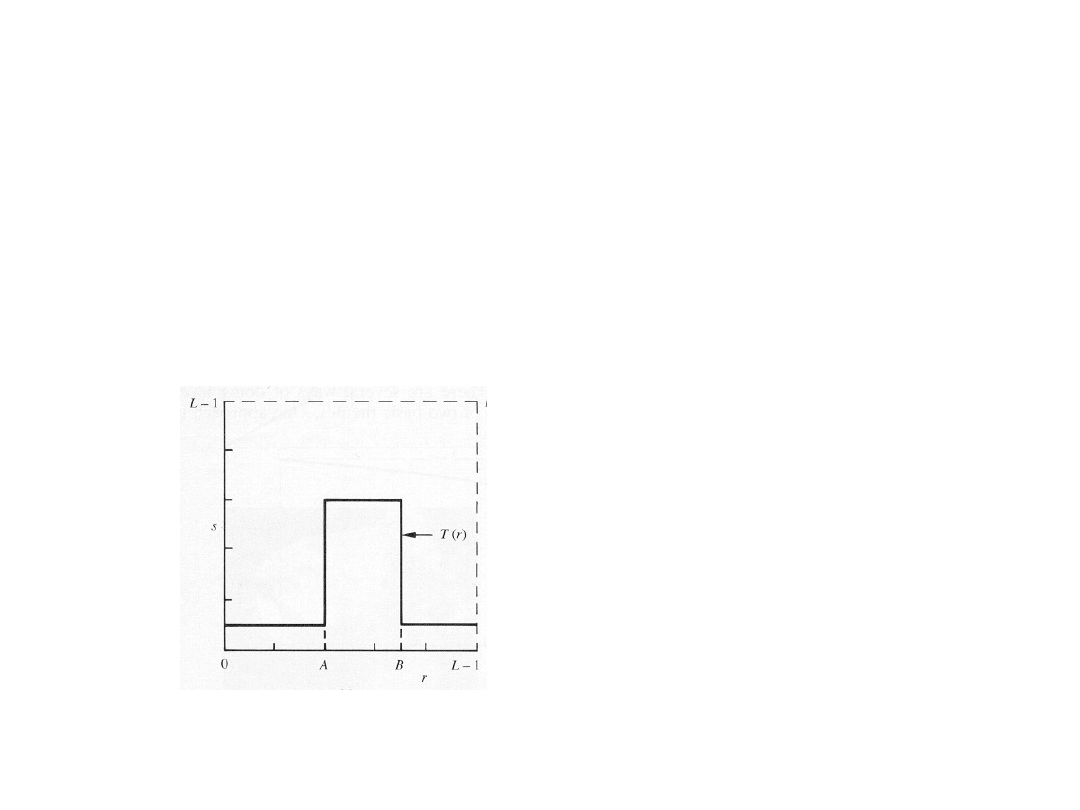
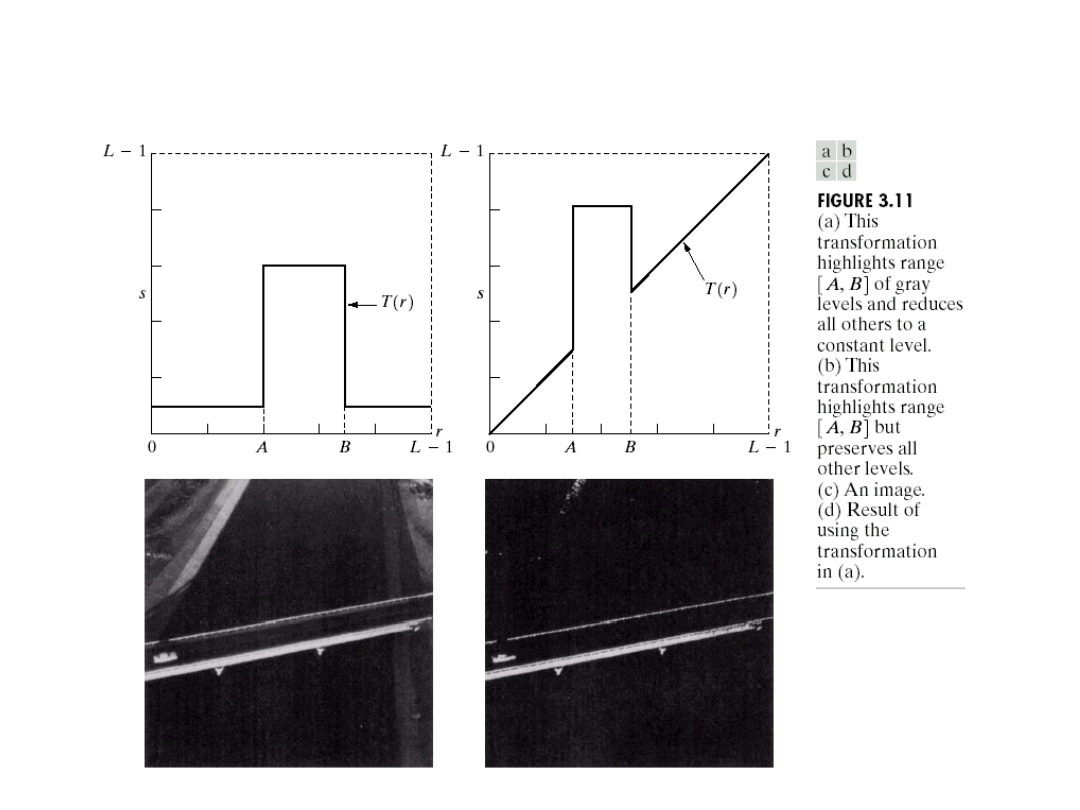
Gray-Level Slicing

• To highlight a specific range of gray levels

in an image (e.g. to enhance certain
features).

One way is to display
a high value for all
gray levels in the
range of interest and
a low value for all
other gray levels
(binary image).

7

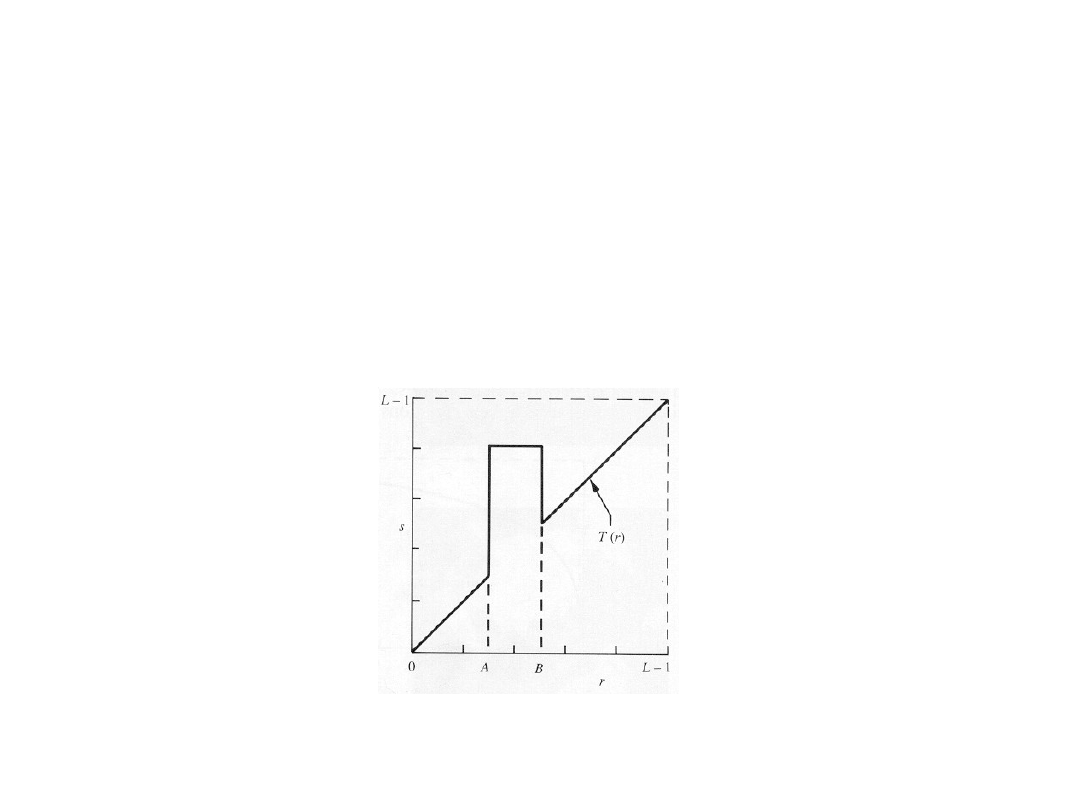
Gray-Level Slicing

– The second approach is to brighten the desired

range of gray levels but preserve the
background and gray-level tonalities in the
image:

8

Image Enhancement in the Spatial

Domain

9

Bit-Plane Slicing

To highlight the contribution made to the total

image appearance by specific bits.

– i.e. Assuming that each pixel is represented by

8 bits, the image is composed of 8 1-bit planes.

– Plane 0 contains the least significant bit and

plane 7 contains the most significant bit.

10

Bit-Plane Slicing

More on bit planes:

– Only the higher order bits (top four) contain

visually significant data. The other bit planes
contribute the more subtle details.

– Plane 7 corresponds exactly with an image

thresholded at gray level 128.

11

12

13

Towards binarization

14

Progowanie obrazu

Jednym z podstawowych zadań analizy obrazu jest segmentacja, czyli podział obrazu

na obszary spełniające pewne kryterium jednorodności. Mówiąc inaczej, pojęcie

obszaru jest używane do określenia spójnej grupy punktów obrazu mających

dodatkowo pewną wspólną cechę, która nie występuje poza najbliższym sąsiedztwem.

Jedną z najprostszych metod wydzielania obszarów jest progowanie. Polega ono na

porównywaniu wartości każdego punktu obrazu z zadaną wartością progową.

Odpowiedni wybór wartości progowej umożliwia wyodrębnienie obszarów określonego

typu. Powstało kilka wersji metody wyodrębniania obszarów przez progowanie.

Metoda najprostsza stosuje jedną wartość progu i jest realizowana według zależności













t

y

x

J

t

y

x

J

y

x

J

w

)

,

(

;

0

)

,

(

;

1

)

,

(

(2.16) gdzie t - próg
binaryzacji.

15

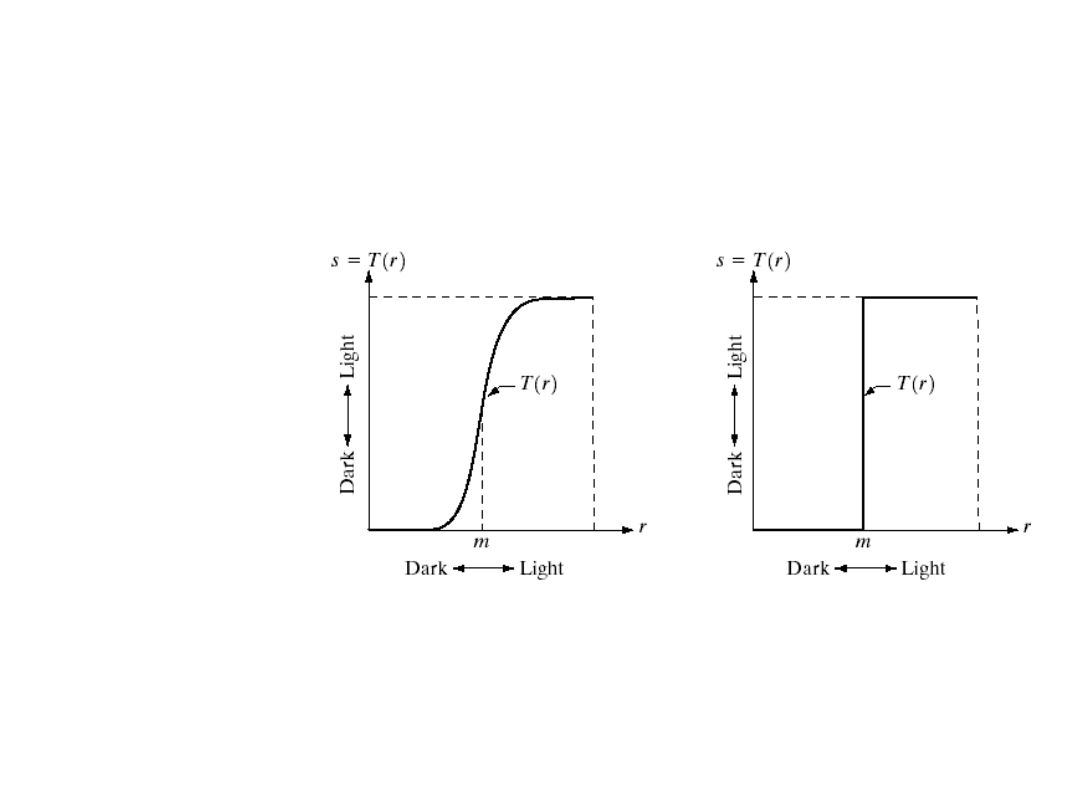
Specjalny przypadek transformacji













.

)

,

(

,

0

)

,

(

,

)

,

(

)

,

(

t

y

x

J

t

y

x

J

y

x

J

y

x

J

w





















t

y

x

J

t

y

x

J

t

t

y

x

J

y

x

J

w

2

2

1

1

)

,

(

,

0

)

,

(

,

1

)

,

(

,

0

)

,

(

Progowanie jest prostą i szybką operacją.

16

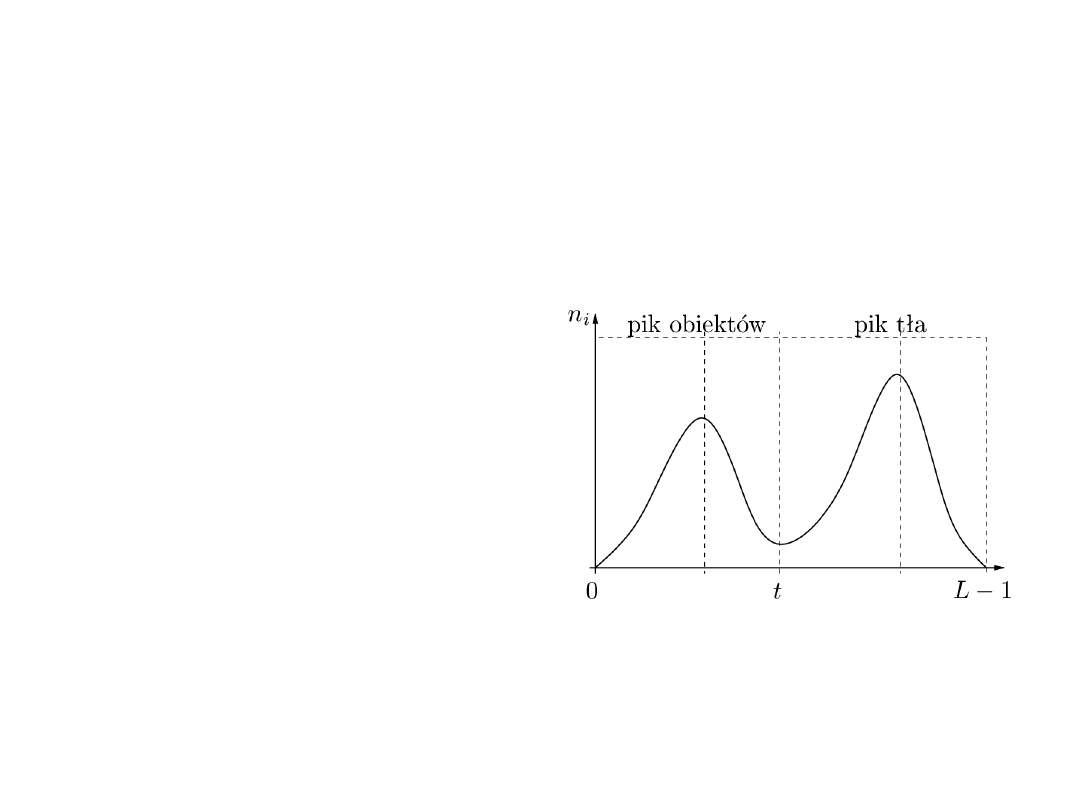
Metody progowania globalnego

Wybór optymalnego progu

podczas przetwarzania

obrazów jest ważny i trudny.

Prostą metodą jest określanie

progu na podstawie

histogramu poziomów jasności

obrazu. Jeżeli histogram będzie

miał rozkład bimodalny, to jako

próg wybiera się takie miejsce,

któremu odpowiada minimum

między pikami histogramu.

Przy użyciu takiego progu treść

obrazu zostanie podzielona na

dwie klasy - obiekty

i tło (rys. 2.12).

Metody tej nie używa się do

znajdowania więcej niż dwóch

progów, nawet jeśli jest więcej

pików w histogramie.

Przykładowy histogram bimodalny

17

Binarizatio
n

18

19

20

•

Wyżej opisane podejście można również zrealizować

w wersji iteracyjnej. Wtedy schemat postępowania dla

rozkładu bimodalnego może być następujący:

•

1. Przyjmij początkową wartość progu t.

•

2. Oblicz średnią wartość czerni tcz wszystkich pikseli poniżej

progu t.

•

3. Oblicz średnią wartość bieli tb wszystkich pikseli powyżej

progu t.

•

4. Oblicz nową wartość progu

•

5. Powtarzaj obliczenia aż t przestanie się zmieniać.

2

b

cz

t

t

t





21

Wyznaczanie progu na podstawie

prostej statystyki obrazu

Zakładamy, że treść analizowanego obrazu można podzielić na
dwie klasy – obiekty i tło. Do wyznaczenia progu skorzystamy z
pewnej statystyki, która nie wymaga konstruowania histogramu.
Algorytm obliczania progu składa się z następujących kroków:
Wyznaczyć moduł gradientu jasności dla każdego punktu obrazu
G(x,y) = max {|Gx(x,y)|, |Gy(x,y)|},
gdzie: Gx(x,y) = J(x+1,y) – J(x-1,y),
Gy(x,y) = J(x,y+1) – J(x,y-1).
- Obliczyć próg według wzoru







x

y

x

y

y

x

G

y

x

G

y

x

J

t

)

,

(

)

,

(

)

,

(

22

Metoda Otsu

Metoda wyznacza się próg t, który dzieli piksele obrazu na dwie

klasy c0 i c1 (obiekty i tło). W dalszych rozważaniach zakładamy,

że:
obraz może mieć L poziomów jasności;
ni oznacza liczbę pikseli o poziomie jasności i, i = 0, 1,... L-1;
całkowita liczba pikseli n = no + n1 + ... nL-1;
histogram obrazu jest unormowany i może być traktowany jak

rozkład prawdopodobieństwa

n

n

p

i

i



, i = 0, 1,...L – 1,

1

1

0









L

i

i

p

;

piksele dzielimy na dwie klasy co i c1 za pomocą progu o wartości t,
gdzie co oznacza piksele o jasności (0,1,... t), zaś c1 oznacza piksele
(t+1,... L-1).

23

Prawdopodobieństwo wystąpienia tych klas i ich

wartości średnie dane są wzorami:







t

i

i

p

P

0

0

= P

t

,

t

L

t

i

i

P

p

P















1

1

1

1

t

t

t

i

i

P

P

ip

/

/

0

0

0













t

t

T

L

t

i

i

P

P

ip

















1

/

1

1

1

1







gdzie P

t

i

t



są odpowiednio momentami zerowego i pierwszego

rzędu dla histogramu obrazu oraz









1

0

L

i

i

T

ip



jest średnią jasnością całego
obrazu.

Można łatwo sprawdzić, że dla dowolnego t jest słuszna następująca relacja:

T

P

P











1

1

0

0

24

Wariancje klas dane są wzorami:

0

2

0

0

2

0

/

)

(

P

p

i

i

t

i













1

2

1

1

1

2

1

/

)

(

P

p

i

i

L

t

i

















Znalezienie optymalnego progu można dokonać na
podstawie optymalizacji jednej
z następujących (równoważnych) funkcji kryterialnych
zależnych od progu t:

2

2

W

B









2

2

W

T









2

2

T

B









2

1

0

1

0

2

1

1

2

0

0

2

)

(

)

(

)

(



























P

P

P

P

T

T

B

- wariancja międzyklasowa,

2

1

1

2

0

0

2







P

P

W





- wariancja wewnątrzklasowa

,











1

0

2

2

)

(

L

i

i

T

i

T

p

n





- wariancja globalna,

przy czym

2

T



jest niezależne od wartości progu t i wyraża się wzorem

2

2

2

B

W

T











,

,

,

25

Warto zwrócić uwagę, że wymaga posługiwania się

statystykami 2‑go rzędu (wariancja), podczas gdy  - 1-
go rzędu (średnie klas). Dlatego jest najprostszą
miarą zależną od t. Stąd optymalny próg t* możemy
obliczyć ze wzoru:

)

(

max

arg

1

0

*

t

t

L

t











1

0

max

arg









L

t

)

(

2

t

B



Ponieważ wariancja jest miarą rozrzutu poziomów
szarości wokół średniej, stąd duża jej wartość oznacza, że
odchylenie od średniej jest duże i piksel obrazu jakby
słabo przynależy do regionu. W związku z tym
maksymalizowanie (2.21) oznacza zwiększanie
odizolowania dwu klas w binaryzowanym obrazie.

(2.21
)

26

Algorithim Otsu

27

Gonzalez’ method for thresholding

(Rafael C. Gonzalez, Richard E. Woods, Steven L. Eddins,

“Digital Image Processing Using Matlab”)

function [bw, t] = threshold_gw(b);
% b bimodal image (dark on bright or bright on dark)
b=double(b);
t=0.5*(min(b(:))+max(b(:)));
told=0;
c=1;
bw(:,:,c)=(b<t);
while abs((told-t)/told)>0.01

c=c+1;
m1 = mean(b(b>t));
m2 = mean(b(b<t));
told=t;
t=0.5*(m1+m2)
bw(:,:,c)=(b<t);

end

28

Problemy

29

• Adaptive thresholding typically takes a grayscale

image as input and, in the simplest implementation,
outputs a binary image.

• There are two main approaches to finding the

threshold:

(i) the Chow and Kaneko approach,
(ii) local thresholding.

• The assumption behind both methods is that smaller image

regions are more likely to have approximately uniform
illumination, thus being more suitable for thresholding. Chow
and Kaneko divide an image into an array of overlapping
subimages and then find the optimum threshold for each
subimage by investigating its histogram. The threshold for each
single pixel is found by interpolating the results of the
subimages. The drawback of this method is that it is
computational expensive and, therefore, is not appropriate for
real-time applications.

Adaptive thresholding

30

An alternative approach

An alternative approach to finding the local threshold is to
statistically examine the intensity values of the local
neighborhood of each pixel. The statistic which is most
appropriate depends largely on the input image. Simple and
fast functions include the mean of the local intensity
distribution,

T=mean,

the median value,

T=median,

or the mean of the minimum and maximum values,

T=(max+min)/2

The size of the neighborhood has to be large enough to cover
sufficient foreground and background pixels, otherwise a poor
threshold is chosen. On the other hand, choosing regions which
are too large can violate the assumption of approximately
uniform illumination.
This method is less computationally intensive than the Chow
and Kaneko approach and produces good results for some
applications.

31

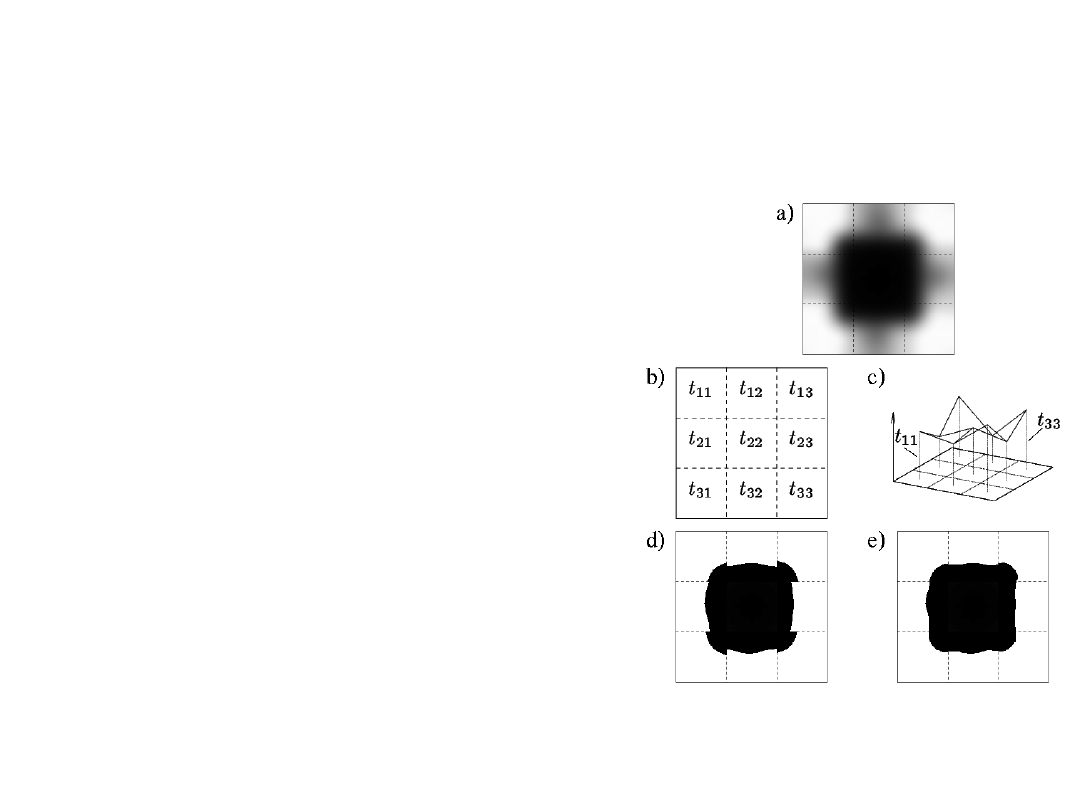
Metody progowania lokalnego

Podczas progowania lokalnego obraz
dzielony jest na podobrazy i próg
określa się dla każdego z nich
niezależnie. To powoduje, że pojawiają
się nieciągłości na granicach dwu
różnych podobrazów (rys. 2.13d).
Dlatego stosuje się różne techniki
wygładzania tych nieciągłości obrazu,
np. poprzez lokalnie liniowe
interpolowanie wartości
progów (rys. 2.13c).
Używając interpolacji skonstruowanej
na podstawie progów sąsiednich
podobrazów otrzymuje się wygładzony
obraz, jak pokazuje rys. 2.13e.

Lokalne progowanie jest formą
progowania adaptacyjnego.

Rys. 2.13

32

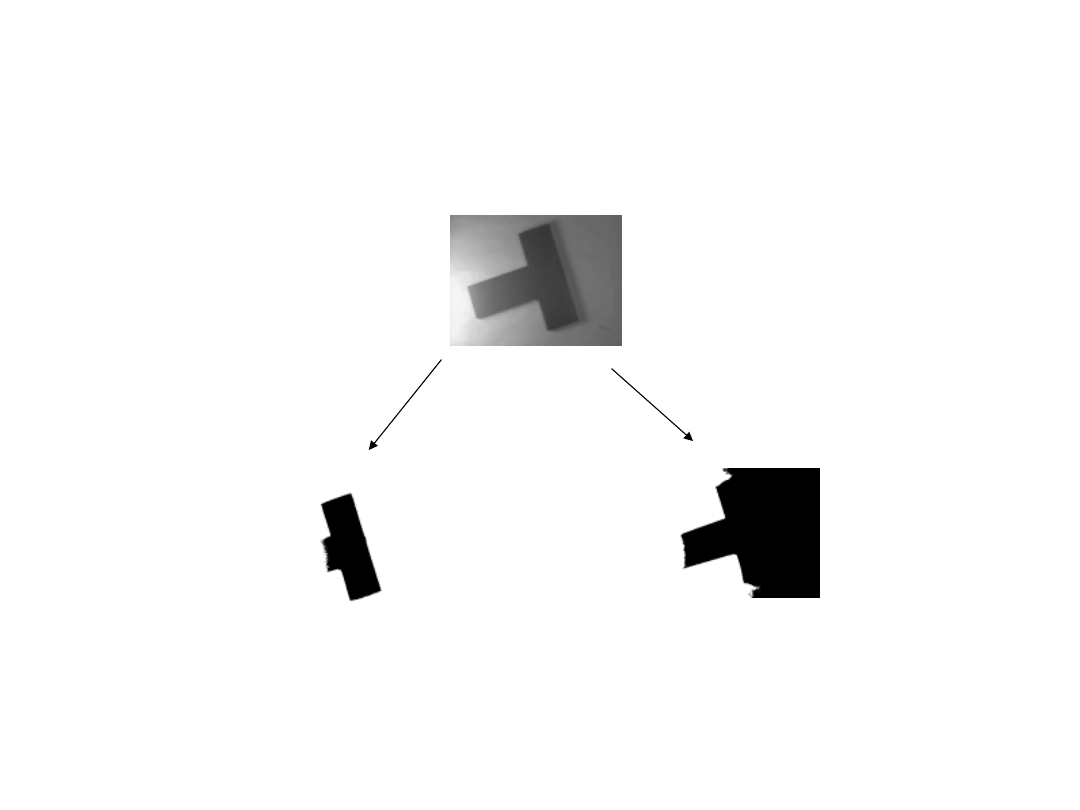
Segmenting text from the image

global

mean of
a 7×7
neighborhood

(mean-C),
C=7,
7×7
neighborhood

(mean-C),
C=10,
75×75
neighborhood

(median-C),
7×7 and C = 4

33

Zakończenie

• Wiele globalnych metod progowania można

rozszerzyć na operację wieloprogowania.

• Uogólnienie metody globalnej na

wieloprogowanie omówimy na przykładzie
metody Otsu.

• Ogólnie trzeba stwierdzić, że problem

wieloprogowania jest trudny i poszukiwania
optymalnego algorytmu ciągle trwają.