Krótki kurs statystyczny czyli jak

poprawnie opracowywać dane przez

nas pozyskiwane ?

Odpowiedzialna za treść – dr Magda Łabieniec

Kiedy możemy stosować

test t-

Studenta

a kiedy tak naprawdę go

stosujemy???

Test t – Studenta

•gdy rozkład jest normalny

•gdy wariancje są jednorodne (równocenne)

czyli nie różnią się (dla prób nieskorelowanych)

•gdy porównujemy tylko 2 próby (populacje)

•dla prób zależnych i niezależnych

Przykłady prób powiązanych

(skorelowanych, zależnych, sparowanych)

- pomiar ciśnienia u człowieka przed podaniem leku i 2h po

podaniu

-gdy 1 dnia prowadzimy badania na tym samym materiale

biologicznym (komórki, krew, błony, mitochondria) – np.

kontrola i testowane stężenia związku na tej samej linii

komórkowej

Przykłady prób niepowiązanych

(nieskorelowanych, niezależnych, niesparowanych)

- gdy porównujemy działanie tego samego związku na

różnych komórkach (liniach komórkowych, krwi od różnych
pacjentów, tkankach/komórkach pochodzących z różnych
organów, lub od różnych zwierząt)

placebo PAMAM G2 PAMAM G4

dalsze badania in vitro

Uwaga!!!!

Gdy dane przedstawiamy

jako

wartości względne

(np. % kontroli) wówczas

próby traktujemy jako

NIESPAROWANE!!!

Kiedy

SD

a kiedy

SEM (SE)

?

• SD – odchylenie standardowe = błąd

pojedynczego pomiaru (wskazuje na
różnice w zakresie tej samej zmiennej
pomiędzy badanymi osobnikami)

• SEM – standardowy błąd średniej; SE –

błąd standardowy = błąd średnich
(wskazuje jak precyzyjnie pracowaliśmy)

SEM = SD/√n

, gdzie n-liczność próby

Gdy liczba wykonanych

przez nas powtórzeń nie

jest na tyle duża by

próbę można uznać za

reprezentacyjną

(odnośnik do populacji)

wówczas należy posłużyć

się

SEM

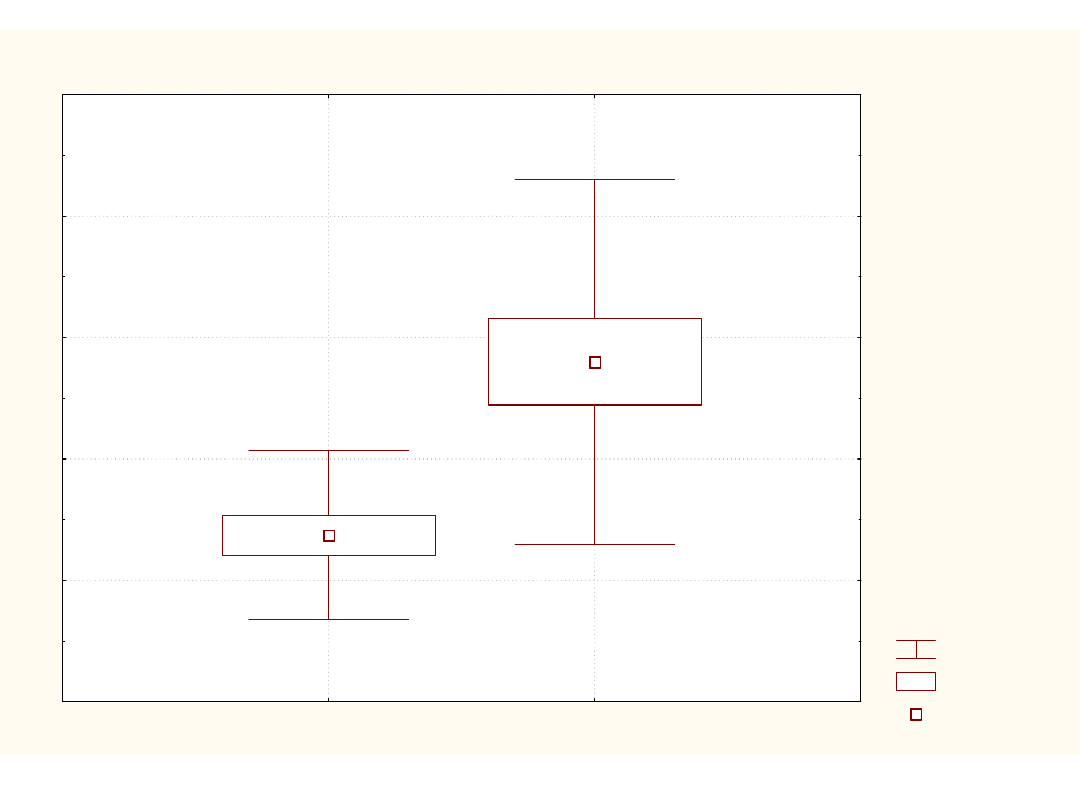
±Odch. std.
±Błąd std.
Średnia

Wykres ramkowy

7.1

7.3

7.5

7.7

7.9

8.1

BSA

BSA_G2

Testy

parametryczne

nieparametryczne

• t-Studenta sparowany
• t-Studenta

niesparowany

• ANOVA – 1 czynnikowa
• ANOVA – 2 czynnikowa

• Korelacja Pearsona

gdy rozkład normalny

• Kolejność par Wilcoxona

-

gdy brak normalności

rozkładu

• Manna Whitneya

• Kruskala-Wallisa

- gdy wariancje nie są

jednorodne

• Friedmana

• Korelacja Spearmana

• Korelacja Kendalla

• Korelacja Gamma

gdy brak jest normalności

Shapiro –Wilk


Schemat postępowania dla prób sparowanych

1. sprawdzić normalność rozkładu rożnic

testem

Shapiro-Wilka

normalny brak

normalności

test rang Wilcoxona

(z popr.

Bonferroniego)

3. test t-Studenta dla prób zależnych
(z popr. Bonferroniego)

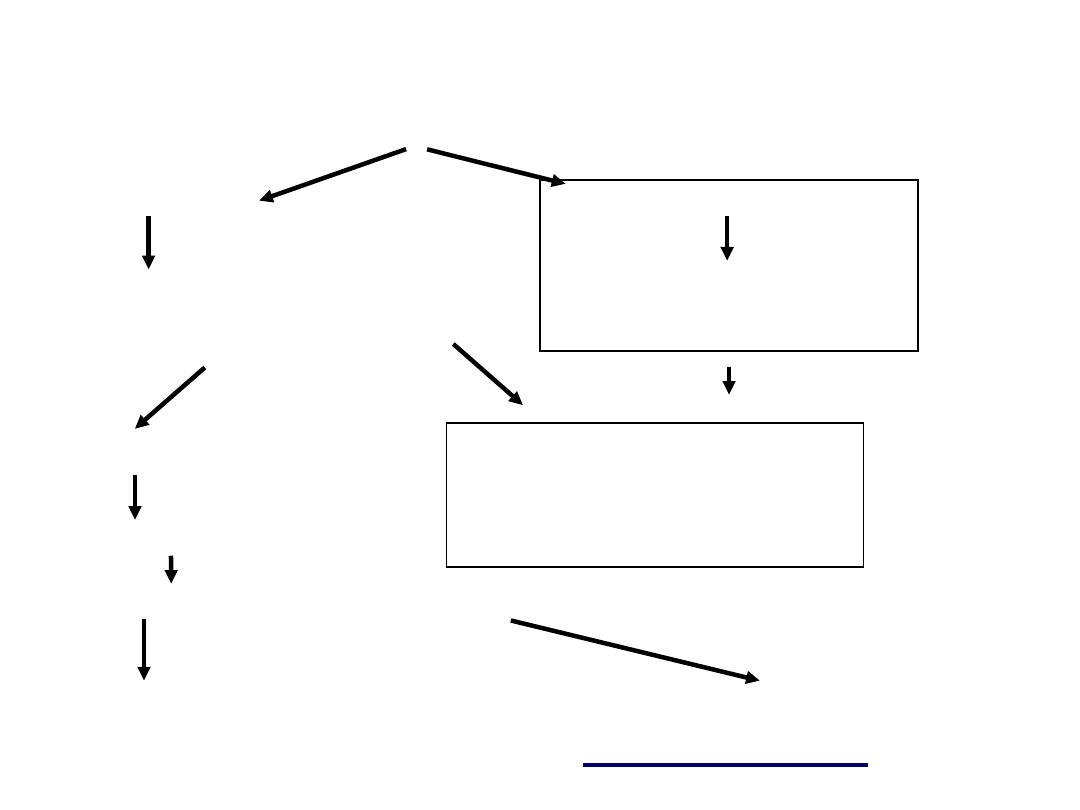
Schemat postępowania dla prób nieskorelowanych

1. sprawdzić normalność rozkładu

testem parametrycznym

Shapiro-Wilka

normalny brak normalności

2. sprawdzić jednorodność

test Manna-Whitneya

(z popr. Bonferroniego)

wariancji

testem Levene’a

jednorodne brak jednorodności

3. analiza wariancji (Anova) test Kruskala-Wallisa

4.Testy porównań wielokrotnych

test Tukeya

test t-Studenta dla prób

niezależnych

(z popr. Bonferroniego)

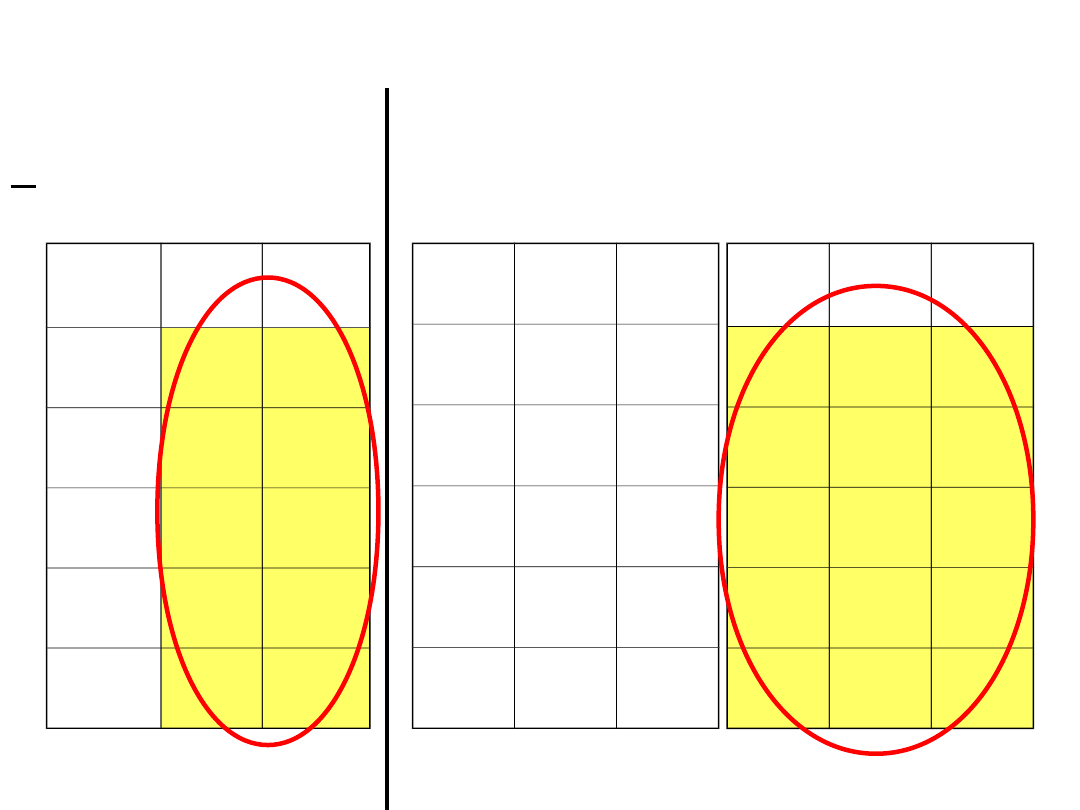
Jak ocenić normalność

testem Shapiro-

Wilka

?

wartości względne wartości

bezwględne

mierzymy różnice

Kontr.
%

10

uM

20

uM

100

89

76

100

74

65

100

87

66

100

91

59

100

85

57

Kont

r

10

uM

20

uM

300

289

156

324

278

134

333

267

156

350

254

178

332

256

165

K-10 K-20 10-

20

11

144

133

46

190

144

66

177

111

96

172

76

76

167

91

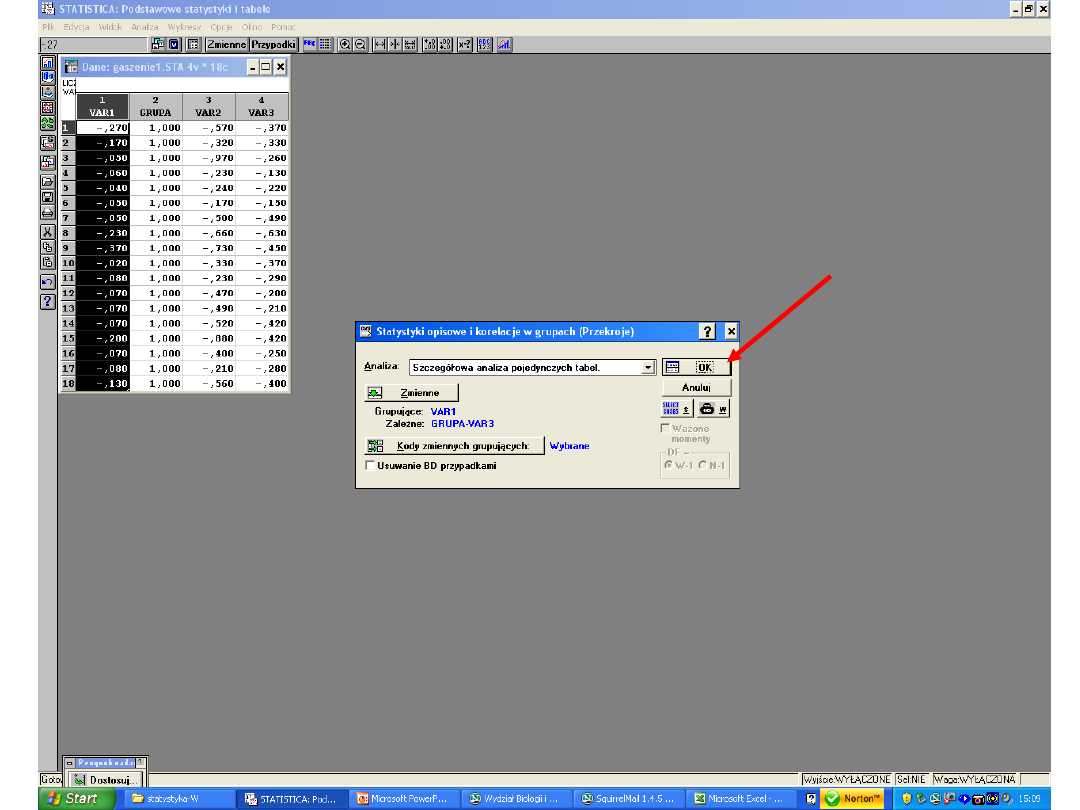
Jak przygotować dane do analizy programem

STATISTICA

1. Wszystkie pomiary/dane wpisać do Excela, w

kolumnach – nie liczyć średniej ani Sd!!! – i zapisać 

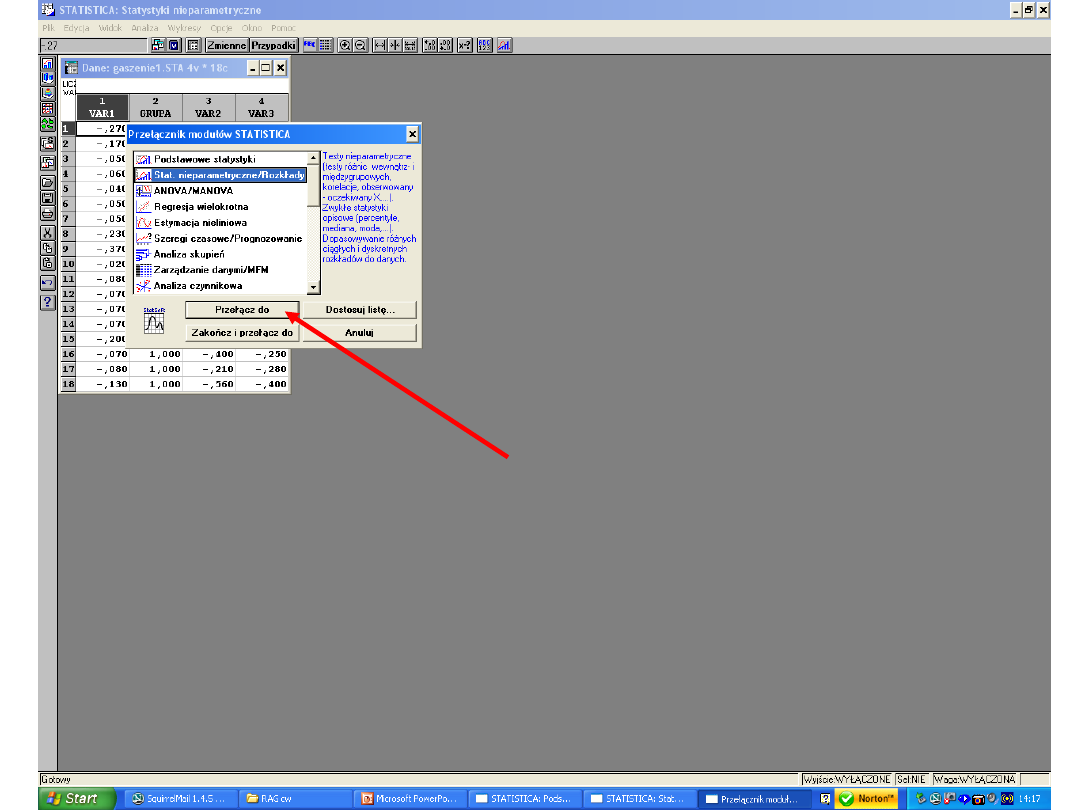
2. Otworzyć program Statistica. Pojawi się okno

dialogowe „Przełącznik modułów Statistica”. Wybrać
opcje „Podstawowe statystyki” i kliknąć „Przełącz do”

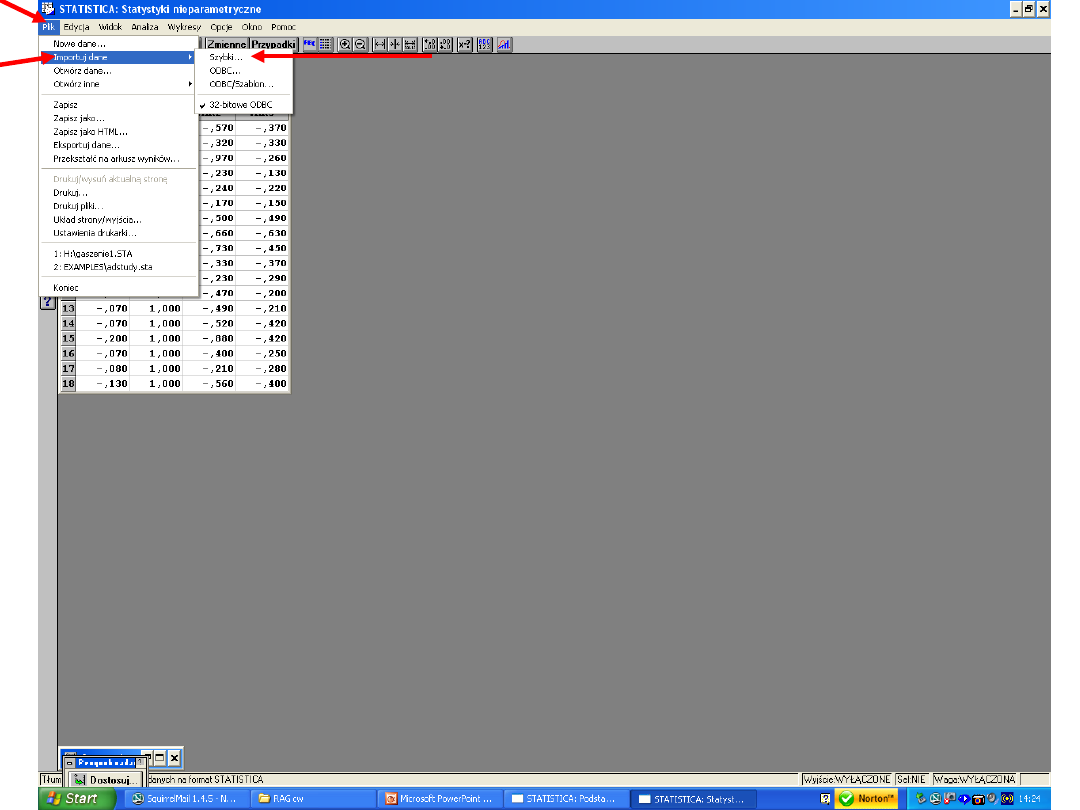
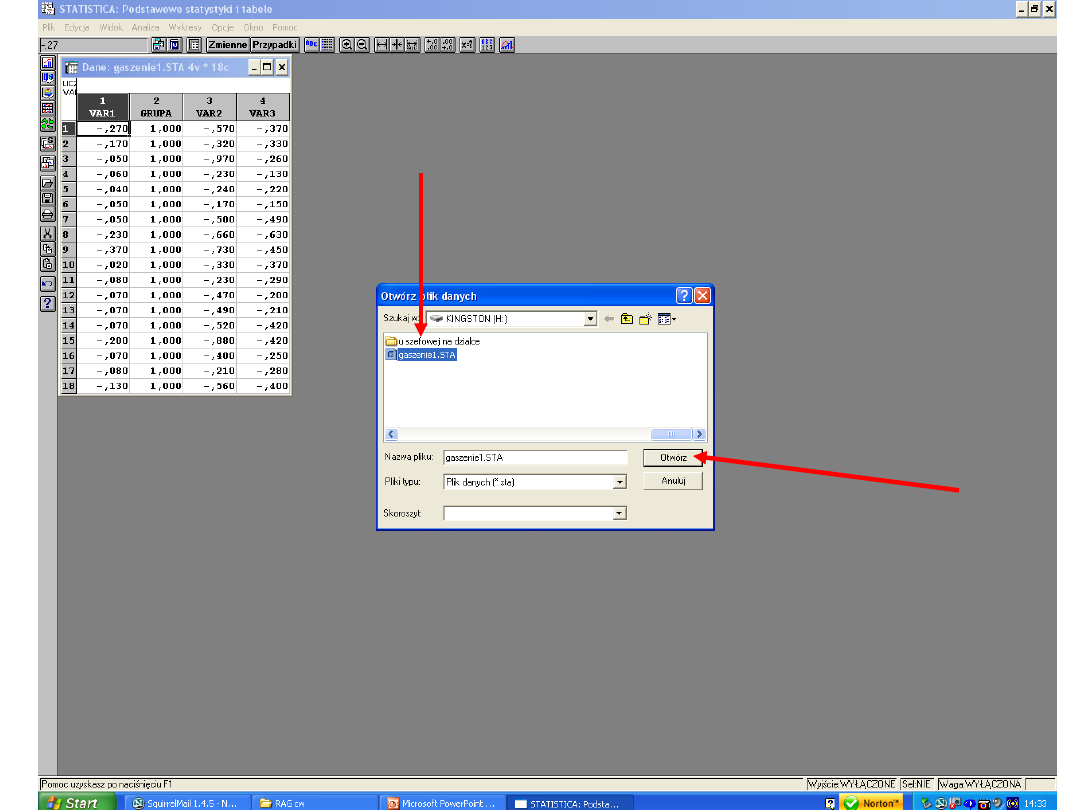
3. Z paska narzędzi wybrać PLIK a potem „Importuj

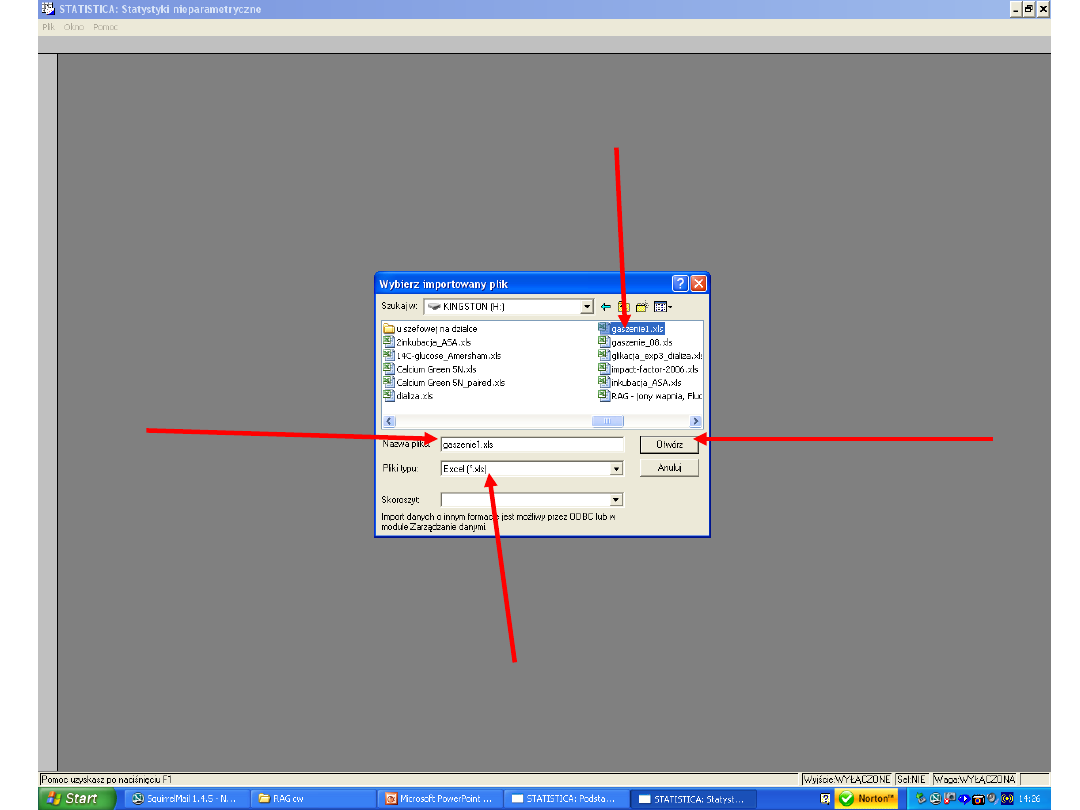
dane” „Szybki”. Pojawi się okno dialogowe „Wybierz
importowany plik”. Wtedy odnajdujemy plik excela z
zapisanymi wcześniej danymi i klikamy „Otwórz”

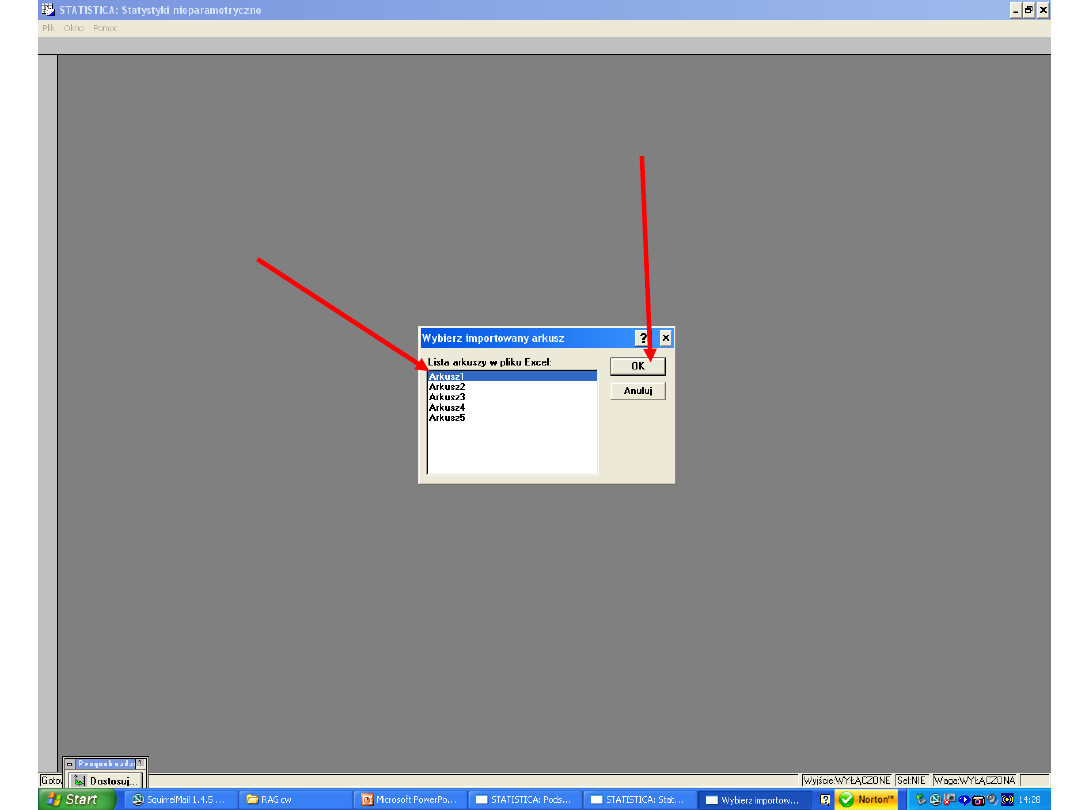
4. Pojawi się kolejne okno „Wybierz importowany

arkusz”. Wybieramy „Arkusz1” i klikamy OK..

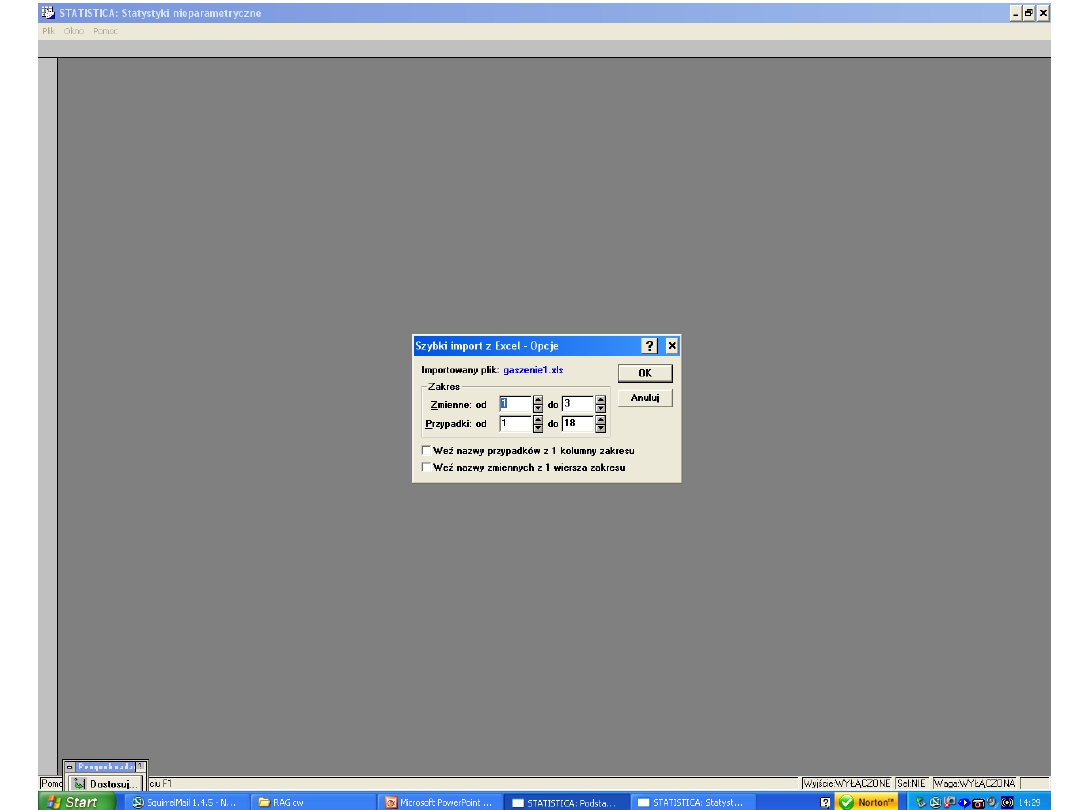
5. Otworzy się okno „Szybki import z Excel-Opcje”,

klikamy Ok.

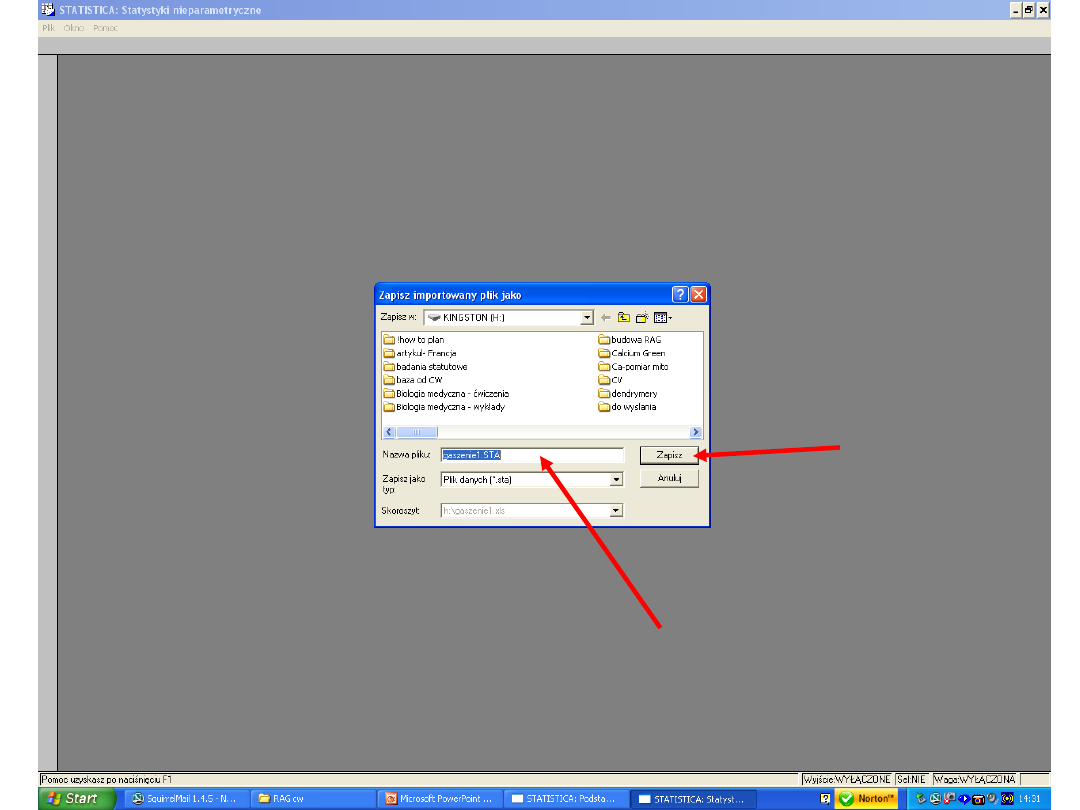
6. Pojawi się kolejne okno „Zapisz importowany plik jako”, wtedy
nasze dane zapiszą się z rozszerzeniem STA i natychmiast ukażą na
ekranie monitora gotowe do dalszej, statystycznej obróbki.

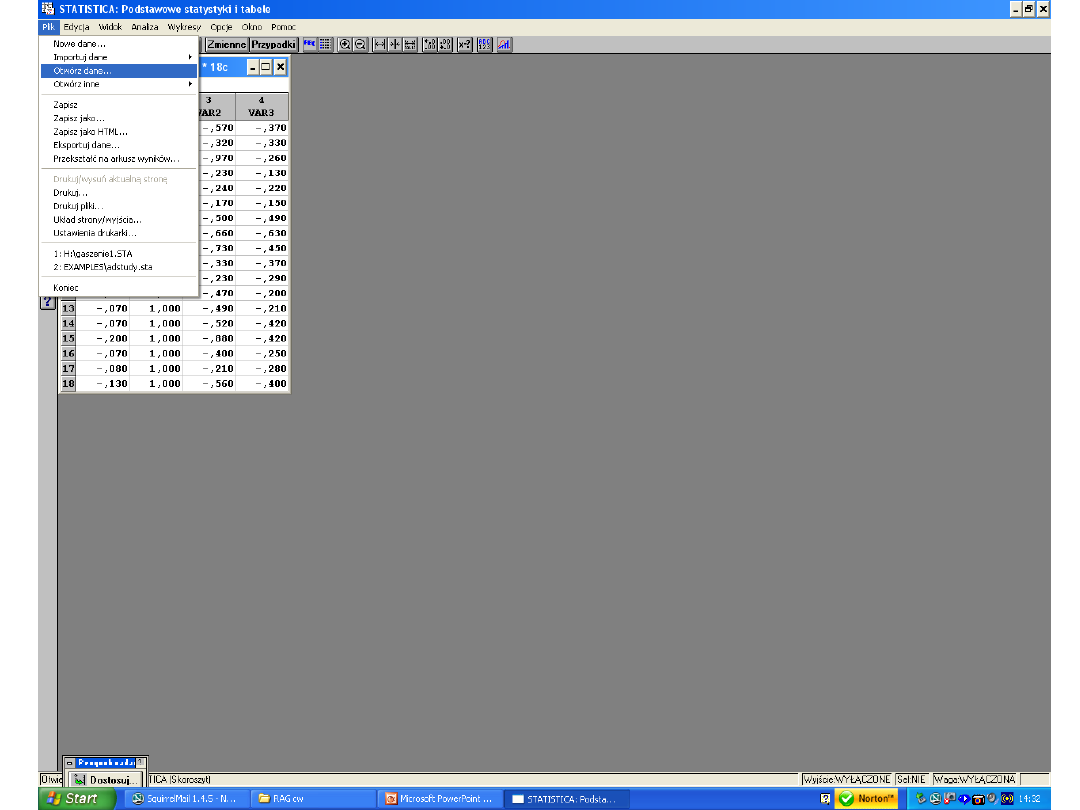
7. Dane zostaną pokazane dokładnie w takiej formie, w jakiej
zapisaliśmy je w pliku excela. Z tym, że sami musimy wpisać nazwy
naszych zmiennych. Póki co istnieją jako VAR1, VAR2 itd. Można też
wybrać pierwszy wiersz arkusza Excela jako wiersz z nazwami
zmiennych.

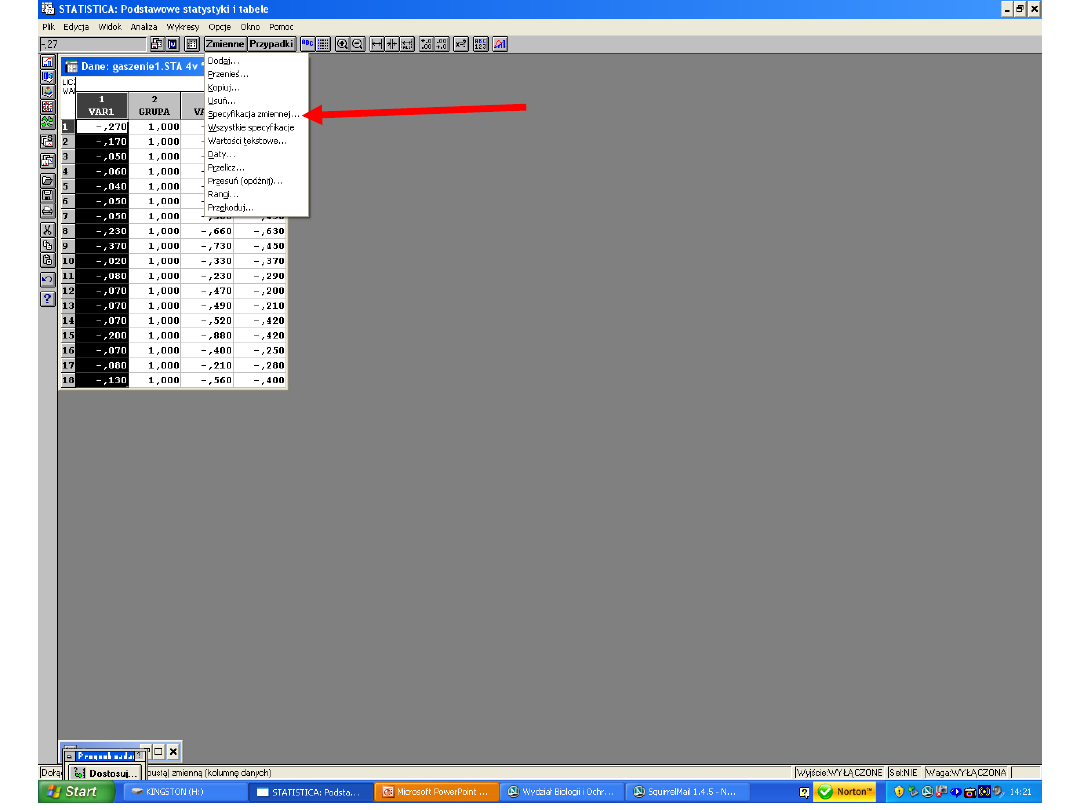
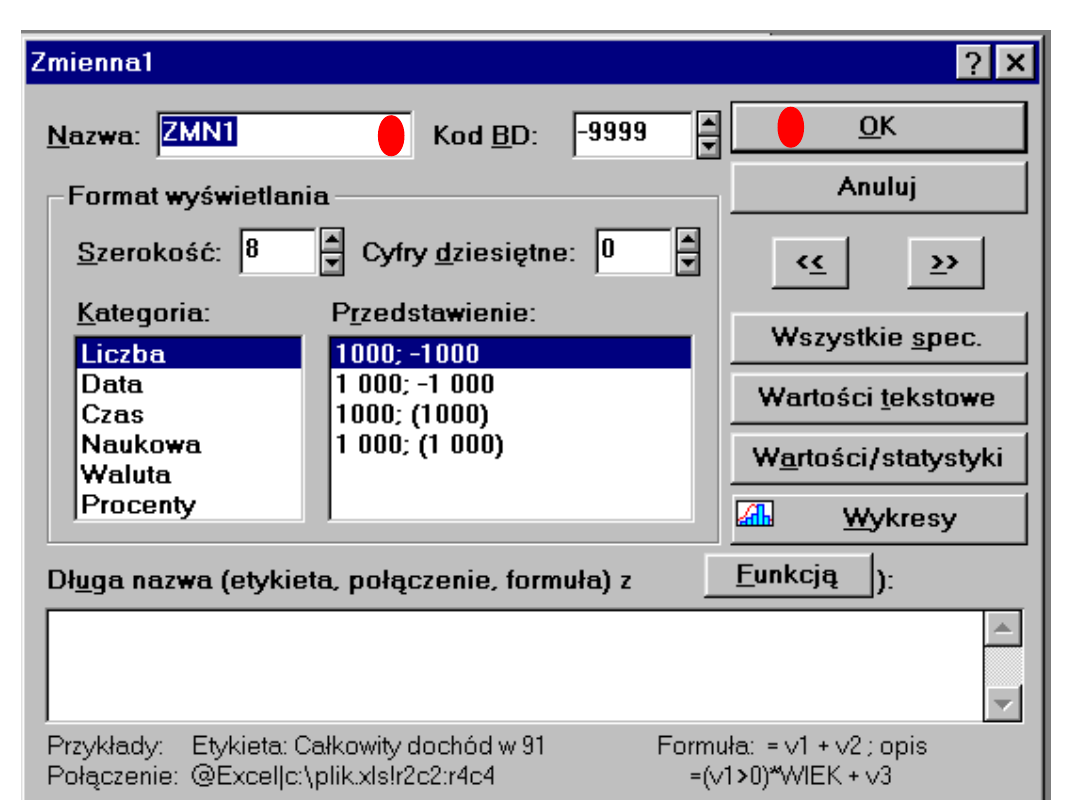
8. Zaznaczamy np. VAR1, następnie wchodzimy w „Zmienne”,
wybieramy opcje „Specyfikacja zmiennej”, klikamy i pojawia nam się
okno dialogowe, w którym pod „Nazwa” wpisujemy własne
oznaczenia. I postępujemy tak dla każdej zmiennej z osobna.
Przykład takiego okna na następnym slajdzie.

c

c

Yhm, świetnie a teraz

sprawdźmy wreszcie tę

normalność!

Jakim testem?

 Shapiro-Wilka 

Stosując test Shapiro-Wilka

musimy pamiętać, że

normalność sprawdzamy dla

każdej kolumny

ODDZIELNIE

.

Zaznaczamy to w punkcie:

„Zmienne”

Uwaga!!!!

• Analiza naszych danych to zawsze

testowanie hipotez. Umiejętność ich

konstruowania to podstawa

interpretacji wyników!

• Hipoteza badawcza (robocza)

• Hipoteza statystyczna:
Ho: hipoteza zerowa x1=x2 (brak różnic)
Ha: hipoteza alternatywna x1</>x2

(różnice)

Gdy badamy normalność .....

Ho: rozkład zmiennej jest normalny

Ha: brak normalności badanej zmiennej

Interpretacja:

Jeśli w wyniku testowania testem Shapiro-Wilka nie

wykażemy istotności przy założonym przez test

poziomie istotności wówczas mówimy,

że

odrzucamy hipotezę alternatywną na korzyść

hipotezy zerowej z określonym

prawdopodobieństwem p (np. p=0.75)

czyli rozkład

naszej zmiennej jest normalny. Dostajemy zielone

światło by przejść do testów parametrycznych

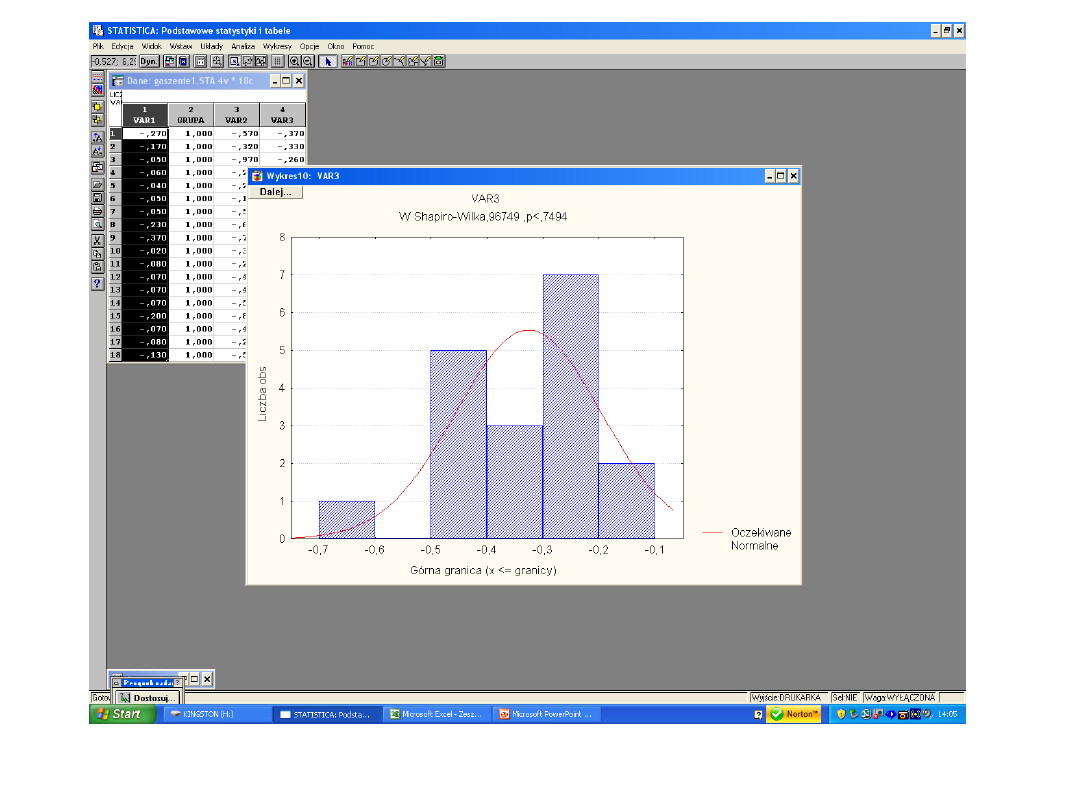
Brak istotności testu oznacza – rozkład normalny badanej

zmiennej

Jeśli rozkład badanych zmiennych

jest

normalny

a grupy, które

badamy są skorelowane (zależne,

powiązane) to następnie

stosujemy test t-Studenta dla

prób zależnych (gdy porównujemy

2 grupy) lub test

t-Studenta z

poprawką Bonferroniego

(gdy

porównujemy więcej niż 2 grupy)

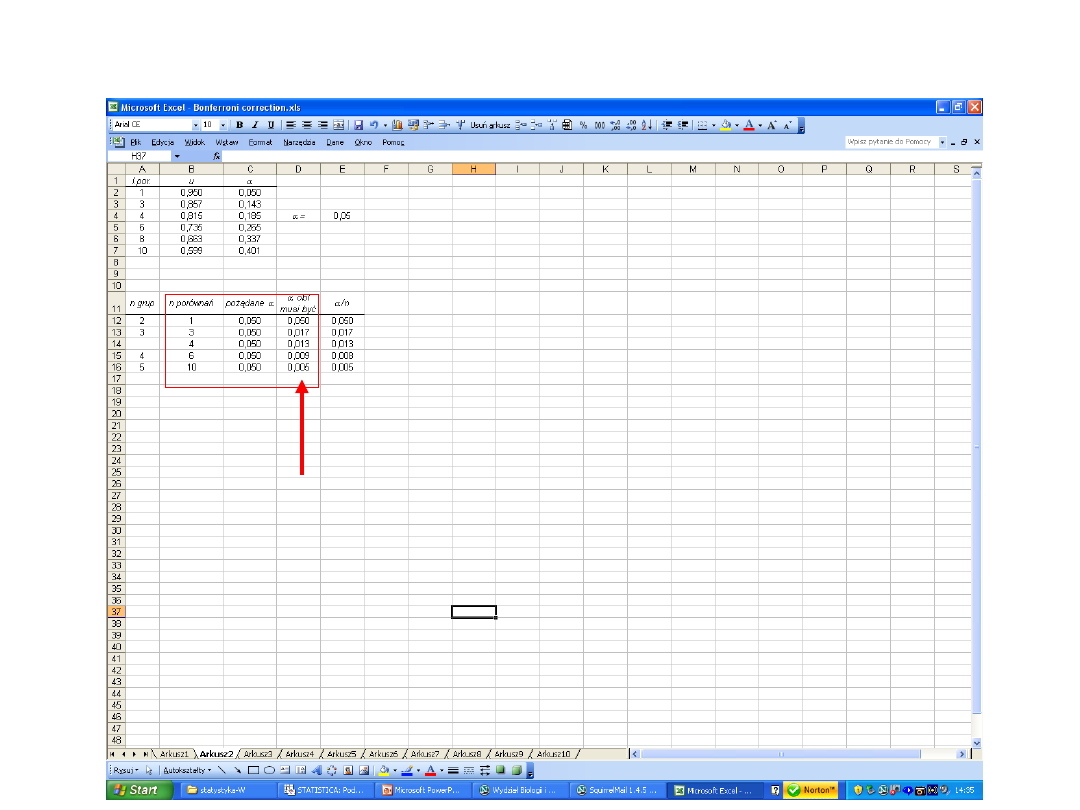
Poprawka Bonferroniego

Wnioskowanie

statystyczne dla prób

zależnych

Uwaga !!!

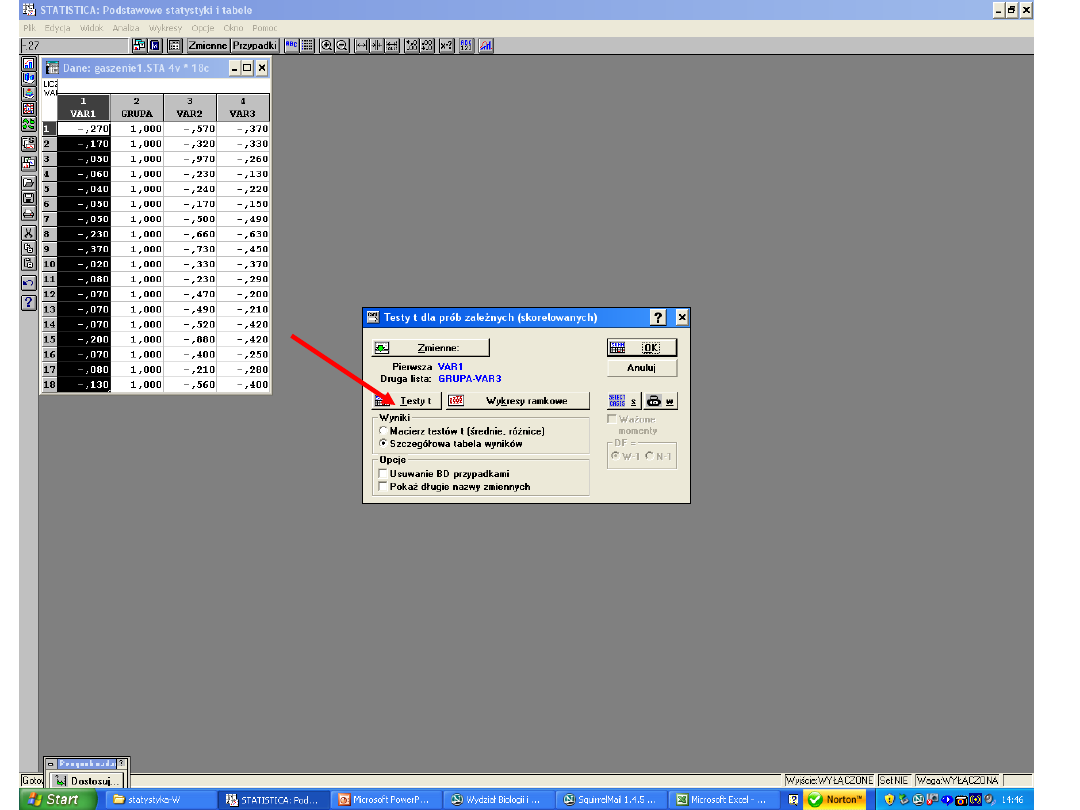
1. Jeśli planujemy potraktować nasze próby

jako zależne (skorelowane) to przedtem

należy się upewnić, że dane przygotowane

do analizy są wyrażone

w postaci wartości

bezwzględnych.

2. Jeśli pierwszy warunek jest spełniony,

wówczas należy zwrócić uwagę na to, że

poza badaniem rozkładu normalnego

naszych zmiennych (gdzie badamy

różnice)

do dalszej analizy statystycznej

wykorzystujemy uzyskane przez nas dane

(wartości bezwzględne) a nie ich

różnice !!!!

3. Rozkład różnic naszych zmiennych musi

być normalny!!!

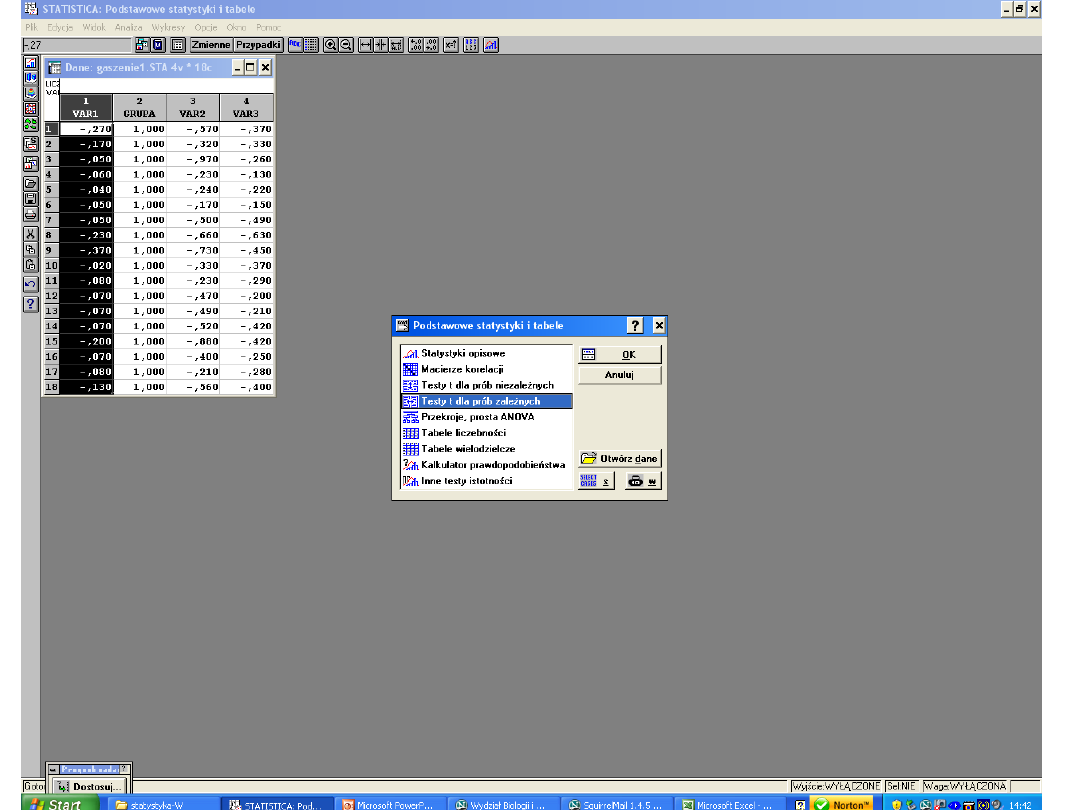
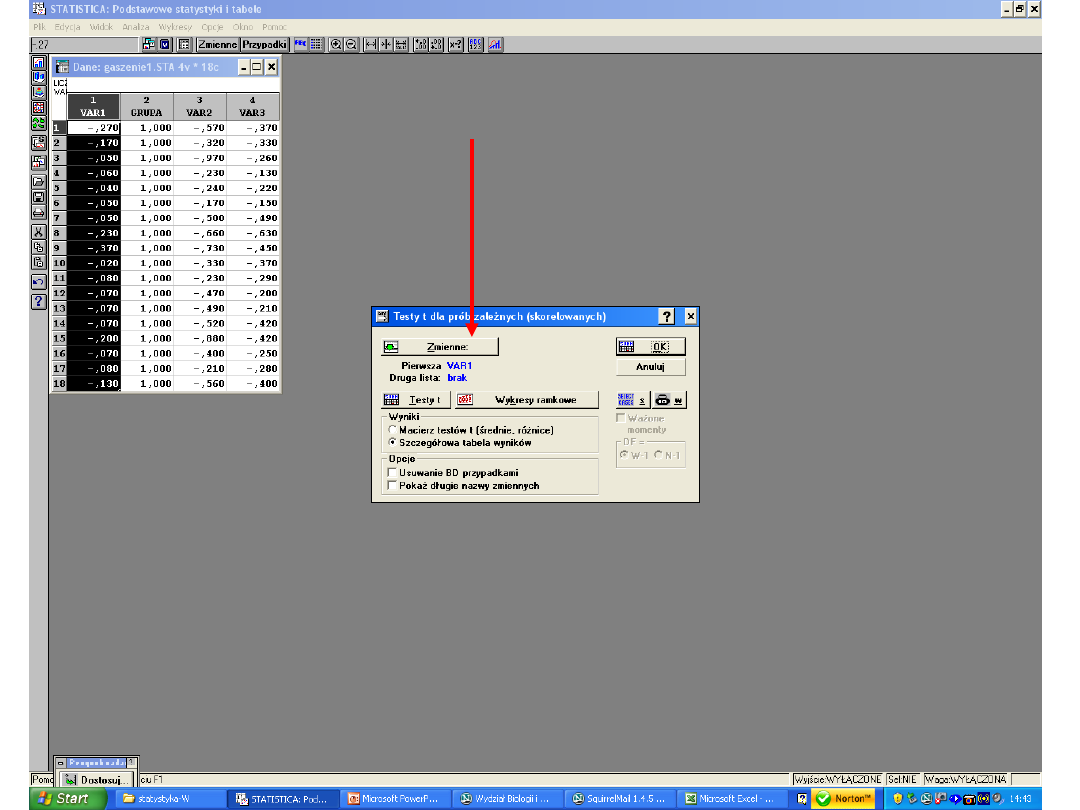
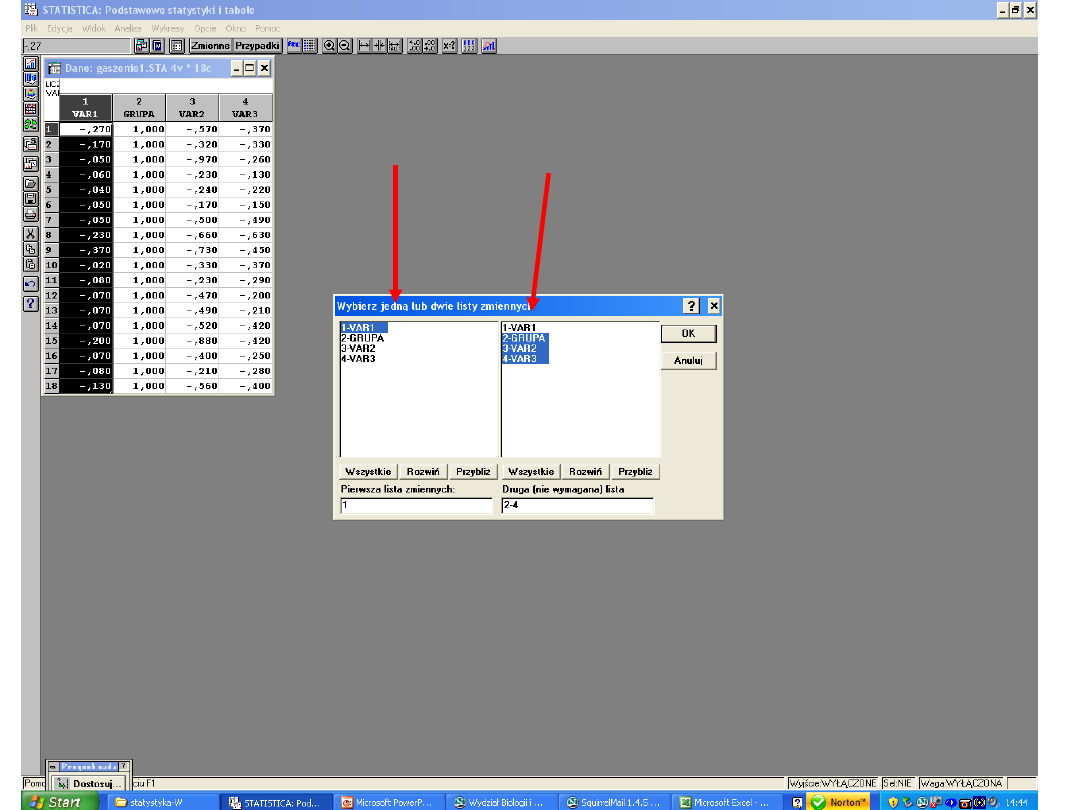
Wnioskowanie

statystyczne dla prób

niezależnych

Uwaga !!!

Jeśli jesteśmy na tym etapie, to upewnijmy się, czy to jest

dobry wybór testów. Czy spełniony jest przynajmniej

1 z poniższych warunków:

-

Próby (nasze wyniki) zostały przedstawione w postaci

wartości względnych

-

Próby zostały wykonane w sposób, który kwalifikuje

je do potraktowania jako badania nieskorelowane

-

rozkład zmiennych jest normalny (uwaga! –

normalność wartości względnych badamy nie biorąc

pod uwagę tych prób, wobec których reszta wyników

była przeliczana a ponadto nie liczymy tu różnic!!! jak

dla testów sparowanych

-

Analiza statystyczna dalsza (poza badaniem

normalności) dotyczy wszystkich zebranych wyników,

nawet tych, które w wyniku zamiany na wartości

względne straciły swoją zmienność

1. sprawdzić normalność rozkładu testem

parametrycznym

Shapiro-Wilka

normalny brak

normalności

2. sprawdzić jednorodność
wariancji

testem Levene’a

jednorodne brak jednorodności

3. analiza wariancji (Anova)

4.Testy porównań wielokrotnych

test t-Studenta (z

popr.

(test Tukeya) Bonferoniego)

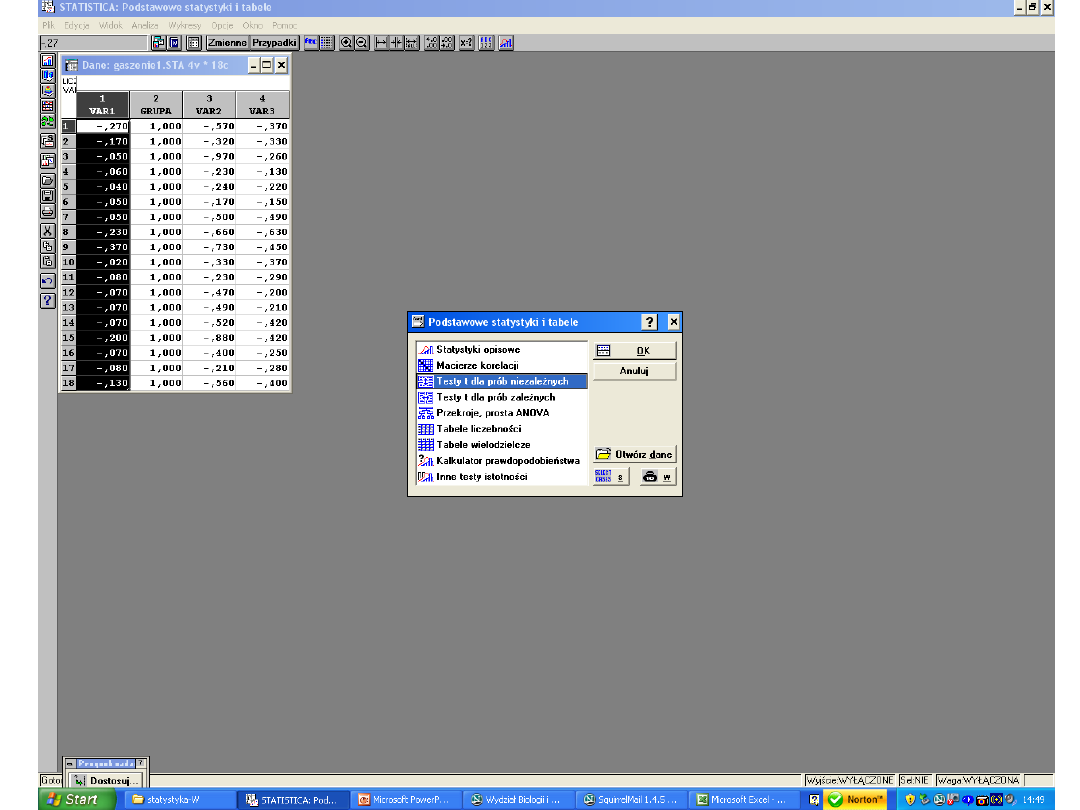
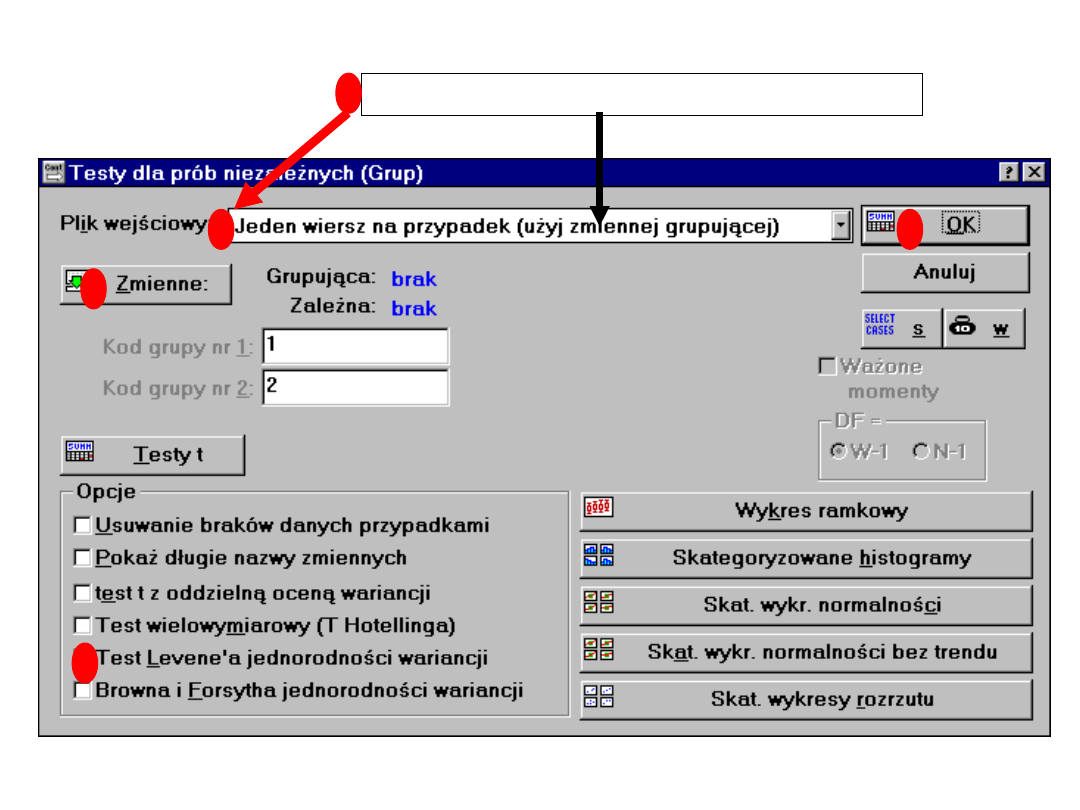
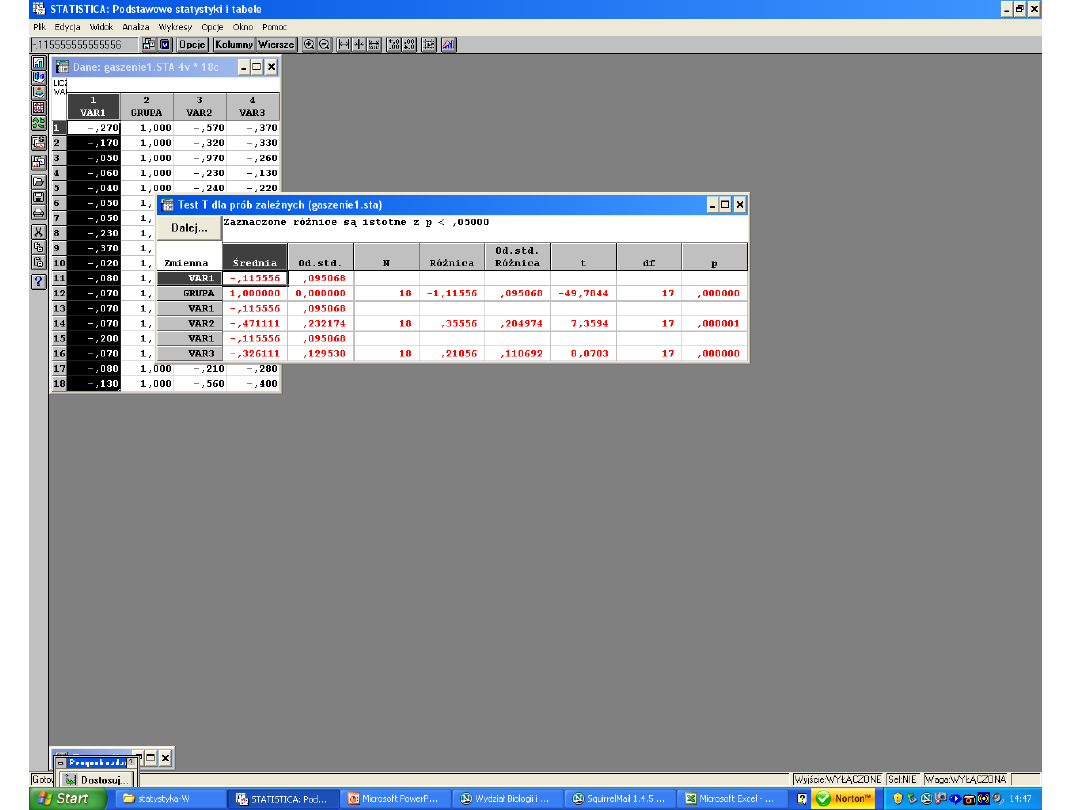
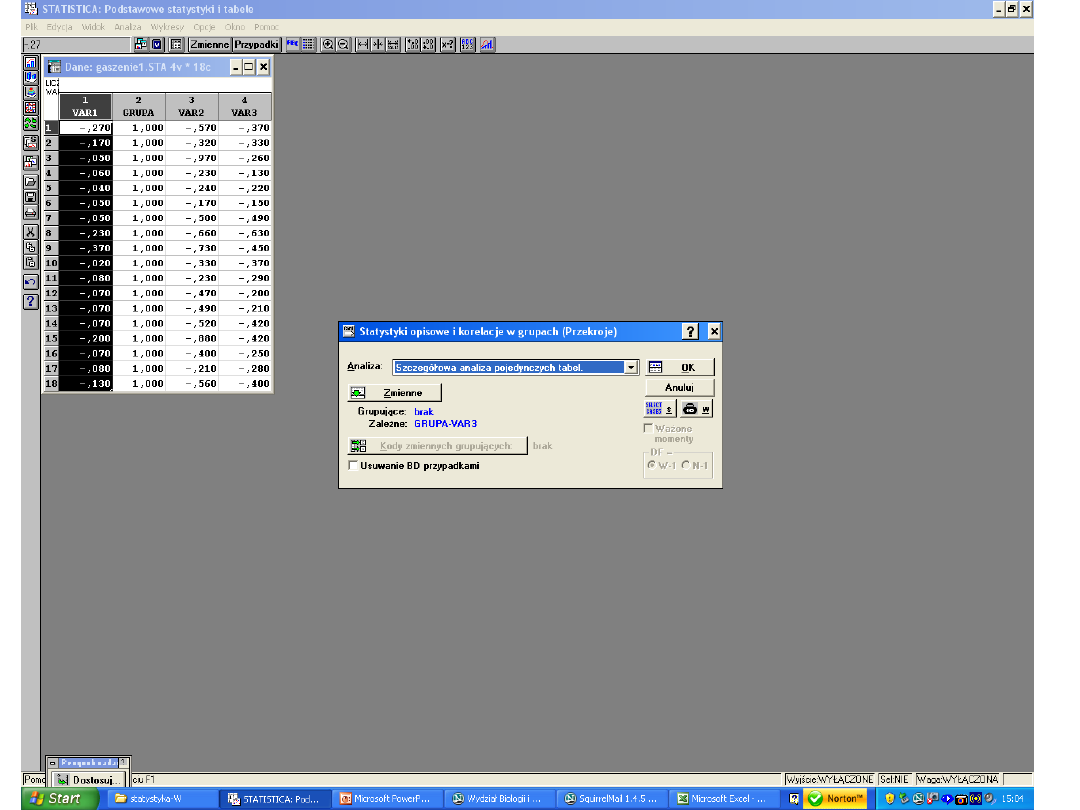
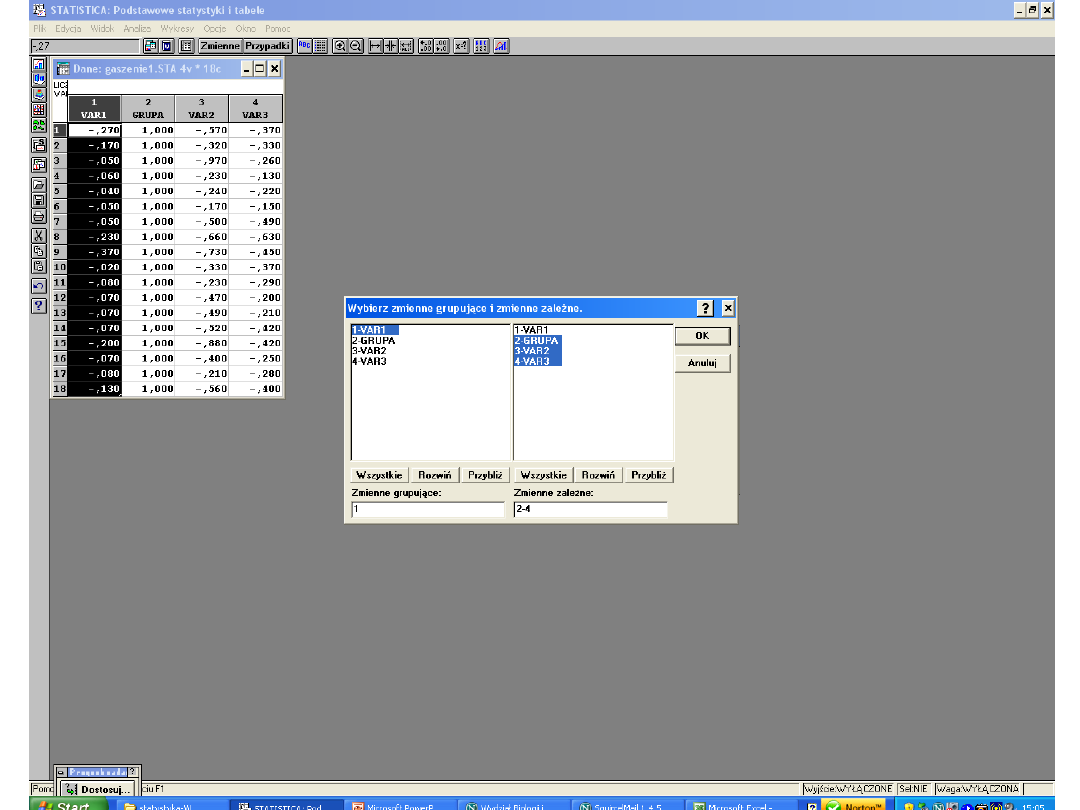
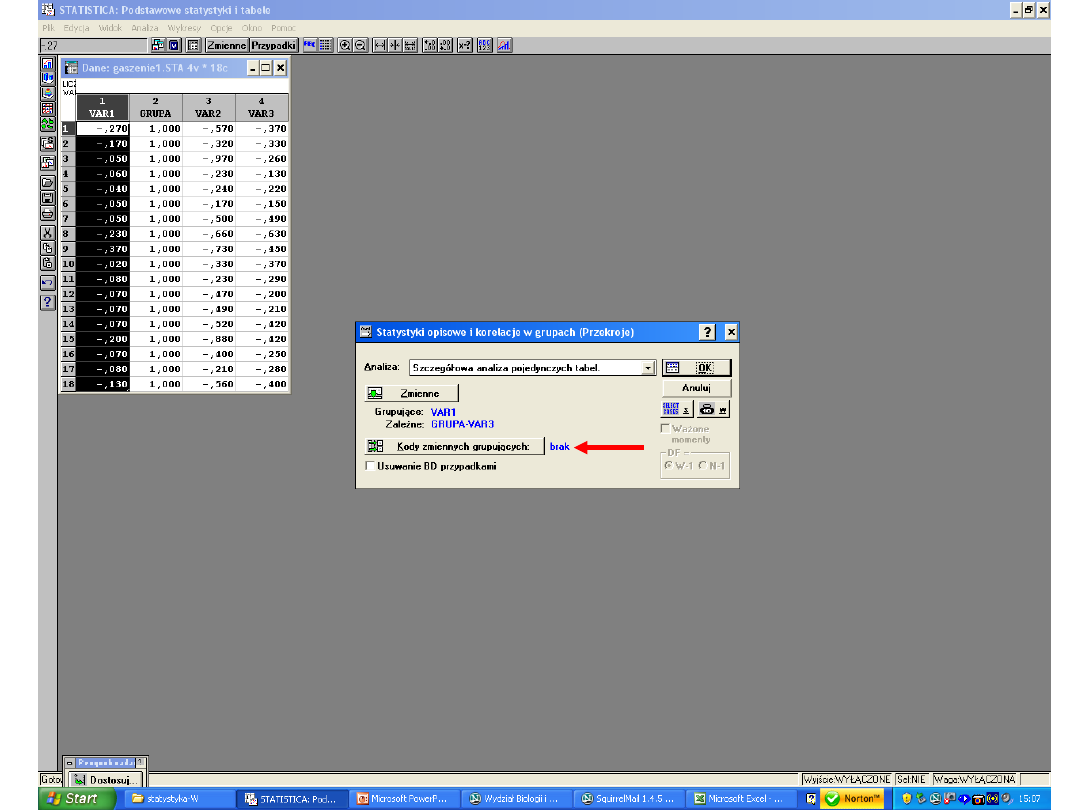
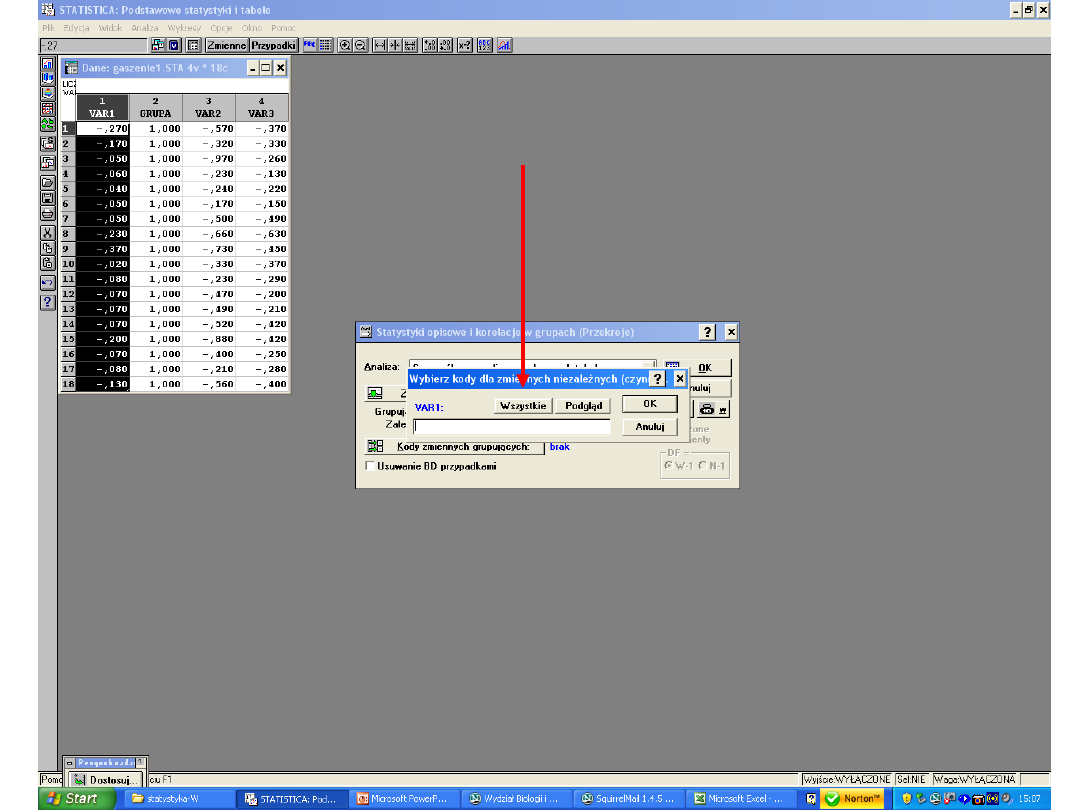
Każda zmienna zawiera dane o 1 grupie

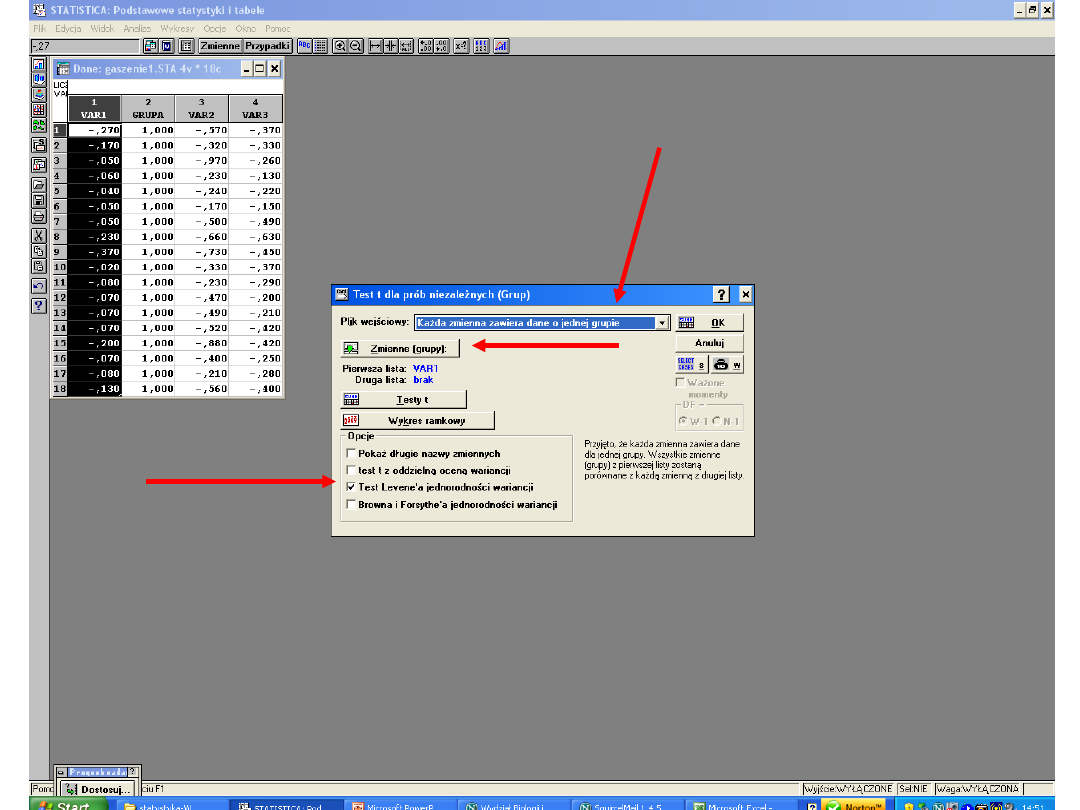
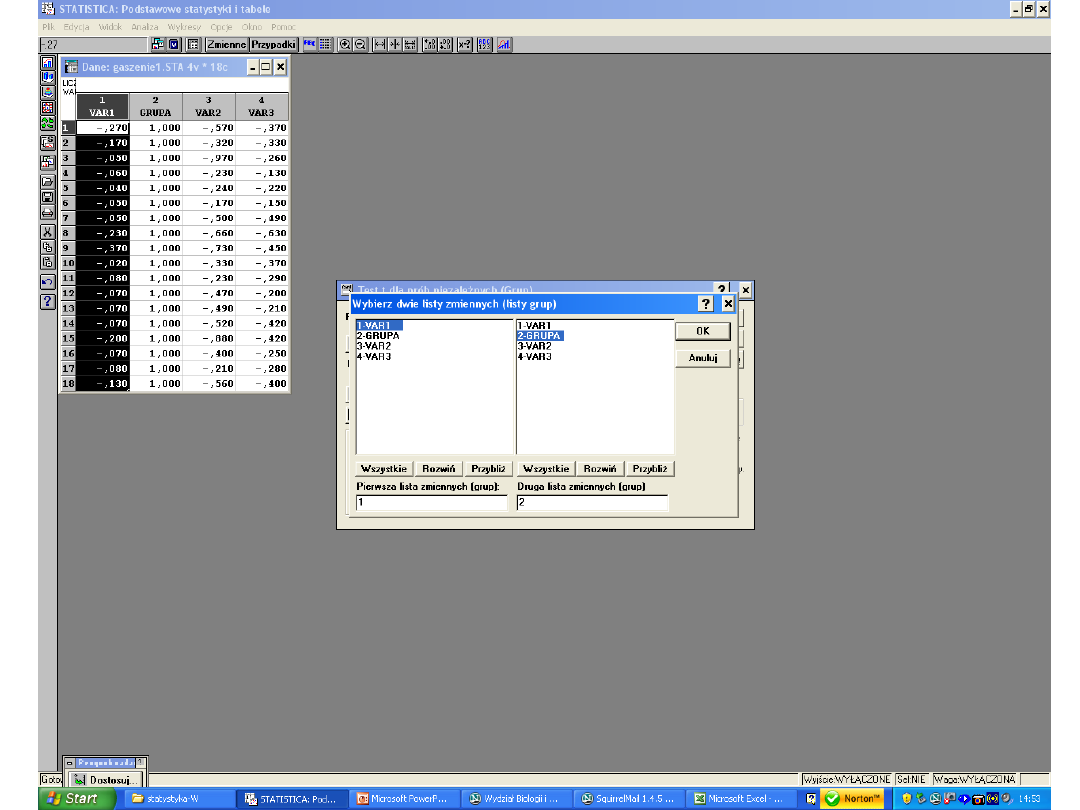
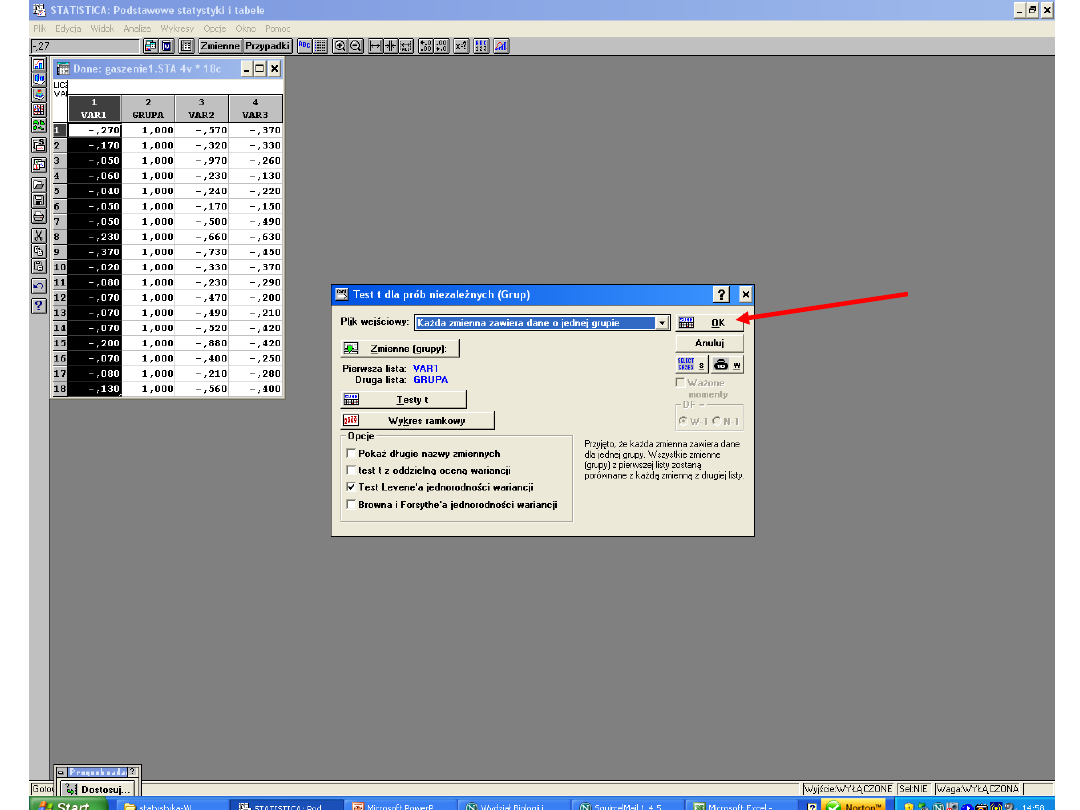
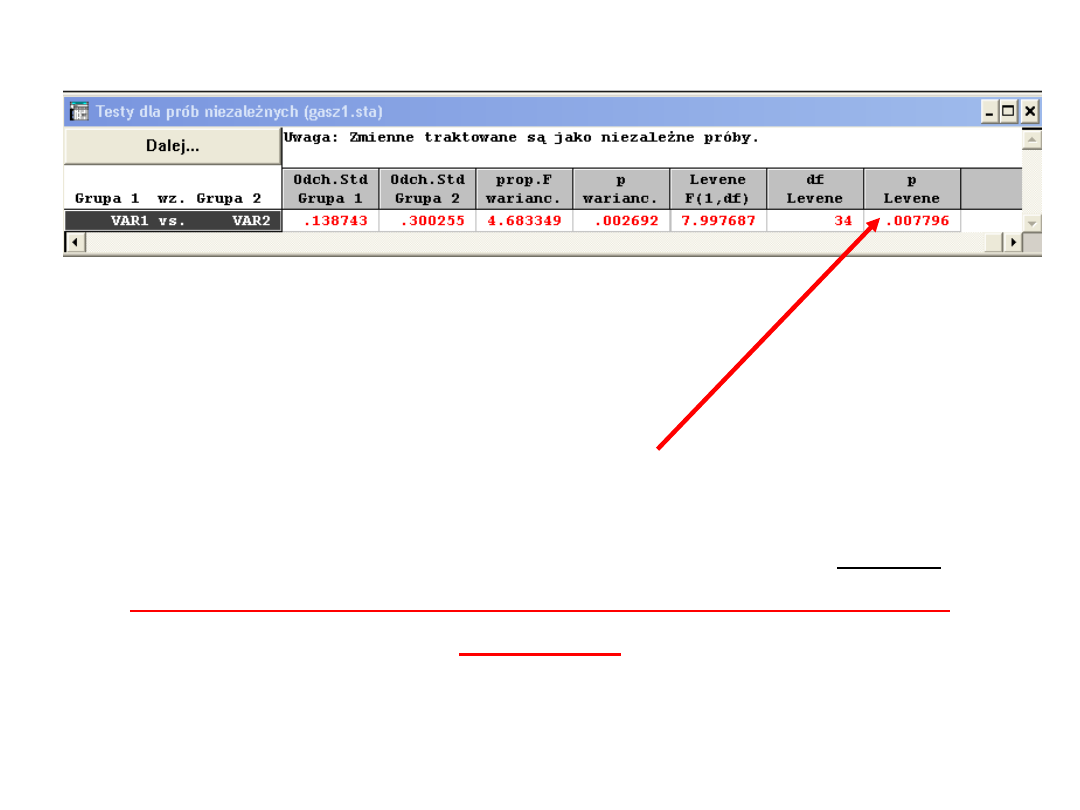
Jeśli w wyniku analizy otrzymamy wynik

istotny statystycznie tj.

zaznaczony na

czerwono

wówczas jest to dla nas informacja,

że wariancje porównywanych zmiennych

nie

są równe

. Dalej musimy stosować testy

NIEPARAMETRYCZNE (np. test Kruskala-

Wallisa)

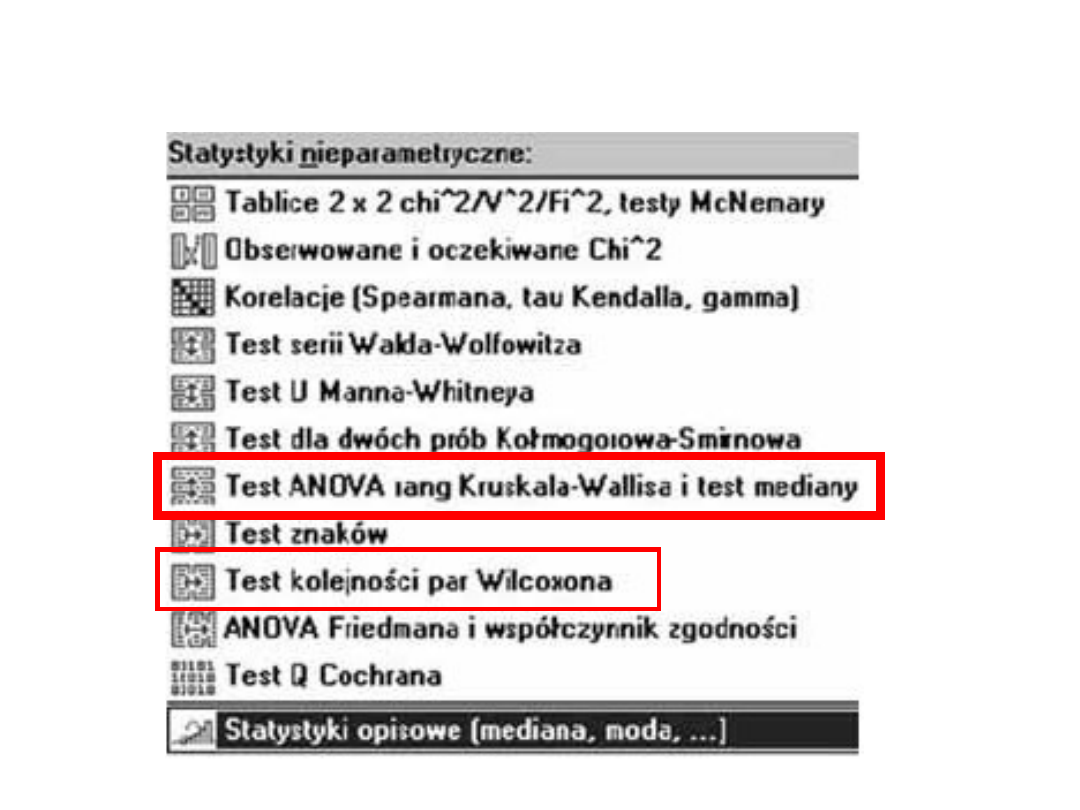
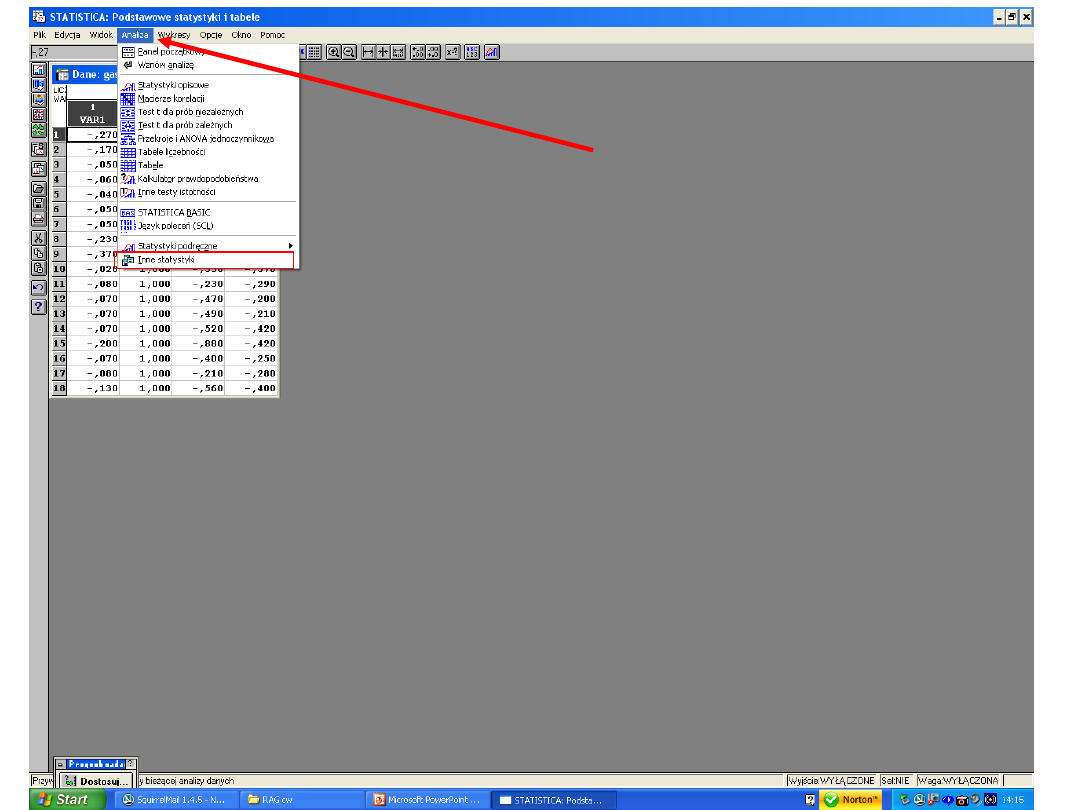
Gdzie szukać testów

nieparametrycznych?

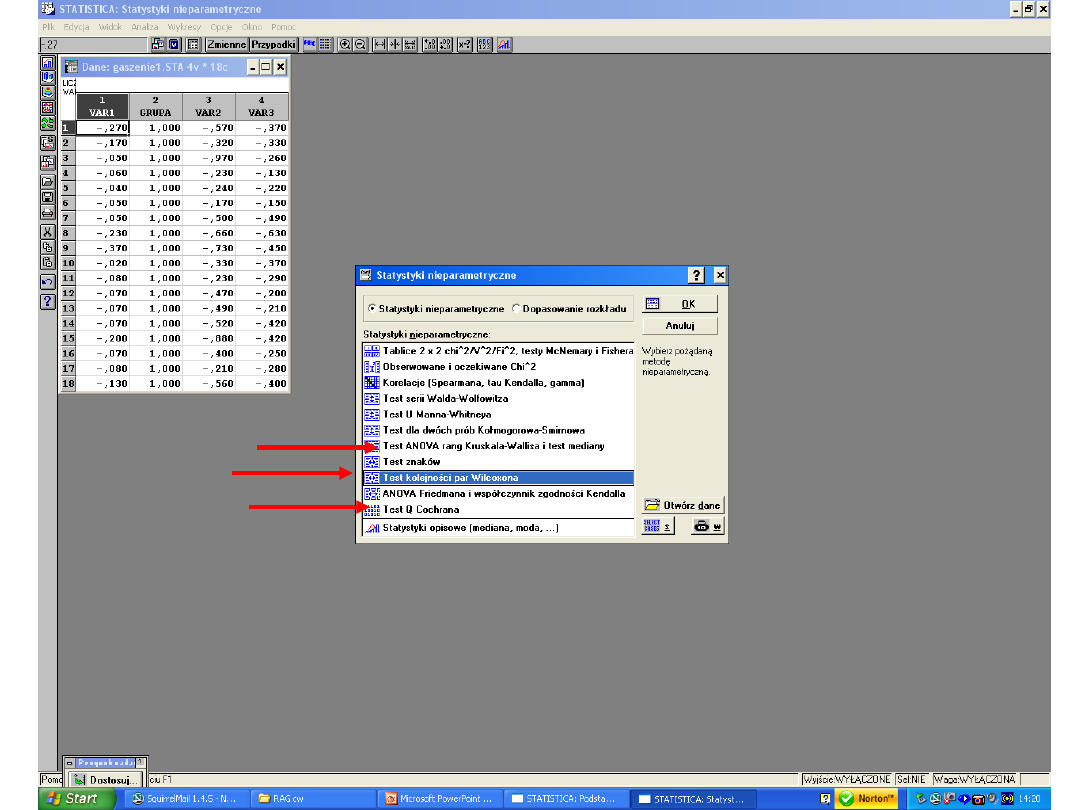
Jeśli wynik testu Levene’a nie wykaże

istotności wówczas dalej stosujemy

test

parametryczny ANOVA

, którym

stwierdzimy różnice pomiędzy

testowanymi zmiennymi lub ich brak.

UWAGA!!!

Test Anova mówi tylko „są różnice

pomiędzy badanymi zmiennymi”, ale nie

wskazuje pomiędzy którymi !!! Dlatego po

wykonaniu analizy wariancji wykonujemy

dalsze analizy, tzw. testy post hoc !!

(czy to się kiedyś skończy??? )

Wyjaśniam pojęcie – „analiza wariancji”

Celem analizy wariancji (ANOVA) jest w istocie

testowanie istotności różnic pomiędzy grupami,
reprezentowanymi przez średnie

Ale zatem dlaczego procedura służąca do

porównywania średnich jest określana nazwą
„analiza wariancji”?

Nazwa ta wywodzi się z faktu, że w celu testowania

statystycznej istotności różnic pomiędzy grupami w

rzeczywistości przeprowadzamy porównanie różnych

wariancji (wariancja węwnątrzgrupowa vs. wariancja

międzygrupowa)

Analiza wariancji ANOVA

jednoczynnikowa

analiza
wariancji

wpływ każdego czynnika

jest rozpatrywany

oddzielnie

wieloczynnikowa

analiza
wariancji

wpływ różnych czynników

jest rozpatrywany

łącznie

Kiedy wolno nam zastosować test

ANOVA?

1. Próba powinna być losowo pobrana

(randomizacja)

2. Porównywane grupy powinny być

równoliczne

3. Wariancje

w porównywanych grupach

powinny być

jednorodne

(homogenne) –

TEST LEVENE’a

4. Rozkłady

zmiennych muszą być

normalne

–

TEST SHAPIRO - WILKA

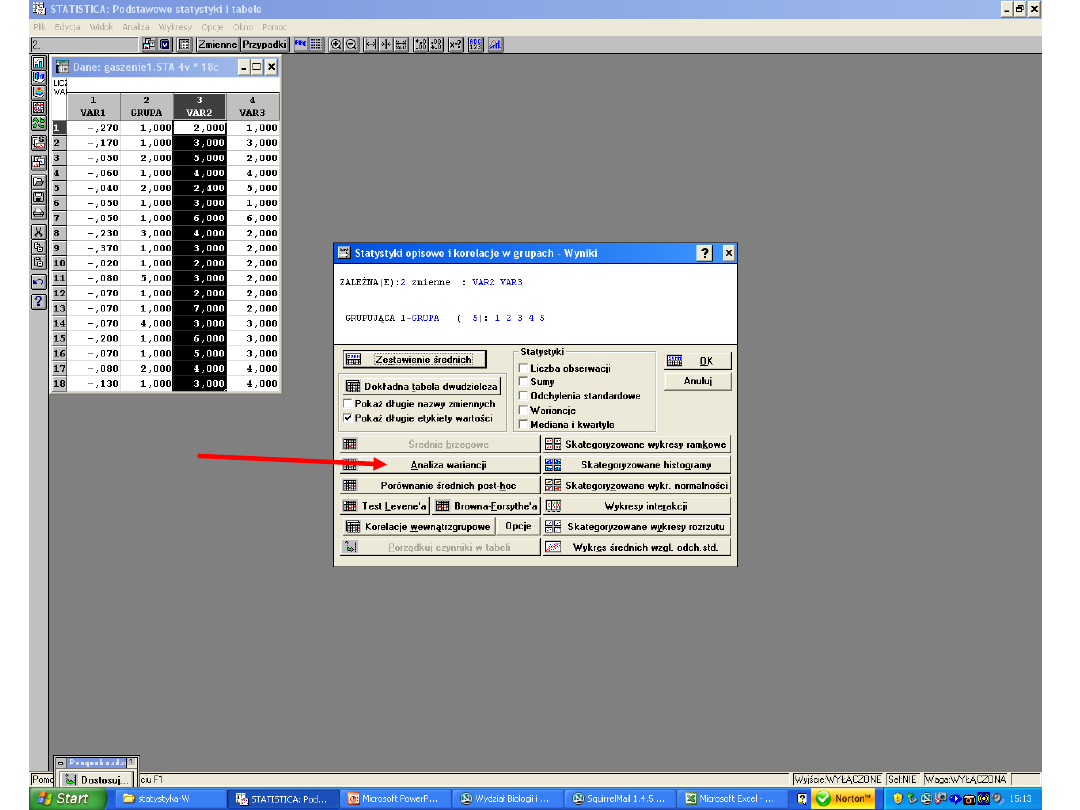
A co zrobić gdy nie są spełnione założenia

ANOVA?

Zastosować

test Kruskala-Wallisa

– jest to nieparametryczny

odpowiednik analizy wariancji

(stosować gdy porównujemy więcej niż 2

grupy!!!)

Nie wolno nam zastosować porównań

wielokrotnych (testu t-Studenta z poprawką

Bonferroniego) dopóki nie wykonamy analizy

wariancji !!!

Dlaczego???

(a) bo testy t-Studenta zawyżają prawdopodobieństwo, często

testem t wykażemy różnice podczas gdy analiza wariancji jej

nie stwierdzi.

(b) jeśli porównujemy więcej niż 2 grupy wyników nie możemy

stosować testu t-Studenta !!!! Chyba, że zastosujemy

poprawkę Bonferroniego.

(c) analiza wariancji jest testem o większej mocy statystycznej

!!!

Interpretacja wyników testów

Nazwa testu

istotność

brak istotności

Shapiro-Wilk
(normalność
rozkładu)

normalny

stosujemy test
parametryczny

brak normalności
stosujemy test
nieparametryczny

(kolejność par

Wilcoxona

)

Test Levene’a
(równość wariancji)

brak równości

Test Kruskala-
Wallisa

wariancje są równe

stosujemy analizę
wariancji (Anova)

Analiza wariancji
(Anova)

ocenia czy występują

różnice pomiędzy

zmiennymi

Testy porównań

wielokrotnych (test

Tukeya) lub test t-

Studenta (z popr. B)

Tak, są różnice

pomiędzy

badanymi
zmiennymi ale nie
wiemy, które
zmienne są za nie

odpowiedzialne

Wskażą które

zmienne różnią się
istotnie
statystycznie

Dane nie różnią się
istotnie (statystycznie)

KONIEC

TESTOWANIA

KONIEC

TESTOWANIA

Analiza regresji - regresja liniowa

• Gdy stosujemy metodę najmniejszych kwadratów

(regresja liniowa II stopnia), wówczas zależy nam na

tym, aby różnice między oczekiwanymi

(obliczonymi, teoretycznymi) a doświadczalnymi

(zmierzonymi) wartościami zmiennej zależnej (y)

były jak najmniejsze. Badamy korelację pomiędzy

zmienną zależną (oś y) i zmienna niezależną

(oś x) – czyli czy zmienna x istotnie wpływa na

zmienną y i odwrotnie.

y= ax + b

gdzie a – współczynnik kierunkowy prostej regresji

Przed przystąpieniem do

analizy regresji najpierw

musimy sprawdzić

normalność

rozkładu różnic

między

oczekiwanymi a zmierzonymi

wartościami zmiennej y; nie

zawsze normalne rozkłady

zmiennych x i y gwarantują

taką normalność różnic – do

zbadania tego służy tzw.

analiza reszt 

rozkład normalny

brak normalności

rozkładu

• Stosujemy test

parametryczny

– współczynnik korelacji

liniowej Pearsona

• Stosujemy test

nieparametryczny

- korelacje Spearmana,

Kendalla, Gamma

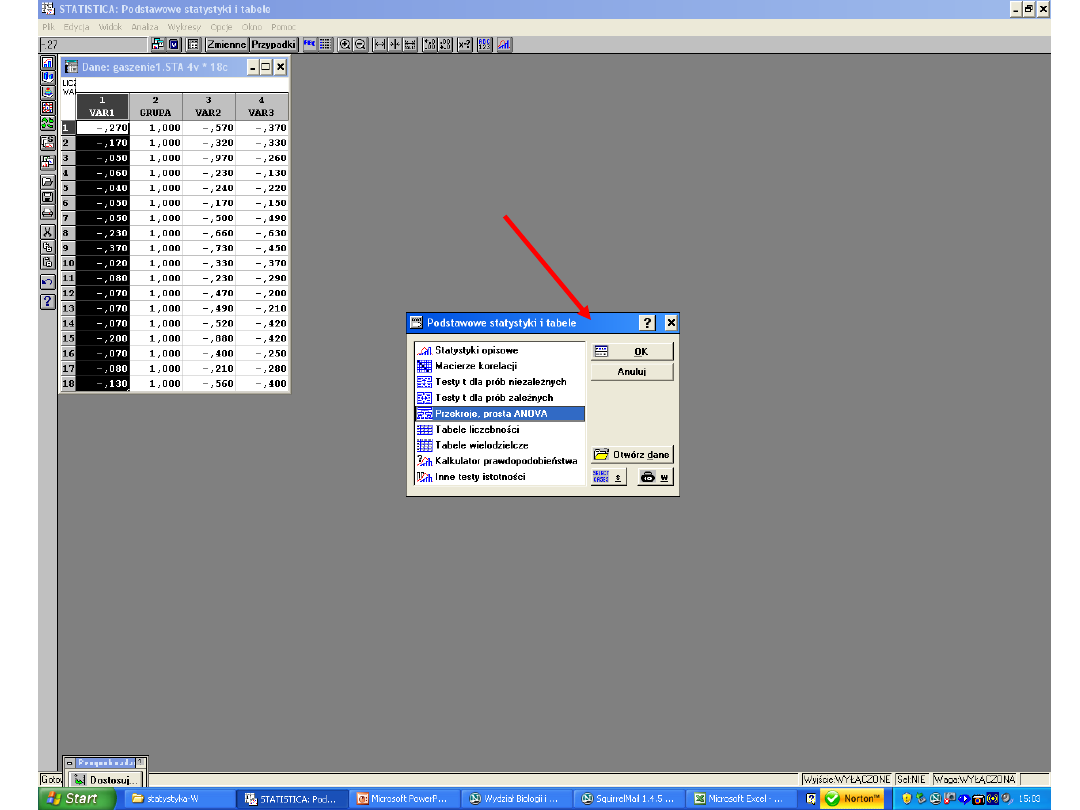
Jak to obliczyć za pomocą

statystyki?

1. Podstawowe statystyki i tabele

2. Macierze korelacji

3. Współczynnik korelacji liniowej Pearsona

4. wybieramy zmienne (jak zawsze)

oraz KORELACJE

Ocena liczności próby i

analiza mocy testu

- w programie STATISTICA ver.

8

Uwaga !!!!

Ocenę liczności próby czyli nasze

„

n

” musimy zawsze obliczyć zanim

zdecydujemy się na zakończenie

eksperymentu. Odpowiednia

liczność gwarantuje nam

pozyskiwanie wyników, których

moc jest na tyle duża iż możemy

uważać te wyniki za

wiarygodne.

Co należy zrobić?

•

Otworzyć program STATISTICA

• Z pasku NARZEDZIA wybrać opcję STATYSTYKA
• W STATYSTYCE wybrać „Analiza mocy testu” – i otworzy się

okno, w którym z lewej strony klikamy na „Liczność próby” a z

prawej na jednym z wybranych testów, którym będziemy

przeprowadzać analizę wyników

• Po dokonaniu powyższych wyborów otworzy się kolejne okno, w

którym musimy wpisać interesujące nas dane,

• Czyli:

• Mi1

– średnia na 1 grupy/kolumny wyników

• Mi2

– średnia na drugiej grupy wyników

• Alfa

– poziom alfa, np. 0.05 lub inny wynikający z poprawki

Bonferoniego

• Sigma 1

– odchylenie standardowe, SD dla 1 grupy

• Sigma 2

– odchylenie standardowe, SD dla 2 grupy

• Ro

– współczynnik autokorelacji – przyjmować domyslnie

• Moc testu

– np.. 0.95; 0.9; 0.8 – sami o tym decydujemy

• I naciskamy OK

następnie ......

• gdy pojawi się kolejne okno wybieramy

opcję

„Oblicz N”

• i pojawia nam się

„wymagana

liczność próby N”

na samym dole.

Kiedy wykonać analizę mocy testu?

Gdy szacujemy minimalną liczność próby

wówczas pojawia nam się tzw. docelowa
moc testu dla liczności opracowanej przez
program. Ta moc zawsze będzie dość
wysoka, nawet może osiągnąć wartość 1.

Ale czasami zdarza się, że recenzent (lub

nasza ciekawość) pyta o moc testu dla
naszej liczności próby (która może być
większa lub mniejsza od tej oszacowanej
przez program statystyczny), więc jak tę
moc sprawdzić ???

Należy wówczas ....

• W pasku narzędzi kliknąć na opcję STATYSTYKA i otworzyć

„Analizę mocy testu”

• Następnie w oknie po lewej stronie należy zaznaczyć „moc

testu” a w oknie po prawej stronie test, którym do tej
pory robiliśmy analizę naszych wyników;

• Po wybraniu tych opcji otworzy nam się okno gdzie

podajemy dane naszego eksperymentu, tj.

N

– czyli naszą

liczność próby, oraz wszystkie inne parametry jak przy
ocenie liczności próby)

• Klikamy Ok. a następnie

„Oblicz moc”

• W końcu pojawi się okno dialogowe, w którym na dole

zostanie wskazana moc testu dla naszych konkretnych
danych. I to jest informacja z jaką mocą
przeprowadziliśmy swoje analizy.

• Jeżeli moc jest poniżej wartości

0.5

– wówczas należy mieć

świadomość, że wynik analizy przez nas otrzymamy jest

niewiarygodny

. Ale nie zdarzy się tak, jeśli nasze badane

próby będą miały liczność taką jaką wcześniej oszacujemy
praogramem STATISTICA – więc warto to zrobić !!!!