Struktura atomów

wieloelektronowych

• Sprzężenie spin-orbita
• Wpływ pola magnetycznego
• Konfiguracje
• Termy atomowe
• Reguły Hunda

Przybliżenie

jednoelektronowe

Każdemu elektronowi
przypisujemy jego
własny orbital

s

l

s

l

m

nlm

m

nlm









Iloczyn funkcji 

nlml

zależącej od

współrzędnych oraz funkcji

spinowej 

ms

Spinorbital

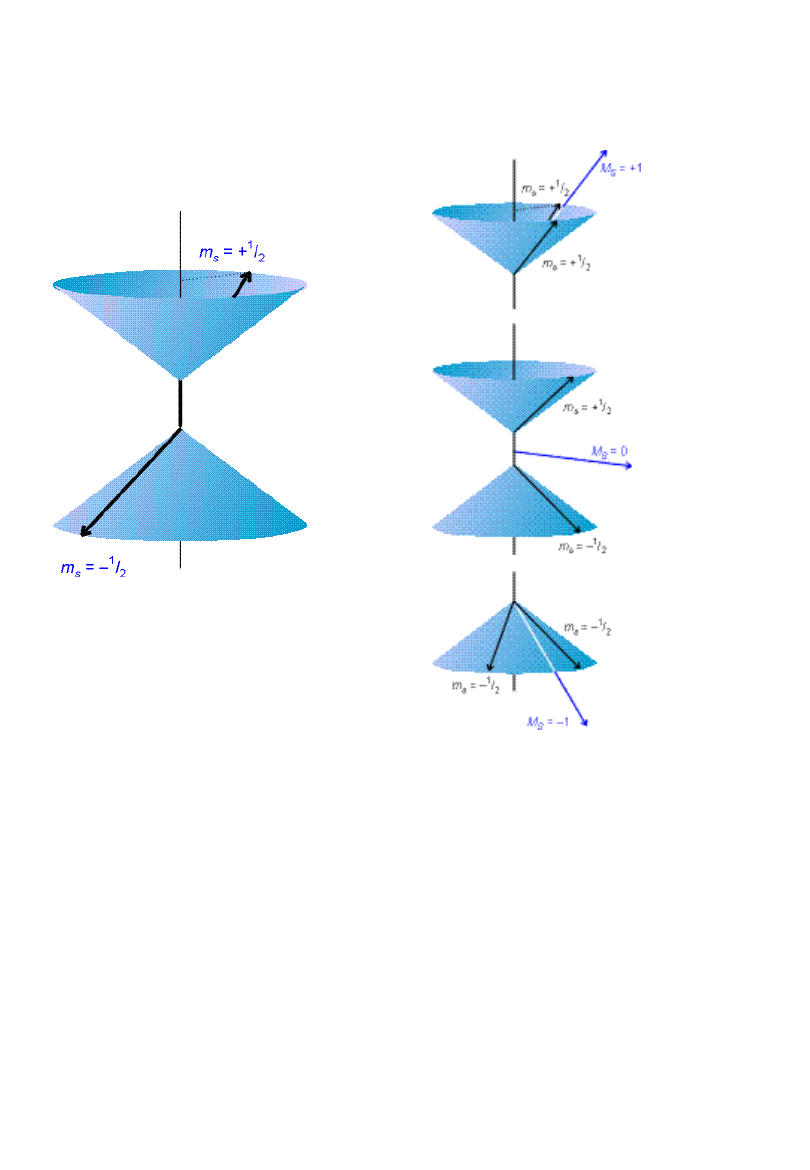
Stany singletowe i

trypletowe

Multipletowość:
2S+1

Dany orbital mogą zajmować co
najwyżej dwa elektrony o
sparowanych spinach

Konfiguracja

elektronowa

Sposób przyporządkowania
poziomów energetycznych
elektronom

Zakaz Pauliego

Okresowość

właściwości

chemicznych

Neon, Z=10 [He]2s

2

2p

6

= 2s

2

2p

6

=

[Ne]

zapełnione powłoki K i L: [Ne]

Lit, Z = 3: [He]3s

1

=

K3s

1

Sód, Z=11: [Ne]3s

1

=KL3s

1

Potas, Z = 19 [Ar]3s

1

Hel Z= 2: 1s

2

=

[He]

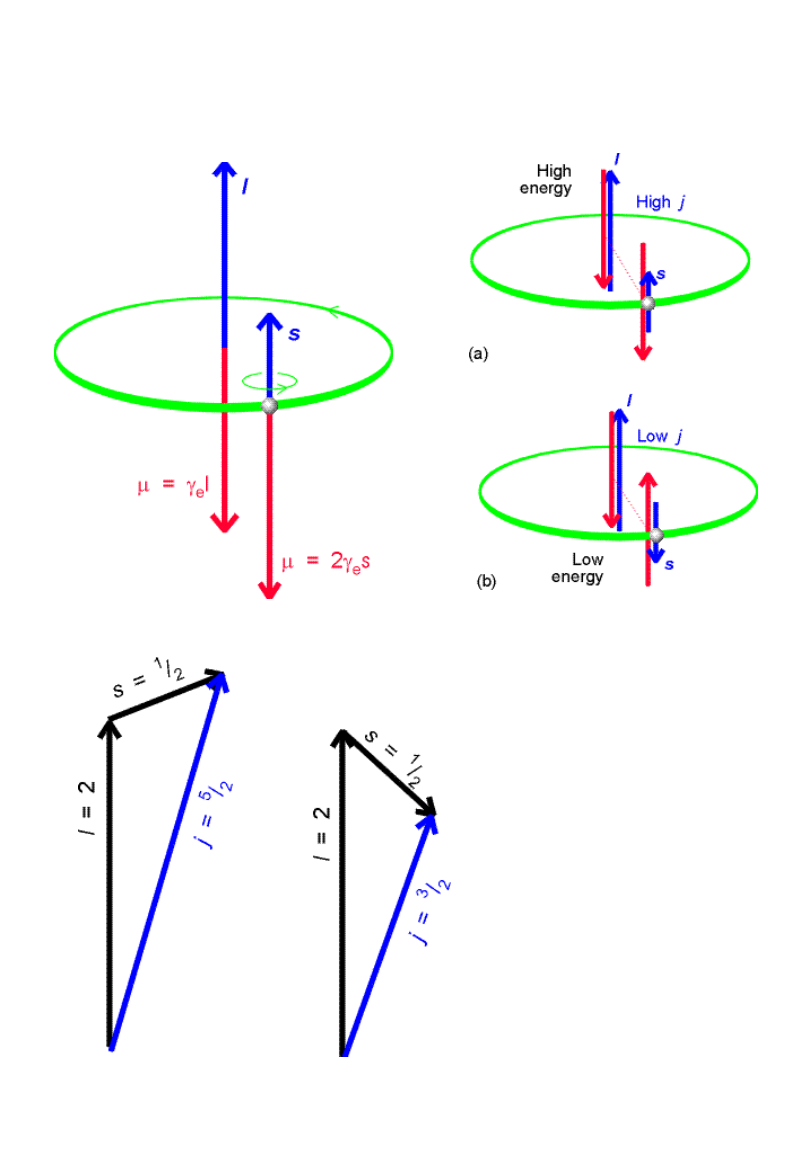
Sprzężenie spinowo-

orbitalne

Całkowit
y
moment
pędu: j

Sprzężenie spinowo-

orbitalne

Energia momentu
magnetycznego  w polu B:

-· B
-· B  s· l









2

2

2

2

2

2

ˆ

ˆ

ˆ

2

1

ˆ

ˆ

2

1

(

s

l

j

s

l

j











































l

s

l

s

l

s

s

s

l

l

s

l

s

l

j

j

s

l

j

2

)

(

)

2

2

2

2

)}

1

(

)

1

(

)

1

(

{

2

1

,

,

ˆ

ˆ

ˆ

|

,

,

2

1

,

,

ˆ

ˆ

|

,

,































s

s

l

l

j

j

s

l

j

s

l

j

s

l

j

s

l

j

s

l

j

|

|

l

s

)}

1

(

)

1

(

)

1

(

{

2

1

,

,













s

s

l

l

j

j

hcA

E

j

s

l

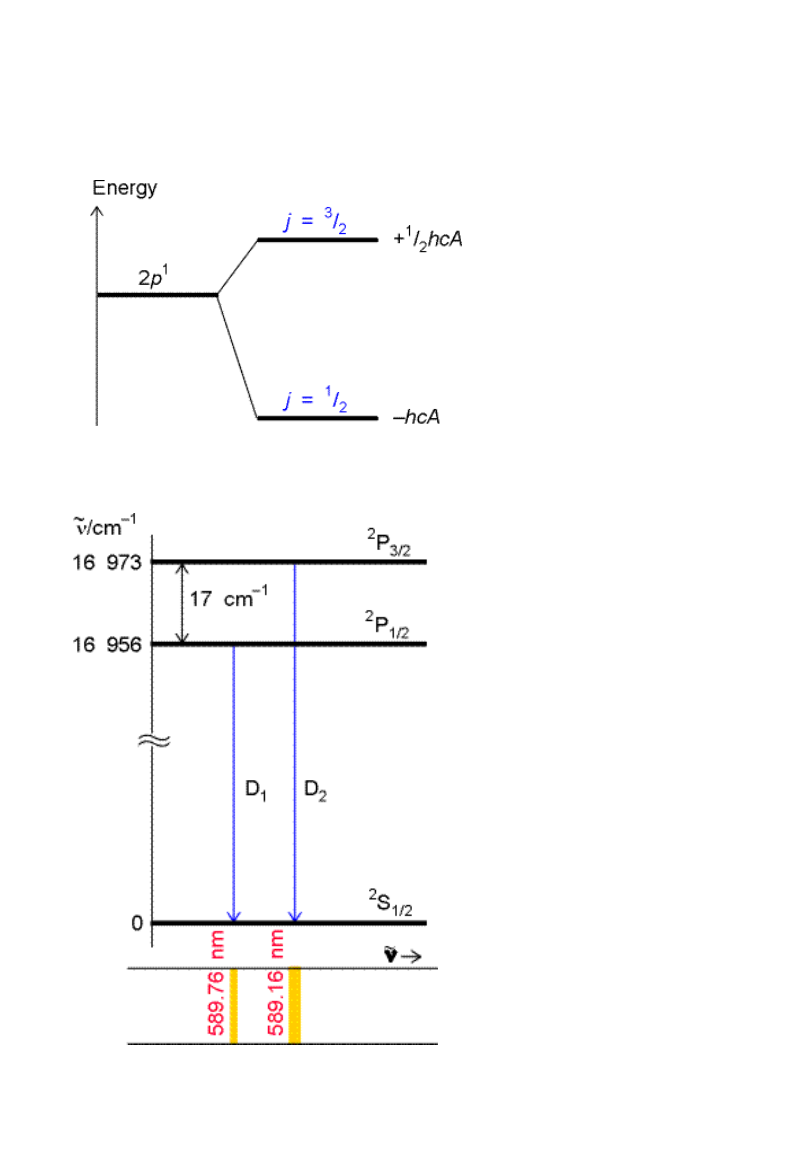
Sprzężenie spinowo-

orbitalne

Struktura
subtelna
widma:
dublet linii
sodu

Wpływ pola

magnetycznego



l

e

z

m







e

e

m

e

2







e

B

B

l

e

z

m

e

m

m

e

2

2

























Energia momentu
magnetycznego  w polu

magnetycznym B:

B

E

z







B

M

E

B

m

E

L

B

M

l

B

m

L

l









lub

Dla momentu spinowego:



s

e

e

z

m

g







...

002319

.

2



e

g

B

M

g

E

B

m

g

E

S

B

e

M

s

B

e

m

s

s









lub

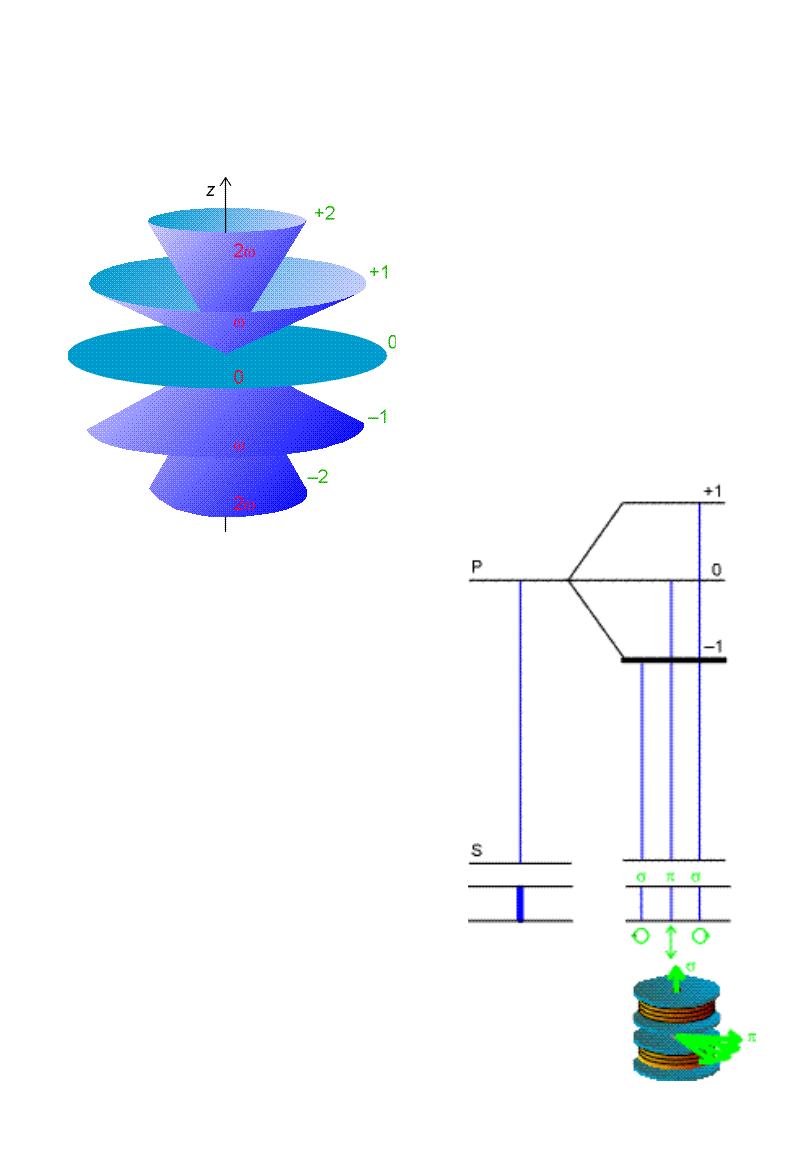
Efekt Zeemana

B

m

E

l

B

m

l





Konfiguracja

elektronowa

Przyporządkowanie elektronów
poziomom energetycznym

Be

Beryl, Z= 4: 1s

2

2s

2

=

[He]2s

2

H

Wodór, Z= 1: 1s

1

B

Bor, Z= 5: 1s

2

2s

2

2p

1

=

[He]2s

2

2p

1

Li

Lit, Z= 3: 1s

2

2s

1

=

[He]2s

1

He

Hel Z= 2: 1s

2

=

[He]

C

Węgiel, Z= 6: 1s

2

2s

2

2p

2

=

[He]2s

2

2p

2

N

Azot, Z= 7: 1s

2

2s

2

2p

3

=

[He]2s

2

2p

3

O

Tlen, Z= 8: 1s

2

2s

2

2p

4

=

[He]2s

2

2p

24

F

Fluor, Z= 9: 1s

2

2s

2

2p

5

=

[He]2s

2

2p

5

Ne

Neon, Z= 10: 1s

2

2s

2

2p

6

=

[Ne]

Na

Sód, Z= 11: 1s

2

2s

2

2p

6

3s

1

=

[Ne]3s

1

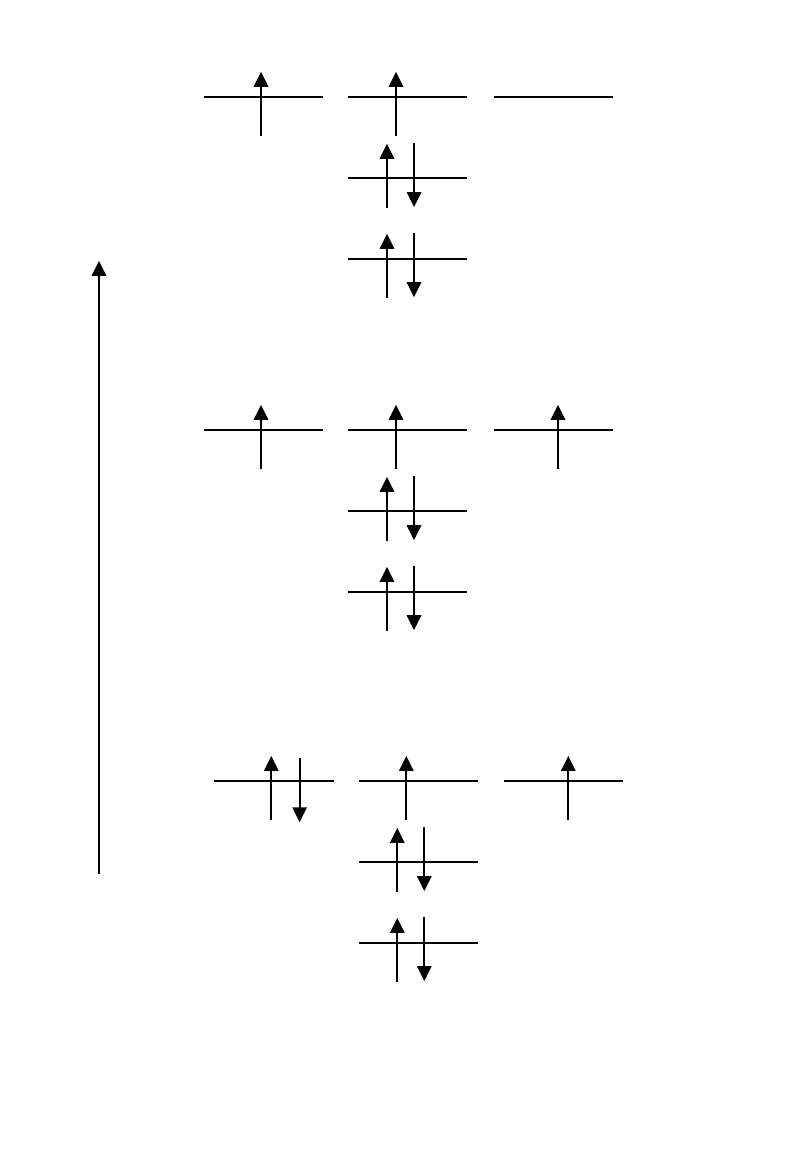
E

[eV]

Atom C

1s

2s

2p

-308.2

-19.2

-11.8

Atom N

1s

2s

2p

-425.3

-25.7

-15.4

Atom O

1s

2s

2p

-562.4

-33.9

-17.2

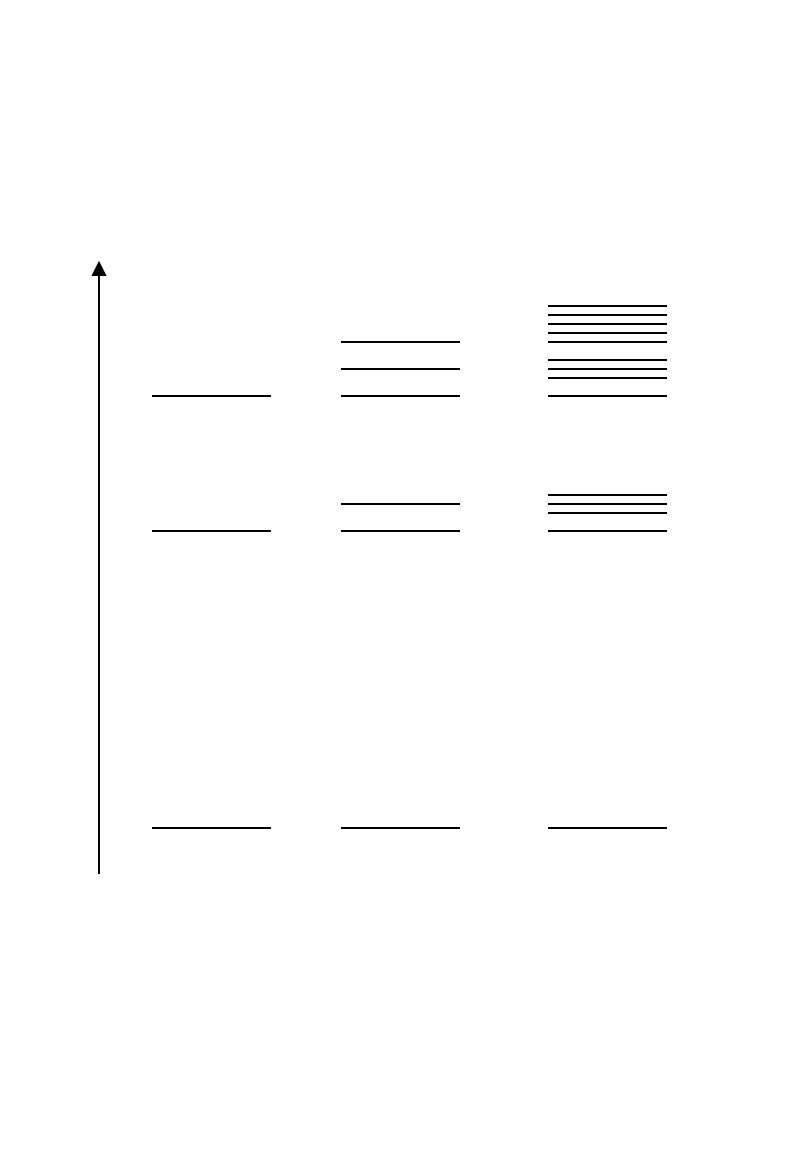
E

n = 3

n = 2

n = 1

Atom H

l = 0

l = 0

l = 1

l = 2

l = 0

l = 1

Atom

wieloel.

l = 1

l = 1

l = 2

l = 0

l = 0

l = 0

Atom

wieloel.

w polu mag.

1s

2s 2p

3s 3p 3d

4s 4p 4d 4f

5s 5p 5d 5f

6s 6p 6d

7s 7p

Schemat obsadzania poziomów

w atomie wieloelektronowym

K

Potas, Z= 19:

1s

2

2s

2

2p

6

3s

2

3p

6

4s

1

Sc

Skand, Z= 21:

1s

2

2s

2

2p

6

3s

2

3p

6

4s

2

3d

1

Ca

Wapń, Z= 20:

1s

2

2s

2

2p

6

3s

2

3p

6

4s

2

Energia orbitalna; suma energii

kinetycznej

oddziaływania z jądrem

oddziaływania z pozostałymi elektronami

Energia orbitalna

nie

jest równa energii całkowitej atomu

Sc

Skand, Z= 21:

1s

2

2s

2

2p

6

3s

2

3p

6

4s

2

3d

1

E(4s) = -0.420 j.at; E(3d) = -0.687 j.at

Dlatego: nie wszystkie orbitale obsadzone

wg rosnących energii

Atomy zamkniętopowłokowe:

Gazy szlachetne

Be (1s

2

s

2

)

C: 1s

2

2s

2

2p

2

=

[He]2s

2

2p

2

= K

2s

2

2p

2

Atomy: otwartopowłokowe

Na: 1s

2

2s

2

2p

6

3s

1

=

[Ne]3s

1

=

KL3s

1

Stan atomu wieloelektronowego - różnice

w stosunku do atomu wodoropodobnego

1. Nie ma liczby kwantowej

charakteryzującej energię

2. Możliwe różne multipletowości spinowe

Termy atomowe

Informacja o całkowitym
orbitalnym momencie pędu L,
multipletowości (2S+1), oraz
całkowitym momencie pędu J dla
danej konfiguracji elektronowej

(konfiguracja
elektronowa)

2S+1

L

J

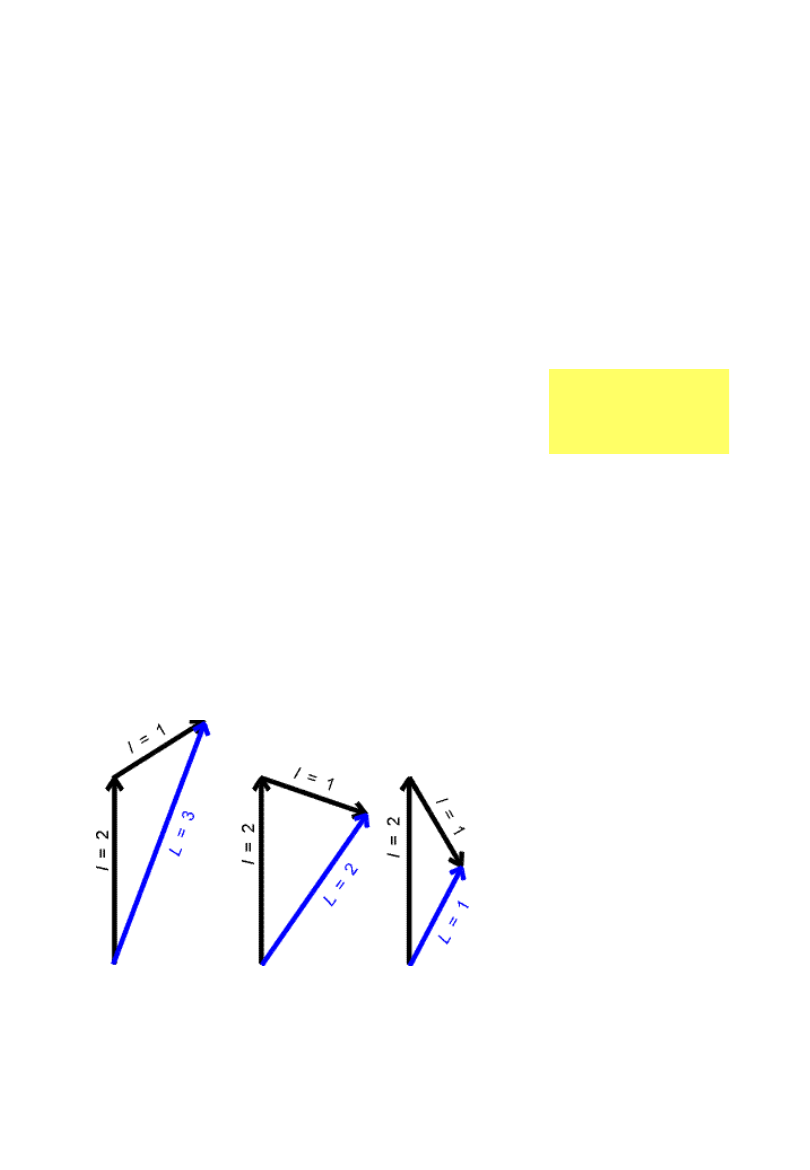
Liczba kwantowa całkowitego
orbitalnym momencie pędu L:

L = l

1

+l

2

, l

1

+l

2

-1,…,| l

1

-l

2

|L

0

S

1

P

2

D

3

F

4

G

5

H

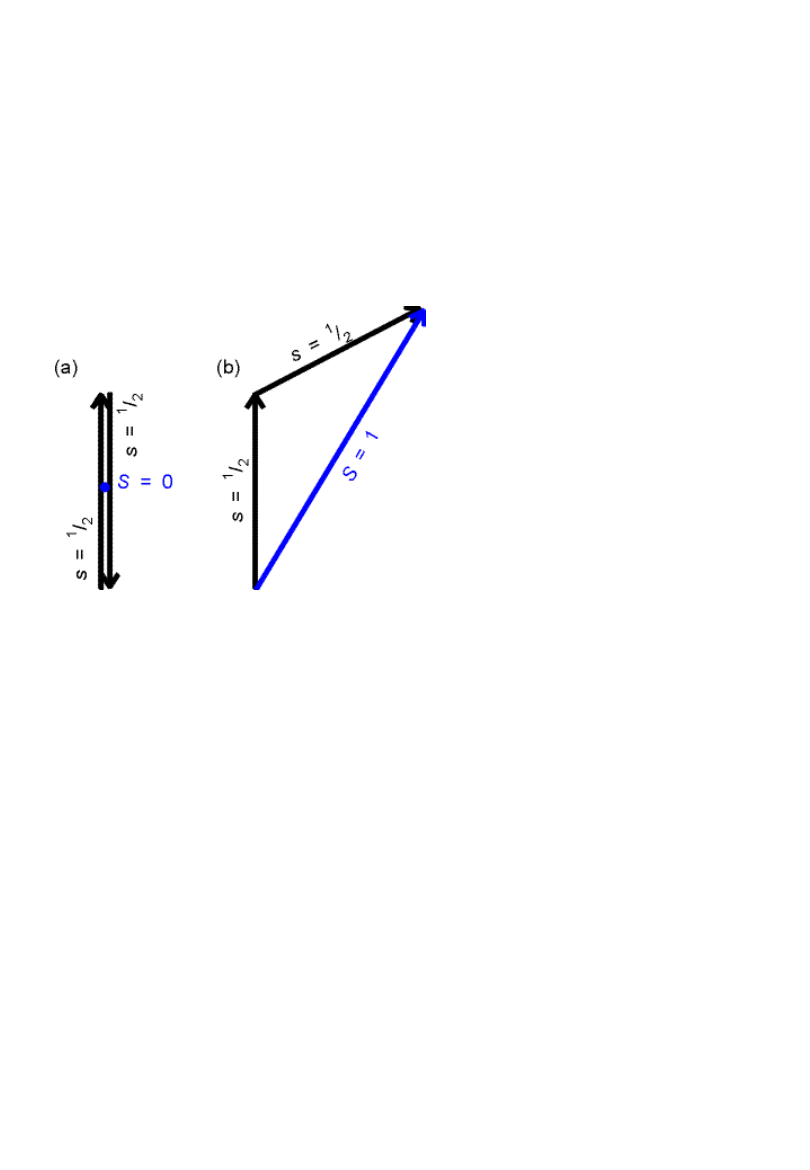
Symbole termów

Multipletowość termu ma
wartość 2S+1

S = s

1

+s

2

, s

1

+s

2

-1,…,| s

1

-s

2

|

Pojedyńczy elektron - dublet,
np [Ne]3s

1

,

[Ne]3p

1

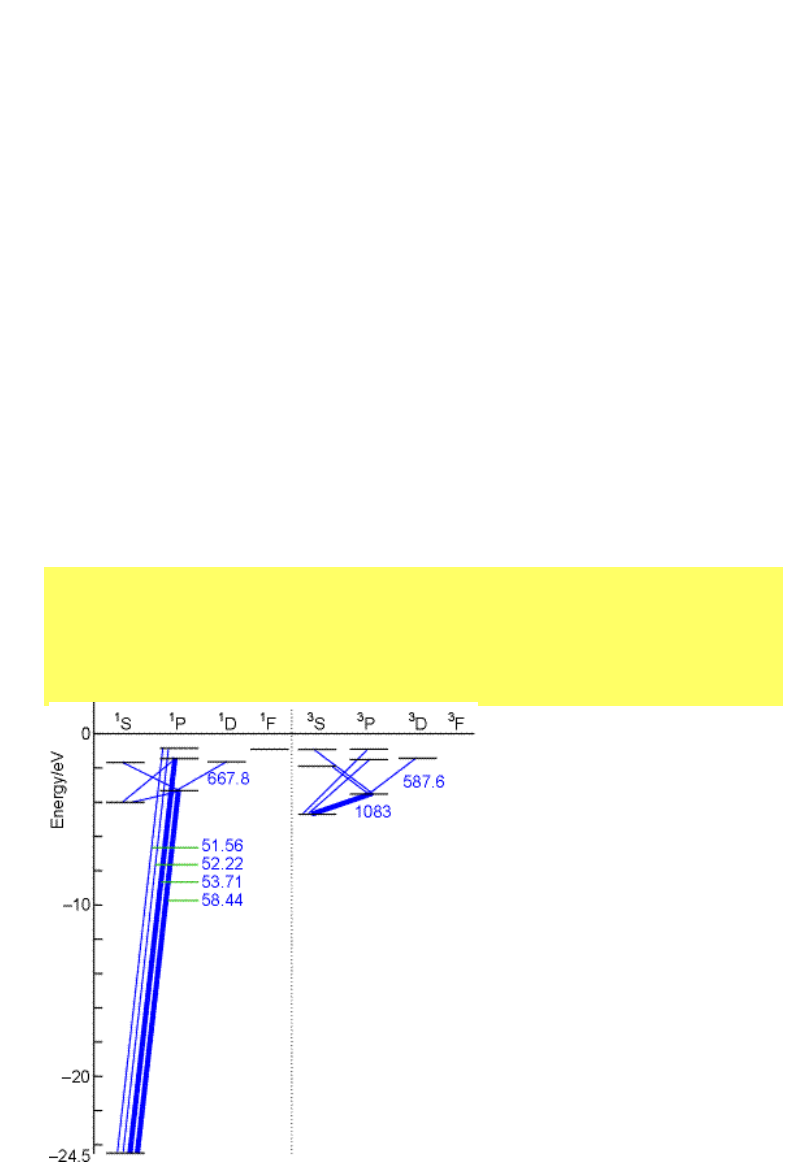
Symbole termów

Całkowity moment pędu J:

Sprzężenie Russela-Saundersa
(L-S)

L = l

1

+l

2

, l

1

+l

2

-1,…,| l

1

-l

2

|

Dla cięższych atomów -
sprzężenie jj

0)

0

wyj.

(z

1

0,

1

1

0,

0





























J

J

J

l

L

S

Reguły wyboru:

Przykłady

termów

Atom H w stanie podstawowym: 1s

1

L = l = 0, S = s = 1/2 =>

2

S

1/2

Atom He w stanie podstawowym: 1s

2

L = l = 0, S = 0 =>

1

S

0

Konfiguracja p

1

(np. Atom B)

L = 1, S = 1/2 =>

2

P

1/2

,

2

P

3/2

Dla zamkniętych powłok S = L = 0

Reguły Hunda

1. Termem podstawowym jest
term o największej
multipletowości.

2. Spośród termów o największej
multipletowości najniższy jest
term o największej wartości L.

3. Dla stanów o tych samych
wartościach L i S, dla powłoki
zapełnionej elektronami mniej
niż w połowie, termem
podstawowym jest term o
najmniejszej wartości J; jeśli
powłoka zapełniona jest więcej
niż w połowie, termem
podstawowym jest term o
największej wartości J.

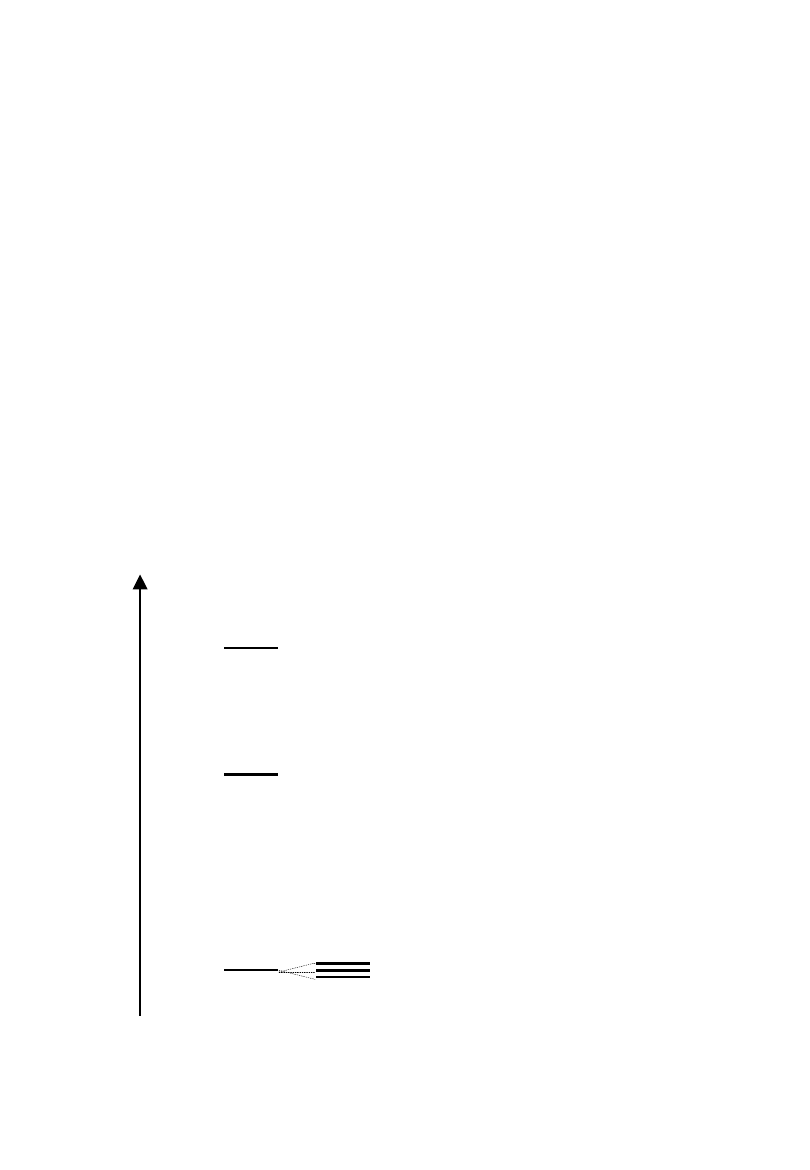
Konfiguracja p

2

(np. Atom C)

Możliwe wartości L: 2, 1,0 (Termy
D, P,S)

Możliwe wartości S: 0, 1
(multipletowość 1lub 3 (singlet lub
tryplet)

Możliwe termy:

1

D

2

3

P

2

3

P

1

3

P

0

1

S

0

E

Atom C (1s

2

2s

2

2p

2

)

1

D

2

1

S

0

3

P

0

3

P

2

3

P

1

Możliwe przyporządkowania
elektronów spinorbitalom dla
konfiguracji p

2

p

1

p

0

p

-1

M

L

2 0 -2 1 0 -1 1 0 -1 1 0 -1

1 0 -1

M

S

0 0 0 1 1 1 0 0 0 -1-1 -1

0 0 0

Mamy M

L

=2 i M

S

=0.

Odpowiada to termowi

1

D

2

Temu termowi opdpowiada

pięć funkcji falowych:

M

L

2 1 0 -1 -2

M

S

0 0 0 0 0

Pozostają:

M

L

0 1 0 -1 1 0 -1 1 0 -1

M

S

0 1 1 1 -1 -1 -1 0 0 0

Mamy M

L

=1 dla której M

S

=-1, 0, 1.

Mamy więc: L=1, S=1.

Odpowiada to termowi

3

P

(

3

P

2

,

3

P

1

,

3

P

0

)

Wykreślamy dziewięć zestawów

Pozostaje jeden człon: M

L

=0,M

S

= 0.

Odpowiada to termowi

1

S

0