Kinetyczno – molekularny model gazu doskonałego

(przełom XIX i XX w. – J.W. Gibbs, L. Boltzmann)

Założenia:

-cząsteczki gazu są to punkty materialne,

-poruszają się ruchem chaotycznym,

-drogę między zderzeniami (fragment prostej) nazywamy drogą
swobodną.

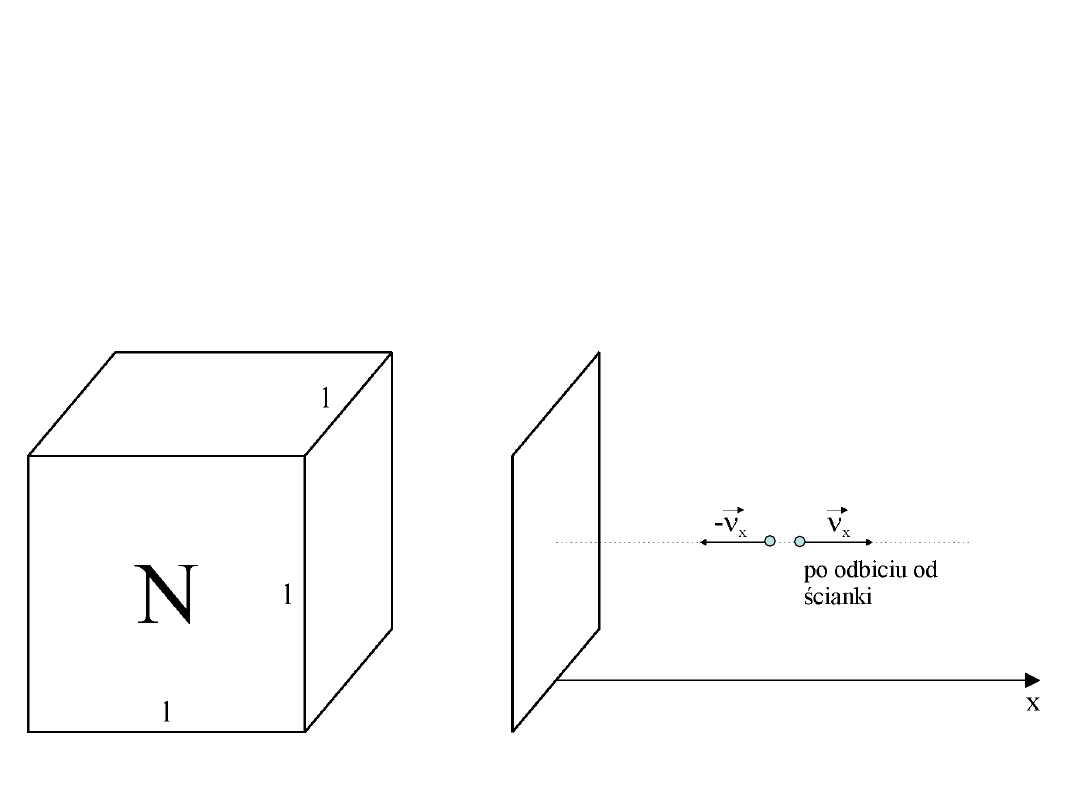
Równanie gazu doskonałego, jako wniosek z teorii kinetyczno – molekularnej

W sześciennym naczyniu o krawędzi l znajduje się N cząsteczek gazu.

m – masa cząsteczki


x

– składowa prędkości cząsteczki w kierunku osi x

Zmiana pędu cząstki przy jednym zderzeniu ze ścianką naczynia:

(

) 2

x

x

x

m

m

m

n

n

n

- -

=

Ile zderzeń następuje w czasie 1 s ?

Czas przelotu cząstki między ścianką lewą i prawą i z powrotem wynosi:

2

x

l

t

n

=

Liczba zderzeń jest równa odwrotności tego czasu (np. jeśli czas wynosi
0,2 s to liczba zderzeń n = 5

1

/s, czyli 5 zderzeń w czasie 1 s).

Zatem liczba zderzeń cząsteczki ze ścianką w czasie 1 s wynosi:

1

2

x

n

t

l

n

= =

Zmiana pędu przy tej samej liczbie zderzeń wynosi:

{

{

{

2

zmiana pędu

liczba

zmiana pędu w

przy jednym zderzeń

czasie 1s dla

zderzeniu

jednej cząstki

2

2

x

x

x

m

m

l

l

n

n

n � =

Zmiana pędu w czasie 1s w przypadku N cząsteczek:

1

2

2

2

2

2

2

2

1

2

(

...

)

...

N

N

x

x

x

x

x

x

m

m

m

m

l

l

l

l

n

n

n

n

n

n

+

+ +

+

+ +

=

Wyrażenie to pomnóżmy i podzielmy przez N

2

2

2

1

2

2

(

...

)

N

x

x

x

x

Nm

m

N

Nl

l

n

n

n

n

+

+ +

=

Ponieważ żaden z kierunków nie jest wyróżniony możemy zapisać:

2

2

1

3

x

n

n

=

Zmiana pędu w czasie 1s N cząsteczek równa się:

2

1

3

m

N

l

n

Z II zasady dynamiki

sr

p

F

t

D

=

D

Oznaczamy:

P – ciśnienie na ściankę
S – powierzchnia ścianki

l

3

– objętość naczynia

Zmiana pędu p spowodowana jest siłą F

śr

(W czasie 1s siła ulega fluktuacji, bierzemy więc F

śr

).

2

1

3

śr

m

F

N

l

n

=

2

2

2

3

1

3

3

śr

F

m

m

P

N

N

S

l l

l

n

n

=

=

=

�

2

2
3

2

m

PV

N

n

=

2
3

k

PV

Ne

=

k

e

równanie gazu doskonałego

-

średnia energia kinetyczna

cząsteczki

Eksperymenty:

1.Robert Boyle (1627 – 1691) – fizyk angielski
Edme Mariotte (1620 – 1684) – fizyk francuski

Prawo Boyle i Mariotte’a:

PV const

=

m = const

T = const

2.Jacques A. Charles (1746 – 1823) – fizyk francuski

Prawo

Charlesa:

P

const

T

=

m = const

V=const

3.Joseph L. Gay-Lussac (1778 – 1850) – fizyk francuski

Prawo Gay-

Lussac’a:

V

const

T

=

m = const

P = const

4.Benoit P. Clapeyron (1799 – 1864) – fizyk francuski

Równanie

Clapeyrona:

PV nRT

=

R = 8,31432

mol

J

K

�

�

�

�

�

�

�

Porównanie wyników eksperymentów z wnioskami z modelu

2
3

A K

PV RT

PV

N e

=

�

�

�

=

�

�

dla 1 mola gazu n = 1, N = N

A

stąd

2
3

3
2

A K

K

A

N

RT

R

T

N

e

e

=

=

A

R

k

N

=

k – stała
Boltzmanna

k = 1,38 * 10

-23

J

K

N

A

- liczba Avogadra

3
2

K

kT

e =

Powyższy wzór pozwala na interpretację temperatury jako miary średniej
energii kinetycznej ruchu postępowego cząsteczek.

Jeśli mamy dwa gazy w tej samej temperaturze, przy czym m

2

> m

1

to

1

2

n n

>

, ponieważ

W tej samej temperaturze atomy gazu cięższego poruszają się wolniej niż
lżejszego (gaz cięższy dyfunduje wolniej niż lżejszy).

1 1

2 2

2

2

m

m

n

n

=

2

2

Energia wewnętrzna

Przy założeniu, ze cząsteczki gazu są punktami materialnymi całkowita
energia gazu jest energią ruchu postępowego cząsteczek.

Nazywamy ją

energią wewnętrzną U.

Zatem

2
3

PV

U

=

Traktując cząsteczki jako układy złożone energią wewnętrzną nazywamy
sumę wszystkich rodzajów energii: kinetycznej ruchu postępowego i
obrotowego, oscylacyjnego, energii potencjalnej oddziaływania atomów,
elektronów, energii wewnątrz-jądrowej, związanej z masą cząstek.

2

m

U N

n

=

2

Energia wewnętrzna układ cząstek gazu wzrasta, gdy nad układem
zostanie wykonana praca sił zewnętrznych.

0

0

zewn

zewn

W

U W

U

>

D =

D >

Przy założeniu, że W

zewn

= 0 energia wewnętrzna układu może wzrastać

na sposób ciepła (w procesie cieplnym).

U Q

D =

Ogólnie:

zewn

U W

Q

D =

+

I zasada termodynamiki

1. W układzie odosobnionym W

zewn

= 0

U Q

D =

2. W układzie izolowanym adiabatycznie Q = 0

zewn

U W

D =

(sprężanie)

(Q – ilość ciepła)

Zasada ekwipartycji energii

3
2

K

kT

e =

Ponieważ

2

2

2

x

y

z

n

n

n

= =

2

2

2

1

2

2

2

2

y

x

z

m

m

m

kT

n

n

n

=

=

=

Energia kinetyczna rozkłada się na trzy niezależne ruchy w kierunkach
wzajemnie prostopadłych – na trzy stopnie swobody.

Na każdy stopień przypada energia równa

1

2

kT

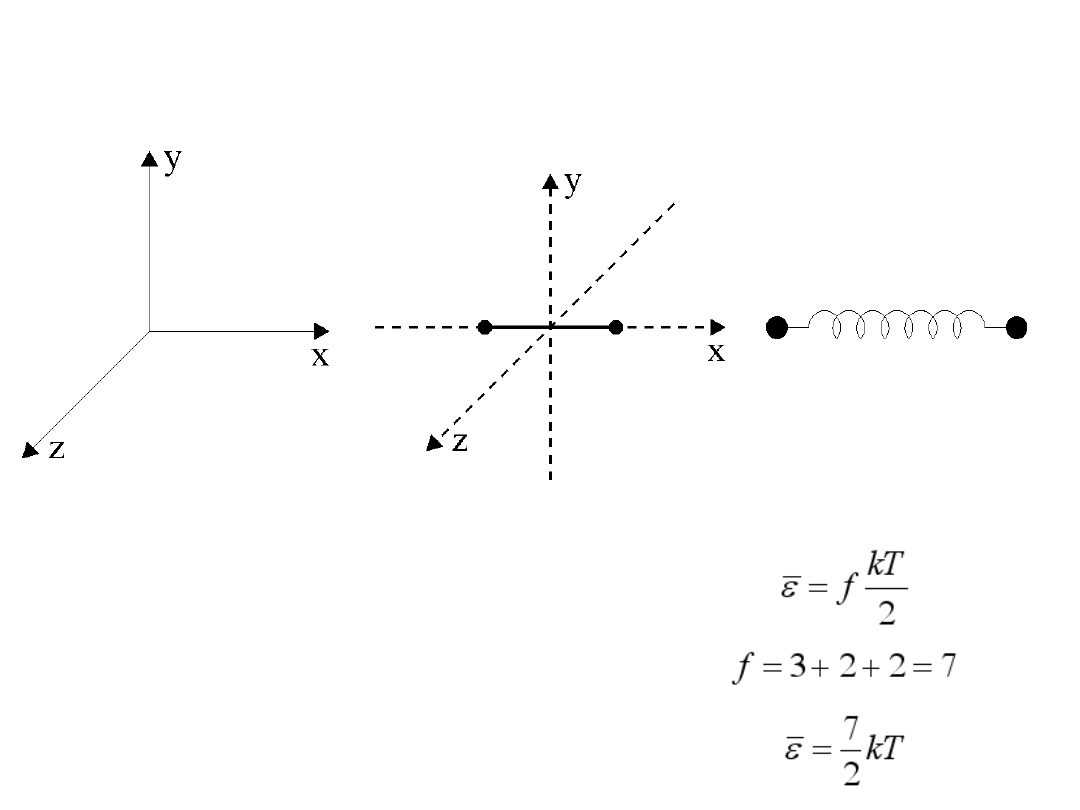
Cząsteczka dwuatomowa ma dodatkowe dwa stopnie swobody na energię
ruchu obrotowego wokół dwóch niezależnych osi obrotu oraz ponadto dwa
stopnie swobody na energie kinetyczną i potencjalną ruchu oscylacyjnego.

ruch postępowy f

1

= 3

ruch obrotowy f

2

= 2

ruch oscylacyjny f

3

= 2

Całkowita średnia energia jaką
ma ta cząsteczka w temperaturze
T wynosi:

Liczbę niezależnych od siebie sposobów
„magazynowania” energii nazywamy liczbą
stopni swobody f

Energia wewnętrzna jednego mola gazu wynosi:

2

2

A

kT

U N f

const

RT

U

f

const

=

+

=

+

Ciepło właściwe gazu (molowe)

Doprowadzanie do 1 mola gazu ciepła o ilości dQ powoduje
wzrost temperatury o dT (V = const).

Ciepłem właściwym nazywamy stosunek

dQ

C

dT

=

Ale

dQ dU

=

zaś

2

RdT

dU

f

=

Zatem

2

RdT

C f

dT

=

2

R

C f

=

2

R

C f

=

W przypadku gazów jednoatomowych (f = 3)

12,47

mol

J

C

K

=

�

W przypadku molekuł dwuatomowych liczba stopni swobody może wynosić 3, 5 lub 7.

Np. dla H2 w temperaturach

poniżej 100 K

12,5

mol

J

C

K

=

�

f=3, ruch postępowy

do 400 K

20,9

mol

J

C

K

=

�

+ rotacja

powyżej 3500 K

29,3

mol

J

C

K

=

�

+ oscylacja

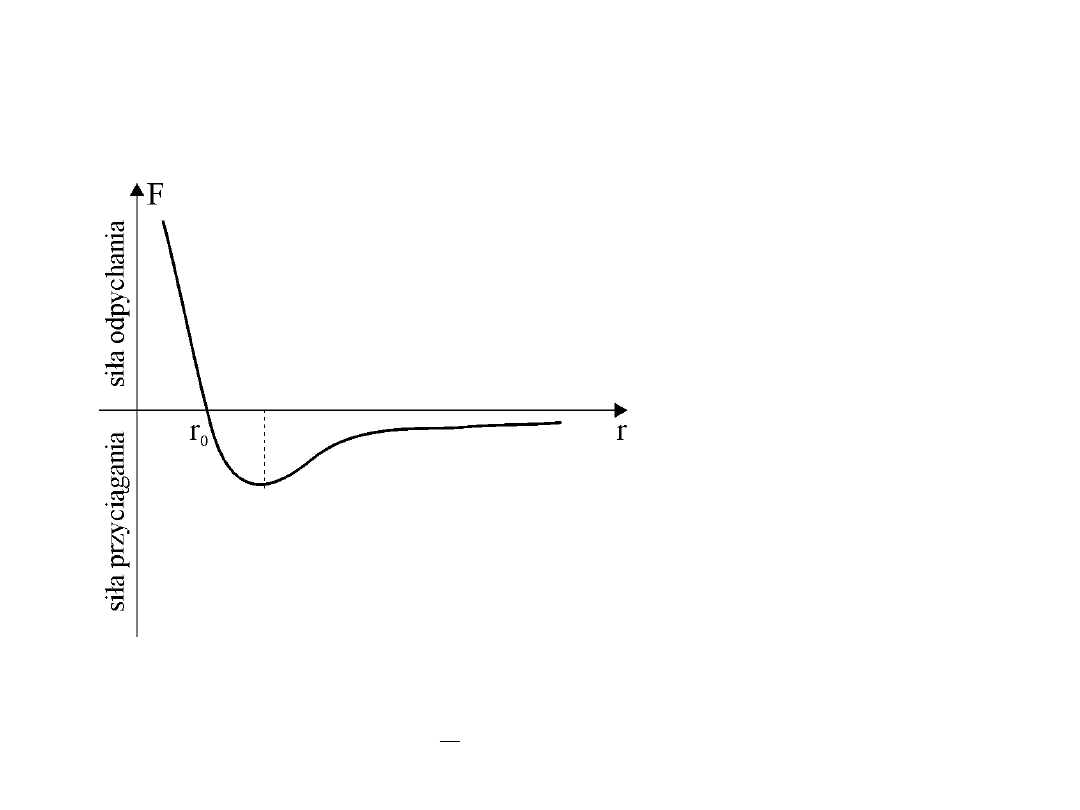
Gazy rzeczywiste

1. Między molekułami gazu rzeczywistego istnieją siły wzajemnego

oddziaływania

(siły międzycząsteczkowe).

r

o

– położenie równowagi

2. Molekuły nie są punktami. Można je traktować jako doskonale
sprężyste kulki

o promieniu r

k

i objętości

3

4
3

k

k

V

r

p

=

Uwzględnienie skończonych wymiarów cząsteczek oraz ich wzajemnego
oddziaływania pozwoliło fizykowi holenderskiemu J. Van der Waalsowi
otrzymanie równania dobrze opisującego właściwości gazów
rzeczywistych.

(

)

2

a

P

V b

RT

V

�

�

+

-

=

�

�

�

�

równanie Van der Waalsa

gdzie:

P – ciśnienie
V – objętość
T – temperatura

gazu

a

4

2

Nm

mol

�

�

�

�

�

�

�

�

b

3

m

mol

�

�

�

�

�

�

�

�

ciało w stanie

lotnym

wodór

0,0032

23,4 * 10

-6

tlen

0,1360

31,9 * 10

-6

para wodna

0,5480

30,6 * 10

-6

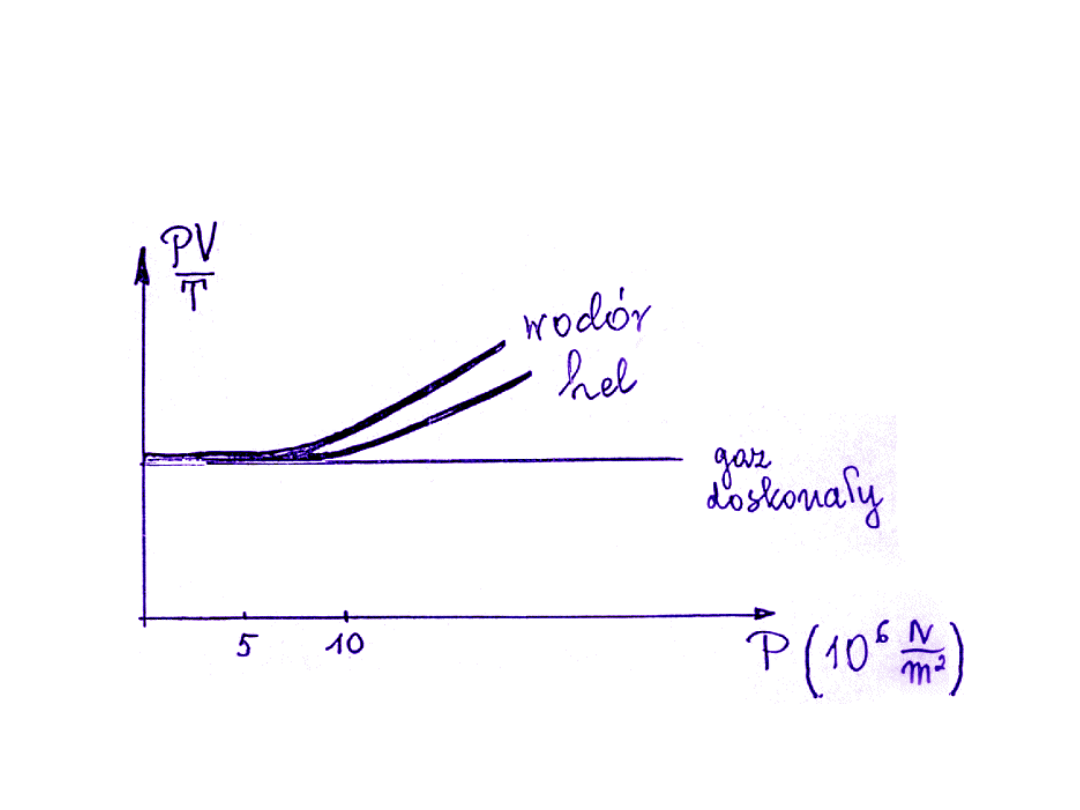
W wysokich temperaturach i przy niskich ciśnieniach gazy
rzeczywiste stosują się do równania Clapeyrona.

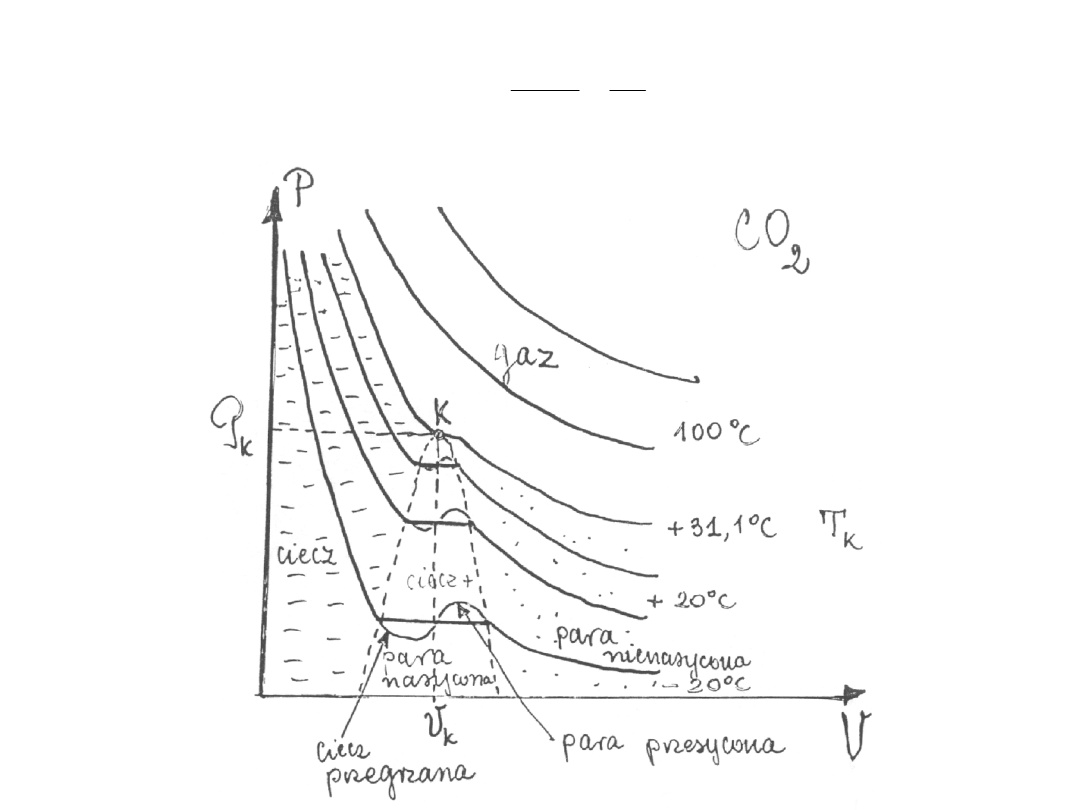
Przy założeniu: T = const

2

RT

a

P

V b V

=

-

-

równanie izotermy

Van der Waalsa

gdzie:

P

k

– ciśnienie krytyczne

V

k

– objętość krytyczna

T

k

– temperatura krytyczna

T

k

[ ]

C

o

P

k

5

2

10

N

m

�

�

�

�

�

�

V

k

4

3

10 m

-

�

�

�

�

Substancja

Azot

-147

34

90,3

Hel

-268

2,3

61,5

Wodór

-240

34

70

CO

2

+ 31

74

98,2

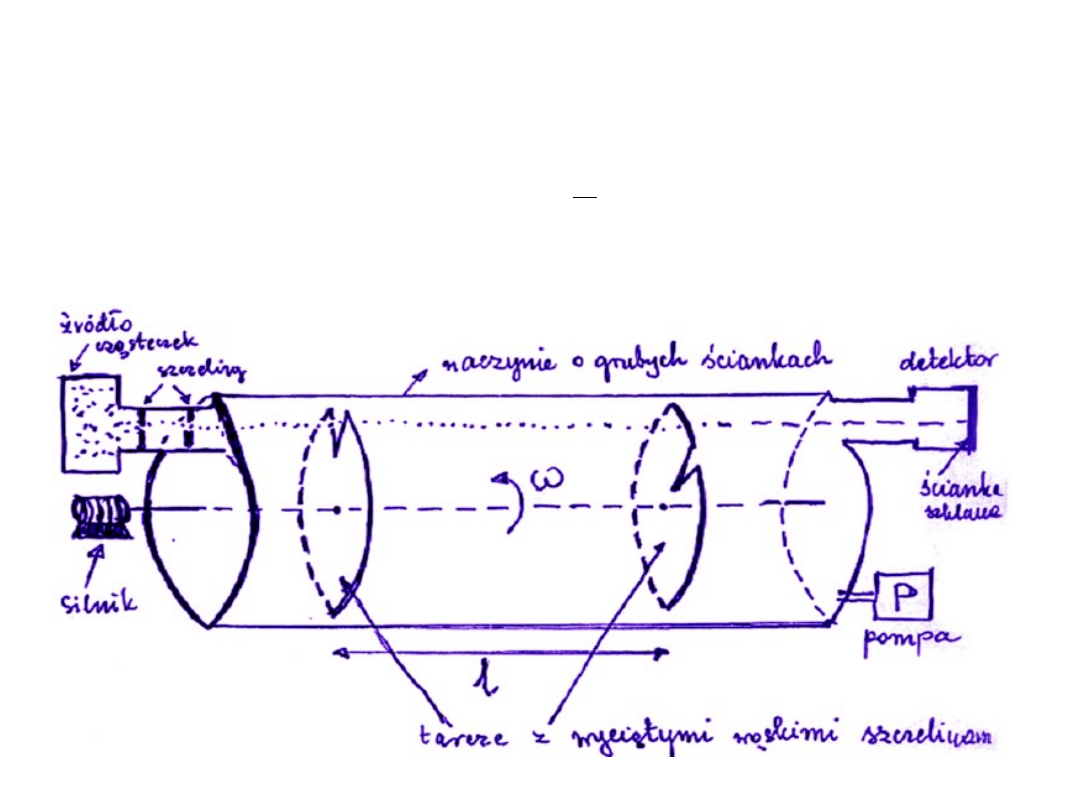
Rozkład prędkości cząsteczek

1.Doświadczenie Lammerta (1929 r.)
2.Równanie Maxwella (rozkład Maxwella)
3.Prędkości charakterystyczne: v

p

,

v

,

v

*

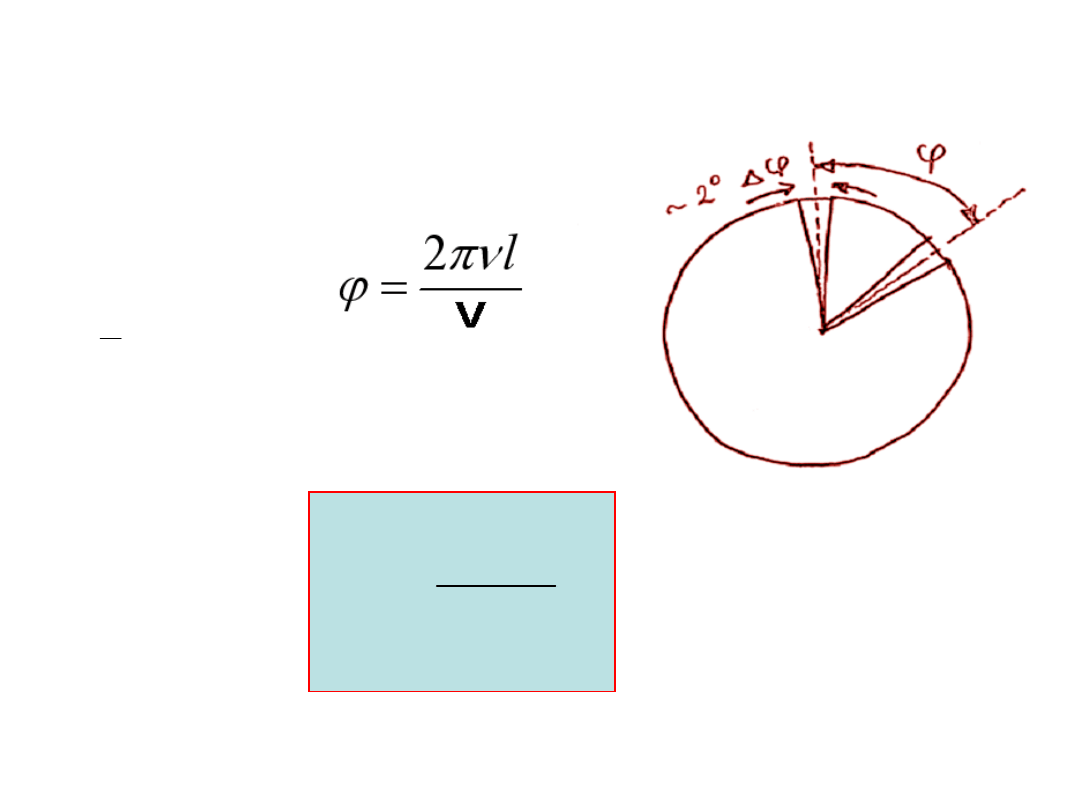
Im większa liczba cząsteczek o
prędkości v,
tym krótszy czas na otrzymanie
dostrzegalnego osadu na ściance
detektora.

�

2

t

l

t

v

j

w

w

pn

=

=

=

V

2 l

v

pn

j

=

V

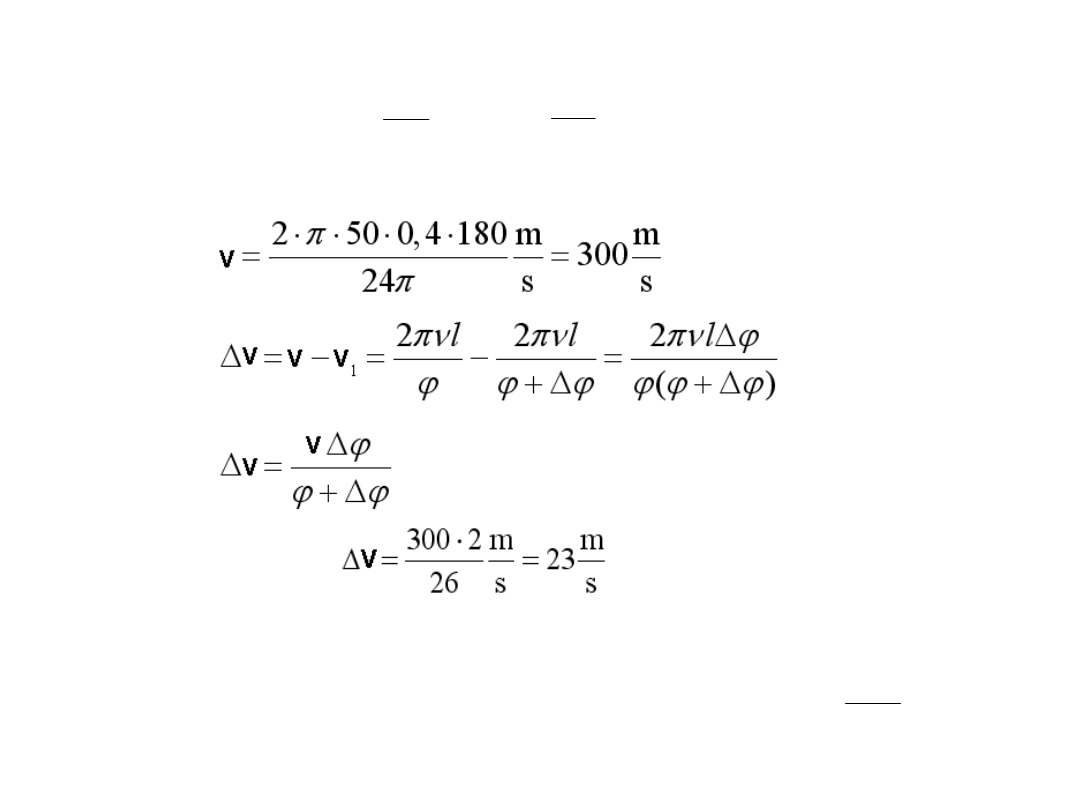
Jeśli

2

j

D =

o

, to

W doświadczeniu Lammerta można było wyznaczyć względną liczbę
cząsteczek, których prędkości leżały w przedziale od v do v+v

tzn. wielkość

N

N t

D

D

Przykład:

l = 0,40 m

24 24

180

p

j =

=

o

obr

50

s

n =

.

N

N t

D

D

N

N t

D

D

N

N t

D

D

Przedział

prędkości

Przedział

prędkości

Przedział

prędkości

60



90

32

270



300

368

480



510

161

90



120

137

300



330

361

510



540

127

120



150

195

330



360

342

540



600

100

150



180

251

360



390

313

600



660

46

180



210

300

390



420

278

660



720

22

210



240

338

420



450

237

720



840

9

240



270

361

450



480

190

840



960

W 1860 r. „rozkład prędkości” został wyprowadzony przez Maxwella.

N

 liczba cząsteczek zamkniętych w naczyniu

d
N



liczba cząsteczek, których prędkości

zawierają się w przedziale: v+v

- względna liczba cząsteczek, których prędkości leżą w przedziale v+v

dN

N

2

3
2

2

2

4

2

mv

kT

dN

m

v e

dv

N

kT

p

p

-

�

�

=

�

�

�

�

�

Na wartość funkcji

dN

N

wpływają: prędkość v i temperatura T.

2

3
2

2

2

( )

4

2

mv

kT

dN

m

f v

v e

Ndv

kT

p

p

-

�

�

=

=

�

�

�

�

�

Maksimum tej funkcji obliczmy:

1
2

( )

0

1,414

p

df v

dv

kT

v

m

=

� �

=

� �

� �

Dla tej prędkości funkcja osiąga maksimum. Prędkość tą nazywamy

prędkością najbardziej prawdopodobną v

p

.

Z taką prędkością porusza się największa liczba cząsteczek (w danej
temp. T).

stąd

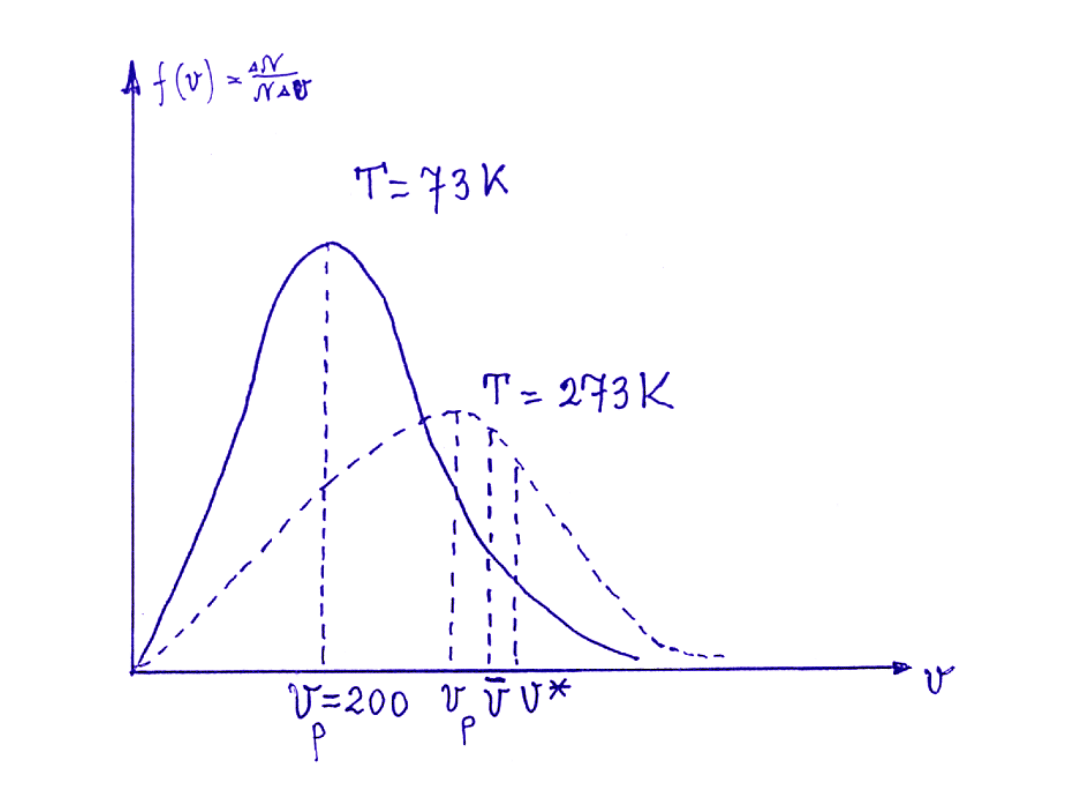
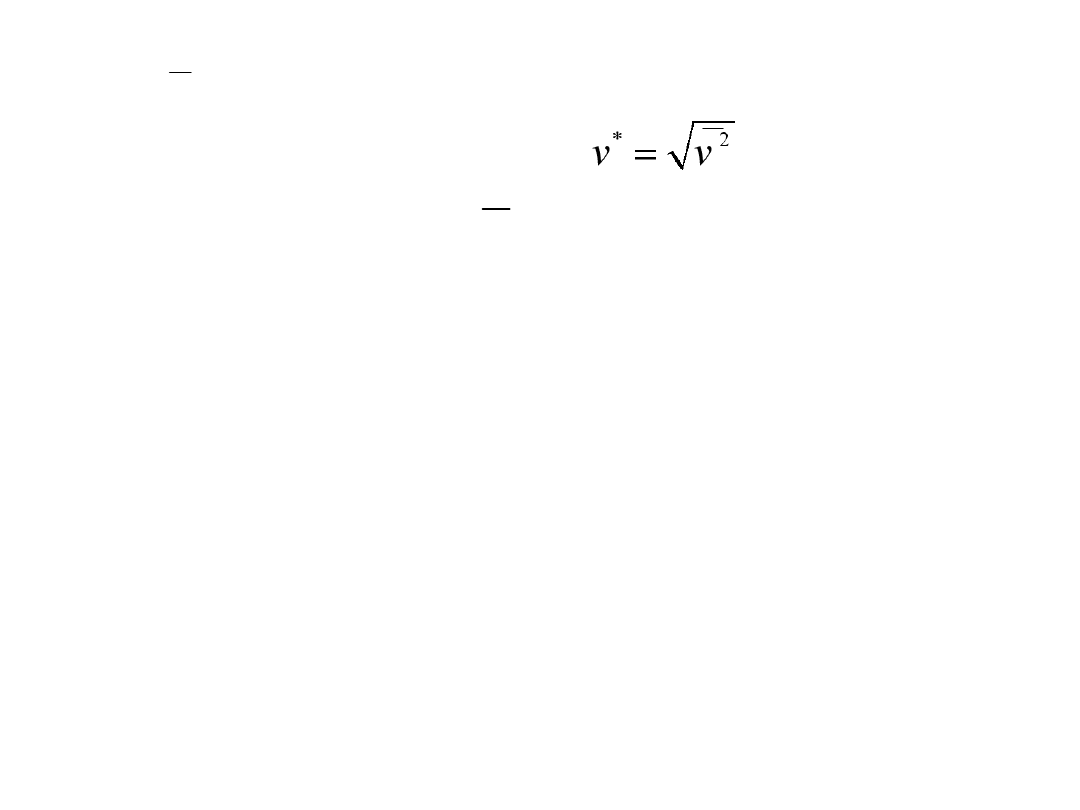
gdzie:

v

 prędkość średnia

*

v

 prędkość średnia kwadratowa;

*

p

v

v v

< <

Cząsteczki O

2

T = 100 K

v

p

= 229 m/s

T = 300 K

v

p

= 394 m/s

T = 1000 K

v

p

= 721 m/s

Cząsteczki H

2

v

p

= 1510 m/s

v

p

= 1765 m/s

Pary Hg

C

o

T = 0

C

o

T = 100

T = 0

T = 100

C

o

C

o

v

p

= 151 m/s

v

p

= 176,5 m/s

*

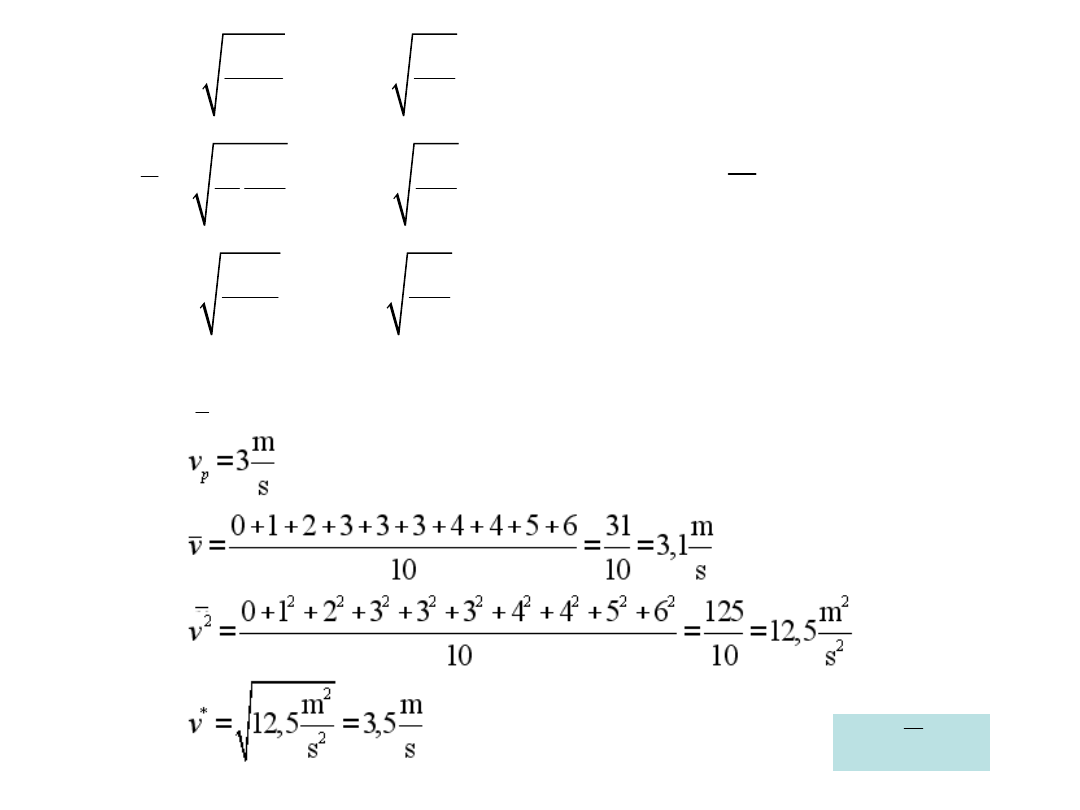
2

1,414

8

1,596

3

1,732

p

kT

kT

v

m

m

kT

kT

v

m

m

kT

kT

v

m

m

p

=

=

=

=

=

=

Przykład:

10 drobin, których prędkości wynoszą: 0, 1, 2, 3, 3, 3, 4, 4, 5, 6 [m/s]

Znaleźć: v

p

,

v

v

*

*

p

v

v v

< <

*

p

v

v v

< <