Wielokąty

Klasyfikacja oraz

własności

czworokątów

Lekcja powtórzeniowa
dla klasy VI szkoły
podstawowej lub klasy I
gimnazjum

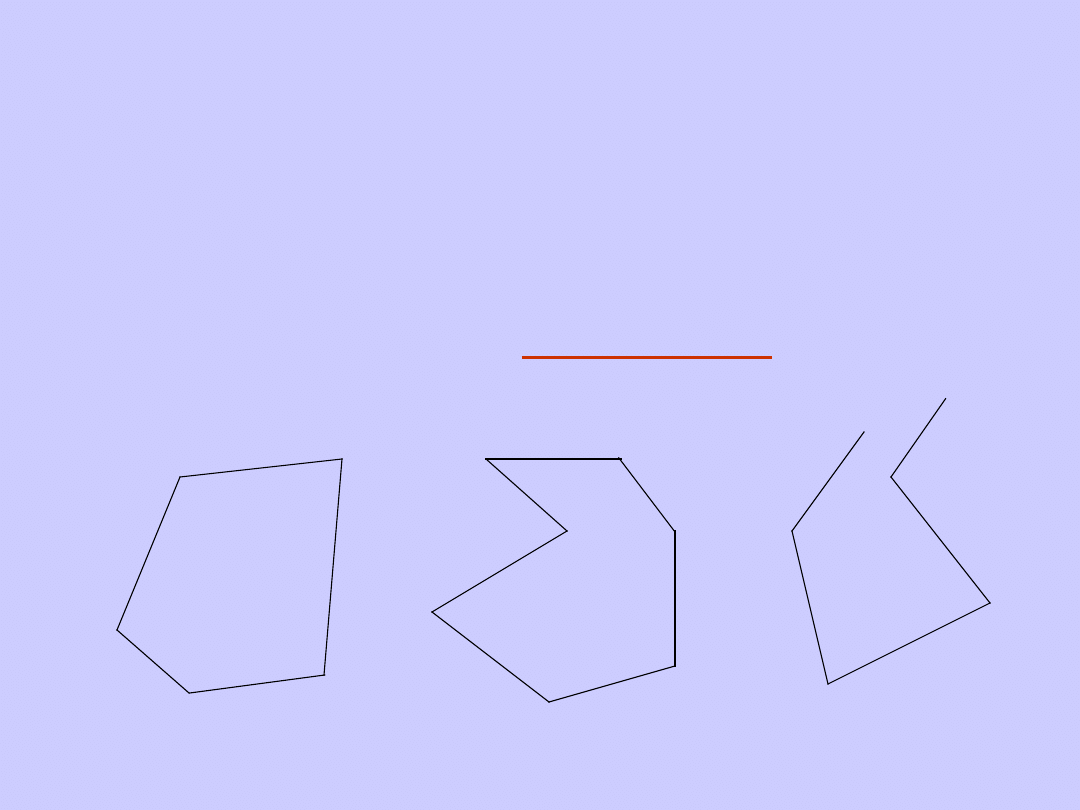
Definicja wielokąta

Część płaszczyzny ograniczoną łamaną

zwyczajną zamkniętą wraz z tą łamaną

nazywamy

wielokątem

A

B

C

D

E

A

B

C

D

E

F

G

A

B

C

D

E

To są
wielokąty

To nie jest
wielokąt

F

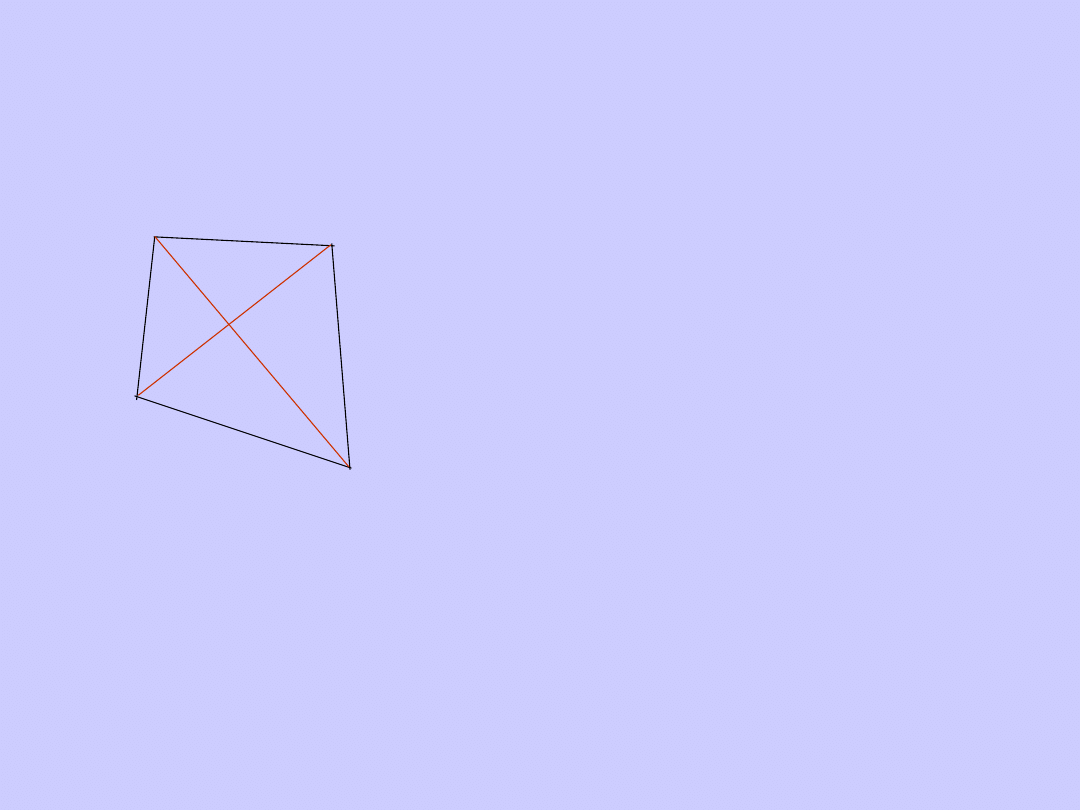
Elementy

wielokąta

A

D

C

B

Wierzchołki łamanej
nazywamy

wierzchołkami

wielokąta

Boki łamanej nazywamy

bokami wielokąta

Odcinek łączący dwa nie
kolejne wierzchołki
wielokąta nazywamy

przekątną wielokąta

Obwód wielokąta

to suma

długości wszystkich jego
boków

A, B, C, D – wierzchołki
wielokąta

AB, AD, BC, DC – boki
wielokąta

AC, DB – przekątne
wielokąta

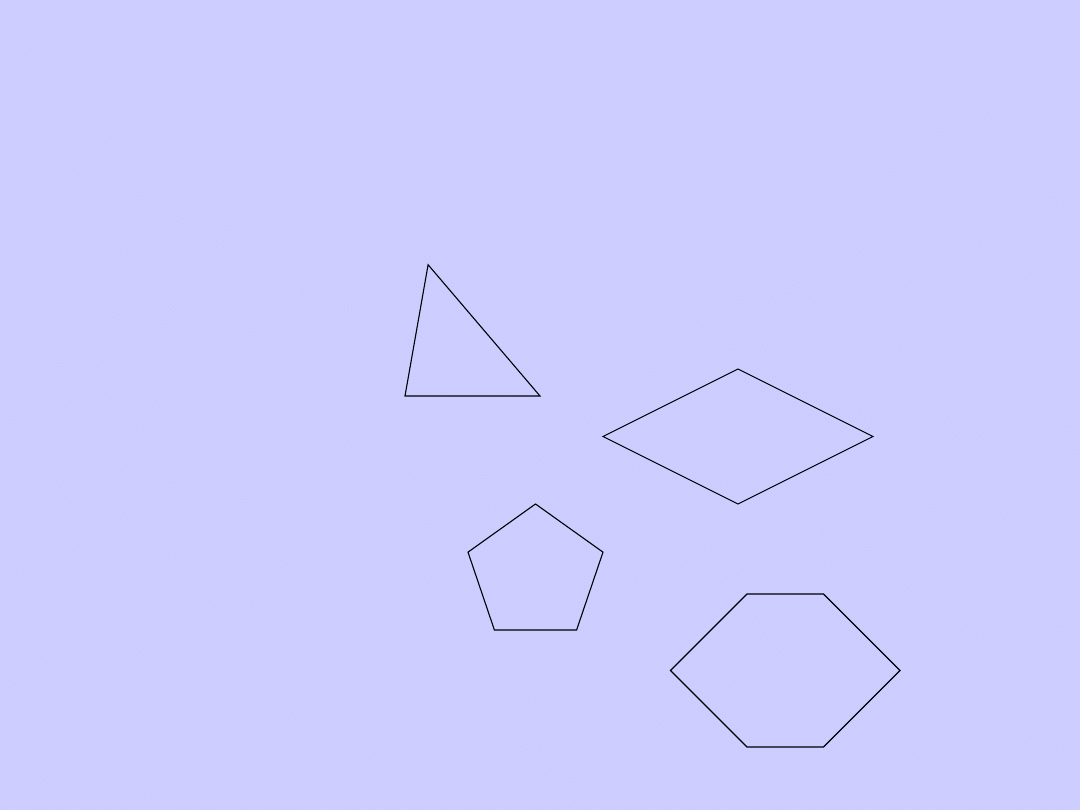
Podstawowy podział

wielokątów

Ze względu na ilość boków wielokąty

dzielimy na:

Trójkąty:

3

boki

Czworokąty:

4

boki

Pięciokąty:

5

boków

Sześciokąty:

6 boków,

itd.

Czworokąty

Czworokąty, to wielokąty mające 4 boki.

Klasyfikacja czworokątów:

C

T

R

P

R

b

K

C - czworokąty

T - trapezy

R

-

równoległoboki

R

b

- romby

P

-

prostokąty

K

-

kwadraty

Trapezy

Trapez to czworokąt mający parę boków
równoległych.

A

B

C

D

E

F

h

Boki równoległe AB i DC

nazywamy
podstawami

AB, DC - podstawa
dolna i podstawa
górna

Boki nierównoległe
AD i BC nazywamy
ramionami

Odcinek DE to wysokość

trapezu

Powyższy trapez nazywa się

różnobocznym

, gdyż jego

boki mają różne długości. Jeśli ramiona trapezu są

równe, to trapez nazywamy

równoramiennym.

.

.

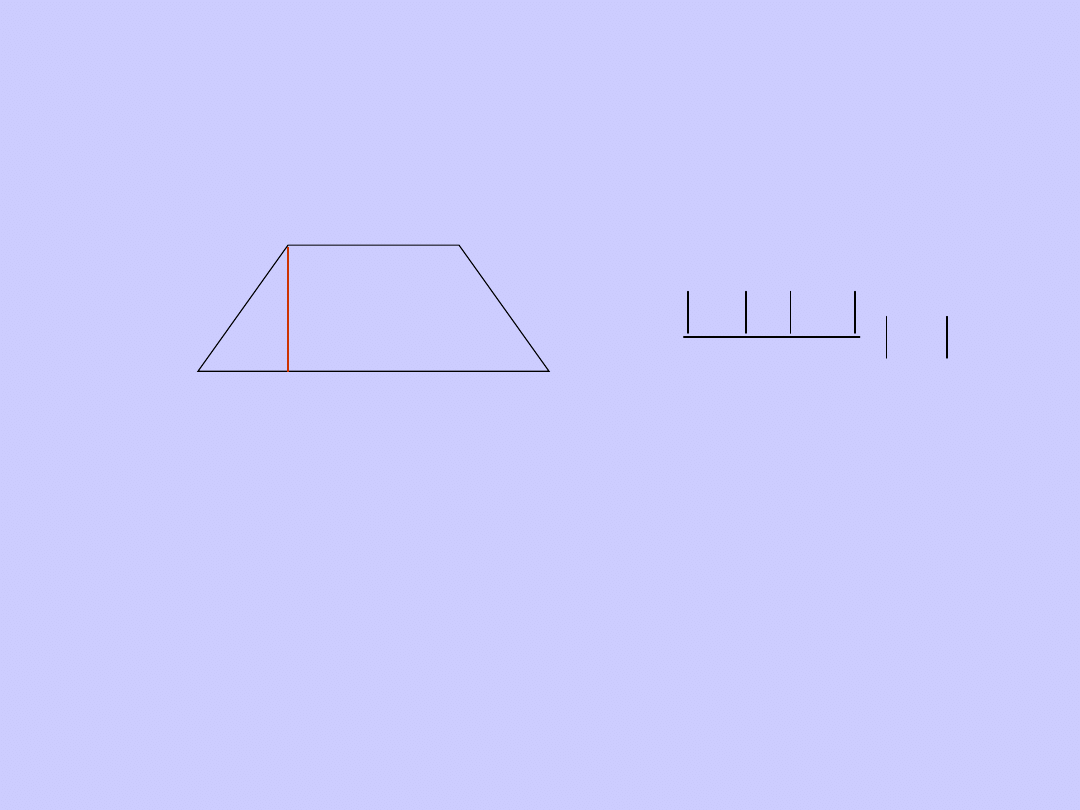
Trapez równoramienny

A

B

C

D









E

WŁASNOŚCI:

1. AD=BC - ramiona mają równe długości
2. kąty przy jednej podstawie są równe
3.  +  =180 suma kątów przy jednym

ramieniu jest równa kątowi półpełnemu

4. suma kątów wewnętrznych jest kątem pełnym
5. przekątne są równej długości

ED

DC

AB

P







2

Pole

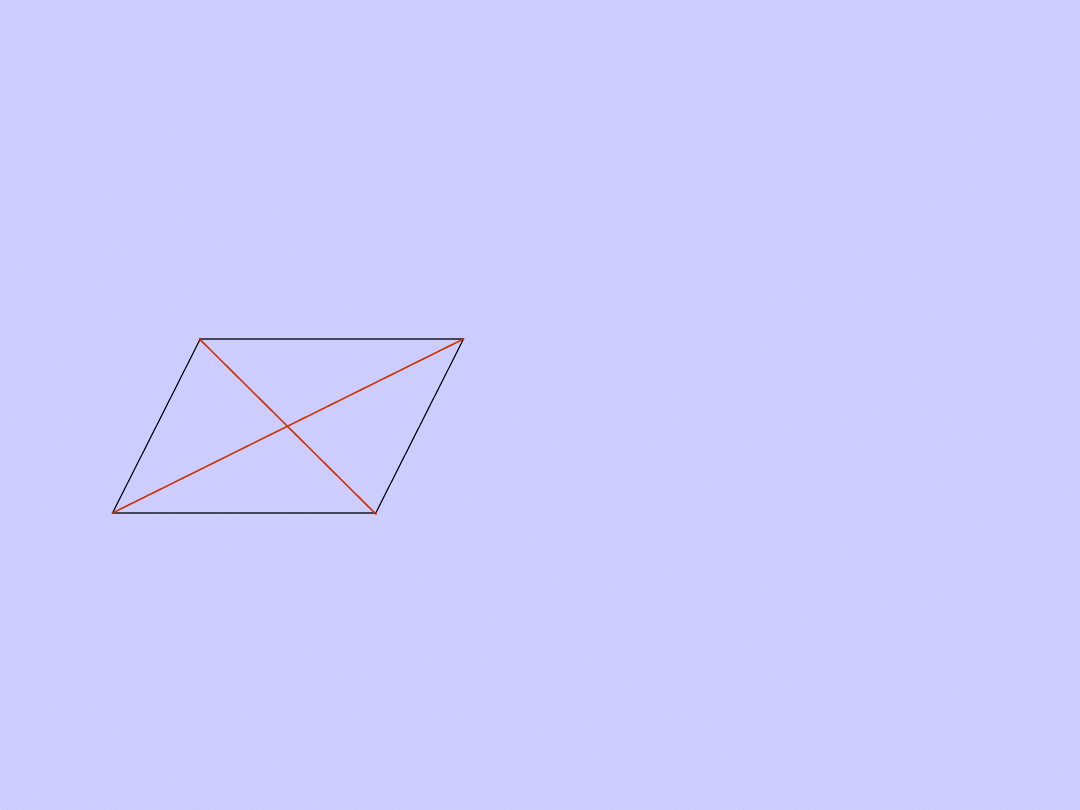
Równoległobok

Jest to czworokąt, który ma dwie pary boków

równoległych

A

B

D

C

O

a

b

Własności:

1. AD



BC oraz AB



DC

2.



AD



=



BC

 i 

AB



=



DC



3. kąt A = kąt C oraz

kąt B = kąt D

4. suma wszystkich kątów wewnętrznych ma
miarę 360 stopni

5. przekątne równoległoboku przecinają się w
połowie

6.suma miar dwóch kolejnych kątów wynosi 180
stopni

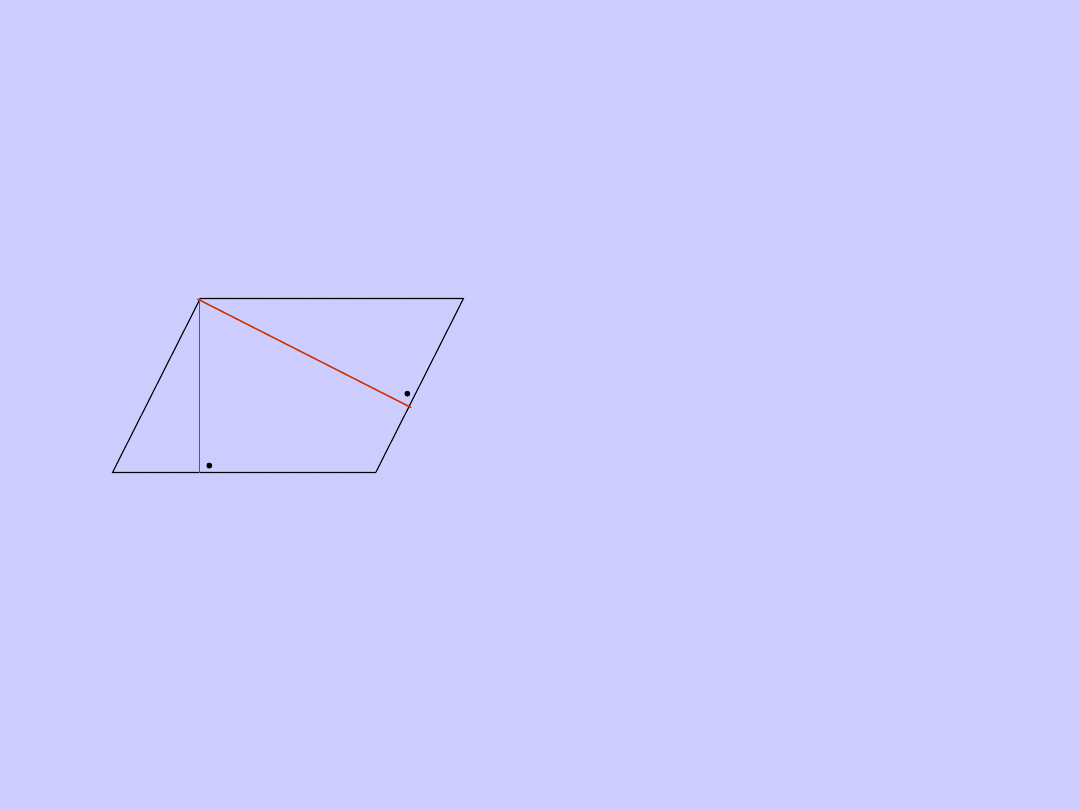
Równoległobok

A

B

D

C

h

a

b

Równoległobok ma
dwie wysokości:

h  AB h

1

 BC

Pole

równoległoboku

P = a ·h lub P= b ·h

1

Obwód

równoległoboku

Obw = 2a + 2b

h

1

Prostokąt

Prostokąt to równoległobok, który ma

wszystkie kąty proste

A

B

C

D

O

Własności

1. AD



BC oraz AB



DC

2.



AD



=



BC

 i 

AB



=



DC



3. kąt A = kąt B = kąt C =

kąt D = = 90

4. suma wszystkich kątów wewnętrznych ma

miarę 360

0

5.



AO



=



OC

 i 

DO



=



OB

 -

przekątne dzielą się na

połowy
6.



AC



=



DB

 -

przekątne są równej długości

Prostokąt

Pole prostokąta

P = a*b

Obwód
prostokąta

Obw = 2a + 2b

A

B

C

D

O

a

b

Romb

Romb jest równoległobokiem, którego

wszystkie boki są równe

A

B

C

D

O

Własności:

1. AD



BC oraz AB



DC

2.



AD



=



DC

 = 

CB



=



BA



3. kąt A = kąt C i kąt B =

kąt D

4. kąt A + kąt B = 180

5. suma wszystkich kątów wewnętrznych ma

miarę 360 stopni
6.



AO



=



OC

 i 

DO



=



OB

 -

przekątne dzielą się na

połowy
7. przekątne dzielą kąty rombu na połowy i są

prostopadłe

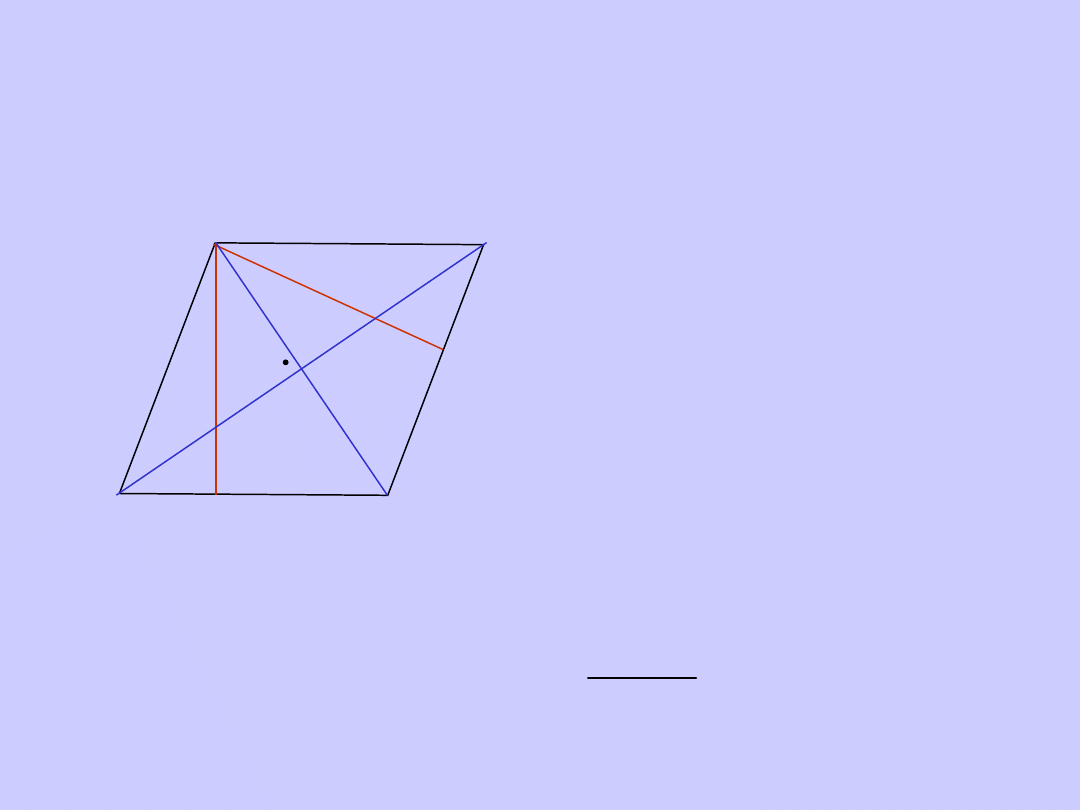
Romb

Romb ma dwie

wysokości takiej

samej długości

Pole

rombu

1. P = a ·h

a

a

h

Jeśli oznaczymy długości przekątnych rombu

przez e i f to:

2

.

2

f

e

P





.

.

Kwadrat

Kwadrat to prostokąt o równych bokach

Kwadrat to romb o równych kątach

A

B

C

D

O

Własności:

1. AD



BC oraz AB



DC

2.



AD



=



DC

 = 

CB



=



BA



3. kąt A = kąt B = kąt C = kąt

D = 90°

4. suma wszystkich kątów wewnętrznych ma

miarę 360 stopni
5.



AO



=



OC

 i 

DO



=



OB

 -

przekątne dzielą się na

połowy
6. przekątne dzielą kąty na połowy, są

prostopadłe i równe

Kwadrat

A

B

C

D

O

Bok kwadratu jest
jednocześnie jego
wysokością

a

a

Pole

kwadratu

P = a ·a

Obwód

kwadratu

Obw = 4a