ELEMENTY TEORII

MODELOWANIA

Komputerowe wspomaganie

prac inżynierskich

Opracował:
Dr hab. inż. Józef Salwiński prof. n

MODEL

• Model –„modus”– „modulus”(miara,

obraz, sposób)

Modelowanie stało się podstawą

badania systemów w matematyce,
fizyce, chemii, biologii, ekonomii,
cybernetyce, analizie dynamicznej
maszyn

Modele

Aby móc badać funkcjonowanie różnego rodzaju

obiektów posługujemy się ich modelami.

MODEL - jest uproszczonym odwzorowaniem

rzeczywistego obiektu i posiada tylko niektóre
cechy obiektu – najistotniejsze ze względu na
konkretny cel modelowania np.:
cechy geometryczne (model geometryczny),
ruch elementów (model kinematyczny)
lub inne cechy.

MODEL

• TEORIA, która jest strukturalnie

podobna do innej, co umożliwia
przechodzenie od jednej teorii do
innej za pomocą zwykłej zmiany
terminologii; w tym znaczeniu
model jest środkiem poznania

MODEL

• SYSTEM, do którego odnosi się

pewna teoria praktyczna lub
teoretyczna dla uproszczonego
odzwierciedlenia badanego
systemu naturalnego; taki model
jest przedmiotem poznania.

MODEL

• Jest to taki dający się pomyśleć lub

materialnie zrealizować układ, który
odzwierciedlając lub odtwarzając przedmiot
badania, zdolny jest zastępować go tak, że
jego badanie dostarcza nam nowej informacji
o tym przedmiocie

MODEL

• Jest zastępującą oryginał, przyjętą

formą reprezentacji,
wykorzystywaną do wyjaśnienia i
przewidywania zachowania się
oryginału w sposób adekwatny z
punktu widzenia celu rozważań

MODELE

• FIZYCZNE – atrybuty obiektu są

przedstawione przez wielkości fizyczne
(napięcie położenie) – np. model w tunelu
aerodynamicznym.

• MATEMATYCZNE – obiekt i jego atrybuty

są przedstawiane przez zmienne
matematyczne, natomiast ich działanie
przez funkcje matematyczne, natomiast
ich działanie przez funkcje matematyczne.

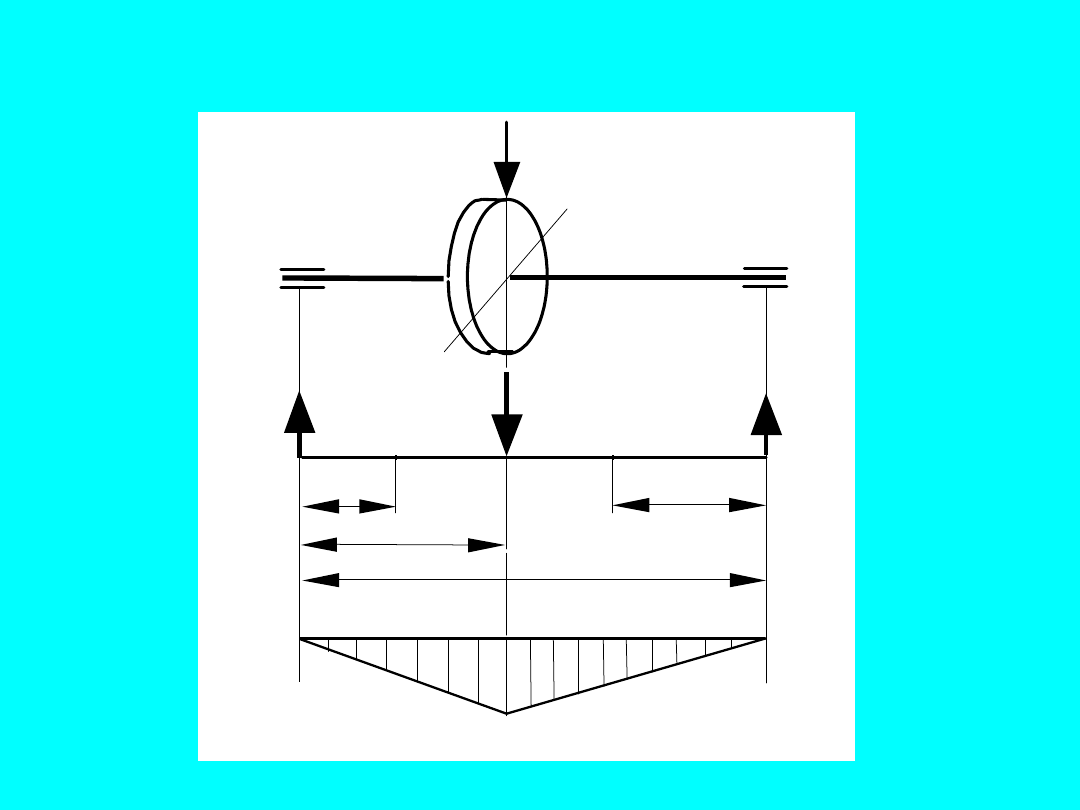
Modelowanie fizyczne

a)

b)

c)

M

g

F

x

1

B

F

A

a

x

2

L

L

R

B

R

A

E

D

C

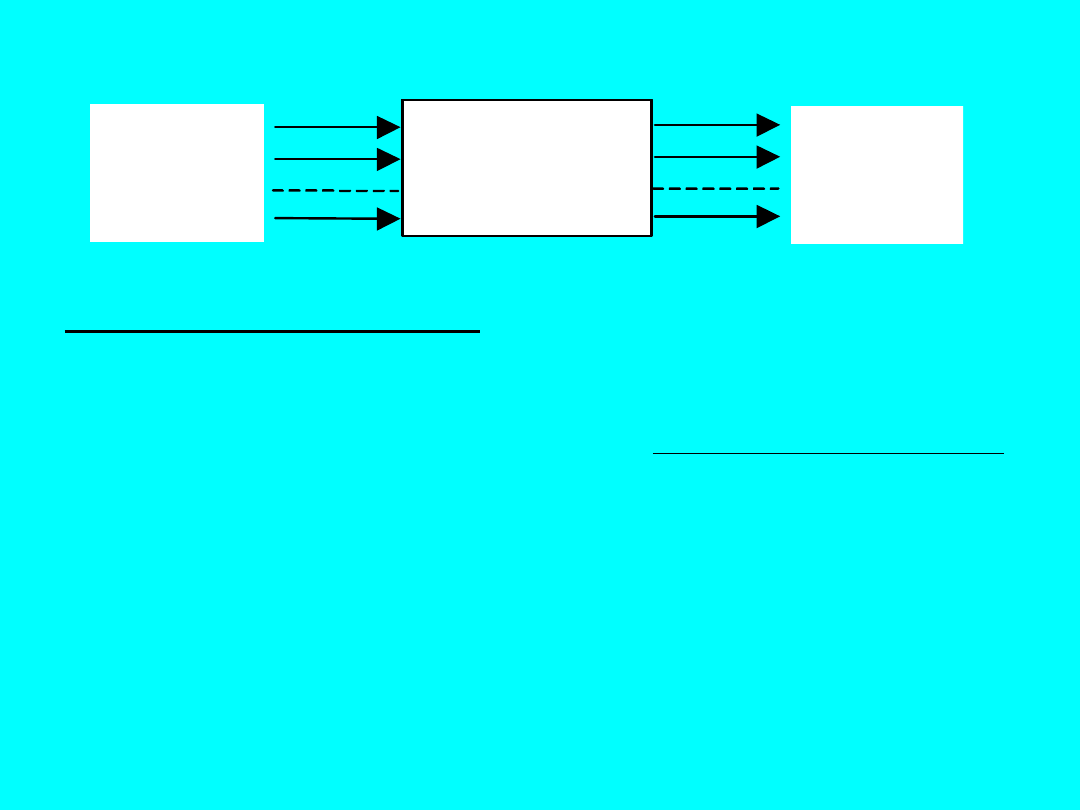
Model matematyczny badanego

układu

Model matematyczny bada zależności zmiennych

wyjściowych od zmiennych wejściowych.

Za zmienne wyjściowe przyjmowane są takie wielkości

fizyczne, których otrzymywanie jest celem działania układu.

Pozostałe wielkości mogą być uznawane za wejściowe.
W maszynach i innego rodzaju układach mechanicznych

zmiennymi są na przykład: siły i momenty obciążeń,
naprężenia i odkształcenia elementów, parametry
geometryczne i materiałowe, nazwy elementów, rodzaje
więzów i wiele innych

Układ

Zmienne
wejściowe

Zmienne
wyjściowe

SYMULACJA

• Można ją zdefiniować jako

technikę rozwiązywania
problemów polegającą na
śledzeniu w czasie zmian
zachodzących w modelu
dynamicznym

KOMPUTEROWY MODEL

SYMULACYJNY

• Jest logiczno matematycznym

przedstawieniem pojęcia systemu lub
działań zaprogramowanym w celu
rozwiązania za pomocą komputera

MODEL DETERMINISTYCZNY

• Jest analitycznym przedstawieniem

pojęcia systemu lub działań, w którym
dla danych wielkości wejściowych
wyniki są określone jednoznacznie

Model deterministyczny

Dla każdego (dopuszczalnego) zestawu

wartości zmiennych wejściowych pozwala
wyznaczyć jednoznaczny i ściśle
określony zestaw wartości na wyjściach

Przykład:

Elementarne wzory obliczeniowe fizyki podające w
sposób analityczny zależności między
poszczególnymi wielkościami i pozwalające dla tych
samych danych uzyskać zawsze ten sam określony
(zdeterminowany) wynik.

Modele matematyczne budowane z użyciem takich

wzorów są więc modelami analitycznymi i
deterministycznymi.

Model stochastyczny

Jest to model w którym powiązania
funkcyjne zależą od wielkości
losowych. Dla danych wielkości
wejściowych wyniki mogą być
jedynie przewidziane zgodnie z
zasadami
probabilistyki

Model wartości

oczekiwanych

Jest to model w którym
wielkościom losowym
zostały nadane ich wartości
oczekiwane lub średnie