11

Zagadnienia...

• W jaki sposób zachodzi dyfuzja?

• Dlaczego odgrywa tak dużą rolę?

• Jak można przewidzieć szybkość dyfuzji
w niektórych prostych przypadkach?

• Jak dyfuzja zależy od temperatury?

Dyfuzja w ciałach stałych

22

Dyfuzja

Dyfuzja -

proces samorzutnego rozprzestrzeniania się

atomów lub cząsteczek w ośrodku (np. w gazie, cieczy lub

ciele stałym), będący konsekwencją chaotycznych zderzeń

atomów (cząsteczek) dyfundującej substancji między sobą

i z atomami (cząsteczkami) otaczającego ośrodka

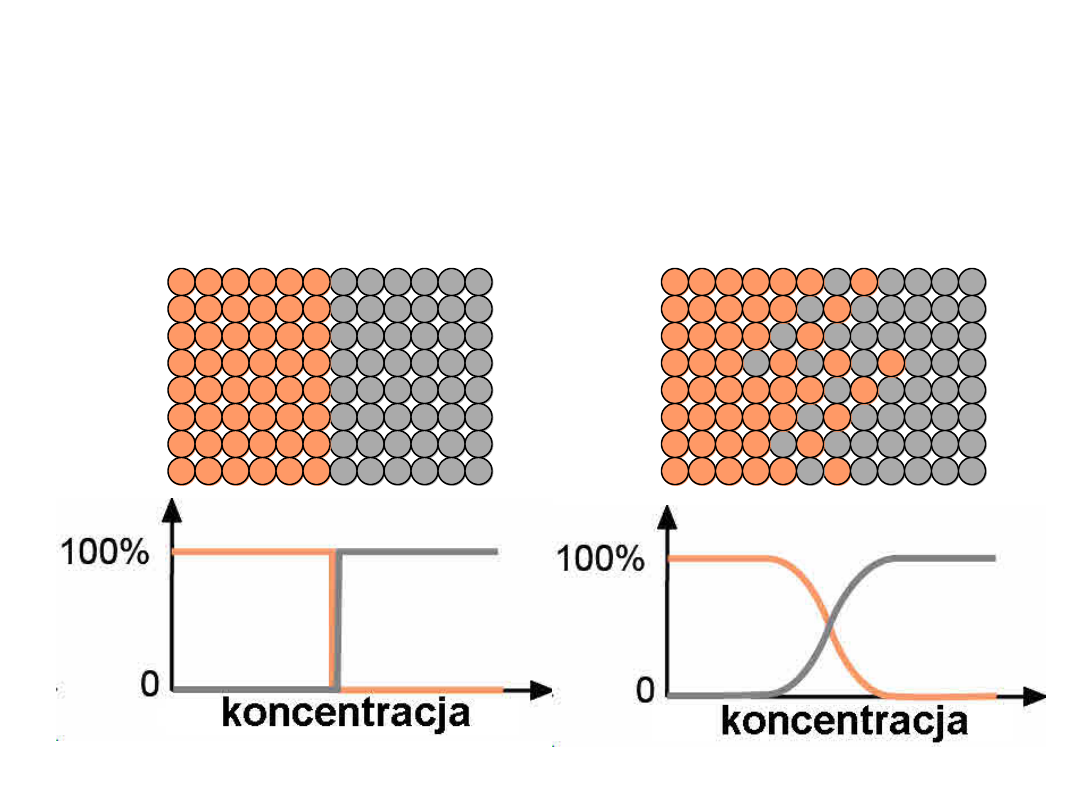
Dyfuzja prowadzi do

ujednorodnienia

się stężeń składników

Mechanizmy

• Gazy i ciecze – ruchy Browna (przypadkowe)
• Ciała stałe – mechanizm wakancyjny lub międzywęzłowy

najszybciej zachodzi dyfuzja w gazach:

2

1

Ponieważ struktury krystaliczne są
na ogół zwarte, migracja atomów
lub jonów w krystalicznych ciałach
stałych jest utrudniona.
Energia konieczna do
przemieszczenia atomu w zwartej
strukturze krystalicznej jest na tyle
wysoka, że niekiedy czyni dyfuzję
prawie niemożliwą.

33

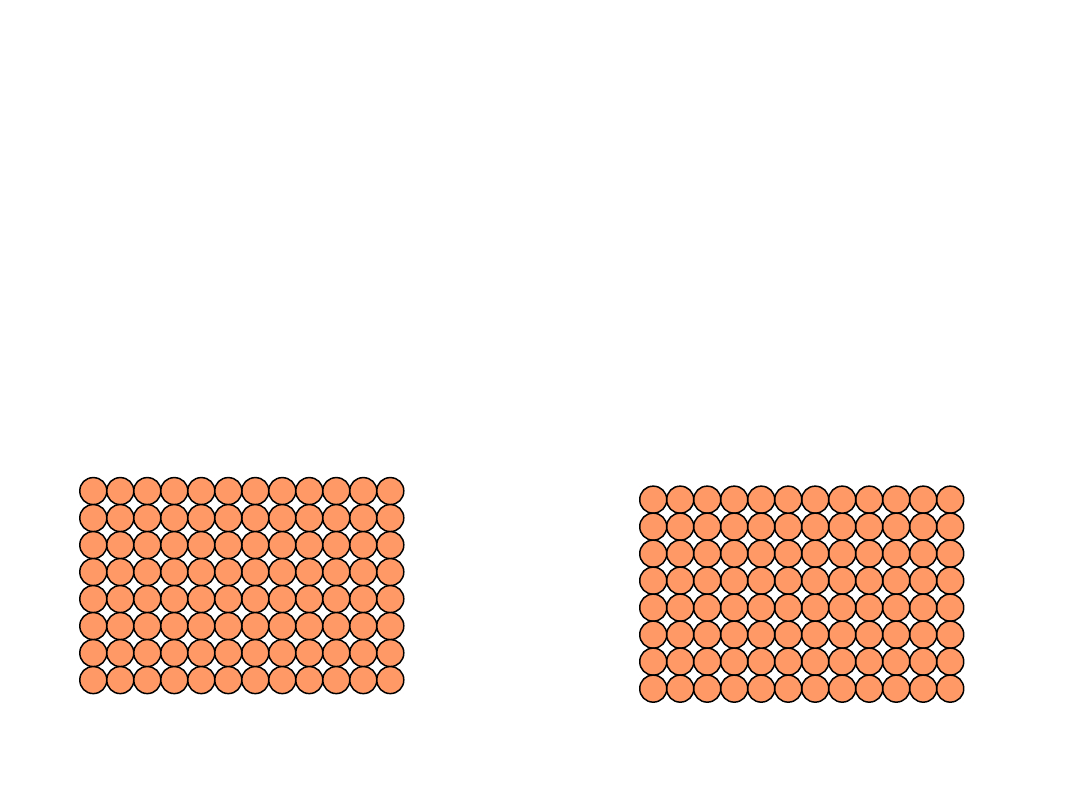
• W stopach atomy mają tendencje do przemieszczania się

z obszarów o większej do obszarów omniejszej koncentracji

Początkowo

Dyfuzja wzajemna

Po pewnym czasie

para

dyfuzyjn

a

44

•

Samodyfuzja

:

W czystych ciałach stałych atomy też migrują

Oznaczmy kilka atomów

Po pewnym czasie

Samodyfuzja

A

B

C

D

A

B

C

D

Samodyfuzja (autodyfuzja),

proces dyfuzji, w

której biorą udział tylko atomy (cząstki) danej
substancji. Samodyfuzja prowadzi m.in. do
wyrównania składu izotopowego pierwiastków
występujących w przyrodzie.

55

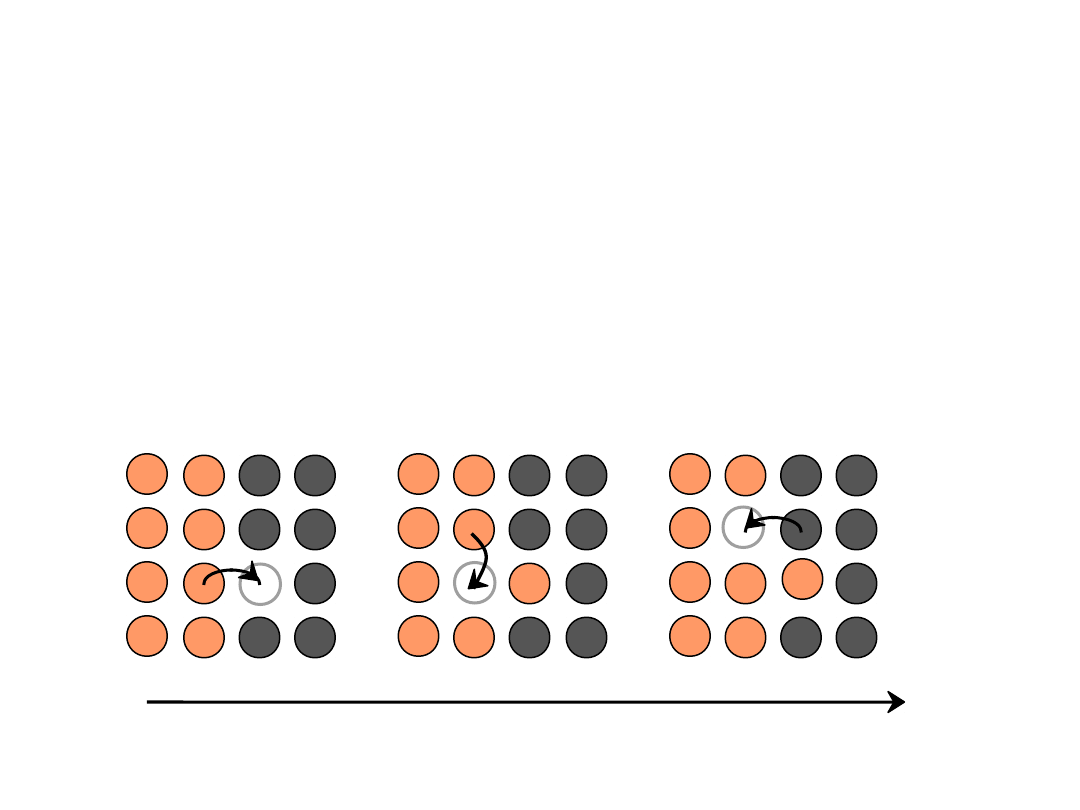
Mechanizmy Dyfuzji

Mechanizm
wakancyjny

:

•

atomy wymieniają się miejscami z wakancjami

• zachodzi w roztworach substytucyjnych
• szybkość dyfuzji zależy od:
- liczby wakancji
- energii aktyacji wymiany: wakancja - atom.

czas

kierunek przemieszczania atomów jest przeciwny do
strumienia wakancji

66

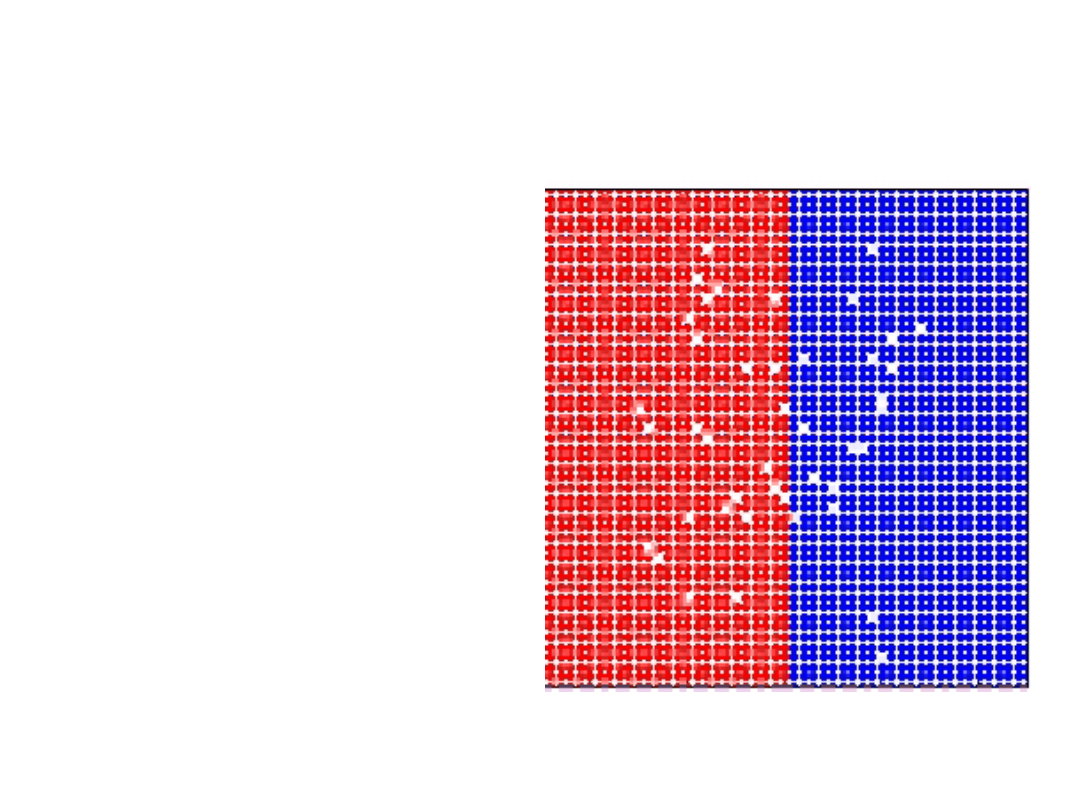
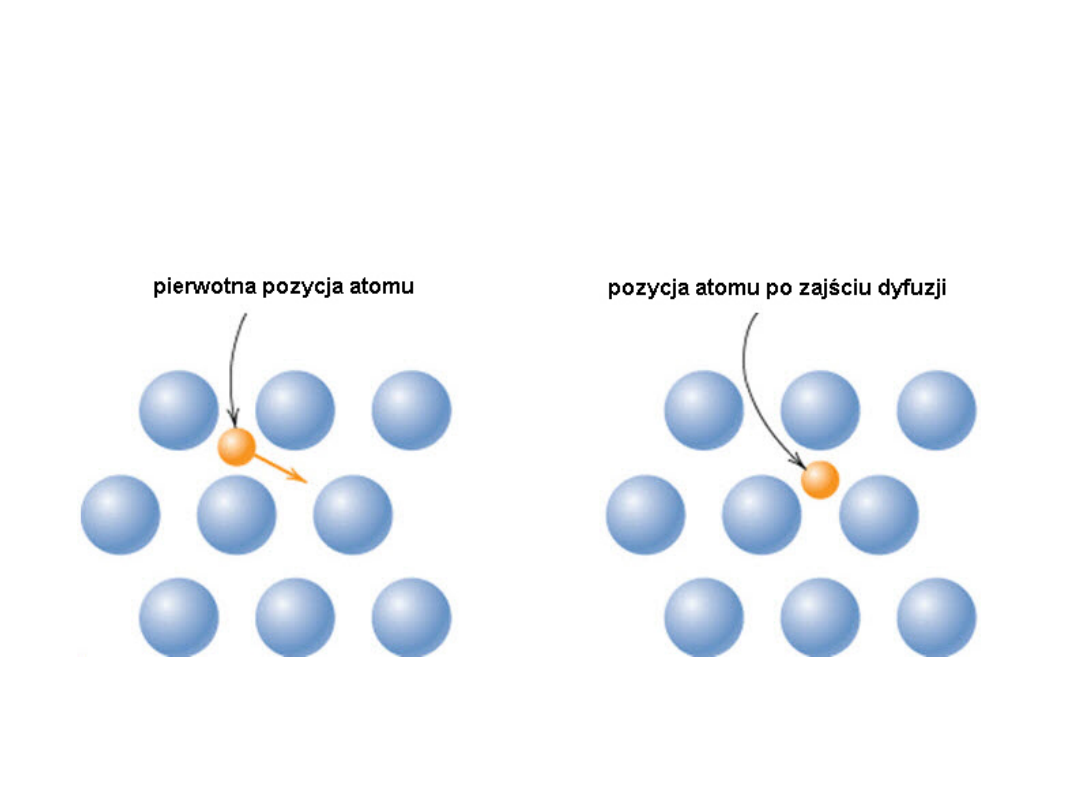
Symulacja dyfuzji na
granicy dwóch
ośrodków:

Szybkość dyfuzji atomów
substytucyjnych zależy od:

- koncentracji wakancji,
- częstotliwości
przeskoków.

Symulacja dyfuzji

77

Mechanizmy dyfuzji

• Dyfuzja międzywęzłowa

– mniejsze atomy

mogą dyfundować pomiędzy atomami
osnowy

Dyfuzja międzywęzłowa jest szybsza niż
dyfuzja mechanizmem wakancyjnym

88

Nawęglanie

:

Dyfuzja atomów węgla do
osnowy stalowej o mniejszej
zawartości węgla
Obecność węgla sprawia, że
stal staje się twardsza i
bardziej odporna na ścieranie

Przykład:

koła zębate w

skrzyniach biegów

Procesy wykorzystujące

dyfuzję

Inne obróbki powierzchniowe związane z dyfuzją:

azotowanie, cyjanowanie, borowanie

(od boru – pierwiastka)

99

•

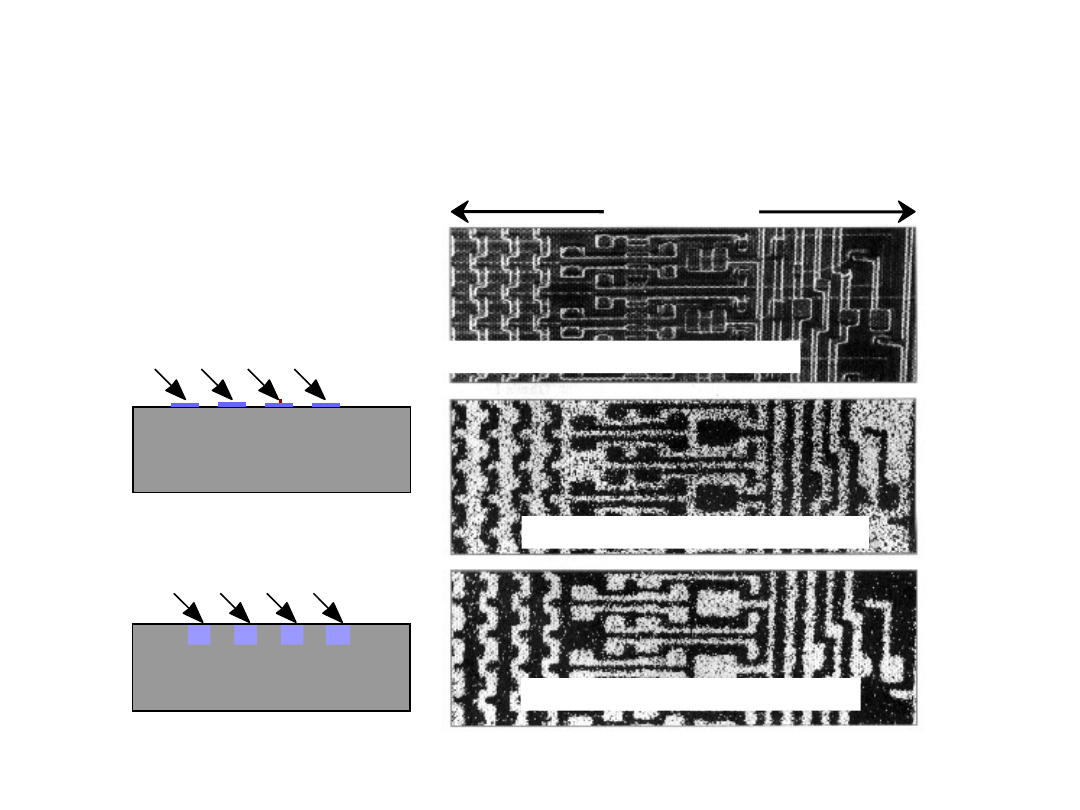
Domieszkowanie

krzemu atomami Al w układach

scalonych

• Proces:

krzem

Procesy wykorzystujące

dyfuzję

powiększony obraz chipu

0.5

mm

jasne obszary: atomy Si

jasne obszary: atomy Al

2. Podgrzanie

1.

Umieszczenie warstwy

bogatej w aluminium na
powierzchni krzemu.

krzem

Chapter 18, Callister 7e.

SEM

1010

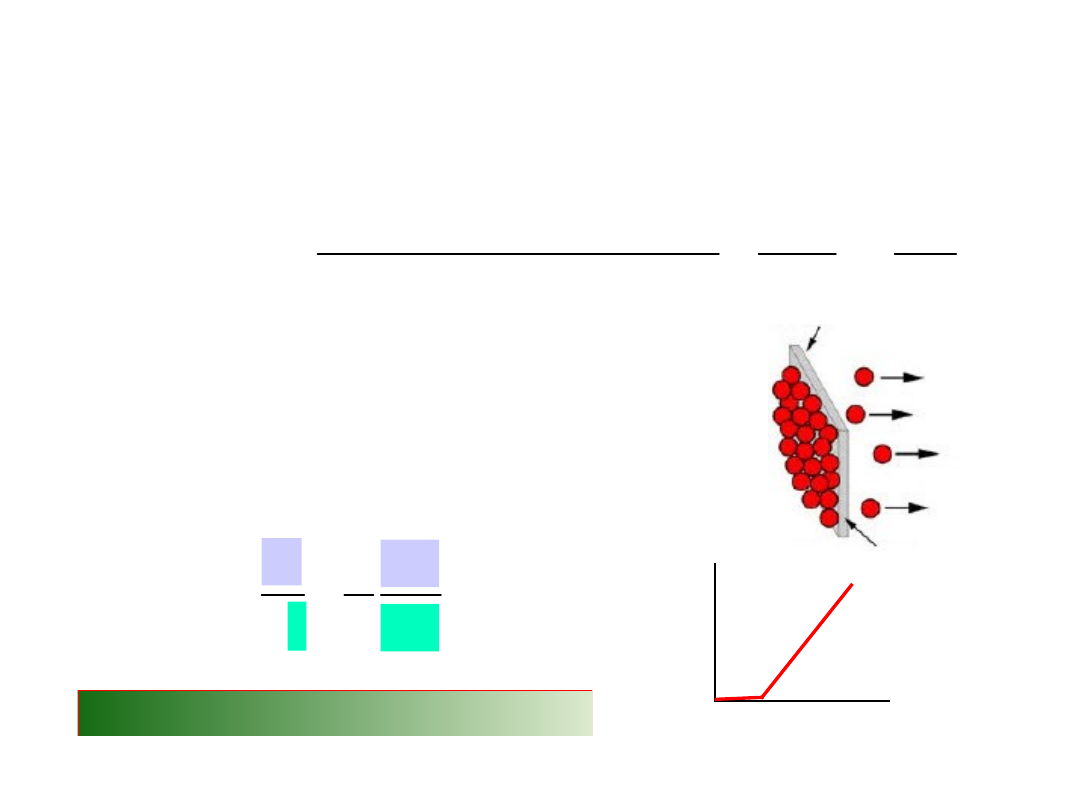
Dyfuzja – opis ilościowy

• Pomiar empiryczny

– Membrana o znanej powierzchni
– Gradient koncentracji
– Pomiar szybkości dyfuzji przez membranę







s

m

kg

lub

s

cm

mol

czas

ia

powierzchn

masa)

(lub

moli

dyf.

liczba

Strumie

ń

2

2







J

dt

dM

A

At

M

J

1





M

=

m

a

sa

czas

J wsp. kier.

Jak ilościowo opisać dyfuzję?

x

gradient koncentracji

A

membrana

duże
stężeni
e

małe
stężeni
e

1111

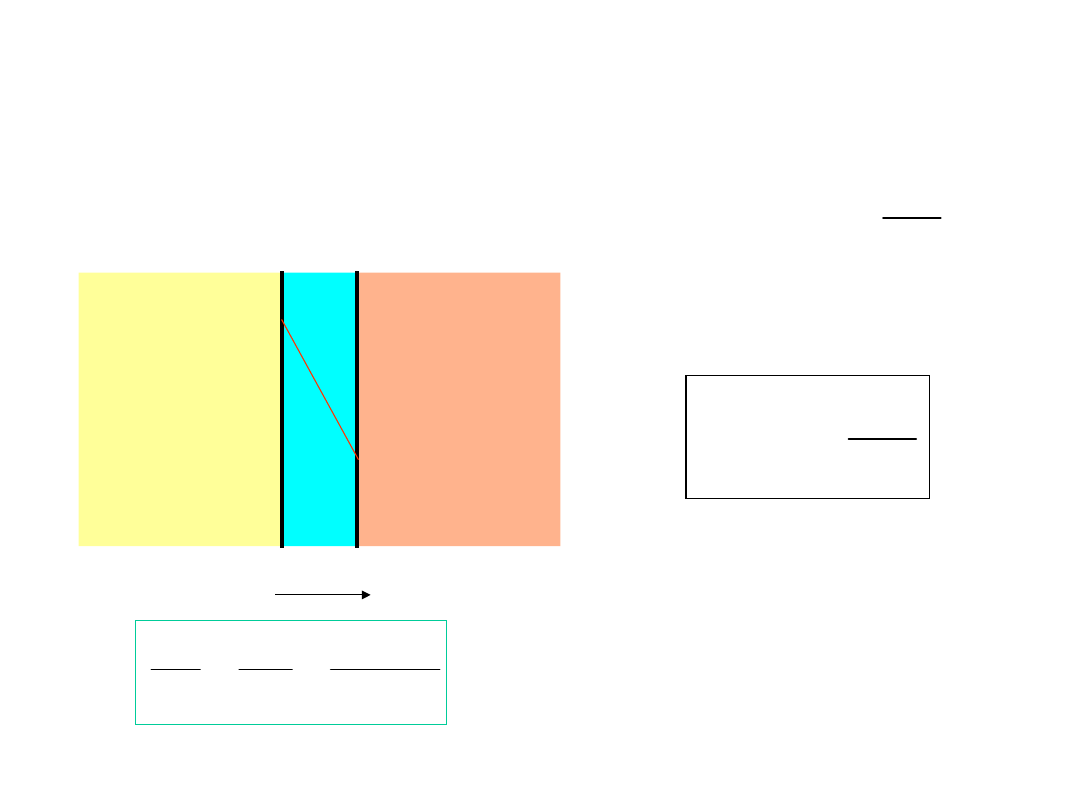
Dyfuzja w Stanie Ustalonym

dx

dC

D

J





Pierwsze prawo
Ficka:

C

1

C

2

x

C

1

C

2

x

1

x

2

D  współczynnik dyfuzji

Szybkość dyfuzji jest niezależna od czasu

Strumień jest proporcjonalny do
gradientukoncentracji

=

dx

dC

1

2

1

2

x

x

C

C

x

C

dx

dC













1212

Przykład: Rękawice ochronne

• Używając rozpuszczalnika farb należy używać rekawiczek

ochronnych, aby rozpuszczalnik nie był absorbowany przez
skórę.

• Jeżeli używamy rękawiczek gumowych o grubości 0.04 cm,

to jaki jest strumień cząsteczek rozpuszczalnika
przenikającego przez gumę?

• Dane:

– współczynnik dyfuzji rozpuszczalnika w gumie:

D = 110 x10

-8

cm

2

/s

– stężenia powierzchniowe:

C

2

= 0.02 g/cm

3

C

1

= 0.44 g/cm

3

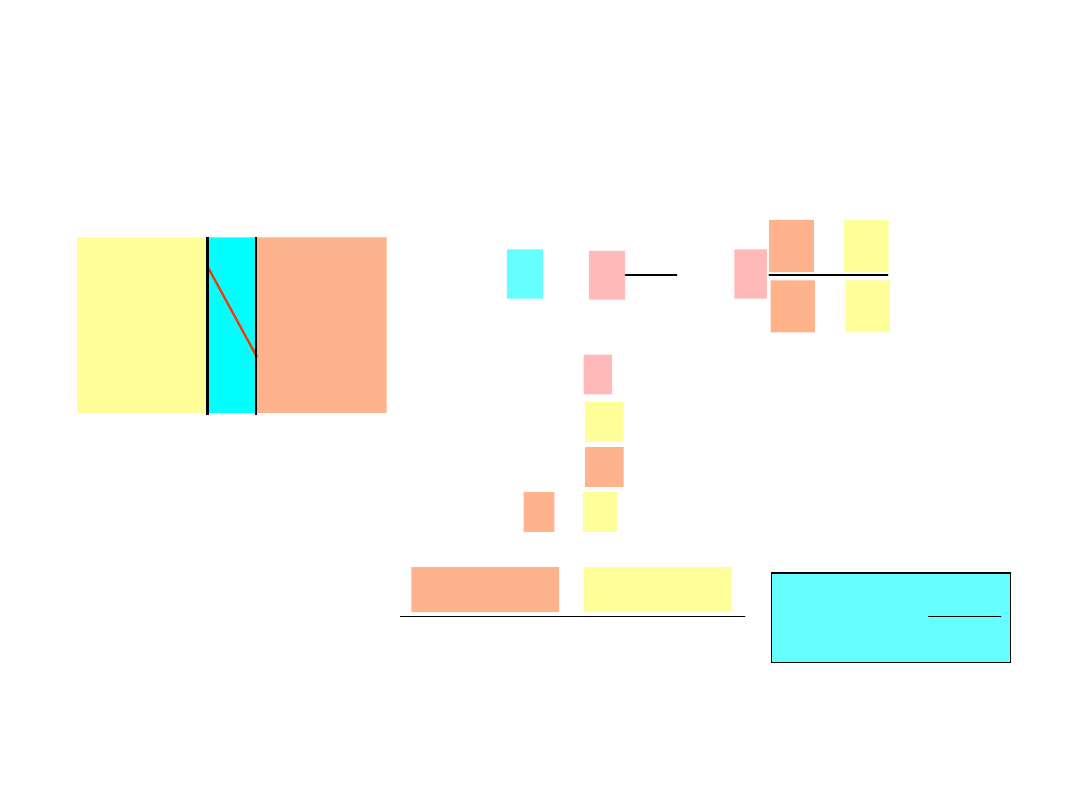
1313

s

cm

g

10

x

16

.

1

cm)

04

.

0

(

)

g/cm

44

.

0

g/cm

02

.

0

(

/s)

cm

10

x

110

(

2

5

-

3

3

2

8

-









J

Przykład - rozwiązanie

1

2

1

2

-

x

x

C

C

D

dx

dC

D

J











D

t

b

6

2





rę

ka

w

ic

zk

a

C

1

C

2

skóra

ro

zp

u

sz

cz

a

ln

ik

x

1

x

2

Rozwiązanie

– zakładamy liniowy gradient koncentracji

D = 110

x

10

-8

cm

2

/s

C

2

= 0.02 g/cm

3

C

1

= 0.44 g/cm

3

x

2

– x

1

= 0.04 cm

Data:

1414

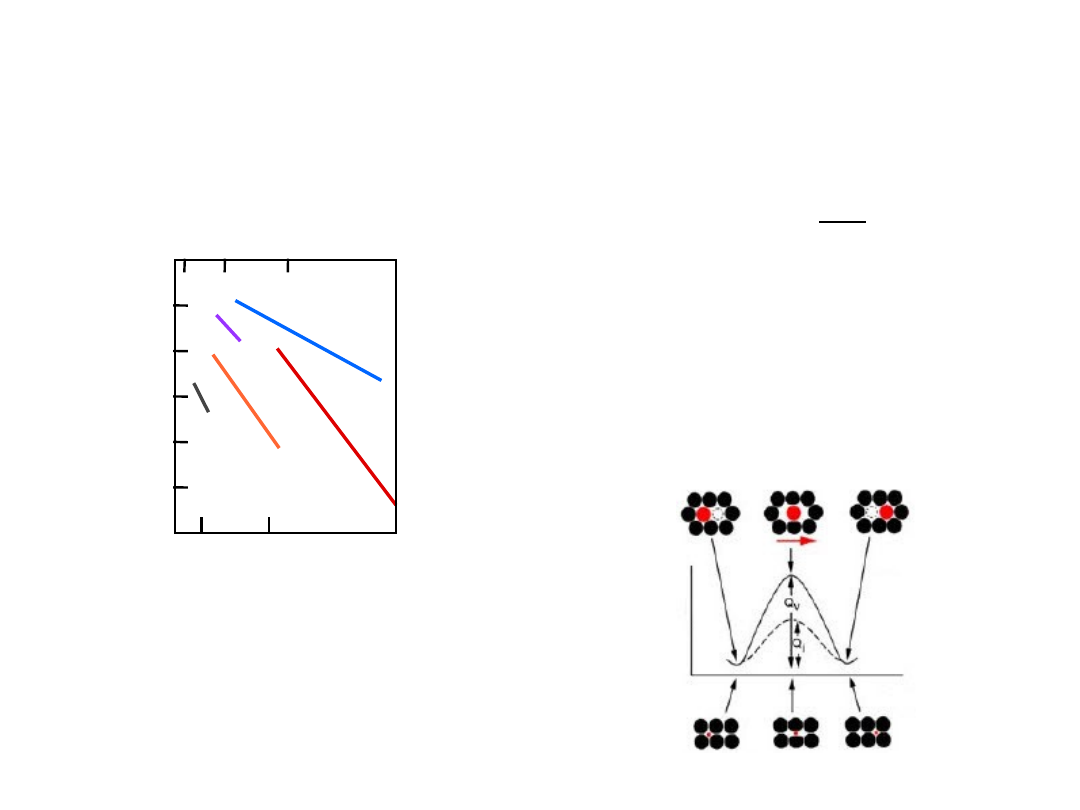
Dyfuzja i temperatura

Zależność D od temperatury T ma charakter
wykładniczy

D



D

o

exp













Q

d

R

T

D

o

= stała [m

2

/s]

D = współczynnik dyfuzji [m

2

/s]

Q

d

= energia aktywacji [J/mol or eV/atom]

R = stała gazowa [8.314 J/mol-K]

T = temperatura bezwzględna [K]

1000 K/T

lnD

C w 

-Fe

C w

-F

e

Al

w

A

l

Fe

w

-

Fe

Fe

w



-F

e

0.5

1.0

1.5

10

-20

10

-14

10

-8

T(C)

1

5

0

0

1

0

0

0

6

0

0

3

0

0

D

międzywęzł.

>> D

subst.

C w -Fe

C w -Fe

Al w Al

Fe w -Fe

Fe w -Fe

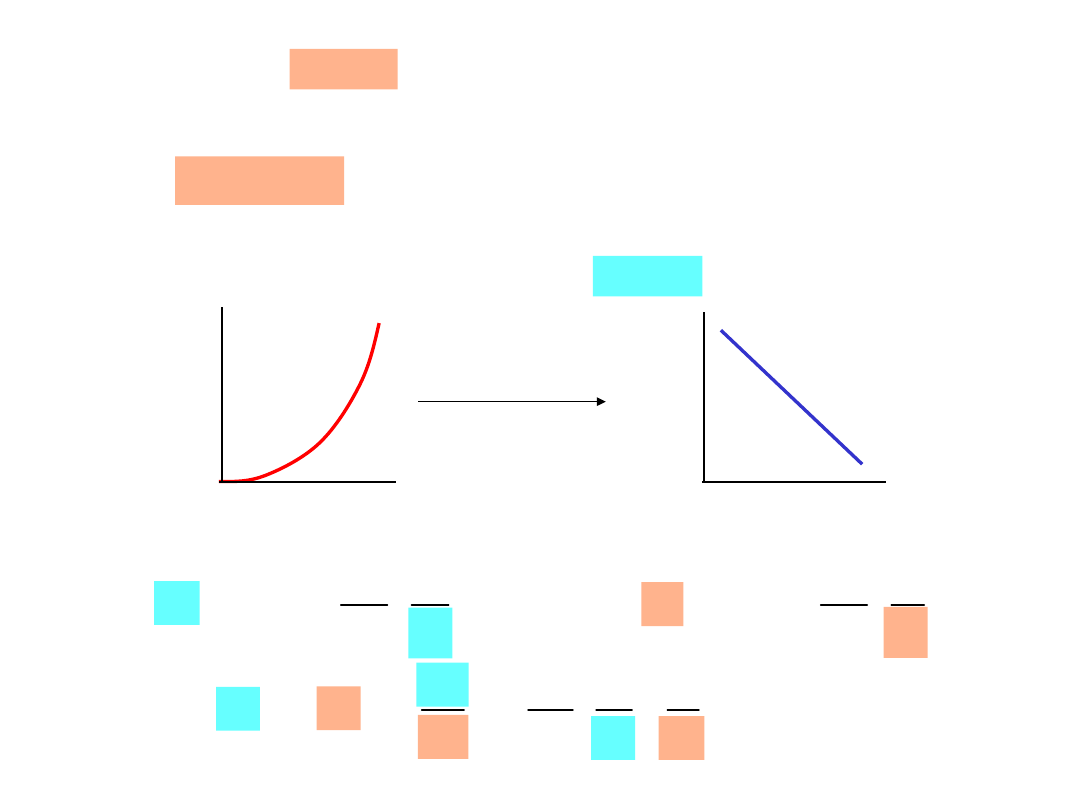
1515

Przykład: W 300ºC współczynnik dyfuzji oraz
energia aktywacji Cu i Si wynoszą:

D(300ºC) = 7.8 x 10

-11

m

2

/s

Q

d

= 41.5 kJ/mol

Jaki jest współczynnik dyfuzji w 350ºC?

































1

0

1

2

0

2

1

ln

ln

and

1

ln

ln

T

R

Q

D

D

T

R

Q

D

D

d

d

























1

2

1

2

1

2

1

1

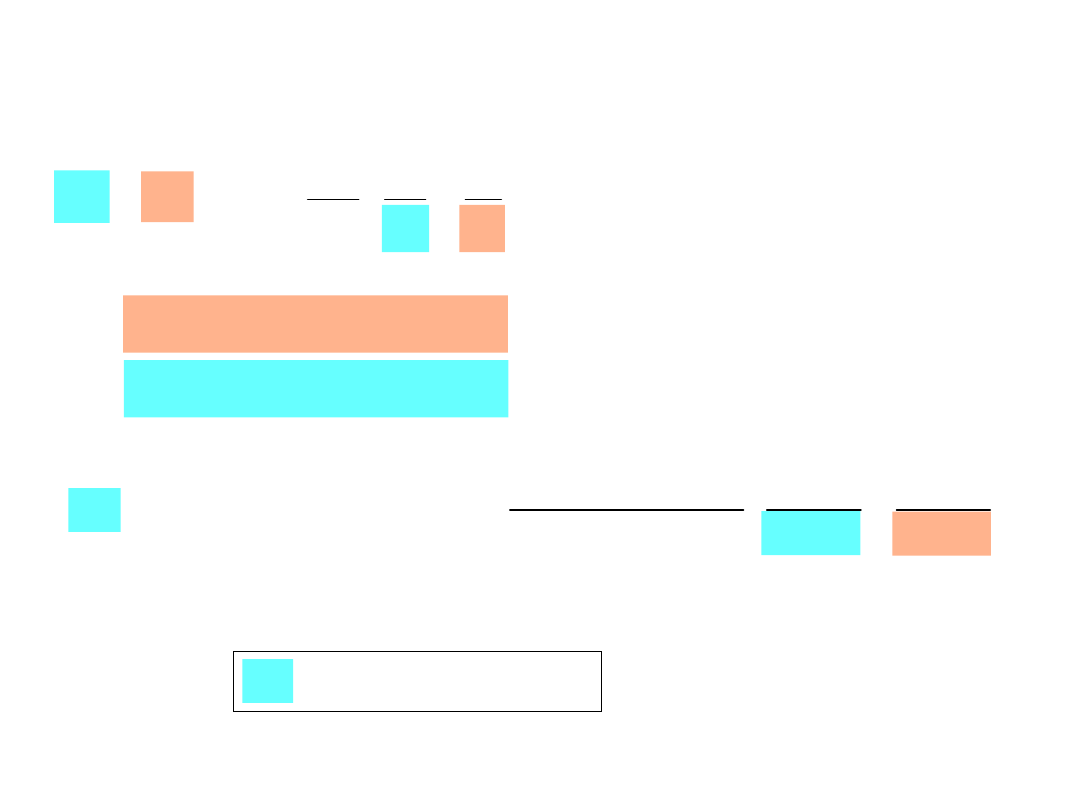
ln

ln

ln

T

T

R

Q

D

D

D

D

d

przekształcen

ie

D

Temp = T

ln D

1/T

1616

Przykład (cd.)

































K

573

1

K

623

1

K

-

J/mol

314

.

8

J/mol

500

,

41

exp

/s)

m

10

x

8

.

7

(

2

11

2

D































1

2

1

2

1

1

exp

T

T

R

Q

D

D

d

T

1

= 273 + 300 = 573

K

T

2

= 273 + 350 = 623

K

D

2

= 15.7 x 10

-11

m

2

/s

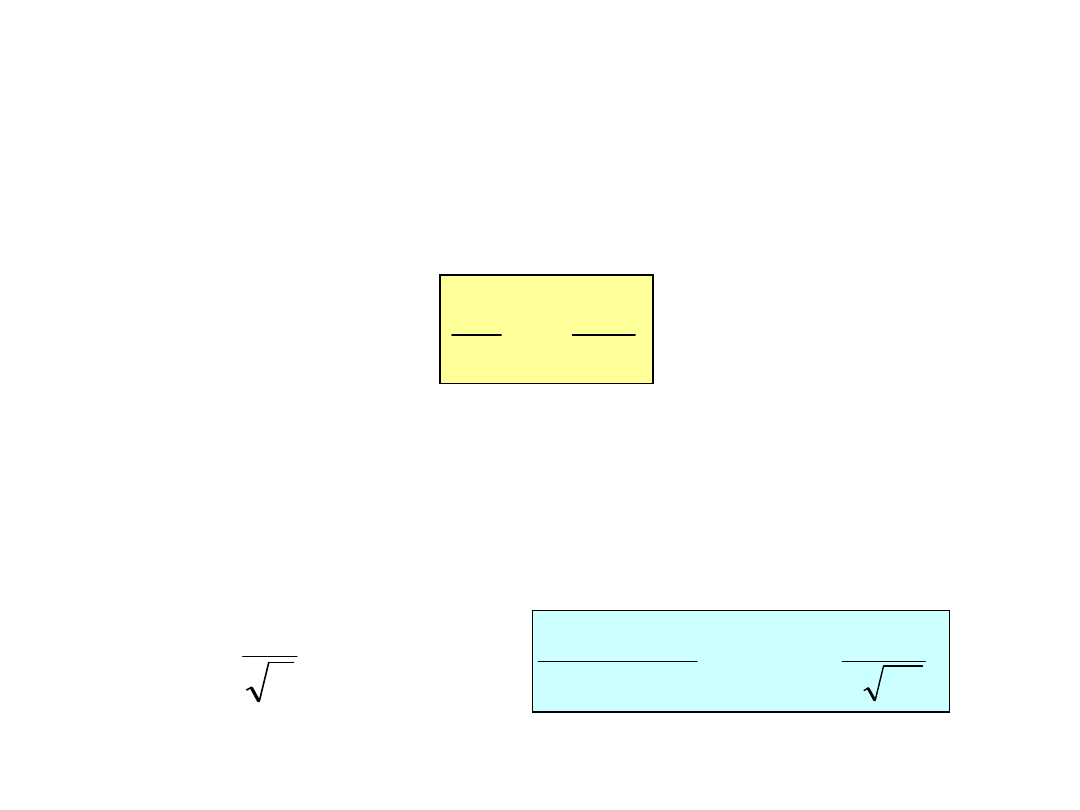
2

2

x

C

D

t

C











1717

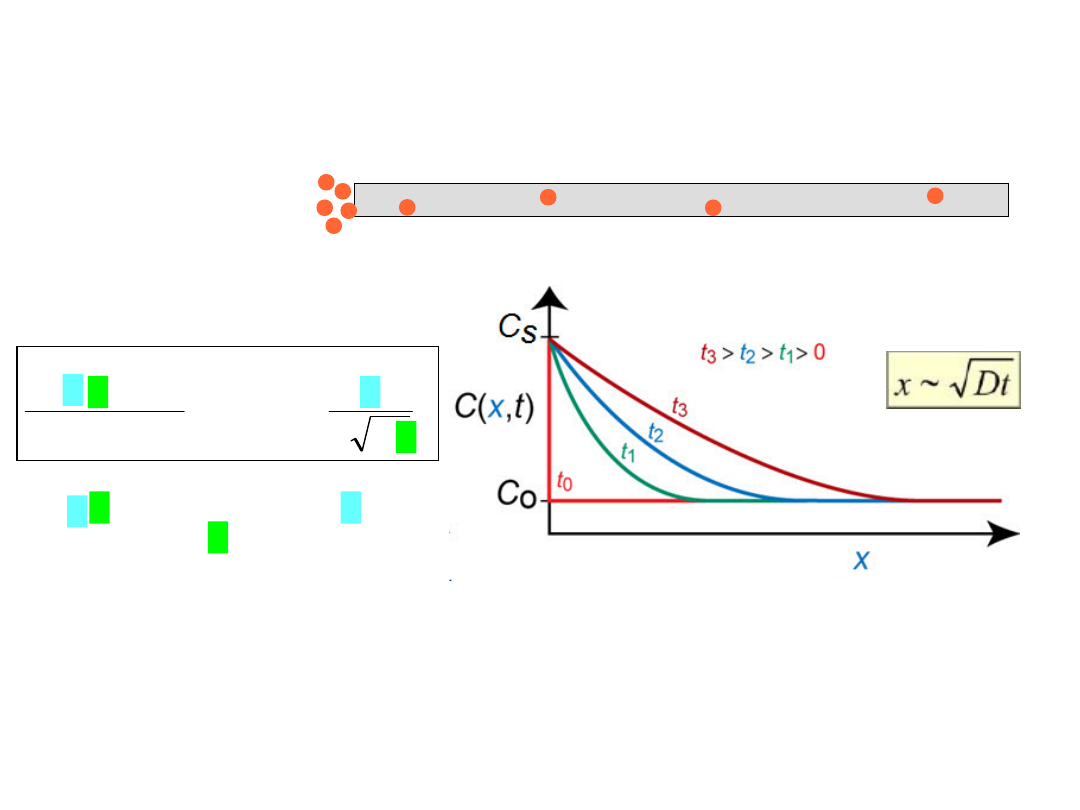
Dyfuzja w stanie

niestacjonarnym

• Koncentracja dyfundującej substancji jest funkcją zarówno czasu, jak i temperatury C = C(x,t)
• W takim przypadku obowiązuje

II Prawo Ficka

Rozwiązanie tego równania jest warunkowane
narzuconymi przez konkretną sytuację warunkami
brzegowymi

 





















Dt

x

C

C

C

t

,

x

C

o

s

o

2

erf

1

dy

e

y

z

2

0

2









erf (z)

C(x,t) = Konc. w punkcie x po

czasie t

erf (z) = funkcja błędów

erf (z) = funkcja błędów

1818

Dyfuzja w stanie

niestacjonarnym

dla t = 0, C = C

o

dla 0 

x

 

dla t > 0, C = C

S

dla

x

= 0 (konc. na pow.

const.)

C = C

o

dla

x

= 

• Cu dyfunduje w pręcie Al

konc. początkowa Cu w pręcie – C

o

Konc. na pow. c

s

,

pręt

 





















Dt

x

C

C

C

t

,

x

C

o

s

o

2

erf

1

C(x,t) = Konc. w punkcie

x po czasie t

wartości erf(z)

są podane w

tabelach

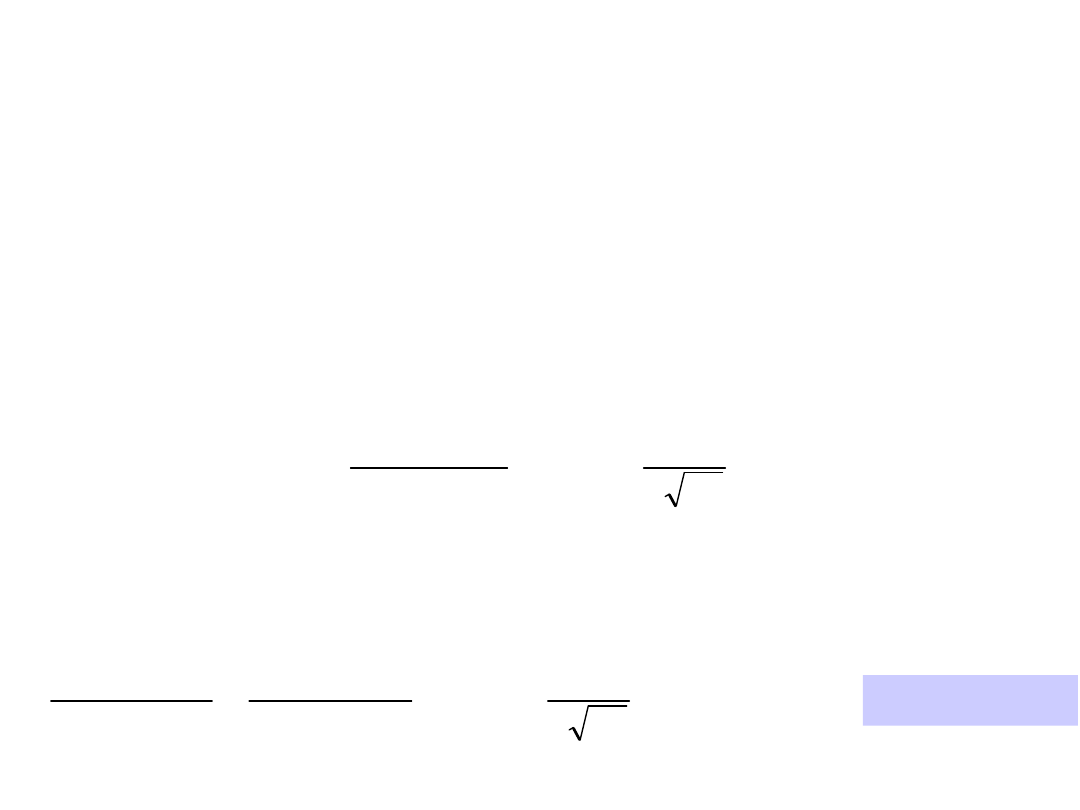
1919

Dyfuzja w stanie niestacjonarnym -

przykład

• Przykład:

żelazo  (struktura RSC) zawierające

początkowo

0.20 %

C (%mas.) jest nawęglane w

podwyższonej temperaturze i w atmosferze, która
wytwarza na powierzchni stałą koncentrację węgla

1.0%

(mas.). Jeżeli po

49.5 h

koncentracja węgla wynosi

0.35%

w warstwie leżącej

4.0 mm

poniżej powierzchni,

to w jakiej temperaturze prowadzono ten proces? .

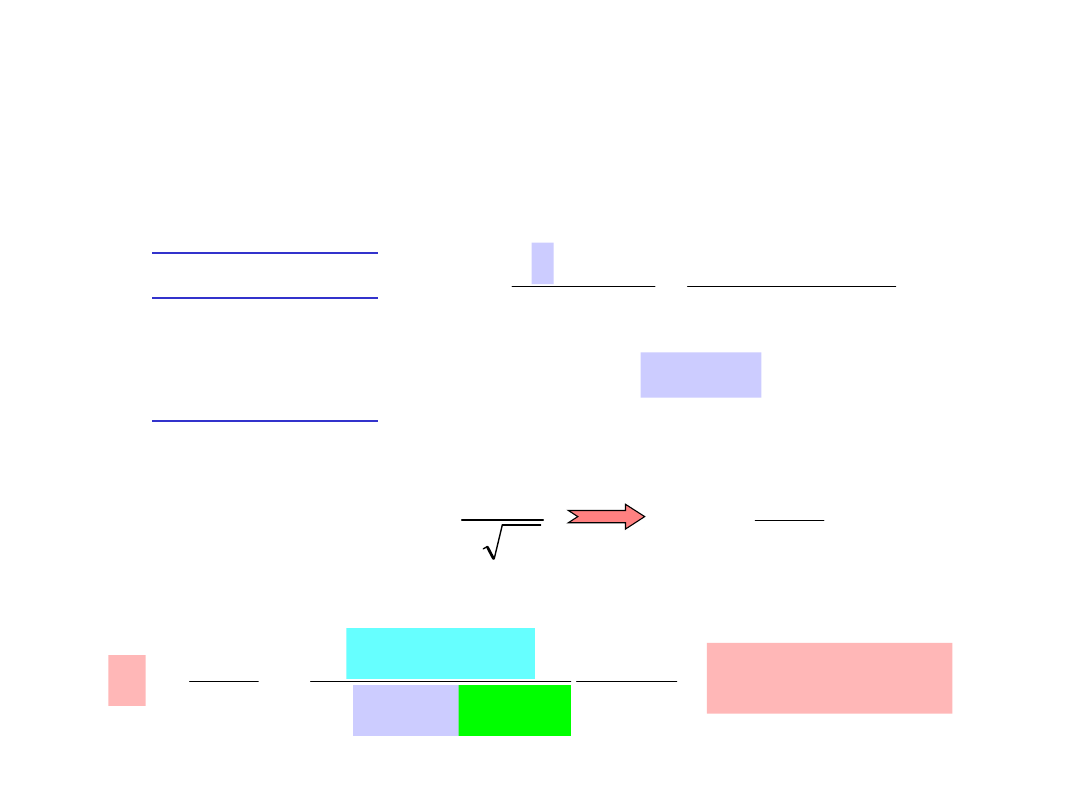
• Rozwiązanie:





















Dt

x

C

C

C

t

x

C

o

s

o

2

erf

1

)

,

(

t = 49.5 h

x = 4 x 10

-3

m

C

x

= 0.35 wt%

C

s

= 1.0 wt%

C

o

= 0.20 wt%

)

(

erf

1

2

erf

1

20

.

0

0

.

1

20

.

0

35

.

0

)

,

(

z

Dt

x

C

C

C

t

x

C

o

s

o































 erf(z) =
0.8125

2020

Rozwiązanie c.d.:

Najpierw musimy znaleźć (z tabeli) wartość z, dla której
funkcja błędów wynosi 0.8125. Należy dokonać
interpolacji:

z

erf(z)

0.90

0.7970

z

0.8125

0.95

0.8209

7970

.

0

8209

.

0

7970

.

0

8125

.

0

90

.

0

95

.

0

90

.

0











z

z  0.93

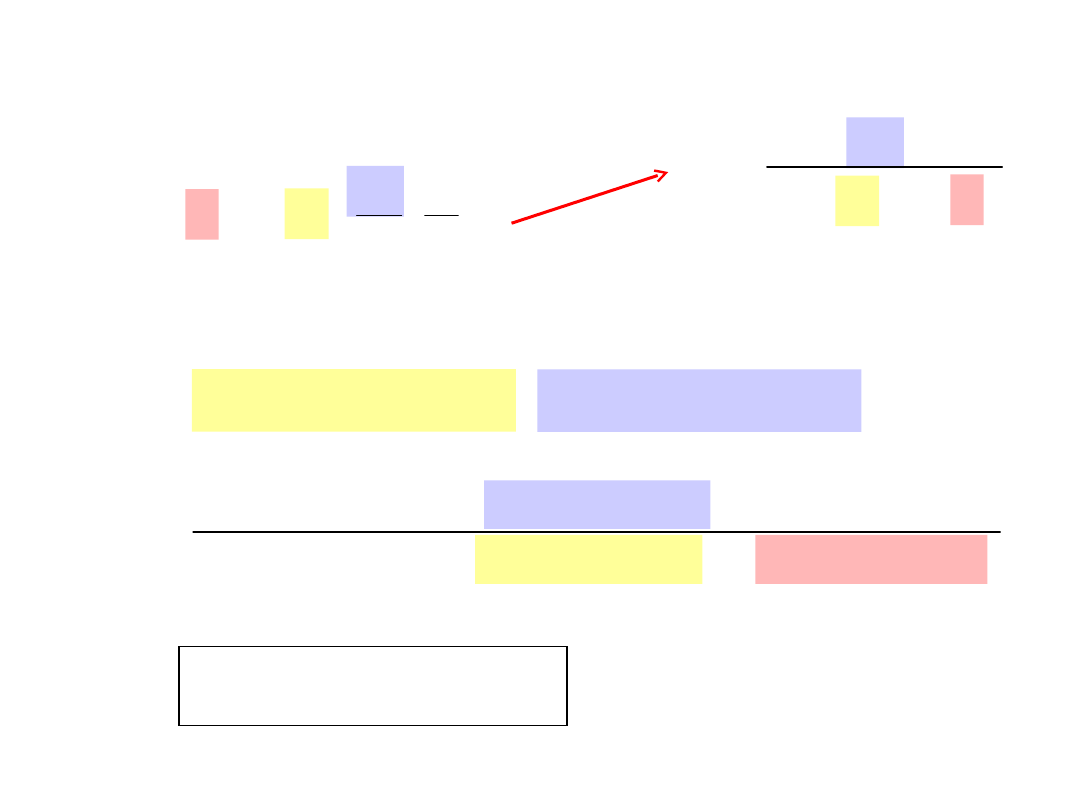
Teraz
rozwiązać
względem D

Dt

x

z

2



t

z

x

D

2

2

4



/s

m

10

x

6

.

2

s

3600

h

1

h)

5

.

49

(

)

93

.

0

(

)

4

(

m)

10

x

4

(

4

2

11

2

2

3

2

2



























t

z

x

D

2121

Aby znaleźć temperaturę, w której D ma powyższą
wartość, należy przekształcić równanie:

)

ln

ln

(

D

D

R

Q

T

o

d





Dla dyfuzji C w Fe-

dane stabelaryzowane



D

o

= 2.3 x 10

-5

m

2

/s Q

d

= 148,000 J/mol

/s)

m

10

x

6

.

2

ln

/s

m

10

x

3

.

2

K)(ln

-

J/mol

314

.

8

(

J/mol

000

,

148

2

11

2

5









T

Rozwiązanie
c.d.:

T = 1300 K = 1027°C

1

ln

ln

0



















T

R

Q

D

D

d

2222

Szybsza

dyfuzja gdy.....

• luźno ułożone struktury

• materiały ze słabszymi
wiązaniami (np. wtórnymi)

• mniejsze atomy
dyfundujące

• materiały o mniejszej
gęstości

Wolniejsza

dyfuzja

gdy.......

• gęsto ułożone struktury

• materiały z mocnymi
wiązaniami (np.
kowalencyjnymi)

• większe atomy
dyfundujące

• materiały o większej
gęstości

Podsumowanie