ZDANIA

KRYTERIA PRAWDY

1. Kryterium św. Tomasza z Akwinu: „prawda jest to zgodność rzeczy z rozumem”
(„veritas est adequatio rei et intellectus”).

2. Kryterium klasyczne (współczesne): za prawdziwe uznajemy te informacje, które
głoszą treści zgodne ze stanem faktycznym, który odnajdujemy w rzeczywistości.

3. Koherencyjne kryterium prawdy: prawda jest zgodnością myśli z samą sobą, a
ściślej – zgodnością z innymi myślami, wcześniej uznanymi za prawdziwe.

4. Pragmatyczna koncepcja prawdy: utożsamiała prawdziwość jakiegoś twierdzenia z
jego użytecznością.

ZDANIE I SĄD, WARTOŚĆ LOGICZNA ZDANIA

Zdaniami w sensie logicznym są tylko zdania oznajmujące.

Zdanie oznajmujące –

to wyrażenie, które jest prawdziwe bądź fałszywe. Znaczenie zdania nazywamy
sądem.

Sąd – to sposób rozumienia danego zdania.

RODZAJE ZDAŃ

Zdanie proste

jest to zdanie, w którym występują wyłącznie funktory zdaniotwórcze od

argumentów nazwowych. Szczególne znaczenie mają tzw. zdania kategoryczne. Należą do nich
takie zdania, jak: „Ziemia jest planetą”, „Słońce świeci”, „Słońce przyciąga Ziemię”, „Niektóre
ptaki nie latają”, „Każdy metal jest pierwiastkiem chemicznym”, „Żaden koziorożec nie fruwa”.
Wspólną cechą tych zdań (to jest zdań kategorycznych) jest to, że dadzą się one rozłożyć na
części, z których jedna jest funktorem zdaniotwórczym od nazw, a pozostałe części są
nazwami.

W klasycznej logice formalnej wyróżniało się pewne postacie zdań kategorycznych, które
nazywa się „

klasycznymi zdaniami kategorycznymi

”. Są to zdania, które dają się zapisać

w następujących postaciach:

1. „Każde S jest P”, 2. „Żadne S nie jest P”, 3. „Niektóre

S są P”, 4. „Niektóre S nie są P”.

WYKŁAD 3

Zdanie złożone

jest to zadnie, w którym występuje funktor od

przynajmniej jednego argumentu zdaniowego. (przynajmniej jedna
negacja)

Negacja (zaprzeczenie) zdania lub : czytamy "nieprawda, że

p ".

Koniunkcja zdań : czytamy "p i q".
Alternatywa zdań : czytamy "p lub q".
Implikacja : czytamy "jeśli p, to q".
Równoważność : czytamy "p wtedy i tylko wtedy, gdy q".
Alternatywa wykluczająca zdań : czytamy "p albo q".

p



q

p

q

p

q

p

q

p

q

p

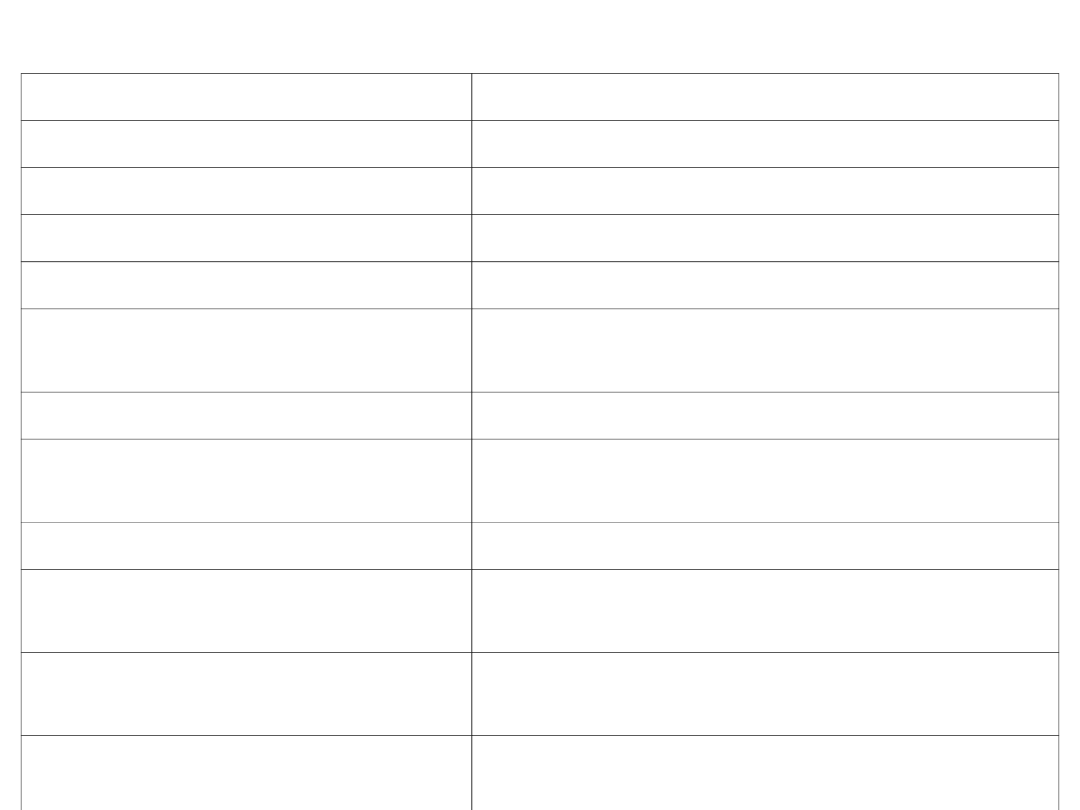
WARTOŚCI LOGICZNE ZDAŃ ZŁOŻONYCH

p

q

1

1

0

1

1

1

1

0

1

0

0

0

1

0

0

1

0

1

1

0

1

1

0

1

0

0

1

0

0

1

1

0

p



q

p

q

p

q

p

q

p

q

p

~
p

Zbuduj schematy następujących zdań:

a)    Jeżeli nie przygotuję się do egzaminu, to go nie zdam.

b)    Jeżeli nie zdam egzaminu, to rodzice zabiorą mi kieszonkowe i
nie wyjadę na narty do Zakopanego.

c)    Jeżeli nie wyjadę na narty, to moja dziewczyna pojedzie w góry
z przyjaciółmi i pozna innego chłopaka albo zostanie w domu i
będzie miała do mnie pretensje z powodu zmarnowanych ferii.

d)    Jeżeli moja dziewczyna będzie suszyła mi głowę, to się z nią
rozstanę i zostanę sam.

e)    Jeżeli zostanę sam, to będzie mi smutno i będę chciał się
pocieszyć.

f)      Będę chodził codziennie do kina lub na imprezy.

g)    Jeżeli nie będę miał czasu na naukę, to nie przygotuję się do
egzaminu i moja sytuacja nie ulegnie poprawie.

h)    Zdam egzamin w pierwszym terminie wtedy i tylko wtedy, gdy
będę uczestniczył w zajęciach i rozwiązywał zadania.

i)      Rozwiążę zadania, jeżeli wysłucham wykładu lub przestudiuję
podręcznik.

j)      Jeżeli przestudiuję podręcznik, to jeśli nie zrozumiem jego
treści, to jeśli znajomi nie będą znali odpowiedzi na dręczące mnie
pytania, to postawię je na zajęciach i dam prowadzącemu szansę
wykazać się wiedzą.

ZDANIA ANALITYCZNE I SYNTETYCZNE

Specjalną kategorię zdań stanowią

zdania analityczne.

O

prawdziwości tych zdań nie decyduje ich zgodność ze stanem
faktycznym, lecz ich wewnętrzna budowa i znaczenie użytych w nich
wyrażeń. Analitycznym jest np. zdanie: „kawaler jest to mężczyzna
nieżonaty”. Prawdziwość tego zdania wynika z analizy użytych w nim
wyrażeń. Na tej samej zasadzie można stwierdzić fałszywość zdania, np.
„trójkąt jest figurą sześciokątną”. Takie zdanie, jak to ostatnie, jest
wewnętrznie sprzeczne. Jego fałszywość stwierdzamy na mocy znaczenia
użytych w nim wyrażeń, w tym przypadku „trójkąt” i „figura
sześciokątna”.

Zdania analityczne nie wymagają weryfikacji w rzeczywistości

doświadczalnej. O ich prawdziwości decyduje niejako ich
struktura syntaktyczna i znaczenie występujących w nim
wyrażeń.

Wymaga takiej weryfikacji, czyli potwierdzenia, inny typ zdań, a
mianowicie tzw.

zdania syntetyczne

. Są to zdania, które wypowiadają

się o konkretnych stanach i zdarzeniach rzeczywistych. Do takich zdań
należą np. zdania następujące: „Warszawa jest stolicą Polski”, „Neapol
jest stolicą Czech”, „Franciszek Józef był cesarzem monarchii Austro-
Węgierskiej” itd. Widzimy, że prawdziwości informacji podawanych przez
zdania syntetyczne nie możemy stwierdzić w oparciu o analizę wyrażeń, z
których zbudowane są te zdania. Ze znaczenia wyrazu „Warszawa” nie
wynika, że jest to stolica Polski. By stwierdzić prawdziwość zdań
syntetycznych, trzeba odwołać się do rzeczywistości, o której one mówią.
Zdania syntetyczne wnoszą coś nowego do naszej wiedzy, tzn. podają
informacje, których nie można wysnuć z analizy znaczenia wyrażeń
występujących w tych zdaniach.

FUNKCJE ZDANIOWE

Do opisu pojęć matematycznych nie starcza sam rachunek zdań. Np.
równanie 3x + 5 = 0 nie jest zdaniem logicznym, ponieważ nie można o
nim powiedzieć ani, że jest prawdziwe, ani, że jest fałszywe.

Funkcja zdaniowa

jest wyrażeniem zawierającym zmienną, które

staje się zdaniem logicznym (fałszywym lub prawdziwym), gdy na miejsce
zmiennej podstawimy nazwę odpowiedniego elementu.

Dziedziną funkcji zdaniowej

jest zbiór tych elementów,  dla których 

zdanie uzyskane z formy zdaniowej jest sensowne.

Zbiór elementów należących do dziedziny funkcji zdaniowej, dla których
zdanie staje się prawdziwe, nazywamy

zbiorem elementów

spełniających daną funkcję zdaniową:

Funkcje zdaniowe oznacza się symbolicznie:

p(x), q(x), r(x),...

Każde równanie i każda nierówność jest funkcją zdaniową, której
dziedziną jest pewien podzbiór liczb rzeczywistych.

Podobnie można określić funkcje zdaniowe dwóch zmiennych lub
większej liczby zmiennych.





)

(

:

x

p

D

x

x

A







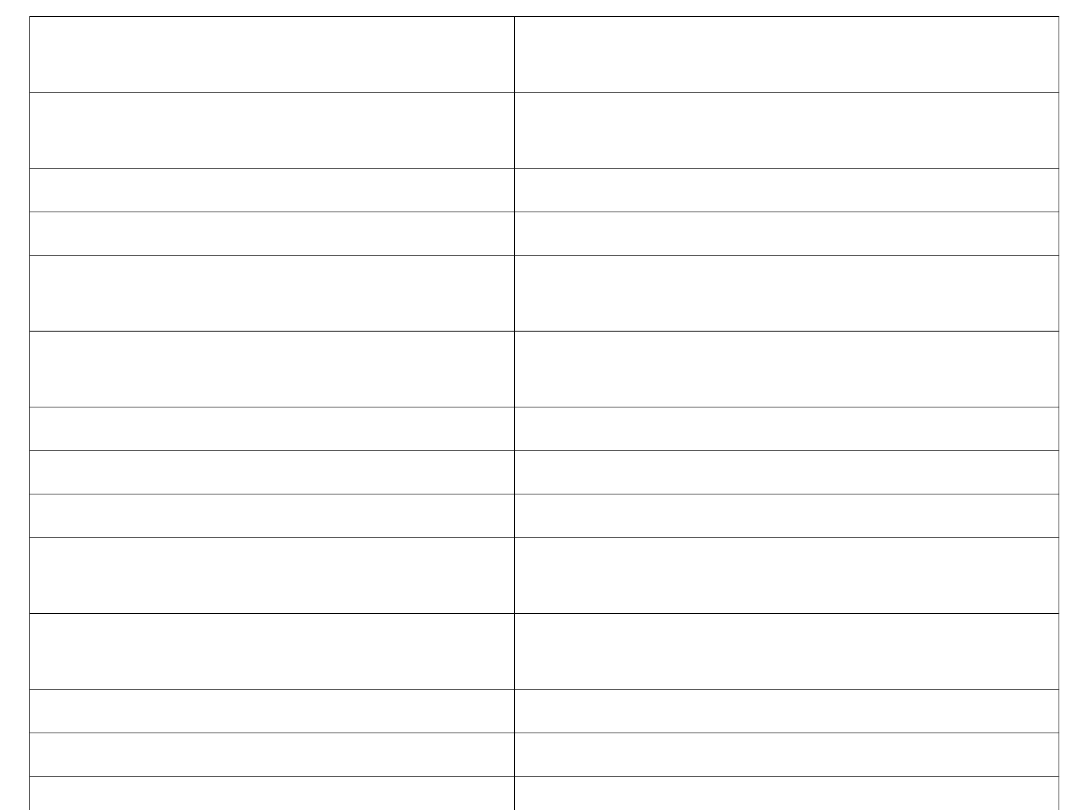
TAUTOLOGIE RACHUNKU ZDAŃ

~~p <=> p

prawo podwójnego przeczenia

p v (~p)

prawo wyłączonego środka

(p v p) <=> p

prawo idempotentności alternatywy

(p ^ p) <=> p

prawo idempotentności koniunkcji

(p ^ q) <=> (q ^ p)

prawo przemienności koniunkcji

[(p ^ q) ^ r] <=> [p ^ (q ^

r)]

prawo łączności koniunkcji

(

p v q) <=> (q v p)

prawo przemienności alternatywy

[(p v q) v r] <=> [p v (q v

r)]

prawo łączności alternatywy

(p <=> q) <=> (q <=> p)

prawo przemienności równoważności

[p ^ (q v r)] <=> [(p ^ q) v

(p ^ r)]

prawo rozdzielności koniunkcji

względem alternatywy

[p v (q ^ r)] <=> [(p v q) ^

(p v r)]

prawo rozdzielności alternatywy

względem koniunkcji

[(p => q) ^ (q => r)] => (p

=> r)

prawo przechodniości implikacji

[(p <=> q) ^ (q <=> r)]

=> (p => r)

prawo przechodniości

równoważności

~(p ^ q) <=> (~p v ~q)

prawo De Morgana zaprzeczenia

koniunkcji

~(p v q) <=> (~p ^ ~q)

prawo De Morgana zaprzeczenia

alternatywy

~(p => q) <=> (p ^ ~q)

prawo zaprzeczenia implikacji

(p => q) <=> (~q => ~p)

prawo kontrapozycji

[(p => q) ^ (q = > p)] => (p

<=> q)

związek między implikacją a

równoważnością

[(p ^ q) => r] <=> [p =>(q =>

r)]

prawo ekstraportacji

(~p => p) => p

prawo Claviusa

(p =>q) <=> [(p ^ ~q) => ~p]

prawo reductio ad absurdum

[p ^ (p => q)] => q

reguła odrywania

[(p => q) ^ (r => s)] => [(p v

r)=>(q v s)]

pierwsze prawo dylematu

konstrukcyjnego

[(p => q) ^ (r => s)] => [(p ^ r)

=> (q ^ s)]

drugie prawo dylematu

konstrukcyjnego

p => (p v q)

prawo wprowadzania alternatywy

(p ^ q) => p

prawo opuszczania koniunkcji

[(p => q) ^ ~q] => ~p

prawo modus tollendo tollens

(zaprzeczenie przy pomocy

zaprzeczenia)

[(p v q) ^ ~p] => q

prawo modus ponendo tollens

(potwierdzenie przy pomocy

zaprzeczenia)

(p q) <=> (p v q) ^ ~(p ^ q)

określenie alternatywy
wykluczającej

