Fizyka

Program przedmiotu:

30 godzin wykładu - dr Krystyna Chłędowska
15 godzin ćwiczeń audytoryjnych
15 godzin laboratorium

www.prz.edu.pl

Wydział Matematyki i Fizyki Stosowanej
Katedra Fizyki
pracownicy

Literatura

1. C. Bobrowski, Fizyka – krótki kurs, WNT Warszawa 2003
2. K. Chłędowska, R. Sikora, Wybrane problemy fizyki z rozwiązaniami

cz. I, Oficyna Wydawnicza Politechniki Rzeszowskiej, Rzeszów 2008

3. K. Chłędowska, R. Sikora, Wybrane problemy fizyki z rozwiązaniami

cz. II, Oficyna Wydawnicza Politechniki Rzeszowskiej, Rzeszów 2010

4. D. Halliday, R. Resnick, J. Walker, Podstawy fizyki ,PWN, Warszawa

1999

5. J. Massalski, M. Massalska, Fizyka dla inżynierów, WNT Warszawa

1980

6. J. Orear, Fizyka, WNT Warszawa 1999
7. I.W. Sawieliew, Wykłady z fizyki, PWN Warszawa 1994

Zaliczenie przedmiotu:

Uzyskanie zaliczenia z ćwiczeń
audytoryjnych

Egzamin po II semestrze:

Część pisemna – zadania + teoria

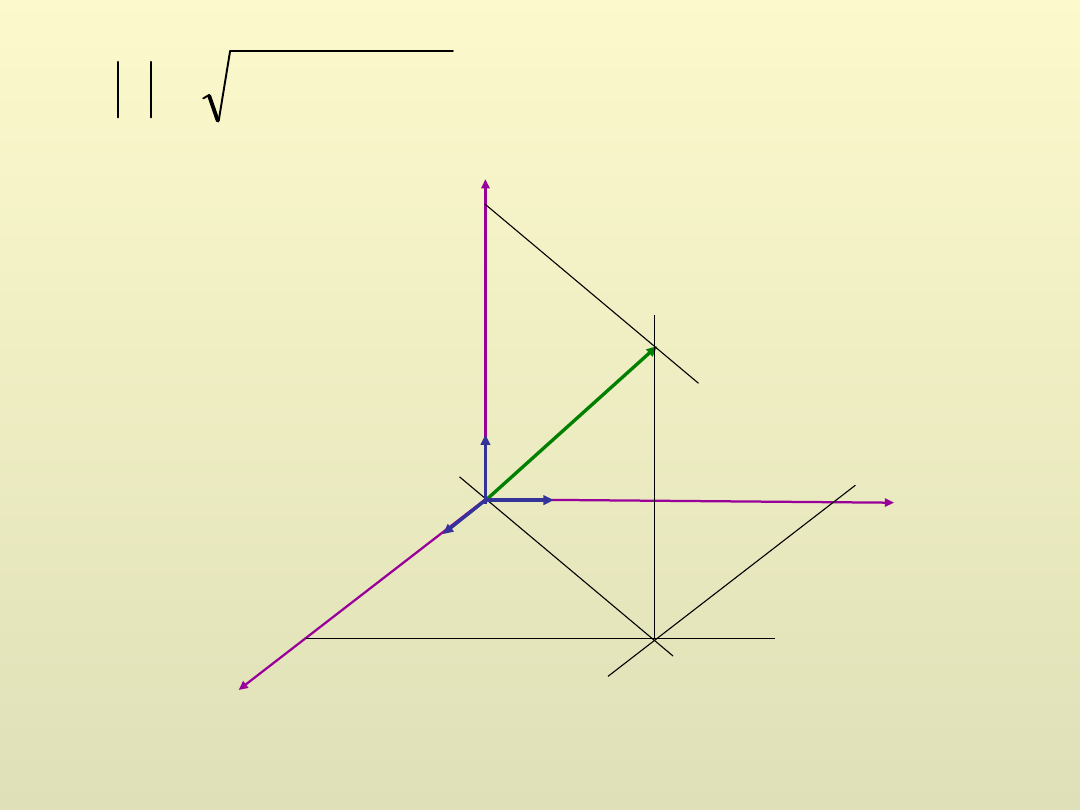
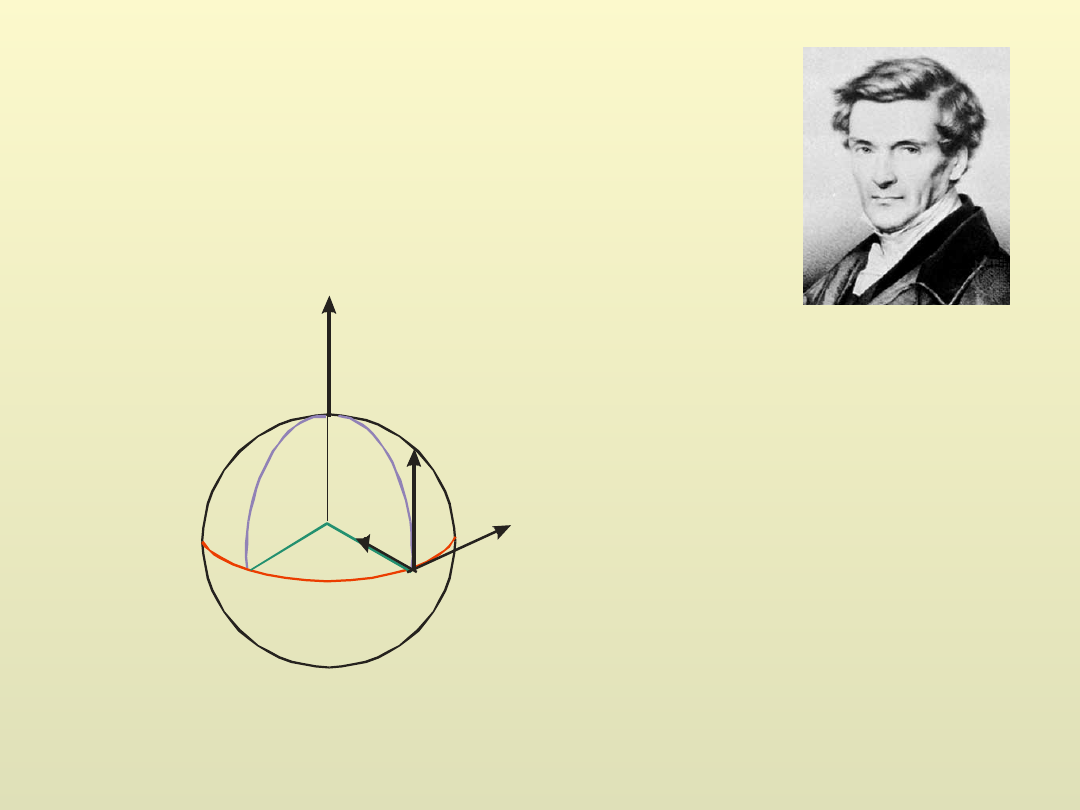
Przestrzeń trójwymiarową

określamy podając trzy wektory, zwane wektorami bazy.
Mogą nimi być trzy wzajemnie prostopadłe wektory
których długości są równe jedności (wersory)

3

2

1

,

,

e

e

e







1

3

2

1







e

e

e







Wektory te definiują tzw. kartezjański układ współrzędnych, w
którym są one zwyczajowo oznaczane jako
Dowolny wektor możemy przedstawić jako kombinację
liniową wersorów

k

j

i







,

,

a





z

y

x

z

y

x

a

a

a

k

a

j

a

i

a

a

,

,

















z

y

x

a

a

a

,

,

gdzie: odpowiednie składowe wektora

a

.

Elementy rachunku wektorowego

a

i

j

k

x

y

z

a

x

a

y

a

z

2

2

2

z

y

x

a

a

a

a

a











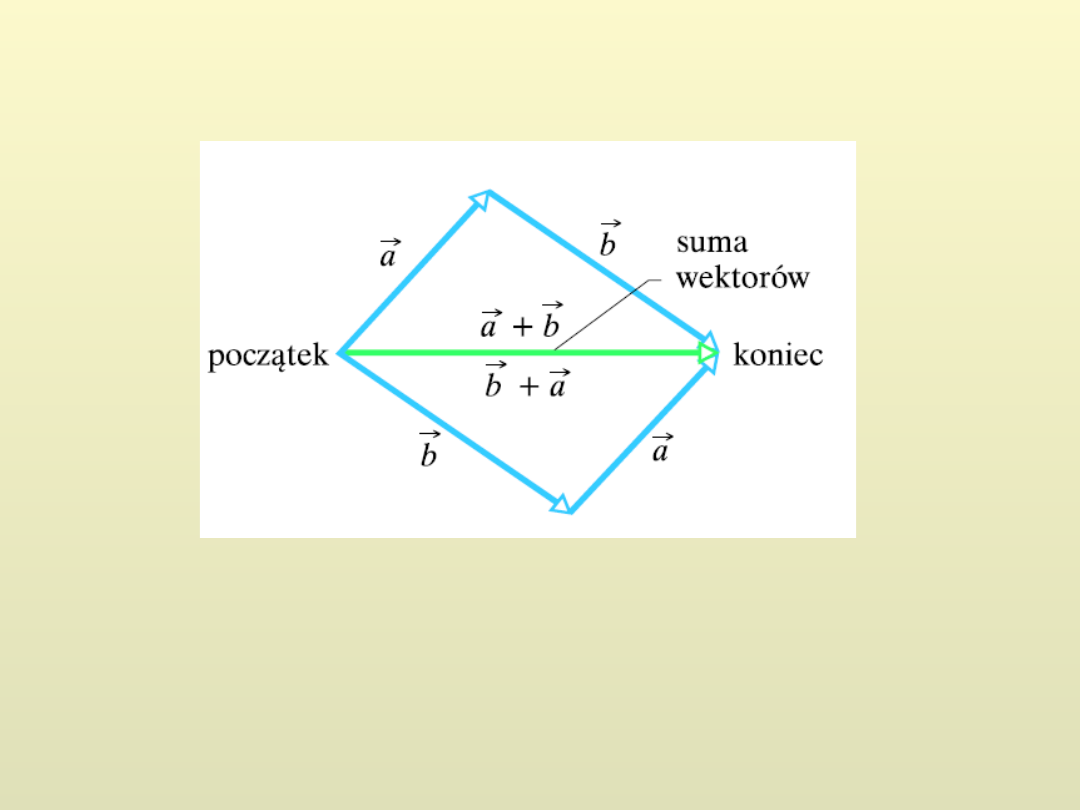
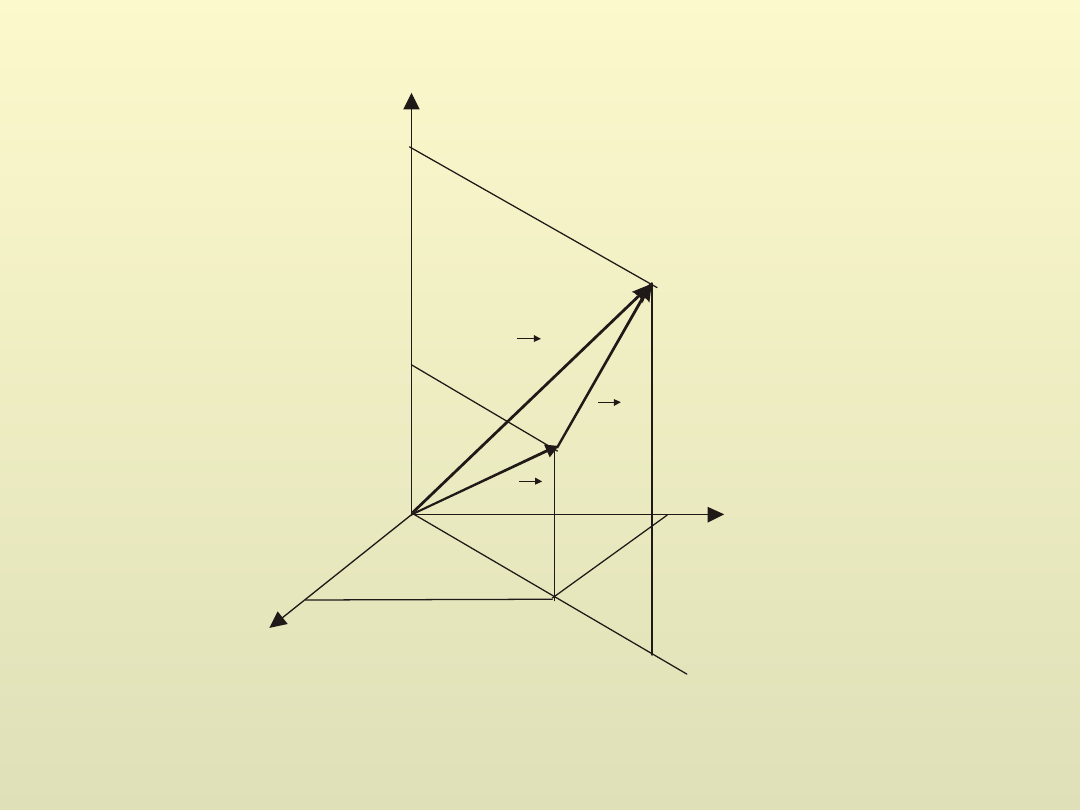
Suma wektorów

c

b

a











W kartezjańskim układzie współrzędnych:

k

b

a

j

b

a

i

b

a

c

z

z

y

y

x

x









)

(

)

(

)

(













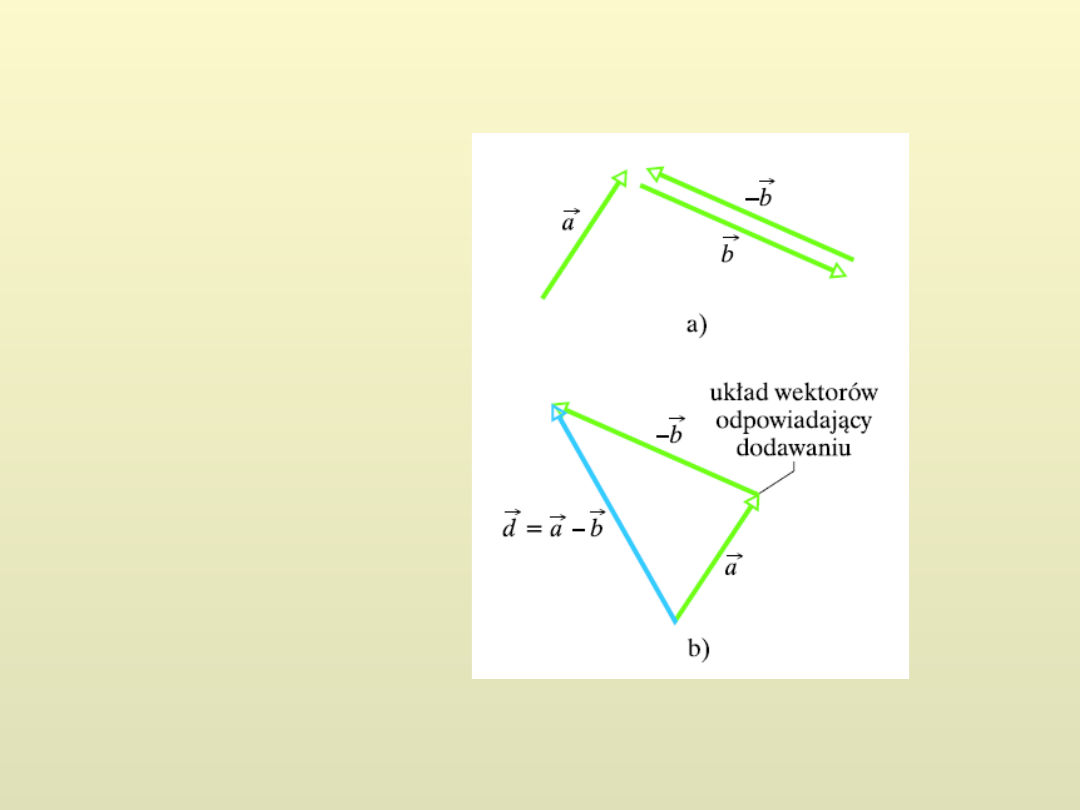
Różnica wektorów:

)

( b

a

b

a

















b

c

a

x

y

z

Iloczyn skalarny wektorów:

)

,

(

cos

b

a

b

a

b

a























lub przy pomocy składowych wektorów w układzie kartezjańskim jako:



 



z

z

y

y

x

x

z

y

x

z

y

x

b

a

b

a

b

a

b

k

b

j

b

i

a

k

a

j

a

i

b

a







































Iloczyn skalarny dla wektorów prostopadłych jest równy zeru.

0

,

0

,

0

90

cos

1

,

1

,

0

cos

0

1













































k

j

k

i

b

a

j

i

b

j

a

i

k

k

j

j

b

a

b

a

i

i

b

i

a

i

y

x

y

x

x

x

x

x

x

x









 

 

















 







)

,

(

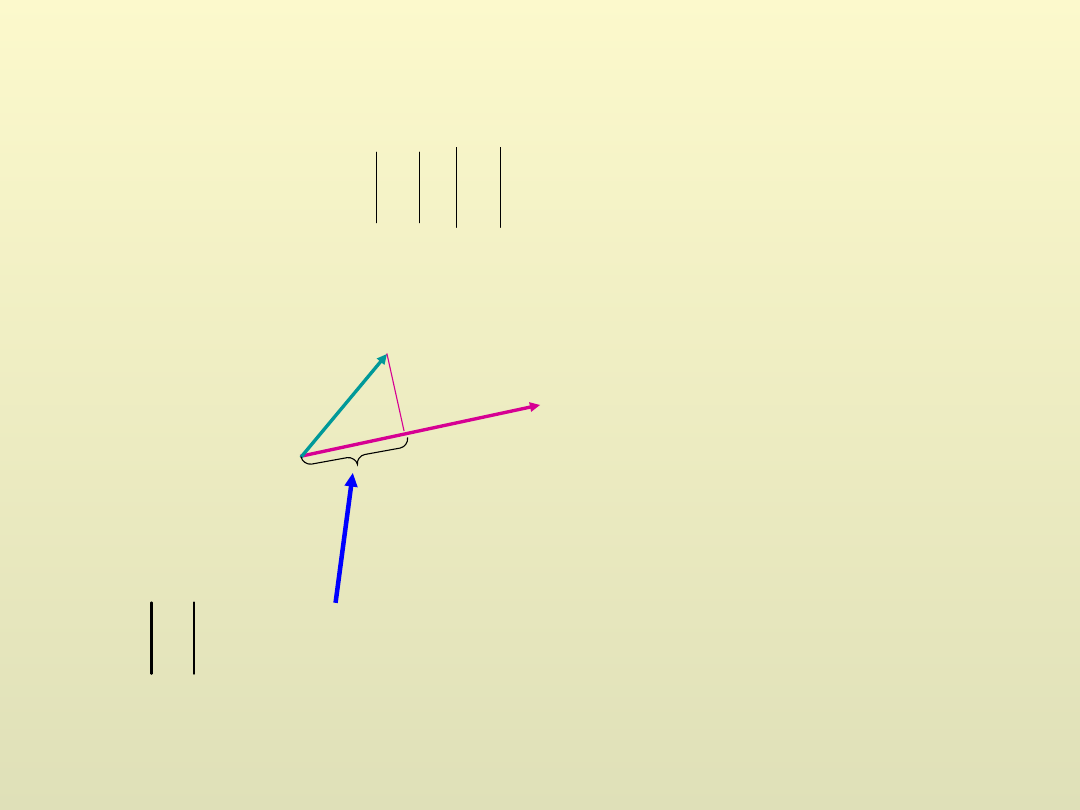
cos

b

a

b

a

b

a























a

b



)

,

(

cos

b

a

a











c

b

a











Iloczyn wektorowy:

jest wektorem prostopadłym do płaszczyzny utworzonej przez
obydwa wektory

Długość wektora

:

)

,

(

sin

b

a

b

a

c

















jest równa polu równoległoboku zbudowanego na wektorach

Iloczyn wektorowy wektorów równoległych jest równy zeru.

c

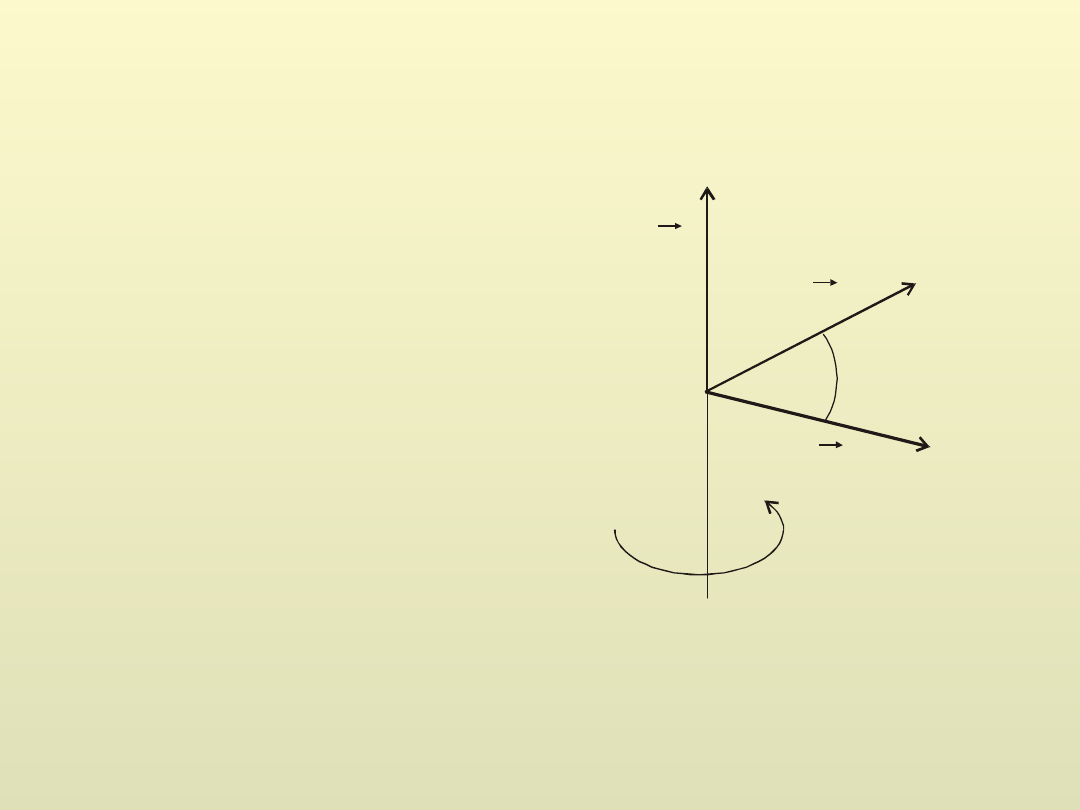
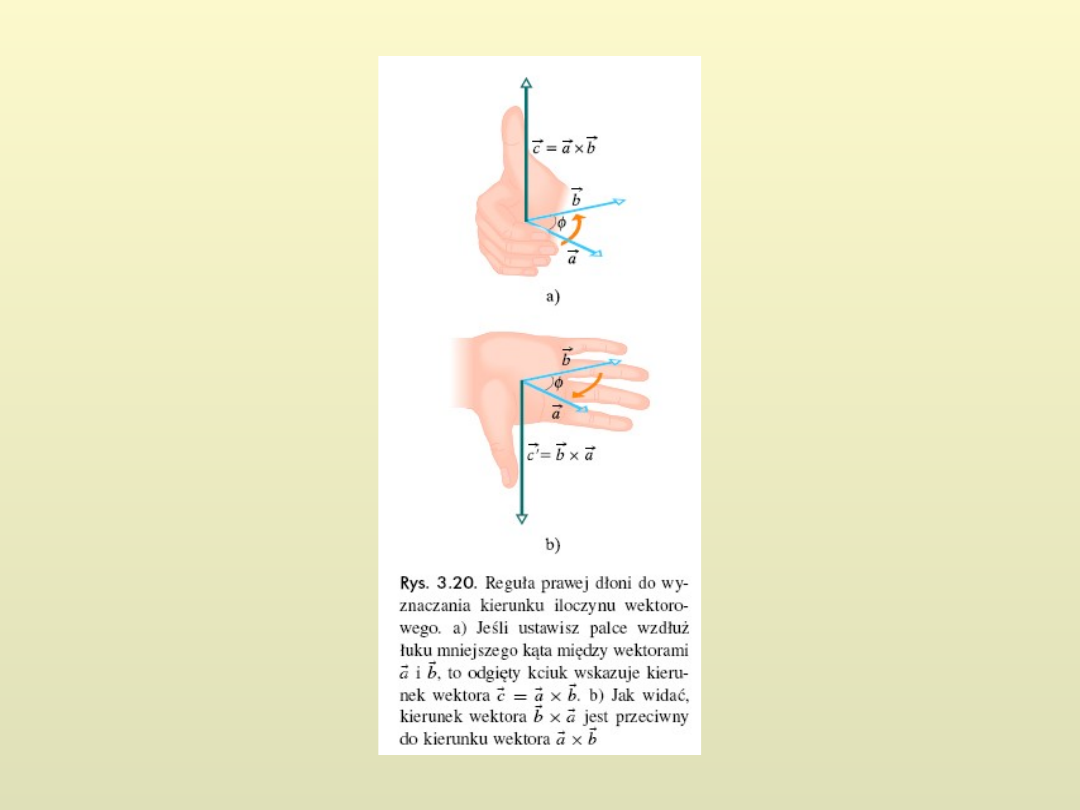
wektor pierwszy w iloczynie
wektorowym obracamy o
mniejszy kąt w prawo tak by
doprowadzić go do pokrycia
się z wektorem drugim w
iloczynie wektorowym. Zwrot
wektora jest zgodny z
kierunkiem ruchu końca śruby
prawoskrętnej.

Zwrot wektora

a

b

c



c

Składowe wektora w układzie kartezjańskim,
możemy wyznaczyć obliczając wyznacznik:

c

)

(

)

(

)

(

x

y

y

x

z

x

x

z

y

z

z

y

z

y

x

z

y

x

b

a

b

a

k

b

a

b

a

j

b

a

b

a

i

b

b

b

a

a

a

k

j

i



























.

Elementy analizy matematycznej

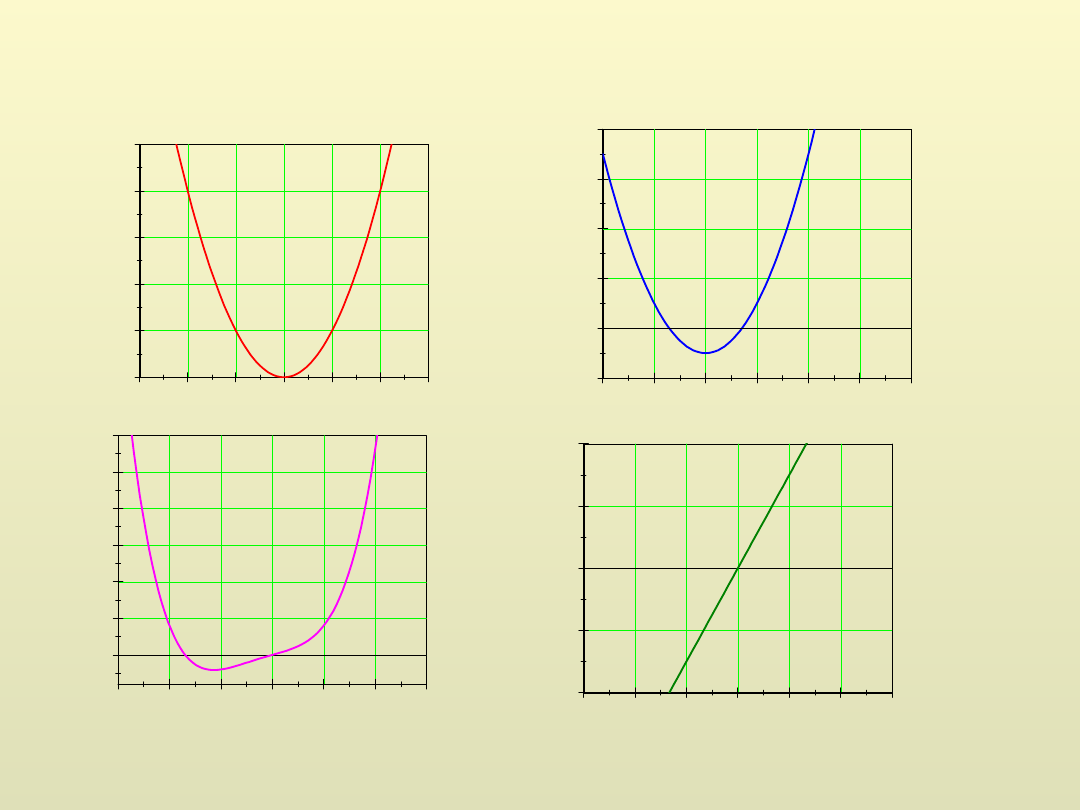
Funkcje

Zmienna

y

nazywa się

zmienną zależną

albo

funkcją

zmiennej x

jeśli przyjmuje określone wartości dla każdej wartości zmiennej x w
jej pewnym przedziale zmienności.

)

(

)

(

x

y

y

x

f

y





lub

-3

-2

-1

0

1

2

3

0

2

4

6

8

10

y

x

-3

-2

-1

0

1

2

3

0

2

4

6

8

10

y

x

2

2x

y 

3

4

2

2







x

x

y

-3

-2

-1

0

1

2

3

0

5

10

15

20

25

30

y

x

x

x

x

y

2

3

4







-3

-2

-1

0

1

2

3

-4

-2

0

2

4

y

x

x

y 3



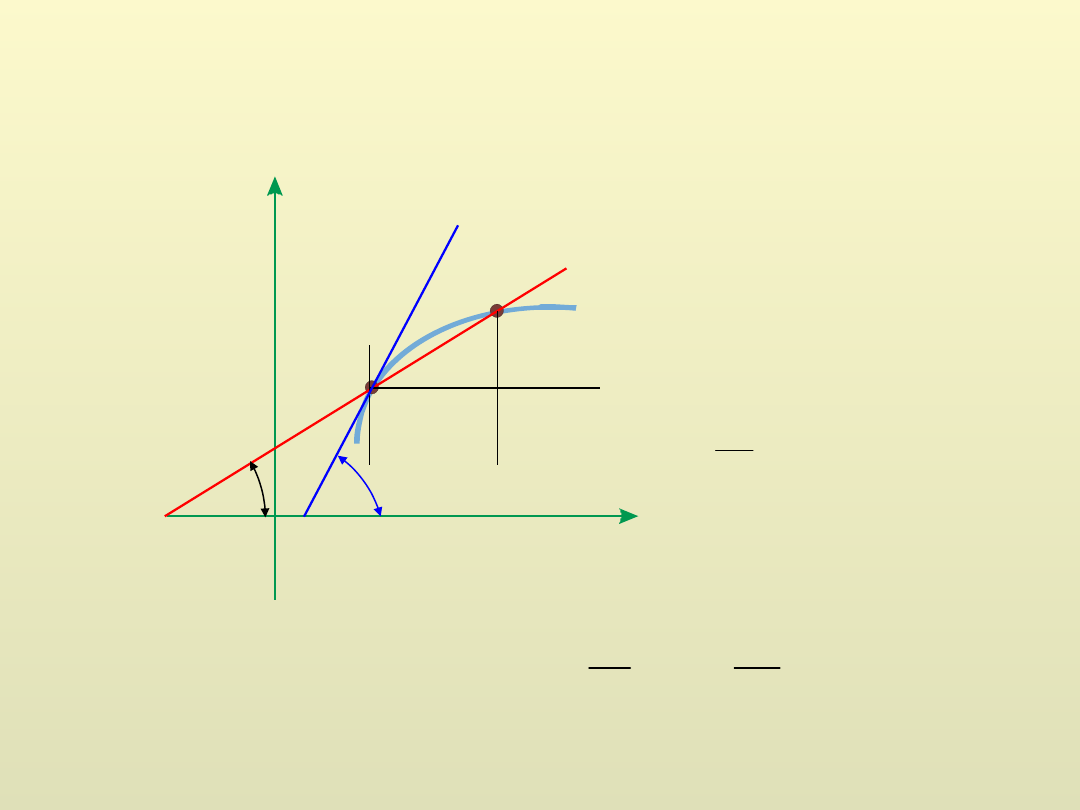
Pochodna funkcji

x

y

A(x

o

,y

o

)

B(x

1

,y

1

)

β

∆y

∆x

y

y

y

x

x

x













1

1

Pochodna funkcji

x

y

dx

dy

y

x















0

lim

α



tan



dx

dy

Pochodna funkcji w danym punkcie jest równa

współczynnikowi

kierunkowemu stycznej

do wykresu funkcji w tym punkcie.

Wyrażenie

dy = y’dx

nazywa się różniczką funkcji y = y(x),

dx

– jest różniczką

argumentu x.

2

2

dx

y

d

dx

dy

dx

d



Różniczkując pierwsza pochodną po x, otrzymamy drugą pochodną

itd……

1

0

)

(





dx

dc

c

x

y

c = const

2

dx

dy

c

dx

cy

d



)

(

3

dx

dy

dx

dy

dx

dy

y

y

y

2

1

2

1









4

dx

dy

y

y

dx

dy

dx

dy

y

y

y

2

1

2

1

2

1











Podstawowe wzory rachunku różniczkowego

5

2

2

2

1

2

1

2

1

y

dx

dy

y

y

dx

dy

dx

dy

y

y

y









6

dx

dy

dy

dz

dx

dz

x

g

y

y

f

z









)

(

),

(

Pochodna funkcji złożonej

Pochodne funkcji elementarnych

y=f(x)

y’

y=f(x)

y’

x

1

cosx

-sinx

x

n

nx

n-1

tgx

1/cos

2

x

e

x

e

x

ctgx

-1/sin

2

x

lnx

x

-1

a

x

a

x

lna

sinx

cosx

Rachunek całkowy – całka nieoznaczona

Całką nieoznaczoną

lub funkcją pierwotną funkcji y =

f(x) nazywamy taką funkcję F(x), której

pochodna

jest równa danej funkcji

f(x)

Całkę nieoznaczoną zapisujemy symbolicznie jako

)

(

)

(

'

)

(

x

f

x

F

dx

x

dF

















)

(

)

(

'

)

(

)

(

x

dF

dx

x

F

dx

x

f

x

F

Całki funkcji elementarnych

1

1

1















n

c

n

x

dx

x

n

n

c

x

x

dx







ln

c

e

dx

e

x

x







1

,

0

,

ln











a

a

c

a

a

dx

a

x

x

c

x

xdx









cos

sin

c

x

xdx







sin

cos

c

x

x

dx







tan

cos

2

c

x

x

dx









cot

sin

2

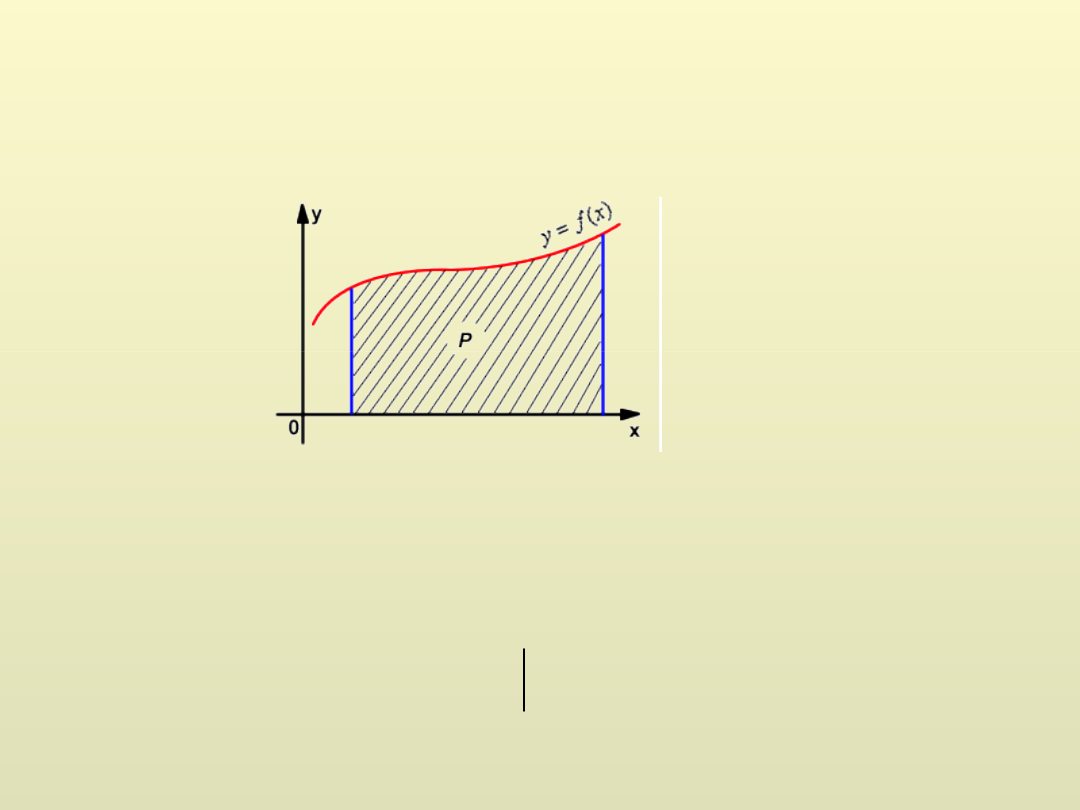
Całka oznaczona

Funkcja y = f(x) jest ciągła w przedziale

<

a,b

>

zmiennej x.

a

b

Całka oznaczona jest równa polu ograniczonemu osią x
i krzywą f(x)









b

a

b

a

a

F

b

F

x

F

dx

x

f

)

(

)

(

)

(

)

(

Przykład

c

x

xdx

x

y









2

2

Całka oznaczona w przedziale

<

-2,3

>





5

.

2

4

9

2

1

2

3

2

2

3

2















x

xdx

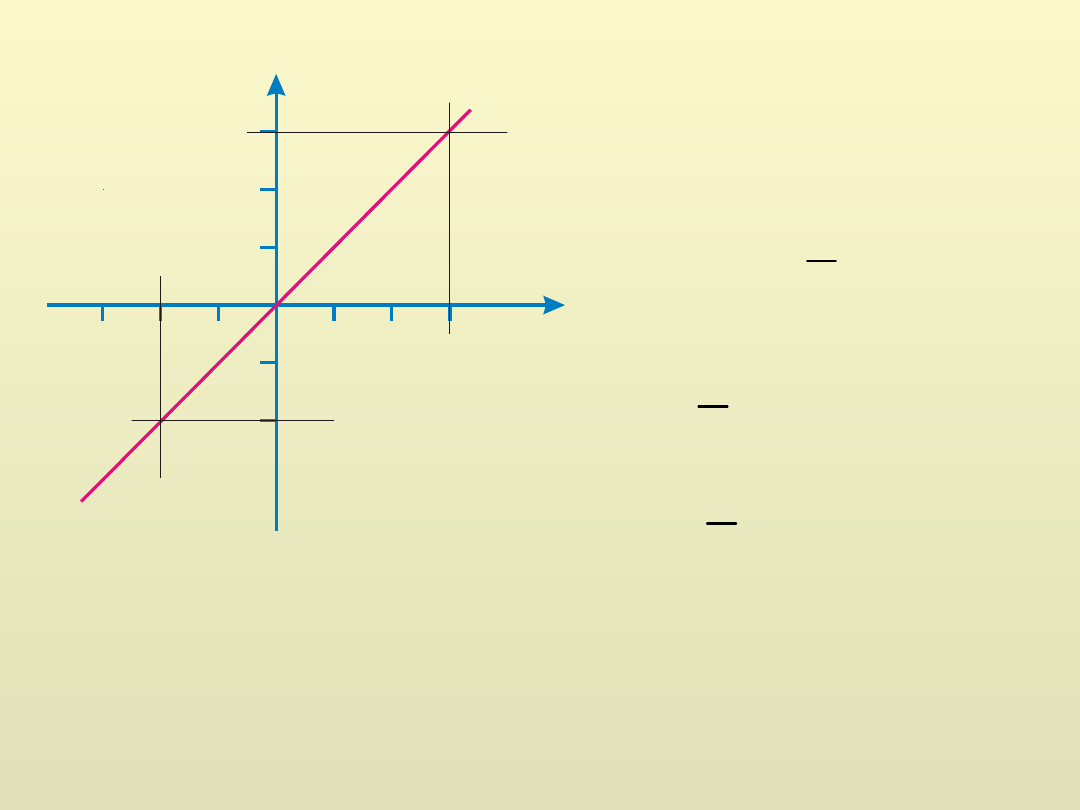
-2

-2

3

3

y = x

Pole trójkąta

ah

P

2

1



+

-

5

.

4

3

3

2

1











P

2

2

2

2

1











P

5

.

2

2

5

.

4















P

P

P

Kinematyka punktu materialnego

Punkt materialny – ciało obdarzone masą, ale nie

posiadające objętości. Ruch postępowy każdego

rzeczywistego obiektu można opisać jako ruch punktu

materialnego.

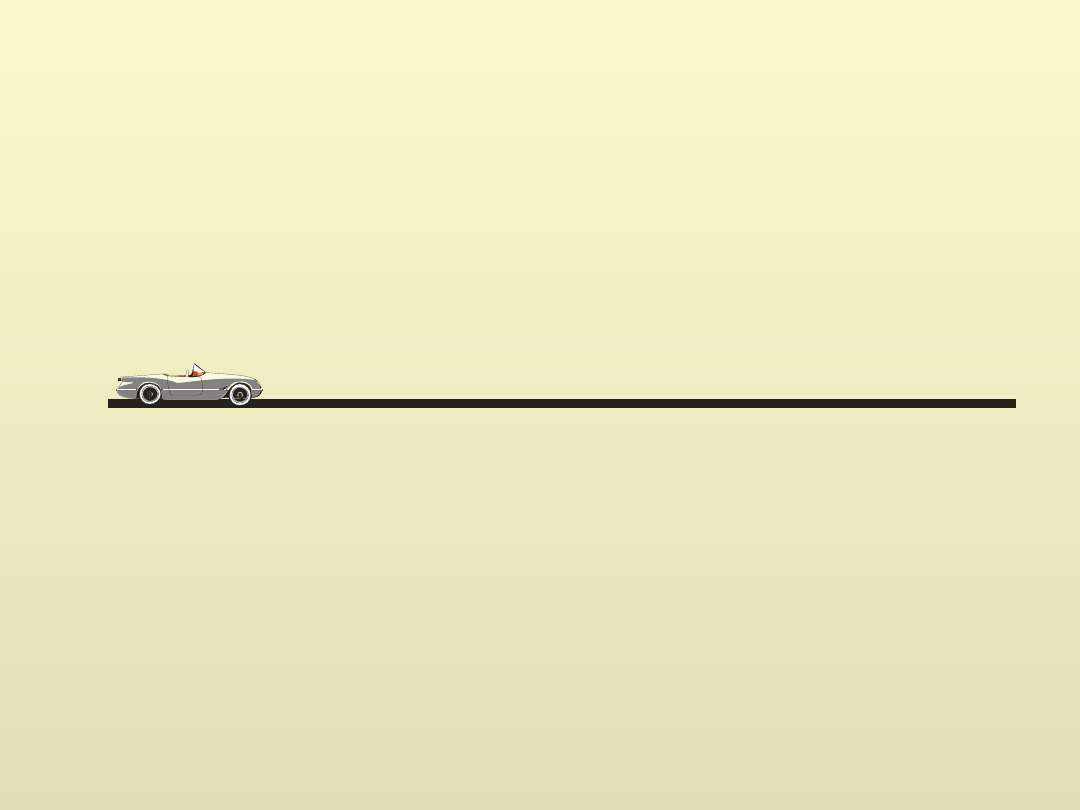
Przemieszczenia liniowe wszystkich elementów samochodu
są

jednakowe

Przemieszczenie liniowe elementów pręta

zależy

od

odległości od osi obrotu

A

B

)

(t

r

Jest to promień wodzący poprowadzony z początku układu
współrzędnych do tego punktu.

y

z

0

1

r

1

2

r

2



r

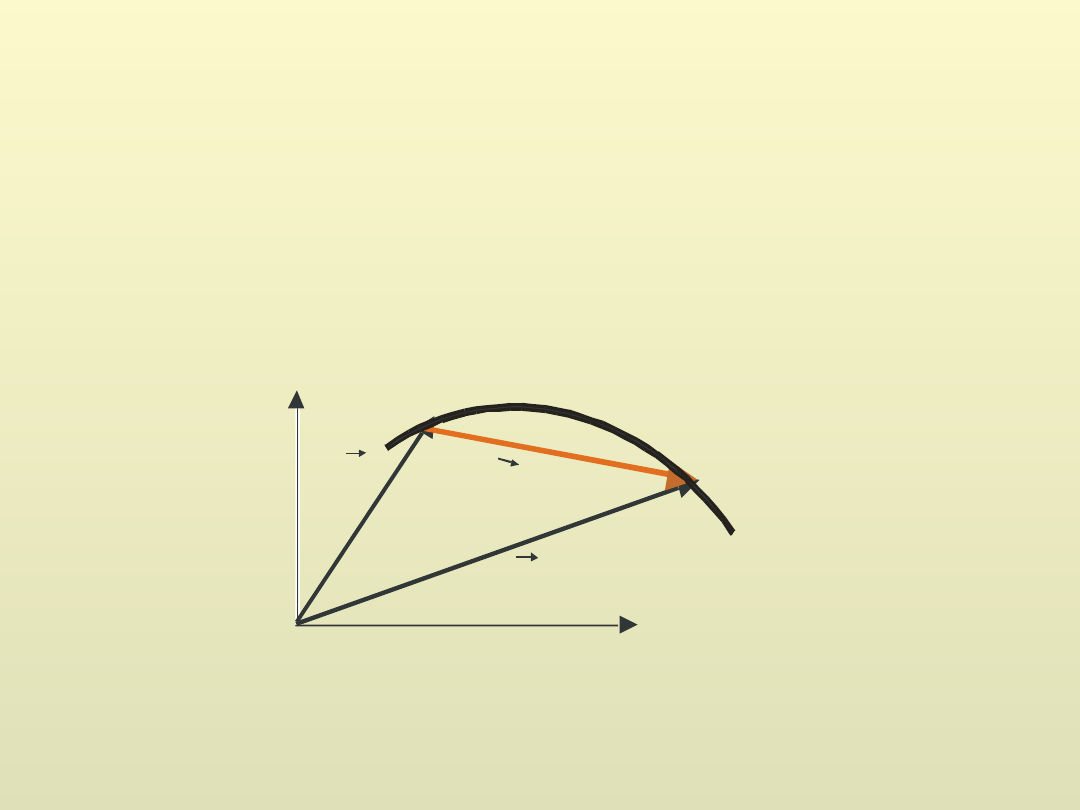
Położenie punktu materialnego określa

wektor położenia

y

z

0

r

1

r

2



r

Punkt 2 wybieramy blisko punktu 1

1

r

2

r

1

2

r

r

r













.

t

r

t

t

r

r

v

śr





















1

2

1

2

.

dt

r

d

t

r

t

v

t



















0

lim

)

(

Wektor przemieszczenia opisujący zmianę położenia punktu
materialnego z punktu opisanego wektorem położenia do
punktu opisanego wektorem

Wektor przemieszczenia podzielony przez czas, w którym to
przemieszczenie nastąpiło jest

prędkością średnią

punktu

materialnego

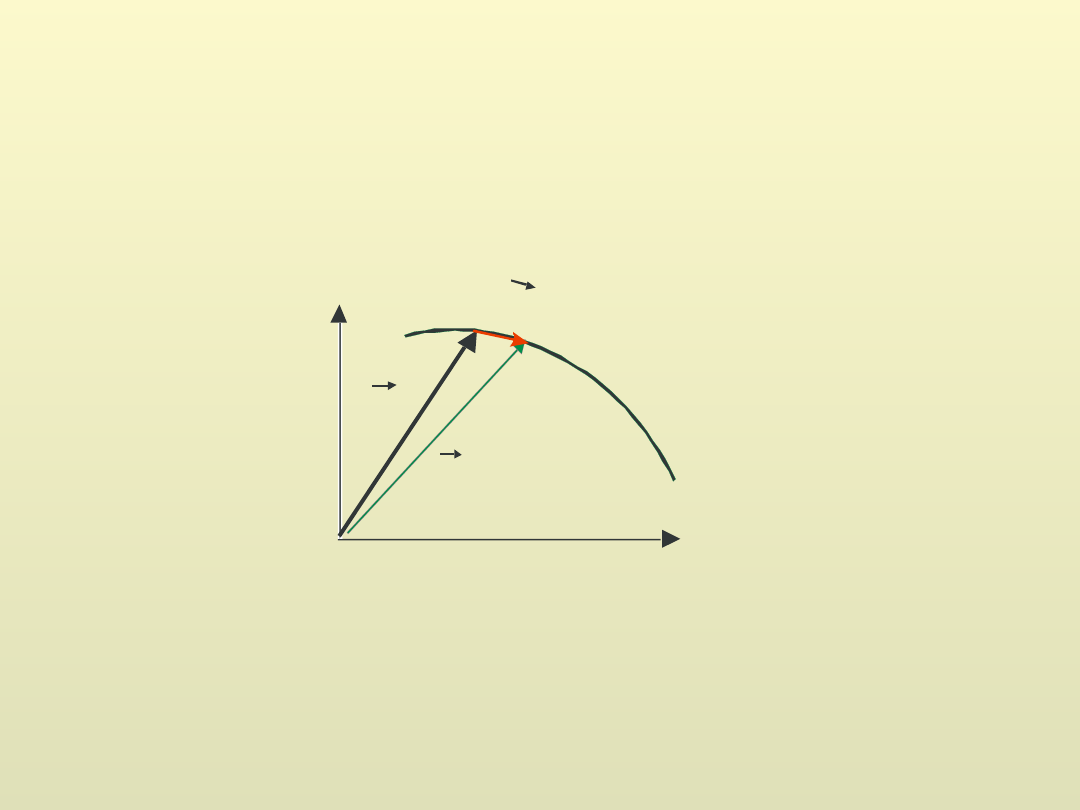
Prędkość punktu materialnego w danej chwili (t0) jest

prędkością chwilową

dt

r

d

v

t

v









)

(

Wartość prędkości chwilowej

jest zawsze liczbą dodatnią.
Wektor prędkości jest

zawsze

styczny do toru

poruszającego się punktu.

v

v

t

v

a

śr











dt

v

d

t

v

t

a

t



















0

lim

)

(

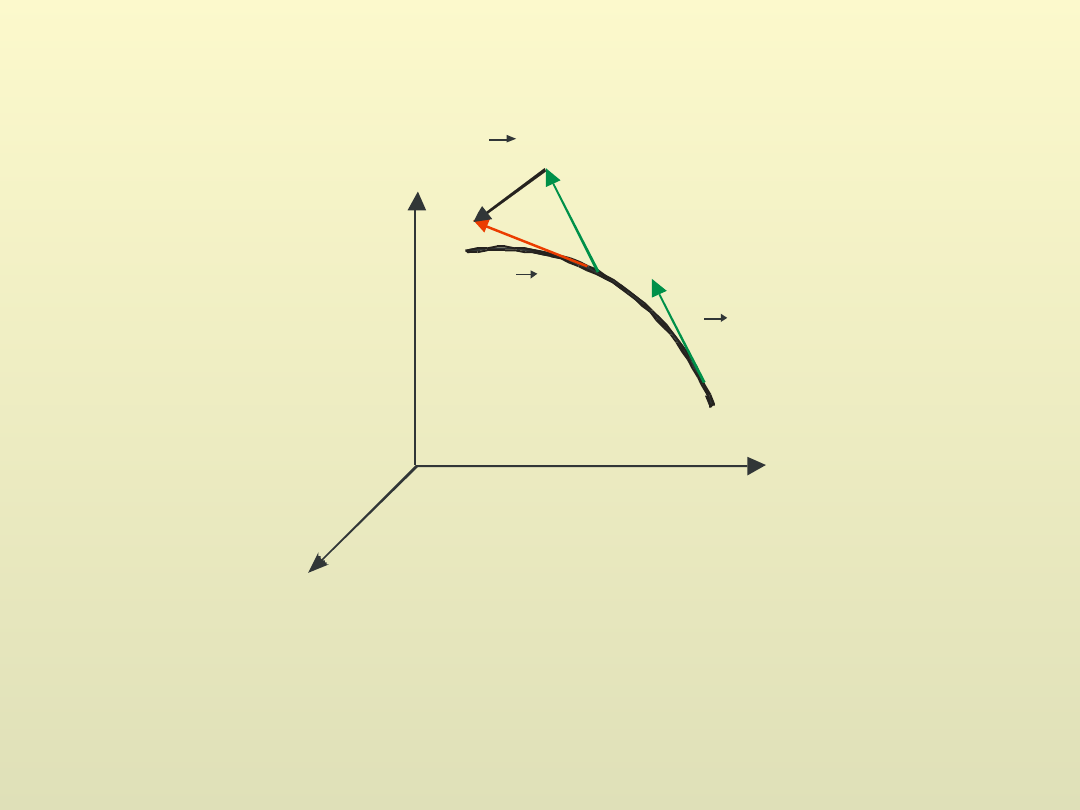
Przyspieszenie

określa zmianę wektora prędkości w czasie.

Przyspieszenie średnie

Jeśli t  0, przyspieszenie chwilowe

z

y

x

0

v

1

v

2



v

t

v

a

śr











dt

v

d

t

v

t

a

t



















0

lim

)

(

Przyspieszenie

określa zmianę wektora prędkości w czasie.

Przyspieszenie średnie

Jeśli t  0, przyspieszenie chwilowe

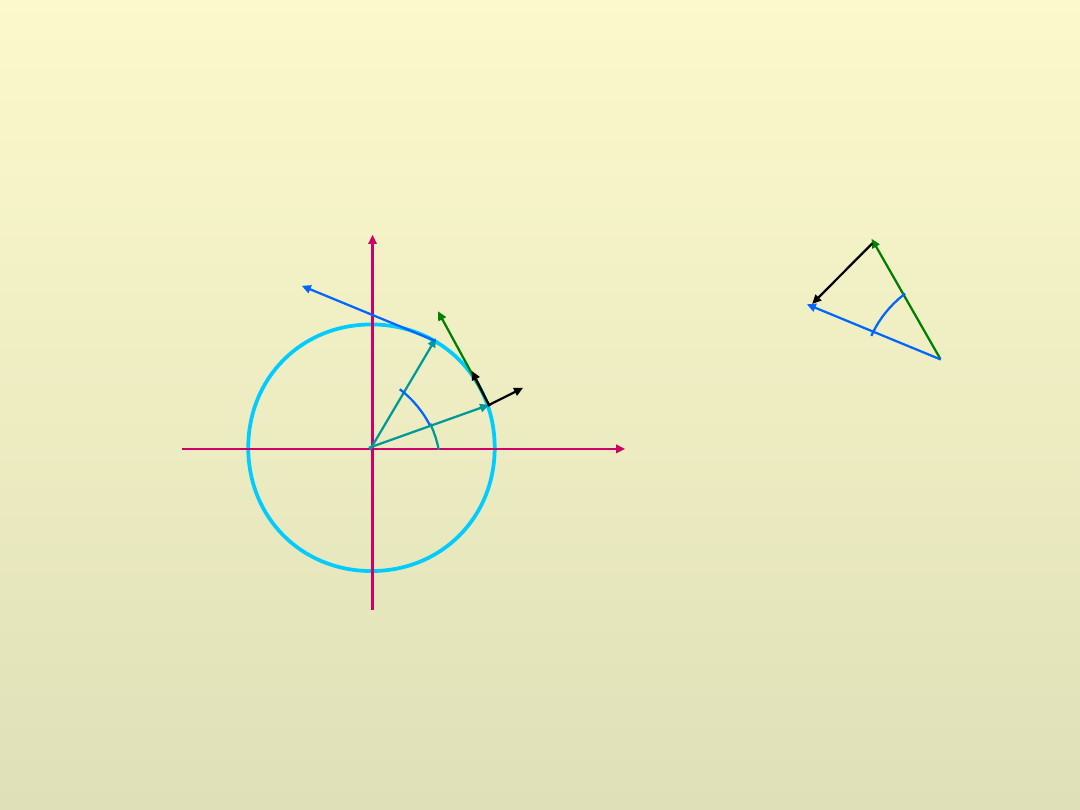
0

x

y

θ

∆θ

v

1

v

2

ε

R

ε

θ

ε

θ,

ε

R

– wektory jednostkowe

ε

θ2

ε

θ1

∆ε

∆θ

Przyspieszenie styczne i normalne

v

v













v

1

v

2

r

1

r

2

Δv

1

2

Jeśli punkt 2 wybierzemy blisko punktu 1 wektor Δv będzie
skierowany do środka okręgu.

v = const

Wektor prędkości w układzie biegunowym

- wektor jednostkowy. Jeżeli

to obydwie wielkości występujące w powyższym wzorze
zmieniają się w czasie Przyspieszenie punktu materialnego

dt

d

v

dt

dv

dt

v

d

a























v

v



















const

v 



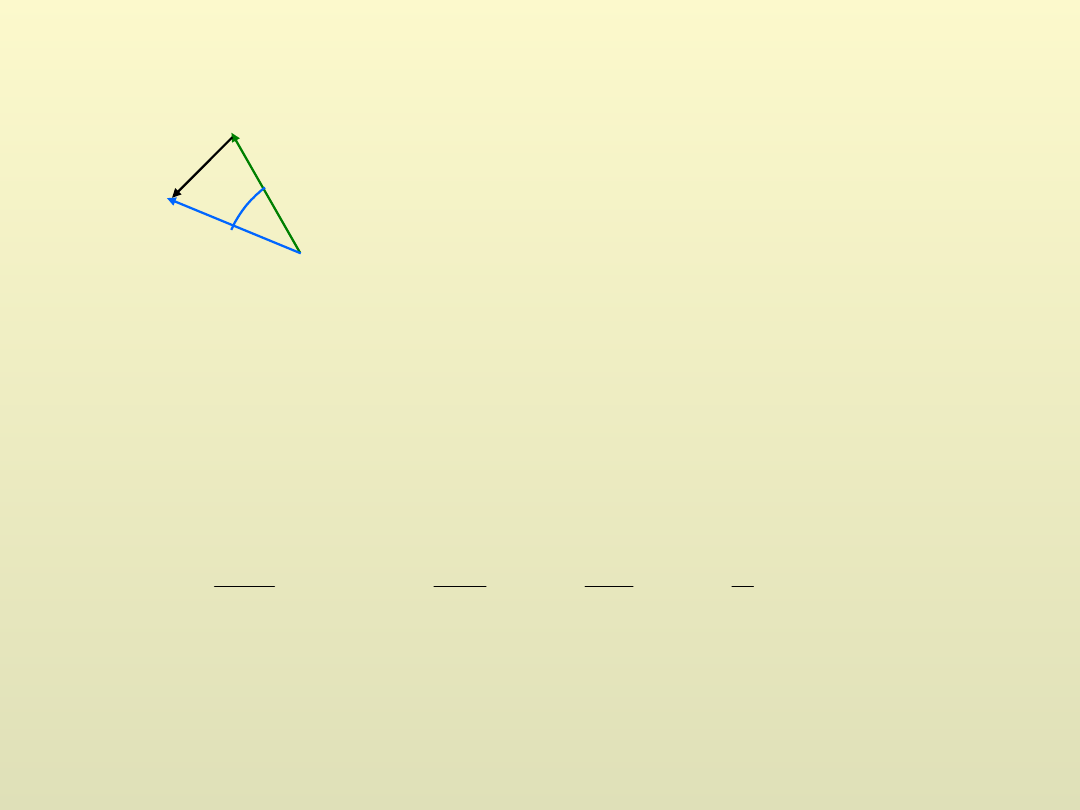
Oznacza to, że w dowolnym punkcie ma kierunek a wartość

Wektor

w przypadku granicznym,
jest skierowany do środka okręgu.

1

2

























0



t









r



















r

v

dt

d

t

dt

d

r

r

t

r











































0

lim

ε

θ2

ε

θ1

∆ε

∆θ

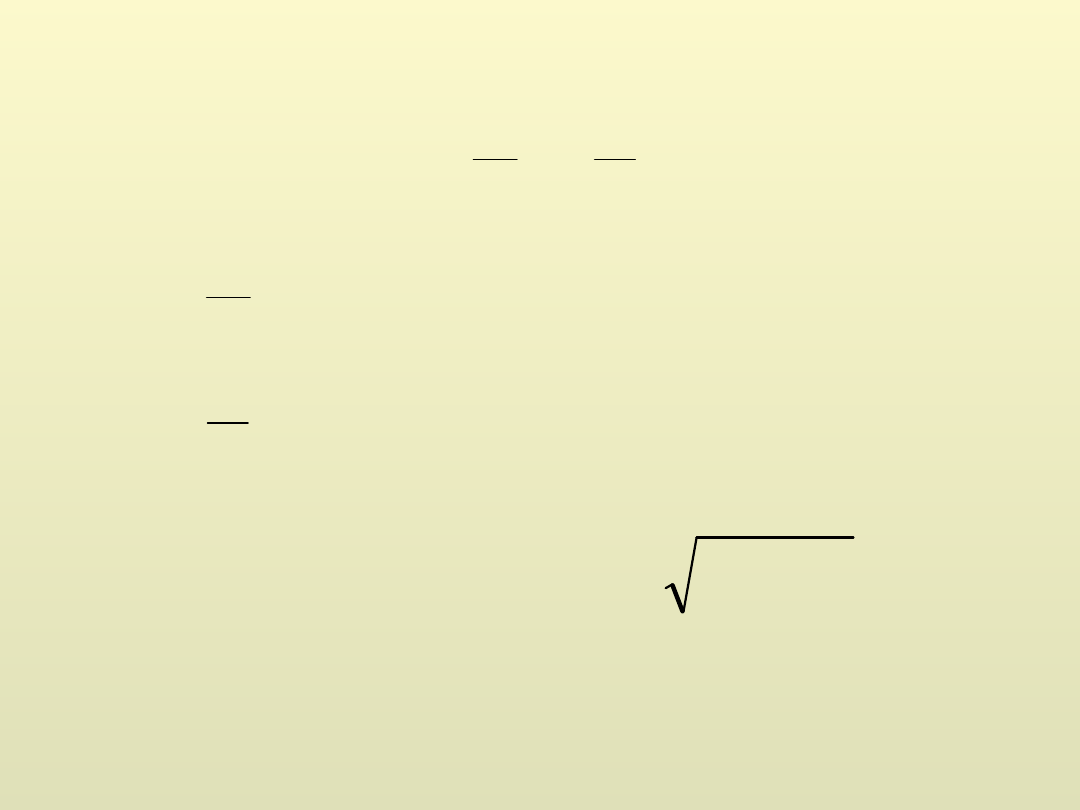
r

v

dt

dv

a

r

2

















dt

dv

a 



r

v

a

n

2



n

r

a

a

a



















2

2

n

a

a

a







przyspieszenie styczne do toru

przyspieszenie normalne, prostopadłe do toru

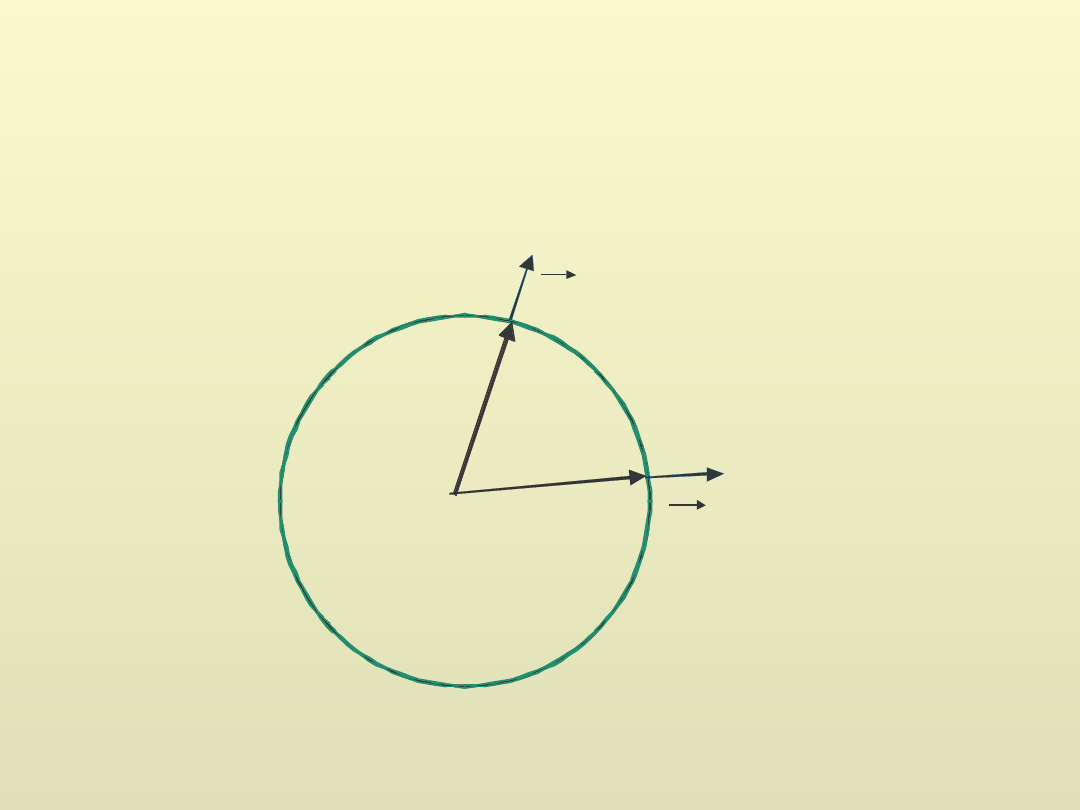
0



r 1



r2



Prędkość kątowa i przyspieszenie kątowe

Punkt materialny porusza się po okręgu o promieniu r. W
czasie wektor jednostkowy opisuje mały kąt

t



r









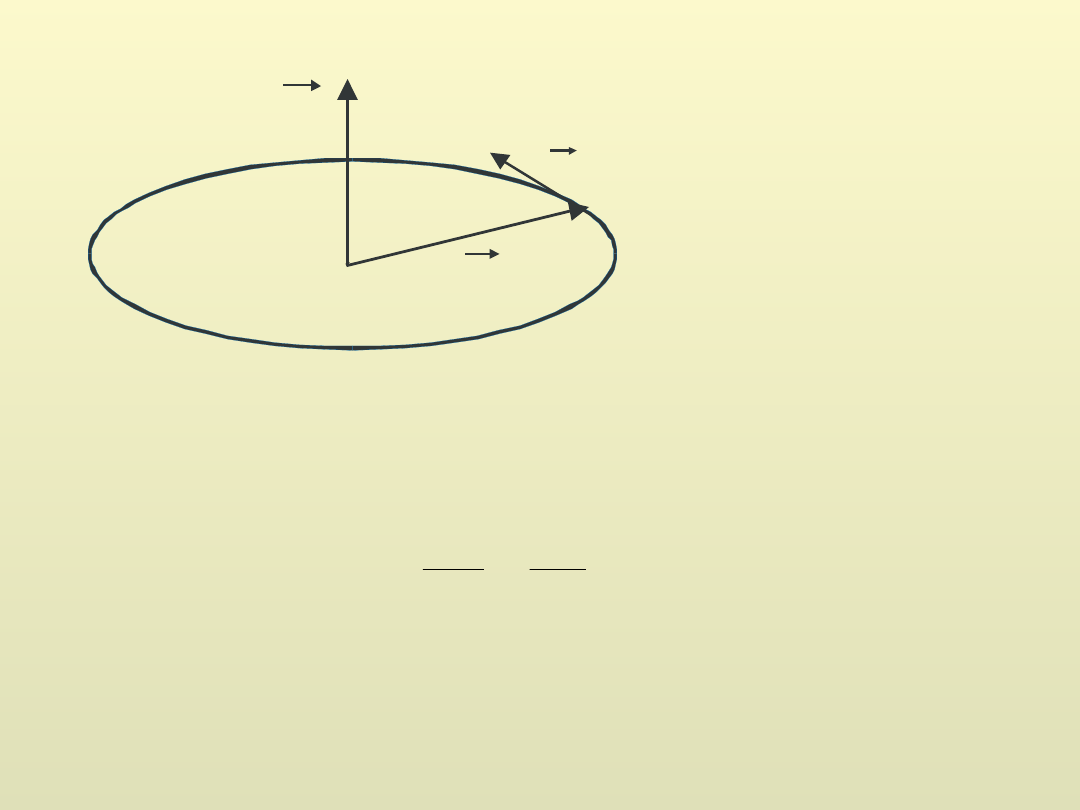
v

r



r

v













r

a

dt

d

t

t





































,

lim

0

Przyspieszenie kątowe

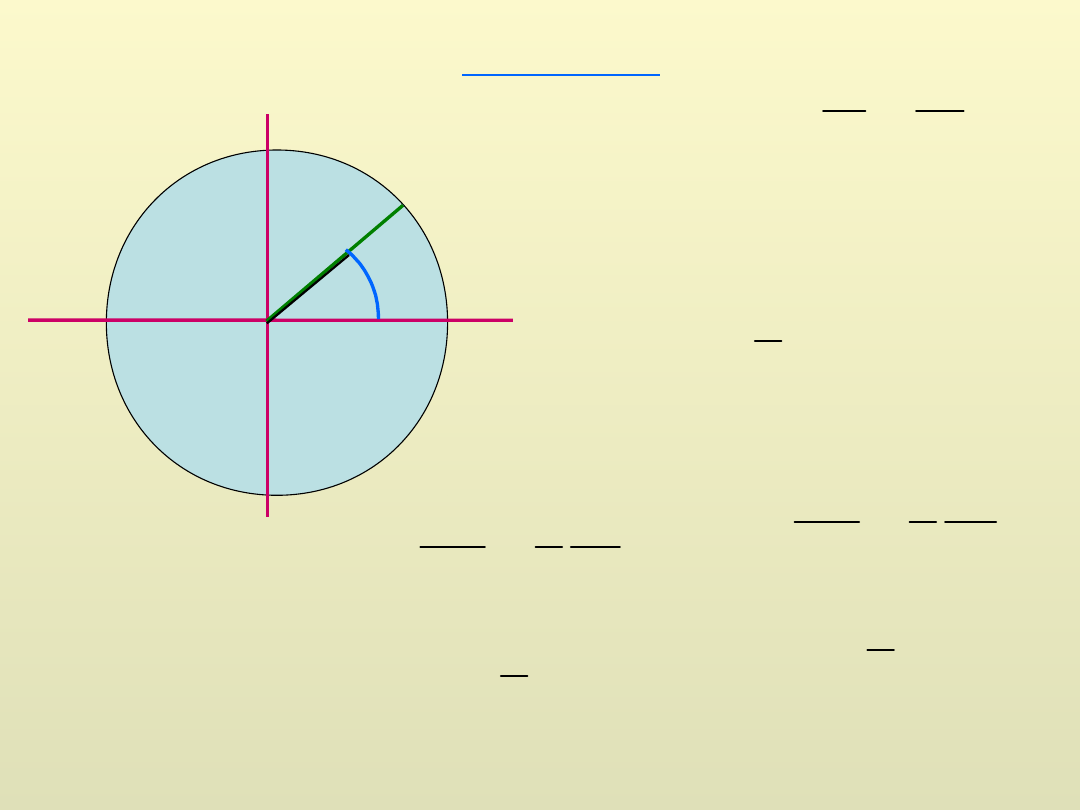
Radian jednostka kąta

długość łuku

promień

r

1

r

2

s

1

s

2

2

2

1

1

r

s

r

s







r

s





v

r

dt

ds

r

dt

d

1

1









a

r

dt

dv

r

dt

d

1

1









Dynamika punktu materialnego

1. Dane jest ciało o ściśle określonych własnościach

2. Ciało umieszczamy w znanym otoczeniu –
potrafimy określić siły, które na niego działają

Pytamy:

jaki będzie ruch tego ciała?

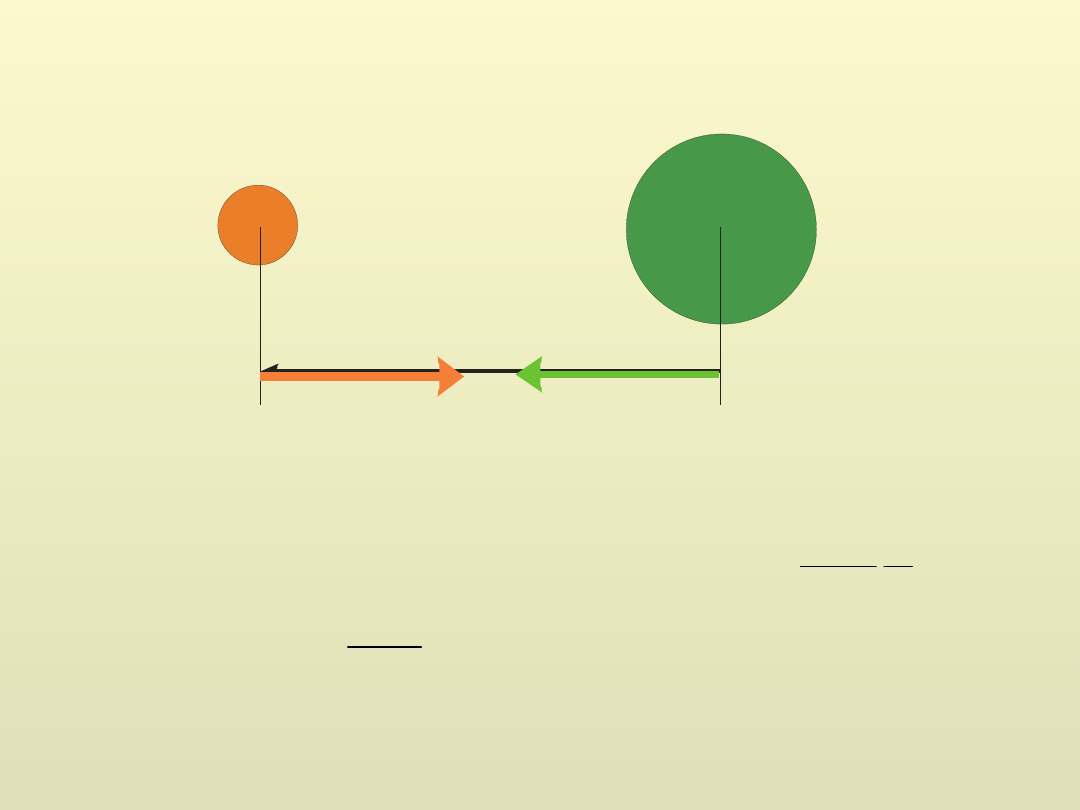
r

F

M

m

r

r

r

Mm

G

F





2





2

2

11

10

66

.

6

kg

Nm

G







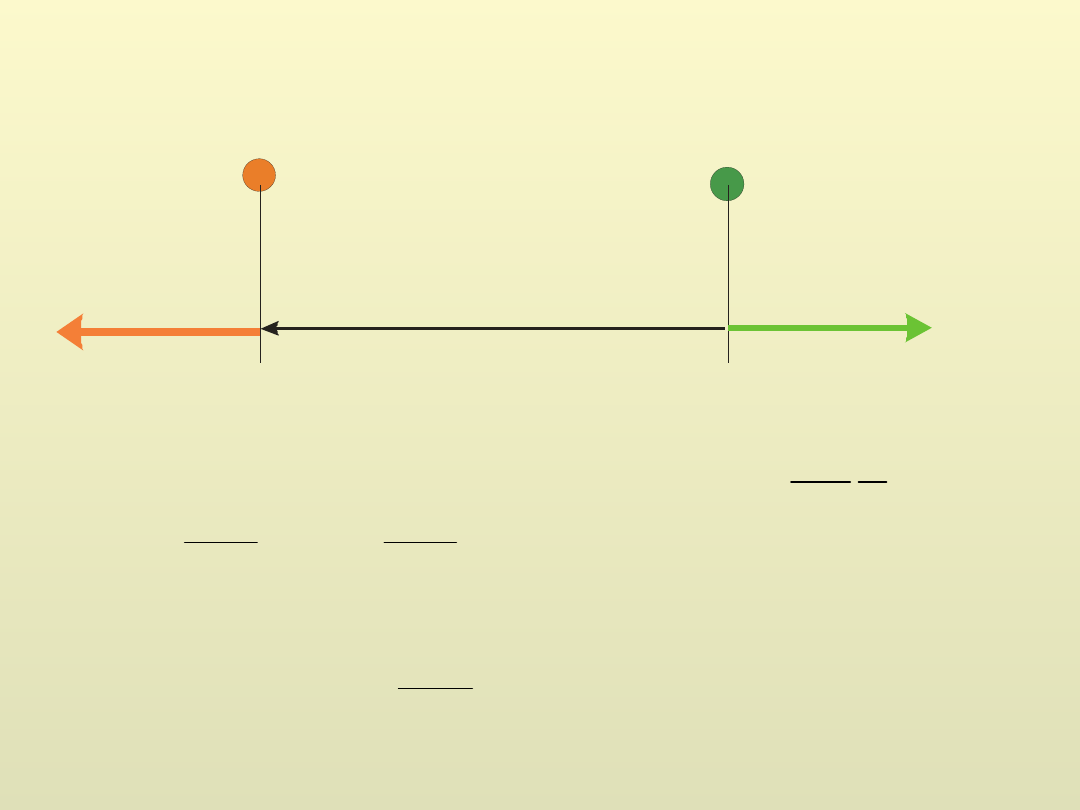
r

+q

+Q

r

r

r

Qq

k

F





2



F

2

2

12

10

8542

,

8

Nm

C

o









2

2

9

10

9

4

1

C

Nm

k

o









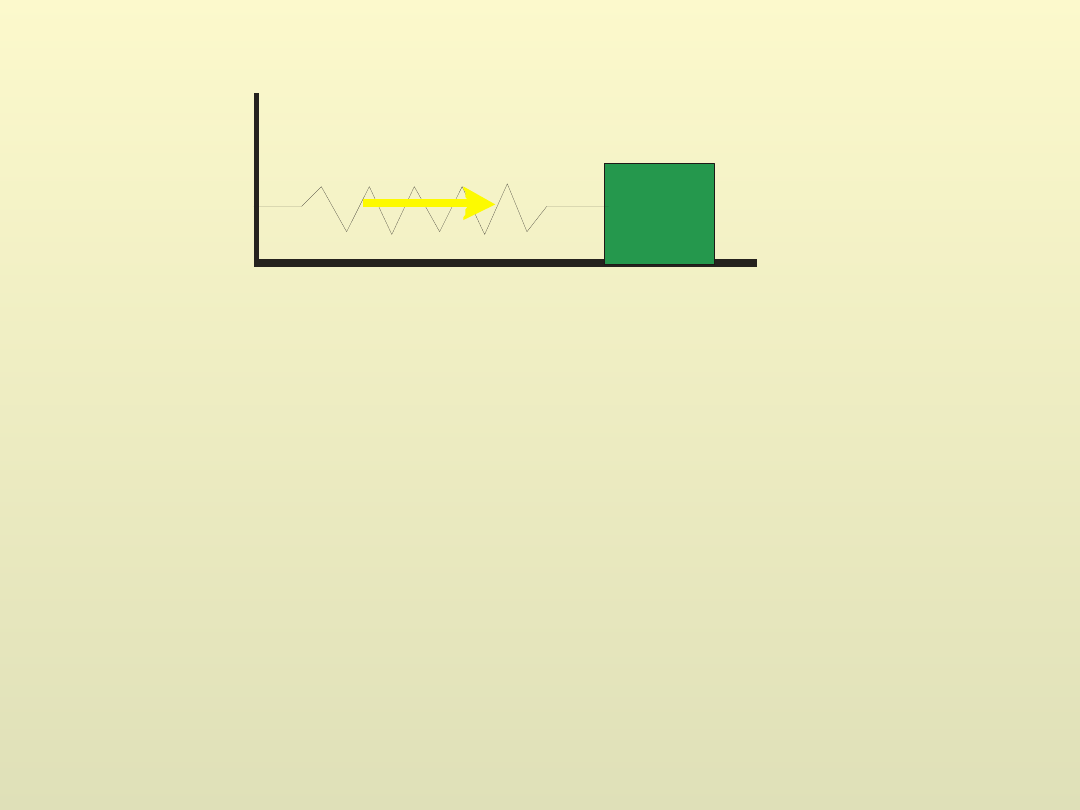
k

m

kx

F 



1

F

1

Jeżeli dodatkowo występuje tarcie pomiędzy masą m a powierzchnią, to

fmg

F 

2

f – współczynnik tarcia

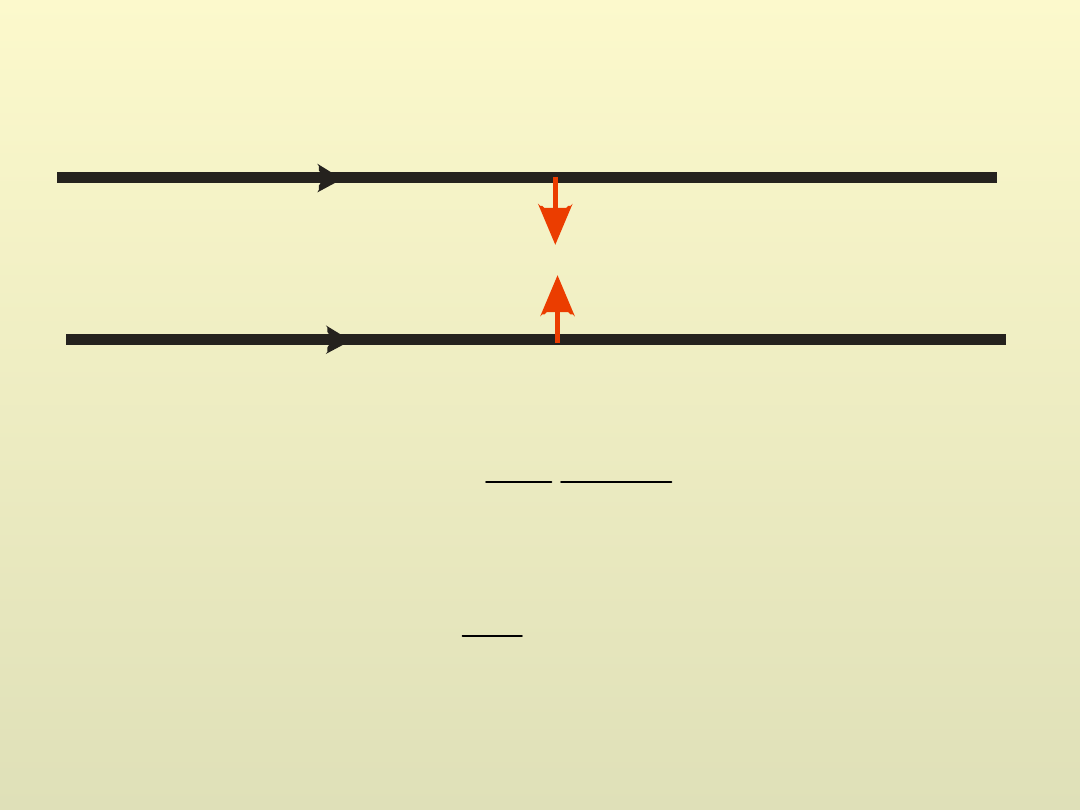
I

1

I

2

F

F

l

a

I

I

F

2

1

0

2

4







Am

Wb

7

0

10

4











Zasady dynamiki Newtona

I zasada dynamiki

Każde ciało pozostaje w stanie spoczynku lub ruchu
jednostajnego po linii prostej dopóty, dopóki nie zostanie
zmuszone za pomocą wywierania odpowiednich sił do zmiany
tego stanu.

I zasada dynamiki stwierdza, że jeżeli w pobliżu danego ciała
nie ma innych ciał (a więc nie działają siły), to można znaleźć

taki układ odniesienia, w którym ciało nie będzie mieć
przyspieszenia.

Isaac Newton 1642-1721

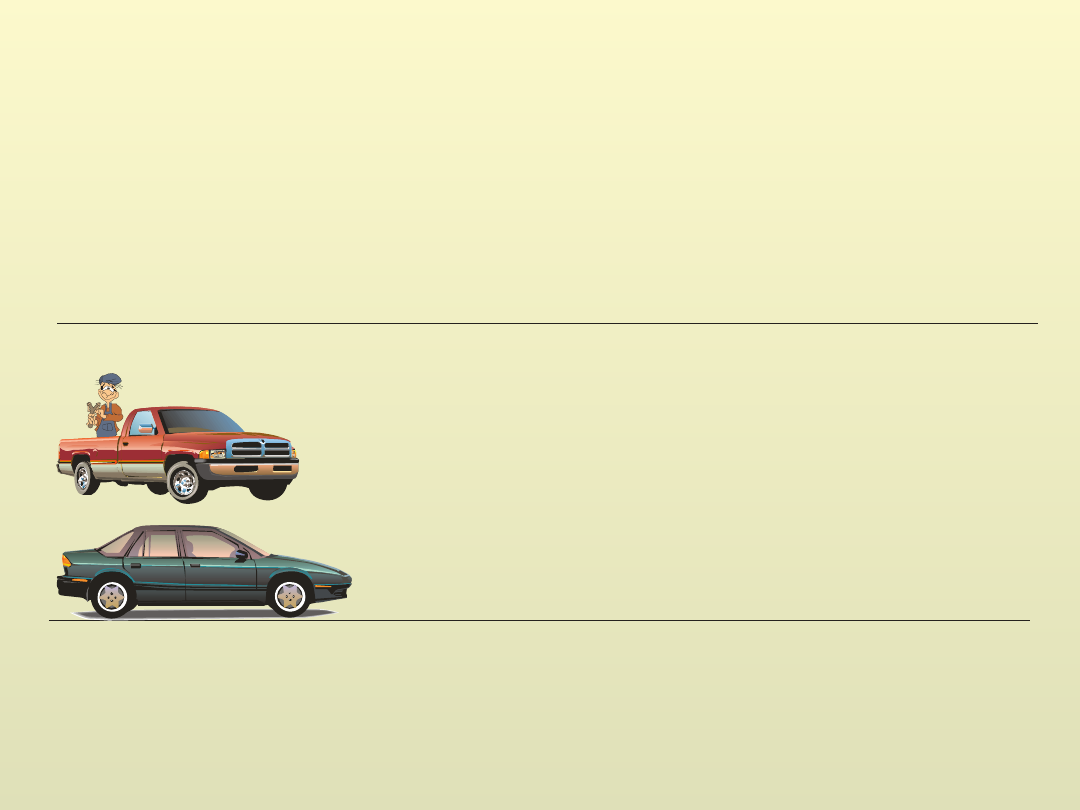
Układ S spoczywa, układ S’ porusza się ze stałą prędkością v.

S’

S

Obserwator znajdujący się w układzie S’ stwierdza:

chłopiec spoczywa

Obserwator znajdujący się w układzie S stwierdza:

chłopiec porusza się z prędkością v = const.

Obydwaj obserwatorzy stwierdzą”

przyspieszenie chłopca a = 0.

Fakt, ze ciało pozostaje w spoczynku lub porusza się ze stałą
prędkością, jeśli nie przykładamy do niego żadnej siły wiąże
się z właściwością materii zwaną bezwładnością (inercją).
Układy, w których obowiązuje I zasada dynamiki nazywamy

układami inercjalnymi.

II zasada dynamiki

Jeżeli na ciało działa wypadkowa siła to przyspieszenie
tego

jest wprost proporcjonalne do działającej siły a odwrotnie do
masy ciała.

Jeśli określimy siły działające na ciało, to znając warunki
początkowe

możemy wyznaczyć położenie ciała, jego prędkość i
przyspieszenie w dowolnej chwili.

F



m

F

a







o

o

r

r

v

v

t















,

,

0

Równanie

jest równaniem wektorowym.

2

2

dt

r

d

m

dt

v

d

m

a

m

F

m

F

a



























z

y

x

F

F

F

F

F

,

,







2

2

2

2

2

2

dt

z

d

m

dt

dz

dt

d

m

dt

dv

m

F

dt

y

d

m

dt

dy

dt

d

m

dt

dv

m

F

dt

x

d

m

dt

dx

dt

d

m

dt

dv

m

F

z

z

y

y

x

x



















Z II zasady dynamiki wynika

- pęd ciała.
Siła działająca na ciało jest równa szybkości zmian pędu ciała.
Rozwiązując ostatnie równanie otrzymamy

Zmiana pędu ciała jest równa popędowi działającej siły

dt

p

d

v

m

dt

d

dt

v

d

m

a

m

F



















 













t

p

p

t

o

dt

F

p

p

dt

F

p

d

dt

F

p

d

o

0

0



















p

v

m







popęd siły

III zasada dynamiki

Wszelkie działanie jest równe przeciwdziałaniu.

Jeżeli ciało A działa na ciało B siłą to ciało B działa na
ciało A siłą równą co do wartości, ale o przeciwnym
zwrocie

AB

F



BA

F



BA

AB

F

F













const

p

p

p

p

dt

d

dt

p

d

dt

p

d

















2

1

2

1

2

1

0













dt

p

d

F

dt

p

d

F

2

2

1

1

,













Zasada zachowania pędu

Założenia:
• układ składa się z dwóch oddziałujących ze sobą cząstek
• nie ma żadnych sił zewnętrznych działających na ten układ.
Z II zasady dynamiki wynika, że

z III zasady dynamiki

Dopóki rozpatrujemy tylko siły

wewnętrzne

całkowity pęd układu

jest stały.

Zwiększenie

pędu jednej cząstki musi spowodować

zmniejszenie

pędu drugiej cząstki.

const

p

p

p

p

p

N

i

i

N















1

3

2

1

........











1

2

2

1

2

2

1

1

0

m

m

v

v

v

m

v

m











Uogólnienie dla układu N ciał

Napęd odrzutowy

x’

y’

S’

0’

z’

P

r’

o

r

r

r









 '

Nieinercjalne układy odniesienia

- układy poruszające się prostoliniowo z przyspieszeniem:
układ S’ porusza się prostoliniowo z przyspieszeniem a

o

względem

układu inercjalnego S

o

r

r

o

r

r

r









 '

o

o

v

v

v

dt

r

d

dt

r

d

dt

r

d























'

'

prędkość punktu P
względem układu S

prędkość punktu P
względem układu S’

prędkość układu S’
(prędkość unoszenia)

Przyspieszenie

o

o

a

a

a

dt

v

d

dt

v

d

dt

v

d

a



























'

'

o

o

a

m

a

m

a

m

a

m

a

m

a

m























'

'

b

o

F

a

m









F

a

m







b

F

F

a

m











'

.

siły bezwładności

działające na

punkt materialny – pseudosiły, siły
pozorne

Zwrot wektora sił bezwładności jest przeciwny do zwrotu
wektora przyspieszenia

siły rzeczywiście działające na punkt
materialny pochodzące od otoczenia

II zasada dynamiki w układzie nieinercjalnym

- układy obracające się:

a) siła odśrodkowa – działa na każde ciało znajdujące się w

odległości od osi obrotu

b) siła Coriolisa – działa na ciało poruszające się z

prędkością względem układu obracającego się

'

r

'

v





'

,

,

'

,

sin

'

2

,'

2

v

F

v

v

m

F

v

m

F

C

C

C





































.





r

r

r

v

m

r

m

r

m

F

o













2

2

'

'





















v





c

a

'

2

v

m

F

C















'

2

v

a

C













Siła Coriolisa na Ziemi

Gustave Gaspard de Coriolis

1792 - 1843.

Czy laboratorium znajdujące się na powierzchni Ziemi jest

układem inercjalnym?

Ziemia wykonuje dwa ruchy obrotowe:
a) wokół własnej osi
przyspieszenie dośrodkowe

b) wokół Słońca
przyspieszenie dośrodkowe





2

2

2

2

6

2

2

2

2

1

s

m

10

38

.

3

s

3600

24

m

10

4

.

6

4

4

























z

z

d

R

T

R

a





2

3

2

2

11

2

2

2

2

2

s

m

10

95

.

5

s

3600

24

365

m

10

5

.

1

4

4































s

z

s

z

d

R

T

R

a

Tak, ale ze względu na niewielkie wartości przyspieszeń tę
„nieinercjalność” można pominąć w zjawiskach, które będziemy
omawiać.

Prawo zachowania energii

• prawa zachowania są niezależne od własności toru, a
często również od własności danej siły
• prawa zachowania mają zastosowanie nawet wtedy, gdy
siły są nieznane
• prawa zachowania stanowią dogodną pomoc w
rozwiązywaniu zagadnienia ruchu cząstki.

Cząstka o masie m nie jest poddana działaniu żadnej siły. W
chwili t = 0 do cząstki przyłożono siłę

p

F



const

F

p





m

F

a

ma

F

p

p





Prędkość cząstki

at

v

t

v





0

)

(

0

0

,

,

0

x

x

v

v

t







 





0

0

)

(

v

t

v

F

m

t

t

m

F

v

t

v

p

p











2

)

(

2

0

0

t

m

F

t

v

x

t

x

p

















 



































2

0

0

2

2

0

0

2

0

2

2

0

0

2

0

0

)

(

2

)

(

2

1

)

(

)

(

2

)

(

2

)

(

v

v

t

v

t

v

v

v

t

v

F

m

v

t

v

F

m

m

F

v

t

v

F

m

v

t

m

F

t

v

x

t

x

p

p

p

p

p





2

0

2

0

)

(

2

)

(

v

t

v

F

m

x

t

x

p











2

0

2

0

2

)

(

2

)

(

v

m

t

v

m

x

t

x

F

p







2

2

mv

energia kinetyczna cząstki

)

(

0

x

x

F

p



p

F

praca wykonana przez przyłożoną siłę jest równa
zmianie energii kinetycznej cząstki





2

0

2

0

2

)

(

2

)

(

v

m

t

v

m

x

t

x

F

p







praca wykonana na cząstce przez siłę

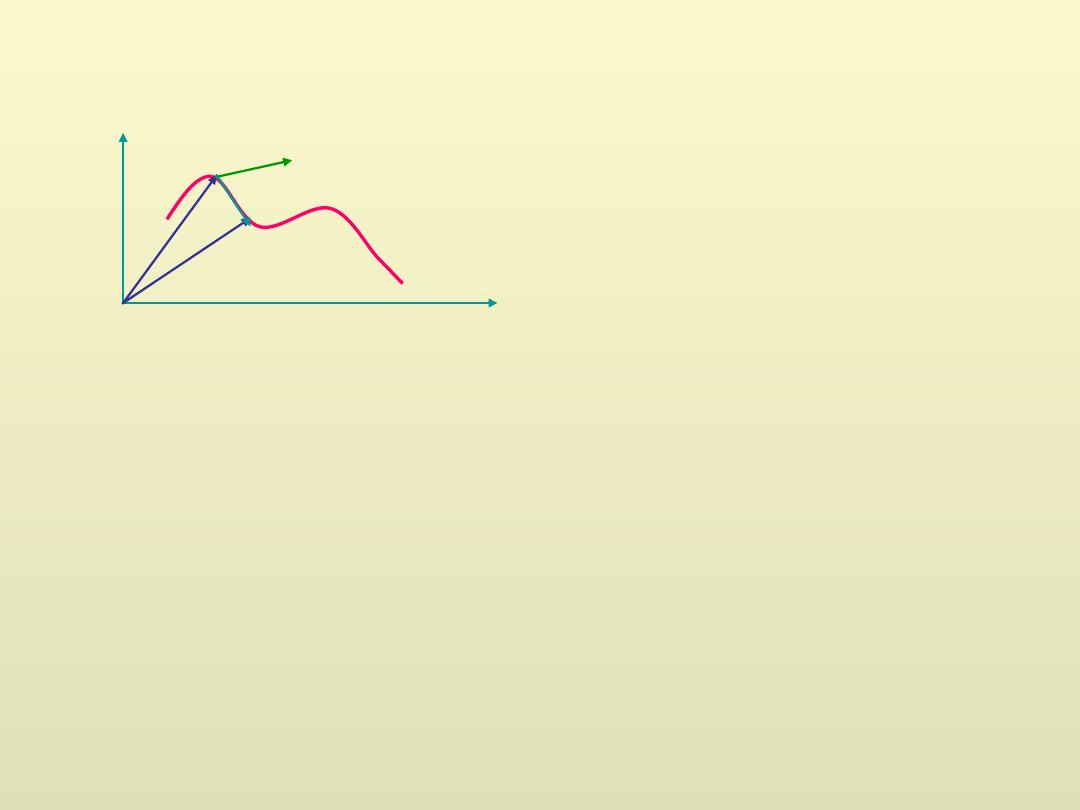
Wówczas

równanie to jest słuszne w granicy, gdy - toru
krzywoliniowego nie można

dokładnie

rozłożyć na skończoną

liczbę odcinków prostoliniowych.

Praca

–

iloczyn skalarny

wektorów siły i przemieszczenia

)

,

(

cos

r

F

r

F

r

F

W

p

p

p























const

r

F

F

p

p





)

(





const

r

F

p



)

(





































N

i

i

i

p

N

N

p

p

p

p

r

r

F

r

r

F

r

r

F

r

r

F

r

r

F

W

1

3

3

2

2

1

1

)

(

)

(

)

(

)

(

)

(

































0





i

r

x

y

F

p

r

1

r

2

r

Drogę rozkładamy na N odcinków liniowych takich, że na każdym z nich

























B

A

i

r

r

p

i

i

i

p

r

r

d

r

F

r

r

F

W



















)

(

)

(

lim

1

0

Pracę definiujemy jako:













B

A

p

r

d

r

F

B

A

W







)

(

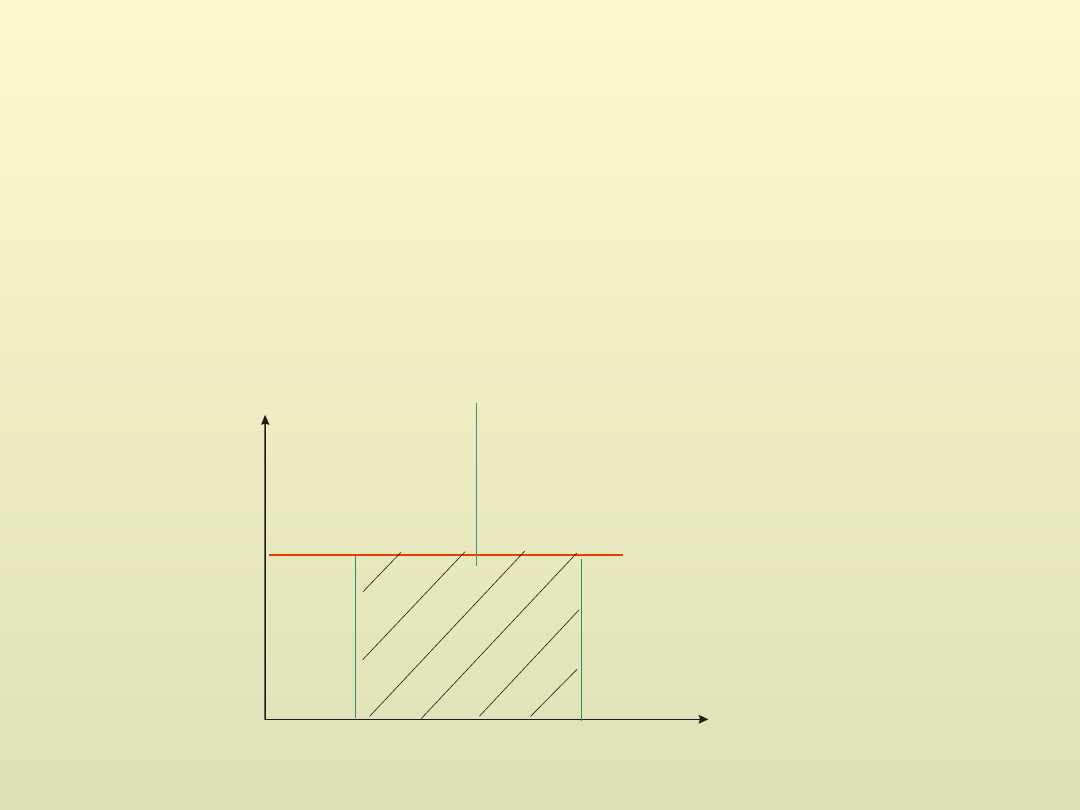
a) Stała siła









A

B

p

B

A

p

x

x

F

dx

F

B

A

W













F

A

x

B

x

x

p

F

W

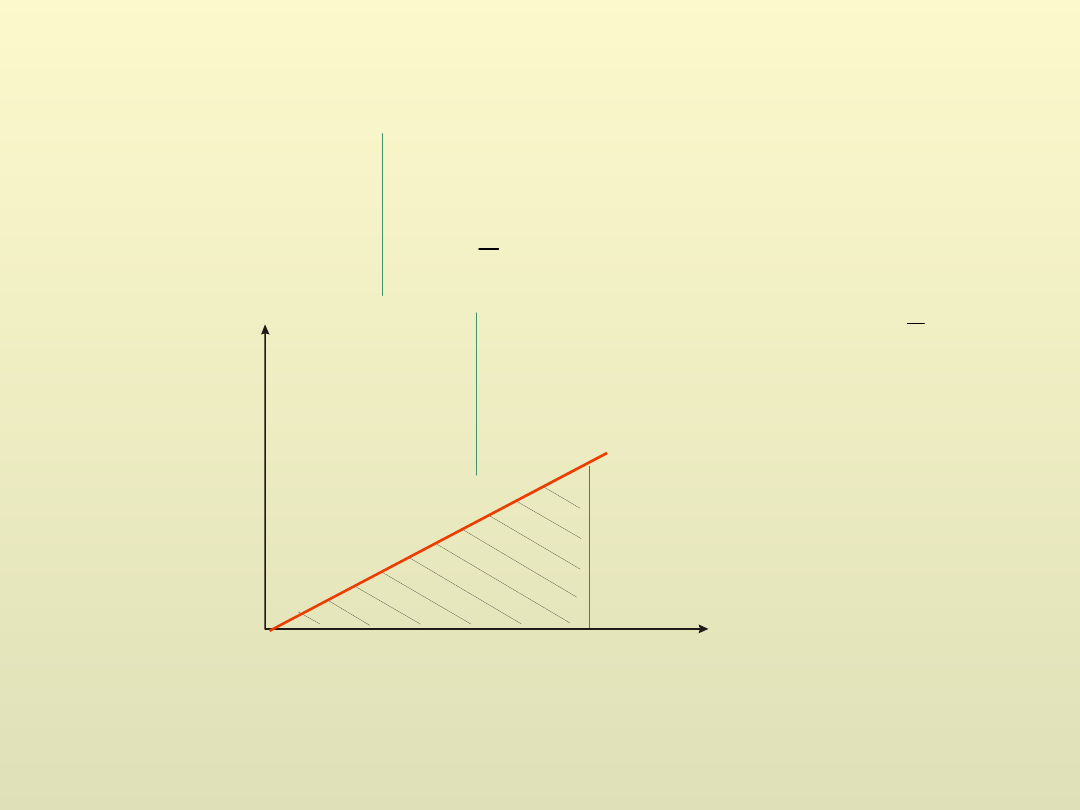
b) Siła zmienna, np. rozciągamy sprężynę:





kx

kx

F

p





























B

A

A

B

x

x

k

dx

kx

B

A

W

2

2

2

1





2

2

1

,

0

kx

B

A

W

x

A







F

x

W

praca wykonana przez dowolną siłę = zmiana energii kinetycznej ciała
(przyjmiemy bez dowodu)

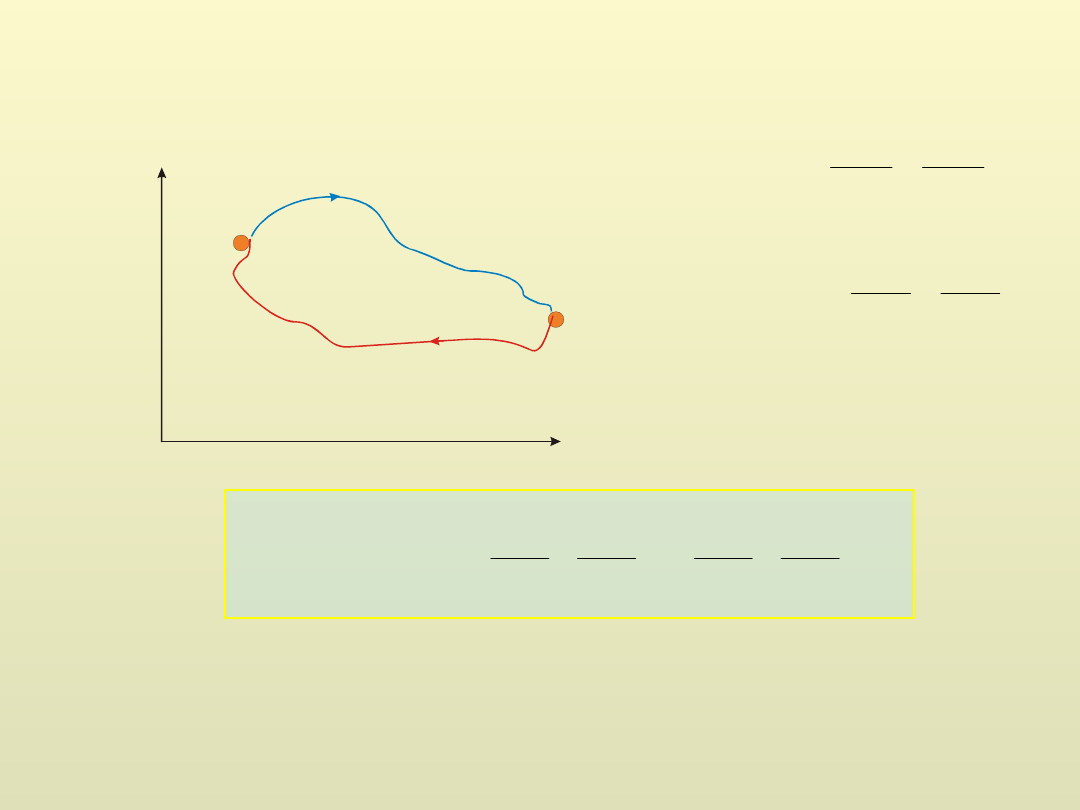
Siły zachowawcze

x

y

A

B

2

2

)

(

2

2

A

B

mv

mv

B

A

W







2

2

)

(

2

2

B

A

mv

mv

A

B

W







0

2

2

2

2

)

(

2

2

2

2







































B

A

A

B

mv

mv

mv

mv

A

B

A

W

Praca wykonana przez siłę zachowawczą po drodze zamkniętej
jest równa zeru.

Praca wykonana przez siłę zachowawczą nie zależy od kształtu

toru.

siły zachowawcze = siły potencjalne













B

A

p

p

p

r

d

F

B

A

W

A

E

B

E





)

(

)

(

)

(









r

A

p

p

p

r

d

F

A

E

r

E









)

(

)

(

Energia potencjalna

Przykładamy do ciała siłę F

p

równoważącą wszystkie inne siły

działające na ciało. Wówczas E

k

= const. Praca wykonana przez

siłę F

p

podczas przenoszenia tego ciała z punktu A do punktu B

pola zachowawczego = zmianie energii potencjalnej ciała

Energia potencjalna ciała w danym punkcie pola

wyznaczona jest z dokładnością do stałej addytywnej

Jeśli siłę przyłożoną zastąpimy siłą rzeczywiście działającą na
ciało
to energia potencjalna ciała w danym punkcie pola

lub względem punktu położonego w nieskończoności

Jeśli punkt A  , wówczas i energia potencjalna
ciała

względem nieskończoności











r

p

r

d

F

r

E









)

(









r

A

p

p

r

d

F

A

E

r

E









)

(

)

(

F

F

p









F



0

)

(





p

E









r

p

p

r

d

F

r

E









)

(

Zasada zachowania energii mechanicznej

N

z

F

F

F











N

z

W

W

W





Na cząstkę działa siła

suma sił

zachowawczych

suma sił

niezachowawczych

Praca wykonana przez siłę

Praca wykonana przez

dowolne siły

podczas przenoszenia ciała

z punktu A do B = zmianie energii kinetycznej ciała

Praca wykonana przez

siły zachowawcze

= zmianie energii

potencjalnej ciała

kA

kB

E

E

B

A

W

W









)

(





pA

pB

z

E

E

B

A

W

W











)

(





N

pA

pB

kA

kB

W

E

E

E

E











0

0

0

















N

N

F

W

const

E

E



Zmiana całkowitej energii mechanicznej układu
równa jest pracy sił niezachowawczych.
Jeśli na ciało (układ ciał) działają tylko siły
zachowawcze wówczas energia mechaniczna jest
stała.

N

cA

cB

W

E

E

E











 



N

pA

kA

pB

kB

W

E

E

E

E









energia całkowita

w punkcie B pola

energia całkowita

w punkcie A pola

Dynamika ruchu obrotowego:
• punktu materialnego
• bryły sztywnej

Bryła sztywna

– zbiór punktów, przy czym dla dowolnych dwóch

punktów A i B ich wzajemna odległość r

AB

jest stała w czasie,

niezależnie od przyłożonej siły.

A

B

r

AB

Moment siły

F

r

M











)

,

(

sin

F

r

rF

M









r



F

1

r

F

a





P

M

O

ramię siły

kierunek działania siły

dla punktu materialnego

p

r

L











Moment pędu punktu materialnego

p

r

L

p

r

rp

L











,

),

,

(

sin







v

m

r

L











L



v

m

r

II zasada dynamiki dla ruchu obrotowego
wokół stałej osi obrotu







I

M 

Moment siły działającej na punkt materialny jest
proporcjonalny do przyspieszenia kątowego jakie ten punkt
uzyskuje.
Współczynnikiem proporcjonalności jest moment
bezwładności.
Dla punktu materialnego

2

mr

I 

na punkt materialny działa zewnętrzny
moment siły, to zmienia się moment pędu
tego punktu materialnego

dt

L

d

M







const

M 



t

L

M











Układy punktów materialnych

Dla układu zawierającego n punktów materialnych zapiszemy:

















n

i

i

n

L

L

L

L

L

L

1

3

2

1















oraz



























n

i

i

i

n

n

n

r

m

r

m

r

m

r

m

r

m

I

I

I

I

I

1

2

2

2

3

3

2

2

2

2

1

1

3

2

1





dt

L

d

M























n

i

i

n

M

M

M

M

M

M

1

3

2

1















Zmiana całkowitego momentu pędu układu
punktów
materialnych w jednostce czasu względem
początku inercjalnego układu odniesienia jest
równa sumie zewnętrznych momentów sił
działających na układ

Ruch postępowo-obrotowy bryły sztywnej

toczenie ciał

Jak opisać taki ruch?

Załóżmy, że cylinder toczy się po poziomej powierzchni bez
poślizgu

Dowolny punkt toczącego się cylindra obraca się wokół
chwilowej osi prostopadłej do płaszczyzny rysunku i
przechodzącej przez punkt P, prędkość liniowa każdego punktu
jest prostopadła do linii łączącej ten punkt z punktem P

wartość bezwzględna tej prędkości jest proporcjonalna do
odległości między punktami

r

v













r

v







,





r





2

2

i

i

ki

v

m

E 





i

i

i

k

v

m

E

2

2

i

i

r

v



















i

i

i

i

i

i

k

r

m

r

m

E

2

2

2

2

2

2











i

i

i

r

m

I

2

moment bezwładności układu punktów materialnych
względem danej osi obrotu

2

2



I

E

k







dm

r

I

2

moment bezwładności bryły sztywnej względem
danej osi obrotu

Energia kinetyczna i-tego
punktu materialnego

Energia kinetyczna układu
punktów materialnych

Energia kinetyczna w ruchu obrotowym

r

2

2

mr

I 

12

4

2

2

ml

mr

I





3

2

ml

I 

5

2

2

mr

I 

2

mr

I 

r

l

Twierdzenie Steinera

2

0

md

I

I





0

I

d

I

2

0

5

2

mr

I 

r

d

3

2



2

2

2

2

45

38

9

4

5

2

3

2

5

2

mr

mr

r

m

mr

I













 



















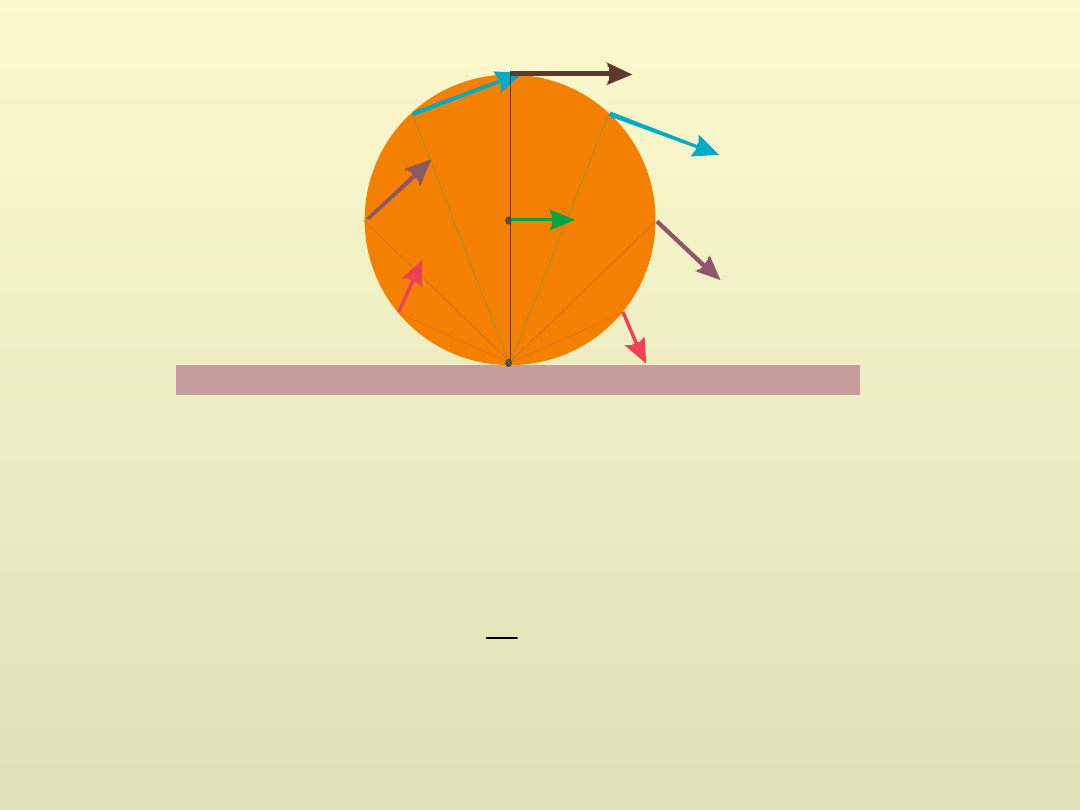
P

S

Cylinder obraca się wokół punktu P z prędkością kątową
w danej chwili – jest to więc czysty ruch obrotowy.
Energia kinetyczna takiego ruchu



2

2

1



I

E

k



Z twierdzenia Steinera wynika

a więc energia kinetyczna cylindra wynosi

2

mr

I

I

S





2

2

2

2

1

2

1





mr

I

E

S

k





Iloczyn jest prędkością liniową środka masy cylindra
względem nieruchomego punktu P



r

2

2

2

1

2

1

S

S

k

mv

I

E







Prędkość środka masy względem punktu P jest taka sama jak
prędkość punktu P względem środka masy stąd prędkość
kątowa środka masy wokół punktu P jest taka sama jak prędkość
kątowa punktu P wokół środka masy

2

2

2

1

2

1

S

S

k

mv

I

E







energia kinetyczna
obracającego się cylindra

energia kinetyczna
cylindra poruszającego
się ruchem postępowym

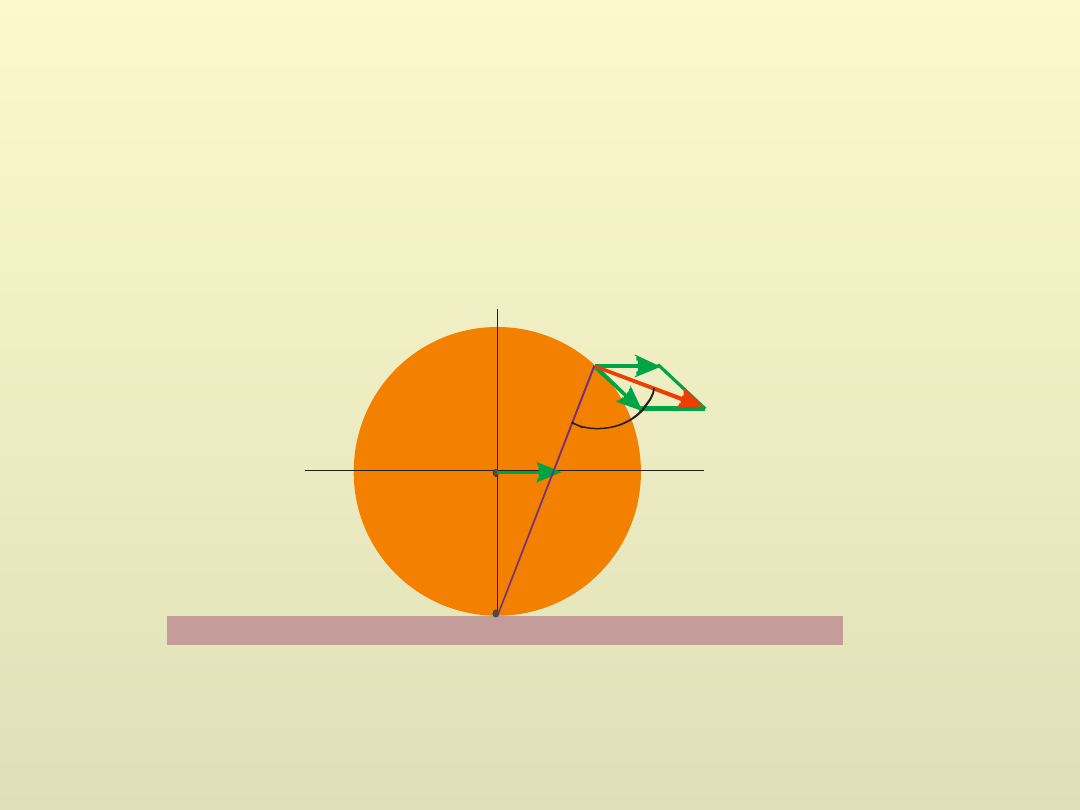
P

S

Dowolny punkt znajdujący się na obwodzie walca obraca
się z prędkością v i z taką samą prędkością porusza się
prostoliniowo

M

dt

L

d







Ogólna postać II zasady dynamiki dla
ruchu obrotowego

Szybkość zmian momentu pędu jest równa momentowi siły

analogicznie do

F

dt

p

d







const

L

dt

L

d

M

















0

0

Zasada zachowania momentu pędu

Moment pędu jest stały gdy nie działa zewnętrzny moment siły.

Związek pomiędzy krętem a prędkością kątową

const

L 



const

I









2

2

1

1















I

I









I

L

Jeśli moment pędu jest zachowany, to