Modele

Oligopolu

Paulina Fisz

Paulina Bełkowska

Ekonomia gr. 2

• Oligopol

– informacje ogólne

• Model

Cournota

• Model

Edgewortha

• Model

Chamberlina

• Model

Stackelberga

• Model Sweezy’ego
• Model Bertranda
• Model Sylos’a – Labinieg’o

Oligopol

• Struktura rynku, w której występuje od dwóch (duopol)

do kilkunastu producentów;

• Istnieje silna współzależność pomiędzy

przedsiębiorstwami;

• Niewielka liczba firm zachowuje się w sposób

strategiczny i działa niezależnie od siebie, ale

uwzględniając istnienie pozostałych firm;

• Na decyzje firmy wpływają decyzje podjęte przez inne

firmy i na odwrót;

• Produkty są jednorodne lub zróżnicowane;
• Niewielka liczba sprzedawców i wielu kupujących;
• Ograniczony dostęp do rynku;
• Dominują pozacenowe formy konkurencji.

Model

Cournota

• Założenia
• Opis
• Interpretacja graficzna

Założenia Modelu

Cournota

• Produkcja jest zmienną decyzyjną, a cena wielkością

wynikową;

• Produkty firm są jednorodne;
• Obaj producenci przyjmują, że ich działania nie wywołują

reakcji przedsiębiorstwa konkurencyjnego;

• Krzywa kosztów krańcowych (MR) pokrywa się z osią

poziomą  MR=0;

• Podaż jest nieograniczona (MR=0);
• Produkcja odbywa się bez kosztów (koszty produkcji

producentów są takie same);

• Wielkość produkcji konkurencji jest dana;
• Doskonała informacja o rynku;
• Cele firm: maksymalizacja zysku!

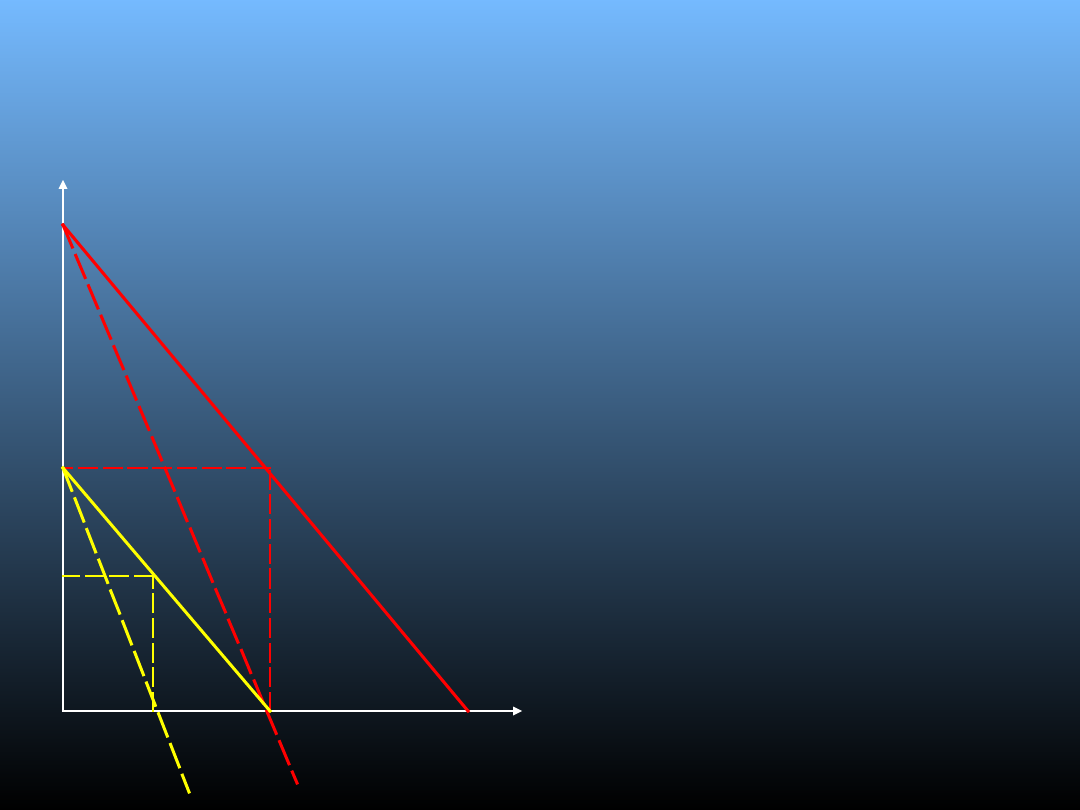
Model Cournota

• Da

- krzywa popytu rynkowego i

krzywa popytu firmy A - przy

założeniu, że A działa jako

monopolista;

• UKa

- utarg krańcowy firmy A;

• Db

- krzywa popytu firmy B;

• UKb

- utarg krańcowy firmy B;

• MC - koszt krańcowy;

• Qa

- wielkość produkcji

maksymalizująca zysk

przedsiębiorstwa A;

• Pa

- cena maksymalizująca zysk

przedsiębiorstwa A przy wielkości

produkcji Qa;

• Qb

– wielkość produkcji

maksymalizująca zysk

przedsiębiorstwa B;

• Pb

– cena maksymalizująca zysk

przedsiębiorstwa B przy wielkości

produkcji Qb

D
a

UKa

Db

UK
b

P

Q

MC=
0

0

Pa

Qa

Qb

Pb

• Na rynku monopolu pełnego (firma A

jako monopolista; Da – krzywa popytu

rynkowego i popytu firmy A) pojawia się

drugi producent tego samego produktu;

• Monopol maksymalizuje zysk sprzedając

wielkość produkcji Qa po cenie Pa;

• Firma B bierze pod uwagę tę część

popytu rynkowego, która pozostała,

jako różnica popytu rynkowego i

wielkości produkcji, która

maksymalizuje zysk firmy A;

• Firma B maksymalizując swój zysk

będzie produkowała połowę wielkości

produkcji, która pozostała po odjęciu

produkcji firmy A od całego produktu

rynkowego;

Model Cournota

D
a

UKa

Db

UK
b

P

Q

MC=
0

0

Pa

Pb

Qb

Qa

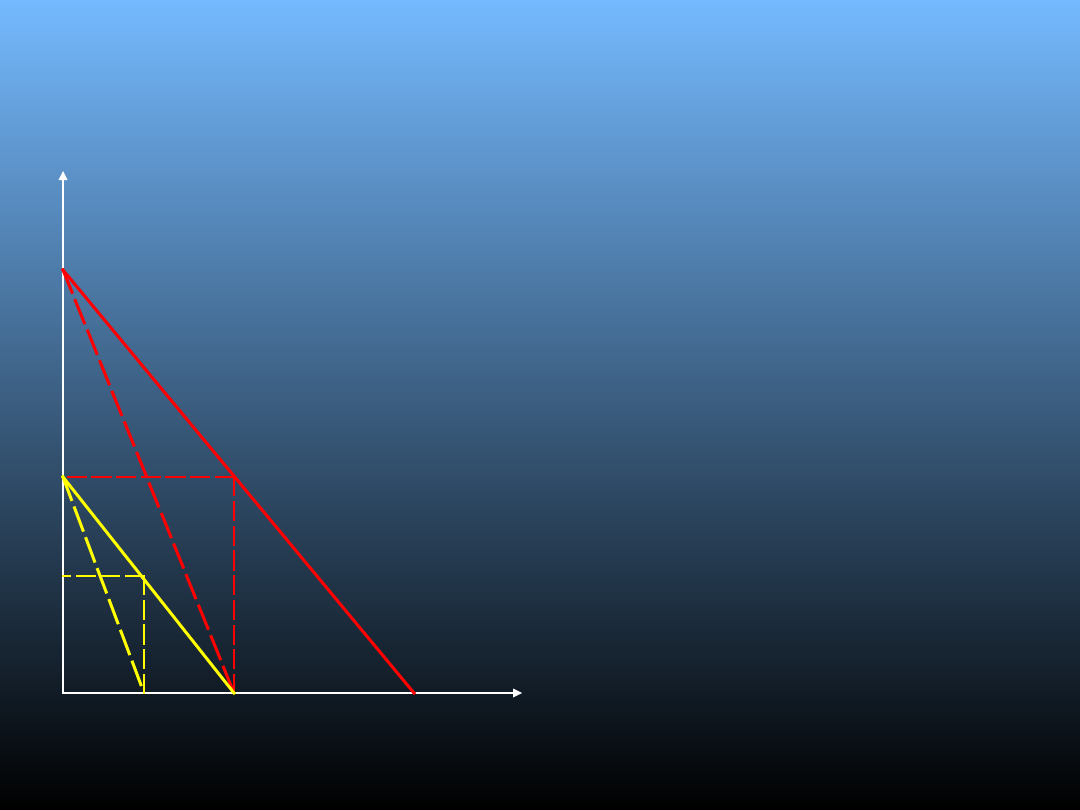
Równowaga Cournota

krzywa reakcji

firmy A;

krzywa reakcji

firmy B;

E – punkt

równowagi
Cournota

Q firmy
A

Q

fi

rm

y

B

E

0

Równowaga Cournota

• Kolejne dostosowania

wielkości produkcji

maksymalizujących zysk

firmy A i B trwają aż do

osiągnięcia równowagi,

tzn. takiego punktu, w

którym żadnej z firm nie

opłaca się zmieniać

osiągniętej wielkości

produkcji;

• Duopol znajduje się w

równowadze wówczas,

gdy Qa= 1/30D oraz Qb=

1/30D.

Q firmy
A

Q

fi

rm

y

B

E

0

Model

Edgewortha

• Założenia
• Opis
• Interpretacja graficzna

Założenia Modelu

Edgewortha

• Cena jest zmienna decyzyjną, a

produkcja wielkością wynikową;

• Produkty firmy są jednorodne;

• Krzywa kosztów krańcowych (MR) pokrywa

się z osią poziomą  MR=0;

• Możliwości produkcyjne przedsiębiorstw

są ograniczone;

• Max wielkość produkcji każdego z

duopolistów jest < od wielkości popytu

jaka wystąpiłaby w przypadku P=0;

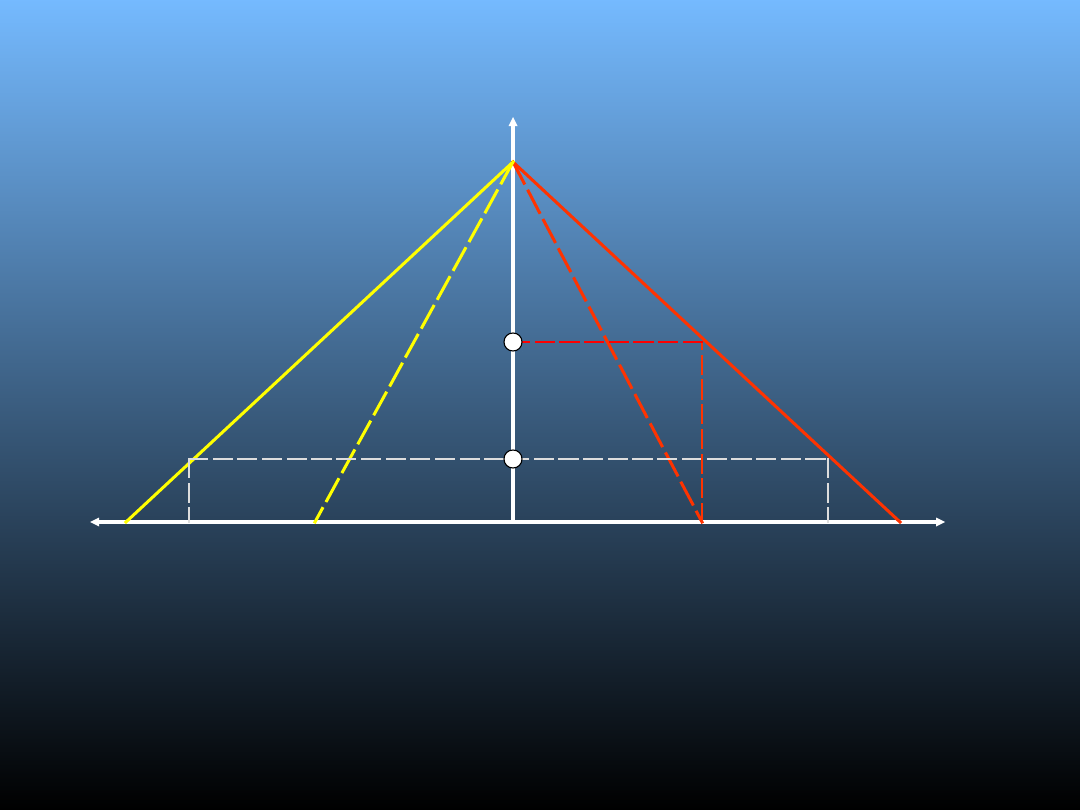
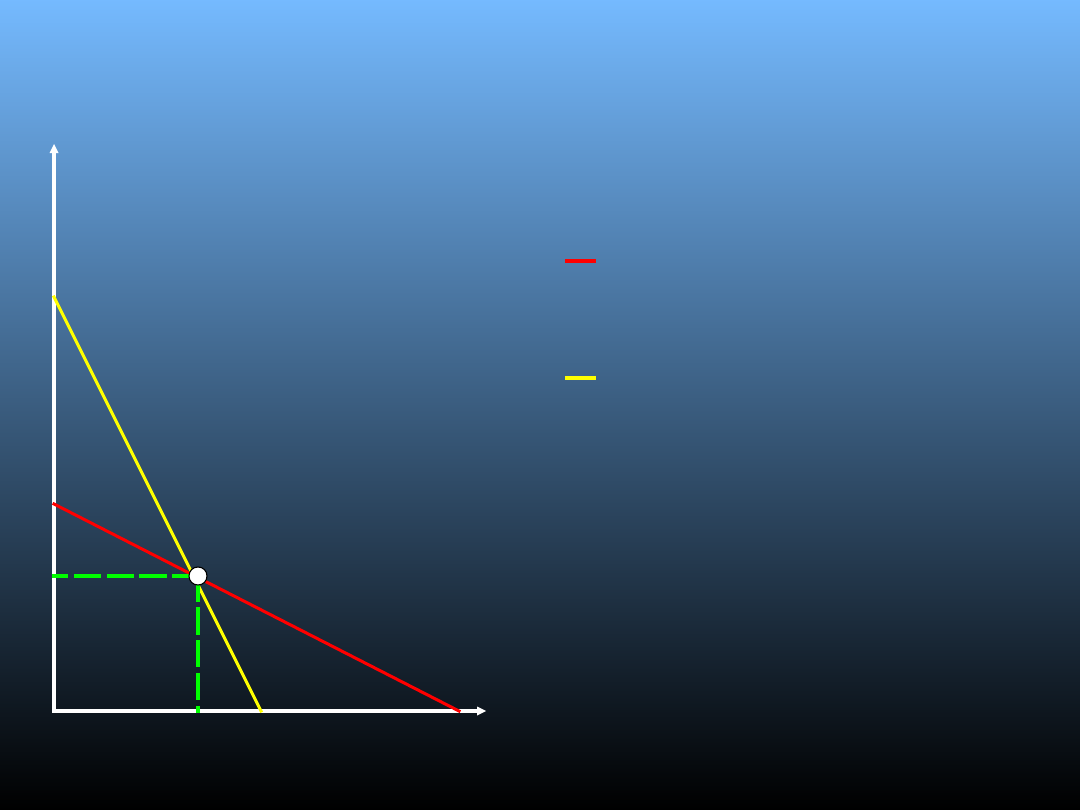
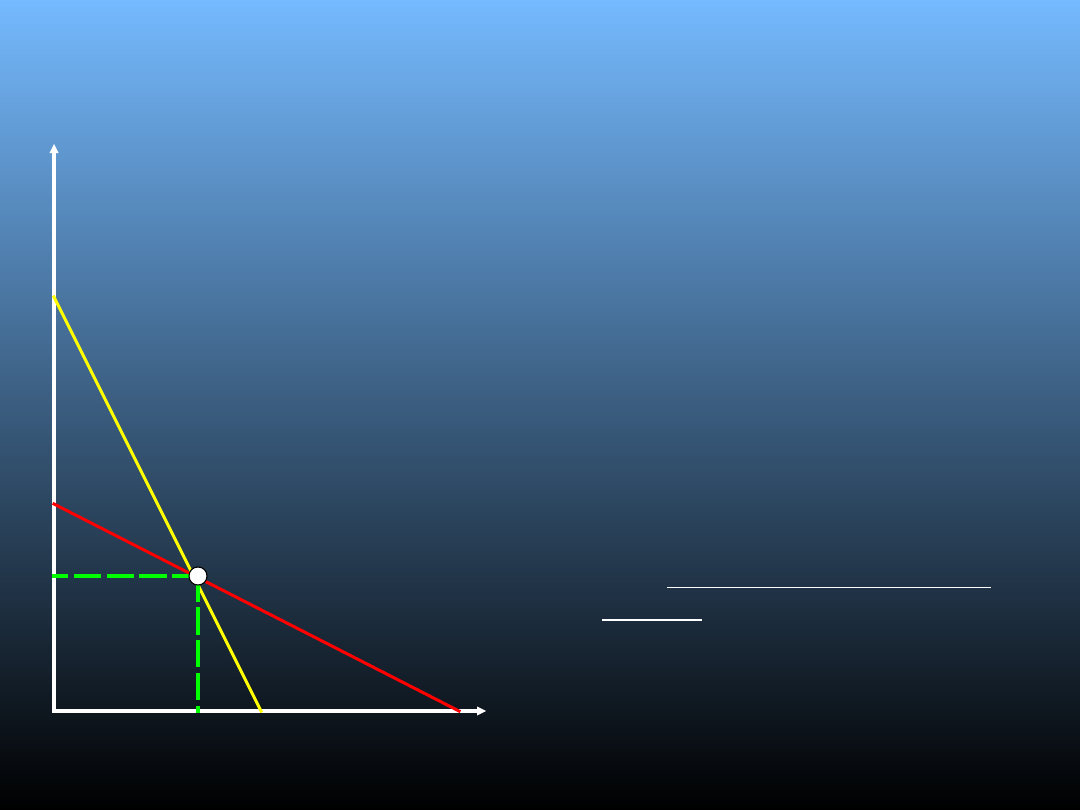
Model Edgewortha

Da

– krzywa popytu firmy A

Db

– krzywa popytu firmy B

UKa

– utarg krańcowy firmy A

UKb

– utarg krańcowy firmy B

Pa

– cena maksymalizująca zysk firmy A

Po

– cena minimalna jaką może ustalić firma

Db

UK
b

Po

P
a

UK
a

Da

0

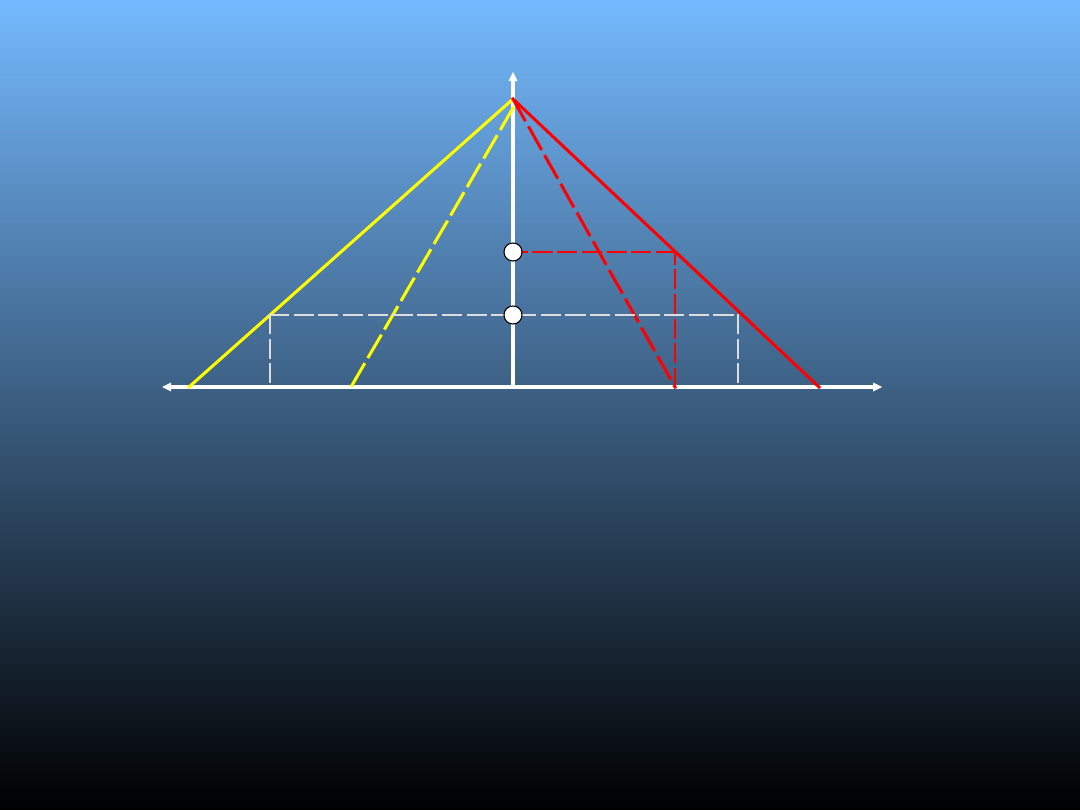
Model Edgewortha

• Producent A początkowo traktowany jako monopolista ustala cenę na poziomie Pa i wielkość produkcji Qa

– max jego zysków;

• Producent B zakłada, że cena producenta A się nie zmieni i ustala cenę poniżej Pa w nadziei, że

przyciągnie część klientów; podobnie postąpi producent A ustalając cenę poniżej, by nie stracić klientów;

• Proces ten trwa do momentu, gdy P = Po, każdy z producentów sprzedając produkty po P = Po dostarcza

max ilość produktów na rynek (nie można zejść poniżej Po ponieważ będzie to przynosiło straty);

• Cena, która max zysk to Pa;
• Dopasowywanie cen zawiera się w przedziale od Po do Pa – tak zmieniać się może cena rynkowa.

Da

Db

UK
a

UK
b

Po

P
a

0

Model

Chamberlina

• Założenia
• Opis
• Interpretacja graficzna

Założenia Chamberlina

• Każdy z duopolistów wyciąga wnioski na

podstawie zdobytych doświadczeń i reaguje
odpowiednio na zmiany decyzji konkurenta;

• Produkt identyczny;
• Koszty produkcji i popyt takie same dla obu

firm;

• Duopoliści dochodzą do wniosku, że

najlepszym rozwiązaniem jest równy
podział zysku monopolowego.

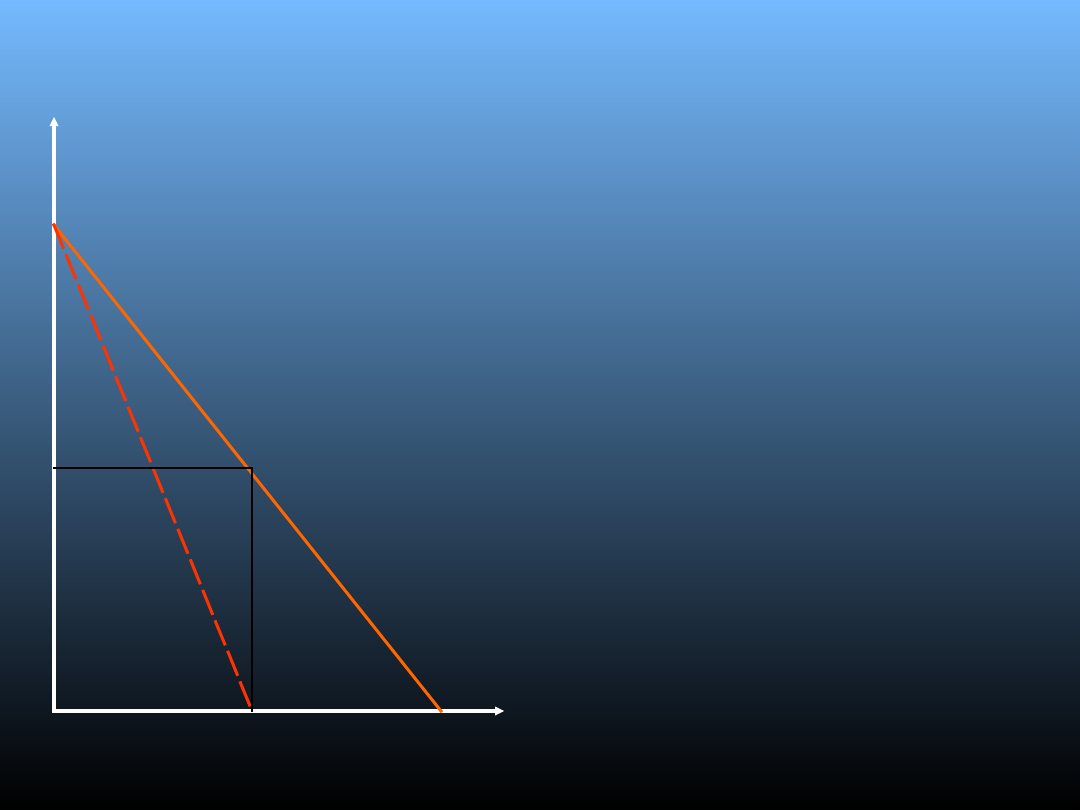
Model Chamberlina

•

Da

– krzywa popytu

firmy A;

•

UKa

– utarg krańcowy

firmy A;

•

Pe

– cena przy której

dana wielkość
produkcji pozwoli
zmaksymalizować zysk;

•

Qe

– wielkość produkcji

maksymalizująca zysk;

UK
a

Da

P
e

Q
e

P

Q

0

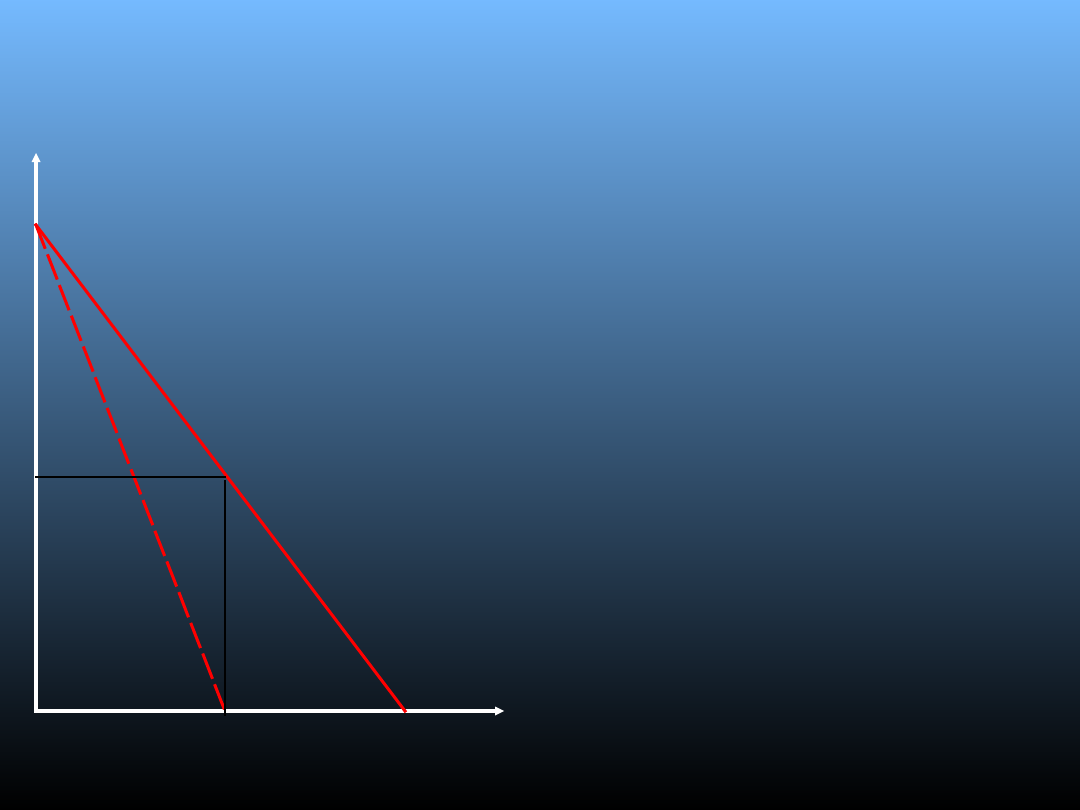
Model Chamberlina

• Każdy ruch cenowy w jednej

firmie wywoła reakcje w

innej – równowaga cenowa;

• Rozwiązanie jest możliwe

gdy firmy mają równą siłę,

produkują po równych

kosztach – zysk można

podzielić na pół;

• Rozwiązanie jest

niekorzystne dla

konsumenta (niższa

produkcja wyższa cena);

• Równowaga na rynku

osiągnięta jest dla Qe i Pe;

• Każdy z duopolistów posiada

taki sam udział rynkowy;

• Sprzedając wielkość Qe/2 po

cenie Pe osiąga zysk

(Qe*Pe)/2.

Da

UK
a

P
e

Q
e

Q

P

0

Model

Stackelberga

• Założenia
• Opis
• Interpretacja geometryczna

Założenia Modelu

Stackelberga

• Występuje przywódca – firma A (ustala

wielkość produkcji przed inna firmą) i

naśladowca – B;

• Naśladowca przyjmuje, że wielkość produkcji,

którą wybierze jest dana;

• Lider przed podjęciem decyzji co do własnej

produkcji chce rozpatrzyć problem max zysku

naśladowcy;

• I lider i naśladowca chcą max swój zysk;
• Decyzja naśladowcy zależy od decyzji lidera;
• KK=0.

Model Stackelberga

krzywa reakcji
firmy B
linie jednakowego
zysku firmy B

Qa – wielkość

produkcji firmy A

Qb – wielkość

produkcji firmy B

Qa

Qb

Model Stackelberga

• Naśladowca przyjmując, że

wielkość produkcji lidera jest

dana, pragnie wybrać taki

wariant produkcji, przy którym

UK=KK (max zysk);

• Za pomocą linii jednakowego

zysku naśladowca tworzy swoją

krzywą reakcji;

• Zysk firmy B (naśladowcy) rośnie

w miarę przesuwania się w lewo

(rośnie produkcja B maleje

produkcja A; B jako monopolista;

A – produkcja zerowa);

• Wzdłuż swojej linii jednakowego

zysku naśladowca wybierze

optymalną dla siebie wielkość

produkcji;

Qa

Qb

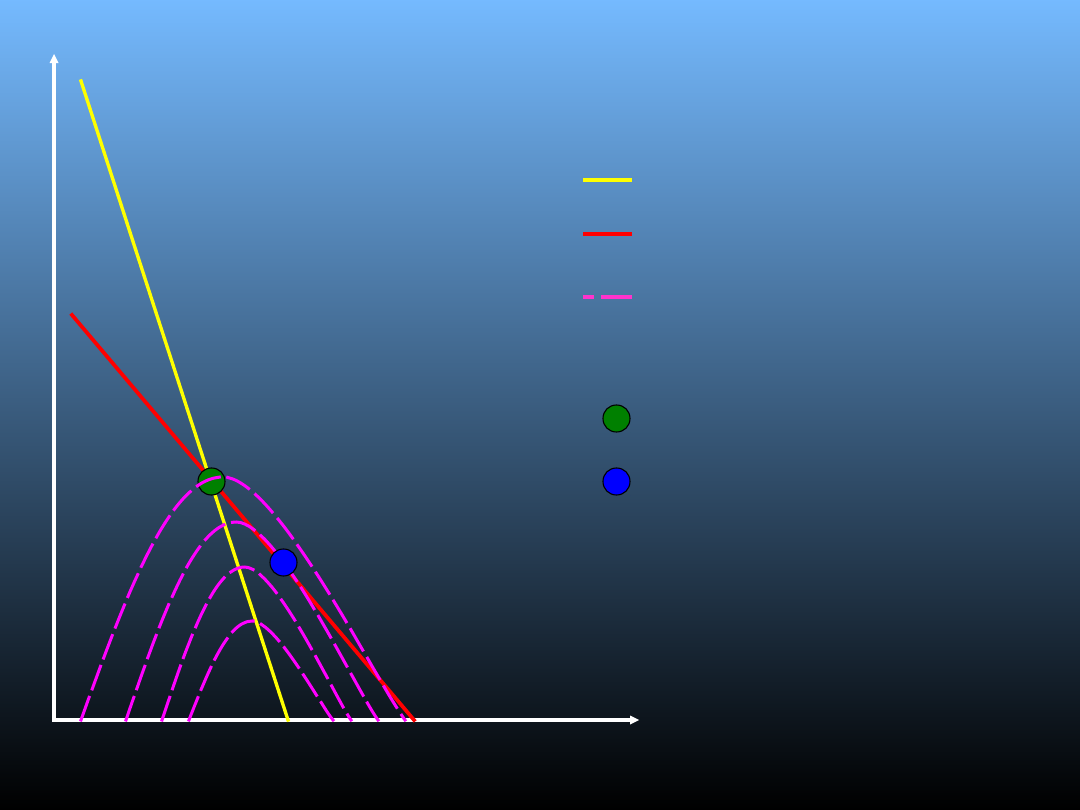
Model Stackelberga

krzywa reakcji firmy A
krzywa reakcji firmy B
linie jednakowego zysku
firmy A
równowaga Cournota
równowaga
Stackelberga

Qa – wielkość produkcji A
Qb – wielkość produkcji B

Qb

Qa

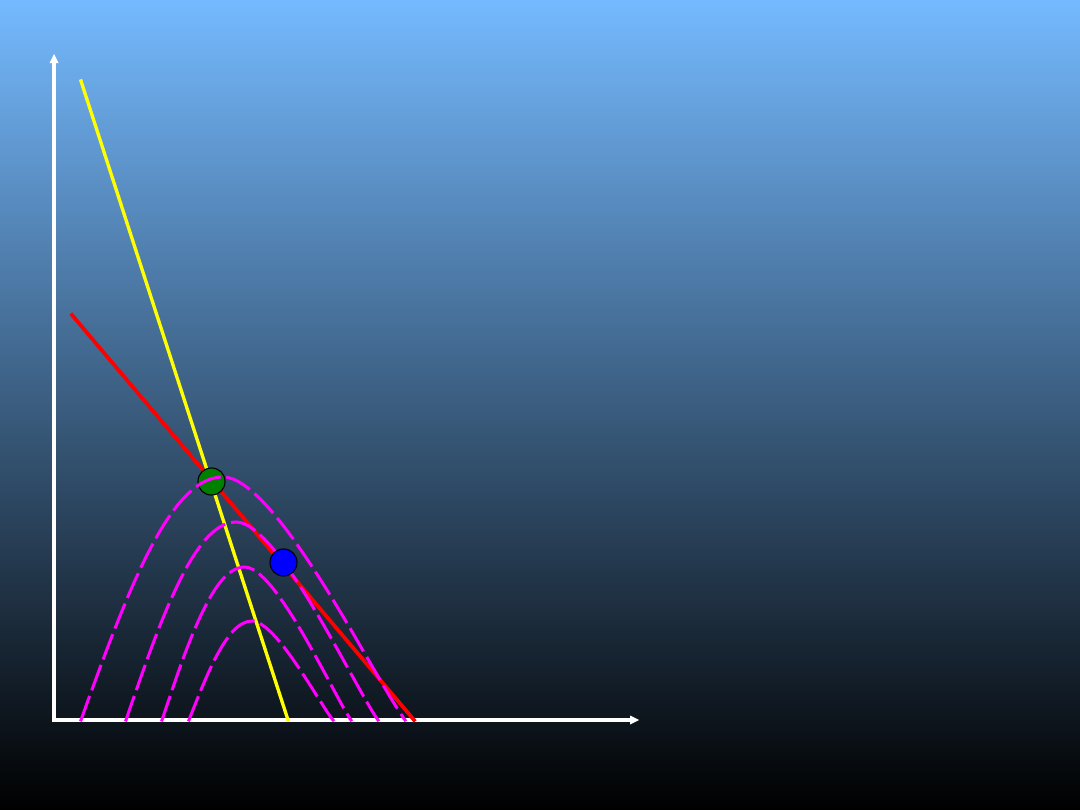
Model Stackelberga

• Lider liczy się z tym, że

jego decyzja wpływa

na decyzję naśladowcy;

• Firma A wybiera taki

punkt na krzywej

reakcji firmy B, który

jest punktem

styczności z jego

najniższą możliwą linią

jednakowego zysku, co

zapewni firmie A

najwyższy możliwy

zysk na liniach

jednakowego zysku

(zysk A wzrasta z

malejącą wielkością

produkcji B).

Qb

Qa

Model

Sweezy’ego

• Założenia
• Opis
• Interpretacja geometryczna

Założenia modelu

Sweezy’ego

• Kiedy jedno przedsiębiorstwo podnosi cenę na swoje

produkty, pozostali producenci nie podnoszą swoich

cen lub robią to w mniejszym stopniu;

• Jeżeli jeden z oligopolistów obniża cenę wówczas

konkurenci także to robią;

• Krzywa popytu na produkty firmy - elastyczna przy

cenach wyższych od wyjściowej (brak reakcji rywali

sprawi, że podwyższając cenę utraci klientów) i

słabo elastyczna przy cenach niższych od

wyjściowej;

• Przyjęcie powyższych założeń odnośnie reakcji

oligopolistów

oznacza,

że

krzywa

popytu

przedsiębiorstwa traci ciągłość (załamuje się).

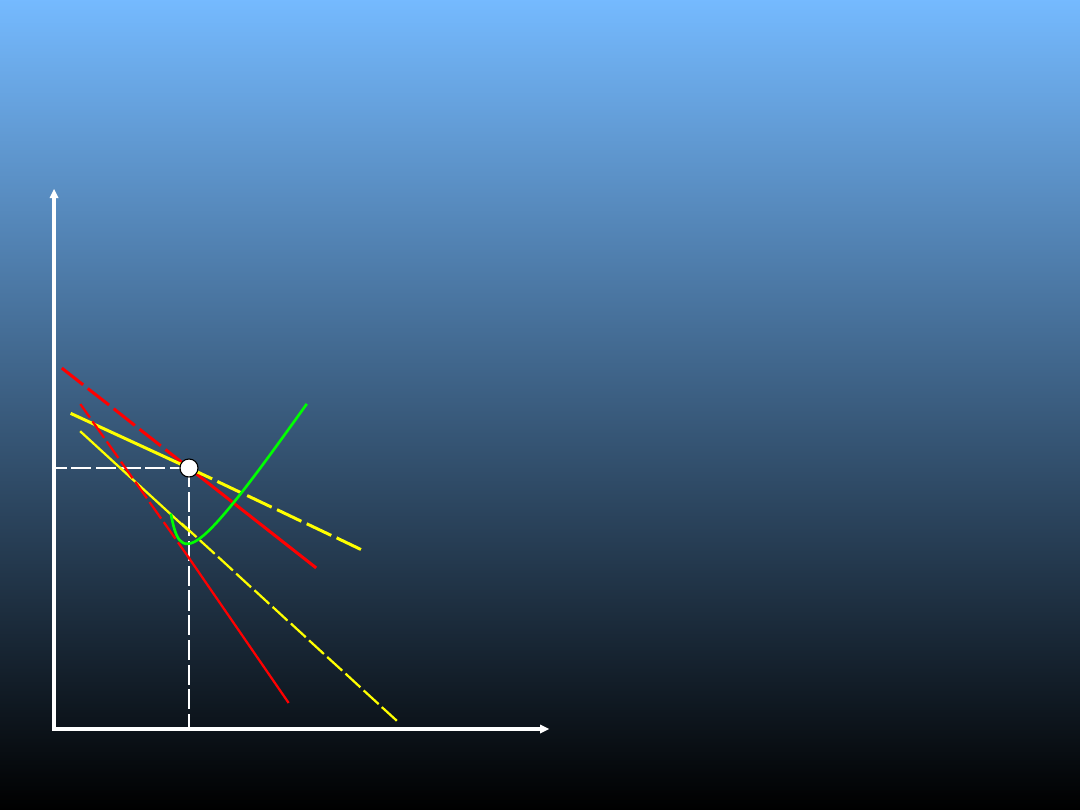
Model Sweezy’ego

• DD

- krzywa relacja – cena; wielkość

sprzedaży kiedy wszystkie

przedsiębiorstwa podnoszą lub

obniżają ceny;

• dd

– popyt na produkty

przedsiębiorstwa wówczas, gdy

przedsiębiorstwo zmienia cenę

swoich produktów, natomiast

konkurenci nie zmieniają cen;

• UKDD

– utarg krańcowy

odpowiadający krzywej DD;

• UKdd

– utarg krańcowy

odpowiadający krzywej dd;

• Qe – wielkość produkcji

maksymalizująca zysk;

• Pe – cena, która pozwoli max zysk.
• E – punkt przecięcia DD i dd;

wyznacza max zysk;

• KK

– koszt krańcowy;

P
e

P

Q

DD

Qe

d
d

 

UKD
D

UKdd

E

KK

0

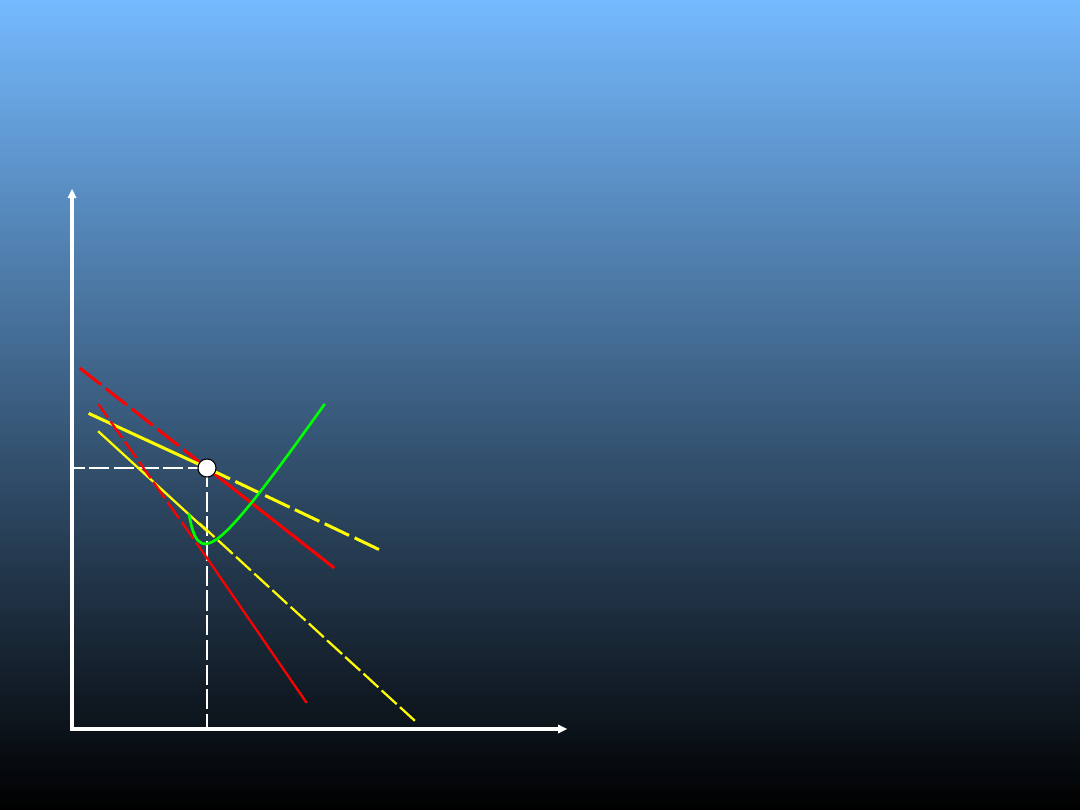
Model Sweezy’ego

• Miejsce przecięcia DD i dd

wyznacza wielkość Qe i Pe
maksymalizującą zysk
(punkt E);

• Jeżeli przedsiębiorstwo

podniesie cenę powyżej Pe
wówczas konkurenci
pozostaną przy
wcześniejszym poziomie cen
(właściwą krzywa na popyt
przedsiębiorstwa w takim
przypadku jest odcinek dE
(odcinek krzywej dd));

• Jeżeli przedsiębiorstwo

obniży cenę poniżej Pe
wówczas konkurenci
również obniżą swoje ceny
(w tym przypadku krzywą
popytu będzie odcinek
krzywej DD, a mianowicie
DE);

P
e

P

Q

D

Q
e

d

 

UKD
D

UKdd

E

KK

d

D

0

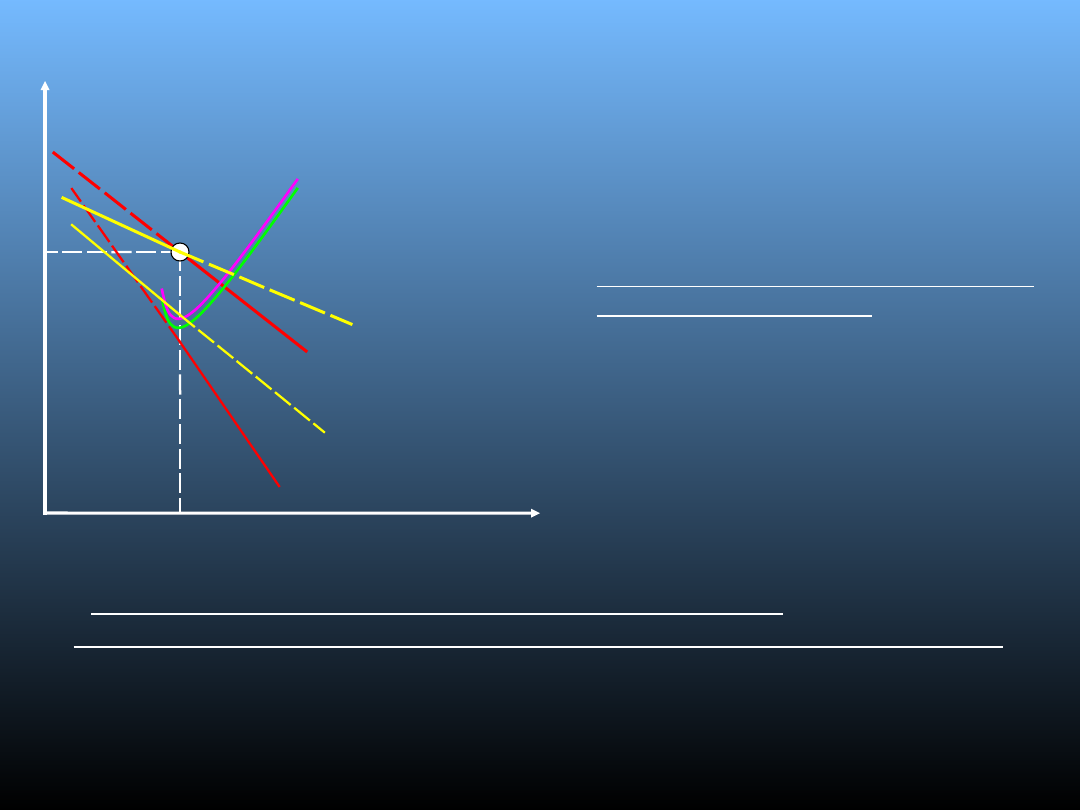
Model Sweezy’ego

• Krzywa popytu

przedsiębiorstwa przybiera

postać załamanej krzywej dED;

• Odcinek dE krzywej popytu jest

bardziej elastyczny niż odcinek

ED ( reakcja konsumentów

przy podwyżce ceny jest

silniejsza niż przy jej obniżce);

• Krzywa przychodu krańcowego

traci swoją ciągłość;

• Załamanie się krzywej popytu i

wynikająca stąd nieciągłość

krzywej UK – cena max zysk

pozostaje stała.

•W granicach nieciągłego odcinka krzywej UK

przedsiębiorstwo nie reaguje na wzrost kosztów krańcowych

(Przypuśćmy, że w sytuacji wyjściowej firma przy kosztach

KM1 max zysk wytwarzając Qe po cenie Pe (KM=UK –

optimum).Kiedy KM wzrosną KM=UK dla wartości Qe i Pe)

P
e

P

Q

D

Q
e

d

 

UKD
D

UKdd

E

KK
1

d

D

KK
2

0

Model

Bertranda

• Założenia
• Opis
• Interpretacja geometryczna

Model Bertranda

• Cena jest zmienną decyzyjną, produkcja to wielkość

wynikowa;

• Produkty są jednorodne;
• Możliwości produkcyjne każdej z firm są na tyle duże, że

jedna firma mogłaby zaspokoić popyt rynkowy;

• Firmy konkurują między sobą cenami;
• Firmy przewidują poziom cen konkurencji i ustalają

własną, która pozwoli im zmaksymalizować zyski;

• Wszystkie firmy na rynku oligopolu maja takie same

koszty, przy czym KK(Koszt Krańcowy) = Kosztowi

Przeciętnemu; gdyby Koszty Krańcowe jakiegoś

przedsiębiorstwa były niższe od innych, to w takiej

sytuacji dana firma wyeliminowałaby wszystkich

konkurentów z rynku.

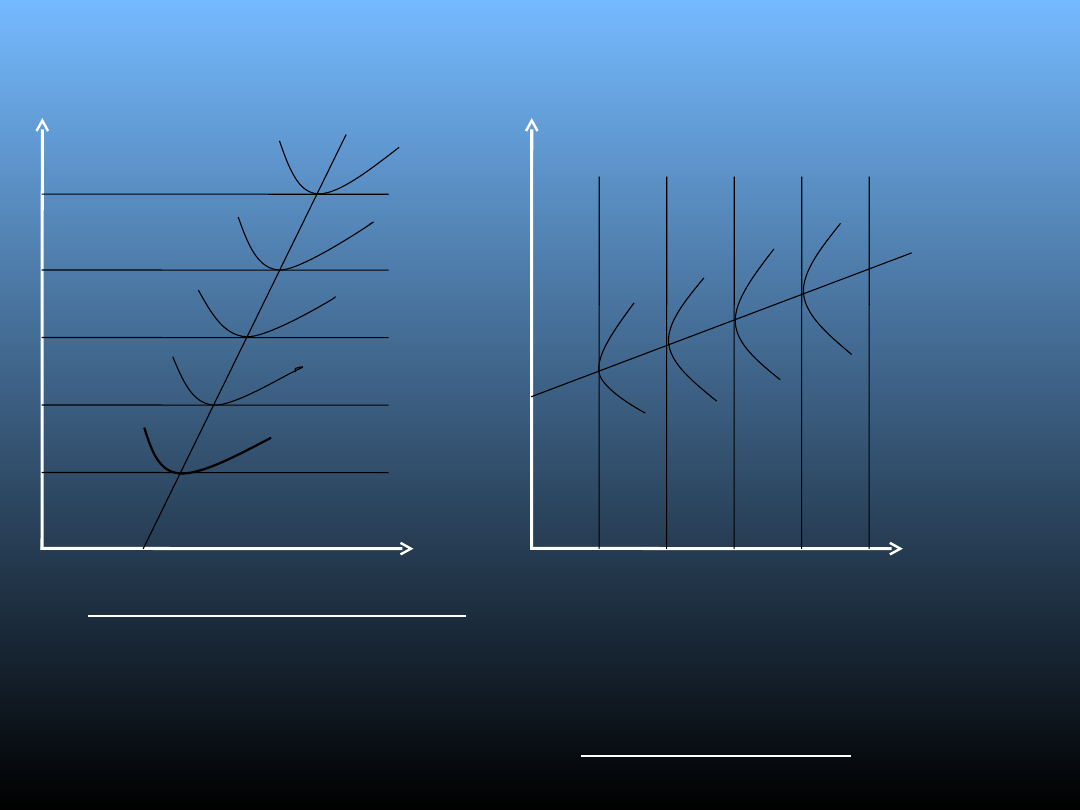
Model Bertranda

• Krzywe jednakowego zysku dla firm tworzą punkty, w których

osiąga ona jednakowy zysk, przy różnych cenach wyznaczanych

przez przedsiębiorstwa. Kształt krzywych świadczy o tym, że firma

obniża cenę do pewnego poziomu w odpowiedzi na obniżki cen

wprowadzane przez konkurencję. Połączenie punktów minimum

krzywych jednakowego zysku tworzy krzywą reakcji firmy.

FIRMA A

FIRMA B

P

b

P

b

P

a

P

a

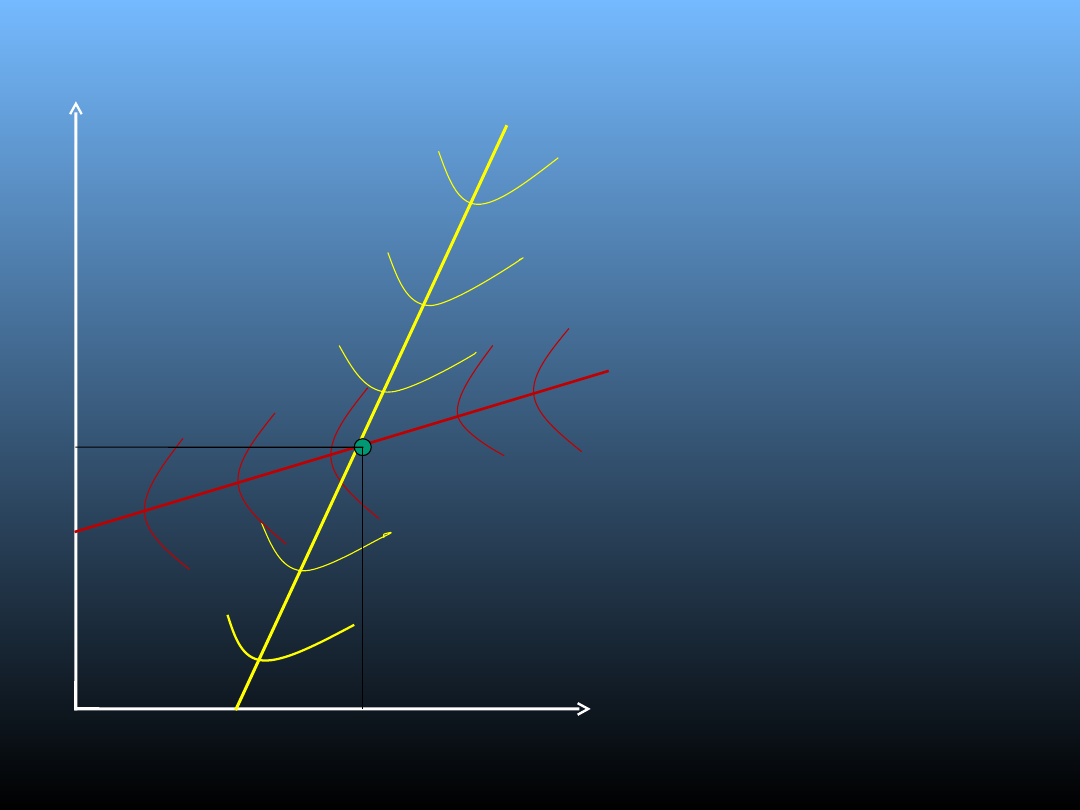
Model Bertranda

• E – punkt

równowagi;

• - krzywa

reakcji firmy A;

• - krzywa

reakcji firmy B;

E

P

b

P

a

KR

A

KR

B

KR

A

KR

B

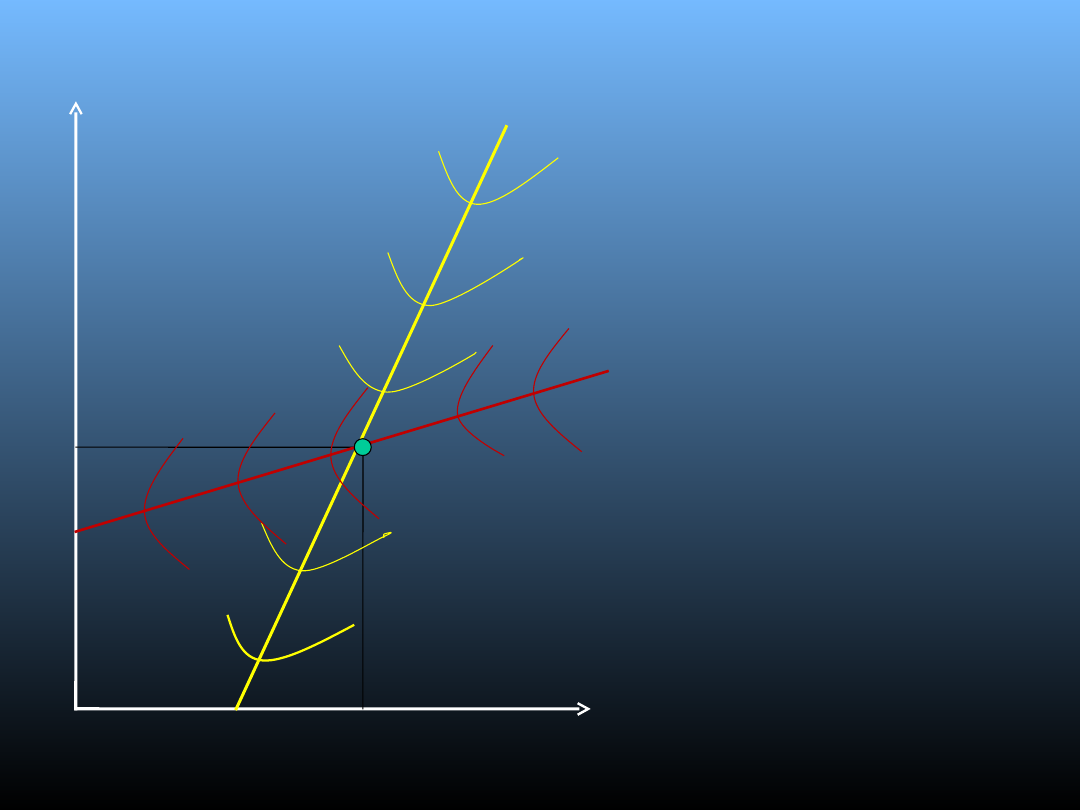
Model Bertranda

●

Równowaga w modelu

Bertranda osiągnięta jest w
punkcie przecięcia się
krzywych reakcji firmy A i
firmy B.

Jeżeli przedsiębiorstwa

sprzedają jednakowy
produkt, to wówczas jedna z
firm, na przykład firma A,
ustalając cenę na poziomie
niewiele niższym niż firma B,
jest w stanie przejąć
praktycznie cały rynek.
Przedsiębiorstwo B zareaguje
jednak na działania firmy A, i
również obniży swoją cenę.
Proces dostosowywania cen
będzie trwał tak długo, aż
dojdzie do osiągnięcia punktu
E.

KR

A

KR

B

P

b

P

a

E

Model

Sylos’a –

Labinieg’o

• Założenia
• Opis
• Interpretacja geometryczna

Założenia modelu

Sylos’a - Labinieg’o

• Przedsiębiorstwa konkurują z potencjalnymi

rywalami, a także między sobą;

• Produkt jest jednorodny, popyt jest dany;
• W branży działają przedsiębiorstwa różnej wielkości:

małe, średnie i duże. Im większe przedsiębiorstwa,
tym Koszt Całkowity Przeciętny jest niższy;

• Przedsiębiorstwo, które produkuje po najniższym

KCP może objąć przywództwo cenowe i ustalić taką
cenę, która chroni wejście do branży. Mniejsze
przedsiębiorstwa akceptują cenę wyznaczoną przez
lidera – same nie mogą jej ustalić. Mogą jednak
wspólnie oddziaływać na lidera, określając wielkość

swojej produkcji. Lider może ustalać tylko taką cenę,

która jest akceptowana przez pozostałe przedsiębiorstwa;

●

Lider zna popyt, koszt przeciętny wszystkich

przedsiębiorstw oraz ich możliwości produkcyjne.
Przyjmuje on, że do branży mogą wejść tylko te
przedsiębiorstwa, które rozpoczną produkcje w
najmniejszym zakresie (KCP będzie najwyższy).
Atrakcyjność wejścia na rynek zależy od tego, jakie są
możliwości zrealizowania nadwyżki ponad KCP;

●

Przedsiębiorstwa działające na rynku oczekują, że

potencjalni konkurenci nie wejdą na rynek, jeśli ich
wejście obniży cenę poniżej ich długookresowego kosztu
przeciętnego. Potencjalni konkurenci oczekują, że po ich
wejściu ogólna podaż branży wzrośnie (przedsiębiorstwa
już tam działające będą produkować tę samą ilość
towaru). Zatem po wejściu na rynek nowych
przedsiębiorstw cena równowagi rynkowej się obniży.

Model Sylos’a – Labinieg’o

1) STRATEGIA NIEDOPUSZCZANIA

NOWYCH FIRM

Polega ona na ustaleniu ceny blokującej wejście

na rynek na takim poziomie P

x,

aby:

- małe i średnie przedsiębiorstwa realizowały co

najmniej normalny zysk, ponieważ wówczas
zaakceptują cenę P

x

- podaż Q

x

była ustalona odpowiednio do ceny P

x

,

a zatem cenę tę akceptują również nabywcy,

- po wejściu nowego konkurenta cena obniżyła się

do poziomu równowagi, niezapewniającego zysku
normalnego najmniejszym przedsiębiorstwom,
wśród których znajdzie się nowa firma.

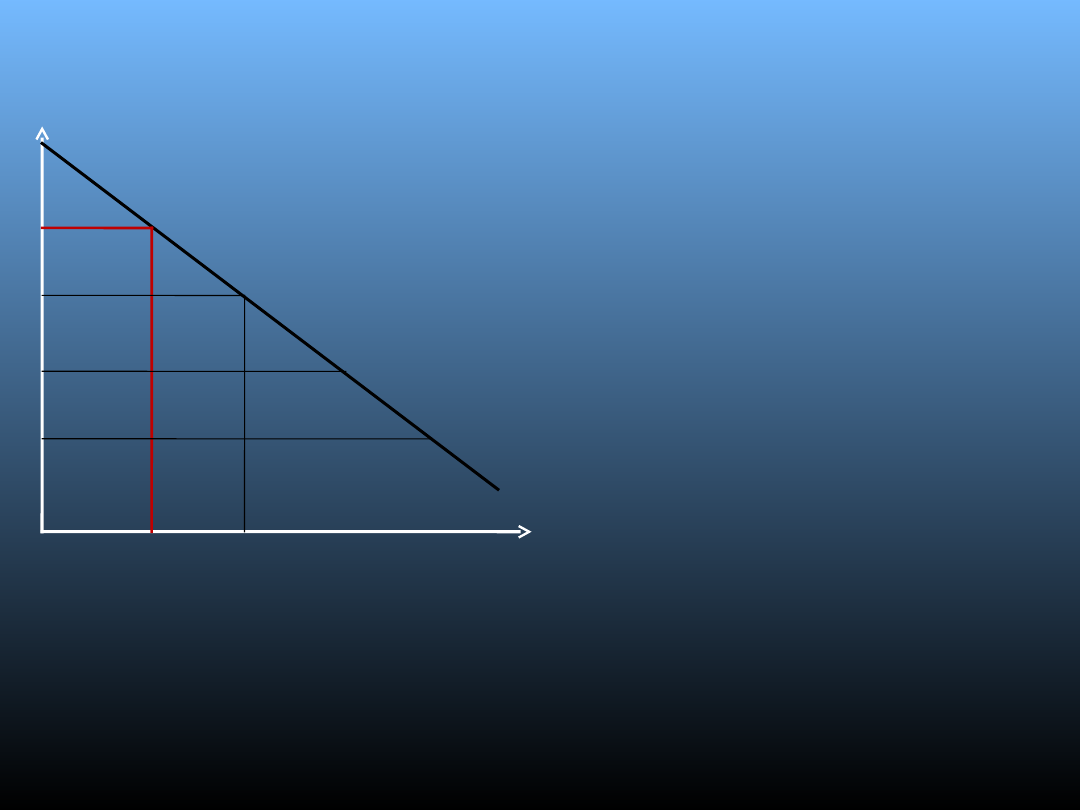
Model Sylos’a – Labinieg’o

• D – linia popytu stała i znana

liderowi (z założenia modelu);

• Jeżeli lider ustali cenę na

poziomie Px, wówczas wejście do
branży jest zablokowane;

• Potencjalni konkurenci, którzy

będą produkować po KCPm i
dostarczą ilość Qe - Qx,
spowodują spadek ceny do
poziomu P3, który nie zapewni im
zysku normalnego;

• CENA NIEDOPUSZCZALNA to

cena na poziomie P3;

●

Blokowanie wejścia na rynek jest osiągane za pomocą ceny

Px, która zapewnia podaż Qx, przy których wszystkie
przedsiębiorstwa realizują zyski większe niż normalne
(strategia niedopuszczenia zakłada istnienie małych i średnich
firm).

Q

Qx

P

x

P

3

P

2

P

1

KCP

d

KCP

s

KCP

m

D

P

Qe

Model Sylos’a – Labinieg’o

2) BLOKOWANIE WEJŚCIA NA RYNEK

●

Występuje ono przy podaży < Qx. Lider może zatem

rozważać wyeliminowanie pewnych małych lub
średnich przedsiębiorstw i przejęcie ich popytu. Aby to
uczynić musiałby narzucić cenę eliminującą, czyli taką,
która nie pokryłaby kosztu stałego w długim okresie.

●

Lider nadal otrzymywałby zysk większy od

normalnego, ponieważ cena ta znajdowałaby się
powyżej ceny Px. Utraci on jednak część zysku, który
ma zapewniony przy cenie Px. Suma utraconych
zysków w czasie, jaki niezbędny jest do
wyeliminowania małych lub średnich firm musi być <
od korzyści, które płyną z odstraszenia potencjalnych
konkurentów.