PODSTAWOWE MODELE 
DUOPOLU I OLIGOPOLU

Prof. ZUT, dr hab. Grażyna Karmowska
Opracowanie na podstawie Ekonomia matematyczna T. Tarnawski, PWE 2011

1

MODELE KONKURENCJI ILOŚCIOWEJ



Modele Cournota i Staclekberga.



Zakładają, że producenci wytwarzają takie 
same dobro lub usługę.



Muszą ustalić taka samą cenę.



Konkurują miedzy sobą wielkościami 
produkcji.

2

MODEL KONKURENCJI CENOWEJ



Model Bertranda.



Wytwarzają produkty będące bliskimi 
substytutami.



Ceny nie muszą być sobie równe



Konkurują między sobą cenami

3

MODEL DUOPOLU COURNOTA



Funkcjonuje 2 producentów o funkcjach 
kosztów:

stały

koszt 

  

krańcowy)

(koszt 

 

przeciętny

koszt 

  

produkcji

 

 wielkość

    

0

0

0

)

(

2

,

1















i

i

i

i

i

i

i

i

f

c

y

f

y

c

y

tc

i

4

MODEL DUOPOLU COURNOTA



Popyt zgłaszany przez konsumentów 
duopolu:

















0;

p

p

 

cenę

 

na

popytu 

 

ść

  wrażliwo

Carnota

duopolu 

 

pojemność

  











0

,

)

(

0

p

p

y

y

d

d

5

MODEL DUOPOLU COURNOTA



Produkcja obu 

producentów dopasowuje 
się do popytu przy cenie p.



Odwrotna funkcja popytu

)

(

)

,

(

1

;

)

,

(

)

(

2

1

2

1

2

1

2

1

2

1

2

1

y

y

b

a

y

y

p

b

a

y

y

y

y

p

p

y

y

p

y

y

y

d











































   

6

MODEL DUOPOLU COURNOTA



Producenci szukają wielkości produkcji 
maksymalizującej zysk, przy danej wielkości 
drugiego producenta:

 

 

const

y

y

const

y

y









1

2

2

1

2

0

1

0

max

max





7

)

(

)

,

(

)

,

(

)

,

(

)

(

1

1

1

2

1

2

1

1

1

2

1

1

1

1

1

y

tc

y

y

y

p

y

y

y

y

y

p

y

tc

py

















  

producenta

 

1.

 

utarg

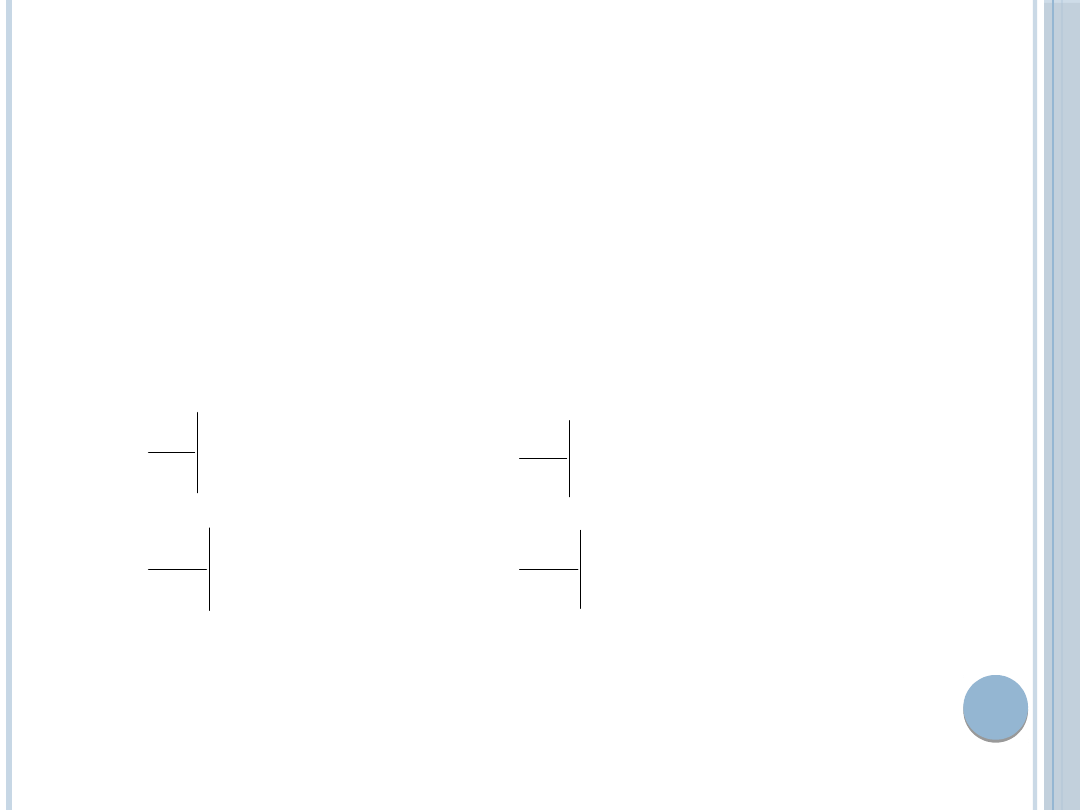
MODEL DUOPOLU COURNOTA



Funkcje zysku



Warunki istnienia ekstremum

8

2

2

1

2

2

2

2

1

2

2

1

2

1

2

1

1

1

2

1

1

)

(

)

,

(

)

(

)

,

(

f

y

by

by

y

c

a

y

y

f

y

by

by

y

c

a

y

y

























0

0

.

2

1

1

2

.

1

1

2

2

















const

y

const

y

y

y





0

0

.

2

2

2

2

.

2

2

1

1

















const

y

const

y

y

y





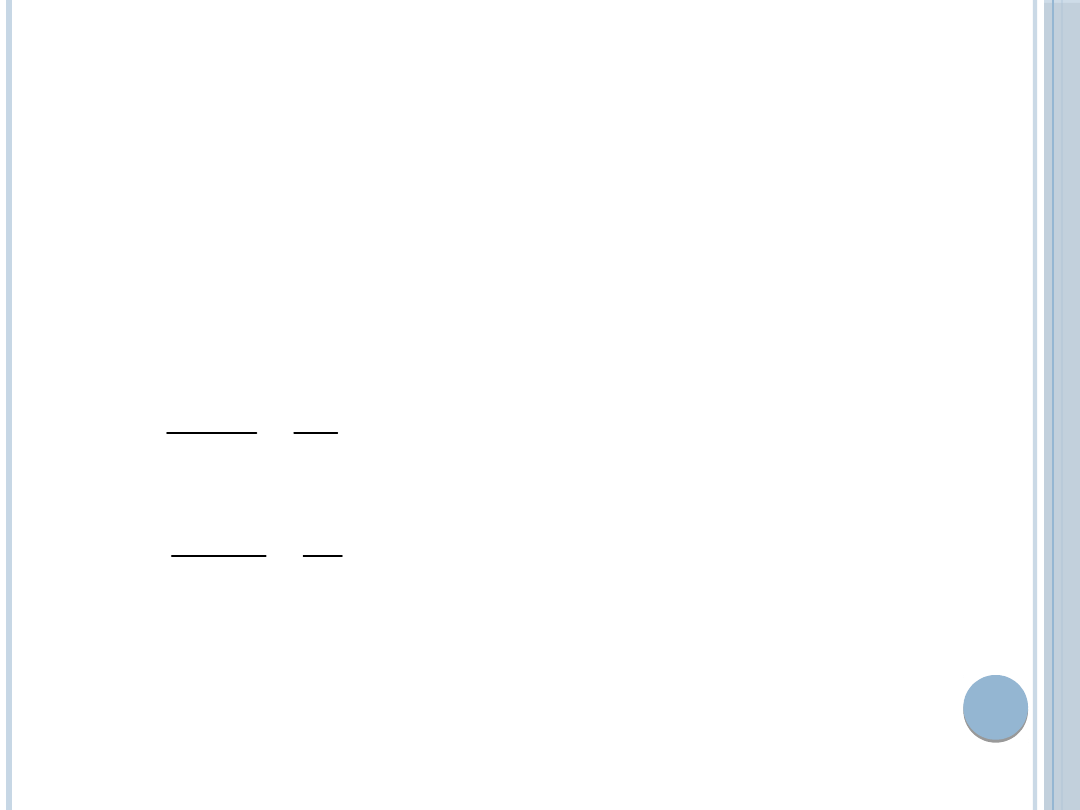
MODEL DUOPOLU COURNOTA



Warunek konieczny ma postać:



Wyznaczają taka wielkość produkcji 
producenta, która przy ustalonej produkcji 
drugiego producenta maksymalizuje jego 
zysk.

9

2

2

2

2

0

2

1

2

2

2

1

1

2

1

1

y

b

c

a

y

y

b

c

a

y

by

by

c

a





















i

RL

 

producenta

 

reakcji

 

linie

 

stąd

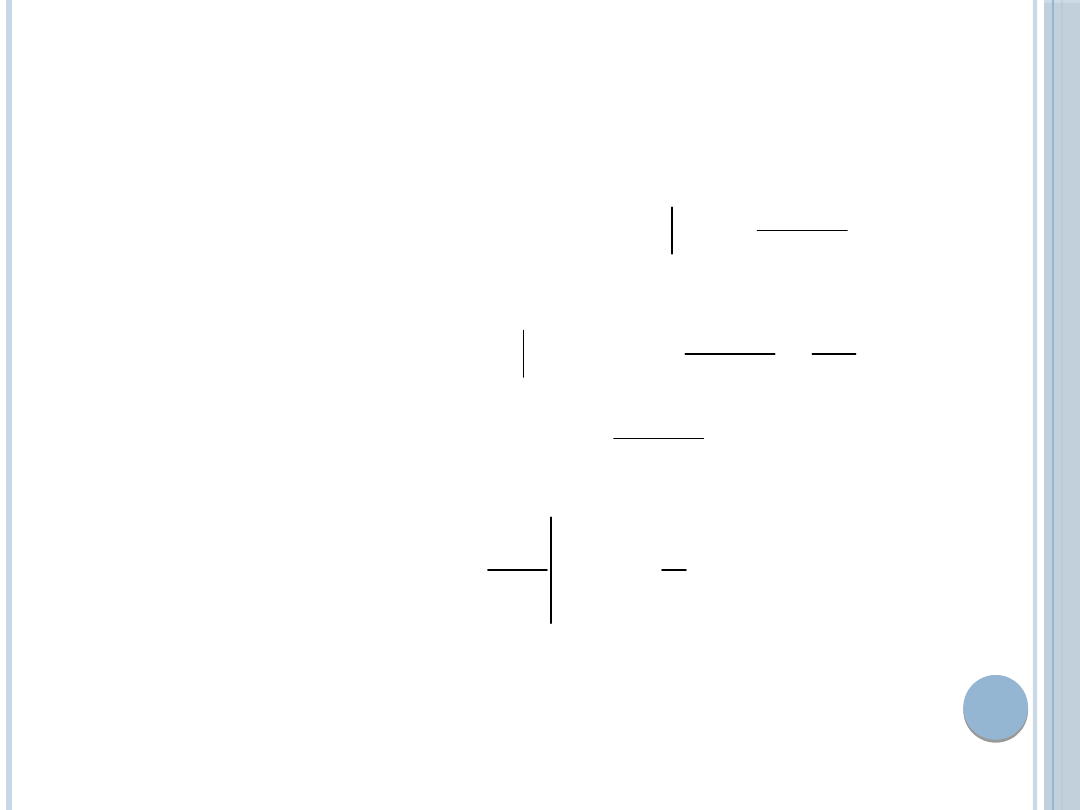
Z LINII REAKCJI WYNIKA, ŻE:



Wielkość produkcji

gdy na rynku jest tylko
jeden producent



Jeśli producent drugi

podnosi swą wielkość 
produkcji o jednostkę, to
producent pierwszy musi obniżyć produkcję o 

0,5jedn.

10

2

1

0

2

2

0

2

0

1

1

1

2

1

1

2

2

1

1

1

1

2































RL

RL

RL

dy

dy

b

c

a

y

y

b

c

a

y

b

c

a

y

y

PUNKT RÓWNOWAGI DUOPOLU 
COURNOTA



punkt przecięcia linii reakcji obu 
producentów.

11

3

)

2

(

3

2

3

)

2

(

3

2

2

2

1

2

1

2

2

2

1

2

1

1

2

2

1

1

2

1

c

c

b

c

c

a

y

c

c

b

c

c

a

y

b

c

a

y

y

b

c

a

y

y

C

C























































:

optymalne

 

wartości

DUOPOL COURNOTA – DUOPOL 
RÓWNORZĘDNYCH PARTNERÓW



Zmiana pojemności rynku oddziałuje na 
podaż każdego z producentów w duopolu w 
takim samym stopniu: jeśli pojemność rynku 
rośnie o jednostkę, to zarówno podaż 
producenta pierwszego jak i drugiego rosną o 
1/3 jedn.

12

3

1

;

3

1

2

1

















C

C

y

y

     



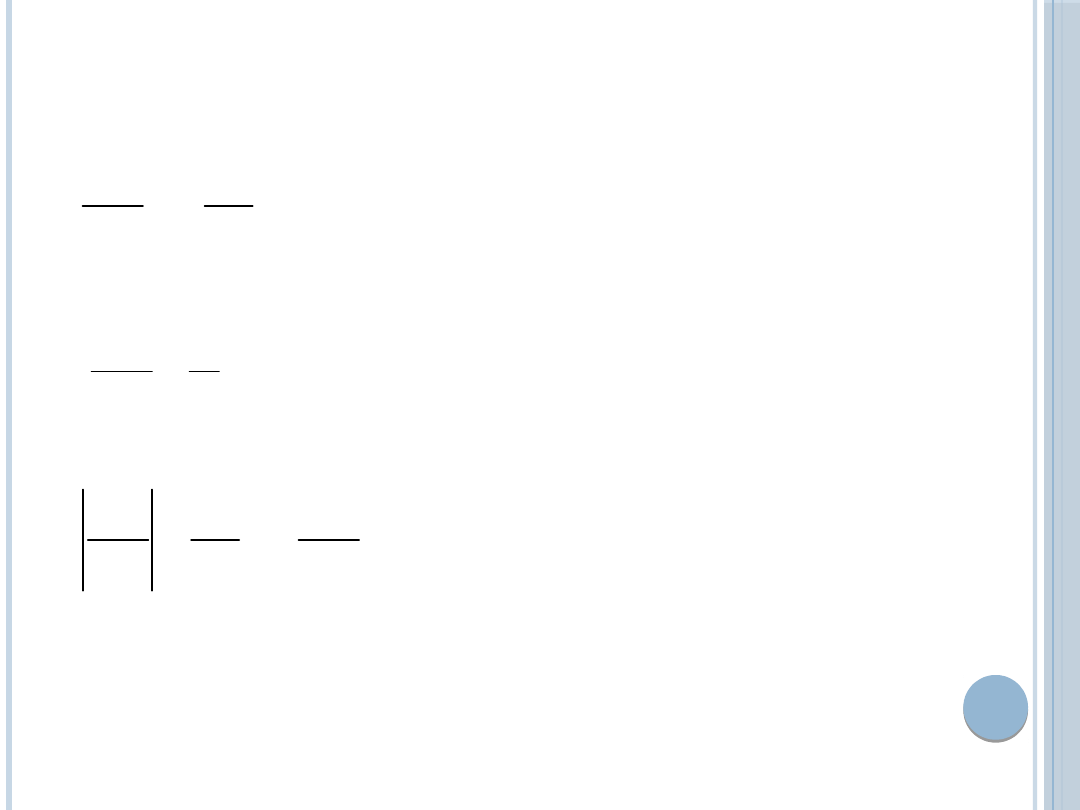
Wzrost kosztów krańcowych 
pierwszego producenta 
prowadzi do spadku jego 
podaży



Wzrostowi kosztów 
krańcowych drugiego 
producenta, towarzyszy 
wzrost podaży pierwszego 
producenta.



Koszty krańcowe pierwszego 
producenta dwa razy silniej 
oddziałują na jego podaż od 
kosztów krańcowych jego 
konkurenta

13

2

1

1

1

2

1

1

1

2

3

2

0

3

;

0

3

2

c

y

c

y

c

y

c

y

C

C

C

C





































 

  

CENA W WARUNKACH RÓWNOWAGI:



zależy od tych samych czynników, które 
determinują podaż każdego z producentów 
duopolu:

14





















3

)

(

)

(

3

2

)

,

(

2

1

2

1

2

1

c

c

p

c

y

y

y

y

y

y

p

p

C

C

C

C

C

C

C

C























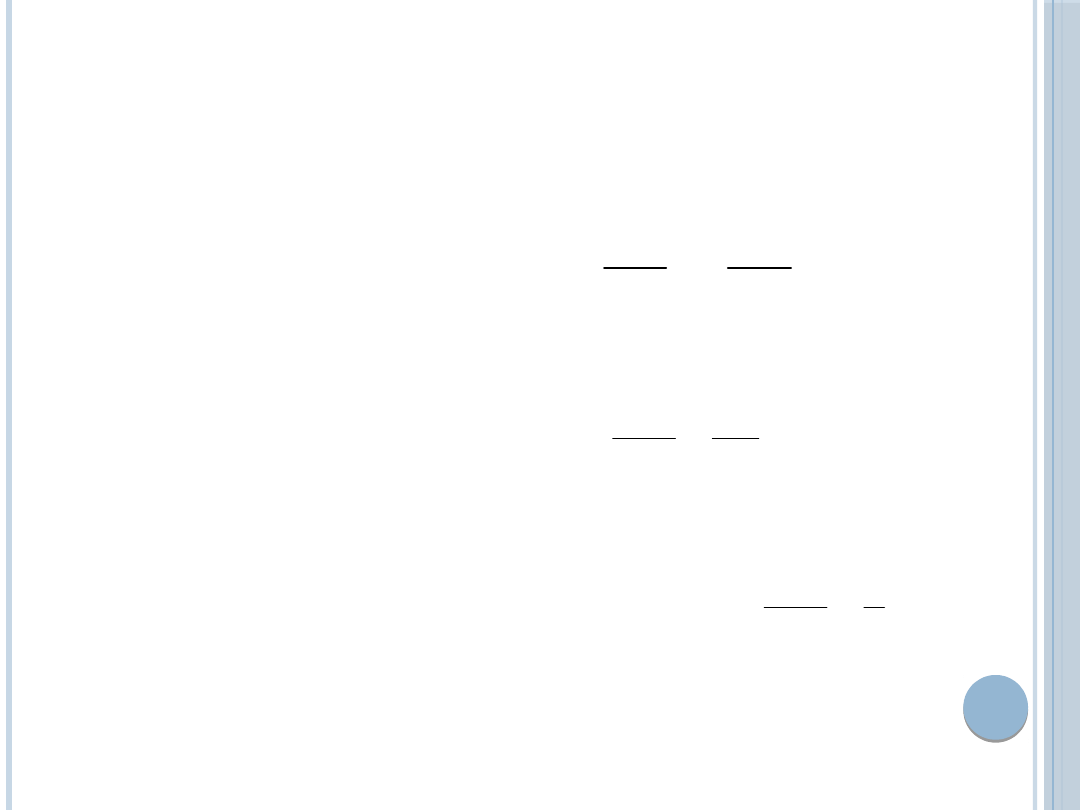
W RÓWNOWADZE DUOPOLU 
COUROTA



Im silniej konsumenci

reagują na zmianę ceny
tym niższa jest cena którą
ustalą producenci.



Wzrostowi pojemności

 rynku towarzyszy wzrost 
ceny.



Wzrost kosztów krańcowych 

pierwszego producenta o 1.
przekłada się na wzrost ceny o 1/3

15

3

1

2

,

1

0

3

1

;

0

3

2





























i

C

C

C

c

p

i

p

p

      

 

  











DUOPOL STACKELBERGA



Założenia podobne jak w modelu Cournota.



Różnica: nie ma równorzędnych partnerów:

•

Lider

•

Naśladowca

16

 

 

const

y

y

y







1

2

1

2

0

1

0

max

max





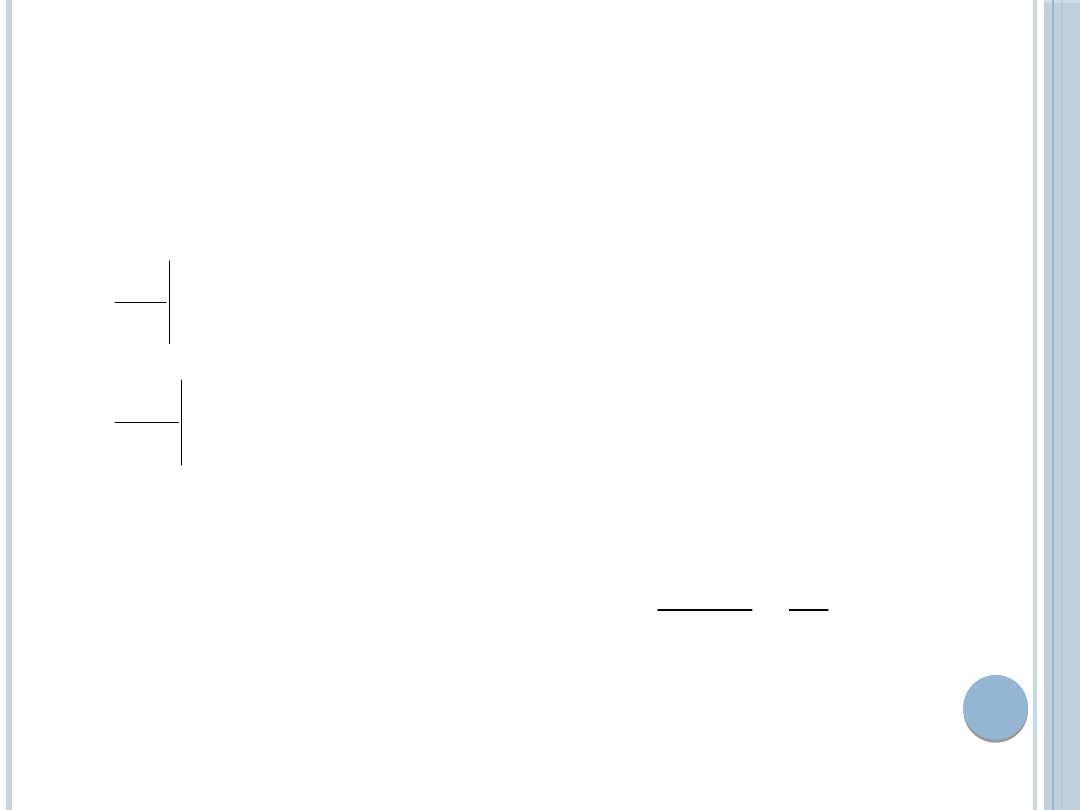
ODWROTNA FUNKCJA POPYTU



Utarg naśladowcy



Naśladowca maksymalizuje swoją funkcję 
zysku względem wielkości produkcji przy 
stałej produkcji lidera.

17

)

(

)

,

(

2

1

2

1

2

1

y

y

b

a

y

y

y

y

p



















2

2

2

2

1

2

2

2

1

2

2

2

2

1

2

2

1

2

2

2

1

2

2

1

2

1

2

)

(

)

,

(

)

(

)

,

(

)

,

(

)]

(

[

)

,

(

)

,

(

f

by

y

by

y

c

a

y

y

y

tc

y

y

r

y

y

y

y

y

b

a

y

y

y

p

y

y

r





























  

WARUNKI ISTNIENIA MAKSIMUM 
FUNKCJI



Warunek konieczny i dostateczny:



Linia reakcji naśladowcy:

18

0

2

0

2

.

2

2

2

2

2

1

2

.

2

2

1

1





























b

y

by

by

c

a

y

const

y

const

y





2

2

)

(

:

1

2

1

2

2

y

b

c

a

y

y

RL







UTARG LIDERA



Utarg lidera

Z uwzględnieniem linii reakcji naśladowcy:



Zysk lidera

19

1

2

1

1

2

1

2

1

1

)]

(

[

)

,

(

)

,

(

y

y

y

b

a

y

y

y

p

y

y

r











1

2

1

1

1

2

1

1

1

1

1

1

1

1

1

1

2

2

2

)

(

)

(

)

(

)

(

f

y

b

y

c

c

a

y

y

tc

y

r

y

tc

py



































2

1

1

2

1

1

2

2

)

(

y

b

y

c

a

y

r







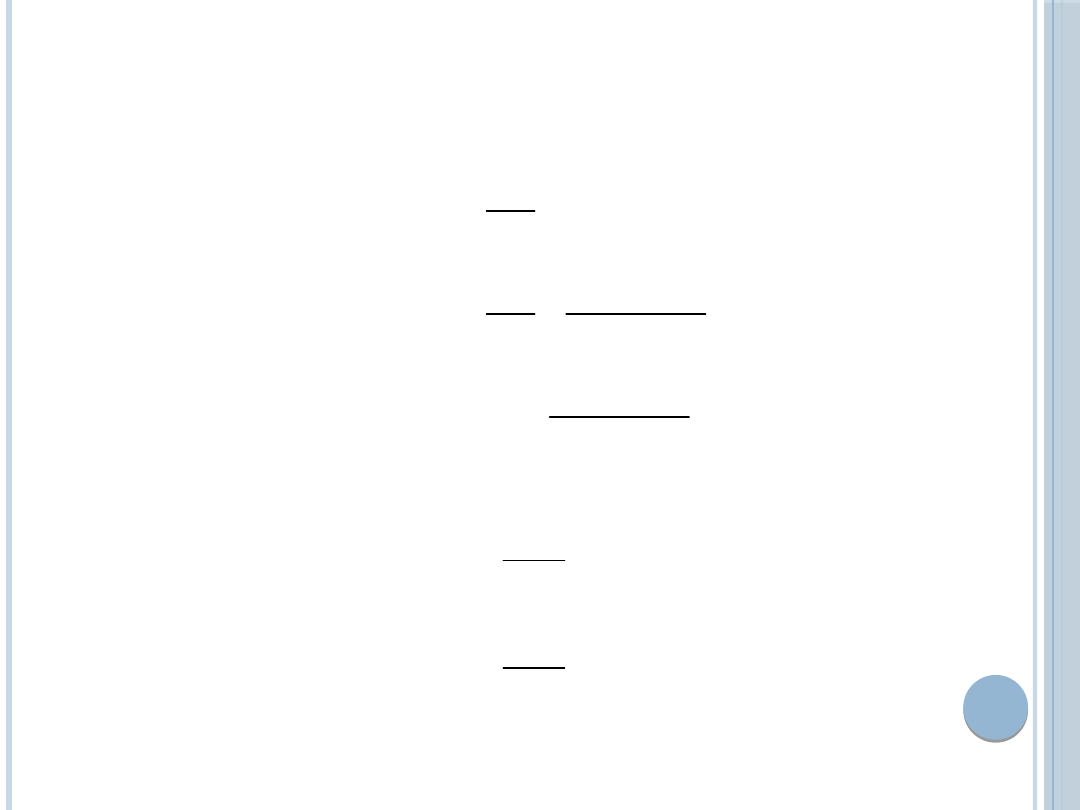
EKSTREMUM LIDERA



Warunek konieczny:



Warunek dostateczny:

20

b

c

c

a

y

by

c

c

a

dy

d

dy

d

S

2

2

0

2

2

0

1

2

1

1

1

2

1

1

1

1























0

0

2

1

1

2

2

1

1

2









b

dy

d

dy

d





EKSTREMUM WIELKOŚCI PRODUKCJI 
LIDERA



Podaż lidera zależy od analogicznych 
czynników jak w modelu Cournota:



Pojemność rynku,



Wrażliwość popytu konsumentów na 
zmianę ceny,



Koszty krańcowe lidera i naśladowcy

21

2

)

2

(

2

2

2

1

1

2

1

c

c

b

c

c

a

y

S



















Wzrost pojemności rynku o jednostkę 
prowadzi do wzrostu podaży lidera o 0,5 jedn.



Wzrost pojemności rynku silniej oddziałuje na 
podaż lidera w modelu Stackelberga, niż na 
podaż każdego z producentów w modelu 
Cournota

22

2

1

1









S

y







































C

C

S

C

S

y

y

y

y

y

2

1

1

1

1

3

1

;

2

1

      



Jeśli koszty krańcowe lidera są mniejsze 
(większe) od połowy kosztów krańcowych 
naśladowcy, to pochodna jest dodatnia 
(ujemna) i wzrost wrażliwości popytu na 
zmianę ceny prowadzi do wzrostu (spadku) 
podaży lidera.



Przy cenie lidera równej połowie ceny 
naśladowcy zmiana wrażliwości popytu 
konsumenta na zmianę ceny nie oddziałuje 
na podaż lidera.

23

b

c

c

y

S

2

2

1

2

1











ŁĄCZNA PODAŻ DUOPOLU 
STACKELBERGA



Łączna podaż zależy od tych samych 
czynników, od których zależy podaż każdego 
z producentów.

24

4

)

2

(

3

4

)

2

3

(

2

)

2

(

2

1

2

1

1

2

2

2

1

1

c

c

y

y

y

c

c

y

c

c

y

S

S

S

S

S





































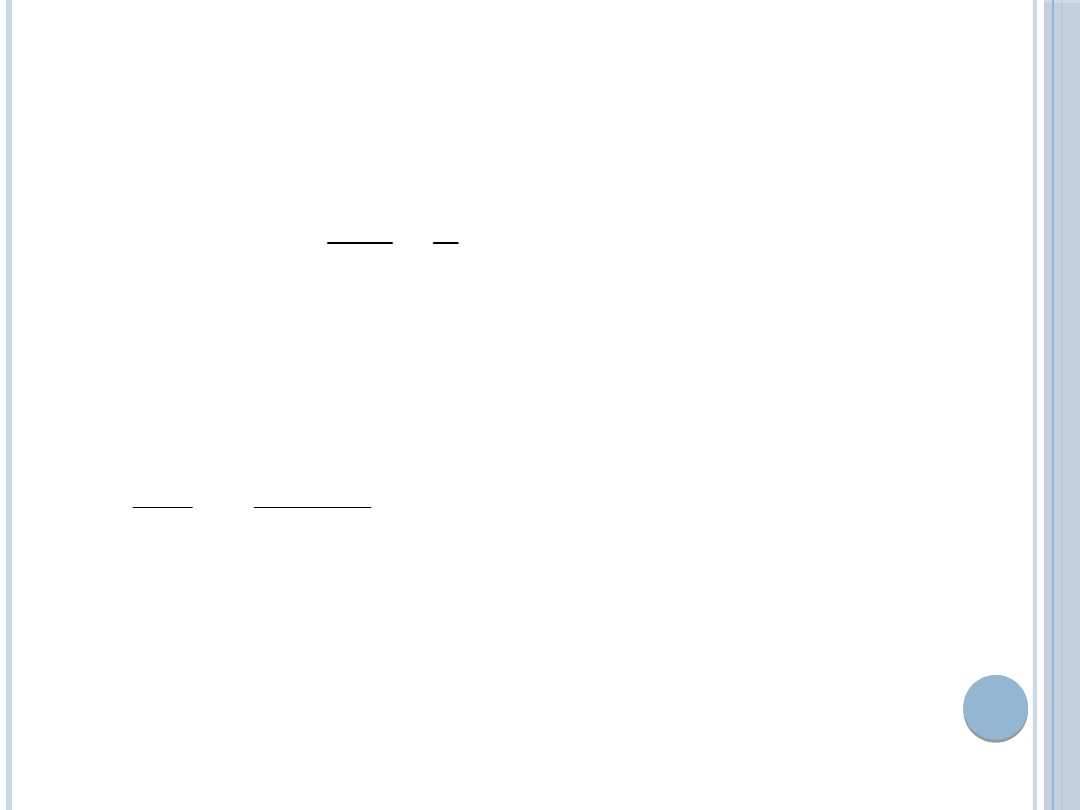
wzrost pojemności rynku prowadzi do 
wzrostu podaży o ¾



Im silniej konsumenci reagują na zmiany 
ceny, tym niższa jest łączna wielkość podaży 
duopolu

25

4

3









S

y

0

4

2

2

1













c

c

y

S





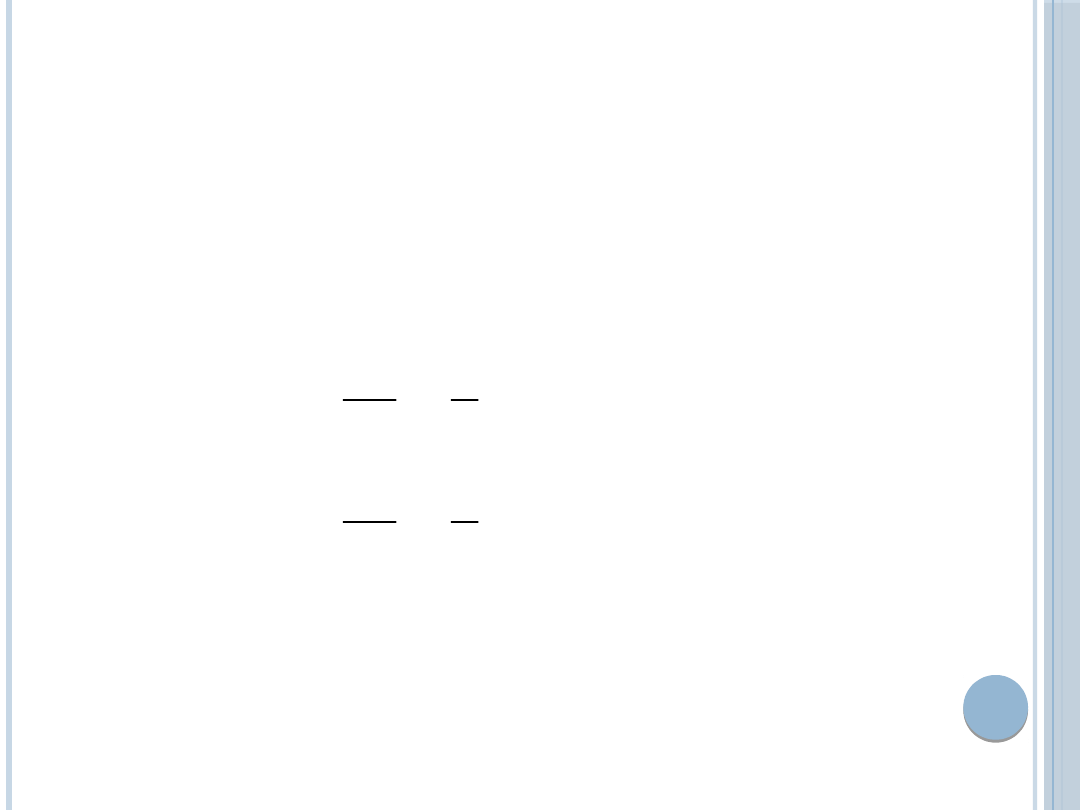
Wzrost kosztów krańcowych każdego z 
producentów przekłada się na spadek łącznej 
podaży owego duopolu, ale koszty krańcowe 
lidera dwa razy silniej oddziałują na łączną 
podaż tego duopolu od kosztów naśladowcy.

26

2

c

0

4

0

2

2

1

























c

y

c

y

S

S

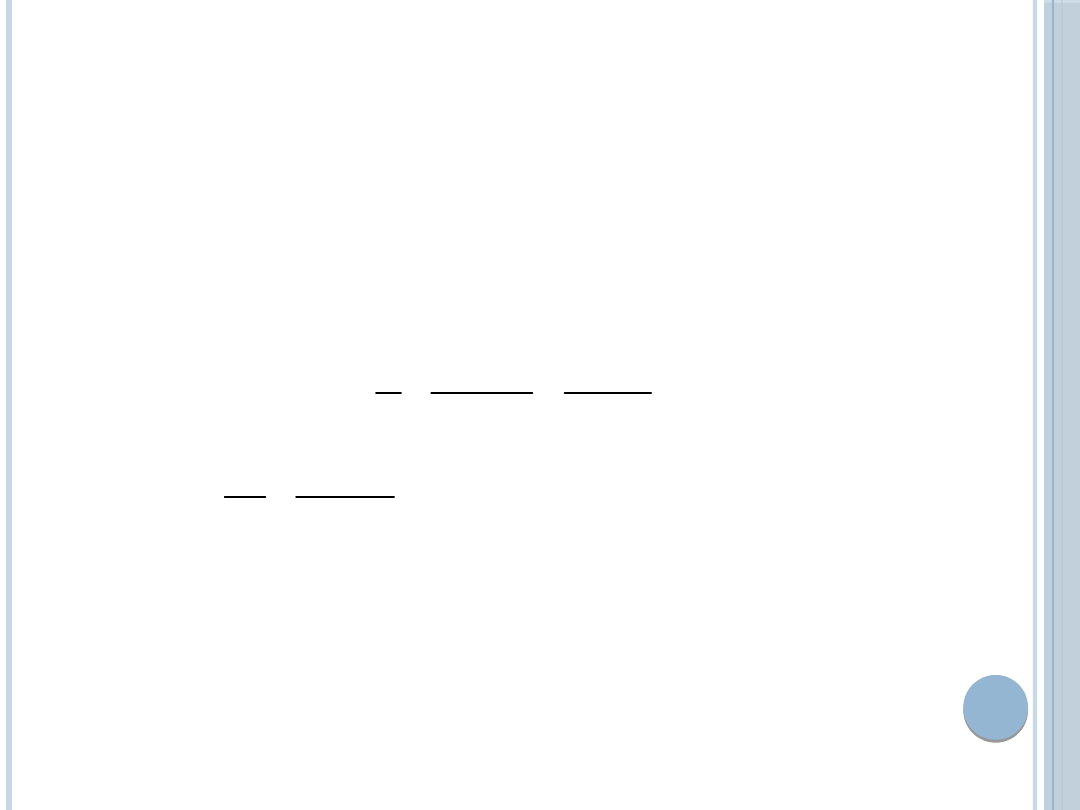
CENA RÓWNOWAGI STACELBERGA



Zależy od pojemności rynku, wrażliwości 
konsumentów na zmianę ceny, kosztów 
krańcowych lidera oraz naśladowcy

27

4

2

4

)

,

(

2

1

2

1

2

1

c

c

p

y

y

y

y

y

p

p

S

S

S

S

S

S

S



































Im większa pojemność

duopolu tym wyższą cenę 
ustalą producenci



Im silniej konsumenci 

reagują na zmianę ceny
tym niższą cenę ustalą producenci

28

0

4

0

4

1

2





























S

S

p

p



Wzrost kosztów krańcowych lidera 
(naśladowcy) o jednostkę przekłada się na 
wzrost ceny w równowadze Stackelberga o 
0,5 (0,25) złotych.

29

4

1

2

1

2

1













c

p

c

p

S

S

DUOPOL BERTRANDA



Model rynku, w którym producenci 
wytwarzają dobra (usługi) będące bliskimi 
substytutami.



Producenci konkurują miedzy sobą ceną 
wytwarzanego dobra (usługi).

30

stały

koszt 

  

krańcowy)

(koszt 

 

przeciętny

koszt 

  

produkcji

 

 wielkość

    

0

0

0

)

(

2

,

1















i

i

i

i

i

i

i

i

f

c

y

f

y

c

y

tc

i

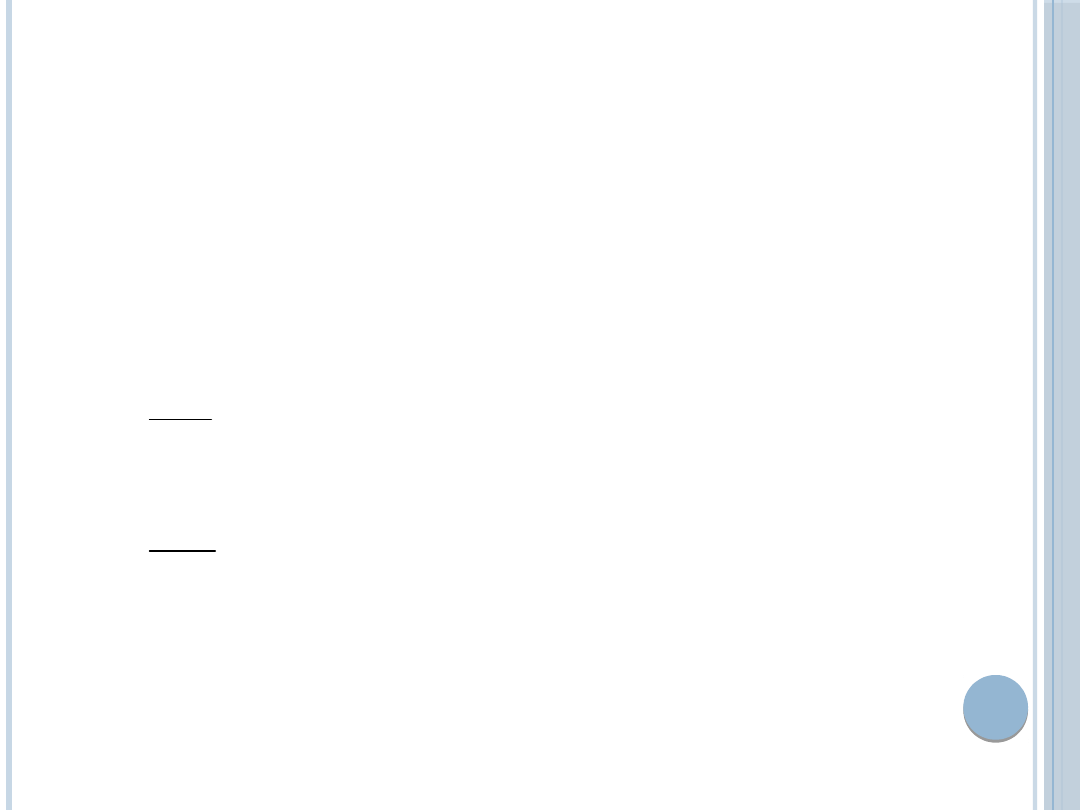
POPYT NA PRODUKT

31

2

2

2

1

1

1

1

2

2

2

2

1

2

2

2

1

1

1

1

2

1

1

)

,

(

)

,

(













































p

y

p

y

p

p

p

p

y

p

p

p

p

y

d

d

d

d

MAKSIMUM ZYSKU

32

 

 

const

p

p

const

p

p









1

2

2

1

2

0

1

0

max

max



