WALEC

O

.

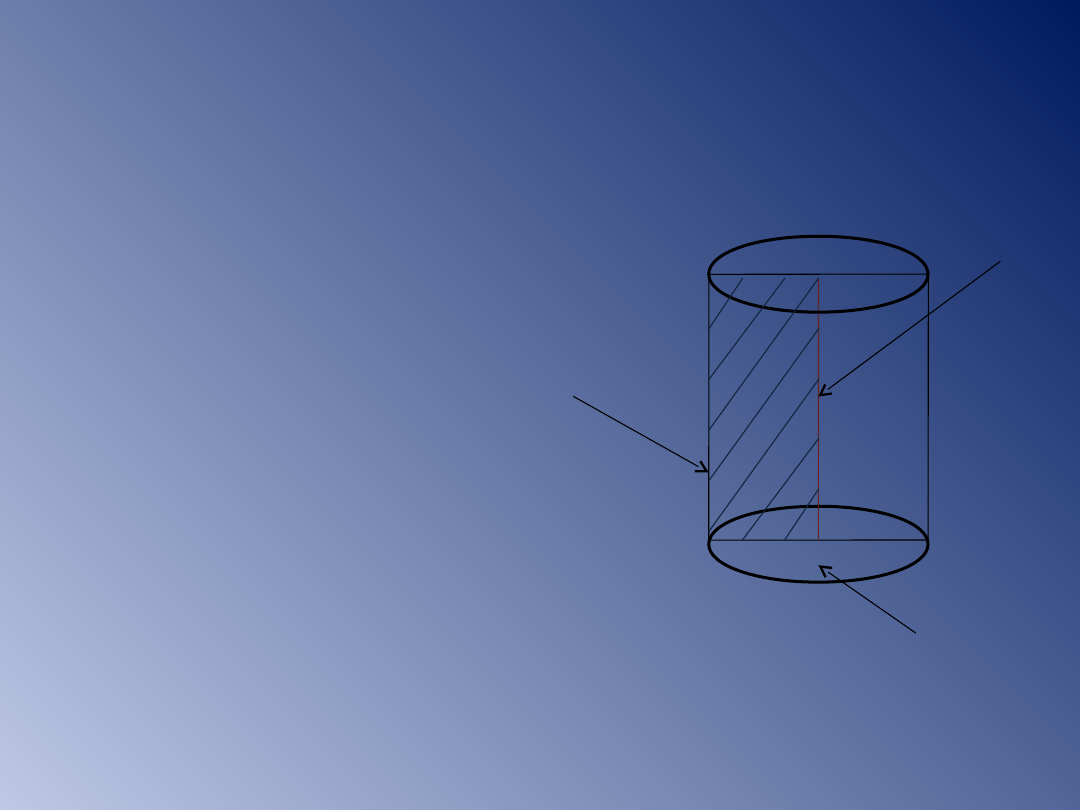
Walec

to bryła

obrotowa powstała

przez obrót

prostokąta wokół

prostej zawierającej

jego bok.

Podstawami walca są

koła o takim samym

promieniu.

tworząc
a walca

podstaw
a

wysokość
walca

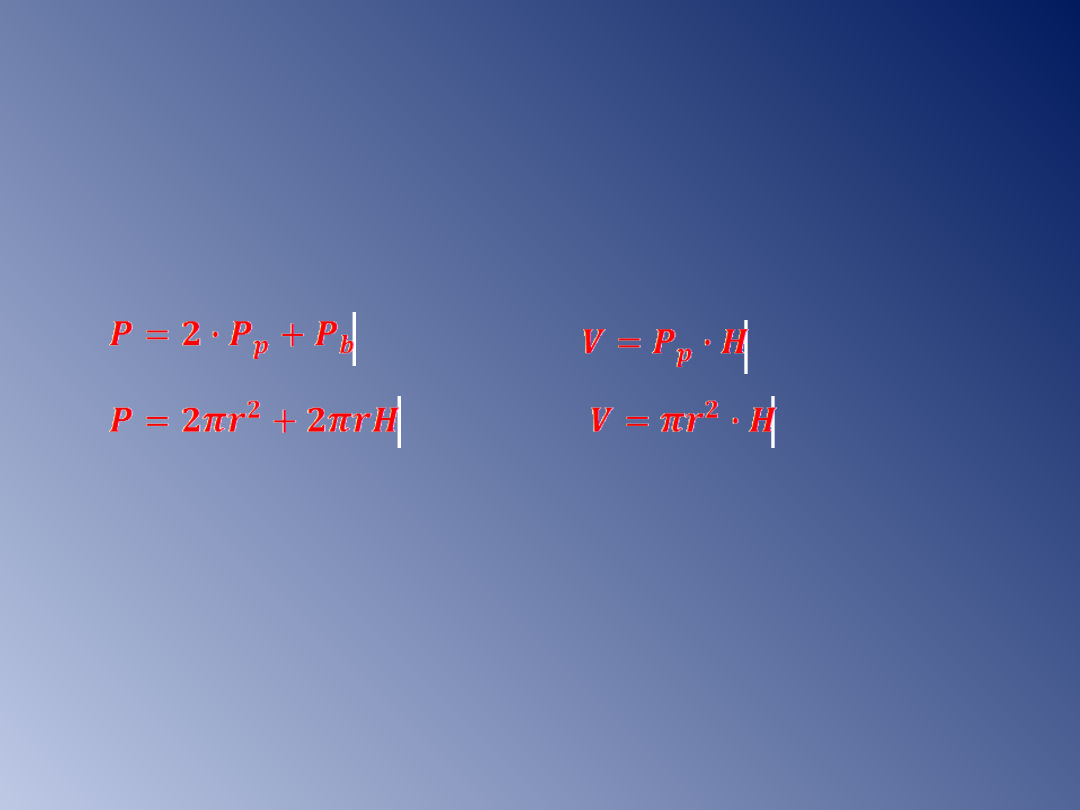
Do rozwiązywania zadań potrzebne

będą wzory na pole powierzchni

(

P

)

i

objętość (

V

) dowolnego walca.

P

p

– pole podstawy

P

b

- pole powierzchni bocznej

H - wysokość walca
r – promień podstawy

O

.

Przykład 1.

Oblicz pole i objętość walca, w którym wysokość
równa się 10cm, promień podstawy 5cm.

Dane:
r=5cm
H=10cm
Szukane: P, V.

Podstawą walca jest koło.

[cm

3

]

H

r

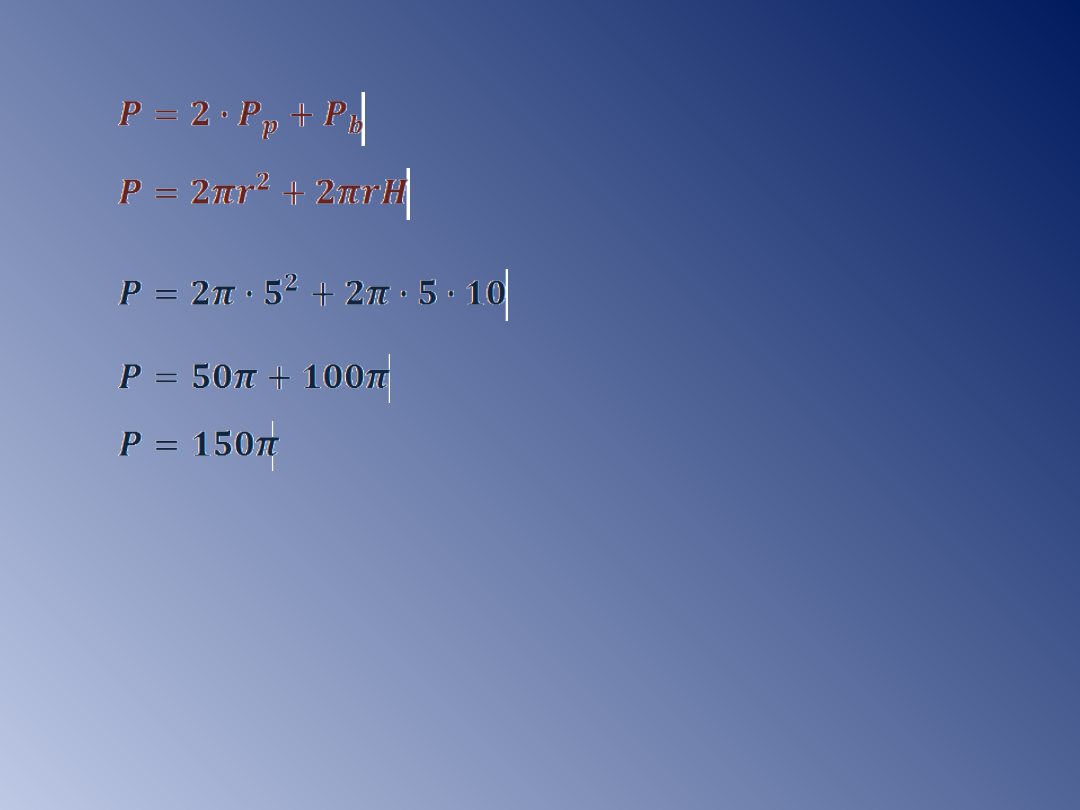
[cm

2

]

Odp: Pole powierzchni walca równa się 150π cm

2

,

jego
objętość 250π cm

3

.

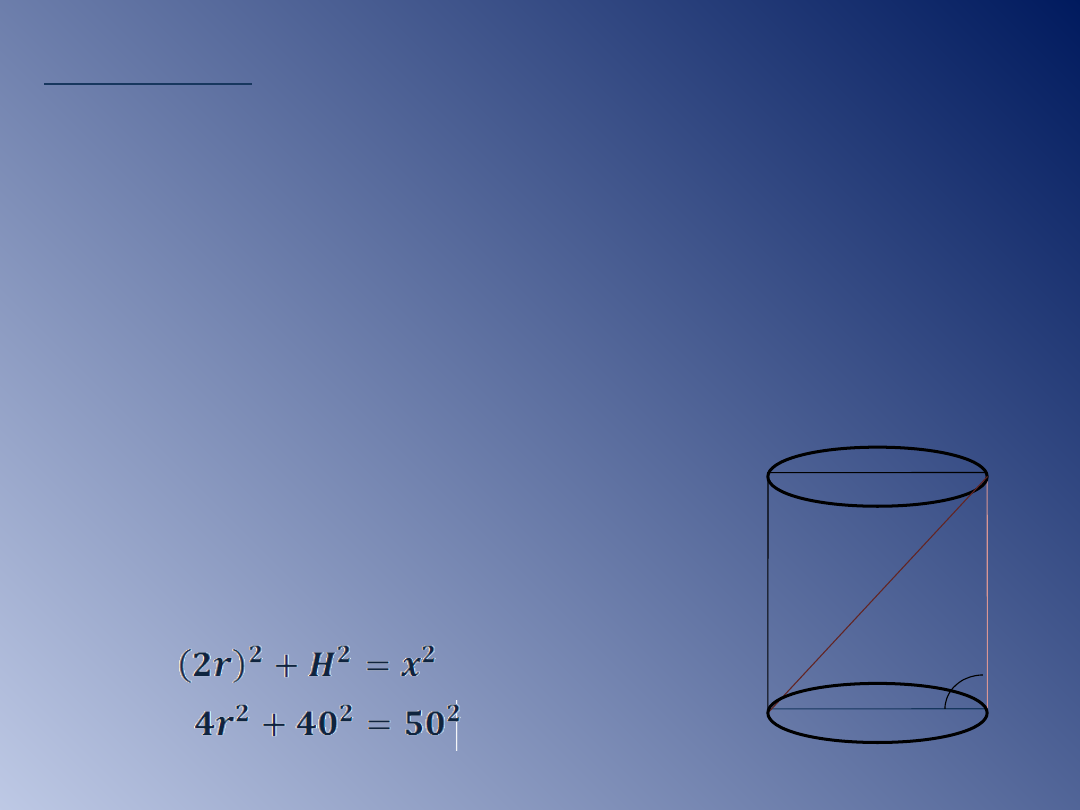
O

.

Przykład 2.

Oblicz pole i objętość walca, w którym wysokość
równa się 40cm, przekrojem osiowym jest
prostokąt, w którym przekątna ma długość 50cm.

Dane:
x=50cm
H=40cm
Szukane: P, V.

Przekrojem walca jest prostokąt ABCD.
Przekątna x dzieli prostokąt na dwa
trójkąty prostokątne.
ΔABC - prostokątny

.

r

r

H

x

A

D

C

B

.

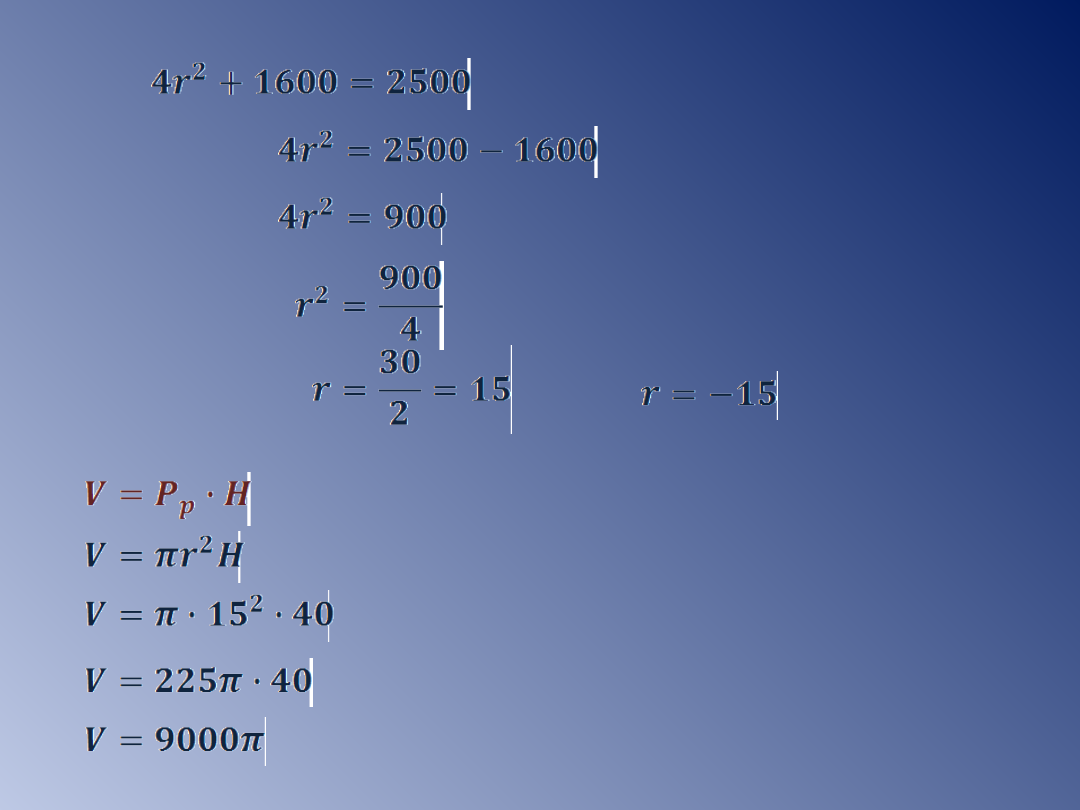
- odpada

[cm

3

]

lub

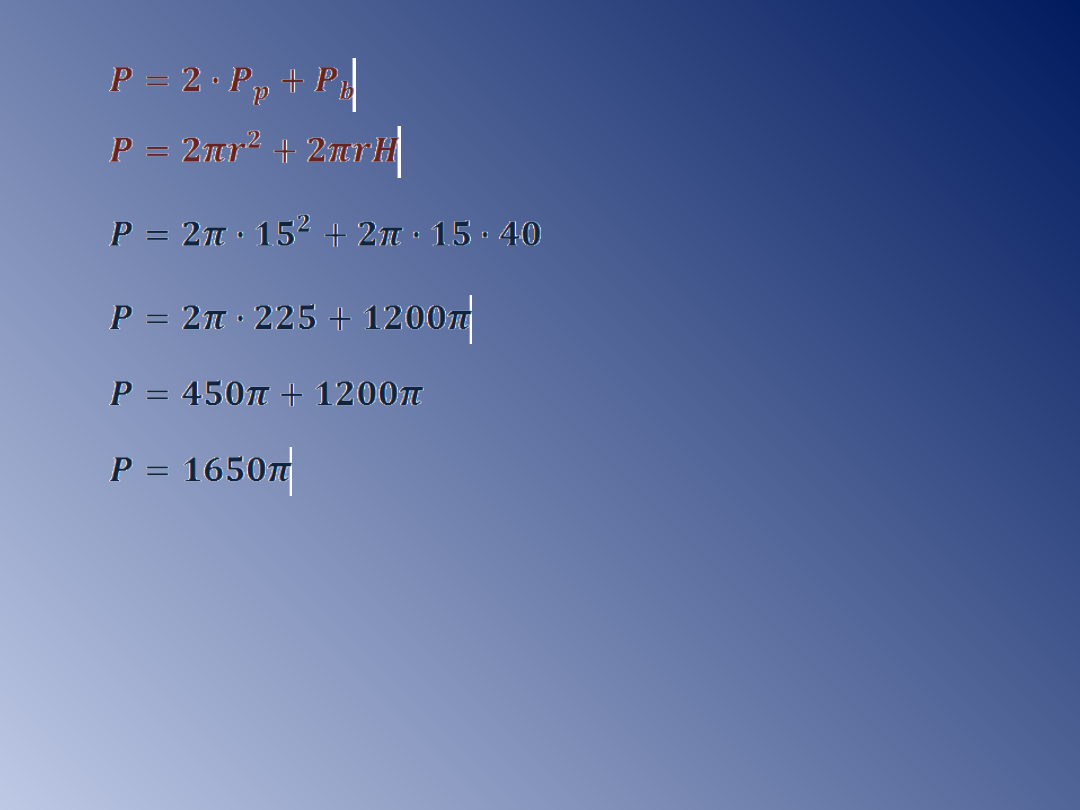
[cm

2

]

Odp: Pole powierzchni walca równa się 1650π cm

2

,

jego
objętość 9000π cm

3

.

O

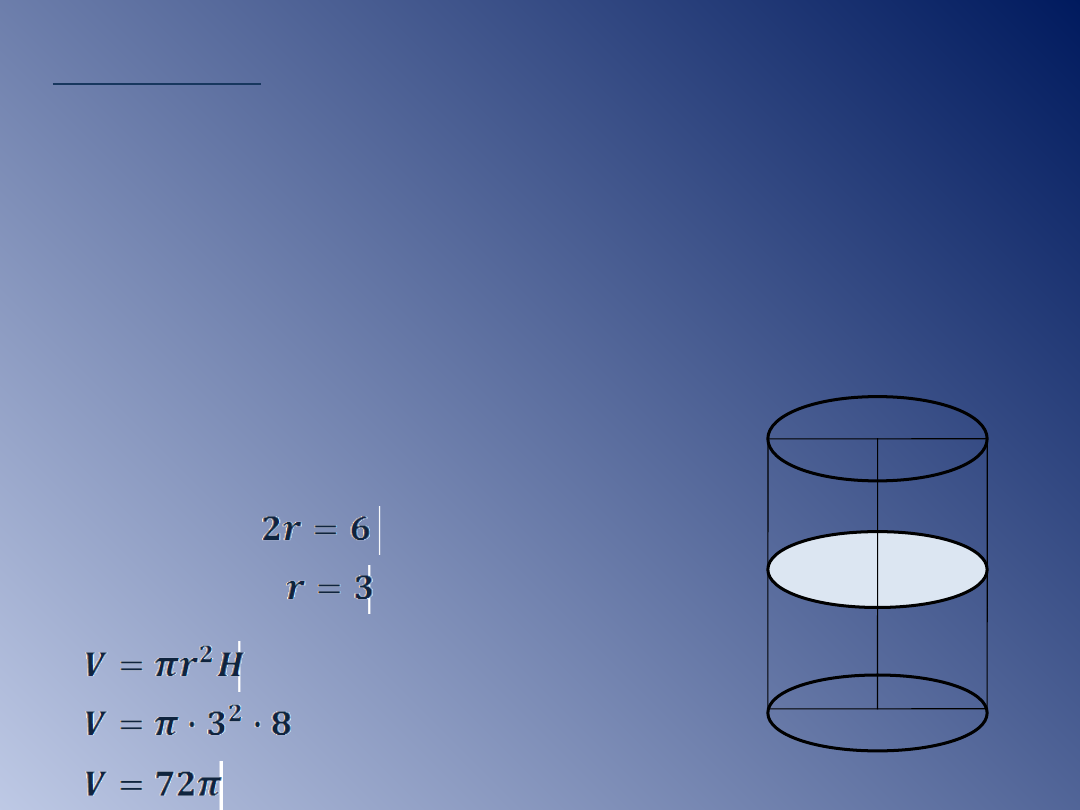
Przykład 3.

Przekrojem walca jest prostokąt o wymiarach 6cm i
8cm. (rys obok) Oblicz pole i objętość walca, oblicz
pole przekroju płaszczyzną równoległą do
płaszczyzny podstawy.

Dane:
2r=6cm
H=8cm
Szukane: P, V,P

przekroju

r

H

r

[cm

3

]

Odp: Pole powierzchni walca równa się 66π cm

2

,

jego
objętość 72π cm

3

; pole przekroju 9π cm

2

.

[cm

2

]

[cm

2

]

O

.

Przykład 4.

Prostokąt o wymiarach 2cm i 4cm obraca się wokół
dłuższego boku. Oblicz pole i objętość powstałej
figury.

Dane:
r=2cm
H=4cm
Szukane: P, V.

W wyniku obrotu powstaje walec,
w którym promień podstawy ma
długość 2cm – długość krótszego boku
prostokąta, wysokość ma długość 4cm – długość
dłuższego boku prostokąta.

r

H

r

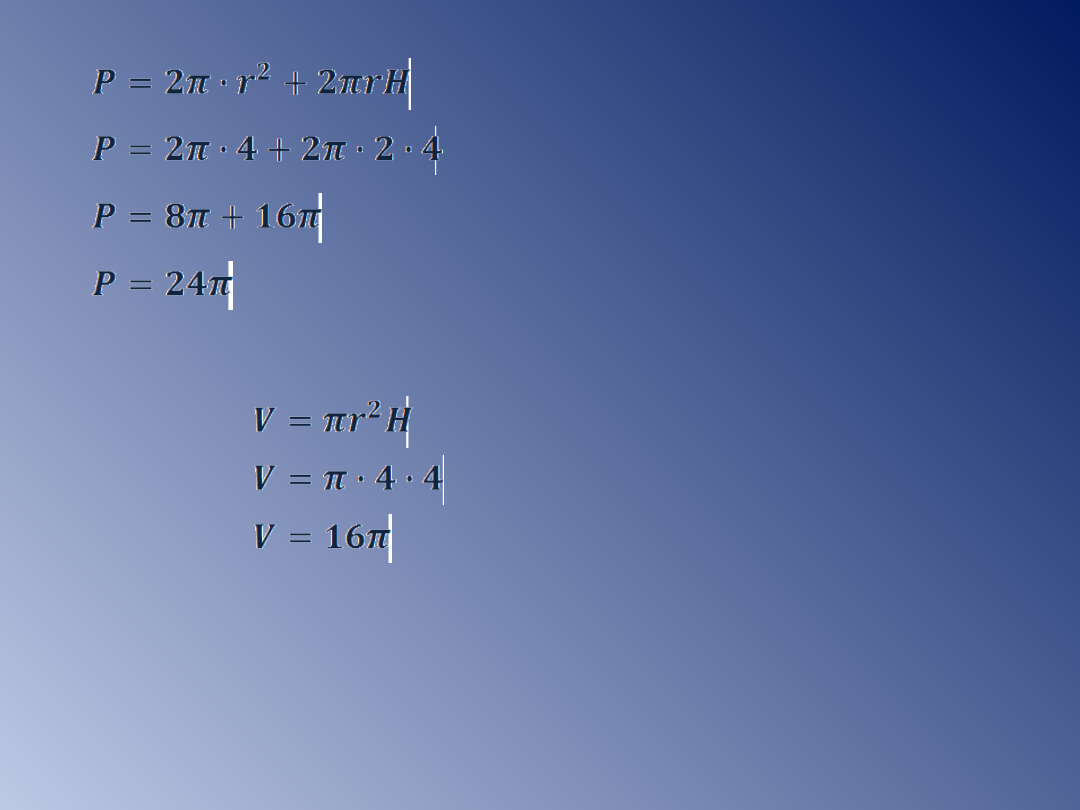
Odp: Pole powierzchni walca równa się 24π cm

2

,

jego
objętość 16π cm

3

.

[cm

3

]

[cm

2

]

O

.

Przykład 5.

Przekrojem walca jest kwadrat o przekątnej
długości 10cm.
Oblicz pole powierzchni i objętość walca.

Dane:
a=10cm
Szukane: P, V.

.

r

r

H

A

C

D

B

Obliczamy długość wysokości
walca, wykorzystując twierdzenie
Pitagorasa.
ΔABC - prostokątny

.

a

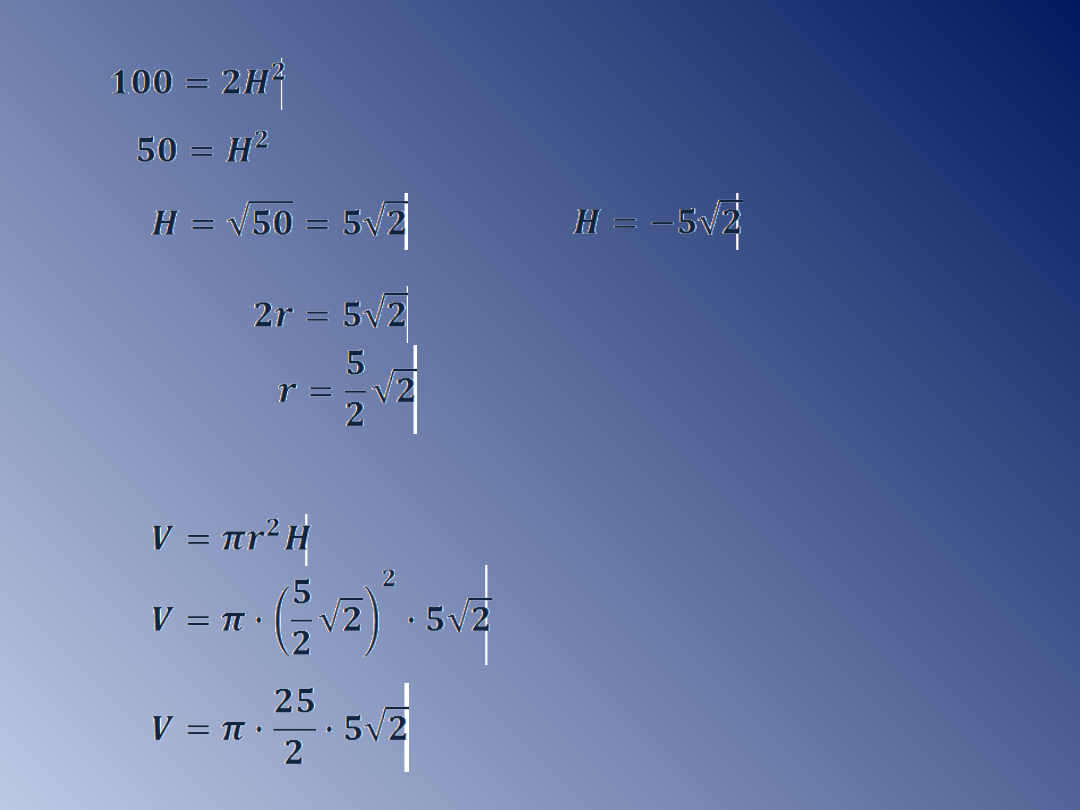
- odpada

lub

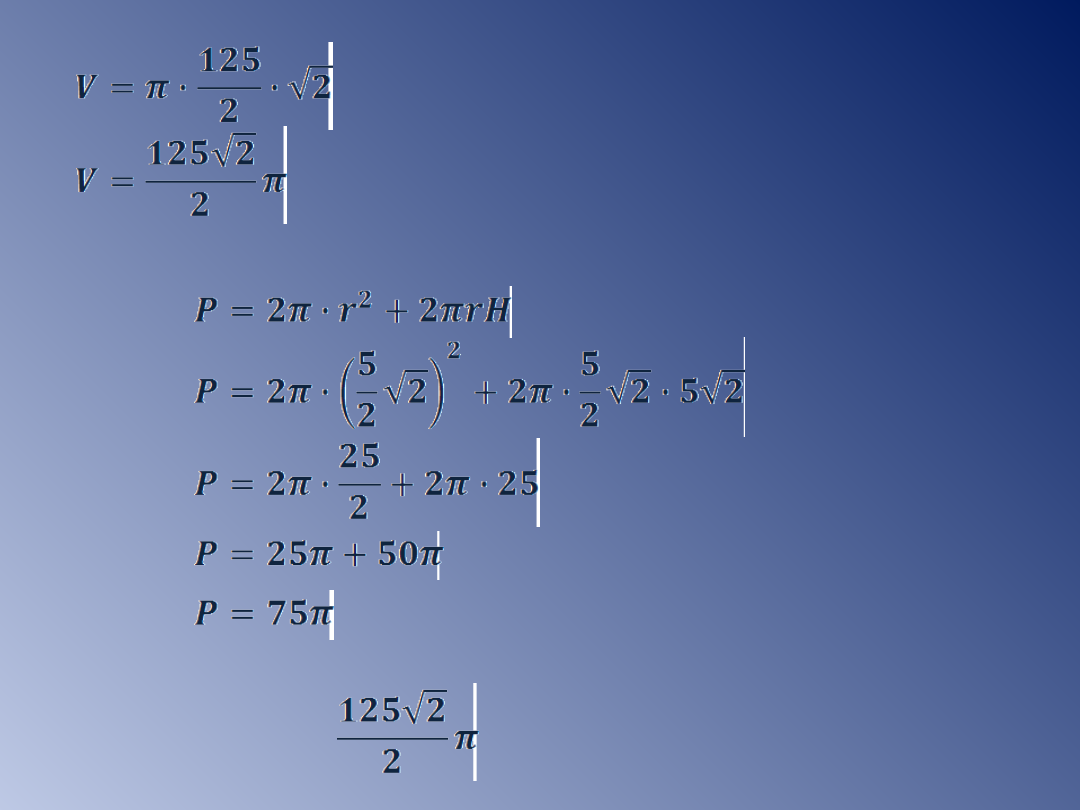
[cm

2

]

[cm

3

]

Odp: Pole powierzchni walca równa się 75π cm

2

,

jego

objętość cm

3

.

O

.

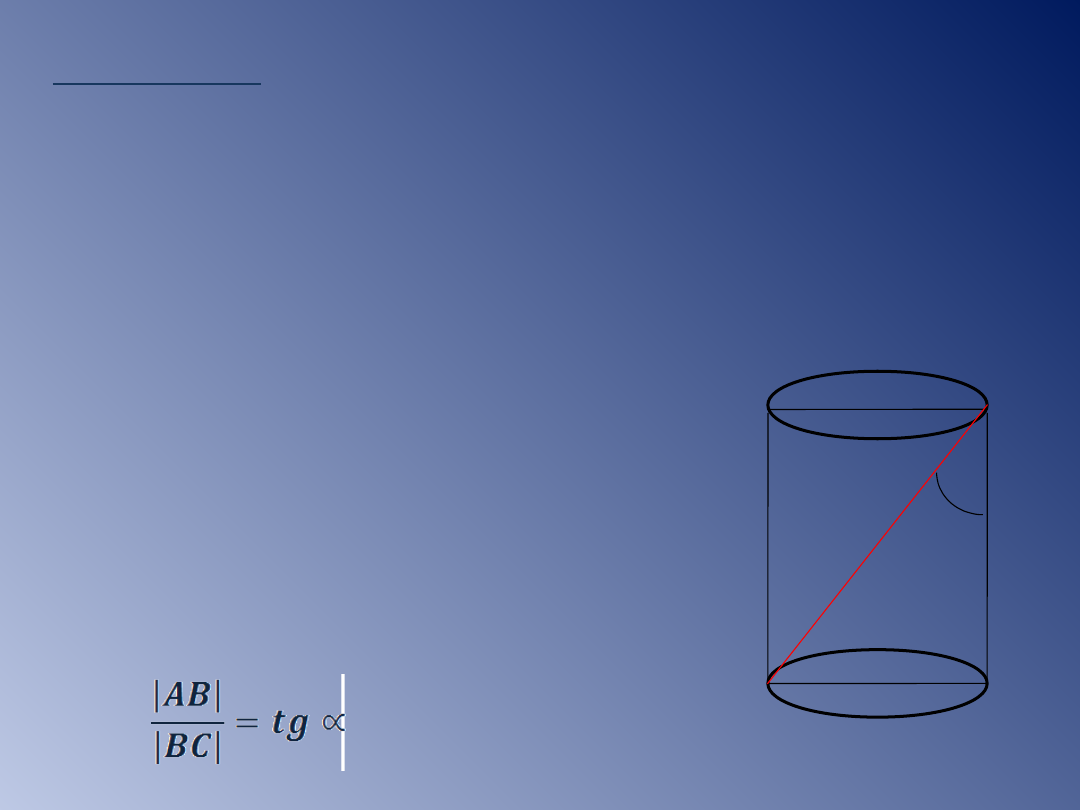
Przykład 6.

Przekrojem walca o wysokości 8cm jest prostokąt,
w którym przekątna tworzy z wysokością kąt o
mierze 30˚. Oblicz pole i objętość walca.

Dane:
=30˚
H=8cm
Szukane: P, V.

α

D

A

C

B

.

r

r

H

Obliczamy długość promienia
podstawy walca, wykorzystując
funkcje trygonometryczne.
ΔABC - prostokątny

α

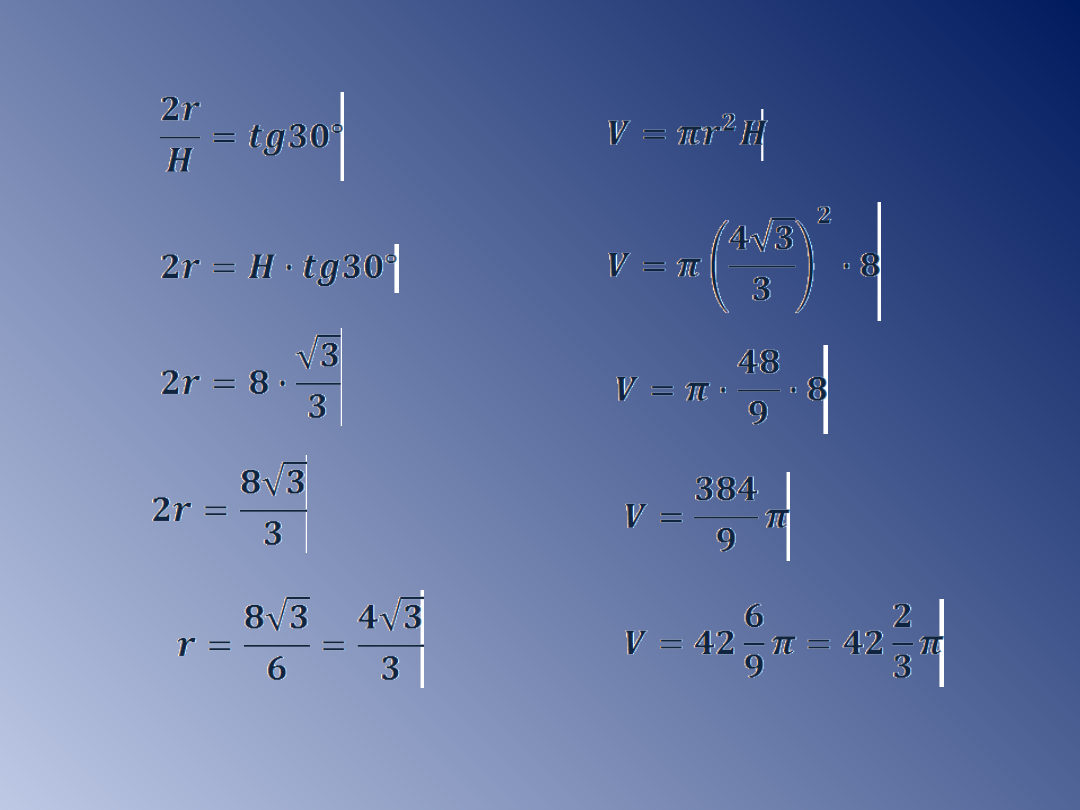
[cm

3

]

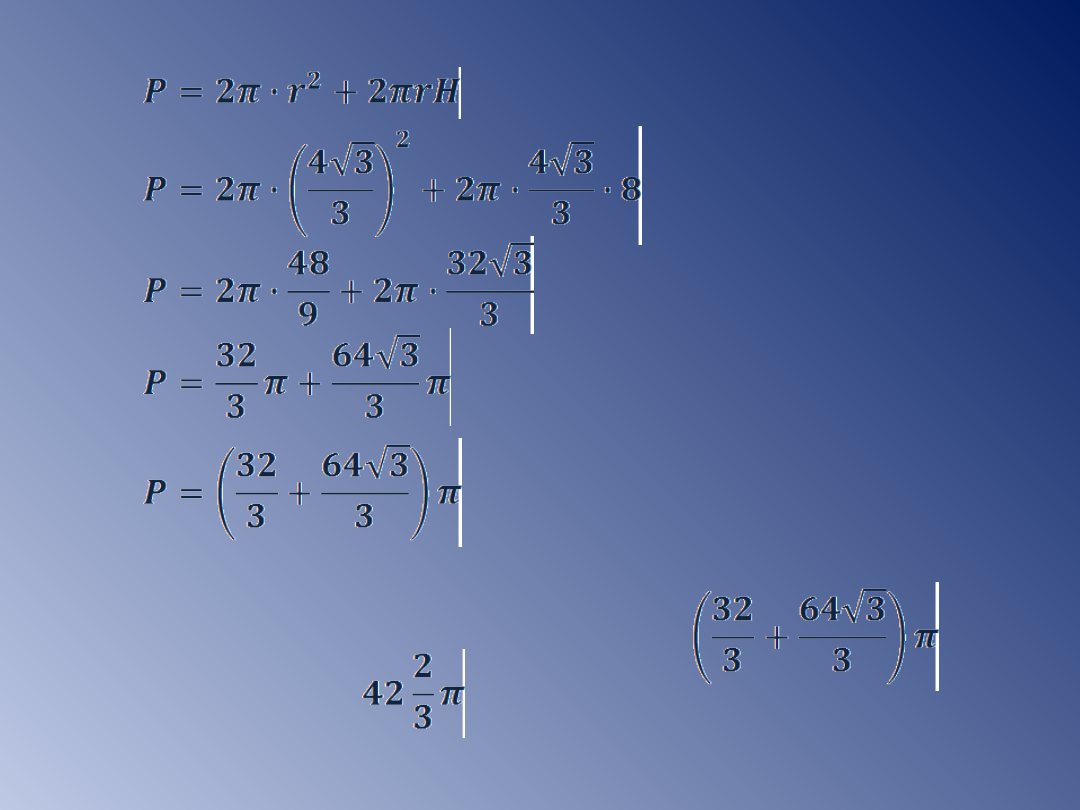
Odp: Pole powierzchni walca równa się

cm

2

,

jego objętość cm

3

.

[cm

2

]