Równania Maxwella

J. C. Maxwell uogólnił prawa uzyskane na drodze doświadczalnej i
opracował jednolitą teorię pola elektromagnetycznego. Jest to teoria
fenomenologiczna, makroskopowa. W sposób ilościowy można ją zapisać
w postaci czterech równań, zwanych równaniami Maxwella:

0

q

E ds

e

� =

�

�

r r

�

1.

prawo Gaussa dla pola elektrostatycznego

2.

0

B ds

� =

�

�

r r

�

prawo Gaussa dla pola magnetycznego

Strumień indukcji magnetycznej przez powierzchnię zamkniętą jest
równy zero. Oznacza to, że linie pola magnetycznego są liniami
zamkniętymi (nie istnieje monopol magnetyczny). Pole magnetyczne
jest polem wirowym. Przez powierzchnię zamkniętą tyle samo linii
pola magnetycznego wchodzi, co i wychodzi.

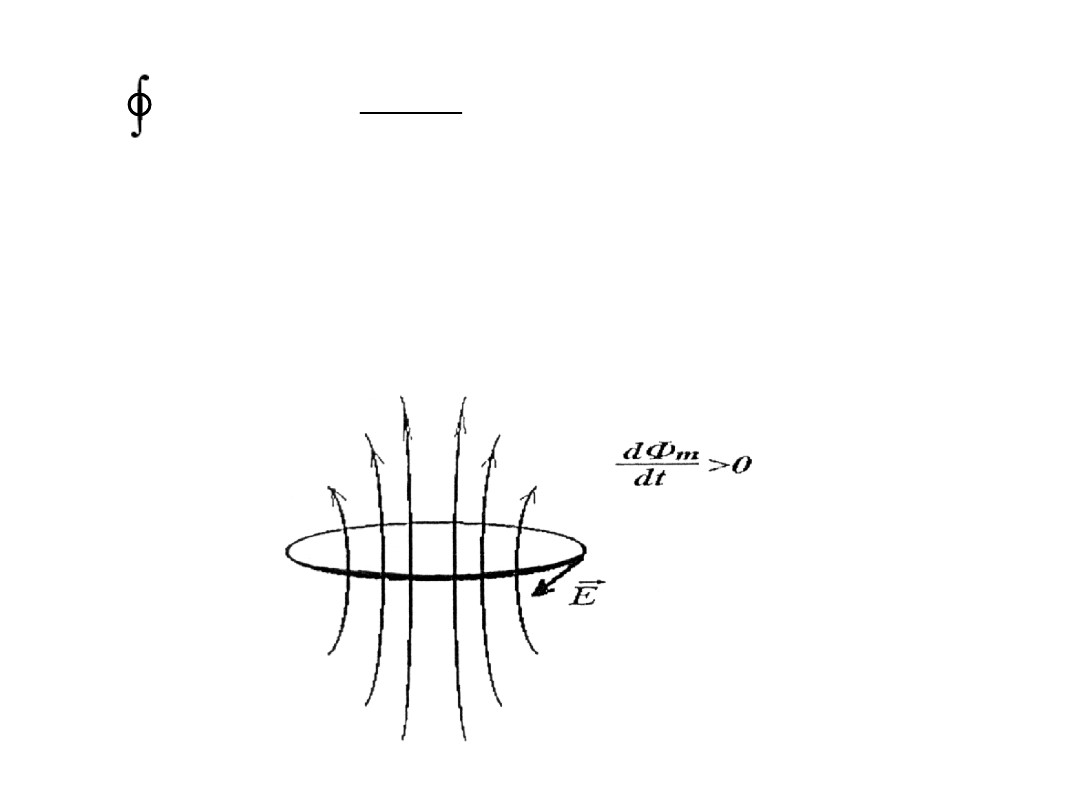
Zmiana strumienia magnetycznego powoduje wytworzenie się
wirowego pola elektrycznego (linie pola są zamknięte). W przypadku
braku nośników ładunku (w próżni) prąd indukcyjny nie powstanie, ale
pojawi się wirowe pole elektryczne.

3.

m

d

E dl

dt

F

� =-

�

r

r

�

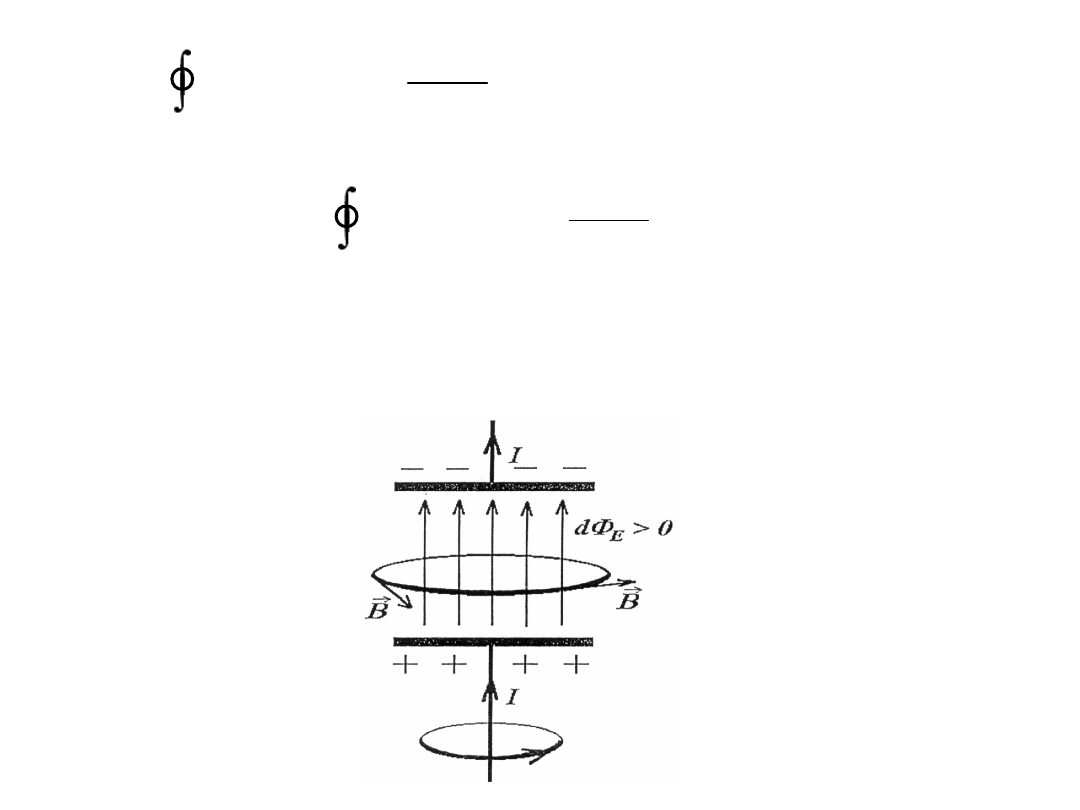
Zmiana strumienia pola elektrycznego powoduje pojawienie się
wirowego pola magnetycznego.

4.

Jeśli I = 0 to :

0 0

E

d

B dl

dt

me

F

� =

�

r

r

�

0 0

0

E

d

B dl

I

dt

me

m

F

� =

+

�

r

r

�

Wniosek z równań 3 i 4:

Między polami: elektrycznym i magnetycznym istnieje ścisły
związek. Zmienne pole magnetyczne powoduje powstanie
wirowego pola elektrycznego, zaś zmienne pole elektryczne
powstawanie wirowego pola magnetycznego.

Pola te wzajemnie wzbudzają się.

m

d

E dl

dt

F

� =-

�

r

r

�

0 0

E

d

B dl

dt

me

F

� =

�

r

r

�

Zmienne pola elektryczne i magnetyczne są ściśle są ściśle ze
sobą związane tworząc jedno pole elektromagnetyczne. Pole te
charakteryzują dwie wartości wektorowe:

E

r

oraz

H

r

(

B

r

)

W przypadku, gdy wzbudzone pole elektromagnetyczne
zmienia się okresowo, rozchodzenie się tego pola w przestrzeni
ma charakter falowy.

Mówimy,

że

w

przestrzeni

rozchodzi

się

fala

elektromagnetyczna.

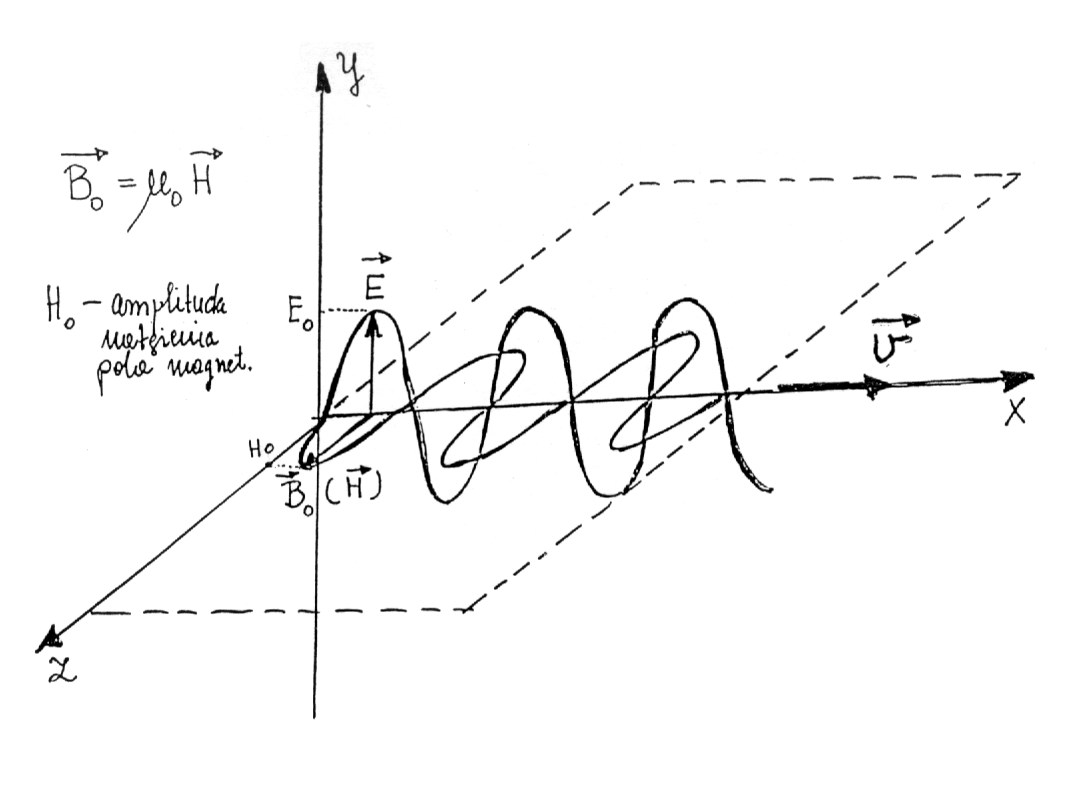
Równanie fali płaskiej:

0

sin(

)

0

x

y

o

z

E
E

E

t kx

E

w

=

=

-

=

0

0

sin(

)

x

y

z

o

H
H
H

H

t kx

w

=

=

=

-

v

v

E H

EH

=

�

r

r

r

s E H

= �

r

r

r

wektor Poyntinga

gdzie:

E, H – chwilowe wartości natężeń pól elektrycznego i magnetycznego

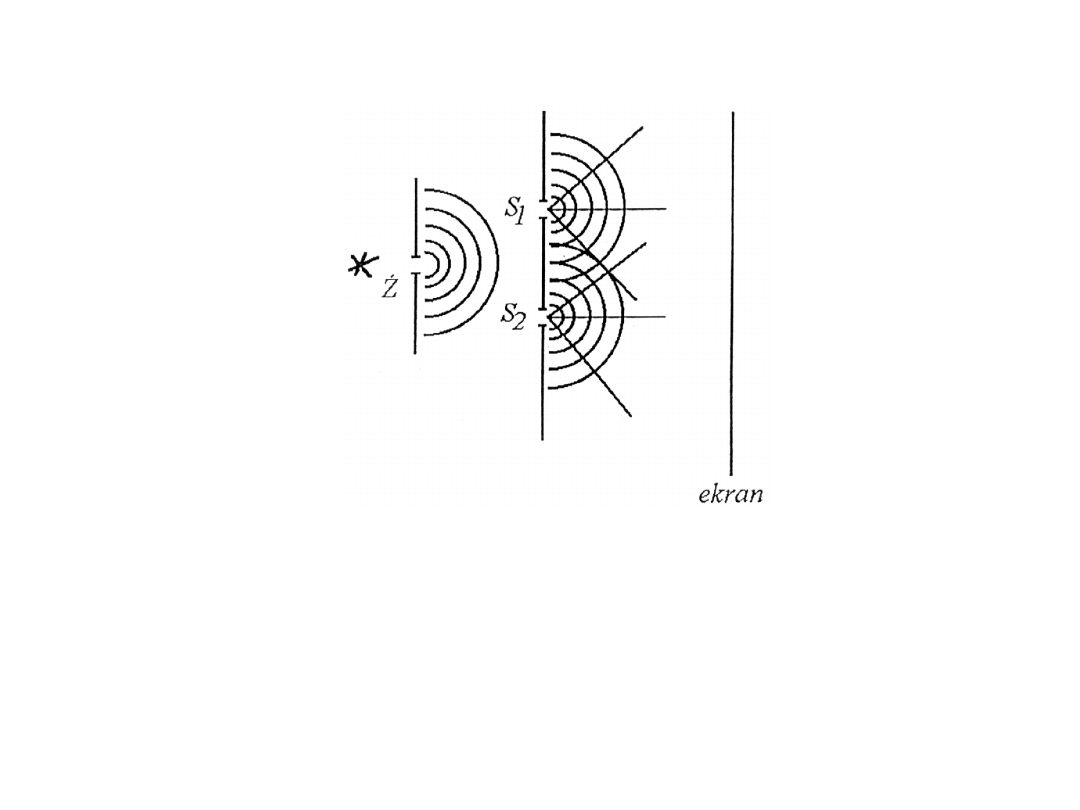
Doświadczenie Younga

Fale świetlne ulegają ugięciu na szczelinach (tak, jak fale na wodzie).
Szczeliny S1 i S2 stają się punktowymi źródłami światła,
rozchodzącego się z każdej szczeliny we wszystkich kierunkach.

Rozważmy punkt P ekranu, do którego dochodzą fale ze
szczelin S

1

i S

2

.

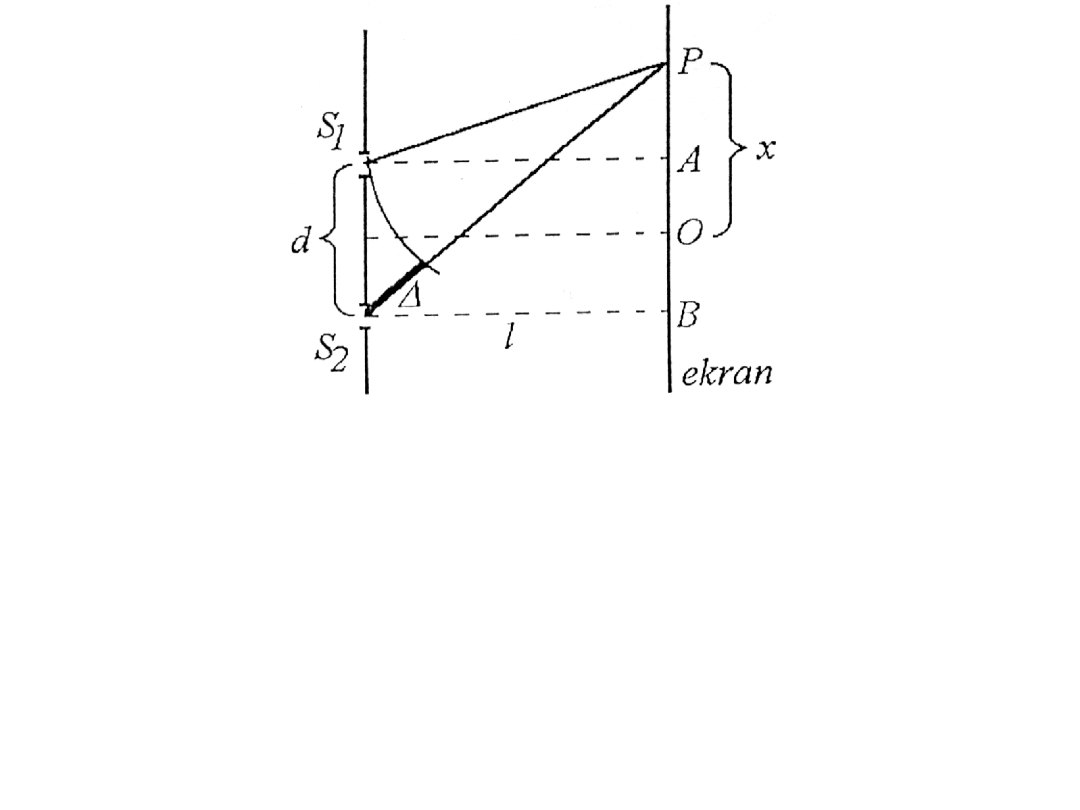
Fale te do punktu P przebywają drogi: S

1

P i S

2

P, których różnica wynosi:

2

1

S P SP

D=

-

W punkcie P nastąpi wzmocnienie w wyniku interferencji, jeśli 

będzie równa wielokrotności długości fali, a więc:

n l

D= �

Obliczmy . Z trójkątów S

1

AP i S

2

BP mamy:

2

2

2

1

2

2

2

2

(

)

2

(

)

2

d

SP

l

x

d

S P

l

x

�

�

= + -

�

�

�

�

�

�

= + +

�

�

�

�

Odejmujemy równanie stronami:

2

2

2

2

2

2

2

1

2

2

2

1

2

(

)

(

)

4

4

(

)

(

)

2

2 2

l

d

d

S P

SP

x

dx

x

dx

S P

SP

dx

l

dx

dx

l

D

�

-

= + +

-

+ -

-

=

D� =

D=

12 3

123

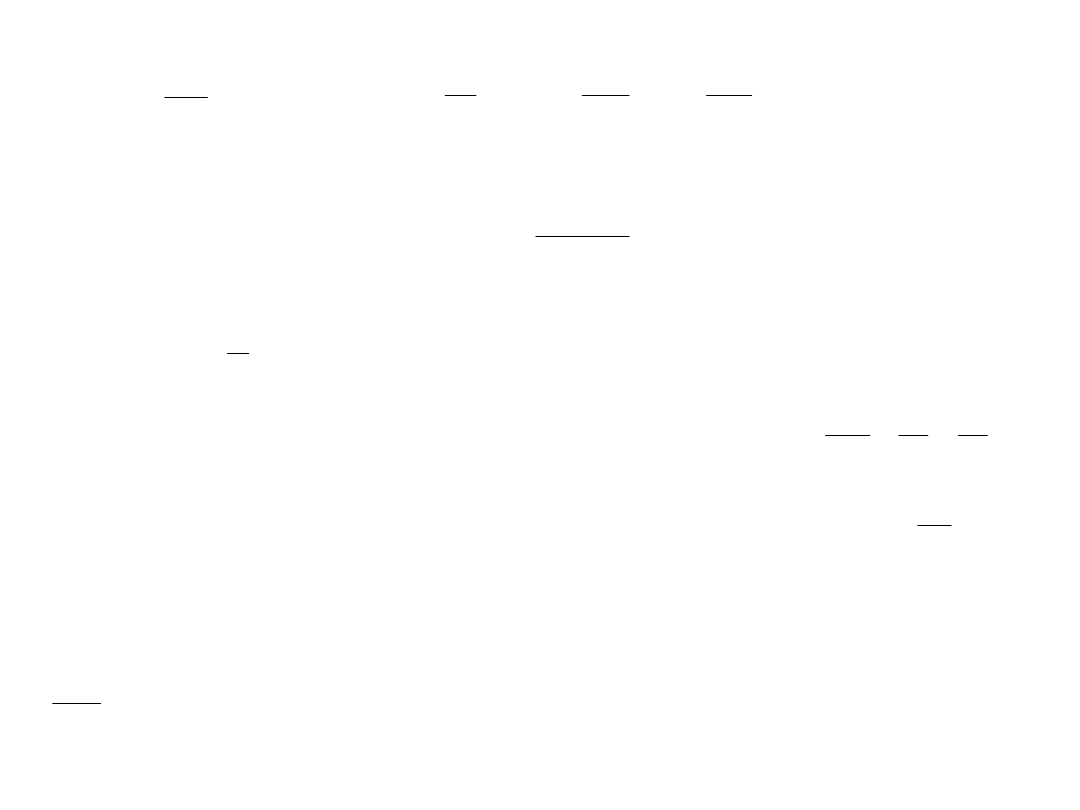
Maksimum pierwszego rzędu mamy, gdy n = 1 tzn.  = 

1

dx

l

l =

stad

1

2

3

2

3

(

,

, ...)

l

l

l

x

x

x

d

d

d

l

l

l

=

=

=

Uogólniając:

n

l

x

d

l

��

=

Jeśli

(2

1) ,

1, 2, ...

2

n

n

l

D=

-

=

to na ekranie obserwujemy wygaszanie
światła, czyli minimum interferencyjne.

Obliczamy odległość między kolejnymi, jasnymi prążkami:

2

1

1

2 l

l

l

x

x

x

d

d

d

l

l

l

-

=

-

=

=

A więc prążki jasne są rozmieszczone w równej od siebie odległości

l

x

d

l

=

W punkcie O na ekranie jest prążek jasny gdyż  = 0; nie ma różnicy dróg

(między spotykającymi się w tym punkcie falami.

n l

x

d

l

=

, więc jeśli światło jest białe (mieszanina promieni różnych barw), to
ponieważ promień czerwony ma

800 nm

cz

l =

a promień
fioletowy

400 nm

f

l =

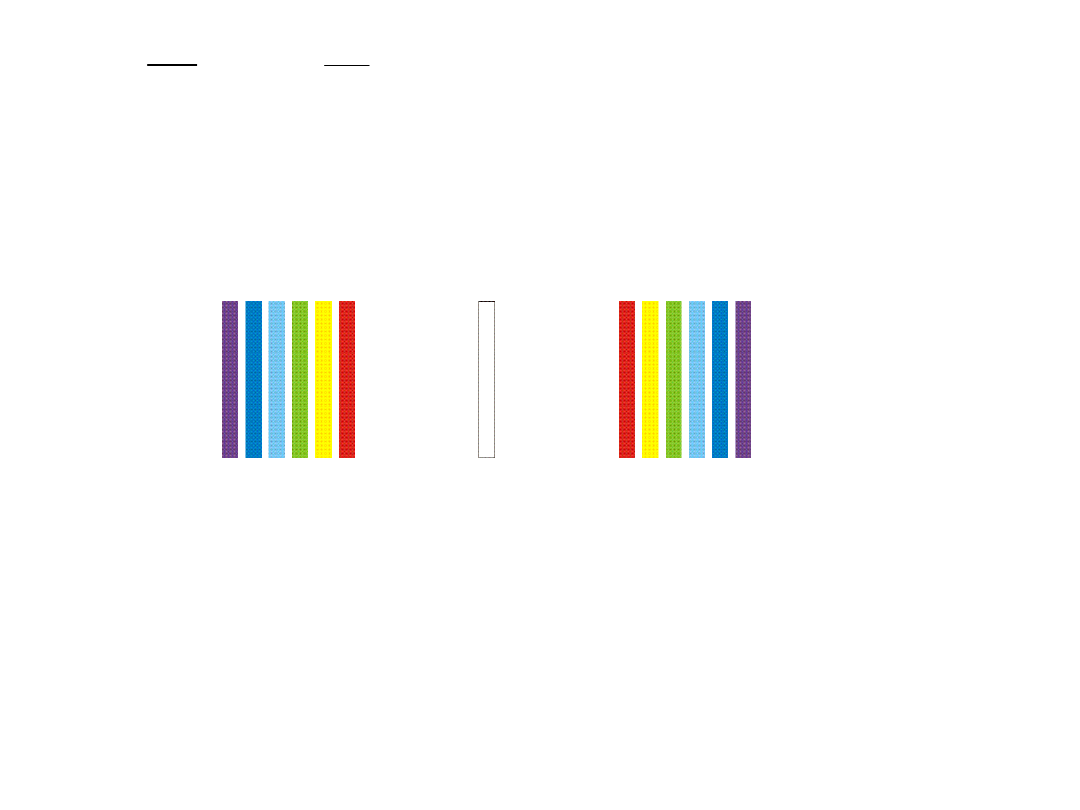
cz

cz

l

x

d

l

=

f

f

l

x

d

l

=

i

to przy

cz

f

l

l

>

mamy

cz

f

x

x

>

Otrzymamy obraz interferencyjny na ekranie w postaci prążków:

Jeśli na szczeliny skierujemy światło monochromatyczny (jednobarwne),
to otrzymujemy obraz interferencyjny, także jednobarwny (prążki na
przemian jasne i ciemne).

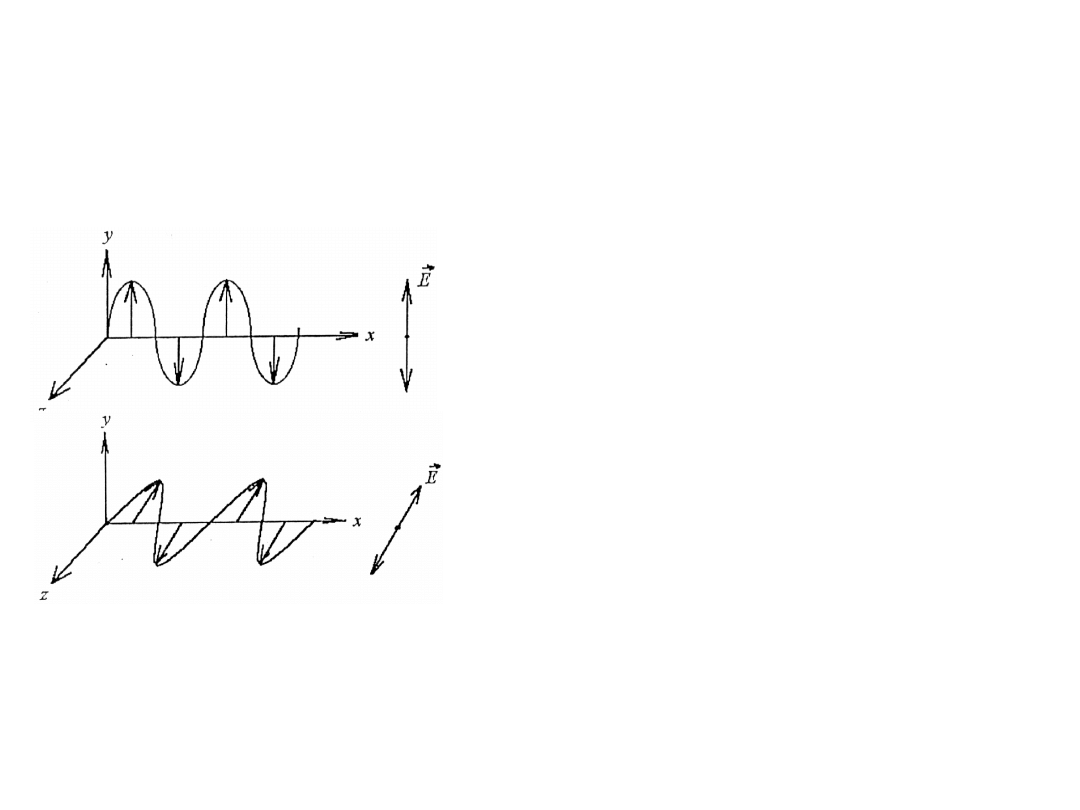
Polaryzacja światła

Przyjmujemy za „reprezentanta” fali świetlnej wektor natężenia pola elektrycznego

E

r

(wszystkie reakcje fotochemiczne na siatkówce oka, kliszy fotograficznej wywołane są
polem elektrycznym).

Model fali świetlnej spolaryzowanej w

kierunku osi Y

Model fali świetlnej spolaryzowanej w

kierunku osi Z

Światło

naturalne

(z

żarówki,

słoneczne)

jest

światłem

niespolaryzowanym,

tzn. że nie można wyróżnić stałego kierunku drgań wektora

E

r

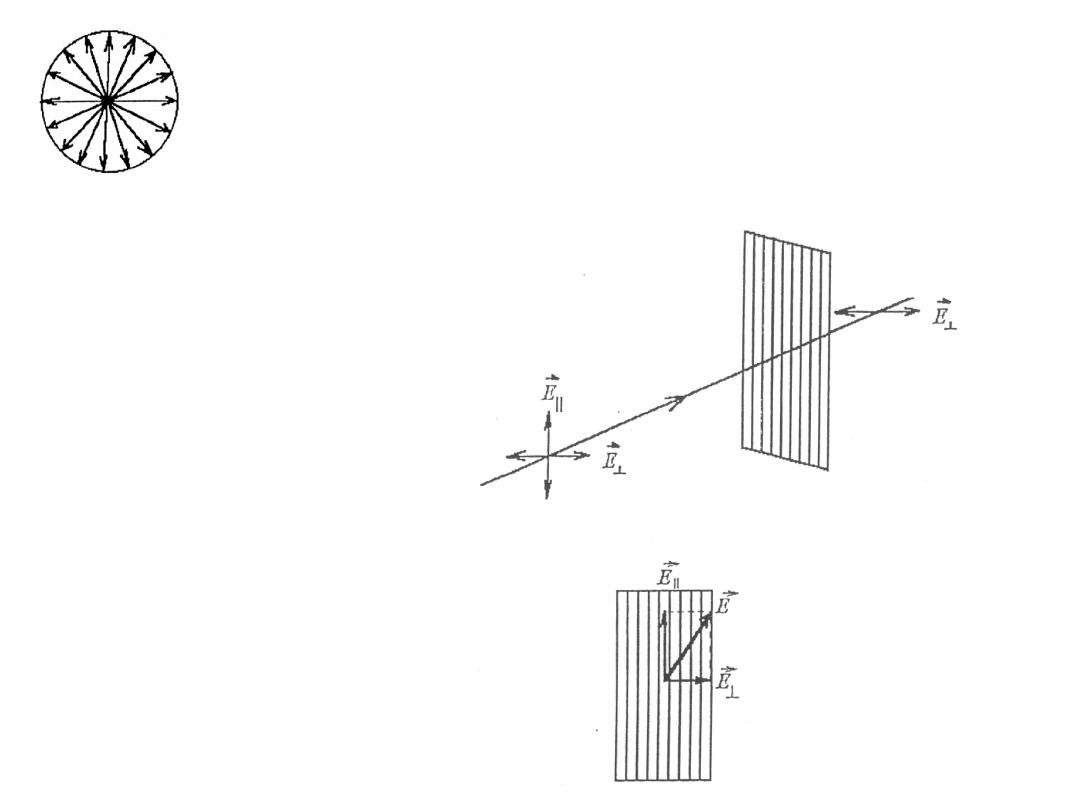
Model światła niespolaryzowanego (w płaszczyźnie prostopadłej

do kierunku promienia możliwe są najrozmaitsze kierunki drgań wektora

E

r

)

W jaki sposób można uzyskać
światło spolaryzowane ?

Ze względu na małą
długość fali świetlnej
grubości drutów i odległości
między nimi muszą być
bardzo małe (na
powierzchni znaczka
pocztowego powinno się
zmieścić 30 000 takich
drutów).

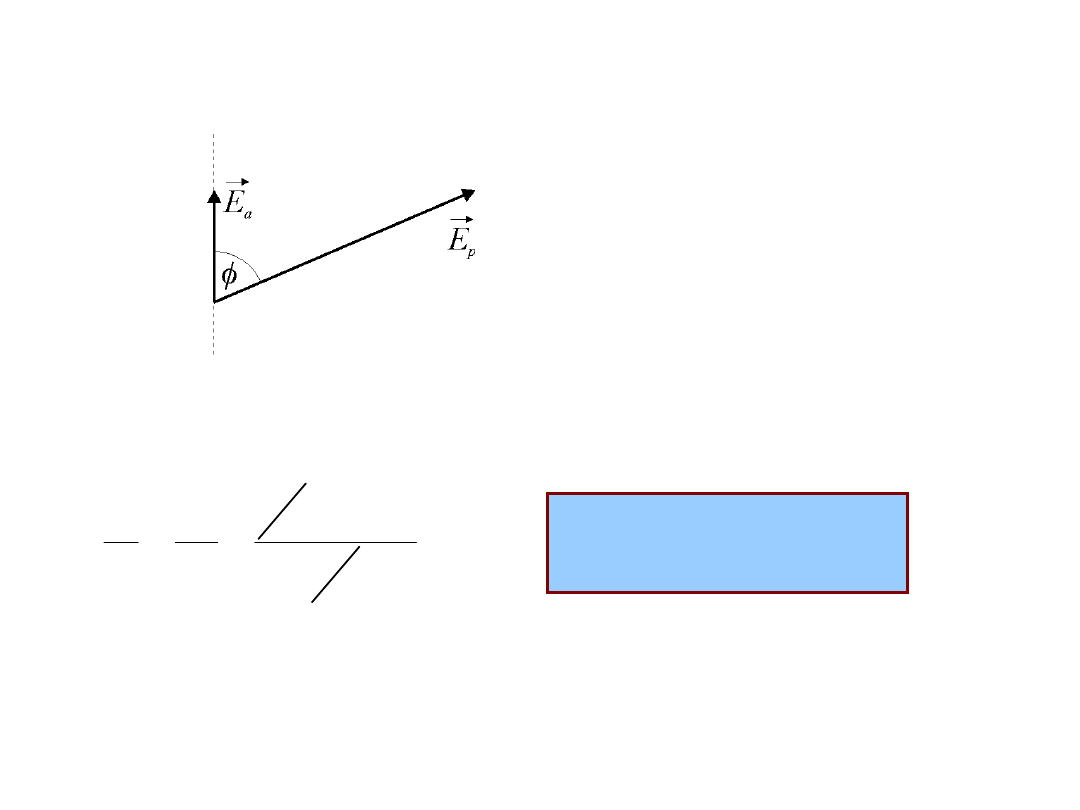
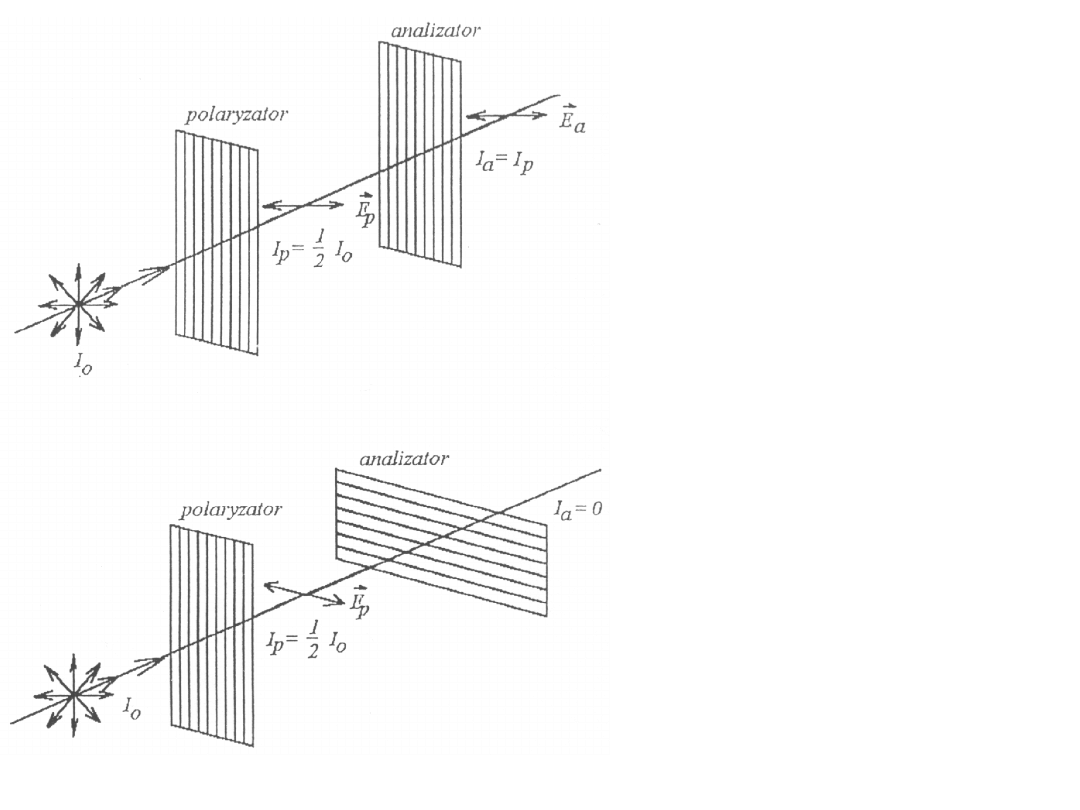
Oznaczamy kierunek „przepuszczania” analizatora linią przerywaną.
Jeśli E

p

(po obrocie polaryzatora) ma dowolny kierunek, to przez

analizator przejdzie tylko składowa E

a

.

cos

a

p

E

E

j

= �

Z teorii ruchu falowego wiadomo, że natężenie fali jest proporcjonalne do
kwadratu amplitudy fali (I ~ A

2

). Zatem natężenie światła przechodzącego

przez analizator jest proporcjonalne do

2

a

E

zaś przez polaryzator

Zatem:

2

2

2

p

a

a

p

p

E

I

E

I

E

=

=

2

2

cos

p

E

j

�

2

cos

a

p

I

I

j

= �

wzór Malusa

Kąt

 jest kątem między kierunkiem przepuszczania polaryzatora i analizatora.

Jeśli

 = 0 to I

a

= I

p

, a jeżeli

 = 2 to I

a

= 0.

2

p

p

I

E

:

~