Transformator
Jest to urządzenie elektromagnetyczne
służące do przetwarzania energii prądu
przemiennego o danym napięciu na energię
prądu przemiennego o innym napięciu.
Zasada działania polega na
elektromagnetycznym oddziaływaniu dwóch
(lub kilku) uzwojeń nie połączonych ze sobą
elektrycznie, nawiniętych na wspólnym
rdzeniu, czyli sprzężonych ze sobą
wspólnym strumieniem magnetycznym.
Transformator
U
1
U
2
I
1
z
1
I
2
z
2
Uzwojenie pierwotne –
to, do którego
doprowadza się energię
– o liczbie zwojów z
1
,
Uzwojenie wtórne – to,
z którego odprowadza
się energię – o liczbie
zwojów z
2
.
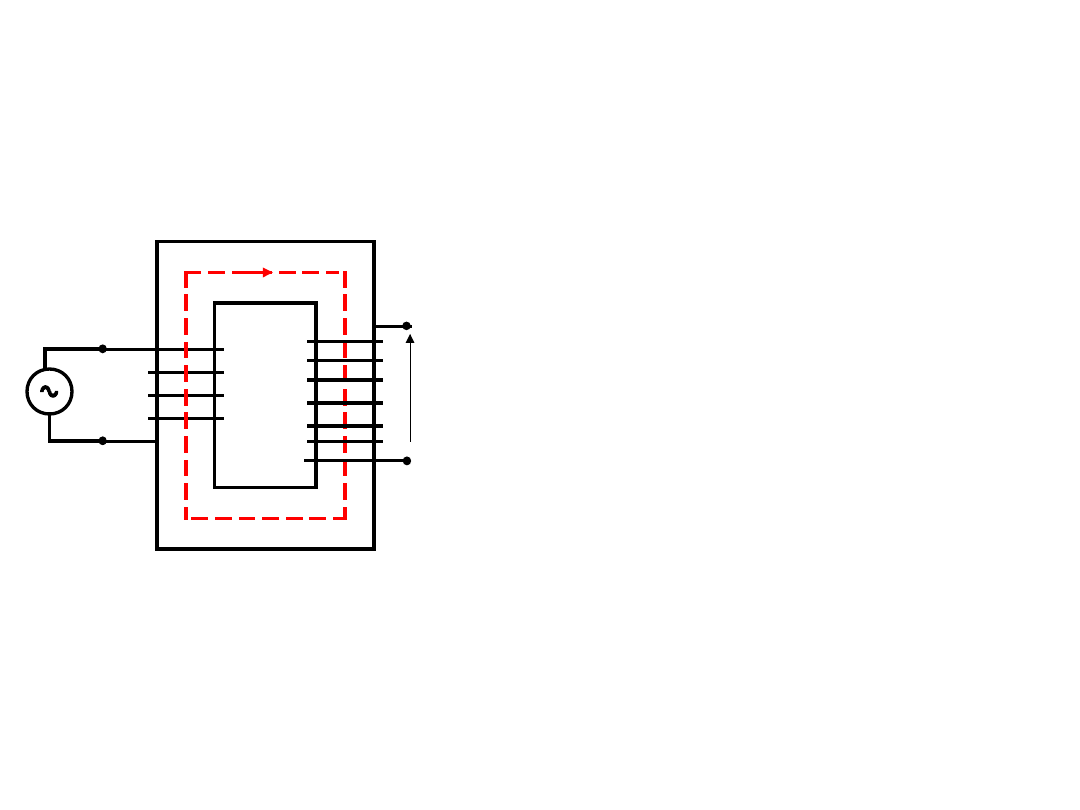
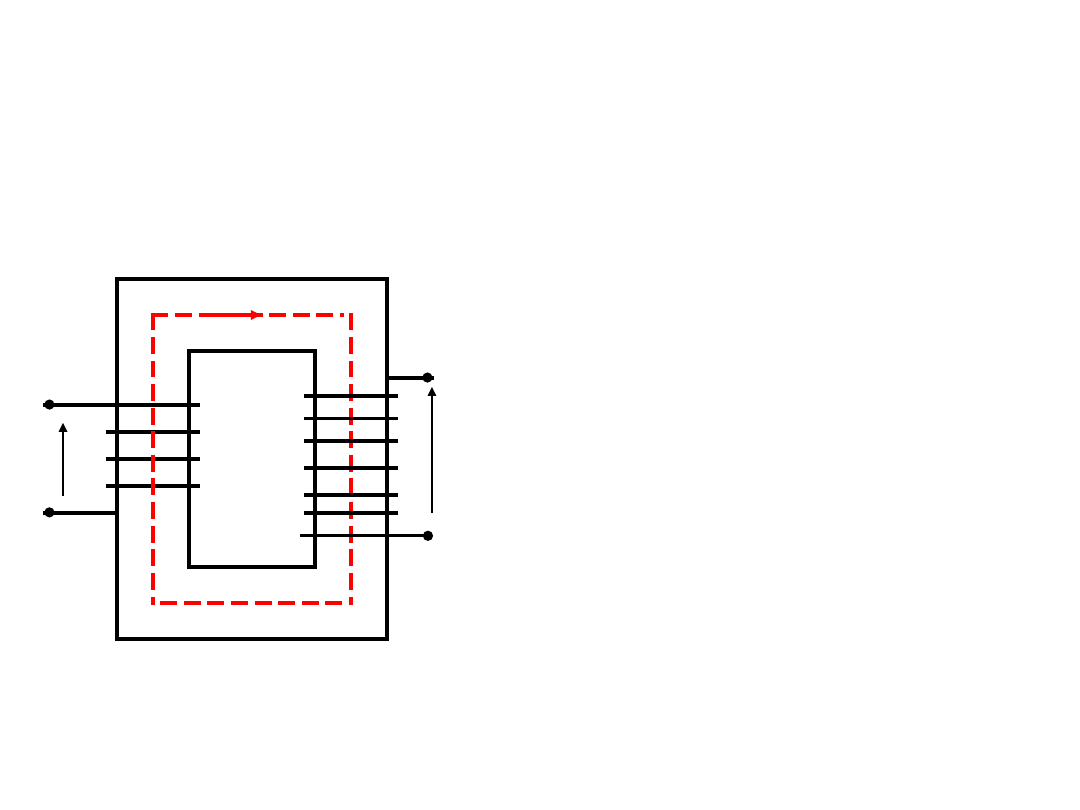
Transformator – stan jałowy
U
2
I
Uzwojenie wtórne jest
rozwarte
.
I
- prąd magnesujący,
wzbudza-jący w rdzeniu
strumień magne-tyczny.
t
m
sin
Strumień ten wywoła, zgodnie z prawem
indukcji elektro-magnetycznej, siły
elektromotoryczne we wszystkich
sprzężonych z nim uzwojeniach.
Transformator – stan jałowy
- w uzwojeniu pierwotnym:
2
sin
cos
1
1
1
1
t
z
t
z
dt
d
z
e
m
m
- w uzwojeniu pierwotnym:
2
sin
cos
2
2
2
2
t
z
t
z
dt
d
z
e
m
m
Transformator – stan jałowy
Wartości maksymalne tych sił wynoszą:
m
m
z
E
1
1
zaś wartości skuteczne:
m
m
z
E
2
2
m
m
fz
z
E
1
1
1
44
,
4
2
m
m
fz
z
E
2
2
2
44
,
4
2
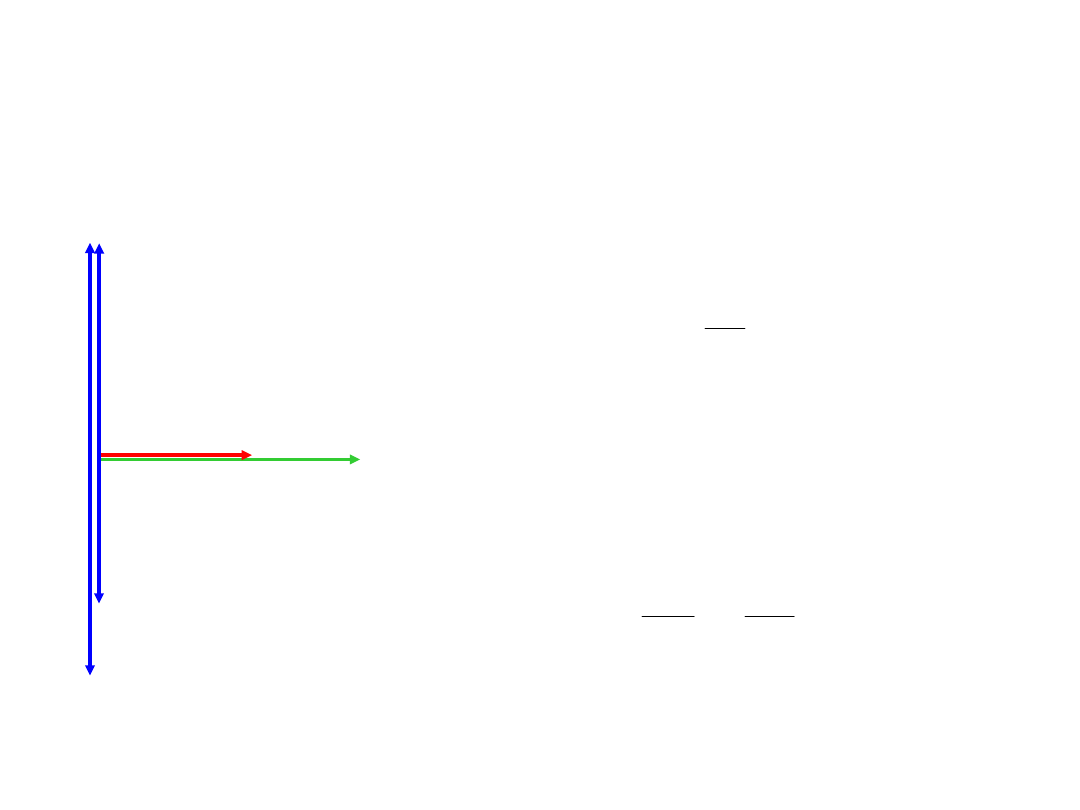
Transformator – stan jałowy
I
-E
1
E
1
U
1
E
2
=U
2
Przekładnia zwojowa
transformatora:
2
1
z
z
Przekładnia napięciowa
transformato-ra:
2
1
2
1
E
E
U
U
Transformator – stan jałowy
Dla transformatora
idealnego:
2
1
2
1
2
1
z
z
E
E
U
U
- przekładnia
transformator
a
Przekładnia transformatora określana jest
zawsze jako stosunek napięcia górnego do
dolnego, czyli
1
Transformator – stan jałowy
Ponieważ:
2
2
1
1
E
z
z
E
Jeżeli
oznaczymy:
2
2
1
'
2
E
z
z
E
to:
'
2
1
E
E
'
2
E
- siła elektromotoryczna obwodu
wtórnego odniesiona do obwodu
pierwotnego.
Jest to siła, która indukowałaby się w
uzwojeniu wtórnym, gdyby uzwojenie to miało
liczbę zwojów równą liczbie zwojów
uzwojenia pierwotnego.
Transformator – stan obciążenia
Transformator zasilany jest po stronie
pierwotnej napięciem U
1
. Jeżeli do zacisków
strony wtórnej przyłączymy obciążenie
(odbiornik), wówczas popłynie prąd w
obwodzie wtórnym i oprócz przepływu
pierwotnego I
1
z
1
powstanie przepływ wtórny
I
2
z
2
.
Zgodnie z regułą Lenza, przepływ wtórny
wytwarza strumień przeciwdziałający
wywołującemu go strumieniowi.
Transformator – stan obciążenia
Wobec tego wypadkowy strumień
magnetyczny jest mniejszy niż strumień w
stanie jałowym, SEM E
1
również jest mniejsza.
Zmniejszenie strumienia wypadkowego
wywoła na zasadzie reakcji w uzwojeniu
pierwotnym zwiększony pobór prądu ze
źródła, tak, aby przywrócić równowagę
między napięciem sieci U
1
i SEM E
1
.
Jest to samoczynne oddziaływanie prądu
wtórnego na wartość prądu pierwotnego
.
Transformator – stan obciążenia
Pomimo powstania prądu obciążenia
strumień magnetyczny sprzęgający oba
uzwojenia pozostaje niezmieniony, a więc
i SEM E
2
również.
Prąd obciążenia w transformatorze
idealnym zależy tylko od SEM E
2
oraz od
impedancji odbiornika.
Transformator – stan obciążenia
W transformatorze idealnym, bez strat, moc
pozorna doprowadzona do strony pierwotnej jest
całkowicie przeniesiona na stronę wtórną, czyli:
2
2
1
1
I
U
I
U
Stąd:
1
1
2
1
2
2
1
z
z
U
U
I
I
Wynika stąd, że w uzwojeniu górnego
napięcia płynie mniejszy prąd a w
uzwojeniu dolnego napięcia płynie większy
prąd.
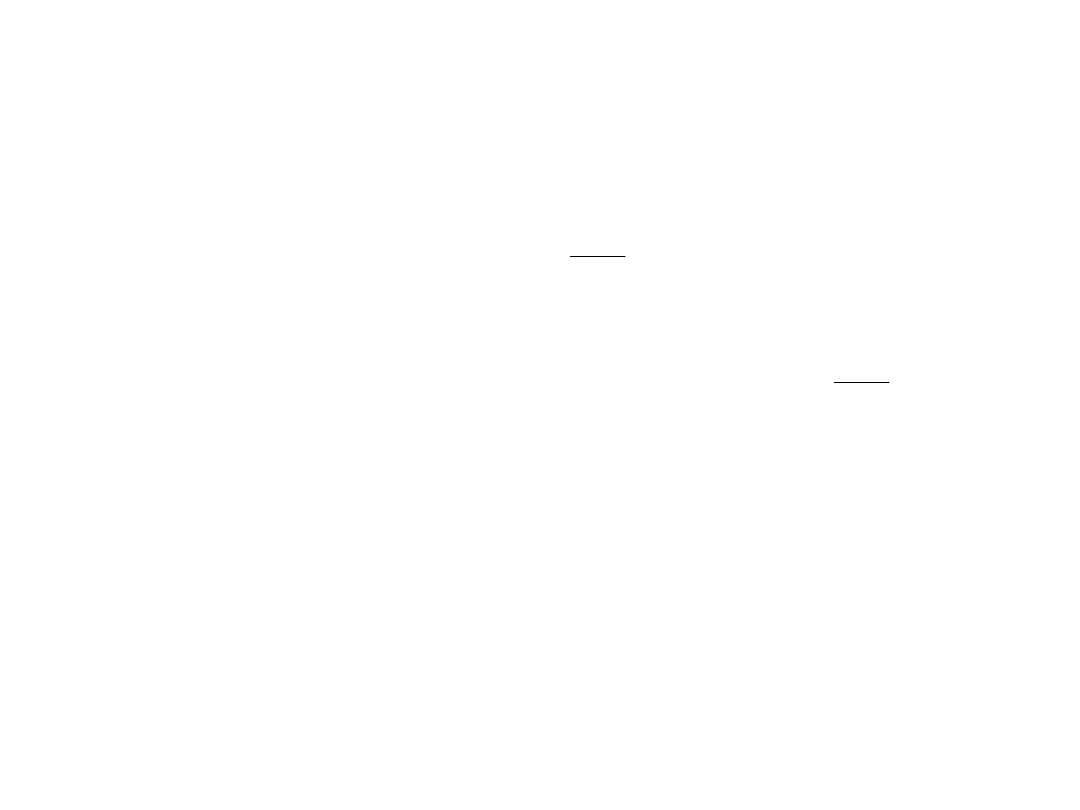
Transformator – stan obciążenia
1
2
2
1
z
z
I
I
Jeżeli oznaczymy:
1
2
2
'
2
z
z
I
I
To:
'
2
1
I
I
'
2
I
- prąd obwodu wtórnego odniesiony
do obwodu pierwotnego. Jest to prąd,
który płynąłby w uzwojeniu wtórnym
w przypadku z
2
= z
1
.
Transformator – stan obciążenia
Jeżeli obwód wtórny zostanie obciążony np.
rezystancją R, to prąd wtórny wyniesie:
1
1
2
2
2
1
E
z
z
R
R
E
I
a prąd
pierwotny:
1
2
1
2
'
2
1
1
E
z
z
R
I
I
lub:
R
E
I
2
1
1
Transformator – stan obciążenia
R
E
I
2
1
1
Wynika stąd, że dla wyznaczenia prądu w
obwodzie pierwotnym należy rezystancję
umieszczoną w obwodzie wtórnym
pomnożyć
przez kwadrat przekładni
.
Transformator – stan obciążenia
Szczególny przypadek, jakim jest włączenie
rezystancji wskazuje na ogólnie
obowiązującą zależność przeliczania
impedancji z obwodu wtórnego do
pierwotnego. Działanie impedancji Z
2
w
obwodzie wtórnym jest takie samo jak
impedancji
w obwodzie pierwotnym.
2
2
'
2
Z
Z
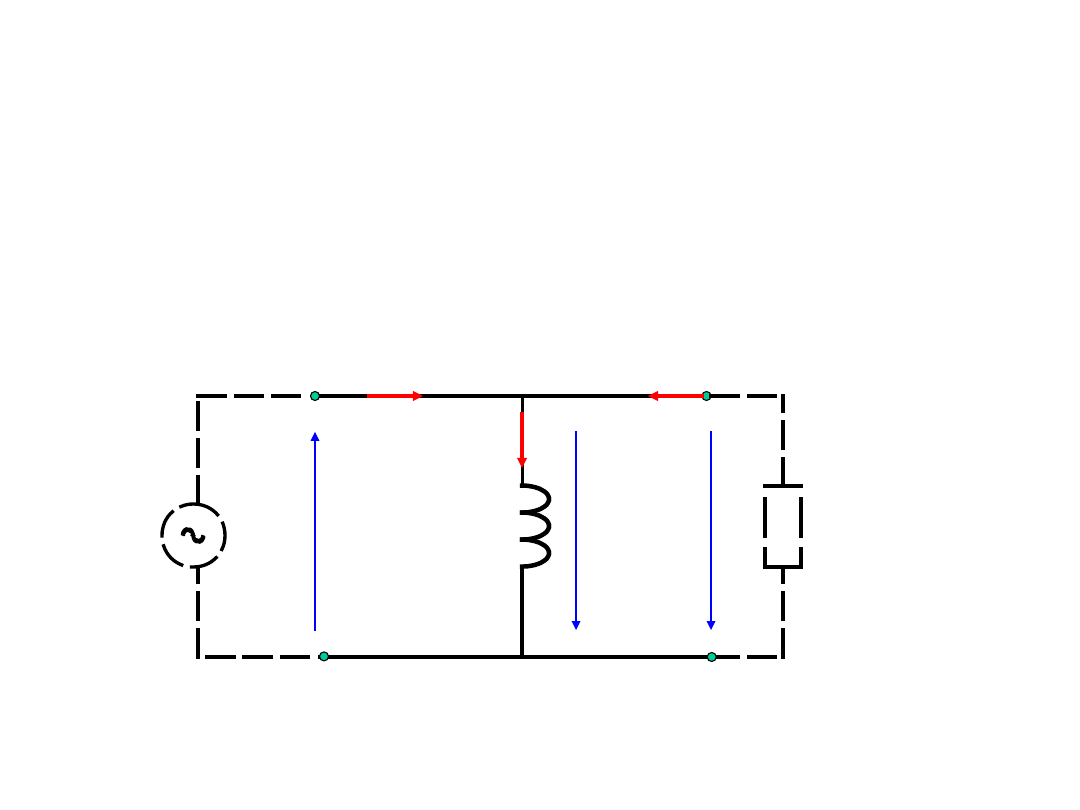
Transformator – stan obciążenia
Schemat zastępczy transformatora
idealnego:
I
1
I
2
’
I
X
Z
obc
’
U
1
E
1
=E
2
’
U
2
’
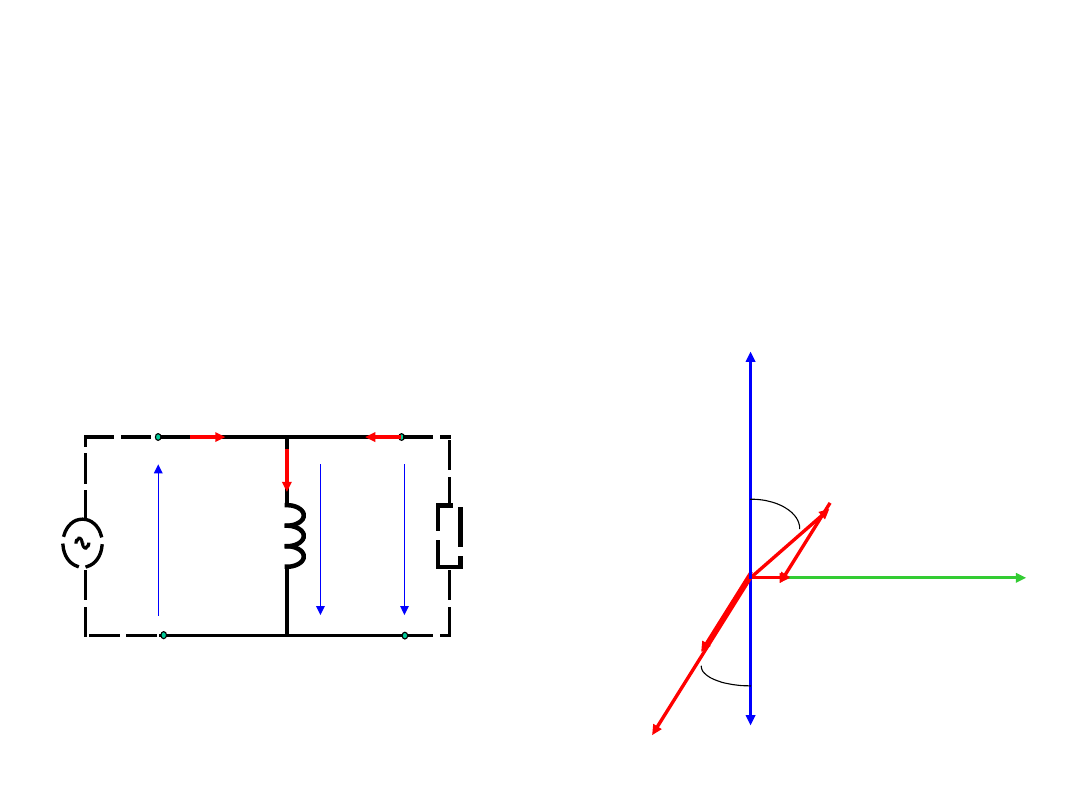
Transformator – stan obciążenia
Wykres wskazowy transformatora
idealnego przy obciążeniu:
I
1
I
2
’
I
X
Z
obc
’
U
1
E
1
=E
2
’
U
2
’
U
1
=-E
1
U
2
=E
2
1
2
I
1
I
2
’
I
I
2
I
2
’
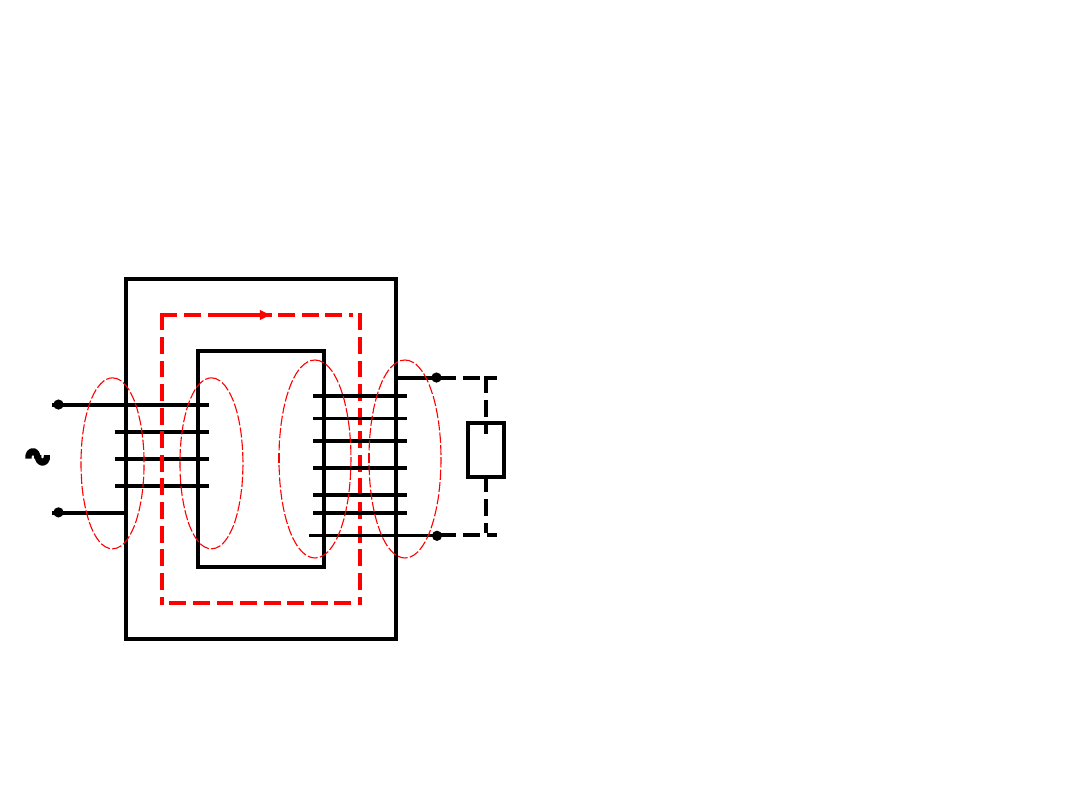
Transformator rzeczywisty
Z
obc
Tym różni się od
idealnego, że
uwzględnia się w
nim rezystancje
uzwojeń (czyli
straty mocy) oraz
reaktancje
(uwzględniają
różne strumienie
rozproszenia
skojarzone z
uzwojenia-mi z
1
oraz z
2
.
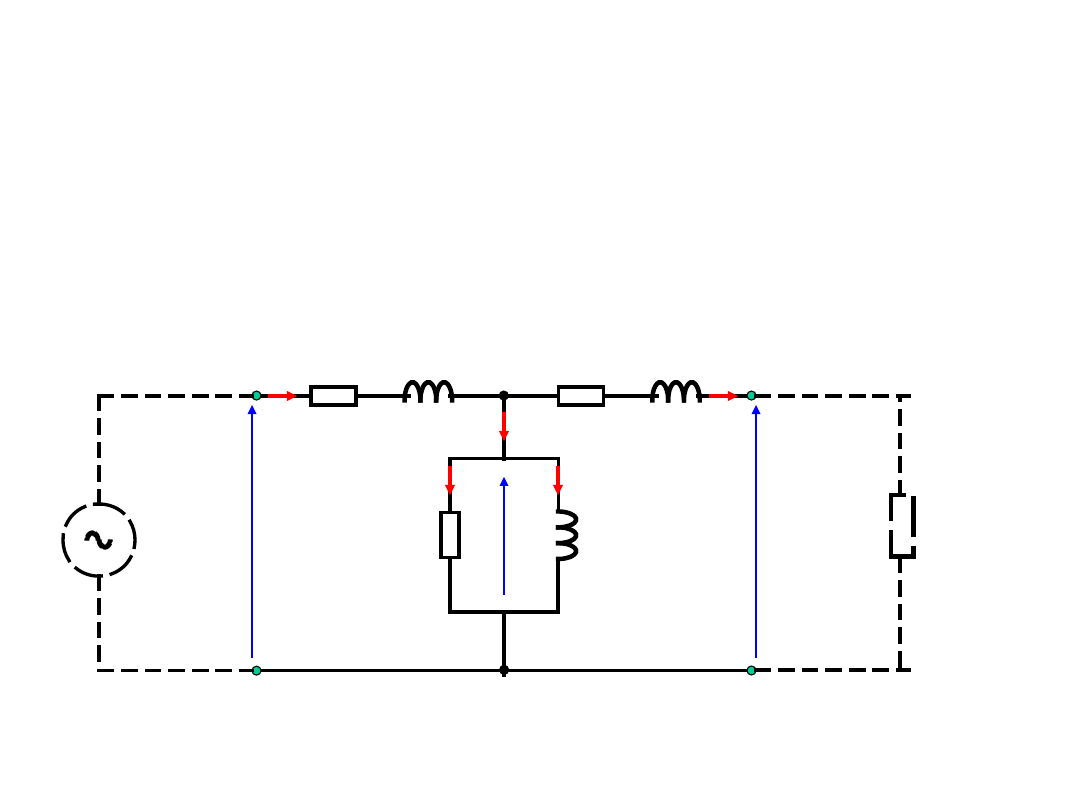
Transformator rzeczywisty
Schemat zastępczy transformatora:
U
1
U
2
’
-E
1
E
2
’
I
1
I
2
’
I
0
I
Fe
I
X
1
X
2
’
R
1
R
2
’
X
R
Fe
Z
obc
’
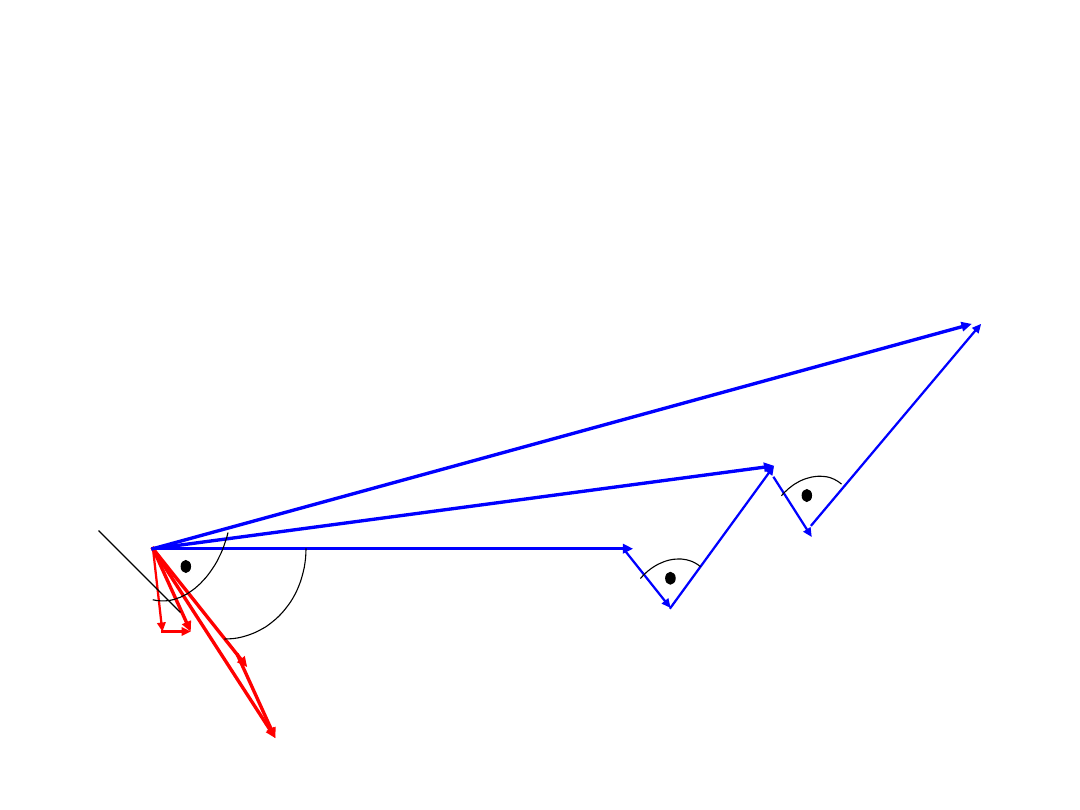
Transformator rzeczywisty
Wykres wskazowy dla stanu obciążenia:
U
2
’
-
E
1
=E
2
’
U
1
R
2
’
I
2
’
X
2
’
I
2
’
R
1
I
1
X
1
I
1
I
2
’
I
0
I
I
F
e
I
0
2
Transformator rzeczywisty – stan
zwarcia
Przy pracy transformatora jest to stan
awaryjny.
W celu zmierzenia niektórych parametrów
charakteryzujących transformator
wykonywane jest zwarcie pomiarowe.
W stanie zwarcia Z
obc
= 0 i napięcie na
zaciskach uzwojenia wtórnego U
2’
= 0.
Wartość prądu (zwarciowego) jaki płynie w
uzwojeniu wtórnym i pierwotnym zależy od
wartości napięcia pierwotnego.
Transformator rzeczywisty – stan
zwarcia
Zwarcie pomiarowe wykonuje się zwykle w
takich warunkach, aby nie uszkodzić
urządzenia.
Do zacisków pierwotnych doprowadza się
napięcie, przy którym w uzwojeniach płyną
prądy znamionowe – napięcie to nazywa się
napięciem zwarciowym
.
Ponieważ U
2’
= 0, to E
2’
jest bardzo mała, a
więc i prąd w gałęzi poprzecznej jest tak
mały, że można tę gałąź pominąć.
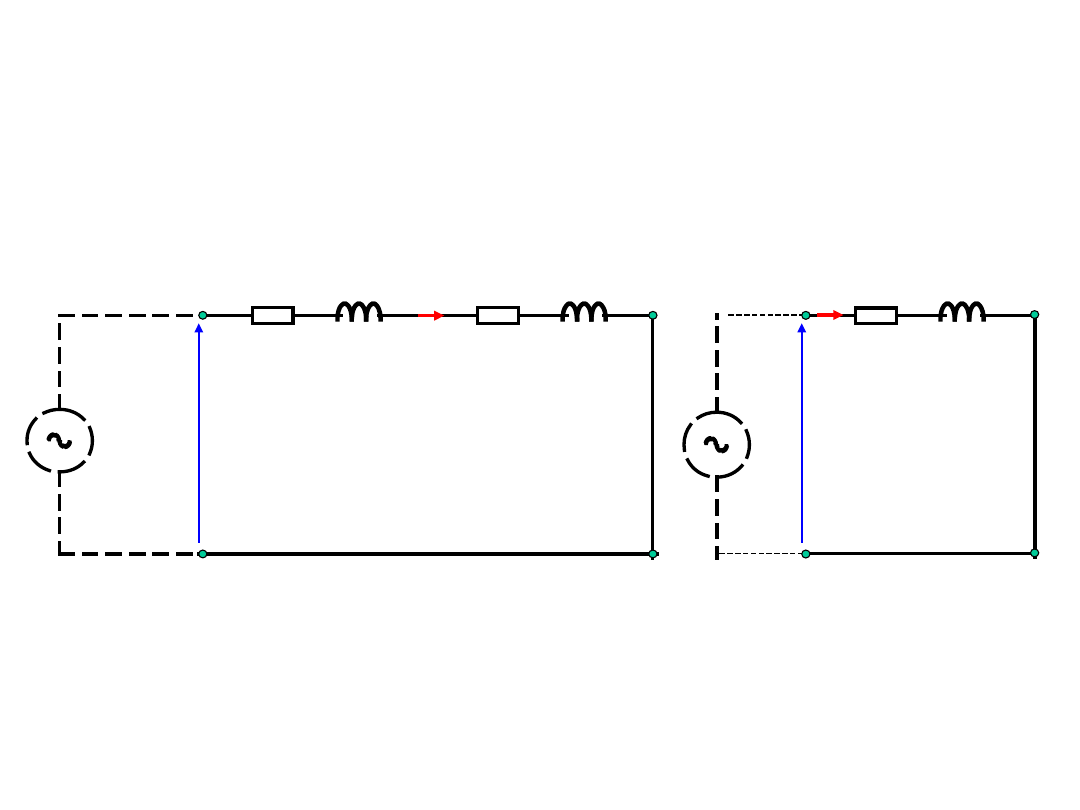
Transformator rzeczywisty – stan
zwarcia
U
1
I
X
1
X
2
’
R
1
R
2
’
U
1
I
X
z
R
z
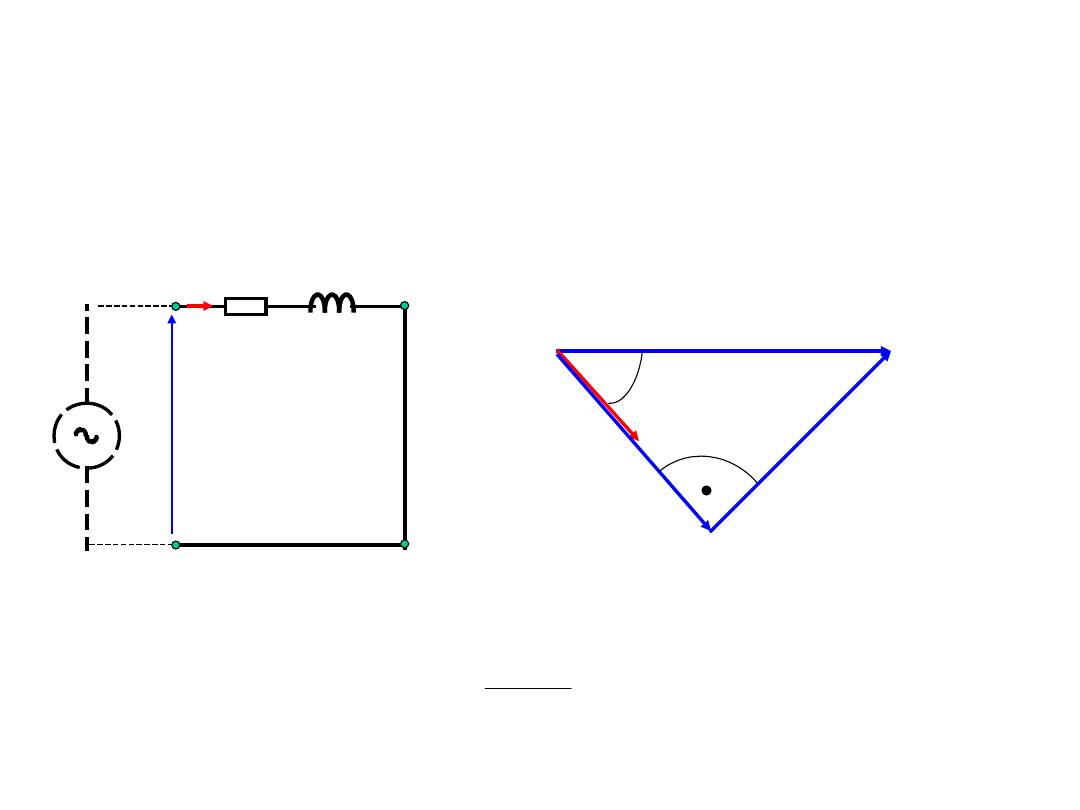
Transformator rzeczywisty – stan
zwarcia
U
1
I
X
z
R
z
z
I
IR
z
IX
z
U
1
%
100
1
n
z
z
U
U
u
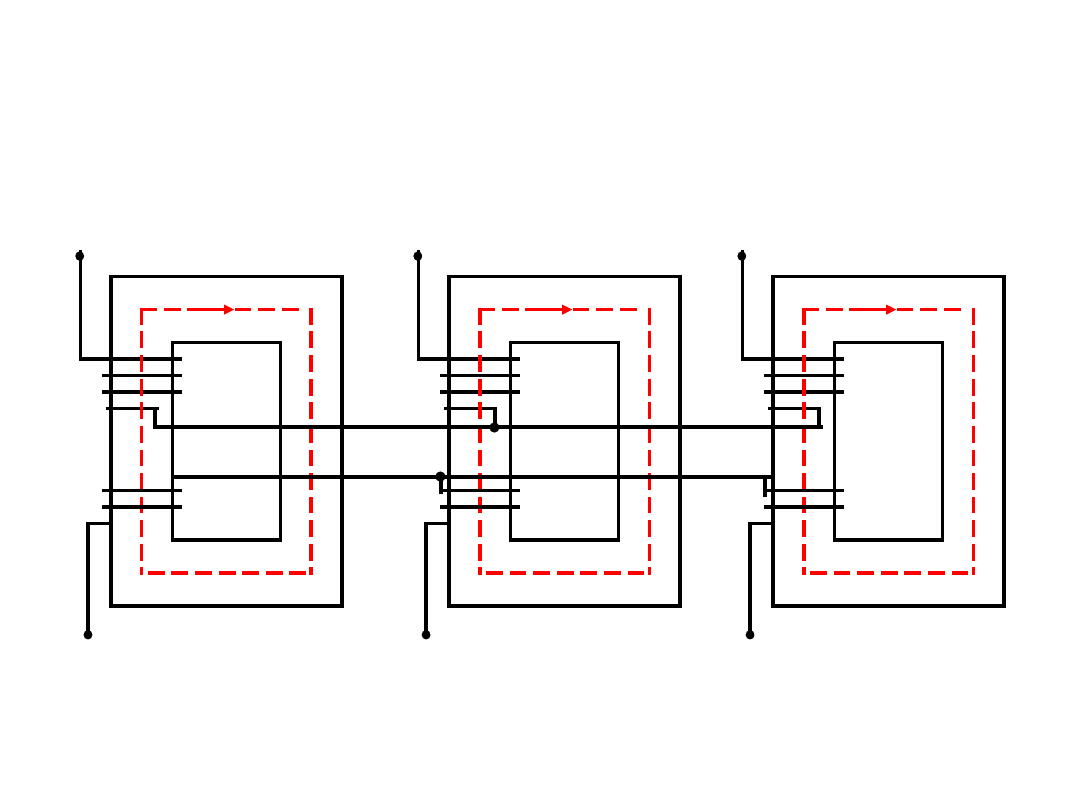
Transformatory trójfazowe
A
B
C
1
A
2
A
1
B
2
B
1
C
2
C
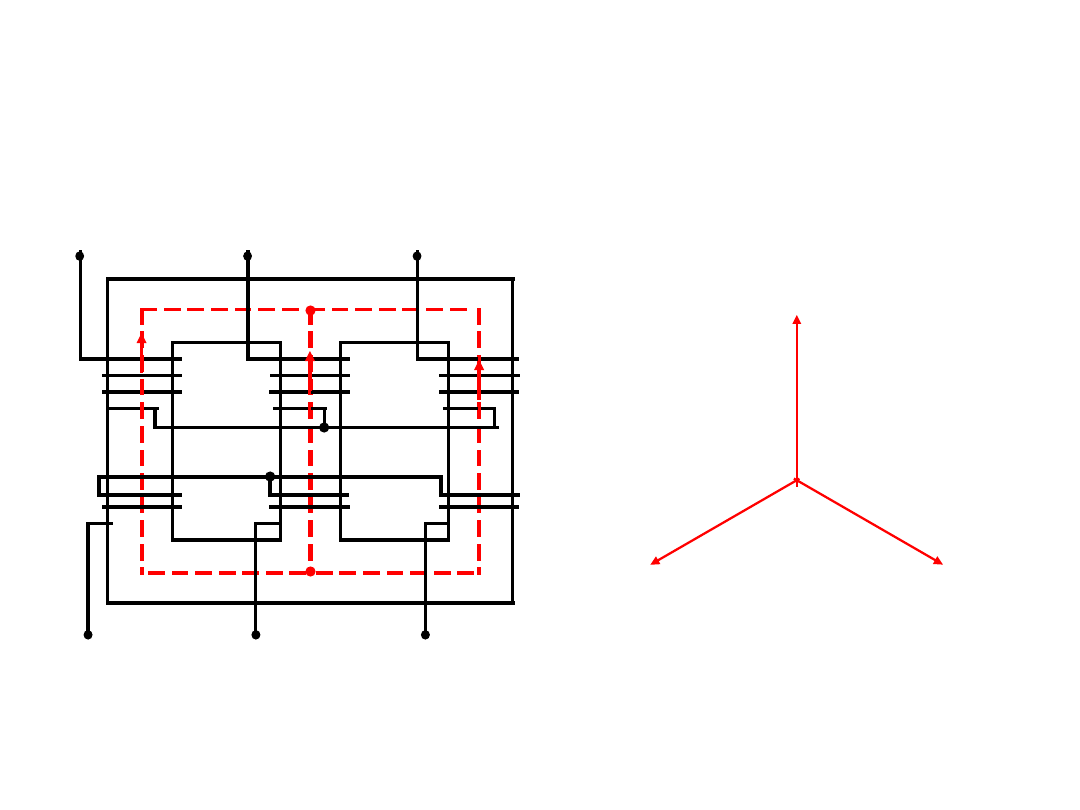
Transformatory trójfazowe
A
1
A
2
A
B
1
B
2
B
1
C
2
C
C
B
A
C
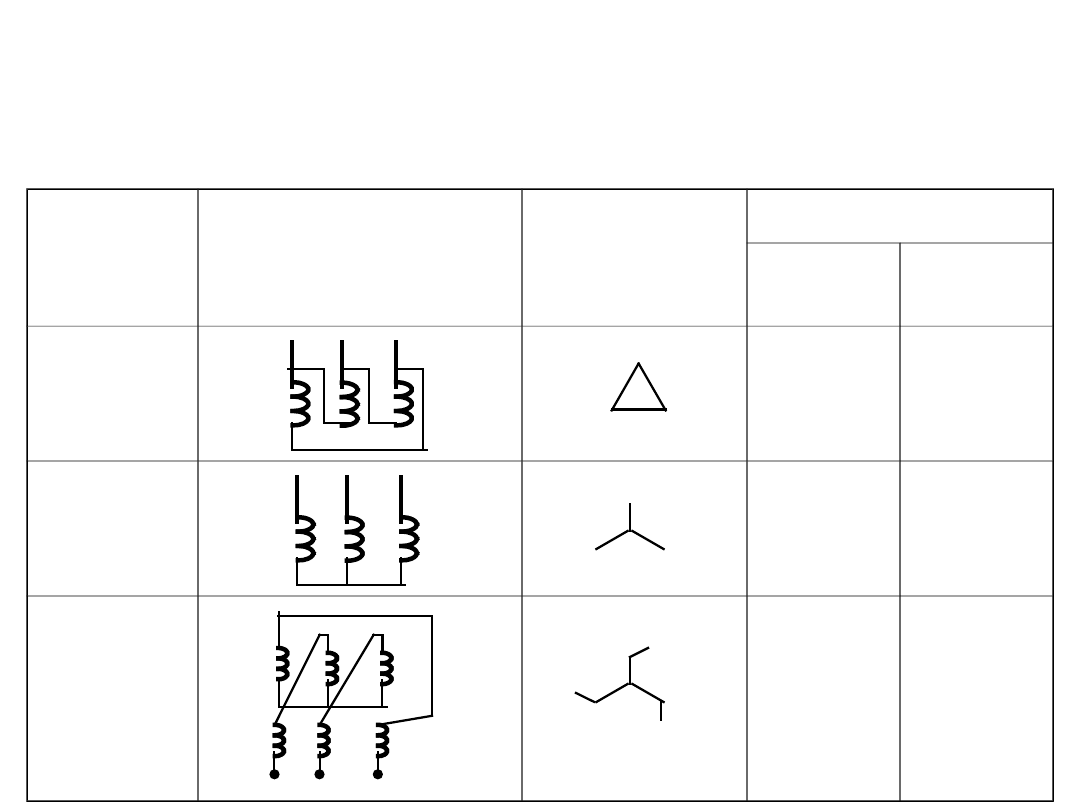
Transformatory trójfazowe
Układ
Schemat
Symbol
graficzny
Symbol literowy
Strona
górna
Strona
dolna
Trójkąt
D
d
Gwiazda
Y
y
Zygzak
-
z
Transformatory trójfazowe
Przekładnia transformatorów
trójfazowych to stosunek napięć
międzyprzewodowych
.
Ponieważ przekładnia zwojowa
odpowiada stosunkowi napięć fazowych,
dla transformatorów trójfazowych
przekładnia zależy nie tylko od liczby
zwojów ale i od układu połączeń
uzwojeń strony górnej i dolnej.
Transformatory trójfazowe
układ
przekładnia
Yy, Dd
Dy, Yz
Yz
Dz
2
1
z
z
2
1
3z
z
2
1
3
2
z
z
2
1
3
2
z
z
Transformatory specjalne -
autotransformator
Stosowane są wówczas, gdy potrzebna jest
transformacja z przekładnią niewiele
różniącą się od 1. Uzwojenie pierwotne jest
galwanicznie połączone z wtórnym.
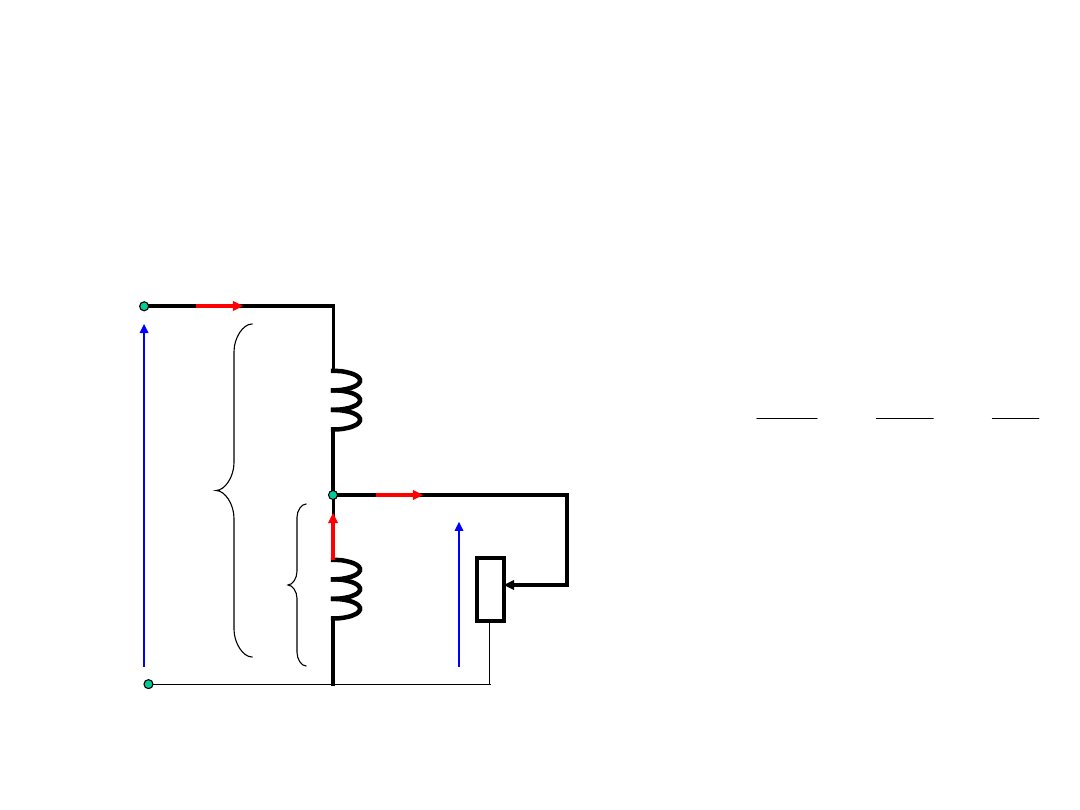
Transformatory specjalne -
autotransformator
z
1
z
2
U
1
I
1
I
2
I
2
-I
1
U
2
Przekładnia:
2
1
2
1
2
1
z
z
E
E
U
U
AT
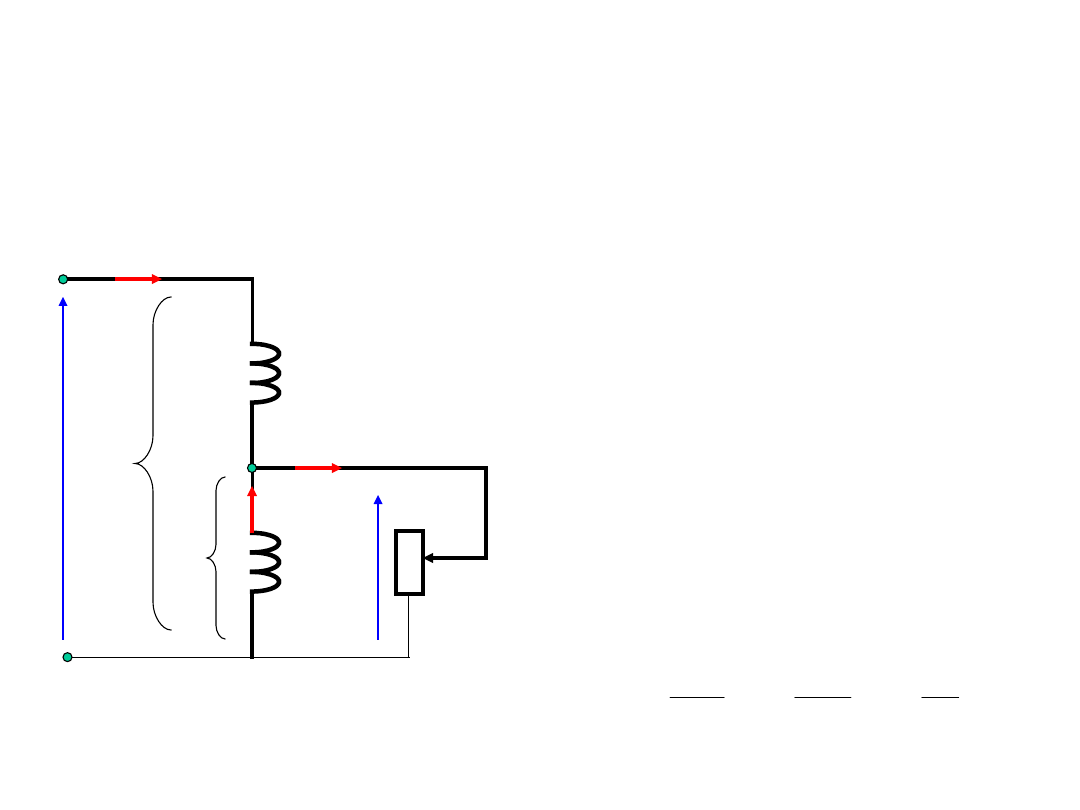
Transformatory specjalne -
autotransformator
z
1
z
2
U
1
I
1
I
2
I
2
-I
1
U
2
Przez zwoje z
1
-z
2
płynie
prąd I
1
, a przez zwoje
z
2
płynie prąd I
2
-I
1
.
Wobec tego przepływy
z uwzględnieniem
zwrotów prądów:
0
2
1
2
2
1
1
z
I
I
z
z
I
czyli:
1
1
2
2
1
z
z
I
I
Transformatory specjalne -
przekładniki
Stosowane w układach pomiarowych w celu
dopasowa-nia mierzonych napięć i prądów
do znormalizowanych zakresów mierników
napięcia, prądu i mocy, również do
rozszerzenia zakresu pomiarowego lub
odizolowania od wysokiego napięcia.
Pośredniczą również w zasilaniu obwodów
wtórnych do regulacji, sterowania i
zabezpieczeń.
Przekładniki napięciowe
Zwykle są jednofazowe – ich działanie i
możliwość pracy jest taka jak dla
transformatorów mocy.
Napięcie pierwotne o różnych
wartościach, napięcie wtórne zwykle
100V lub V.
3
100
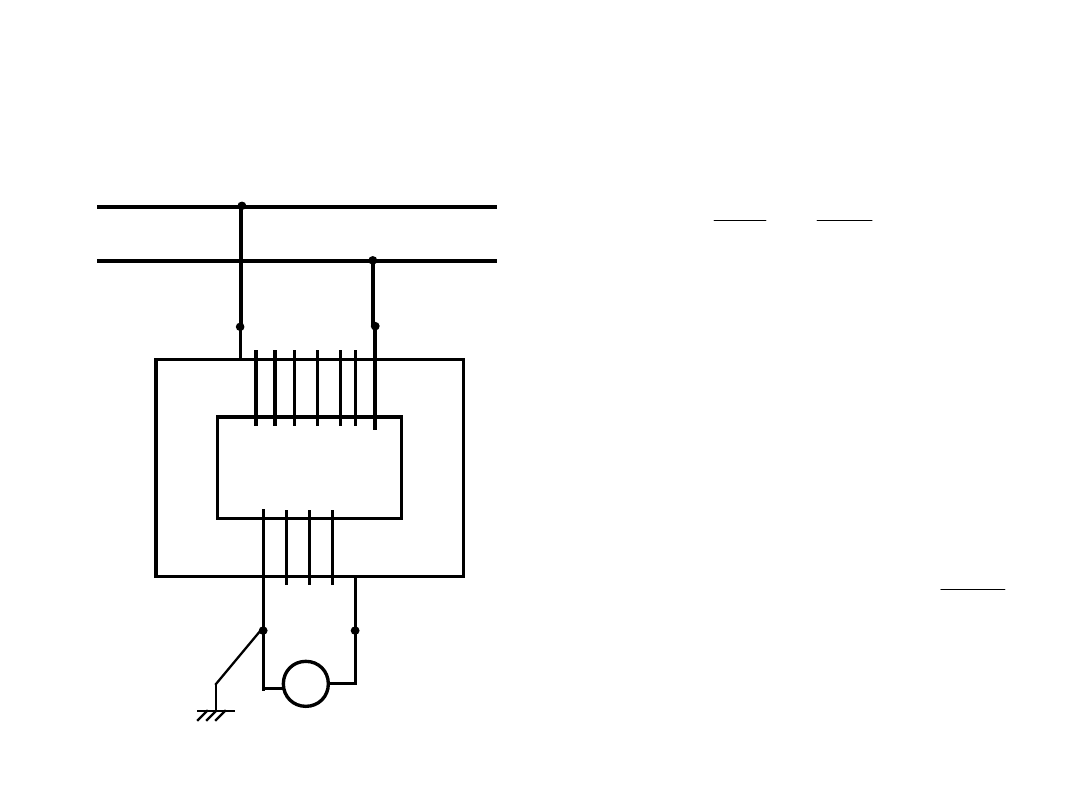
Przekładniki napięciowe
V
a
b
A
B
L1
L2
2
1
2
1
N
N
U
U
N
1
– liczba zwojów
uzwojenia
pierwotnego, N
2
–
liczba zwojów
uzwojenia
wtórnego.
Przekładnia:
2
1
U
U
k
U
Praca w stanie zbliżonym do
stanu jałowego
.
Przekładniki prądowe
Prąd pierwotny o różnych wartościach, prąd
wtórny zwykle 5A lub 1A.
Obwód wtórny przekładnika prądowego
pracuje normalnie prawie w stanie zwarcia
(przyłącza się do niego bardzo małe
impedancje cewek mierników, liczników lub
przekaźników).
Przekładniki prądowe
Przy rozwarciu zacisków obwodu wtórnego
wystąpiłby wzrost strumienia
magnetycznego do wartości występującej w
stanie jałowym. Na zaciskach wtórnych
powstałaby, proporcjonalnie do przekładni
duża wartość napięcia (niebezpieczna dla
użytkownika). Poza tym powstałby wzrost
strat w stali rdzenia, czyli wzrost
temperatury groźny dla izolacji
przekładnika.
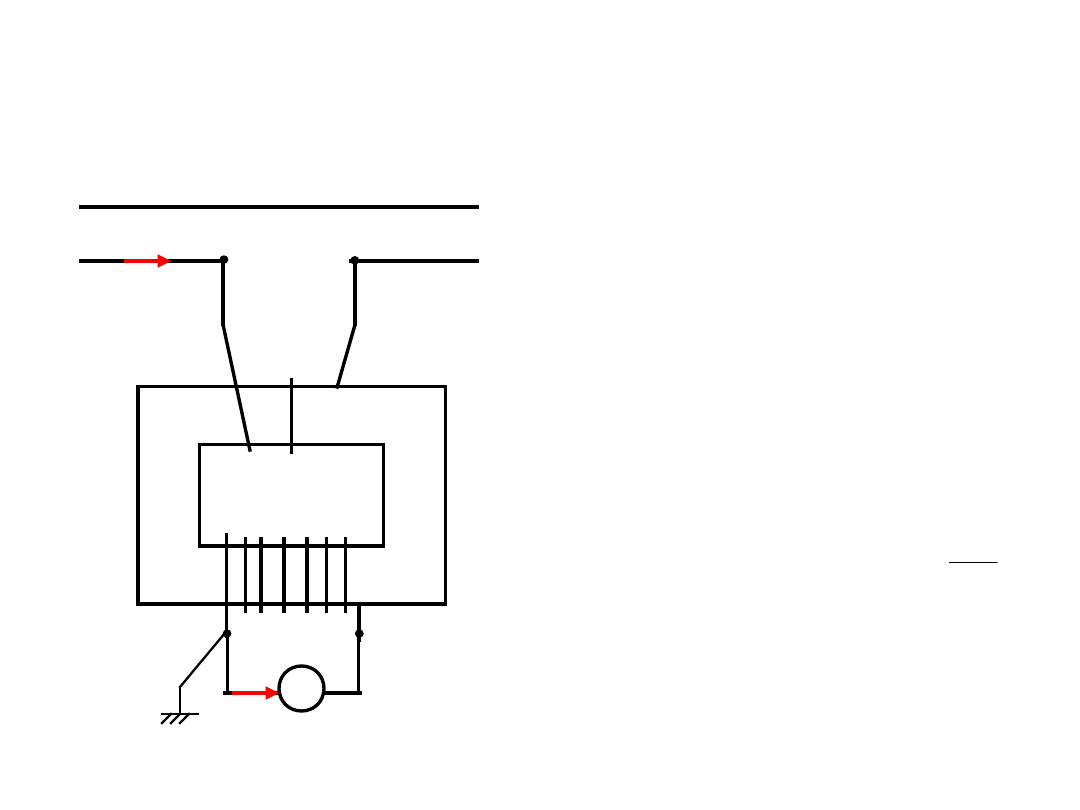
Przekładniki prądowe
2
2
1
1
N
I
N
I
N
1
– liczba zwojów
uzwojenia
pierwotnego, N
2
–
liczba zwojów
uzwojenia
wtórnego.
Przekładnia:
2
1
I
I
k
I
A
P
1
P2
L1
L2
I
1
I
2
S
2
S
1
Pomiary wielkości elektrycznych
Pomiar mocy prądu stałego
Można:
1. - zmierzyć napięcie U na zaciskach
odbiornika i prąd I płynący przez
odbiornik i obliczyć moc pobieraną:
P = U I
2. - użyć watomierza
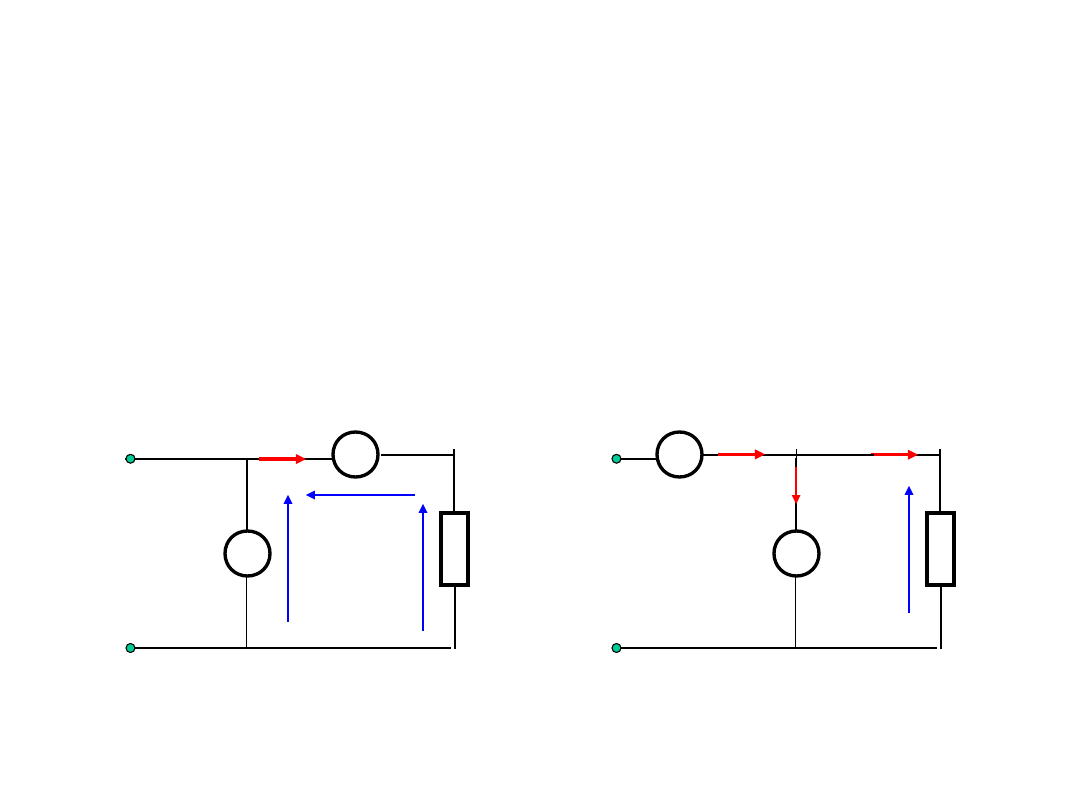
Pomiary wielkości elektrycznych
Pomiar mocy prądu stałego
Pomiar napięcie U na zaciskach odbiornika i prądu I
płynącego przez odbiornik.
A
V
U
A
U
V
U
R
A
R
V
R
I
A
= I
1
)
A
V
U
V
=
U
R
A
R
V
R
I
2
)
I
A
I
V
Moc obliczona za wskazań mierników:
P’=U
V
I
A
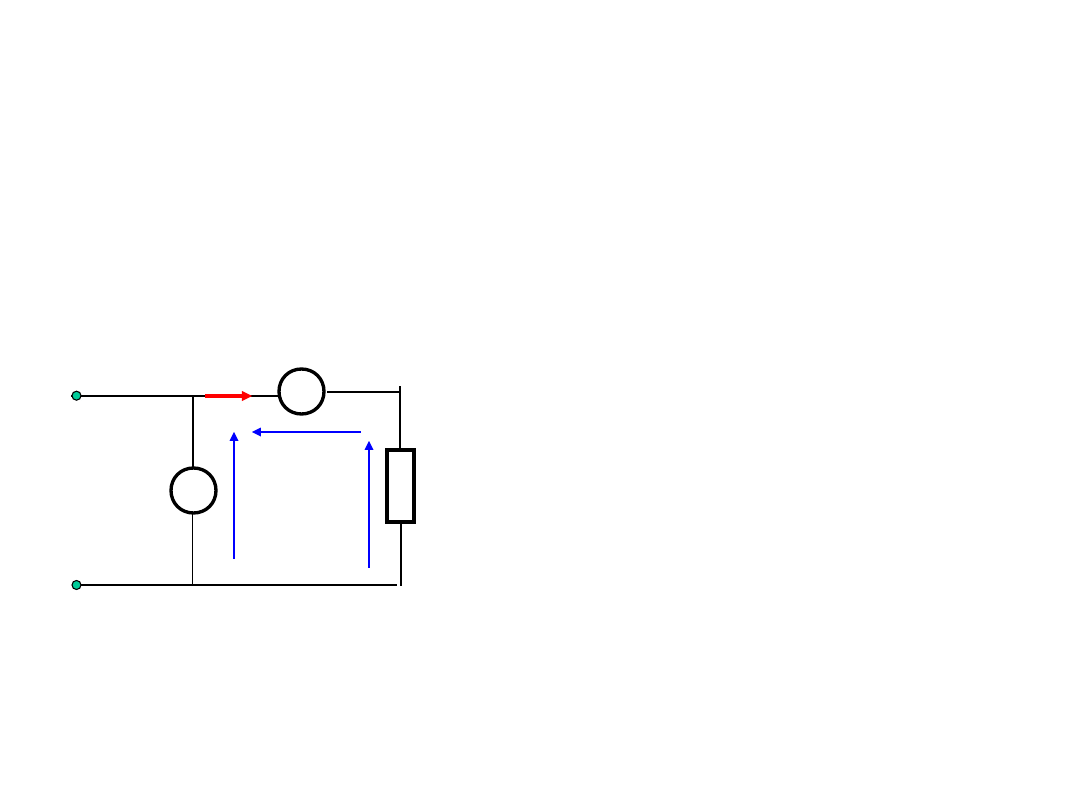
Pomiary wielkości elektrycznych
Pomiar mocy prądu stałego
Przyrządy pomiarowe pobierają pewna moc.
A
V
U
A
U
V
U
R
A
R
V
R
I
A
= I
1
)
Moc pobierana przez
odbiornik:
a
A
A
A
V
A
A
A
V
P
P
I
R
I
U
I
I
R
U
UI
P
'
2
Poprawka obliczeniowa –
moc
pobierana przez amperomierz:
A
A
a
R
I
P
2
Poprawkę można
zaniedbać gdy:
A
R
R
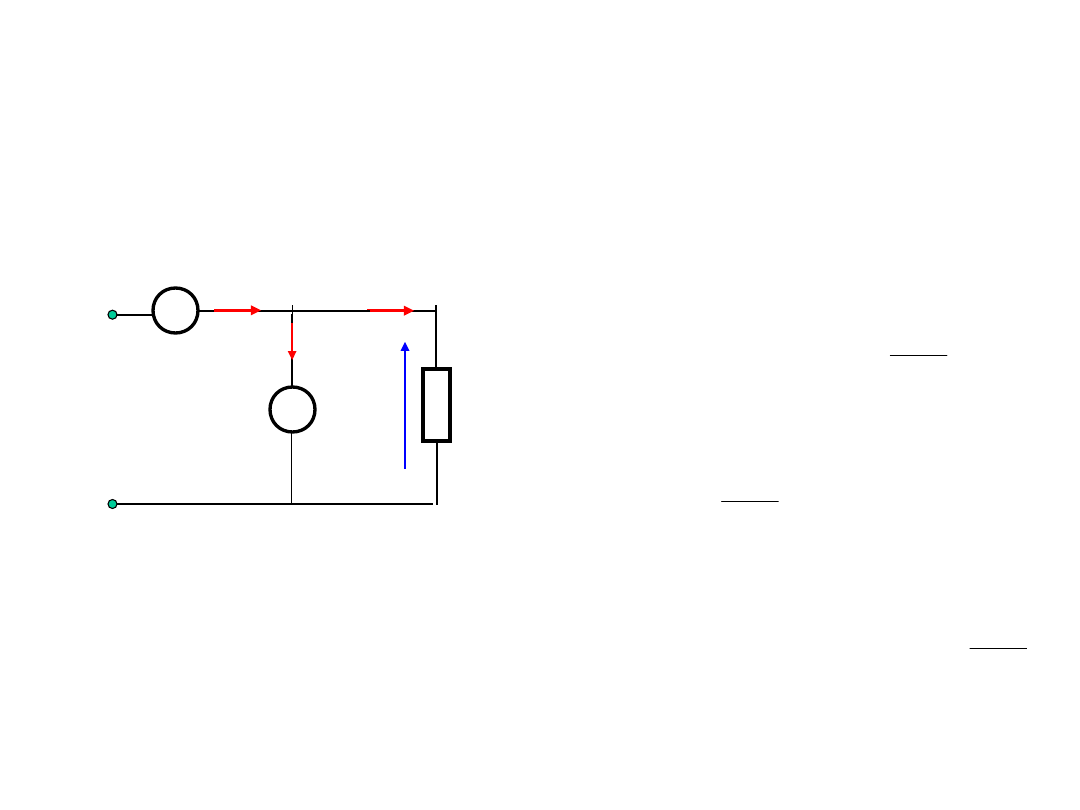
Pomiary wielkości elektrycznych
Pomiar mocy prądu stałego
Moc pobierana przez
odbiornik:
b
V
V
A
V
V
V
A
V
P
P
R
U
I
U
R
U
I
U
UI
P
'
2
Poprawka – moc pobierana przez
woltomierz:
V
V
b
R
U
P
2
Poprawkę można
zaniedbać gdy:
V
R
R
A
V
U
V
=
U
R
A
R
V
R
I
2
)
I
A
I
V
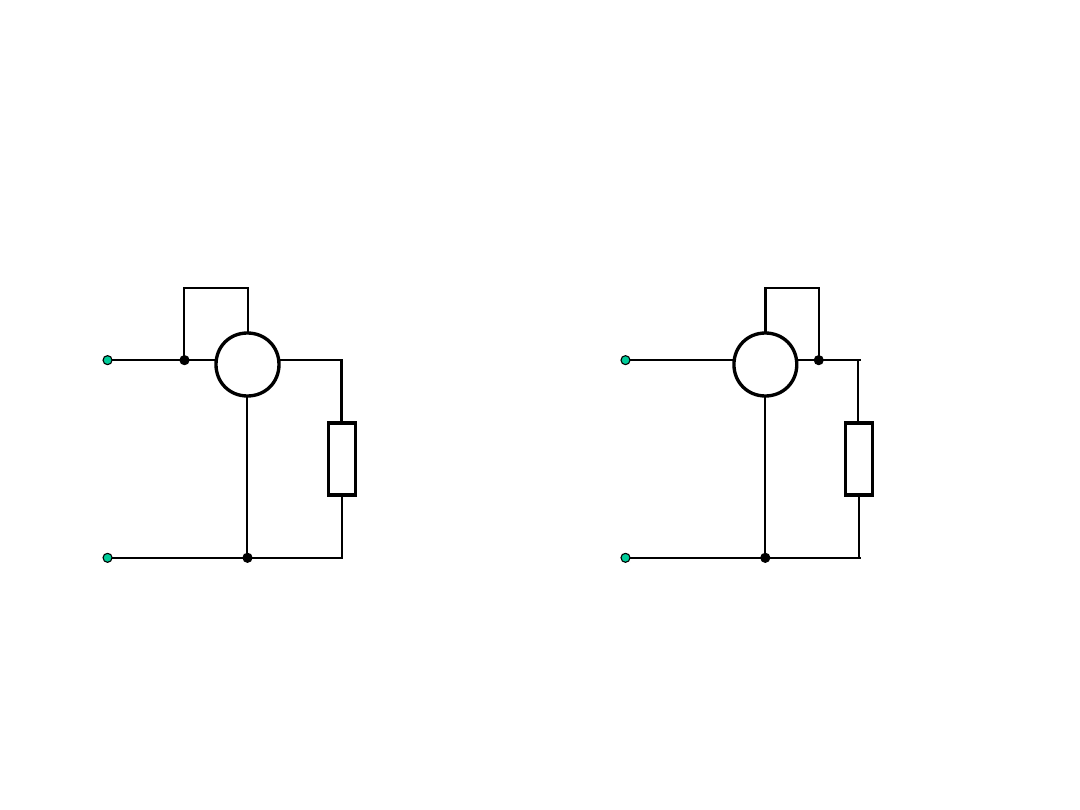
Pomiary wielkości elektrycznych
Pomiar mocy prądu stałego lub
mocy czynnej prądu
sinusoidalnego
R
W
W
R
lub
Układ dla dużych
rezystancji
odbiornika
Układ dla małych
rezystancji
odbiornika
Pomiary wielkości elektrycznych
Pomiar mocy czynnej w układzie
trójfazowym
Można zastosować jeden z układów:
- jeden watomierz (jeżeli obciążenie jest
symetryczne, czyli moce pobierane we
wszystkich fazach są jednakowe),
-układ trzech watomierzy,
-jeden watomierz trójfazowy,
-układ dwóch watomierzy.
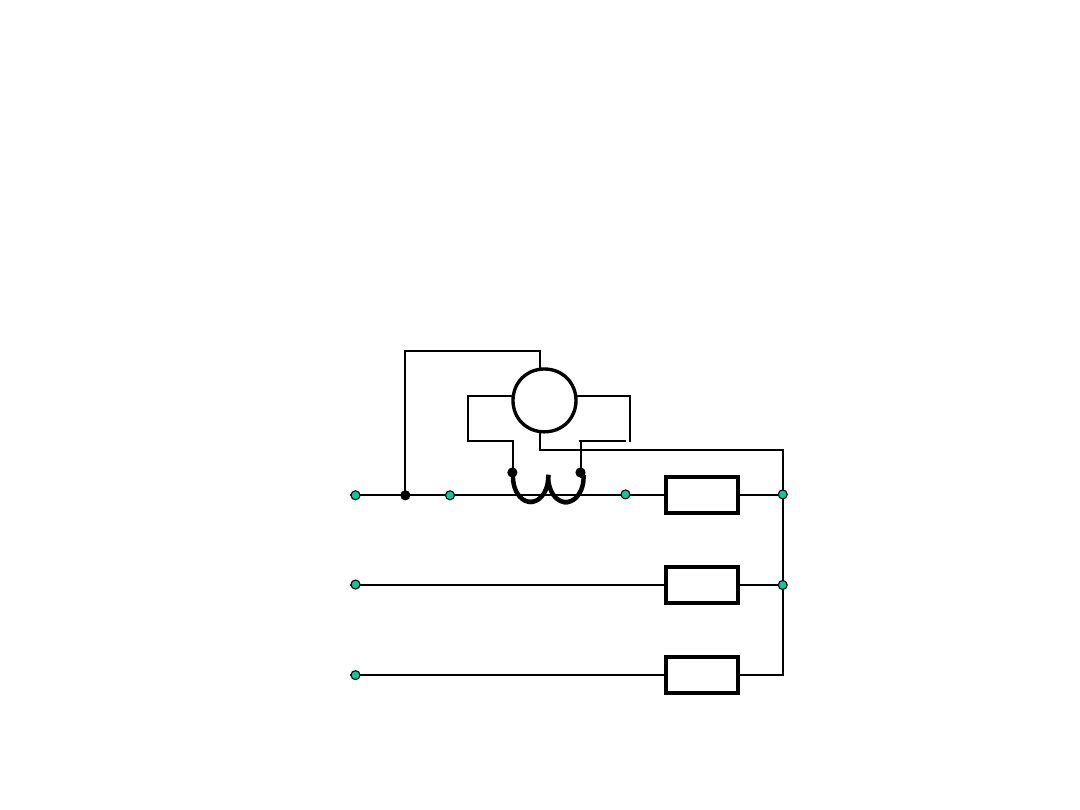
Pomiar mocy czynnej w układzie
trójfazowym
Układ jednego watomierza z zastosowaniem
przekładnika prądowego.
W
S1
S2
P1
P2
Z
Z
Z
L1
L2
L3
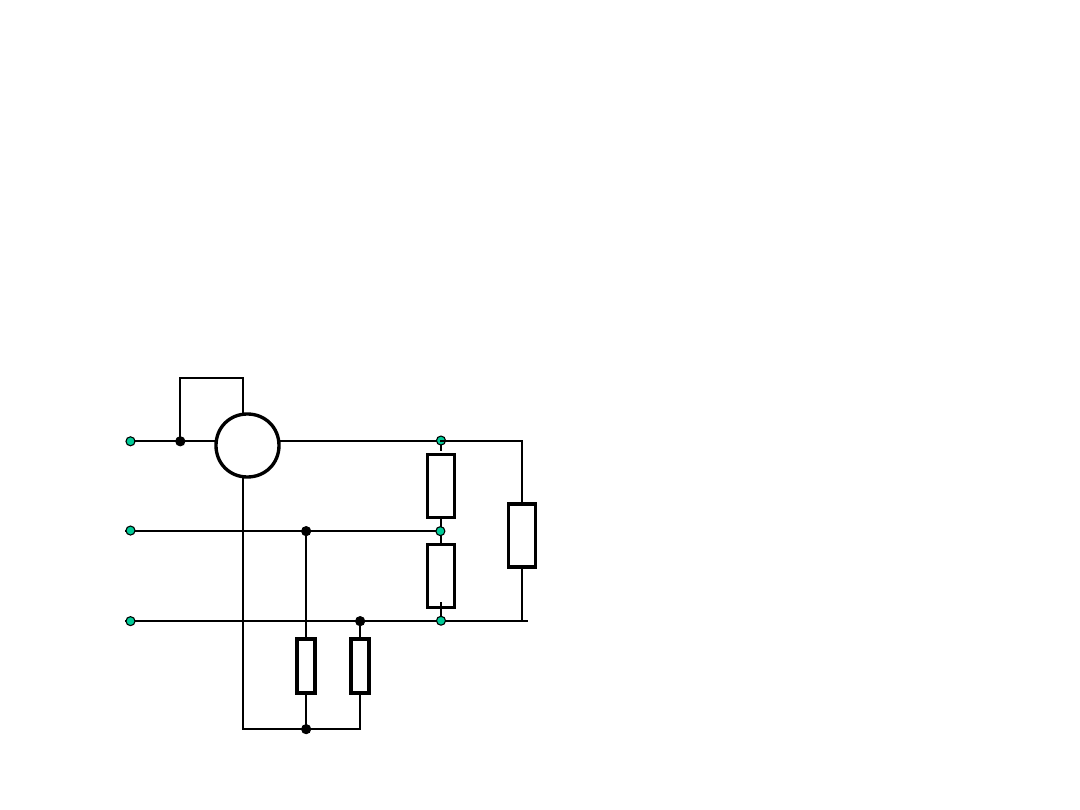
Pomiar mocy czynnej w układzie
trójfazowym
Układ jednego watomierza z zastosowaniem
sztucznego punktu neutralnego.
W
Z
Z
Z
L1
L2
L3
R
1
R
2
R
1
= R
2
= R
Wn
–
wprowadza
symetrię
zakłóconą przez
pojedynczą
cewkę
napięciową
watomierza.
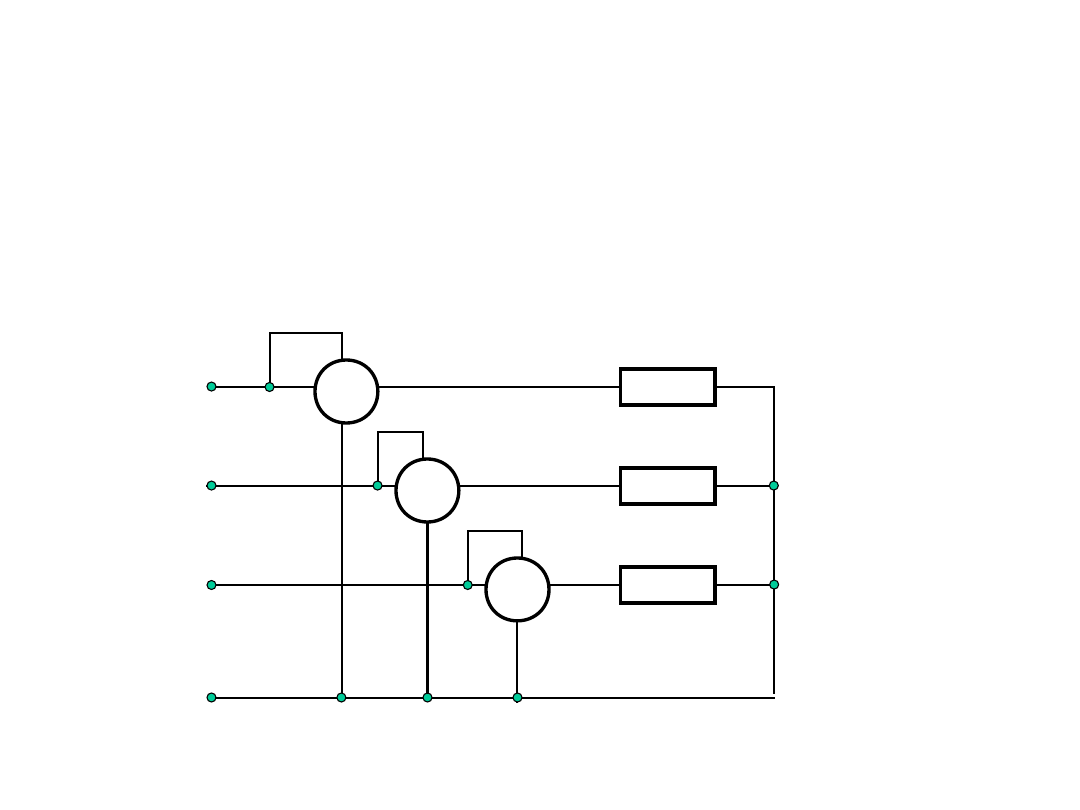
Pomiar mocy czynnej w układzie
trójfazowym
Układ trzech watomierzy.
W
W
W
L3
L2
L1
N
Z3
Z2
Z1
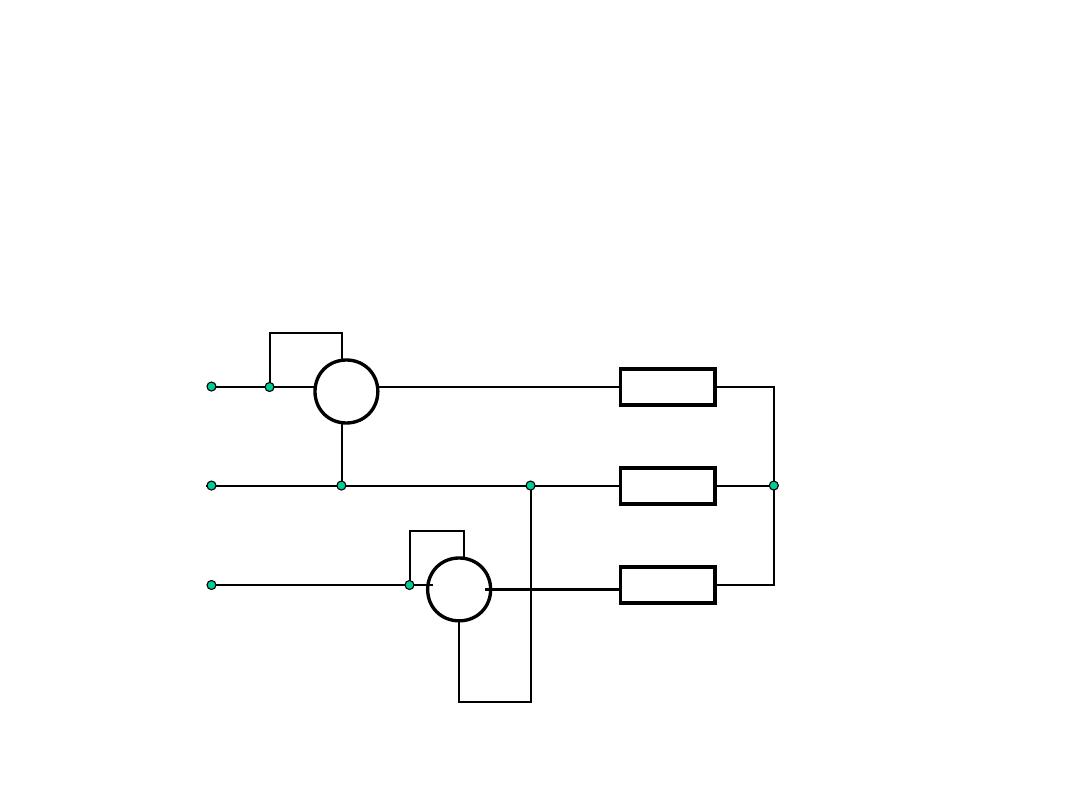
Pomiar mocy czynnej w układzie
trójfazowym
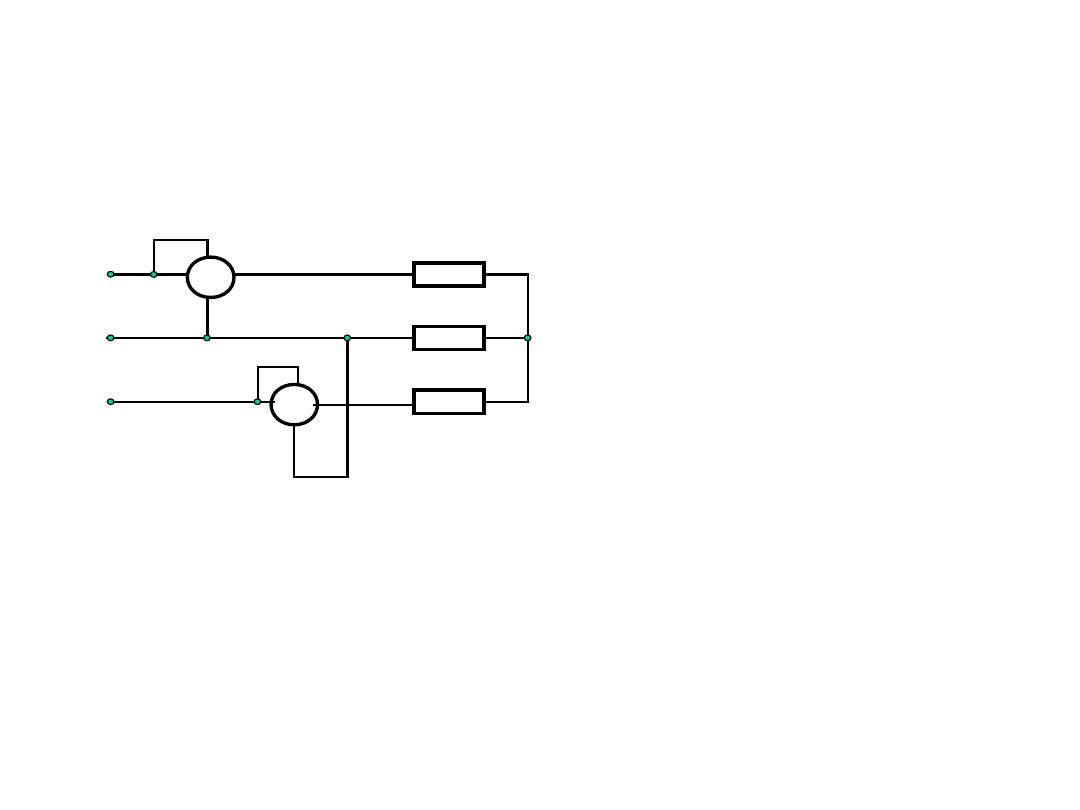
Układ dwóch watomierzy – układ Arona.
W
W
L3
L2
L1
Z3
Z2
Z1
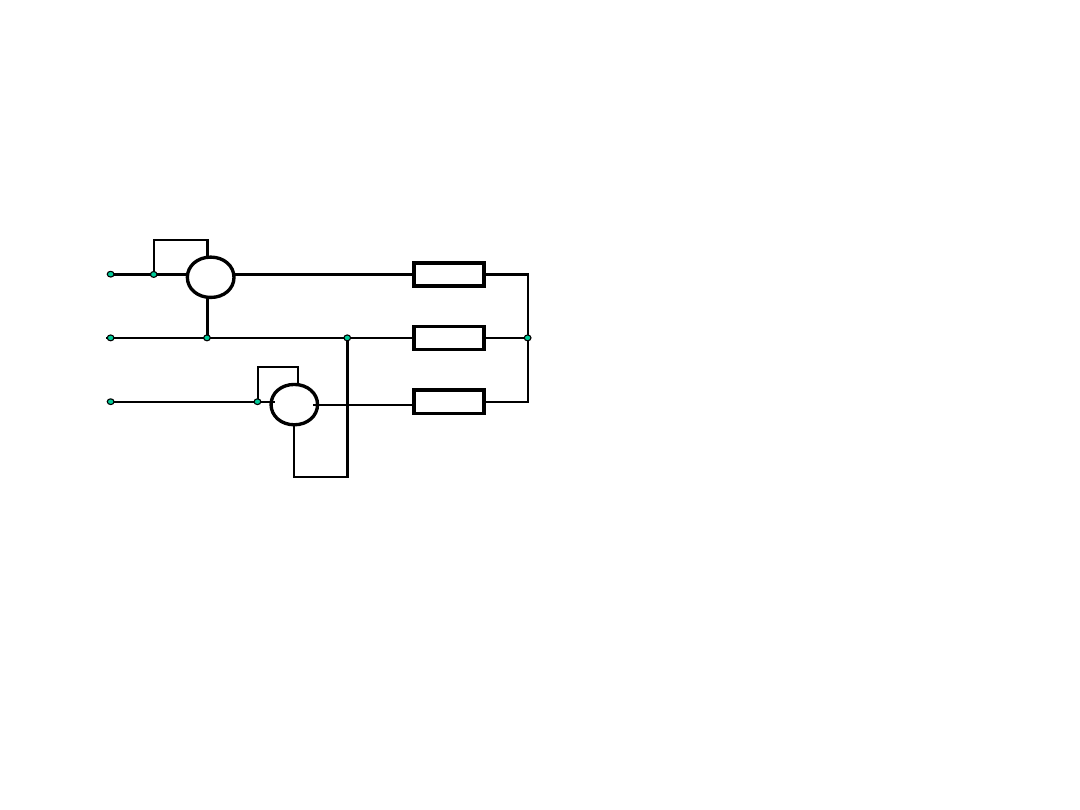
Pomiar mocy czynnej w układzie
trójfazowym
W
W
L
3
L
2
L
1
Z
3
Z
2
Z
1
0
3
2
1
L
L
L
i
i
i
Wartość chwilowa
mocy mierzonej
przez oba
watomierze:
3
2
3
1
2
1
2
1
L
L
L
L
L
L
i
u
i
u
p
p
3
2
3
1
2
1
L
L
L
L
L
L
i
u
u
i
u
u
2
2
3
3
1
1
3
1
2
3
3
1
1
L
L
L
L
L
L
L
L
L
L
L
L
L
i
u
i
u
i
u
i
i
u
i
u
i
u
Pomiar mocy czynnej w układzie
trójfazowym
W
W
L
3
L
2
L
1
Z
3
Z
2
Z
1
Moc czynna
wskazana przez
poszczególne
watomierze (wartość
skuteczna):
1
2
1
1
2
1
1
cos
L
L
L
L
L
L
I
U
I
U
P
2
2
3
2
2
3
2
cos
L
L
L
L
L
L
I
U
I
U
P
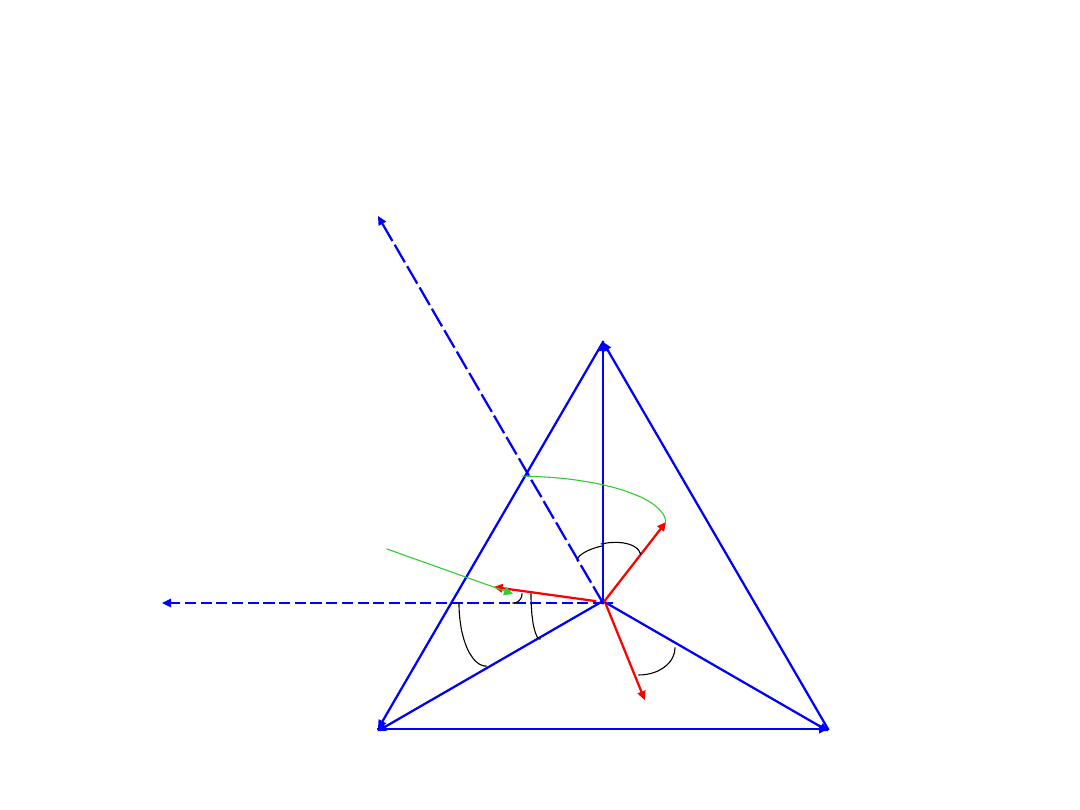
Pomiar mocy czynnej w układzie
trójfazowym
L1
L2
L3
U
L1
U
L3
U
L2
U
L1L2
U
L2L3
U
L3L1
I
L3
I
L2
I
L1
U
L1L2
30
o
30
o
U
L3L2
+30
o
-30
o
Pomiar mocy czynnej w układzie
trójfazowym
1
2
1
1
2
1
1
cos
L
L
L
L
L
L
I
U
I
U
P
2
2
3
2
2
3
2
cos
L
L
L
L
L
L
I
U
I
U
P
Kąt między U
L1L2
a I
L1
wynosi + 30
o
, a
kąt między U
L3L2
a I
L3
wynosi - 30
o
.
Wobec tego:
30
cos
30
cos
2
1
UI
UI
P
P
P
cos
3UI