MECHANIKA 2

Wykład Nr 14

Teoria uderzenia

DYNAMIKA PUNKTU NIESWOBODNEGO

Punkt, którego ruch ograniczony jest
jakimiś

więzami,

nazywamy

punktem

nieswobodnym.

Więzy oddziaływają na poruszający się punkt
pewnymi siłami, które nazywamy reakcjami
więzów. Istnienie więzów powoduje więc
pojawienie

się

w

równaniach

rucha

dodatkowych sił – reakcji więzów.

(1)

Równanie ruchu przyjmie postać

Równania ruchu:

Po przekształceniu
otrzymujemy:

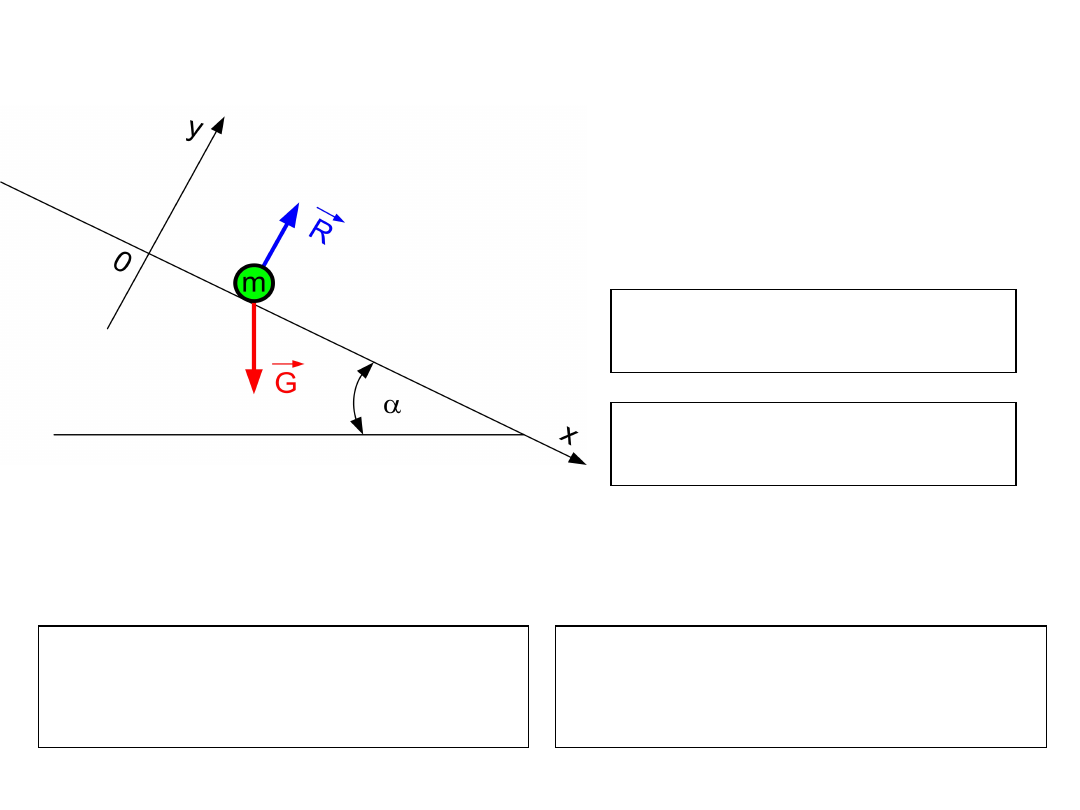
Ruch punktu po gładkiej równi

pochyłej

Rys.
7

Równania

ruchu:

gdzie:

Po podstawieniu:

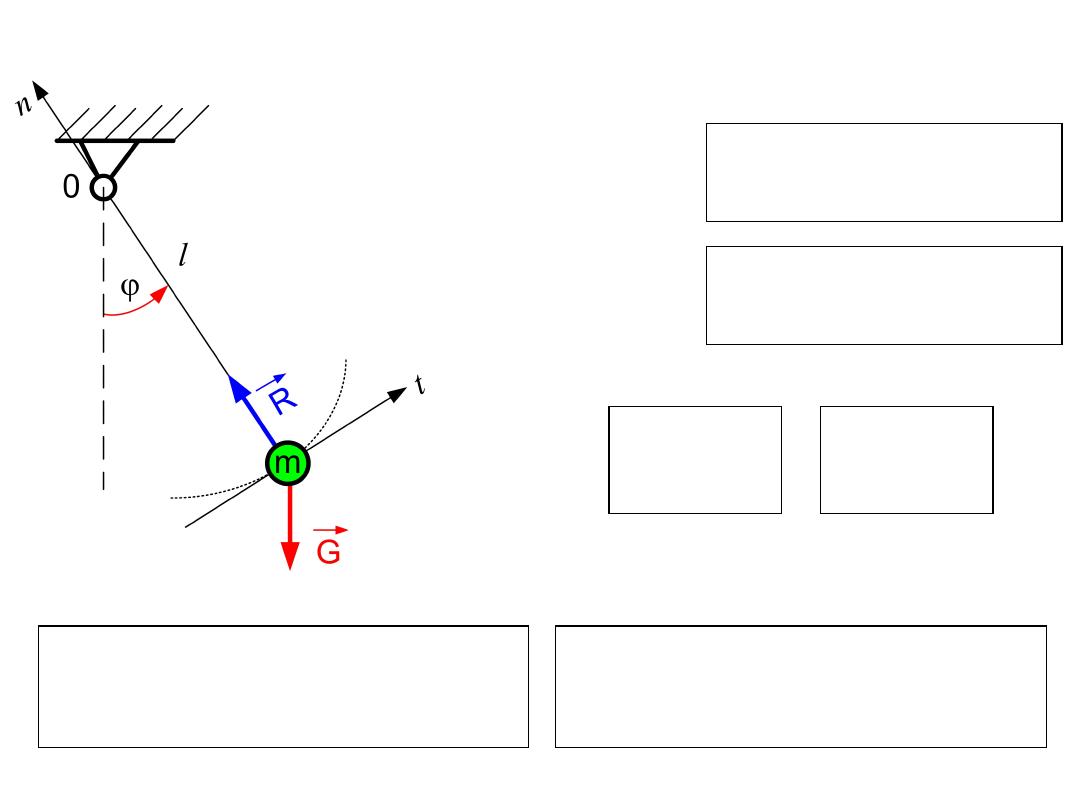
Ruch wahadła matematycznego

Przy małych wychyleniach wahadła sin = wówczas

więc równanie ruchu przybiera postać:

Jest to równanie ruchu
harmonicznego prostego.

Przypomnijmy, że równanie ruchu harmonicznego
prostego ma postać:

Zatem dla wahadła:

Równanie ruchu ma postać:

0





max







t

Warunek początkowy:

dla

Po scałkowaniu względem czasu otrzymamy wzór na prędkość:

Po wyznaczeniu stałej c i podstawieniu do wzoru na v:

Ponieważ

to

Załóżmy, że dla t = 0,
wówczas:

0





Rys.
2

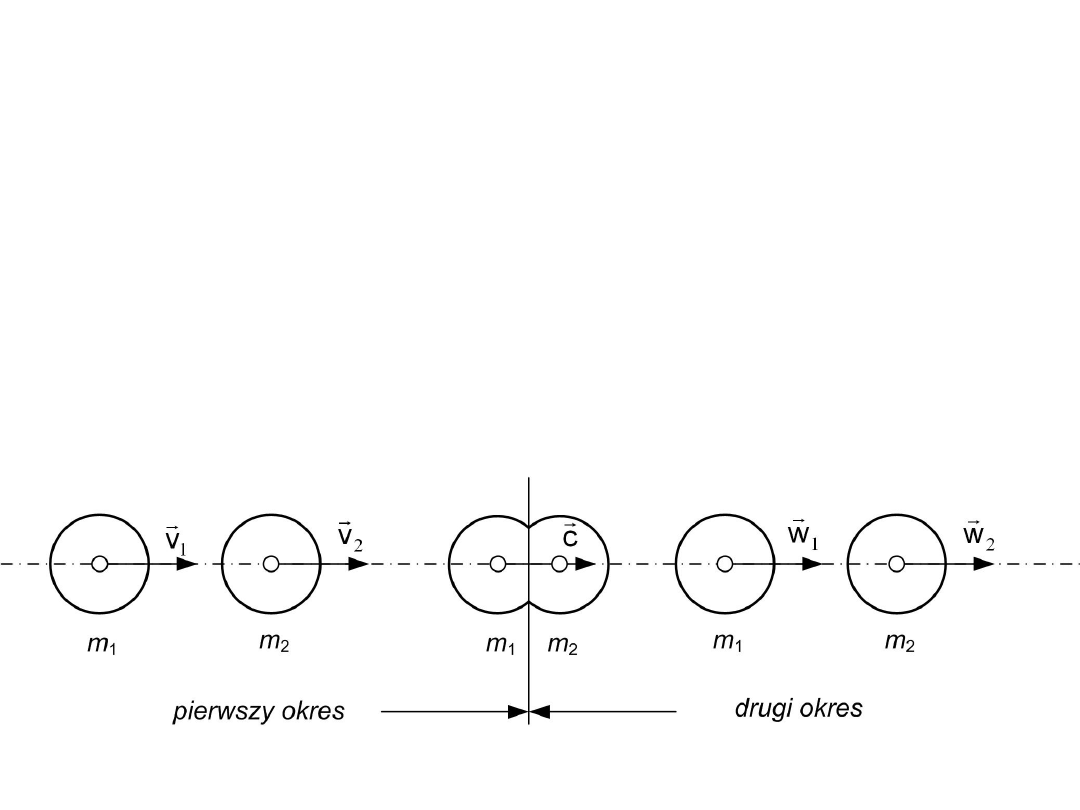
Zderzenie proste środkowe

Zderzenie zachodzi w przypadku działania na
siebie dwu ciał siłą o skończonej wartości w
bardzo krótkim przedziale czasu.

Zderzenie środkowe charakteryzuje się
tym, że normalna do płaszczyzny styku w
punkcie styku obu ciał przechodzi przez
środki masy tych ciał.

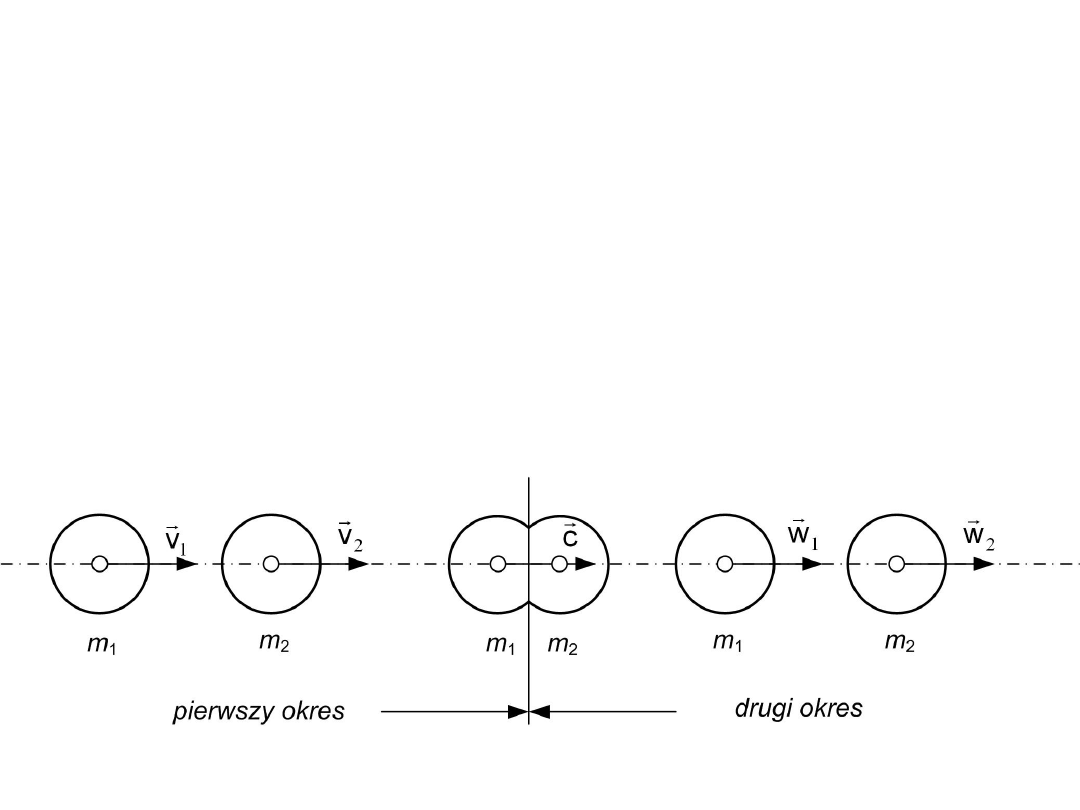
W procesie zderzenia rozróżniamy dwa

charakterystyczne okresy:

a)        - pierwszy okres: od chwili zetknięcia się

ciał aż do chwili największego zbliżenia ich
środków mas, przy równoczesnym
odkształcaniu się obu ciał,

Okresy zderzenia

b)       - drugi okres: od chwili rozpoczęcia oddzielania
się obu mas.

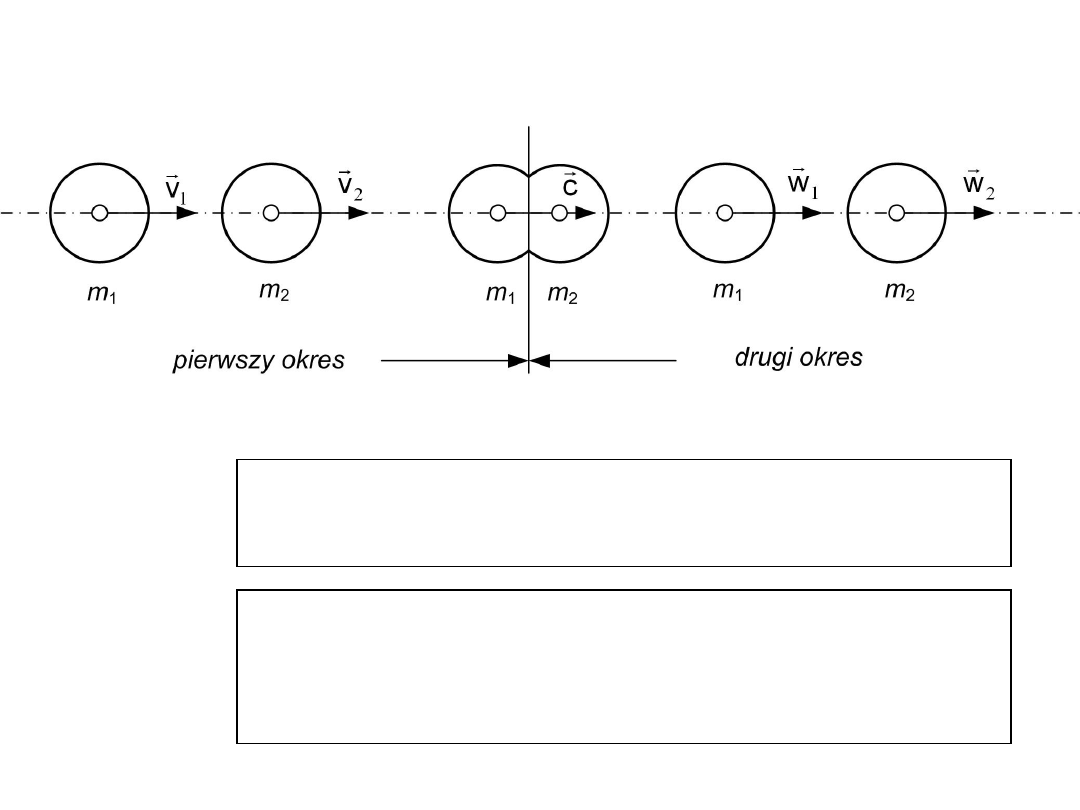
Pęd zderzających się mas

Pęd przed po zderzeniu jest
taki sam

Rys.
2

c

– wspólna prędkość obu mas przy końcu pierwszego
okresu.

Stąd

Energia kinetyczna

W wyniku odkształcania się ciał przy zderzeniu
występuje zmiana energii kinetycznej układu w pewnej
jej części na pracę odkształcenia. Strata ta może być
pozorna lub rzeczywista, w zależności od tego, czy
zostanie zwrócona w drugim okresie zderzenia.
Oznaczmy ją przez

Uwzględniając wzór
otrzymamy

(23)

(23a
)

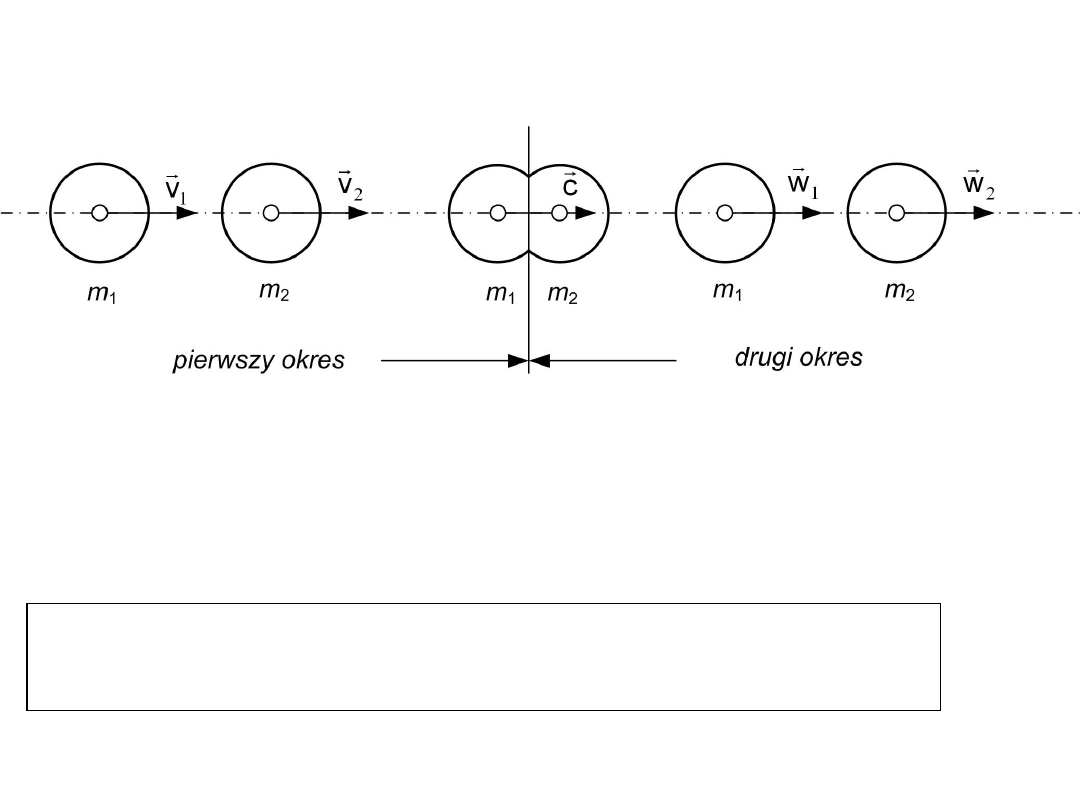
Pęd układu w drugim okresie

zderzenia

Przechodząc do drugiego okresu zauważamy, że
obowiązuje nadal zasada zachowania pędu badanego
układu, czyli że

(2
4)

Prędkości oraz zależeć będą od tego, czy

strata energii kinetycznej została:

1

w

2

w

Zderzenie sprężyste i plastyczne

a) zwrócona w 100% (zderzenie ciał doskonale
sprężystych),

b) pochłonięta w 100% (zderzenie ciał idealnie
plastycznych),
c)

pochłonięta

częściowo

(zderzenie

ciał

rzeczywistych).

Współczynnik zderzenia

przy czym
oczywiście

Wartości graniczne współczynnika

odpowiadają:

k

1



k

0



k

dla ciała idealnie
sprężystego,

dla ciała idealnie plastycznego.

(2
5)

Prędkości po zderzeniu

Uwzględniając równania (24) i (25) otrzymamy po

podstawieniu i przekształceniu

(2
6)

Dla zderzenia ciał idealnie
sprężystych





1



k

(2
7)

Dla

zderzenia

ciał

idealnie

plastycznych





0



k

(2
8)

Rzeczywista strata energii kinetycznej

Rzeczywista strata energii
kinetycznej wynosi

Po podstawieniu wartości oraz ze wzoru (26)
otrzymamy

1

w

2

w

Charakterystyczne
przypadki:

Po zderzeniu nastąpiła więc wymiana
prędkości pomiędzy obiema masami.

1. (ciało doskonale sprężyste).

1



k

2

1

m

m 

Ze wzorów (27)
otrzymamy:

ZDERZENIE PROSTE ŚRODKOWE ORAZ

UKOŚNE ŚRODKOWE

2. , (nieruchoma ściana), .

0

2









2

m

1



k

Ze wzorów (27)
otrzymamy:

Masa m

1

odbija się z tą samą

prędkością.

3. , (nieruchoma ściana), (ciało
rzeczywiste).

0

2









2

m

0



k

Wykorzystując wzory (26) napiszemy:

ZDERZENIE PROSTE ŚRODKOWE ORAZ

UKOŚNE ŚRODKOWE

Przypadek ten podaje zarazem prosty sposób wyznaczania

współczynnika zderzenia k. Jak wiadomo bowiem z

kinematyki, ciało spadające z wysokości H na stałą

podstawę ma w początkowej chwili zderzenia prędkość

. Po odbiciu wznosi się na wysokość h, czyli przy

końcu drugiego okresu zderzenia miało ono prędkość

.

Ponieważ

(pomijając znak minus, gdyż interesuje

nas tylko moduł), zatem

gH

2

1





gh

2

w

1



1

1

–

w



k



Masa m

2

odbije się z prędkością zmniejszoną o

k .

k =

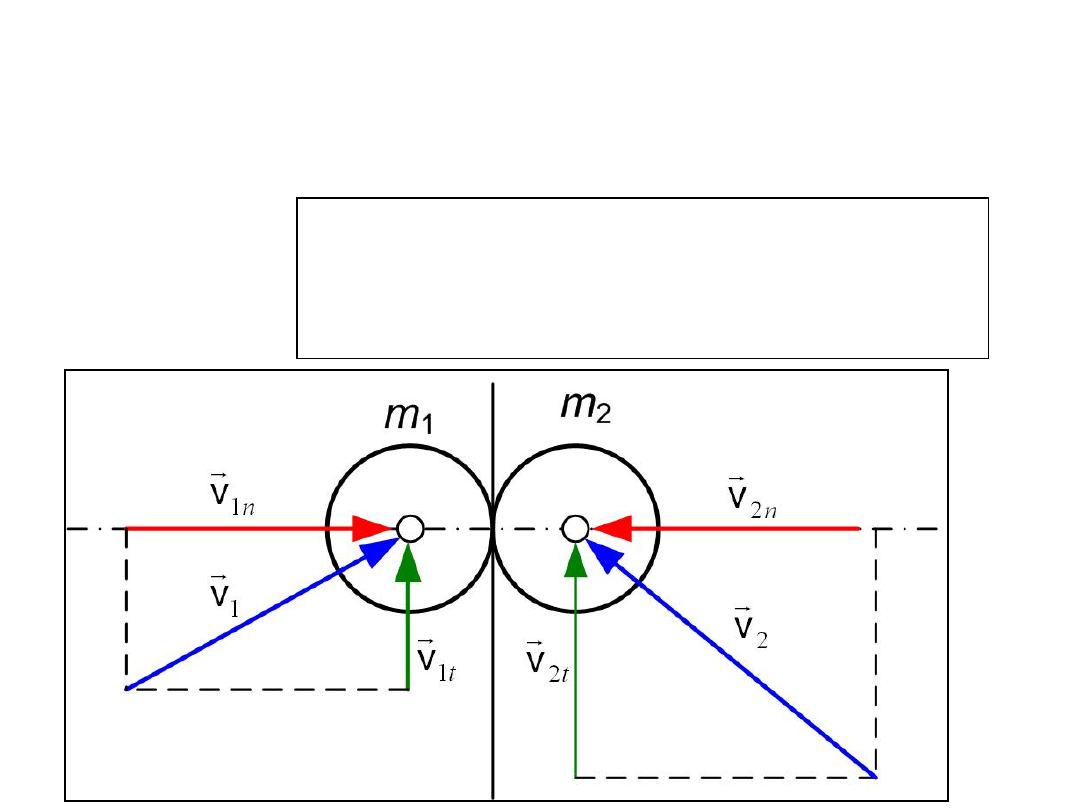
Przejdźmy teraz do omówienia zderzenia ukośnego
środkowego (rys. 3). Rozkładamy wektory prędkości na
składowe normalne i styczne do płaszczyzny styku

Rys.
3

ZDERZENIE PROSTE ŚRODKOWE ORAZ

UKOŚNE ŚRODKOWE

ZDERZENIE PROSTE ŚRODKOWE ORAZ

UKOŚNE ŚRODKOWE

Jeżeli pominiemy straty tarcia przy zderzeniu i możliwości,

ewentualnych obrotów mas (przyjęto je jako punkty

materialne) w wyniku na ogół różnych wartości składowych

stycznych oraz (przyjmując idealnie gładkie powierzchnie

styku mas), to w wyniku zderzenia zmienią się tylko składowe

normalne.

t

1



t

2



oraz

Do oceny zmian składowych normalnych wykorzystamy wzory
(26), wprowadzając jedynie odpowiednie wskaźniki n,
składowe zaś styczne pozostaną bez zmiany, czyli:

Ostatecznie składając wektorowo otrzymamy po zderzeniu

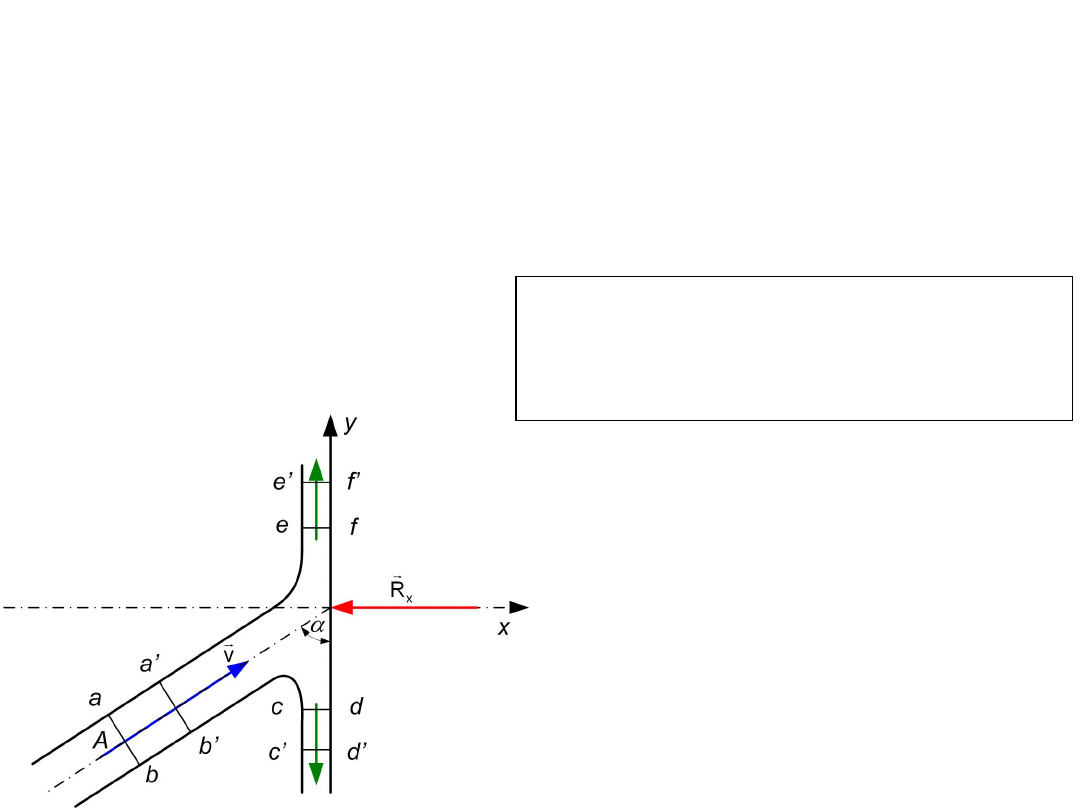
Oddziaływanie strumienia padającego na

przegrodę

Do wyznaczenia reakcji przegrody na działanie
strumienia, padającego pod kątem (rys. 4),
wykorzystamy zasadę pędu i impulsu według wzoru

R



Załóżmy,

że

dane

są

ponadto

przekrój

strumienia A, gęstość ρ

(niezmienna

w

czasie)

oraz

średnia

prędkość

strumienia v.

Rys.
4

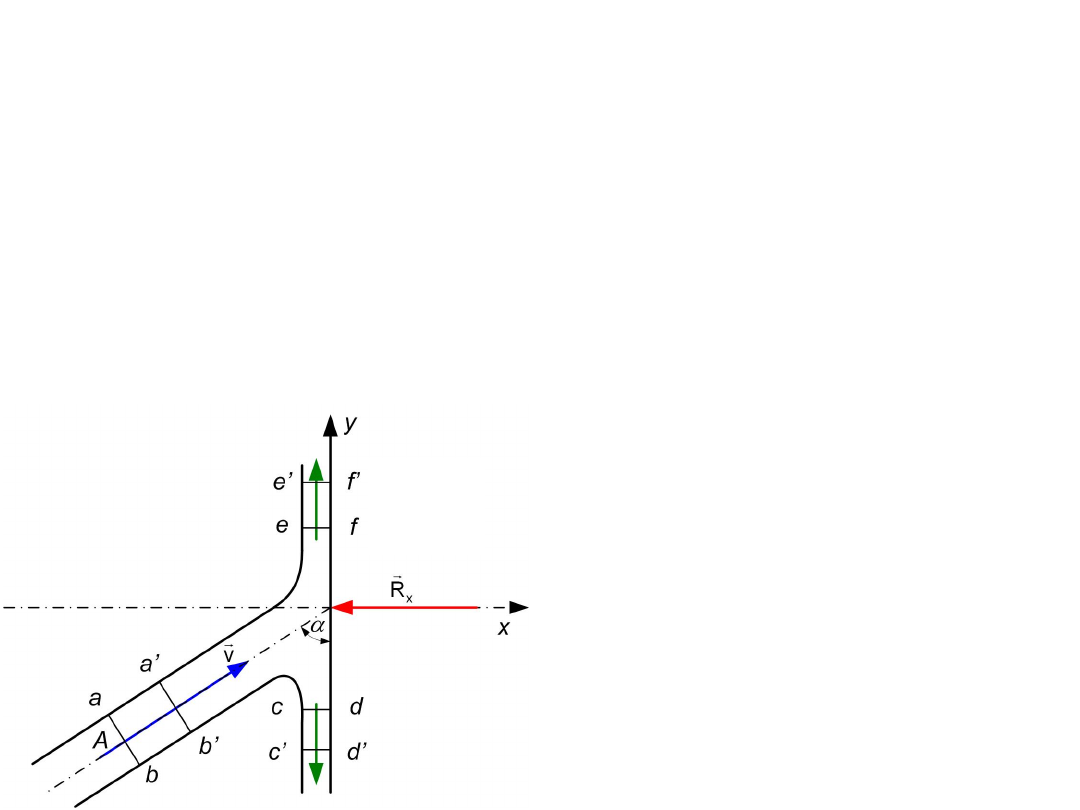
W czasie dt wystąpi przemieszczenie przekroju ab w
położenie a'b' (rys. 4) o od vdt. Równocześnie strumień
rozdzielając się na przegrodzie przemieści się w swych
strugach z położeń ef w e'f' oraz z położeń cd w c'd'
(rys. 4). Zauważmy, że kierunki wektorów prędkości
tych rozdzielonych na przegrodzie strug są przeciwne i
styczne do przegrody.

Oddziaływanie strumienia padającego na

przegrodę

Rys.
4

Zgodnie więc z zasadą pędu i impulsu (19)

napiszemy rzutując wektory pędów pulsu na oś

,

prostopadłą do przegrody

x

Oddziaływanie strumienia padającego na

przegrodę

Oddziaływanie strumienia padającego na

przegrodę

Gdyż wektory pędów tych strug są styczne do
przegrody, zatem

Stąd ostatecznie
otrzymujemy reakcję
przegrody w kierunku osi

x

oraz