Algebra Boole’a

Zapoczątkowana w 1854 r. przez
George’a Boole’a

Algebrą Boole’a nazywamy system
algebraiczny

<

K,o,i,+,·

>

,

w którym

K

jest zbiorem,

o

oraz

i

wyróżnionymi elementami tego zbioru,

„

+

”

oraz

„

·

”

operacjami (nazywanymi

także

działaniami

lub

operatorami)

dwuargumentowymi

określonymi

w

zbiorze K

Terminologia

Terminologia

Zamiast terminów suma w odniesieniu

do symbolu

[

+

]

używane są

także

terminy

:

alternatywa lub dysjunkcja

A+B czytamy A lub B

Zamiast terminu iloczyn [

·

]

możemy

używać zamiennie terminu

koniunkcja

A·B

(możemy używać zapisu A*B)

czytamy A i B

Zmienne logiczne

Algebra Boole'a

różni się od zwykłej algebry tym, że

zmienne w definicji określone jako wyróżnione
elementy mogą przybierać tylko dwie możliwe

wartości

0

lub

1

.

Zmienne logiczne 0 i 1 mogą reprezentować

Logiczne 0

Logiczna 1

Fałsz (False)

Prawda (True)

Przełącznik

otwarty

-

Wyłączony (Off)

Przełącznik zamknięty

Włączony (On)

Niski poziom

napięcia (Low )

Wysoki poziom

napięcia (High)

Nie (No)

Tak (Yes)

Operacje logiczne

W algebrze Boole'a, dozwolone są trzy

podstawowe

operacje

:

OR

(suma logiczna, suma boolowska

dysjunkcja); np.:

A+B=C

AND

(iloczyn logiczny, iloczyn

boolowski, koniunkcja); np.:

A*B=C

NOT

(negacja, inwersja);np.:A=C

(czasem zapisujemy to w postaci A’= C)

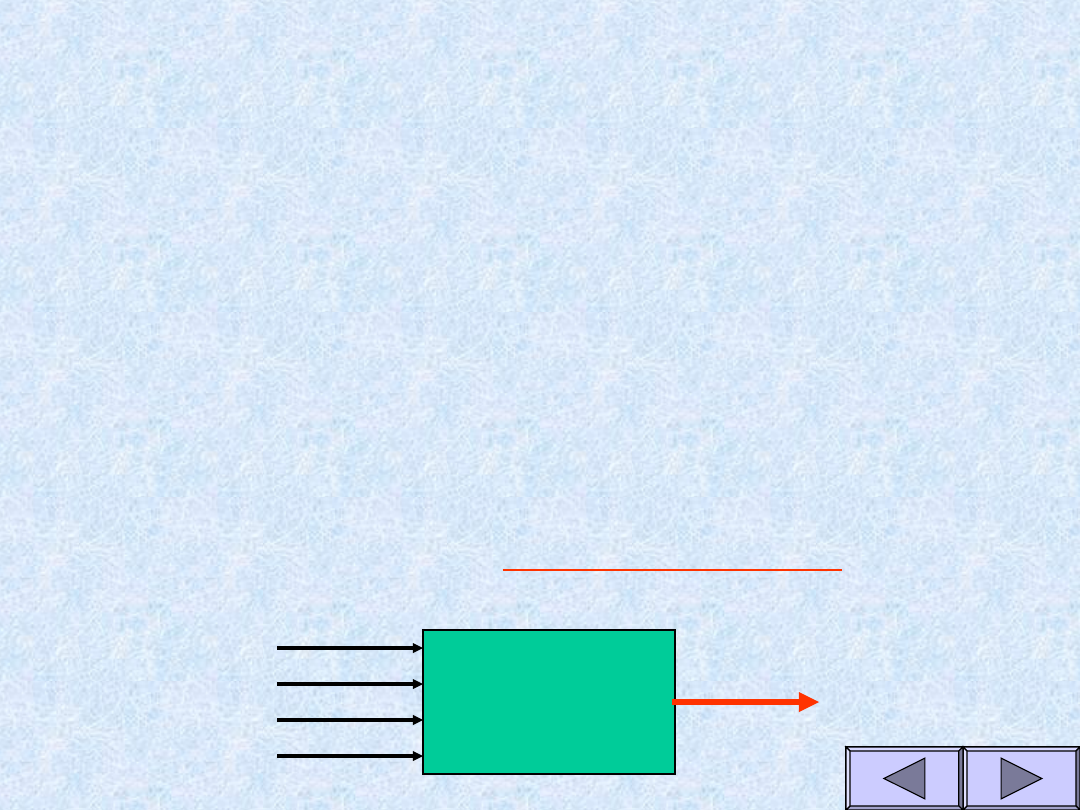
Układy logiczne

wejścia

• Dowolny układ logiczny może mieć

n

wejść

i co najmniej

jedno wyjście

.

• Może realizować podstawowe, czy też

bardziej złożone funkcje algebry Boole’a.

• Niezależnie od konstrukcji wewnętrznej

układu zależność pomiędzy stanem
wyjścia układu, a stanami wejść można
opisać za pomocą

tablicy prawdy

lub

analitycznie za pomocą wyrażenia
algebraicznego

wyjście

Układ

logiczny

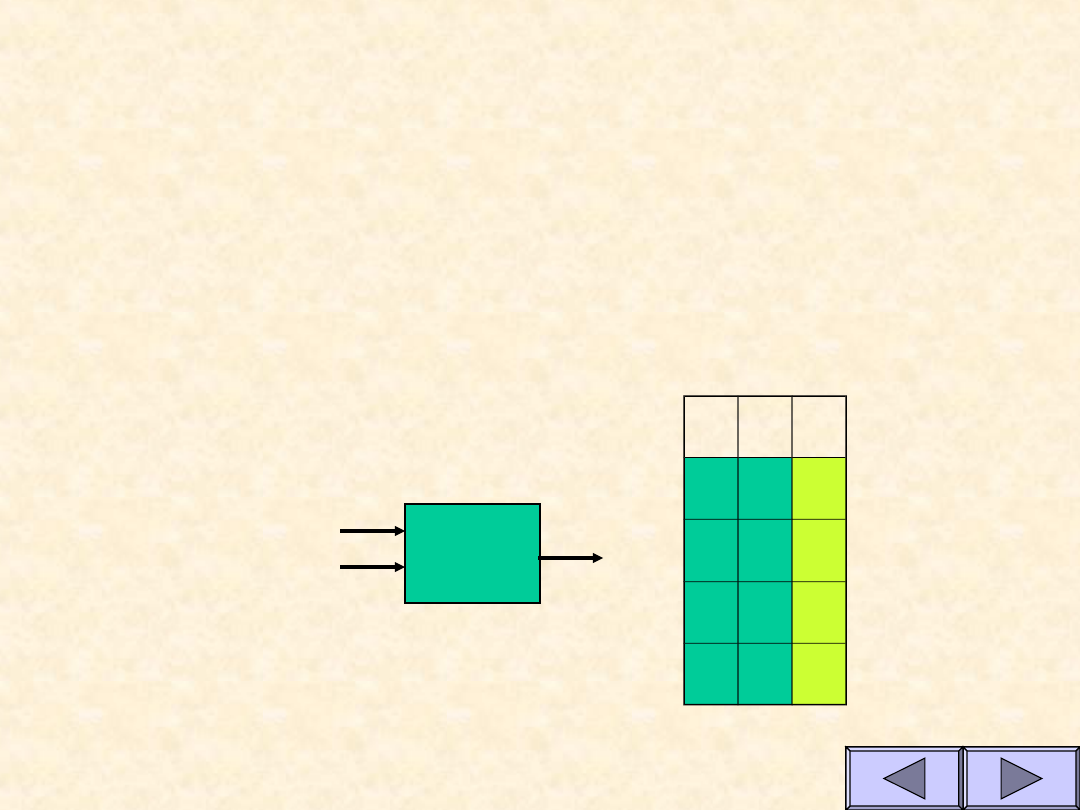
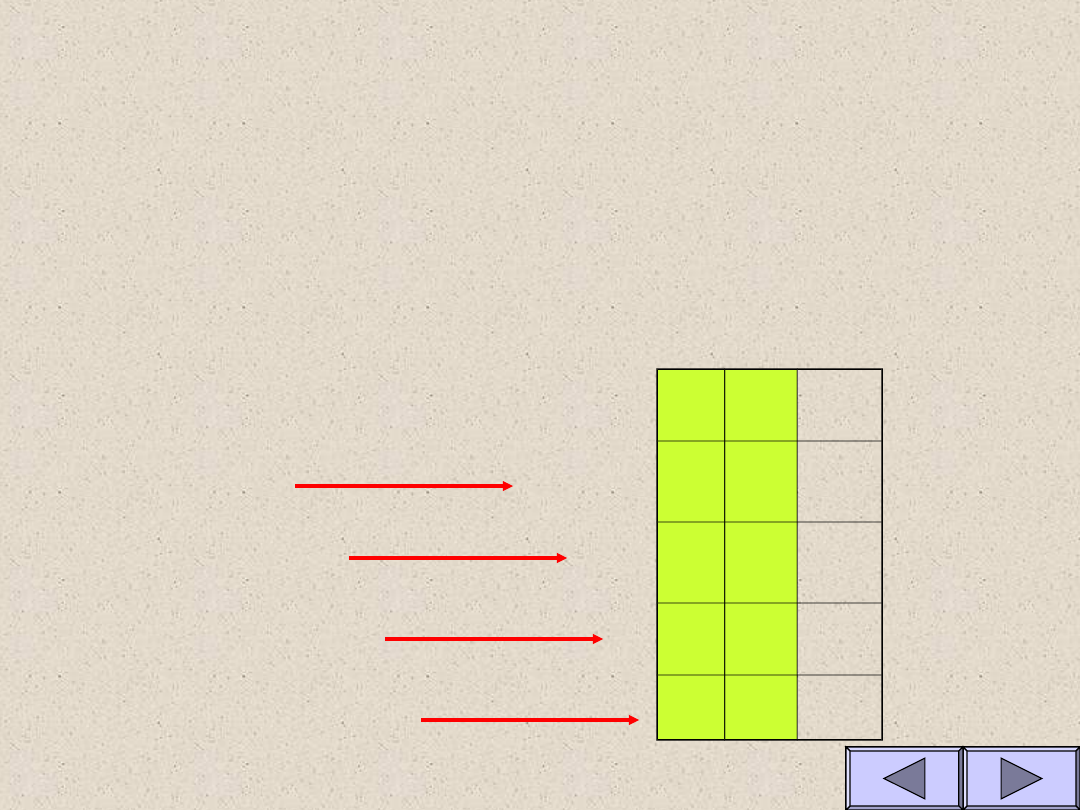
Co to jest tablica prawdy?

Tablica prawdy przedstawia zależność pomiędzy

stanem logicznym wyjścia układu logicznego,
a stanami logicznymi na wejściach tego
układu.

Dla układu o n wejściach ma ona 2

n

wierszy

uwzględniających wszystkie możliwe kombinacje
sygnałów wejściowych i odpowiadające im stany
wyjścia (lub wyjść).

A B

Y

0 0

0

0 1

1

1 0

1

1 1

1

Np.:dla układu o 2 wejściach A i
B oraz wyjściu Y realizującego
funkcję sumy logicznej

Y

=A+B

ma ona postać:

A

B

Y

Własności funkcji

logicznej

Własności funkcji

logicznej

Tablicę prawdy możemy określić na

podstawie

wyrażenia

algebraicznego

określającego

funkcję

logiczną

podstawiając

wartości

argumentów.

Np.:dla

wyrażenia:

Y=

(A*B)+B

otrzymamy

A B

Y

0 0

0

0 1

1

1 0

0

1 1

1

Y=(0*0)+0=0

Y=(0*1)+1=1

Y=(1*0)+0=0

Y=(1*1)+1=1

Fizyczna realizacja

• Fizyczną

realizacją

podstawowych

operacji logicznych są układy nazywane
bramkami.

Są

to

układy

scalone

wykonane

w

technologii

półprzewodnikowej. Produkowany jest
bardzo szeroki asortyment układów od
najprostszych

do

bardzo

skomplikowanych

.

•

Stanom

logicznym

0

oraz

1

przyporządkowano napięcia elektryczne

0

logiczne – napięcia < 0,8 V

1

logiczna - napięcia > 2,4 V

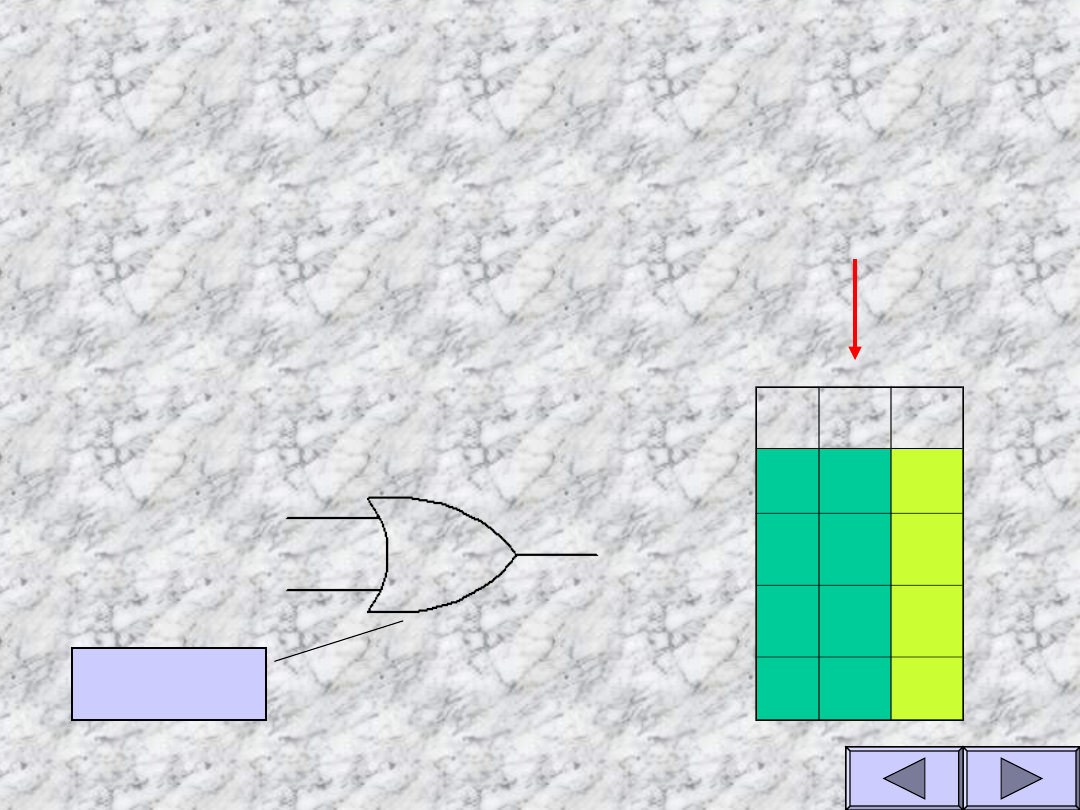
Własności funkcji OR

Własności funkcji OR

A B Y

0 0

0

0 1

1

1 0

1

1 1

1

Tablica prawdy dla funkcji OR (sumy

logicznej)

Y=A+
B

Funkcja przyjmuje

wartość 1 wtedy gdy co

najmniej jedno z wejść

przyjmuje stan 1

A

B

Y

Symbol

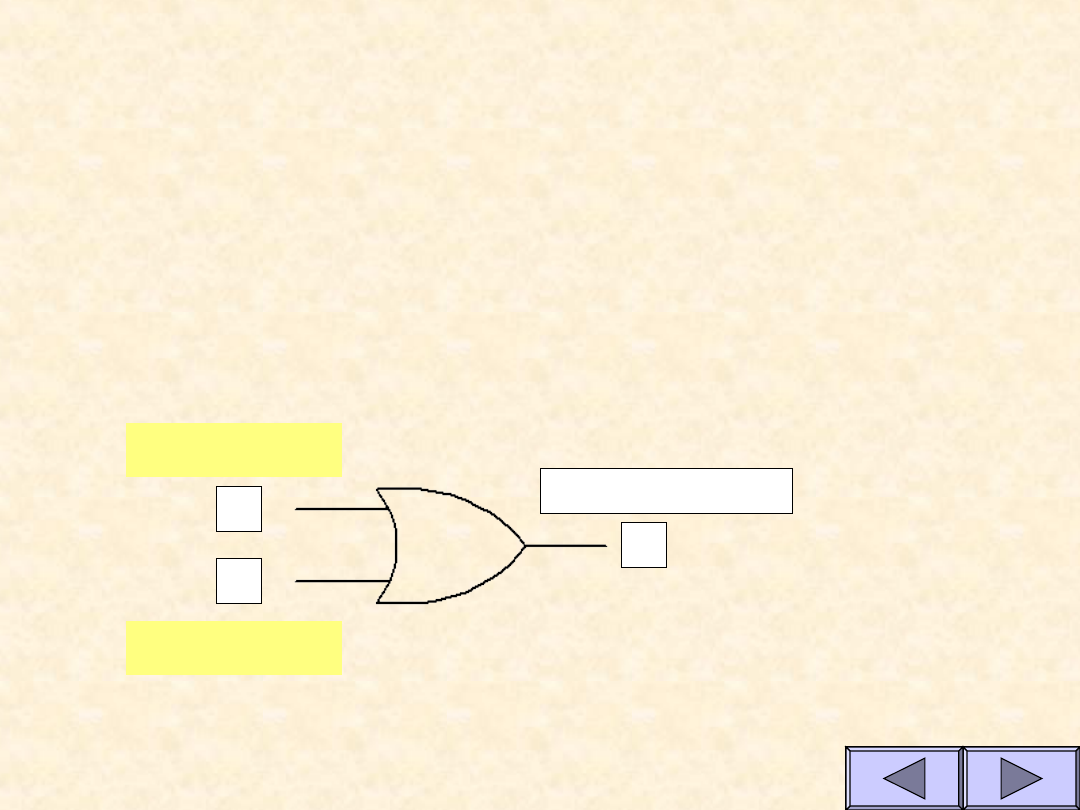
Symulacja bramki OR

Symulacja bramki OR

Stan wejścia A

Stan wejścia B

Stan wyjcia Y

1

1

1

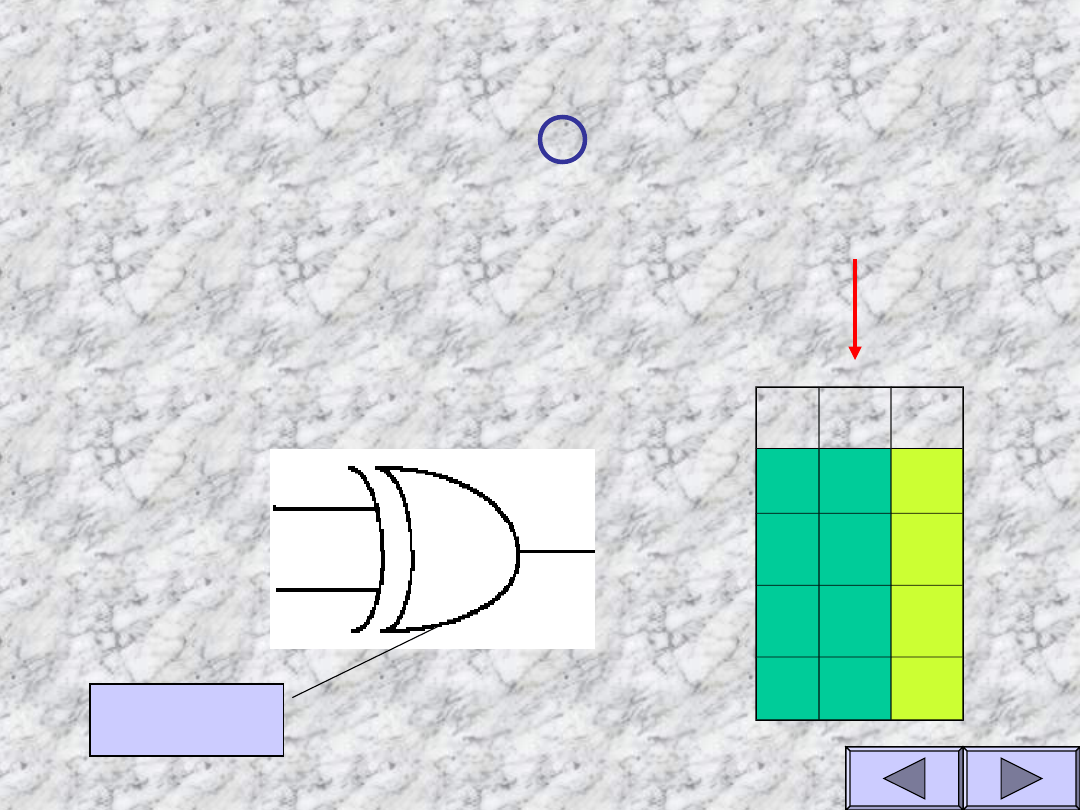
Własności funkcji EXOR

Własności funkcji EXOR

A B Y

0 0

0

0 1

1

1 0

1

1 1

0

Tablica prawdy dla funkcji EXOR (sumy

modulo 2)

Y=A +
B

Funkcja przyjmuje

wartość 1 wtedy gdy

tylko jedno z wejść

przyjmuje stan 1

A

B

Y

Symbol

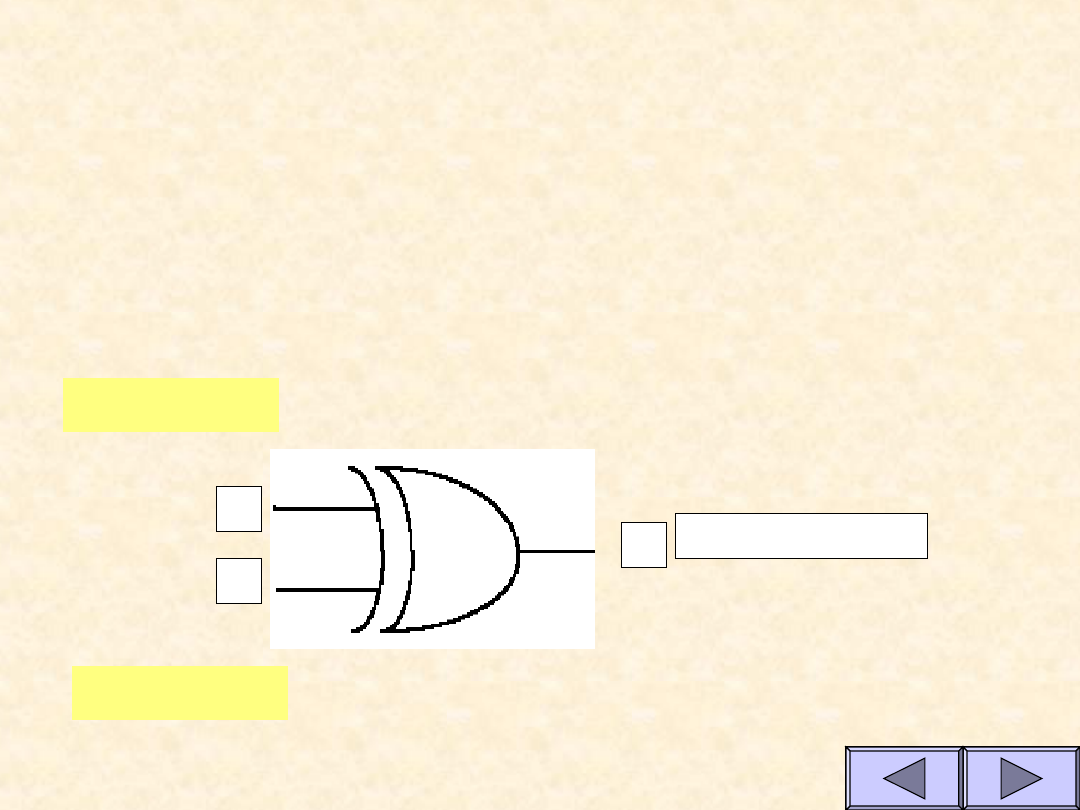
Symulacja bramki

EXOR

Symulacja bramki

EXOR

Stan wejścia A

Stan wejścia B

0

Stan wyjcia Y

0

0

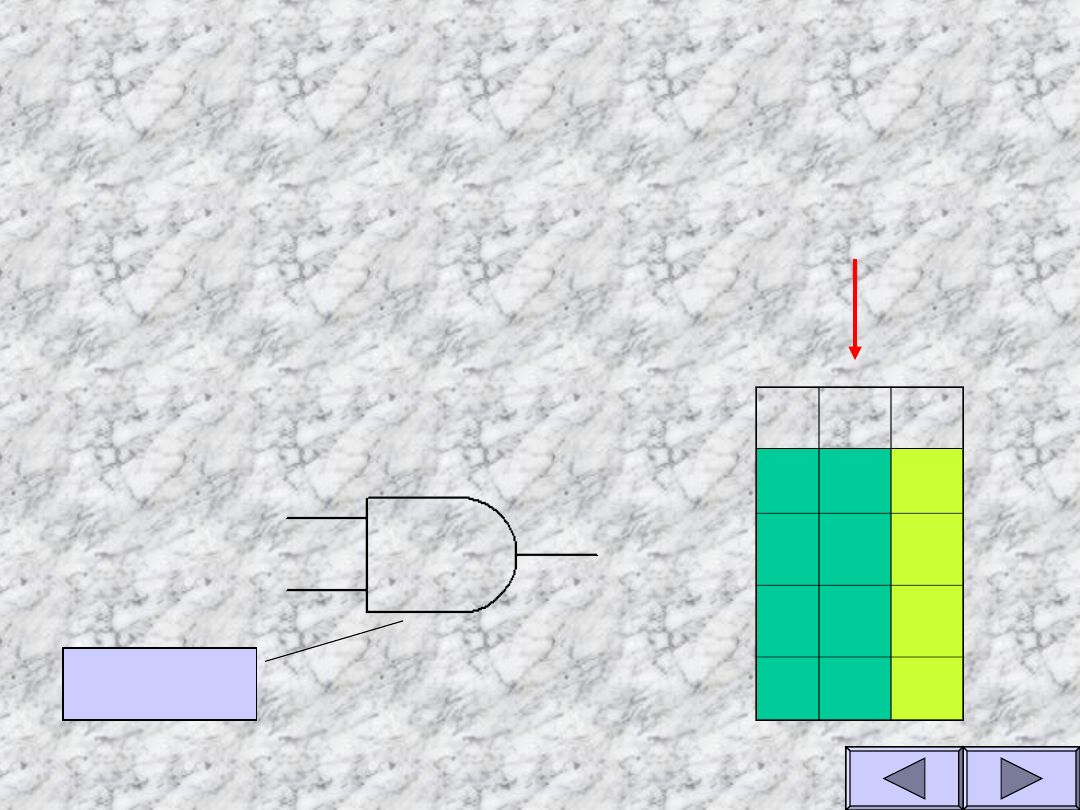
Własności funkcji AND

Własności funkcji AND

A B Y

0 0

0

0 1

0

1 0

0

1 1

1

Tablica prawdy dla funkcji

AND

(iloczynu logicznego)

Y=A*B

Funkcja przyjmuje

wartość 1 tylko wtedy gdy

oba wejścia przyjmują

stan 1

A

B

Y

Symbol

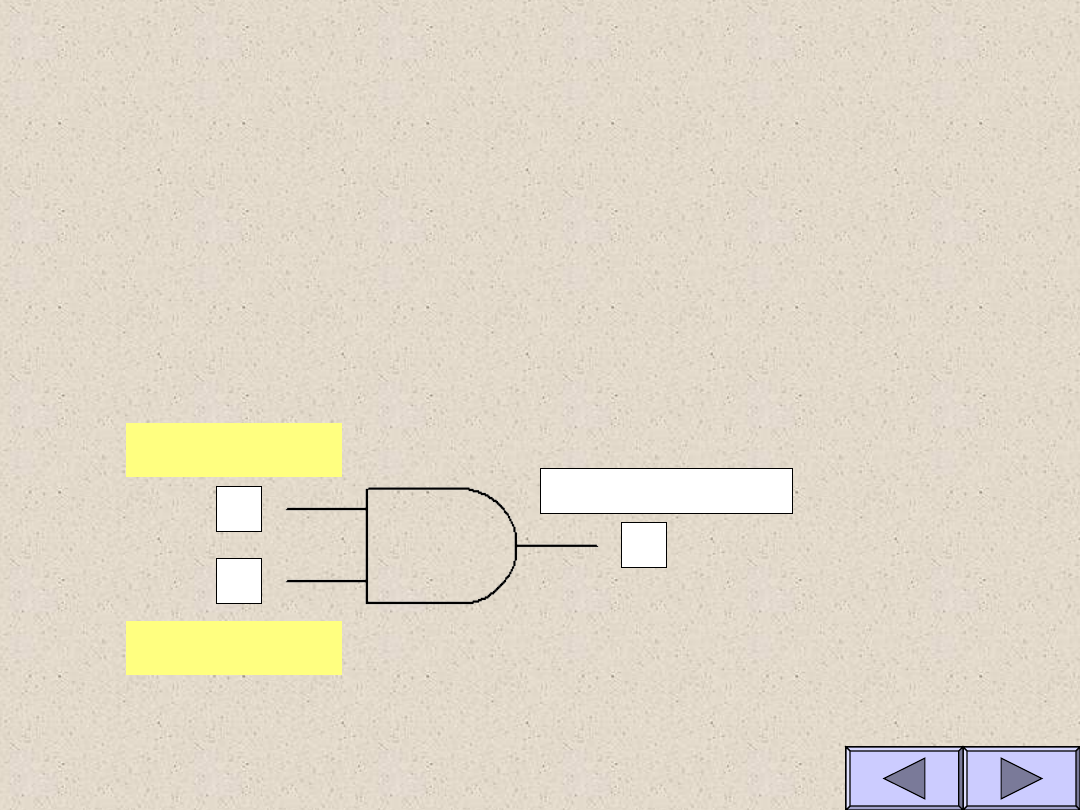
Symulacja bramki AND

Symulacja bramki AND

Stan wejścia A

Stan wejścia B

Stan wyjcia Y

1

1

1

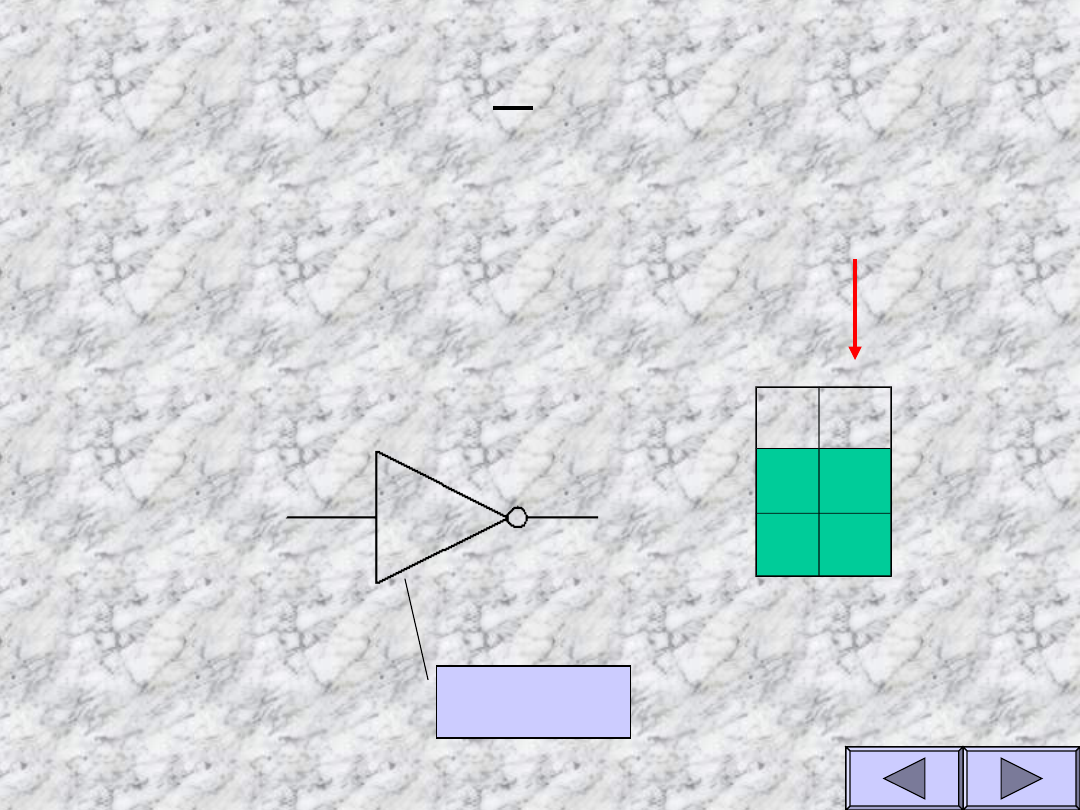
Własności funkcji NOT

Własności funkcji NOT

A Y

0

1

1

0

Tablica prawdy dla funkcji NOT

(negacji)

Y=A

Funkcja przyjmuje

wartość przeciwną do

stanu wejścia

A

Y

Symbol

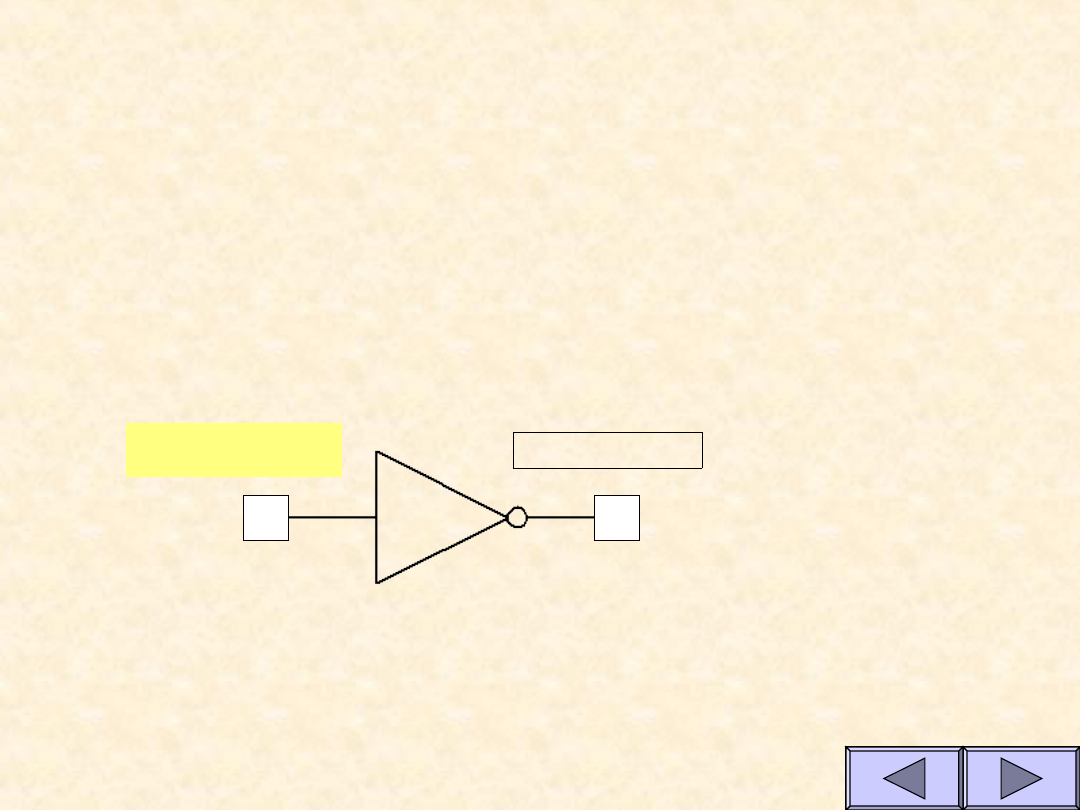
Symulacja bramki NOT

Symulacja bramki NOT

Stan wejścia A

Stan wyjś...

0

1

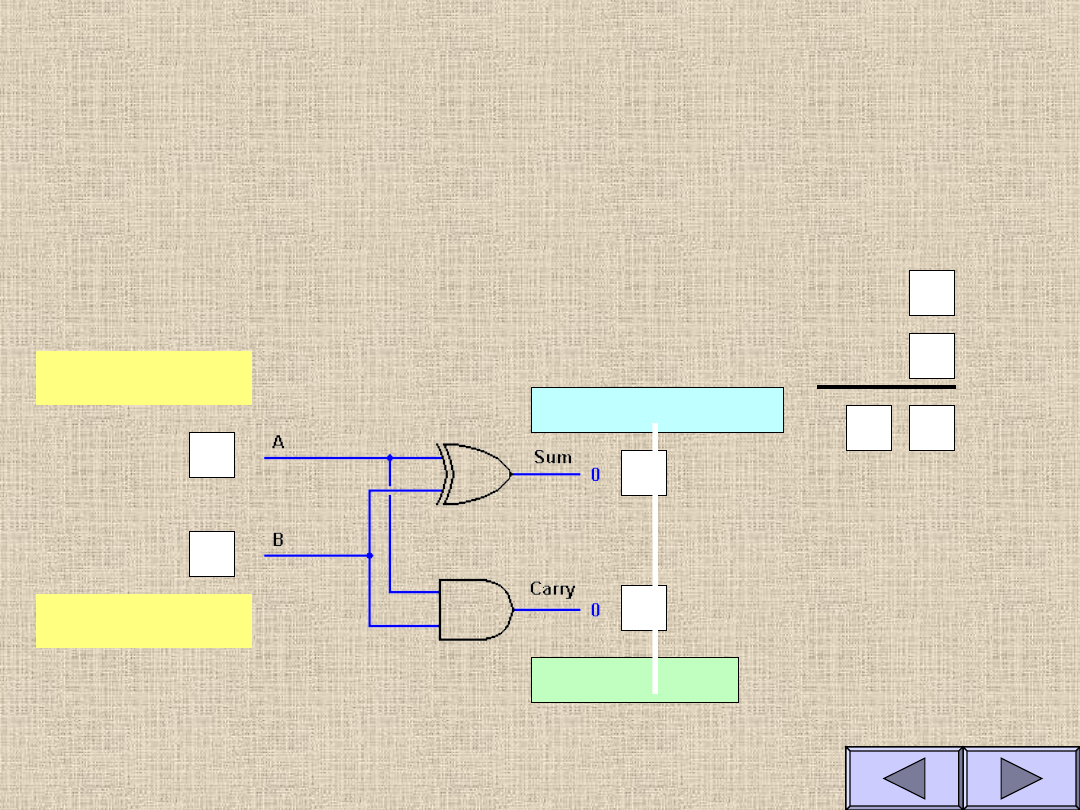
Jak działa półsumator

Jak działa półsumator

Składnik A

Składnik B

1

0

SUMA

0

1

1

1

0

0

Przeniesienie

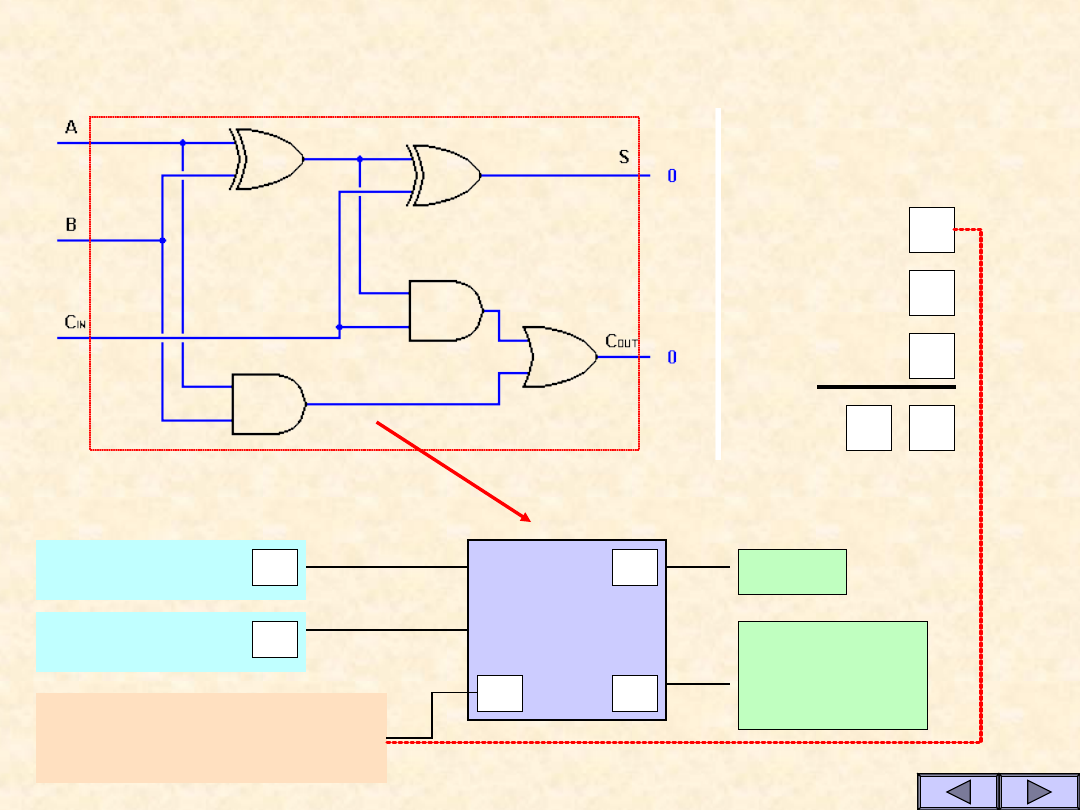
Sumator pełny

Sumator pełny

SUMA

Składnik A

Składnik B

Przeniesienie z

młodszej pozycji

Przeniesieni

e na

starszą po...

1

1

1

1

1

1

1

1

1

1

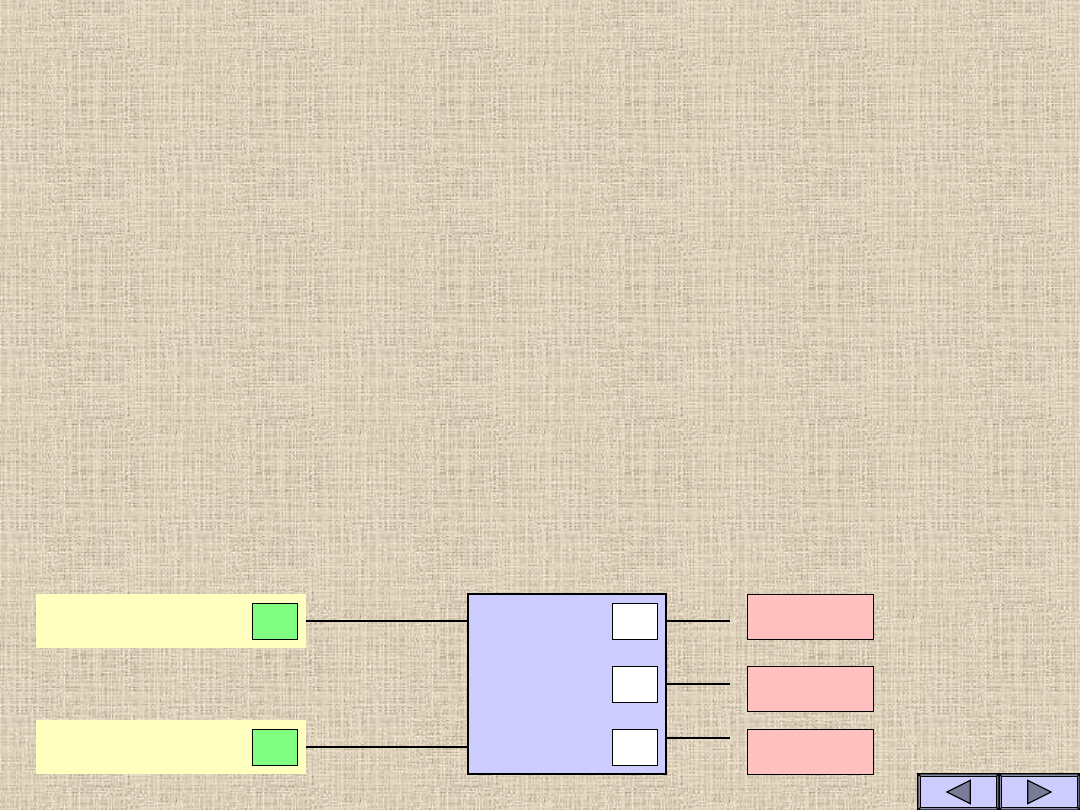
Porównujemy liczby

binarne

- komparator

Porównujemy liczby

binarne

- komparator

bit A

bit B

0

1

0

0

1

A>B

A=B

A<B

Komparatorem

nazywamy

układ logiczny wskazujący fakt
równości

lub

nierówności

dwóch

binarnych

słów

wejściowych tego układu.