OPIS DYNAMIKI UKŁADÓW

• Modelowanie fizyczne procesu
• Modelowanie matematyczne procesu
• Uproszczenia modelu
• Linearyzacja
• Redukcja modelu
• Przekształcanie modelu

Równanie dynamiki układu

•

Własności dynamiczne wielu układów, niezależnie od tego czy są one

mechaniczne, elektryczne, cieplne, a nawet biologiczne lub ekonomiczne,

zazwyczaj mogą zostać opisane za pomocą równań różniczkowych. Ogólna

postać liniowego równania różniczkowego elementu czy układu o jednym

wejściu i jednym wyjściu jest następująca:

•

•

Skrócona postać tego równania używana przy analizie numerycznej jest

następująca:

•

•

gdzie wyrażenia w nawiasach , określają rząd pochodnej.

•

u

r

b

dt

du

r

b

r

dt

u

r

d

b

r

dt

u

r

d

b

y

m

a

dt

dy

m

a

m

dt

y

m

d

a

m

dt

y

m

d































1

1

1

1

0

1

1

1

1













1

0

czym

przy

,

0

0



















a

j

r

j

j

r

u

j

b

i

m

y

m

i

i

a

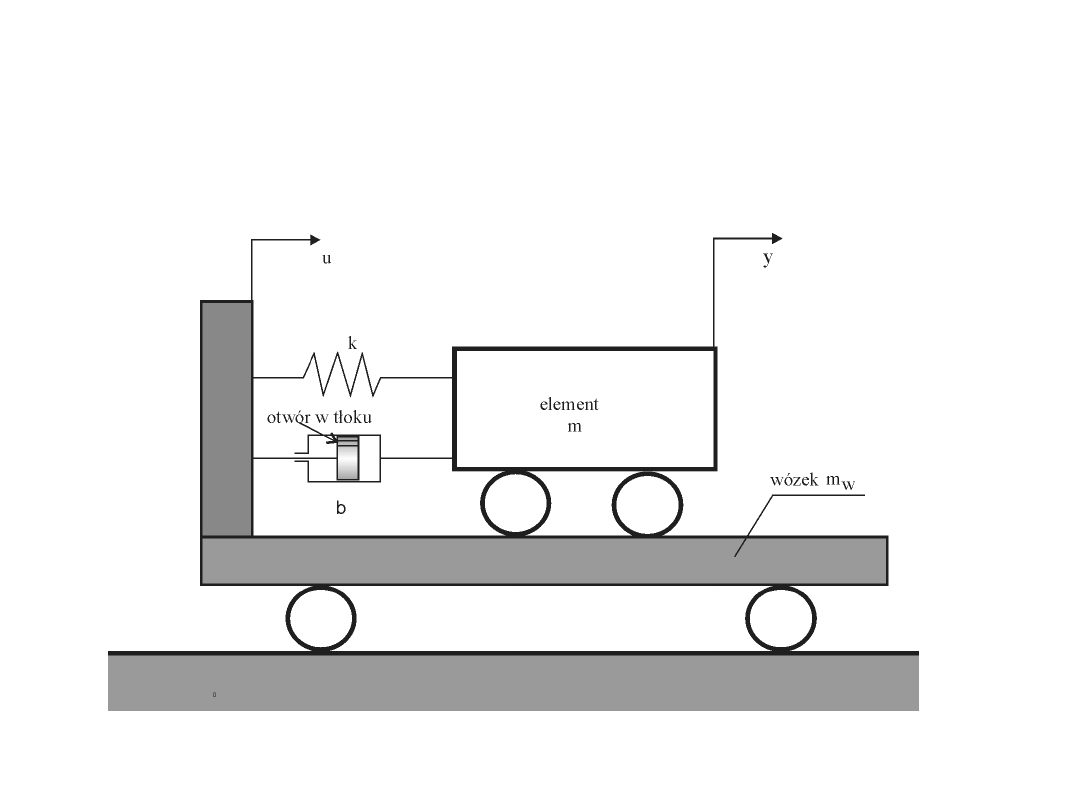
Przykład 1. Wózek z układem

drgająco‑tłumiącym

Przykład 1

•

Rozwiązanie

•

Dla rozpatrywanego układu II prawo Newtona ma postać:

•

,

•

naszym przypadku na masę działa siła sprężystości i siła tłumienia. Stosując II

prawo Newtona dla przedstawionego układu przy założeniu, że masa wózka jest

równa zeru, otrzymujemy:

•
•

.

•

Po przekształceniach:

•
•

Standardową postacią tego równania jest:

•

,

•

gdzie poszczególne współczynniki: a1, a2, b0, b1, b2 mają następujące wartości:

Opis za pomocą równania różniczkowego, zwanego w tym przypadku równaniem ruchu

układu, jest w zasadzie jedyną jednoznaczną formą opisu dynamiki układu. Jak

wiemy z kursu matematyki, aby rozwiązać równanie różniczkowe zwyczajne należy

jeszcze znać warunki początkowe.





F

a

m

2

2

(

)

d y

du dy

m

b

k u y

dt

dt dt

�

�

=

-

+

-

�

�

�

�

ku

dt

du

b

ky

dt

dy

b

dt

y

d

m









2

2

u

b

u

b

u

b

y

a

y

a

y

2

1

0

1

1



















m

k

b

m

b

b

b

m

k

a

m

b

a











2

,

1

,

0

0

,

2

,

1

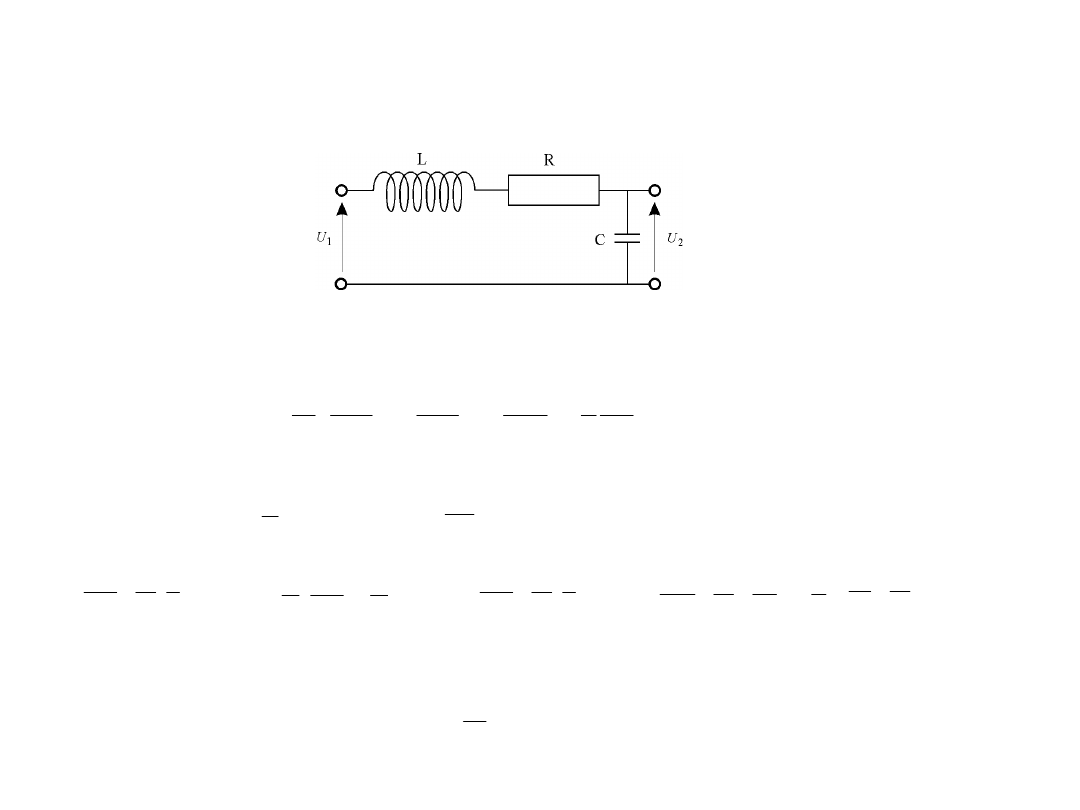
Przykład 2. Czwórnik elektryczny

•

Wyprowadzić równanie dynamiczne czwórnika elektrycznego, przedstawionego na rysunku , utworzonego z połączonych

szeregowo indukcyjności , oporności i pojemności C. Sygnałem wejściowym jest , zaś wyjściowym .

•

Rozwiązanie

•

Przy wyznaczaniu równań można stosować równania Lagrange’a:

•

•

Za współrzędną uogólnioną w tym przypadku przyjmuje się ładunek kondensatora . Wymuszeniem zewnętrznym

układu jest tu sygnał wejściowy . Energia kinetyczna, potencjalna i moc rozproszona wyrażają się wzorami:

•

Stąd składniki równania Lagrange’a mają postać:

•

,

•

,

•

,

.

•

Jeśli wstawimy otrzymane wyrażenia do równania Lagrange’a, to równanie opisujące dynamikę czwórnika

elektrycznego LRC będzie miało postać:

•

.

 

2

2

q

L

k

E





 

t

X

y

P

y

E

y

E

y

E

dt

d

i

i

i

p

i

k

i

k





























































2

1

2

2

1

q

C

p

E 

 

2

q

R

P





 

q

L

q

L

q

y

k

E





























2

2

 

q

L

q

L

dt

d

y

k

E

dt

d



























 

0

2

2





















q

L

q

y

k

E



C

q

C

q

q

y

p

E









































2

2

 

q

R

q

R

q

y

P









2

2 



















1

1

Lq Rq

q U

C

+

+

=

&&

&

MODELOWANIE OBIEKTÓW

STEROWANIA

Automatyka wytworzyła własny aparat pojęciowy i własną metodykę

rozwiązywania problemów analizy i syntezy układów sterowania.
Istotną rolę odgrywa odpowiednie przygotowanie modelu
matematycznego zarówno obiektu, układu otwartego, jak i układu
zamkniętego na potrzeby tej metodyki. W tym celu przekształca się
równania dynamiczne do jednej z wybranych postaci modelu układu. W
niniejszym podręczniku będziemy posługiwali się następującymi
modelami matematycznymi:

---schematy blokowe,
---modele w przestrzeni stanu,
---modele operatorowe.
W tym rozdziale omówimy kolejno te modele i pokażemy

podstawowe związki pomiędzy nimi. Oprócz wymienionych modeli
istotną rolę w automatyce ogrywają inne modele, np. model ARMAX,
model wykorzystujący parametry i łańcuchy Markowa, grafy i sieci,
automat skończony, itd.

Wiadomości podstawowe o

schematach blokowych

• Inżynierowie projektujący układy dynamiczne często stosują do

wizualizacji tych układów różnego rodzaju schematy. Schemat

jest zazwyczaj bardziej komunikatywny niż równania

matematyczne opisujące badany lub projektowany układ

sterowania. Budowanie schematów zazwyczaj zaczynamy od

podzielenia układu na mniejsze podukłady. Następnie rysujemy

schemat ukazując połączenia pomiędzy podukładami.

• Podział na podukłady może odbywać się na różnych poziomach.

Jeśli badany układ jest bardzo rozbudowany, to często buduje

się schematy w sposób zagnieżdżony. To znaczy, dzielimy układ

na duże podukłady i rysujemy połączenia pomiędzy nimi. Tak

wydzielone podukłady rysujemy na osobnych schematach

dzieląc je dalej na podpodukłady. Postępując tak kolejno

dochodzimy do takiego poziomu schematów, że te detalicznie

opisują pewne fragmenty układu. Takim podejściem do

modelowania układów dynamicznych charakteryzuje się na

przykład program SIMULINK.

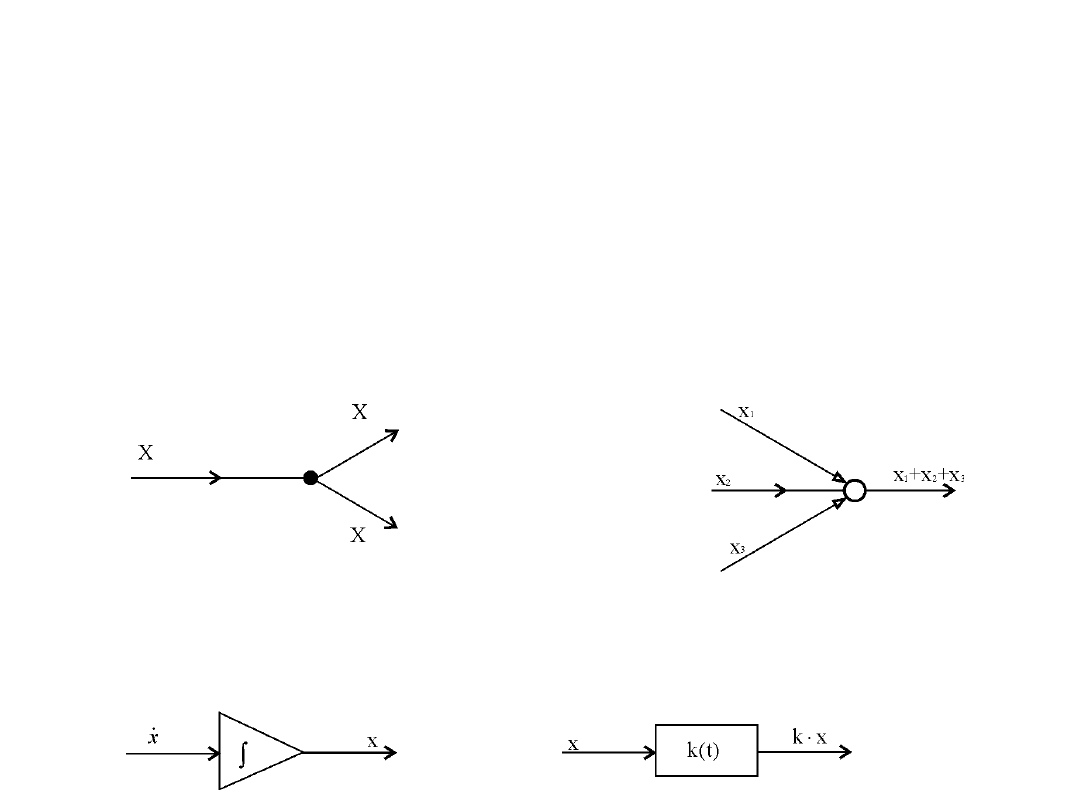
Elementy schematów blokowych

• Jednym z możliwych schematów jest schemat blokowy. W schemacie

blokowym związki pomiędzy zmiennymi w układzie liniowym można wyrazić

jedynie przez cztery elementarne podukłady (zwane popularnie

elementami):

– Element informacyjny – reprezentowany przez kropkę.

– Element sumacyjny – reprezentowany przez okrąg.

– Element całkujący – reprezentowany przez trójkąt.

– Element przetwarzający (wzmacniający) - reprezentowany przez kwadrat lub

prostokąt.

Przykład 3. Wózek z układem

drgająco‑tłumiącym

•

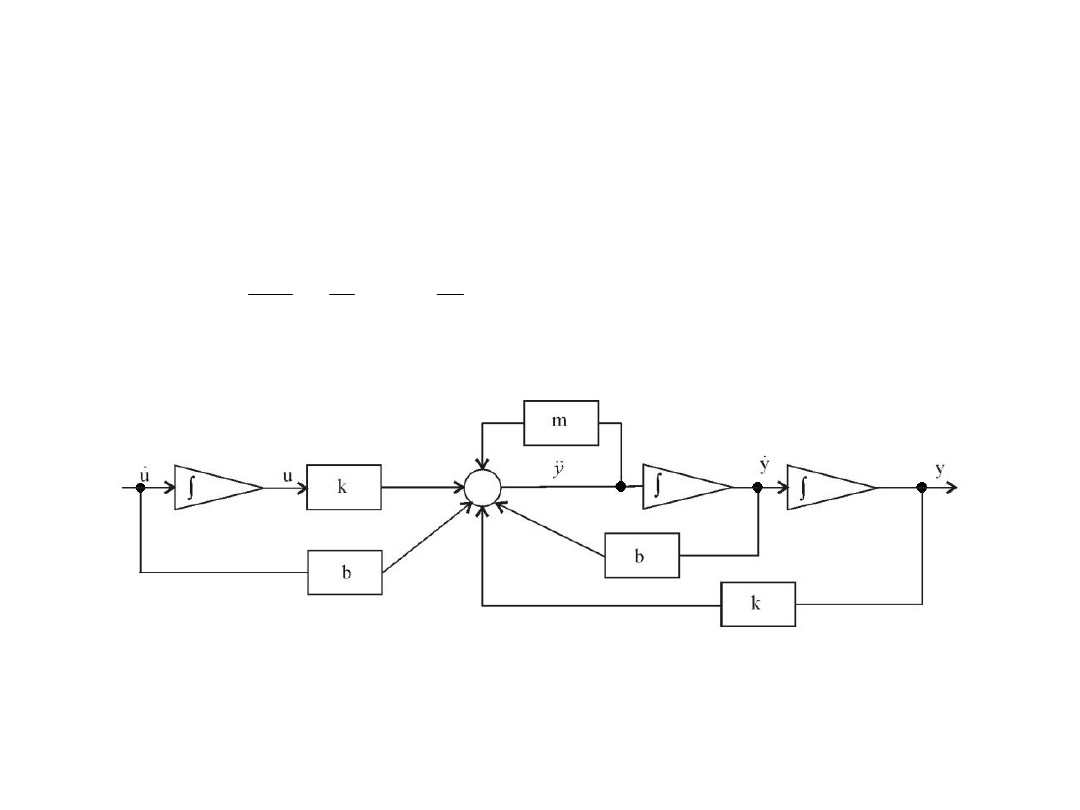
Narysować schemat blokowy układu opisanego w przykładzie 1.

•

Rozwiązanie

•

Równanie dynamiczne opisujące ruch masy przymocowanej poprzez sprężynę i tłumik z

ruchomym wózkiem w następującej postaci:

•

.

•

Na bazie tego równania narysujemy schemat blokowy. Jako regułę przyjmuje się, że dla

każdego równania rysujemy jeden element sumacyjny. Jeśli wyjściem z integratora jest

pochodna, to oznacza, że wejściem jest pochodna drugiego rzędu, itd.

•

Jak podkreślono w przykładzie 1, sygnałem wejściowym jest sygnał (opisujący ruch wózka),

natomiast sygnałem wyjściowym jest sygnał y (opisujący ruch masy). Niestety, tu jako

sygnał wejściowy mamy pochodną sygnału u, gdyż nie jesteśmy w stanie narysować innego

schematu bezpośrednio na podstawie równania ruchu. Poprawne narysowanie schematu jest

możliwe w przypadku zastosowania modelu operatorowego lub modelu przestrzeni stanu.

ku

dt

du

b

ky

dt

dy

b

dt

y

d

m









2

2

Pojęcie stanu układu

•

Stan układu czy jego elementów składowych jest jednym z najważniejszych pojęć w teorii

układów dynamicznych i teorii sterowania. Stan charakteryzuje układ odznaczający się

pewnego rodzaju pamięcią, tzn. stan zawiera informację zakumulowaną z całej przeszłości

układu aż do danej chwili oraz nie może ulegać nagłym skokowym zmianom.

•

Pojęcie stanu wyjaśnimy na prostym przykładzie zbiornika z cieczą. Zawartość zbiornika

(objętość cieczy) mówi nam wszystko o jego stanie, a więc jest to zmienna stanu tego

zbiornika. Wiedząc bowiem, ile jest cieczy w zbiorniku, nie musimy już pamiętać o tym, w jaki

sposób i kiedy ta ciecz wpłynęła do zbiornika – zmienna stanu „pamięta” całą historię

dopływów i odpływów ze zbiornika i bilansuje tę historię. Dopływ lub odpływ można uznać za

zmienną sterującą zbiornika; łatwo dostrzec, że ustalając np. określony dopływ, mierzony w

jednostkach objętości na jednostkę czasu, regulujemy stan, ale nie możemy go zmienić nagle

– co najwyżej wpływamy na prędkość zmian stanu. Zauważmy również, że znajomość

aktualnego stanu jest niezbędna, jeśli interesujemy się przyszłym zachowaniem układu – np.,

jeśli chcemy określić, w jaki sposób zbiornik opróżni się z cieczy przy swobodnym jej

wypływie. Stan zbiornika jest jego zmienną wewnętrzną, bowiem zawartość zbiornika można

określić tylko pośrednio, np. mierząc poziom cieczy w zbiorniku lub ciśnienie na jego dnie. Przy

bezpośrednim pomiarze objętości konieczne byłoby całkowite opróżnienie zbiornika. Poziom

lub ciśnienie można oczywiście uznać za zmienne wyjściowe; nie zawsze są one

proporcjonalne do stanu. W tym przypadku mogą zależeć od kształtu zbiornika.

•

Przykład zbiornika uwidacznia kilka istotnych spraw. Najważniejszą jest spostrzeżenie, że

wybór zmiennej stanu jest w gruncie rzeczy arbitralny.. Drugie spostrzeżenie dotyczy

potencjalnych ograniczeń fizycznych stanu, np. zbiornik może zostać przepełniony lub

całkowicie opróżniony. Oznacza to, że stan może (choć nie musi) podlegać pewnym

ograniczeniom fizycznym. Zauważmy wreszcie, że znajomość stanu daje nam bardzo wiele,

ale jeszcze więcej wiedzielibyśmy o układzie, gdybyśmy znali związki zmiennej stanu z innymi

ważnymi zmiennymi. Można więc przypuszczać, że w opisie układu (w jego modelu

matematycznym) kluczową rolę będzie odgrywał związek (np. równanie) rządzący

zachowaniem się zmiennej stanu.

Zbiornik

•

W przykładzie zbiornika można taki związek podać bardzo łatwo w postaci równania różniczkowego:

•
•

w którym x(t) oznacza wartość zmiennej stanu w danej chwili (objętość cieczy w [m3]), zaś u(t) –

wypadkowy dopływ w danej chwili (w [m3 s-1]). Rozwiązanie powyższego równania ma postać:

•

•

lub może przyjąć postać alternatywną:

•

•

gdzie zmienna jest zmienną całkowania.

•

Pierwsze z tych wyrażeń pokazuje, że zawartość zbiornika jest całką wypadkowego dopływu, liczoną przez

cały czas jego istnienia (w czasie zbiornik był pusty). Drugie wyrażenie jest bardziej dogodne, ponieważ

podkreśla postulowaną przez nas właściwość zmiennej stanu. Jeśli rozpatrywany jest przebieg zmian

zawartości zbiornika od chwili: , to wówczas konieczna jest znajomość stanu , która zawiera pełną informację

o jego przeszłości. Dalsze zachowanie zmiennej stanu określa całka wielkości , liczona od chwili początkowej

0 do bieżącej t, przy czym dla , i stan pozostałby stały („zapamiętany”) również w następnych chwilach

czasu t.

•

Analogiczne właściwości do omówionego zbiornika miałyby takie układy, jak: kondensator ładowany prądem

elektrycznym (zmienną stanu jest spadek napięcia lub ładunek zgromadzony na kondensatorze), kalorymetr

bilansujący ciepło doprowadzone i odprowadzone, zbiornik ciśnieniowy powietrza. Podobnie można

rozpatrywać magazyn towaru lub zasób finansowy. Wspólną cechą wymienionych układów jest fakt

magazynowania (zachowania, pamiętania, akumulowania) pewnej wielkości fizycznej – masy, ładunku,

energii, ciepła, kapitału przez elementy, które dalej będziemy nazywali elementami całkującymi. Wyjścia

elementów całkujących nazywane są zmiennymi stanu, ponieważ mogą być rozważane jako zmienne, które

definiują stan wewnętrzny systemu.

)

(

)

(

t

u

dt

t

dx











t

d

u

t

x





)

(

)

(







t

d

u

x

t

x

0

)

(

)

0

(

)

(





Przestrzeń stanu

Liczba zmiennych stanu jest równa liczbie niezależnych elementów magazynujących (lub niezależnych
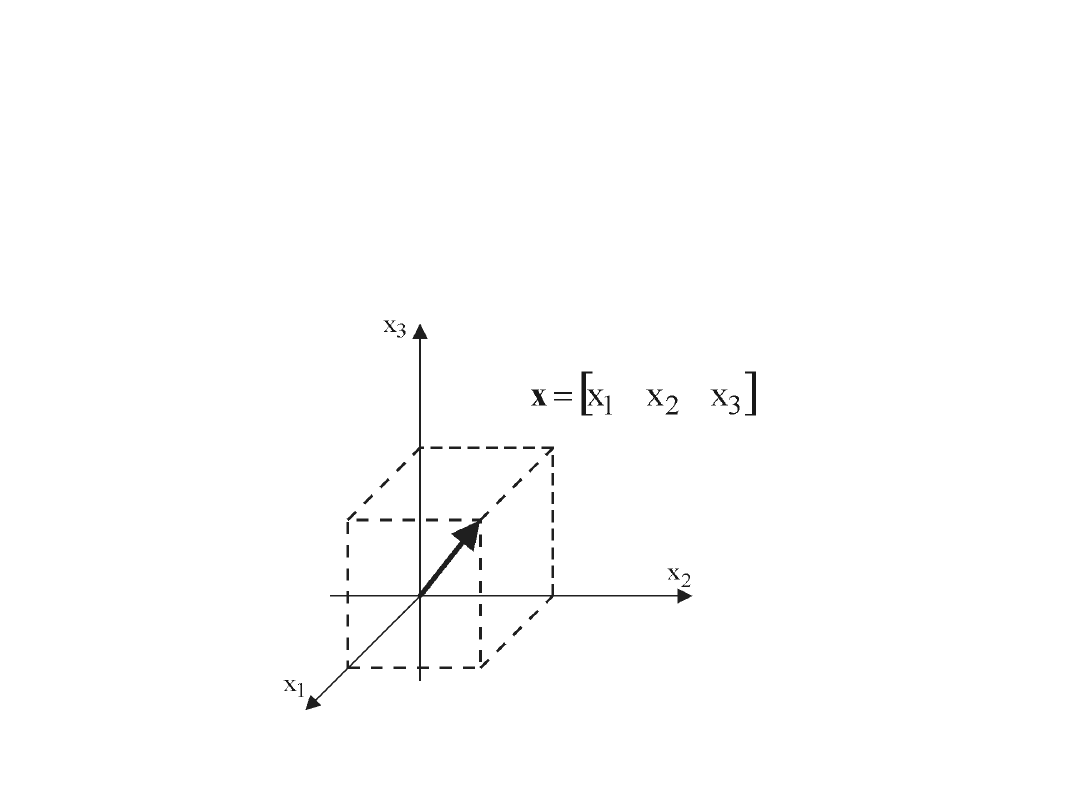
wielkości magazynowanych). Można to interpretować w taki sposób, że stan ma postać wektora,
określonego w

–wymiarowej przestrzeni stanów, gdzie n oznacza liczbę zmiennych stanu. Osiami (współrzędnymi)
przestrzeni stanów są więc poszczególne współrzędne (zmienne) stanu. Każdy punkt przestrzeni
stanów reprezentuje określony stan rozumiany jako zbiór wartości wszystkich zmiennych stanu
układu. Można więc zapisać symbolicznie wektor stanu

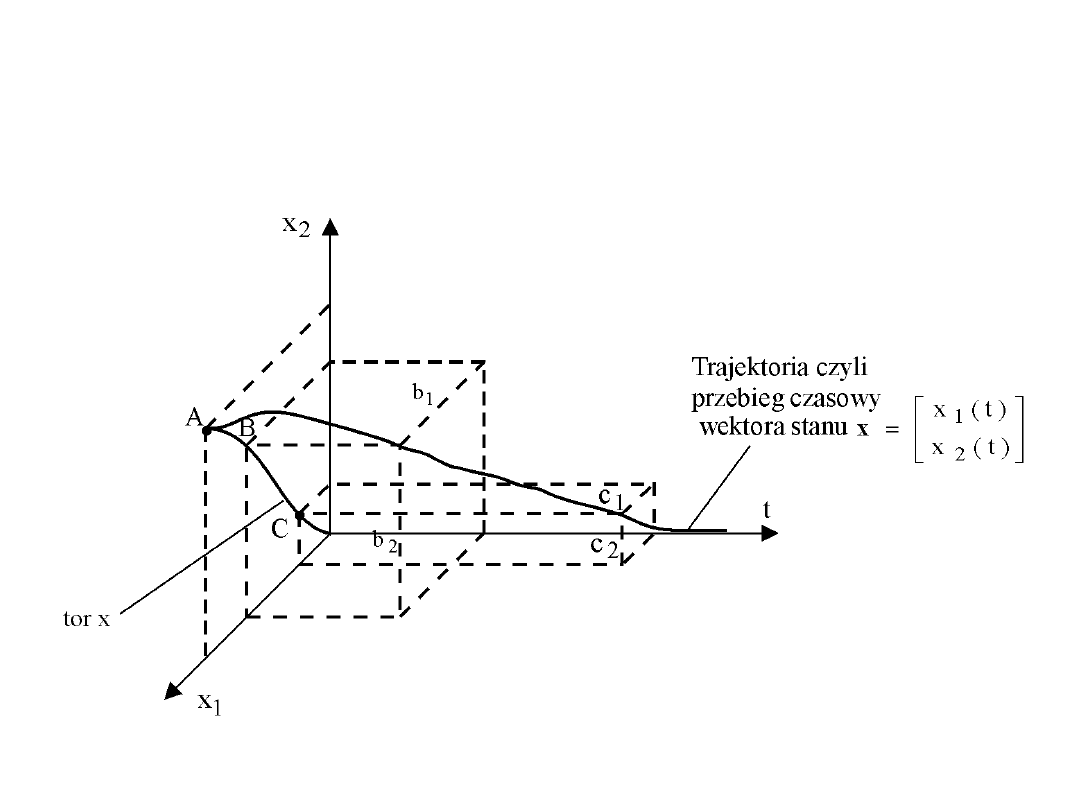
Trajektoria i tor

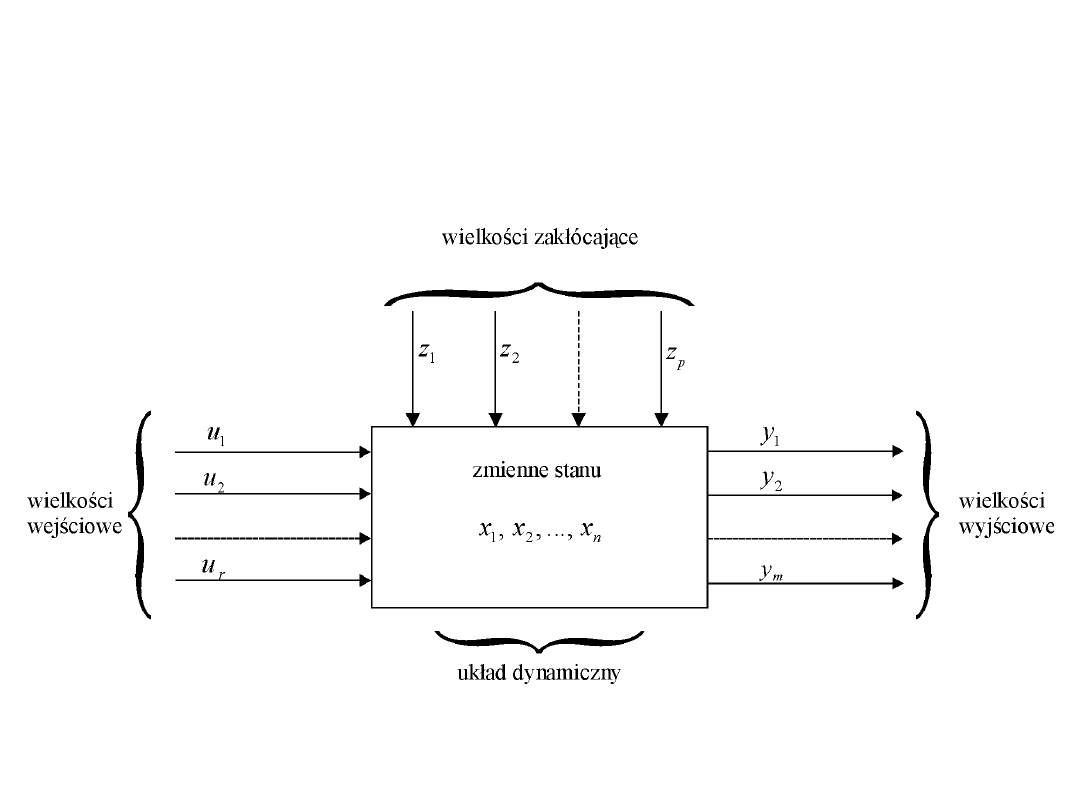
Sygnały w układzie dynamicznym

Równania stanu

)

;

2

1

;

...,

,

2

,

1

;

...,

,

2

,

1

(

)

(

)

;

2

1

;

...,

,

2

,

1

;

...,

,

2

,

1

(

2

)

(

2

)

;

2

1

;

...,

,

2

,

1

;

...,

,

2

,

1

(

1

)

(

1

t

p

...,z

,

z

,

z

r

u

u

u

n

x

x

x

m

g

t

m

y

t

p

...,z

,

z

,

z

r

u

u

u

n

x

x

x

g

t

y

t

p

...,z

,

z

,

z

r

u

u

u

n

x

x

x

g

t

y









)

;

2

1

;

...,

,

2

,

1

;

...,

,

2

,

1

(

)

(

)

;

2

1

;

...,

,

2

,

1

;

...,

,

2

,

1

(

2

)

(

2

)

;

2

1

;

...,

,

2

,

1

;

...,

,

2

,

1

(

1

)

(

1

t

p

...,z

,

z

,

z

r

u

u

u

n

x

x

x

n

f

t

n

x

t

p

...,z

,

z

,

z

r

u

u

u

n

x

x

x

f

t

x

t

p

...,z

,

z

,

z

r

u

u

u

n

x

x

x

f

t

x















 





t

f

t

,

,

,

z

u

x

x 



 





t

g

t

,

,

,

z

u

x

y 

 

 

 

 

t

t

t

t

Ez

Bu

Ax

x









 

 

 

 

t

t

t

t

Fz

Du

Cx

y







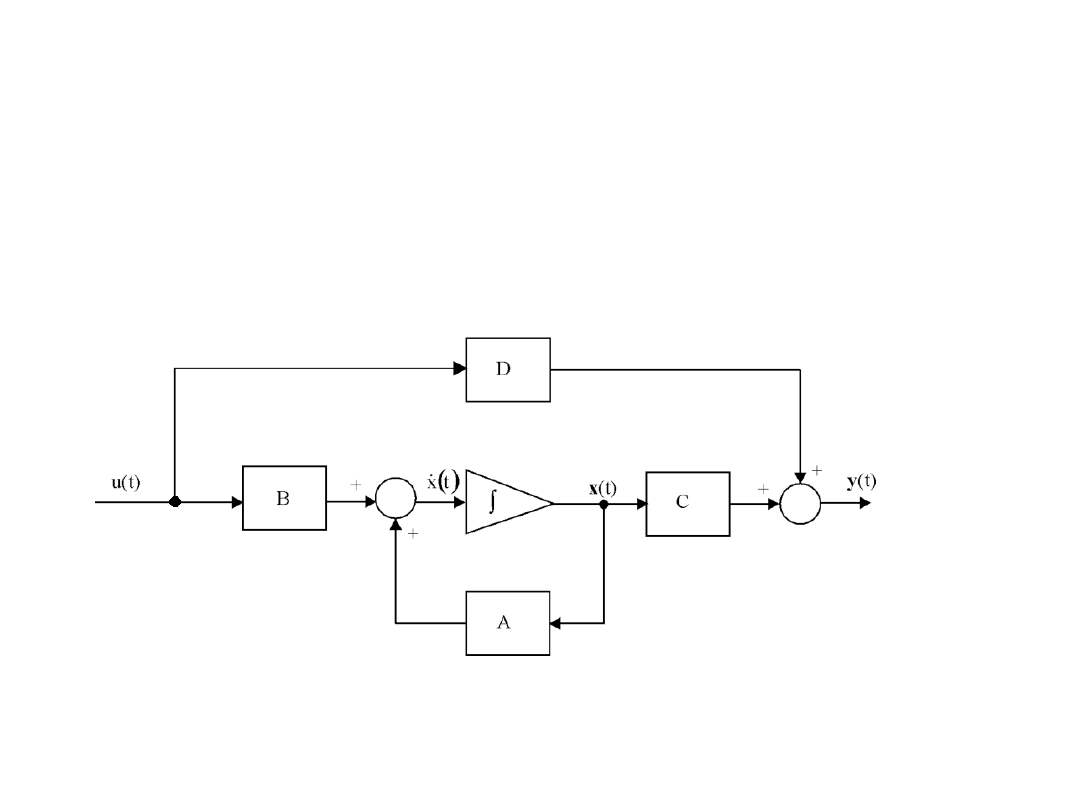
Schemat modelu układu w przestrzeni

stanu

 

 

 

t

t

t

Bu

Ax

x







 

 

 

t

t

t

Du

Cx

y





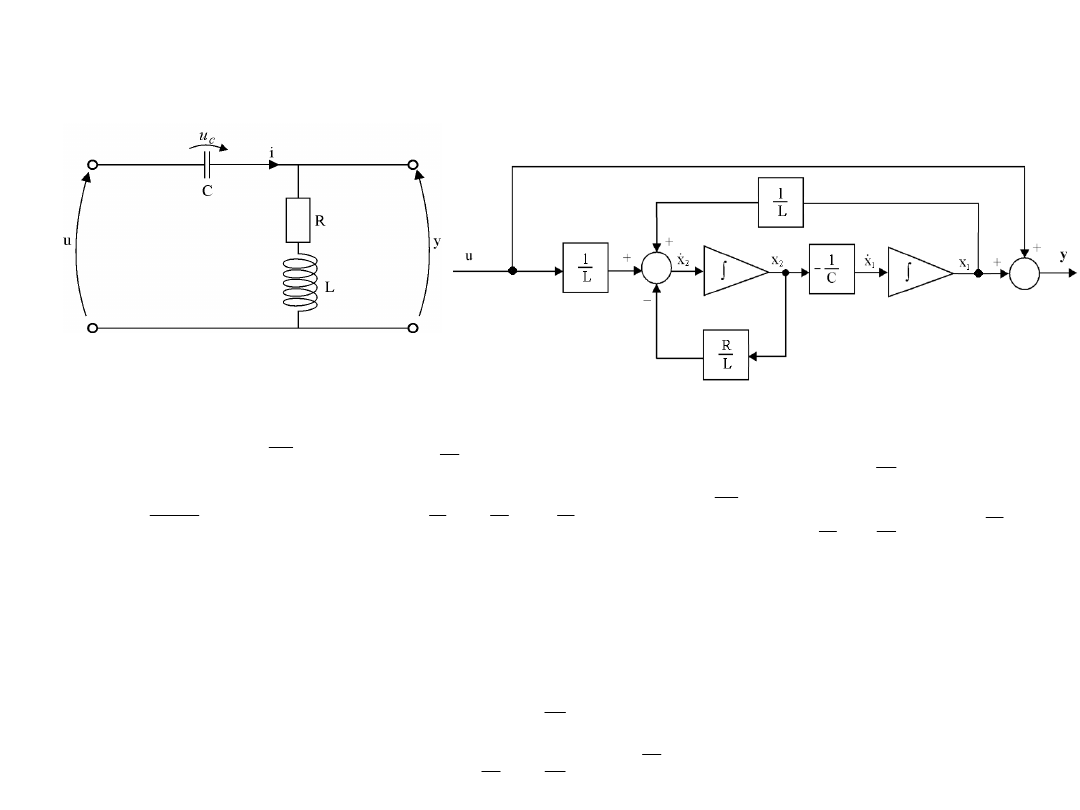
Przykład 4. Obwód elektryczny

.

,

,

u

C

u

y

i

dt

C

du

C

dt

di

L

Ri

C

u

u















u

L

x

L

R

x

L

x

x

C

x

1

2

1

1

2

2

1

1















u

x

y



 1

1

1

2

2

1

0

0

1

1

x

x

d

C

u

x

x

R

dt

L

L

L

�

�

-

� �

�

�

� �

� � � �

=

+

�

�

� �

� � � �

� �

� �

�

�

-

� �

�

�

�

�





 

u

x

x

y

1

2

1

0

1





















 

1

;

0

1

;

1

0

;

1

1

0















































D

C

L

B

L

R

L

C

A