Lista II (do wykładu III 06.03, IV 13.03, V 27.03)

Zasady zachowania

Drgania

1. Sprawdzić, czy siła F=(2xz²-2y,-2x-6yz,2x²z-3y²) jest siłą zachowawczą. Jeśli tak, to wyznaczyć odpowiadającą jej energię potencjalną. (Wykład, Skrypt, Cząstki i pola, AR, I.3.3, s. 32)

2. Energia potencjalna siły F ma postać: U(x,y)=3x²y-7x. Wyznaczyć zależność siły F od współrzędnych x,y. (Wykład, Skrypt, Cząstki i pola, AR, I.3.3, s.32)

3. Walec o promieniu podstawy R i wysokości H pływa (pionowo) w cieczy o gęstości ρ, przy czym jest w niej zanurzony do połowy swojej objętości. Obliczyć pracę potrzebną do wyciągnięcia walca na powierzchnię.

4. W drewniany klocek o masie M=1 kg zawieszony na linie o długości L=1 m trafia pocisk o masie m=5 g i pozostaje w nim. Jaka była prędkość pocisku v, jeśli lina klocka odchyliła się o kąt =60o od pionu? Jaka ilość ciepła Q wydziela się w trakcie wbijania się pocisku w klocek?

5. Poziomo lecący strumień wody uderza o ścianę i spływa po niej swobodnie. Prędkość strumienia wynosi v, a jego pole przekroju poprzecznego S. Wyznaczyć siłę, z jaką ten strumień działa na ścianę.

6. Z działa stojącego na płaskiej powierzchni oddano strzał pod katem α do poziomu. Masa pocisku m, a wartość jego prędkości przy wylocie z lufy v. Jak daleko przesunie się działo po wystrzale, jeśli siła tarcia działa o podłoże wynosi F? Masa działa, M.

7. Jaką najmniejszą prędkość należy nadać ciału, aby wynieść je na orbitę okołoziemską? (I prędkość kosmiczna)

8. A jaką, aby uwolnić je od grawitacyjnego wpływu Ziemi? (II prędkość kosmiczna)

9. Jaką wartość ma wyrażenie,
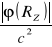
   , gdzie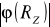
   oznacza wartość potencjału grawitacyjnego na powierzchni Ziemi? (Wykład, Skrypt, Cząstki i pola, AR, I.4.2, s. 35)

10. Dwie kule zawieszone na równoległych niciach o tej samej długości stykają się. Kula o masie M zostaje odchylona od pionu tak, że jej środek ciężkości wznosi się na wysokość h, a następnie puszczona swobodnie. Na jaką wysokość wzniesie się ta kula po zderzeniu doskonale niesprężystym z drugą kulą o masie m?

11. Z równi pochyłej o wysokości h=1.8 m i kącie =30o zsuwa się skrzynia uzyskując na końcu równi prędkość v=2 m/s. Ile wynosi współczynnik tarcia f skrzyni o równię?

12. Ciało o masie m znajduje się początkowo na wierzchołku równi pochyłej w kształcie jednorodnego klina o masie M, wysokości h i długości L, mogącej przesuwać się po poziomej płaszczyźnie. Zakładając, że tarcie nie występuje, wyznaczyć położenie równi w momencie, gdy ciało zsunie się z równi.

13. Obliczyć pracę siły F=(3y+x²)j pomiędzy punktami (0,0) oraz (5,5) na drodze: a) po bokach kwadratu: (0,0) -> (0,5) -> (5,5) b) po bokach kwadratu (0,0) -> (5,0) -> (5,5) c) po przekątnej kwadratu (0,0) -> (5,5). Czy jest to siła zachowawcza? (Wykład, Skrypt, Cząstki i pola, AR, I.3.2, s. 30)

14. Napisać i rozwiązać równanie jednowymiarowego oscylatora harmonicznego. (Wykład, Skrypt, Cząstki i pola, AR, I.2.3, s.20)

15. Jeśli amplituda drgań harmonicznych wynosi A, a okres T, to ile wynosi maksymalna prędkość i maksymalne przyspieszenie? Znając fazę drgań wyznaczyć stosunek energii potencjalnej do energii kinetycznej.

16. Na poziomym doskonale gładkim stole leży ciało o masie M, przymocowane sprężyną do ściany. W ciało to uderza pocisk o masie m, lecący z prędkością v w kierunku poziomym i pozostaje w nim. Układ zaczyna wykonywać harmoniczne drgania w kierunku poziomym z amplitudą A. Wyznaczyć częstość tych drgań.

17. Ciało o masie m spada z wysokości h na szalkę wagi sprężynowej i przykleja się do niej. Układ zaczyna wykonywać harmoniczne drgania w kierunku pionowym. Wyznaczyć amplitudę tych drgań i ich energię. Współczynnik sprężystości sprężyny wynosi k, a masa szalki M.

18. Podać równanie ruchu ciała, które wpadło w szyb, przecinający na wskroś kulę ziemską wzdłuż jej średnicy (wziąć pod uwagę zmienną wartość siły ciężkości w jej wnętrzu). Podać czas, po jakim ciało osiągnie środek Ziemi oraz prędkość, z jaką go minie.

19. Napisać i rozwiązać równanie jednowymiarowego tłumionego oscylatora harmonicznego. (Wykład, Skrypt, Cząstki i pola, AR, I.2.3, s. 21)

20. Na pionowo wiszącej sprężynie zawieszono ciężarek, co spowodowało wydłużenie sprężyny o Δl. Ciężarek ten wprawiono w drgania. Jaką wartość powinien mieć współczynnik tłumienia β, aby: a) amplituda zmalała 100 razy w przeciągu czasu t, b) ciężarek powrócił aperiodycznie do położenia równowagi.

21. Logarytmiczny dekrement tłumienia drgań tłumionych oscylatora wynosi λ=0.02. Obliczyć, ile razy zmniejszy się amplituda drgań po 100 całkowitych wahnięciach.

22. Napisać i rozwiązać równanie jednowymiarowego wymuszonego oscylatora harmonicznego. (Wykład, Skrypt, Cząstki i pola, AR, I.2.3, s. 23)

23. Obliczyć amplitudę rezonansową drgań harmonicznych wymuszonych punktu materialnego, gdy jego masa m=0.2 kg, okres drgań własnych wynosi T₀=1s, odwrotność współczynnika tłumienia 1/β=1/3 s, a amplituda siły wymuszającej F₀=10 N.

24. Ciało o masie M wykonuje drgania harmoniczne tłumione. W chwili t=0 faza drgań była równa zeru, a amplituda wynosiła A₀. Na ciało zaczęła działać okresowa siła zewnętrzna, pod wpływem której ustaliły się drgania wymuszone o równaniu: x=Bcos(2πt-0.75π). Wyznaczyć: a) równanie drgań nietłumionych, b) amplitudę i częstość siły wymuszającej. Stała tłumienia wynosi β.

---