Wykres Gantta, Metoda 

CPM, Metoda PERT.

Opracowane 

przez

Adrian 

Ciepielewski

Łukasz 

Wesołowski

Z6R2S1

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

2

Spis Treści

1.

Wykres Gantta
1.1. Definicja;
1.2. Wykonanie wykresu Gantta;
1.3. Kamienie milowe.

2. 

Metoda CPM i PERT
2.1. Definicja, powstanie.
2.1.1. PERT.
2.1.2. CPM.
2.2. Opracowanie sieci.
2.3. Ścieżka krytyczna.
2.4. Ustalanie czasu realizacji projektu i analiza działań.
2.4.1. Metoda CPM.
2.4.2. Metoda PERT.

3. 

Zadania
3.1. Wykres Gantta.
3.2. Metoda CPM.
3.3. Metoda PERT.

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

3

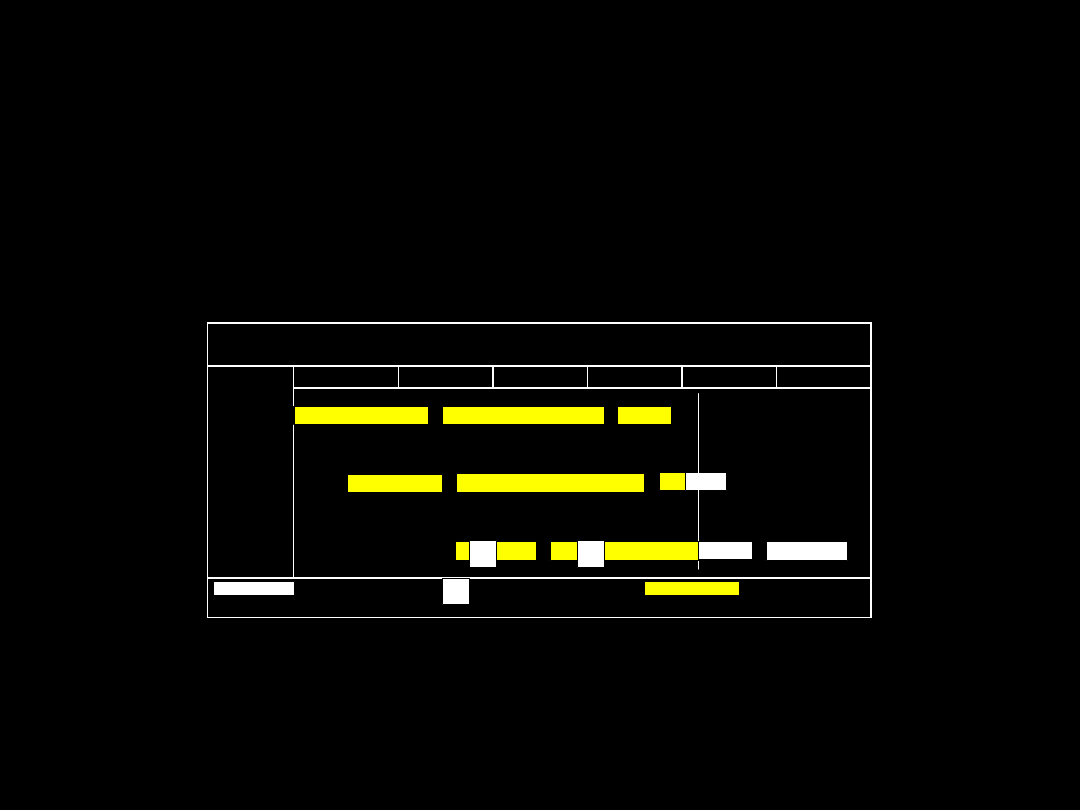
1. Wykres Gantta

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

4

1.1. Definicja

• Wykres Gantta – graficzny sposób 

planowania i kontroli

1

1

J.A.F. Stoner, Ch. Wankel, Kierowanie, Polskie Wydawnictwo Ekonomiczne, 

Warszawa 1996, s. 162.

Wydział X 

Miesiąc 1 – Miesiąc 6 

Miesiąc 1 

Miesiąc 2  Miesiąc 3  Miesiąc 4  Miesiąc 5  Miesiąc 6 

 

 

Wyrób A 

 

 

Wyrób B 

 

 

Wyrób C 

Zaopatrzenie               Produkcja                  Wysyłka 

 

 

             Zaopatrzenie           Produkcja                    Wysyłka 

 

 

                                 Zaopatrzenie               Produkcja                    Wysyłka 

                    Plan                                Kamień milowy                                   Wykonanie 

 

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

5

1.2. Tworzenie Wykresu 

Gantta

W  celu  zrealizowania  wykresu  Gantta  należy  wykonać 

następujące kroki:

1.    Na  wstępie  należy  podzielić  projekt  na  drobne 

zadania;

2. Dla każdego zadania wyznacza się czas w jakim dane 

zadanie  ma  być  wykonane  oraz  datę  jego  realizacji, 

które  są  konieczne  do  sfinalizowania  całego 

przedsięwzięcia  w  uprzednio  wyznaczonym  czasie; 

Informacja ta na wykresie Gantta zobrazowana jest w 

formie „klamry”. Jej początek wskazuję termin startu, 

a koniec wyznacza dzień, w którym dane zadanie ma 

zostać zakończone;

3. Przenosi się wszystkie ustalenia na formę graficzną.

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

6

1.3. Kamienie milowe.

• Kamienie milowe - sformalizowane 

punkty kontrolne, w których można 
zanalizować koszty, postęp prac czy 
potrzebę modyfikacji lub zmiany planu

2

.

2

J.A.F. Stoner, Ch. Wankel, Kierowanie, Polskie Wydawnictwo Ekonomiczne, 

Warszawa 1996, s. 163.

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

7

2. Metoda CPM i PERT

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

8

2.1. Definicja, powstanie.

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

9

2.1.1. PERT.

• PERT – Program Evaluation and Review Technique – 

Technika  oceny  i  kontroli  programu  –  metoda 

szacowania 

i 

kontroli 

czasów 

na 

potrzeby 

planowania. 

• PERT  jest  jedną  z  dwóch  najistotniejszych  metod 

sieciowych. 

• Opracowana została w altach 1957-1958 przez Biuro 

Projektów  Specjalnych  Marynarki  Wojennej  Stanów 

Zjednoczonych,  przy  współdziałaniu  z  korporacją 

Lockheed, firmą doradztwa Booz, Allen i Hamilton

3

.

3

J.A.F. Stoner, Ch. Wankel, Kierowanie, Polskie Wydawnictwo Ekonomiczne, 

Warszawa 1996, s. 164.

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

10

2.1.2. Definicja, 

powstanie.

• CPM  –  Critical  Path  Metod  –  Metoda  ścieżki  krytycznej  –  to 

jedna z dwóch, obok PERT, najważniejszych metod sieciowych. 

• Opracowana przez grupę DuPont w latach 1957-1958. 
• Jej  zadaniem  jest  ułatwianie  kontroli  wielkich,  złożonych 

projektów 

przemysłowych. 

Wykorzystuje 

się 

ją 

do 

cyklicznych/systematycznych  procesów,  gdzie  poszczególne 

zadania  mają  niezmienny  czas  trwania                      i  znany  jest 

termin ich zakończenia

4

.

4

J.A.F. Stoner, Ch. Wankel, Kierowanie, Polskie Wydawnictwo Ekonomiczne, 

Warszawa 1996, s. 164.

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

11

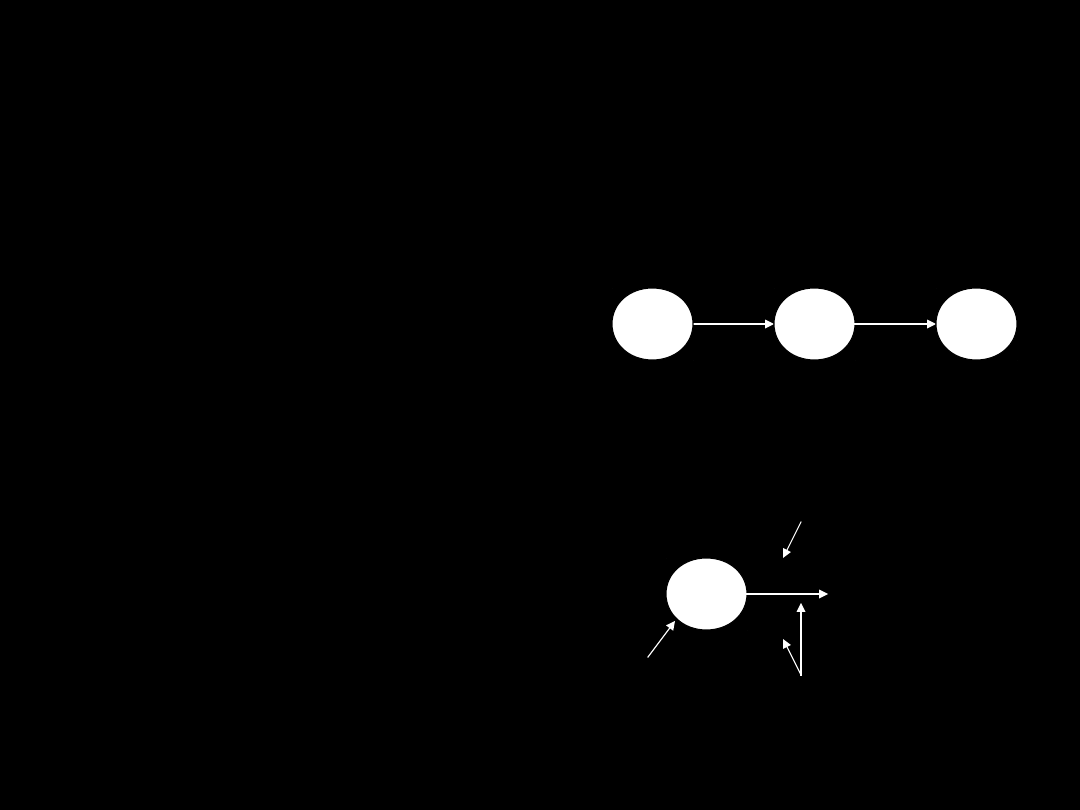
2.2. Opracowanie sieci.

1. 

Całe 

działanie 

musi 

być 

podzielone na odrębne zadania.

2. 

Zdarzenia 

i 

działania 

umieszcza się na wykresie w 
sposób 

logiczny, 

sekwencyjny i zintegrowany.

3. 

Do 

sieci 

wpisuje 

się 

oszacowany  czas  potrzebny 
na każde działanie.

4.  Należy  ustalić  krytyczną 

ścieżkę przebiegającą przez 
sieć.

1

2

3

3

2

A

B

1

3

A

Wydarzeni
e

Działanie

Czas

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

12

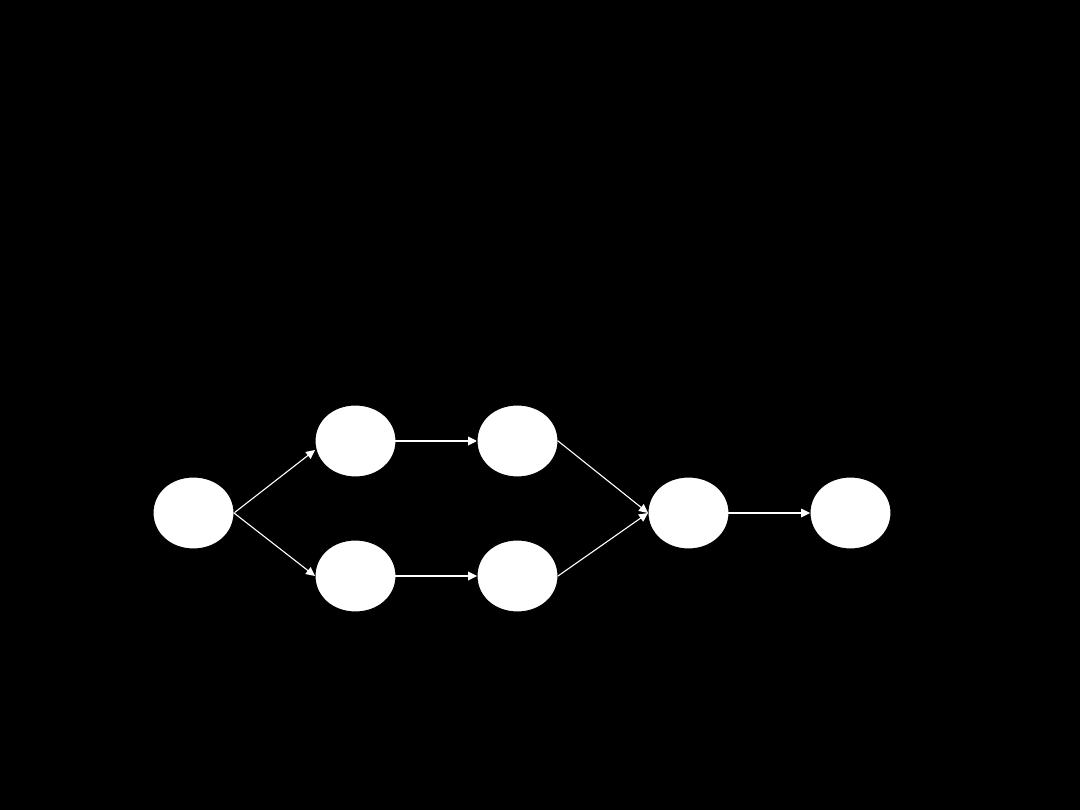
2.3. Ścieżka krytyczna

Ścieżka krytyczna – najdłuższa pod względem czasu trasa przechodząca 

przez  sieć.  Wyznacza  się  ją  dodając  do  siebie  wszystkie  czasy 

niezbędne  do  wykonania  wszystkich  zadań  w  każdej  ich  sekwencji. 

Ścieżką krytyczną jest łańcuch zadań o najdłuższym czasie

5

.

1

2

3

3

2

4

5

2

1

6

7

3

5

2

A

B

C

G

D

E

F

5

J.A.F. Stoner, Ch. Wankel, Kierowanie, Polskie Wydawnictwo Ekonomiczne, Warszawa 1996, s. 165.

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

13

2.4. Ustalenie czasu 

realizacji projektu i 

analiza działań.

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

14

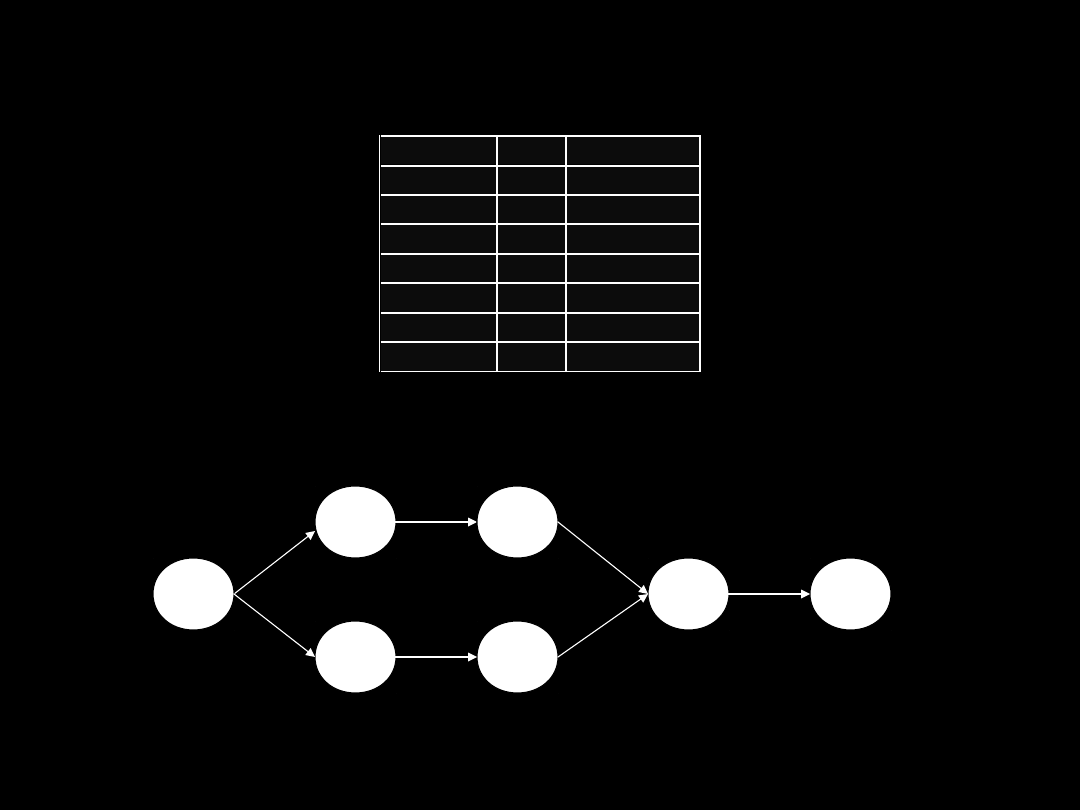
2.4.1. CPM

1. Znalezienie najwcześniejszego czasu 

zaistnienia wydarzeń, przy rozpoczęciu 
projektu w momencie zerowym.

2. Określenie w jakim czasie projekt zostanie 

wykonany – drogą ścieżki krytycznej.

3. Znalezienie najpóźniejszego możliwego 

czasu zaistnienia wydarzenia – 
wykonywane odwrotnie do pkt. 1 a więc 
od końca projektu do jego początku.

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

15

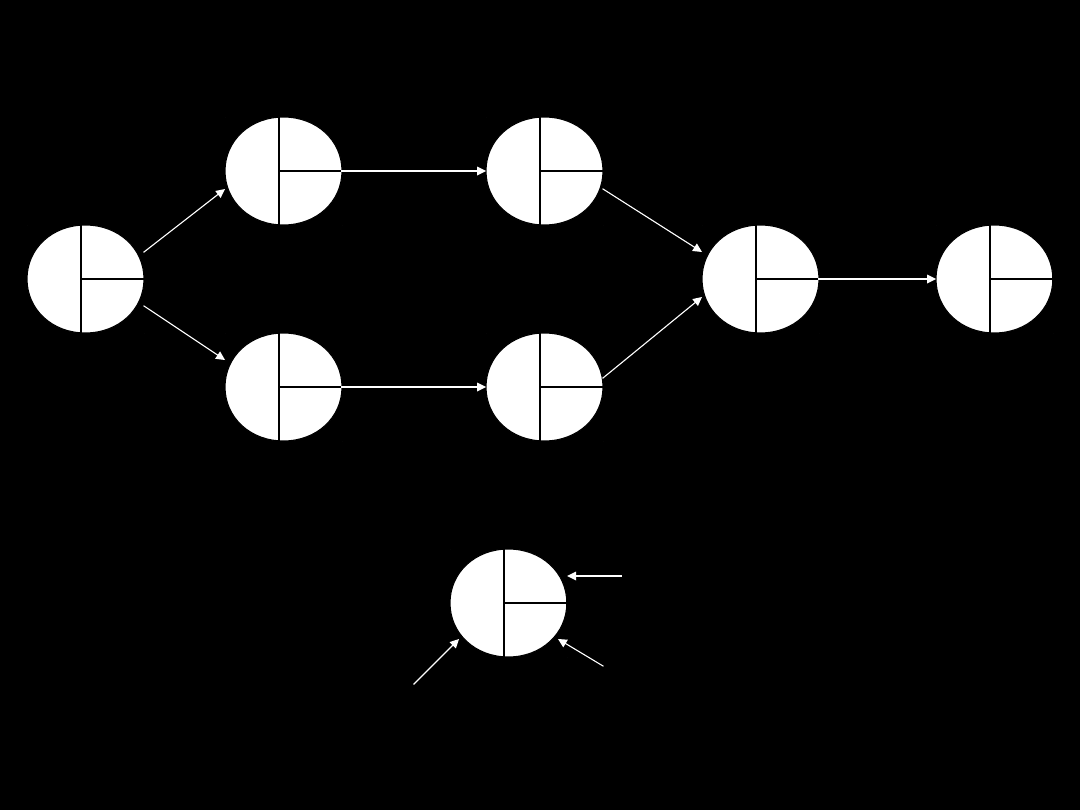
2.4.1. CPM

1

2

3

3

2

4

5

2

1

6

7

3

5

2

A

B

C

G

D

E

F

Działania  Czas  Poprzednik 
A 

3 

- 

B 

2 

A 

C 

5 

B 

D 

2 

- 

E 

1 

D 

F 

3 

E 

G 

2 

C, F 

 

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

16

3

A

1

2

4

3

5

6

7

B

C

G

3

1

2

2

5

F

E

D

2

0

3

5

1
0

1
2

2

3

1
2

1
0

5

3

0

6

7

1

0

0

Wydarzeni
e

Najpóźniejszy 
czas

Najwcześniejsz
y czas

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

17

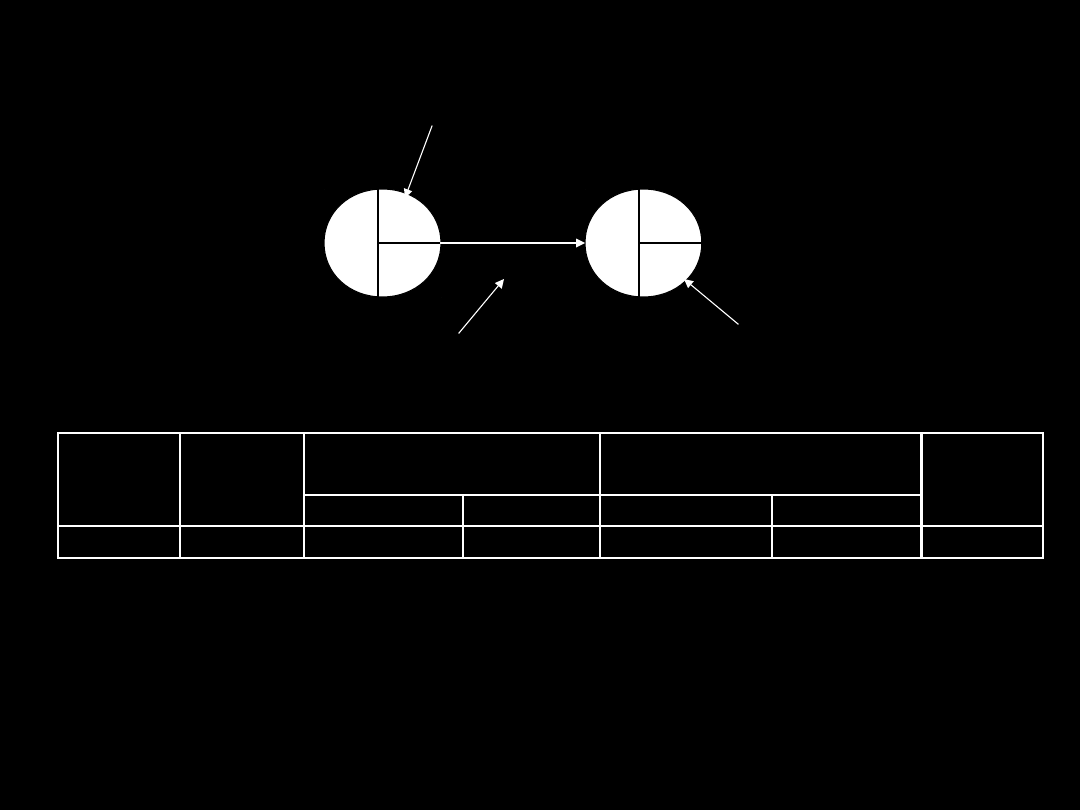
Analiza działań

• Margines, to ograniczenie opóźnień.
• Margines 

= 

najpóźniejszy 

możliwy 

czas 

zakończenia  –  najwcześniejszy  możliwy  czas 
rozpoczęcia – czas trwania

• Najwcześniejszy  czas  rozpoczęcia  działania  to 

najwcześniejszy czas poprzedzającego wydarzenia

• Najwcześniejszy  czas  zakończenia  to  czas 

rozpoczęcia plus czas trwania

• Najpóźniejsze  rozpoczęcie  zadania  to  czas 

następującego  wydarzenia  minus  czas  trwania 
działania

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

18

4

5

1

E

2

3

6

7

Najwcześniejszy czas 
rozpoczęcia zadania = 
najwcześniejszy czas 
zaistnienia wydarzenia(NP)

Najpóźniejszy czas 
zaistnienia wydarzenia = 
najpóźniejszy czas 
rozpoczęcia zadania(NpK)

Czas 
trwania(t)

Najwcześniejszy możliwy 

czas(N) 

Najpóźniejszy możliwy 

czas(Np) 

Działanie 

Czas 

trwania(t) 

Początku(NP)  Końca(NK)  Początku(NpP)  Końca(NpK) 

Margines 

(NpK-

NP-t) 

E 

1 

2 

3(NP+t) 

6(NpK-t) 

7 

4 

 

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

19

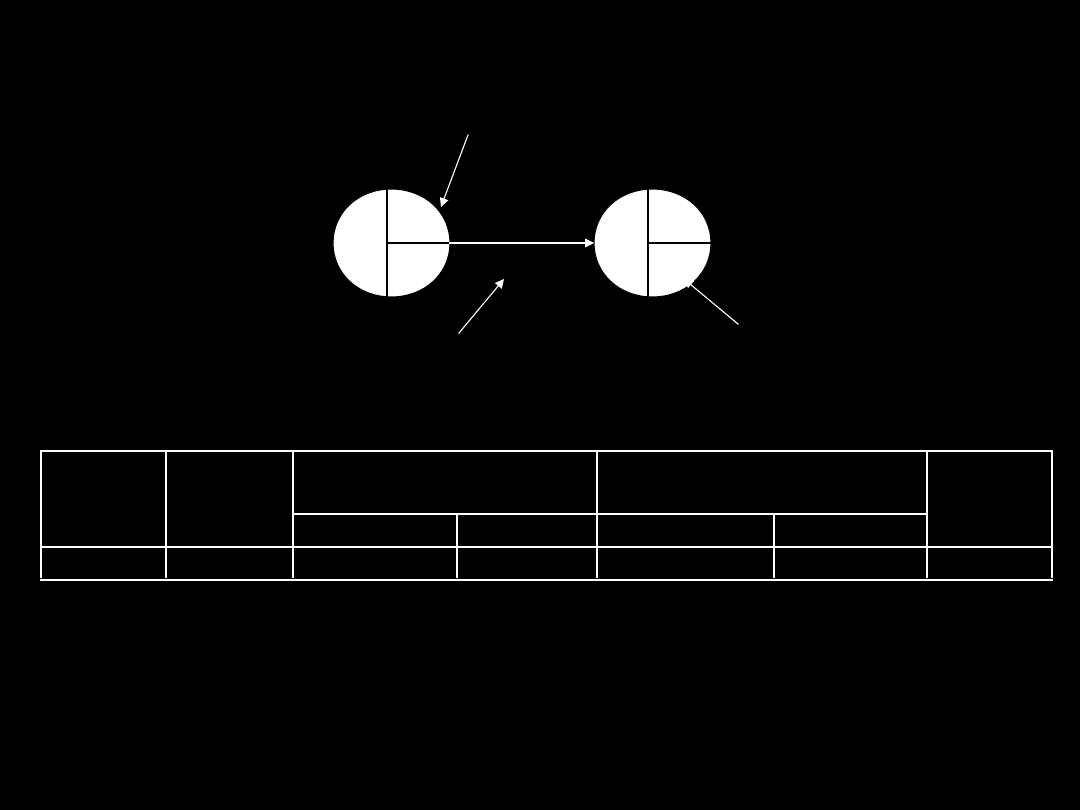
Działanie krytyczne

Działanie krytyczne – działanie, które ma 

jeden  stały  moment,  w  którym  musi 
zostać  wykonane(margines  wynosi  0). 
Działania 

krytyczne 

tworzą 

nieprzerwaną  linię,  zwaną  ścieżką 
krytyczną, prowadzącą przez sieć

6

.

6

D. Waters, Zarządzanie operacyjne: towary i usługi, Wydawnictwo Naukowe PWN, Warszawa 2001, s. 499.

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

20

2

3

B

2

3

5

5

3

Najwcześniejszy możliwy 

czas(N) 

Najpóźniejszy możliwy 

czas(Np) 

Działanie 

Czas 

trwania(t) 

Początku(NP)  Końca(NK)  Początku(NpP)  Końca(NpK) 

Margines 

(NpK-

NP-t) 

B 

2 

3 

5(NP+t) 

3(NpK-t) 

5 

0 

 

Najwcześniejszy czas 
rozpoczęcia zadania = 
najwcześniejszy czas 
zaistnienia wydarzenia(NP)

Najpóźniejszy czas 
zaistnienia wydarzenia = 
najpóźniejszy czas 
rozpoczęcia zadania(NpK)

Czas 
trwania(t)

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

21

2.4.2. PERT

• Ustalenie czasu realizacji projektu oraz w analizie działań, a 

wiec przy wyznaczaniu marginesu wykorzystuje się 
oczekiwaną wartość czasu, a nie czas trwania działania jak w 
metodzie CPM

• Oczekiwaną wartość wylicza się wykorzystując

– Optymistyczny czas realizacji(O)
– Czas prawdopodobny(M)
– Czas pesymistyczny(P)
Według wzoru:
Wartość oczekiwana = (O + 4M + P)/6

• Wariancję oblicza się ze wzoru:

Wariancja = (O – P)

2

/36

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

22

•

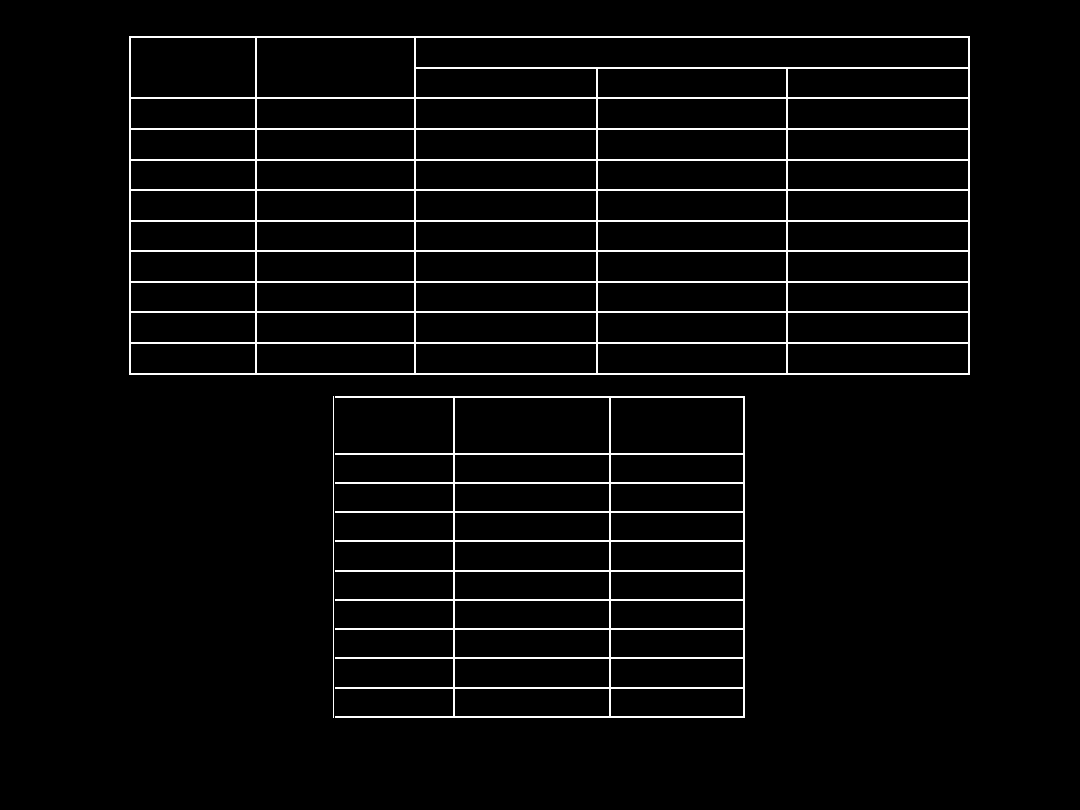
Obliczamy również prawdopodobieństwo ukończenia 

danego projektu w jakimś czasie, przy wykorzystaniu tabel 

rozkładu normalnego, według schematu:

1.

Wyznaczamy okres względem, którego będziemy obliczać 

prawdopodobieństwo. >(Ot) – W; <(Ot) – M;

2.

Obliczamy oczekiwany czas zakończenia(Ot) projektu 

podążając ścieżką krytyczną;

3.

Obliczamy wariancje dla tych punktów i je sumujemy;

4.

Z sumy wariancji(SW) wyliczamy odchylenie standardowe(OS) 

w następujący sposób: OS=√SW

5.

Wyliczamy poszukiwane odchylenie standardowe(POS) ze 

wzoru:

•

POS=(W-Ot)/OS, jeśli czas ukończenia dla, którego liczymy 

prawdopodobieństwo jest większy od oczekiwanego czasu 

zakończenia

•

POS=(Ot-M)/OS, jeśli czas ukończenia dla, którego liczymy 

prawdopodobieństwo jest mniejszy od oczekiwanego czasu 

zakończenia

6.

Wyszukujemy w tabeli rozkładu normalnego wartość dla 

otrzymanego POS

7.

Wyszukaną wartość odejmujemy od jedności(1) i otrzymujemy 

prawdopodobieństwo ukończenia projektu przed wyznaczonym 

okresem.

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

23

Czas trwania 

Działanie  Poprzednicy 

Optymistyczny  Prawdopodobny  Pesymistyczny 

A 

- 

2 

3 

10 

B 

- 

4 

5 

12 

C 

- 

8 

10 

12 

D 

AG 

4 

4 

4 

E 

B 

3 

6 

15 

F 

B 

2 

5 

8 

G 

B 

6 

6 

6 

H 

C,F 

5 

7 

15 

I 

D,E 

6 

8 

10 

 

Działanie  Oczekiwany  

czas trwania  Wariancja 

A 

4 

1,78 

B 

6 

1,78 

C 

10 

0,44 

D 

4 

0 

E 

7 

4,00 

F 

5 

1,00 

G 

6 

0 

H 

8 

2,78 

I 

8 

0,44 

 

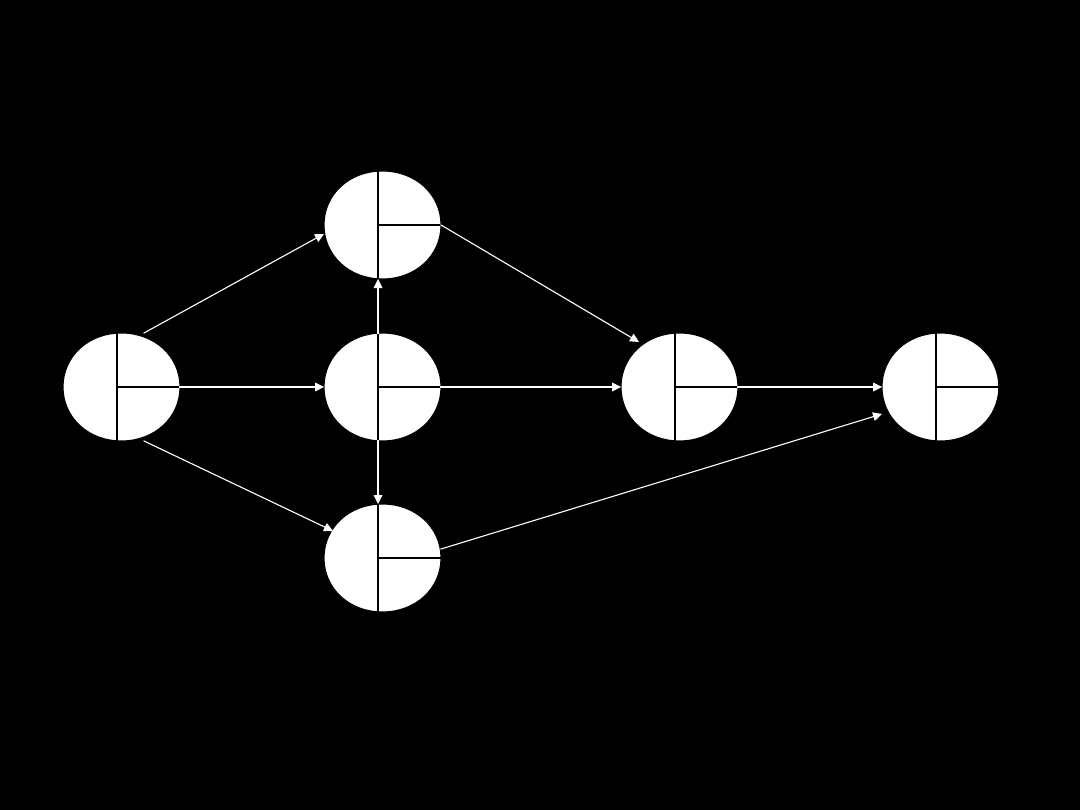
 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

24

1

2

B

6

0

6

6

0

3

1
2

1
2

A

4

G

6

5

1
6

1
6

D

4

4

1
1

1
6

6

2
4

2
4

E

7

F

5

C

10

I

8

H

8

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

25

Najwcześniejszy możliwy 

czas(N) 

Najpóźniejszy możliwy 

czas(Np) 

Działanie 

Oczekiwany 

czas 

trwania(Ot)  Początku(NP)  Końca(NK)  Początku(NpP)  Końca(NpK) 

Margines 

(NpK-

NP-Ot) 

A 

4 

0 

4(NP+Ot) 

8(NpK-Ot) 

12 

8 

B 

6 

0 

6(NP+Ot) 

0(NpK-Ot) 

6 

0 

C 

10 

0 

10(NP+Ot) 

6(NpK-Ot) 

16 

6 

D 

4 

12 

16(NP+Ot)  12(NpK-Ot) 

16 

0 

E 

7 

6 

13(NP+Ot) 

9(NpK-Ot) 

16 

3 

F 

5 

6 

11(NP+Ot)  11(NpK-Ot) 

16 

5 

G 

6 

6 

12(NP+Ot) 

6(NpK-Ot) 

12 

0 

H 

8 

11 

19(NP+Ot)  16(NpK-Ot) 

24 

5 

I 

8 

16 

24(NP+Ot)  16(NpK-Ot) 

24 

0 

 

Oczekiwany czas zakończenia projektu wyznaczają działania krytyczne 
B, G, D i I. Oczekiwane czasy wynoszą kolejno 6, 6, 4 i 8. Ich suma 
wynosi 24. Wariancje kolejno, to 1,78; 0; 0 i 0,44. Suma Wariancji dla 
tych 4 wydarzeń wynosi 2,22. Odchylenie standardowe to √2,22=1,49

Prawdopodobieństwo ukończenia zadania przed np. 26 dniem wynosi: 

Z=(26-24)/1,49=1,34

gdzie Z jest odchyleniem standardowym

Odczytujemy więc z tablic rozkładu normalnego, że wartość Z wynosi 
0,0901, z czego wynika, że prawdopodobieństwo wynosi 1-
0,0901=0,9099, tj. prawie 91%

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

26

3. Zadania

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

27

3.1. Wykres Gantta

Polecenie
Wykonaj wykres Gantta na podstawie podanych 

informacji i danych:

1.Wykres obejmuje 7 kolejnych miesięcy
2.Wykres obejmuje 5 produktów
3.Mamy obecnie połowę miesiąca nr. 6
4.Działania w obrębie każdego produktu: 

Zaopatrzenie, Produkcję, Wysyłkę

5.Wykorzystaj dane z tabeli

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

28

Zaopatrzenie 

Produkcja 

Wysyłka 

Wyrób 

Początek  Koniec  Wykonano  Początek  Koniec  Wykonano  Początek  Koniec  Wykonano 

1 

0 

1,5 

100% 

2 

3 

100% 

3,5 

5,5 

100% 

2 

1,5 

2,5 

100% 

3 

4,5 

100% 

5 

6 

25% 

3 

1,5 

3 

100% 

3,5 

4,5 

100% 

5 

6,5 

33,3% 

4 

3 

4 

100% 

4,5 

5,5 

100% 

6 

7 

0% 

5 

0 

2 

100% 

2,5 

4,5 

100% 

5 

7 

25% 

 

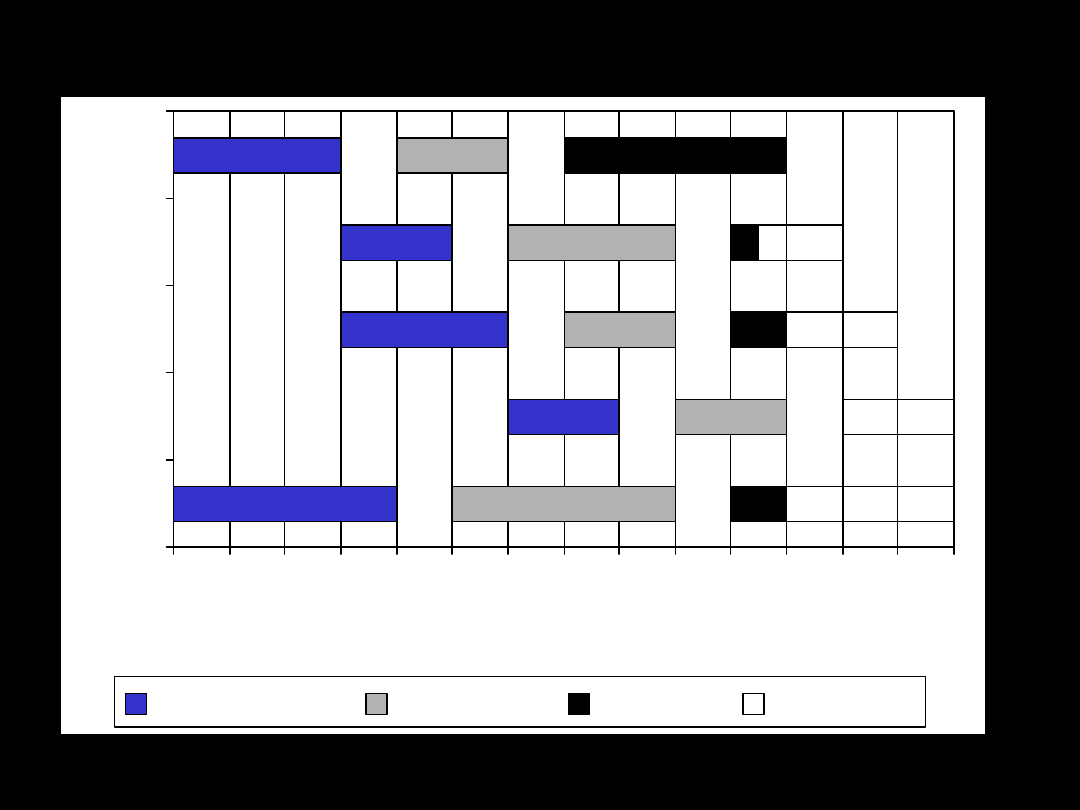
 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

29

0

0,5

1

1,5

2

2,5

3

3,5

4

4,5

5

5,5

6

6,5

7

5

4

3

2

1

Pr

od

uk

ttt

Miesiąc

Zaopatrzenie Produkcja Wysyłka Pozostało

Rozwiązanie

3.2. Metoda CPM.

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

31

Polecenie:
1. Wypełnij sieć wykonując odpowiednie obliczenia 

i zaznacz ścieżkę krytyczną

2. Na podstawie wypełnionej sieci wykonaj tabelę 

przedstawiającą:

a) Działania
b) Czas trwania
c) Najwcześniejszy możliwy czas początku
d) Najwcześniejszy możliwy czas końca
e) Najpóźniejszy możliwy czas początku
f) Najpóźniejszy możliwy czas końca
g) Margines

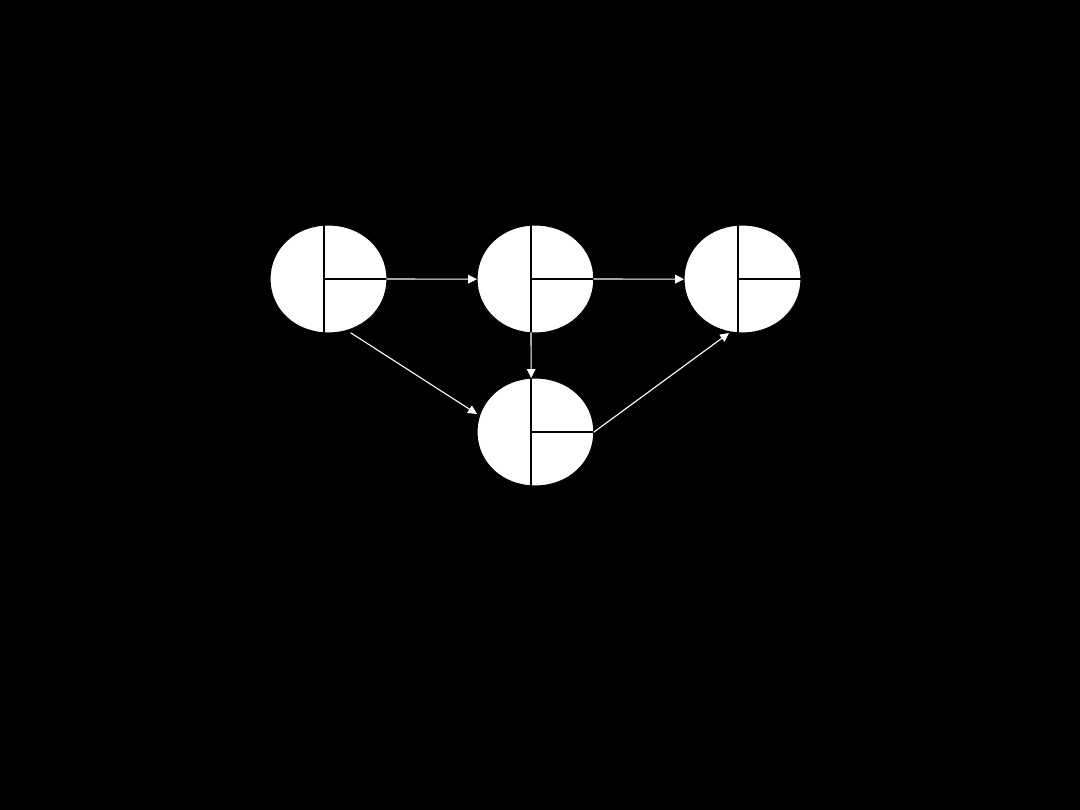
 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

32

1

2

A

6

3

C 5

B

10

4

D

E

1

4

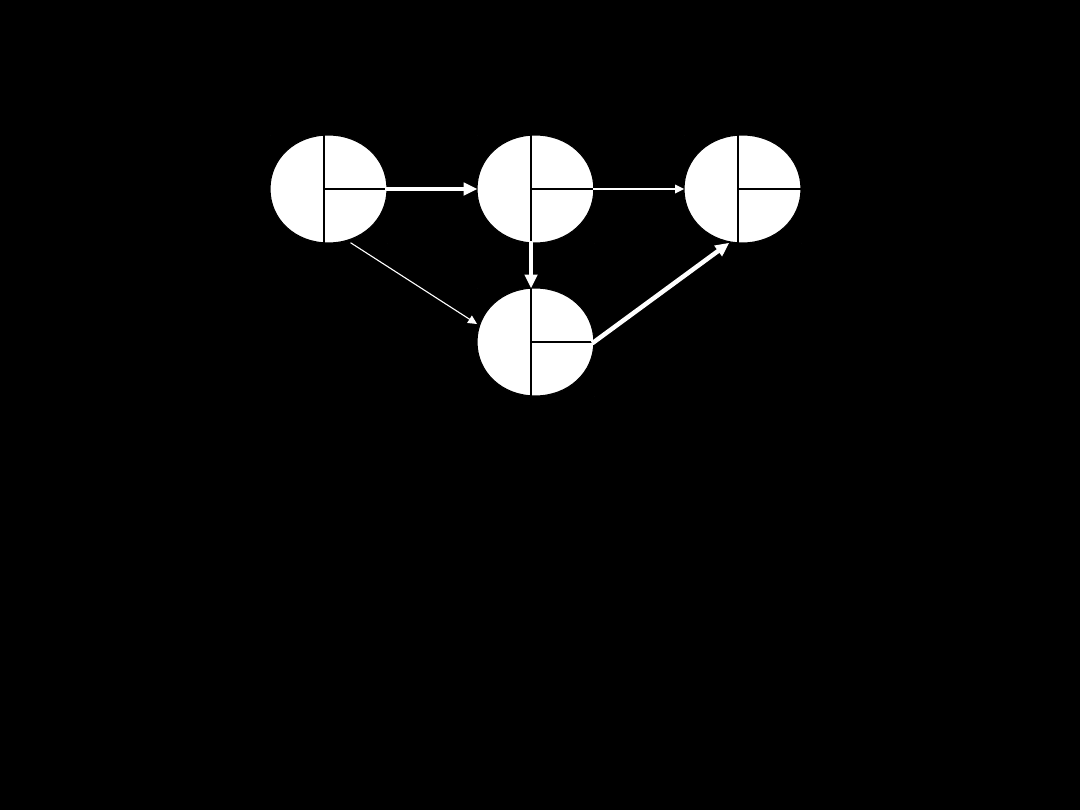
 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

33

1

2

A

6

0

6

6

0

3

1
1

1
1

C 5

B

10

4

1
5

1
5

D

E

1

4

Rozwiązanie

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

34

Najwcześniejszy 

możliwy czas 

Najpóźniejszy możliwy 

czas 

Działanie 

Czas 

trwania 

Początku 

Końca 

Początku 

Końca 

Margines 

A 

6 

0 

6 

0 

6 

0 

B 

10 

0 

10 

1 

11 

1 

C 

5 

6 

11 

6 

11 

0 

D 

1 

6 

7 

14 

15 

8 

E 

4 

11 

15 

11 

15 

0 

 

Rozwiązanie c.d.

3.3. Metoda PERT.

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

36

Polecenie:
1.

Na podstawie tabeli oblicz i umieść w tabeli pomocniczej:

a)

Działania

b)

Oczekiwany czas trwania

c)

Wariancję

2.

Na podstawie danych z tabeli pomocniczej oraz podanej tabeli wykonaj 

rysunek sieci i zaznacz ścieżkę krytyczną

3.

Na podstawie rysunku wykonaj tabelę, która będzie przedstawiała:

a)

Działanie

b)

Czas trwania

c)

Najwcześniejszy możliwy czas początku

d)

Najwcześniejszy możliwy czas końca

e)

Najpóźniejszy możliwy czas początku

f)

Najpóźniejszy możliwy czas końca

g)

Margines

4.  Oblicz prawdopodobieństwo ukończenia projektu przed 22 dniem.

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

37

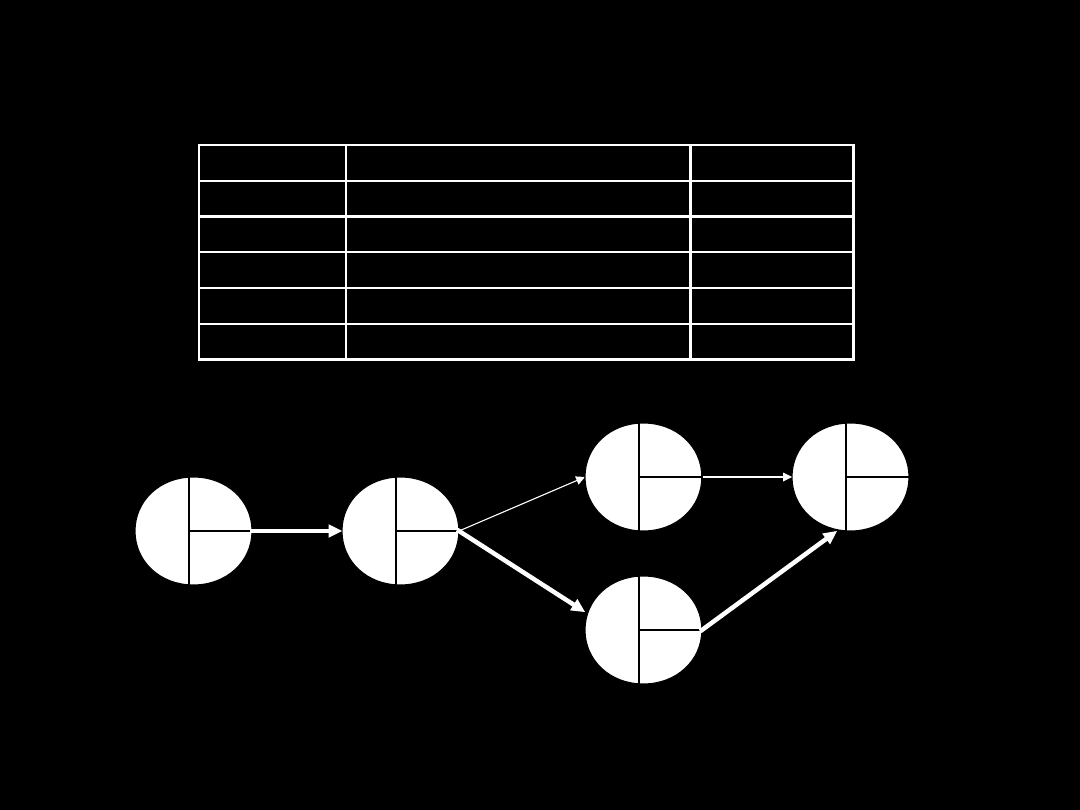
Czas trwania 

Działanie  Poprzednicy 

Optymistyczny  Prawdopodobny  pesymistyczny 

A 

- 

4 

5 

12 

B 

A 

2 

5 

8 

C 

A 

8 

10 

12 

D 

C 

2 

3 

10 

E 

B 

4 

4 

4 

 

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

38

1

2

A

6

0

6

6

0

3

1
6

1
6

C

5
B

10

5

2
0

2
0

D

E

4

4

4

1
1

1
6

Działanie  Oczekiwany czas trwania  Wariancja 

A 

6 

1,78 

B 

10 

1,00 

C 

5 

0,44 

D 

4 

1,78 

E 

4 

0 

 

Rozwiązanie

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

39

Najwcześniejszy 

Najpóźniejszy 

Działanie  Oczekiwany 

czas trwania  Początek  Koniec 

Początek 

Koniec 

Margines 

A 

6 

0 

6 

0 

6 

0 

B 

10 

6 

16 

6 

16 

0 

C 

5 

6 

11 

11 

16 

5 

D 

4 

11 

15 

16 

20 

5 

E 

4 

16 

20 

16 

20 

0 

 

Rozwiązanie c.d.

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

40

Ścieżka krytyczna: A-B-E
Suma  oczekiwanego  czasu  dla  ścieżki  krytycznej 

= 20

Suma wariancji ścieżki krytycznej = 2,78
Odchylenie standardowe = 1,68
Poszukiwane odchylenie standardowe = 1,2
Wartość prawdopodobieństwa dla poszukiwanego 

odchylenia standardowego = 0,1151

Prawdopodobieństwo  ukończenia  projektu  przed 

22 dniem = ~ 88,5%

Rozwiązanie c.d.

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

41

Zadanie dodatkowe

Polecenie
1.

Na podstawie danych z tabeli stwórz i wypełnij sieć wykonując odpowiednie obliczenia

2.

Stwórz tabelę(zgodnie z otrzymaną siecią), która będzie przedstawiała

a)

Działanie

b)

Czas trwania

c)

Najwcześniejszy możliwy czas początku

d)

Najwcześniejszy możliwy czas końca

e)

Najpóźniejszy możliwy czas początku

f)

Najpóźniejszy możliwy czas końca

g)

Margines

3. 

Na podstawie sieci i danych w tabeli narysuj wykres Gantta zawierający:
a) Czas  trwania  działań  krytycznych  –  przedstaw  je  na  wykresie  tak  by  odróżniały  się 

od działań niekrytycznych
b) Przedstaw na wykresie działania niekrytyczne(w inny sposób niż działania krytyczne) 

oraz ich marginesy.

Podpowiedź
Aby narysować czas trwania poszczególnych działań wykorzystujemy jedynie Najwcześniejszy początek i koniec.

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

42

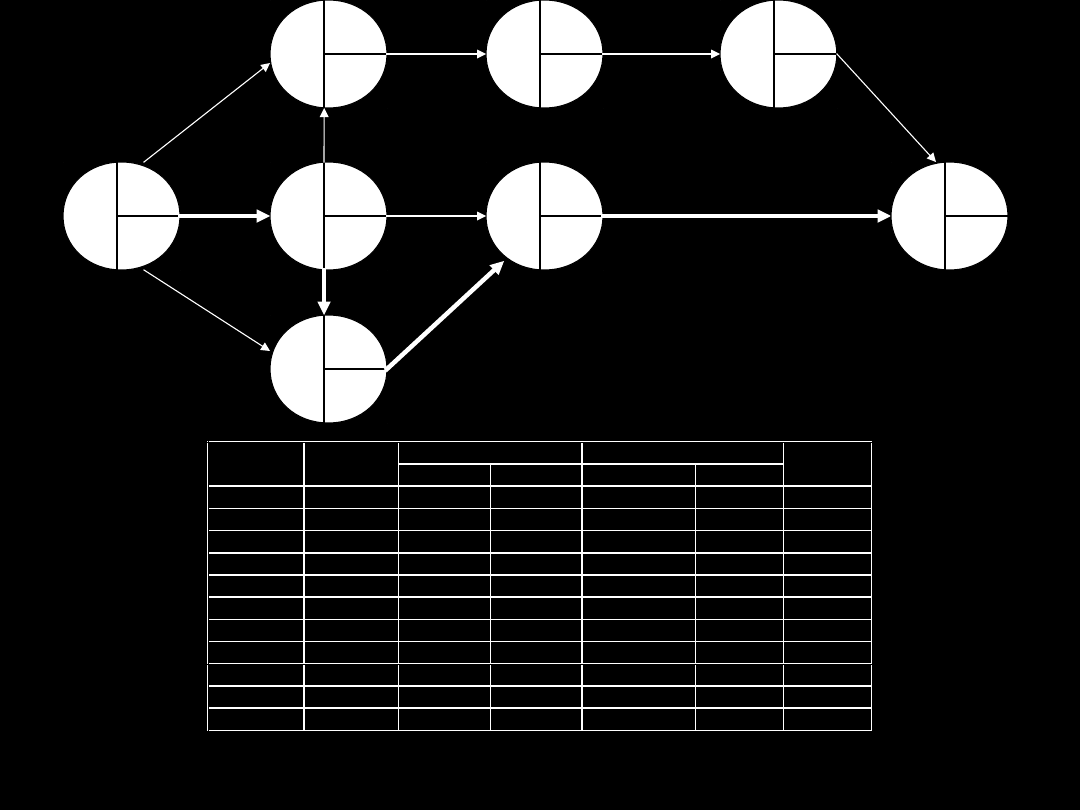
Działanie  Czas  Poprzednik 

A 

4 

- 

B 

6 

- 

C 

10 

- 

D 

6 

B 

E 

5 

B 

F 

8 

B 

G 

7 

E,C 

H 

4 

A,D 

I 

2 

H 

J 

4 

F,G 

K 

3 

I 

 

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

43

1

2

B

6

0

6

6

0

3

1
2

1
3

A

4

D

6

5

1
6

1
7

G

4

1
1

1
1

6

1
8

1
8

E

7

F

5

C

10

I

4

H

8

7

1
8

1
9

8

2
2

2
2

J

K

2

3

4

Najwcześniejszy 

Najpóźniejszy 

Działanie 

Czas 

trwania  Początek  Koniec 

Początek 

Koniec 

Margines 

A 

4 

0 

4 

11 

13 

9 

B 

6 

0 

6 

0 

6 

0 

C 

10 

0 

10 

1 

11 

1 

D 

6 

6 

12 

7 

13 

1 

E 

5 

6 

11 

6 

11 

0 

F 

8 

6 

14 

10 

18 

4 

G 

7 

11 

18 

11 

18 

0 

H 

4 

12 

16 

13 

17 

1 

I 

2 

16 

18 

17 

19 

1 

J 

4 

18 

22 

18 

22 

0 

K 

3 

18 

21 

19 

22 

1 

 

Rozwiązanie

 Adrian Ciepielewski

Łukasz Wesołowski

Z6R2S1

44

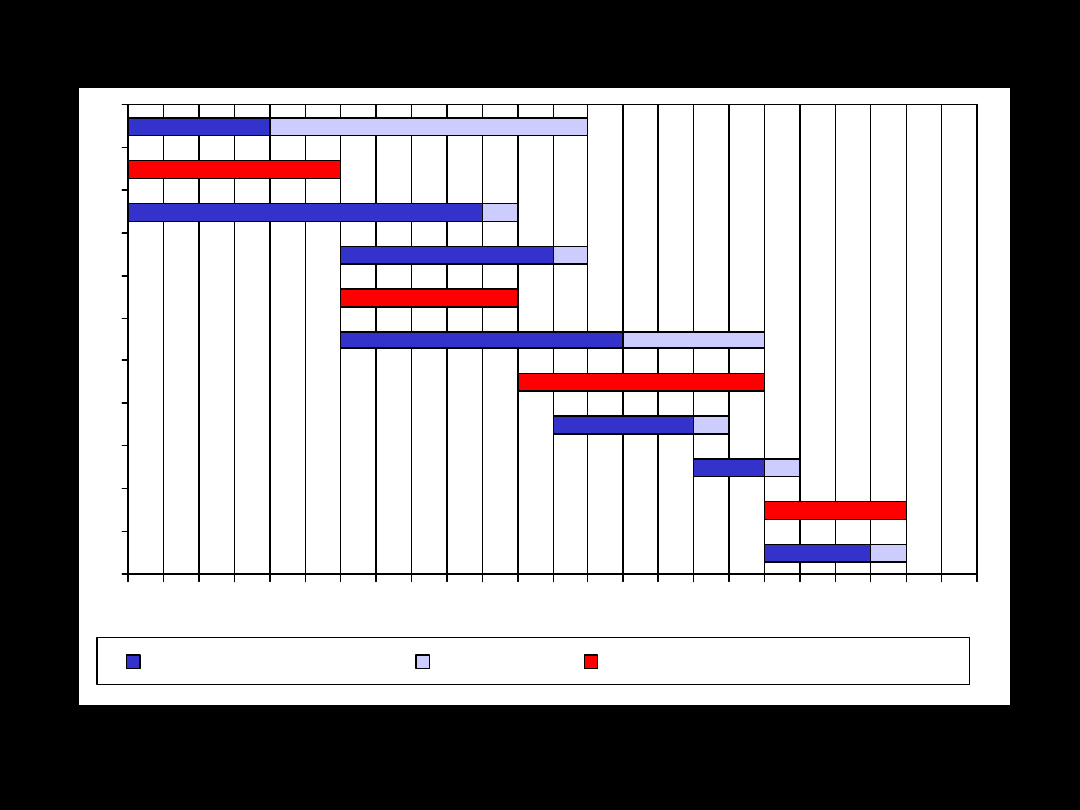
0 1 2 3 4 5 6 7 8 9 10 11 1213 14 15 16 17 18 19 20 21 22 23 24

K

J

I

H

G

F

E

D

C

B

A

Czas trwania działania

Margines

Czas trwania działania krytycznego

Rozwiązanie c.d.

DZIĘKUJEMY