Autor:

CIEPIELEWSKI

Adrian

Z9R1S2

WOJSKOWA AKADEMIA TECHNICZNA

im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

PREZENTACJA NA ĆWICZENIA Z PRZEDMIOTU ZARZĄDZANIE JAKOŚCIĄ

STACJONARNE STUDIA II°

Temat:

Metoda CPM, Metoda PERT

Adrian Ciepielewski

Z9R1S2

2

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

Spis Treści

1. Metoda CPM i PERT

1.1. Definicja, powstanie.

1.1.1. PERT.
1.1.2. CPM.

1.2. Opracowanie sieci.
1.3. Ścieżka krytyczna.
1.4. Ustalanie czasu realizacji projektu i analiza
działań.

1.4.1. Metoda CPM.
1.4.2. Metoda PERT.

Adrian Ciepielewski

Z9R1S2

3

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

1. Metoda CPM i PERT

Adrian Ciepielewski

Z9R1S2

4

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

1.1. Definicja, powstanie.

Adrian Ciepielewski

Z9R1S2

5

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

1.1.1. PERT.

• PERT – Program Evaluation and Review Technique –

Technika oceny i kontroli programu – metoda

szacowania

i

kontroli

czasów

na

potrzeby

planowania.

• PERT jest jedną z dwóch najistotniejszych metod

sieciowych.

• Opracowana została w altach 1957-1958 przez Biuro

Projektów Specjalnych Marynarki Wojennej Stanów

Zjednoczonych, przy współdziałaniu z korporacją

Lockheed, firmą doradztwa Booz, Allen i Hamilton

3

.

3

J.A.F. Stoner, Ch. Wankel, Kierowanie, Polskie Wydawnictwo Ekonomiczne,

Warszawa 1996, s. 164.

Adrian Ciepielewski

Z9R1S2

6

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

1.1.2. Definicja,

powstanie.

• CPM – Critical Path Metod – Metoda ścieżki krytycznej – to

jedna z dwóch, obok PERT, najważniejszych metod sieciowych.

• Opracowana przez grupę DuPont w latach 1957-1958.
• Jej zadaniem jest ułatwianie kontroli wielkich, złożonych

projektów

przemysłowych.

Wykorzystuje

się

ją

do

cyklicznych/systematycznych procesów, gdzie poszczególne

zadania mają niezmienny czas trwania i znany jest

termin ich zakończenia

4

.

4

J.A.F. Stoner, Ch. Wankel, Kierowanie, Polskie Wydawnictwo Ekonomiczne,

Warszawa 1996, s. 164.

Adrian Ciepielewski

Z9R1S2

7

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

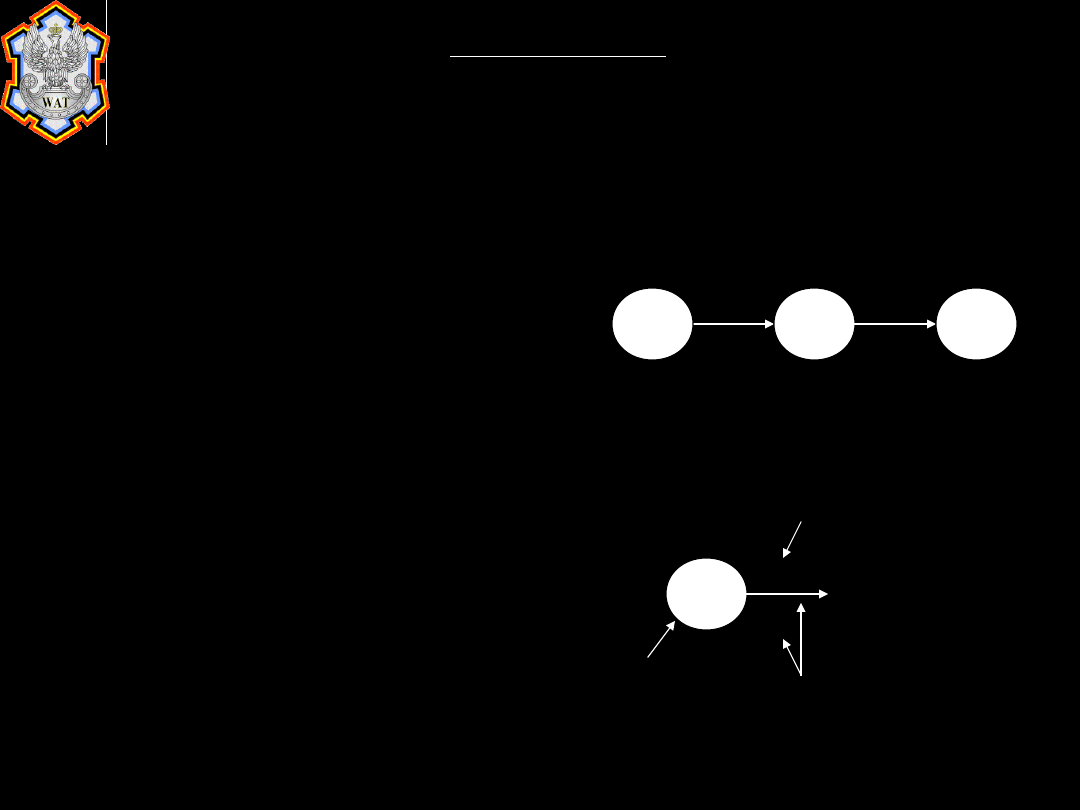
1.2. Opracowanie sieci.

1.

Całe

działanie

musi

być

podzielone na odrębne zadania.

2.

Zdarzenia

i

działania

umieszcza się na wykresie w
sposób

logiczny,

sekwencyjny i zintegrowany.

3.

Do

sieci

wpisuje

się

oszacowany czas potrzebny
na każde działanie.

4. Należy ustalić krytyczną

ścieżkę przebiegającą przez
sieć.

1

2

3

3

2

A

B

1

3

A

Wydarzeni
e

Działanie

Czas

Adrian Ciepielewski

Z9R1S2

8

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

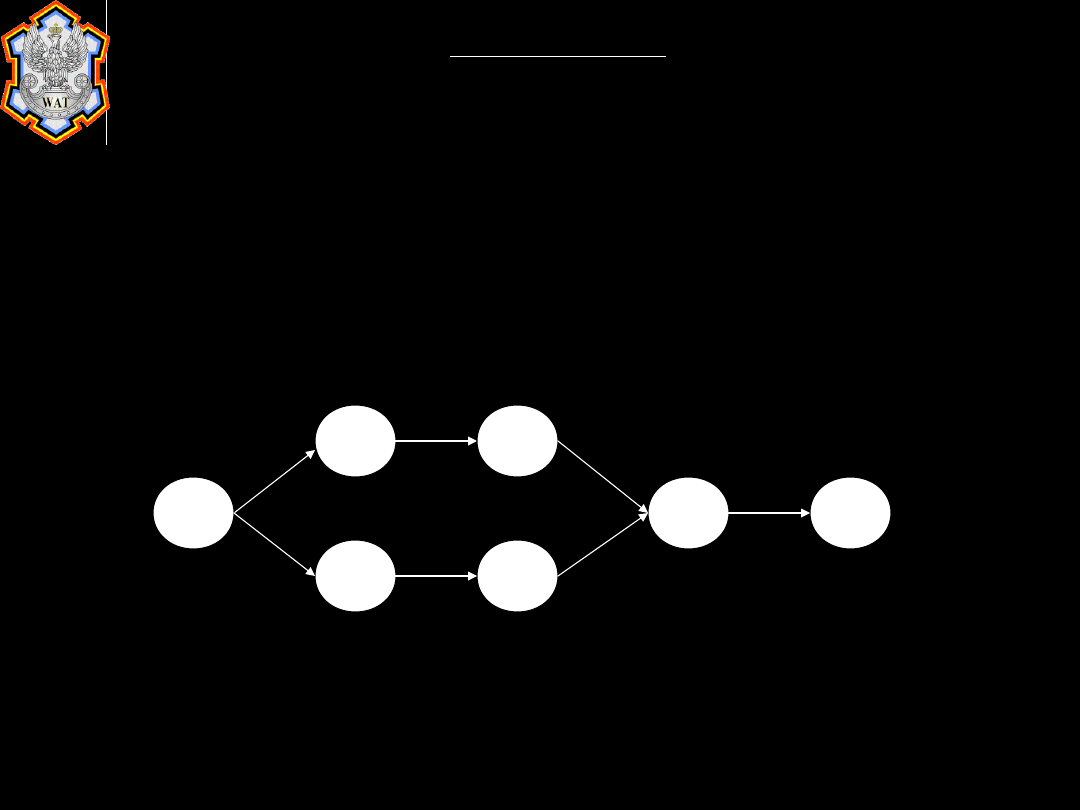
1.3. Ścieżka krytyczna

Ścieżka krytyczna – najdłuższa pod względem czasu trasa przechodząca

przez sieć. Wyznacza się ją dodając do siebie wszystkie czasy

niezbędne do wykonania wszystkich zadań w każdej ich sekwencji.

Ścieżką krytyczną jest łańcuch zadań o najdłuższym czasie

5

.

1

2

3

3

2

4

5

2

1

6

7

3

5

2

A

B

C

G

D

E

F

5

J.A.F. Stoner, Ch. Wankel, Kierowanie, Polskie Wydawnictwo Ekonomiczne, Warszawa 1996, s. 165.

Adrian Ciepielewski

Z9R1S2

9

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

1.4. Ustalenie czasu

realizacji projektu i

analiza działań.

Adrian Ciepielewski

Z9R1S2

10

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

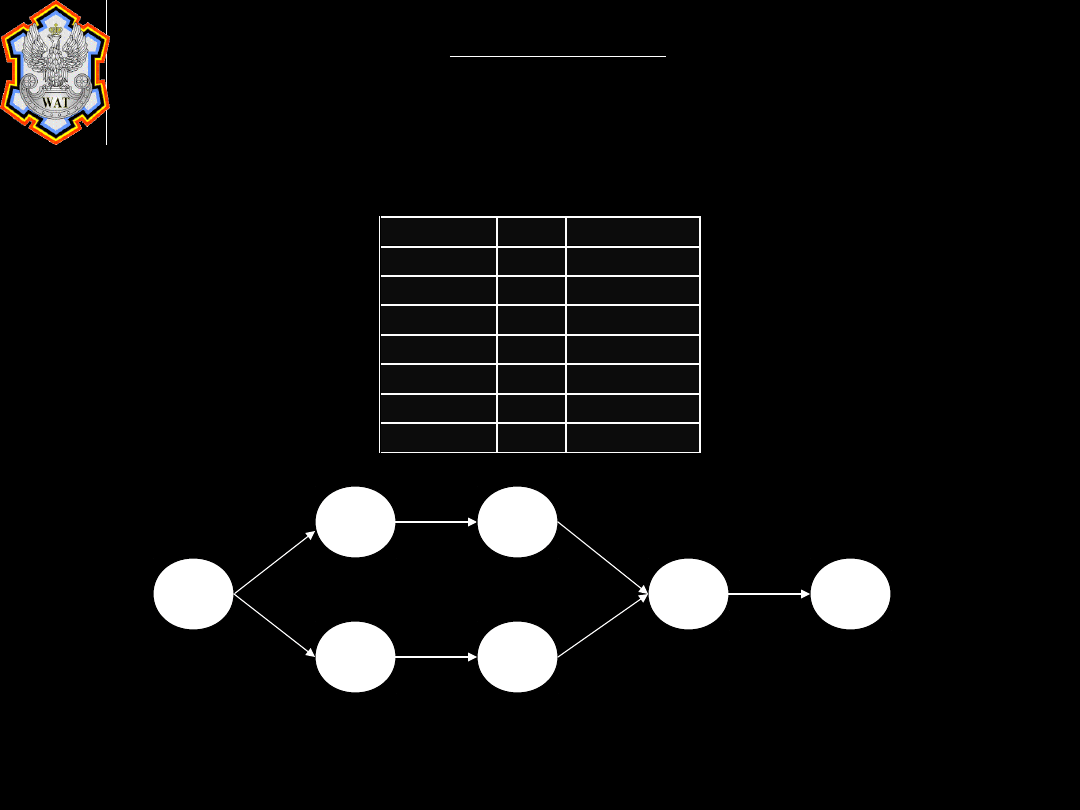
1.4.1. CPM

1. Znalezienie najwcześniejszego czasu

zaistnienia wydarzeń, przy rozpoczęciu
projektu w momencie zerowym.

2. Określenie w jakim czasie projekt zostanie

wykonany – drogą ścieżki krytycznej.

3. Znalezienie najpóźniejszego możliwego

czasu zaistnienia wydarzenia –
wykonywane odwrotnie do pkt. 1 a więc
od końca projektu do jego początku.

Adrian Ciepielewski

Z9R1S2

11

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

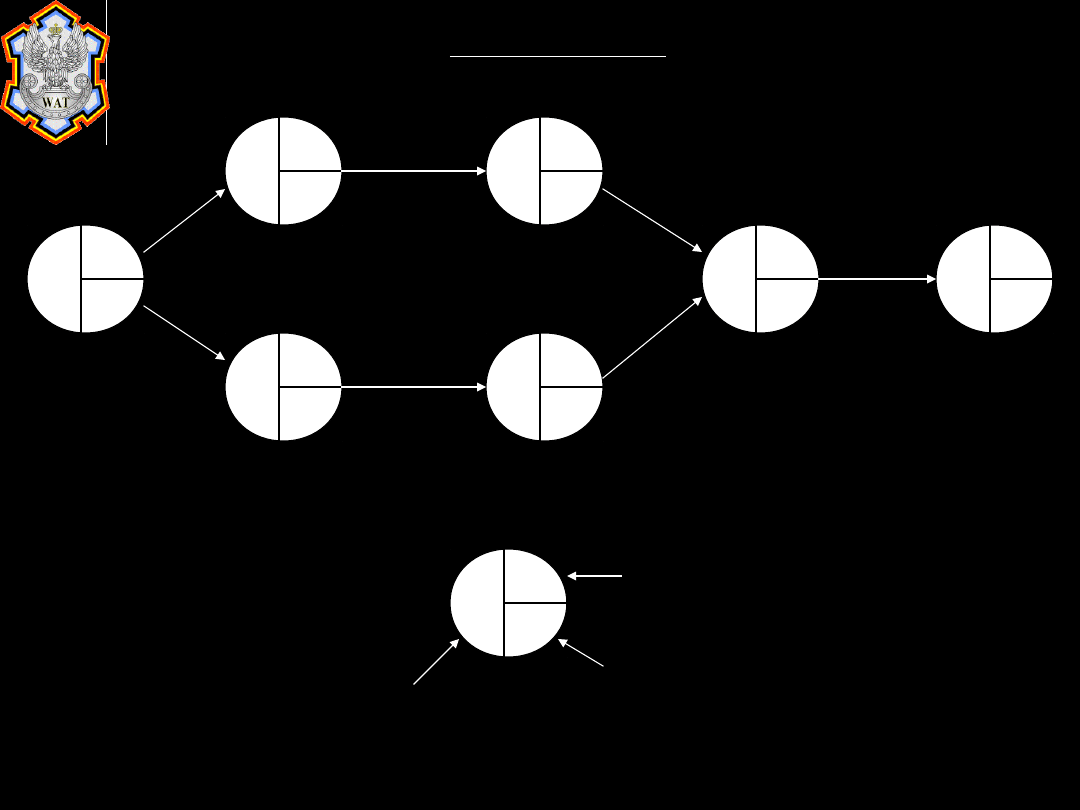
1.4.1. CPM

1

2

3

3

2

4

5

2

1

6

7

3

5

2

A

B

C

G

D

E

F

Działania Czas Poprzednik
A

3

-

B

2

A

C

5

B

D

2

-

E

1

D

F

3

E

G

2

C, F

Adrian Ciepielewski

Z9R1S2

12

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

3

A

1

2

4

3

5

6

7

B

C

G

3

1

2

2

5

F

E

D

2

0

3

5

1
0

1
2

2

3

1
2

1
0

5

3

0

6

7

1

0

0

Wydarzeni
e

Najpóźniejszy
czas

Najwcześniejsz
y czas

Adrian Ciepielewski

Z9R1S2

13

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

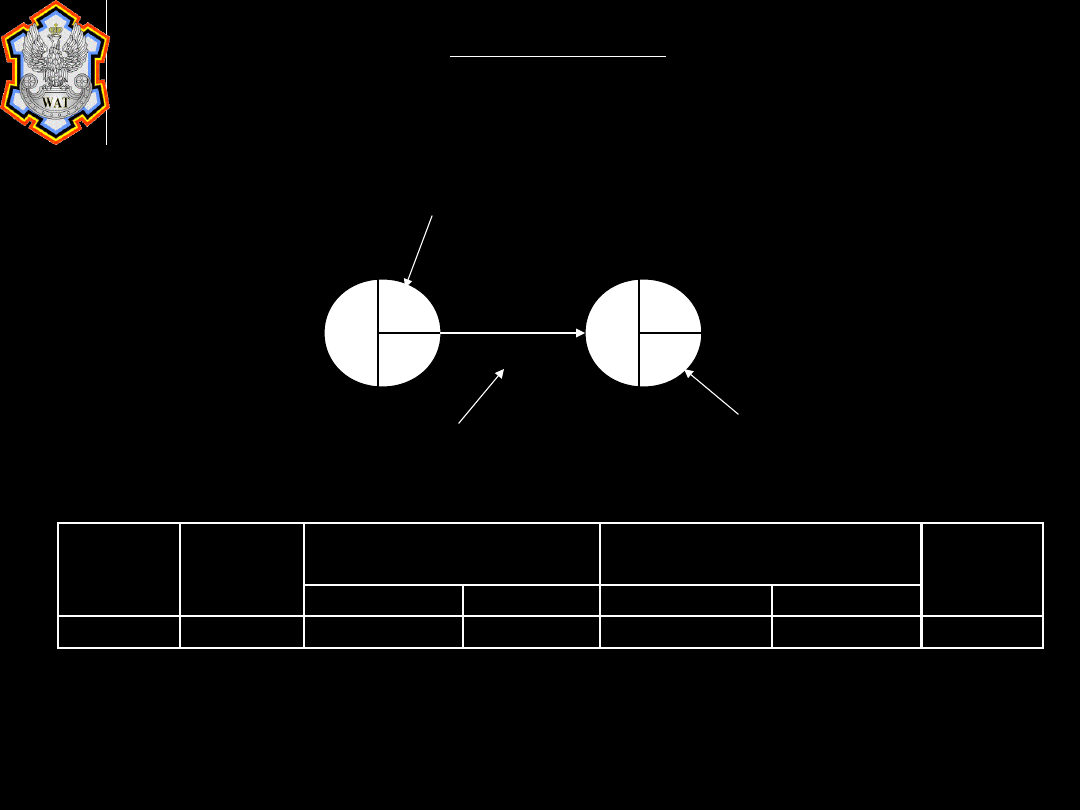
Analiza działań

• Margines, to ograniczenie opóźnień.
• Margines

=

najpóźniejszy

możliwy

czas

zakończenia – najwcześniejszy możliwy czas
rozpoczęcia – czas trwania

• Najwcześniejszy czas rozpoczęcia działania to

najwcześniejszy czas poprzedzającego wydarzenia

• Najwcześniejszy czas zakończenia to czas

rozpoczęcia plus czas trwania

• Najpóźniejsze rozpoczęcie zadania to czas

następującego wydarzenia minus czas trwania
działania

Adrian Ciepielewski

Z9R1S2

14

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

4

5

1

E

2

3

6

7

Najwcześniejszy czas
rozpoczęcia zadania =
najwcześniejszy czas
zaistnienia wydarzenia(NP)

Najpóźniejszy czas
zaistnienia wydarzenia =
najpóźniejszy czas
rozpoczęcia zadania(NpK)

Czas
trwania(t)

Najwcześniejszy możliwy

czas(N)

Najpóźniejszy możliwy

czas(Np)

Działanie

Czas

trwania(t)

Początku(NP) Końca(NK) Początku(NpP) Końca(NpK)

Margines

(NpK-

NP-t)

E

1

2

3(NP+t)

6(NpK-t)

7

4

Adrian Ciepielewski

Z9R1S2

15

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

Działanie krytyczne

Działanie krytyczne – działanie, które ma

jeden stały moment, w którym musi
zostać wykonane(margines wynosi 0).
Działania

krytyczne

tworzą

nieprzerwaną linię, zwaną ścieżką
krytyczną, prowadzącą przez sieć

6

.

6

D. Waters, Zarządzanie operacyjne: towary i usługi, Wydawnictwo Naukowe PWN, Warszawa 2001, s. 499.

Adrian Ciepielewski

Z9R1S2

16

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

2

3

B

2

3

5

5

3

Najwcześniejszy możliwy

czas(N)

Najpóźniejszy możliwy

czas(Np)

Działanie

Czas

trwania(t)

Początku(NP) Końca(NK) Początku(NpP) Końca(NpK)

Margines

(NpK-

NP-t)

B

2

3

5(NP+t)

3(NpK-t)

5

0

Najwcześniejszy czas
rozpoczęcia zadania =
najwcześniejszy czas
zaistnienia wydarzenia(NP)

Najpóźniejszy czas
zaistnienia wydarzenia =
najpóźniejszy czas
rozpoczęcia zadania(NpK)

Czas
trwania(t)

Adrian Ciepielewski

Z9R1S2

17

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

1.4.2. PERT

• Ustalenie czasu realizacji projektu oraz w analizie działań, a

wiec przy wyznaczaniu marginesu wykorzystuje się
oczekiwaną wartość czasu, a nie czas trwania działania jak w
metodzie CPM

• Oczekiwaną wartość wylicza się wykorzystując

– Optymistyczny czas realizacji(O)
– Czas prawdopodobny(M)
– Czas pesymistyczny(P)
Według wzoru:
Wartość oczekiwana = (O + 4M + P)/6

• Wariancję oblicza się ze wzoru:

Wariancja = (O – P)

2

/36

Adrian Ciepielewski

Z9R1S2

18

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

•

Obliczamy również prawdopodobieństwo ukończenia danego projektu w
jakimś czasie, przy wykorzystaniu tabel rozkładu normalnego, według
schematu:

1.

Wyznaczamy okres względem, którego będziemy obliczać
prawdopodobieństwo. >(Ot) – W; <(Ot) – M;

2.

Obliczamy oczekiwany czas zakończenia(Ot) projektu podążając ścieżką
krytyczną;

3.

Obliczamy wariancje dla tych punktów i je sumujemy;

4.

Z sumy wariancji(SW) wyliczamy odchylenie standardowe(OS) w
następujący sposób: OS=√SW

5.

Wyliczamy poszukiwane odchylenie standardowe(POS) ze wzoru:

•

POS=(W-Ot)/OS, jeśli czas ukończenia dla, którego liczymy
prawdopodobieństwo jest większy od oczekiwanego czasu zakończenia

•

POS=(Ot-M)/OS, jeśli czas ukończenia dla, którego liczymy
prawdopodobieństwo jest mniejszy od oczekiwanego czasu
zakończenia

6.

Wyszukujemy w tabeli rozkładu normalnego wartość dla otrzymanego POS

7.

Wyszukaną wartość odejmujemy od jedności(1) i otrzymujemy
prawdopodobieństwo ukończenia projektu przed wyznaczonym okresem.

Adrian Ciepielewski

Z9R1S2

19

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

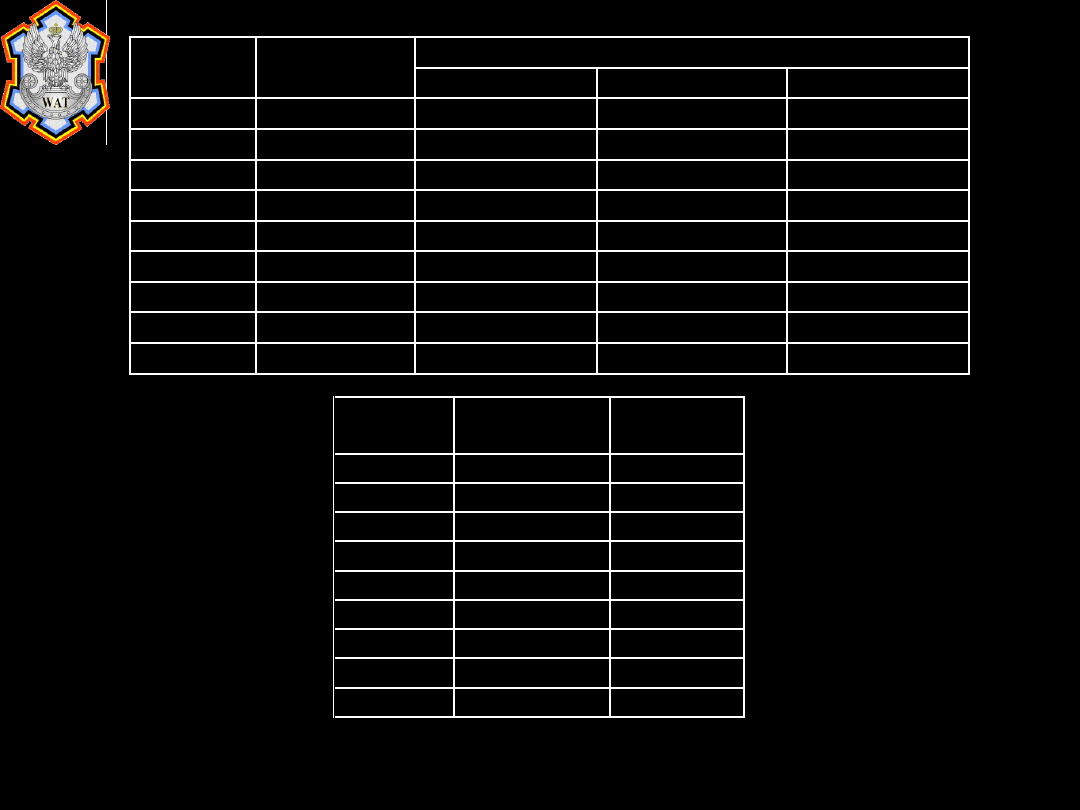
Czas trwania

Działanie Poprzednicy

Optymistyczny Prawdopodobny Pesymistyczny

A

-

2

3

10

B

-

4

5

12

C

-

8

10

12

D

AG

4

4

4

E

B

3

6

15

F

B

2

5

8

G

B

6

6

6

H

C,F

5

7

15

I

D,E

6

8

10

Działanie Oczekiwany

czas trwania Wariancja

A

4

1,78

B

6

1,78

C

10

0,44

D

4

0

E

7

4,00

F

5

1,00

G

6

0

H

8

2,78

I

8

0,44

Adrian Ciepielewski

Z9R1S2

20

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

1

2

B

6

0

6

6

0

3

1
2

1
2

A

4

G

6

5

1
6

1
6

D

4

4

1
1

1
6

6

2
4

2
4

E

7

F

5

C

10

I

8

H

8

Adrian Ciepielewski

Z9R1S2

21

WOJSKOWA AKADEMIA TECHNICZNA

Im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Instytut Organizacji i Zarządzania

Najwcześniejszy możliwy

czas(N)

Najpóźniejszy możliwy

czas(Np)

Działanie

Oczekiwany

czas

trwania(Ot) Początku(NP) Końca(NK) Początku(NpP) Końca(NpK)

Margines

(NpK-

NP-Ot)

A

4

0

4(NP+Ot)

8(NpK-Ot)

12

8

B

6

0

6(NP+Ot)

0(NpK-Ot)

6

0

C

10

0

10(NP+Ot)

6(NpK-Ot)

16

6

D

4

12

16(NP+Ot) 12(NpK-Ot)

16

0

E

7

6

13(NP+Ot)

9(NpK-Ot)

16

3

F

5

6

11(NP+Ot) 11(NpK-Ot)

16

5

G

6

6

12(NP+Ot)

6(NpK-Ot)

12

0

H

8

11

19(NP+Ot) 16(NpK-Ot)

24

5

I

8

16

24(NP+Ot) 16(NpK-Ot)

24

0

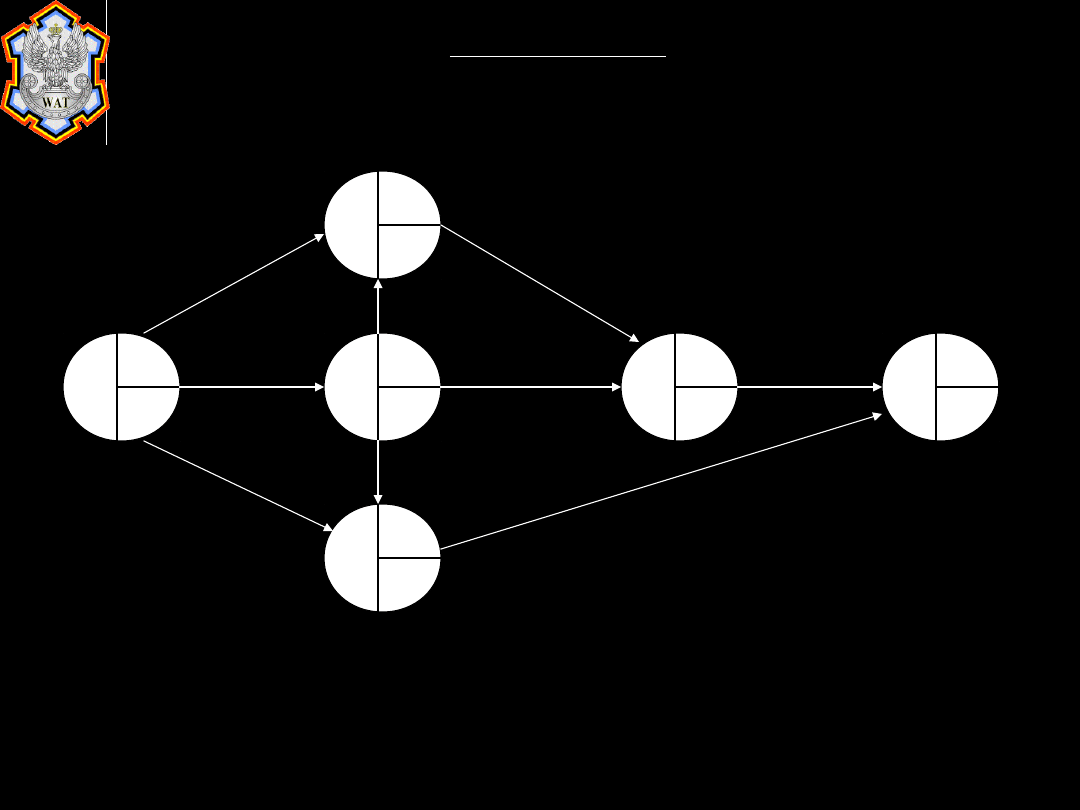
Oczekiwany czas zakończenia projektu wyznaczają działania krytyczne
B, G, D i I. Oczekiwane czasy wynoszą kolejno 6, 6, 4 i 8. Ich suma
wynosi 24. Wariancje kolejno, to 1,78; 0; 0 i 0,44. Suma Wariancji dla
tych 4 wydarzeń wynosi 2,22. Odchylenie standardowe to √2,22=1,49

Prawdopodobieństwo ukończenia zadania przed np. 26 dniem wynosi:

Z=(26-24)/1,49=1,34

gdzie Z jest odchyleniem standardowym

Odczytujemy więc z tablic rozkładu normalnego, że wartość Z wynosi
0,0901, z czego wynika, że prawdopodobieństwo wynosi 1-
0,0901=0,9099, tj. prawie 91%

DZIĘKUJĘ