Parametry zbioru

Parametry zbioru

ziarn

ziarn



Wielkość ziarna.

Wielkość ziarna.



Skład ziarnowy materiału.

Skład ziarnowy materiału.



Analizy granulometryczne (składu

Analizy granulometryczne (składu

ziarnowego).

ziarnowego).



Gęstość nasypowa, porowatość i

Gęstość nasypowa, porowatość i

wilgotność materiału

wilgotność materiału

uziarnionego.

uziarnionego.



Analiza sedymentacyjna

Analiza sedymentacyjna

1

m 10m 100m 1000m 1cm 10cm

1

10

100

1 000

10 000

100 000

Wielkość ziarna,

m

Separatory strumieniowo-zwojowe

Płuczki strumieniowe, stożki Reicherta

Stoły powietrzne

(węgiel)

(rudy)

Stoły szlamowe

Stoły koncentracyjne

węgiel

Hydrocyklony

(węgiel)

Separator Bartles-Mozley

Sep. Tasmowy Bartles

Flotacja

(węgiel)

Floculacja selektywna

Mokra separacja magnetyczna LI

Mokra separacja magnetyczna HI (wysokie natężenie)

Sucha separacja magnetyczna LI

Separacja elektryczna

Wychwytywanie

Osadazarki

wêgiel

os.

promieniowe

Sortowanie (przebieranie)

Rospuszczalność

Hydrocyklony

Separatory głębokie Separatory płytkie

Przewodnictwo elektrycz.

Gęstość i wielkość ziarn

podatność magnetyczna

własności powierzchniowe

Kolor, postać

Gęstość (ciecze ciężkie)

Wielkość ziarn

Mokre Przesiewanie Suche

Klasyfikacja hydrauliczna

Średnica ziarna d, m

Średnica ziarna d, m

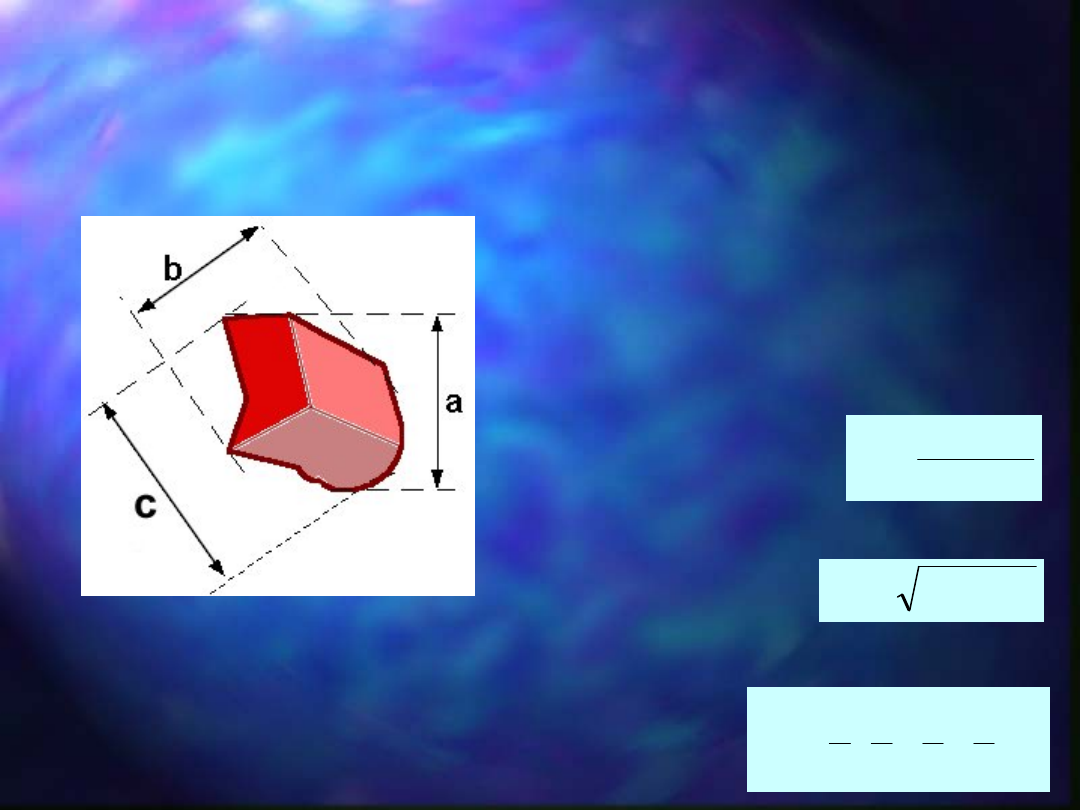
średnia arytmetyczna:

średnia arytmetyczna:

średnia geometryczna:

średnia geometryczna:

średnia harmoniczna:

średnia harmoniczna:





3

c

b

a

d

g







2

c

b

a

d

a







1

h

c

1

b

1

a

1

3

1

d

































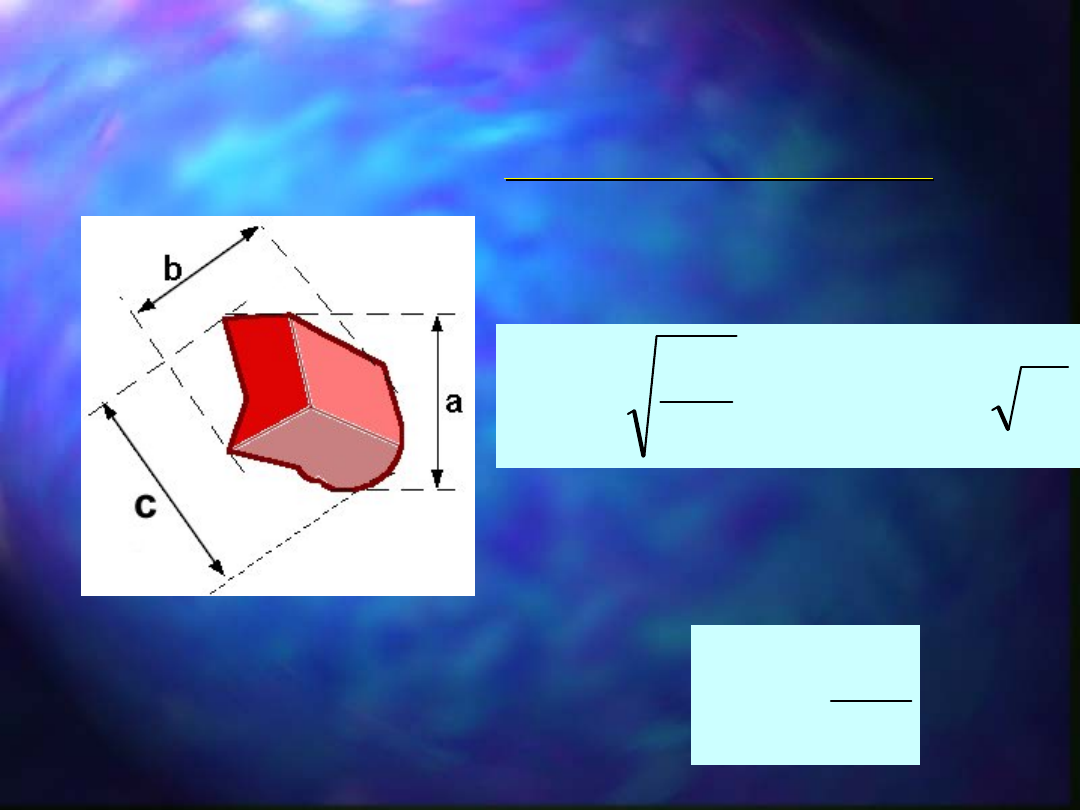
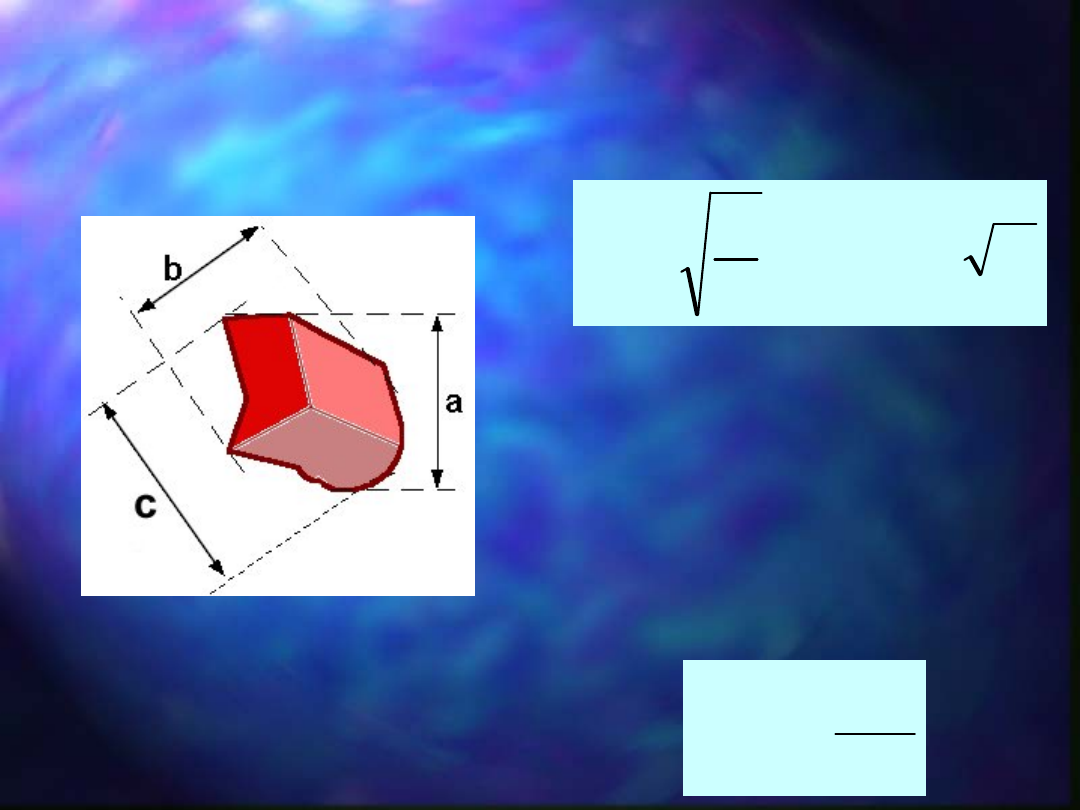
Rozmiary główne ziarna 3D:

Rozmiary główne ziarna 3D:

a - długość, m

a - długość, m

b - szerokość, m

b - szerokość, m

c - wysokość, m

c - wysokość, m

Jeżeli możliwy jest bezpośredni pomiar

Jeżeli możliwy jest bezpośredni pomiar

ziarna, to średnica może być okreslona

ziarna, to średnica może być okreslona

jako:

jako:

Średnica zastępcza ziarna:

Średnica zastępcza ziarna:

3

3

2407

,

1

6

z

z

z

V

V

d









Średnica ziarna d, m

Średnica ziarna d, m

gdzie:

gdzie:

V

V

z

z

-

-

objętość ziarna, m

objętość ziarna, m

3

3

Średnica zastępcza ziarna

Średnica zastępcza ziarna

odpowia-dająca średnicy kuli o tej

odpowia-dająca średnicy kuli o tej

samej objętości co rozpatrywane

samej objętości co rozpatrywane

ziarno:

ziarno:

Objętość

Objętość

kuli:

kuli:

6

3

d

V

K





Średnica zastępcza ziarna:

Średnica zastępcza ziarna:





z

z

A

d

Średnica ziarna d, m

Średnica ziarna d, m

gdzie:

gdzie:

A

A

z

z

- pole powierzchni ziarna,

- pole powierzchni ziarna,

m

m

Średnica zastępcza ziarna

Średnica zastępcza ziarna

równa

równa

średnicy kuli o tej samej powierz-

średnicy kuli o tej samej powierz-

chni co rozpatrywane ziarno:

chni co rozpatrywane ziarno:

pole powierzchni

pole powierzchni

kuli:

kuli:

2

K

d

A





Średnica projekcyjna ziarna:

Średnica projekcyjna ziarna:

Średnica ziarna d, m

Średnica ziarna d, m

gdzie:

gdzie:

A - pole powierzchni rzutu

A - pole powierzchni rzutu

ziarna na płaszczyznę

ziarna na płaszczyznę

Średnica projekcyjna jest

Średnica projekcyjna jest

średnicą koła, które ma takie

średnicą koła, które ma takie

samo pole powierzchni F jak rzut

samo pole powierzchni F jak rzut

prostopadły ziarna na

prostopadły ziarna na

płaszczyznę

płaszczyznę

A

1284

,

1

A

d

p









4

d

A

2





koło

Sferyczność ziarna

Sferyczność ziarna





określa stosunek powierzchni kuli

określa stosunek powierzchni kuli

o tej samej objętości co rozpatrywane ziarno do

o tej samej objętości co rozpatrywane ziarno do

powierzchni tego ziarna:

powierzchni tego ziarna:

A

A

K

K

- pole powierzchni kuli

- pole powierzchni kuli

A

A

z

z

- pole powierzchni ziarna

- pole powierzchni ziarna

1

A

A

z

K

V

V

z

K





















Wartości współczynników

Wartości współczynników

sferyczności wybranych figur:

sferyczności wybranych figur:

walec h=d 0,874

walec h=d 0,874

regularny ośmiościan 0,846

regularny ośmiościan 0,846

sześcian 0,806

sześcian 0,806

czworościan foremny 0,670

czworościan foremny 0,670

dysk d=10h 0,471

dysk d=10h 0,471

Sferyczność ziarna:

Sferyczność ziarna:

Współczynnik kształtu

Współczynnik kształtu

ziarna

ziarna

stanowi odwrotność sferycznosci:

stanowi odwrotność sferycznosci:

1

1







k

Dla procesów przesiewania

Dla procesów przesiewania

:

:

stosuje się

stosuje się

współczynnik kształtu oparty na wyznaczaniu

współczynnik kształtu oparty na wyznaczaniu

wymiarów głównych

wymiarów głównych

ziarn:

ziarn:

c

b

k 

b lub a - szerokość, długość, m.

b lub a - szerokość, długość, m.

c - wysokość, m

c - wysokość, m

1. Skład ziarnowy (rozkład wielkości ziarn)

1. Skład ziarnowy (rozkład wielkości ziarn)

2. Minimalna i maksymalna średnica ziarn

2. Minimalna i maksymalna średnica ziarn

3. Średni rozmiar ziarn

3. Średni rozmiar ziarn

4. Powierzchnia właściwa zbioru ziarn

4. Powierzchnia właściwa zbioru ziarn

5. Porowatość

5. Porowatość

6. Sferyczność zbioru ziarn

6. Sferyczność zbioru ziarn

Parametry zbioru ziarn

Parametry zbioru ziarn

Zbiór ziarn może być scharakteryzowany przez

Zbiór ziarn może być scharakteryzowany przez

średnicę reprezentatywną zbioru lub przez

średnicę reprezentatywną zbioru lub przez

funkcję opisującą rozkład wielkości ziarn

funkcję opisującą rozkład wielkości ziarn

wyrażonych masą, objętością, powierzchnią lub

wyrażonych masą, objętością, powierzchnią lub

pewną cechą morfologiczną ziarna. W praktyce

pewną cechą morfologiczną ziarna. W praktyce

rozkłady wielkości ziarn mineralnych wyrażamy

rozkłady wielkości ziarn mineralnych wyrażamy

najczęściej przez

najczęściej przez

rozkład ich masy

rozkład ich masy

, ze względu

, ze względu

na łatwość jej oszacowania.

na łatwość jej oszacowania.

Jeżeli zbiór ziarn o masie

Jeżeli zbiór ziarn o masie

Q

Q

przesiejemy

przesiejemy

kolejno na sitach o średnicach oczek:

kolejno na sitach o średnicach oczek:

d

d

m

m

>d

>d

m-

m-

1

1

>. . . >d

>. . . >d

i

i

. . . . >d

. . . . >d

2

2

>d

>d

1

1

, to otrzymamy n=m+1

, to otrzymamy n=m+1

podzbiorów ziarn o masach q

podzbiorów ziarn o masach q

i

i

. Średnice ziarn

. Średnice ziarn

zawarte w przedziale

zawarte w przedziale

d

d

i-1

i-1

÷ d

÷ d

i

i

nazywamy

nazywamy

klasą ziarnową

klasą ziarnową

,

,

a ilość (masę) tych ziarn

a ilość (masę) tych ziarn

wychodem

wychodem

tej klasy.

tej klasy.

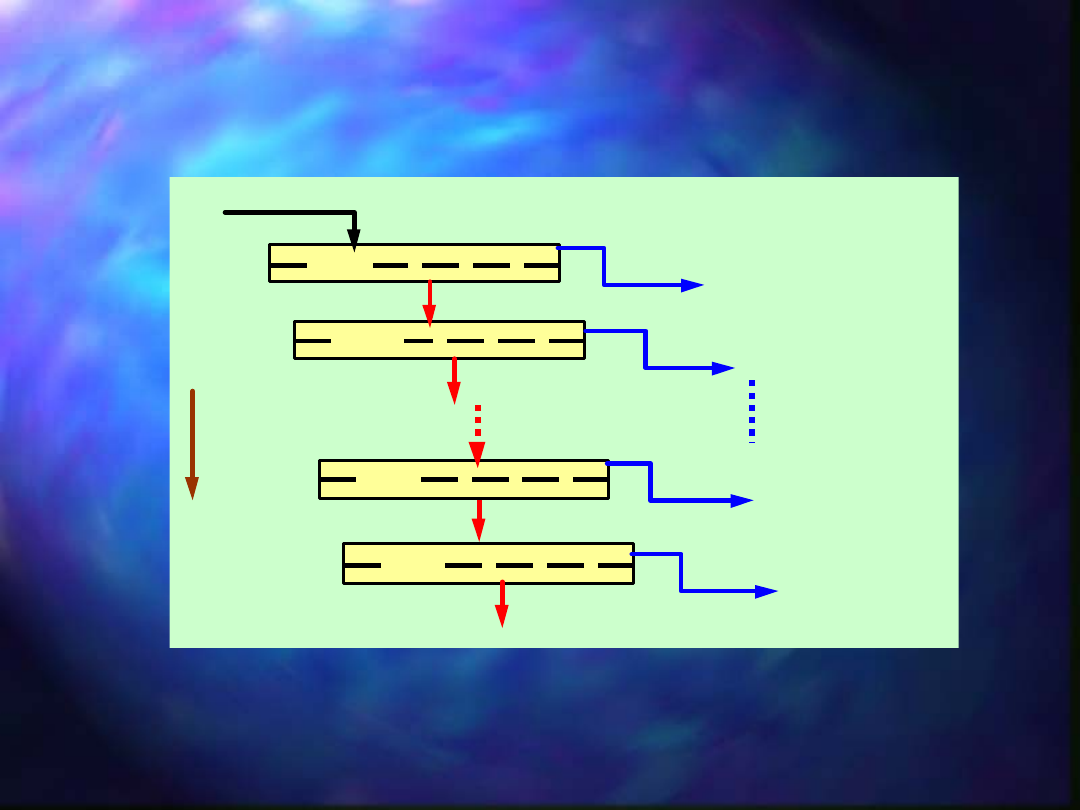
Skład ziarnowy

Skład ziarnowy

=d

m

=d

m-1

=d

2

NADAWA, Q

+d

m

, q

m

(+d

m-1

-d

m

), q

m-1

Klasy ziarnowe:

Sita o coraz
mniejszych
otworach

=d

1

(+d

2

-d

3

), q

3

(+d

1

-d

2

), q

2

-d

1

, q

1

Badania składu ziarnowego - analiza ziarnowa

Badania składu ziarnowego - analiza ziarnowa

(granulometryczna, sitowa)

(granulometryczna, sitowa)

Aparat do wykonywania analiz

Aparat do wykonywania analiz

składu ziarnowego

składu ziarnowego

W analizach ziarnowych posługujemy się

W analizach ziarnowych posługujemy się

najczęściej

najczęściej

wychodami względnymi klasy:

wychodami względnymi klasy:

które możemy nazywać

które możemy nazywać

częstością klasy

częstością klasy

.

.

Posługujemy się też

Posługujemy się też

funkcją

funkcją

skumulowaną:

skumulowaną:

 







n

i

i

i

1

d

f

)

d

(

F

co oznacza:

co oznacza:

F(d

F(d

1

1

)=f(d

)=f(d

1

1

)

)

F(d

F(d

2

2

)=f(d

)=f(d

1

1

) + f(d

) + f(d

2

2

)

)

F(d

F(d

3

3

)=f(d

)=f(d

1

1

) + f(d

) + f(d

2

2

) + f(d

) + f(d

3

3

)

)

itd

itd







Q

i

i

q

)

d

(

f

 





max

min

d

f

)

(

F

d

d

i

i

i

d

d

d

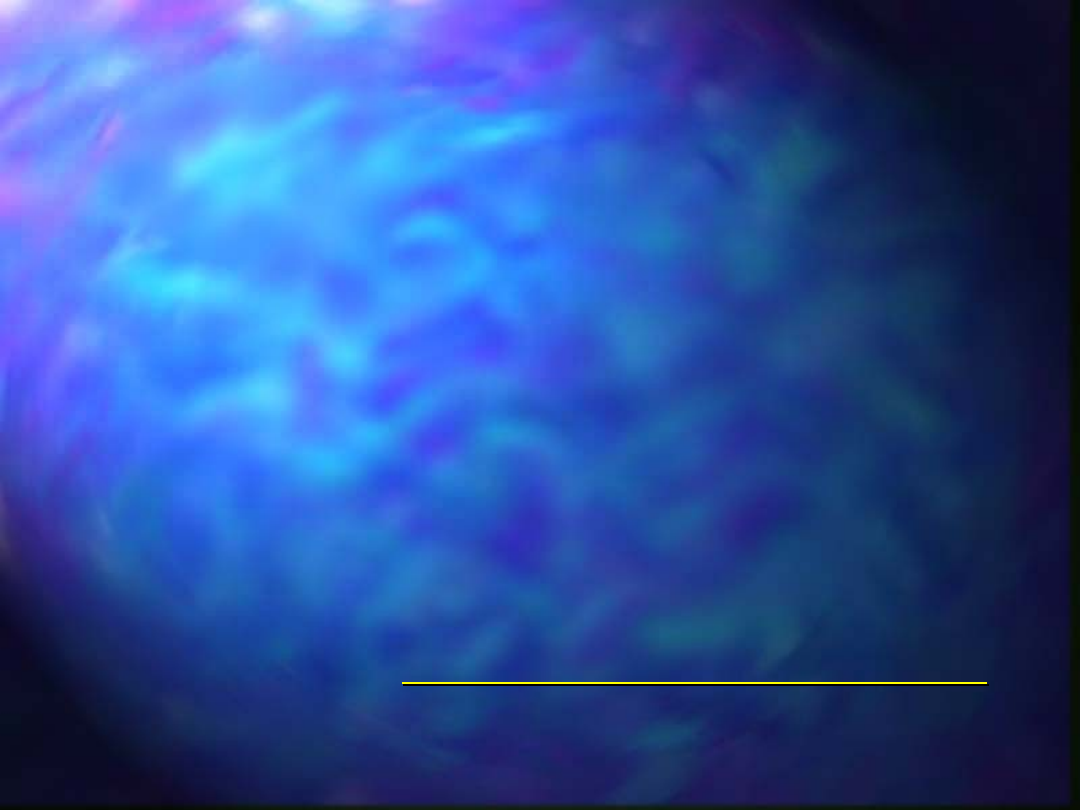
Wartość argumentu d

Wartość argumentu d

i

i

w funkcji F(d

w funkcji F(d

i

i

) oznacza

) oznacza

prawostronną granicę przedziału wartości

prawostronną granicę przedziału wartości

reprezentującego i-tą klasę ziarnową czyli

reprezentującego i-tą klasę ziarnową czyli

dokładnie d

dokładnie d

i

i

F(d

F(d

0

0

)=0, F(d

)=0, F(d

n

n

)=1, gdzie n - liczba klas

)=1, gdzie n - liczba klas

ziarnowych

ziarnowych

Funkcje

Funkcje

F(d

F(d

i

i

)

)

f(d

f(d

i

i

)

)





(d

(d

i

i

) = 1-F(d

) = 1-F(d

i

i

)

)

nazywamy

nazywamy

krzywymi składu ziarnowego

krzywymi składu ziarnowego

,

,

charakterystykami ziarnowymi,

charakterystykami ziarnowymi,

charakterystykami granulometrycznymi

charakterystykami granulometrycznymi

Wyniki badania składu ziarnowego

Wyniki badania składu ziarnowego

(analizy ziarnowej)

(analizy ziarnowej)

Klasa

ziarnowa, mm

d

i -1

–

d

i

Środek

przedziału

d

i

*

prawostronna

granica

d

i

q

i

, g f(d

i

), %

F(d

i

)

%

(d

i

),

%

-2,0+0,0

1,0

0,0

0,0

0,0

0,0

100,0

-5,0+2,0

3,5

2,0

3,0

4,1

4,1

95,9

-8,0+5,0

6,5

5,0

13,0

17,6

21,6

78,4

-10,0+8,0

9,0

8,0

28,0

37,8

59,5

40,5

-14,0+10,0

12,0

10,0

25,0

33,8

93,2

6,8

+14,0

14,0

5,0

6,8

100,0

0,0

suma

74,0

100,0

(

(

)

)









n

n

i=1

i=1

i

i

i

d

d

f

f

)

)

d

d

(

(

F

F





(d

(d

i

i

) = 100-F(d

) = 100-F(d

i

i

)

)

0

10

20

30

40

0,0

5,0

10,0

15,0

20,0

Wielkość ziarna d

i

, mm

f(

d

i

),

%

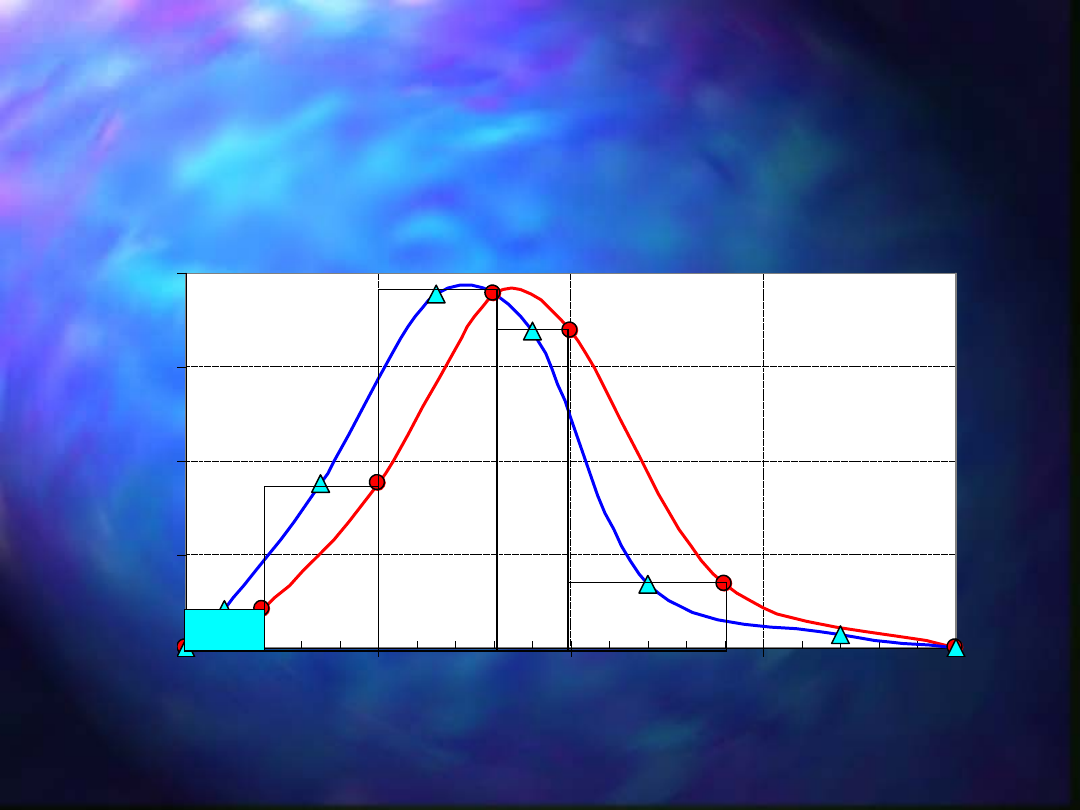
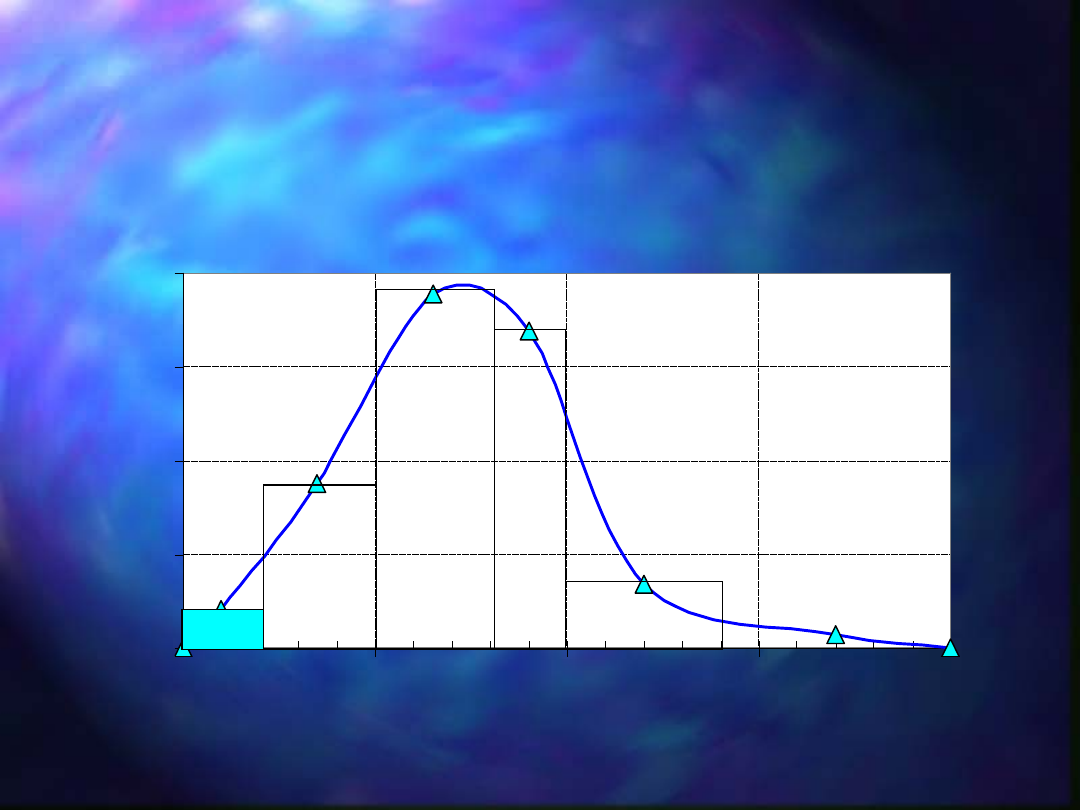
Rozkład wielkości ziarn: krzywa częstości f(d

Rozkład wielkości ziarn: krzywa częstości f(d

i

i

)

)

(

(

funkcja gęstości rozkładu wielkości ziarn

funkcja gęstości rozkładu wielkości ziarn

)

)

0

10

20

30

40

0,0

5,0

10,0

15,0

20,0

Wielkość ziarna d

i

, mm

f(

d

i

),

%

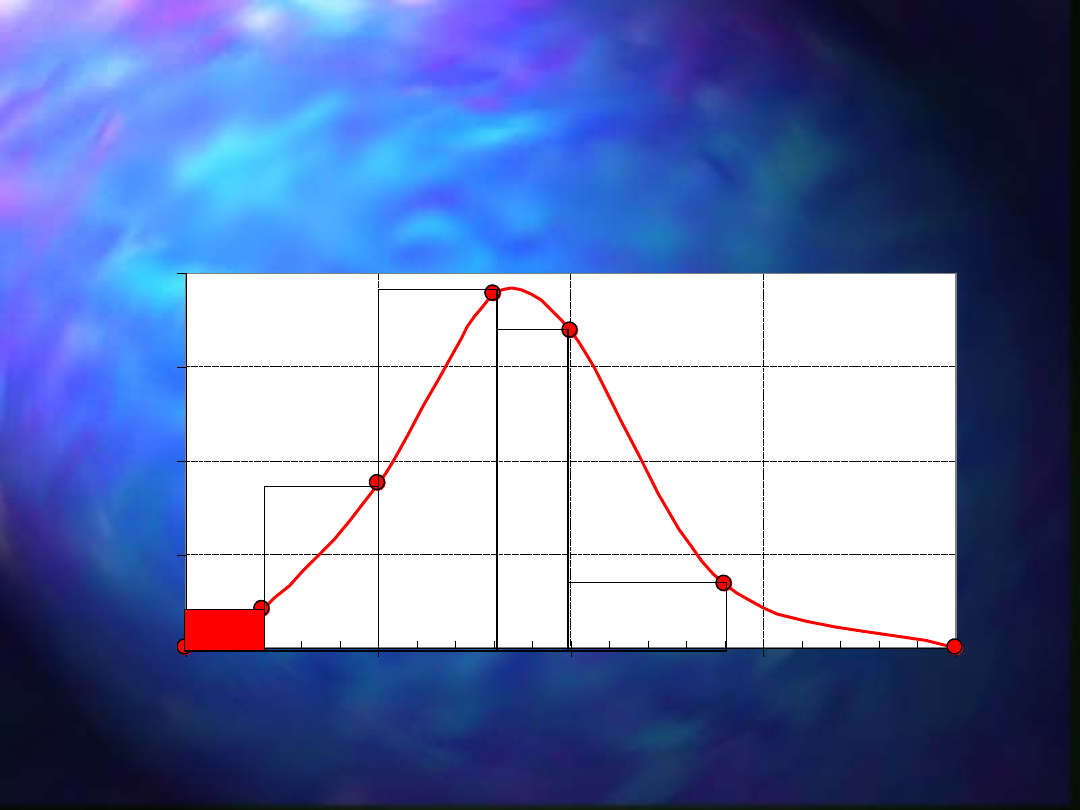
Rozkład wielkości ziarn: krzywa częstości f(d

Rozkład wielkości ziarn: krzywa częstości f(d

i

i

)

)

(

(

funkcja gęstości rozkładu wielkości ziarn

funkcja gęstości rozkładu wielkości ziarn

)

)

0

10

20

30

40

0

5

10

15

20

Wielkość ziarna d

i

, mm

f(

d

i

),

%

Rozkład wielkości ziarn: krzywa częstości f(d

Rozkład wielkości ziarn: krzywa częstości f(d

i

i

)

)

(

(

funkcja gęstości rozkładu wielkości ziarn

funkcja gęstości rozkładu wielkości ziarn

)

)

G

G

ęstość rozkładu określa udział cząstek w przedziale

ęstość rozkładu określa udział cząstek w przedziale

d

d

i-

i-

1

1

÷ d

÷ d

i

i

0

20

40

60

80

100

0,0

5,0

10,0

15,0

20,0

Wielkość ziarna d

i

, mm

f(

d

i

),

F

(d

i

),

%

f(d

i

)

F(d

i

)

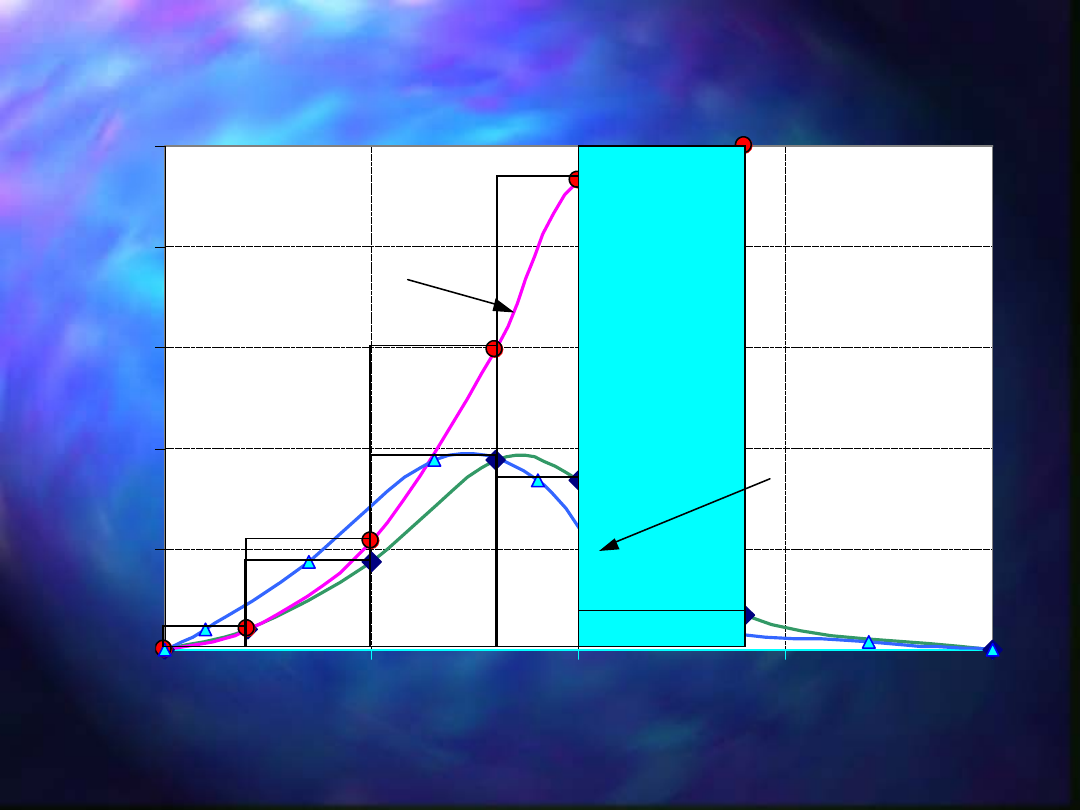
Rozkład wielkości ziarn: krzywa częstości f(d

Rozkład wielkości ziarn: krzywa częstości f(d

i

i

)

)

i krzywa skumulowana F(d

i krzywa skumulowana F(d

i

i

)

)

0

20

40

60

80

100

0,0

5,0

10,0

15,0

20,0

Wielkość ziarna d

i

, mm

f(

d

i

),

F

(d

i

),

%

f(d

i

)

F(d

i

)

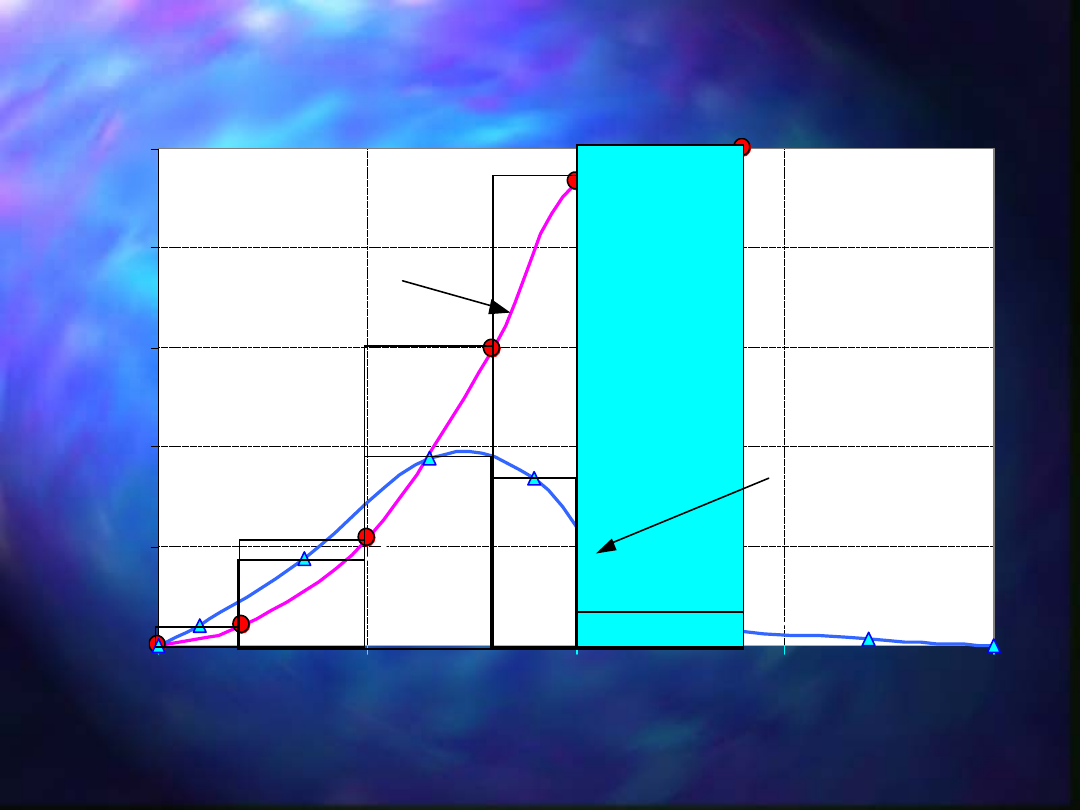
Rozkład wielkości ziarn: krzywa częstości f(d

Rozkład wielkości ziarn: krzywa częstości f(d

i

i

)

)

i krzywa skumulowana F(d

i krzywa skumulowana F(d

i

i

)

)

0

20

40

60

80

100

0,0

5,0

10,0

15,0

20,0

wielkość ziarna d

i

, mm

F

(d

i

),



(d

i

),

%

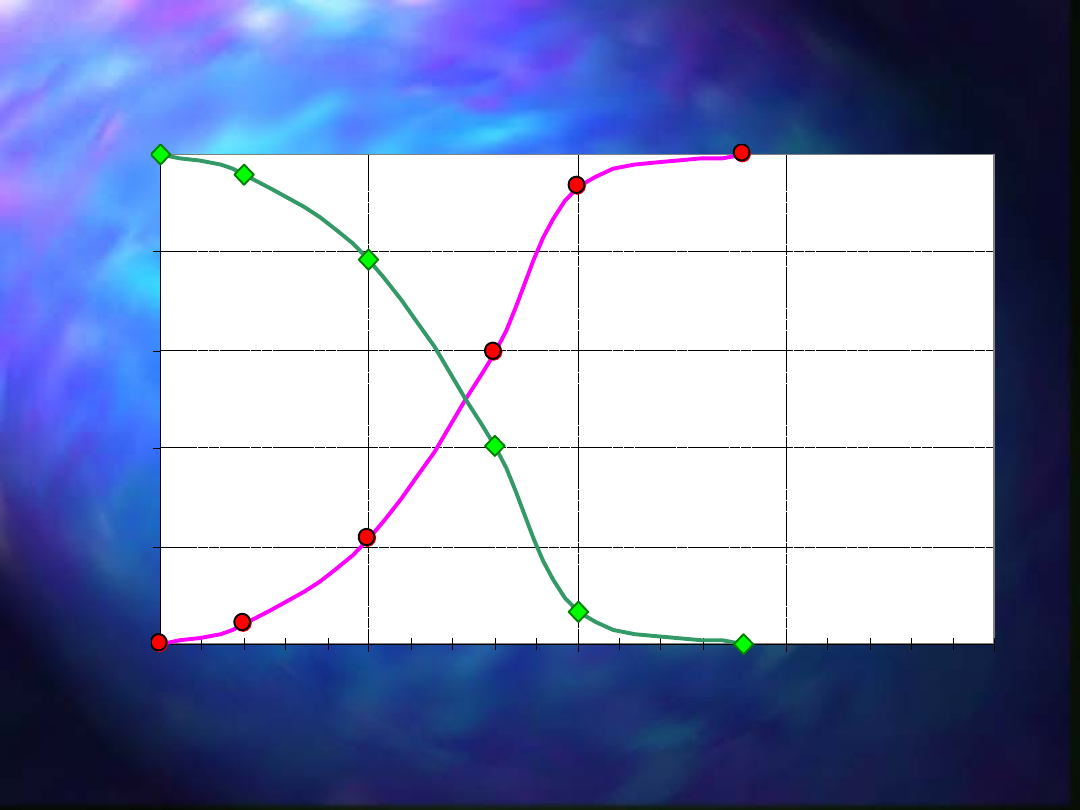
Wykresy krzywych składu ziarnowego

Wykresy krzywych składu ziarnowego

F(d

F(d

i

i

) i

) i





(d

(d

i

i

)

)

(d

i

)

F(d

i

)

Opisywane krzywe składu ziarnowego F(d

Opisywane krzywe składu ziarnowego F(d

i

i

)

)

i

i





(d

(d

i

i

) są krzywymi całkowymi i można

) są krzywymi całkowymi i można

je zapisać w postaci:

je zapisać w postaci:

- funkcji rosnącej

- funkcji rosnącej

 

 

 









d

0

d

d

dx

x

f

dx

x

f

d

F

min

- funkcji malejącej

- funkcji malejącej

 

 

 

d

F

1

dx

x

f

d

max

d

d











W prognozowaniu procesów przeróbczych,

W prognozowaniu procesów przeróbczych,

badaniach teoretycznych i w analizach

badaniach teoretycznych i w analizach

statystycznych zjawisk fizycznych związanych z

statystycznych zjawisk fizycznych związanych z

przeróbką kopalin, ważną rolę odgrywają

przeróbką kopalin, ważną rolę odgrywają

modele matematyczne krzywych składu

modele matematyczne krzywych składu

ziarnowego

ziarnowego

.

.

Rozkład Gausa (normalny)

Rozkład Gausa (normalny)



















































x

2

G

dx

x

2

1

exp

2

1

)

x

(

F

Y

x - średnica ziarna
 - wartość średnia
 =

 = - odchylenie

standardowe zmiennej x

 







n

1

i

i

i

x

x

f

  













n

1

i

2

i

i

x

x

f

Rozkład Gatesa-Gaudina-Schumana

Rozkład Gatesa-Gaudina-Schumana

Y

Y

GGS

GGS

= F(x) = x

= F(x) = x

b

b

, b>0

, b>0

gdzie:

gdzie:

b - parametr kształtu funkcji

b - parametr kształtu funkcji

0

0





x

x





1

1

jest względną średnicą ziarna:

jest względną średnicą ziarna:

min

max

min

d

d

d

d

x







Parametr kształtu funkcji b można oszacować na

Parametr kształtu funkcji b można oszacować na

podstawie empirycznej krzywej składu

podstawie empirycznej krzywej składu

ziarnowego metodą największej wiarygodności:

ziarnowego metodą największej wiarygodności:

 























n

1

i

i

i

x

ln

x

f

1

b

gdzie:

gdzie:

f(x

f(x

i

i

) - częstość klasy ziarnowej

) - częstość klasy ziarnowej

Rozkład Rosina-Ramlera-Sperlinga (RRS)

Rozkład Rosina-Ramlera-Sperlinga (RRS)

(Rozkład Weibulla)

(Rozkład Weibulla)

gdzie a – wielkość charakterystyczna ziarna

x – względna lub bezwzględna średnica
ziarn
b – parametr kształtu określany analitycznie

b

RRS

a

x

exp

1

)

x

(

F

Y

































 

0

b

,

632

,

0

e

1

1

x

F

x

a











Parametry równania RRS wyznacza się graficznie nanosząc
dane punkty doświadczalne krzywej składu ziarnowego w
układzie współrzędnych linearyzyjącym funkcję F(x):
log x – log log lub ln x – ln ln

F

1

F

1

Średni rozmiar ziarna w zbiorze ziarn

Średni rozmiar ziarna w zbiorze ziarn

 

z

d

d

z

z

z

d

d

d

d

d

f

max

min







 

x

d

x

f

x

x

max

min

x

x











ROZKŁAD

ZASTOSOWANIE

N (normalny,

Gausa)

Mielenie zboża, produkty z

suszarek rozpylających

RRSB

Mielenie surowców mineralnych

(rozdrabnianie drobne)

GGS

Kruszenie surowców

(rozdrabnianie grube)

Powierzchnia właściwa zbioru ziarn

Powierzchnia właściwa zbioru ziarn

Powierzchnia zbioru ziarn odnoszona jest zwykle do ich

Powierzchnia zbioru ziarn odnoszona jest zwykle do ich

jednostki objętości lub masy. Bezwzględna wartość

jednostki objętości lub masy. Bezwzględna wartość

powierzchni zbioru N (

powierzchni zbioru N (

N=

N=





) ziarn kulistych opisywana jast

) ziarn kulistych opisywana jast

wzorem:

wzorem:

natomiast ich objętość zależnością:

natomiast ich objętość zależnością:

 

z

d

d

z

i

z

z

d

d

d

N

S

z

z

d

f

max

min

2









 

z

d

d

z

i

z

z

d

d

d

N

V

z

z

d

f

6

max

min

3









Powierzchnia właściwa

Powierzchnia właściwa

odniesiona do jednostki

odniesiona do jednostki

objętości:

objętości:

z

z

V

V

S

s 

Gęstość i gęstość nasypowa

Gęstość i gęstość nasypowa

materiału uziarnionego

materiału uziarnionego

3

s

s

s

m

kg

,

V

Q





3

,

m

N

g

V

g

s

s

s

s









Q

Ciężar

Ciężar

właściwy:

właściwy:

3

p

s

p

s

0

.

nas

m

kg

,

V

V

V















Q

Q

Q

Gęstość objętościowa

Gęstość objętościowa

materiału

materiału

uziarnionego

uziarnionego

(nasypowa, usypowa, pozorna):

(nasypowa, usypowa, pozorna):

gdzie:

gdzie:

Q

Q

s

s

-

-

masa ziarn (ciała stałego)

masa ziarn (ciała stałego)

Q

Q

p

p

- masa medium w porach między ziarnami.

- masa medium w porach między ziarnami.

Q

Q

s

s

+

+

Q

Q

p

p

=

=

Q

Q

V

V

s

s

,

,

V

V

p

p

-

-

objętość ziarn (ciała stałego) i porów,

objętość ziarn (ciała stałego) i porów,

V

V

s

s

+

+

V

V

p

p

V =

V =

V

V

Q, V

Q, V

- masa i objętość ziarn wraz z medium w porach

- masa i objętość ziarn wraz z medium w porach

g - przyspieszenie ziemskie

g - przyspieszenie ziemskie

Wilgotność materiału uziarnionego

Wilgotność materiału uziarnionego

Porowarość materiału uziarnionego

Porowarość materiału uziarnionego

V

V

p





Q

Q

=

=

Q

Q

s

s

+

+

Q

Q

p

p

=

=





s

s

V(1-

V(1-





)+

)+









p

p

V,

V,

V

0

Q









0

0

=

=





s

s

(1-

(1-





)

)

ponieważ

ponieważ





p

p





0

0

s

0

s













%

,

100

W

w

Q

Q



Q

Q

w

w

-

-

masa wody w próbce materiału,

masa wody w próbce materiału,

Q =

Q =

Q

Q

s

s

+

+

Q

Q

w

w

Określanie składu ziarnowego, a zatem rozkładu

Określanie składu ziarnowego, a zatem rozkładu

wielkości ziarn materiału ziarnistego dokonuje się

wielkości ziarn materiału ziarnistego dokonuje się

metodami bezpośrednimi oraz pośrednimi.

metodami bezpośrednimi oraz pośrednimi.

•

Metody bezpośrednie:

Metody bezpośrednie:

-

-

analiza sitowa

analiza sitowa

- pomiary liniowych rozmiarów ziarn:

- pomiary liniowych rozmiarów ziarn:

mechaniczne i

mechaniczne i

optyczne (makro- lub mikroskopowa analiza

optyczne (makro- lub mikroskopowa analiza

obrazu)

obrazu)

•

Metody pośrednie:

Metody pośrednie:

-

-

analizy sedymentacyjne

analizy sedymentacyjne

(stacjonarne i

(stacjonarne i

przepływowe)

przepływowe)

- optyczne (rozproszenie promieniow. laser., rtg,

- optyczne (rozproszenie promieniow. laser., rtg,

izotop.)

izotop.)

Dolną granicą wielkości ziarna jaka można w

Dolną granicą wielkości ziarna jaka można w

praktyce uzyskać za pomocą przesiewania

praktyce uzyskać za pomocą przesiewania

(analizy sitowe) jest klasa ± 0,025 mm. Już

(analizy sitowe) jest klasa ± 0,025 mm. Już

przesiewanie przez sita o średnicach otworów

przesiewanie przez sita o średnicach otworów

<0,05mm staje się bardzo trudne. Wówczas

<0,05mm staje się bardzo trudne. Wówczas

korzystnie jest zastosować

korzystnie jest zastosować

analizę

analizę

sedymentacyjną

sedymentacyjną

Na ziarno zanurzone w cieczy i znajdujące

Na ziarno zanurzone w cieczy i znajdujące

się w ruchu działają następujące siły:

się w ruchu działają następujące siły:

OPADANIE ZIARN W O

OPADANIE ZIARN W O

Ś

Ś

RODKACH P

RODKACH P

Ł

Ł

YNNYCH

YNNYCH

kie

ru

n

e

k

kie

ru

n

e

k

ru

ch

u

ru

ch

u

F

F

1

1

F

F

1

1

F

F

2

2

F

F

3

3

siła ciężkości:

siła ciężkości:

F

F

1

1

=V·

=V·





s

s

·g

·g

siła ciężkości:

siła ciężkości:

F

F

1

1

=V·

=V·





s

s

·g

·g

siła wyporu:

siła wyporu:

F

F

2

2

=V·

=V·





c

c

·g

·g

siła wyporu:

siła wyporu:

F

F

2

2

=V·

=V·





c

c

·g

·g

siła wyporu i ciężkości dają razem tzw.

siła wyporu i ciężkości dają razem tzw.

ciężar pozorny ziarna wywołujący jego

ciężar pozorny ziarna wywołujący jego

ruch

ruch

F

F

4

4

= V·g(

= V·g(





s

s

-

-





c

c

)

)

siła wyporu i ciężkości dają razem tzw.

siła wyporu i ciężkości dają razem tzw.

ciężar pozorny ziarna wywołujący jego

ciężar pozorny ziarna wywołujący jego

ruch

ruch

F

F

4

4

= V·g(

= V·g(





s

s

-

-





c

c

)

)

siła oporu hydrodynamicznego:

siła oporu hydrodynamicznego:

F

F

3

3

=0,5

=0,5





·V·

·V·





c

c

v

v

2

2

A

A

siła oporu hydrodynamicznego:

siła oporu hydrodynamicznego:

F

F

3

3

=0,5

=0,5





·V·

·V·





c

c

v

v

2

2

A

A

F

F

4

4

d

d

we wzorach tych:

we wzorach tych:

V – objętość ziarna, v - prędkość ruchu ziarna

V – objętość ziarna, v - prędkość ruchu ziarna





s

s

,

,





c

c

– gęstość ziarna i ośrodka

– gęstość ziarna i ośrodka

g – przyspieszenie ziemskie

g – przyspieszenie ziemskie

A – pole przekroju ziarna

A – pole przekroju ziarna





–

–

współczynnik oporu hydrodynamicznego

współczynnik oporu hydrodynamicznego

Wypadkowa sił:

Wypadkowa sił:

F

F

1

1

=V·

=V·





s

s

·g

·g

F

F

2

2

=V·

=V·





c

c

·g

·g

F

F

3

3

=0,5

=0,5





·V·

·V·





c

c

v

v

2

2

A

A

Siłę wywołującą ruch przyspieszony można

Siłę wywołującą ruch przyspieszony można

także

także

opisać równaniem:

opisać równaniem:

F

F

v

v

=V·

=V·

(

(





s

s

- a

- a





c

c

)

)

dt

dt

dv

dv

F

F

v

v

=F

=F

1

1

– F

– F

2

2

– F

– F

3

3

i

i

jeśli

jeśli





s

s

>

>





c

c

nadaje przyspieszenie ziarnu oraz pewnej

nadaje przyspieszenie ziarnu oraz pewnej

masie p

masie p

ł

ł

ynu poruszaj

ynu poruszaj

ą

ą

cej si

cej si

ę

ę

wraz z

wraz z

ziarnem

ziarnem

gdzie: a - współczynnik wyznaczany z

gdzie: a - współczynnik wyznaczany z

bilansu energetycznego przepływu

bilansu energetycznego przepływu

Gdy siła wywołującą ruch zrówna się z siłą oporu ziarno

Gdy siła wywołującą ruch zrówna się z siłą oporu ziarno

porusza się ze stałą prędkością końcową =0

porusza się ze stałą prędkością końcową =0

dt

dt

dv

dv

Współczynnik oporu hydrodynamicznego jest funkcją liczby

Współczynnik oporu hydrodynamicznego jest funkcją liczby

Reynoldsa. Liczba Reynoldsa wyraża stosunek siły

Reynoldsa. Liczba Reynoldsa wyraża stosunek siły

bezwładności do siły tarcia i określony jest wzorem:

bezwładności do siły tarcia i określony jest wzorem:







c

d

Re

v

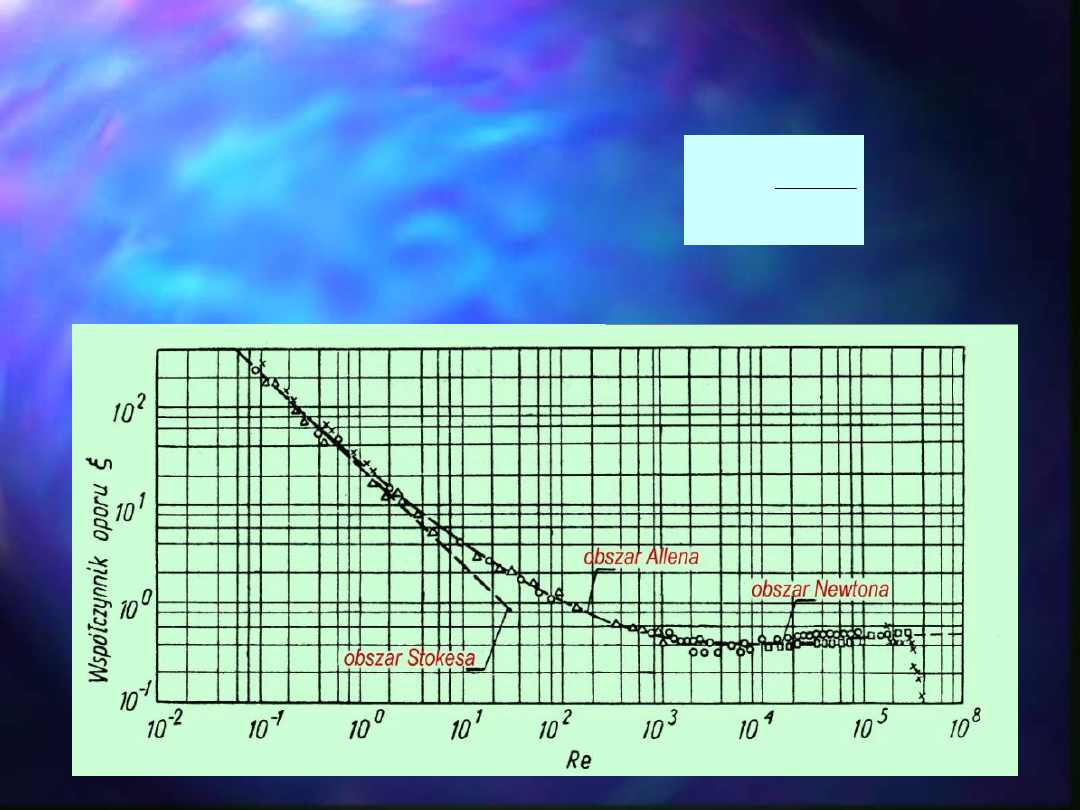
Zależność oporu hydrodynamicznego

Zależność oporu hydrodynamicznego

od liczby Reynoldsa przedstawiono na

od liczby Reynoldsa przedstawiono na

wykresie

wykresie

Rayleigha:

Rayleigha:

Zgodnie z wykresem Rayleigha można przyjąć, ze

Zgodnie z wykresem Rayleigha można przyjąć, ze

znacznym przybliżeniem, że w określonych

znacznym przybliżeniem, że w określonych

zakresach liczby Reynoldsa funkcja

zakresach liczby Reynoldsa funkcja





=f(Re) wyraża

=f(Re) wyraża

się następującymi wzorami

się następującymi wzorami

1. Dla Re<0,2, zatem dla małych ziarn kulistych o

1. Dla Re<0,2, zatem dla małych ziarn kulistych o

średnicy 0,005 - 0,1 mm (

średnicy 0,005 - 0,1 mm (

ruch laminarny, zakres

ruch laminarny, zakres

Stokesa

Stokesa

)

)

Re

24





2. Dla 0,2<Re<5

2. Dla 0,2<Re<5

·

·

10

10

2

2

, zatem dla ziarn kulistych o średnicy

, zatem dla ziarn kulistych o średnicy

0,1 - 1,0 mm (

0,1 - 1,0 mm (

zakres przejściowy Allena

zakres przejściowy Allena

)

)

6

,

0

Re

5

,

18







3. Dla 5

3. Dla 5

·

·

10

10

2

2

<Re< 3

<Re< 3

·

·

10

10

5

5

, zatem dla ziarn kulistych o

, zatem dla ziarn kulistych o

średnicy >1,0 mm (

średnicy >1,0 mm (

zakres ruchu burzliwego

zakres ruchu burzliwego

Newtona-Rittingera

Newtona-Rittingera

)

)

44

,

0





OPADANIE ZIARN W O

OPADANIE ZIARN W O

Ś

Ś

RODKACH P

RODKACH P

Ł

Ł

YNNYCH

YNNYCH

Wzór Stokesa na pr

Wzór Stokesa na pr

ę

ę

dko

dko

ść

ść

opadania ziarna

opadania ziarna

kulistego (dla ruchu laminarnego), dotyczy ziarn o

kulistego (dla ruchu laminarnego), dotyczy ziarn o

rozmiarach 0,01 - 0,1 mm

rozmiarach 0,01 - 0,1 mm

, m/s





















c

s

2

1

c

s

2

d

k

d

18

g

v

gdzie:

gdzie:

d -

d -

ś

ś

rednica ziarna, m

rednica ziarna, m

v

v

- ko

- ko

ń

ń

cowa (sta

cowa (sta

ł

ł

a) prędko

a) prędko

ść

ść

opadania ziarna , m/s

opadania ziarna , m/s





s

s

- gęsto

- gęsto

ść

ść

ziarna, kg/m

ziarna, kg/m

3

3





c

c

- gęsto

- gęsto

ść

ść

o

o

ś

ś

rodka, kg/m

rodka, kg/m

3

3





- wspó

- wspó

ł

ł

czynnik lepko

czynnik lepko

ś

ś

ci dynamicznej, Ns/m

ci dynamicznej, Ns/m

2

2

k

k

1

1

, k

, k

2

2

,

,

k

k

3

3

- wspó

- wspó

ł

ł

czynniki oporu zale

czynniki oporu zale

ż

ż

ne od kszta

ne od kszta

ł

ł

tu ziarna oraz

tu ziarna oraz

od

od

charakteru ruchu ziarna wzgl

charakteru ruchu ziarna wzgl

ę

ę

dem cieczy, tj. od

dem cieczy, tj. od

charakteryzuj

charakteryzuj

ą

ą

cej

cej

dany ruch liczby Reynodsa

dany ruch liczby Reynodsa

Wzór

Allena

dla

zakresu

Wzór

Allena

dla

zakresu

przej

przej

ść

ść

iowego (ziarna 0,1-1,0 mm):

iowego (ziarna 0,1-1,0 mm):





3

c

2

c

s

2

d

k











v

Wzór Newtona - Rittingera dla ruchu

Wzór Newtona - Rittingera dla ruchu

burzliwego (ziarna >1 mm):

burzliwego (ziarna >1 mm):

, m/s

, m/s

c

c

s

3

d

k











v

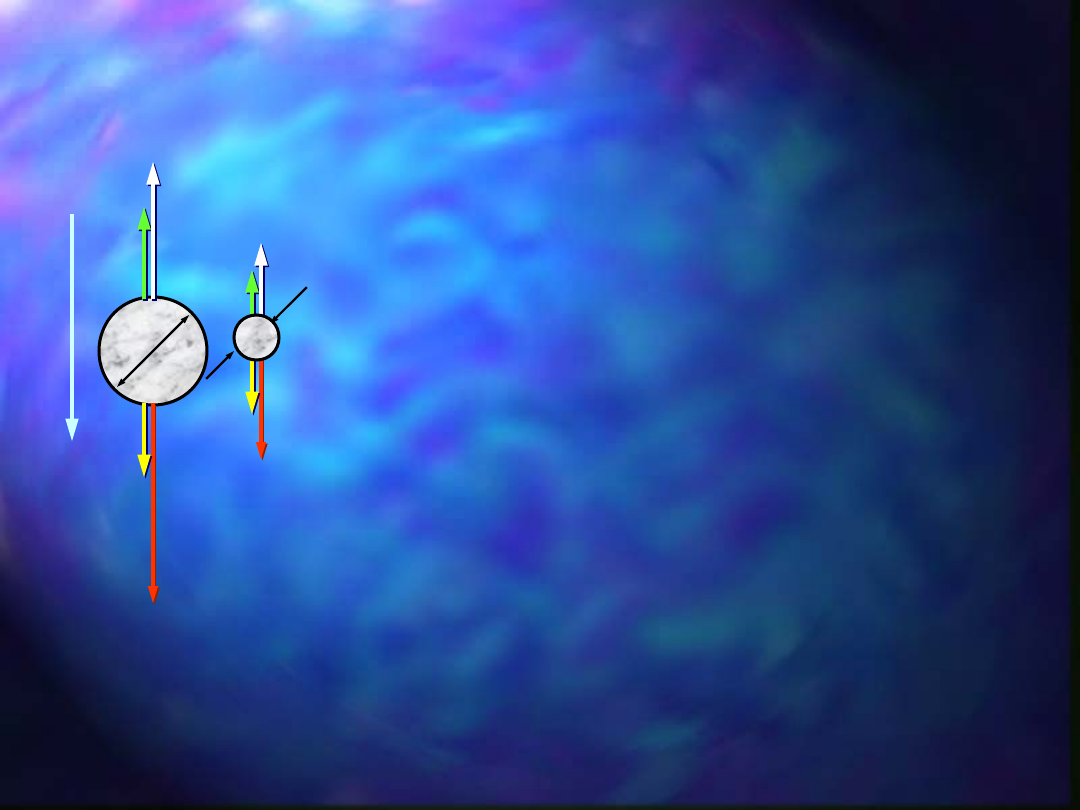
Na ziarna o różnej masie zanurzone w

Na ziarna o różnej masie zanurzone w

cieczy i znajdujące się w ruchu działają

cieczy i znajdujące się w ruchu działają

siły:

siły:

OPADANIE ZIARN W O

OPADANIE ZIARN W O

Ś

Ś

RODKACH P

RODKACH P

Ł

Ł

YNNYCH

YNNYCH

siła ciężkości:

siła ciężkości:

F

F

1

1

=V·

=V·





s

s

·g

·g

siła ciężkości:

siła ciężkości:

F

F

1

1

=V·

=V·





s

s

·g

·g

siła wyporu:

siła wyporu:

F

F

2

2

=V·

=V·





c

c

·g

·g

siła wyporu:

siła wyporu:

F

F

2

2

=V·

=V·





c

c

·g

·g

ciężar pozorny ziarna

ciężar pozorny ziarna

F

F

4

4

= V·g(

= V·g(





s

s

-

-





c

c

)

)

ciężar pozorny ziarna

ciężar pozorny ziarna

F

F

4

4

= V·g(

= V·g(





s

s

-

-





c

c

)

)

siła oporu hydrodynamicznego:

siła oporu hydrodynamicznego:

F

F

3

3

=0,5

=0,5





·V·

·V·





c

c

v

v

2

2

A

A

siła oporu hydrodynamicznego:

siła oporu hydrodynamicznego:

F

F

3

3

=0,5

=0,5





·V·

·V·





c

c

v

v

2

2

A

A

gdzie:

gdzie:

V – objętość ziarna, v - prędkość ruchu

V – objętość ziarna, v - prędkość ruchu

ziarna

ziarna





s

s

,

,





c

c

– gęstość ziarna i ośrodka

– gęstość ziarna i ośrodka

g – przyspieszenie ziemskie

g – przyspieszenie ziemskie

A – pole przekroju ziarna

A – pole przekroju ziarna





–

–

współczynnik oporu hydrodynamicznego

współczynnik oporu hydrodynamicznego

m – masa ziarna

m – masa ziarna

kie

ru

n

e

k

kie

ru

n

e

k

ru

ch

u

ru

ch

u

F

F

1

1

F

F

1

1

F

F

2

2

F

F

3

3

F

F

4

4

d

1

d

2

Jeśli d

Jeśli d

1

1

> d

> d

2

2

to

to

przy

przy





s1

s1

=

=





s2

s2

m

m

1

1

> m

> m

2

2

,

,

a zatem

a zatem

v

v

1

1

>v

>v

2

2







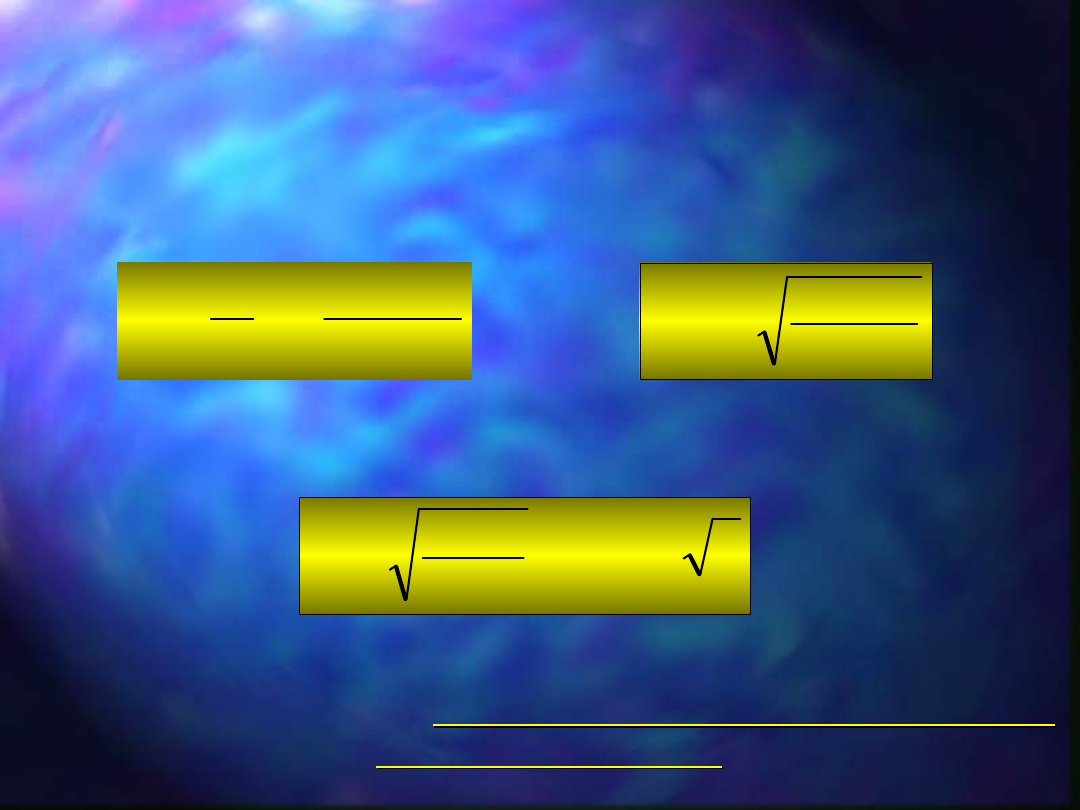
c

s

d

g





2

18

v

Przekształcając wzór Stokesa:

Przekształcając wzór Stokesa:

Analiza sedymentacyjna

Analiza sedymentacyjna





g

c

s











v

d

18

lub do postaci ogólnej:

lub do postaci ogólnej:





v

d

v

k

d

c

s

1

k















Poszczególne ziarna w zawiesinie będą opadały z

Poszczególne ziarna w zawiesinie będą opadały z

różną prędkością w

różną prędkością w

zależności od ich masy, a zatem

zależności od ich masy, a zatem

od ich rozmiarów.

od ich rozmiarów.

Określanie składu ziarnowego ziarn < 0,1mm rozpro-

Określanie składu ziarnowego ziarn < 0,1mm rozpro-

szonych w wodzie w postaci zawiesiny

szonych w wodzie w postaci zawiesiny

polidyspersyjnej

polidyspersyjnej

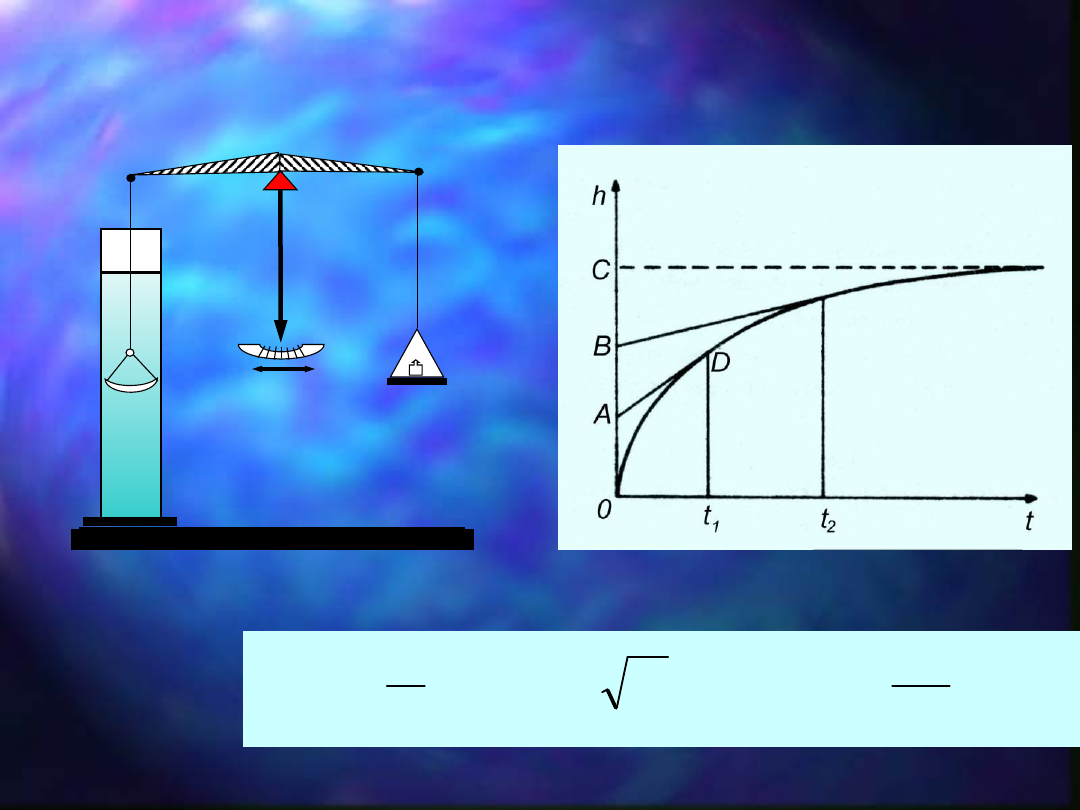
Zasada działania

Zasada działania

wagi

wagi

sedymentacyjnej

sedymentacyjnej

Krzywa sedymentacji

Krzywa sedymentacji

,%

100

0

0

1

1

1

1

C

A

k

d

t

h











1

1

v

v

H

H

Po czasie t

Po czasie t

1

1

w punkcie D:

w punkcie D:

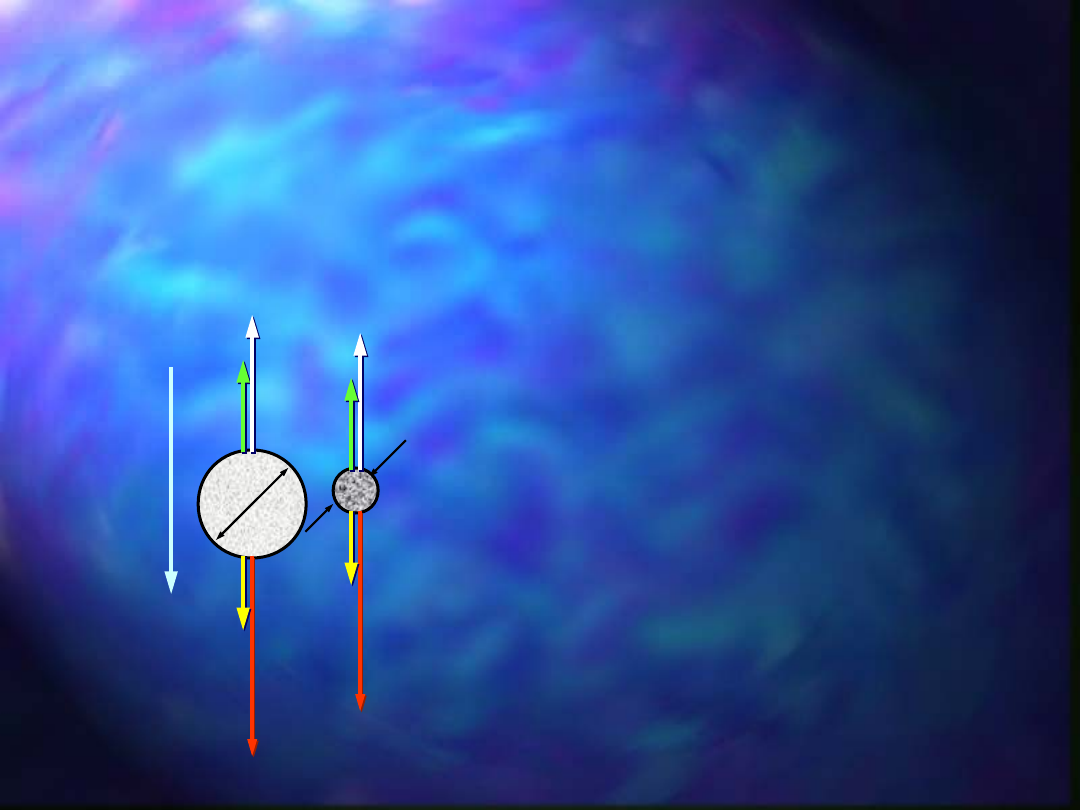
Na ziarna o jednakowej

Na ziarna o jednakowej

masie zanurzone w cieczy

masie zanurzone w cieczy

i znajdujące się w ruchu

i znajdujące się w ruchu

działają siły:

działają siły:

OPADANIE ZIARN W O

OPADANIE ZIARN W O

Ś

Ś

RODKACH P

RODKACH P

Ł

Ł

YNNYCH

YNNYCH

Jeśli d

Jeśli d

1

1

> d

> d

2

2

to

to

przy

przy





s1

s1

<

<





s2

s2

może się zdarzyć, że

może się zdarzyć, że

m

m

1

1

= m

= m

2

2

i wówczas

i wówczas

v

v

1

1

= v

= v

2

2

,

,

a ziarna nazywa się

a ziarna nazywa się

równoopadającymi

równoopadającymi

kie

ru

n

e

k

kie

ru

n

e

k

ru

ch

u

ru

ch

u

F

F

1

1

F

F

1

1

F

F

2

2

F

F

3

3

F

F

4

4

d

1

d

2

W

W

spó

spó

ł

ł

czynnik równoopadania

czynnik równoopadania

v

1

= v

2

 np. dla ziarn grubych >1mm w wodzie, 

c

=1000

kg/m

3

:

1000

1000

1000

1000

2

1

2

3

1

3







s

s

d

k

d

k







d

d

1

2

e

d

d

s

s









1

2

1

2

1000

1000





Jeśli

Jeśli

to im mniejsza warto

to im mniejsza warto

ść

ść

e

e

,

,

tym

tym

mniejsza jest ostro

mniejsza jest ostro

ść

ść

rozdzia

rozdzia

ł

ł

u

u

 

s

s

2

1

