
Wykład 6
Modulacje dyskretne
1. Modulacje impulsowe
2. Modulacje przyrostowe
3. Modulacje dyskretne
4. Widma zmodulowanych
sygnałów
5. Widma impulsów
TD6-1 / 31
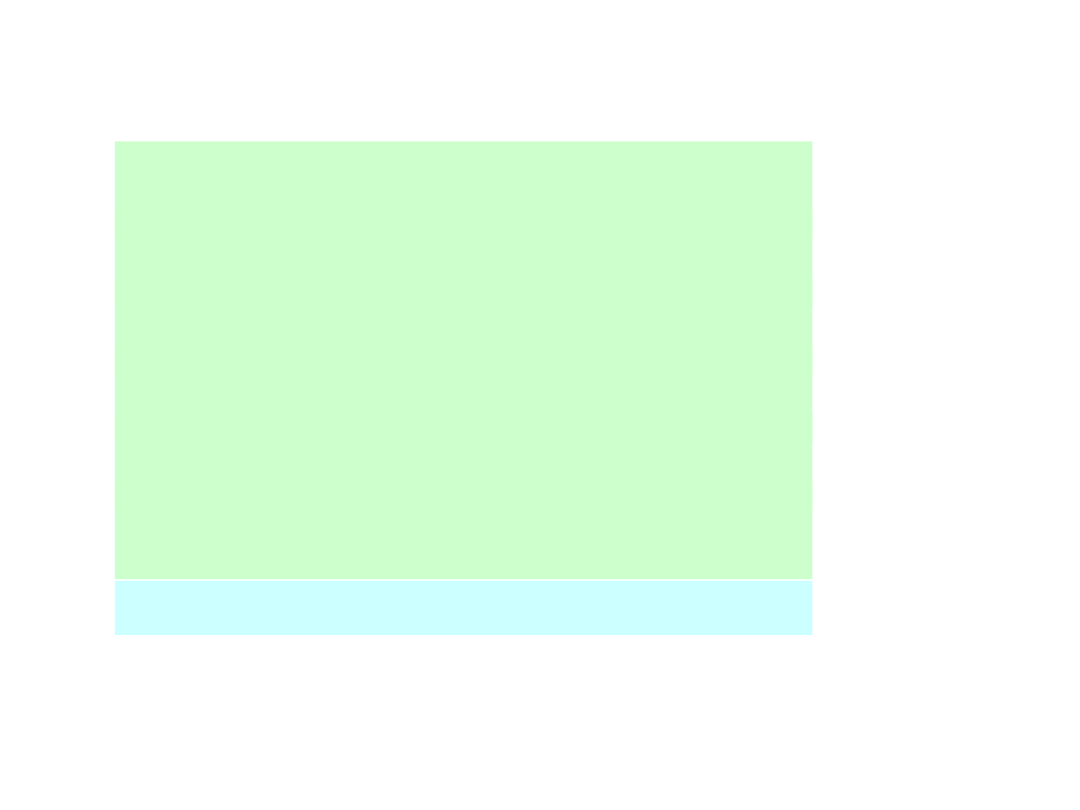
Modulacje impulsowe
PAM – modulacja amplitudy
impulsów
TD6-2 / 31
PFM – modulacja częstotliwości
impulsów
PPM – modulacja położenia
impulsów
PDM – modulacja długości
impulsów
PNM – modulacja liczby
impulsów
PCM – modulacja kodowo
impulsowa
PΔM – modulacje przyrostowe
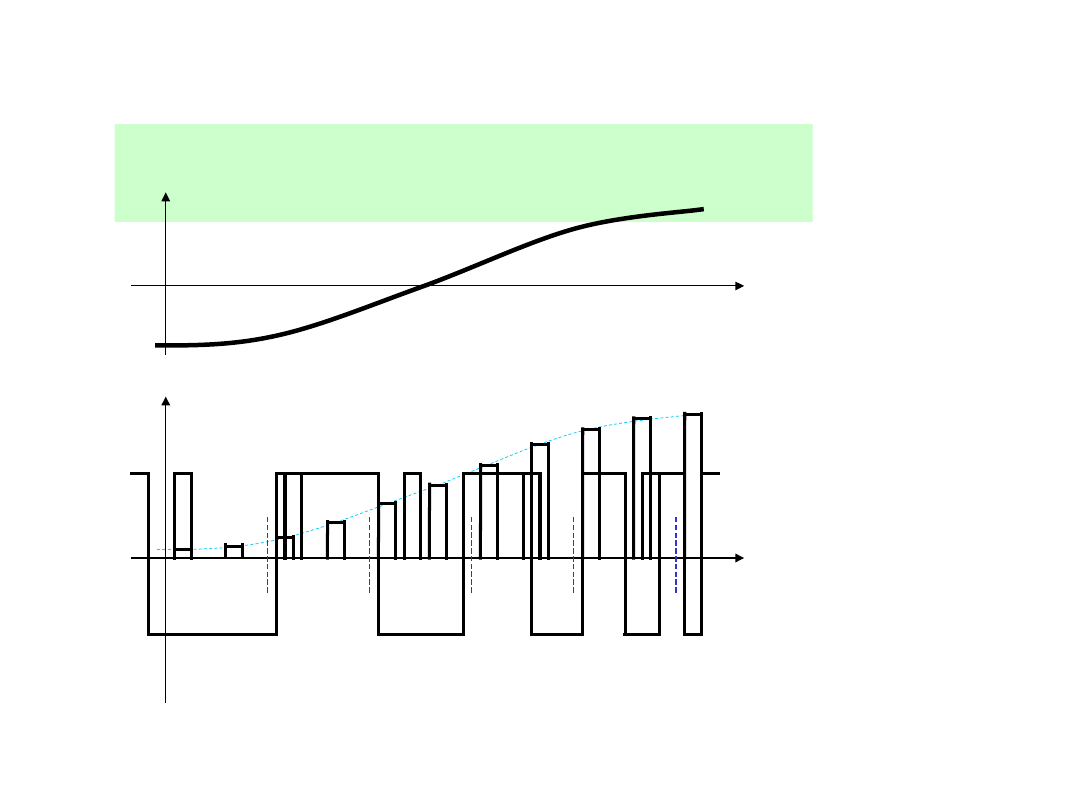
Modulacje impulsowe
PAM – modulacja amplitudy
impulsów
TD6-3 / 31
PFM – modulacja częstotliwości
impulsów
PPM – modulacja położenia
impulsów
x(t
)
t
u
x
(t
)
t
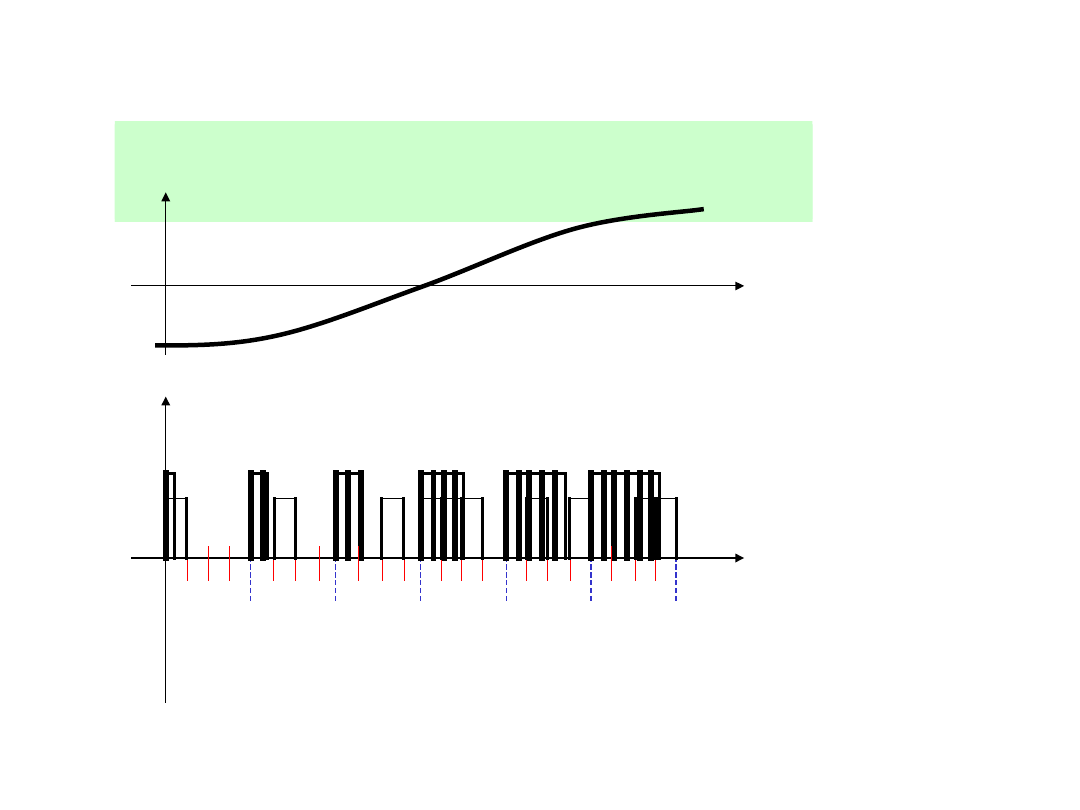
Modulacje impulsowe
TD6-4 / 31
PDM – modulacja długości
impulsów
PNM – modulacja liczby
impulsów
PCM – modulacja kodowo
impulsowa
x(t
)
t
u
x
(t
)
t
1 2 4 7 10 12
1 0 0 0
0 0 1 1
1 1 1 0
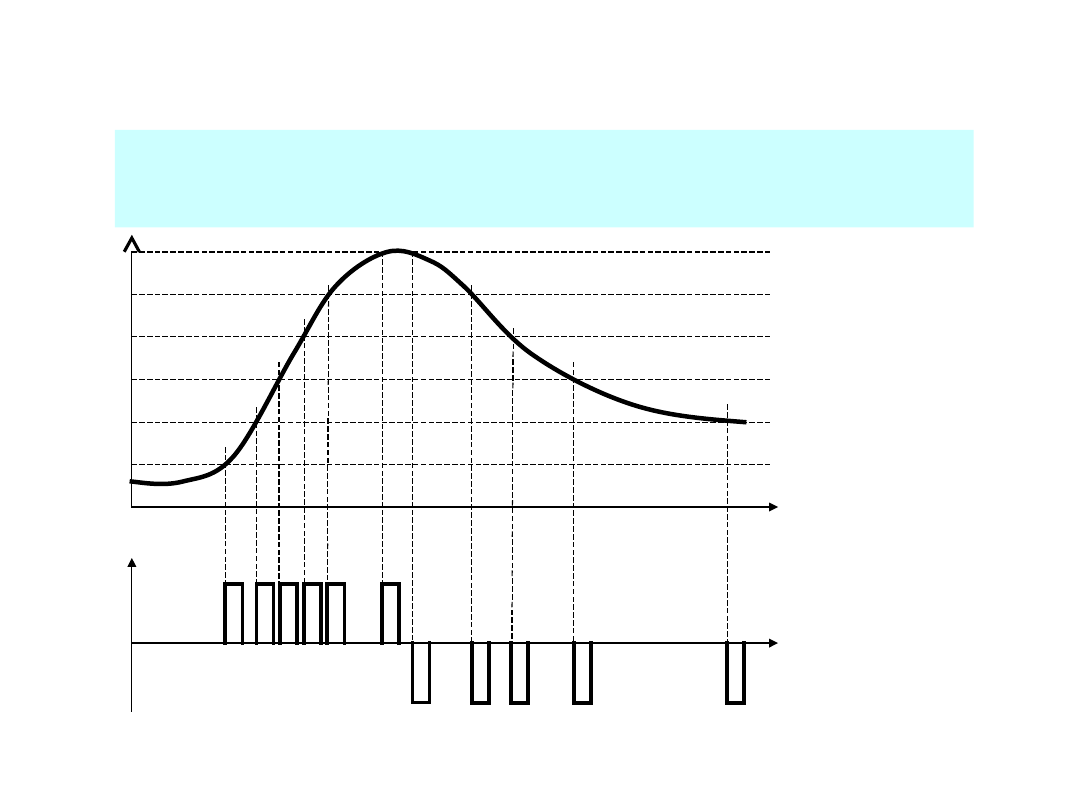
Modulacje przyrostowe
TD6-5 / 31
PΔM – modulacja przyrostowa (delta –
modulacja)
x(t
)
t
t
u
x
(t
)
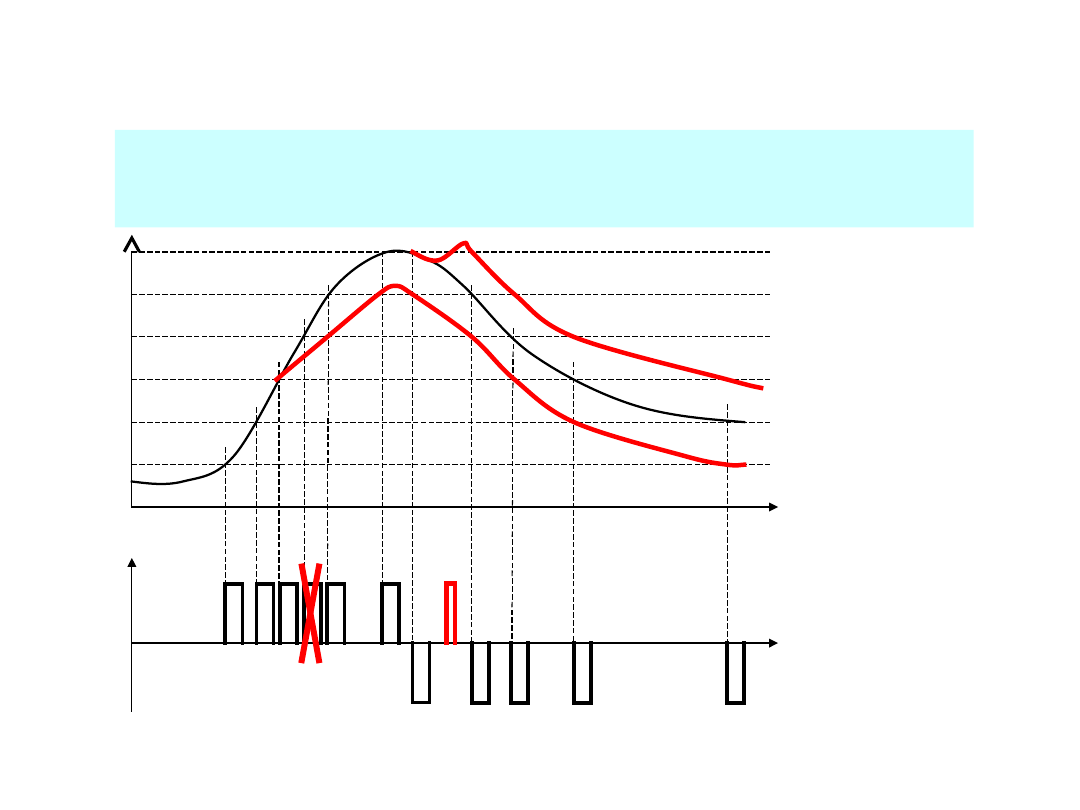
Modulacje przyrostowe
TD6-6 / 31
PΔM – modulacja przyrostowa (delta –
modulacja)
x(t
)
t
t
u
x
(t
)

Modulacje
dyskretne
TD6-7 / 31
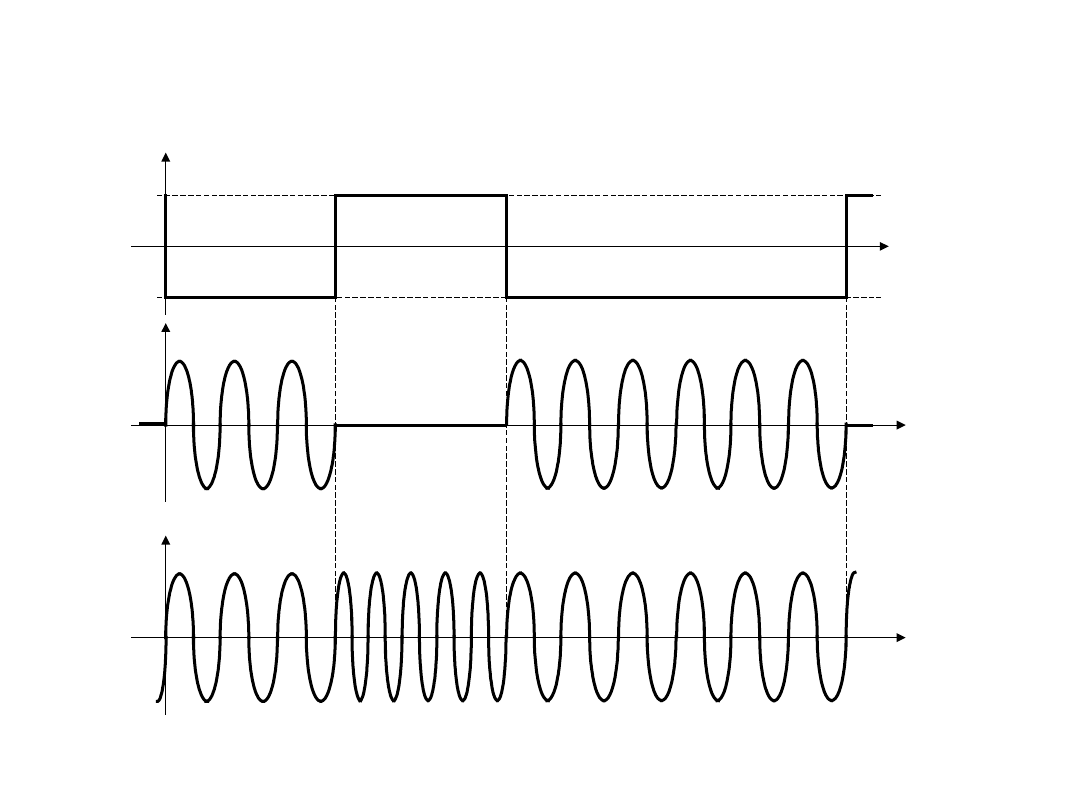
Modulacje binarne AM i FM
TD6-8 / 31
x(t
)
t
AM
t
+U
–U
t
FM
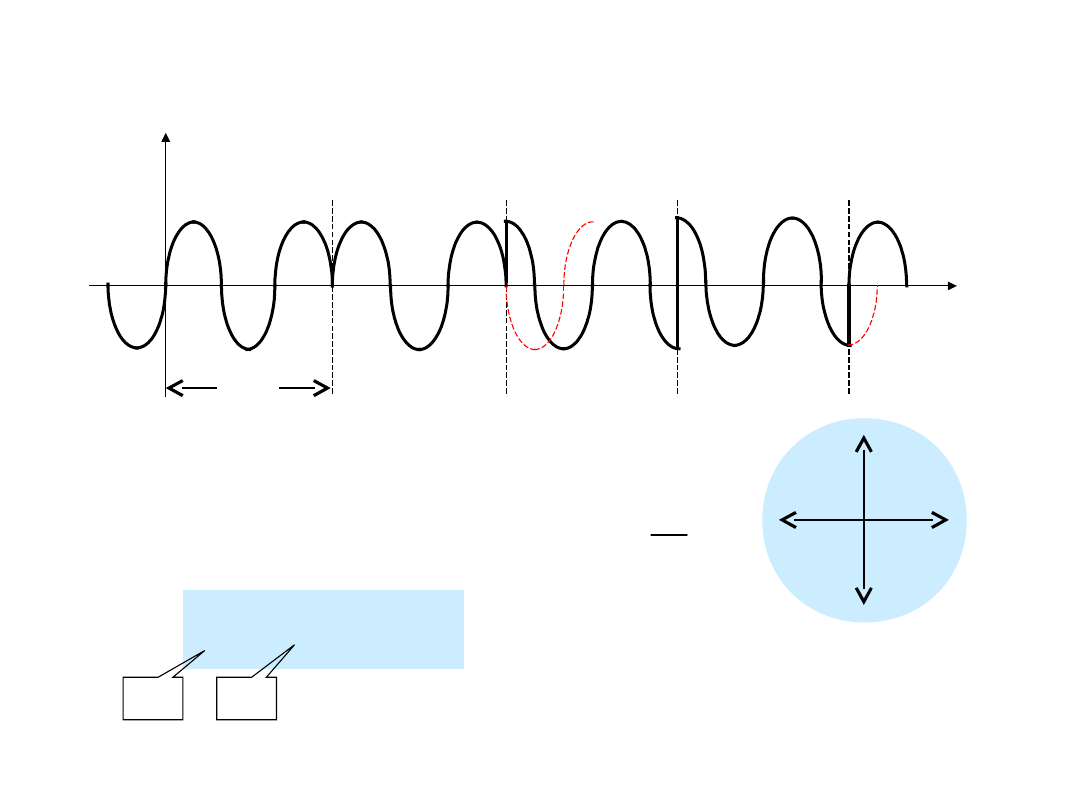
Modulacja DCPSK
m
m
T
1
TD6-9 / 31
t
0
00
180
11
90
01
180
11
270
10
T
m
T
m
– okres modulacji
w
– wartościowość modulacji
m
– szybkość modulacji
t
– szybkość transmisji
00
01
11
10
w
m
t
log
b/
s
B
d
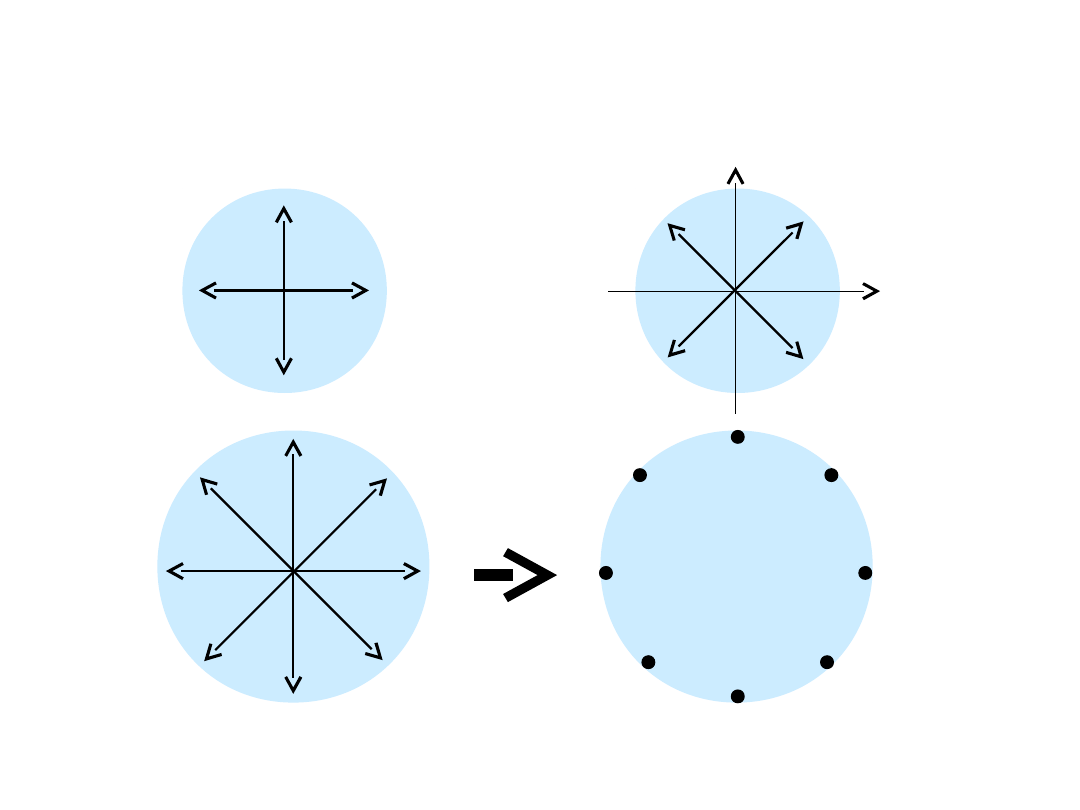
Modulacje DCPSK
TD6-10 / 31
00
01
11
10
00
01
11
10
000
011
110
101
001
010
111
100
Konstelacja
8 – wartościowej
DCPSK
000
011
110
101
001
010
111
100
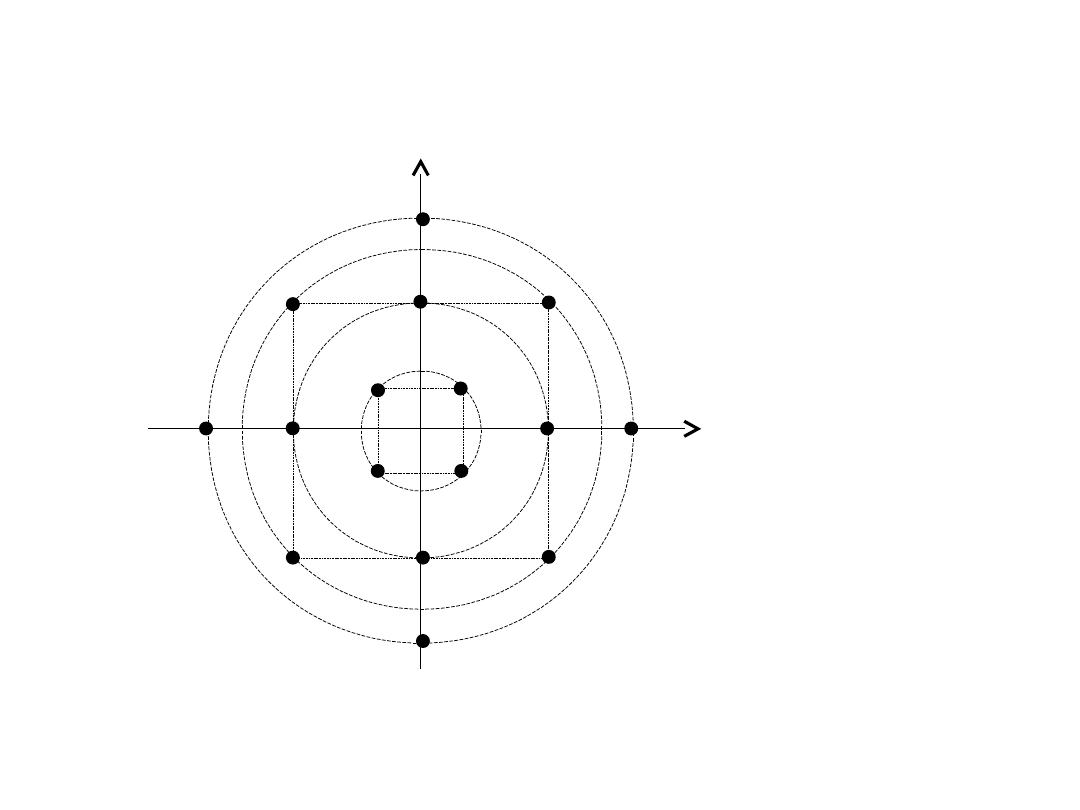
Modulacja QAM (AM-PM)
TD6-11 / 31
1000
1011
1110
1101
1001
1010
1111
1100
0000
0011
0110
0101
0010
0111
0100
0001
ITU-T
V.29
1
1
3
5
3
5
w
= 16
m
= 2 400 Bd
t
= 9 600 b/s
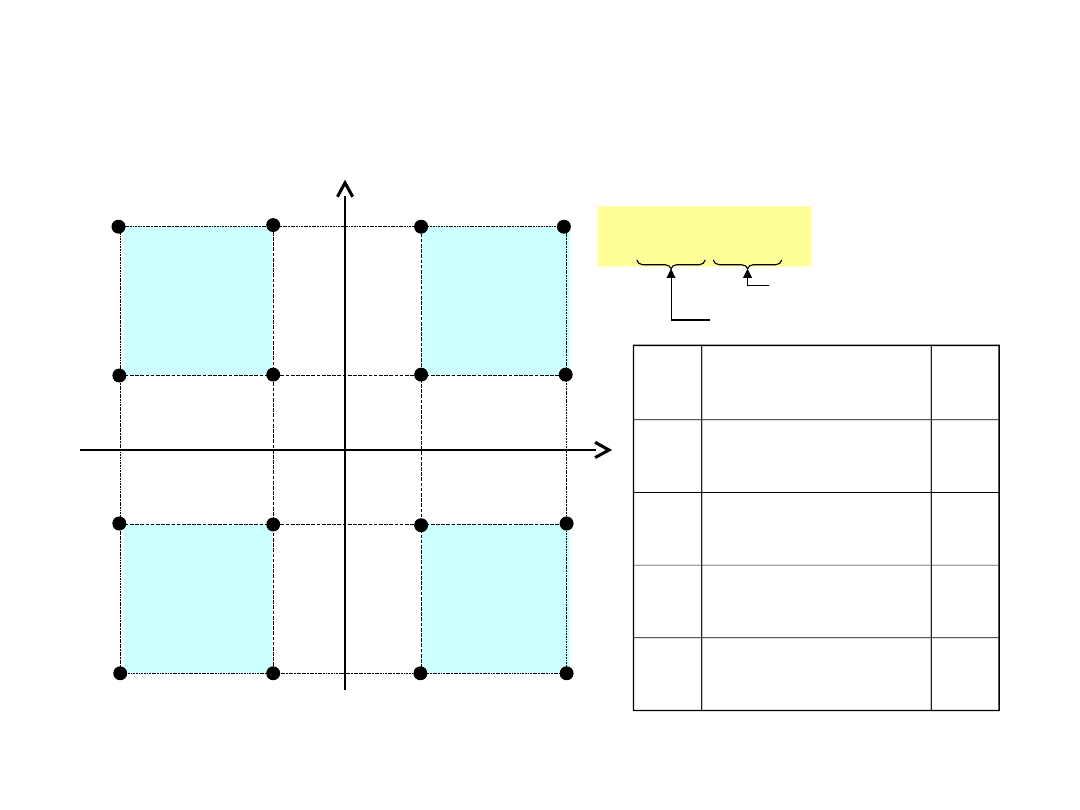
Modulacja QAM (AM-PM)
TD6-12 / 31
11
10
11
11
01
10
11
10
00
00
00
10
01
01
01
00
ITU-T V.22bis i
V.32
1
1
3
3
1
4
2
3
B
1
B
2
B
3
B
4
punkt w kwadracie
zmiana kwadratu
B
1
B
2
Zmiana
kwadratu
Faz
a
00 1 2, 2 3
3 4, 4 1
90
01 1 1, 2 2
3 3, 4 4
0
11 1 4, 2 1
3 2, 4 3
270
10 1 3, 2 4
3 1, 4 2
180
-1
-3
-1
-3

Widma
zmodulowanyc
h sygnałów
TD6-13 / 31
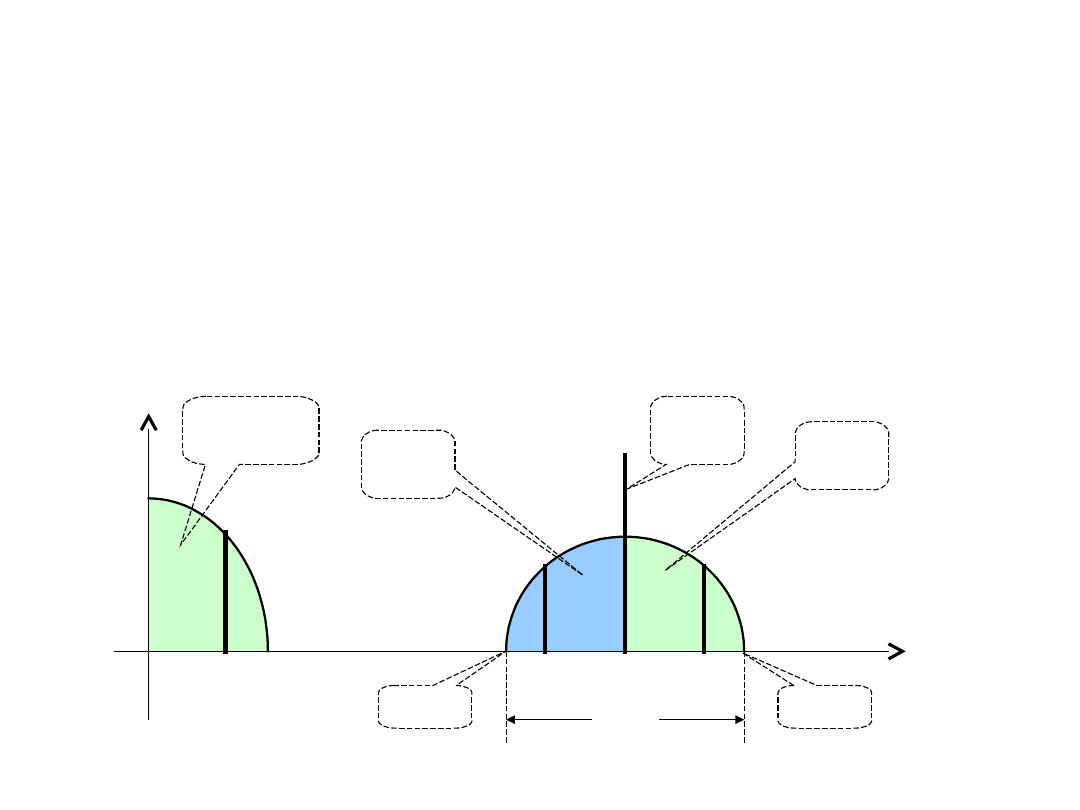
Widmo sygnału AM
TD6-14 / 31
u
x
(A, t ) = U
0
[1 + m cos(t +
)] cos(
0
t +
) =
= U
0
cos(
0
t +
) + mU
0
cos(t +
) cos(
0
t +
) =
= U
0
cos(
0
t +
) +
+ ½mU
0
cos[(
0
– )t + (
–
)] +
+ ½mU
0
cos[(
0
+ )t + (
+
)]
g
0
–
0
0
+
Widmo
podstawo
we
Wstęg
a
górna
Wstęg
a
dolna
Prąże
k
nośnej
0
+
g
0
–
g
2
g
x(t
)=m
cos(t +
)
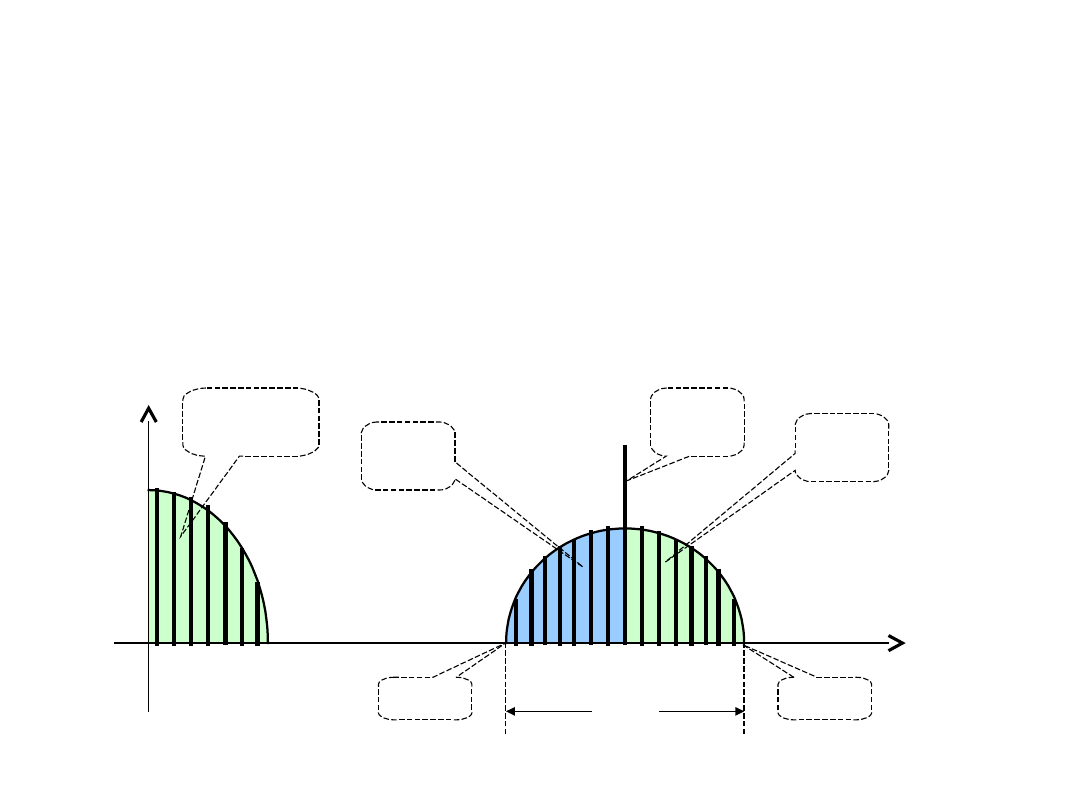
Widmo sygnału AM
TD6-15 / 31
u
x
(A, t ) = U
0
[1 +
k
m
k
cos(
k
t +
k
)] cos(
0
t +
) =
= U
0
cos(
0
t +
) + U
0
k
m
k
cos(
k
t +
k
) cos(
0
t +
) =
= U
0
cos(
0
t +
) +
+ ½U
0
k
m
k
cos[(
0
–
k
)t + (
–
k
)] +
+ ½U
0
k
m
k
cos[(
0
+
k
)t + (
+
k
)]
k
g
0
–
k
0
0
+
k
Widmo
podstawo
we
Wstęg
a
górna
Wstęg
a
dolna
Prąże
k
nośnej
0
+
g
0
–
g
2
g
x(t
)=
k
m
k
cos(
k
t +
k
)
Związek FM i PM
t
t
d
t
d
t
x
t
x
t
x
0
0
0
0
0
TD6-16 / 31
Niech w modulacji FM
(x (t )) =
0
+
x
(t )
gdzie
t
x
x
d
t
0
t
dt
t
d
dt
t
x
d
t
x
x
0
0
Niech w modulacji PM
(x (t )) =
0
t +
x
(t ) + φ
0

Widmo sygnału FM
TD6-17 / 31
Niech
(x (t )) =
0
+
x
(t )
Niech
x
(t ) = M cos(t +
)
u
x
(
, t ) = A cos[
0
t +
+ M cos(t +
) ] =
= A cos(
0
t +
) cos[M cos(t +
) ] +
– A sin(
0
t +
) sin[M cos(t +
) ]
Zakładając modulację wąskopasmową gdzie |M| << 1 mamy
cos[M cos(t +) ] 1
sin[M cos(t +) ] M cos(t + )
Zatem
u
x
(
, t ) A cos(
0
t +
) – AM cos(t +
) sin(
0
t +
)
t
t
A
d
t
A
d
x
A
t
u
x
t
x
t
x
0
0
0
0
cos
cos
cos
,
u
x
(
, t ) A cos(
0
t +
) – AM cos(t +
) sin(
0
t +
) =
= A cos(
0
t +
) +
– ½AM sin[(
0
– ) t + (
–
)] +
+ ½AM sin[(
0
+ ) t + (
+
)]
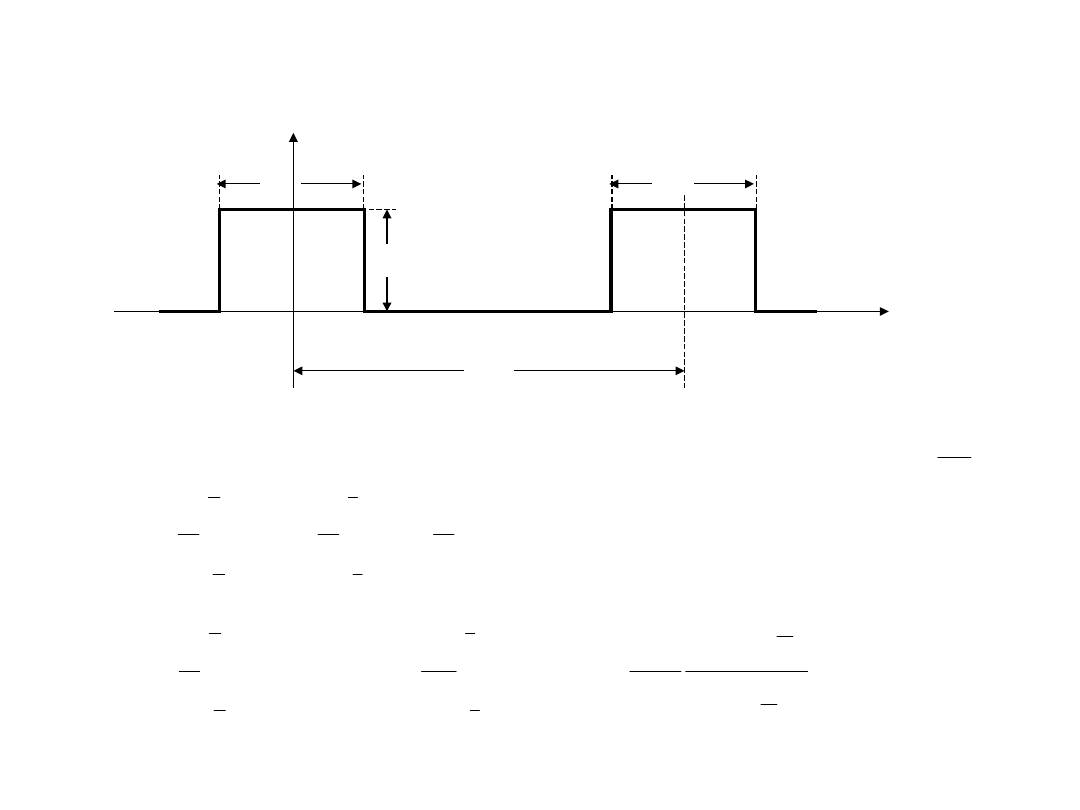
Widmo ciągu impulsów
2
2
sin
2
cos
2
cos
2
,
1
cos
0
0
2
2
0
2
2
0
2
2
2
2
0
1
0
0
n
n
T
A
dt
t
n
T
A
dt
t
n
t
f
T
a
T
A
dt
T
A
dt
t
f
T
a
t
n
a
a
t
f
T
T
n
T
T
n
n
TD6-18 / 31
A
f (t
)
2
T
2
2
T+
2
T
T
2
t
T
2
0
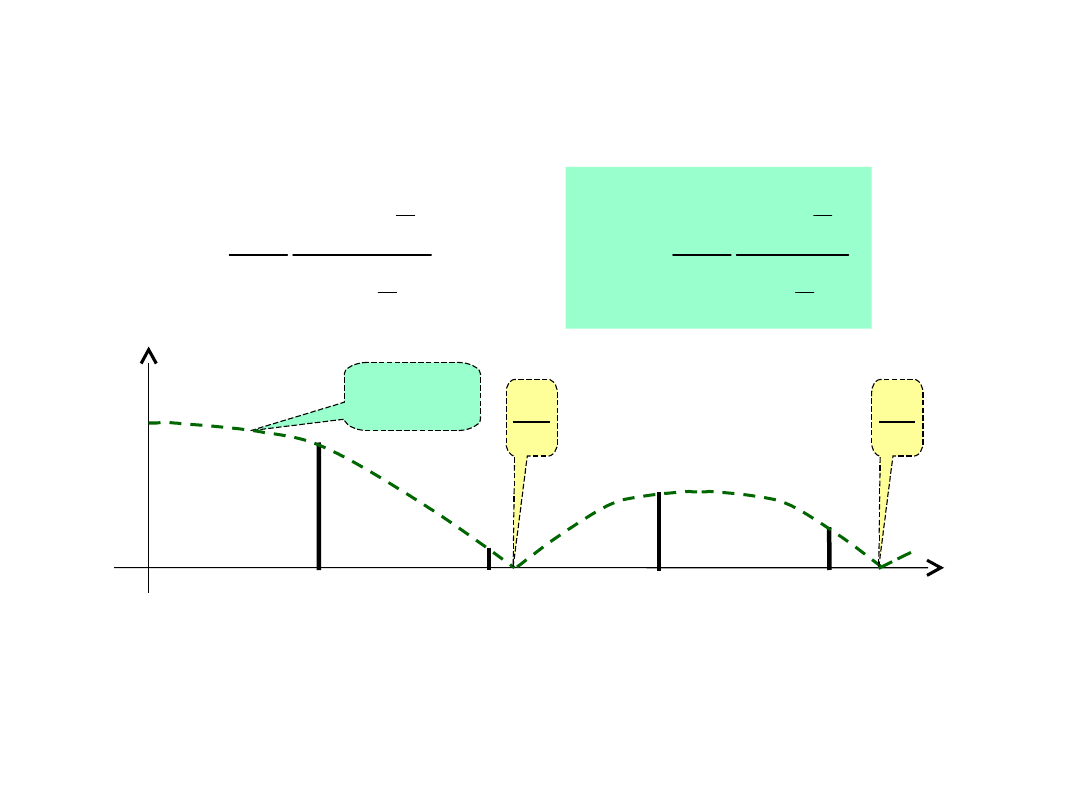
Widmo ciągu impulsów
2
2
sin
2
2
2
sin
2
0
0
T
A
A
n
n
T
A
a
n
TD6-19 / 31
Oznaczając = n
0
otrzymujemy równanie obwiedni
0
Obwiedni
a A()
2
0
3
0
4
0
|F(
)|
2
4
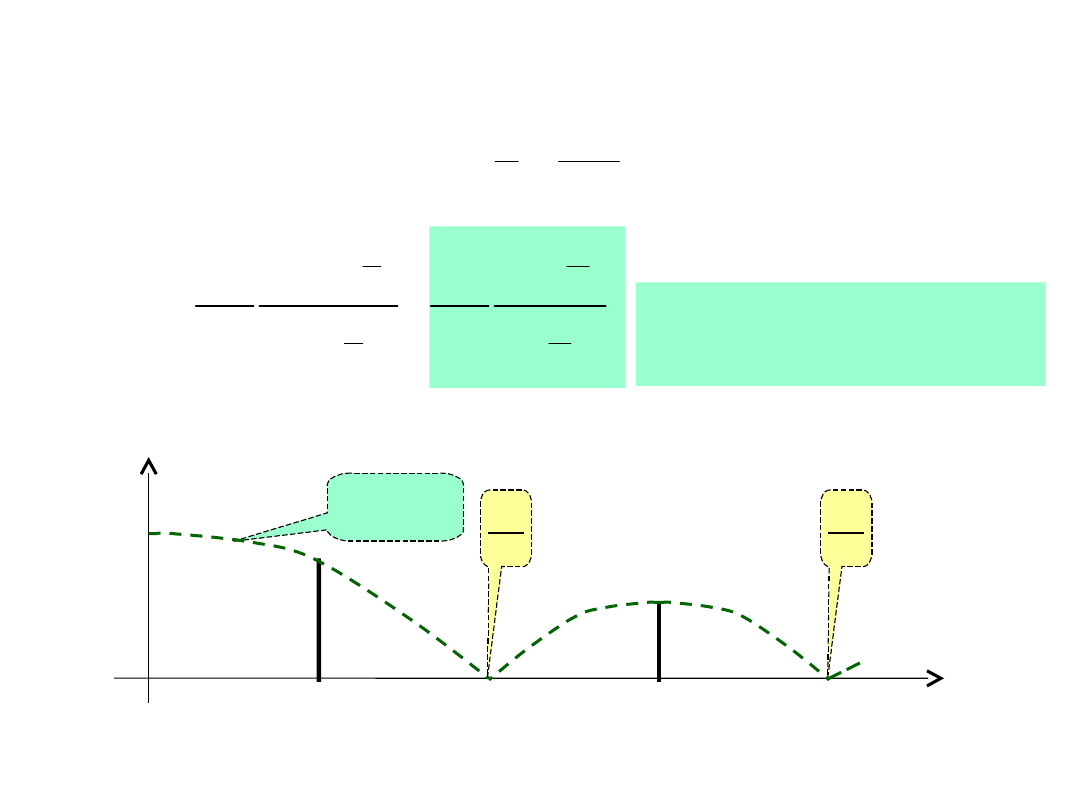
Widmo fali prostokątnej
2
2
sin
2
2
2
sin
2
0
0
n
n
T
A
n
n
T
A
a
n
TD6-20 / 31
Mamy
= ½T,
zatem
0
Obwiedni
a A()
2
0
3
0
4
0
|F(
)|
2
4
0
2
2
Dla n
0 i parzystych
a
n
=
0.
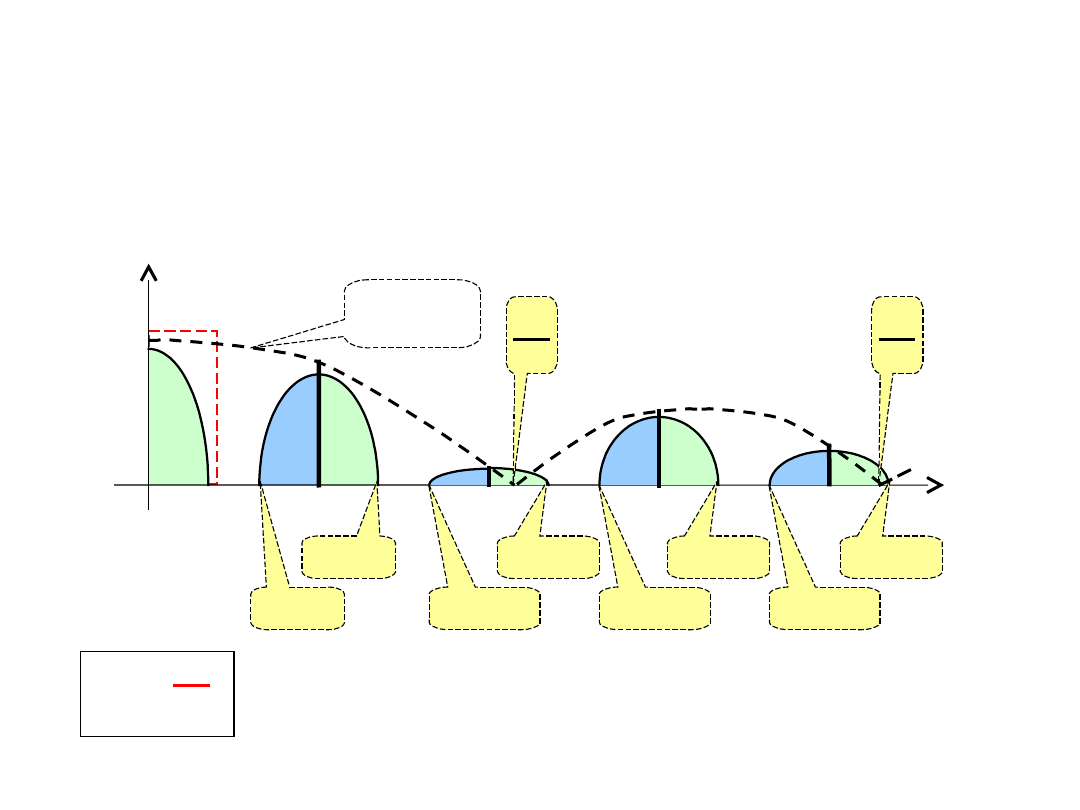
Widmo sygnału PAM
TD6-21 / 31
g
0
Obwiedni
a A()
0
+
g
0
–
g
2
0
2
0
+
g
3
0
3
0
+
g
4
0
4
0
+
g
2
0
–
g
3
0
–
g
4
0
–
g
|F(
)|
2
4
1
0
0
1
0
0
cos
cos
n
n
n
n
x
t
n
a
t
U
t
U
a
t
n
a
a
t
U
t
f
g
0
g
2 f
g
f
0
T
1
2f
g
T = okres próbkowania

Widma
impulsów
TD6-22 / 31
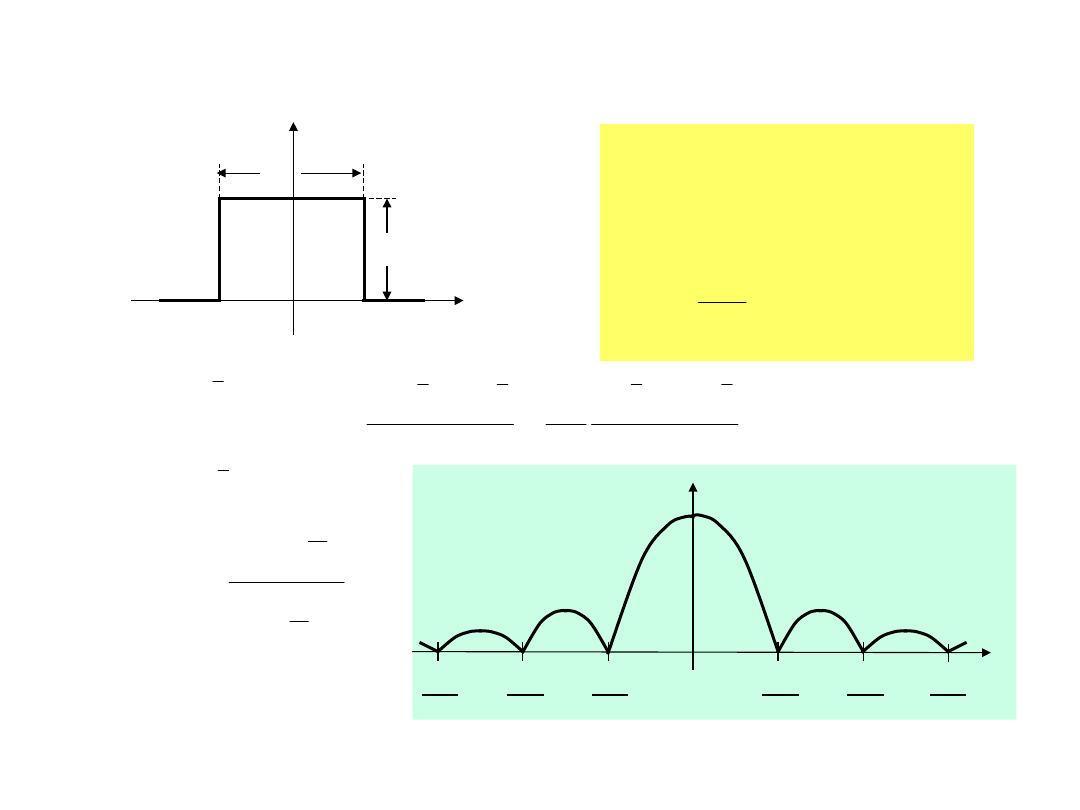
Impuls prostokątny
d
e
j
S
t
x
dt
e
t
x
j
S
t
j
t
j
2
1
2
2
sin
)
(
2
2
)
(
2
2
2
2
2
2
A
j
S
j
e
e
A
j
e
e
A
dt
e
A
j
S
j
j
j
j
t
j
TD6-23 / 31
A
x(t
)
2
2
t
|S(j)|
1
=
2
f
2
3
-1
-3
-2
0
A
f
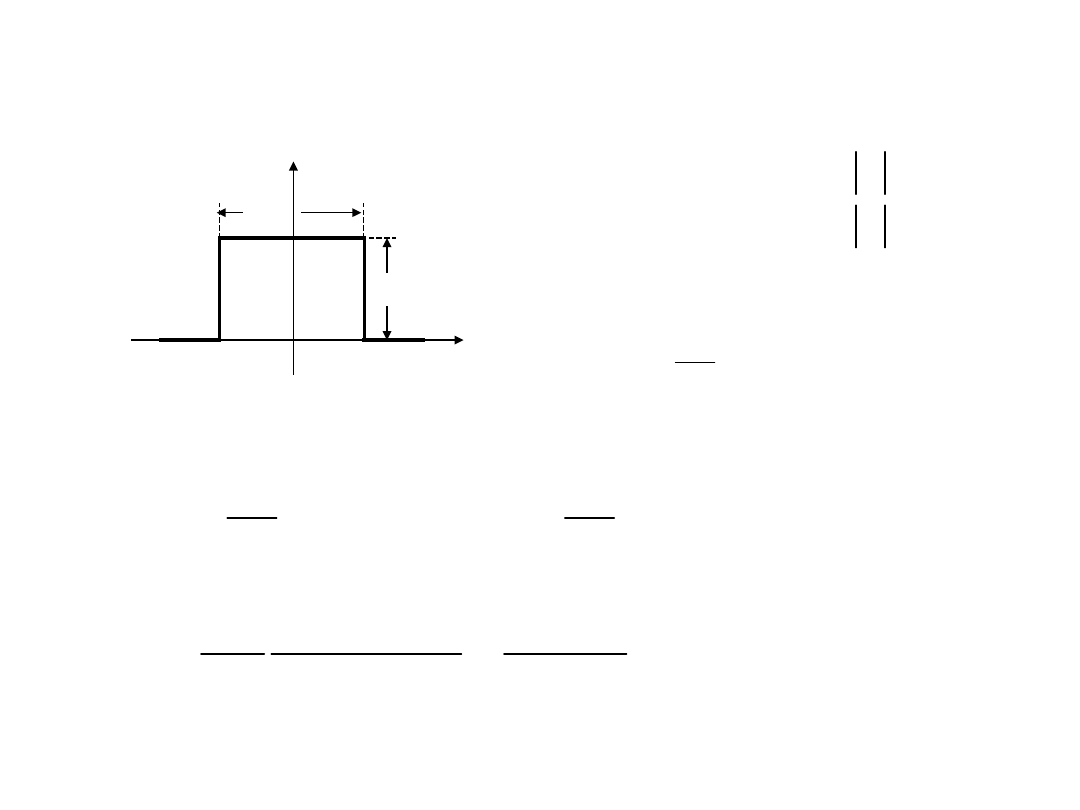
Impuls o widmie
prostokątnym
0
0
0
gdzie
dla
0
dla
T
T
j
S
TD6-24 / 31
T
S( j
)
2
0
0
-
0
t
t
jt
d
T
d
j
S
t
x
e
e
e
e
t
j
t
j
t
j
t
j
o
0
0
0
sin
2
1
2
2
1
0
0
0
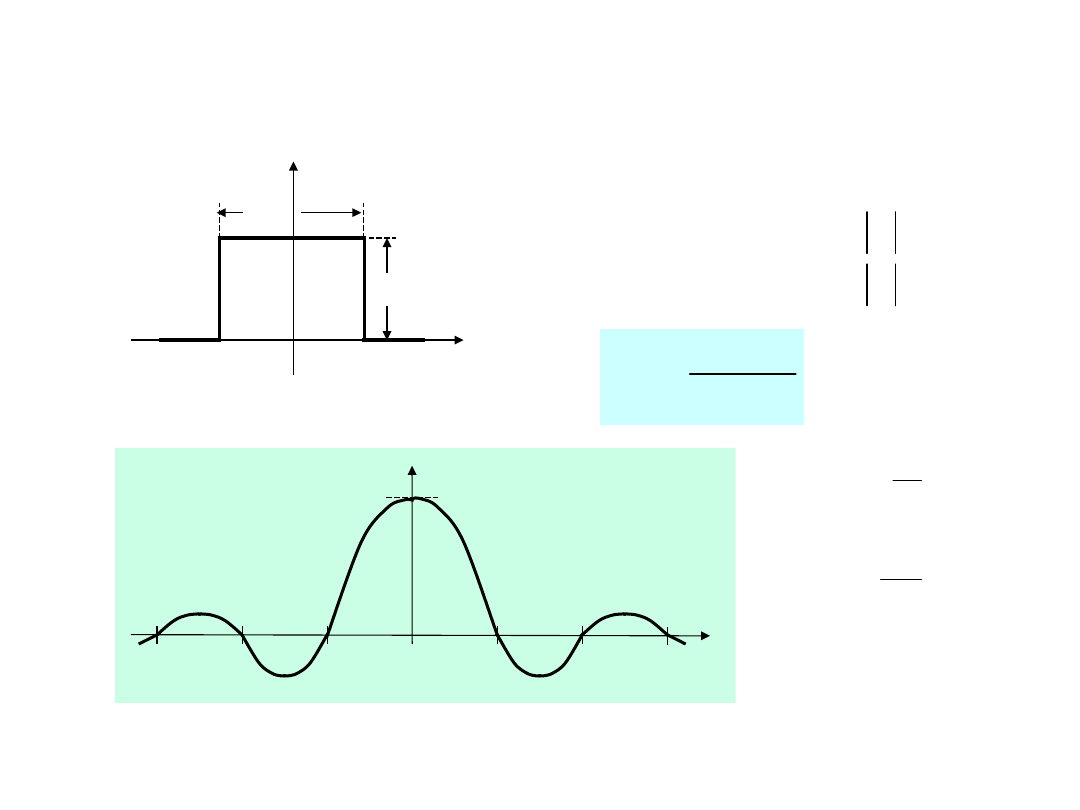
Impuls o widmie
prostokątnym
0
0
dla
0
dla
T
j
S
TD6-25 / 31
T
S( j
)
2
0
0
-
0
t
t
t
x
0
0
sin
0
0
T
T
x(t
)
0
1
t
T
2T
3T
-T
-2T
-3T

Impuls o widmie
ograniczonym
)
1
(
dla
0
)
1
(
)
1
(
dla
1
2
sin
1
2
)
1
(
dla
0
0
0
0
0
T
T
j
S
0
0
T
T
TD6-26 / 31
T
S( j
)
0
(1)
-
0
0,5T
0
(1+)
0
-
0
(1)
-
0
(1+)
t
t
t
t
t
x
0
0
2
0
2
0
sin
1
cos
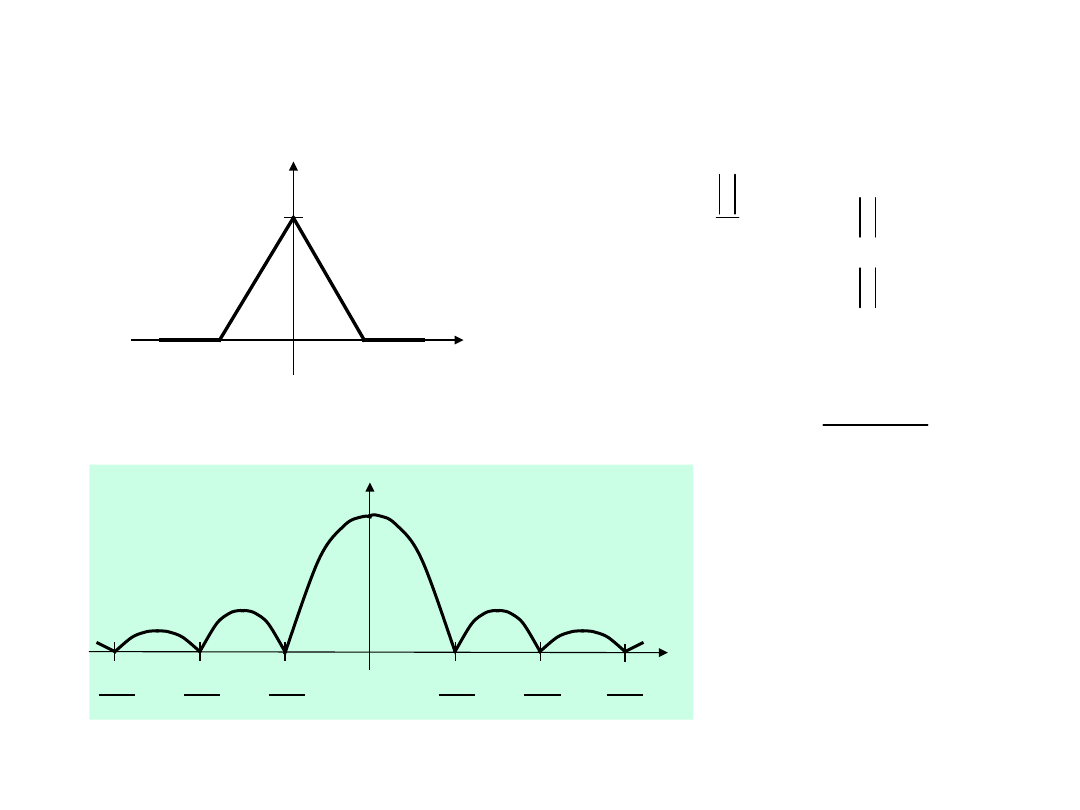
Impuls trójkątny
TD6-37 / 31
t
t
t
A
t
x
dla
0
dla
1
2
sin
A
j
S
x(t
)
A
t
-
S(j)
1
=
2
f
2
3
-1
-3
-2
0
A
f
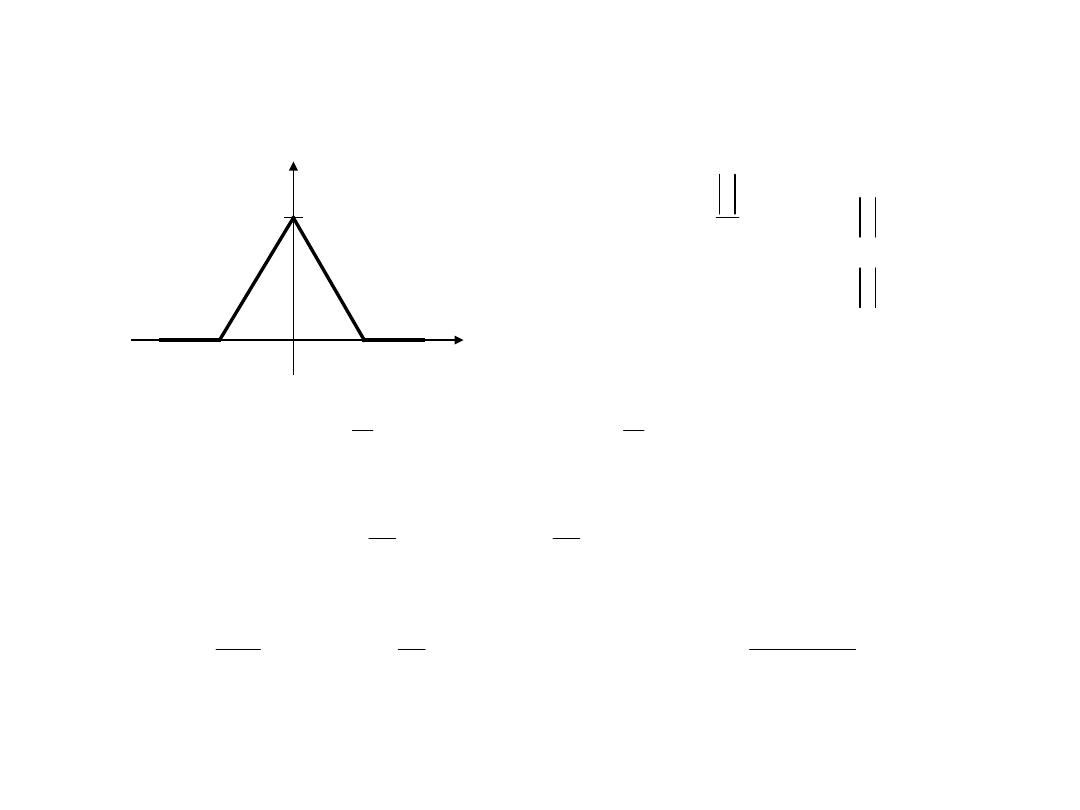
Impuls trójkątny
TD6-28 / 31
t
t
t
A
t
x
dla
0
dla
1
2
0
0
0
0
0
sin
sin
2
1
1
A
dt
t
A
A
dt
t
A
dt
t
A
dt
A
dt
t
A
dt
t
A
j
S
e
e
e
e
e
e
e
t
j
t
j
t
j
t
j
t
j
t
j
t
j
x(t
)
A
t
-
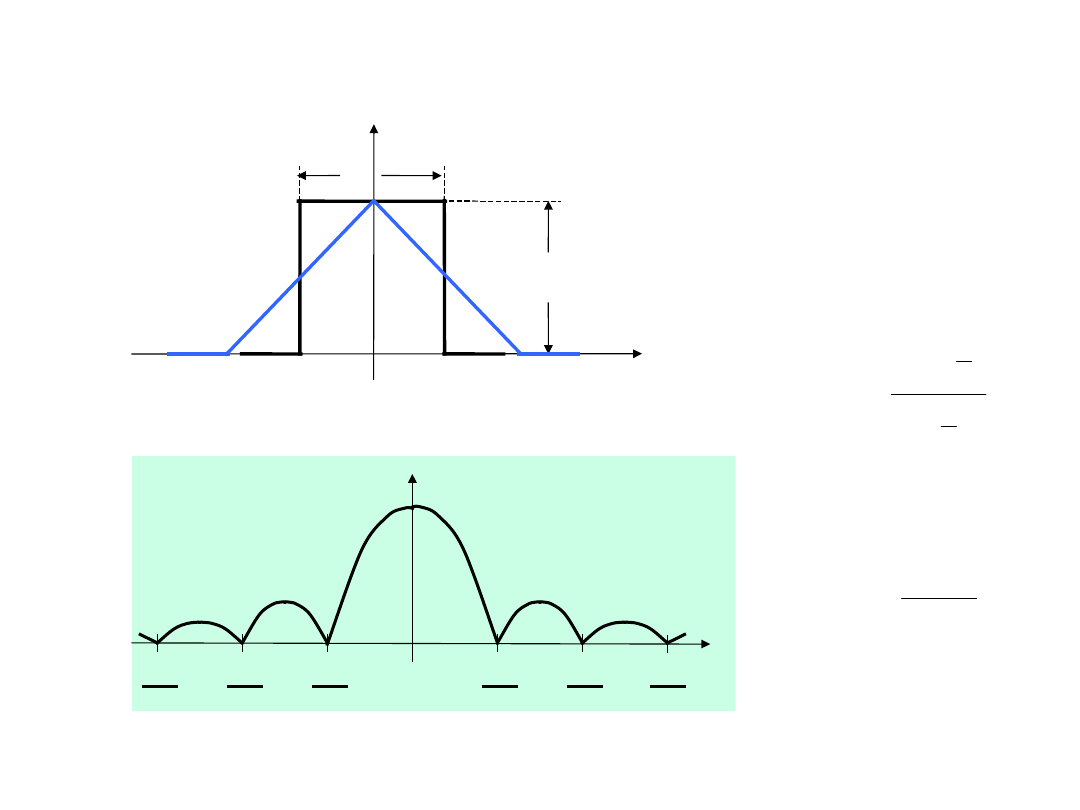
Impuls trójkątny i
prostokątny
2
2
sin
)
(
A
j
S
TD6-29 / 31
|S(j)|
1
=
2
f
2
3
-1
-3
-2
0
A
f
A
x(t
)
2
2
t
-
2
sin
A
j
S
Impuls prostokątny
Impuls trójkątny
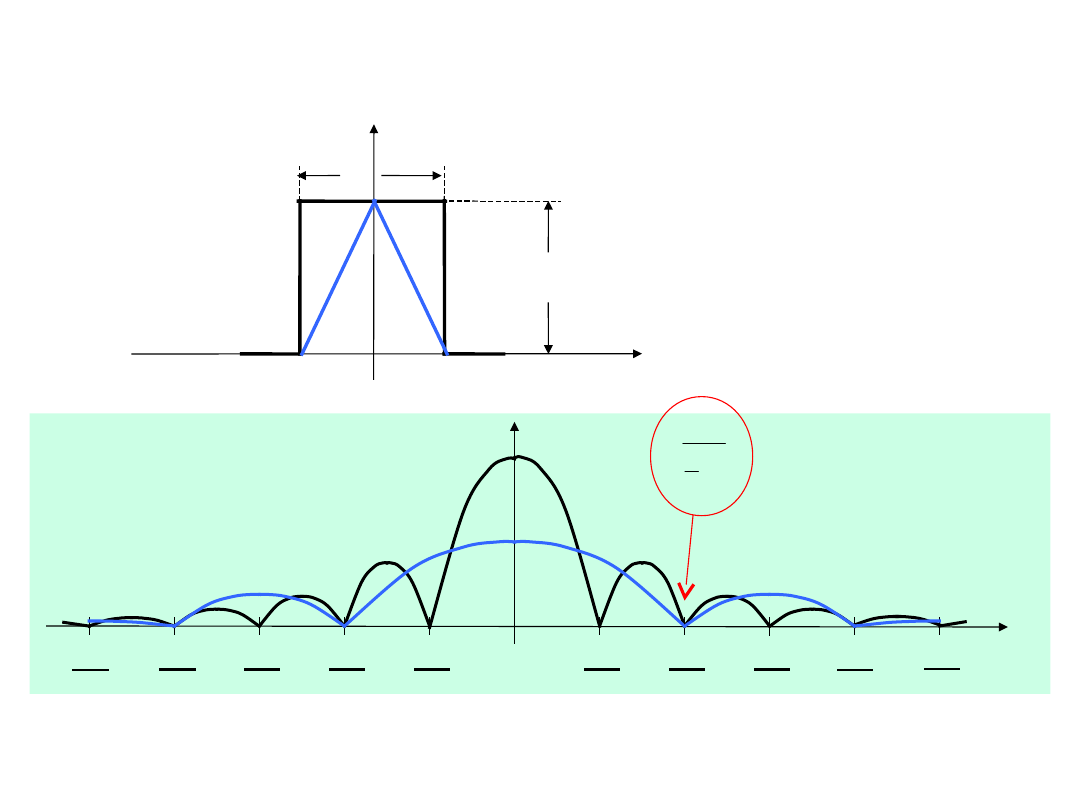
Impuls trójkątny i
prostokątny
TD6-30 / 31
A
x(t
)
2
2
t
|S(j)|
1
=
2
f
2
3
-1
-3
-2
0
A
f
4
5
-5
-4
2
1
1
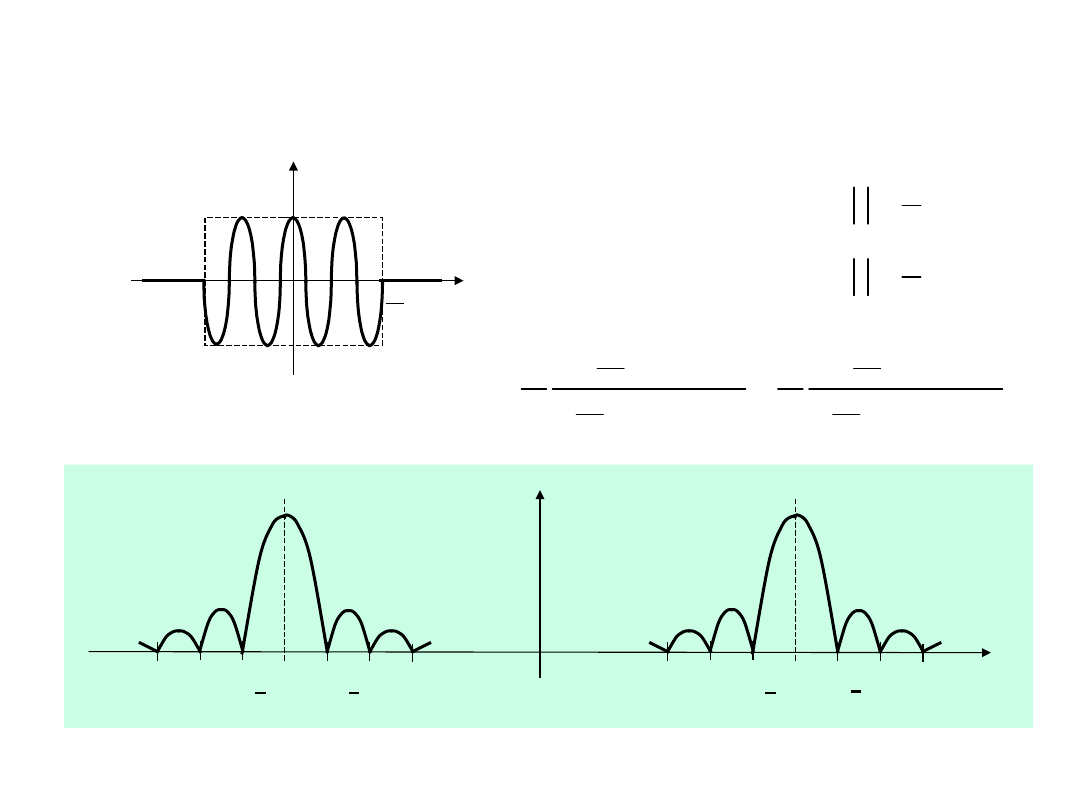
Impuls sinusoidalny RF
2
dla
0
2
dla
cos
0
t
t
t
A
t
x
t
t
A
t
t
A
j
S
0
2
0
2
0
2
0
2
sin
2
sin
2
TD6-31 / 31
x(t
)
A
t
2
2
|S(j)|
=
2
f
0
=2
f
0
f
f
0
1
f
0
+
1
f
0
–
-f
0
1
-f
0
+
1
-f
0
–
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
Wyszukiwarka
Podobne podstrony:
Hydronic D5WZ 25 2216 TD 06 2003 JE
TD 01
MT st w 06
Kosci, kregoslup 28[1][1][1] 10 06 dla studentow
06 Podstawy syntezy polimerówid 6357 ppt
06
06 Psych zaburz z somatoformiczne i dysocjacyjne
GbpUsd analysis for July 06 Part 1
Probl inter i kard 06'03
06 K6Z4
06 pamięć proceduralna schematy, skrypty, ramyid 6150 ppt
Sys Inf 03 Manning w 06
Ustawa z dnia 25 06 1999 r o świadcz pien z ubezp społ w razie choroby i macierz
więcej podobnych podstron