Relacje binarne

Definicja
Niech X i Y będą dowolnymi zbiorami. Dowolny
podzbiór R zbioru X  Y nazywamy relacją binarną

(dwuargumentową, dwuczłonową) na zbiorze X  Y.
UWAGA: Ponieważ R XY, R jest zatem zbiorem par

uporządkowanych. Jeśli xX, yY oraz <x,y>R

to mówimy, że x jest w relacji (R) z y. Inny zapis to x R y.

Relacją n-członową nazywamy relację, której
wszystkie elementy są n-kami uporządkowanymi
RX

1

X

2

..X

n

Definicja
Mając dowolną relację R XY, zbiór D(R)={x : yY <x,y>R}

nazywamy dziedziną relacji R, zbiór V(R)={y : xX <x,y>R}

przeciwdziedziną relacji R, a zbiór D(R)V(R) polem relacji R.

Relacje binarne –

przykłady

Przykład Relacja < w zbiorze liczb rzeczywistych jest to
podzbiór produktu

R  R, do którego należą wszystkie pary <x,y> takie, że

x,yR i x<y.

Przykład Niech P(X) będzie niepustą rodziną zbiorów. Relacja
inkluzji jest

własnością par uporządkowanych <A,B>

takich, że

A B oraz A, B P(X). Jest to relacja binarna w P(X) 

P(X).

UWAGA: Elementy należące do relacji posiadają
zatem jakieś

szczególne własności

(takie, jakie definiuje relacja).

Inne przykłady:

Podzielność liczb w zbiorze liczb naturalnych

Równoległość prostych na płaszczyźnie
Stosunki pokrewieństwa pomiędzy ludźmi („być ojcem”)

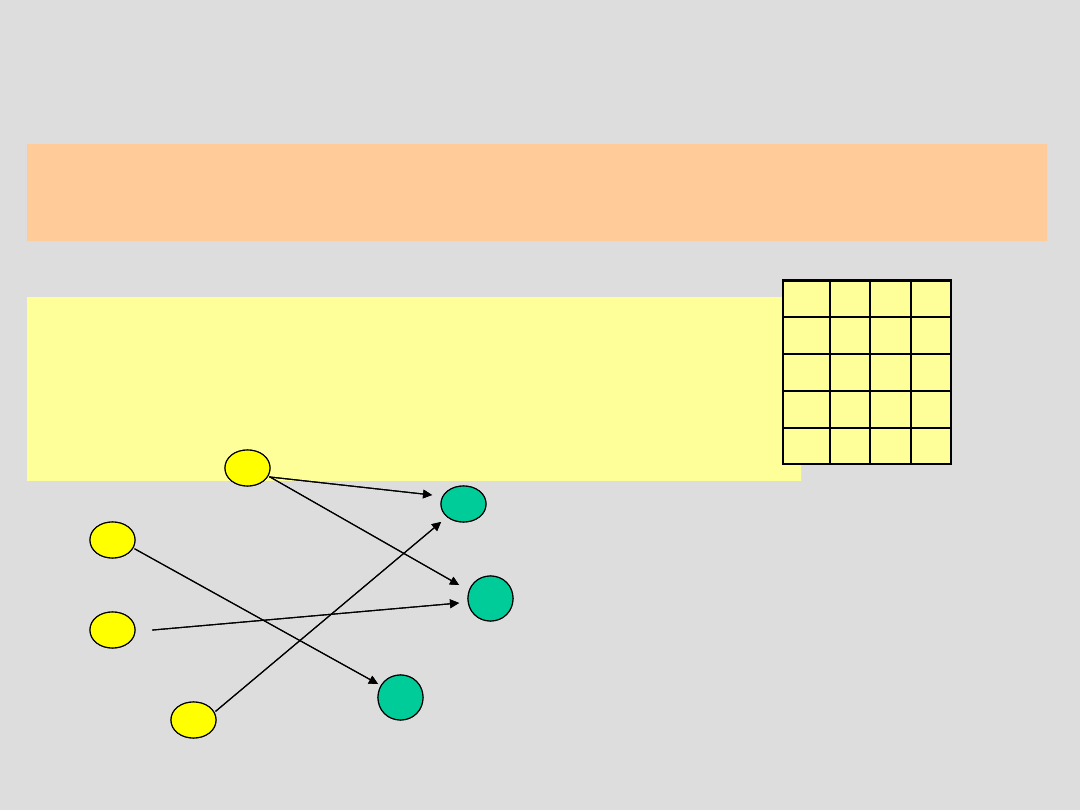
Relacje binarne –

reprezentacje

UWAGA: Każdą relację binarną określoną w zbiorze skończonym

można przedstawić w postaci macierzowej lub diagramu

Niech X= {1,2,3,4} i Y = {5,7,8} oraz R
XY

R={<1,5>, <3,7>, <2,8>, <4,5>,
<1,7> }

5 7 8

1 + +
2 +
3 +
4 +

5

7

1

2

3

4

8

5

7

1

2

3

4

8

Specjalne rodzaje

relacji binarnych

Rozważmy relację RXX
R jest zwrotna w X, jeśli xX <x,x>R
R jest przeciwzwrotna w X, jeśli xX <x,x>R
R jest symetryczna w X, jeśli x,yX <x,y>R <y,x>R
R jest antysymetryczna w X, jeśli

x,yX <x,y>R  <y,x>R  x=y

R jest przeciwsymetryczna w X, jeśli x,yX <x,y>R <y,x>R
R jest przechodnia w X, jeśli

x,y,zX <x,y>R  <y,z>R  <x,z> R

R jest spójna w X, jeśli x,yX <x,y>R  <y,x>R  x=y

Odwracanie i składanie

relacji

Definicja
Jeżeli R jest relacją binarną w X  Y, to R

-1

jest

relacją binarną w
Y  X, zdefiniowaną następująco: R

–1

={<y,x> :

<x,y>R }.

Definicja
Jeśli RXY oraz SYZ, to relację

T={<x,z> : y <x,y>R  <y,z>S} nazywamy

złożeniem relacji R i S (zamiast T można zapisać SR).

Przykład: L zbiór ludzi RLL

R={<x,y> : x dzieckiem y}

R

-1

={<x,y> : x jest rodzicem y}

Relacja równoważności

Definicja
Relację RXX nazywamy relacją równoważności

wttw R jest relacją zwrotną, symetryczną i
przechodnią.

Przykłady

1. L – zbiór wszystkich prostych na płaszczyźnie, RLL l, hL l R h  l || h

2. L – zbiór chorych RLL l, hL

l R h  l jest chory na tę samą chorobę co h

3. L – zbiór samochodów RLL l, hL

l R h  l został wyprodukowany przez tę samą firmę co h

Skoda

Mazda

Toyota

Fiat

Klasa abstrakcji

Definicja
Niech R będzie relacją równoważności w zbiorze X,
wtedy dla dowolnego x X, zbiór [x]

R

= {y  X : x R y}

nazywamy klasą
abstrakcji relacji R o reprezentancie x.

Stwierdzenie
Jeżeli R jest relacją równoważności w zbiorze X, to

dla dowolnych x,y



X, prawdziwe są następujące

warunki:
x



[x]

[x] = [y] wttw x R y
Jeżeli [x]  [y] , to [x]  [y] = 

UWAGA: Zbiór wszystkich klas abstrakcji relacji R w X oznacza się

X\R i nazywa się zbiorem ilorazowym

Zasady abstrakcji

Definicja
Rodzinę P podzbiorów zbioru X nazywamy podziałem

zbioru

X wttw
i) F dla każdego FP

ii) P=X

iii) i,j F

i

F

j

 F

1

 F

2

=

Twierdzenie
Każda relacja równoważności R w zbiorze X ustala podział tego

zbioru. Podział ten tworzą klasy abstrakcji tej relacji (relacji R).
Zachodzi również twierdzenie odwrotne
Każdy podział H={ H

i

: iI } zbioru X wyznacza relację

równoważności R

H

w zbiorze X, w myśl wzoru

x, y  X x R

H

y  iI ( xH

i

 yH

i

)

Skoda

Mazda

Toyota

Fiat

Funkcja jako relacja

Definicja
Niech X i Y będą dowolnymi zbiorami. Relację RXY nazywamy

Funkcją, jeśli spełnia ona następujące warunki:
i) xX yY x R y

ii) xX y

1

,y

2

Y ( x R y

1

 x R y

2

)  y

1

=y

2

UWAGA: To jedyne y, które pozostaje w relacji z x oznaczamy

R(x). Zazwyczaj funkcje oznaczamy jako f, g, h itd.

Funkcja różnowartościowa (injekcja)

x,yX [ f(x)=f(y) ]  x=y

Funkcja „na” (surjekcja)

yY xX ( y=f(x) )

Odwzorowanie wzajemnie jednoznaczne (bijekcja)

injekcja + surjekcja

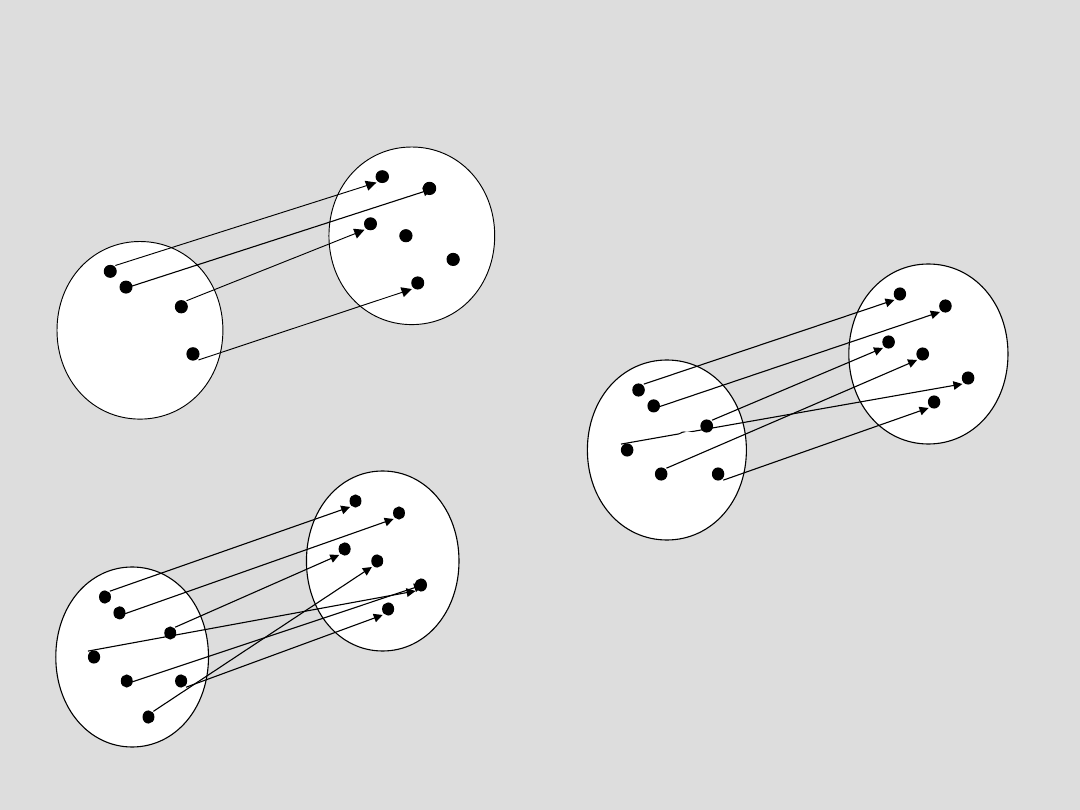
Przykłady funkcji

Y

X

„na”

różnowartościowa

Y

X

Y

X

odwzorowanie
wzajemnie jednoznaczne

Y

X

Obraz i przeciwobraz

zbioru

Definicja
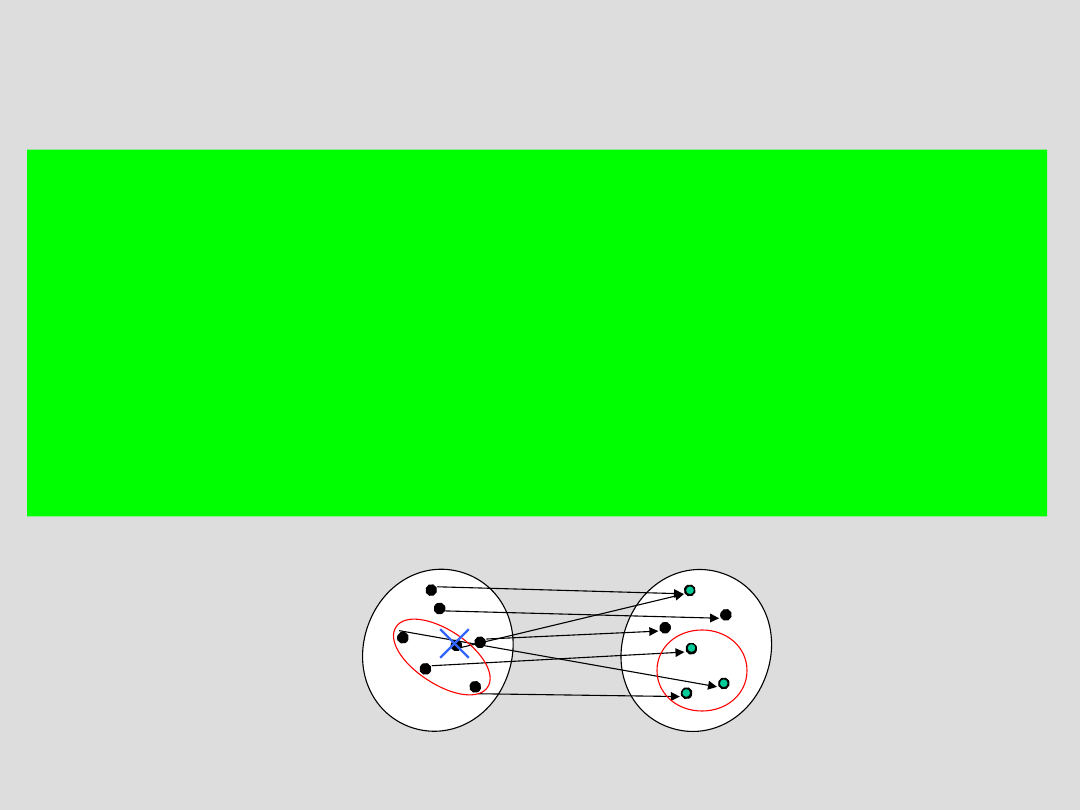
Załóżmy, że AX oraz fXY (f:XY) jest funkcją.

Obrazem zbioru A przez funkcję f nazywamy zbiór

f(A)={y : xA y=f(x) }

Definicja
Załóżmy, że ZY oraz fXY (f:XY) jest funkcją.

Przeciwobrazem zbioru Z przez funkcję f nazywamy zbiór

f

-1

(Z)={x : yZ f(x)=y }

z

Relacje porządkujące

Definicja
Relację binarną R w zbiorze X nazywamy porządkiem
(częściowym porządkiem) wttw R jest relacją zwrotną,
antysymetryczną i przechodnią.

Przykłady

1. R – rodzina zbiorów <R, >

2. Zbiór N jest uporządkowany przez relację podzielności
n | m  n jest dzielnikiem m

3. Każdy niepusty podzbiór zbioru R uporządkowany jest przez relację 

Zbiór X wraz z porządkiem R nazywamy zbiorem
uporządkowanym. Ozn. <X, R>.

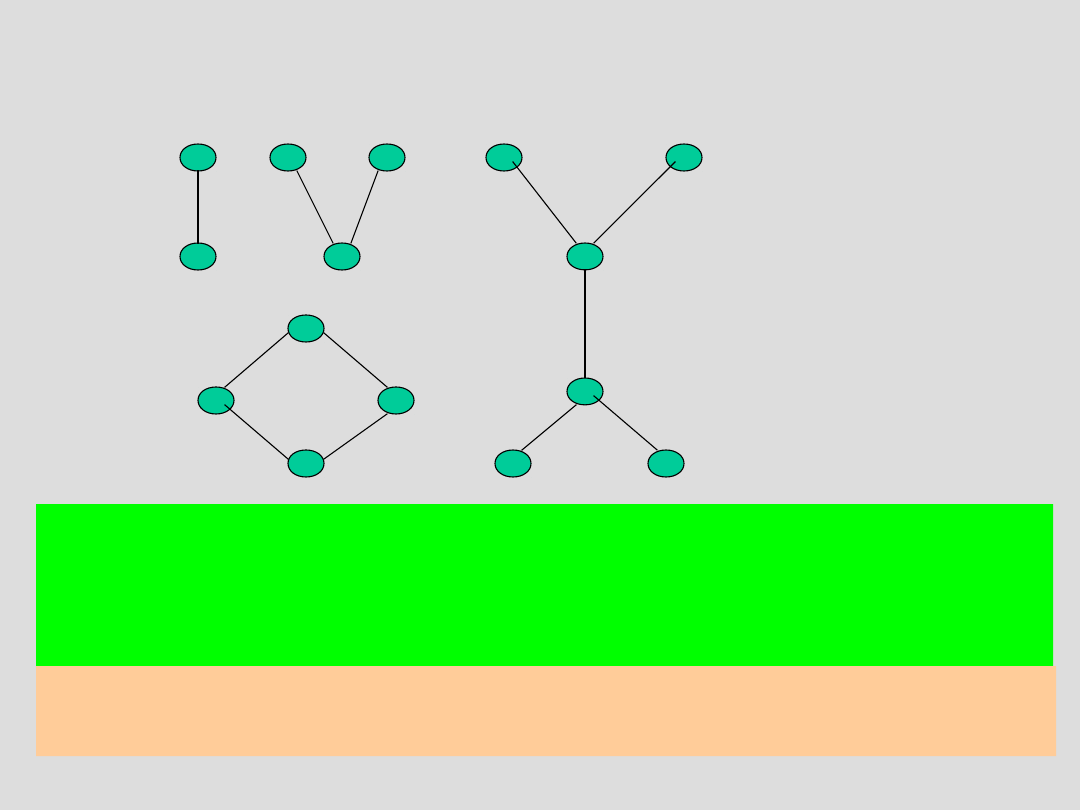
Reprezentacja graficzna

b

a

b

a

c

b

d

c

a

a

c

b

d

f

e

Diagramy Hassego

1. a R b – a znajduje się poniżej b
2. a

i

R a

j

- od a

i

do a

j

prowadzi łamana skierowana w górę

UWAGA: Skończoność zbioru X gwarantuje istnienie
Diagramu Hassego dla <X, R>.

Elementy wyróżnione

Definicja
Niech <X, R> jest zbiorem uporządkowanym
1. Element a X nazywamy maksymalnym w zbiorze <X, R> wttw

xX, (a R x  x=a)

2. Element a X nazywamy minimalnym w zbiorze <X, R> wttw

xX, (x R a  x=a)

Definicja
Niech <X, R> jest zbiorem uporządkowanym
1. Element a X nazywamy największym w zbiorze <X, R> wttw

xX, x R a

2. Element a X nazywamy najmniejszym w zbiorze <X, R> wttw

xX, a R x

Elementy wyróżnione

cd.

Twierdzenie
W zbiorze uporządkowanym <X, R> istnieje co najwyżej
jeden element największy (najmniejszy).
Element największy (najmniejszy) jest maksymalny (minimalny)
Dowód: ćwiczenia

Definicja
Jeśli relacja R spełnia warunki porządku częściowego oraz jest
relacją spójną, to R nazywamy relacją liniowo porządkującą

Definicja
Niech dany jest zbiór uporządkowany <X, R>
Podzbiór AX, nazywamy łańcuchem jeśli,

x,yA, ( x R y  y R x )

Czyli łańcuch

jest liniowo

uporządkowany

Kresy

Definicja
Niech AX, gdzie <X, R> zb. up. Element x

0

nazywamy ograniczeniem

górnym (dolnym) zbioru A, jeśli

 xA, x R x

0

( x

0

R x )

Najmniejsze ograniczenie górne zbioru A (jeśli istnieje)
nazywamy
kresem górnym zbioru A (sup A)
Największe ograniczenie dolne zbioru A (jeśli istnieje)
nazywamy
kresem dolnym zbioru A (inf A).

Twierdzenie
W każdym niepustym skończonym zbiorze liniowo
uporządkowanym istnieje element największy (ostatni)
i element najmniejszy (pierwszy)

Porządek leksykograficzny

Definicja
Niech <X

1

,R

1

>,.,<X

n

,R

n

> są zbiorami częściowo uporządkowanymi.

Relację R

*

określoną w produkcie X

1

X

2

..X

n

:

 
<x

1

,x

2,

..,x

n

> R

*

<y

1

,y

2

,..,y

n

> wttw albo dla wszystkich in x

i

=y

i

albo istnieje takie k (0<kn), że dla 0<i<k, x

i

=y

i

oraz x

k

R

k

y

k

, x

k

y

k

nazywamy porządkiem leksykograficznym w X

1

X

2

..X

n

.

Przykład

Mamy ={a,b,..,z}, na którym określamy zwykły porządek liniowy liter w alfabecie.

Wówczas R

*

określona w 

m

, mN jest zwykłym porządkiem alfabetycznym w 

m

.

 
kos R

*

kot R

*

ros

Porządek słownikowy

Definicja
Niech  będzie ustalonym alfabetem uporządkowanym liniowo

przez relację R. W zbiorze 

*

(wszystkich słów nad alfabetem ),

definiujemy relację porządku słownikowego R

L

:

 

<x

1

,..,x

n

> R

L

<y

1

,..,y

m

> wttw albo nm i dla wszystkich i (1<in) x

i

=y

i

albo istnieje takie k (1<kmin(n,m)), że dla każdego i (0<i<k) x

i

=y

i

oraz x

k

Ry

k

, dla x

k

y

k

Przykład

kos R

L

kosa R

L

ros R

L

rosomak

Alfabet identyczny jak w poprzednim przypadku, nie zakładamy długości słów