Układy funkcyjne.

Kształtowanie

przebiegów nieliniowych

mk, 2006

Układy funkcyjne

1. Układy funkcyjne (przekształtniki) służą do

nieliniowego przekształcania sygnałów

• realizacja funkcji nieliniowych, jednej lub wielu

zmiennych

Układy funkcyjne

2. Typowe zastosowania układów funkcyjnych:

• aproksymacja funkcji nieliniowych,
• przekształcanie sygnałów (np. zamiana fali trójkątnej w

przebieg sinusoidalny),

• modulacja i demodulacja, itd.
• prostowanie, obcinanie i  ograniczanie,
• logarytmowanie i  delogarytmowanie,
• potęgowanie i pierwiastkowanie (ogólnie - funkcje

potęgowe),

• mnożenie i dzielenie sygnałów,
• obliczanie modułu, wartości maksymalnej, itp.

Układy funkcyjne

3. Przekształcane są napięciowe lub prądowe

sygnały analogowe:

• stałoprądowe

• wolnozmienne (wąskopasmowe)

• szybkozmienne (szerokopasmowe)

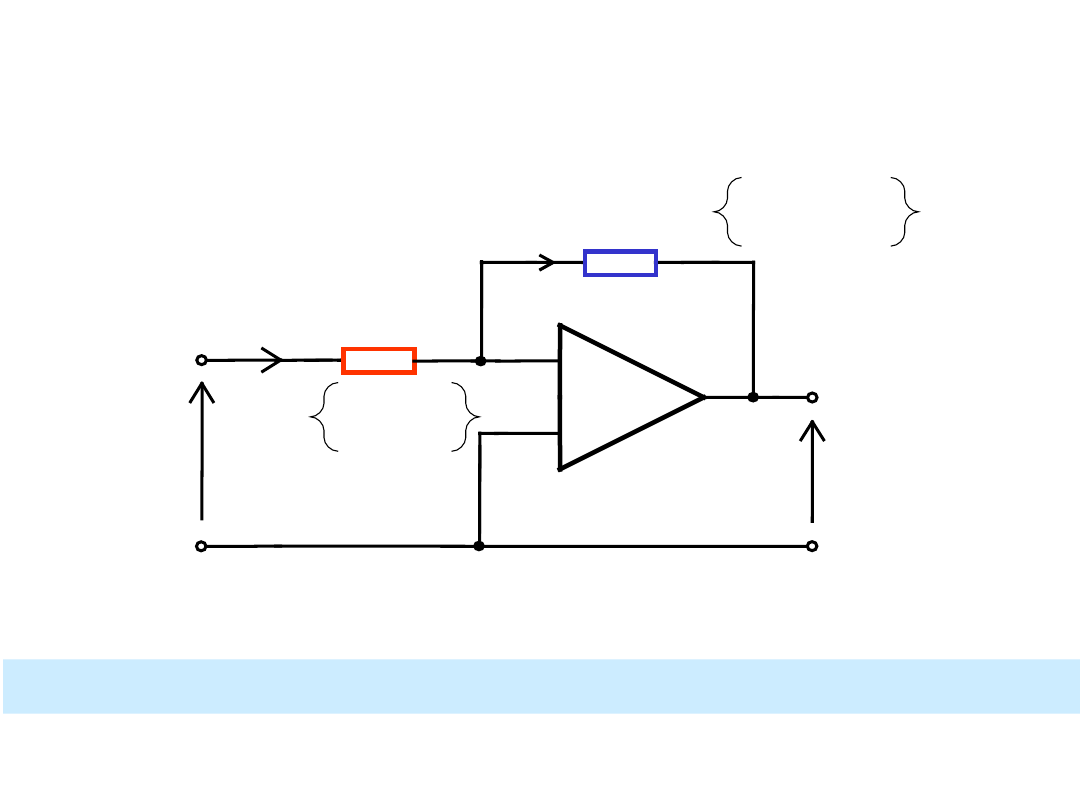
Zasada działania układów funkcyjnych

ze wzmacniaczem operacyjnym

Struktura układu funkcyjnego; R1 albo R2 jest nieliniowy

R1

R2

U

I

U

1

1

2

-

+

I

2

= f(U

2

)

I

1

= f(U

1

)

I

2



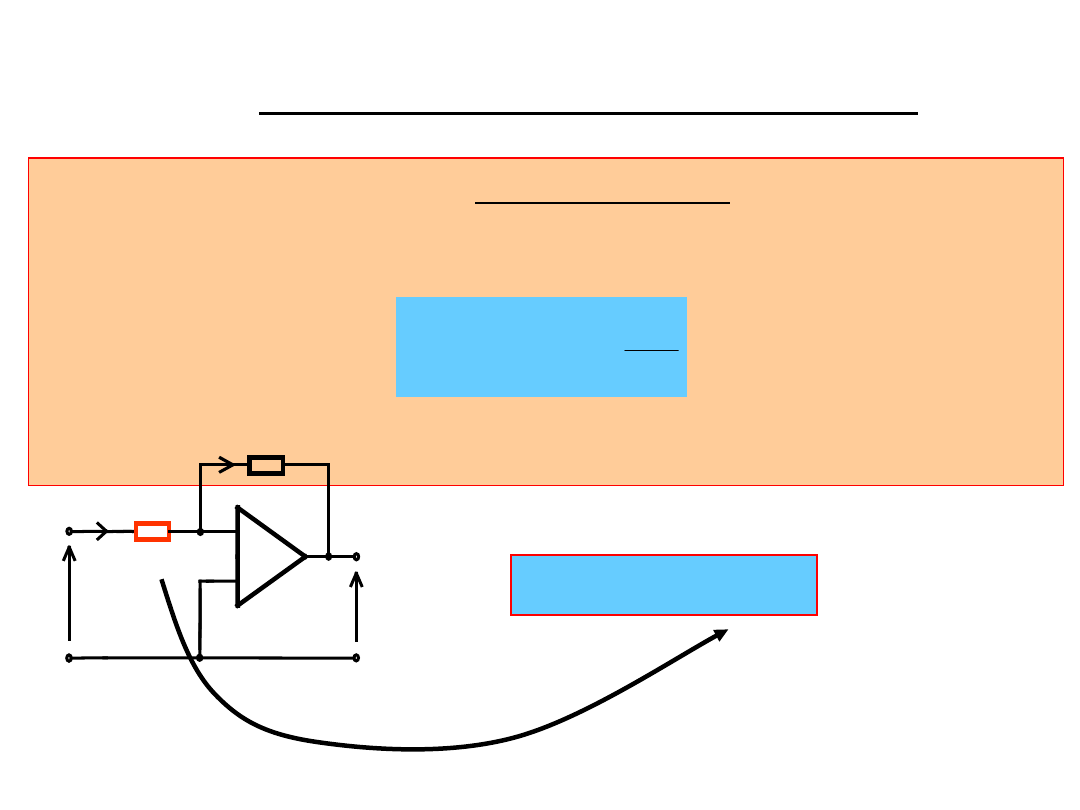
Zasada działania układu funkcyjnego:

tzw. METODA FUNKCJI JAWNEJ

Układ realizuje metodę funkcji jawnej, gdy rezystor R2
jest liniowy, a

R1

- nieliniowy o charakterystyce

prądowo - napięciowej I

1

=f(U

1

).

Prąd I

1

( = I

2

) wynosi:

Układ ten realizuje bezpośrednio funkcję:

)

U

(

f

R

U

1

2

2







R1

R2

U

I

U

1

1

2

-

+

I

1

= f(U

1

)

I

2



2

R

U

)

U

(

f

I

2

1

1







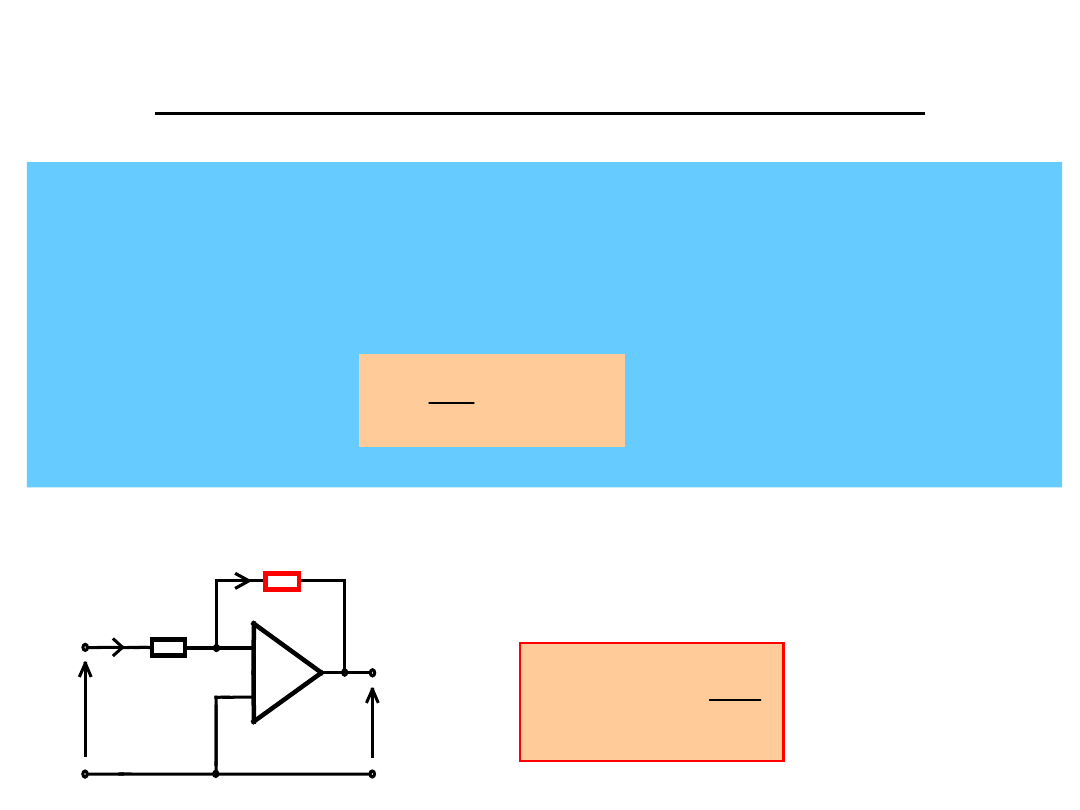
Zasada działania układu funkcyjnego:

METODA FUNKCJI ODWROTNEJ

Funkcję odwrotną uzyskuje się gdy rezystor R1 jest
liniowy, a

R2

nieliniowy, opisany równaniem I

1

f(U

2

)

(zakładamy, że funkcja ta jest ściśle monotoniczna).

Prąd I

1

jest równy:

)

R

U

(

f

U

1

1

1

2







R1

R2

U

I

U

1

1

2

-

+

I

2

= f(U

2

)

I

2



Układ realizuje funkcję odwrotną:

)

U

(

f

1

R

U

I

2

1

1







Realizacja nieliniowych układów funkcyjnych

metodą funkcji odwrotnej i jawnej

na przykładzie u. logarytmujacego i delogarytmujacego

W metodzie

f. jawnej

wykorzystuje się

wprost

charakterystyki

prądowo-napięciowe elementów półprzewodnikowych

(diod, diod Zenera, tranzystorów unipolarnych,

bipolarnych, itp.)

albo charakterystyki złożonych układów (np.

charakterystykę przejściową I

C

(U

WEr

) pary różnicowej).

W metodzie

f. odwrotnej

wykorzystuje się

odwrotność

funkcji opisującej charakterystyki prądowo-napięciowe

elementów półprzewodnikowych (diod, diod Zenera,

tranzystorów unipolarnych, bipolarnych, itp.)

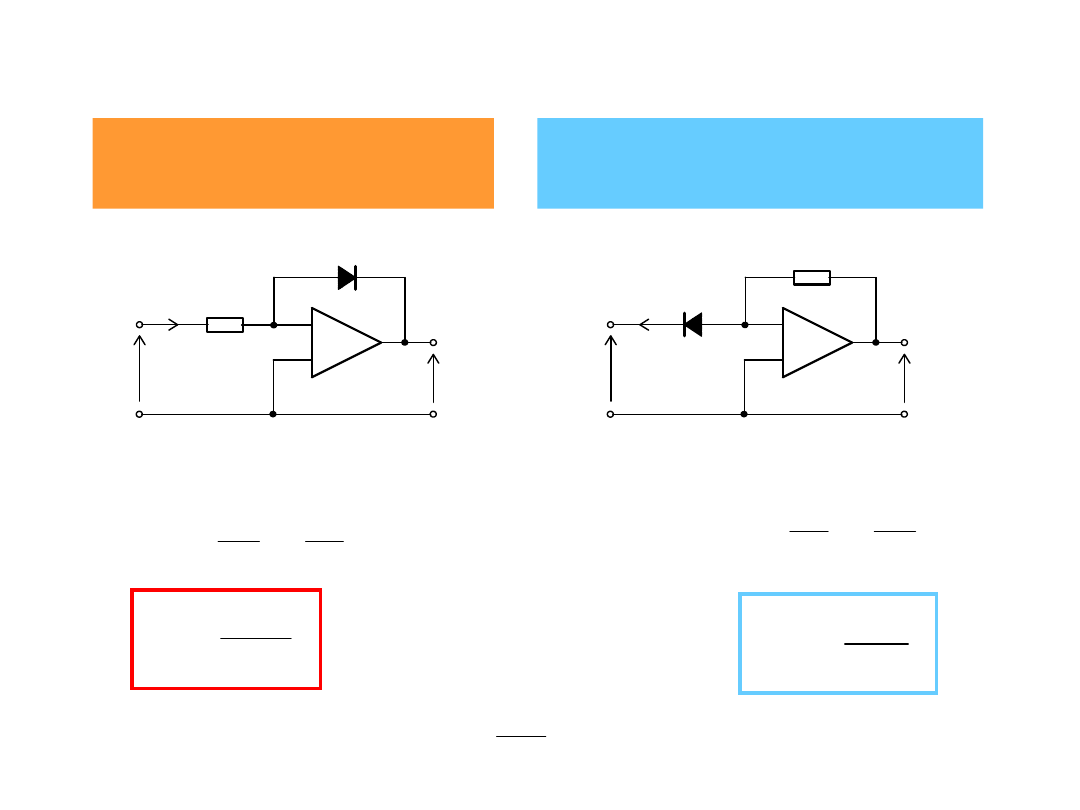
Układ logarytmujący i delogarytmujący z diodami

Układ logarytmujący

(funkcja odwrotna)

Układ delogarytmujący

(funkcja jawna)

1

1

T

2

s

R

U

U

exp

I

I























U

exp

I

R

U

T

1

s

1

2













































s

1

1

T

2

I

R

U

ln

U

mV

25

e

T

k

T









R1

D

U

I

U1

2

-

+

R1

D

U

I

U1

2

-

+

U

WE

=0

U

WE

=0

1

2

T

1

s

R

U

U

exp

I

I























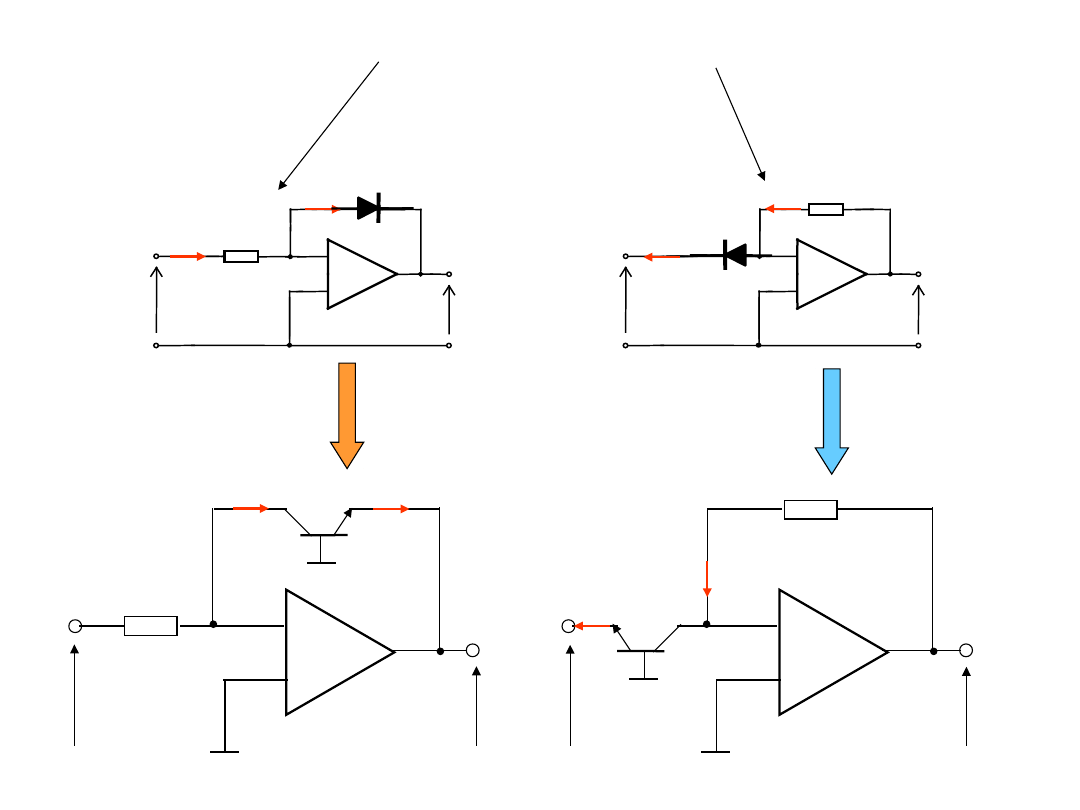
Układ logarytmujący i delogarytmujący

z tranzystorami

U

1

-

+

U

2

R1

T

U

1

-

+

U

2

T

R1

R1

D

U

I

U1

2

-

+

R1

D

U

I

U1

2

-

+

U

=0

U

=0

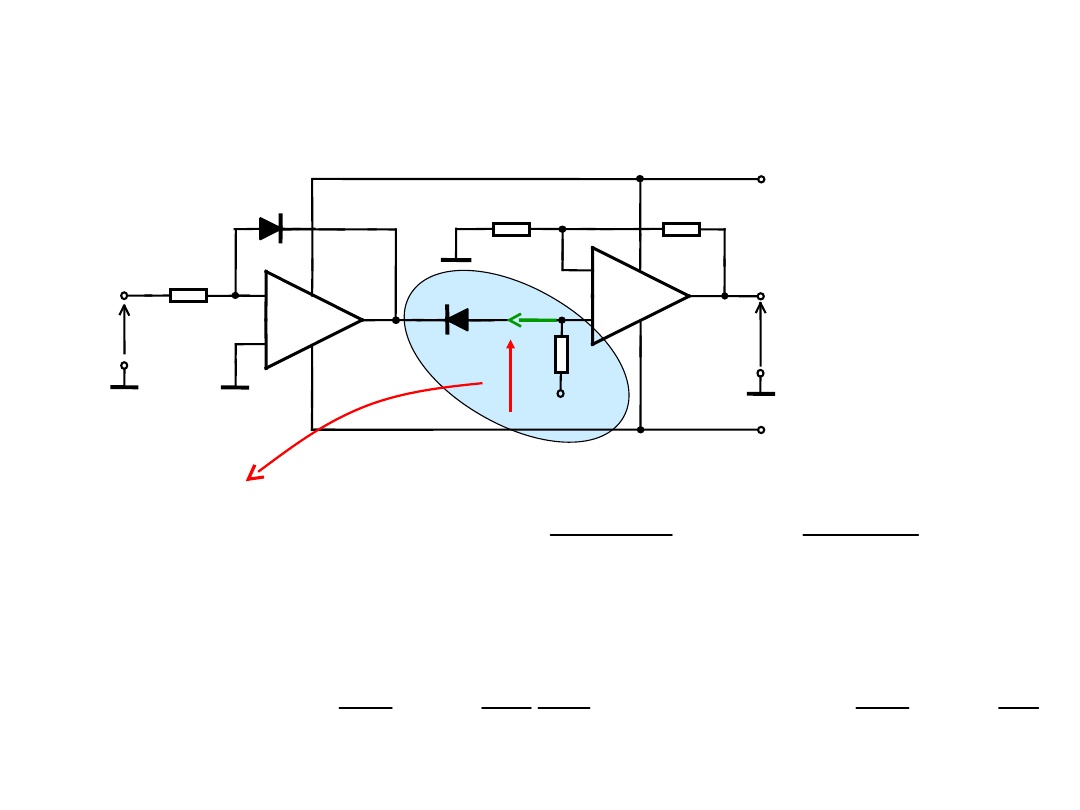
Układ logarytmujący z kompensacją termiczną

prądów zerowych diod D1 i D2

R1

U

+

Ucc (+15V)

Rp

R2

-

+

W2

W1

U

R3

U

D1

Uee (-15V)

+Up

D2

-

1

2

1

s

1

1

T

2

s

T

1

D

2

D

I

R

U

ln

I

Rp

Up

ln

U

U

U

























































































P

1

2

3

T

1

1

2

3

T

2

I

I

ln

R

R

1

)

T

(

Up

Rp

R

U

ln

R

R

1

)

T

(

U

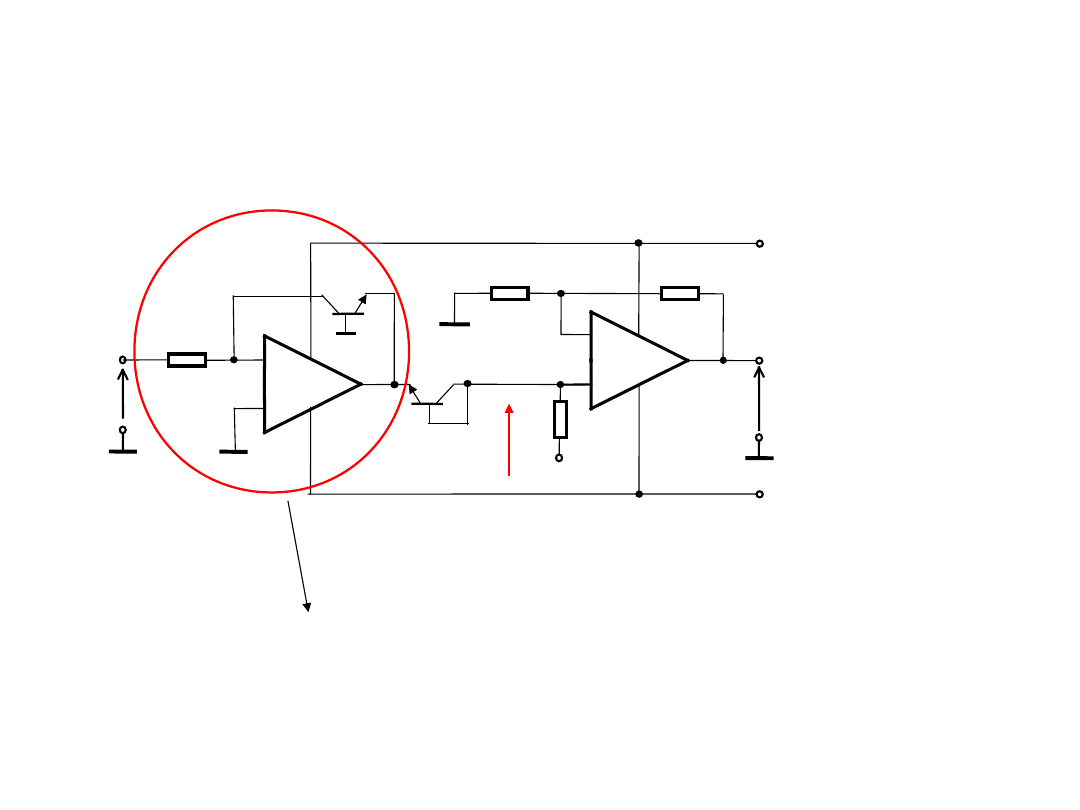
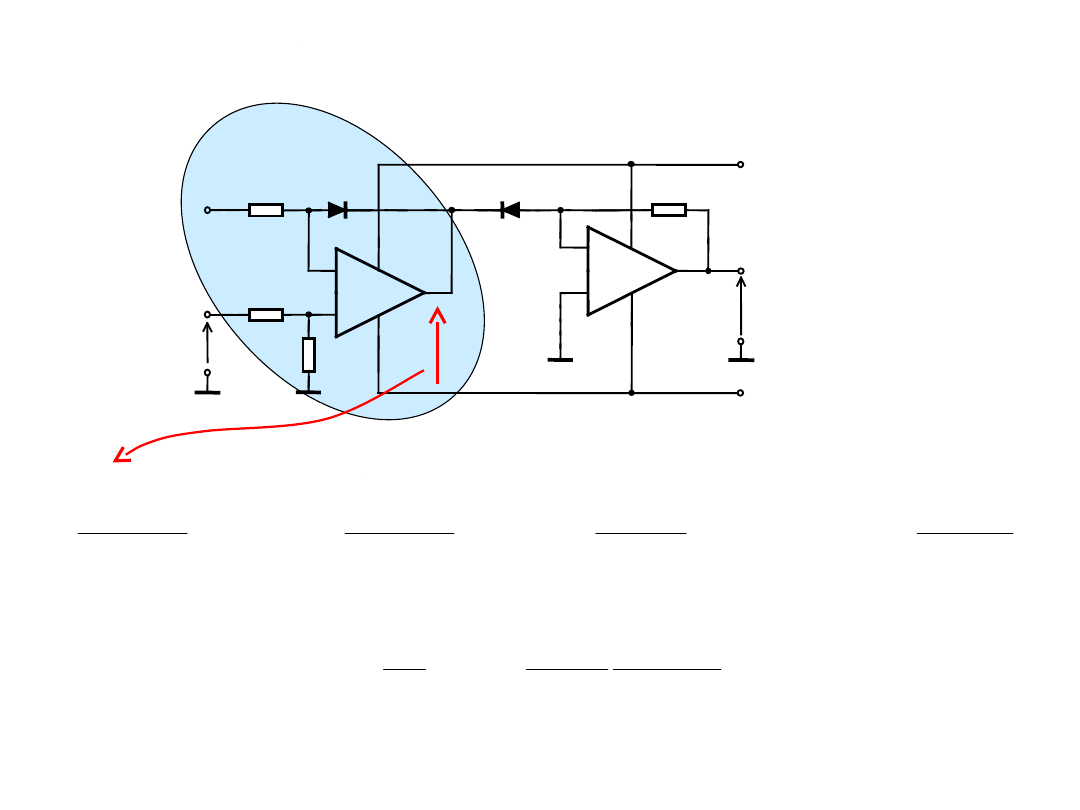
Układ logarytmujący z kompensacją termiczną

prądów zerowych i parą różnicową

R1

U

+

Ucc (+15V)

Rp

R2

-

+

W2

W1

U

R3

U

T1

Uee (-15V)

+Up

T2

-

1

2

STABILNOŚĆ !

Układ delogarytmujący

z kompensacją termiczną prądów zerowych diod

Rp

U

+

Ucc (+15V)

-

+

W2

W1

U

R3

U

D1

Uee (-15V)

+Up

D2

-

1

2

R2

R1

2

s

3

2

T

2

D

1

s

T

1

2

1

1

1

D

1

2

1

1

I

R

U

ln

U

I

Rp

Up

ln

U

R

R

R

U

U

R

R

R

U























































1

2

1

1

T

3

2

U

R

R

R

)

T

(

1

exp

Rp

Up

R

U

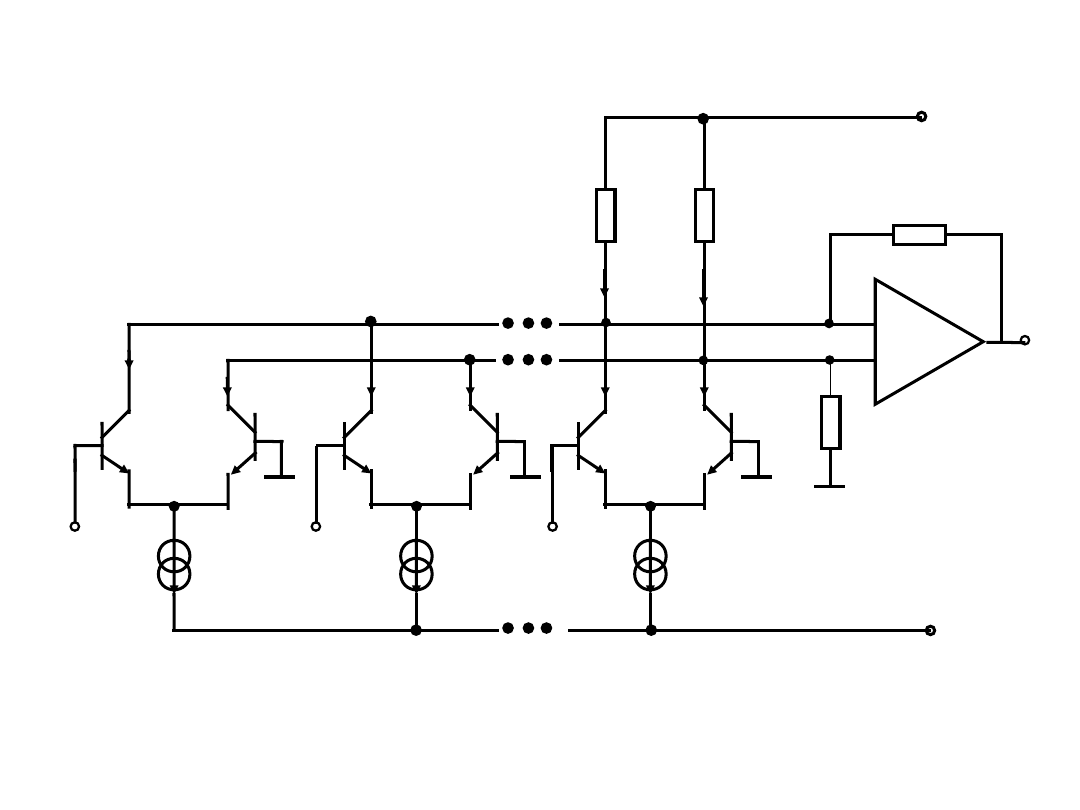
Szerokopasmowy układ logarytmujący

(metoda funkcji jawnej)

I

1A

I

2A

b

1

I

u

R1

=
α

1

u

I

I

1B

I

2B

b

2

I

U

0

I

nA

I

nB

b

n

I

-

+

R

0

R

0

R

C

R

C

u

R2

=

α

2

u

I

u

Rn

=

α

n

u

I

-E

EE

E

CC

T

1A

T

1

B

T

2A

T

2B

T

nA

T

nB

A

B

i

WA

i

WB



















T

R

R

2

u

h

tg

I

i

Dla każdej pary różnicowej, ze źródłem stałoprądowym w emiterze,
zachodzi związek:

gdzie : i

R

- różnicowy prąd kolektora

u

R

- wejściowe napięcie różnicowe

Dla n par różnicowych wynikowy prąd różnicowy I

WR

można

opisać zależnością:





































n

1

j

n

1

j

T

j

j

j

Rj

WB

WA

WR

2

u

h

tg

b

I

i

i

i

i

Wprowadzając zmienne unormowane

T

I

WR

2

u

x

;

I

i

y









otrzymujemy















n

1

j

j

j

x

h

tg

b

y

aproksymującą z założoną dokładnością funkcję logarytmiczną

x

lg

b

a

y







Wzmacniacz operacyjny spełnia rolę przetwornika przetwarzającego
prąd różnicowy i

WR

na napięcie wyjściowe u

0

.

Zapisując równania bilansów prądów dla węzłów A i B mamy :

WB

0

C

CC

WA

0

0

C

CC

i

R

u

R

u

E

i

R

u

u

R

u

E























Rozwiązując powyższy układ równań otrzymujemy

C

0

WR

0

R

R

1

K

K

i

u







Ponieważ

K >> 1 + R

0

/ R

C

,

otrzymujemy:

u

0

= i

WR

R

0

Układ monolityczny SN76502 :
- dwa układy logarytmiczne,
- każdy z układów składa się z czterech par
różnicowych (n=4),
- dokładność realizacji charakterystyki
logarytmicznej +/- 0,5 dB,
- zakres napięć wejściowych około 60 dB,
- częstotliwość graniczna f

3dB

= 40 MHz.

Układy mnożące i dzielące

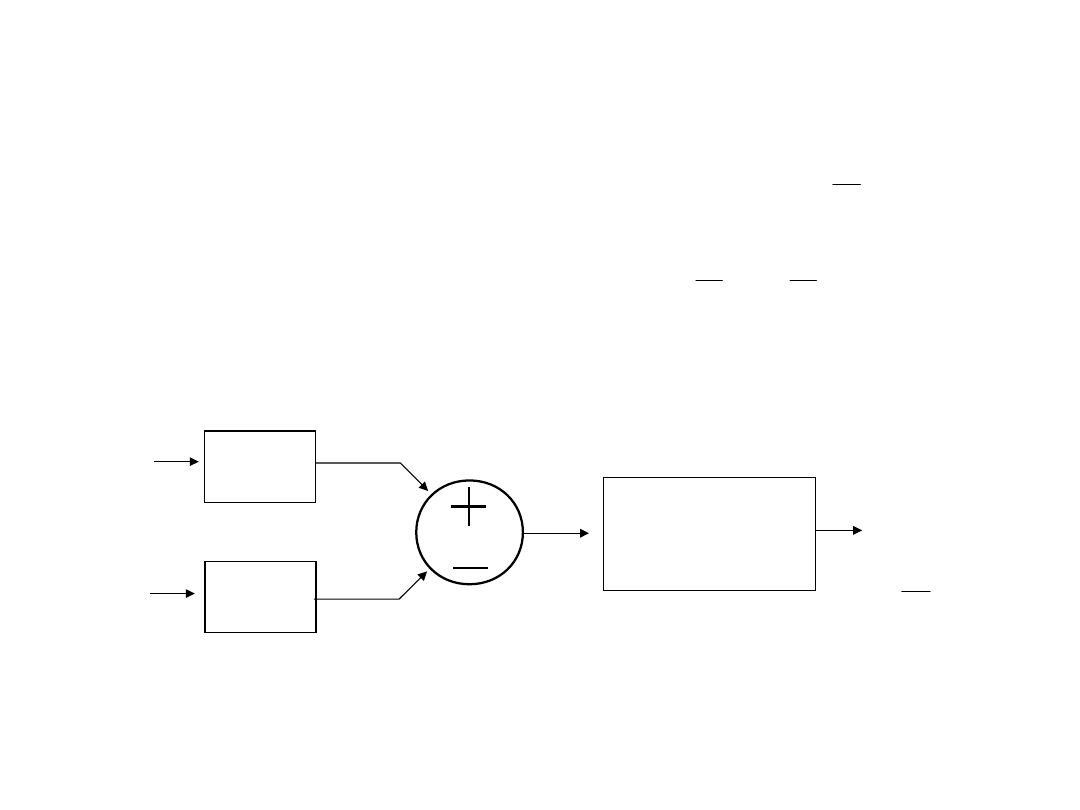
Zasada działania układów mnożących i

dzielących

)

y

x

ln(

y

ln

x

ln







y

x

)]

y

x

exp[ln(







)

y

x

ln(

y

ln

x

ln





y

x

)]

y

x

exp[ln( 

ln(x)

ln(y)

)

z

exp(

y

x 

z

y

x

x

y

lub

lub

Aproksymacja funkcji nieliniowych

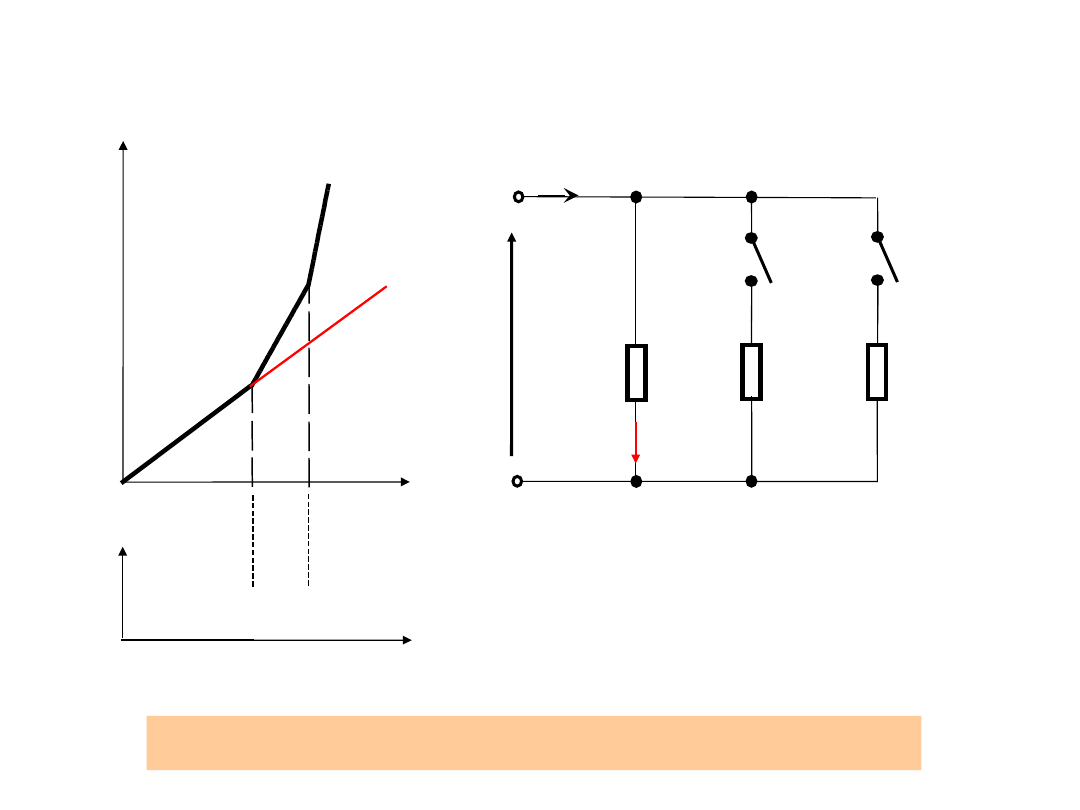
Aproksymacja funkcji odcinkami linii prostych

U

I

G2

G3

K2

I

U

U1

U2

G1

G1+G2

G1+G2+G3

K1

G1

K - klucze diodowe ( diody przełączające)

I

1

=G1U

I

2

=G2U

I

3

=G3U

I

1

I

2

I

3

U

1

0

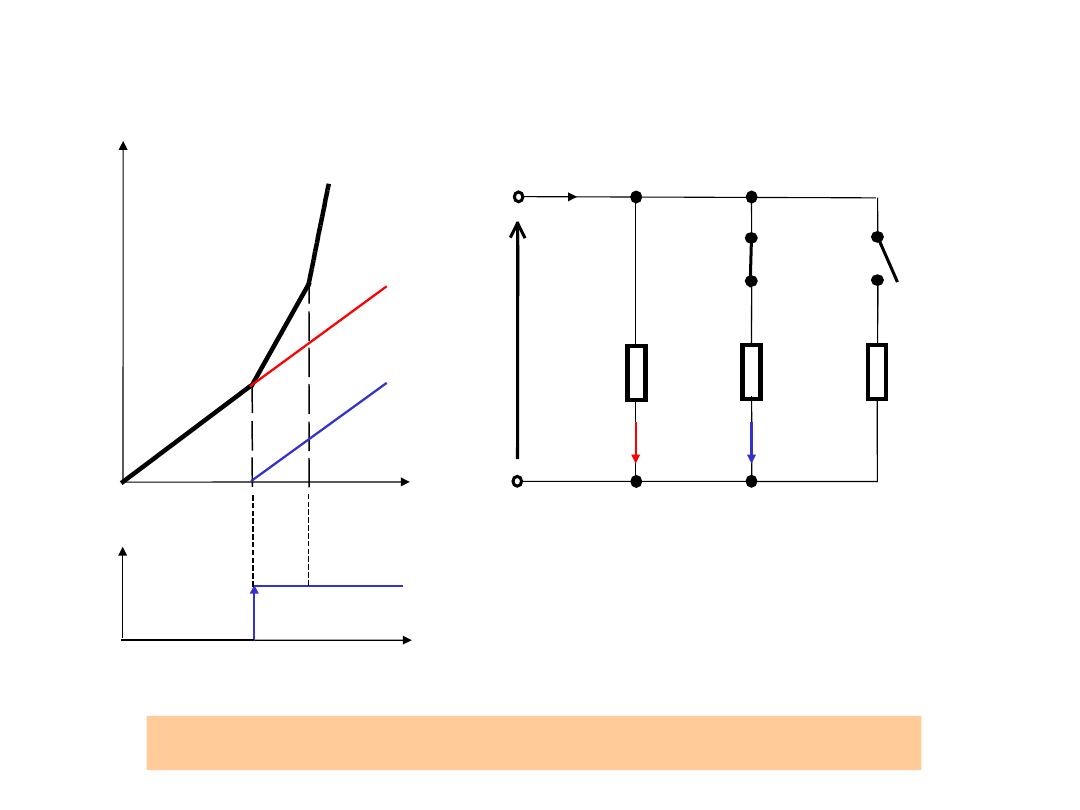
Aproksymacja funkcji odcinkami linii prostych

U

I

G2

G3

K2

I

U

U1

U2

G1

G1+G2

G1+G2+G3

K1

G1

K - klucze diodowe ( diody przełączające)

I

1

=G1U

I

2

=G2U

I

3

=G3U

I

1

I

2

I

3

U

K1

1

0

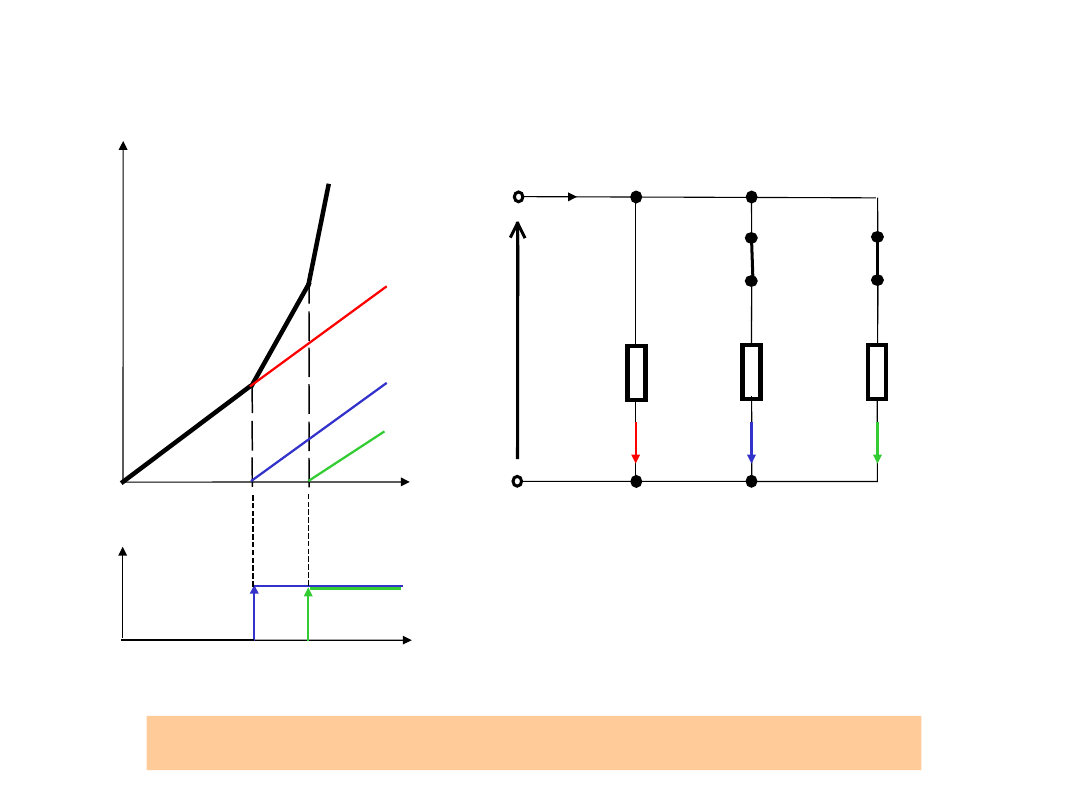
Aproksymacja funkcji odcinkami linii prostych

U

I

G2

G3

K2

I

U

U1

U2

G1

G1+G2

G1+G2+G3

K1

G1

K - klucze diodowe ( diody przełączające)

I

1

=G1U

I

2

=G2U

I

3

=G3U

I

1

I

2

I

3

U

K1

K2

1

0

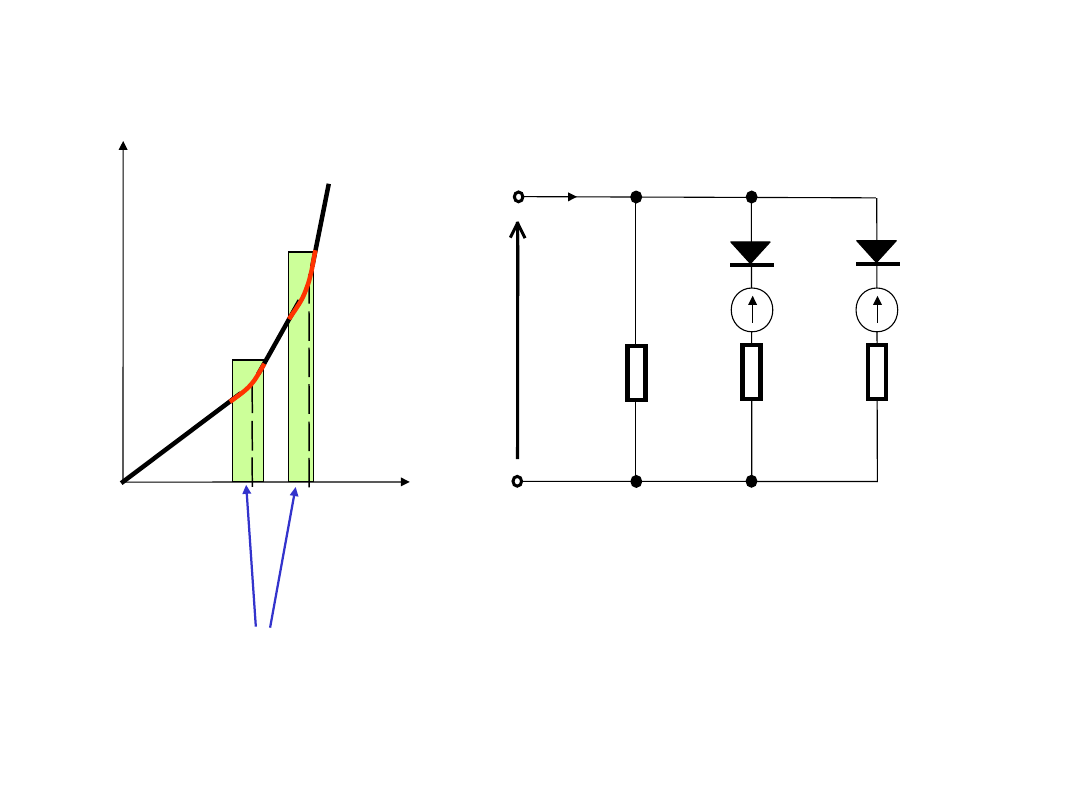
Aproksymacja funkcji odcinkami linii prostych

U

I

G2

G3

D2

I

G1

G1+G2

G1+G2+G3

D1

G1

U1

U2

U

U1

U2

Obszary włączania się diod

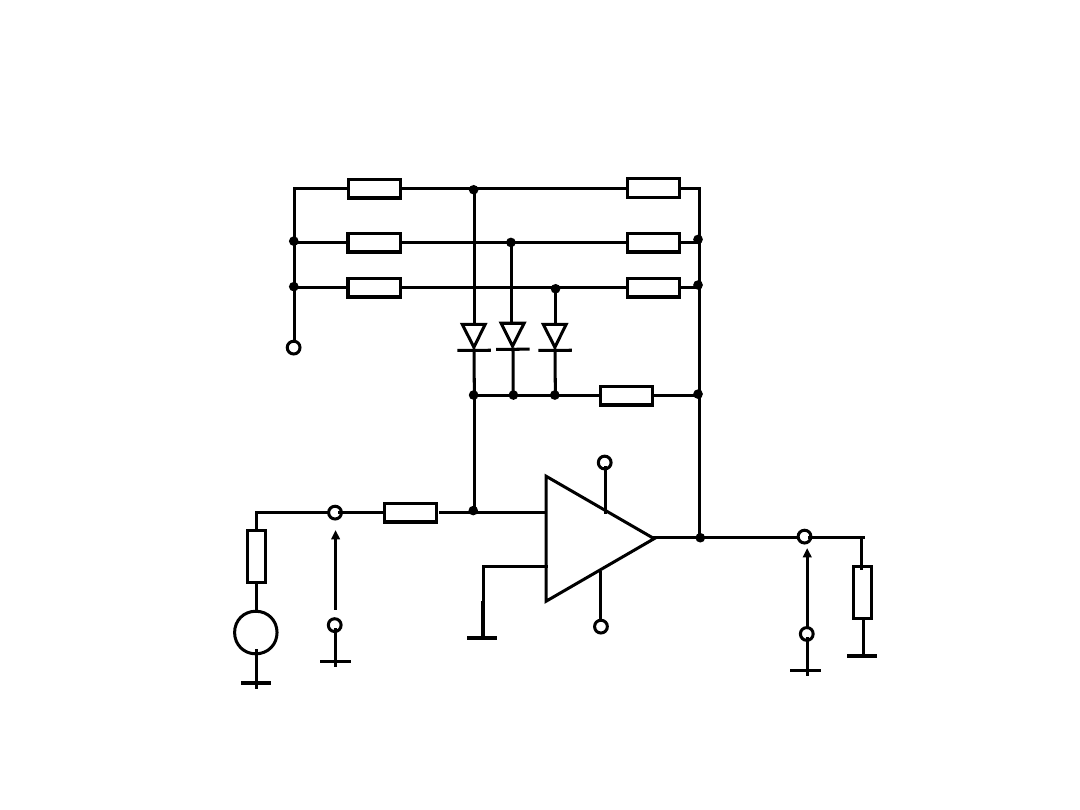
U

1

-

+

R

1

D

1

-V

B

E

g

R

G

-V

EE1

+V

CC1

U

2

R

L

R

2

R

3

R

4

R

5

R

6

R

7

R

8

D

2

D

3

Przykład układu logarytmującego z kluczami

diodowymi (aproksymacja

czterema

odcinkami

linii prostej)

Odcinek 1; R2 ..

Odcinek 2; D3 ...

Odcinek 3; D2 ...

Odcinek 4; D1 ...

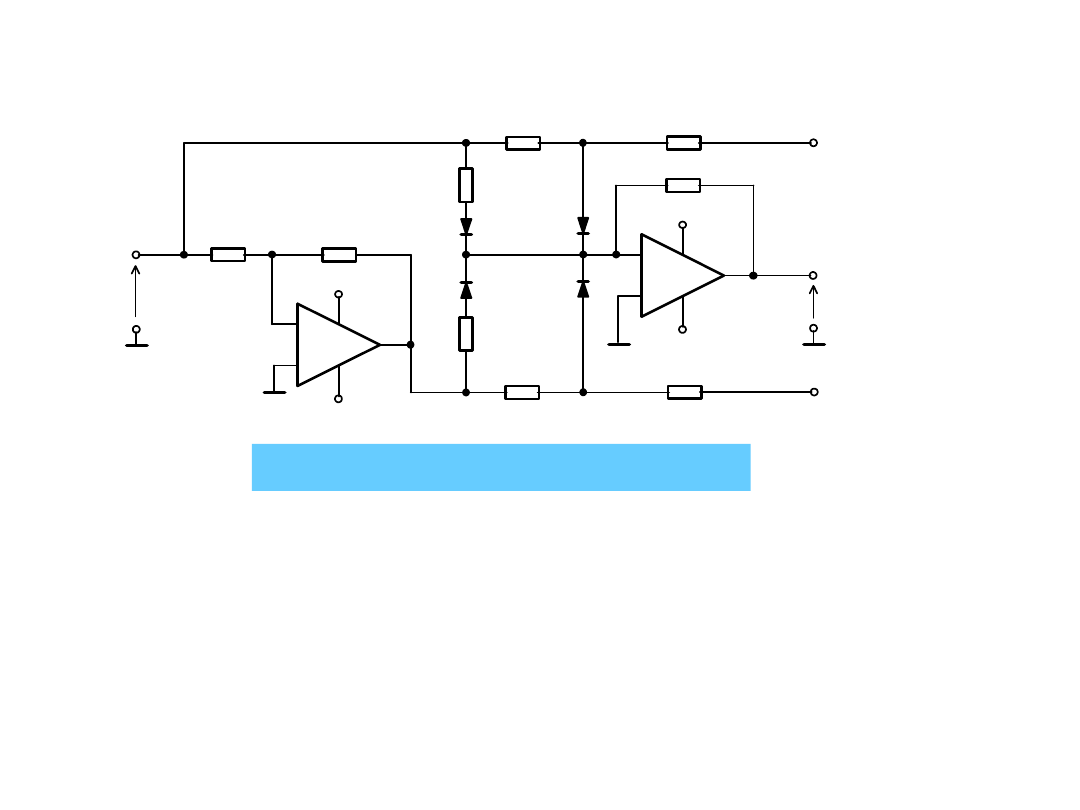
Układ paraboliczny:

W2

-

+

+Ucc (+15V)

-Uee (-15V)

R2

U

R21

R

R

-Up

R

R

R21'

-Up

D1 D2

D1'

2

D2'

W1

-

+

+Ucc (+15V)

-Uee (-15V)

Rf2

U

1

Rf1

Przykład układu parabolicznego

Przy napięciu wejściowym mniejszym od napięcia przewodzenia
diod napięcie wyjściowe jest równe zeru. W miarę wzrostu
napięcia wejściowego między wejście wzmacniacza operacyjnego
W2 i całego układu są dołączane równolegle kolejne rezystory R,
zmniejszając

rezystancję

gałęzi

sprzężenia

zwrotnego

i zwiększając wzmocnienie układu. Układ umożliwia realizację
funkcji kwadratowej w zakresie napięć wejściowych od 2,5V do
+2,5V z błędem mniejszym od +/3% wartości maksymalnej
napięcia wyjściowego.

2

1

2

U

a

U





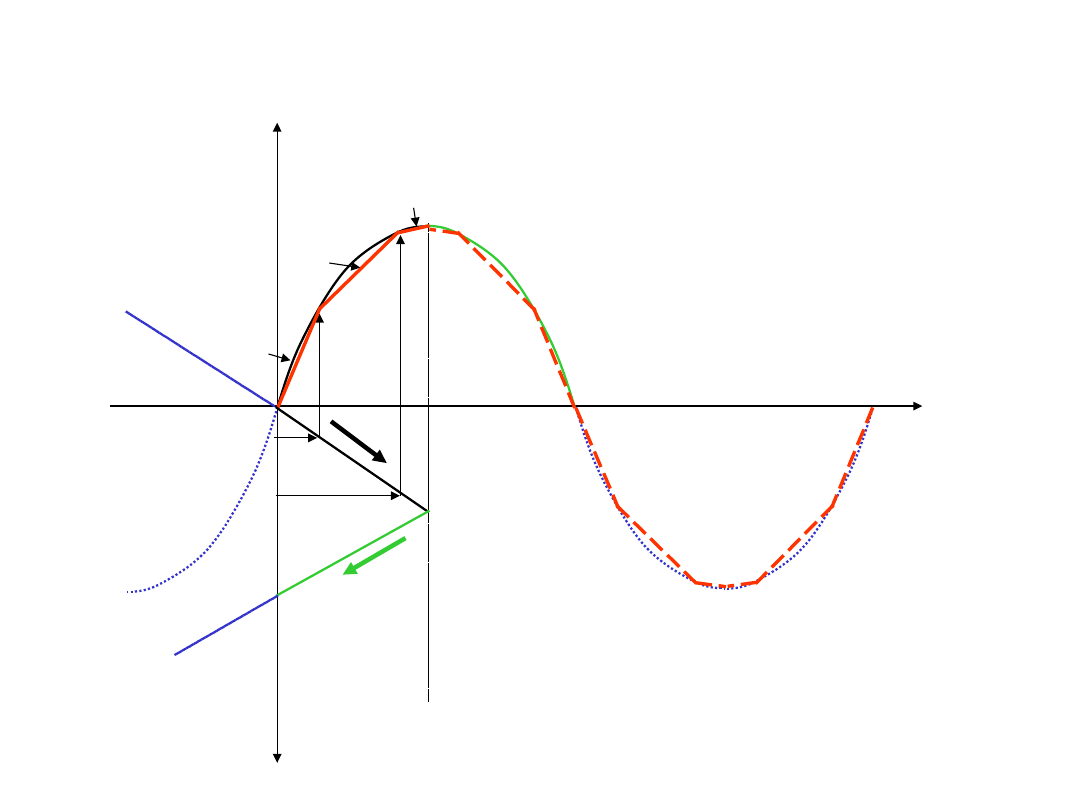
Przetwornik trójkąt-sinus

U

WY

(t)

t

U

WE

U

WE

(t)

K1

K2

Aproksymacja trójodcinkowa

1

2

3

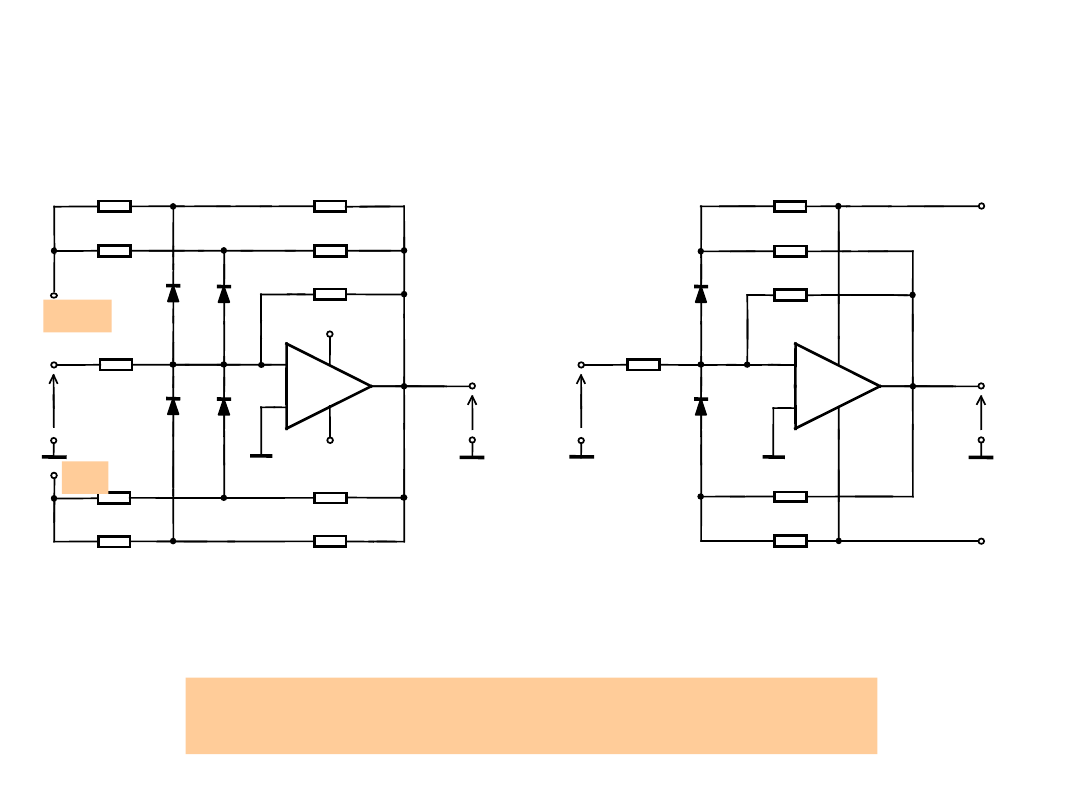
Przetwornik trójkąt-sinus z OPA

R4

W

-

+

+Ucc

-Uee

R2

U

R3

R1

R31

R41

R31'

R41'

R4'

R3'

D2 D1

D2'

2

D1'

U

1

+Up

-Up

W

-

+

+Ucc

-Uee

R2

U

R3

R1

R31

R31'

R3'

D1

2

D1'

U

1

Przetworniki z napięciami pomocniczymi U

P

Aproksymacja trójodcinkowa Aproksymacja dwuodcinkowa

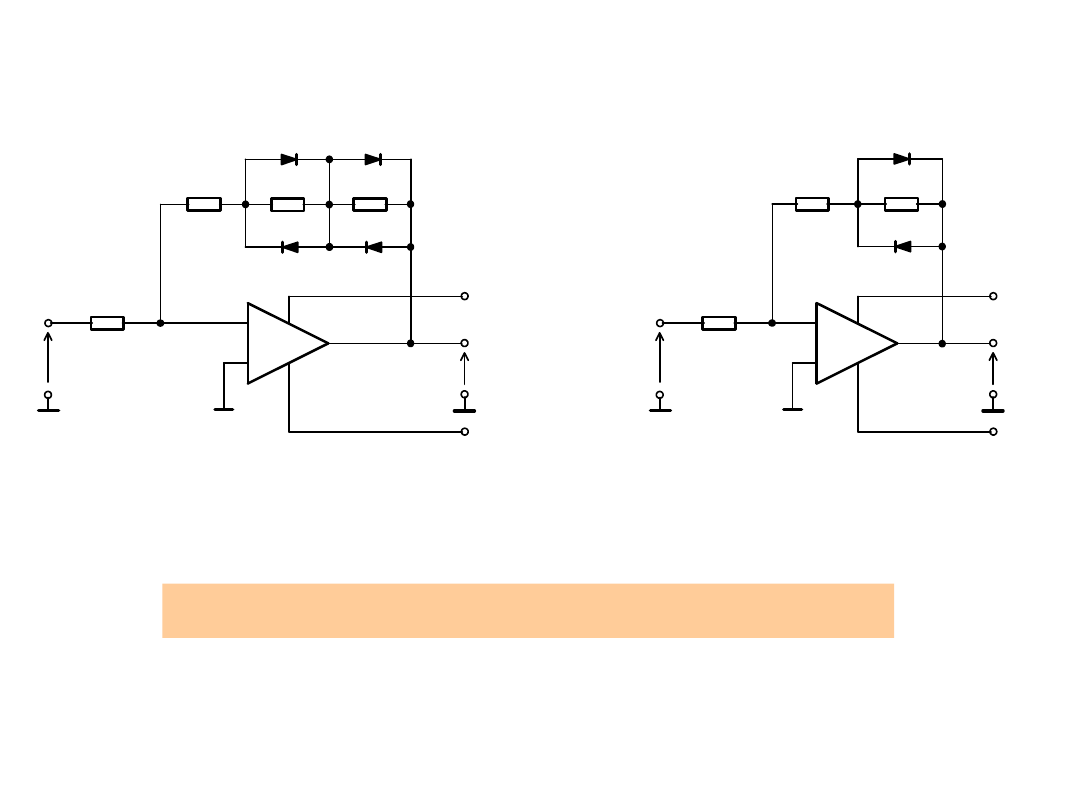
Przetwornik trójkąt-sinus

W

-

+

+Ucc

-Uee

R2

U

R4

R1

D2'

2

U

1

D2

D1'

R3

D1

W

-

+

+Ucc

-Uee

R2

U

R3

R1

D1'

2

U

1

D1

Przetworniki bez napięć pomocniczych

Aproksymacja trójodcinkowa Aproksymacja dwuodcinkowa

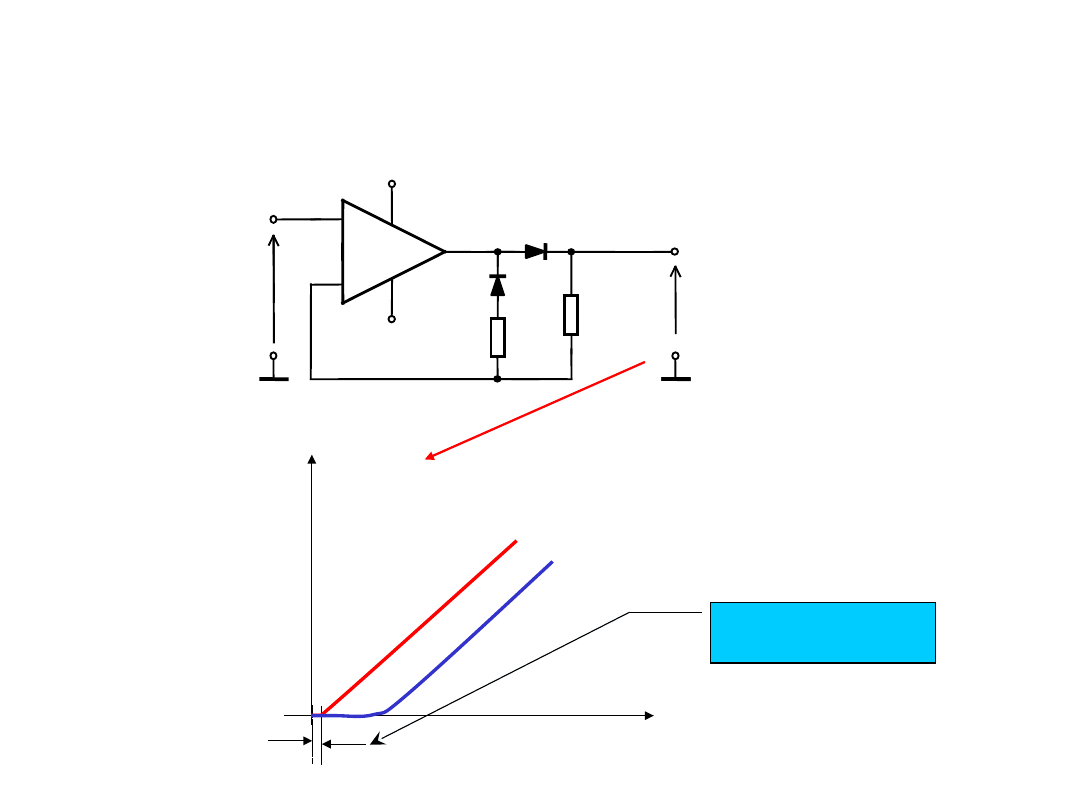
Prostownik precyzyjny jednopołówkowy;

tzw. układ progowy: próg  0V

U

-

+

+ Ucc (+15V)

-Uee (-15V)

U

D1

D2

R

R

2

1

K

U

U

D

/K

U

mV

U

1

U

2

U

D

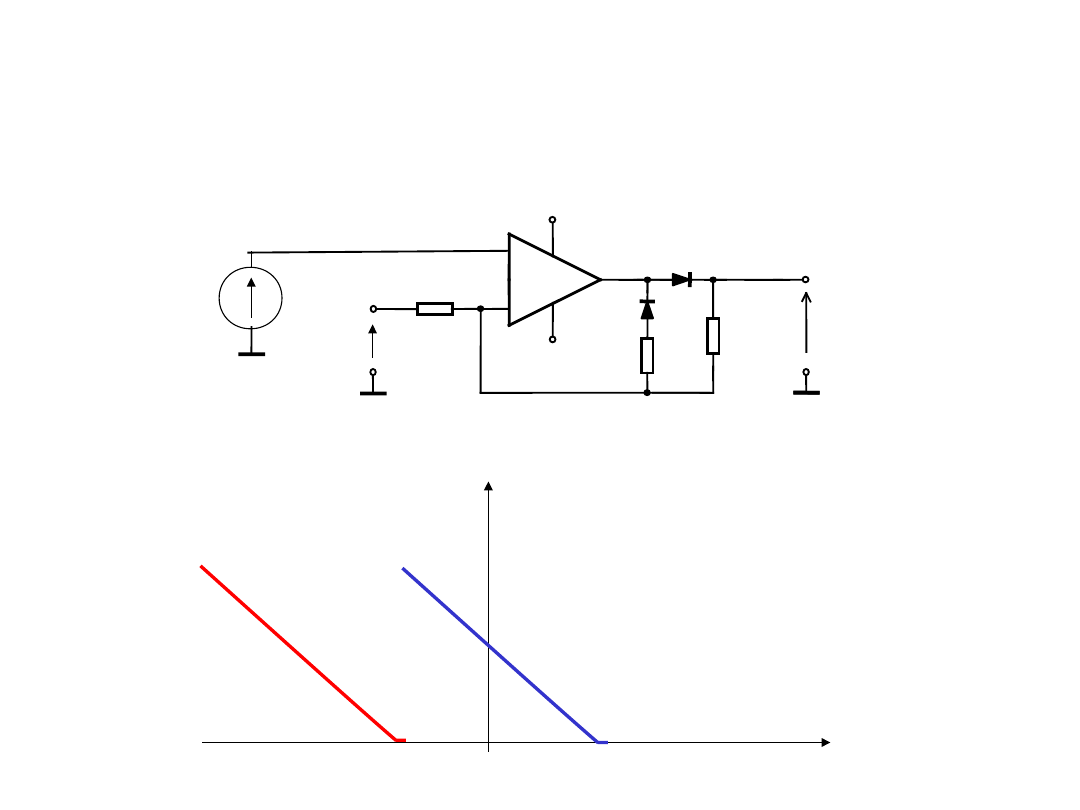
Układ z regulowanym progiem U

P

U

1

U

2

U

P

>0

U

P

<0

-

+

+ Ucc (+15V)

-Uee (-15V)

R1

U

D1

D2

R2

R

2

U

1

W

U

P

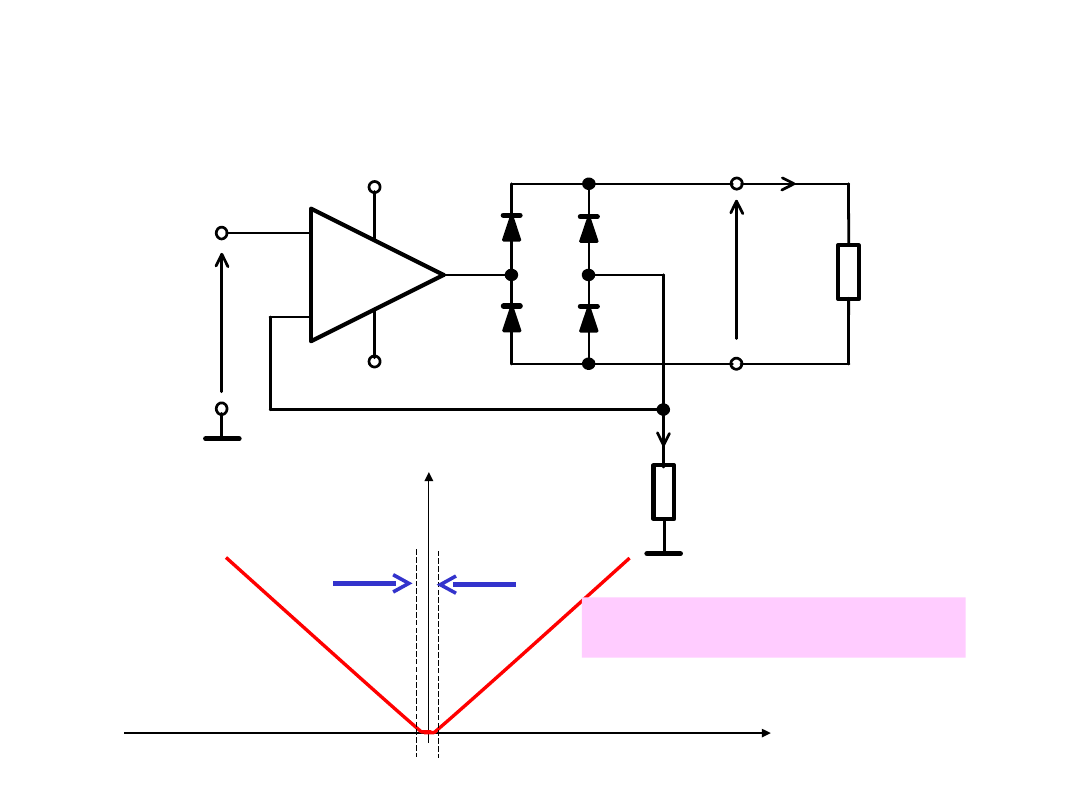
Prostownik precyzyjny dwupołówkowy

U

-

+

+ Ucc (+15V)

-Uee (-15V)

R

U

D1

D2

RL

2

1

W

D3

D4

I

I

U

2

U1

Nachylenie: 1+R

L

/R

mV

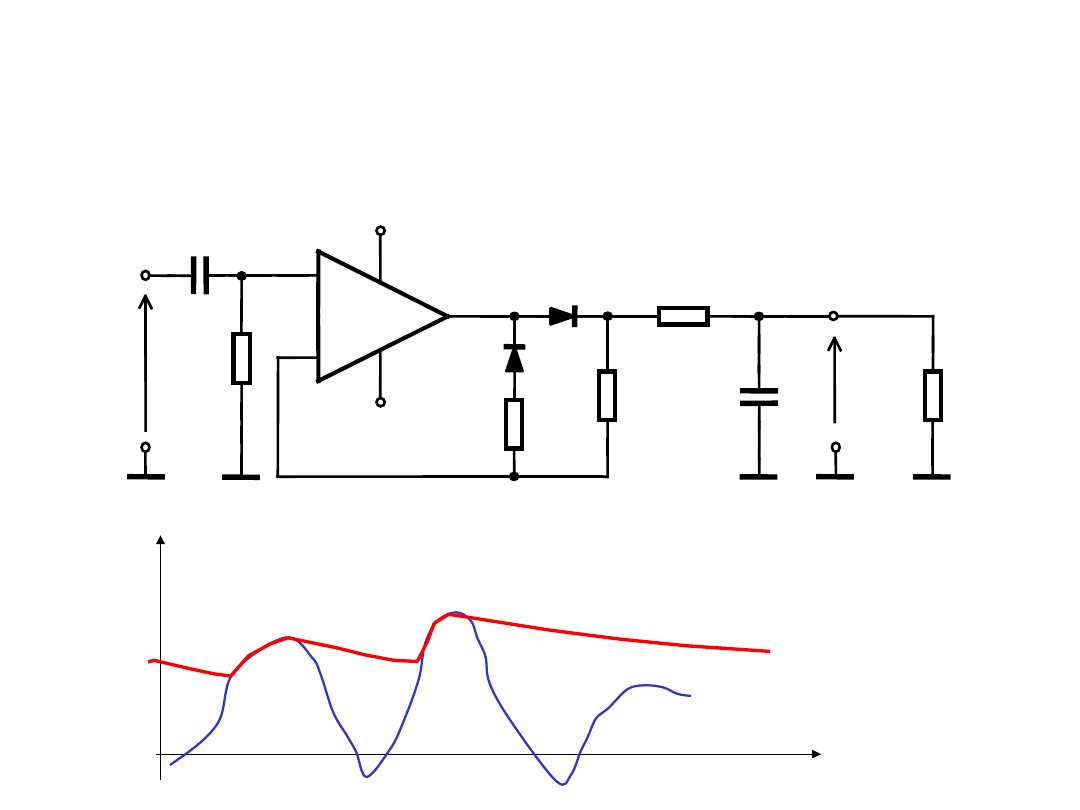
Prostownik quasi-szczytowy

Oblicza wartość zbliżoną do szczytowej sygnału

U

-

+

+ Ucc (+15V)

-Uee (-15V)

U

D1

D2

R2

R

2

1

W

R3

C1

C2

R4

RL

U2

t

U1

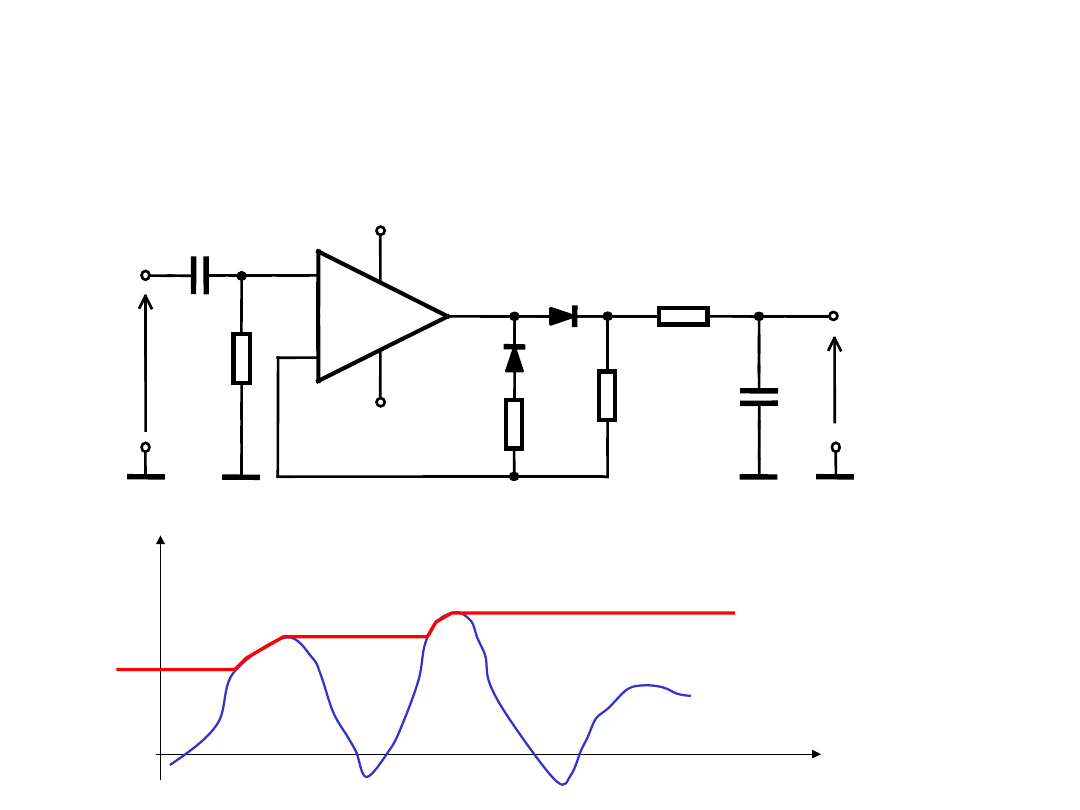
Prostownik szczytowy

+ Ucc (+15V)

U

-

+

-Uee (-15V)

U

D1

D2

R2

R

2

1

W

R3

C1

C2

R4

Oblicza wartość szczytową sygnału

U2

t

U1

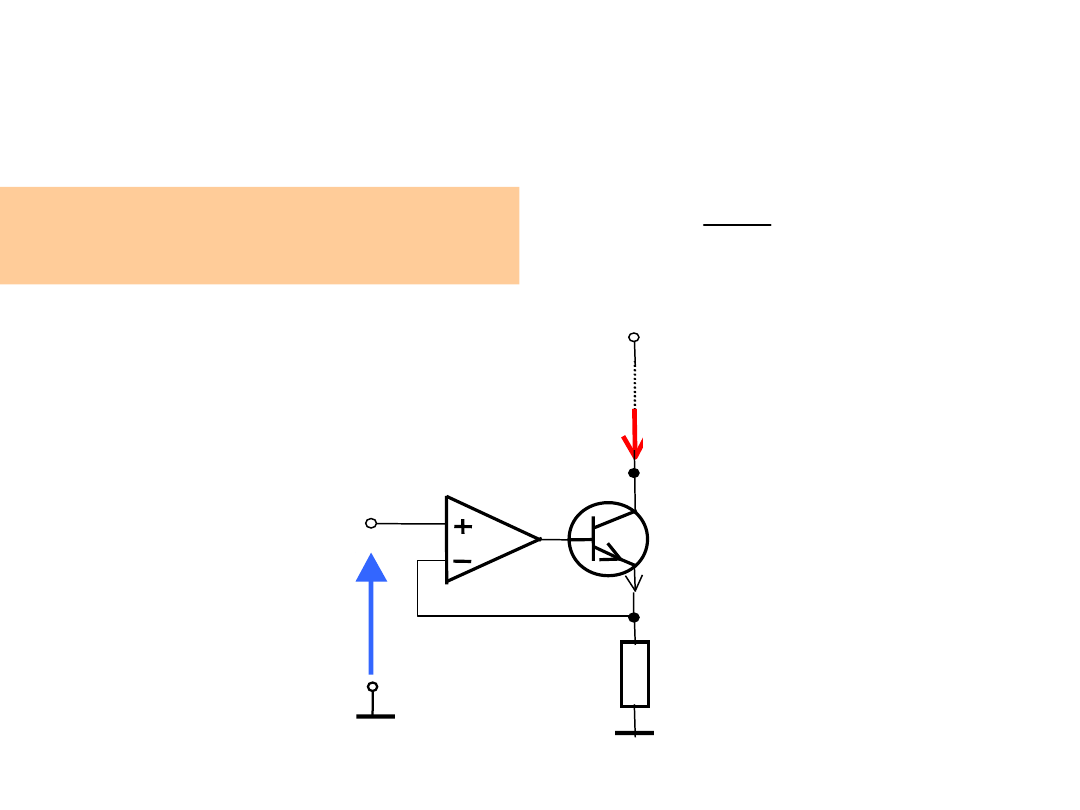
Przetwornik napięcie-prąd

R

E

i

L



i

R

I

ź

u

in

+U

CC

E

in

ź

R

u

I 

Przetwornik napięcie-prąd:
(sterowane źródło prądowe)

U=0