ŚCIANY

ŚCIANY

OBLICZENIA

OBLICZENIA

RODZAJE MURÓW

RODZAJE MURÓW



ODPOWIEDNIO DO ZASTOSOWANYCH ELEMENTÓW

ODPOWIEDNIO DO ZASTOSOWANYCH ELEMENTÓW

MUROWYCH ROZRÓŻNIA SIĘ :

MUROWYCH ROZRÓŻNIA SIĘ :



MURY CERAMICZNE

MURY CERAMICZNE



MURY SILIKATOWE

MURY SILIKATOWE



MURY BETONOWE

MURY BETONOWE



MURY Z AUTOKLAWIZOWANEGO BETONU KOMÓRKOWEGO

MURY Z AUTOKLAWIZOWANEGO BETONU KOMÓRKOWEGO



MURY Z KAMIENIA NATURALNEGO.

MURY Z KAMIENIA NATURALNEGO.

ODPOWIEDNIO DO GRUBOŚCI SPOIN ROZRÓŻNIA SIĘ :

ODPOWIEDNIO DO GRUBOŚCI SPOIN ROZRÓŻNIA SIĘ :



MURY NA SPOINACH ZWYKŁYCH (O GRUBOŚCI 8 – 15 mm),

MURY NA SPOINACH ZWYKŁYCH (O GRUBOŚCI 8 – 15 mm),



MURY NA SPOINACH CIENKICH (O GRUBOŚCI 1 -3 mm)

MURY NA SPOINACH CIENKICH (O GRUBOŚCI 1 -3 mm)

MURY NA SPINACH ZWYKŁYCH MOGĄ BYĆ WYKONYWANE

MURY NA SPINACH ZWYKŁYCH MOGĄ BYĆ WYKONYWANE

PRZY UŻYCIU ZAPRAWY ZWYKŁEJ LUB LEKKIEJ.

PRZY UŻYCIU ZAPRAWY ZWYKŁEJ LUB LEKKIEJ.

JEŻELI W OKREŚLENIU MURU NIE PODANO JAKIEJ UŻYTO

JEŻELI W OKREŚLENIU MURU NIE PODANO JAKIEJ UŻYTO

ZAPRAWY I GRUBOŚCI SPOINY, TO PRZYJMUJE SIĘ, ŻE MUR

ZAPRAWY I GRUBOŚCI SPOINY, TO PRZYJMUJE SIĘ, ŻE MUR

WYKONANO NA ZAPRAWIE ZWYKŁEJ.

WYKONANO NA ZAPRAWIE ZWYKŁEJ.

Z UWAGI NA SPECYFIKĘ OBCIĄŻENIA I WYNIKAJĄCE STĄD

Z UWAGI NA SPECYFIKĘ OBCIĄŻENIA I WYNIKAJĄCE STĄD

WARUNKI WYZNACZANIA NOŚNOŚCI, ŚCIANY

WARUNKI WYZNACZANIA NOŚNOŚCI, ŚCIANY

KONSTRUKCYJNE DZIELI SIĘ ZGODNIE Z PN-B-

KONSTRUKCYJNE DZIELI SIĘ ZGODNIE Z PN-B-

03002:1999" NA:

03002:1999" NA:



ŚCIANY OBCIĄŻONE GŁÓWNIE PIONOWO,

ŚCIANY OBCIĄŻONE GŁÓWNIE PIONOWO,



ŚCIANY OBCIĄŻONE GŁÓWNIE POZIOMO,

ŚCIANY OBCIĄŻONE GŁÓWNIE POZIOMO,



ŚCIANY USZTYWNIAJĄCE.

ŚCIANY USZTYWNIAJĄCE.



DO ŚCIAN OBCIĄŻONYCH

DO ŚCIAN OBCIĄŻONYCH

GŁÓWNIE PIONOWO

GŁÓWNIE PIONOWO

NALEŻĄ

NALEŻĄ

ŚCIANY W BUDYNKACH PRZENOSZĄCE OBCIĄŻENIA Z

ŚCIANY W BUDYNKACH PRZENOSZĄCE OBCIĄŻENIA Z

GÓRNYCH KONDY GNACJI (CIĘŻAR WŁASNY I - KIEDY NA

GÓRNYCH KONDY GNACJI (CIĘŻAR WŁASNY I - KIEDY NA

ŚCIANACH TYCH OPARTE SĄ STROPY - OBCIĄŻENIE OD

ŚCIANACH TYCH OPARTE SĄ STROPY - OBCIĄŻENIE OD

STROPÓW), A TAKŻE ODDZIAŁUJĄCE NA NIE

STROPÓW), A TAKŻE ODDZIAŁUJĄCE NA NIE

BEZPOŚREDNIO OBCIĄŻENIE POZIOME. O NOŚNOŚCI TYCH

BEZPOŚREDNIO OBCIĄŻENIE POZIOME. O NOŚNOŚCI TYCH

ŚCIAN DECYDUJE WYTRZYMAŁOŚĆ MURU NA ŚCISKANIE.

ŚCIAN DECYDUJE WYTRZYMAŁOŚĆ MURU NA ŚCISKANIE.



ŚCIANAMI OBCIĄŻONYMI

ŚCIANAMI OBCIĄŻONYMI

GŁÓWNIE POZIOMO

GŁÓWNIE POZIOMO

SĄ NIE

SĄ NIE

PRZENOSZĄCE OBCIĄŻENIA Z GÓRNYCH KONDYGNACJI

PRZENOSZĄCE OBCIĄŻENIA Z GÓRNYCH KONDYGNACJI

ZEWNĘTRZNE ŚCIANY WYPEŁNIAJĄCE, PODDANE PARCIU

ZEWNĘTRZNE ŚCIANY WYPEŁNIAJĄCE, PODDANE PARCIU

WIATRU. O NOŚNOŚCI TYCH ŚCIAN DECYDUJE

WIATRU. O NOŚNOŚCI TYCH ŚCIAN DECYDUJE

WYTRZYMAŁOŚĆ MURU NA ROZCIĄGANIE.

WYTRZYMAŁOŚĆ MURU NA ROZCIĄGANIE.



ŚCIANY PIWNIC, KTÓRYCH NOŚNOŚĆ ZALEŻY RÓWNIEŻ W

ŚCIANY PIWNIC, KTÓRYCH NOŚNOŚĆ ZALEŻY RÓWNIEŻ W

DUŻEJ MIERZE OD OBCIĄŻENIA POZIOMEGO - W TYM

DUŻEJ MIERZE OD OBCIĄŻENIA POZIOMEGO - W TYM

PRZYPADKU WYWOŁANEGO PARCIEM GRUNTU -

PRZYPADKU WYWOŁANEGO PARCIEM GRUNTU -

WYMIARUJE SIĘ JAKO ŚCIANY OBCIĄŻONE

WYMIARUJE SIĘ JAKO ŚCIANY OBCIĄŻONE

GŁÓWNIE

GŁÓWNIE

PIONOWO.

PIONOWO.



ŚCIANY USZTYWNIAJĄCE

ŚCIANY USZTYWNIAJĄCE

SĄ TO ŚCIANY PRZEJMUJĄCE NA

SĄ TO ŚCIANY PRZEJMUJĄCE NA

SIEBIE SIŁY POZIOME WYNIKŁE Z DZIAŁANIA NA BUDYNEK

SIEBIE SIŁY POZIOME WYNIKŁE Z DZIAŁANIA NA BUDYNEK

OBCIĄŻENIA POZIOMEGO RÓWNOLEGŁEGO DO PŁASZCZYZNY

OBCIĄŻENIA POZIOMEGO RÓWNOLEGŁEGO DO PŁASZCZYZNY

ŚCIANY.

ŚCIANY.



KIEDY

KIEDY

ŚCIANAMI USZTYWNIAJĄCYMI

ŚCIANAMI USZTYWNIAJĄCYMI

SĄ ŚCIANY OBCIĄŻONE

SĄ ŚCIANY OBCIĄŻONE

GŁÓWNIE PIONOWO, NOŚNOŚĆ TAKICH ŚCIAN SPRAWDZA SIĘ

GŁÓWNIE PIONOWO, NOŚNOŚĆ TAKICH ŚCIAN SPRAWDZA SIĘ

Z UWZGLĘDNIENIEM SIŁ WEWNĘTRZNYCH WYWOŁANYCH

Z UWZGLĘDNIENIEM SIŁ WEWNĘTRZNYCH WYWOŁANYCH

PRZEZ OBCIĄŻENIE POZIOME RÓWNOLEGŁE DO PŁASZCZYZNY

PRZEZ OBCIĄŻENIE POZIOME RÓWNOLEGŁE DO PŁASZCZYZNY

ŚCIANY.

ŚCIANY.

PARAMETRY WYTRZYMAŁOŚCIOWE MURU

PARAMETRY WYTRZYMAŁOŚCIOWE MURU



WARTOŚCI CZĘŚCIOWYCH WSPÓŁCZYNNIKÓW

WARTOŚCI CZĘŚCIOWYCH WSPÓŁCZYNNIKÓW

BEZPIECZEŃSTWA

BEZPIECZEŃSTWA

γ

γ

m

m

UZALEŻNIONE SĄ WG

UZALEŻNIONE SĄ WG

PN-B-

PN-B-

03002:1999

03002:1999

OD KATEGORII WYKONANIA ROBÓT NA

OD KATEGORII WYKONANIA ROBÓT NA

BUDOWIE I WYNOSZĄ:

BUDOWIE I WYNOSZĄ:



DLA KATEGORII A -

DLA KATEGORII A -

γ

γ

m

m

= 1,7

= 1,7



DLA KATEGORII B -

DLA KATEGORII B -

γ

γ

m

m

= 2,2

= 2,2



PRZY CZYM, ODMIENNIE NIŻ W

PRZY CZYM, ODMIENNIE NIŻ W

PN-87/B-03002

PN-87/B-03002

, NIE

, NIE

ROZRÓŻNIA SIĘ WARTOŚCI

ROZRÓŻNIA SIĘ WARTOŚCI

γ

γ

m

m

PRZY ŚCISKANIU I PRZY

PRZY ŚCISKANIU I PRZY

ROZCIĄGANIU.

ROZCIĄGANIU.



KATEGORIE

KATEGORIE

A

A

I

I

B

B

WYKONANIA ROBÓT NA BUDOWIE

WYKONANIA ROBÓT NA BUDOWIE

DEFINIUJE SIĘ NASTĘPUJĄCO:

DEFINIUJE SIĘ NASTĘPUJĄCO:



Kategoria A

Kategoria A

wykonania robót: roboty murarskie wykonuje

wykonania robót: roboty murarskie wykonuje

należycie wyszkolony zespół pod nadzorem majstra murarskiego,

należycie wyszkolony zespół pod nadzorem majstra murarskiego,

stosuje się zaprawy produkowane fabrycznie, a jeżeli zaprawy

stosuje się zaprawy produkowane fabrycznie, a jeżeli zaprawy

wykonywane sana budowie, kontroluje się dozowanie składników,

wykonywane sana budowie, kontroluje się dozowanie składników,

a także wytrzymałość zaprawy; jakość robót kontroluje osoba o

a także wytrzymałość zaprawy; jakość robót kontroluje osoba o

odpowiednich kwalifikacjach, niezależna od wykonawcy.

odpowiednich kwalifikacjach, niezależna od wykonawcy.



Kategoria B

Kategoria B

wykonania robót: warunki określające kategorię

wykonania robót: warunki określające kategorię

A

A

nie są spełniane, a nadzór nad jakością robót może wykonywać

nie są spełniane, a nadzór nad jakością robót może wykonywać

osoba odpowiednio wykwalifikowana, upoważniona przez

osoba odpowiednio wykwalifikowana, upoważniona przez

wykonawcę.

wykonawcę.



Decyzję, czy do obliczeń sprawdzających niezawodność

Decyzję, czy do obliczeń sprawdzających niezawodność

konstrukcji murowych przyjąć można wartości

konstrukcji murowych przyjąć można wartości

y

y

m

m

odpowiadające

odpowiadające

kategorii

kategorii

A

A

czy kategorii

czy kategorii

B

B

, podejmuje projektant, odpowiednio

, podejmuje projektant, odpowiednio

do informacji uzyskanych od inwestora, który w przypadku

do informacji uzyskanych od inwestora, który w przypadku

ustalenia, że będzie to kategoria

ustalenia, że będzie to kategoria

A

A

- zobowiązuje się do

- zobowiązuje się do

dopilnowania poprzez swojego inspektora nadzoru

dopilnowania poprzez swojego inspektora nadzoru

inwestorskiego, że zadane warunki wykonania robót zostaną

inwestorskiego, że zadane warunki wykonania robót zostaną

dotrzymane.

dotrzymane.

WYTRZYMAŁOŚĆ OBLICZENIOWA MURU

WYTRZYMAŁOŚĆ OBLICZENIOWA MURU



WYTRZYŁAŁOŚĆ OBLICZENIOWĄ MURU NA

WYTRZYŁAŁOŚĆ OBLICZENIOWĄ MURU NA

ŚCISKANIE OBLICZAĆ NALEŻY WEDŁUG WZORU:

ŚCISKANIE OBLICZAĆ NALEŻY WEDŁUG WZORU:



Gdzie

Gdzie



f

f

k

k

– wytrzymałość charakterystyczna muru na ściskanie

– wytrzymałość charakterystyczna muru na ściskanie



γ

γ

m

m

– częściowy współczynnik bezpieczeństwa muru

– częściowy współczynnik bezpieczeństwa muru

m

k

d

γ

f

f 

ŚCIANY GŁÓWNIE OBCIĄŻONE

ŚCIANY GŁÓWNIE OBCIĄŻONE

PIONOWO

PIONOWO



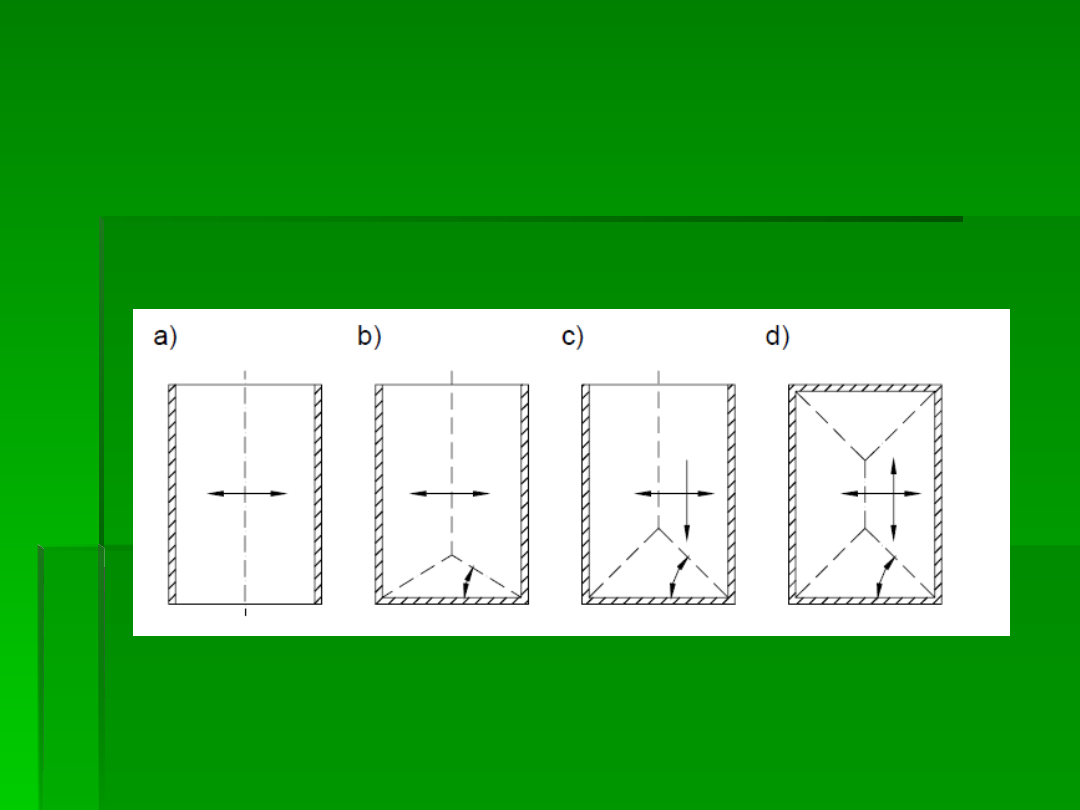
Obciążenie pionowe od stropów należy wyznaczać

zgodnie z zasadami podanymi na rysunku 1. Jeżeli

strop przylega do nieoddylatowanej ściany

samonośnej, do obciążenia pionowego tej ściany

należy dodać obciążenie z trójkąta stropu wg

rysunku 1b lub zastępczo – obciążenie z pasma o

szerokości równej 0,3 rozpiętości stropu.

ŚCIANY GŁÓWNIE OBCIĄŻONE

ŚCIANY GŁÓWNIE OBCIĄŻONE

PIONOWO

PIONOWO

ŚCIANY GŁÓWNIE OBCIĄŻONE PIONOWO

ŚCIANY GŁÓWNIE OBCIĄŻONE PIONOWO



WARUNEK NIEPRZEKROCZENIA STANU GRANICZNEGO

WARUNEK NIEPRZEKROCZENIA STANU GRANICZNEGO

NOŚNOŚCI ŚCIANY OBCIĄŻONEJ GŁÓWNIE PIONOWO.

NOŚNOŚCI ŚCIANY OBCIĄŻONEJ GŁÓWNIE PIONOWO.

OBCIĄŻENIE PONOWE ŚCIAN OBCIĄŻONYCH GŁÓWNIE

OBCIĄŻENIE PONOWE ŚCIAN OBCIĄŻONYCH GŁÓWNIE

PIONOWO STANOWIĄ:

PIONOWO STANOWIĄ:



CIĘŻAR WŁASNY,

CIĘŻAR WŁASNY,



OBCIĄŻENIE PIONOWE OD STROPÓW (W TYM RÓWNIEŻ OD

OBCIĄŻENIE PIONOWE OD STROPÓW (W TYM RÓWNIEŻ OD

DACHÓW, SCHODÓW, BALKONÓW) I ŚCIAN OPARTYCH NA

DACHÓW, SCHODÓW, BALKONÓW) I ŚCIAN OPARTYCH NA

ROZPATRYWANEJ ŚCIANIE, A TAKŻE SIŁY WEWNĘTRZNE ,

ROZPATRYWANEJ ŚCIANIE, A TAKŻE SIŁY WEWNĘTRZNE ,

WYNIKAJĄCE Z POŁĄCZENIA TEJ ŚCIANY ZE ŚCIANAMI

WYNIKAJĄCE Z POŁĄCZENIA TEJ ŚCIANY ZE ŚCIANAMI

PRZYLEGŁYMI, JEŚLI ICH OKSZTAŁCENIE PIONOWE JEST

PRZYLEGŁYMI, JEŚLI ICH OKSZTAŁCENIE PIONOWE JEST

ZNACZĄCO RÓŻNE OD ODKSZTAŁCENIA ŚCIANY

ZNACZĄCO RÓŻNE OD ODKSZTAŁCENIA ŚCIANY

ROZPATRYWANEJ.

ROZPATRYWANEJ.



STAN GRANICZNY NOŚNOŚCI ŚCIAN OBCIĄŻONYCH

STAN GRANICZNY NOŚNOŚCI ŚCIAN OBCIĄŻONYCH

GŁÓWNIE PIONOWO NALEŻY SPRAWDZIĆ ZA POMOCĄ

GŁÓWNIE PIONOWO NALEŻY SPRAWDZIĆ ZA POMOCĄ

WARUNKU:

WARUNKU:

N

N

Sd

Sd

< N

< N

Rd

Rd

GDZIE:

GDZIE:

N

N

Sd

Sd

– OBLICZENIOWE OBCIĄŻENIE ŚCIANY

– OBLICZENIOWE OBCIĄŻENIE ŚCIANY

N

N

Rd

Rd

– OBLICZENIOWA NOŚNOŚĆ ŚCIANY

– OBLICZENIOWA NOŚNOŚĆ ŚCIANY



SPRAWDZENIA NOŚNOŚCI NALEŻY WYKONAC – W

SPRAWDZENIA NOŚNOŚCI NALEŻY WYKONAC – W

ODNIESIENIU DO PRZEKROJÓW POD I NAD STROPEM

ODNIESIENIU DO PRZEKROJÓW POD I NAD STROPEM

ORAZ W STREFIE ŚRODKOWEJ ŚCIANY – Z

ORAZ W STREFIE ŚRODKOWEJ ŚCIANY – Z

UWZGLĘDNIENIEM GEOMETRII ŚCIAN, MIMOŚRODOEGO

UWZGLĘDNIENIEM GEOMETRII ŚCIAN, MIMOŚRODOEGO

DZIAŁANIA OBCIĄŻENIA PIONOWEGO I WŁAŚCIWOŚCI

DZIAŁANIA OBCIĄŻENIA PIONOWEGO I WŁAŚCIWOŚCI

MATERIAŁOWYCH MURU. W ŚCIANACH Z OTWORAMI

MATERIAŁOWYCH MURU. W ŚCIANACH Z OTWORAMI

NALEŻY SPRAWDZIĆ TAKŻE NOŚNOŚĆ NADPROŻY.

NALEŻY SPRAWDZIĆ TAKŻE NOŚNOŚĆ NADPROŻY.



PRZY WYZNACZANIU MIEJSCA PRZYŁOŻENIA

PRZY WYZNACZANIU MIEJSCA PRZYŁOŻENIA

OBLICZENIOWEGO OBCIĄŻENIA PIONOWEGO

OBLICZENIOWEGO OBCIĄŻENIA PIONOWEGO

N

N

Sd

Sd

NALEŻY UWZGLĘDNIĆ NIEZAMIERZONY MIMOŚRÓD

NALEŻY UWZGLĘDNIĆ NIEZAMIERZONY MIMOŚRÓD

PRZYPADKOWY

PRZYPADKOWY

e

e

a

a

= h/300

= h/300

GDZIE h TO WYSOKOŚĆ W mm ŚCIANY W ŚWIETLE

GDZIE h TO WYSOKOŚĆ W mm ŚCIANY W ŚWIETLE



Przy wyznaczaniu wielkości mimośrodu działania

Przy wyznaczaniu wielkości mimośrodu działania

obliczeniowego obciążenia pionowego nsd należy uwzględnić

obliczeniowego obciążenia pionowego nsd należy uwzględnić

niezamierzony mimośród przypadkowy ea = h/300 (h w mm,

niezamierzony mimośród przypadkowy ea = h/300 (h w mm,

wysokość jednej kondygnacji w świetle stropów), lecz nie mniej

wysokość jednej kondygnacji w świetle stropów), lecz nie mniej

niż 10 mm.

niż 10 mm.



Nośność obliczeniową ściany wyznacza się:

Nośność obliczeniową ściany wyznacza się:



W przekroju pod stropem górnej kondygnacji n1rd oraz w

W przekroju pod stropem górnej kondygnacji n1rd oraz w

przekroju nad stropem dolnej kondygnacji -n2r d ze wzoru

przekroju nad stropem dolnej kondygnacji -n2r d ze wzoru

N

N

iRd

iRd

=

=

Φ

Φ

i

i

Af

Af

d

d

GDZIE:

GDZIE:



i = 1

i = 1

- dla przekroju pod stropem oraz i = 2 dla przekro ju nad

- dla przekroju pod stropem oraz i = 2 dla przekro ju nad

stropem;

stropem;



Φ

Φ

i

i

- współczynnik redukcyjny, zależny od wielkości mimośrodu

- współczynnik redukcyjny, zależny od wielkości mimośrodu

e

e

i

i

, na którym w w rozpatrywanym przekroju działa siła

, na którym w w rozpatrywanym przekroju działa siła

obliczeniowa, oraz wielkość miomośrodu przypadkowego

obliczeniowa, oraz wielkość miomośrodu przypadkowego



A

A

– pole przekroju

– pole przekroju



f

f

d

d

- wytrzymałość obliczeniowa muru na ściskanie

- wytrzymałość obliczeniowa muru na ściskanie



W środkowej strefie ściany

N

N

m

m

R

R

,d

,d

= Φ

= Φ

m

m

Af

Af

d

d



w którym:

Φ

m

– współczynnik redukcyjny

wyrażający wpływ efektów drugiego

rzędu na

nośność ściany, zależny od mimośrodu początkowego
e

o

= e

m

,

smukłości ściany h

ef

/t, zależności σ(ε) muru i czasu

trwania obciążenia.



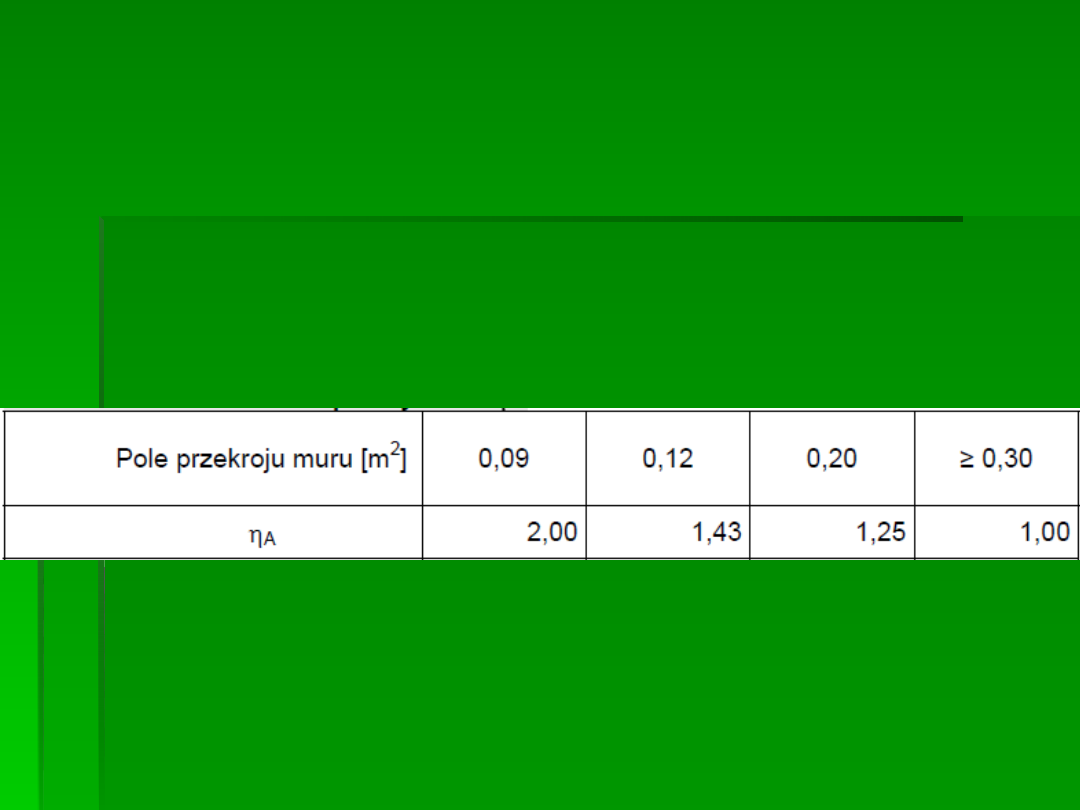
Kiedy pole przekroju konstrukcji murowej jest mniejsze niż

Kiedy pole przekroju konstrukcji murowej jest mniejsze niż

0,30 m2, wytrzymałość obliczeniową muru należy

0,30 m2, wytrzymałość obliczeniową muru należy

podzielić współczynnik ηA wg tabeli 1.

podzielić współczynnik ηA wg tabeli 1.



Tabela 1 Wartość współczynnika

Tabela 1 Wartość współczynnika

η

η

A

A



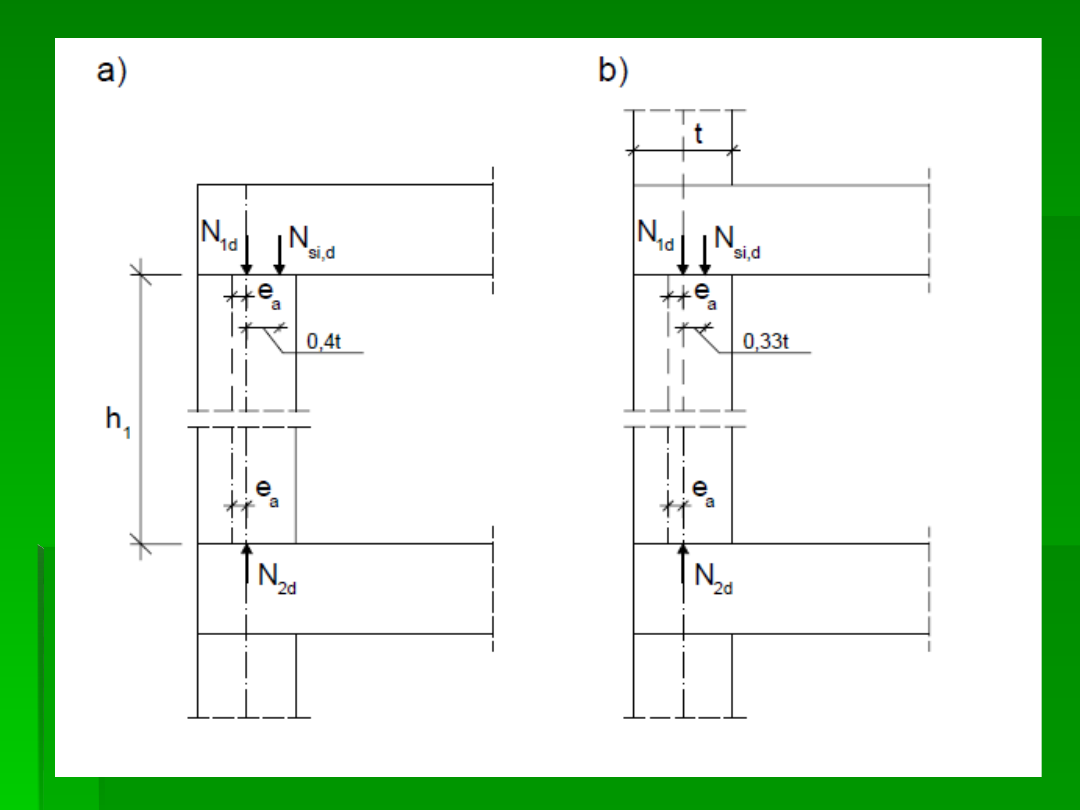
Model przegubowy traktuje ścianę jako wydzielony pręt

podparty przegubowo w poziomie stropów. W modelu

przegubowym, najczęściej wykorzystywanym do obliczania

ścian obciążonych głównie pionowo, można przyjąć:

a) na najwyższej kondygnacji:



− w przekroju pod stropem siła z dachu

N

N

1d

1d

działa w

stosunku do nominalnej osi ściany na mimośrodzie

e

e

a

a

, a

obciążenie od stropu

N

N

si,d

si,d

– na mimośrodzie

0,4t + e

0,4t + e

a

a

,



− w przekroju nad stropem dolnej kondygnacji siła N

2d

,

stanowiąca sumę

N

N

1d

1d

i

N

N

si,d

si,d

oraz ciężaru ściany, działa na

mimośrodzie

e

e

a

a

,

b) dla ścian niższych kondygnacji:



− w przekroju pod stropem siła z górnych kondygnacji N

1d

działa na mimośrodzie e

a

, a obciążenie od stropu

N

N

si,d

si,d

– na

mimośrodzie

0,33t + e

0,33t + e

a

a

,



− w przekroju nad stropem dolnej kondygnacji –

analogicznie jak w wypadku ściany najwyższej kondygnacji.

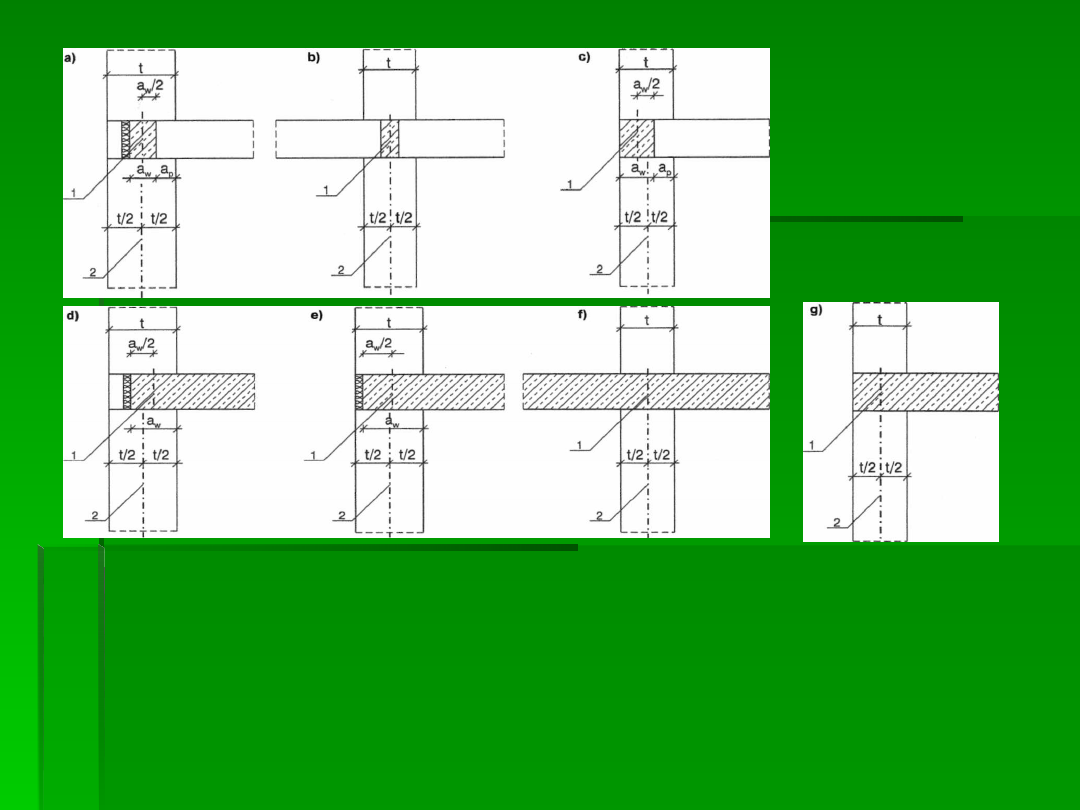
Oparcie stropu na ścianie zewnętrznej i wewnętrznej i położenia osi złącza

Oparcie stropu na ścianie zewnętrznej i wewnętrznej i położenia osi złącza

ściana/strop:

ściana/strop:

a) oparcie stropu z płyt na ścianie zewnętrznej z warstwą wełny mineralnej

a) oparcie stropu z płyt na ścianie zewnętrznej z warstwą wełny mineralnej

wewnątrz ściany; b) oparcie stropu z płyt na ścianie wewnętrznej z obu stron; c) oparcie

wewnątrz ściany; b) oparcie stropu z płyt na ścianie wewnętrznej z obu stron; c) oparcie

stropu z płyt z jednej strony; d) oparcie stropu z betonu zwykłego na ścianie zewnętrznej z

stropu z płyt z jednej strony; d) oparcie stropu z betonu zwykłego na ścianie zewnętrznej z

warstwą styropianu wewnątrz ściany; e) oparcie stropu z betonu zwykłego na ścianie

warstwą styropianu wewnątrz ściany; e) oparcie stropu z betonu zwykłego na ścianie

zewnętrznej z warstwą styropianu od strony zewnętrznej; f) oparcie stropu z betonu

zewnętrznej z warstwą styropianu od strony zewnętrznej; f) oparcie stropu z betonu

zwykłego na ścianie wewnętrznej z obu stron; g) oparcie stropu z betonu zwykłego na

zwykłego na ścianie wewnętrznej z obu stron; g) oparcie stropu z betonu zwykłego na

ścianie wewnętrznej z jednej strony;

ścianie wewnętrznej z jednej strony;

1

1

- nominalna oś złącza ściana/strop;

- nominalna oś złącza ściana/strop;

2

2

- nominalna

- nominalna

oś ściany.

oś ściany.



WARTOŚĆ e

WARTOŚĆ e

m

m

WYZNACZA SIĘ ZE WZORU:

WYZNACZA SIĘ ZE WZORU:



W KTÓRYM N

W KTÓRYM N

md

md

– OBCIĄŻENIE OBLICZENIOWE ŚCIANY W POŁOWIE WYSOKOŚCI

– OBCIĄŻENIE OBLICZENIOWE ŚCIANY W POŁOWIE WYSOKOŚCI



W SCIANIE ZEWNĘTRZNEJ Z WIEŃCEM OCIEPLONYM OD ZEWNĄTRZ MOMENT M

W SCIANIE ZEWNĘTRZNEJ Z WIEŃCEM OCIEPLONYM OD ZEWNĄTRZ MOMENT M

1d

1d

W

W

PRZEKROJU POD STROPEM GÓRNEJ KONDYGNACJI WYNOSI:

PRZEKROJU POD STROPEM GÓRNEJ KONDYGNACJI WYNOSI:



NA KONDYGNACJI NIŻSZEJ

NA KONDYGNACJI NIŻSZEJ



MOMENT W PRZEKROJU NAD STROPEM DOLNEJ KONDYGNACJI

MOMENT W PRZEKROJU NAD STROPEM DOLNEJ KONDYGNACJI



W ŚCIANIE WEWNĘTRZNEJ

W ŚCIANIE WEWNĘTRZNEJ

md

d

2

d

1

m

N

M

4

,

0

M

6

,

0

e





)

e

10

a

2

t

(

N

)

e

2

a

t

(

N

M

a

w

d

,

sl

a

w

d

1

d

1













)

e

6

a

2

t

(

N

)

e

2

a

t

(

N

M

a

w

d

,

sl

a

w

d

1

d

1













)

e

2

a

t

(

N

M

a

w

d

2

d

2







)

e

t

33

,

0

(

N

N

(

e

N

M

a

p

,

sl

d

,

sl

a

d

1

d

1









)

e

N

M

a

d

2

d

2





WYSOKOŚĆ EFEKTYWNA ŚCIANY

WYSOKOŚĆ EFEKTYWNA ŚCIANY

GDZIE:

GDZIE:

ρ

ρ

h

h

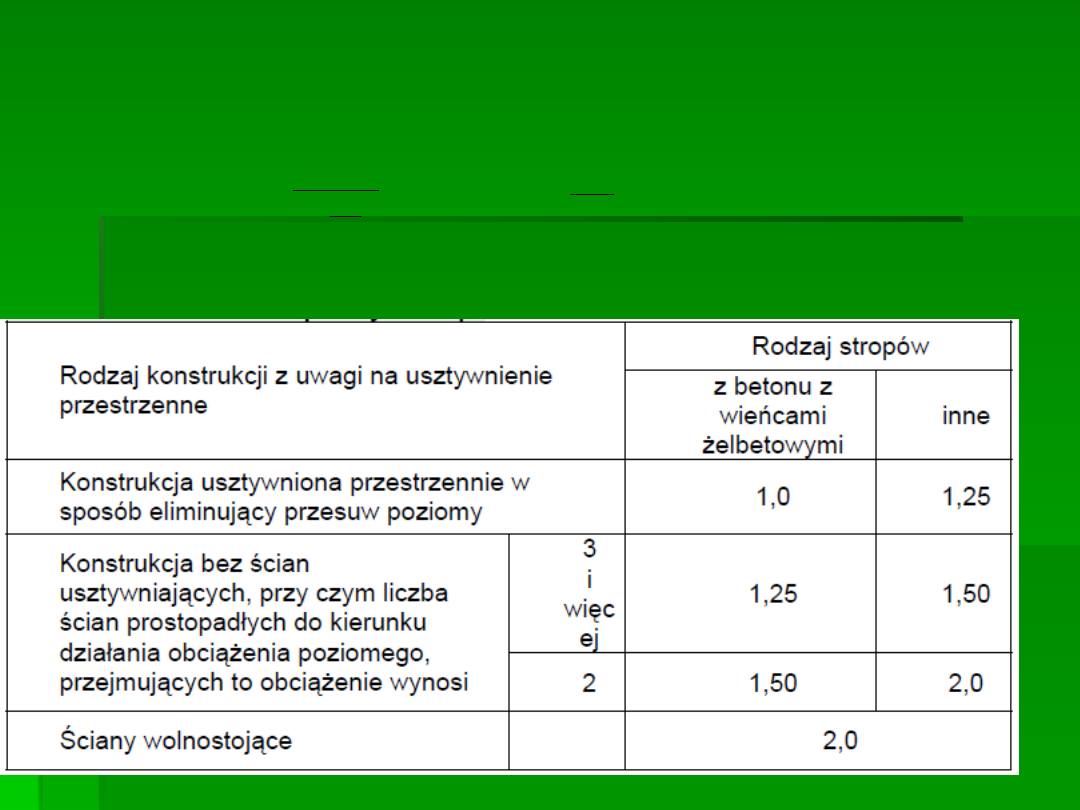
– WSPÓŁCZYNNIK REDUKCYJNY ZALEŻNY OD PRZESTRZENNEGO

– WSPÓŁCZYNNIK REDUKCYJNY ZALEŻNY OD PRZESTRZENNEGO

USZTYWNIENIA BUDYNKU (tabela3.)

USZTYWNIENIA BUDYNKU (tabela3.)

ρ

ρ

n

n

– WSPÓŁCZYNNIK REDUKCYJNY

– WSPÓŁCZYNNIK REDUKCYJNY

ρ

ρ

2

2

,

,

ρ

ρ

3

3

ODPOWIEDNIO OD USZTYWNIENIA

ODPOWIEDNIO OD USZTYWNIENIA

ŚCIANYWZDŁUŻ DWÓCH, TRZECH LUB CZTERECH KRAWĘDZI

ŚCIANYWZDŁUŻ DWÓCH, TRZECH LUB CZTERECH KRAWĘDZI

ZA WARTOŚĆ

ZA WARTOŚĆ

ρ

ρ

n

n

PRZYJMOWAĆ MOŻNA:

PRZYJMOWAĆ MOŻNA:

DLA ŚCIAN PRZYTRZYMANYCH U GÓRY I U DOŁU

DLA ŚCIAN PRZYTRZYMANYCH U GÓRY I U DOŁU

ρ

ρ

2

2

= 1,00

= 1,00

DLA ŚCIAN PRZYTRZYMYWANYCH U GÓRY I U DOŁU, USZTYWNIONYCH

DLA ŚCIAN PRZYTRZYMYWANYCH U GÓRY I U DOŁU, USZTYWNIONYCH

WZDŁUŻ JEDNEJ KRAWĘDZI PIONOWEJ (Z JEDNĄ SWOBODNĄ KRAWĘDZIĄ

WZDŁUŻ JEDNEJ KRAWĘDZI PIONOWEJ (Z JEDNĄ SWOBODNĄ KRAWĘDZIĄ

PIONOWĄ)

PIONOWĄ)

JEŻELI h<3,5L

JEŻELI h<3,5L

JEŻELI h>3,5L

JEŻELI h>3,5L

GDZIE L- ODLEGŁOŚĆ KRAWĘDZI SWOBODNEJ OD OSI ŚCIANY

GDZIE L- ODLEGŁOŚĆ KRAWĘDZI SWOBODNEJ OD OSI ŚCIANY

USZTYWNIAJĄCEJ

USZTYWNIAJĄCEJ

h

h

n

h

f







2

)

L

3

h

(

1

2

2

3











3

,

0

h

L

5

,

1

3







DLA ŚCIAN PRZYTRZYMYWANYCH U GÓRY I U DOŁU, USZTYWNIONYCH

DLA ŚCIAN PRZYTRZYMYWANYCH U GÓRY I U DOŁU, USZTYWNIONYCH

WZDŁUŻ OBU KRAWĘDZI PIONOWYCH

WZDŁUŻ OBU KRAWĘDZI PIONOWYCH

Tabela 2. Wartość współczynnika ρ

Tabela 2. Wartość współczynnika ρ

h

h

2

2

4

)

L

3

h

(

1

2











3

,

0

h

L

5

,

0

4







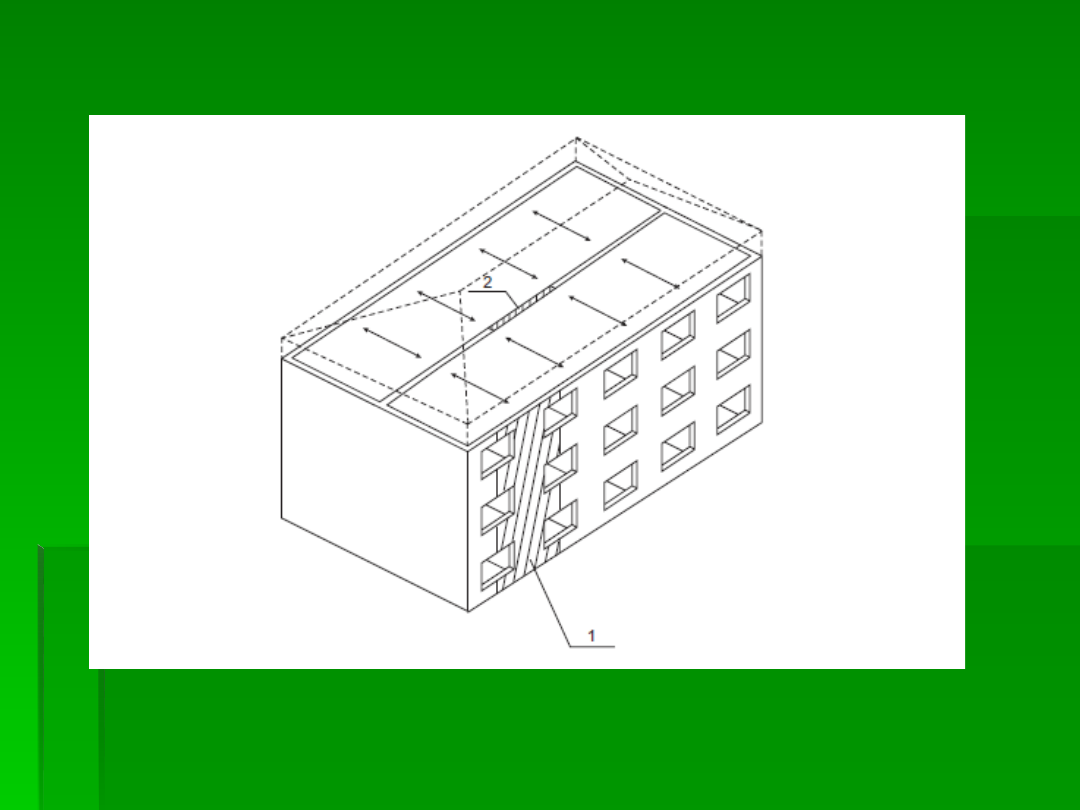
ŚCIANA ZEWNĘTRZNA

ŚCIANA ZEWNĘTRZNA

PASMA ŚCIAN SPRAWDZANE W OBLICZENIACH –

PASMA ŚCIAN SPRAWDZANE W OBLICZENIACH –

BUDYNEK W UKŁADZIE POPRZECZNYM

BUDYNEK W UKŁADZIE POPRZECZNYM

1

1

– ŚCIANA ZEWNĘTRZNA GRUBOŚCI 365 mm OBCIĄŻONA STROPAMI,

– ŚCIANA ZEWNĘTRZNA GRUBOŚCI 365 mm OBCIĄŻONA STROPAMI,

2

2

– ŚCIANA WEWNĘTRZNA GRUBOŚCI 240

– ŚCIANA WEWNĘTRZNA GRUBOŚCI 240

mm OBCIĄŻONA OBUSTRONNIE STROPAMI,

mm OBCIĄŻONA OBUSTRONNIE STROPAMI,

3

3

- ŚCIANA WEWNĘTRZNA PRZY DYLATACJI GRUBOŚCI 200 mm

- ŚCIANA WEWNĘTRZNA PRZY DYLATACJI GRUBOŚCI 200 mm

OBCIĄŻONA JEDNOSTRONNIE STROPAMI

OBCIĄŻONA JEDNOSTRONNIE STROPAMI

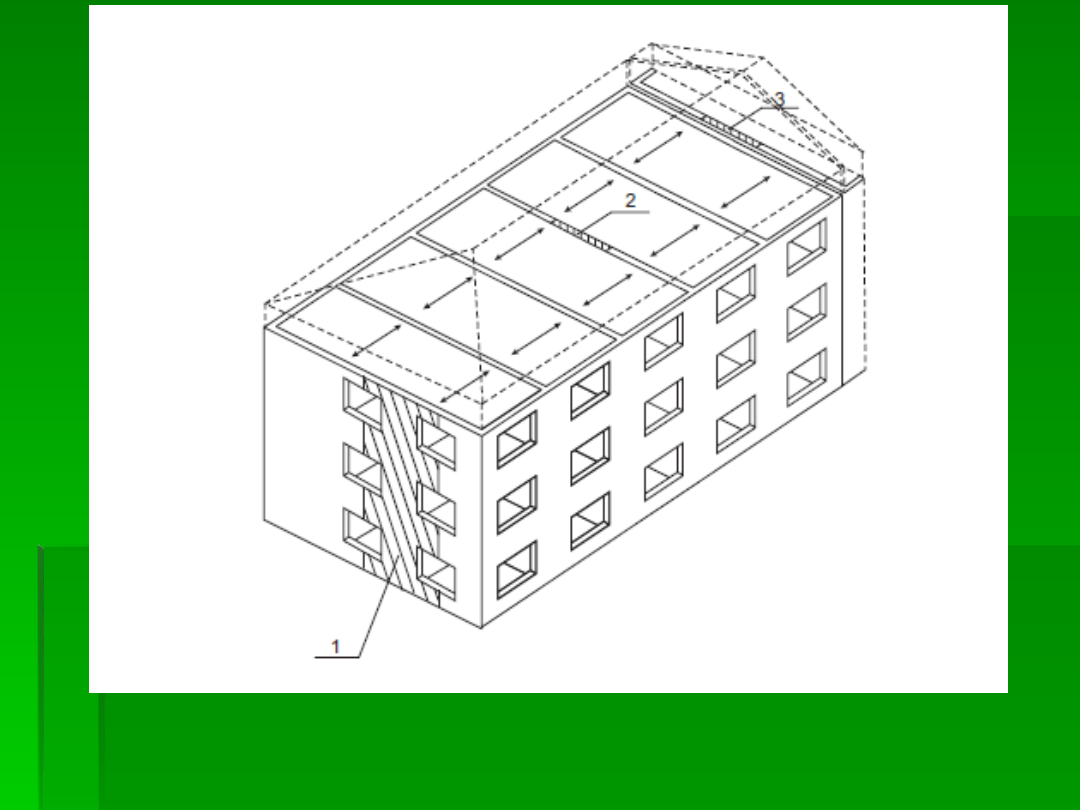
PASMA ŚCIAN SPRAWDZANE W OBLICZENIACH –

PASMA ŚCIAN SPRAWDZANE W OBLICZENIACH –

BUDYNEK W UKŁADZIE POPRZECZNYM

BUDYNEK W UKŁADZIE POPRZECZNYM

1

1

– ŚCIANA ZEWNĘTRZNA GRUBOŚCI 365 mm OBCIĄŻONA STROPAMI,

– ŚCIANA ZEWNĘTRZNA GRUBOŚCI 365 mm OBCIĄŻONA STROPAMI,

2

2

– ŚCIANA

– ŚCIANA

WEWNĘTRZNA GRUBOŚCI 240 mm OBCIĄŻONA OBUSTRONNIE STROPAMI,

WEWNĘTRZNA GRUBOŚCI 240 mm OBCIĄŻONA OBUSTRONNIE STROPAMI,

3

3

- ŚCIANA

- ŚCIANA

WEWNĘTRZNA PRZY DYLATACJI GRUBOŚCI 200 mm OBCIĄŻONA JEDNOSTRONNIE STROPAMI

WEWNĘTRZNA PRZY DYLATACJI GRUBOŚCI 200 mm OBCIĄŻONA JEDNOSTRONNIE STROPAMI

Przykład obliczeniowy 1.



Sprawdzić stan graniczny nośności dla filarka międzyokiennego

Sprawdzić stan graniczny nośności dla filarka międzyokiennego

na poziomie parteru w domu jednorodzinnym piętrowym z

na poziomie parteru w domu jednorodzinnym piętrowym z

poddaszem użytkowym. Dach jest wykonany w konstrukcji

poddaszem użytkowym. Dach jest wykonany w konstrukcji

drewnianej jako krokwiowo - płatwiowy o nachyleniu 45° z

drewnianej jako krokwiowo - płatwiowy o nachyleniu 45° z

pokryciem z blachy stalowej, długość krokwi 5 m. Stropy

pokryciem z blachy stalowej, długość krokwi 5 m. Stropy

gęstożebrowe Teriva – I bis o rozpiętości 7 m oparte na ścianach

gęstożebrowe Teriva – I bis o rozpiętości 7 m oparte na ścianach

trójwarstwowych z pustaków betonowych TAB ( pustak elewacyjny

trójwarstwowych z pustaków betonowych TAB ( pustak elewacyjny

9 cm, styropian 10 cm , pustak konstrukcyjny t = 24 cm) na

9 cm, styropian 10 cm , pustak konstrukcyjny t = 24 cm) na

zaprawie cementowej marki M5. Kategoria robót murarskich - A.

zaprawie cementowej marki M5. Kategoria robót murarskich - A.



Filarek międzyokienny o wymiarach 120/24 cm (3 pustaki)

Filarek międzyokienny o wymiarach 120/24 cm (3 pustaki)

umieszczony jest pomiędzy dwoma oknami 150/150 cm, a więc

umieszczony jest pomiędzy dwoma oknami 150/150 cm, a więc

przenosi obciążenia z pasa o szerokości 2,70 m.

przenosi obciążenia z pasa o szerokości 2,70 m.



W związku z wymiarami filarka 1,2 ⋅ 0,24 = 0,288 m

W związku z wymiarami filarka 1,2 ⋅ 0,24 = 0,288 m

2

2

< 0,3 m

< 0,3 m

2

2

należy zastosować współczynnik zmniejszający η

należy zastosować współczynnik zmniejszający η

A

A

= 1,03

= 1,03



Zestawienie obciążeń

Zestawienie obciążeń



Obliczeniowe wartości obciążeń działających na sprawdzany

Obliczeniowe wartości obciążeń działających na sprawdzany

filarek :

filarek :

1. obciążenia pionowe z dachu

1. obciążenia pionowe z dachu

- pokrycie dachowe z uwzględnieniem krokwi, łat i deskowań (0,35

- pokrycie dachowe z uwzględnieniem krokwi, łat i deskowań (0,35

kN/m2)

kN/m2)

0,35 ⋅ 2,7 ⋅ 5,0 ⋅ 0,5 ⋅ 1,2 =

0,35 ⋅ 2,7 ⋅ 5,0 ⋅ 0,5 ⋅ 1,2 =

2,84 kN

2,84 kN



- wełna mineralna gr. 15 cm

- wełna mineralna gr. 15 cm



0,6 ⋅ 0,15 ⋅ 2,7 ⋅ 5,0 ⋅ 0,5 ⋅

0,6 ⋅ 0,15 ⋅ 2,7 ⋅ 5,0 ⋅ 0,5 ⋅

1,3 = 0,79 kN

1,3 = 0,79 kN



- płyta gipsowo - kartonowa

- płyta gipsowo - kartonowa

12,0 ⋅ 0,012 ⋅ 2,7 ⋅ 5,0 ⋅ 0,5 ⋅ 1,3 =

12,0 ⋅ 0,012 ⋅ 2,7 ⋅ 5,0 ⋅ 0,5 ⋅ 1,3 =

1,27 kN

1,27 kN



- murłata

- murłata

6,0 ⋅ 0,14 ⋅ 0,14 ⋅ 2,7 ⋅ 1,1 = 0,35 kN

6,0 ⋅ 0,14 ⋅ 0,14 ⋅ 2,7 ⋅ 1,1 = 0,35 kN



- obciążenie dachu śniegiem ( I strefa , C=0,6)

- obciążenie dachu śniegiem ( I strefa , C=0,6)

0,7 ⋅ 0,6 ⋅ 2,7 ⋅ 5,0 ⋅ 0,5 ⋅ cos 45° ⋅ 1,4 =

0,7 ⋅ 0,6 ⋅ 2,7 ⋅ 5,0 ⋅ 0,5 ⋅ cos 45° ⋅ 1,4 =

2,81 kN

2,81 kN



- obciążenie wiatrem prostopadłe do połaci dachowej ( I strefa,

- obciążenie wiatrem prostopadłe do połaci dachowej ( I strefa,

teren B)

teren B)

0,25 ⋅ 0,8 ⋅ 0,475 ⋅ 1,8 ⋅ 2,7 ⋅ 5,0 ⋅ 0,5 ⋅ cos 45° ⋅ 1,3 =

0,25 ⋅ 0,8 ⋅ 0,475 ⋅ 1,8 ⋅ 2,7 ⋅ 5,0 ⋅ 0,5 ⋅ cos 45° ⋅ 1,3 =

1,10 kN

1,10 kN

razem 9,16

razem 9,16

kN

kN



2. ściana kolankowa wys. 0,60 m

2. ściana kolankowa wys. 0,60 m



- pustaki elewacyjne TAB gr. 9 cm

- pustaki elewacyjne TAB gr. 9 cm



1,50 ⋅ 2,7 ⋅ 0,6 ⋅ 1,1 = 2,68 kN

1,50 ⋅ 2,7 ⋅ 0,6 ⋅ 1,1 = 2,68 kN



- styropian gr. 10 cm

- styropian gr. 10 cm



0,1 ⋅ 0,45 ⋅ 2,7 ⋅ 0,6 ⋅ 1,2 = 0,08 kN

0,1 ⋅ 0,45 ⋅ 2,7 ⋅ 0,6 ⋅ 1,2 = 0,08 kN



- pustaki konstrukcyjne TAB gr 19 cm

- pustaki konstrukcyjne TAB gr 19 cm



2,30 ⋅ 2,7 ⋅ 0,6 ⋅ 1,1 = 4,10 kN

2,30 ⋅ 2,7 ⋅ 0,6 ⋅ 1,1 = 4,10 kN



- tynk cementowo - wapienny

- tynk cementowo - wapienny



0,015 ⋅ 19,0 ⋅ 2,7 ⋅ 0,6 ⋅ 1,3 = 0,60 kN

0,015 ⋅ 19,0 ⋅ 2,7 ⋅ 0,6 ⋅ 1,3 = 0,60 kN



razem 7,45 kN

razem 7,45 kN



3. strop nad piętrem ( Teriva – I bis ) oraz strop nad

3. strop nad piętrem ( Teriva – I bis ) oraz strop nad

parterem

parterem



- klepka

- klepka



0,23 ⋅ 2,7 ⋅ 7,0 ⋅ 0,5 ⋅ 1,2 = 2,61 kN

0,23 ⋅ 2,7 ⋅ 7,0 ⋅ 0,5 ⋅ 1,2 = 2,61 kN



- szlichta cementowa 3 cm

- szlichta cementowa 3 cm



0,03 ⋅ 21,0 ⋅ 2,7 ⋅ 7,0 ⋅ 0,5 ⋅ 1,3 = 7,74 kN

0,03 ⋅ 21,0 ⋅ 2,7 ⋅ 7,0 ⋅ 0,5 ⋅ 1,3 = 7,74 kN



- styropian 3 cm

- styropian 3 cm



0,03 ⋅ 0,45 ⋅ 2,7 ⋅ 7,0 ⋅ 0,5 ⋅ 1,2 = 0,15 kN

0,03 ⋅ 0,45 ⋅ 2,7 ⋅ 7,0 ⋅ 0,5 ⋅ 1,2 = 0,15 kN



- strop Teriva – I bis

- strop Teriva – I bis



3,57 ⋅ 2,7 ⋅ 7,0 ⋅ 0,5 ⋅ 1,1 = 37,11 kN

3,57 ⋅ 2,7 ⋅ 7,0 ⋅ 0,5 ⋅ 1,1 = 37,11 kN



- tynk cementowo-wapienny

- tynk cementowo-wapienny



0,015 ⋅ 19,0 ⋅ 2,7 ⋅ 7,0 ⋅ 0,5 ⋅ 1,3 = 3,50 kN

0,015 ⋅ 19,0 ⋅ 2,7 ⋅ 7,0 ⋅ 0,5 ⋅ 1,3 = 3,50 kN



- obciążenie od ścianek działowych

- obciążenie od ścianek działowych



1,25 ⋅ 2,7 ⋅ 7,0 ⋅ 0,5 ⋅ 1,2 = 14,18 kN

1,25 ⋅ 2,7 ⋅ 7,0 ⋅ 0,5 ⋅ 1,2 = 14,18 kN



- obciążenie użytkowe

- obciążenie użytkowe



1,5 ⋅ 2,7 ⋅ 7,0 ⋅ 0,5 ⋅ 1,4 = 19,85 kN

1,5 ⋅ 2,7 ⋅ 7,0 ⋅ 0,5 ⋅ 1,4 = 19,85 kN



razem 85,13 kN

razem 85,13 kN



ściana piętra wys. 2,7m ( również ściana parteru) – dla

ściana piętra wys. 2,7m ( również ściana parteru) – dla

uproszczenia bez potrącania powierzchni okien

uproszczenia bez potrącania powierzchni okien



- pustaki elewacyjne TAB gr. 9 cm

- pustaki elewacyjne TAB gr. 9 cm



1,50 ⋅ 2,7 ⋅ 2,7 ⋅ 1,1 = 12,03 kN

1,50 ⋅ 2,7 ⋅ 2,7 ⋅ 1,1 = 12,03 kN



- styropian gr. 10 cm

- styropian gr. 10 cm



0,1 ⋅ 0,45 ⋅ 2,7 ⋅ 2,7 ⋅ 1,2 = 0,40 kN

0,1 ⋅ 0,45 ⋅ 2,7 ⋅ 2,7 ⋅ 1,2 = 0,40 kN



- pustaki konstrukcyjne TAB gr 24 cm

- pustaki konstrukcyjne TAB gr 24 cm



2,75 ⋅ 2,7 ⋅ 2,7 ⋅ 1,1 = 22,05 kN

2,75 ⋅ 2,7 ⋅ 2,7 ⋅ 1,1 = 22,05 kN



- tynk cementowo - wapienny

- tynk cementowo - wapienny



0,015 ⋅ 19,0 ⋅ 2,7 ⋅ 2,7 ⋅ 1,3 = 2,70 kN

0,015 ⋅ 19,0 ⋅ 2,7 ⋅ 2,7 ⋅ 1,3 = 2,70 kN



razem 37,18 kN

razem 37,18 kN

5. obciążenie poziome od ssania wiatru

5. obciążenie poziome od ssania wiatru



q

q

k

k

= 250 Pa – strefa I

= 250 Pa – strefa I



C

C

e

e

= 0,8 – teren zabudowany przy wysokości

= 0,8 – teren zabudowany przy wysokości

istniejących budynków do 10 m

istniejących budynków do 10 m



C = 0,4 – ssanie wiatru H/L< 2 , B/L< 1

C = 0,4 – ssanie wiatru H/L< 2 , B/L< 1



β = 1,8

β = 1,8



γ

γ

f

f

= 1.3

= 1.3



p = q

p = q

k

k

⋅ C

⋅ C

e

e

⋅ C ⋅ β ⋅ γ

⋅ C ⋅ β ⋅ γ

f

f

= 0,25 ⋅ 0,8 ⋅ 0,4 ⋅ 1,8 ⋅ 1,3

= 0,25 ⋅ 0,8 ⋅ 0,4 ⋅ 1,8 ⋅ 1,3

= 0,19 kN/m2

= 0,19 kN/m2



w

w

d

d

= p ⋅ 2,7 m = 0,19 ⋅ 2,7 = 0,51 kN/m

= p ⋅ 2,7 m = 0,19 ⋅ 2,7 = 0,51 kN/m



Sprawdzanie nośności filarka :

Sprawdzanie nośności filarka :



Siła

Siła

N

N

1d

1d

obciążająca filarek w poziomie stropu nad

obciążająca filarek w poziomie stropu nad

parterem

parterem



N

N

1d

1d

= 9,16 + 7,45 + 85,13 + 37,18 = 138,92 kN

= 9,16 + 7,45 + 85,13 + 37,18 = 138,92 kN



Siła

Siła

N

N

si,d

si,d

obciążająca filarek od stropu nad parterem

obciążająca filarek od stropu nad parterem



N

N

si,d

si,d

= 85,13 kN

= 85,13 kN



Siła

Siła

N

N

2d

2d

obciążająca filarek w poziomie podłogi

obciążająca filarek w poziomie podłogi

parteru

parteru



N

N

2d

2d

= 138,92 + 85,13 + 37,18 = 261,23 kN

= 138,92 + 85,13 + 37,18 = 261,23 kN



Siła

Siła

N

N

md

md

obciążająca filarek w połowie wysokości

obciążająca filarek w połowie wysokości

ściany parteru

ściany parteru



N

N

md

md

= 138,92 + 85,13 + 0,5 ⋅ 37,18 = 242,64 kN

= 138,92 + 85,13 + 0,5 ⋅ 37,18 = 242,64 kN



Mimośród przypadkowy

Mimośród przypadkowy



e

e

a

a

= h/300 = 2,7 m / 300 = 8,1 mm < 10 mm

= h/300 = 2,7 m / 300 = 8,1 mm < 10 mm



e

e

a

a

= 10 mm

= 10 mm



Moment zginający zgodnie z wzorem

Moment zginający zgodnie z wzorem



M

M

1d

1d

= N

= N

1d

1d

e

e

a

a

+ N

+ N

si,d

si,d

(0,33t + e

(0,33t + e

a

a

) = 138,92 ⋅ 0,01 +

) = 138,92 ⋅ 0,01 +

85,13 ⋅ (0,33 ⋅ 0,24 + 0,01) = 8,98 kN⋅m

85,13 ⋅ (0,33 ⋅ 0,24 + 0,01) = 8,98 kN⋅m



Moment zginający zgodnie z wzorem

Moment zginający zgodnie z wzorem



M

M

2d

2d

= N

= N

2d

2d

e

e

a

a

= 261,23 ⋅ 0,01 = 2,61 kN⋅m

= 261,23 ⋅ 0,01 = 2,61 kN⋅m



Wysokość efektywna ściany zgodnie z wzorem oraz

Wysokość efektywna ściany zgodnie z wzorem oraz

Tabelą 2

Tabelą 2



h

h

ef

ef

= ρ

= ρ

h

h

ρ

ρ

n

n

h = 1,0 ⋅ 1,0 ⋅ 2,7 = 2,7 m

h = 1,0 ⋅ 1,0 ⋅ 2,7 = 2,7 m



Moment zginający zgodnie z wzorem

Moment zginający zgodnie z wzorem



M

M

wd

wd

= w

= w

d

d

hef

hef

2

2

/ 8 = 0,51 ⋅ 2,72 / 8 = 0,47 kN⋅m

/ 8 = 0,51 ⋅ 2,72 / 8 = 0,47 kN⋅m



Zastępczy mimośród początkowy zgodnie z wzorami

Zastępczy mimośród początkowy zgodnie z wzorami



e

e

m

m

= (0,6 M

= (0,6 M

1d

1d

+ 0,4 M

+ 0,4 M

2d

2d

+ M

+ M

wd

wd

) / N

) / N

md

md

= (0,6 ⋅ 8,98 +

= (0,6 ⋅ 8,98 +

0,4 ⋅ 2,61 + 0,47) / 242,64 = 2,84 cm

0,4 ⋅ 2,61 + 0,47) / 242,64 = 2,84 cm



Współczynnik redukcyjny nośności zgodnie ze

Współczynnik redukcyjny nośności zgodnie ze

wzorami

wzorami



λ = 0,0378 h

λ = 0,0378 h

ef

ef

/ t = 0,0378 ⋅ 2,7 / 0,24 = 0,4253

/ t = 0,0378 ⋅ 2,7 / 0,24 = 0,4253



u = (λ – 0,063) / (0,73 – 1,17e

u = (λ – 0,063) / (0,73 – 1,17e

m

m

/ t) = (0,4253 –

/ t) = (0,4253 –

0,063) /

0,063) /

(0,73 – 1,17 ⋅ 2,84 / 24,0) = 0,61

(0,73 – 1,17 ⋅ 2,84 / 24,0) = 0,61



Φ

Φ

m

m

= (1-2 e

= (1-2 e

m

m

/ t) e

/ t) e

-u⋅u/2

-u⋅u/2

= (1 – 2 ⋅ 2,84 / 24,0) ⋅ e –

= (1 – 2 ⋅ 2,84 / 24,0) ⋅ e –

0,61 ⋅ 0,61 / 2 = 0,63

0,61 ⋅ 0,61 / 2 = 0,63



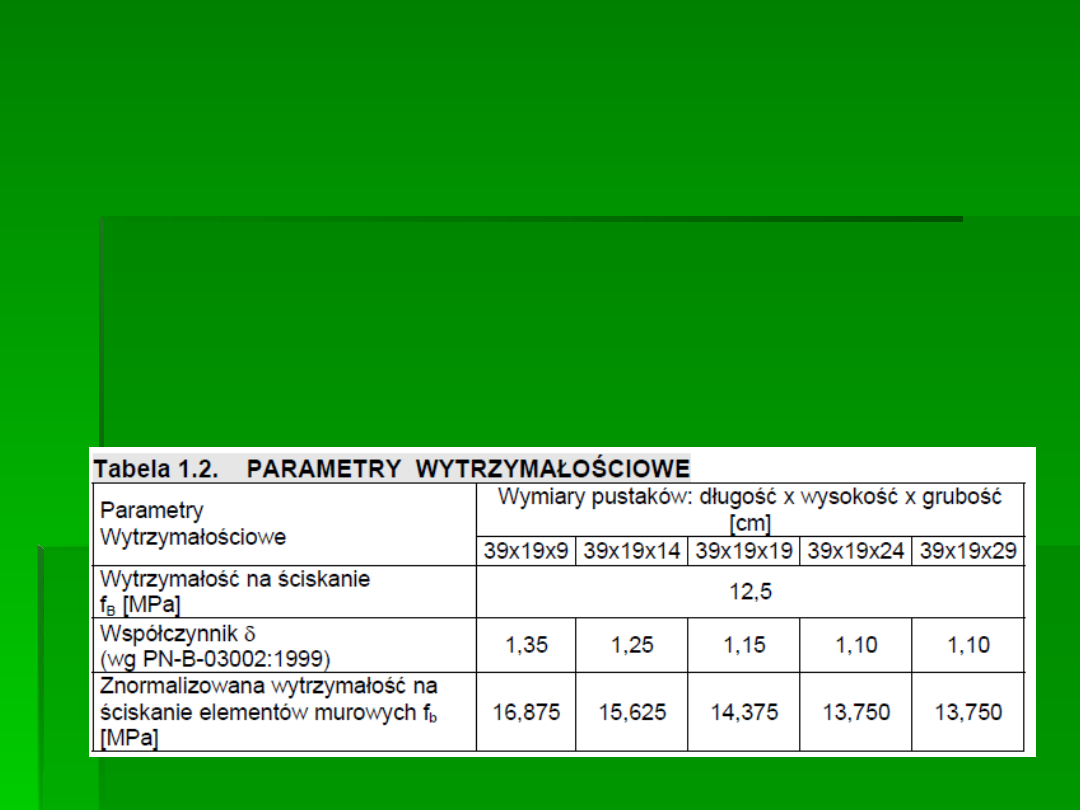
Wytrzymałość obliczeniową muru TAB na ściskanie zgodnie ze

Wytrzymałość obliczeniową muru TAB na ściskanie zgodnie ze

wzorami oraz Tabelą 1.2

wzorami oraz Tabelą 1.2



f

f

d

d

= 0,45 f

= 0,45 f

b

b

0,65 f

0,65 f

m

m

0,25 / γ

0,25 / γ

m

m

η

η

A

A

= 0,45 ⋅ 14,375 0,65 ⋅ 5,0

= 0,45 ⋅ 14,375 0,65 ⋅ 5,0

0,25 / 1,7⋅ 1,03 = 2,17 MPa =

0,25 / 1,7⋅ 1,03 = 2,17 MPa =

0,217 kN / cm

0,217 kN / cm

2

2



Nośność ściany zgodnie ze wzorem

Nośność ściany zgodnie ze wzorem



N

N

mR,d

mR,d

= Φ

= Φ

m

m

Af

Af

d

d

= 0,63 ⋅ 24 ⋅ 120 ⋅ 0,217 = 393,72 kN > N

= 0,63 ⋅ 24 ⋅ 120 ⋅ 0,217 = 393,72 kN > N

md

md

=

=

242,64

242,64

kN

kN



Nośność filarka jest wystarczająca.

Nośność filarka jest wystarczająca.

ZASADY OBLICZEŃ STATYCZNYCH ŚCIAN

WYPEŁNIAJĄCYCH



Ściany wypełniające zakwalifikowane są przez

Ściany wypełniające zakwalifikowane są przez

normę jako ściany obciążone głównie poziomo.

normę jako ściany obciążone głównie poziomo.

Dotyczy to przypadków gdy na ścianę działa

Dotyczy to przypadków gdy na ścianę działa

obciążenie wiatrem lub obciążenie wyjątkowe.

obciążenie wiatrem lub obciążenie wyjątkowe.

Nośność takich ścian, uzależnioną od wytrzymałości

Nośność takich ścian, uzależnioną od wytrzymałości

muru na rozciąganie sprawdza się z warunku :

muru na rozciąganie sprawdza się z warunku :



M

M

Sd

Sd

≤ W f

≤ W f

xd

xd



W = b t

W = b t

2

2

/ 6

/ 6



w którym:

w którym:

M

M

Sd

Sd

– obliczeniowy moment zginający od

– obliczeniowy moment zginający od

obliczeniowego obciążenia

obliczeniowego obciążenia



pionowego

pionowego



f

f

xd

xd

– wytrzymałość obliczeniowa muru na

– wytrzymałość obliczeniowa muru na

rozciąganie przy zginaniu,

rozciąganie przy zginaniu,



W

W

– wskaźnik wytrzymałości przekroju muru

– wskaźnik wytrzymałości przekroju muru



Przy zginaniu muru wywołanego rozciąganiem w

Przy zginaniu muru wywołanego rozciąganiem w

przekroju równoległym do warstw muru należy

przekroju równoległym do warstw muru należy

zastosować zbrojenie stalowe w spoinach

zastosować zbrojenie stalowe w spoinach

wspornych, a nośność sprawdzać z zależności :

wspornych, a nośność sprawdzać z zależności :



M

M

Sd

Sd

≤ A

≤ A

s

s

f

f

y

y

0,8 d

0,8 d



M

M

Sd

Sd

≤ f

≤ f

d

d

0,4 d

0,4 d

2

2

b

b



Dodatkowo w konstrukcjach murowych

Dodatkowo w konstrukcjach murowych

obciążonych poprzecznie należy sprawdzać

obciążonych poprzecznie należy sprawdzać

nośność muru na ścinanie przy zginaniu :

nośność muru na ścinanie przy zginaniu :



V

V

Sd

Sd

≤ 0,75 f

≤ 0,75 f

xd

xd

b d

b d



Gdzie:

Gdzie:

A

A

s

s

f

f

y

y

–pole przekroju i wytrzymałość

–pole przekroju i wytrzymałość

obliczeniowa rozciąganego zbrojenia w spoinie

obliczeniowa rozciąganego zbrojenia w spoinie

muru

muru



d

d

– wysokość efektywna przekroju

– wysokość efektywna przekroju



b

b

– szerokość zginanego przekroju muru

– szerokość zginanego przekroju muru



W przypadku ścian wypełniających obciążonych

W przypadku ścian wypełniających obciążonych

głownie poziomo parciem wiatru w

głownie poziomo parciem wiatru w

najniekorzystniejszej sytuacji znajduje się filar

najniekorzystniejszej sytuacji znajduje się filar

ograniczony przez dwa otwory. Naprężenia

ograniczony przez dwa otwory. Naprężenia

rozciągające wywołane zginaniem w przekroju

rozciągające wywołane zginaniem w przekroju

równoległym do warstw muru muszą być

równoległym do warstw muru muszą być

przejęte przez zbrojenie stalowe umieszczone w

przejęte przez zbrojenie stalowe umieszczone w

zabetonowanych kanałach pionowych muru.

zabetonowanych kanałach pionowych muru.



Pojedynczy filar można traktować jak pręt

Pojedynczy filar można traktować jak pręt

obustronnie zamocowany, gdy zbrojenie

obustronnie zamocowany, gdy zbrojenie

pionowe w kanałach przechodzi przez kilka

pionowe w kanałach przechodzi przez kilka

przęseł, a moment zginający w połowie

przęseł, a moment zginający w połowie

wysokości filara wynosi :

wysokości filara wynosi :



M

M

Sd

Sd

= w

= w

wd

wd

h

h

2

2

/ 12

/ 12



gdzie :

gdzie :



w

w

wd

wd

– obciążenie obliczeniowe wiatrem

– obciążenie obliczeniowe wiatrem



h

h

– wysokość filara w świetle stropów

– wysokość filara w świetle stropów

Przykład obliczeniowy 2.



Należy sprawdzić stan graniczny nośności dla ściany

Należy sprawdzić stan graniczny nośności dla ściany

wypełniającej obciążonej parciem wiatru. Ściana wykonana jest

wypełniającej obciążonej parciem wiatru. Ściana wykonana jest

z pustaków grubości t = 19 cm na zaprawie cementowej marki

z pustaków grubości t = 19 cm na zaprawie cementowej marki

M5. Kategoria robót murarskich - A.

M5. Kategoria robót murarskich - A.



Dane dla obliczenia obciążenia wiatrem :

Dane dla obliczenia obciążenia wiatrem :



q

q

k

k

= 250 Pa – strefa I

= 250 Pa – strefa I



C

C

e

e

= 0,8 – teren zabudowany przy wysokości istniejących

= 0,8 – teren zabudowany przy wysokości istniejących

budynków do 10 m

budynków do 10 m



C

C

= 0,7 – parcie wiatru H/L< 2 , B/L< 1

= 0,7 – parcie wiatru H/L< 2 , B/L< 1



β

β

= 1,8

= 1,8



γ

γ

f

f

= 1.3

= 1.3



p = q

p = q

k

k

⋅ C

⋅ C

e

e

⋅ C ⋅ β ⋅ γ

⋅ C ⋅ β ⋅ γ

f

f

= 0,25 ⋅ 0,8 ⋅ 0,7 ⋅ 1,8 ⋅ 1,3 = 0,33 kN/m

= 0,25 ⋅ 0,8 ⋅ 0,7 ⋅ 1,8 ⋅ 1,3 = 0,33 kN/m

2

2



Rozstaw ścian usztywniających b

Rozstaw ścian usztywniających b

e

e

= 7,0 m.

= 7,0 m.



Moment zginający w ścianie od parcia wiatru dla

Moment zginający w ścianie od parcia wiatru dla

pasma ściany wysokości 1 m:

pasma ściany wysokości 1 m:



M

M

Sd

Sd

= p ⋅ 1,0 ⋅ b

= p ⋅ 1,0 ⋅ b

e

e

2

2

/ 8 = 0,33 ⋅ 1,0 ⋅ 7,0

/ 8 = 0,33 ⋅ 1,0 ⋅ 7,0

2

2

/ 8 = 2,02

/ 8 = 2,02

kNm

kNm



Wskaźnik wytrzymałości przekroju ściany zgodnie

Wskaźnik wytrzymałości przekroju ściany zgodnie

ze wzorem

ze wzorem



W = b

W = b

e

e

t

t

2

2

/ 6 = 100 ⋅ 192 / 6 = 6016 cm

/ 6 = 100 ⋅ 192 / 6 = 6016 cm

3

3



Wytrzymałość obliczeniowa muru na rozciąganie

Wytrzymałość obliczeniowa muru na rozciąganie

przy zginaniu zgodnie ze wzorem dla zaprawy

przy zginaniu zgodnie ze wzorem dla zaprawy

marki M5 i kategorii robót A

marki M5 i kategorii robót A



f

f

xd

xd

= f

= f

xk

xk

/ γ

/ γ

m

m

= 0,2 / 1,7 = 0,117 MPa = 117 kN/m

= 0,2 / 1,7 = 0,117 MPa = 117 kN/m

2

2



Warunek nośności zgodnie ze wzorem

Warunek nośności zgodnie ze wzorem



M

M

Sd

Sd

= 2,02 kNm > W f

= 2,02 kNm > W f

xd

xd

= 0,006 ⋅ 117 = 0,702 kNm

= 0,006 ⋅ 117 = 0,702 kNm

nie jest spełniony.

nie jest spełniony.



Dla wzmocnienia ściany zastosowano w spoinach

Dla wzmocnienia ściany zastosowano w spoinach

wspornych zbrojenie w postaci prętów o średnicy 5

wspornych zbrojenie w postaci prętów o średnicy 5

mm z zachowaniem 20 mm otuliny od lica ściany. W

mm z zachowaniem 20 mm otuliny od lica ściany. W

paśmie wysokości 1 m znajduje się 5 prętów co 20

paśmie wysokości 1 m znajduje się 5 prętów co 20

cm.

cm.



Tak zazbrojony mur należy sprawdzić z zależności

Tak zazbrojony mur należy sprawdzić z zależności



M

M

Sd

Sd

= 2,02 kNm ≤ A

= 2,02 kNm ≤ A

s

s

f

f

y

y

0,8 d = 5 ⋅ 0,196 ⋅ 21 ⋅

0,8 d = 5 ⋅ 0,196 ⋅ 21 ⋅

0,8 ⋅ 17 = 2,80 kNm

0,8 ⋅ 17 = 2,80 kNm



M

M

Sd

Sd

= 2,02 kNm ≤ f

= 2,02 kNm ≤ f

d

d

0,4 d

0,4 d

2

2

b = 0,381 / 1,7 ⋅ 0,4 ⋅

b = 0,381 / 1,7 ⋅ 0,4 ⋅

172 ⋅ 100 = 25,91 kNm

172 ⋅ 100 = 25,91 kNm



Warunek nośności na zginanie spełniony.

Warunek nośności na zginanie spełniony.



Nośność muru na ścinanie przy zginaniu według

Nośność muru na ścinanie przy zginaniu według

zależności :

zależności :



V

V

Sd

Sd

= 0,5 ⋅ p ⋅ 1,0 ⋅ 7,0 = 0,5 ⋅ 0,33 ⋅ 1,0 ⋅ 7,0 =

= 0,5 ⋅ p ⋅ 1,0 ⋅ 7,0 = 0,5 ⋅ 0,33 ⋅ 1,0 ⋅ 7,0 =

1,15 kN ≤ 0,75 f

1,15 kN ≤ 0,75 f

xd

xd

b d = 0,75 ⋅ 117 ⋅ 1,0 ⋅ 0,17 =

b d = 0,75 ⋅ 117 ⋅ 1,0 ⋅ 0,17 =

14,92 kN

14,92 kN



Warunek nośności na ścinanie spełniony.

Warunek nośności na ścinanie spełniony.

OGÓLNE ZASADY OBLICZEŃ

STATYCZNYCH ŚCIAN PIWNIC



Nośność ścian piwnic poddanych poziomemu parciu

Nośność ścian piwnic poddanych poziomemu parciu

ziemi oblicza się jak nośność ścian obciążonych

ziemi oblicza się jak nośność ścian obciążonych

głównie pionowo z warunku, a dodatkowo należy

głównie pionowo z warunku, a dodatkowo należy

stwierdzić czy w spoinie wspornej, w której jest ułożona

stwierdzić czy w spoinie wspornej, w której jest ułożona

izolacja przeciwwilgociowa, nie następuje poślizg.

izolacja przeciwwilgociowa, nie następuje poślizg.



Sprawdzenie to odbywa się z warunku

Sprawdzenie to odbywa się z warunku



V

V

Sd

Sd

< f

< f

vd

vd

A

A



W którym:

W którym:

V

V

Sd

Sd

– obliczeniowa siła pozioma wywołana

– obliczeniowa siła pozioma wywołana

parciem gruntu (wg PN-88/B-20014)

parciem gruntu (wg PN-88/B-20014)

f

f

vd

vd

– obliczeniowa wytrzymałość na ścinanie w spoinie,

– obliczeniowa wytrzymałość na ścinanie w spoinie,

w

w

której znajduje się warstwa

której znajduje się warstwa

przeciwpoślizgowa

przeciwpoślizgowa

A

A

– pole przekroju ściany

– pole przekroju ściany

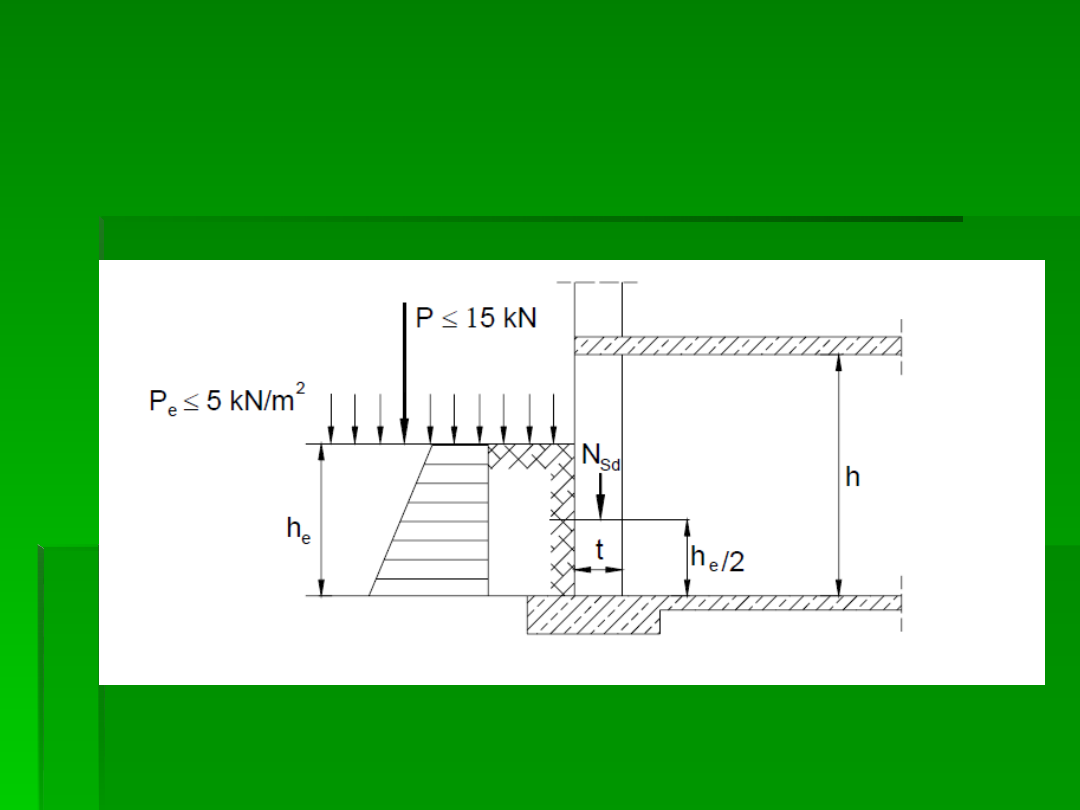
Siły obliczeniowe oddziałujące na ścianę piwnicy.



Jeżeli powyższy warunek nie jest spełniony należy

Jeżeli powyższy warunek nie jest spełniony należy

wykonać odpowiednie zabezpieczenie

wykonać odpowiednie zabezpieczenie

przeciwpoślizgowe, np. w postaci warstwy

przeciwpoślizgowe, np. w postaci warstwy

chudego betonu powyżej wierzchu fundamentu.

chudego betonu powyżej wierzchu fundamentu.

Przy takim zabezpieczeniu warunek sprawdza się

Przy takim zabezpieczeniu warunek sprawdza się

przyjmując za

przyjmując za

f

f

vd

vd

obliczeniową wytrzymałość na

obliczeniową wytrzymałość na

ścinanie zwykłej spoiny poziomej w murze TABELA

ścinanie zwykłej spoiny poziomej w murze TABELA



Jeżeli warunek braku poślizgu w spoinie wspornej, w której jest

Jeżeli warunek braku poślizgu w spoinie wspornej, w której jest

ułożona izolacja przeciwwilgociowa jest spełniony norma

ułożona izolacja przeciwwilgociowa jest spełniony norma

PN-B-

PN-B-

03002:1999

03002:1999

dopuszcza sprawdzanie stanu granicznego nośności

dopuszcza sprawdzanie stanu granicznego nośności

ścian piwnic obciążonych poziomym parciem gruntu w sposób

ścian piwnic obciążonych poziomym parciem gruntu w sposób

uproszczony, jeśli również :

uproszczony, jeśli również :

−

−

wysokość w świetle ściany piwnicy

wysokość w świetle ściany piwnicy

h ≤ 2600 mm

h ≤ 2600 mm

, a grubość

, a grubość

t ≥ 240 mm,

t ≥ 240 mm,

−

−

strop nad ścianą działa jako przepona pozioma i zdolny jest

strop nad ścianą działa jako przepona pozioma i zdolny jest

przejąć siły wywołane parciem gruntu,

przejąć siły wywołane parciem gruntu,

−

−

obciążenie zmienne powierzchni gruntu (obciążenie

obciążenie zmienne powierzchni gruntu (obciążenie

naziomem)

naziomem)

P

P

e

e

≤ 5 kN/m

≤ 5 kN/m

2

2

, a obciążenie skupione w odległości

, a obciążenie skupione w odległości

od ściany nie większej niż

od ściany nie większej niż

1500 mm

1500 mm

nie przekracza

nie przekracza

15 kN

15 kN

,

,

−

−

powierzchnia gruntu nie podnosi się, a głębokość zasypania

powierzchnia gruntu nie podnosi się, a głębokość zasypania

ściany gruntem

ściany gruntem

h

h

e

e

nie przekracza wysokości ściany,

nie przekracza wysokości ściany,

−

−

nie występuje parcie hydrostatyczne,

nie występuje parcie hydrostatyczne,

−

−

pionowe obciążenie obliczeniowe ściany na jednostkę

pionowe obciążenie obliczeniowe ściany na jednostkę

długości

długości

N

N

Sd

Sd

, wynikające ze stałego obciążenia ściany w

, wynikające ze stałego obciążenia ściany w

połowie wysokości zasypania gruntem spełnia następujące

połowie wysokości zasypania gruntem spełnia następujące

zależności :

zależności :



kiedy

kiedy

b

b

e

e

≥ 2 h

≥ 2 h

:

:



t f

t f

k

k

/ 3 γ

/ 3 γ

m

m

≥ N

≥ N

Sd

Sd

≥ ρ

≥ ρ

e

e

h h

h h

e

e

2

2

/ 20 t

/ 20 t



w której:

w której:

b

b

e

e

– odległość między ścianami poprzecznymi lub

– odległość między ścianami poprzecznymi lub

innymi elementami usztywniającymi

innymi elementami usztywniającymi

h

h

– wysokość w świetle ściany piwnicy

– wysokość w świetle ściany piwnicy

f

f

k

k

– wg zależności

– wg zależności

h

h

e

e

– głębokość zasypania ściany gruntem

– głębokość zasypania ściany gruntem

t

t

– grubość ściany

– grubość ściany

ρ

ρ

e

e

– gęstość objętościowa gruntu

– gęstość objętościowa gruntu



kiedy

kiedy

b

b

e

e

≤ h

≤ h

:

:



t f

t f

k

k

/ 3 γ

/ 3 γ

m

m

≥ N

≥ N

Sd

Sd

≥ ρ

≥ ρ

e

e

h h

h h

e

e

2

2

/ 40 t

/ 40 t

kiedy

kiedy

h < b

h < b

e

e

< 2

< 2

h dopuszcza się interpolację

h dopuszcza się interpolację

liniową wartość prawej strony nierówności

liniową wartość prawej strony nierówności

uzyskanych z równań

uzyskanych z równań



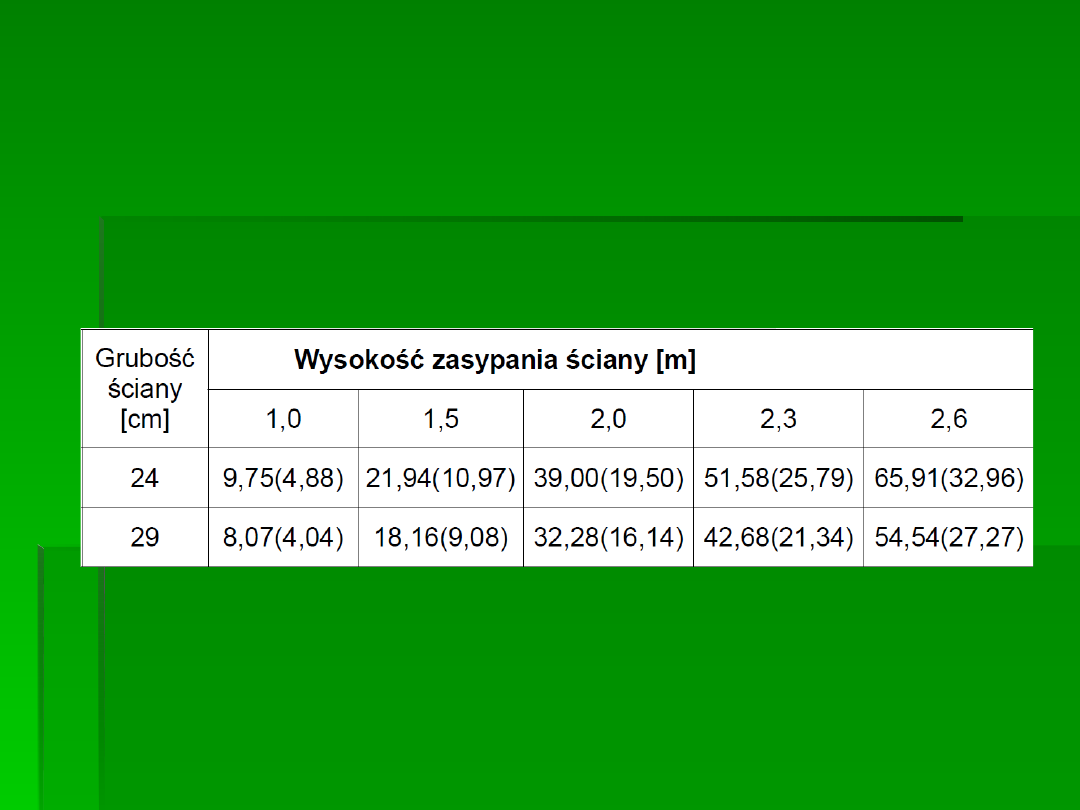
Tabela 7.5. Wartości minimalne siły N

Sd

[kN/m], przy

której można stosować sposób uproszczony
obliczeń

Przykład obliczeniowy 3.

Należy sprawdzić stan graniczny nośności

Należy sprawdzić stan graniczny nośności

ściany piwnic w budynku z przykładu 1.

ściany piwnic w budynku z przykładu 1.



Szerokość sprawdzanego pasma wynosi 1

Szerokość sprawdzanego pasma wynosi 1

m. Wysokość ściany piwnicznej w świetle 2.6

m. Wysokość ściany piwnicznej w świetle 2.6

m. Odległość pomiędzy ścianami

m. Odległość pomiędzy ścianami

usztywniającymi wynosi be = 7m. Wysokość

usztywniającymi wynosi be = 7m. Wysokość

zasypania gruntem o gęstości objętościowej

zasypania gruntem o gęstości objętościowej

18kN/m3 wynosi 1,8 m.

18kN/m3 wynosi 1,8 m.



Zestawienie obciążeń

Zestawienie obciążeń



Obliczeniowe wartości obciążeń stałych działających

Obliczeniowe wartości obciążeń stałych działających

na pasmo szerokości 1 m ściany piwnicy w połowie

na pasmo szerokości 1 m ściany piwnicy w połowie

wysokości zasypania gruntem :

wysokości zasypania gruntem :



1. obciążenia pionowe z dachu

1. obciążenia pionowe z dachu



- pokrycie dachowe z uwzględnieniem krokwi, łat i

- pokrycie dachowe z uwzględnieniem krokwi, łat i

deskowań (0,35 kN/m2)

deskowań (0,35 kN/m2)



0,35 ⋅ 1,0 ⋅ 5,0 ⋅ 0,5 ⋅ 1,2 = 1,05 kN

0,35 ⋅ 1,0 ⋅ 5,0 ⋅ 0,5 ⋅ 1,2 = 1,05 kN



- wełna mineralna gr. 15 cm

- wełna mineralna gr. 15 cm



0,6 ⋅ 0,15 ⋅ 1,0 ⋅ 5,0 ⋅ 0,5 ⋅ 1,3 = 0,29 kN

0,6 ⋅ 0,15 ⋅ 1,0 ⋅ 5,0 ⋅ 0,5 ⋅ 1,3 = 0,29 kN



- płyta gipsowo - kartonowa

- płyta gipsowo - kartonowa



12,0 ⋅ 0,012 ⋅ 1,0 ⋅ 5,0 ⋅ 0,5 ⋅ 1,3 = 0,47 kN

12,0 ⋅ 0,012 ⋅ 1,0 ⋅ 5,0 ⋅ 0,5 ⋅ 1,3 = 0,47 kN



- murłata

- murłata



6,0 ⋅ 0,14 ⋅ 0,14 ⋅ 1,0 ⋅ 1,1 = 0,13 kN

6,0 ⋅ 0,14 ⋅ 0,14 ⋅ 1,0 ⋅ 1,1 = 0,13 kN

razem

razem

1,94 kN

1,94 kN



2. ściana kolankowa wys. 0,60 m

2. ściana kolankowa wys. 0,60 m



- pustaki elewacyjne TAB gr. 9 cm

- pustaki elewacyjne TAB gr. 9 cm



1,50 ⋅ 1,0 ⋅ 0,6 ⋅ 1,1 = 0,99 kN

1,50 ⋅ 1,0 ⋅ 0,6 ⋅ 1,1 = 0,99 kN



- styropian gr. 10 cm

- styropian gr. 10 cm



0,1 ⋅ 0,45 ⋅ 1,0 ⋅ 0,6 ⋅ 1,2 = 0,03 kN

0,1 ⋅ 0,45 ⋅ 1,0 ⋅ 0,6 ⋅ 1,2 = 0,03 kN



- pustaki konstrukcyjne TAB gr 19 cm

- pustaki konstrukcyjne TAB gr 19 cm



2,30 ⋅ 1,0 ⋅ 0,6 ⋅ 1,1 = 1,52 kN

2,30 ⋅ 1,0 ⋅ 0,6 ⋅ 1,1 = 1,52 kN



- tynk cementowo - wapienny

- tynk cementowo - wapienny



0,015 ⋅ 19,0 ⋅ 1,0 ⋅ 0,6 ⋅ 1,3 = 0,22 kN

0,015 ⋅ 19,0 ⋅ 1,0 ⋅ 0,6 ⋅ 1,3 = 0,22 kN



razem 2,76 kN

razem 2,76 kN



3. strop nad piętrem ( Teriva – I bis ), strop

3. strop nad piętrem ( Teriva – I bis ), strop

nad parterem oraz strop nad piwnicą

nad parterem oraz strop nad piwnicą



- klepka

- klepka



0,23 ⋅ 1,0 ⋅ 7,0 ⋅ 0,5 ⋅ 1,2 = 0,97 kN

0,23 ⋅ 1,0 ⋅ 7,0 ⋅ 0,5 ⋅ 1,2 = 0,97 kN



- szlichta cementowa 3 cm

- szlichta cementowa 3 cm



0,03 ⋅ 21,0 ⋅ 1,0 ⋅ 7,0 ⋅ 0,5 ⋅ 1,3 = 2,87 kN

0,03 ⋅ 21,0 ⋅ 1,0 ⋅ 7,0 ⋅ 0,5 ⋅ 1,3 = 2,87 kN



- styropian 3 cm

- styropian 3 cm



0,03 ⋅ 0,45 ⋅ 1,0 ⋅ 7,0 ⋅ 0,5 ⋅ 1,2 = 0,06 kN

0,03 ⋅ 0,45 ⋅ 1,0 ⋅ 7,0 ⋅ 0,5 ⋅ 1,2 = 0,06 kN



- strop Teriva – I bis

- strop Teriva – I bis



3,57 ⋅ 1,0 ⋅ 7,0 ⋅ 0,5 ⋅ 1,1 = 13,74 kN

3,57 ⋅ 1,0 ⋅ 7,0 ⋅ 0,5 ⋅ 1,1 = 13,74 kN



- tynk cementowo-wapienny

- tynk cementowo-wapienny

0,015 ⋅ 19,0 ⋅ 1,0 ⋅ 7,0 ⋅ 0,5 ⋅ 1,3 = 1,30 kN

0,015 ⋅ 19,0 ⋅ 1,0 ⋅ 7,0 ⋅ 0,5 ⋅ 1,3 = 1,30 kN



- obciążenie od ścianek działowych

- obciążenie od ścianek działowych



1,25 ⋅ 1,0 ⋅ 7,0 ⋅ 0,5 ⋅ 1,2 = 5,25 kN

1,25 ⋅ 1,0 ⋅ 7,0 ⋅ 0,5 ⋅ 1,2 = 5,25 kN



razem 24,19 kN

razem 24,19 kN



4. ściana piętra wys. 2,7m ( również ściana

4. ściana piętra wys. 2,7m ( również ściana

parteru) – dla uproszczenia bez potrącania

parteru) – dla uproszczenia bez potrącania

powierzchni okien

powierzchni okien



- pustaki elewacyjne TAB gr. 9 cm

- pustaki elewacyjne TAB gr. 9 cm



1,50 ⋅ 1,0 ⋅ 2,7 ⋅ 1,1 = 4,46 kN

1,50 ⋅ 1,0 ⋅ 2,7 ⋅ 1,1 = 4,46 kN



- styropian gr. 10 cm

- styropian gr. 10 cm



0,1 ⋅ 0,45 ⋅ 1,0 ⋅ 2,7 ⋅ 1,2 = 0,15 kN

0,1 ⋅ 0,45 ⋅ 1,0 ⋅ 2,7 ⋅ 1,2 = 0,15 kN



- pustaki konstrukcyjne TAB gr 24 cm

- pustaki konstrukcyjne TAB gr 24 cm



2,75 ⋅ 1,0 ⋅ 2,7 ⋅ 1,1 = 8,17 kN

2,75 ⋅ 1,0 ⋅ 2,7 ⋅ 1,1 = 8,17 kN



- tynk cementowo - wapienny

- tynk cementowo - wapienny



0,015 ⋅ 19,0 ⋅ 1,0 ⋅ 2,7 ⋅ 1,3 = 1,00 kN

0,015 ⋅ 19,0 ⋅ 1,0 ⋅ 2,7 ⋅ 1,3 = 1,00 kN



razem 13,78 kN

razem 13,78 kN



5. ściana piwnicy odcinek 1,7 m od stropu piwnicy

tj. do połowy wysokości zasypania gruntem



- pustaki konstrukcyjne TAB gr. 9 cm



1,50 ⋅ 1,0 ⋅ 1,7 ⋅ 1,1 = 2,81 kN



- styropian gr. 8 cm



0,08 ⋅ 0,45 ⋅ 1,0 ⋅ 1,7 ⋅ 1,2 = 0,07 kN



- pustaki konstrukcyjne TAB gr 24 cm



2,75 ⋅ 1,0 ⋅ 1,7 ⋅ 1,1 = 5,14 kN



razem 8,02 kN



Siła

Siła

N

N

Sd

Sd

przypadająca na pasmo ściany szerokości 1m wynosi :

przypadająca na pasmo ściany szerokości 1m wynosi :



N

N

Sd

Sd

= 1,94 + 2,76 + 3 ⋅ 24,19 + 2 ⋅ 13,78 + 8,02 = 112,85

= 1,94 + 2,76 + 3 ⋅ 24,19 + 2 ⋅ 13,78 + 8,02 = 112,85

kN / 1,0 m

kN / 1,0 m



b

b

e

e

= 7 m > 2 ⋅ h = 2 ⋅ 2,6 = 5,2 m

= 7 m > 2 ⋅ h = 2 ⋅ 2,6 = 5,2 m



f

f

k

k

= 3,7 Mpa = 3,7 ⋅ 103 kN/m2

= 3,7 Mpa = 3,7 ⋅ 103 kN/m2



t f

t f

k

k

/ 3 γ

/ 3 γ

m

m

= 0,24 ⋅ 3,7 ⋅ 103 / 3 ⋅ 1,7 = 174,12 kN/m

= 0,24 ⋅ 3,7 ⋅ 103 / 3 ⋅ 1,7 = 174,12 kN/m



ρ

ρ

e

e

h h

h h

e

e

2

2

/ 20 t = 18,0 ⋅ 2,6 ⋅ 1,82 / 20 ⋅ 0,24 = 31,59 kN/m

/ 20 t = 18,0 ⋅ 2,6 ⋅ 1,82 / 20 ⋅ 0,24 = 31,59 kN/m



174,12 kN/m ≥ N

174,12 kN/m ≥ N

Sd

Sd

= 112,85 kN/m ≥ 31,59 kN/m

= 112,85 kN/m ≥ 31,59 kN/m



Ściana piwnicy spełnia warunek nośności.

Ściana piwnicy spełnia warunek nośności.

Konstrukcyjnie zaleca się wykonanie rdzeni betonowych w

Konstrukcyjnie zaleca się wykonanie rdzeni betonowych w

narożach, miejscach połączeń ścian i co ~ 4,5 mb ściany.

narożach, miejscach połączeń ścian i co ~ 4,5 mb ściany.

ŚCIANY USZTYWNIAJĄCE

ŚCIANY USZTYWNIAJĄCE



W budynkach o ustroju ścianowym nośność ścian

W budynkach o ustroju ścianowym nośność ścian

usztywniających sprawdza się jak nośność ścian obciążonych

usztywniających sprawdza się jak nośność ścian obciążonych

głównie pionowo, przy czym siłę

głównie pionowo, przy czym siłę

N

N

Sd

Sd

przyjmuje się jako sumę

przyjmuje się jako sumę

obciążenia obliczeniowego z górnych kondygnacji i od stropu

obciążenia obliczeniowego z górnych kondygnacji i od stropu

oraz wypadkowej naprężeń ściskających wywołanych przez

oraz wypadkowej naprężeń ściskających wywołanych przez

przypadającą na rozpatrywaną ścianę część obliczeniowego

przypadającą na rozpatrywaną ścianę część obliczeniowego

obciążenia poziomego, oddziałującego na budynek.

obciążenia poziomego, oddziałującego na budynek.



Przy dostatecznym nasyceniu budynku ścianami

Przy dostatecznym nasyceniu budynku ścianami

usztywniającymi, przy sprawdzeniu nośności ścian, można

usztywniającymi, przy sprawdzeniu nośności ścian, można

pominąć wpływ sił wewnętrznych, wywołanych przez

pominąć wpływ sił wewnętrznych, wywołanych przez

obciążenie poziome. W takim przypadku obliczenia statyczne

obciążenie poziome. W takim przypadku obliczenia statyczne

budynku o ustroju ścianowym sprowadzają się tylko do

budynku o ustroju ścianowym sprowadzają się tylko do

obliczeń ścian obciążonych głównie pionowo.

obliczeń ścian obciążonych głównie pionowo.



Kiedy usztywnienie przestrzenne budynku w rozpatrywanym

Kiedy usztywnienie przestrzenne budynku w rozpatrywanym

kierunku działania obciążenia poziomego stanowi zespół ścian

kierunku działania obciążenia poziomego stanowi zespół ścian

usztywniających, maksymalne naprężenie krawędziowe

usztywniających, maksymalne naprężenie krawędziowe

σ

σ

max

max

, jakie

, jakie

występuje w ścianach usztywniających pod działaniem obciążenia

występuje w ścianach usztywniających pod działaniem obciążenia

poziomego – a jest to naprężenie krawędziowe w najbardziej

poziomego – a jest to naprężenie krawędziowe w najbardziej

sztywnej ścianie w rozpatrywanym zespole ścian usztywniających –

sztywnej ścianie w rozpatrywanym zespole ścian usztywniających –

wyznaczyć można w sposób przybliżony ze wzoru:

wyznaczyć można w sposób przybliżony ze wzoru:



Gdzie:

Gdzie:



w

w

– obliczeniowe obciążenie poziome, wywołane łącznym oddziaływaniem parcia i

– obliczeniowe obciążenie poziome, wywołane łącznym oddziaływaniem parcia i

ssania wiatru, kN/m

ssania wiatru, kN/m

2

2



L,H

L,H

– długość i wysokość budynku

– długość i wysokość budynku



b

b

– długość muru najbardziej sztywnej ściany zespołu ścian usztywniających,

– długość muru najbardziej sztywnej ściany zespołu ścian usztywniających,



b

b

i

i

, t

, t

i

i

- długość i grubość muru poszczególnych ścian występujących w zespole

- długość i grubość muru poszczególnych ścian występujących w zespole

ścian usztywniających

ścian usztywniających



α

α

i

i

– stosunek modułu sprężystości muru ściany „i” do modułu sprężystości muru

– stosunek modułu sprężystości muru ściany „i” do modułu sprężystości muru

ściany najbardziej sztywnej

ściany najbardziej sztywnej



η

η

i

i

- współczynnik uwzględniający wpływ obecności pionowych szeregów otworów

- współczynnik uwzględniający wpływ obecności pionowych szeregów otworów

na sztywność ściany.

na sztywność ściany.



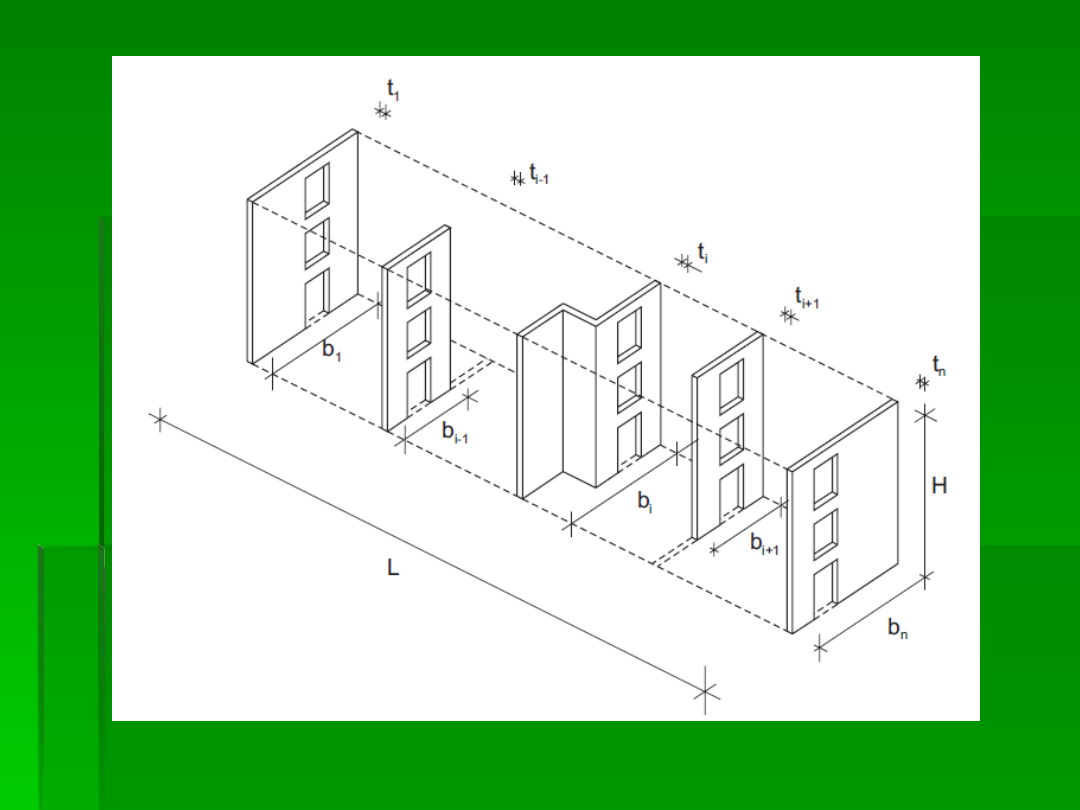
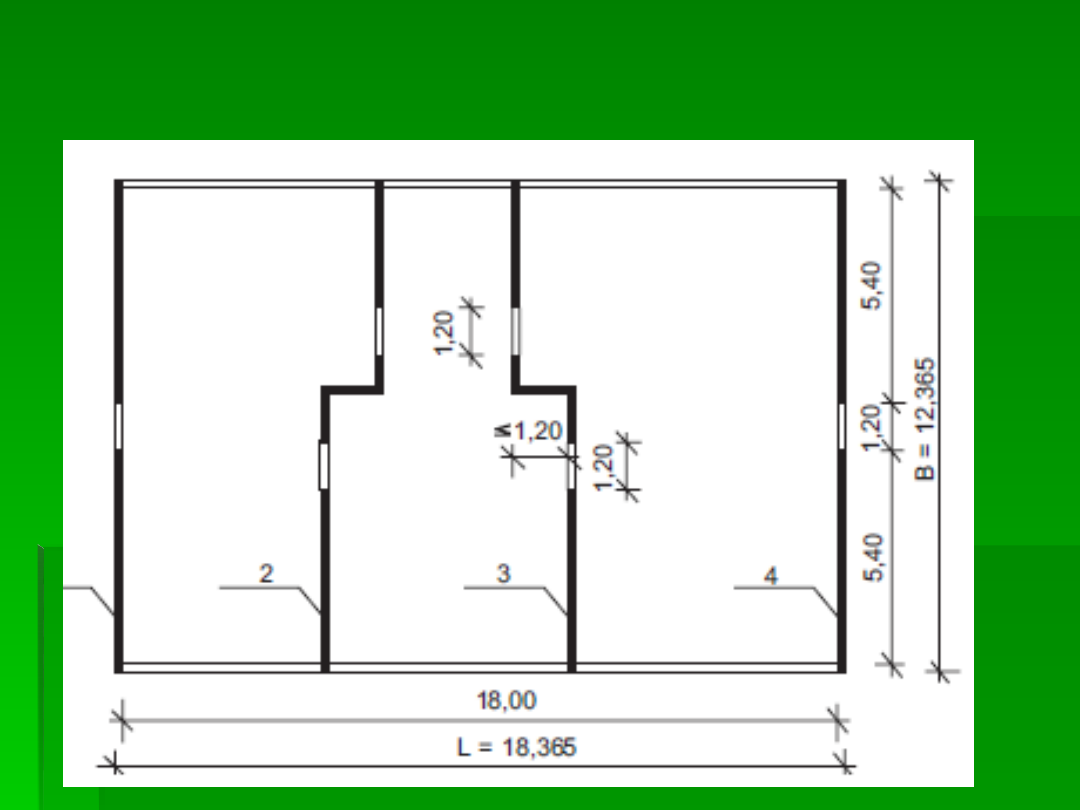
Wzór dotyczy ścian o przekroju prostokątnym (bez

Wzór dotyczy ścian o przekroju prostokątnym (bez

uwzględniania współpracy ścian usytuowanych

uwzględniania współpracy ścian usytuowanych

prostopadle do rozpatrywanych ścian usztywniających), a

prostopadle do rozpatrywanych ścian usztywniających), a

przy jego wyprowadzaniu przyjęto, że w przypadku, kiedy

przy jego wyprowadzaniu przyjęto, że w przypadku, kiedy

w ścianie najbardziej sztywnej występuje jeden lub kilka

w ścianie najbardziej sztywnej występuje jeden lub kilka

pionowych szeregów otworów, stosunek

pionowych szeregów otworów, stosunek

σ

σ

max

max

ściany z

ściany z

otworami do

otworami do

σ

σ

max

max

ściany bez otworów jest identyczny z

ściany bez otworów jest identyczny z

parametrem

parametrem

η

η

i

i

wyrażającym stosunek sztywności ściany

wyrażającym stosunek sztywności ściany

bez otworów do sztywności ściany z otworami.

bez otworów do sztywności ściany z otworami.

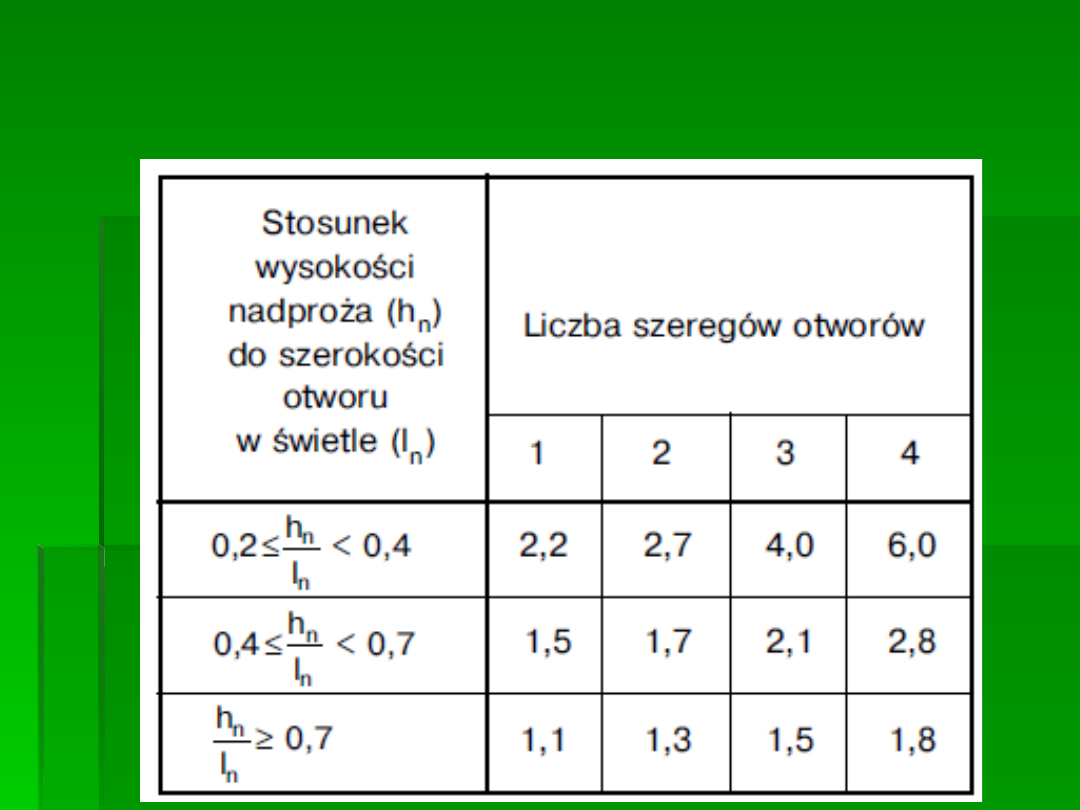
Wartości współczynnika

Wartości współczynnika

η

η

i

i

dla ścian

dla ścian

osłabionych pionowymi szeregami

osłabionych pionowymi szeregami

otworów

otworów

ŚCIANY USZTYWNIAJĄCE

ŚCIANY USZTYWNIAJĄCE

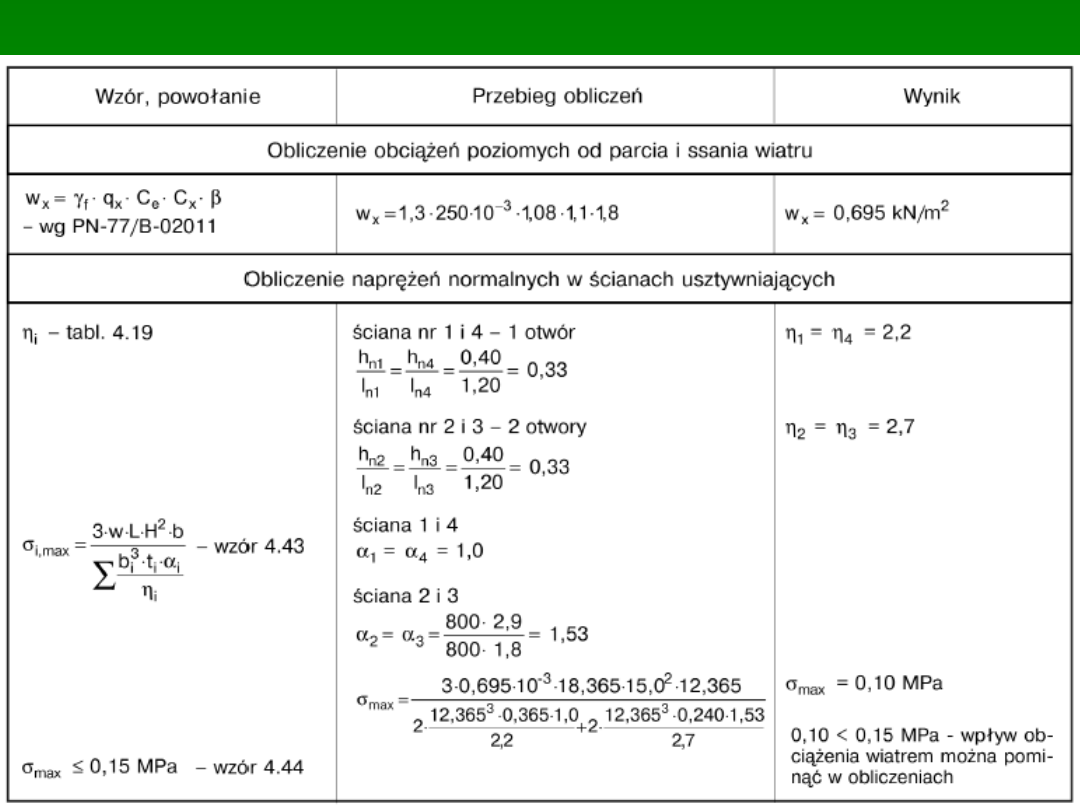
PRZEBIEG OBLICZEŃ

PRZEBIEG OBLICZEŃ