„Zwiększenie liczby wysoko wykwalifikowanych absolwentów kierunków ścisłych Uniwersytetu Jagiellońskiego”

POKL.04.01.02-00-097/09-00

Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego

Spektroskopia elektronowa związków

nieorganicznych

Zaawansowana Chemia Nieorganiczna

kurs dla III roku Chemii UJ

moduł Chemia Nieorganiczna i Strukturalna

Prowadzący

mgr Tomasz Baran

[e-mail]

p. 205
konsultacje: Pon. 17-18

Plan seminarium

L.p

.

Temat

Data

1

Spektroskopia

elektronowa

związków

nieorganicznych.

20.11.2013

2

Fotochemia związków nieorganicznych.

27.11.2013

3

Właściwości

magnetyczne

i

elektrochemiczne

związków nieorganicznych.

4.12.2013

4

Kinetyka

i

mechanizmy

reakcji

w

chemii

nieorganiczne.

11.12.2013

5

Termodynamika w chemii nieorganicznej.

18.12.2013

6

Kataliza

homo-

i

heterogeniczna.

Elementy

nieorganicznej nanochemii.

3.01.2014

(Pt)

7

Elementy biologicznej chemii nieorganicznej.

15.01.2014

8

Kolokwium.

?

Zaliczenie

Kolokwium zaliczeniowe

18

Kolokwia wstępne

62

BONUS: Aktywność

71

Maksymalnie

30

0,0 – 15,0 ndst
15,1 – 18,0 dst
18,1 – 21,0 dst+
21,1 – 24,0 db
24,1 – 27,0 db+
27,1 – 30,0 bdb

5

Spektroskopia - tematyka

• Widma elektronowe związków nieorganicznych

• Energia elektronu w atomach – przypomnienie

• Konfiguracja elektronowa pierwiastków –

przypomnienie

• Termy:

• wyznaczenie termu stanu podstawowego – reguły Hunda
• termy w stanie wzbudzonym
• energia termów
• diagramy Tanabe – Sugano

• Orbitale w polu krystalicznym ligandów

6

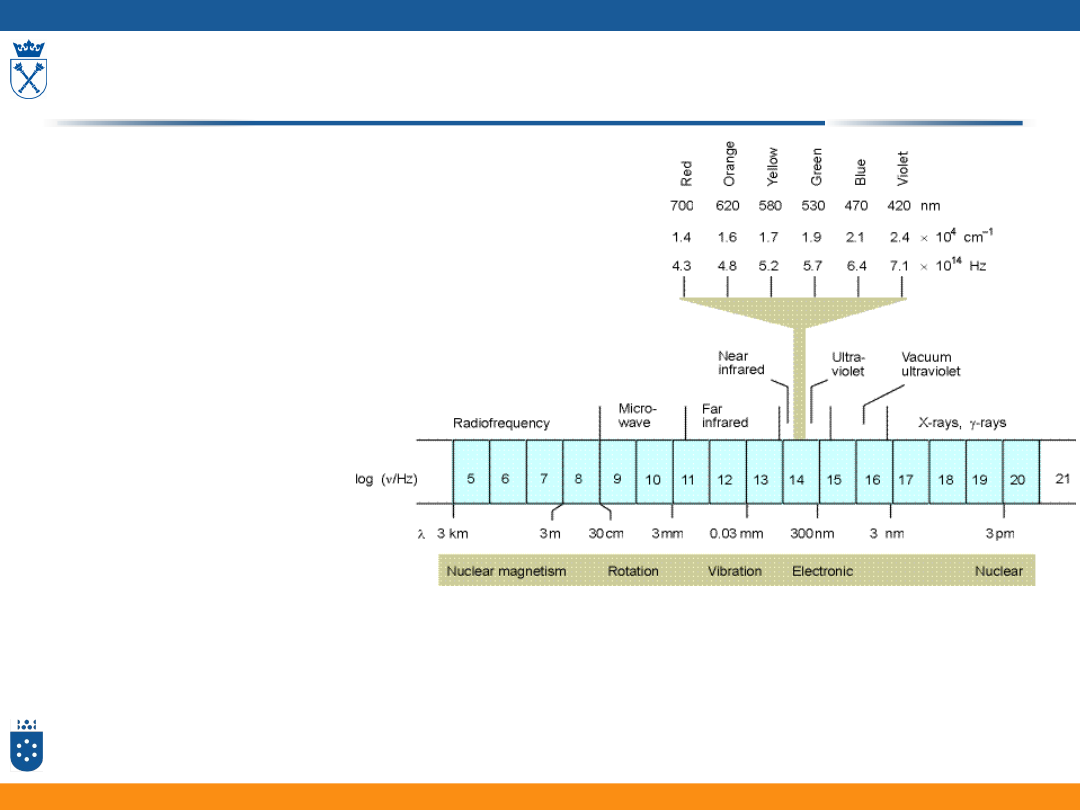
Formy energii molekuł

• Energia translacji 3/2kT
• Energia rotacji
• Energia oscylacji
• Energia elektronowa
• Energia wewnątrzjądrowa

7

Konfiguracja elektronowa metali bloku d i f

• Cr

2+

---

• Mn

2+

---

• Co

2+

---

• Pr ---
• Eu ---
• Tb ---

Podaj zapis konfiguracji elektronowej dla
następujących atomów i jonów:

1s

2

2s

2

2p

6

3s

2

3p

6

3d

4

1s

2

2s

2

2p

6

3s

2

3p

6

3d

5

1s

2

2s

2

2p

6

3s

2

3p

6

3d

7

1s

2

2s

2

2p

6

3s

2

3p

6

3d

10

4s

2

4p

6

4d

10

4f

3

5s

2

5p

6

6s

2

1s

2

2s

2

2p

6

3s

2

3p

6

3d

10

4s

2

4p

6

4d

10

4f

7

5s

2

5p

6

6s

2

1s

2

2s

2

2p

6

3s

2

3p

6

3d

10

4s

2

4p

6

4d

10

4f

9

5s

2

5p

6

6s

2

8

Energia elektronu w atomie wodoropodobnym

Energia elektronu - liczby kwantowe:

• n = 1,2,3… - główna liczba kwantowa

• l = 0, 1, 2, …, n-1 – orbitalna liczba kwantowa,

• moment pędu elektronu:
• rodzaj orbitalu - s, p, d, f

• m

l

= -l … +l - magnetyczna orbitalna liczba kwantowa,

• rzut orbitalnego momentu pędu na kierunek pola:

• s = ½ - spin

• m

s

= ± ½ - magnetyczna spinowa liczba kwantowa

h

)

1

l

(

l 

h

l

m

9

Energia atomu wieloelektronowego

Momenty pędu elektronów sumują się wektorowo dając

wektory wypadkowe.

Wartość energii określają liczby kwantowe:
• L = m

l

– całkowita orbitalna liczba kwantowa

• L = 0, 1, 2…
• rodzaj termu – S, P, D, F, G, H

• S = m

s

– całkowita spinowa liczba kwantowa

Wypadkowe wektory spinu i momentu pędu orbitalnego

dają całkowity moment pędu orbitalnego J

wynikający ze

sprzężenia spinowo-orbitalnego J=L+S

• dla pierwiastków lekkich – sprzężenie LS (Russella-Sandersa) –

oddziaływanie wypadkowego momentu orbitalnego i spinowego
J = |L - S|; … ;L + S

• dla bloku f – sprzężenie j-j - momenty pędu elektronów

charakteryzuje liczba j wynikająca ze sprzężenia l i s dla
poszczególnych elektronów

Z zasady
dodawania wektorów

10

Termy – sposób zapisu

2S+1

L

J

warto

ść

L

0

1

2

3

4

5

6

7

oznaczenie

S

P

D

F

G

H

I

K

J = |L-S|, …. , L+S

•J = |L-S| dla f

n

, n<7

•J = L+S dla f

n

, n>7

S = s

multipletowo
ść
(term
singletowy,
dubletowy,
trypletowy
itd.)

11

Termy – sposób zapisu

2S+1

L

J

multipletowo
ść
(term
singletowy,
dubletowy,
trypletowy
itd.)

Multipletowość:

S=0

S=1/2

Term singletowy – wszystkie elektrony
są sparowane np. wapń

Term dubletowy – jeden
niesparowany elektron np.
scand

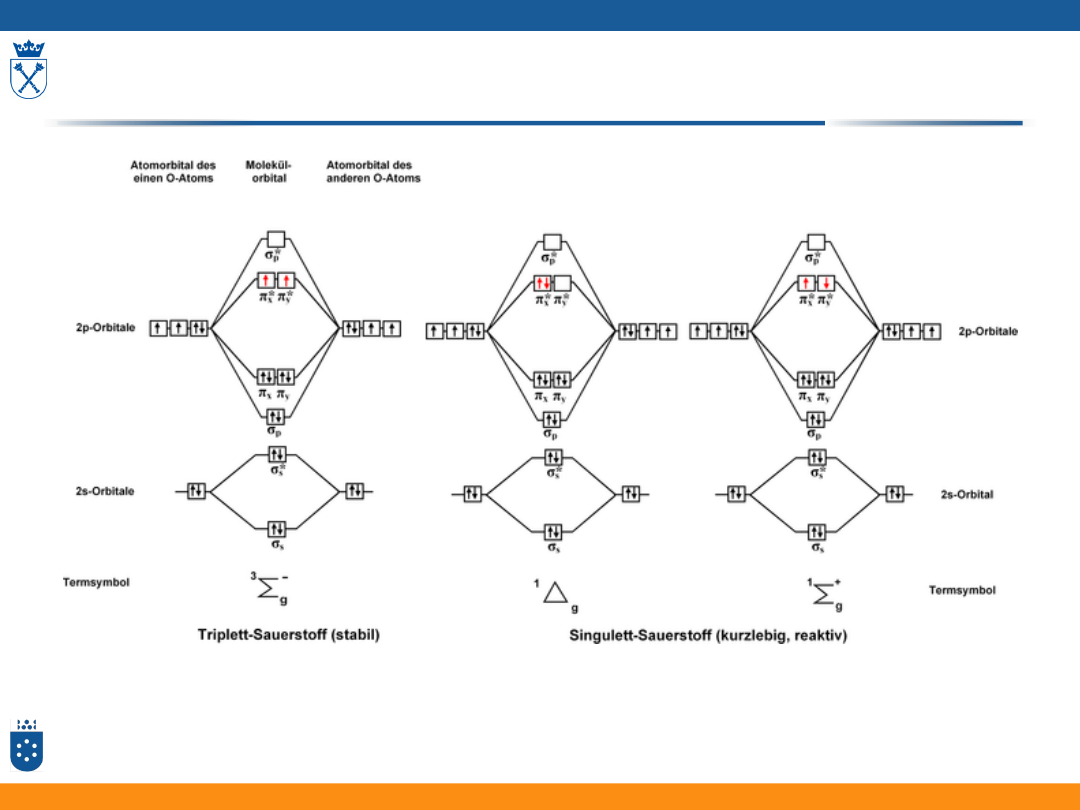
12

Termy

Mikrostany

13

różne sposoby rozmieszczenia elektronów na orbitalach dla
danej konfiguracji elektronowej ⇒ mikrostany

mikrostan (1

+

, 1

-

) ⇒ m

l

= +1; „+„ ⇒ m

s

= +½, „-„ ⇒ m

s

= - ½

mikrostan (-1

+

, 0

+

) ⇒ m

l

= +1, 0; m

s

= +½

odpychanie międzyelektronowe ⇒ mikrostany odpowiadające
różnej względnej kątowej gęstości elektronowej mają różne
energie

mikrostany o takiej samej energii przy uwzględnieniu
odpychania międzyelektronowego ⇒ termy

Mikrostany

14

m

s

M

L

+1

0

-1

+2:

1

+

1

-

 

+1:

1

+

0

+

1

+

0

-

1

-

0

+

1

-

0

-

0:

-1

+

1

+

-1

+

1

-

0

+

0

-

-1

-

1

+

-1

-

1

-

-1:

-1

+

0

+

-1

+

0

-

-1

-

0

+

-1

-

0

-

-2:

-1

+

-1

-

Dla konfiguracji p

2

:

m

l

+1 0 -1

Skoro l=1

15

Wyznaczanie termu stanu podstawowego

• Czy energia

poszczególnych
konfiguracji jest taka
sama czy różna?

• Który mikrostan powinien

odpowiadać cząsteczce
w stanie podstawowym?

m

l

= 2 1 0 -1 -2

Różne sposoby
rozmieszczenia
elektronów dla
konfiguracji d

2

:

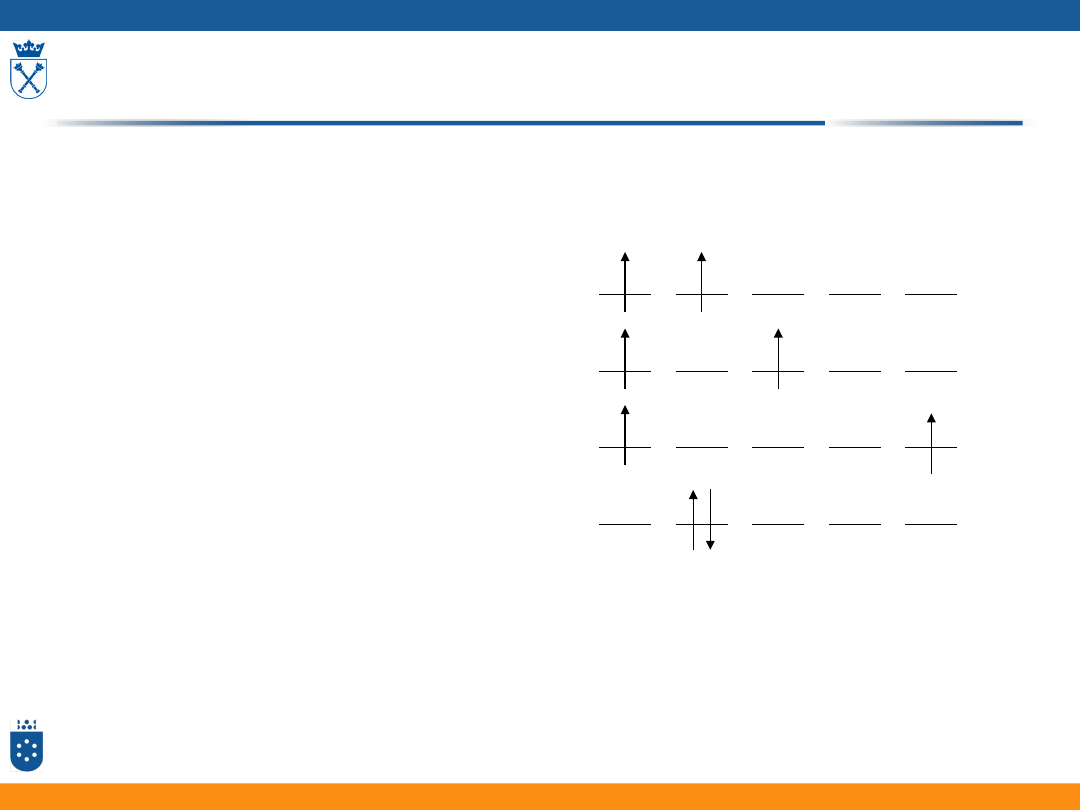
16

Termy atomowe

• mikrostany danej

konfiguracji elektronowej
mają różne energie na
skutek odpychania
międzyelektronowego

• zbiory mikrostanów o takiej

samej energii  termy

m

l

= 2 1 0 -1 -2

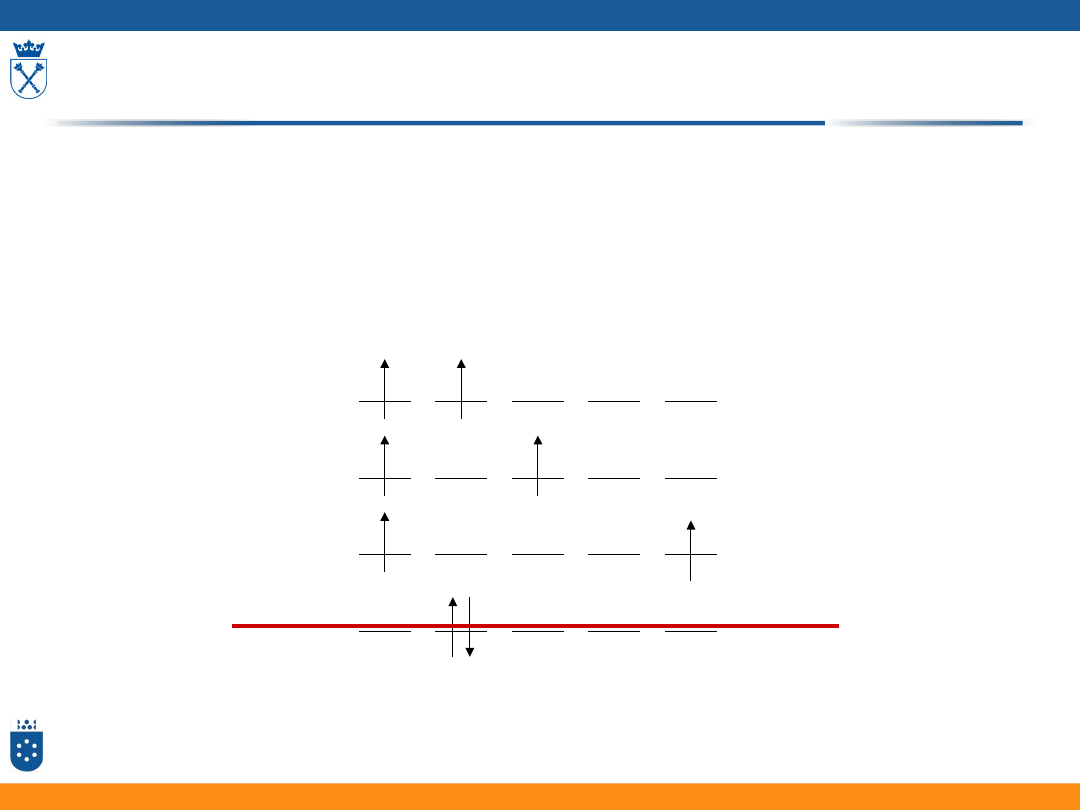
17

Reguły Hunda

1. Dla danej konfiguracji termem o najniższej energii

jest term o największej multipletowości:

m

L

= 2 1 0 -1 -2

a)
b)

c)

d)

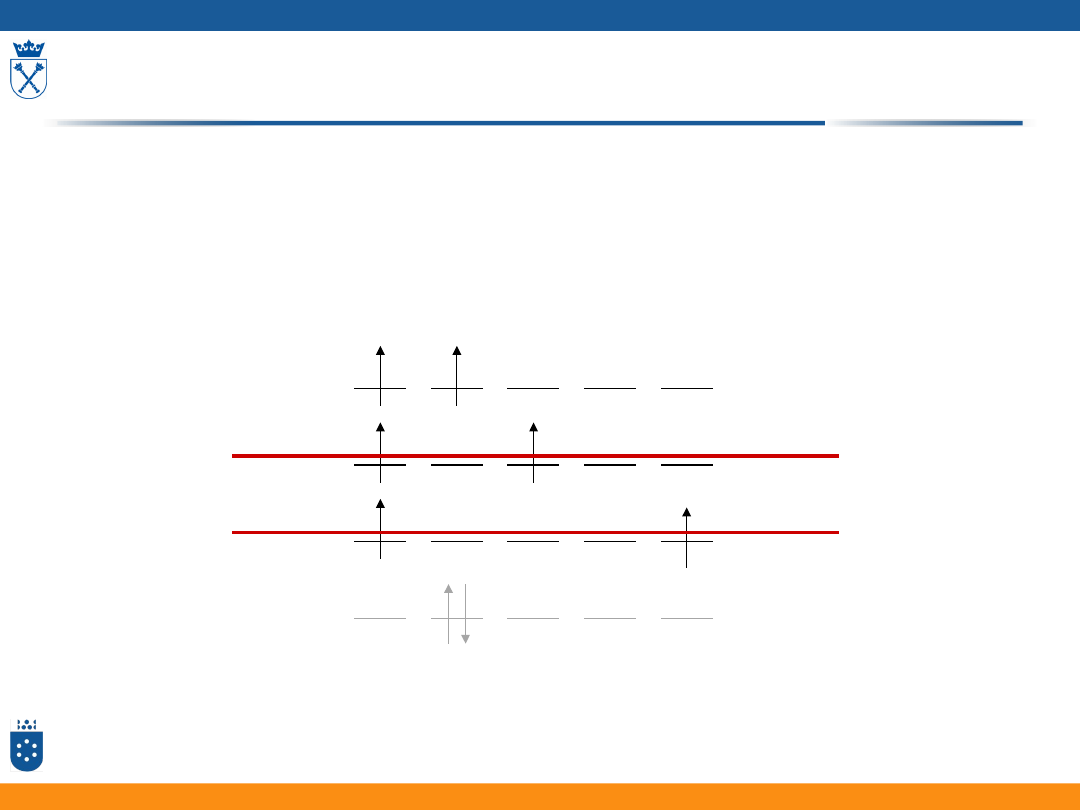
18

Reguły Hunda

2. Dla termu o określonej multipletowości niższą
energię ma

term o większej wartości L

m

L

= 2 1 0 -1 -2

a)
b)

c)

d)

19

Reguły Hunda

3. Dla tych samych wartości S i L:

• Term o najmniejszej wartości J dla

powłok zapełnionych do połowy

• Term o najwyższej wartości J dla powłok

zapełnionych ponad połowę

Wyznaczanie termu stanu podstawowego

20

m

L

= 2 1 0 -1 -2

Ustalić term stanu podstawowego dla konfiguracji

d

3

:

S = 3*1/2 = 3/2
L = 2+1+0 = 3 => term F

Term stanu podstawowego:

4

F

Wyznaczanie termu stanu podstawowego

21

m

L

= 2 1 0 -1 -2

Ustalić term stanu podstawowego dla konfiguracji

d

6

:

S = 5*1/2+1*(-1/2) = 2
L = 2+2+1+0-1-2= 2 => term D

Term stanu podstawowego:

5

D

22

Wyznaczanie termu stanu podstawowego

m

L

= 3 2 1 0 -1 -2

-3

Ustalić term stanu podstawowego dla konfiguracji

f

7

:

S = 7*1/2 = 7/2
L = 3+2+1+0-1-2-3 = 0 =>
term S
J=S=7/2

Term stanu podstawowego:

8

S

7/2

23

Wyznaczanie termu stanu podstawowego - ćwiczenia

Stosując reguły Hunda wyznaczyć term stanu

podstawowego dla izolowanych jonów:

• Cr

2+

--- d

4

• Mn

2+

--- d

5

• Co

2+

--- d

7

• Pr --- f

3

• Tb --- f

9

---

5

D

---

6

S

---

4

F

---

4

I

9/2

---

6

H

5/2

24

Spektroskopia elektronowa

25

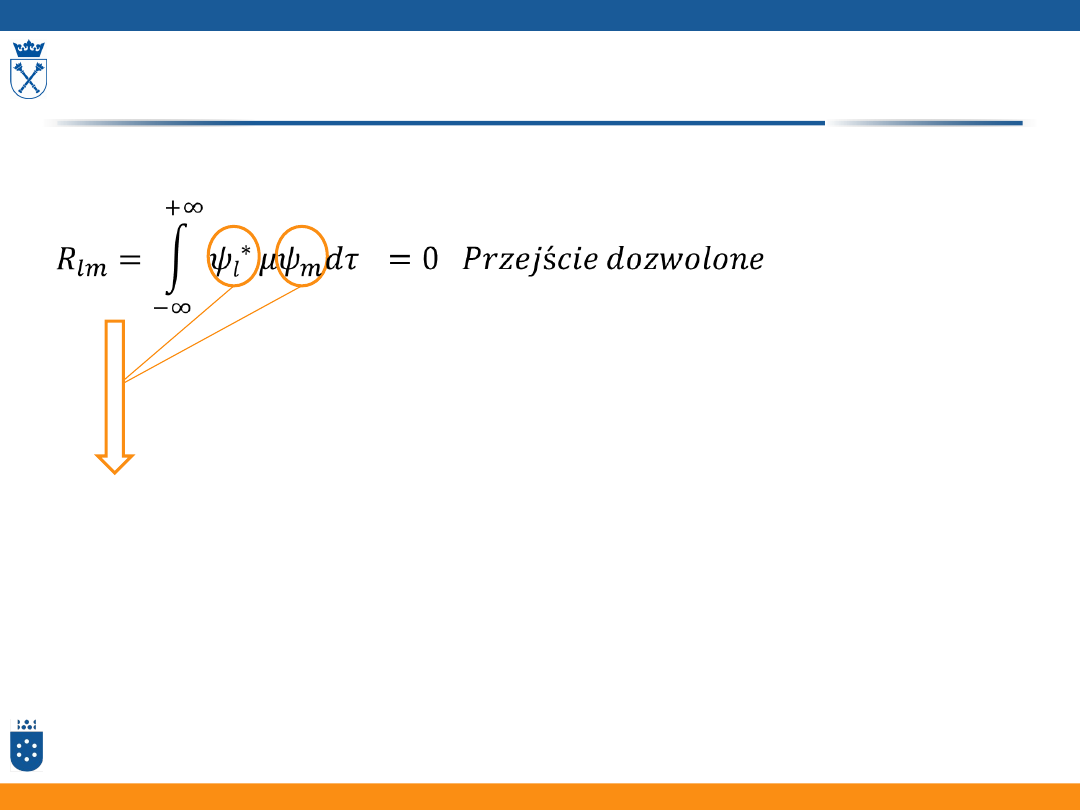
Reguły wyboru przejść elektronowych

Funkcje falowe termów elektronowych

S=0 dla przejść dozwolonych

!!przejścia między termami elektronowymi o tej samej multipletowości!!

- sprzężenie wibronowe
-elektryczny moment kwadrupolowy
-magnetyczny moment dipolowy

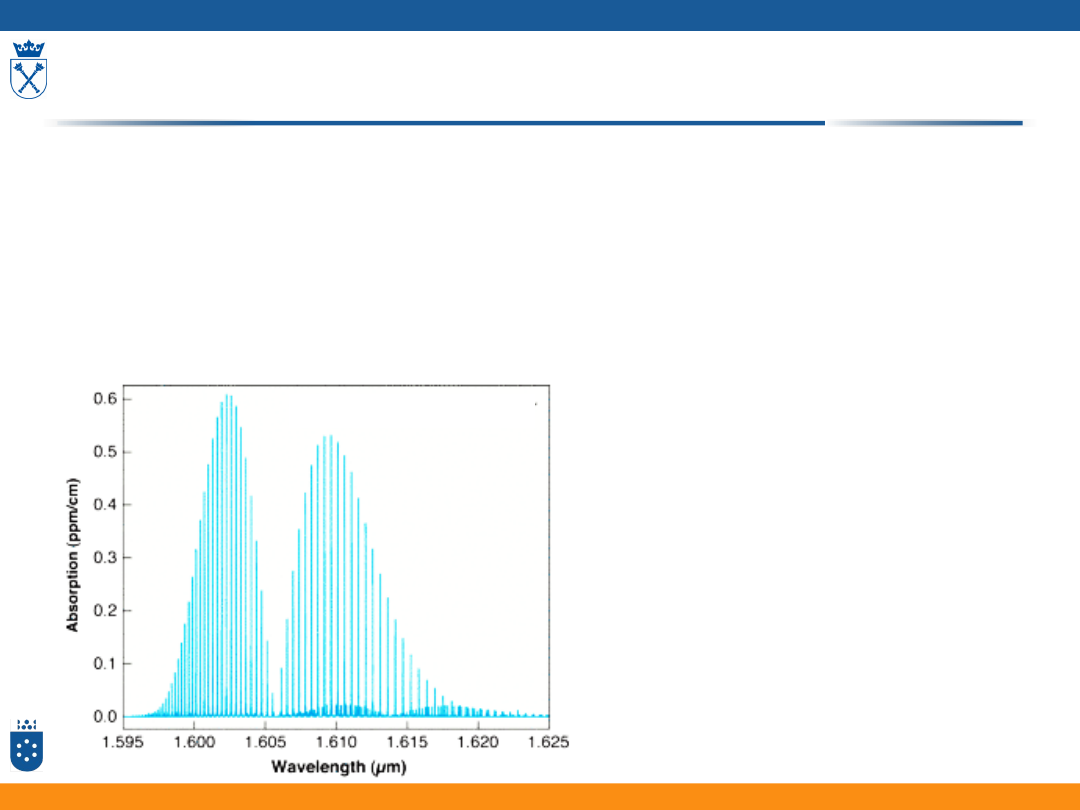
Proste molekuły w fazie gazowej

Pasma przejść elektronowych składają się z:

• szeregu pasm oscylacyjno-elektronowych, a te z kolei z:

• blisko leżących składowych przejść rotacyjnych

• Widma składają się z szeregu linii – interpretacja konturu widma

jest trudna

• Widma mogą dostarczyć informacji o:

• długościach wiązań
• kątach między wiązaniami
• stałych siłowych
• rozkładzie ładunków elektronów walencyjnych

26

Skąd bierze się kontur widma elektronowego?

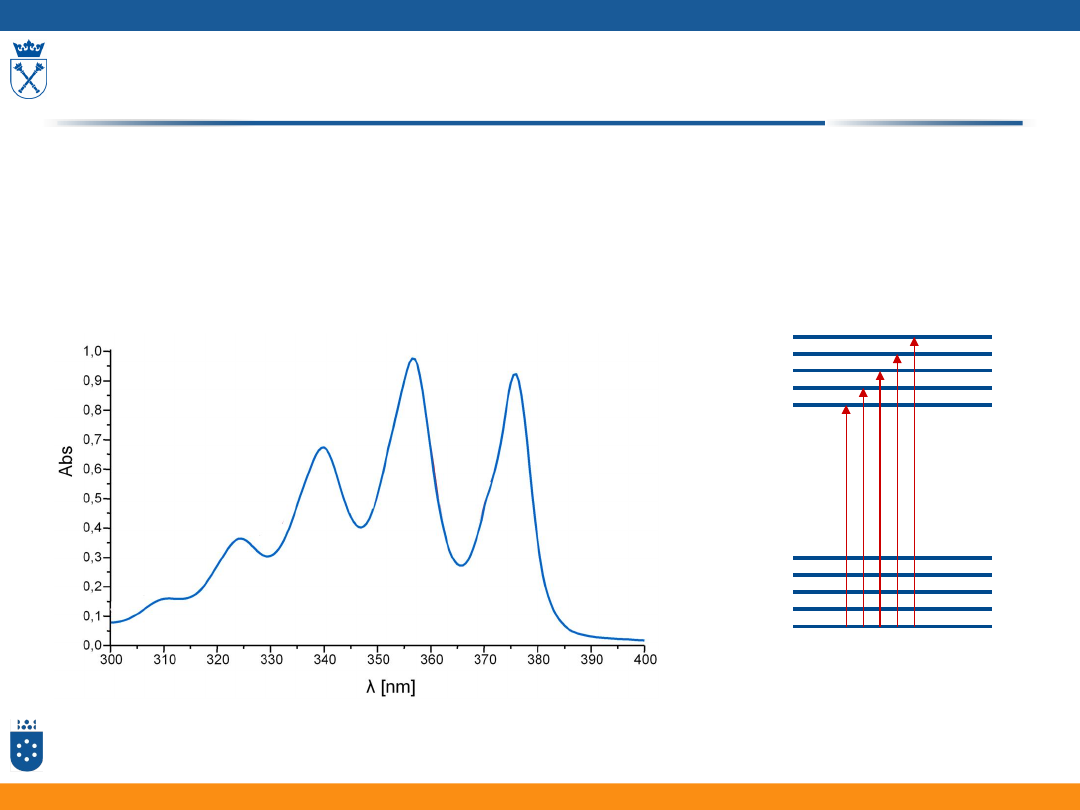
Widma oscylacyjne cząsteczek w fazie ciekłej

• W większości przejścia obserwowane na widmach UV-Vis

są przejściami elektronowymi.

• Na widmie związków w fazie ciekłej nie można obserwować pasm przejść rotacyjnych.

• W pewnych warunkach można otrzymać widmo struktury oscylacyjnej związku chemicznego.

27

S

0

S

1

28

Ogólna charakterystyka widm

• Pełną

strukturę

pasm

elektronowo-oscylacyjno-

rotacyjnych można obserwować tylko dla substancji w
fazie gazowej pod zmniejszonym ciśnieniem.

• W FAZIE CIEKŁEJ:

• rotacje są zahamowane
• składowe oscylacyjne są szerokie i poszczególne pasma

zlewają się ze sobą

• pasma elektronowe są szerokie i rozmyte

29

Typy przejść elektornowych

• Przejścia z przeniesieniem ładunku

Pochłonięcie fotonu powoduje przeniesienie elektronu z

jednej molekuły (donor) na inną (akceptor)

• LMCT
• MLCT
• MMCT
• MSCT
• …

• Przejścia typu d-d

30

Przejścia z przeniesieniem ładunku

• Po absorpcji fotonu elektron ulega przemieszczeniu w

obrębie cząsteczki

• Wiązanie liganda przez jon metalu pociąga za sobą

pojawienie się nowego pasma. Jest ono zwykle przesunięte

względem widma składników w stronę wyższych długości fal.

• Tego typu przejścia są obserwowane dla:

• kompleksów jonów metali przejściowych – przeniesienie

elektronu metal  ligand

• halogenków metali alkalicznych w stanie gazowym
• jonów MnO

4

lub CrO

22

– przeniesienie elektronu typu n(tlenu)

 * (metalu)

• Pasma tego typu są zazwyczaj bardzo szerokie i mają dużą

intensywność

31

ORBITALE W POLU KRYSTALICZNYM

LIGANDÓW

Spektroskopia kompleksów metali przejściowych

32

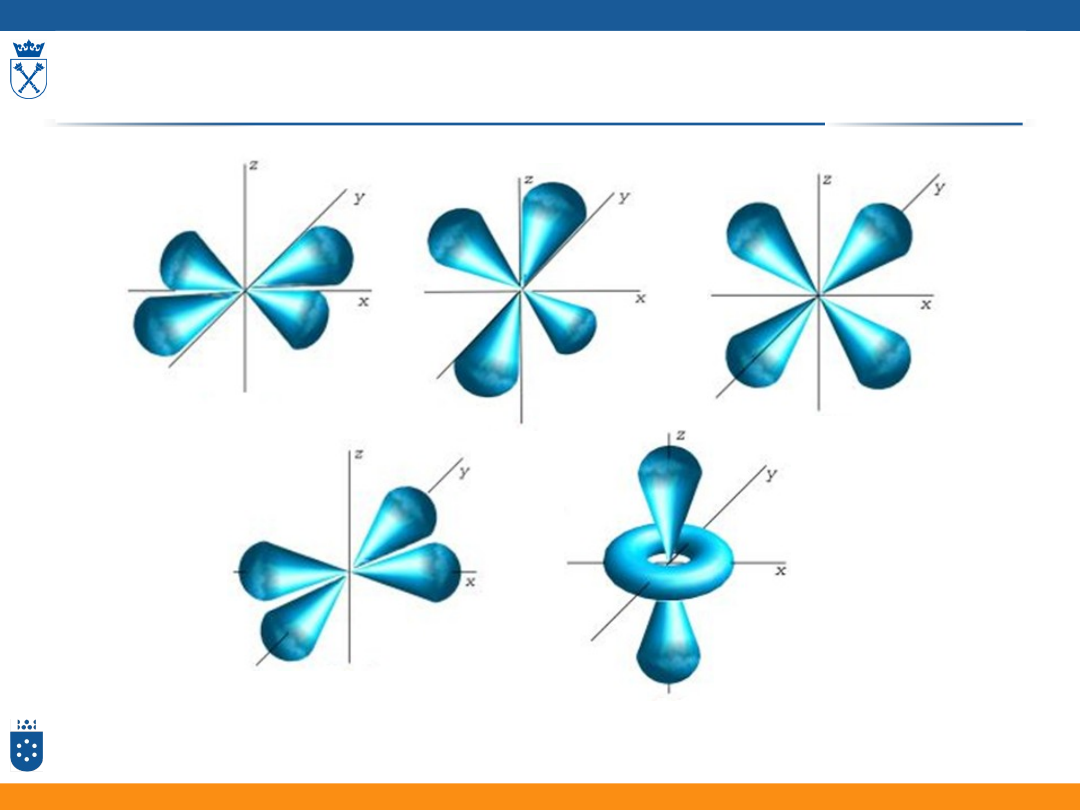
Kształty orbitali d

rysunek pobrano ze strony:

http://www.uni-graz.at/exp2www/Physik-HAKB/start.html

d

xy

d

yz

d

xz

d

x2-y2

d

z2

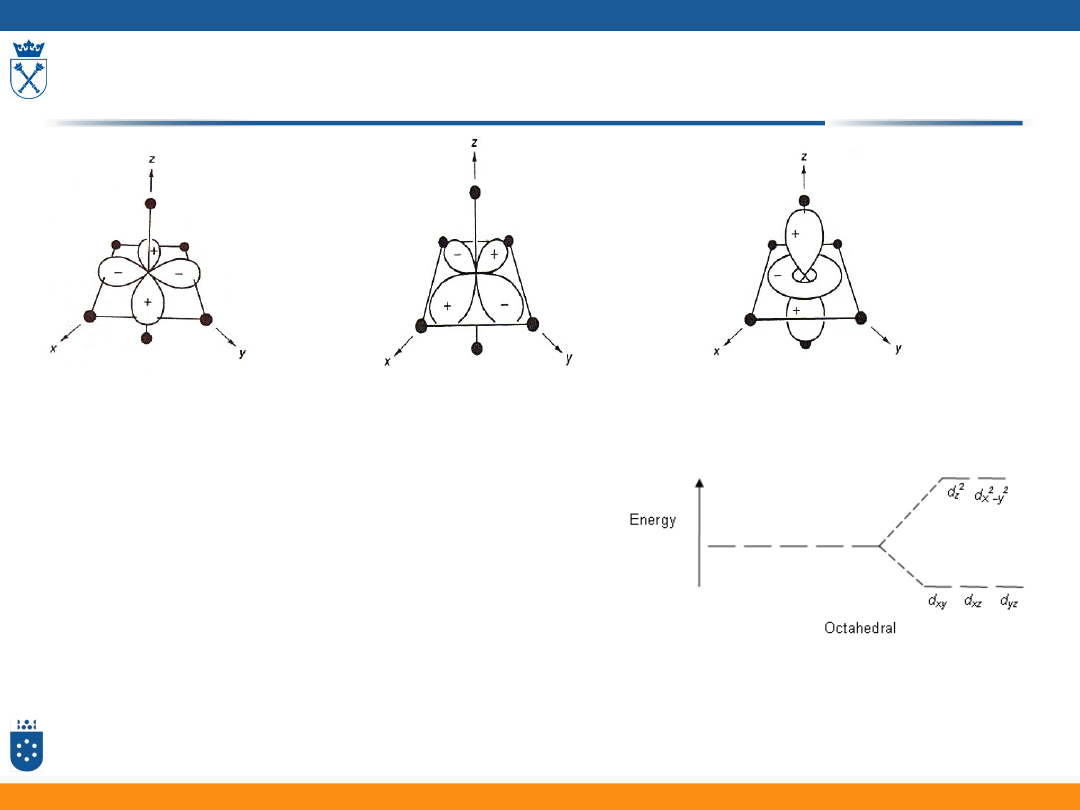
Orbitale d w oktaedrycznym polu ligandów

• Oddziaływanie poszczególnych orbitali d metalu

z orbitalami ligandów nie jest jednakowe

• Orbitale d w oktaedrycznym polu ligandów

dzielą się na dwa zespoły orbitali o różnej
energii:

• 3 orbitale mają energię niższą
• 2 orbitale mają energię wyższą

33

rysunki: Fizyczna chemia nieorganiczna, S.F.A Kettle, Wydawnictwo Naukowe PWN, Warszawa 1999

d

xy

analogicznie d

yz

oraz d

xz

d

x2-y2

d

z2

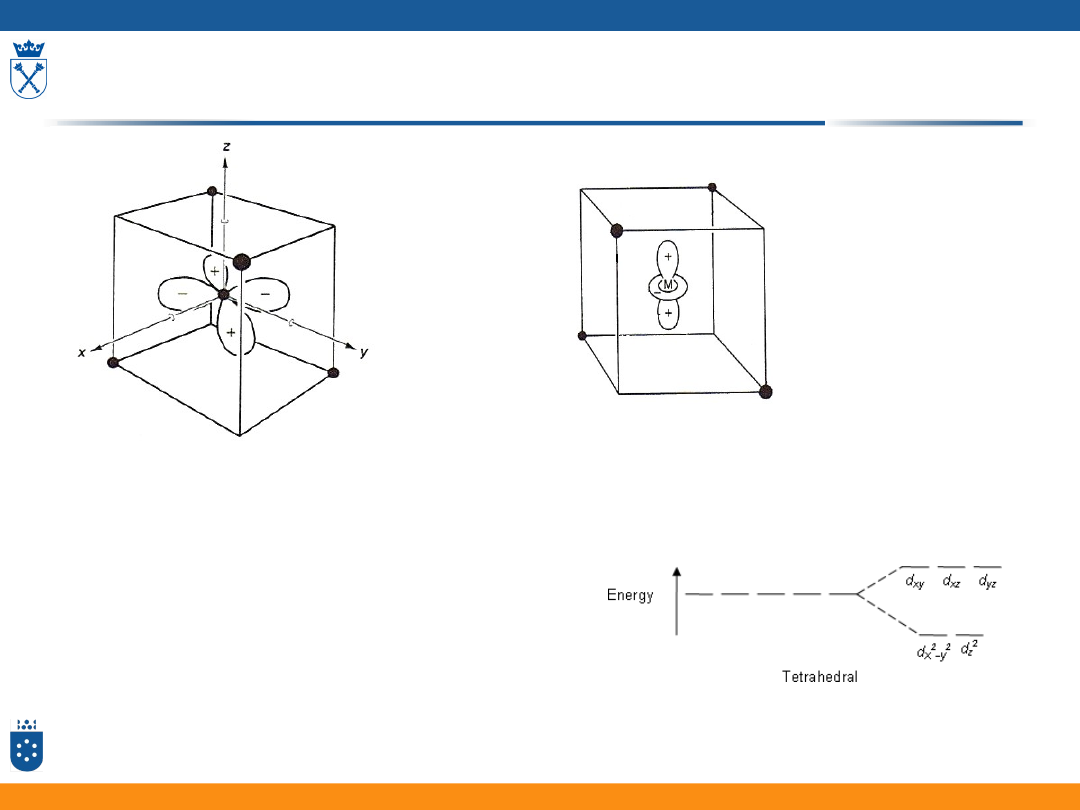
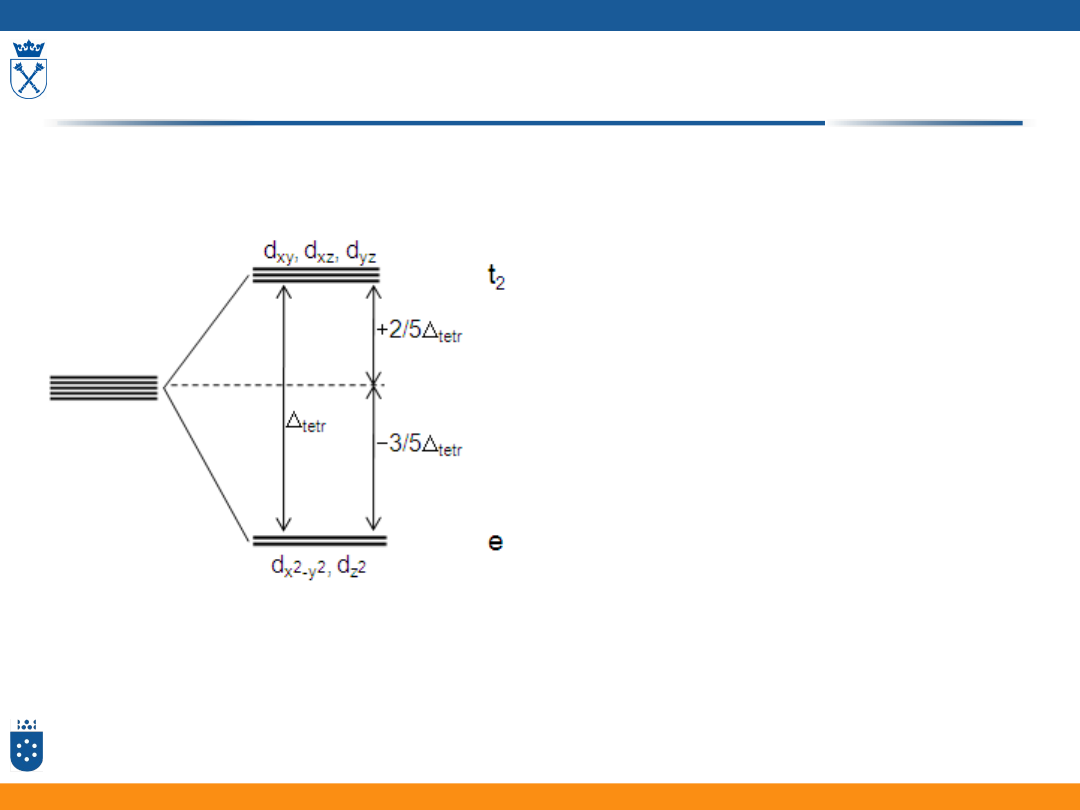
Orbitale d w tetraedrycznym polu ligandów

• Oddziaływanie poszczególnych orbitali d metalu

z orbitalami ligandów nie jest jednakowe

• Orbitale d w tetraedrycznym polu ligandów

dzielą się na dwa zespoły orbitali o różnej
energii:

• 2 orbitale mają energię niższą
• 3 orbitale mają energię wyższą

34

rysunki: Fizyczna chemia nieorganiczna, S.F.A Kettle, Wydawnictwo Naukowe PWN, Warszawa 1999

analogicznie d

yz

oraz d

xz

d

xy

d

z2

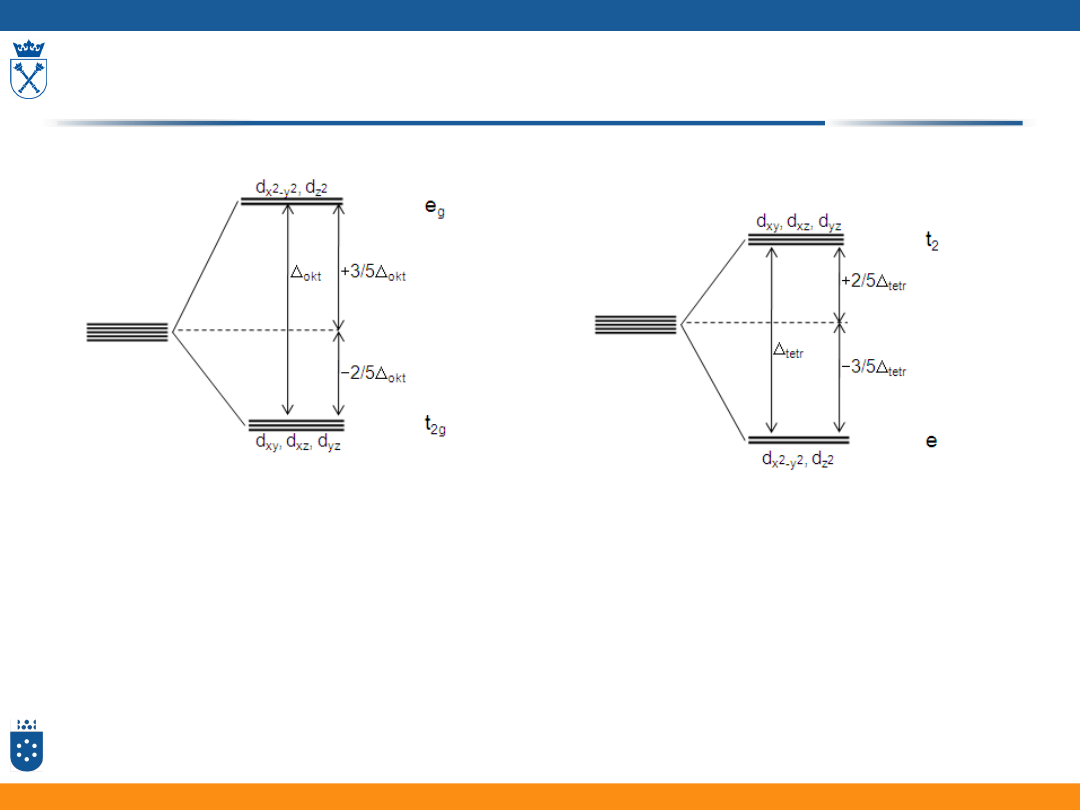
Rozszczepienie orbitali d w polu ligandów

• Różnica energii orbitali d w polu oktaedrycznym jest większa niż

w tetraedrycznym: 

tetr

= 4/9

okt

• Zależnie od siły pola ligandów kompleksu  przyjmuje różne wartości

35

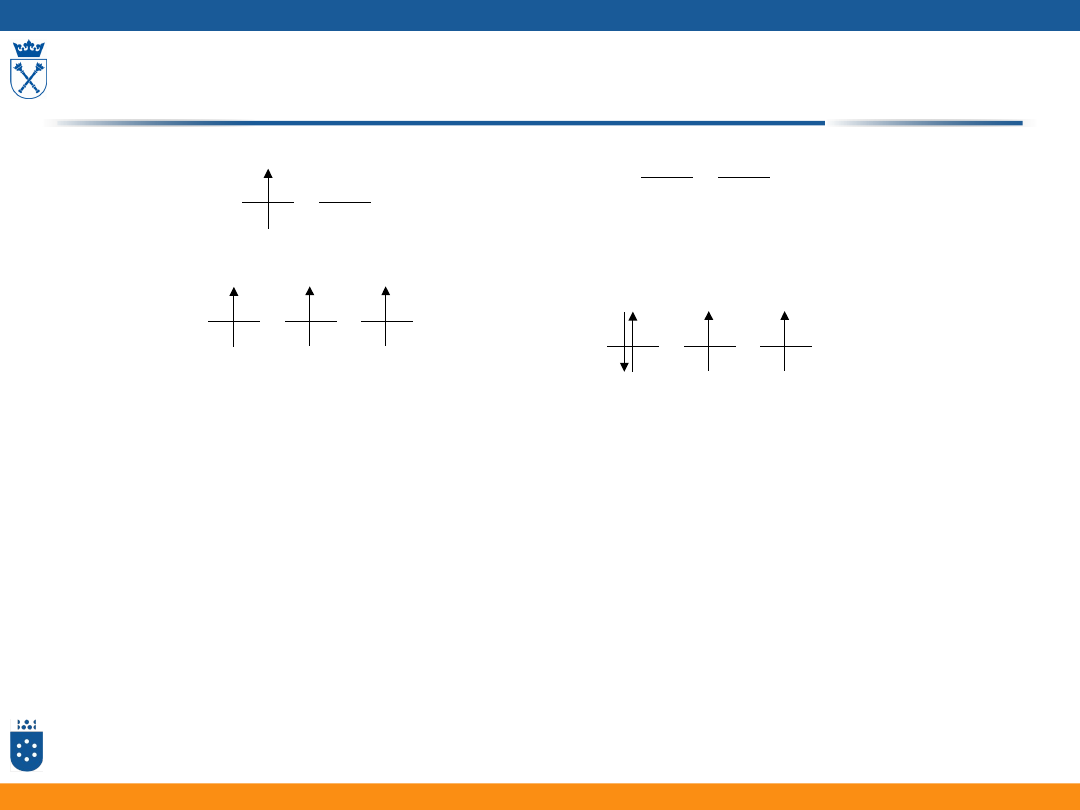
Konfiguracja wysokospinowa i niskospinowa

w oktaedrycznym polu ligandów

• Dla jonów o konfiguracji d

4

-d

7

możliwe dwa różne rodzaje

rozmieszczenia elektronów na rozszczepionych poziomach d

• Konfiguracje wysokospinowe występują dla małych wartości 

• Konfiguracje niskospinowe występują dla dużych wartości 

36

t

2g

e

g

t

2g

e

g

konfiguracja

wysokospinowa

konfiguracja

niskospinowa

37

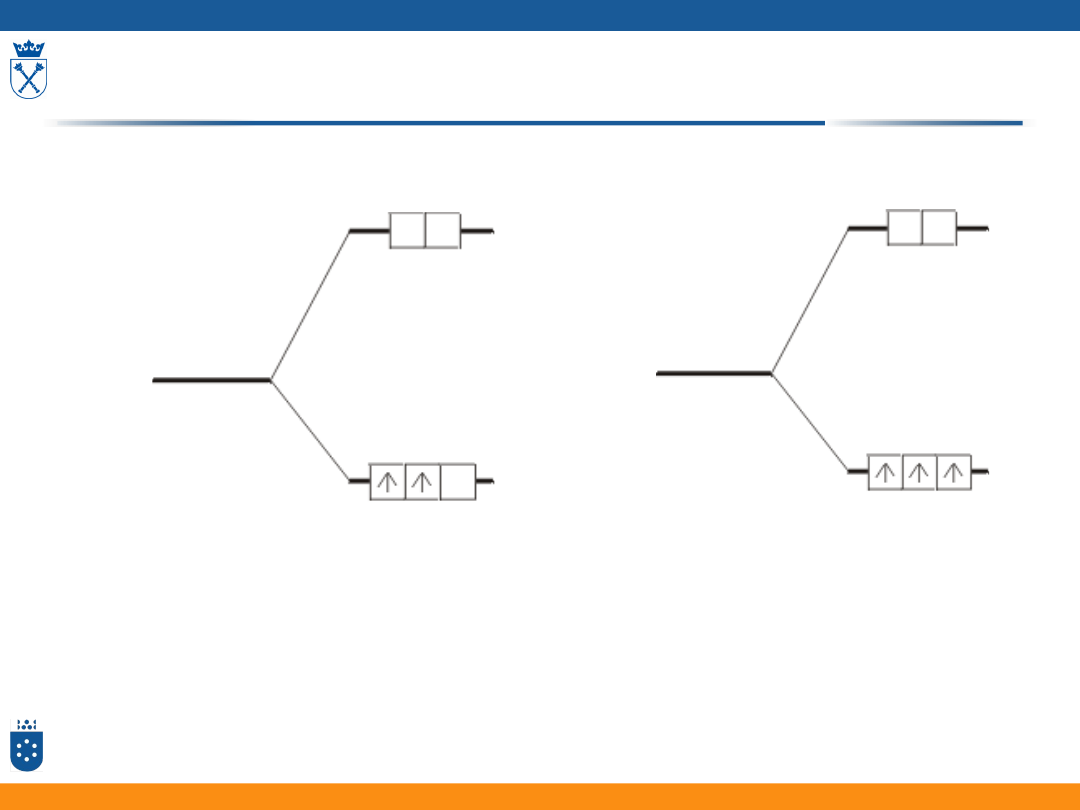
Konfiguracja wysokospinowa i niskospinowa

w tetraedrycznym polu ligandów

• Wartości rozszczepienia w

polu tetraedrycznym są
mniejsze niż w
oktaedrycznym

• Powstają zwykle kompleksy

wysokospinowe

• Konfiguracja niskospinowa

pojawia się rzadko

Przybliżenie słabego i silnego pola

[Ti

2+

]

3d

2

LFSE = 2  0.4 

O

=

0.8

O

[V

2+

]

3d

3

LFSE = 3  0.4 

O

=

1.2

O

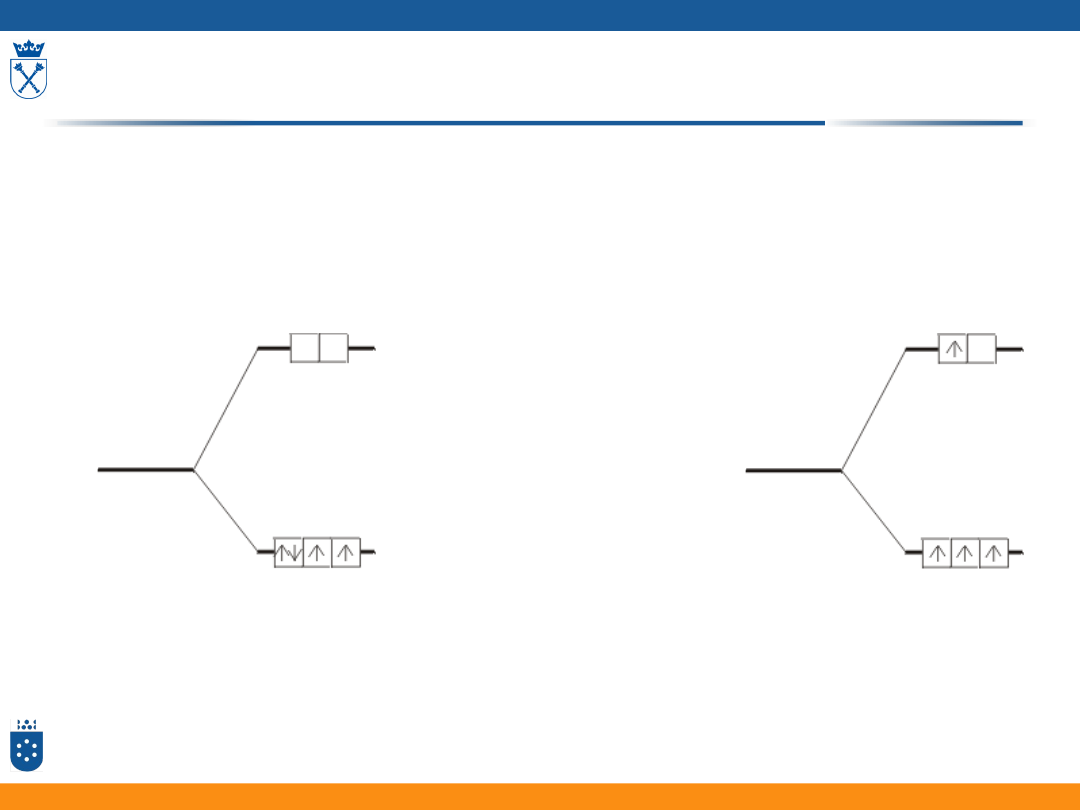
[Cr

2+

] 3d

4

Silne pole

Konfiguracj
a
niskospino
wa

Słabe pole

Konfiguracja
wysokospinow
a

Konkurencja między
tendencją elektronów
do pozostawania
możliwie daleko od
siebie a tendencją do
obsadzania pustych
orbitali o
najmniejszej energii

Przybliżenie słabego i silnego pola

40

Od czego zależy wielkość

rozszczepienia w polu ligandów:

• wartość  w kompleksach jonów danego okresu przejściowego o tej

samej wartościowości i z tymi samymi ligandami zmienia się w

stosunkowo wąskich granicach,

• wartość  w kompleksach tego samego ligandu szybko rośnie ze

wzrostem wartościowości kationu,

• wartość  w kompleksach tego samego ligandu rośnie

o ok. 30% przy przejściu od jonu metalu jednego okresu

przejściowego do odpowiadającego mu jonu metalu następnego

okresu,

• najczęściej spotykane ligandy można uszeregować według

wzrastającego pola ligandów tak, by  wzrastało w sposób

praktycznie niezależny od rodzaju kationu.

I

–

< Br

–

< Cl

–

< F

–

< OH

–

<H

2

O < NH

3

< NO

2–

< CN

–

Konfiguracja wysoko- i niskospinowa - ćwiczenie

Jaka jest preferowana konfiguracja orbitali d dla
metalu w poniższych kompleksach? (wysoko- czy
niskospinowa).

• [MnCl

6

]

4

• [Mn(CN)

6

]

4

• [MnCl

4

]

2

41

oktaedryczny wysokospinowy
oktaedryczny niskospinowy
tetraedryczny

Parametry rozszczepienia pola ligandów

[CoX(NH

3

)

5

]

n+

X = I

-

, Br

-

, Cl

-

, H

2

O i

NH

3



[CoI(NH

3

)

5

]

2+

głęboko purpurowy

[CoCl(NH

3

)

5

]

2+

różowy

[Co(NH

3

)

6

]

3+

żółty

Wzrost energii przejścia elektronowego o
najniższej energii, a więc wzrost 

O

ze zmianą

liganda w serii

1. wartości 

O

wzrastają ze wzrastającym

stopniem utlenienia metalu

[Ru(OH

2

)

6

]

2+



O

= 19 800 cm

-1

[Ru(OH

2

)

6

]

3+



O

= 28 600 cm

-1

2. wartości 

O

wzrastają w dół grupy:

3d < 4d < 5d

44

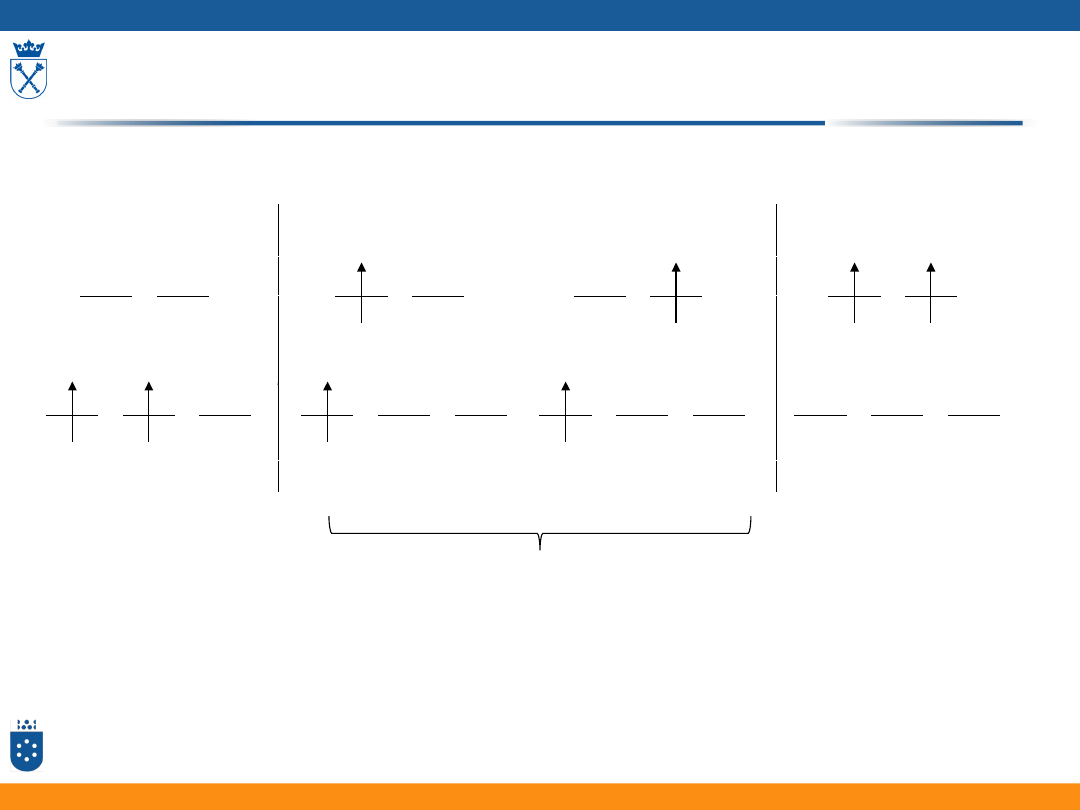
Rozmieszczenie elektronów

w oktaedrycznym kompleksie o konfiguracji d

2

t

2g

e

g

t

2g

2

t

2g

1

e

g

1

e

g

2

wzbudzenia jednoelektronowe wzbudzenie

dwuelektronowe

stan podstawowy

Przejścia d-d

• Pasma d-d dla kompleksów oktaedrycznych mają niską

intensywność

• Przejścia d-d w kompleksach oktaedrycznych są

zabronione ze względu na symetrię (reguła Laporte’a)

• Pasma tych przejść pojawiają się dzięki chwilowym

deformacjom symetrii kompleksu na skutek oscylacji
ligandów

• Dla kompleksów tetraedrycznych nie obowiązuje reguła

Laporte’a

• Pasma d-d dla takich kompleksów mają większą

intensywność niż dla kompleksów oktaedrycznych

45

Energia termu - parametry Racah

Parametry Racah określają wpływ odpychania międzyelektronowego na
energię termów dla określonej konfiguracji.

Parametry Racah są ilościowym wyrażeniem reguły Hunda

i odstępstw od niej.

Energia termu: kombinacja liniowa 3 parametrów Racah A, B i C np. dla

konfiguracji d

2

:

E(

1

S) = A + 14B + 7C

E(

1

G) = A + 4B + 2C

E(

1

D) = A - 3B + 2C

E(

3

P) = A + 7B

E(

3

F) = A - 8B

Energia przejścia między poziomami

3

P i

3

F:

E(

3

P) - E(

3

F) = 15 B

C > 5B 

3

F <

3

P <

1

D <

1

G <

1

S

C < 5B 

3

F <

1

D <

3

P <

1

G <

1

S

46

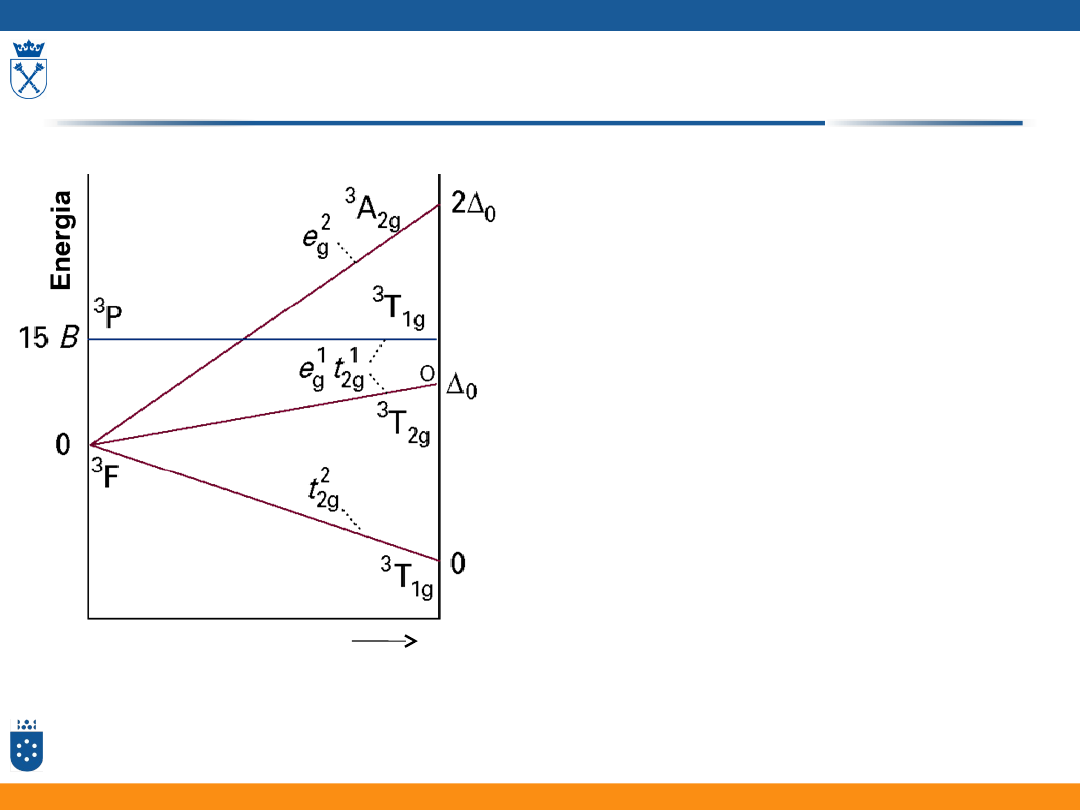
Energia termów w polu ligandów

• W polu ligandów energia

poszczególnych termów różnicuje się

• Energia termów zależy od mocy pola

ligandów

• Zmienia się sposób zapisu termów

• Symbole termów zależą od rodzajów

elementów symetrii danego układu

• Energia potrzebna do wzbudzenia

elektronów zależy od mocy pola
ligandów

47

diagram: Fizyczna chemia nieorganiczna, S.F.A Kettle, Wydawnictwo Naukowe PWN, Warszawa 1999

moc pola ligandów

Diagram dla konfiguracji d

2

w polu oktaedrycznym

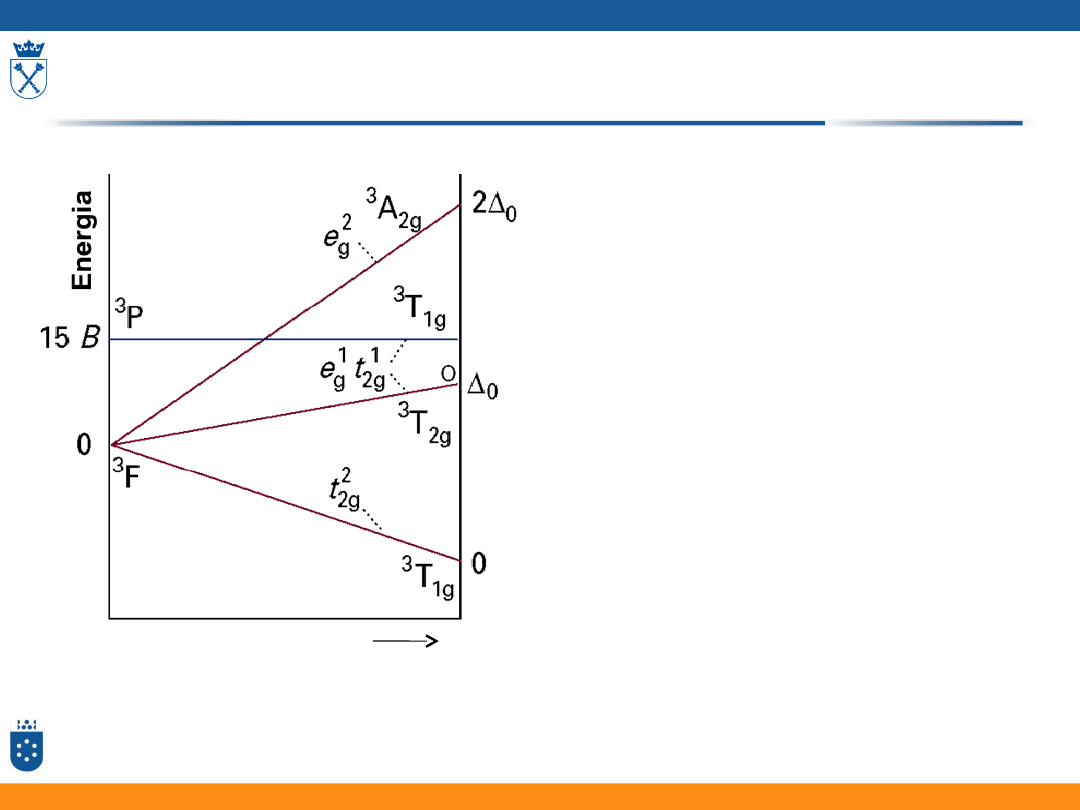
Diagramy Tanabe – Sugano

• Zależność energii poszczególnych

termów od mocy pola ligandów
przedstawiają tzw. diagramy Tanabe
– Sugano

• Parametry na osiach diagramu to:

• moc pola: /B
• energia: E/B
(gdzie B, to jeden z parametrów Racah)

• B oraz  to tzw. parametry pola

ligandów

48

diagram: Fizyczna chemia nieorganiczna, S.F.A Kettle, Wydawnictwo Naukowe PWN, Warszawa 1999

moc pola ligandów

Diagram dla konfiguracji d

2

w polu oktaedrycznym

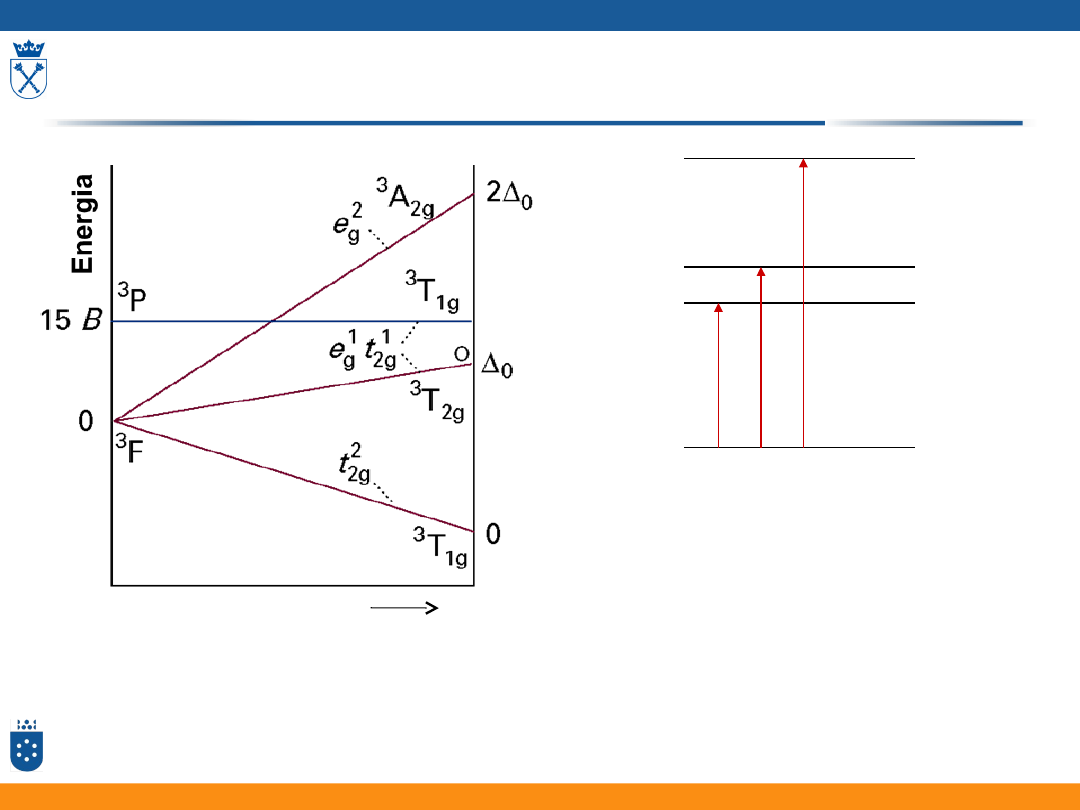
moc pola ligandów

49

Diagramy Tanabe – Sugano

Przejścia elektronowe

Z diagramu TS można odczytać,

że:

• Możliwe są 3 przejścia

elektronowe

• W zależności od mocy pola

ligandów przejścia wystąpią
przy innych długościach fali

diagram: Fizyczna chemia nieorganiczna, S.F.A Kettle, Wydawnictwo Naukowe PWN, Warszawa 1999

Diagram dla konfiguracji d

2

w polu oktaedrycznym

0

Δ

0

3

T

1g

2Δ

0

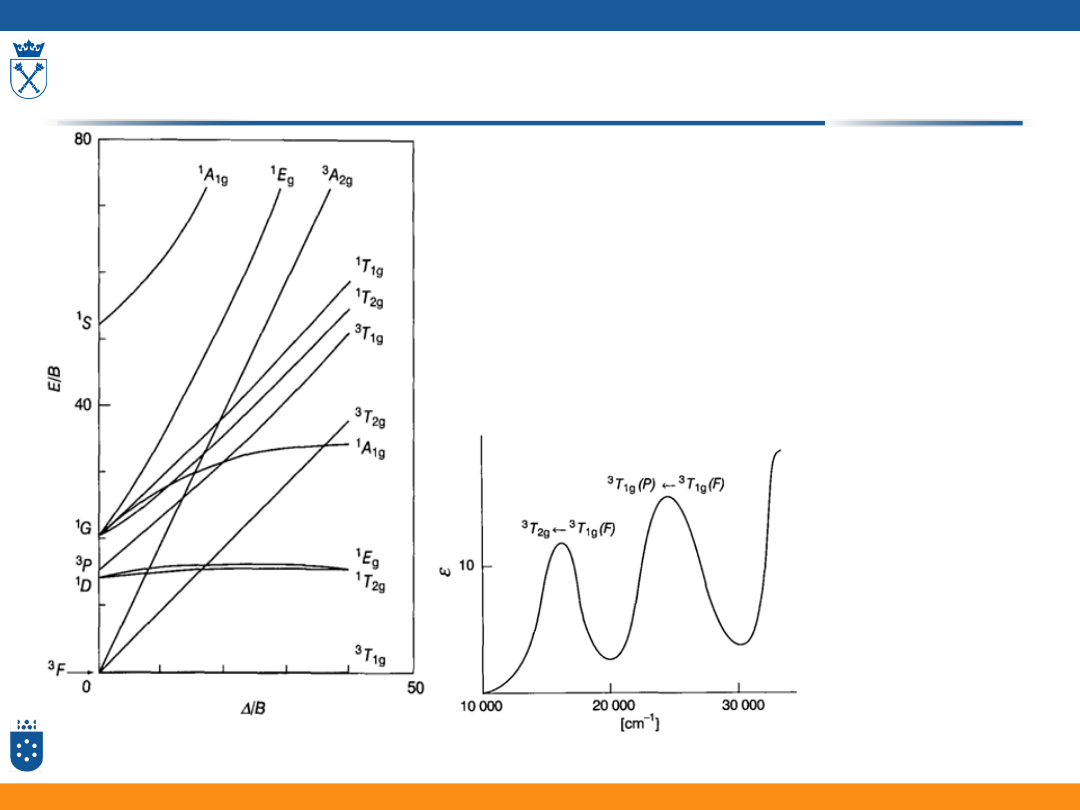
Diagramy Tanabe – Sugano

Widma przejść d-d

Dla znanych wartości parametru
rozszczepienia i B z diagramu TS
można odczytać energię
poszczególnych przejść,
a następnie obliczyć przy jakich
długościach fali pojawią się
pasma

50

diagram dla konfiguracji d

2

: Fizyczna chemia nieorganiczna, S.F.A Kettle, Wydawnictwo Naukowe PWN,

Warszawa 1999

Dwa przejścia d-
d w widmie
kompleksu
[V(mocznik)

6

]

3+

dla /B = 4,42

Diagramy Tanabe – Sugano

Reguła niekrzyżowania się termów

Jeśli wzrastające pole ligandów
powoduje zbliżanie się termów
słabego pola (niebieskie linie) to
one się nie krzyżują lecz
zmieszają (czerwone linie) i
zapobiegną przecięciu – termy o
tej samej symetrii



Zakrzywione linie na diagramach
Tanabe-Sugano są wynikiem
mieszania termów o tej samej
symetrii

51

moc pola ligandów

Stan 1

Stan 2

52

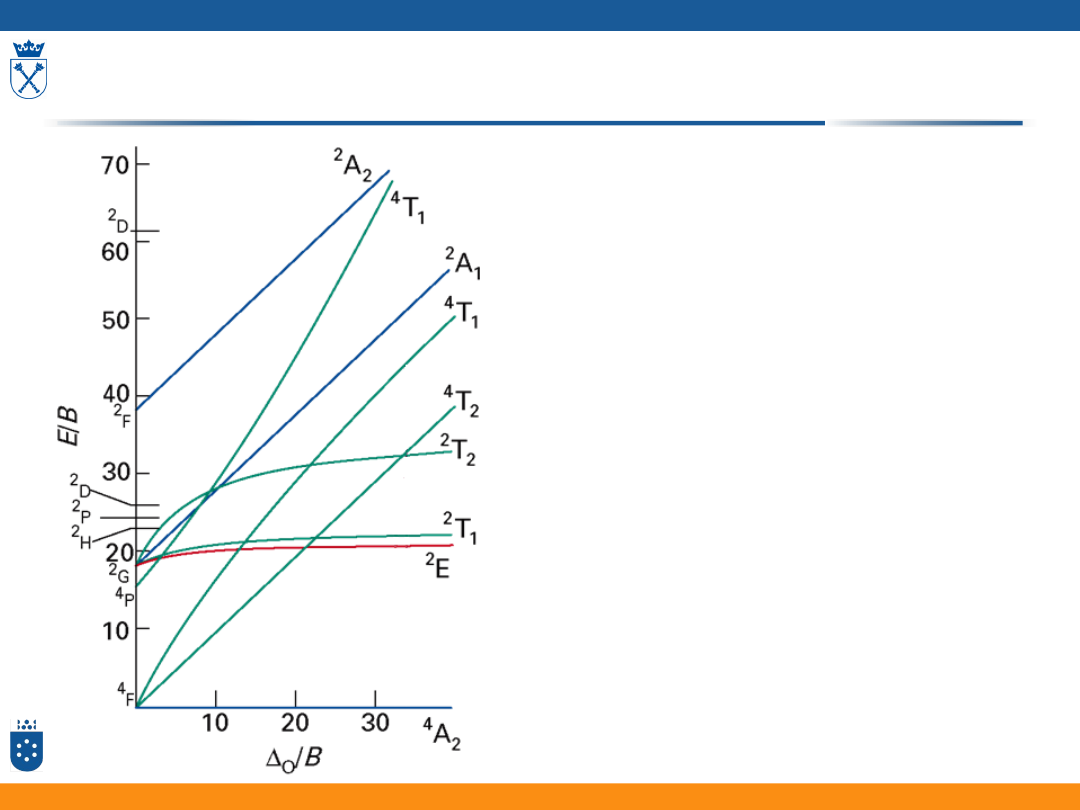
Korzystając z zamieszczonego
diagramu oblicz energię dwóch
pierwszych przejść kwartetowych
w widmie kompleksu
[Cr(H

2

O)

6

]

3+

,

dla którego:
Δ

O

= 17 600 cm

-1

i B = 700 cm

-1

Sposób rozwiązania:

1. Identyfikacja przejść:

4

T

2g



4

A

2g

E

1

=?

4

T

1g



4

A

2g

E

2

=?

2. Wyliczenie wartości Δ

O

/B

Δ

O

/B = 17 600/700 = 25.14

Wyznaczanie energii przejść z diagramu TS - Zadanie

53

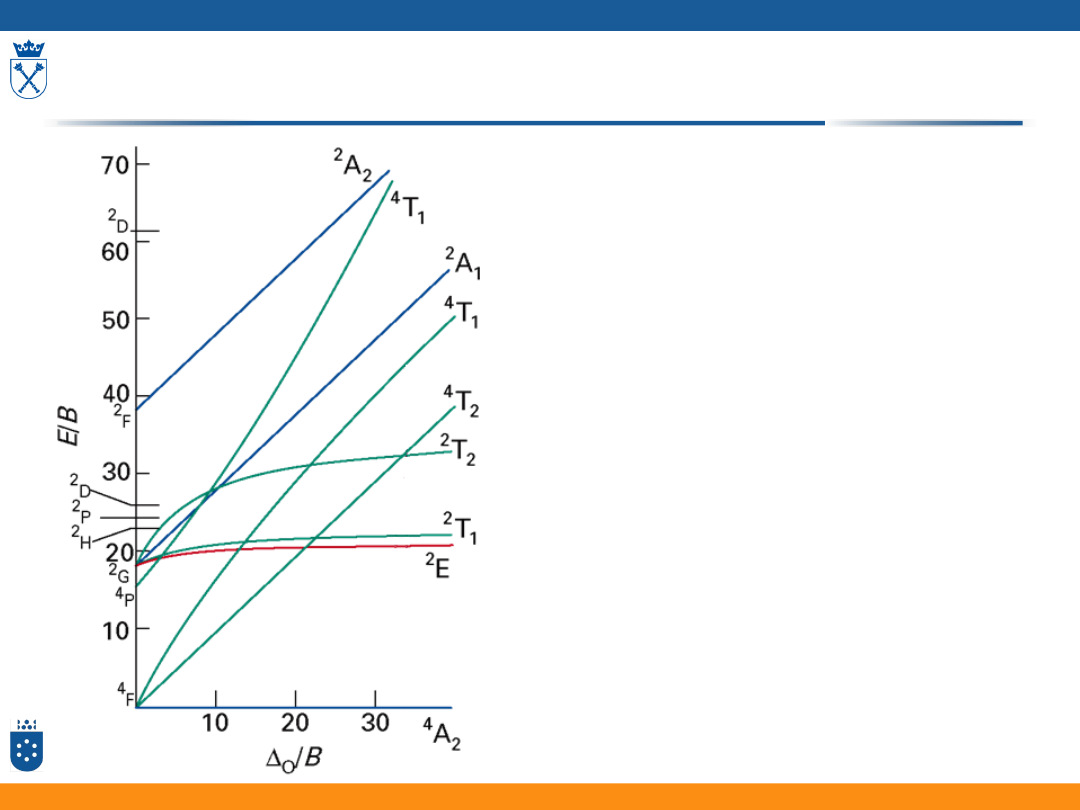
Korzystając z zamieszczonego
diagramu oblicz energię dwóch
pierwszych przejść
kwartetowych w widmie
kompleksu [Cr(H

2

O)

6

]

3+

,

dla którego:
Δ

O

= 17 600 cm

-1

i B = 700 cm

-

1

Sposób rozwiązania:

3. Odczytanie wartości E/B z

diagramu TS dla Δ

O

/B =

25.14:
E

1

/B =25 i E

2

/B =32

4.Obliczenie wartości energii:
E

1

= 25  700 = 17 500 cm

-1

E

2

= 32  700 = 22 400 cm

-1

Wyznaczanie energii przejść z diagramu TS - Zadanie

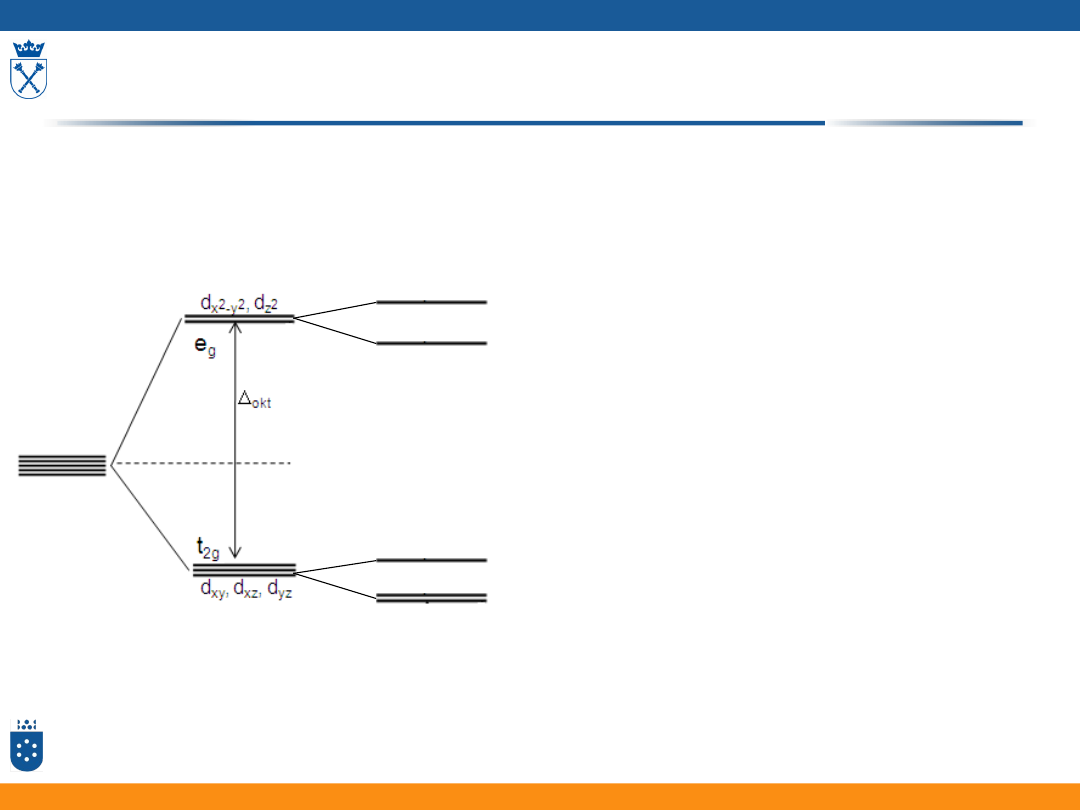
Rozszczepienie orbitali d

w kompleksach płaskich - kwadratowych

• Kompleksy płaskie-kwadratowe

wyprowadzane są z
oktaedrycznych, gdzie
płaszczyzna kwadratu to xy

• Trudno określić, która wartość to



• Nie ma jasnego związku

pomiędzy wartościami
poszczególnych rozszczepień

• Interpretacja widm tego typu

kompleksów jest skomplikowana.

54

e

g

b

2g

b

1g

a

1g

Efekt Jahna-Tellera

Jeśli konfiguracja elektronowa
stanu podstawowego cząsteczki
nieliniowej jest zdegenerowana, to
cząsteczka ulega deformacji
usuwając degenerację i uzyskując
niższą energię.

deformacja tetragonalna – efekt Jahna-
Tellera

deformacja płaska kwadratowa –
ekstremalny przypadek efektu Jahna-
Tellera

Widma elektronowe układów elektronów f

• W widmach lantanowców i aktynowców występują trzy

typy przejść elektronowych:

• f – f – wiele słabych, ostrych pasm w zakresie

promieniowania widzialnego i podczerwonego

• nf – (n+1)d – gdzie n to główna liczba kwantowa; pasma

szerokie o dużej intensywności

• ligand  orbital f metalu (pasma CT) – intensywne,

szerokie pasma w zakresie nadfioletu

• W przypadku orbitali f rozszczepienie poziomów w polu

krystalicznym ligandów nie odgrywa znaczącej roli.

56

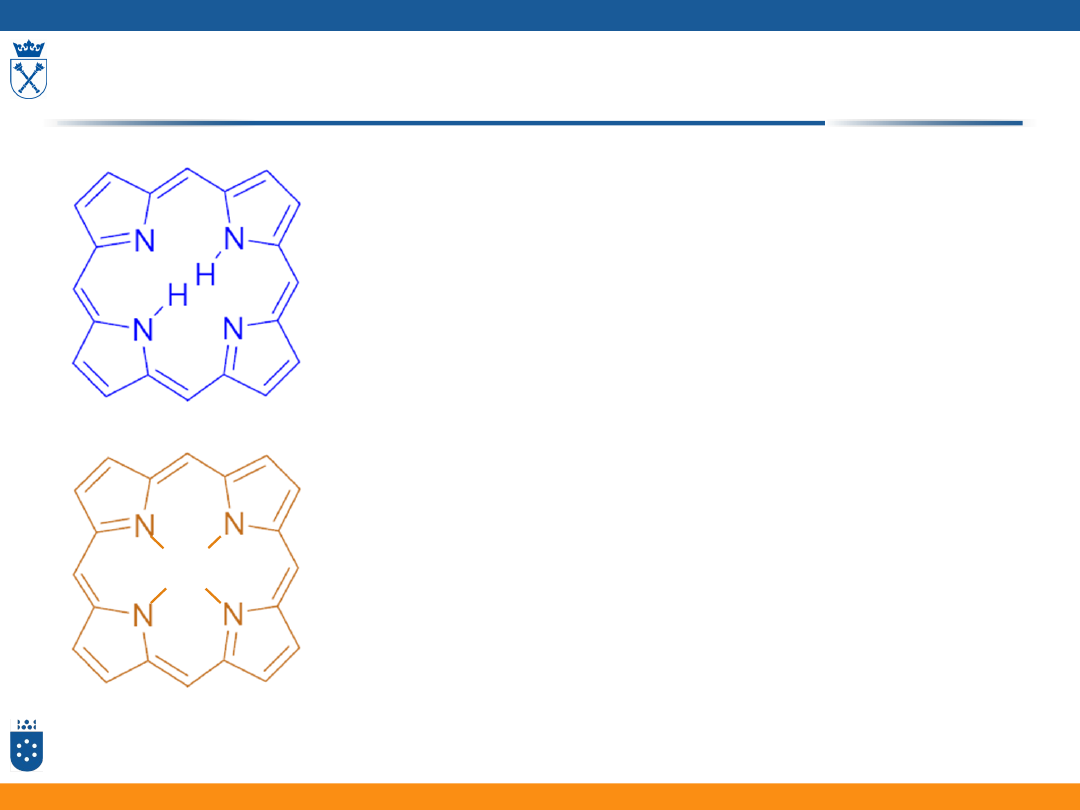
Porfiryny i metaloporfiryny

57

M

II

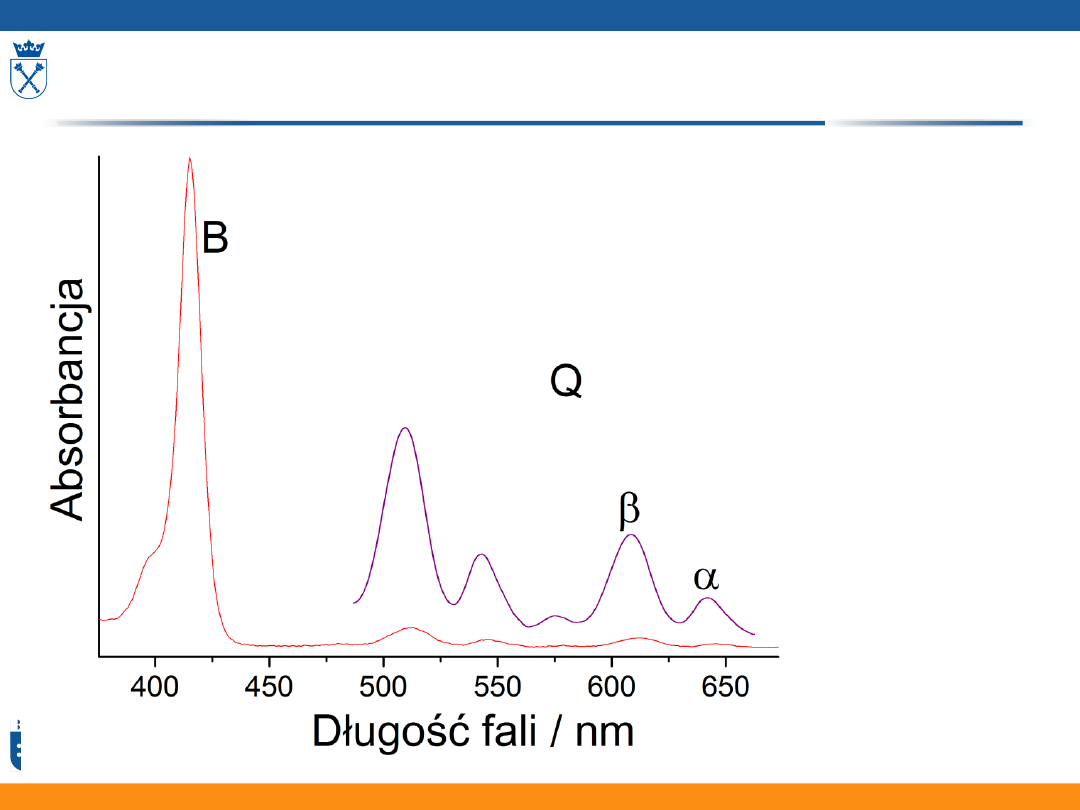
• Na widmach porfiryn można

wyróżnić 3 zbiory pasm:

• Q – 450-700 nm – zwykle 2 - 4

pasma

• B – tzw. pasmo Soreta – 380-400

nm – najbardziej intensywne

• N, L, M – 215-325 nm – niezbyt

intensywne, ich położenie zależy
od rozpuszczalnika

• Są to głównie przejścia  → *

Porfiryny i metaloporfiryny

58

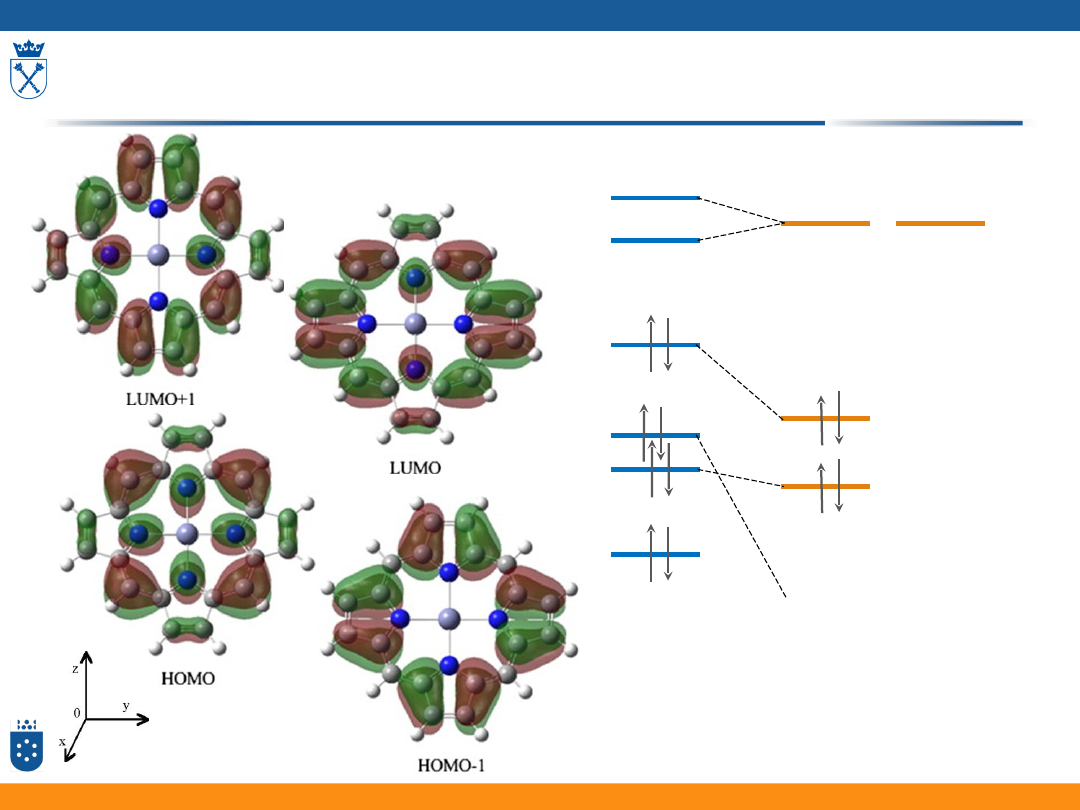
Zmiana symetrii z D

2h

(H

2

P) na D

4h

(MP)

prowadzi do uproszczenia widma UV-Vis.
Zmniejsza się liczba pasm Q wskutek
pojawienia się degeneracji poziomów LUMO.

59

Porfiryny i metaloporfiryny

e

g

(π*)

a

2u

(π)

a

1u

(π)

H

2

P

(D

2h

)

M

II

P

(D

4h

)

(a

2u

)

2

(e

g

)

0

→ (a

2u

)

1

(e

g

)

1

(a

1u

)

2

(a

2u

)

2

(e

g

)

0

→ (a

1u

)

1

(a

2u

)

2

(e

g

)

1

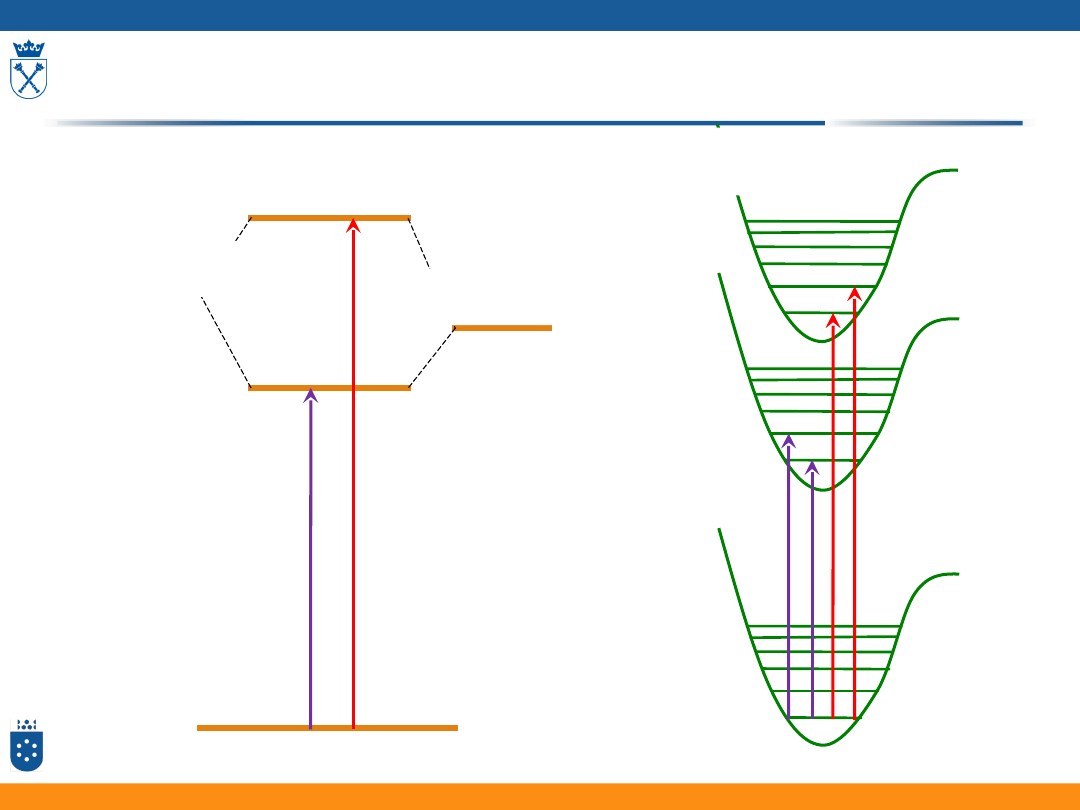
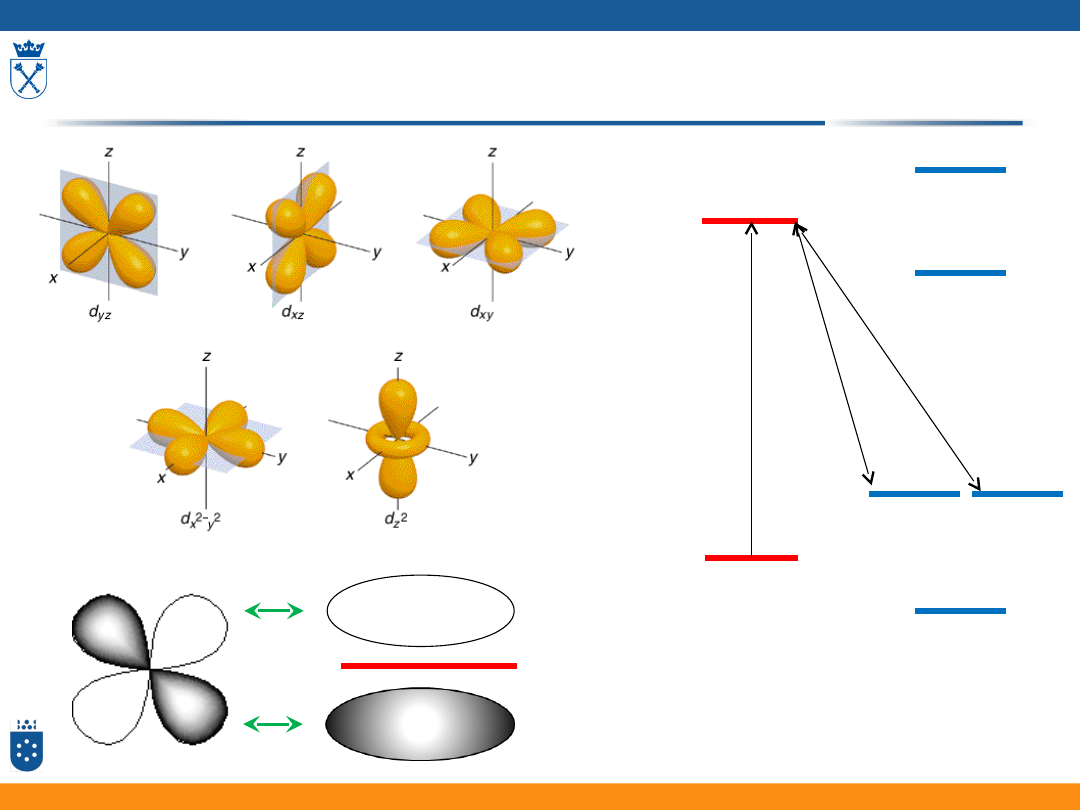
Model czterech orbitali Goutermana

Porfiryny i metaloporfiryny

S

0

S

1

S

2

(a

1u

)

1

(a

2u

)

2

(e

g

)

1

(a

1u

)

2

(a

2u

)

2

(a

1u

)

2

(a

2u

)

1

(e

g

)

1

Pa

sm

o

Q

(

α

)

Pa

sm

o

B

(

S

o

re

ta

)

S

0

S

1

S

2

S

o

re

t

α

β

Porfiryny i metaloporfiryny

61

d

x

2

-d

y

2

d

z

2

d

xz

d

yz

d

xy

π

π*

ΔE

d

π

•

Kompleksy

niskospinowe

wykazują

ostrzejsze

pasma

absorpcyjne

niż

kompleksy wysokospinowe.

•

Dla kompleksów wysokospinowych (np.
Fe(II)-porfiryna) można obserwować pasma
CT w podczerwieni.

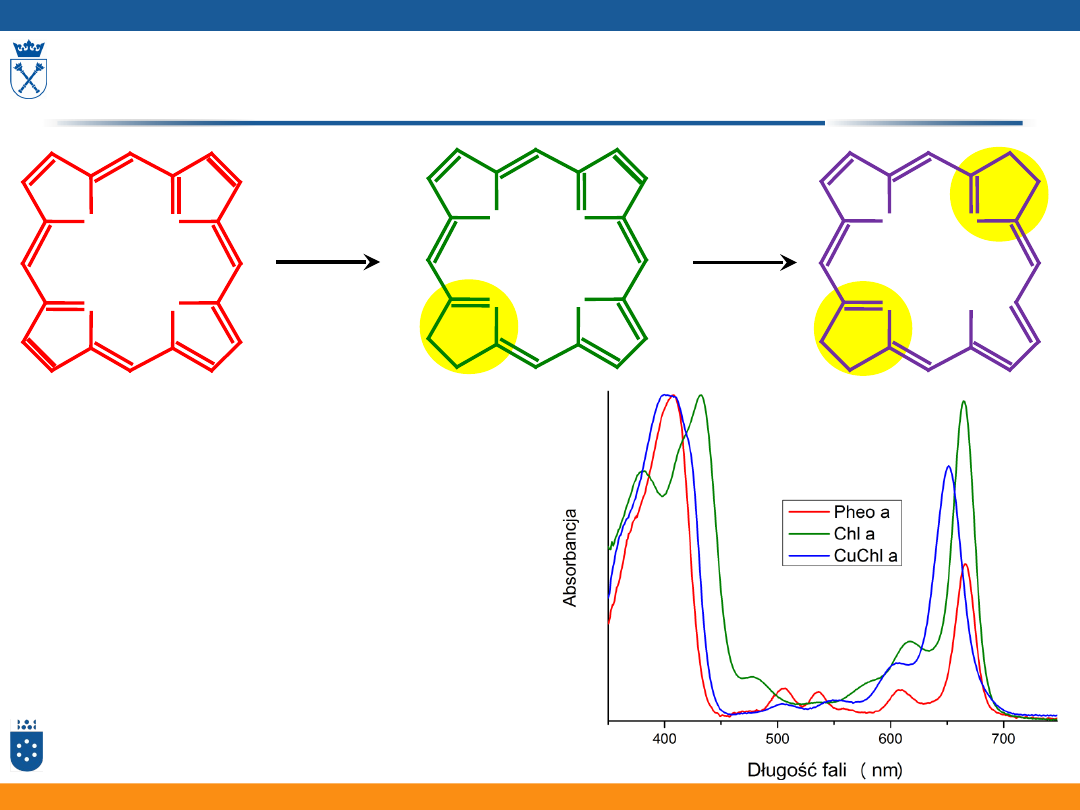
Porfiryny i metaloporfiryny

62

+ 2e

–

+ 2e

–

N

NH

N

N

H

porfiryna

NH

N

N

H

N

chloryna

N

NH

N

N

H

bakteriochloryna

Niezależnie od metalu, zmiany
struktury elektronowej
pierścienia tetrapirolowego
pociągają za sobą zmiany
symetrii:

P >> Chl < BChl

Wynikiem tych zmian jest
zwiększenie intensywności
pasma α.

Absorpcja i emisja porfiryn

Absorpcja

Emisja

Metal

Regularne

Fluorescencyjne

Φ

f

> 10

-3

, Φ

em

> 10

-3

Mg(II), Zn(II), Cd(II),

Sn(IV), Al(III)

Nieregularne – hipso

Fosforescencyjne

Φ

f

< 10

-4

, Φ

em

> 10

-3

Pd(II), Pt(II), Ru(II),

Os(II), Rh(III)

Nieregularne - hipso

Nie emitujące

Φ

em

< 10

-4

Co(II), Ni(II), Fe(II),

Fe(III), Ag(III)

Nieregularne – hiper

Nie emitujące

Φ

em

< 10

-4

Sn(II), Pb(II), Sb(III),

Bi(III), Mn(III), Mo(V),

W(V)

Nieregularne - hiper

Luminescencyjne

Φ

em

> 10

-4

Cr(III)

Kompleksy tetrapirolowe z jonami metali otwartopowłokowych bardzo
słabo

lub

w ogóle nie wykazują emisji fuorescencji/fosforescencji.

63

64

Literatura:

• „Podstawy spektroskopii molekularnej” Z. Kęcki,

Wydawnictwo Naukowe PWN, Warszawa 1998

• „Fizyczna chemia nieorganiczna” S.F.A Kettle,

Wydawnictwo Naukowe PWN, Warszawa 1999

• „Chemia nieorganiczna - podstawy” F.A. Cotton,

G. Wilkinson, P.L. Gaus, Wydawnictwo Naukowe PWN,
Warszawa 1995