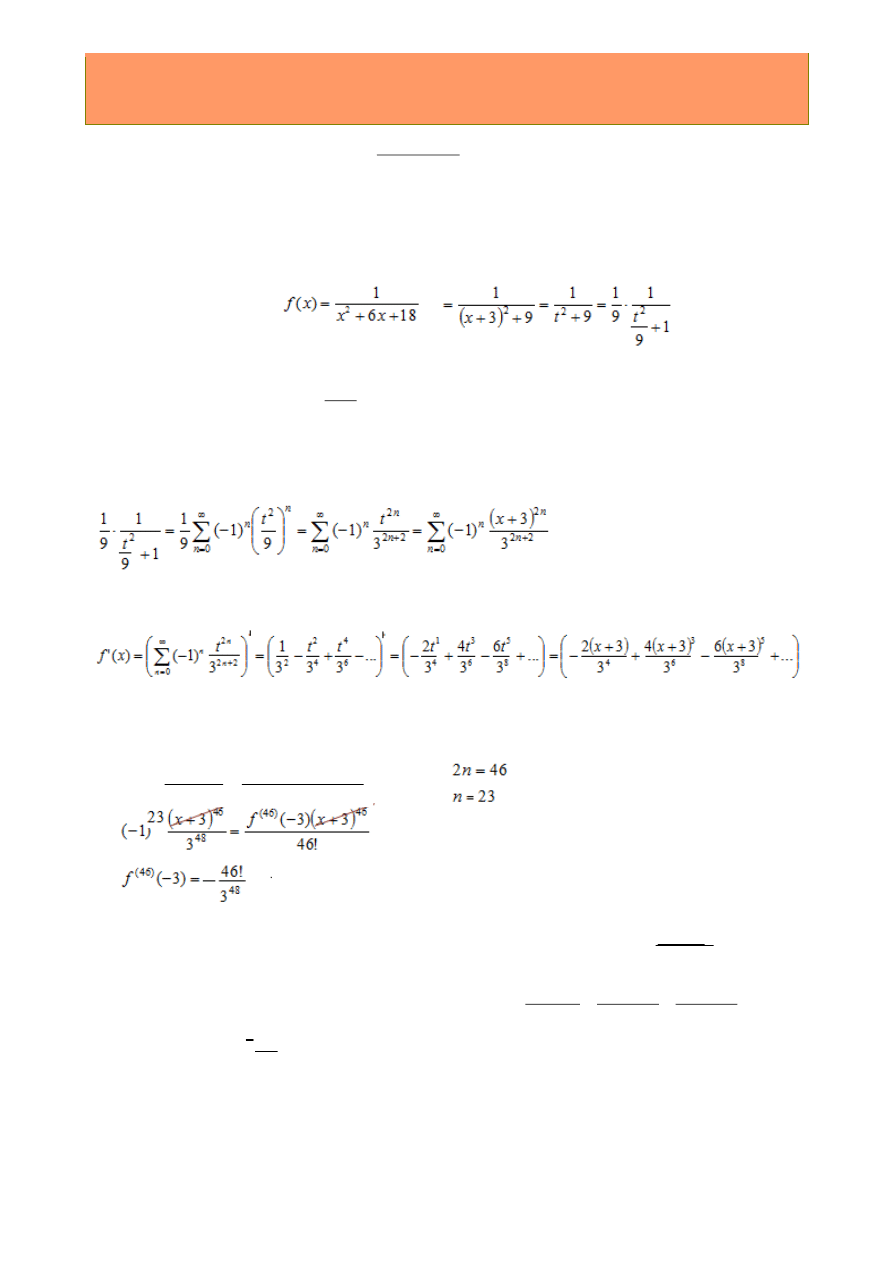
Egzamin
rok 2012/2013
Zadanie 4:
Dana jest funkcja
Rozwinąć funkcje f(x) i f'(x)w szereg Taylora w otoczeniu x
0
= -
3. Obliczyć
Rozwiązanie:
z kartki z gotowymi rozwinięciami:
1)
Rozwinięcie f(x) w szereg Taylora w otoczeniu x
0
= -3 wynosi:
2) Rozwinięcie f'(x) w szereg Taylora w otoczeniu x
0
= -3 wynosi:
3) wynosi:
Odpowiedź:
Rozwinięcie f(x) w szereg Taylora w otoczeniu x
0
= -3 wynosi:
Rozwinięcie f'(x) w szereg Taylora w otoczeniu x
0
= -3 wynosi:
Natomiast:
Autor:
Michał Z.
grupa
2
26.01.2014
18
6
1
)
(
2
x
x
x
f
)
3
(
)
46
(
f
3
0
3
3
0
0
0
x
t
x
x
0
)
1
(
1
1
n
n
n
x
x
!
46
3
)
3
(
3
3
)
1
(
46
)
46
(
2
2
2
x
f
x
n
n
n
)
3
(
)
46
(
f
2
2
2
0
3
3
)
1
(
n
n
n
n
x
...
3
3
6
3
3
4
3
3
2
8
5
6
3
4
x
x
x
48
)
46
(
3
!
46
)
3
(
f