
PORÓWNANIE SPRAWNOŚCI UKŁADÓW
Janusz Kotowicz
Instytut Maszyn i Urządzeń Energetycznych
P O L I T E C H N I K A Ś L Ą S
K A
Wydział Inżynierii Środowiska i
Energetyki
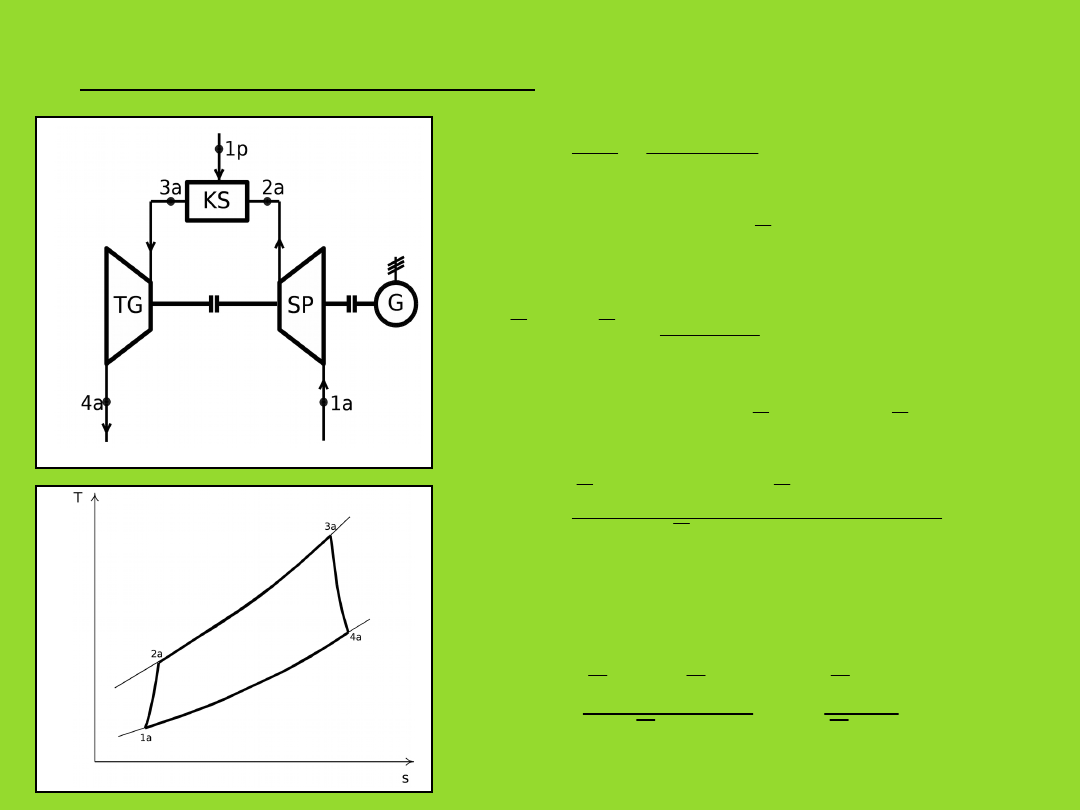
2. Układ turbiny gazowej
a
a
a
a
a
a
a
a
a
a
a
a
Ea
a
a
S
S
a
a
a
a
S
S
a
a
Wa
S
S
a
a
a
a
Da
a
a
a
a
a
a
S
S
a
a
Da
Da
Wa
Da
Da
ob
Ea
S
S
T
S
S
T
S
S
T
S
S
T
dS
T
dS
S
T
Q
dS
S
T
S
S
T
T
S
S
T
dS
S
T
Q
Q
Q
Q
Q
L
a
a
a
a
a
a
a
a
2
3
3
2
1
4
1
4
2
3
3
2
1
4
1
4
1
4
1
4
3
2
2
3
3
2
2
3
3
2
3
2
4
1
4
1
3
2
3
2
1
Przy założeniu odwracalności
przemian:
a
a
a
a
a
a
a
a
a
a
Ea
T
T
T
T
T
3
2
1
4
3
2
1
4
3
2
1
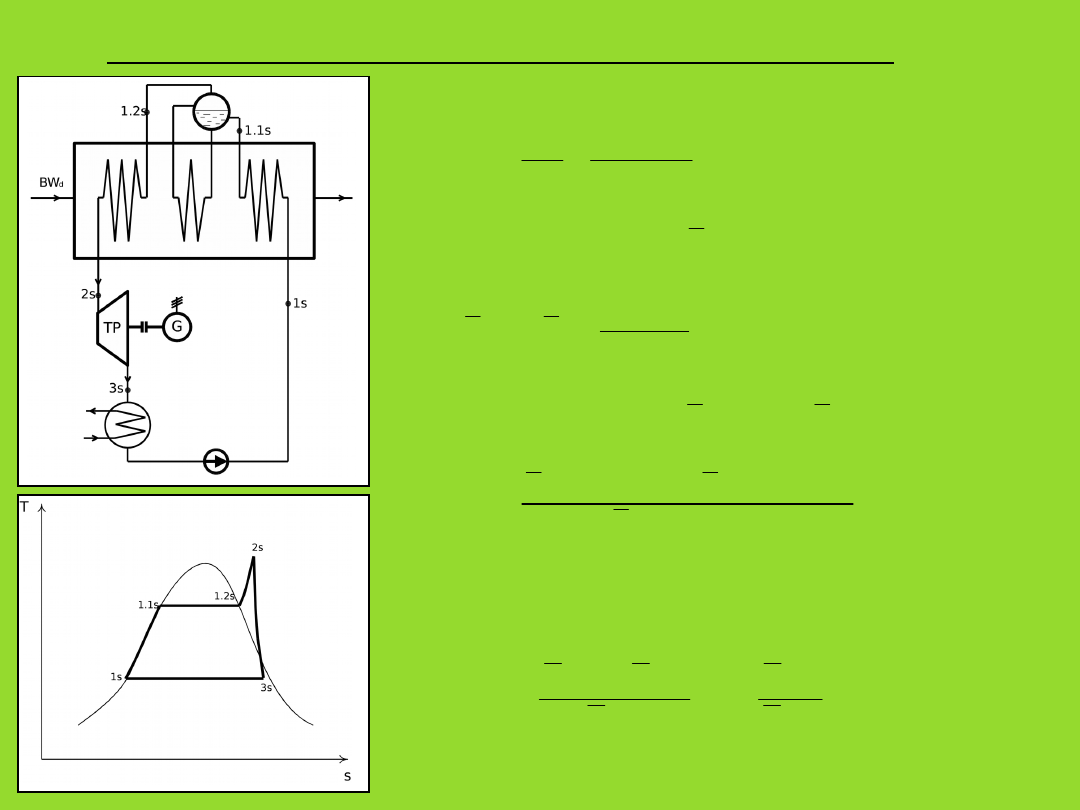
3. Konwencjonalny układ siłowni parowej
s
s
s
s
s
s
s
s
s
s
s
s
Es
s
s
S
S
s
s
s
s
S
S
s
s
Ws
S
S
s
s
s
s
Ds
s
s
s
s
s
s
S
S
s
s
Ds
Ds
Ws
Ds
Ds
ob
Es
S
S
T
S
S
T
S
S
T
S
S
T
dS
T
dS
S
T
Q
dS
S
T
S
S
T
T
S
S
T
dS
S
T
Q
Q
Q
Q
Q
L
a
a
s
s
s
s
s
s
1
2
2
1
1
3
1
3
1
2
2
1
1
3
1
3
1
3
1
3
2
1
1
2
2
1
1
2
2
1
2
1
3
1
3
1
2
1
2
1
1
Przy założeniu odwracalności
przemian:
s
s
s
s
s
s
s
s
s
s
Es
T
T
T
T
T
2
1
1
3
2
1
1
3
2
1
1
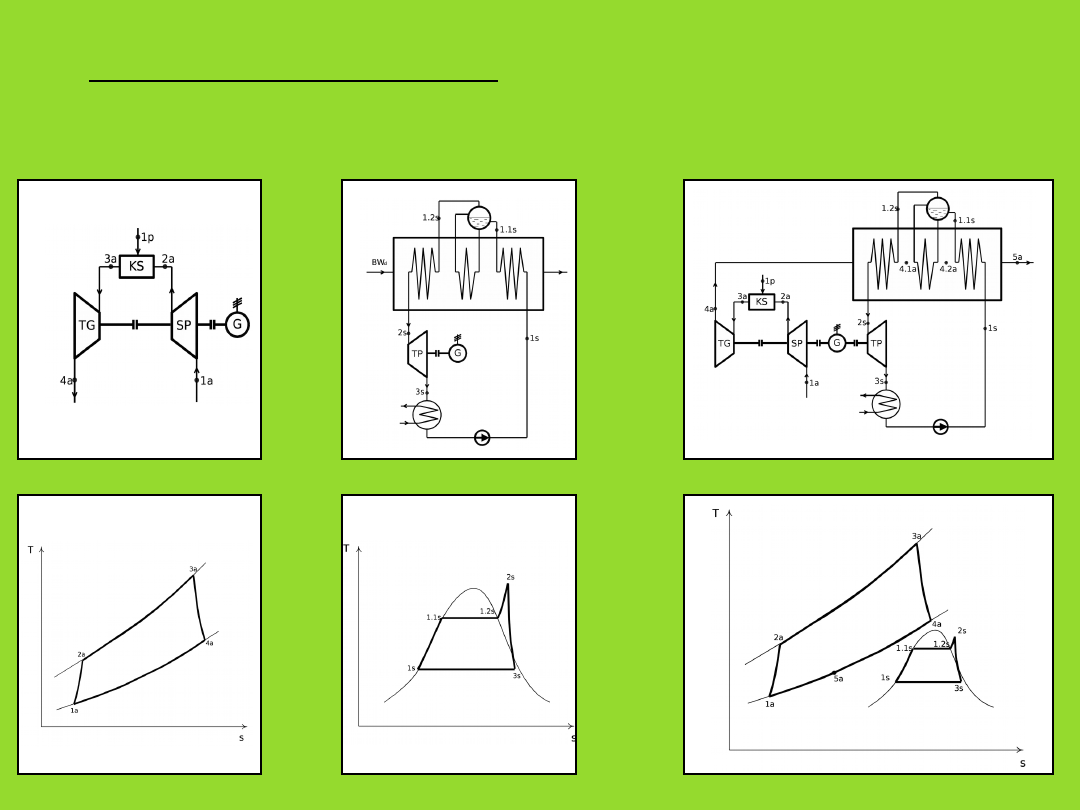
4. Układ kombinowany
+
=
=
+
5. Układ kombinowany
a
a
a
a
s
s
s
s
a
a
a
s
a
a
a
a
E
s
s
S
S
s
s
s
a
S
S
s
s
Ws
a
a
S
S
a
a
a
a
S
S
a
a
Wa
Ws
Wa
W
a
a
a
a
S
S
a
a
D
D
W
D
D
ob
E
S
S
T
S
S
T
S
S
T
S
S
T
S
S
T
ds
T
dS
S
T
Q
S
S
T
dS
T
dS
S
T
Q
Q
Q
Q
S
S
T
dS
S
T
Q
Q
Q
Q
Q
L
s
s
s
s
a
a
a
a
a
a
2
3
3
2
1
3
1
3
1
5
1
5
2
3
3
2
1
3
1
3
1
3
1
3
1
5
1
5
1
5
1
5
2
3
3
2
3
2
3
1
3
1
5
1
5
1
3
2
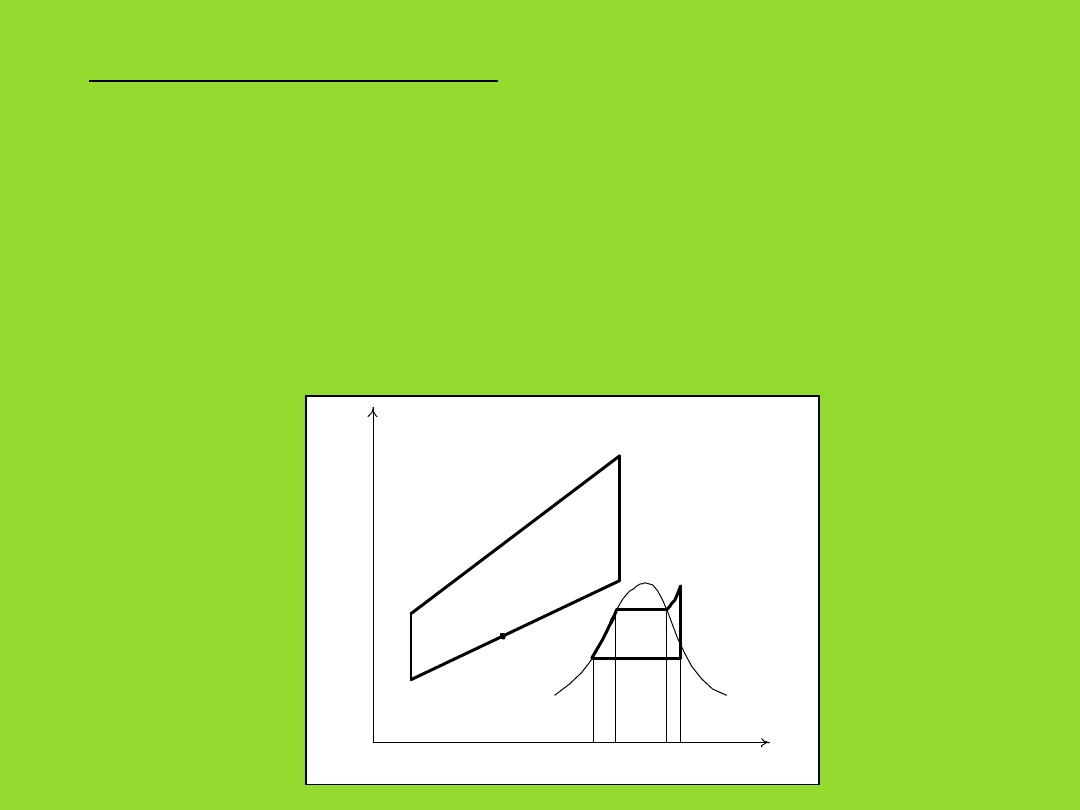
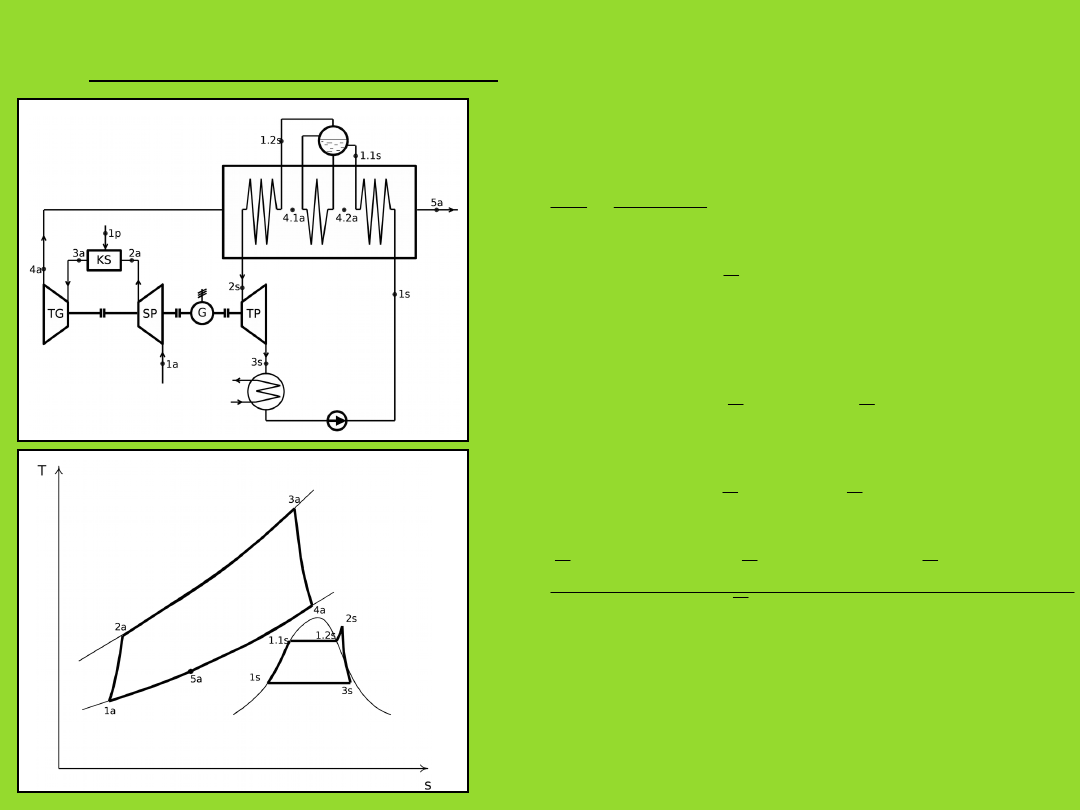
6. Układ kombinowany
Przy pewnych upraszczających założeniach możliwe jest zapisanie sprawności
energetycznej układu kombinowanego wyłącznie w funkcji temperatur czynników
roboczych.
Założenia:
1) Procesy sprężania oraz rozprężania odbywają się bez strat ciepła (wg. przemian
izentropowych)
2) Przyrost temperatury czynników roboczych opisany pomiędzy punktami
charakterystycznymi jest liniową funkcją przyrostu entropii
3) W części parowej układu średnia temperatura czynnika roboczego w kotle jest
równa temperaturze wody w stanie nasycenia
2a
1a
1s
4a
1.1s
1.2s
3a
3s
2s
5a
T
s
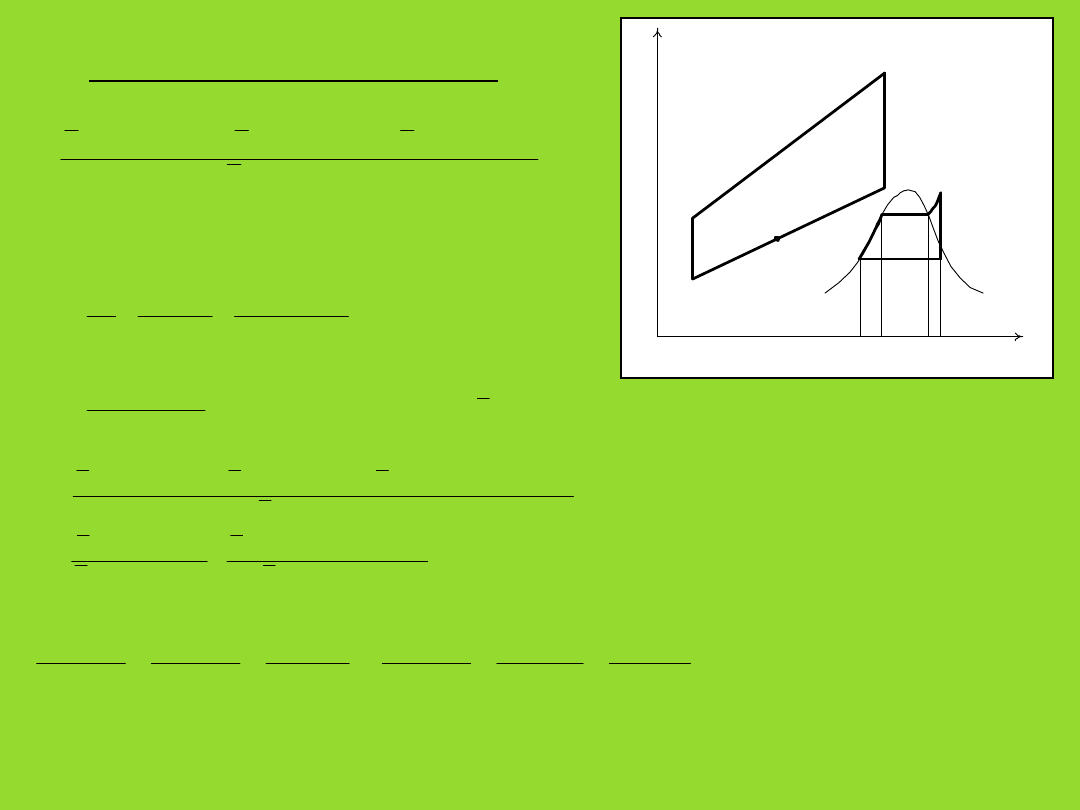
7. Układ kombinowany
a
a
a
a
s
s
s
s
a
a
a
a
a
a
a
a
E
S
S
T
S
S
T
S
S
T
S
S
T
2
3
3
2
1
3
1
3
1
5
1
5
2
3
3
2
Dla części parowej możemy napisać
Es
a
a
a
a
Es
a
a
s
s
a
a
s
s
a
a
Es
a
a
s
s
s
s
s
s
s
s
D
W
D
D
ob
Es
S
S
T
Q
Q
Q
Q
Q
Q
Q
Q
Q
Q
Q
Q
Q
Q
L
1
1
5
4
5
4
5
4
1
3
5
4
1
3
5
4
5
4
2
1
2
1
1
3
2
1
a
a
a
a
Es
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
Es
a
a
a
a
a
a
a
a
a
a
a
a
E
S
S
T
S
S
T
S
S
T
S
S
T
S
S
T
S
S
T
S
S
T
S
S
T
2
3
3
2
5
4
5
4
2
3
3
2
1
5
1
5
2
3
3
2
5
4
5
4
1
5
1
5
2
3
3
2
1
1
1
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
T
T
T
T
S
S
S
S
S
S
S
S
T
T
T
T
S
S
S
S
S
S
S
S
1
4
1
5
1
4
1
5
2
3
1
5
1
4
5
4
1
4
5
4
2
3
5
4
;
2a
1a
1s
4a
1.1s
1.2s
3a
3s
2s
5a
T
s
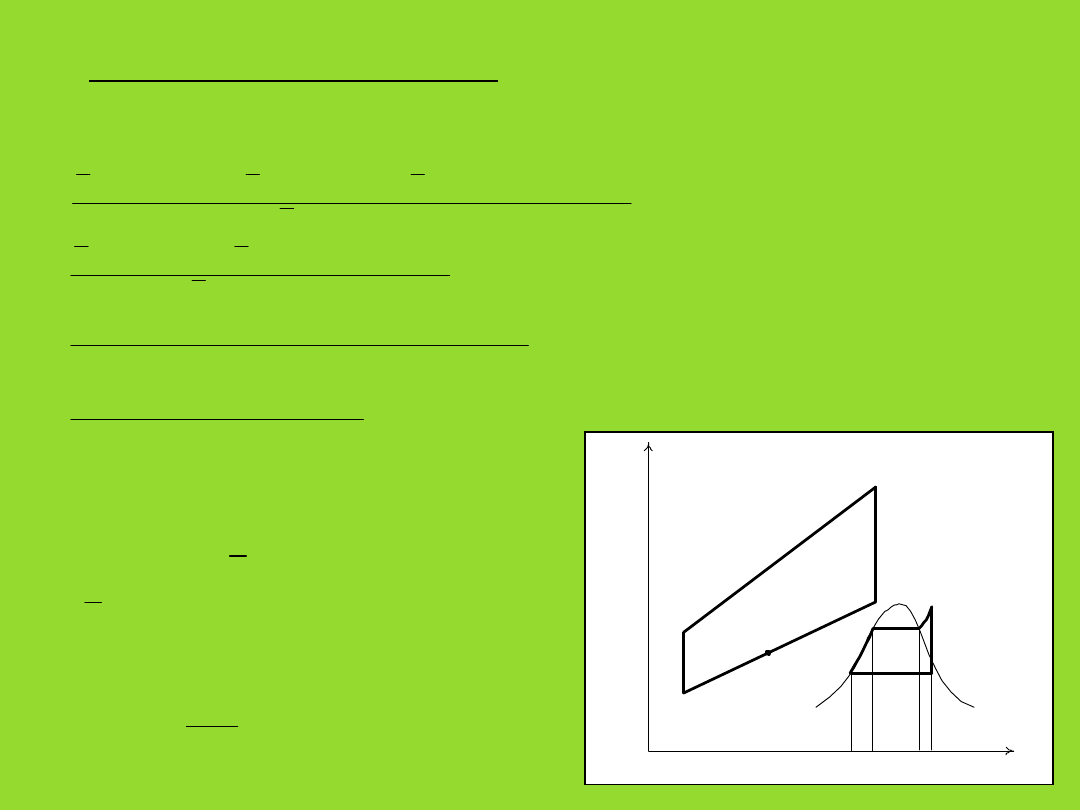
8. Układ kombinowany
Ostatecznie możemy napisać
a
a
a
a
Es
a
a
a
a
a
a
a
a
Es
a
a
a
a
a
a
a
a
a
a
a
a
Es
a
a
a
a
a
a
a
a
a
a
a
a
Es
a
a
a
a
a
a
a
a
a
a
a
a
E
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
S
S
T
S
S
T
S
S
T
S
S
T
1
4
3
2
2
5
2
4
2
1
2
5
1
4
3
2
5
4
5
4
1
5
1
5
1
4
3
2
5
4
5
4
1
5
1
5
2
3
3
2
5
4
5
4
1
5
1
5
2
3
3
2
1
1
1
1
1
1
1
Ponadto przy obliczaniu sprawności energetycznej
części parowej, stosując założenie 3, mamy
)
(
)
(
)
(
1
3
1
.
1
1
3
2
.
1
1
.
1
1
2
2
1
2
1
s
s
s
s
s
s
s
s
s
s
s
s
s
Ds
S
S
T
S
S
T
S
S
T
Q
Q
A więc
s
s
Es
T
T
1
.
1
1
1
2a
1a
1s
4a
1.1s
1.2s
3a
3s
2s
5a
T
s
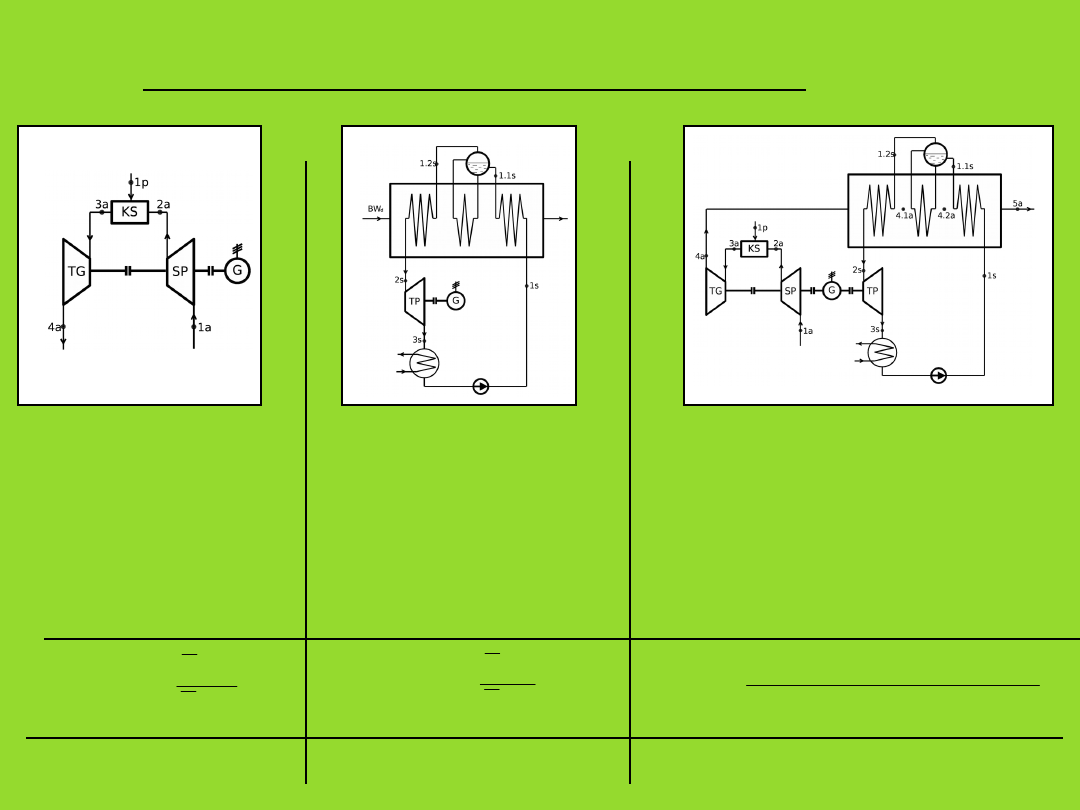
9. Porównanie sprawności układów
C
t
C
t
C
t
C
t
a
a
a
a
525
1100
300
15
4
3
2
1
C
t
C
t
C
t
s
s
s
525
295
30
2
1
.
1
1
C
t
C
t
C
t
C
t
C
t
a
a
a
a
a
80
525
1100
300
15
5
4
3
2
1
a
a
a
a
Ea
T
T
3
2
1
4
1
s
s
s
s
Es
T
T
2
1
1
3
1
a
a
a
a
Es
a
a
a
a
E
T
T
T
T
T
T
T
T
1
4
3
2
2
5
2
4
2
1
2
5
1
1
442
,
0
Ea
466
,
0
Es
421
,
0
Es
659
,
0
E
C
t
C
t
C
t
s
s
s
480
250
30
2
1
.
1
1
Document Outline
Wyszukiwarka
Podobne podstrony:
Analiza porównawcza współpracy układów płucznych i odstojnik 24K224FCJB5HLJRFWNQ6VQAMW66ZWDL467L36XQ
Napęd hybrydowy, na czym polega, przykładowe rozwiązania, porównanie do układów pojedyńczych
Porównywanie układów chłodzenia pośredniego i bezpośredniego, studium rolnicze, Mechanizacja, Układ
Rozwiązywanie układów równań
PORÓWNYWANIE TECHNOLOGII
Złote standardy w diagnostyce chorób układowych 3
Metodyka harcerska i starszoharcerska porównanie
8 ocena jakości układów regulacji
Porównanie dwóch regionalnych strategii innowacji
19 Teorie porównanie
Wykład VIII Synteza układów sekwencyjnych
Wykład XI Metody opisu układów cyfrowych
KOLOKWIUM 2 zadanie wg Adamczewskiego na porownawczą 97
więcej podobnych podstron