1

GEODEZYJNA OBSŁUGA

GEODEZYJNA OBSŁUGA

REALIZACJI I KONTROLI

REALIZACJI I KONTROLI

BUDOWY DŻWIGNIC

BUDOWY DŻWIGNIC

Kazimierz Ćmielewski

Instytut Geodezji i Geoinformatyki

Uniwersytet Przyrodniczy we Wrocławiu

2

Na terenie każdego portu, stoczni, hali
produkcyjnej

czy

zakładu

przemysłowego, znajdują się urządzenia
dźwigowe, wśród których przeważającą
grupę stanowią suwnice. Są one
wykorzystywane jako środki transportu
bliskiego i służą do załadunku i
rozładunku materiałów, towarów, itp.,
oraz ich przenoszenia z miejsca na
miejsce.

Wprowadzenie

3

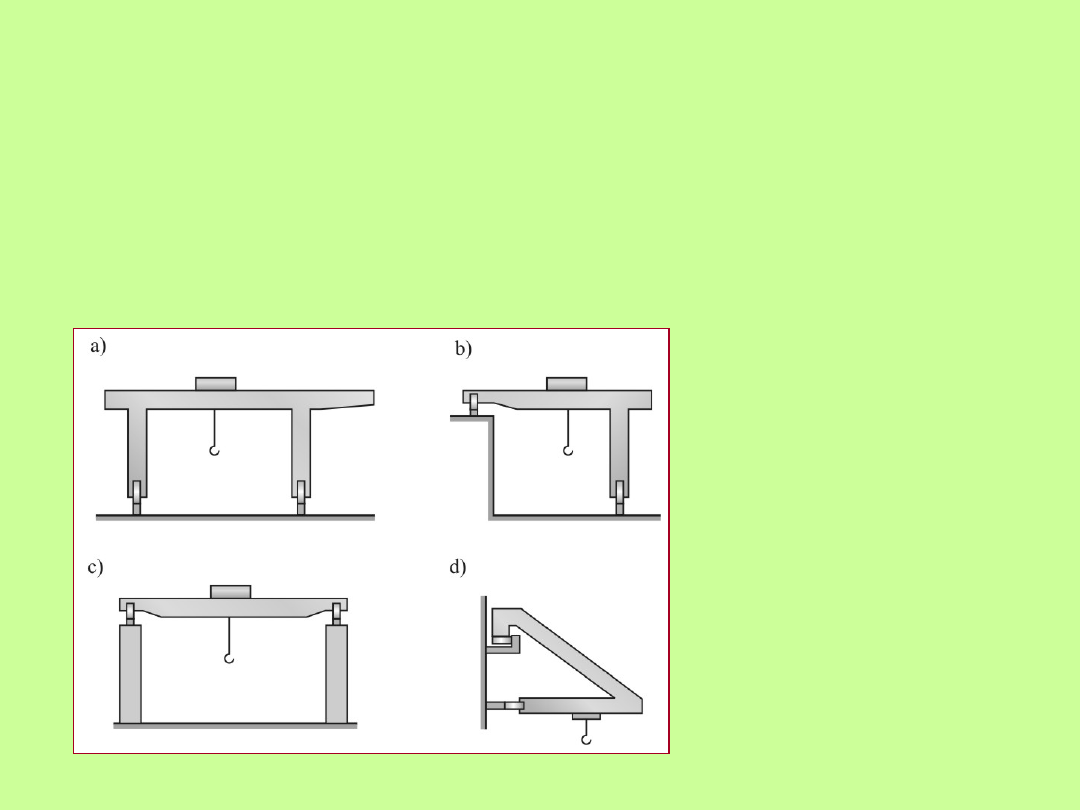
a - suwnica bramowa

(portalowa)

b - suwnica półbramowa

(półportalowa)
pracująca przy ścianie

c - suwnica pomostowa
d - suwnica wspornikowa

Rodzaje suwnic

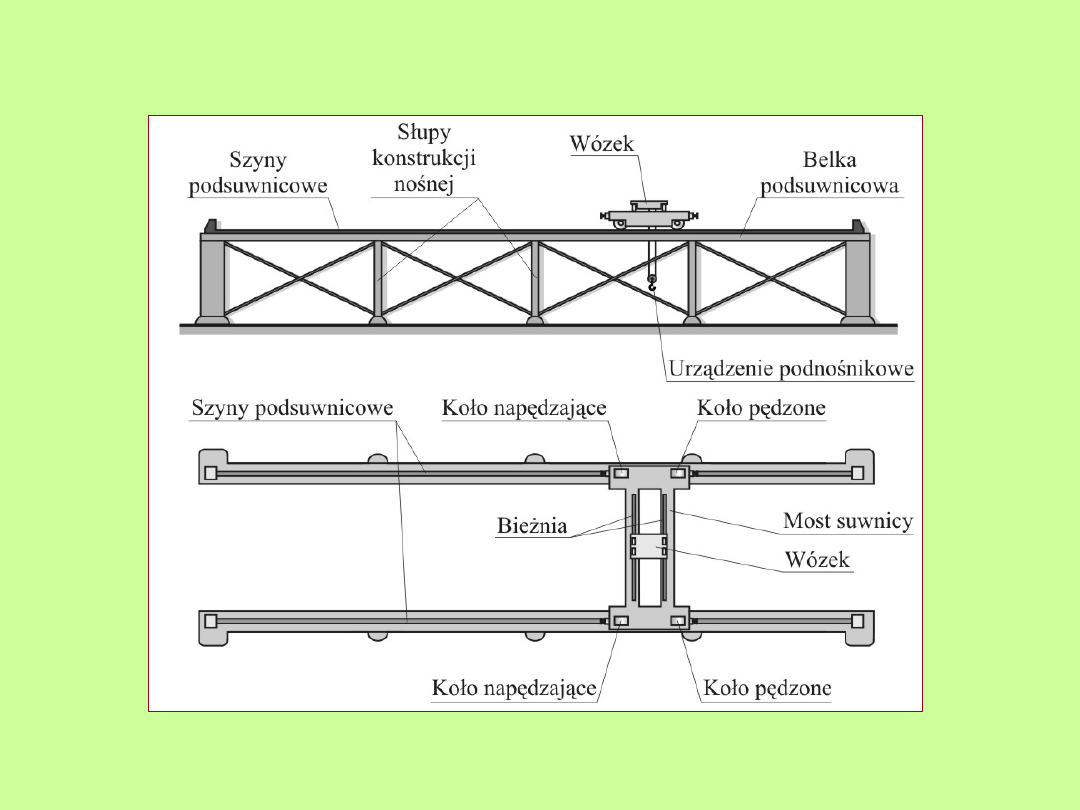
Suwnica jest to urządzenie transportowe złożone z toru

podsuwnicowego, po którym porusza się ustrój nośny mostu
(pomostu) oraz poruszającego się po nim na bieżni wózka z
wciągarką. Torem podsuwnicowym najczęściej jest zespół dwóch
szyn zajmujących położenie w przestrzeni określone kierunkiem,
pochyleniem i rozstawem.

4

Budowa suwnicy

Suwnica pomostowa

5

Wskutek osiadania podłoża gruntowego a tym samym
konstrukcji

nośnej

toru

podsuwnicowego

oraz

oddziaływania różnych czynników geologicznych, w
trakcie

wieloletniej

współpracy

zespołu:

tory

podsuwnicowe-suwnica, występują:

Powyższe zjawiska powodują możliwość wystąpienia
awarii i naruszenie obowiązujących zasad bhp oraz
zmianę projektowego ułożenia geometrycznego osi szyn
toru w okresie jego wieloletniej eksploatacji.

• stopniowe rozregulowania się

torów i

suwnic

• pogorszenie się pracy suwnicy

• nieuzasadniony pobór energii

elektrycznej

• nadmierne zużywanie się

mechanizmów suwnic

6

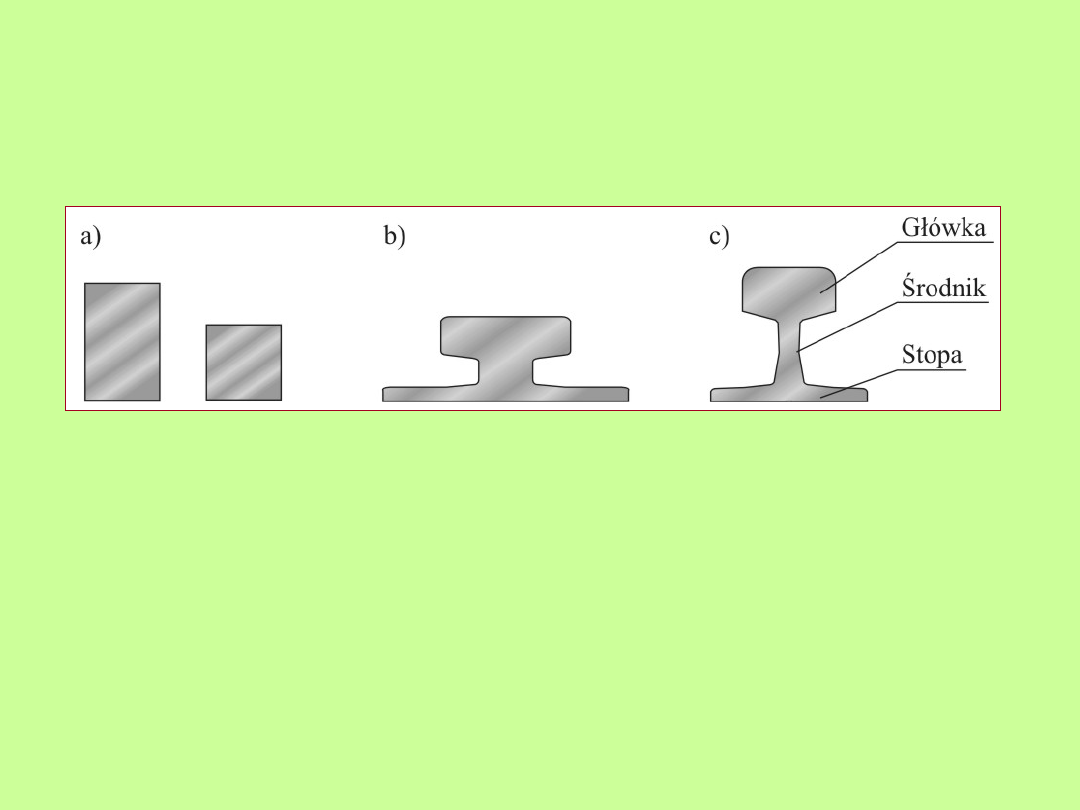
Przekrój poprzeczny odmian szyn stosowanych w torach

suwnicowych

a) szyny kwadratowe lub prostokątne stosowane przy dużych nośnościach

suwnic (powyżej 100 t)

b) typowe szyny dźwigowe o szerokości główki od 65 do 100 mm (PN-62/H-

93410) stosowane przy średnich nośnościach suwnic (do 100 t)

c) szyny normalnotorowe (kolejowe) o szerokości główki 62 lub 72 mm

stosowane dla suwnic o nośnościach małych (od kilku do kilkudziesięciu
ton)

W zależności od długości torowiska występuje następujący podział: tory

krótkie (do 100 m), średnie (od 100 do 300 m) i długie (powyżej 300 m).

W zależności od nośności suwnicy stosuje się następujące odmiany
przedstawione na rysunku:

Szyny suwnic

7

Pomiary inwentaryzacyjne suwnic obejmują:

• pomiar elementów geometrycznych toru jezdnego

mostu i wózka suwnicy

• pomiar kształtu mostu suwnicowego

(podstawowych wymiarów)

• pomiar położenia mostu w lokalnym układzie całej

suwnicy

• pomiar średnic i położenia kół suwnicy
• pomiary dynamiczne zmian położenia konstrukcji

suwnicy podczas ruchu

• pomiary ugięć konstrukcji związanych z

obciążeniem suwnicy.

8

Główne wymagania geometryczne dla torów

podsuwnicowych

Prawidłowa praca suwnicy związana jest ze
spełnieniem następujących warunków
geometrycznych:

• szyny toru stanowią elementy prostoliniowe,

• toki szyn są oddalone od siebie w płaszczyźnie

poziomej i pionowej o wielkości projektowe,

• szyny i belki ułożone są w odpowiednich

odległościach od elementów konstrukcji nośnej
hali lub estakady oraz innych urządzeń w
szczególności elektrycznych,

• część toczna szyny ma określony wymiar i ułożenie

przestrzenne (nachylenie)

Dla suwnic pomostowych obowiązującą jest norma PN-
91/M-45457, a dla suwnic półbramowych i bramowych
PN-M-45495.

9

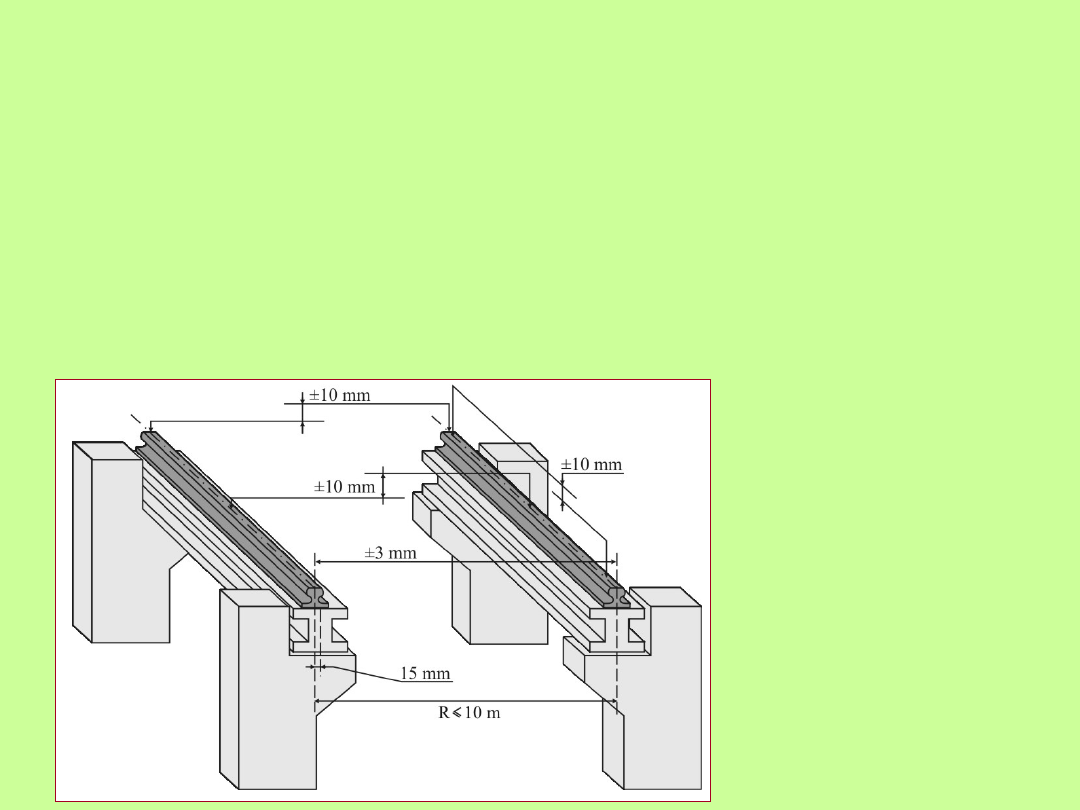
Podstawowe parametry torów suwnicowych

• rozstaw szyn R (rozpiętość): dla torów o rozstawie R≤10 m

dopuszczalna różnica (odchyłka) między rzeczywistym a
teoretycznym rozstawem nie może przekraczać wartości =±3 mm,

a dla torów o rozstawie R≥10 m, wartości =±(3+1/4(R-10)) a

zarazem być mniejsza od wartości ≤15 mm

• różnica poziomów główek szyn (przechyłka boczna) nie powinna

przekraczać wartości odchyłki =±10 mm

• różnica wysokości przekrojów główek szyn w przekroju podłużnym

(pochylenie wzdłużne) nie powinna przekraczać wartości odchyłki
=±10 mm

Dopuszczalne
wartości odchyłek
wzajemnego ułożenia
osi szyn toru
podsuwnicowego

10

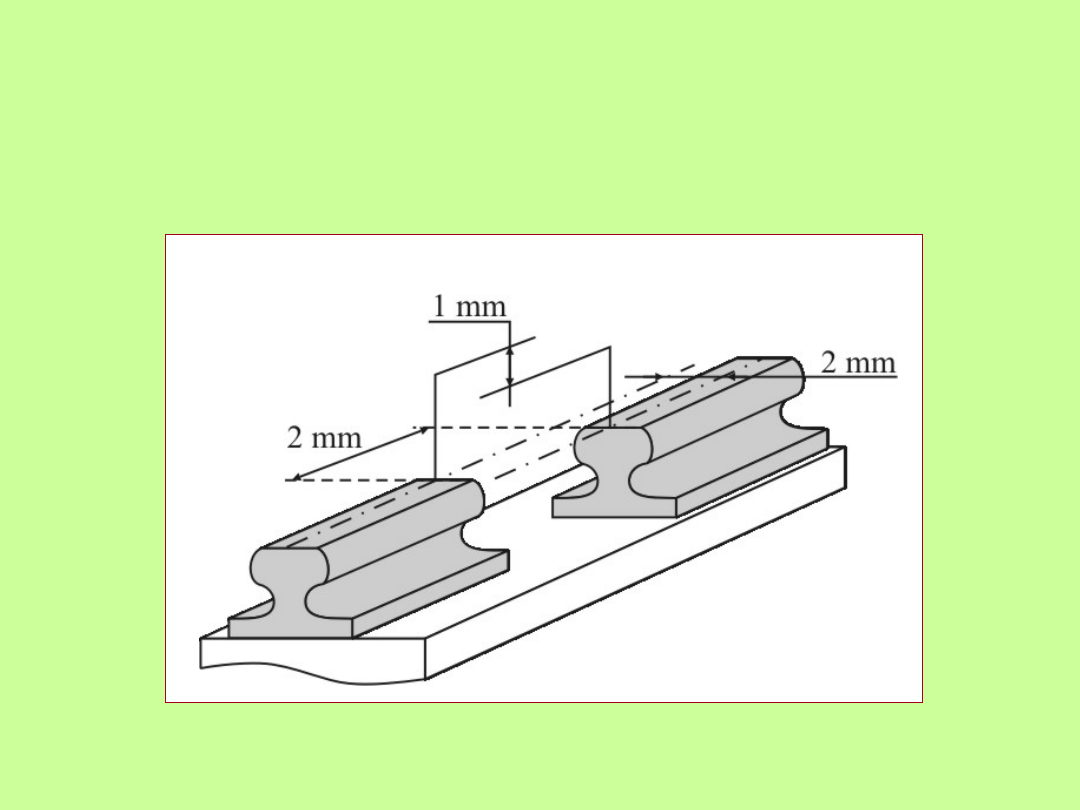
Dopuszczalne odchyłki przesunięcia główek szyn

w styku

• wzajemne przesunięcie w styku sąsiednich szyn nie powinno

przekraczać wartości odchyłki w poziomie D≤2 mm, w pionie D≤1
mm, natomiast końce łączonych odcinków szyn nie powinny
wykazywać szczeliny większej od 2 mm.

Podstawowe parametry torów suwnicowych

11

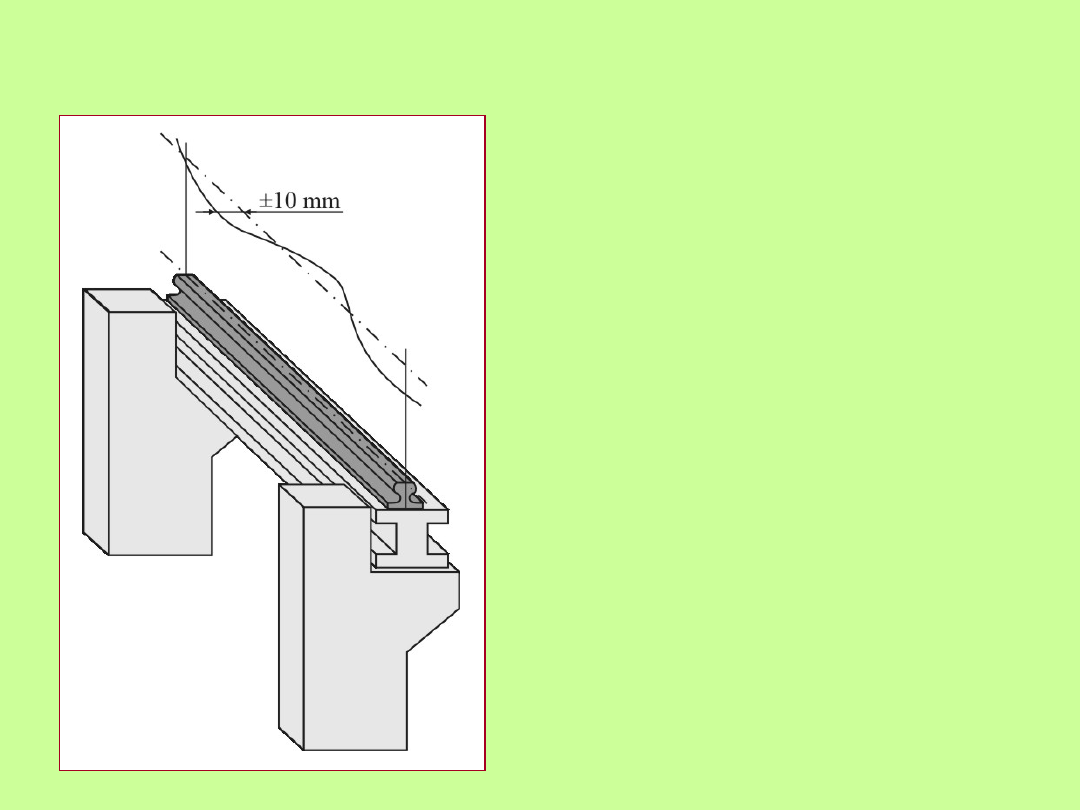
Dopuszczalna odchyłka osi
szyny od prostoliniowości

• odchylenie osi szyn od prostej w

płaszczyźnie poziomej nie powinno
przekraczać wartości odchyłki
D=±10 mm

Podstawowe parametry torów suwnicowych

12

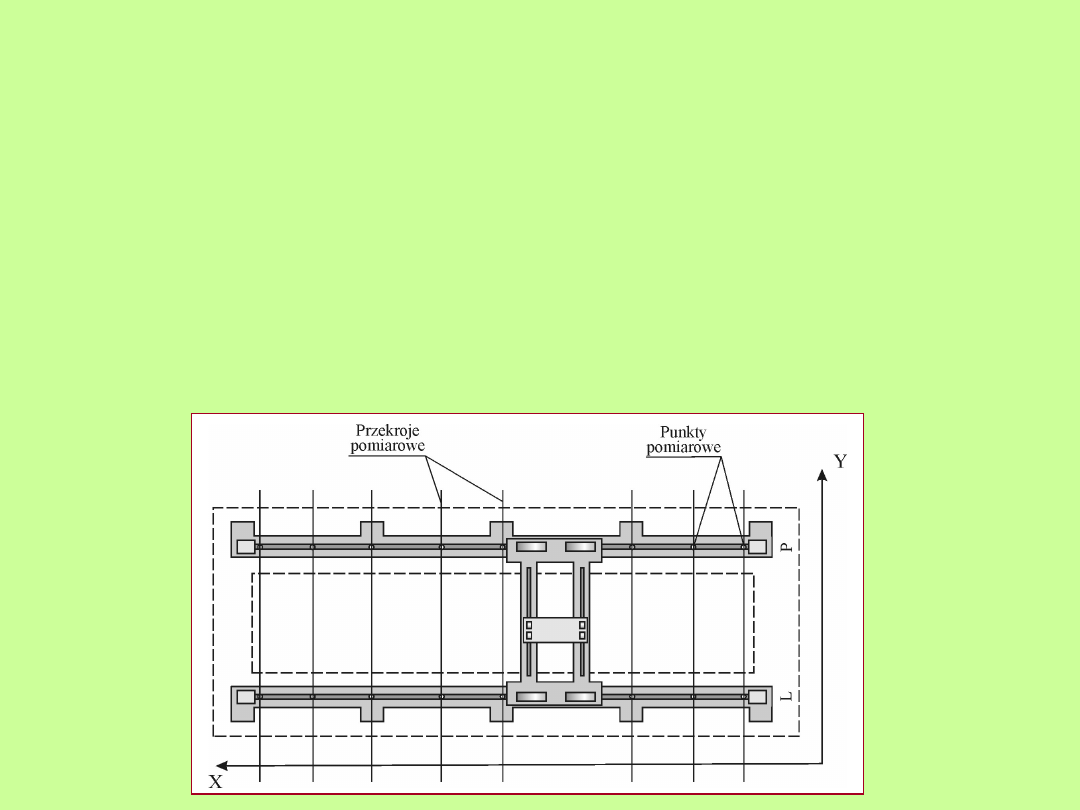
Rozmieszczenie punktów pomiarowych na

torach podsuwnicowych

Podczas oznaczania punktów pomiarowych na torze suwnicy
należy wykonać następujące czynności:

• most suwnicy ustawiony w skrajne położenie toku szyn,

• ustawienie teodolitu nad jedną z szyn w drugim końcu

toku,

• centrowanie instrumentu na wyznaczony środek główki

szyny,

• nacelowanie na środek główki szyny w pobliżu mostu

suwnicy,

• odłożenie kąta prostego i zaznaczenie punktu na drugiej

szynie toru.

W ten sposób wyznaczony zostaje pierwszy przekrój
pomiarowy od którego wyznacza się kolejne w rozmierzonych
miejscach jak na rysunku.

13

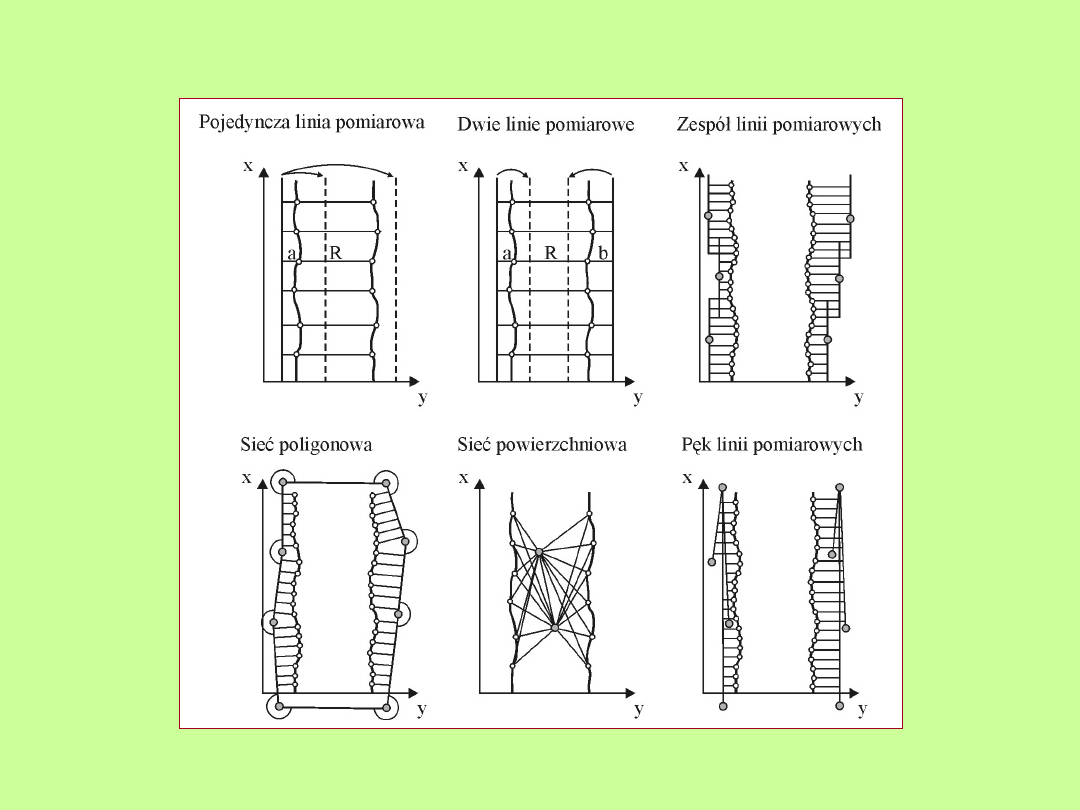
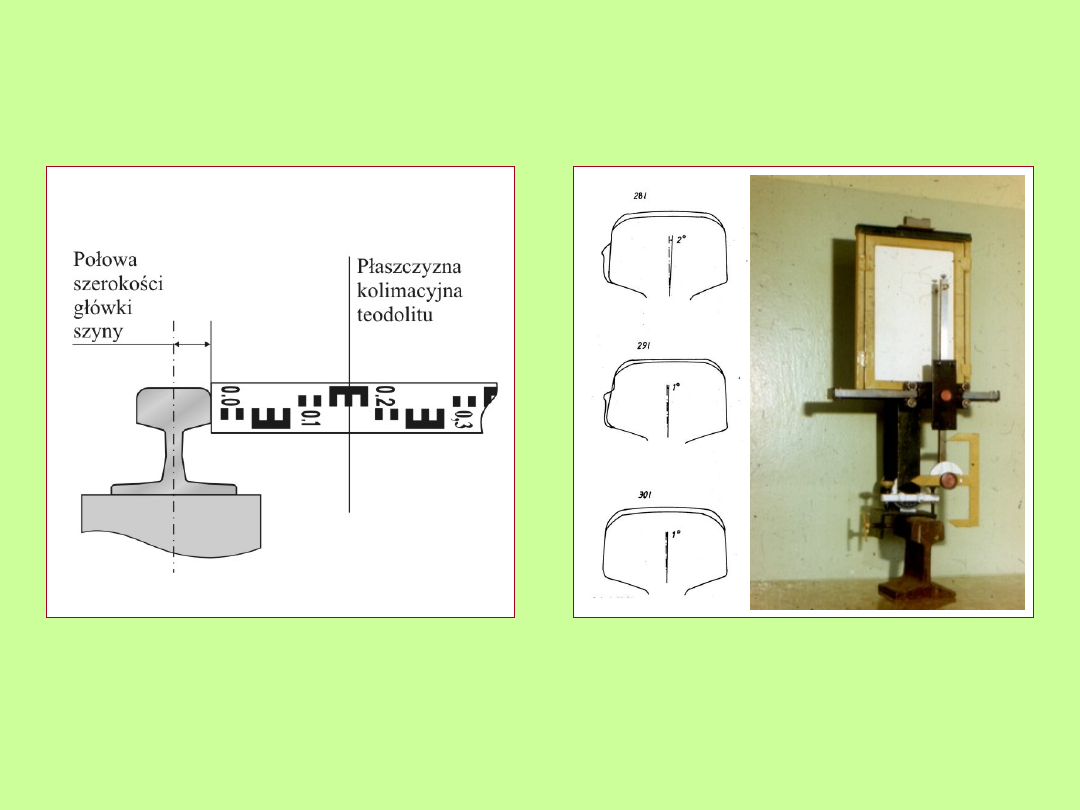
Poziome osnowy pomiarowe

Warianty poziomych osnów pomiarowych

14

Pomiary prostoliniowości szyn

Sposób przyłożenia

łaty do szyny

Deformacje główek

szyn (profilograf)

15

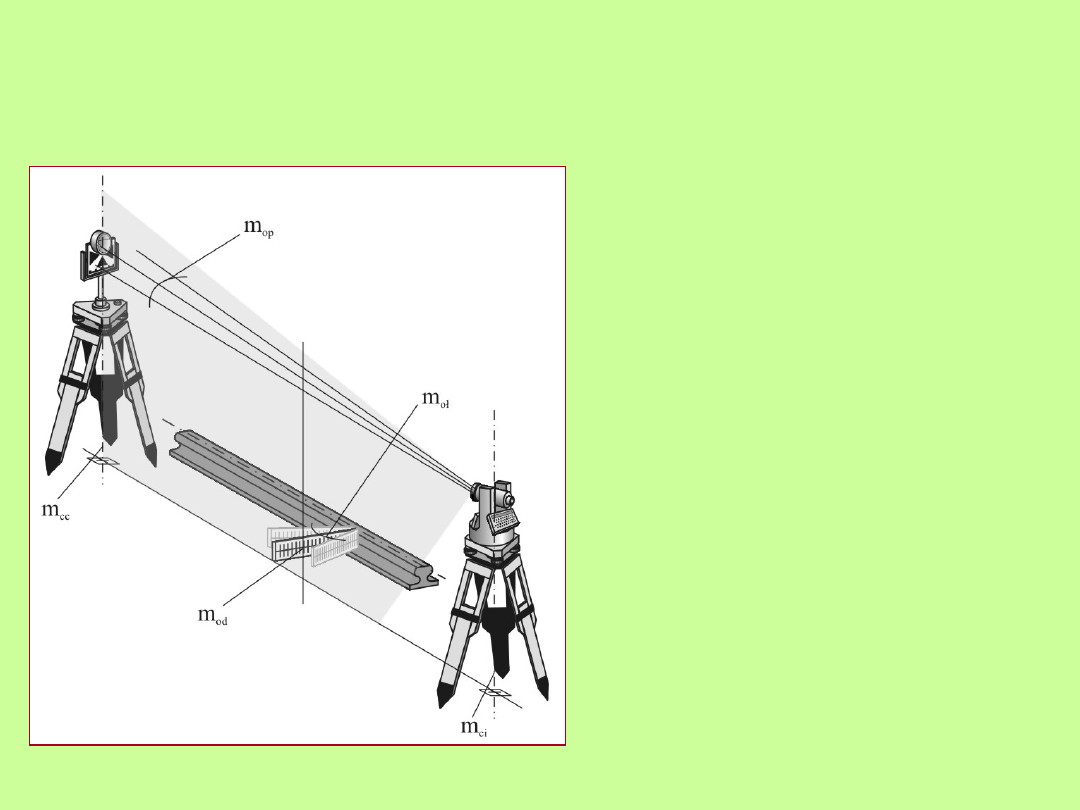
Błędy występujące przy pomiarach

inwentaryzacyjnych metodą aliniometryczną (tj.

metodą stałej prostej)

Rodzaje błędów

m

ci

- błąd centrowania

instrumentu oraz tarczy (celu)
na punktach osnowy,

m

op

- błąd zorientowania

pionowej płaszczyzny
odniesienia na tarczę (cel),

m

od

- błąd odczytu na podziałce

łaty,

m

oł

- błąd pomiaru odchylenia

od prostej na wskutek
nieprostopadłego ustawienia
podziału łaty do prostej
odniesienia,

m

xp

- błąd położenia punktu

kontrolowanego na szynie
(wyznaczenie punktu, miara
bieżąca na torze).

16

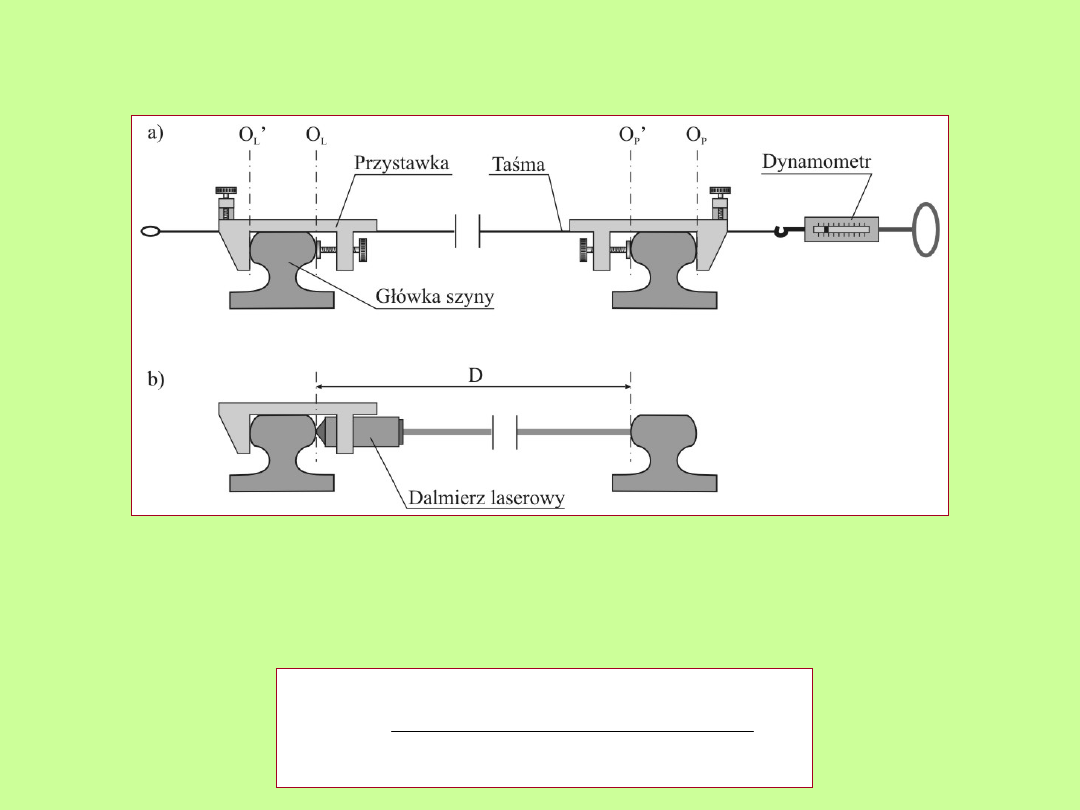
Pomiary rozstawu torów jednopoziomowych

Pomiar rozstawu szyn: a) bezpośredni - przy pomocy
przystawek oraz taśmy i dynamometru, b) pośredni -
dalmierzem laserowym Disto (Leica)
Bezpośredni rozstaw pomierzony na obiekcie taśmą oblicza się
z następującego wzoru:

2

)

'

'

(

)

(

'

L

P

L

P

O

O

O

O

R









17

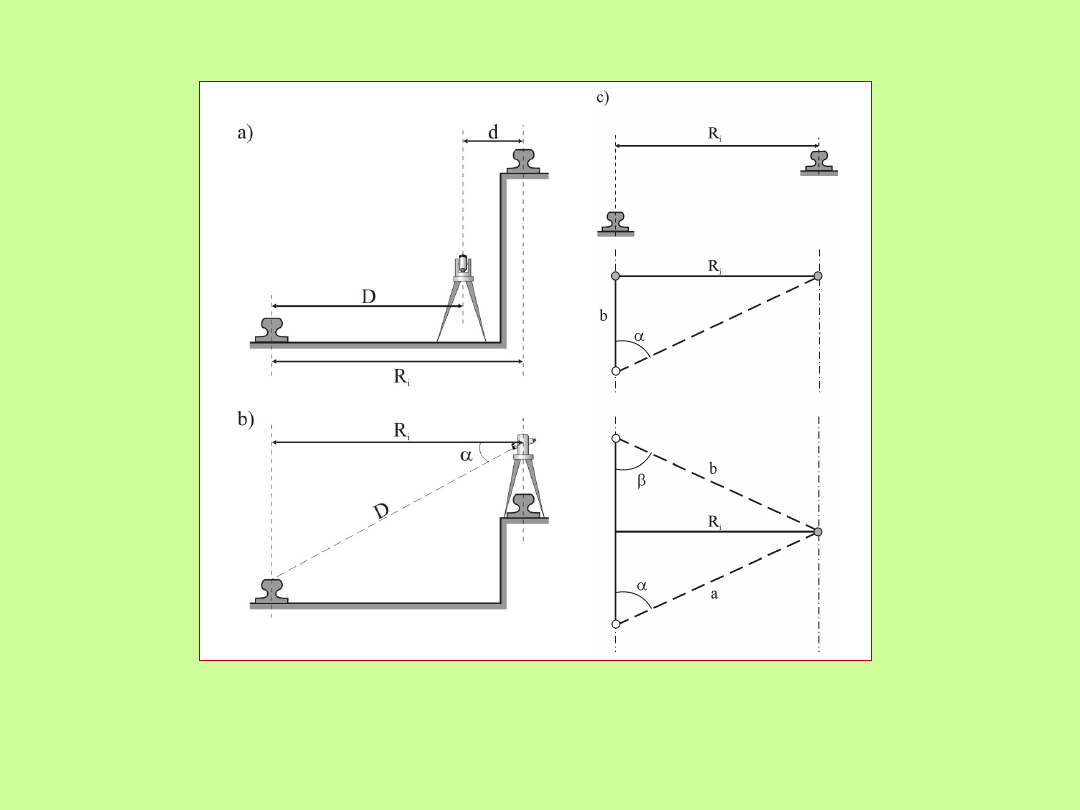
Pomiary rozstawu torów dwupoziomowych

Sposób pośredniego pomiaru rozstawu torów dwupoziomowych z

wykorzystaniem:

a) metody rzutowania teodolitem, b) metody trygonometrycznej,

c) metoda wcięcia w przód

18

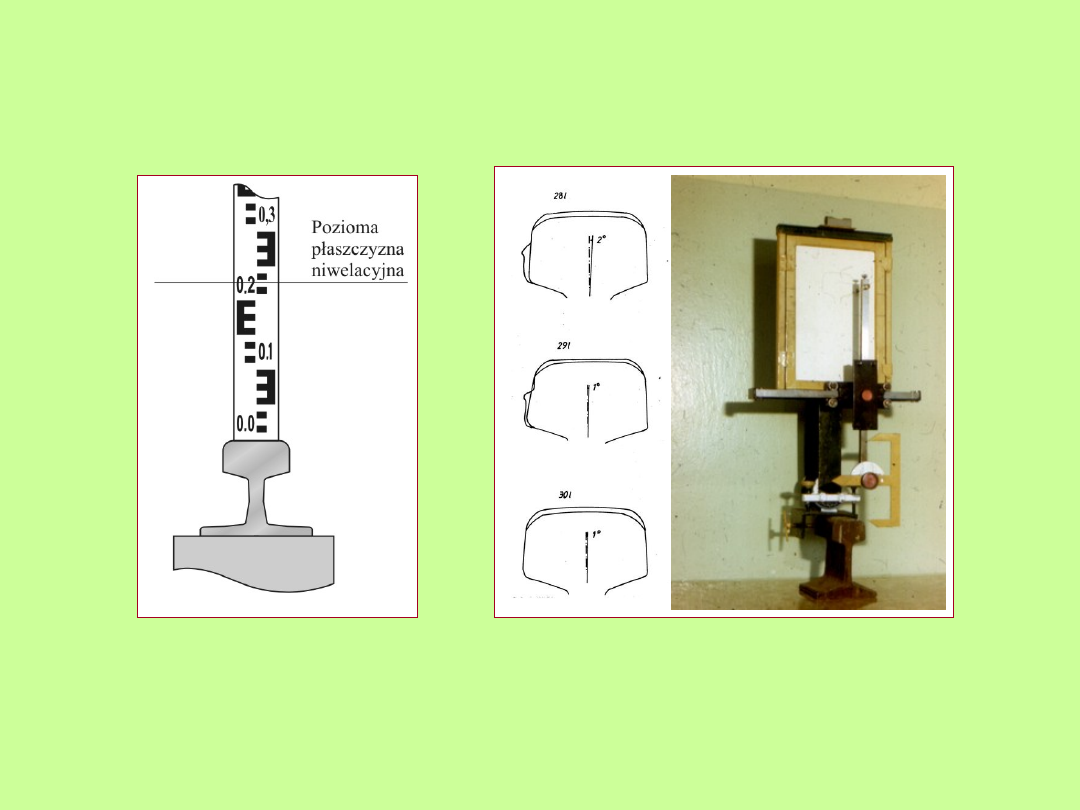
Pomiary niwelacyjne położenia wysokościowego główki szyn

Pomiary bezpośrednie metodą niwelacji geometrycznej punktów rozproszonych

Ustawienie łaty

niwelacyjnej na główce

szyny

Deformacje główek

szyn (profilograf)

26

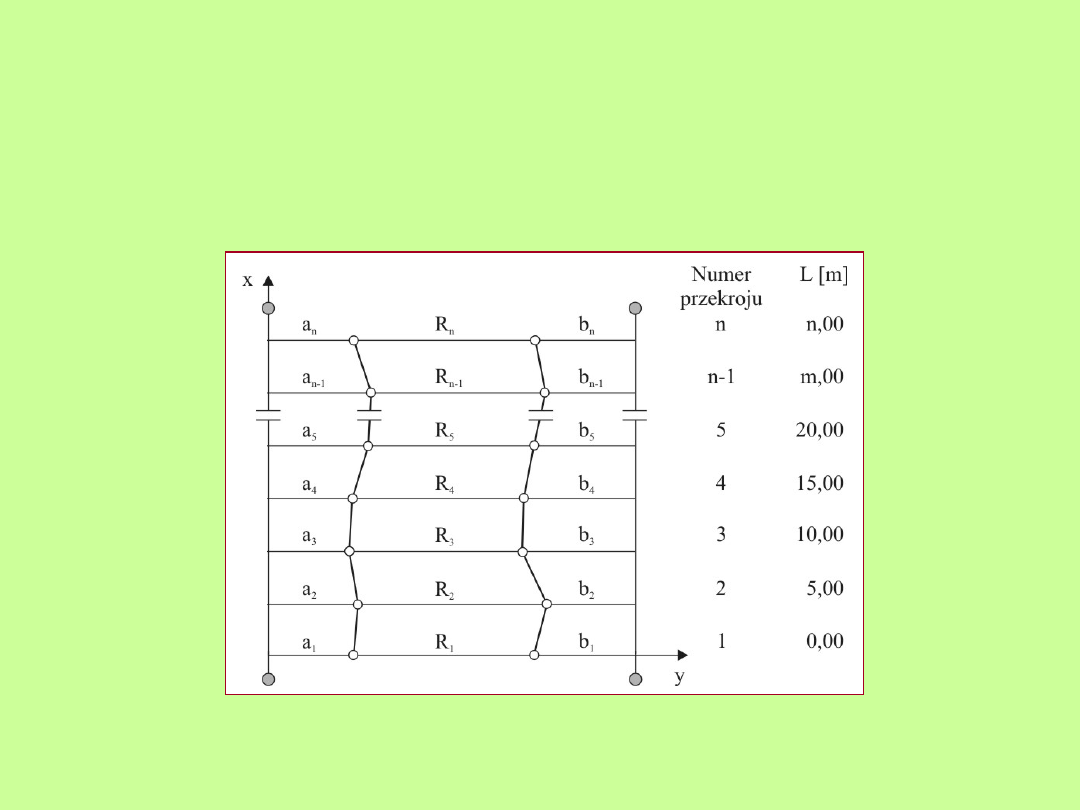
Określenie dokładności pomiarów polowych

w płaszczyźnie poziomej

Przyjęcie lokalnego układu współrzędnych przy założeniu, że oś X
pokrywa się z pierwszą prostą odniesienia, a oś Y z pierwszym
przekrojem pomiarowym

Schemat konstrukcji osnowy pomiarowej dla prostych

odniesienia z lokalizowanych na zewnątrz szyn

27

Określenie dokładności pomiarów polowych

w płaszczyźnie poziomej

Wielkości a i b oraz R obarczone są niedokładnościami wskutek błędów
pomiarowych występujących w procesie pomiarowym (praca na
wysokości, ograniczona pomiarowa przestrzeń operacyjna, drgania belek
podsuwnicowych, itp.), użytych instrumentów (teodolit, tachymetr) i
przyrządów (taśmy, łaty, itp.) oraz obserwatora (niedoświetlenie, hałas,
itp.).
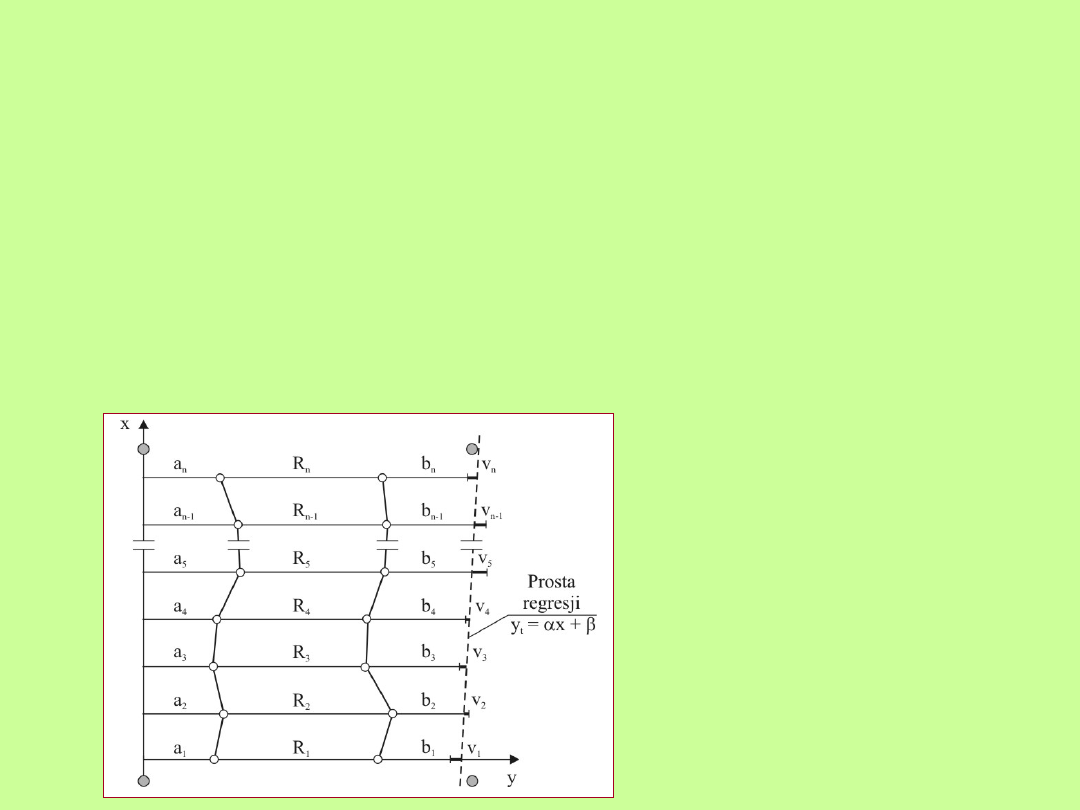
Wyrównanie spostrzeżeń poziomych deformacji toru przeprowadza się
poprzez wpasowanie prostej wyrównującej y

t

w wyniki pomiarów w

oparciu o zasadę metody najmniejszych kwadratów –

min

2





v

Szkic do wyrównania

spostrzeżeń poziomych

deformacji toru

28

Określenie dokładności pomiarów polowych

w płaszczyźnie poziomej







 x

y

t

p

t

y

y

v





n

n

n

p

b

R

a

y







n

n

n

b

R

a

x

v















Etapy wyrównania obserwacji
- zapisanie równania prostej wyrównującej według wzoru 1:

gdzie:
 – kierunek prostej wyrównującej,

 – punkt przecięcia prostej z osią Y,

- zestawienie równań poprawek według wzoru 2:

gdzie
:

Stąd równanie poprawek można zapisać według wzoru 4:

Liczba równań poprawek jest równa liczbie pomierzonych
przekrojów.

(2)

(3)

(4)

(1)

29

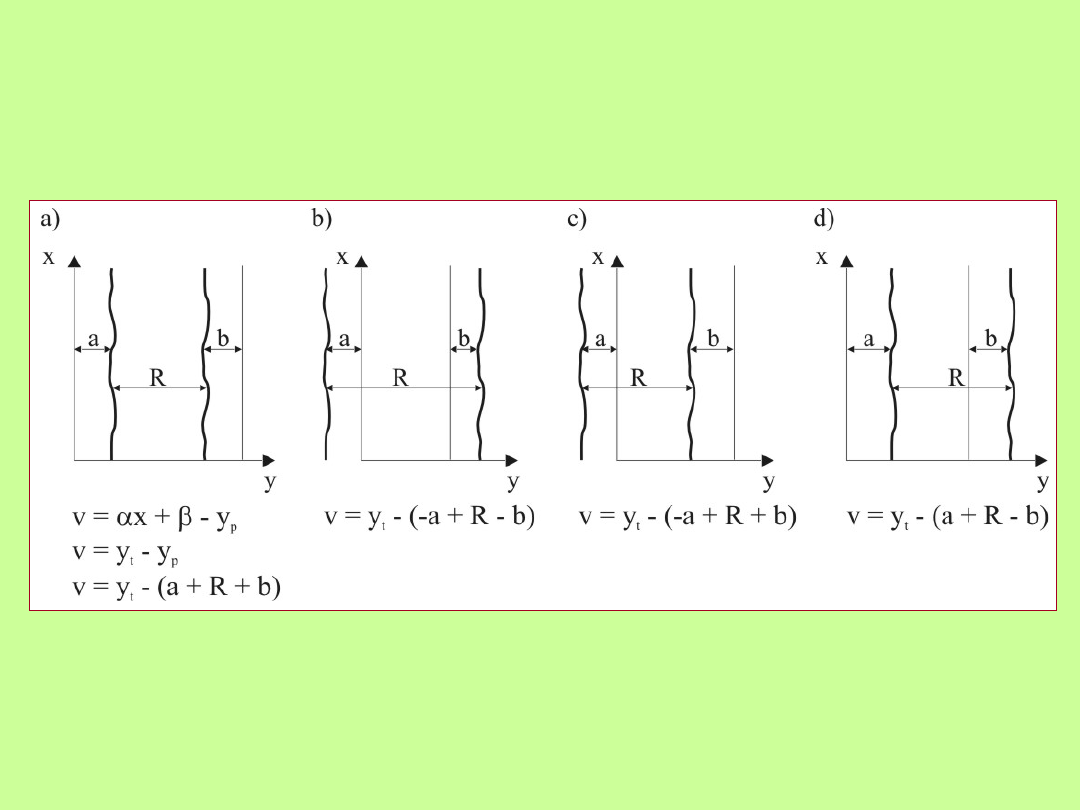
Określenie dokładności pomiarów polowych

w płaszczyźnie poziomej

Warianty równań poprawek w zależności od

usytuowania prostych odniesienia

30

Określenie dokładności pomiarów polowych

w płaszczyźnie poziomej

min

2





v

0

0

2





























p

p

y

n

x

xy

x

x









Po nałożeniu na układ równań poprawek (wzór 4) warunku

otrzymuje się układ równań normalnych (5):

Z przedstawionego układu równań (wzór 6) wyznacza się niewiadome a
i b (np. metodą wyznaczników), a następnie wartości poszczególnych
poprawek v. Zakładając że pomiary prostoliniowości i rozstawu osi szyn
toru są jednakowodokładne, można wyrównać wartości pomierzone a,
b, R, według wzoru 6:

v

a

a

3

1

'





v

b

b

3

1

'





v

R

R

3

1

'





(6)

(4)

(5)

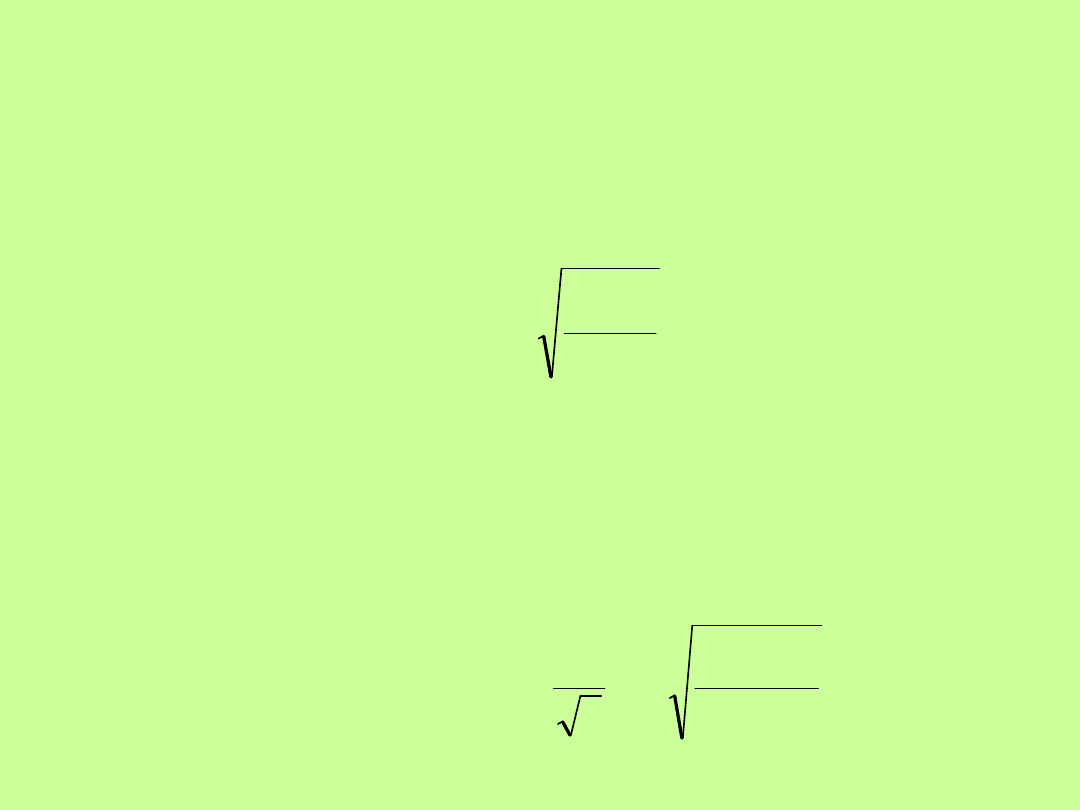
31

2

2

0









n

v

m

mm

m

5

,

2

0









2

3

3

2

0















n

v

m

m

m

m

R

b

a

Ocenę dokładności pomiarów polowych dla pojedynczego przekroju
pomiarowego korzystając z wzoru 7:

Przyjmuje się że wartość średniego błędu pomiaru pojedynczego
przekroju pomiarowego m

0

dla prawidłowo wykonanych obserwacji

przyjmuje wartość

Średni błąd pojedynczego pomiaru poszczególnej wielkości a, b lub R
można wyznaczyć z wzoru:

(8)

Określenie dokładności pomiarów polowych

w płaszczyźnie poziomej

(7)

32

Wyznaczenie położenia osi szyn suwnicowych

Zasadniczą czynnością przy opracowaniu projektu jest

rektyfikacji osi szyn w płaszczyźnie poziomej najkorzystniejsze
wpasowanie w układ osi rzeczywistych, teoretycznego układu
osi. Od tej czynności, w głównej mierze zależeć będzie ilość i
wielkość przesunięcia osi szyn, a zatem zakres i czas
rektyfikacji w terenie. W zależności od stosowanego sposobu,
wpasowanie to opiera się na zasadzie:

• Metodą graficznego opracowania

– doprowadzenia do

wizualnie uchwytnych najmniejszych rozbieżności między
osiami rzeczywistymi, a wpasowanym graficznie układem
teoretycznych osi.

• Metodą analityczną

– doprowadzenie do położenia osi

szyn tak, aby był zachowany warunek minimum sumy
kwadratów odchyleń osi rzeczywistej toru (a nie szyn) od
jego osi teoretycznej.

Często stosowanym sposobem był sposób graficzny. Aktualnie
stosuje się na ogół sposób analityczny.

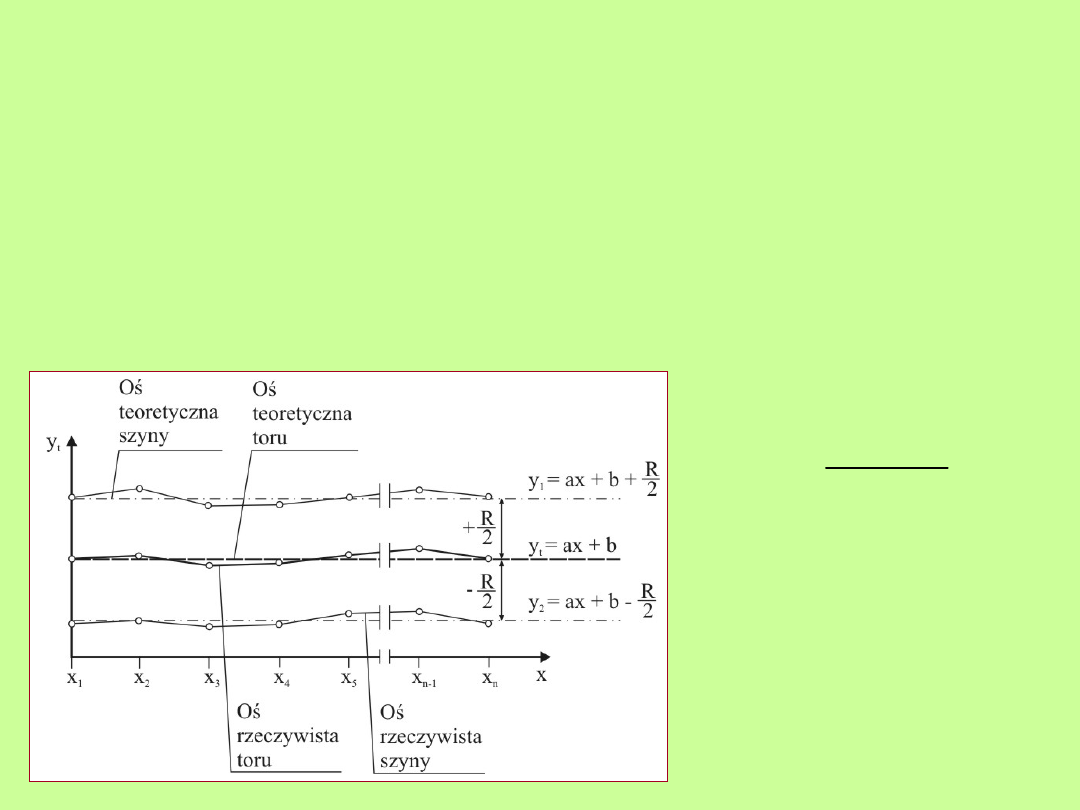
33

Wyznaczenie położenia osi szyn suwnicowych

sposobem analitycznym

Stosowanie tego sposobu jest możliwe gdy:

• punkty pomiaru osi rzeczywistych na obu szynach są rozmieszczone

w jednakowych przekrojach poprzecznych,

• dokładność wyznaczenia położenia punktów jest jednakowa,

• współrzędne punktów obu osi rzeczywistych są obliczone we

wspólnym układzie, tak zorientowanym, że oś Y jest równoległa do
linii przekrojów poprzecznych, a oś X przechodzi przez dwa skrajne
punkty osi jednej z szyn lub jest przesunięta równolegle do niej

Ilustracja wyznaczenia

układu teoretycznego osi

szyn

L

P

t

p

x

x

x

y

y

y









2

2

1

(9)

34

Wyznaczenie położenia osi szyn suwnicowych

sposobem analitycznym

b

ax

Y

t









min

2

2











t

t

y

Y

d

p

p

t

y

b

ax

y

Y

d











Proces obliczeń w tej metodzie polega na wyznaczeniu równania jednej
prostej wyrównującej (regresji) postaci:

dla punktów osi rzeczywistej toru ze spełnieniem warunku minimum dla
sumy kwadratów odchyleń – d osi rzeczywistej toru od prostej
wyrównującej, czyli:

Prostą wyrównującą określa się jako oś teoretyczną toru.

W celu wyznaczenia niewiadomych parametrów a i b w równaniu, układa
się tzw. równanie odchyłek o postaci ogólnej:

których liczba będzie równa ilości przekrojów poprzecznych.

(10)

(11)

(12)

35

0

0

2





























p

p

y

nb

a

x

xy

b

x

a

x

2

R

b

ax

Y

t







2

R

b

ax

Y

t







Rozwiązanie układu (13) pozwala wyznaczyć wartości liczbowe
niewiadomych równania (10). Na podstawie otrzymanego równania osi
toru (10) i znanej z dokumentacji rozpiętości teoretycznej osi – R, określa
się równania teoretycznych obydwu osi szyn – lewej i prawej:

Szyna 2: (15)

Z równań (12) tworzy się układ równań normalnych o postaci:

Wyznaczenie położenia osi szyn suwnicowych

sposobem analitycznym

(13)

Szyna 1: (14)

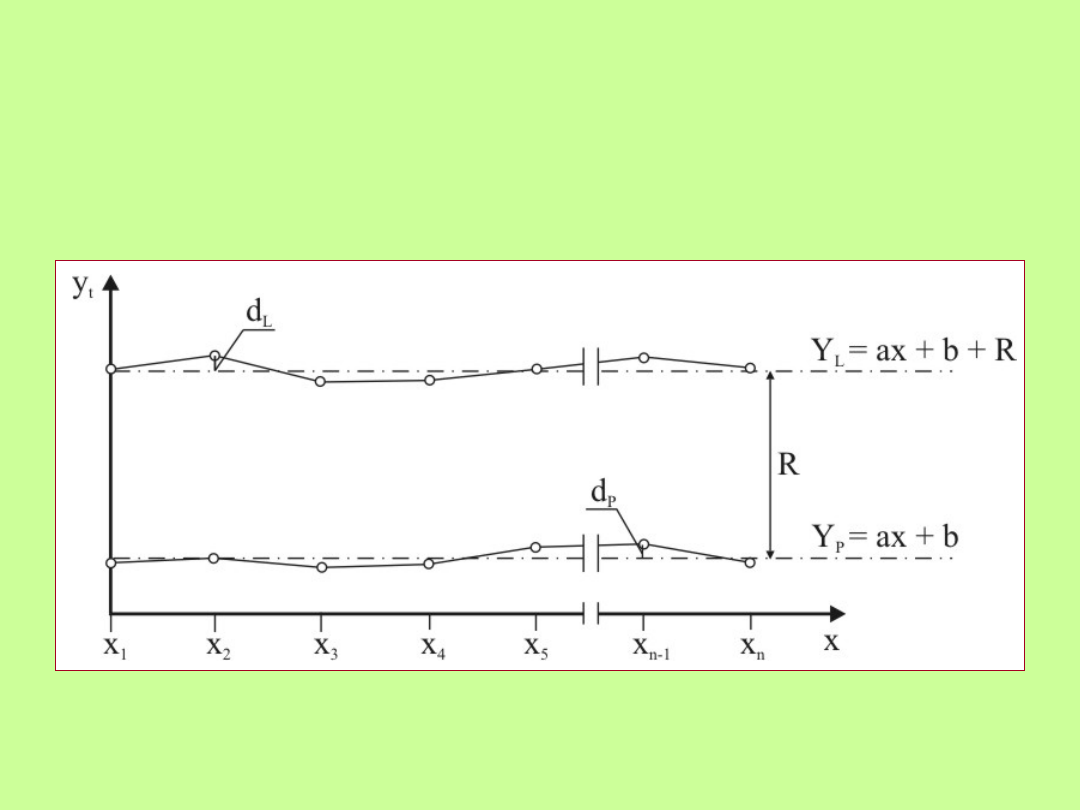
36

Układ osi średnich wpasowanych w osie rzeczywiste przy zadanej rozpiętości

Wyznaczenie położenia osi szyn suwnicowych

sposobem analitycznym

Drugi sposób wyznaczenia średnich osi, stosujemy gdy znany jest
rozstaw szyn R dla suwnicy (rozstaw nominalny - projektowy).

37

Wówczas w osie rzeczywiste szyny lewej (x

L

, y

L

) i prawej (x

P

, y

P

)

wpasowuje się układ dwóch prostych równoległych oddalonych o
wartość rozstawu nominalnego R. Równania prostych mają postać:

 

(16)

 

Wyznaczenie osi średnich odbywa się przy zachowaniu warunku

najmniejszych kwadratów o postaci:

 

(17)

R

b

ax

Y

b

ax

Y

L

L

P

P













 







min

2

2

2

2

















L

p

L

L

P

P

d

d

y

Y

y

Y

Wyznaczenie położenia osi szyn suwnicowych

sposobem analitycznym

38

W celu wyznaczenia niewiadomych parametrów a i b w równaniach
wzór 16 układa się równania odchyłek w postaci ogólnej dla szyny
prawej i lewej:

(18)

Równań odchyłek będzie tyle ile pomierzonych przekrojów
poprzecznych.

nL

nL

nL

L

L

L

nP

nP

nP

P

P

P

y

R

b

ax

d

y

R

b

ax

d

y

b

ax

d

y

b

ax

d

































1

1

1

1

1

1

Wyznaczenie położenia osi szyn suwnicowych

sposobem analitycznym

39

Z równań odchyłek (wzór 18) tworzy się równania normalne o postaci:
 

(19)

 

Rozwiązanie równań pozwala wyznaczyć osie teoretyczne szyny lewej i
prawej odległe o zadaną wartość rozstawu, a następnie odchyłki
rzeczywistych osi od teoretycznych.

 

 













 









0

2

2

0

2

2

2



































L

P

L

P

y

R

y

nb

a

x

x

y

R

xy

b

x

a

x

Wyznaczenie położenia osi szyn suwnicowych

sposobem analitycznym

40

Trzecim sposobem jest jednoczesne wyznaczenie dla obu osi rzeczywistych

dwóch odpowiadających im równań optymalnych osi teoretycznych

wzajemnie równoległych, przy zastosowaniu metody najmniejszych

kwadratów o postaci.

dla szyny 1

dla szyny 2

z zachowaniem warunku:

(20)

Rozstaw między wyznaczonymi osiami optymalnymi wyznacza się z

równania:

(21)

Wyznaczenie położenia osi szyn suwnicowych

sposobem analitycznym

1

1

b

ax

Y

i

i





2

2

b

ax

Y

i

i







 







min

2

2

21

2

1

1











i

i

i

y

Y

y

Y

2

1

2

1 a

b

b

R

opt







41

Równania odchyłek dla omawianego sposobu mają następującą postać:

(22)

Na podstawie zestawionych równań odchyłek tworzy się równania

normalne o postaci: 

(23)

Wyznaczenie położenia osi szyn suwnicowych

sposobem analitycznym

nL

L

nL

nL

L

L

L

L

nP

P

nP

nP

p

P

P

P

y

b

ax

d

y

b

ax

d

y

b

ax

d

y

b

ax

d





























1

1

1

1

1

1

 

 





 

 













 

 

 

 

0

0

0

2

2













































L

L

L

P

P

P

L

L

P

P

L

L

P

P

L

P

y

nb

a

x

y

nb

a

x

y

x

y

x

b

x

b

x

a

x

x

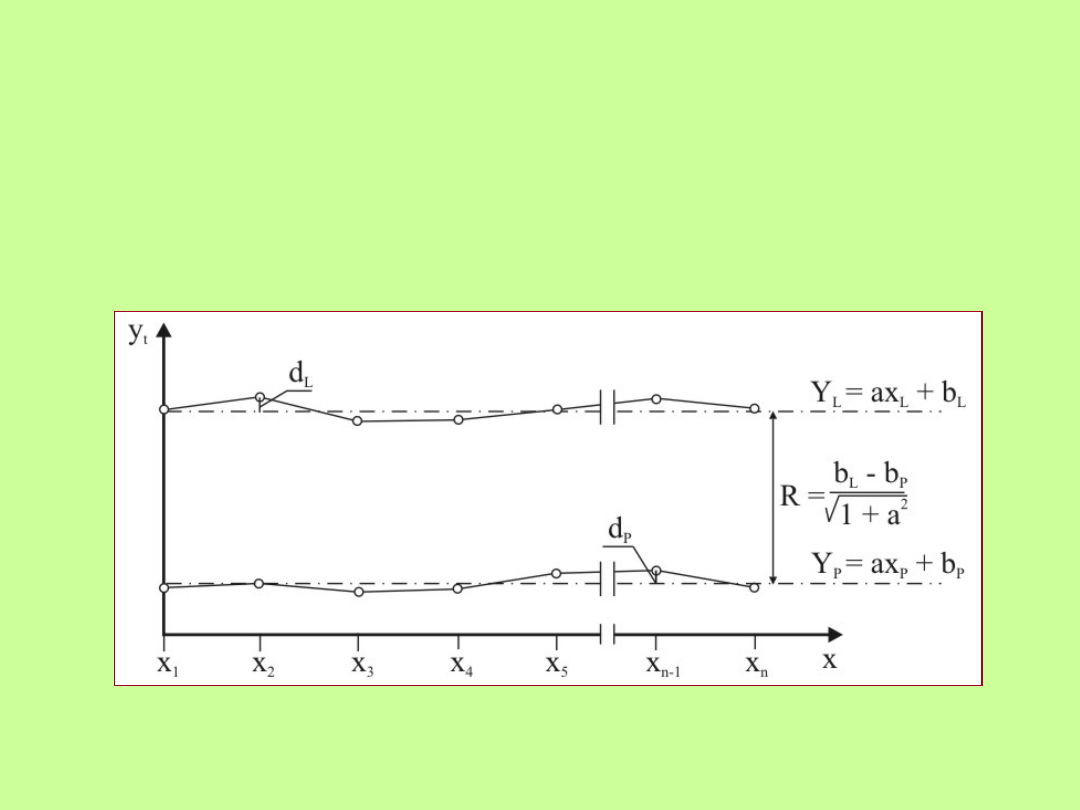
42

Układ osi optymalnych wpasowanych w osie rzeczywiste przy

rozstawie optymalnym

Rozwiązanie

równań

normalnych

pozwala

na

wyznaczenie

niewiadomych, a, b

L

, b

P

, które po podstawieniu do równań odchyłek

(wzór 22) pozwalają na określenie wartości odchyleń osi rzeczywistych

od teoretycznych (optymalnych) i są podstawą do wyznaczenia wartości

koniecznych przesunięć osi toru do położenia teoretycznego

(optymalnego), co przedstawiono na rysunku.

Wyznaczenie położenia osi szyn suwnicowych

sposobem analitycznym

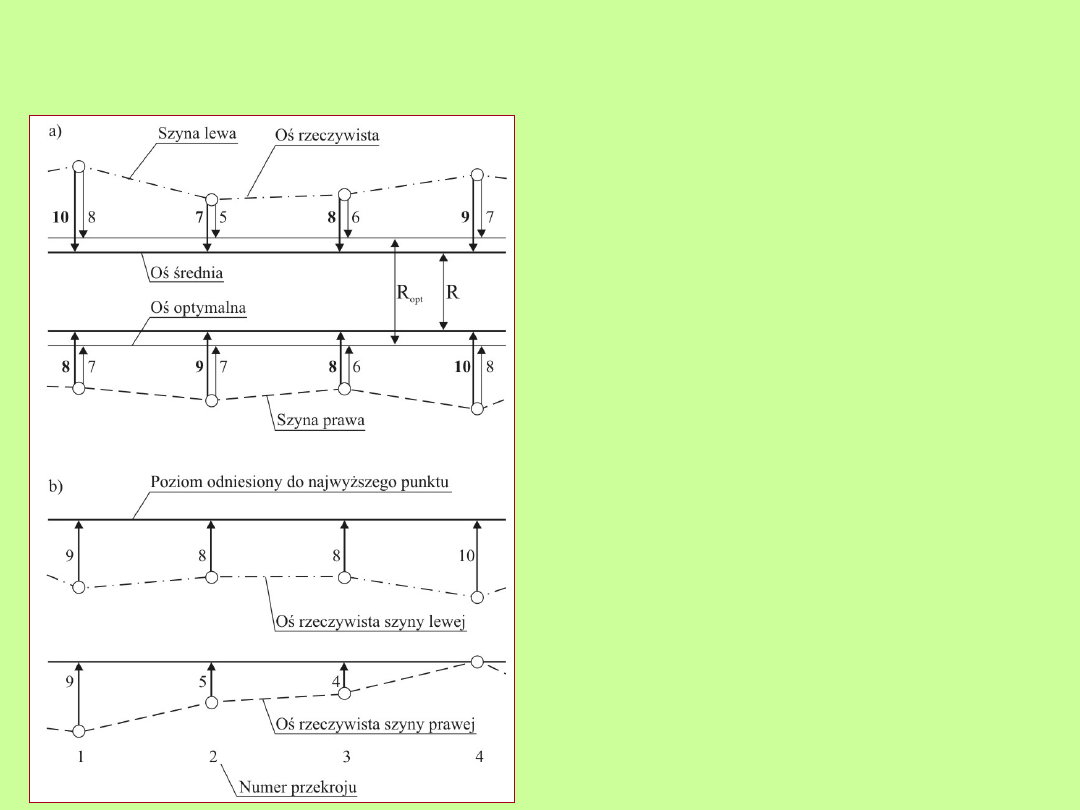
43

Opracowanie projektu rektyfikacji

szyn toru podsuwnicowego

Projekt rektyfikacji przedstawia się
w

formie

szkicu,

na

którym

umieszczone są poprawki (odchyłki
usytuowania)

pozwalające

na

dostosowanie układu szyn toru do
wymagań określonych przepisami
technicznymi.

Szkic projektu rektyfikacji fragmentu
toru podsuwnicowego: a) w
płaszczyźnie poziomej, b) w
płaszczyźnie pionowej