Pomiary fizyczne i niepewności

pomiarowe

Klasyfikacja pomiarów:
• Podział dychotomiczny
• Skalowanie nominalne
• Skalowanie porządkowe
• Pomiar na skali przedziałowej
• Pomiar bezwzględny.

Pomiary fizyczne i niepewności

pomiarowe

• Ilościowo każdą wielkość fizyczną

wyrażamy jej miarą

• A={A}A
•

A wielkość fizyczna

•

{A} wielkość liczbowa

•

A

jednostka dowolnie wybrany

stan wielkości fizycznej układ SI

Pomiary fizyczne i niepewności

pomiarowe

• Pomiary bezpośrednie wykonujemy

za pomocą narzędzi pomiarowych na
które składają się wzorce miar

• Pomiary pośrednie. Wielkość fizyczna

jest funkcją zmiennych, które
mierzymy w pomiarach
bezpośrednich z = f(x1, x2, x3,...)

Niepewności pomiarowe i błędy

pomiarowe

• ỹ - wartość rzeczywista nikt jej nie zna
• y - wartość zmierzona
• Δỹ - rzeczywisty błąd nikt go nie zna
• Δỹ = y - ỹ
• W pomiarach określamy przedział y ±

Δy lub (y - Δy, y + Δy), w którym z

założoną niepewności mieści się

wartość rzeczywista ỹ. Δy nazywamy

niepewnością pomiarową

Niepewności pomiarowe i błędy

pomiarowe

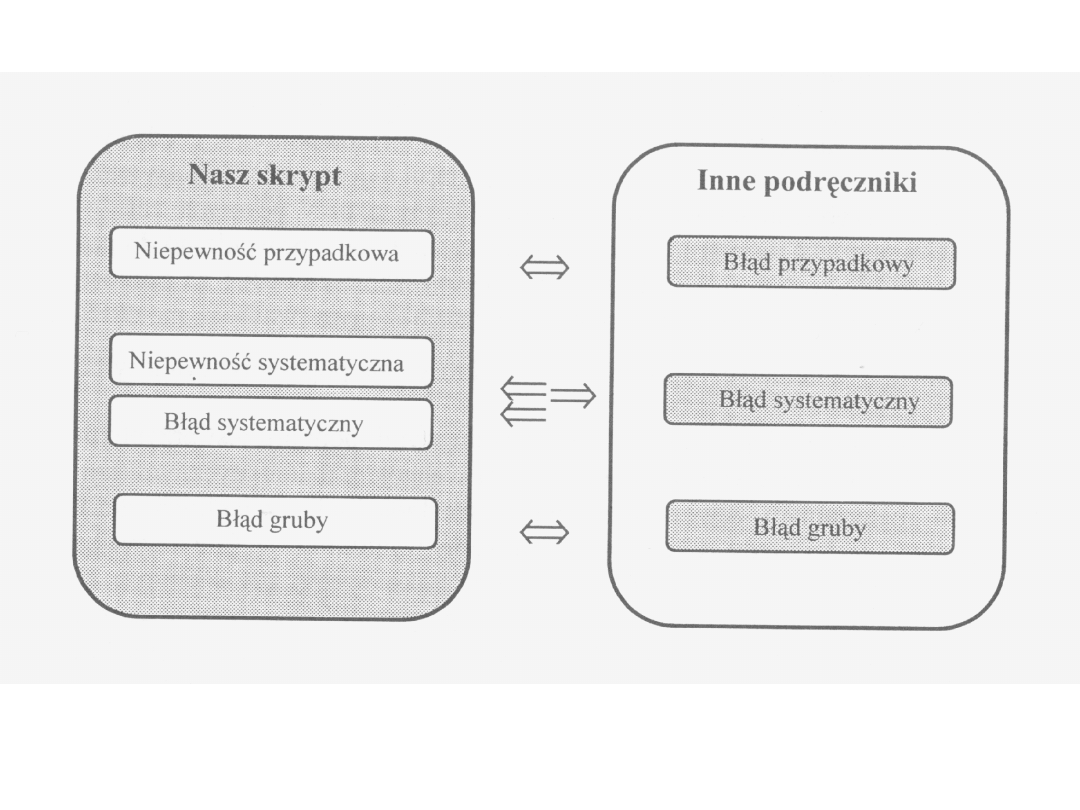
• Niepewność systematyczna
• Niepewność przypadkowa
• Błąd systematyczny
• Błąd gruby

Nazwa

niepewności

W jaki sposób

się objawia

Przyczyna

Przykład

Niepewność
systematycz

na

Na podziałce
przyrządu nie
można odczytać
dowolnej liczby
miejsc wyniku
pomiarowego.

Można odczytać części
setne:1.96A lub 1.98A,
a nie można odczytać
tysięcznych części

Niepewności
systematyczne
występują w
każdym
pomiarze.
Dominują gdy, w
kolejnych
pomiarach
uzyskuje się
identyczne
wyniki

Ograniczona
liczba kresek
podziałki
przyrządu

Niepewność
systematyczna
podziałki , na której
kolejne kreski
oznaczają
wartości1.96A, 1.98A
wynosi ΔI=0.02A

Klasa przyrządu
pomiarowego

Niepewność
systematyczna
miernika klasy 0.5 jest
równa 0.5%
stosowanego zakresu

Ograniczona
dokładność
odczytu

Niepewność
systematyczna równa
szerokości wskazówki
odczytanej na
podziałce

Niepewność
obserwatora
spowodowana
drżeniem lub
ruchem
wskazówki

Niepewność
systematyczna równa
odczytanej na
podziałce przyrządu
szerokości obszaru, w
obrębie którego
zachodzą drgania
wskazówki

Nazwa

niepewności

W jaki sposób się

objawia

Przyczyna

Przykład

Niepewnoś
ć

przypadko

we

Przy powtarzaniu
pomiarów nie

uzyskujemy

identycznych wyników

Pomiary
długości: 8.36,

8.25, 8.48,

8.39, ...

Niepewnoś

ć

przypadko

we obiektu

Rozrzut statystyczny

wyników pomiarów

poszczególnych

elementów zbioru

Brak

identyczności

elementów

Pomiar średnicy

serii

„identycznych”

kulek

Rozrzut wyników

wielokrotnego

pomiaru tego samego

obiektu

Niezgodność

przyjętego

modelu z

mierzonym

obiektem

Pomiar średnicy

pręta

Niepewnoś

ć

przypadko

we metody

Pomiar

precyzyjny

Rozrzut wyników

wielokrotnego

pomiaru wzorca

Przyrząd

pomiarowy

Wiele

przyrządów

Metoda

pomiarowa

Różne metody

Warunki

pomiarowe

Różne warunki

atmosferyczne

Zmysły

obserwatora

Różne rodzaje

oświetlenia

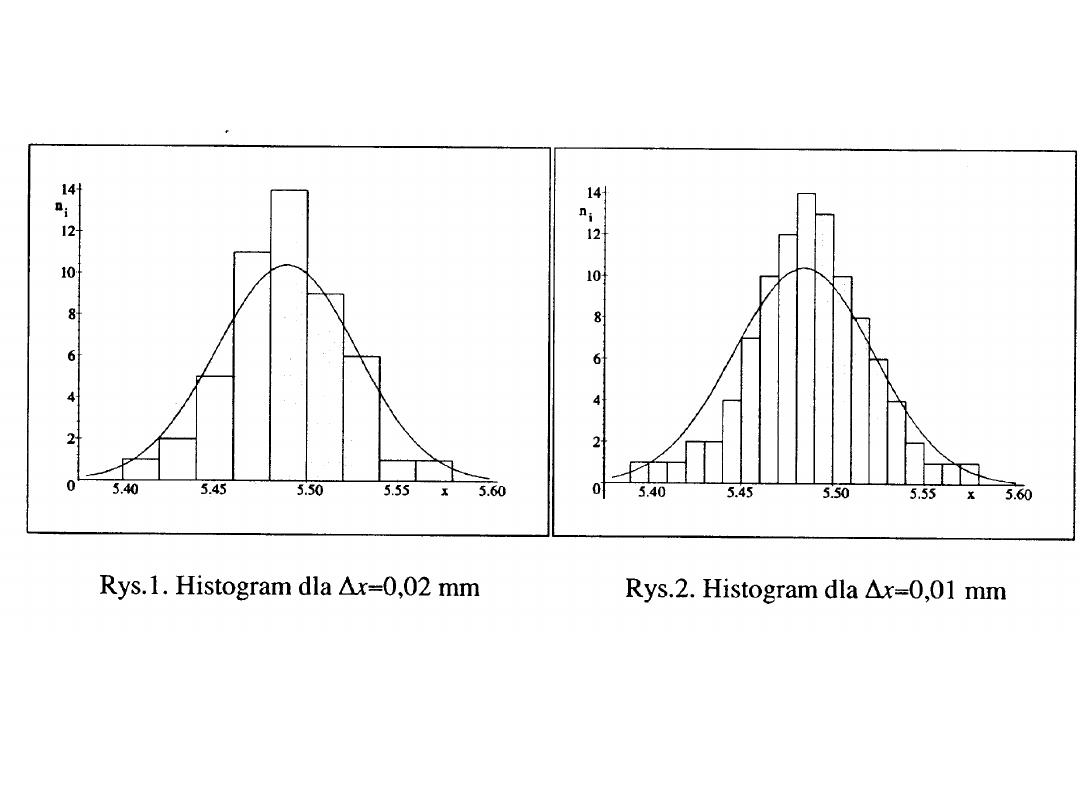
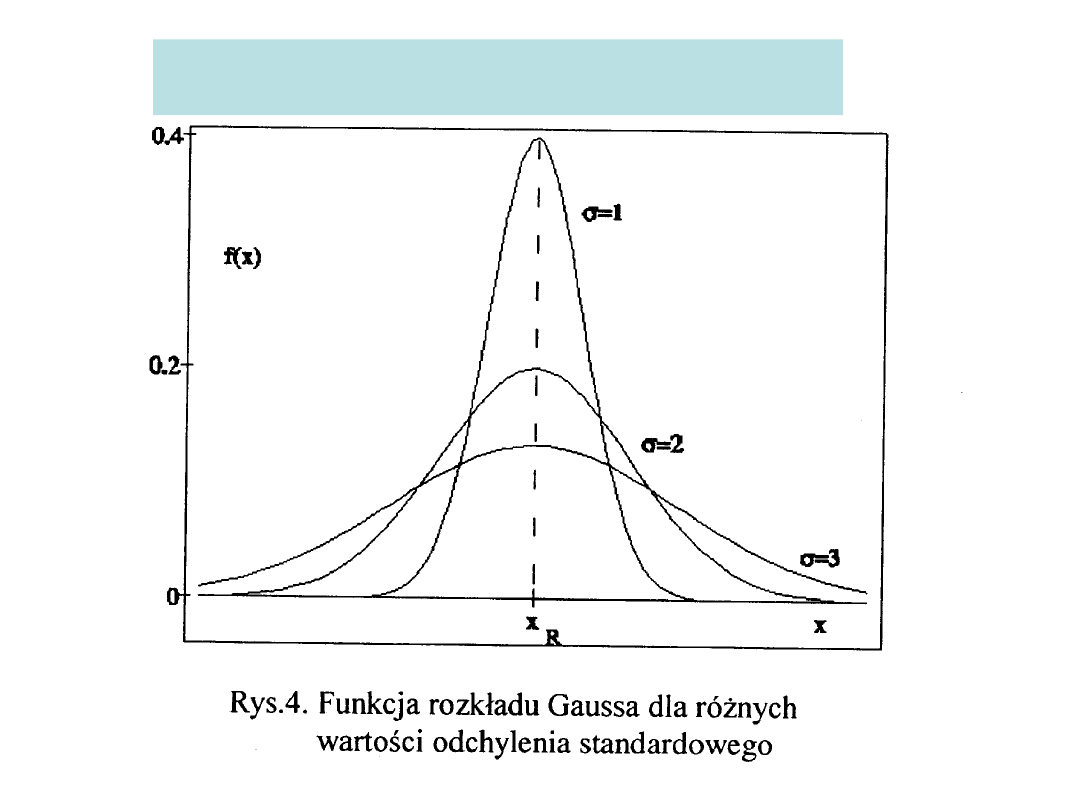
Funkcja rozkładu Gaussa

Wartośc najbardziej

prawdopodobna









 





































































































n

i

i

R

n

i

R

i

n

i

R

i

R

n

i

R

i

c

n

n

c

R

i

i

x

x

n

x

x

x

x

x

x

g

x

x

A

P

x

P

x

P

x

P

x

P

P

x

x

A

P

1

1

1

2

2

1

2

3

3

2

2

1

1

2

2

1

0

2

2

exp

)

(

)

(

)

(

)

(

2

exp







Procedura pomiarowa:

• Pomiar wykonujemy 3 razy.
• Jeśli się powtarzają to dominuje

niepewność systematyczna.

• Δx= Δx

systematyczna

Procedura pomiarowa:

• Jeżeli są różne wyniki mierzymy

wielkość przynajmniej 10 razy np. N
razy.

• Wyznaczamy średnią:
• Wyznaczamy odchylenie

standardowe średniej (przedział
ufności 68.3%):

Procedura pomiarowa:

• Niepewność pomiarowa przy

poziomie ufności 99% z
uwzględnieniem niepewności
systematycznej

• Δx= Δx

systematyczna

+ 3∙δ

x

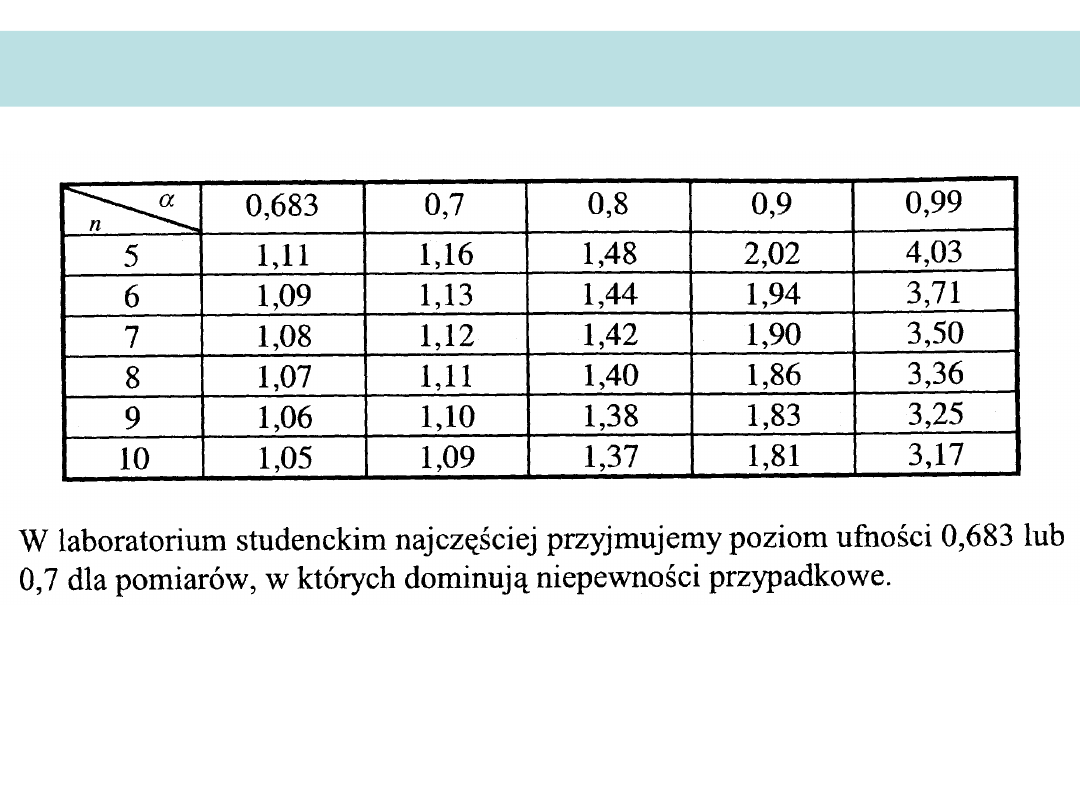
Współczynnik rozkładu Studenta-Fishera

Procedura pomiarowa:

• Dla pomiaru pośredniego z = f(x1,

x2, x3,...) niepewność maksymalną
wyliczamy z różniczki zupełnej:

• Maksymalna niepewność względna
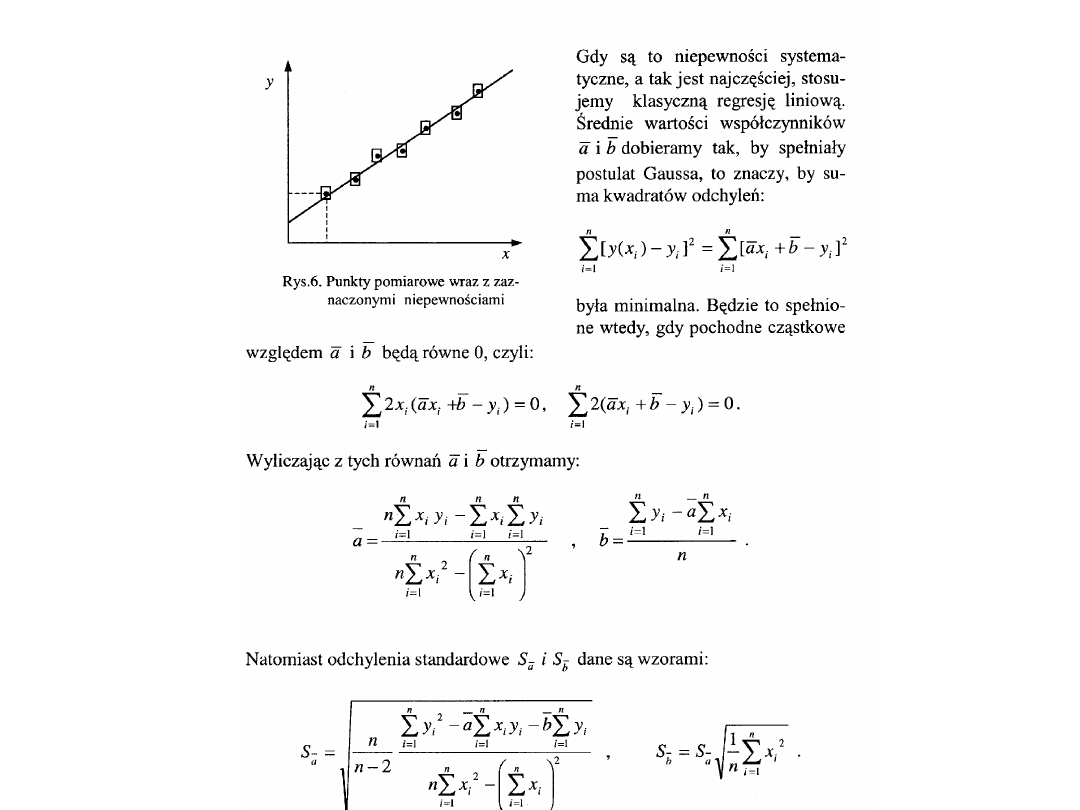
• Regresja liniowa (metoda

algebraiczna, graficzna)

Zapis wyników

• Zaokrąglanie zaczynamy od

niepewności

• Niepewność pomiarową zaokrąglamy

do jednego miejsca znaczącego wtedy,
gdy pierwsza cyfra znacząca jest
większa od trzech. W przeciwnym razie
zaokrąglamy do dwóch.

• Wynik zaokrąglamy do tego samego

miejsca rozwinięcia dziesiętnego co
niepewność

Porównywanie pomiarów

• Pomiar uważamy za błędny, jeżeli

wartość rzeczywista nie mieści się w
przedziale wyznaczonym przez
pomiar.

• Dwa pomiary dają ten sam wynik

jeśli przedziały wyznaczone w tych
pomiarach maja wspólną część.