UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

1

PODSTAWY AUTOMATYKI

PODSTAWY AUTOMATYKI

Prowadzący

Prowadzący

:

:

dr ing. Sebastian

dr ing. Sebastian

Kula

Kula

e-mail: [e-mail]

e-mail: [e-mail]

Uniwersytet Kazimierza Wielkiego w

Bydgoszczy

wykład III

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

2

zajęcia realizowane są w ramach

projektu pt. “Mechatronika

kierunkiem przyszłości –

dostosowanie oferty edukacyjnej

Uniwersytetu Kazimierza

Wielkiego do potrzeb rynku

pracy”, Działanie 4.1.1, Programu

Operacyjnego Kapitał Ludzki,

współfinansowanego ze środków

Europejskiego Funduszu

Społecznego”.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

3

Plan wykładu

• Badanie stabilności

- warunek stabilności układu
- kryterium stabilności Routha - Hurwitza
- kryterium stabilności Nyquista
- kryterium Michajłowa
- stabilność obiektów nieliniowych

• Projektowanie liniowych układów regulacji w

dziedzinie czasu i częstotliwości.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

4

Badanie stabilności(1)

Podstawową właściwością, jaką powinien spełniać

każdy system automatyki jest stabilność. Pojęcie

stabilności mówi, że gdy podamy na wejście

systemu dowolny sygnał ograniczony, wówczas na

jego wyjściu y(t) otrzymamy również sygnał

ograniczony (definicja według Laplace’a).
Każdy układ regulacji automatycznej musi być

stabilny jeżeli ma działać prawidłowo. Sprawdzenie

jego stabilności jest podstawowym kryterium oceny

jakości układu regulacji i musi być kontrolowane w

czasie doboru rodzaju i optymalnych nastaw

poszczególnych członów tego układu a w

szczególności – w czasie doboru nastaw regulatora.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

5

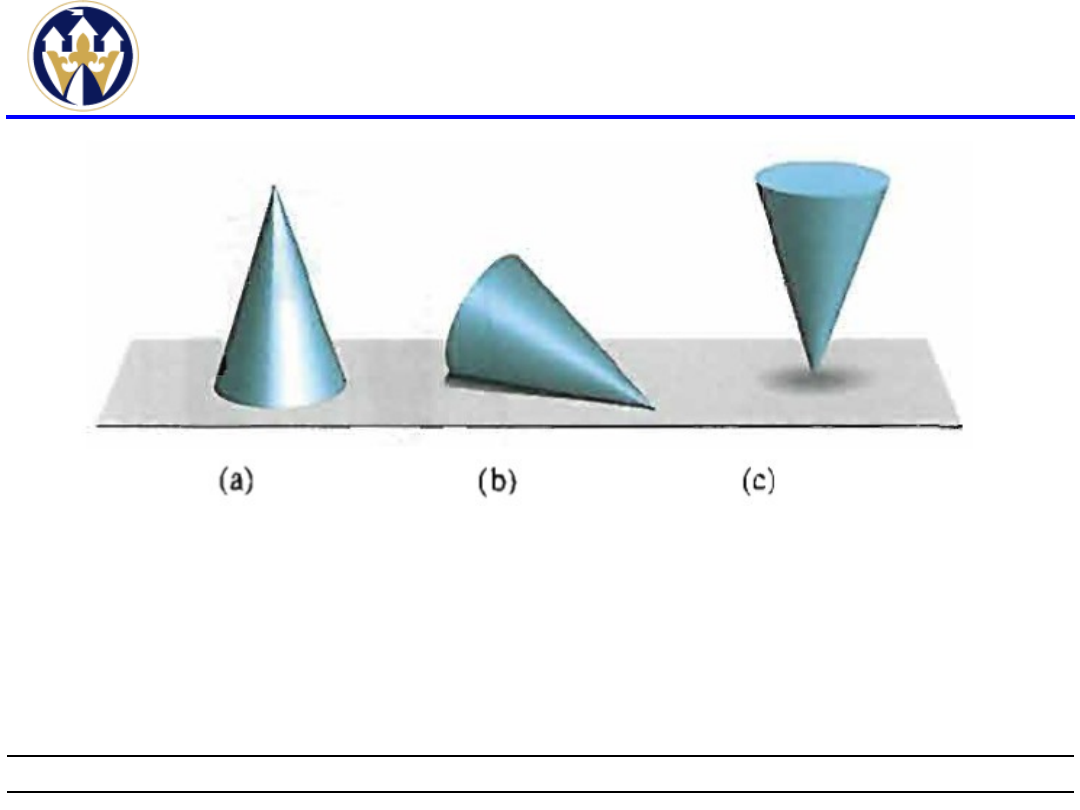
Koncepcja stabilności na przykładzie stożka a)

układ stabilny b) neutralny c) niestabilny.

Badanie stabilności(2)

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

6

Badanie stabilności(3)

Most Tacoma Narrows w Puget Sound, USA.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

7

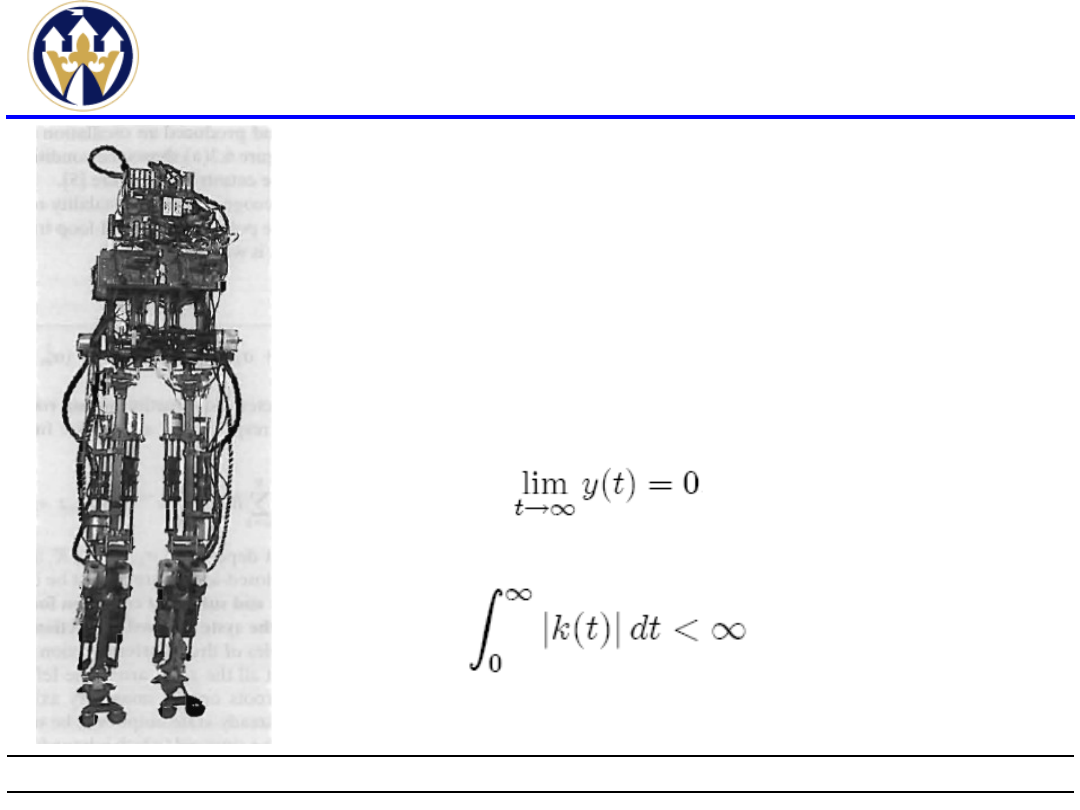
Badanie stabilności(4)

Robot M2 charakteryzujący się
małym zapasem stabilności.

Definicja stabilności mówi, że
system

nazywamy

stabilnym

(asymptotycznie),

jeśli

przy

dowolnym warunku początkowym i
zerowym pobudzeniu zachodzi:

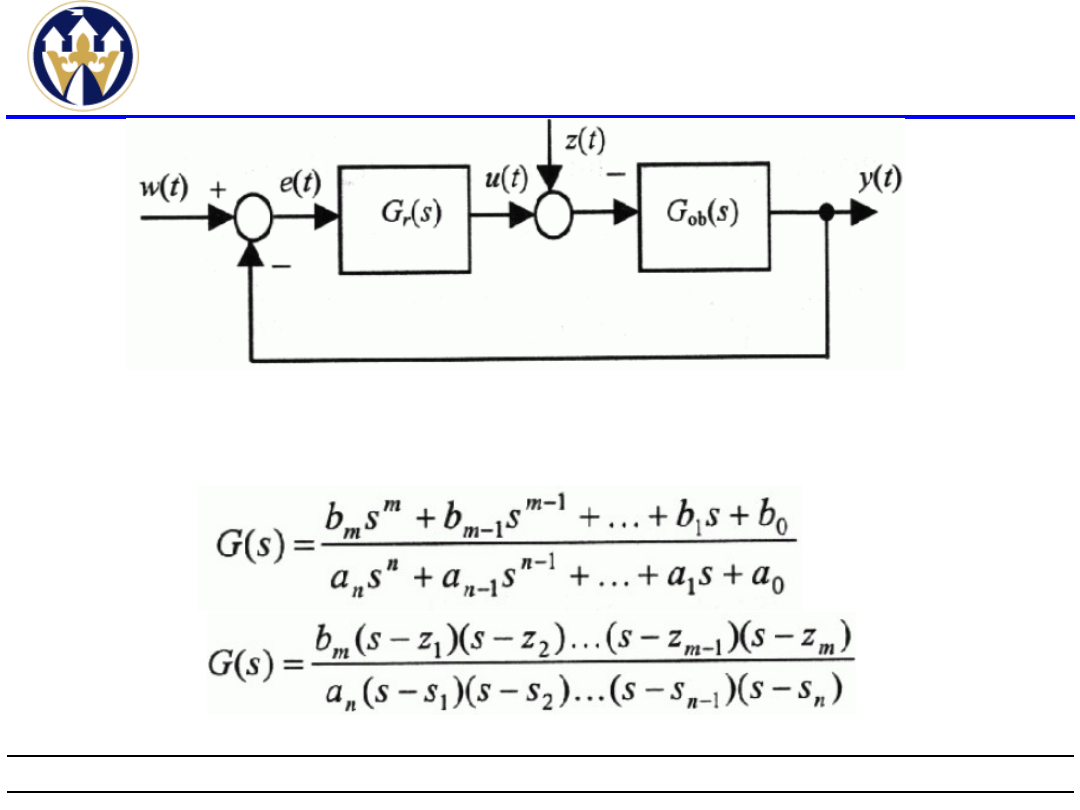
Dla systemu stabilnego zachodzi
również:

k(t)- charakterystyka impulsowa

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

8

Schemat liniowego układu automatycznej

regulacji. G

r

(s), G

ob

(s) transmitancje regulatora

oraz obiektu.

Badanie stabilności(5)

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

9

Badanie stabilności(6)

Odpowiedź impulsowa tego układu:

gdzie

s

i

są

pierwiastkami

(biegunami)

transmitancji

układu

zamkniętego

G(s)

powstałymi

po

rozwiązaniu

równiania

charakterystycznego:

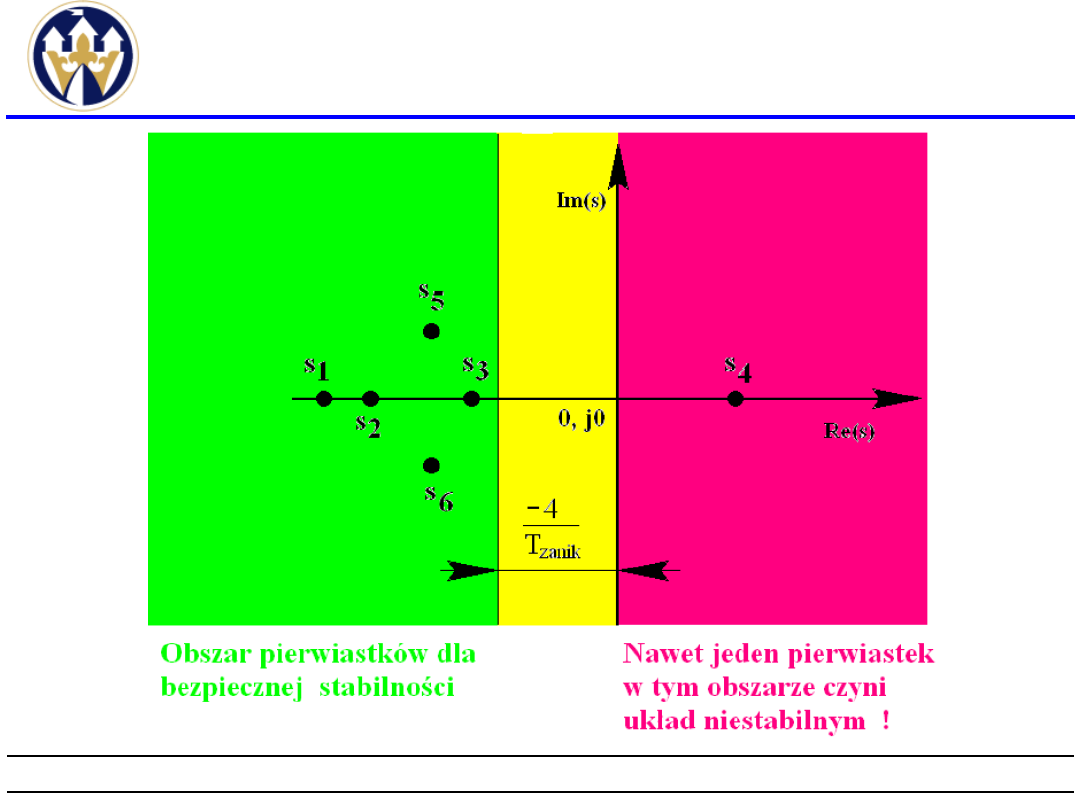
Jeżeli wszystkie bieguny G(s) znajdują się w
lewej półpłaszczyźnie zmiennej zespolonej, czyli
mają części rzeczywiste ujemne to odpowiedź
impulsowa dąży do zera przy t dążącym do
nieskończoności. Wtedy układ jest układem
stabilnym.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

10

Badanie stabilności(7)

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

11

Badanie stabilności(8)

Warunek powyżej sformułowany jest warunkiem
stabilności liniowego układu automatycznej
regulacji. Transmitancja operatorowa stabilnego
liniowego układu automatycznej regulacji nie
ma biegunów w prawej domkniętej płaszczyźnie
zmiennej zespolonej s.

Jeżeli chociaż jeden z biegunów transmitancji
układu zamkniętego znajduje się na osi urojonej
płaszczyzny zmiennej zespolonej s, to taki układ
zamknięty nie będzie układem stabilnym.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

12

Badanie stabilności(9)

Jeżeli jeden z biegunów transmitancji układu
zamkniętego G(s) jest biegunem zerowym, czyli
znajduje się w początku układu współrzędnych
na płaszczyźnie zmiennej zespolonej s, to
odpowiedź impulsowa g(t) dąży do wartości
stałej przy t dążącym do nieskończoności. Układ
zamknięty nie jest stabilny.

Jeżeli transmitancja układu zamkniętego ma
dwa bieguny urojone sprzężone: jω i -jω, czyli
znajdujące się na osi urojonej płaszczyzny
zmiennej zespolonej s, odpowiedź impulsowa
g(t) będzie przebiegiem sinusoidalnym i układ
zamknięty nie jest stabilny.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

13

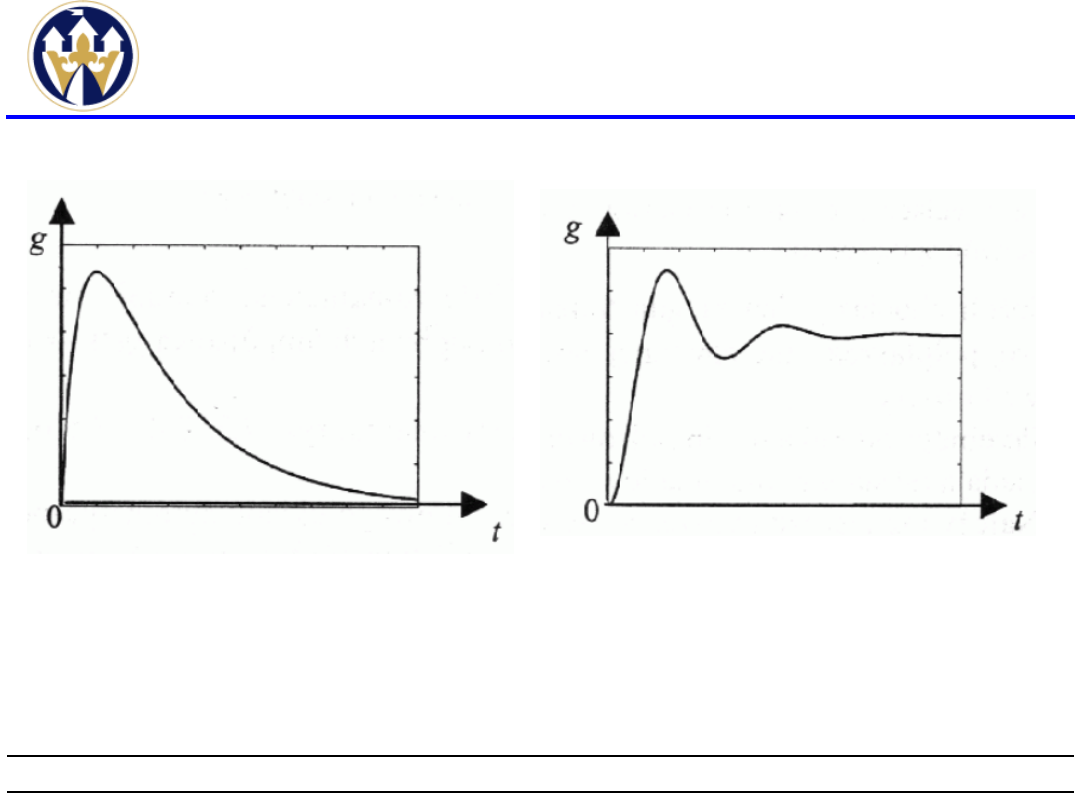
Badanie stabilności(10)

Odpowiedź impulsowa

stabilnego układu

regulacji.

Odpowiedź impulsowa

układu regulacji z

biegunem zerowym.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

14

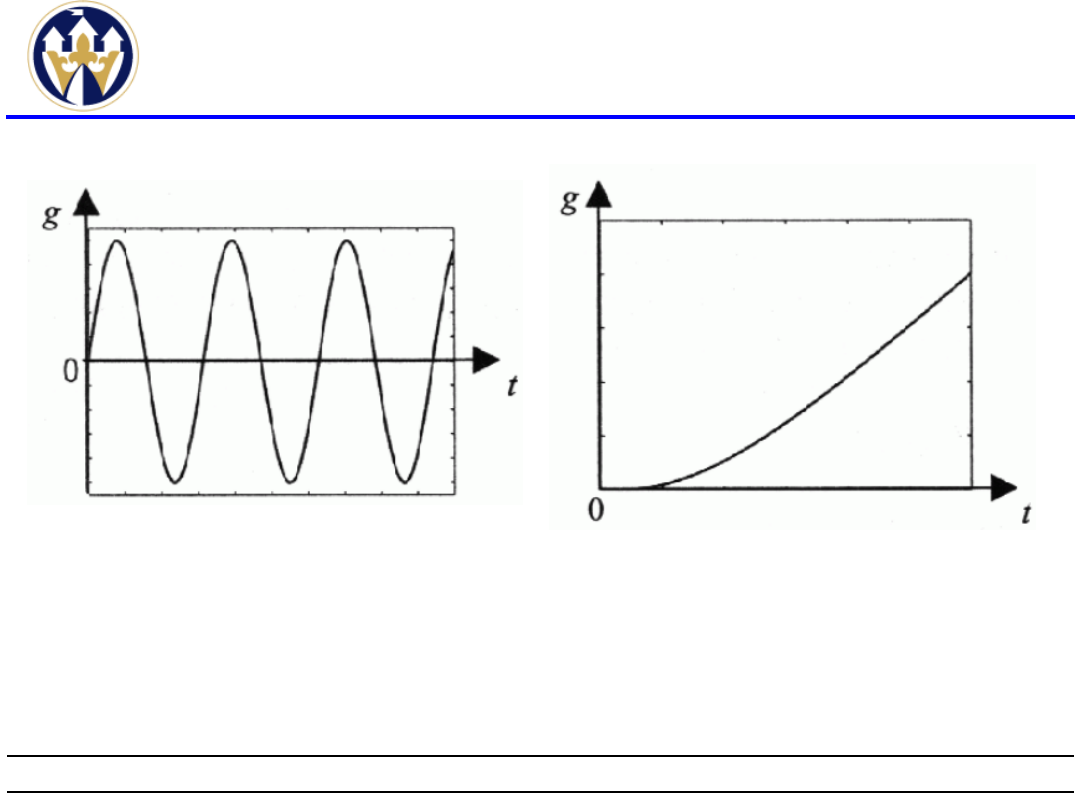
Badanie stabilności(11)

Odpowiedź impulsowa

układu regulacji z

dwoma biegunami

urojonymi

sprzężonymi.

Odpowiedź impulsowa

układu niestabilnego.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

15

Badanie stabilności(12)

Badania stabilności można przeprowadzać
metodami

analitycznymi

jeżeli

opis

matematyczny wszystkich członów układu
regulacji jest znany, stabilność można też
oceniać

eksperymentalnie

jeżeli

układ

regulacji istnieje i można na nim przeprowadzać
eksperymenty.
Badanie

stabilności

układu

regulacji

automatycznej

polega

na

wprowadzeniu

krótkotrwałego sygnału zakłócającego stan
równowagi układu i na ocenie przebiegu
sygnału wyjściowego lub uchybu regulacji po
zaniknięciu zakłócenia. Sygnałem zakłócającym
może być np. krótkotrwała (impulsowa) zmiana
sygnału wejściowego, którym jest wartość
zadana.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

16

Ocena stabilności układu opiera się na
sprawdzeniu

położenia

biegunów

jego

transmitancji.

Z

warunków

biegunowych

wiadomo, że wiąże się to z rozwiązaniem
równania charakterystycznego. Odpowiedź na
pytanie o stabilność układu automatycznej
regulacji można uzyskać bez rozwiązywania
układu

charakterystycznego,

poprzez

zastosowanie kryteriów stabilności (np.
kryterium

Routha-Hurwitza,

Hurwitza,

Michajłowa i Nyquista. Różnią się one między
sobą metodyką postępowania i bazują na różnej
formie wyjściowej wiedzy o układzie.

Kryterium Hurwizta(1)

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

17

Kryterium Hurwizta(2)

Dysponując równaniem charakterystycznym
można sprawdzić stabilność układu bez
wyliczania jego pierwiastków. Skorzystać w tym
celu można z kryterium Hurwitza.
Według Hurwitza równanie algebraiczne

o współczynnikach rzeczywistych a

i

(i = 1, 2,...,

n) ma pierwiastki s

i

o ujemnych częściach

rzeczywistych wtedy i tylko wtedy, gdy
wszystkie współczynniki a

i

istnieją i są dodatnie

oraz gdy dodatni jest następujący wyznacznik n-
tego rzędu (zwany wyznacznikiem Hurwitza)

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

18

Kryterium Hurwizta(3)

Wyznacznik Hurwiza.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

19

oraz wszystkie jego podwyznaczniki główne:

Kryterium Hurwizta(4)

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

20

Kryterium Hurwizta(5)

Przykład

badania

stabilności

przy

wykorzystaniu

kryterium

Hurwitza.

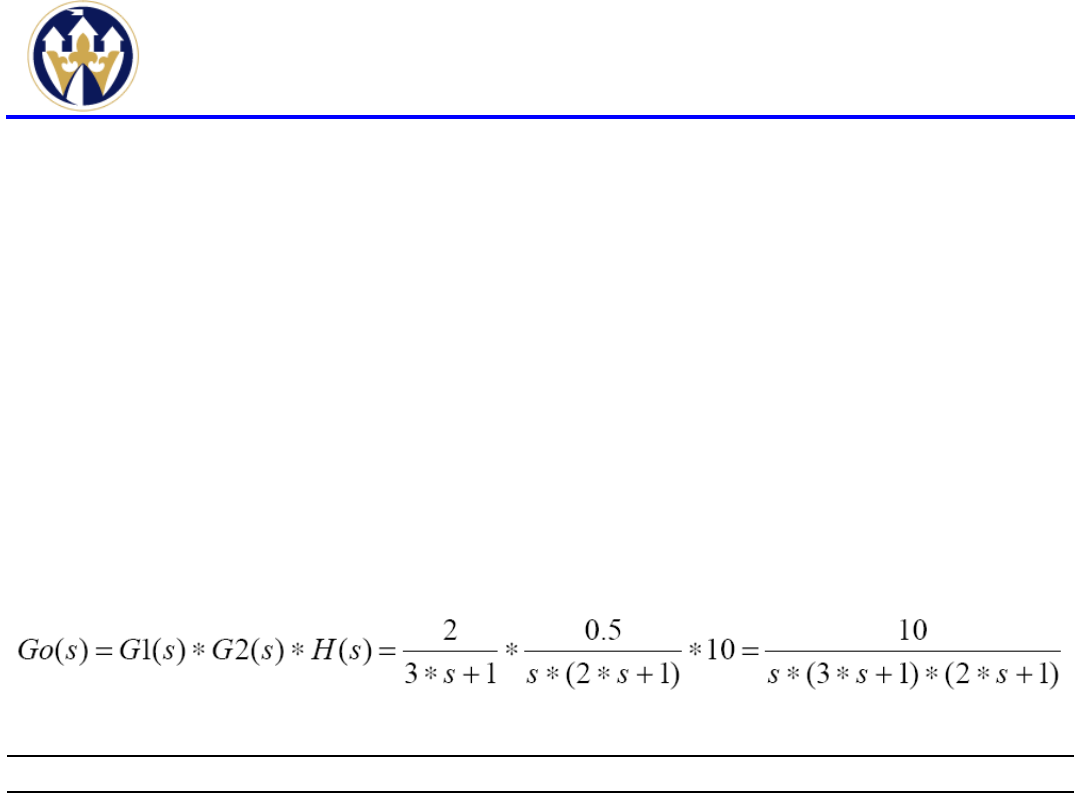
Układ

regulacji

automatycznej

z

ujemnym

sprzężeniem zwrotnym zawiera w torze
głównym człon nastawczy o transmitancji
operatorowej G1(s)=2/(3*s+1) i obiekt regulacji
o transmitancji G2(s)=0.5/(s*(2*s+1)) oraz w
torze

sprzężenia

zwrotnego

człon

proporcjonalny o transmitancji H(s)=10.
Transmitancja operatorowa układu otwartego:

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

21

Kryterium Hurwizta(6)

Równanie

charakterystyczne

układu

zamkniętego:

po kolejnych przekształceniach

ostateczna postać równania to wielomian 3
stopnia, w którym wszystkie stałe współczynniki
a

0

, a

1

, a

2

, a

3

, istnieją i są dodatnie a więc

spełniają pierwszy konieczny warunek kryterium
Hurwitza.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

22

Kryterium Hurwizta(7)

Główny wyznacznik 3 - stopnia utworzony z tych
współczynników:

ma wartość ujemną, a więc układ jest
niestabilny i nie ma potrzeby przeprowadzania
dalszych obliczeń.
Można sprawdzić podwyznacznika 2 - stopnia
utworzonego, który także jest ujemny.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

23

Kryterium Routha(1)

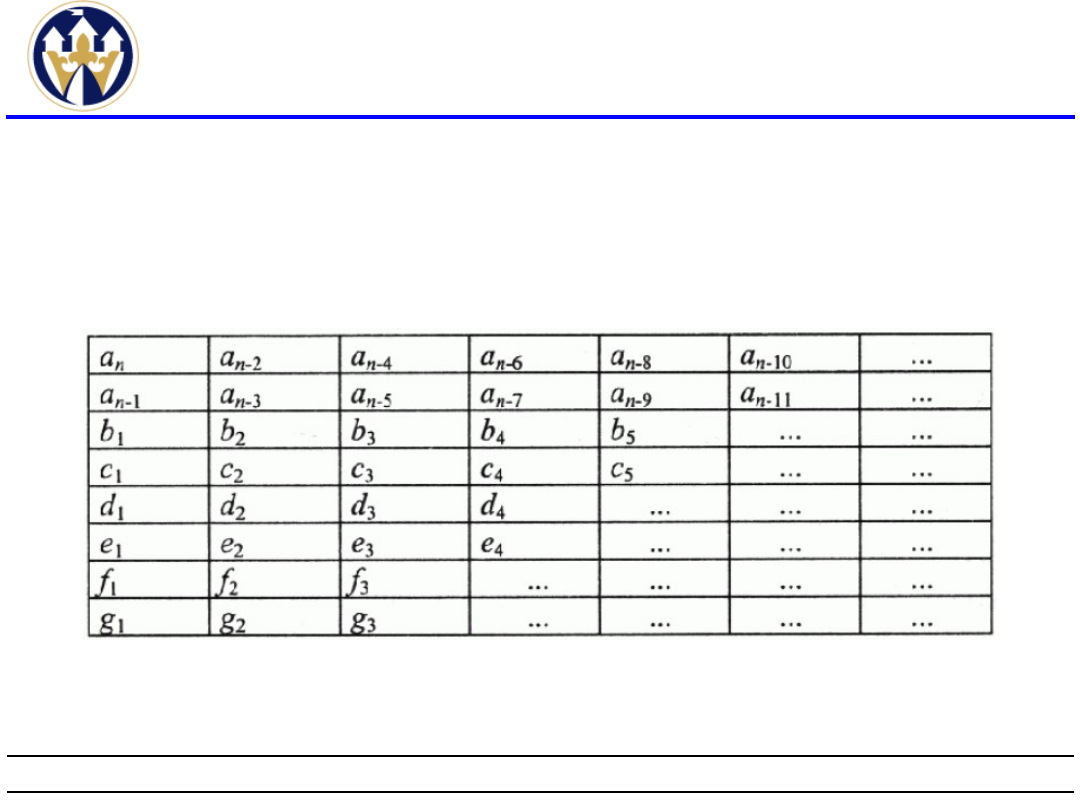
Według Routha układ automatycznej regulacji
będzie stabilny wtedy i tylko wtedy, gdy
wszystkie wyrazy pierwszej kolumny tablicy
Routha są różne od zera oraz mają ten sam
znak.

Tablica Routha.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

24

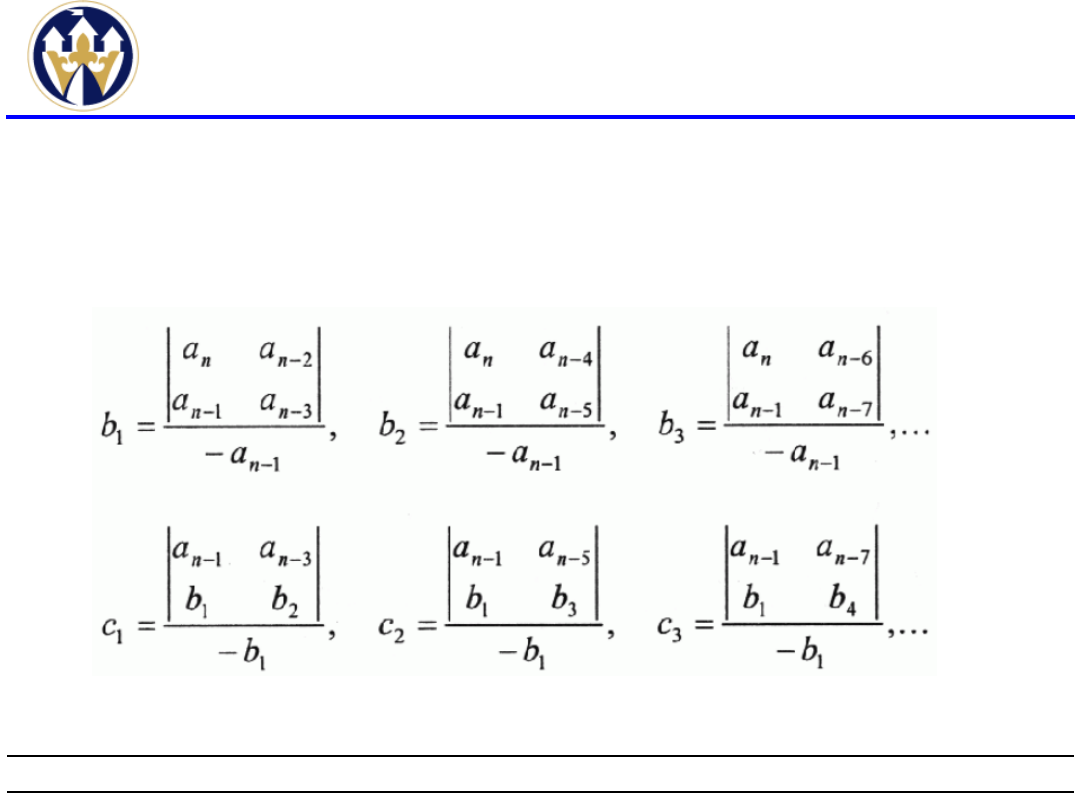
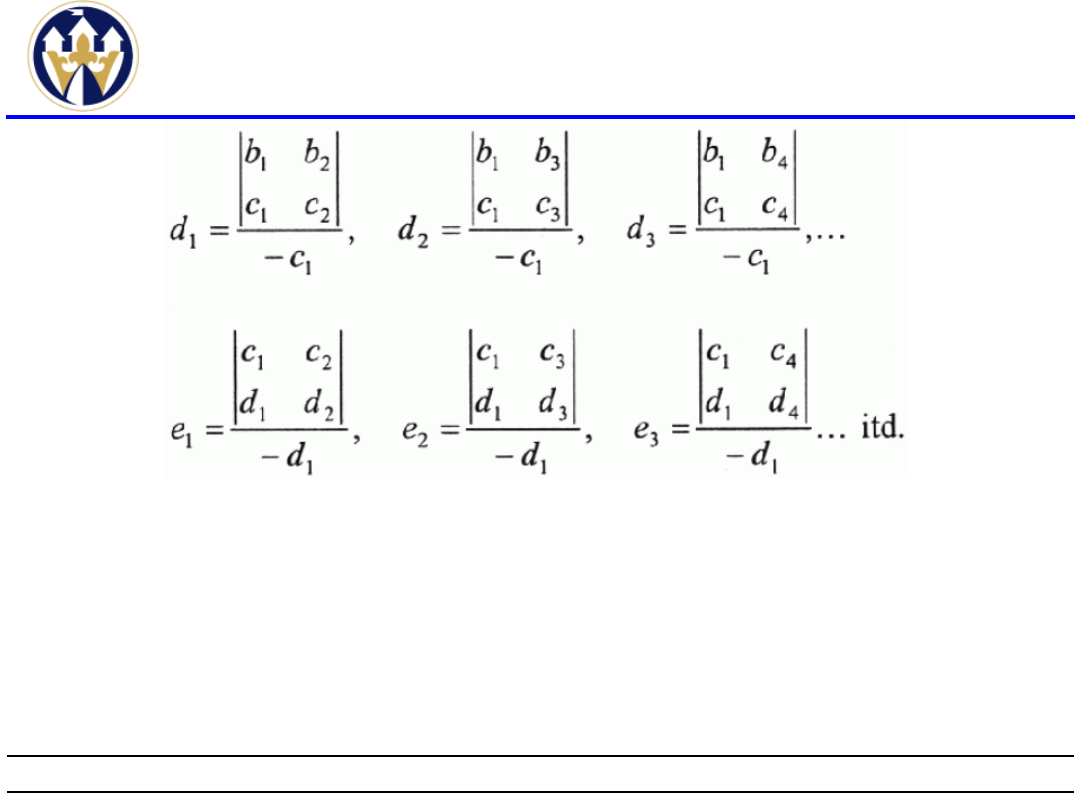
Kryterium Routha(2)

Poszczególne wyrazy b

1

, b

2

, ... , c

1

, c

2

, ... d

1

,

d

2

, ...

znajdujące się w kolejnych wierszach i

kolumnach określają wzory:

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

25

Kryterium Routha(3)

Jeżeli w pierwszej kolumnie tablicy Routha
występują wyrazy o rożnych znakach, to układ
jest niestabilny, a liczba zmian znaku jest równa
liczbie

pierwiastków

równania

charakterystycznego znajdujących się w prawej
półpłaszczyźnie zmiennej zespolonej s.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

26

Kryterium Nyquista(1)

Kryterium Nyquista to kryterium o bardzo
dużym znaczeniu praktycznym. Ocenia ono
stabilność układu zamkniętego na podstawie
badania

przebiegu

charakterystyki

częstotliwościowej

układu

otwartego

powstałego przez otwarcie pętli sprzężenia
zwrotnego układu automatycznej regulacji.
Jeżeli sygnał sinusoidalnie zmienny, który może
być

składnikiem

widma

wszechobecnych

szumów wniknie w dowolnym miejscu do
układu, to po obiegnięciu pętli
jaką tworzą elementy układu zamkniętego
ulega przetworzeniu polegającemu na zmianie
amplitudy i fazy. Ze względu na
ujemny znak sprzężenia

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

27

zwrotnego, sygnał o takiej częstotliwości, przy

której po przejściu przez elementy tworzące

pętlę zmieni fazę na przeciwną, ulegnie

podtrzymaniu.

Jeżeli

moduł

transmitancji

widmowej pętli będzie dla tej częstotliwości

większy od jedności to po każdym obiegnięciu

pętli amplituda sygnału zwiększy się. Sygnał

będzie rósł teoretycznie nieograniczenie, a więc

układ będzie niestabilny.

Gdy w układzie zamkniętym występują drgania

o określonej amplitudzie i pulsacji to:

Kryterium Nyquista(2)

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

28

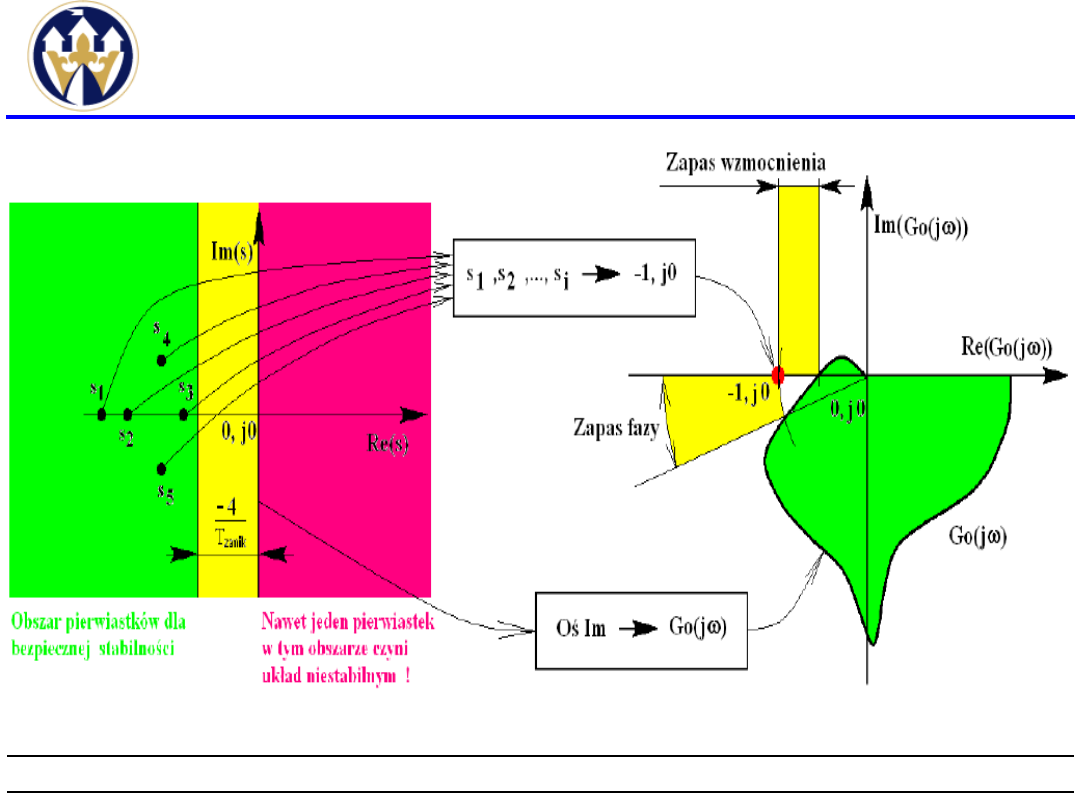
Kryterium Nyquista(3)

Wobec powyższego wnioskujemy, że gdy w

układzie zamkniętym występują drgania to

charakterystyka

amplitudowo-fazowa

stabilnego układu otwartego przechodzi przez

punkt (-1,j0).

Warunkiem stabilności układu z ujemnym

sprzężeniem zwrotnym jest by punkt o

współrzędnych

(-1,j0) - nazywany „punktem Nyquista” leżał

poza obszarem płaszczyzny ograniczonym linią

charakterystyki amplitudowo - fazowej układu

otwartego. Do oceny stabilności układu

niezbędny jest jeden wykres charakterystyki

amplitudowo - fazowej.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

29

Kryterium Nyquista(4)

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

30

Kryterium Nyquista(5)

Istotną

zaletą

kryterium

Nyquista

jest

możliwość bardzo łatwego oszacowania zapasu

stabilności układu określanego jedną z dwu

charakterystycznych wielkości:

a)

zapas

współczynnika

wzmocnienia

występującego w układzie otwartym

b)

zapas

kąta

fazowego

przesunięcia

występującego w układzie otwartym

Znajomość tych dwu wielkości pozwala łatwo

zoptymalizować

nastawy

poszczególnych

członów układu regulacji występujących w torze

głównym i w torze ujemnego sprzężenia

zwrotnego.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

31

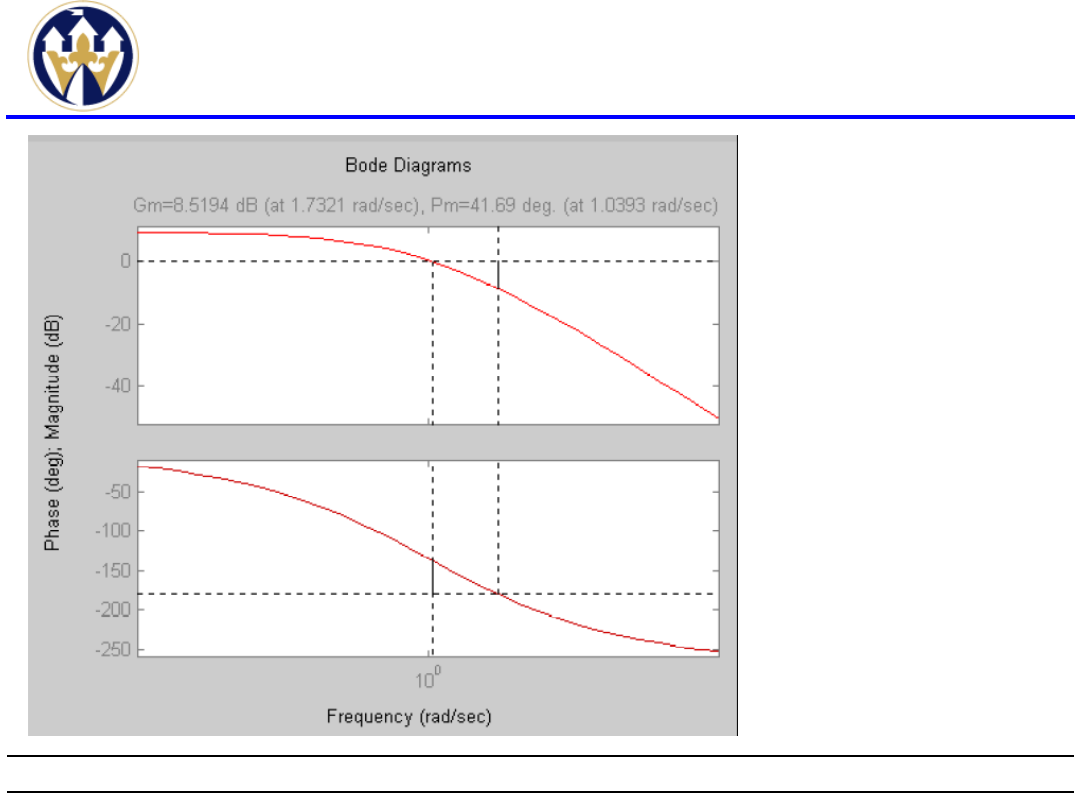
Kryterium Nyquista(6)

Zapas

amplitudy

oraz fazy,

wykres

logarytmiczn

y Bodego.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

32

Kryterium Michajłowa(1)

Kryterium Michajłowa umożliwia badanie

stabilności liniowego układu automatycznej

regulacji na podstawie przebiegu wielomianu

M(jω) będącego mianownikiem transmitancji

widmowej G(jω) na płaszczyźnie zmiennej

zespolonej s.

Równanie charakterystyczne M(jω) może

być przedstawione w postaci:

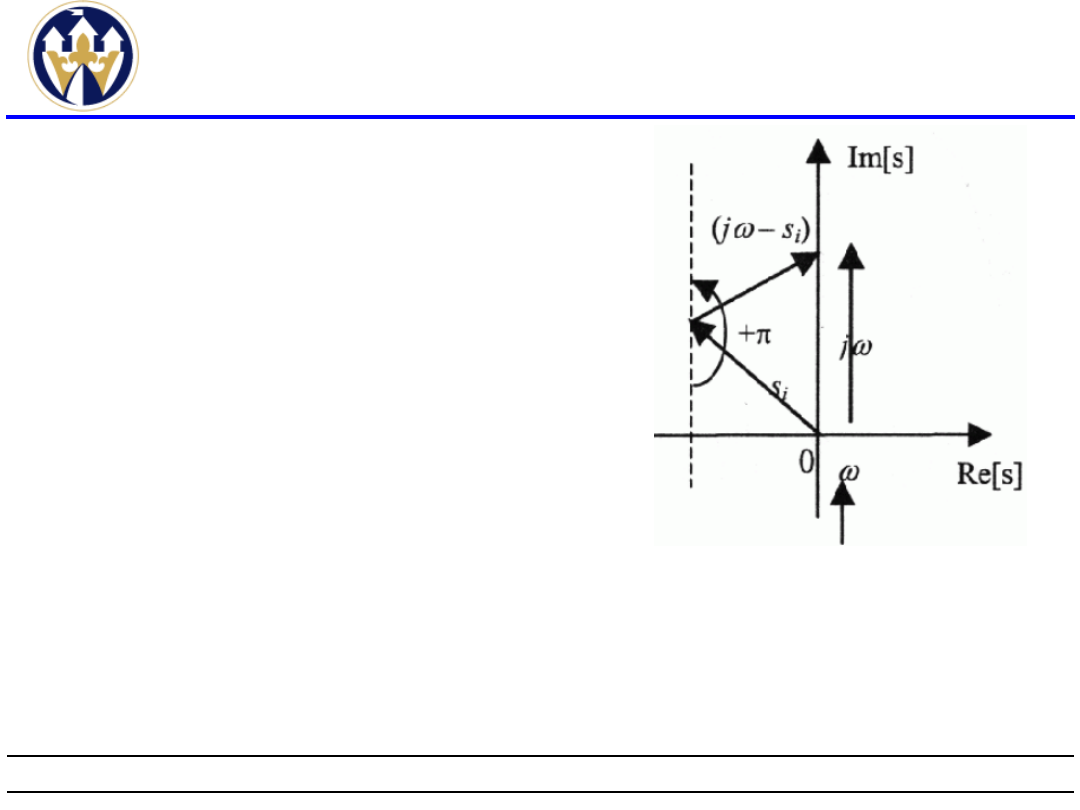
każdy z czynników (jω - s

i

) można przedstawić

na płaszczyźnie zmiennej zespolonej s jako

różnicę dwóch wektorów.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

33

Kryterium Michajłowa(2)

Zmiana

argumentu

każdego czynnika (jω - s

i

)

przy zmianie pulsacji ω

od

-∞

do

+∞

dla

pierwiastków leżących w

lewej

półpłaszczyźnie

płaszczyzny

zespolonej

wynosi +π w kierunku

przeciwnym do ruchu

wskazówek zegara , a w

prawej -π w kierunku

zgodnym

do

ruchu

wskazówek zegara.

Zmiana argumentu

wektora (jω - s

i

)

przy zmianie ω od

-∞ do +∞ dla

Re(s

i

)<0.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

34

Kryterium Michajłowa(3)

Ponieważ w układzie stabilnym wszystkie

pierwiastki

musza

leżeć

w

lewej

półpłaszczyźnie

płaszczyzny

zespolonej

zmiennej s, to dla układu stabilnego mamy:

Wykorzystując fakt symetrii funkcji M(jω)

względem osi rzeczywistej dla dodatnich i

ujemnych ω, sprawdzenie stabilności można

ograniczyć

do

sprawdzenia

przyrostu

argumentu tylko dla dodatnich ω i przyrostu

argumentu stabilnego układu wynosi:

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

35

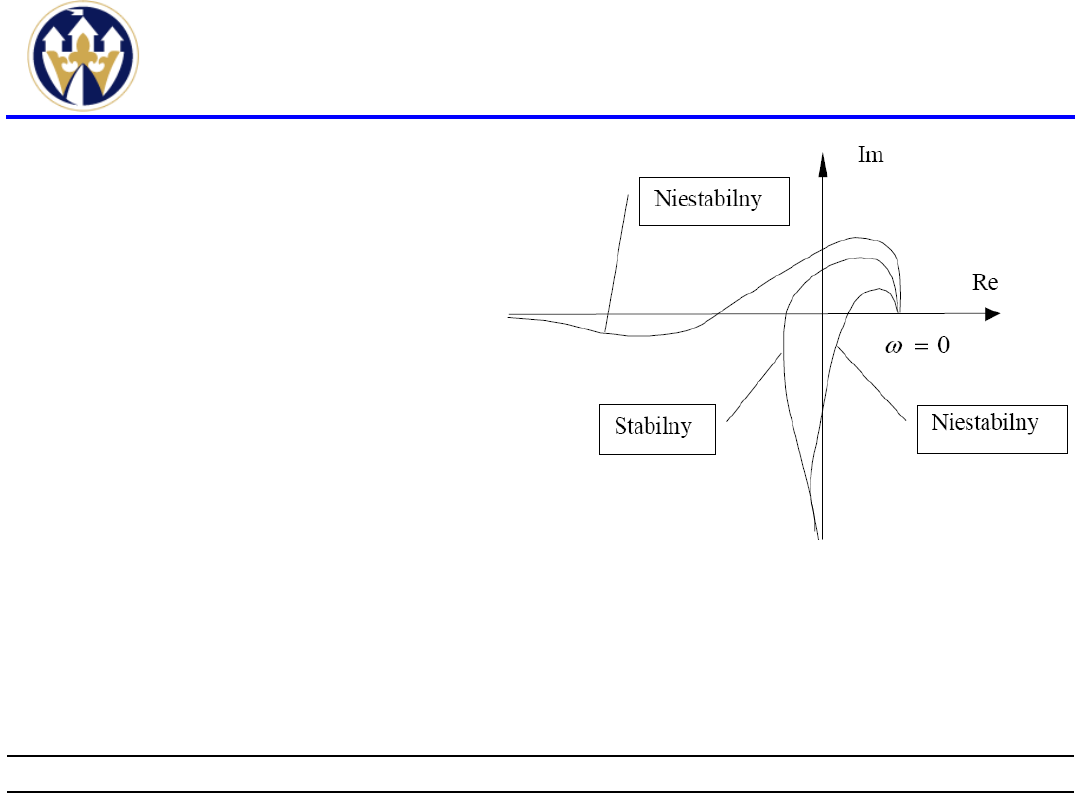
Kryterium Michajłowa(4)

Wykres

krzywej

M(jω) odpowiadający

stabil-nemu

układowi

przejdzie

przy zmianie ω od -∞

do +∞ przez n

ćwiartek w kierunku

przeciwnym

do

ruchu

wskazówek

zegara (w stosunku

do początku układu

współrzędnych),

gdzie

n

jest

najwyższą potęgą s

równania

charakterystycznego

.

Przykładowe

przebiegi krzywej

M(jω) dla obiektów

trzeciego rzędu.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

36

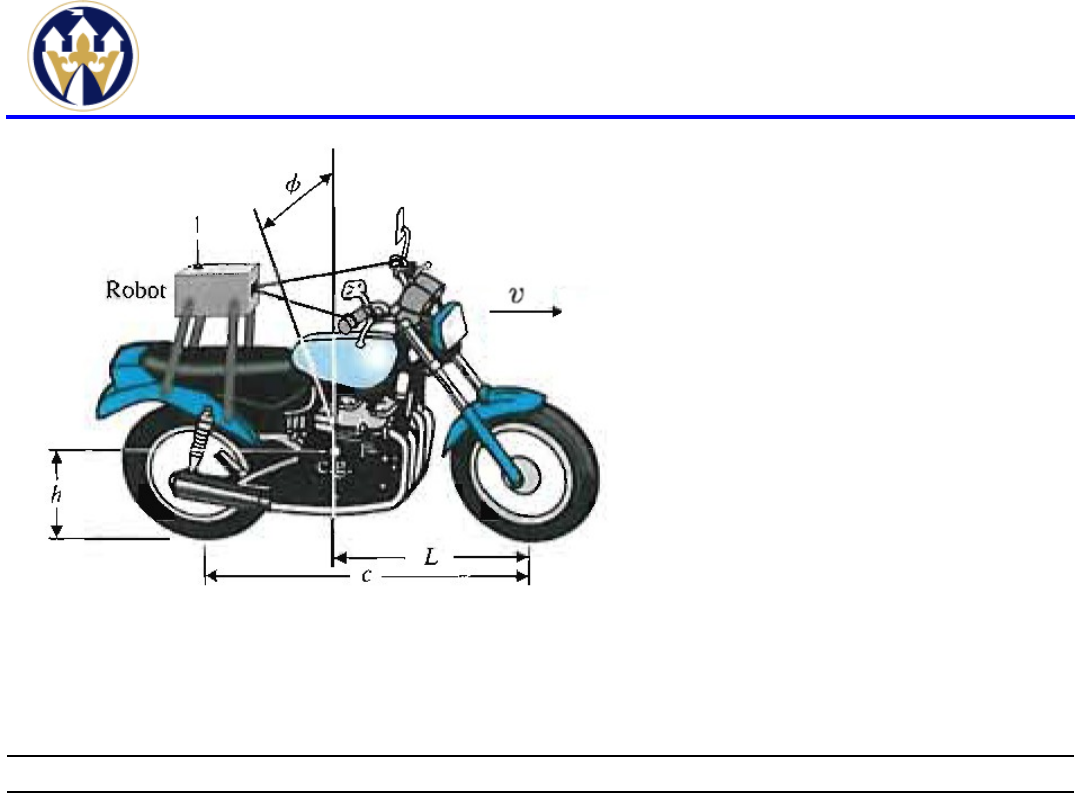
Przykład badania

stabilności(1)

Motor sterowany

robotem, gdzie v-

stała prędkość,

c.g.-środek

ciężkości, h-

wysokość podłoża

do c.g., c-

odległość

pomiędzy środkami

kół, L- pozioma

odległość

pomiędzy kołem

przednim a c.g., φ-

kąt odchylenia od

pionu.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

37

Przykład badania

stabilności(2)

Motor ma być tak sterowany aby poruszał się

po linii prostej, ze stałą prędkością. Oczekiwany

kąt odchylenia od pionu powinien wynosić

zero:

Model motoru opisuje następująca funkcja

przejścia:

gdzie:

Model motoru w układzie otwartym jest

niestabilny.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

38

Przykład badania

stabilności(3)

Model regulatora opisuje następująca funkcja

przejścia:

gdzie:

- stała czasowa określająca szybkość

odpowiedzi

regulatora

Aby otrzymać układ stabilny wprowadzamy

pętlę sprzężenia zwrotnego i określamy

zakresy wzmocnień sprzężonych K

P

i K

D

dla

jakich układ zamknięty będzie stabilny.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

39

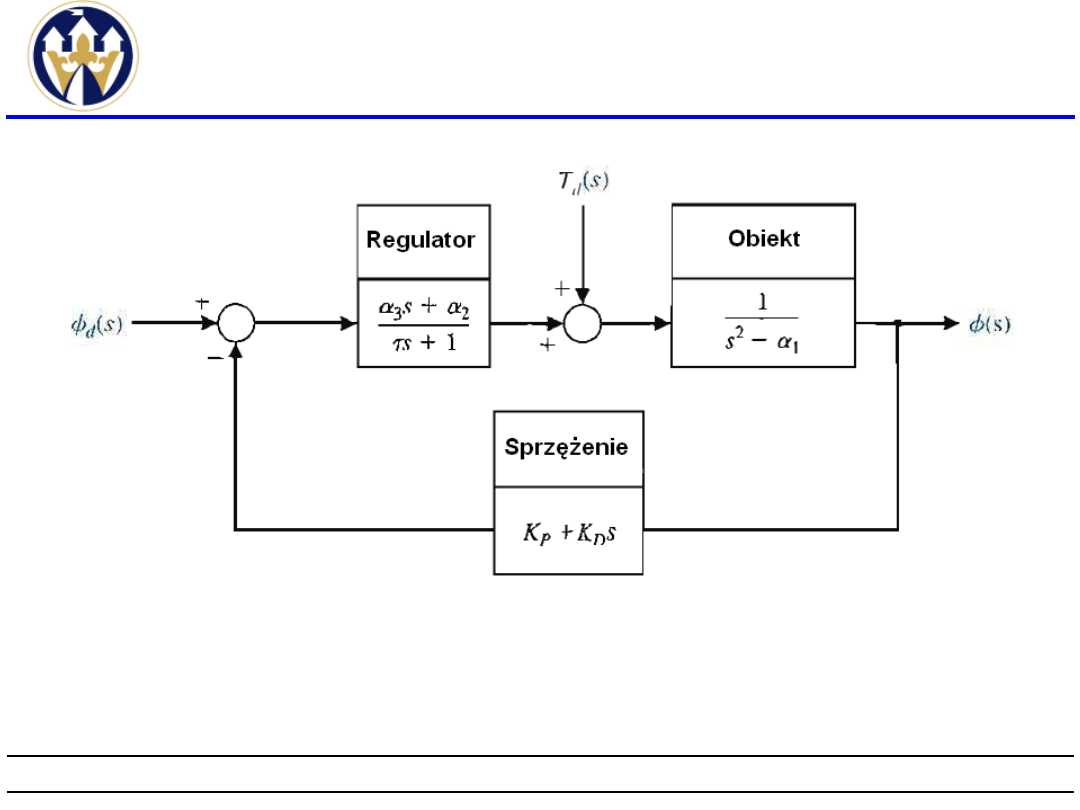
Przykład badania

stabilności(4)

Schemat układu zamkniętego dla modelu

motocykla sterowanego robotem.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

40

Przykład badania

stabilności(5)

Wartości parametrów fizycznych dla modelu

motocykla sterowanego robotem.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

41

Przykład badania

stabilności(6)

Funkcja przejścia układu zamkniętego wynosi:

gdzie:

Równanie charakterystyczne to:

Należy wyznaczyć dla jakich wartości K

P

i K

D

pierwiastki

równania

charakterystycznego

znajdują się w lewej półpłaszczyźnie.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

42

Przykład badania

stabilności(7)

Na podstawie Kryterium Routha:

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

43

Przykład badania

stabilności(8)

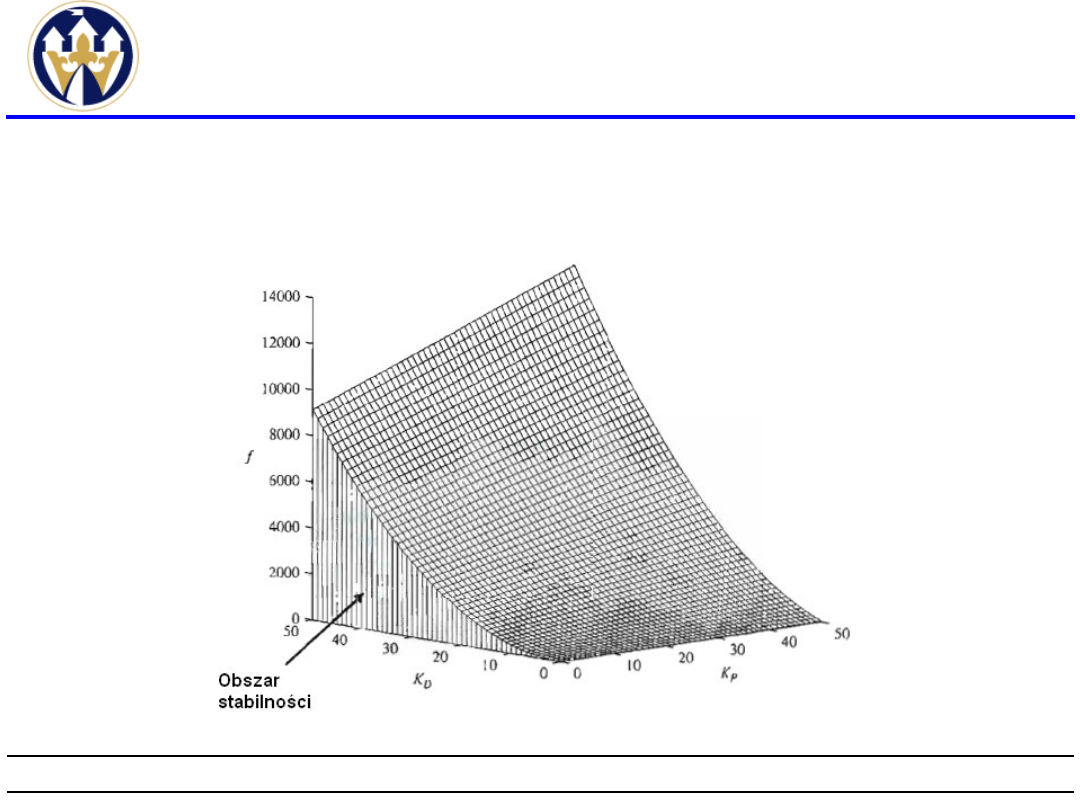
Po uwzględnieniu wszystkich warunków obszar

stabilności występuje przy K

D

>0 i K

P

>3,33.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

44

Stabilność obiektów

nieliniowych(1)

Cechy obiektów nieliniowych mogą zależeć

od poziomu sygnałów zewnętrznych. Jednemu

poziomowi sterowania może odpowiadać jeden,

dwa, lub więcej stanów równowagi.

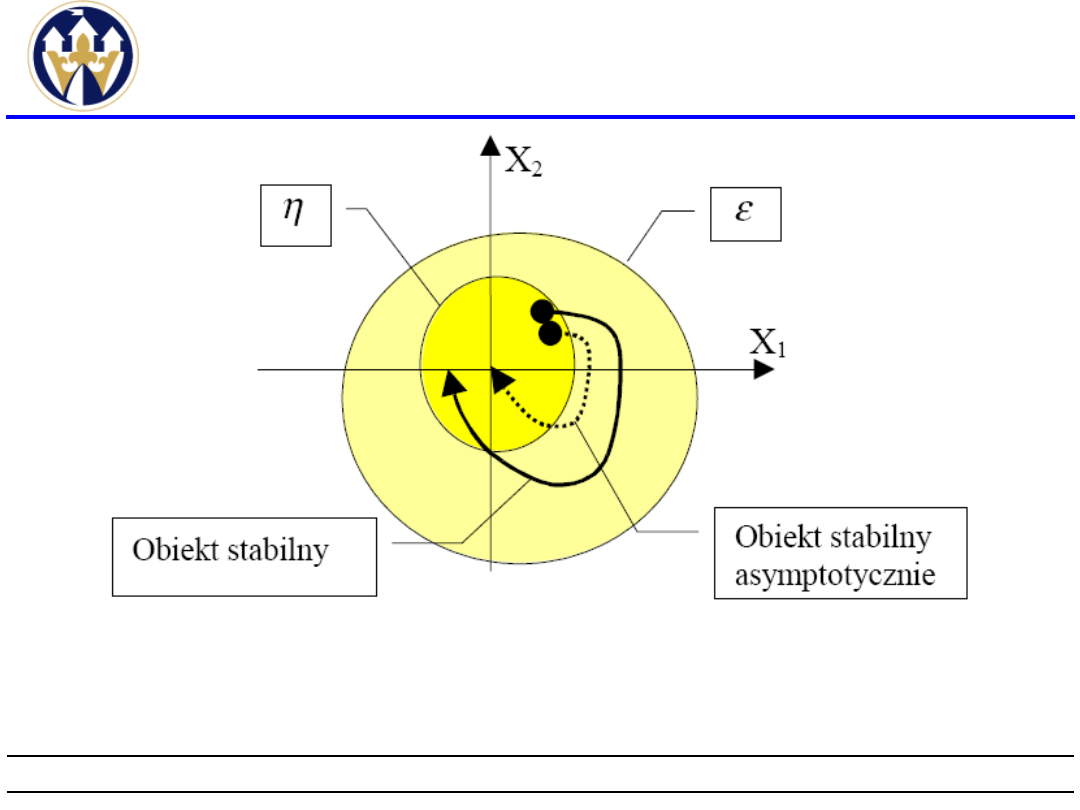
Do oceny stabilność punktu równowagi

posługuje się definicją stabilności lokalnej

Lapunowa: punkt równowagi nazywamy

stabilnym, jeżeli dla każdego, dowolnie małego

obszaru ε odchyleń od stanu równowagi można

dobrać taki obszar η warunków początkowych,

że cała trajektoria startująca z obszaru η

będzie zawarta w obszarze ε. Jeżeli dodatkowo

trajektoria zmierza do wymienionego punktu

równowagi to stan równowagi w tym punkcie

nazywamy stabilnym asymptotycznie.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

45

Stabilność obiektów

nieliniowych(2)

Definicja Lapunowa dla obiektu nieliniowego

drugiego rzędu.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

46

Projektowanie liniowych

układów regulacji(1)

Projektowanie

układu

wymaga

przeanalizowania wymogów przejściowych.

Charakter

przebiegów

przejściowych

w

liniowych układach sterowania w dziedzinie

czasu jest badany po podaniu funkcji skokowej

(jednostkowej) 1(t) na wejście układu.

Na podstawie tej odpowiedzi definiowane są

następujące wskaźniki jakości w stanie

przejściowym:

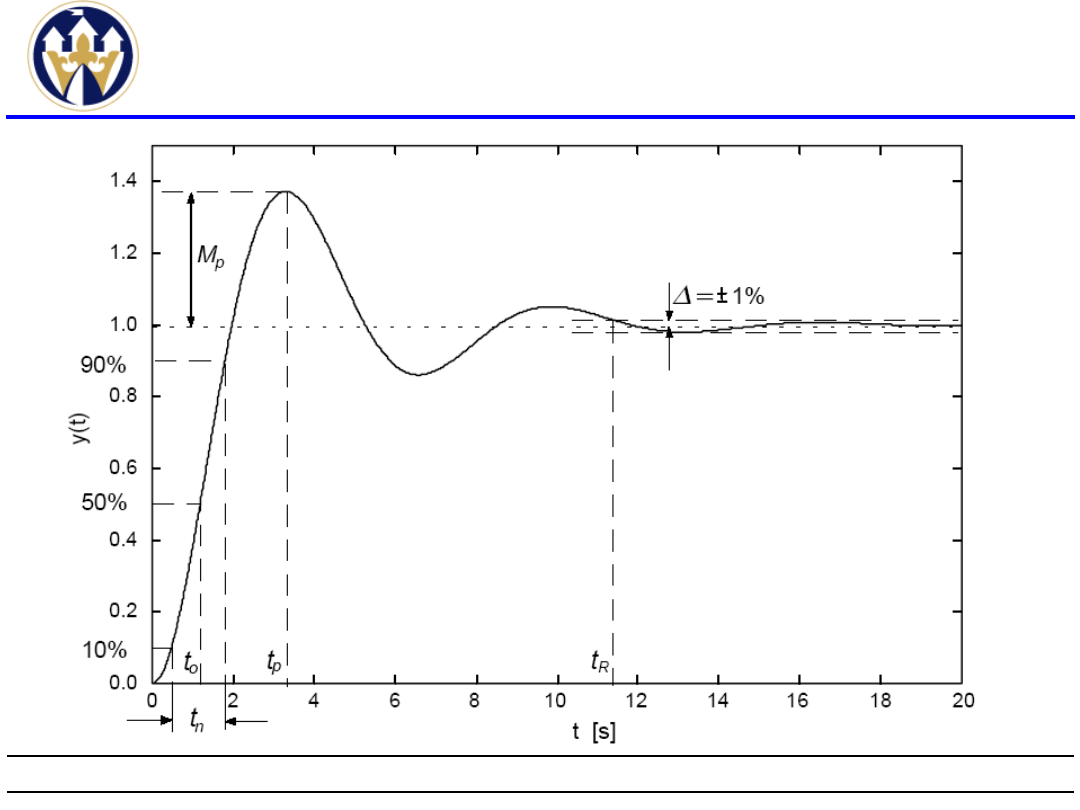
Maksymalne przeregulowanie M

p

M

p

= y

max

− y

u

gdzie:

y(t) − odpowiedź skokowa układu,

y

max

− maksymalna wartość y(t),

y

u

− wartość y(t) w stanie ustalonym (y

u

≤

y

max

).

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

47

Projektowanie liniowych

układów regulacji(2)

Czas opóźnienia t

o

definiowany jako czas po

którym odpowiedź skokowa osiąga 50% swojej

wartości końcowej.

Czas narastania t

n

definiowany jest jako czas

potrzebny do wzrostu odpowiedzi skokowej

układu od 10% do 90% wartości ustalonej.

Czas ustalania (regulacji) t

R

definiowany

jako czas potrzebny do tego aby przejściowa

odpowiedź skokowa znalazła się i pozostała w

pewnej określonej strefie dokładności (% 1 ± ,

% 2 ± , itd.) od wartości ustalonej. Najczęściej

jest to 5% wartości ustalonej.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

48

Projektowanie liniowych

układów regulacji(3)

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

49

Projektowanie liniowych

układów regulacji(4)

Wskaźniki jakości w stanie ustalonym:

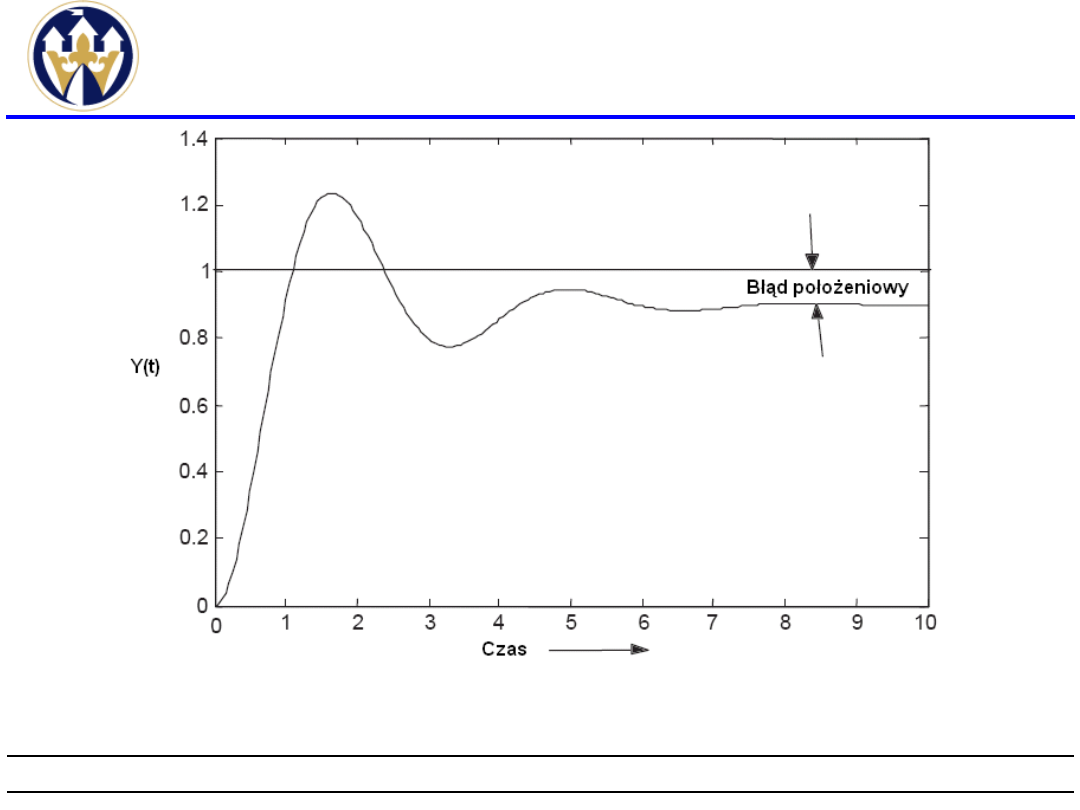
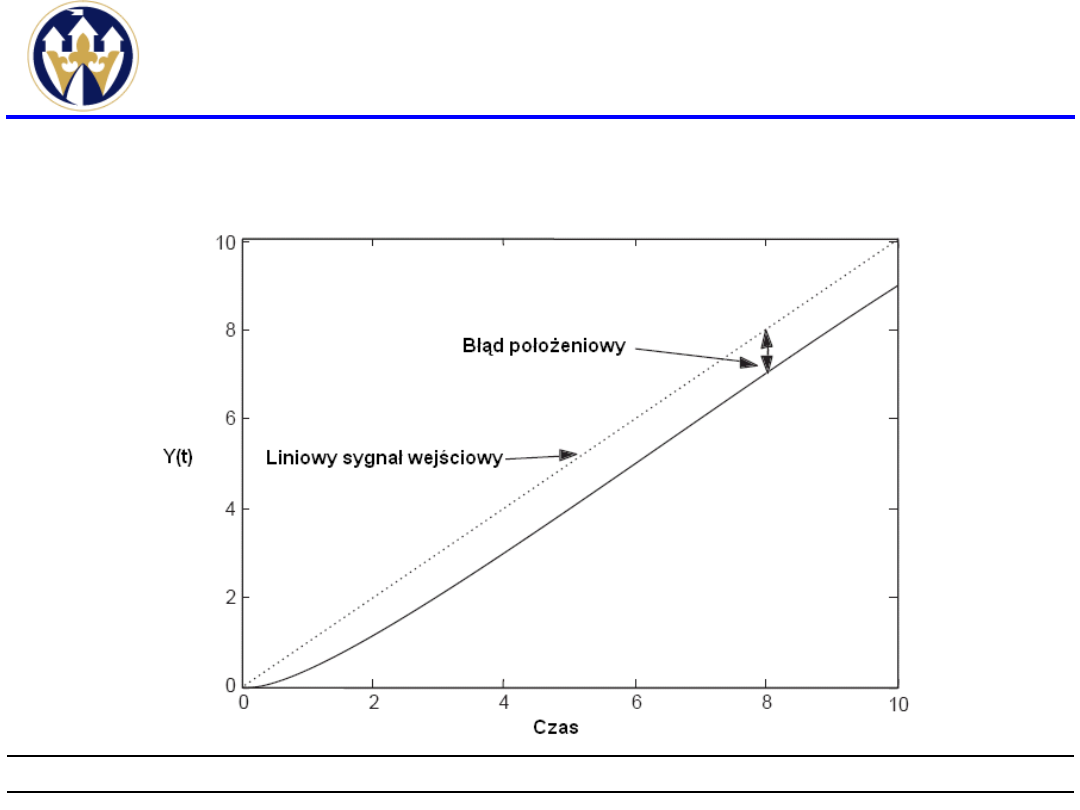
Błąd statyczny e

u

Przez błąd statyczny (zwany również błędem

położeniowym) rozumiemy wielkość błędu,

który

pozostaje

po

zaniku

stanów

dynamicznych. W układzie liniowym poziom

danego sygnału jaki odpowiada nowemu

stanowi równowagi, po zmianach wielkości

wejściowych, możemy wyliczyć na podstawie

znajomości transformat sygnałów wejściowych

i transmitancji łączących te sygnały z

interesującym nas wyjściem.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

50

Projektowanie liniowych

układów regulacji(5)

Przy analizowaniu układu automatyki, ze

sprzężeniem

zwrotnym

wpływ

sygnału

zadanego w(t) i zakłócenia z(t) można

rozpatrywać oddzielnie, co oznacza, że błąd

położeniowy jest sumą dwóch składowych i

wynosi:

gdzie:

e

wu

- błąd położeniowy wywołany zmianą

sygnału wymuszającego przy z(t)=0

e

zu

- błąd położeniowy wywołany zmianą

zakłócenia przy w(t)=0

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

51

Projektowanie liniowych

układów regulacji(6)

Odpowiedź na skok jednostkowy z

zaznaczonym błędem położeniowym.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

52

Projektowanie liniowych

układów regulacji(7)

Błąd prędkościowy e

v

czyli błąd w stanie

ustalonym przy wymuszeniu sygnałem liniowo

narastającym.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

53

Projektowanie liniowych

układów regulacji(8)

W projektowaniu liniowych układów sterowania

z użyciem metod w dziedzinie częstotliwości,

konieczne jest zdefiniowanie zbioru nowych

wskaźników jakości układu.

Najczęściej używane wskaźniki w dziedzinie

częstotliwości:

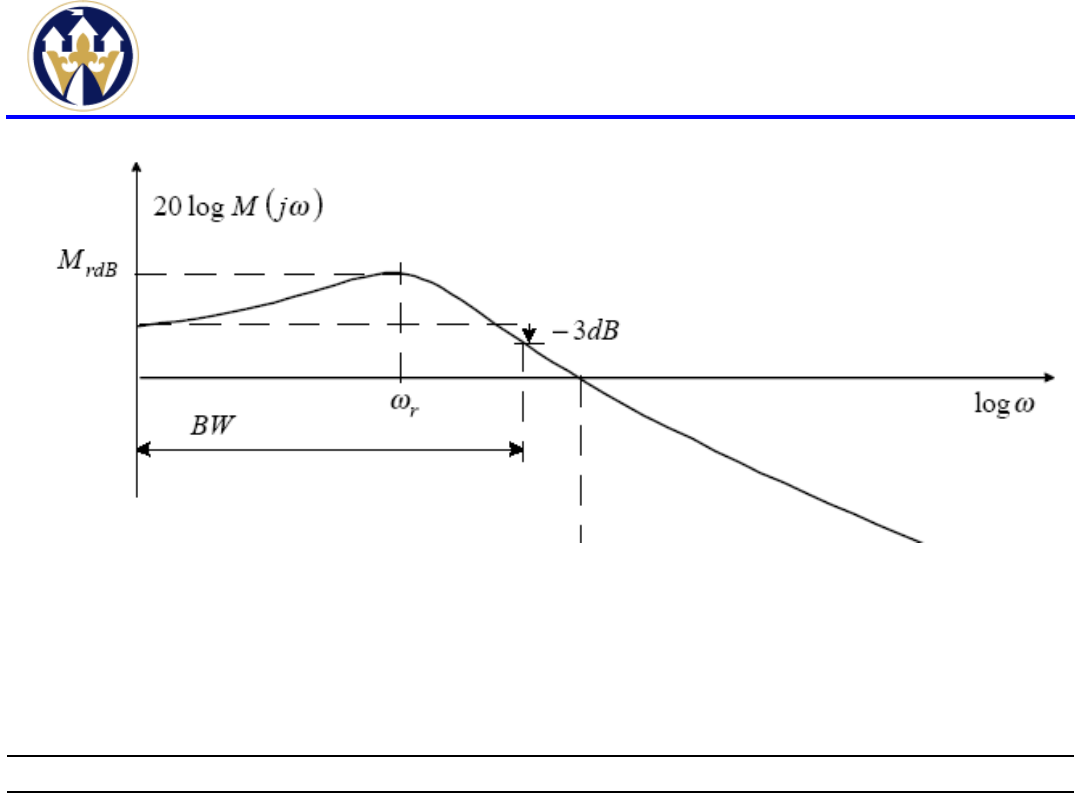
Moduł rezonansowy M

rdB

wyrażony w

decybelach (dB) jest maksymalną wartością

charakterystyki

amplitudowej

20logM(jω).

Amplituda

M

rdB

pozwala

na

określenie

stabilności

względnej

stabilnego

układu

zamkniętego. Zazwyczaj duże wartości M

rdB

odpowiadają

dużym

wartościom

maksymalnego przeregulowania odpowiedzi

skokowej.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

54

Projektowanie liniowych

układów regulacji(9)

Częstotliwość

rezonansowa

ω

r

jest

częstotliwością przy której występuje moduł

rezonansowy.

Szerokość pasma BW (pasmo przenoszenia)

jest zakresem częstotliwości od zera do

częstotliwości (zwanej częstotliwością odcięcia)

przy której charakterystyka amplitudowa

20logM(jω) różni się o conajmniej 3 dB od jego

amplitudy przy zerowej częstotliwości. Pasmo

BW określa szybkość odpowiedzi układu i

wzrost

częstotliwości

odcięcia

powoduje

zwiększenie szybkości odpowiedzi układu.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

55

Projektowanie liniowych

układów regulacji(10)

Przykładowa logarytmiczna charakterystyka

amplitudy.

UKW, dr ing. Sebastian Kula 2010

Podstawy Automatyki

56

•Thank you !

•Vielen Dank !

•Cпасибо !

•Dziękuje !