Problem Transportowy

Metoda NW

(Pn.- Zach. Kąta)

mkw

Dane:

• Liczba producentów: 3 [ P1, P2, P3] dysponujących odpowiednio
zasobami

[46, 34, 40]

• Liczba odbiorców: 4 [O1, O2, O3, O4] o zapotrzebowaniu
odpowiednio

[40, 35, 30, 15]

Zadanie jest zbilansowane: (46+34+40) = (40+35+30+15)

Mamy jak najmniejszym kosztem porozwozić wszystkie zasoby,
znając koszty drogi od danego producenta do każdego odbiorcy.
Koszty te zostały zestawione w tabeli.

Macierz kosztów jednostkowych

4

3

2

5

1

1

6

4

3

5

9

4

Zestawienie danych zadania w postaci

tabelki

40

35

30

15

O1

O1

O2

O2

O3

O3

O4

O4

4

3

2

5

P1

P1

46

1

1

6

4

P2

P2

34

3

5

9

4

P3

P3

40

Odbiorcy

produce
nci

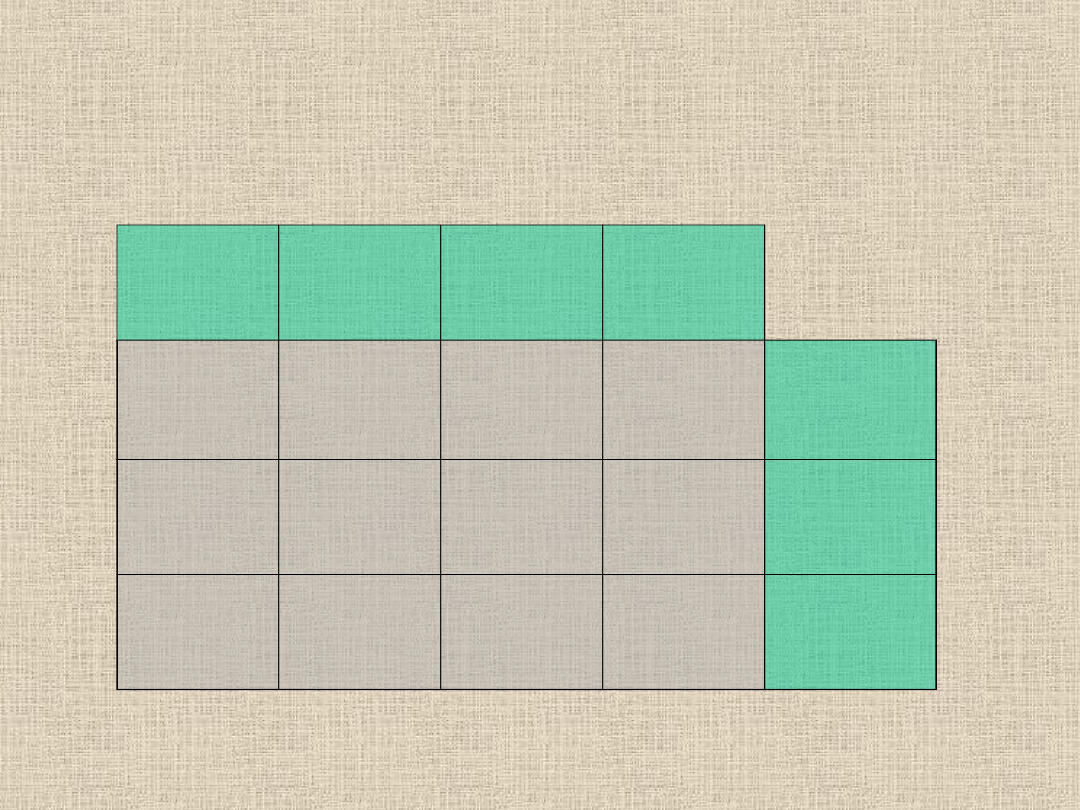
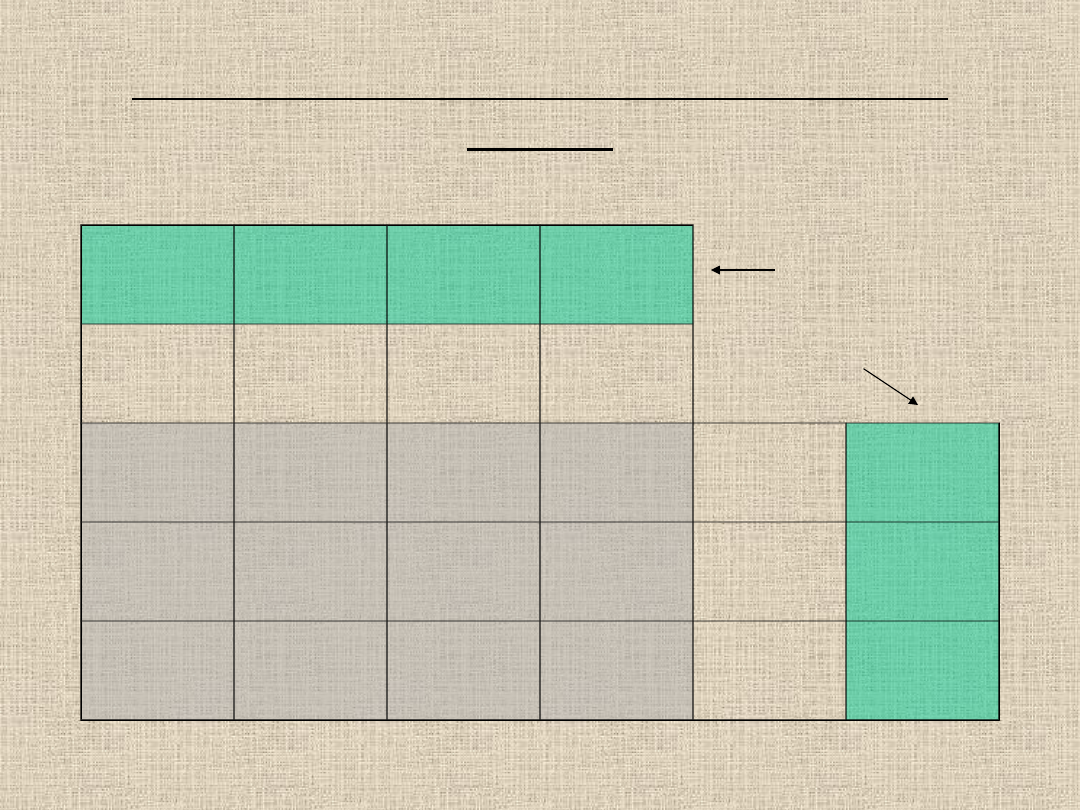
Czysta tabela o wymiarze n-wierszy i m-kolumn gdzie n-
liczba producentów, m- liczba odbiorców.

40

35

30

15

46

34

40

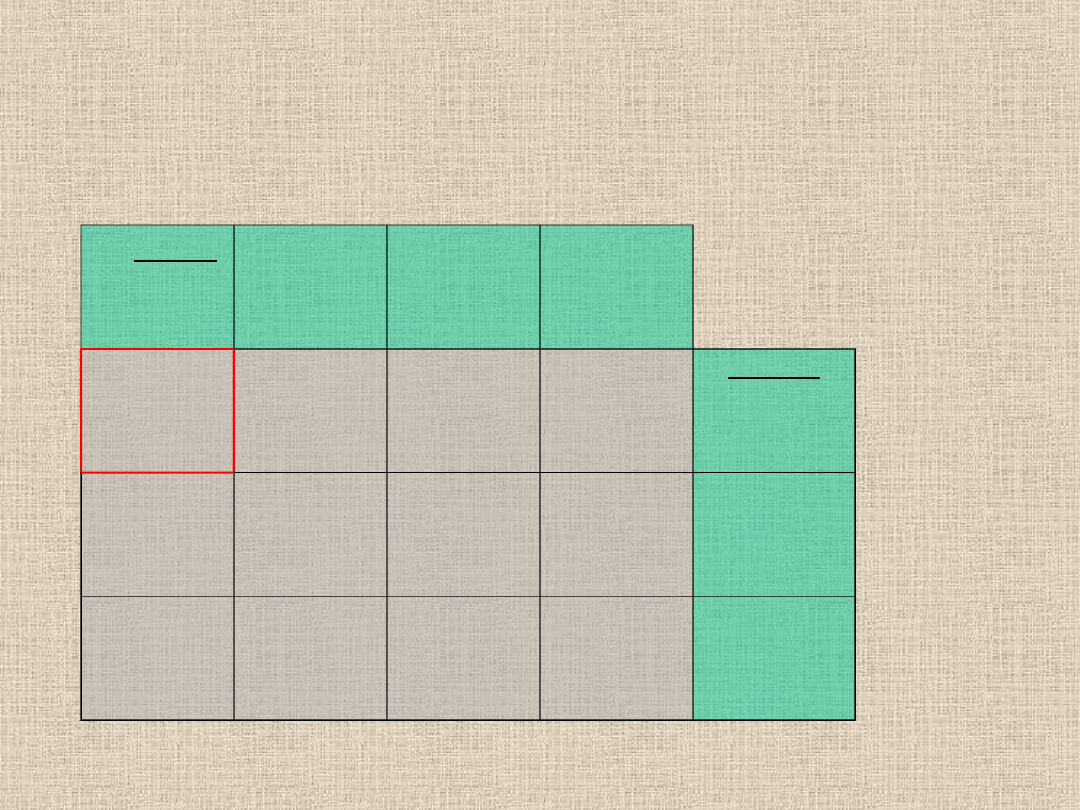
40-40=0

40

35

30

15

40

46

0

34

0

40

46-
40=6

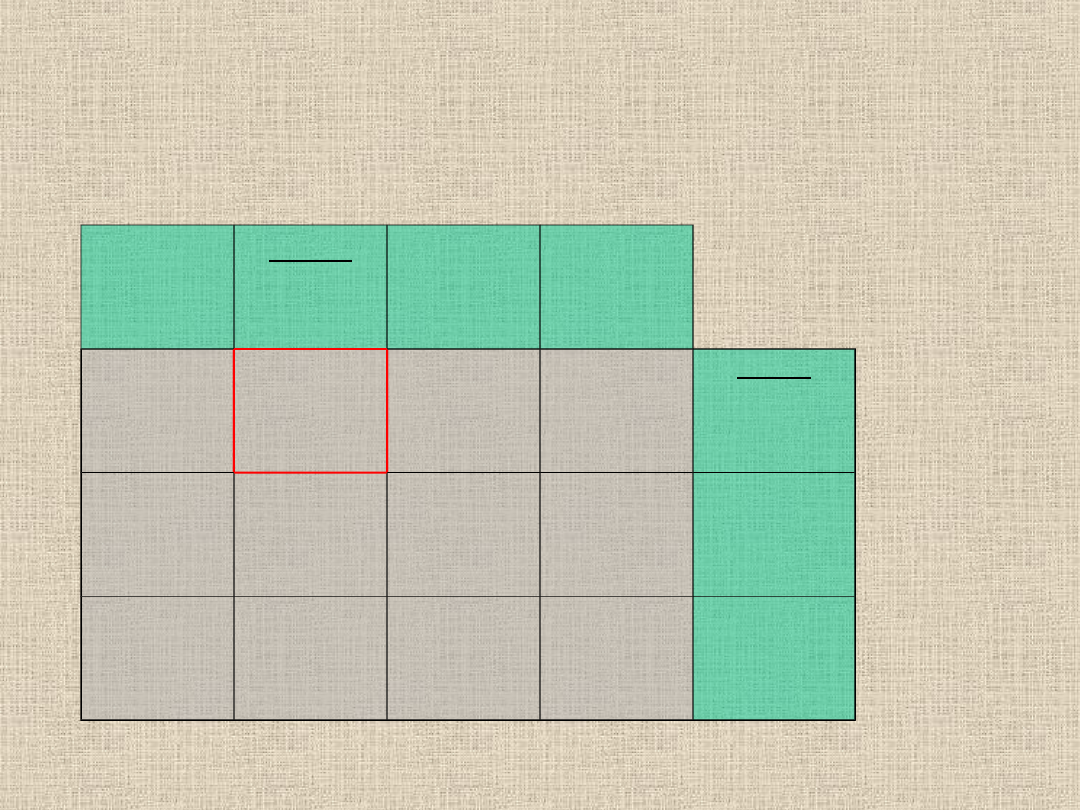
0

35

30

15

40

6

0

0

6

0

34

0

40

6-6=0

35-
6=29

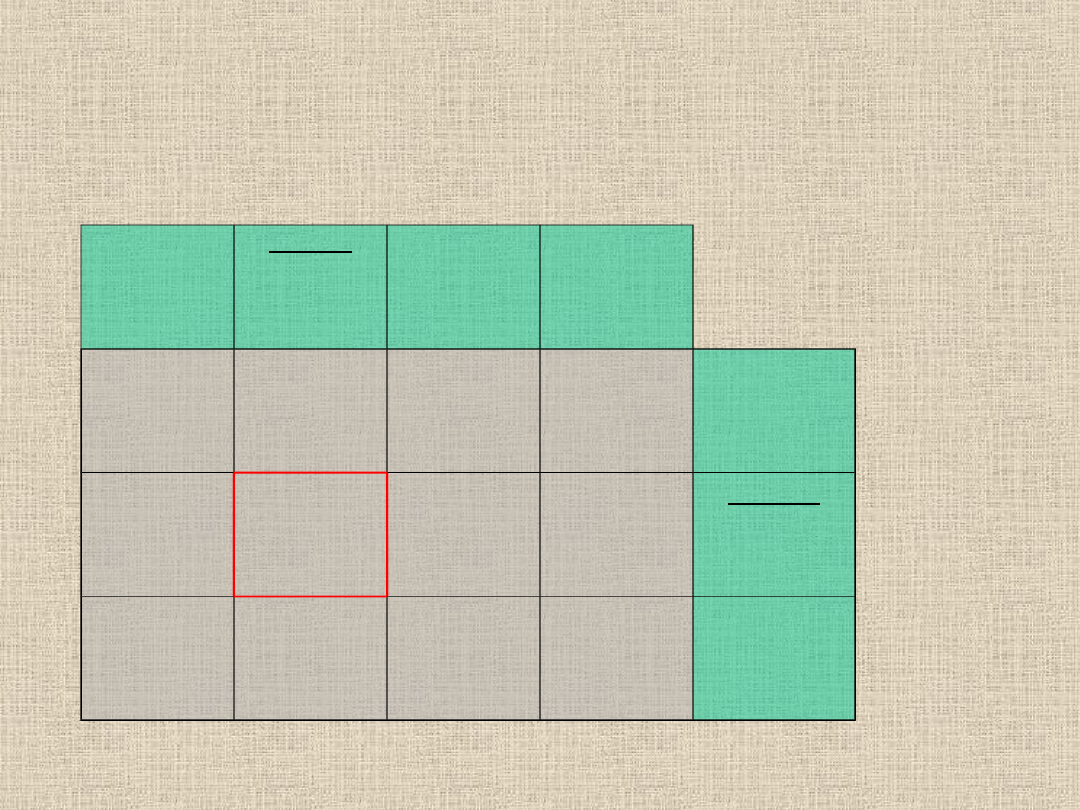
0

29

30

15

40

6

0

0

0

0

29

34

0

0

40

29-
29=0

34-
29=5

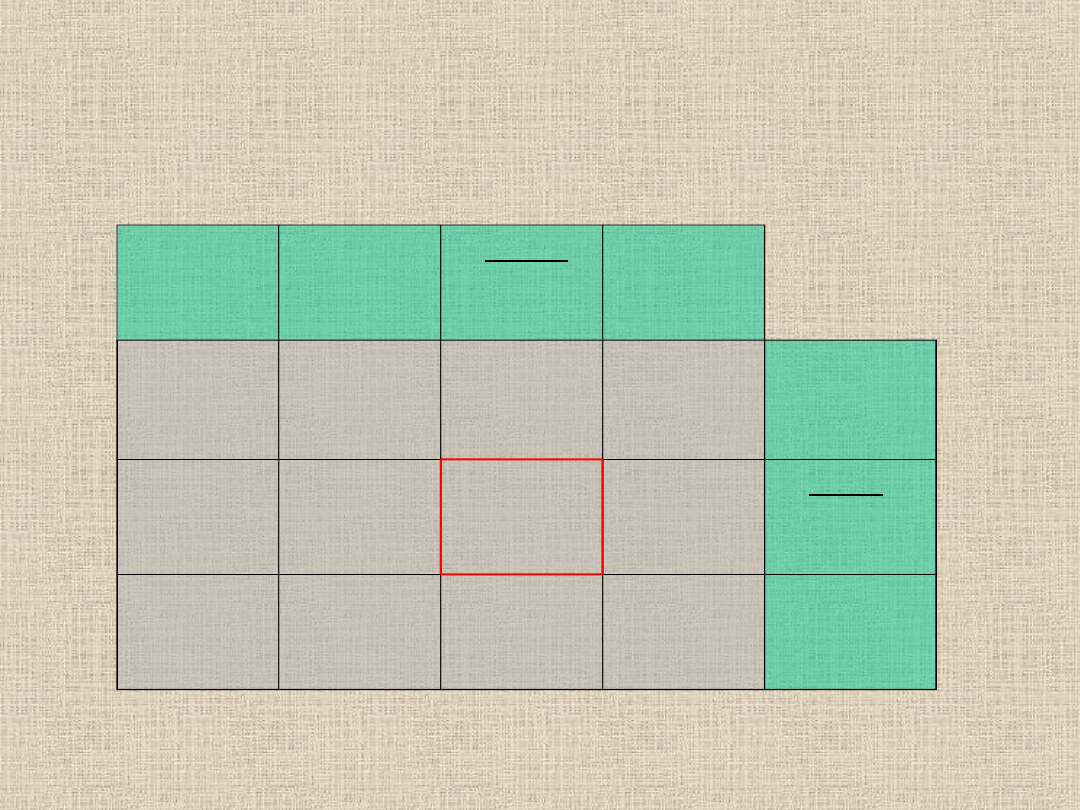
0

0

30

15

40

6

0

0

0

0

29

5

0

5

0

0

40

30-
5=25

5-
5=0

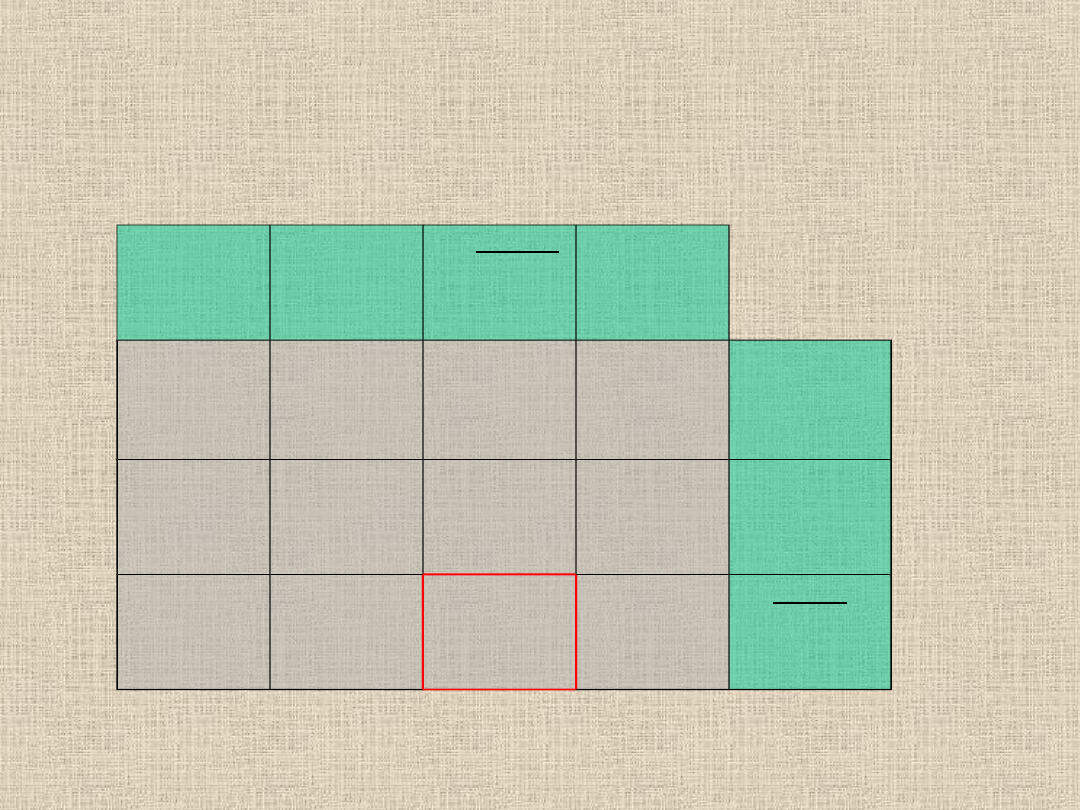
0

0

25

15

40

6

0

0

0

0

29

5

0

0

0

0

25

40

25-
25=0

40-
25=15

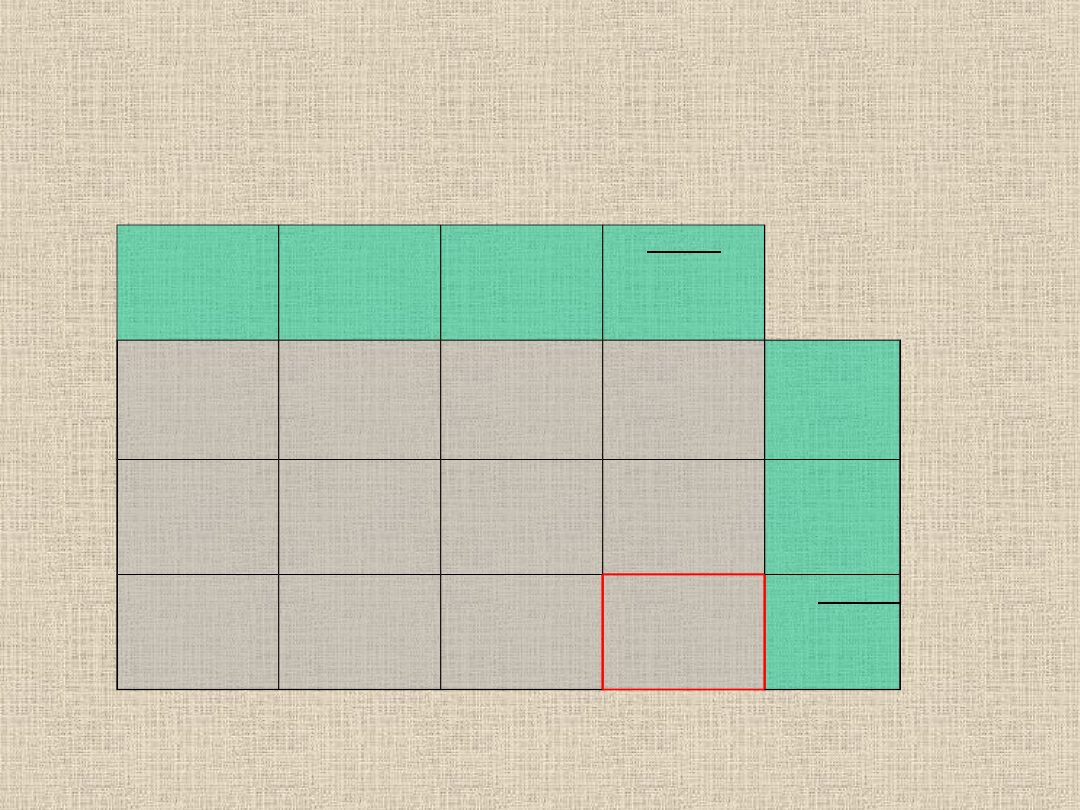
0

0

0

15

40

6

0

0

0

0

29

5

0

0

0

0

25

15

15

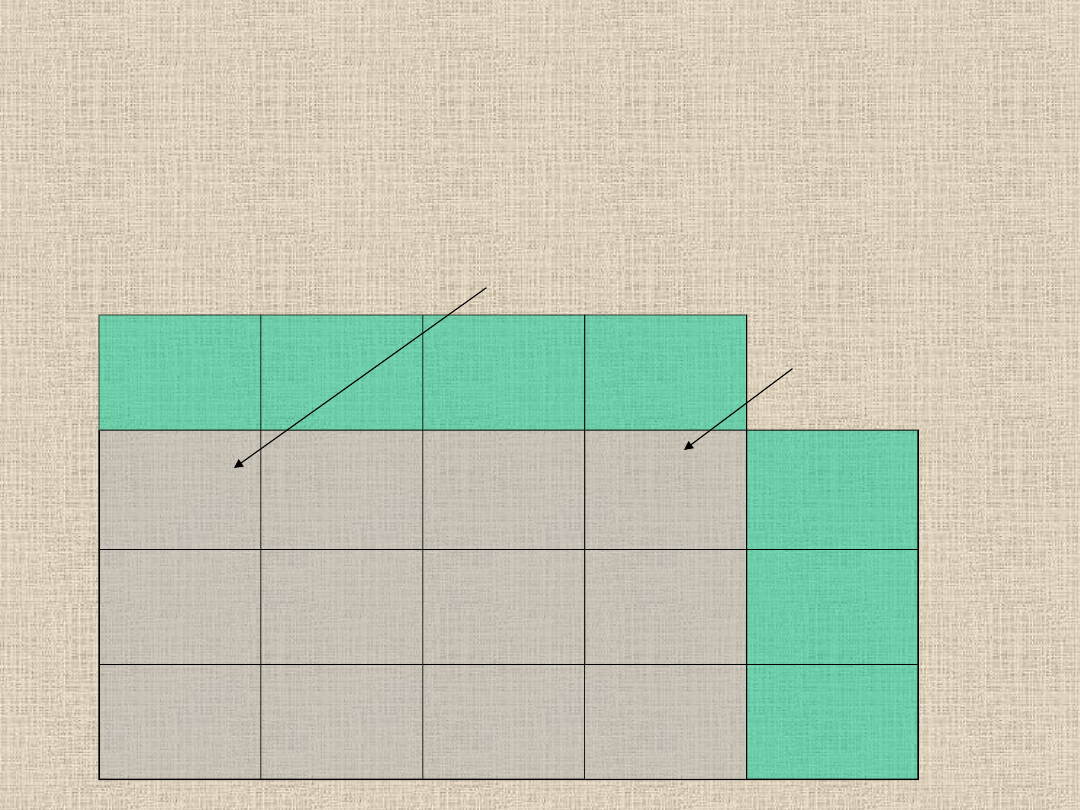
Wartość podaży i popytu dla ostatniego elementu
zawsze powinna być taka sama. Tabelka po tym
kroku powinna mieć wszystkie wartości popytu i
podaży równe zero.

15-
15=0

15-
15=0

0

0

0

0

40

6

0

0

0

0

29

5

0

0

0

0

25

15

0

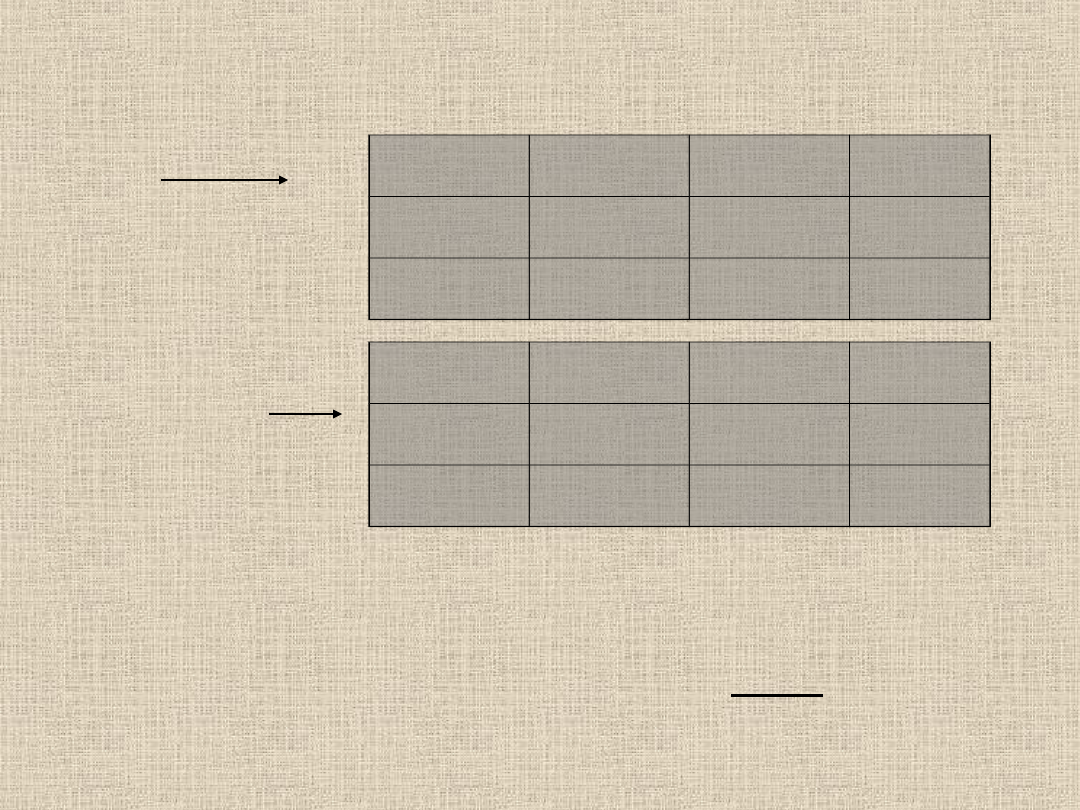
W ten sposób uzyskaliśmy rozwiązanie dopuszczalne. Wszystkie
zerowe elementy rozwiązania nazywamy elementami
niebazowymi. Natomiast elementami bazowymi nazywamy
wszystkie elementy niezerowe. Przy czym el. bazowych powinno
być m+n-1 (4+3-1=6), wówczas rozwiązanie nazywamy
zdegenerowanym.

El. bazowe

El.
niebazowe

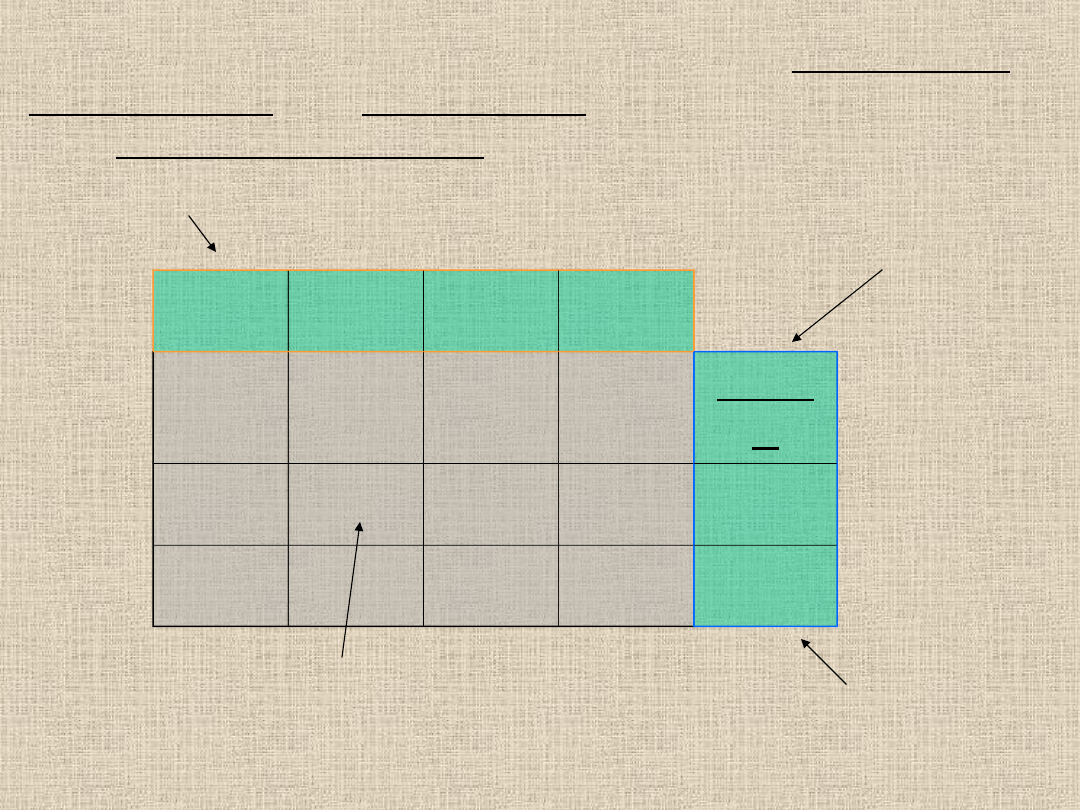
Koszt jaki uzyskaliśmy stosując tą metodę.

4

3

2

5

1

1

6

4

3

5

9

4

40

6

0

0

0

29

5

0

0

0

25

15

Koszt rozwiązania:

4*40+3*6+1*29+6*5+9*25+4*15=

522

koszty

Rozwiązanie

dopuszczalne

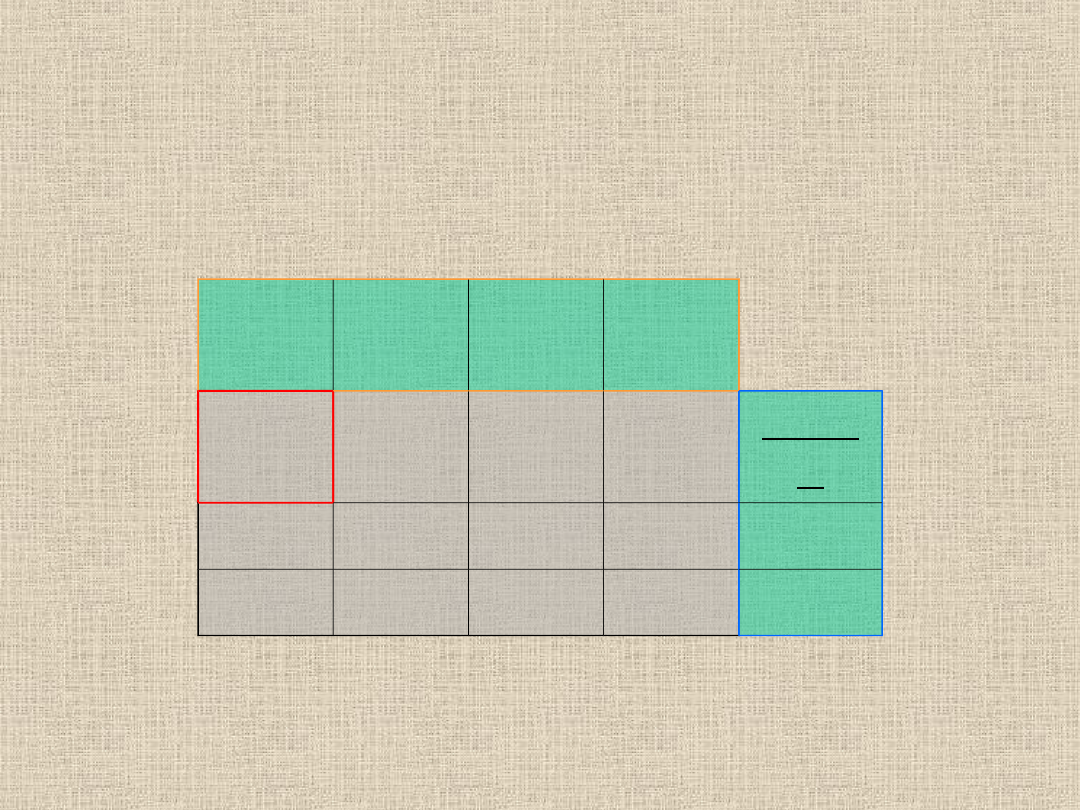
Przystępujemy do sprawdzenia czy nasze rozwiązanie
dopuszczalne jest optymalnym. Posłużymy się w tym
celu metodą potencjałów.

4

3

U1=

0

1

6

9

4

Potencjały V

Potencjały U

Koszty (tylko w miejscach baz)

Ustawiamy
U1=0

V1=

4
4

3

U1=

0

1

6
9

4

V1=4-
0

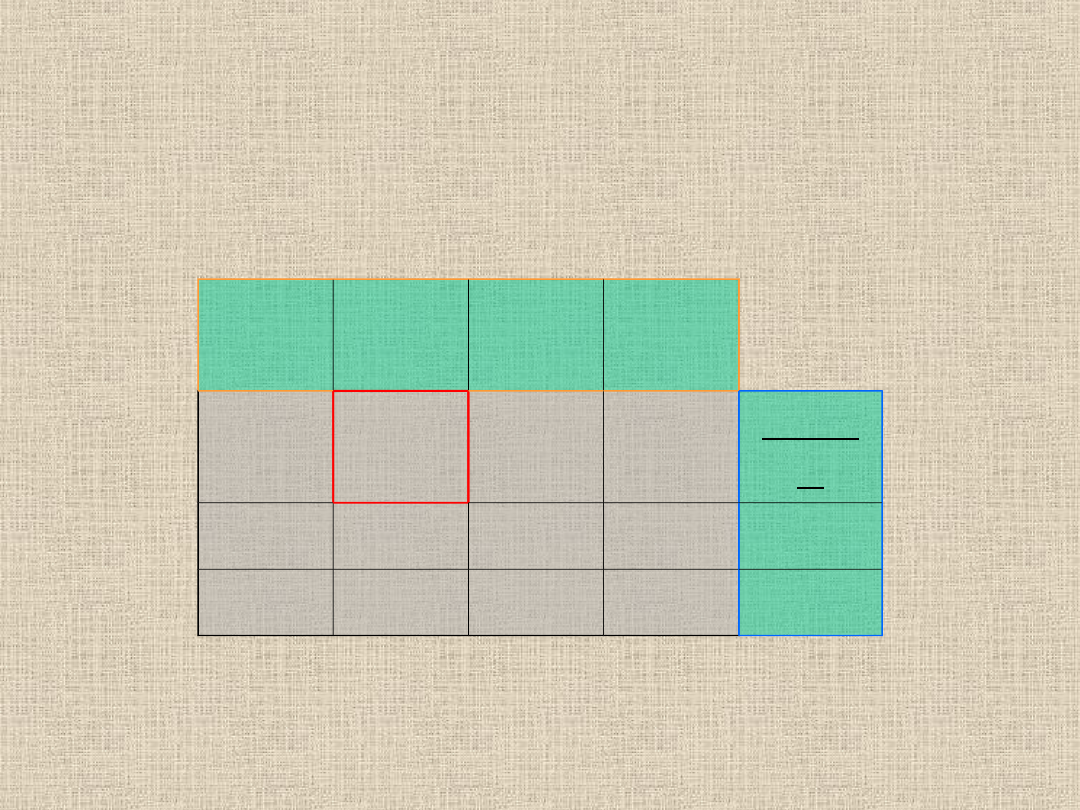
Mamy na wejście ustawioną wartość potencjału U1 = 0, więc szukamy w
wierszu odpowiadającym temu U1 (czyli w pierwszym wierszu) kosztu - jest
nim koszt = 4 w pierwszej komórce. Następnie w potencjał V odpowiadający
znalezionemu kosztowi (czyli V1) wpisujemy wartość równą różnicy kosztu i
potencjału U1 (V1=4-0=4).

V1=

4

V2=

3

4

3

U1=

0

1

6
9

4

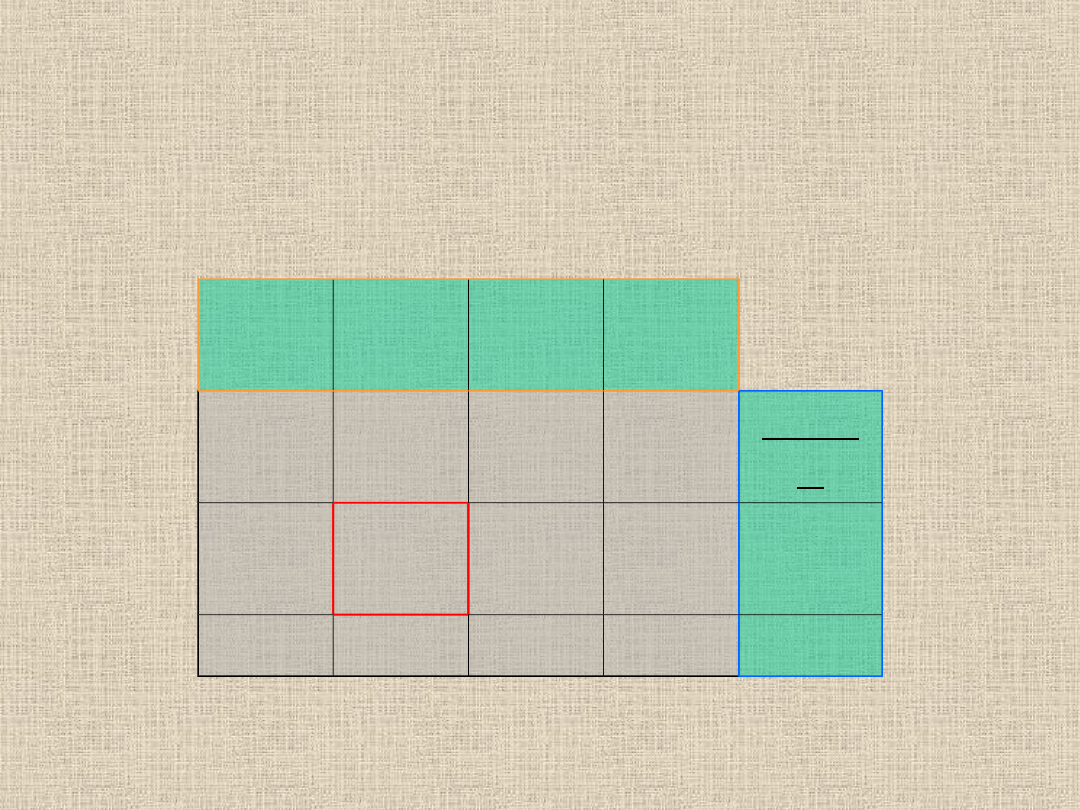
V2=3-0

V1=

4

V2=

3

4

3

U1=

0

1

6

U2=-

2

9

4

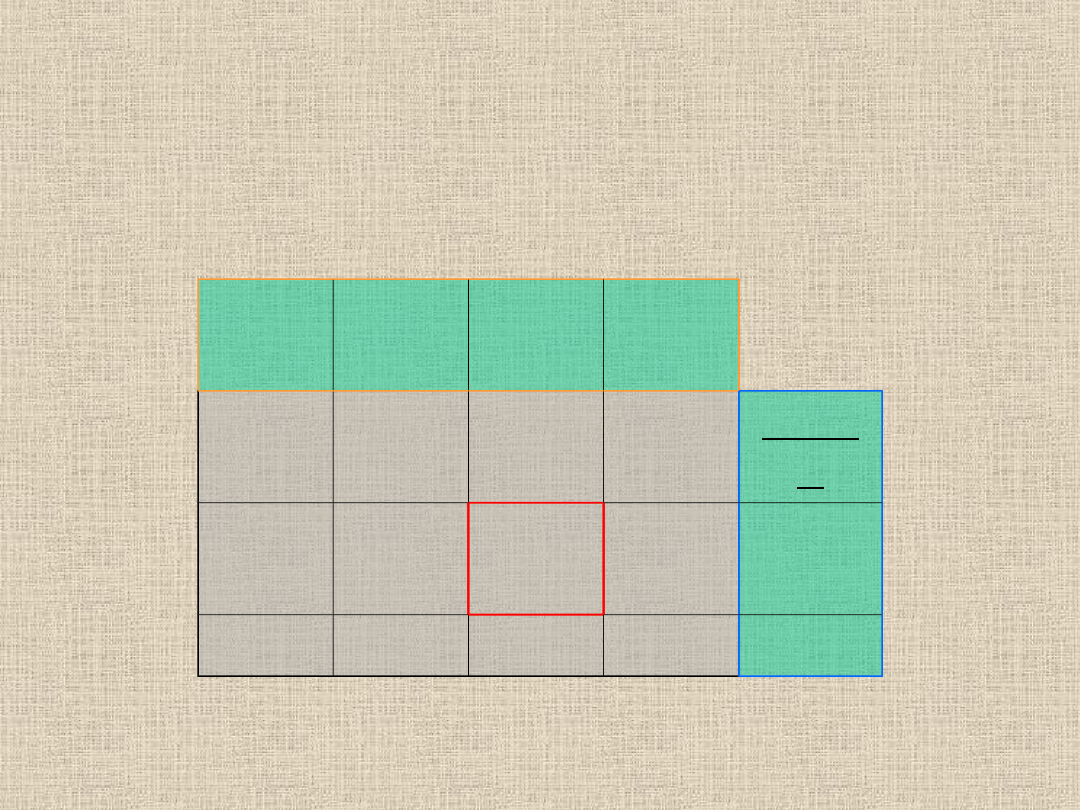
U2=1-3

V1=

4

V2=

3

V3=

8

4

3

U1=

0

1

6

U2=-

2

9

4

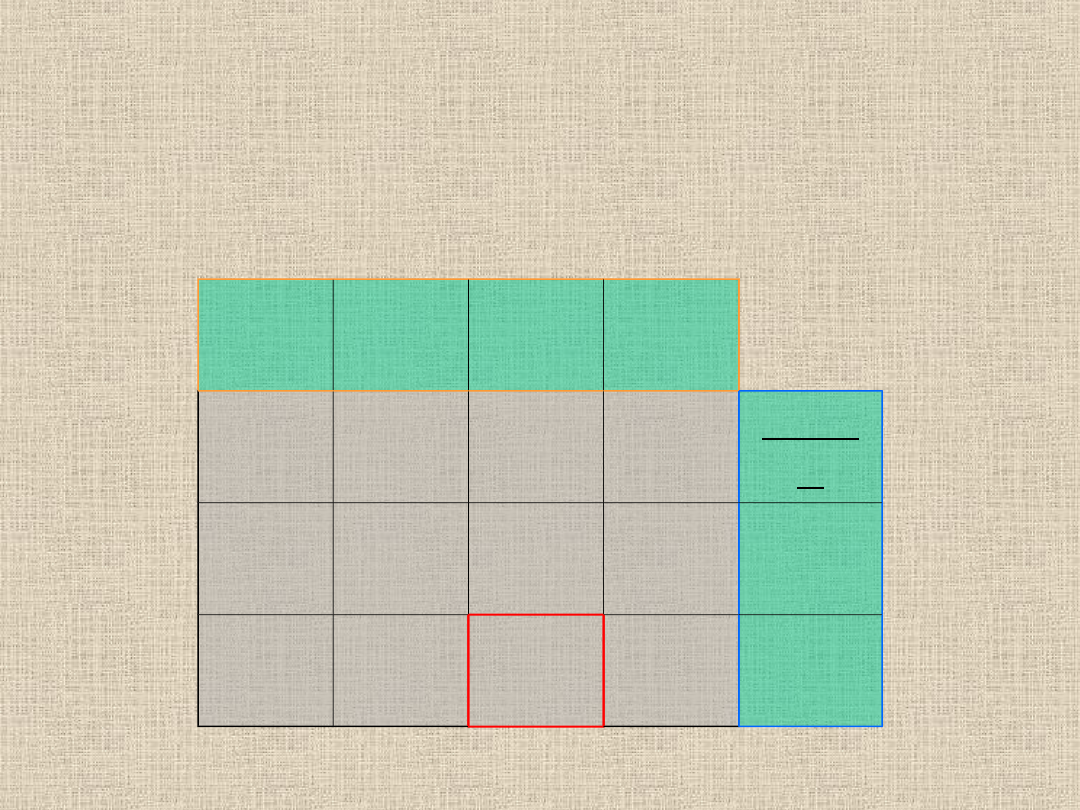
V3=6-(-
2)

V1=

4

V2=

3

V3=

8

4

3

U1=

0

1

6

U2=-

2

9

4

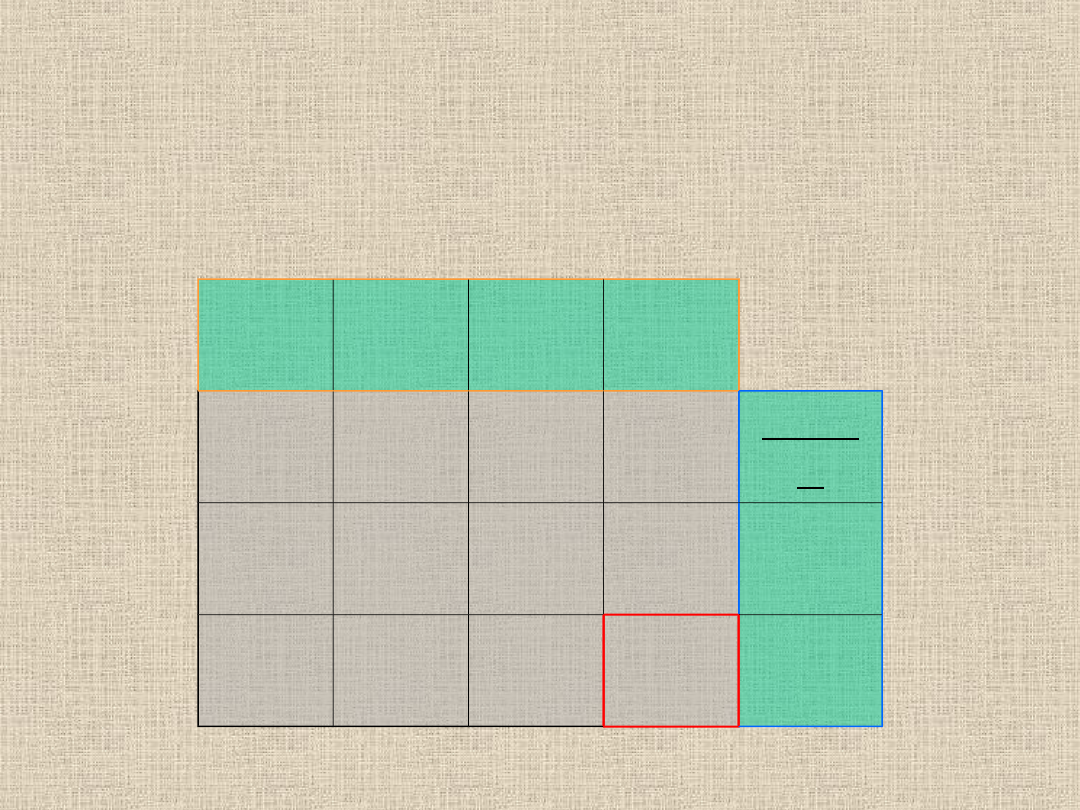
U3=

1

U3=9-8

V1=

4

V2=

3

V3=

8

V4=

3

4

3

U1=

0

1

6

U2=-

2

9

4

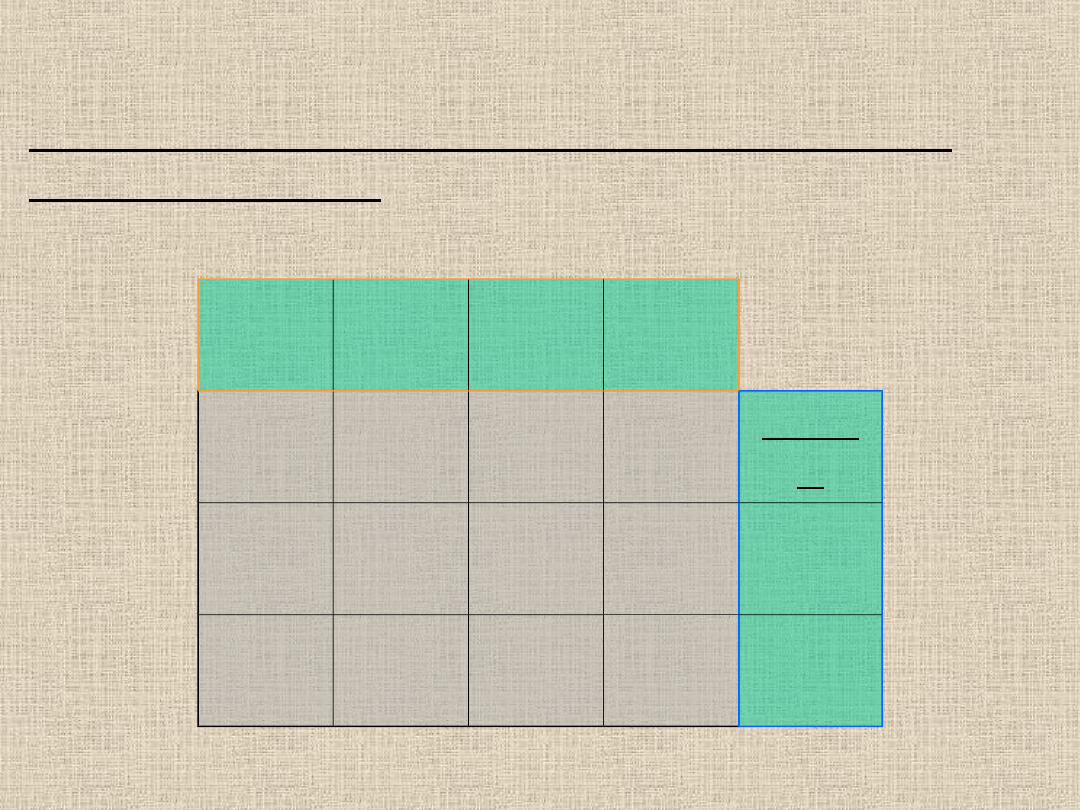
U3=

1

V4=4-1

V1=

4

V2=

3

V3=

8

V4=

3

4

3

U1=

0

1

6

U2=-

2

9

4

U3=

1

Poniższa tabelka przedstawia już wyliczone
potencjały U i V

V1=

4

V2=

3

V3=

8

V4=

3

4

3

8+0=8

3+0=3

U1=

0

4+(-2)=2

1

6

3+(-2)=1

U2=-

2

4+1=5

3+1=4

9

4

U3=

1

Kolejnym krokiem jest wyliczenie kosztów
pośrednich.
Należy pozostałe (puste) komórki tabelki z wynikami
wypełnić sumami potencjału Vi i Uj

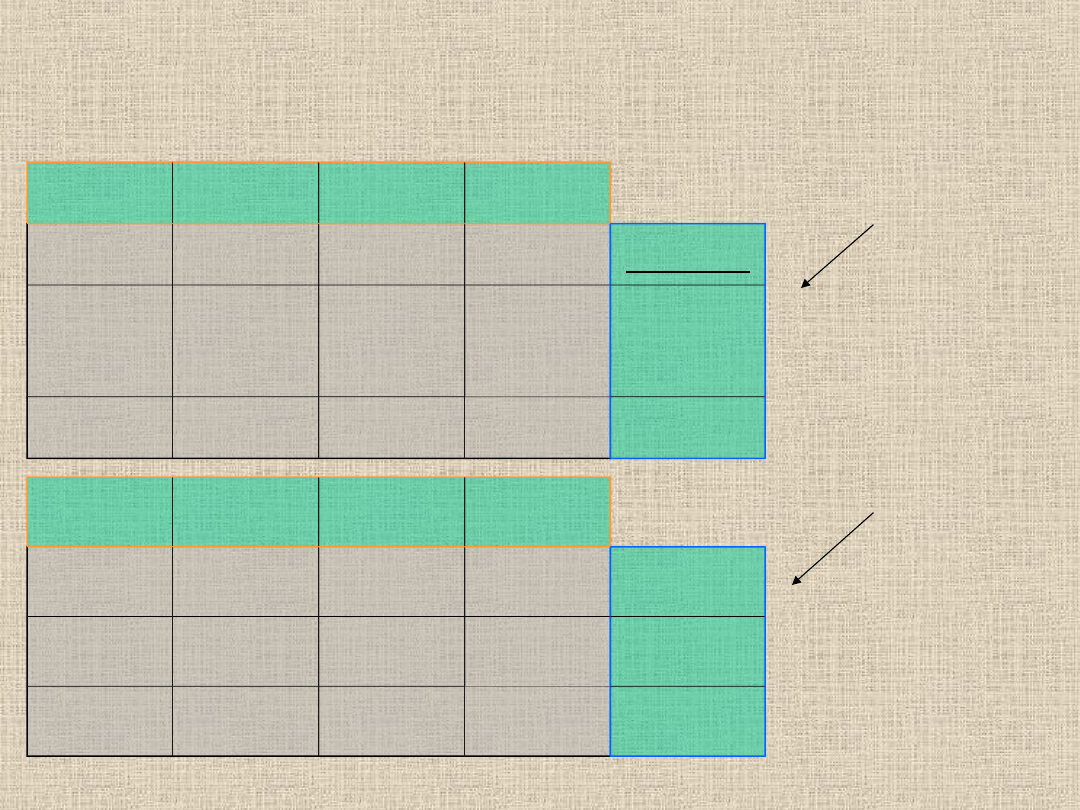
Następnie wyliczamy wskaźniki optymalności.
W tym celu zestawmy obok siebie dwie tabelki: tabelkę
obliczonych przed chwilą kosztów pośrednich i tabelkę
kosztów z początku zadania

V1=4 V2=3 V3=8 V4=3

4

3

8

3

U1=0

2

1

6

1

U2=-

2

5

4

9

4

U3=1

40

35

30

15

4

3

2

5

46

1

1

6

4

34

3

5

9

4

40

Koszty

pośrednie

Koszty

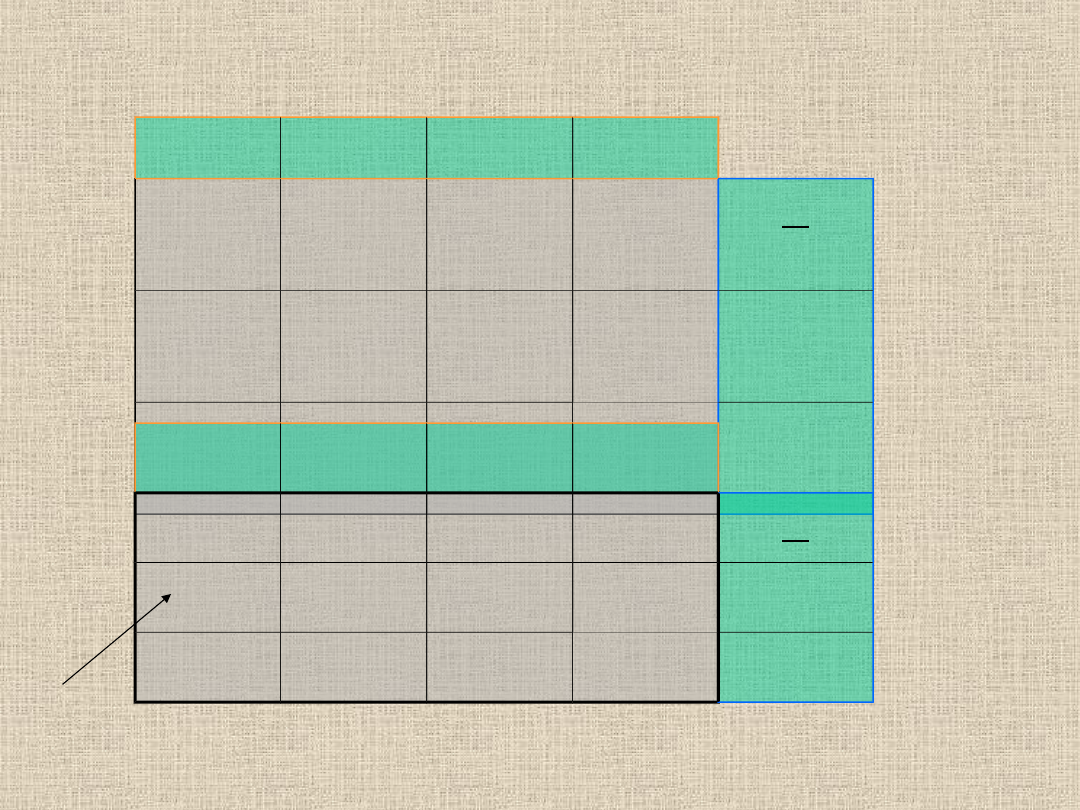
Wskaźniki optymalności wyliczamy odejmując od kosztów
pośrednich koszty.

4

3

8

3

4-

4=0

3-

3=0

8-

2=6

3-5=-

2

0

2-

1=1

1-

1=0

6-

6=0

1-4=-

3

-2

5-

3=2

4-5=-

1

9-

9=0

4-

4=0

1

V

U

4

3

8

3

0

0

6

-2

0

1

0

0

-3

-2

2

-1

0

0

1

V

U

Wskaźniki optymalności

Jeżeli wśród wskaźników optymalności znajdują się liczby
dodatnie wówczas rozwiązanie nie jest rozwiązaniem
optymalnym.
Rozwiązanie jest więc optymalne kiedy wszystkie liczby
są niedodatnie.

Następnym etapem jest więc budowa cyklu w celu
uzyskania rozwiązania dopuszczalnego o niższym koszcie
a w rezultacie rozwiązania optymalnego.

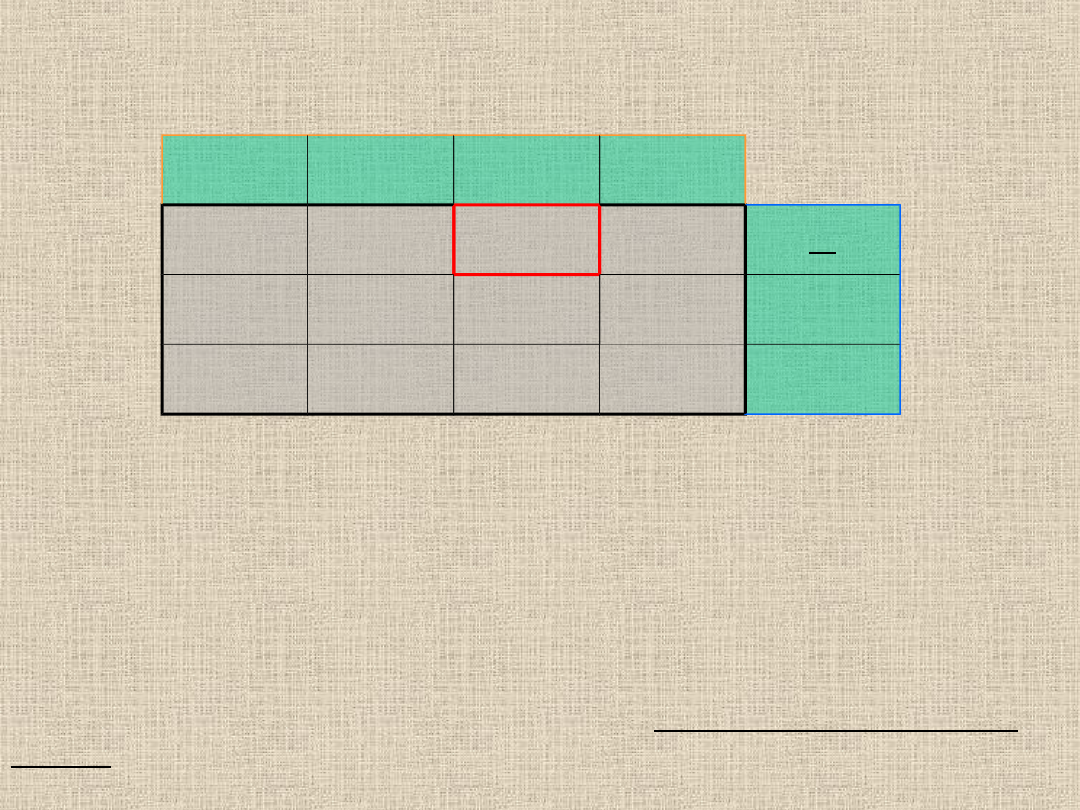
Cykl składa się zawsze z półcyklu dodatniego i
półcyklu ujemnego.

4

3

8

3

0

0

6

-2

0

1

0

0

-3

-2

2

-1

0

0

1

Aby stworzyć cykl trzeba mieć rozwiązanie dopuszczalne, które
będziemy "polepszać" sprawdzone uprzednio metodą potencjałów.
Niezbędna jest nam tabelka wskaźników optymalności z metody
potencjałów. Wśród wskaźników szukamy największej wartości na
plusie.

40

35

30

15

40

6

0+

0

46

0

29

5

0

34

0

0

25

15

40

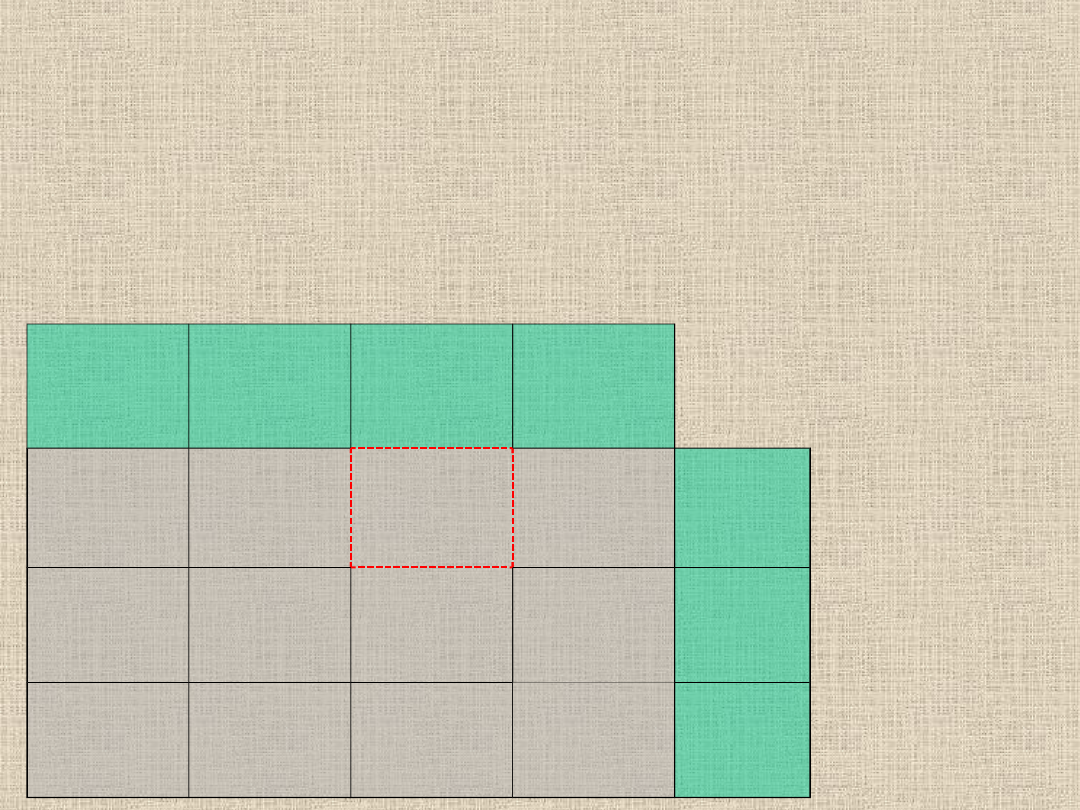
Potrzebujemy tabelkę z rozwiązaniem dopuszczalnym uzyskanym
metodą NW, na którą będziemy nanosić cykl,

Zaznaczamy w tabelce znaczkiem "+" pierwszy element cyklu dodatniego,
który zawsze znajduje się w miejscu odpowiadającym największemu
dodatniemu wskaźnikowi w tabelce wskaźników. Oznacza to, że w to miejsce
opłaca się przenieść towar z innych elementów bazowych.

40

35

30

15

40

6

0+

0

46

0

29

5-

0

34

0

0

25

15

40

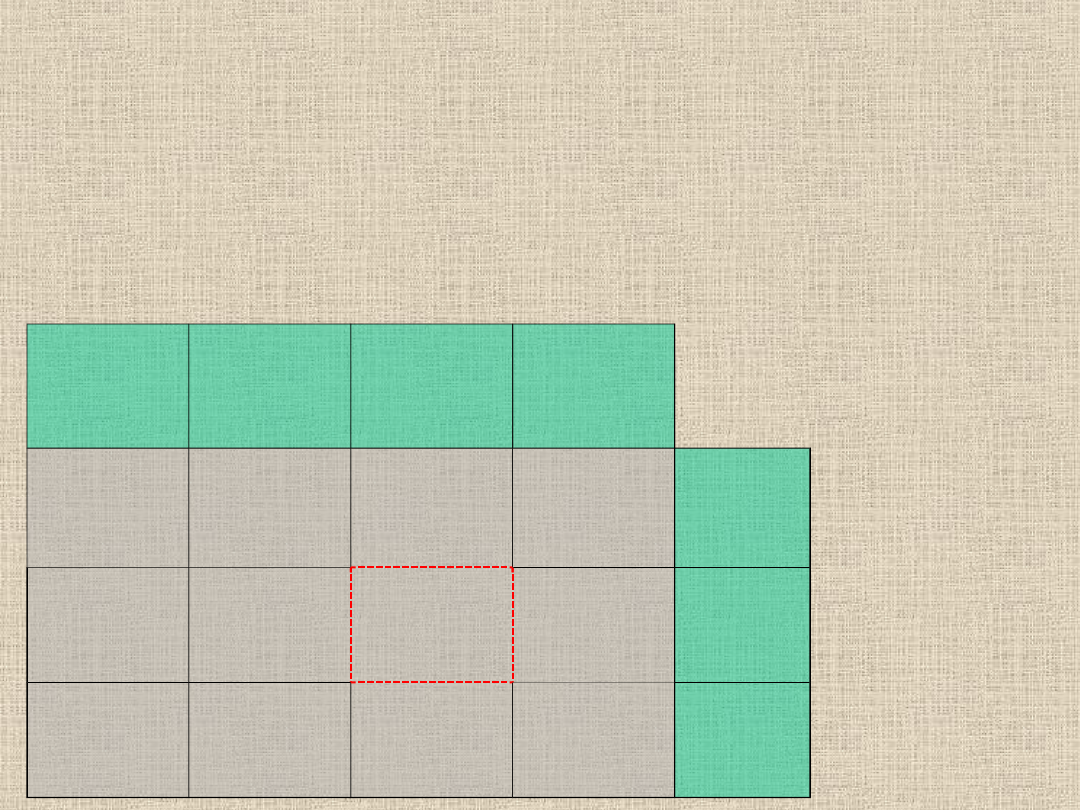
Mamy już element półcyklu dodatniego więc należy teraz stworzyć
element półcyklu ujemnego. Szukamy w kolumnie, w której stoimy
elementu bazowego, takiego który z kolei będzie miał element
bazowy w wierszu . Jest nim element o wartości 5 - zaznaczamy go
znaczkiem "-"

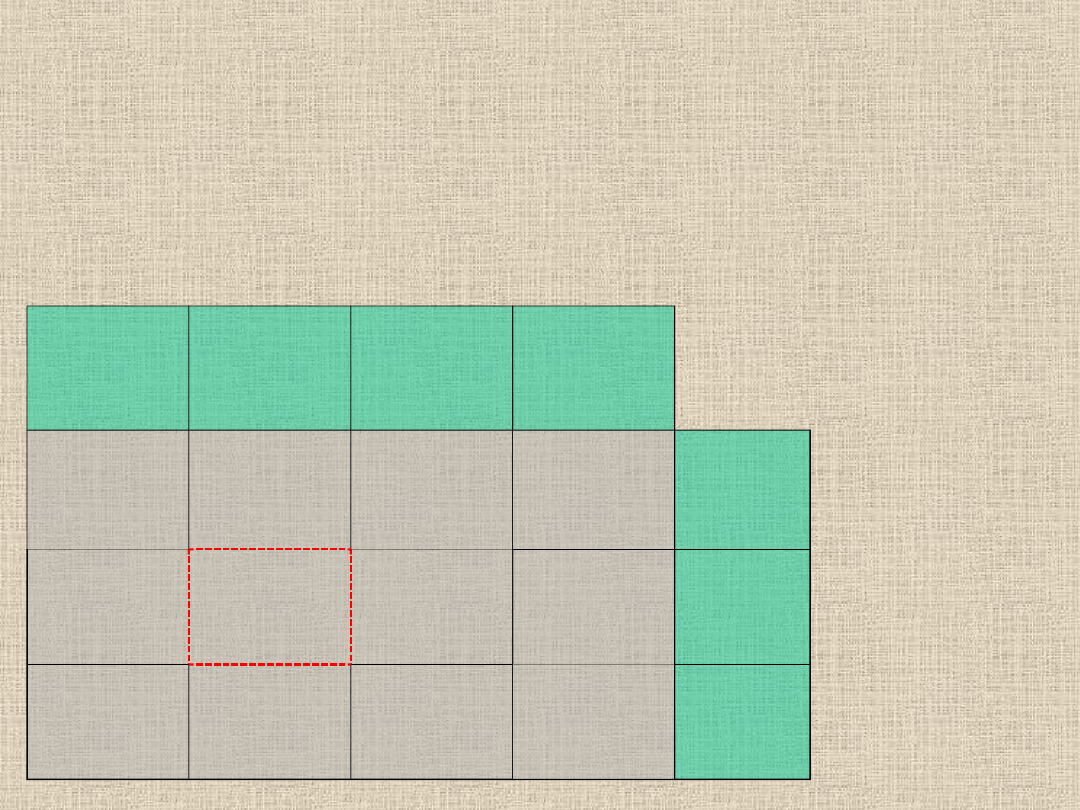
Mając element półcyklu ujemnego tworzymy kolejny element
półcyklu dodatniego. Stoimy na komórce stworzonego elementu
półcyklu ujemnego. Szukamy w wierszu, w której stoimy elementu
bazowego, który jednocześnie ma element bazowy w kolumnie. Jest
nim element o wartości 29 - zaznaczamy go znaczkiem "+"

40

35

30

15

40

6

0+

0

46

0

29+

5-

0

34

0

0

25

15

40

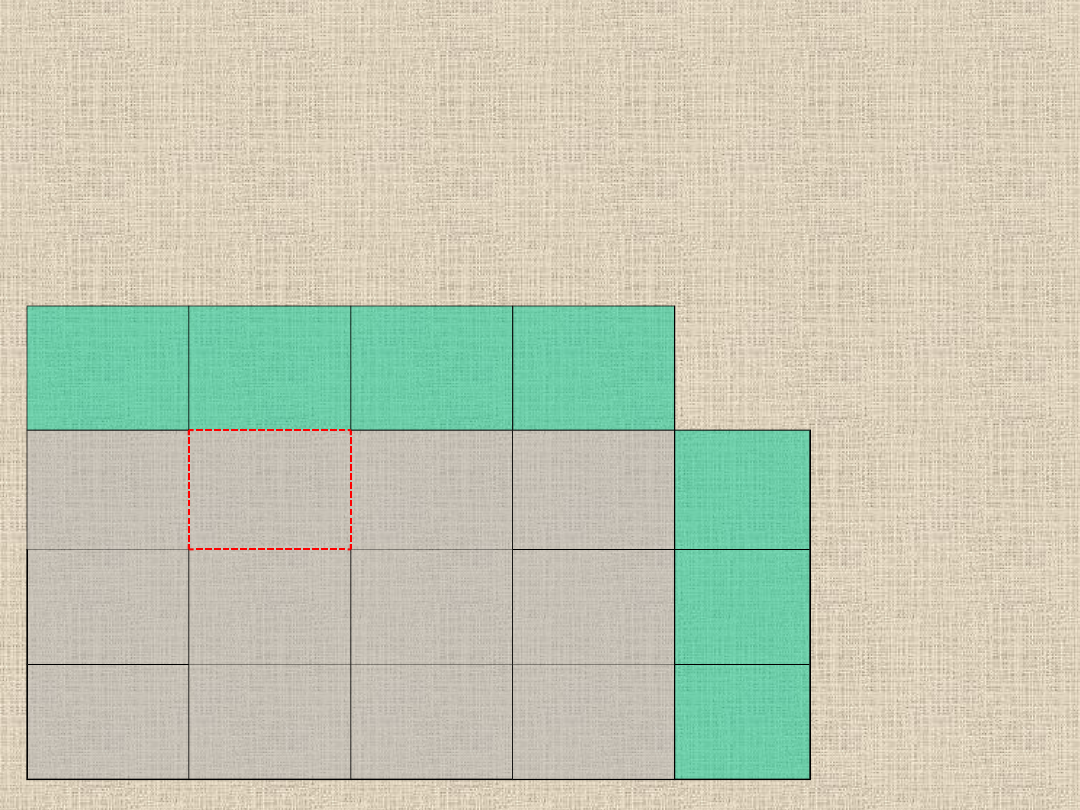
Stworzywszy element półcyklu dodatniego tworzymy kolejny element
półcyklu ujemnego. Stoimy na komórce stworzonego elementu
półcyklu dodatniego. Szukamy w wierszu, w której stoimy elementu
bazowego, który jednocześnie ma element bazowy w kolumnie. Jest
nim element o wartości 5 - zaznaczamy go znaczkiem "-"

40

35

30

15

40

6-

0+

0

46

0

29+

5-

0

34

0

0

25

15

40

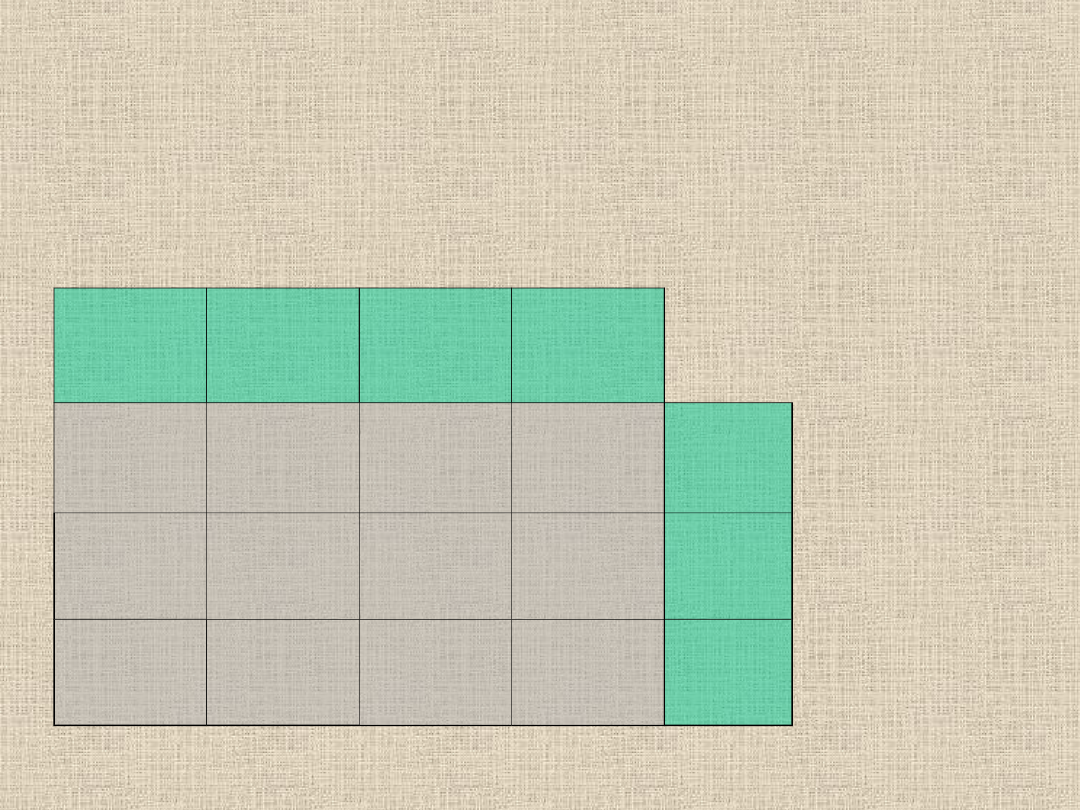
40

35

30

15

40

6-

0+

0

46

0

29+

5-

0

34

0

0

25

15

40

Mamy stworzony cykl. Należy teraz znaleźć wartość minimalną
wśród elementów cyklu ujemnego - poczym odjąć tą wartość od
wszystkich elementów cyklu ujemnego oraz dodać do wszystkich
elementów cyklu dodatniego. Elementami cyklu ujemnego są: 6, 5.
Najmniejszą spośród nich jest 5 i tę liczbę odejmujemy od
elementów cyklu ujemnego i dodajemy do elementów cyklu
dodatniego.

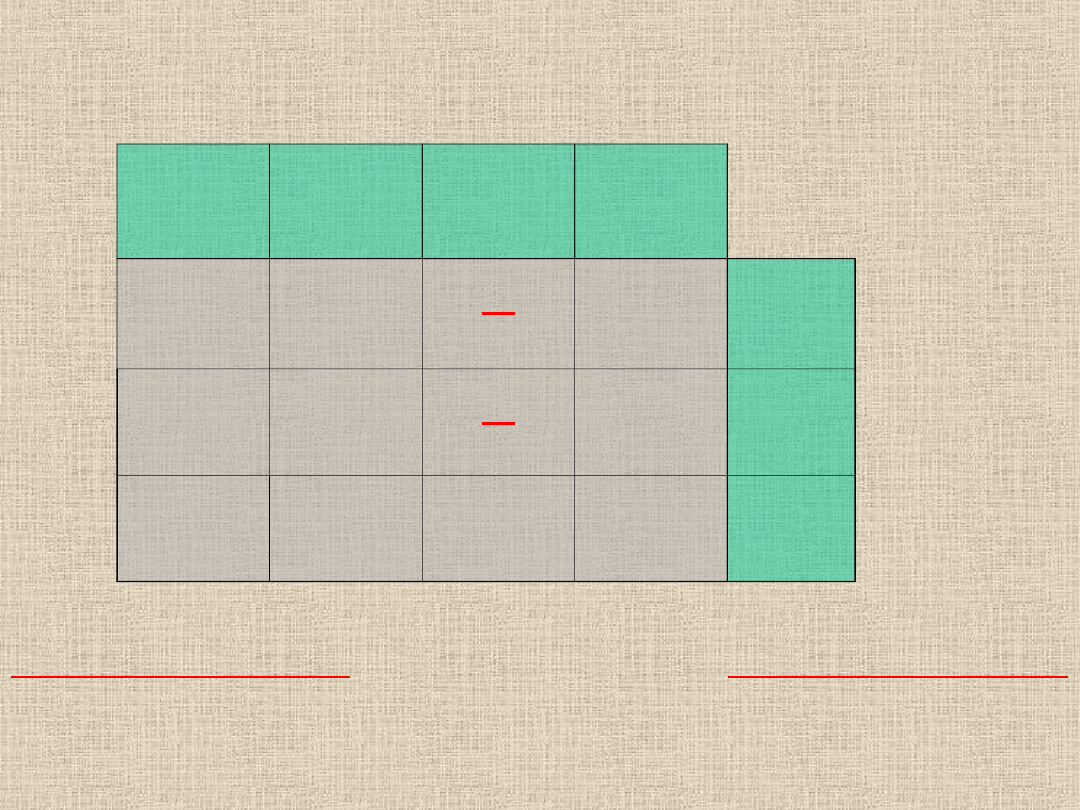
W wyniku czego otrzymujemy nowe rozwiązanie dopuszczalne.

40

35

30

15

40

1

5

0

46

0

34

0

0

34

0

0

25

15

40

Procedura cyklu spowodowała, że doszła nam jedna nowa baza

(wiersz 1, kolumna 3),

oraz jedna nam odeszła

(wiersz 2, kolumna 3).

Stąd nadal mamy 6 elementów bazowych - rozwiązanie jest
zdegenerowane.

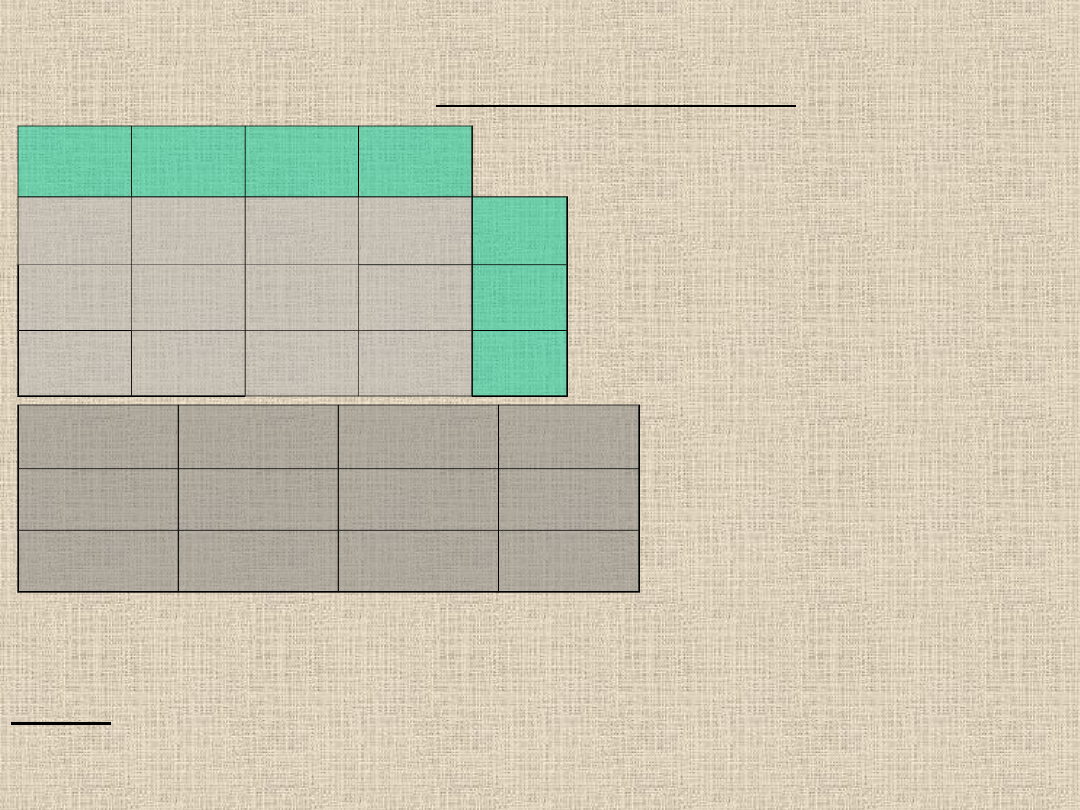
Obliczmy koszt nowego rozwiązania dopuszczalnego i
porównajmy ze starym (stary koszt = 522)

40

35

30

15

40

1

5

0

46

0

34

0

0

34

0

0

25

15

40

4

3

2

5

1

1

6

4

3

5

9

4

Koszt nowego rozwiązania: 40*4+1*3+2*5+34*1+25*9+15*4=

492

Uzyskaliśmy niższy koszt - rozwiązanie jest lepsze. Pozostało teraz sprawdzić metodą
potencjałów optymalność rozwiązania i powtórzyć procedurę jeżeli rozwiązanie nie
jest optymalne.

Sprawdzenie metodą potencjałów optymalności
rozwiązania:

Wyliczamy wskaźniki optymalności:

V1=4 V2=3 V3=-

2

V4=-

3

4

3

2

3

U1=0

0

1

-6

-1

U2=-

4

-3

-4

9

4

U3=-

7

40

35

30

15

4

3

2

5

46

1

1

6

4

34

3

5

9

4

40

4

3

8

3

4-4=0 3-3=0 2-2=0 3-5=-

2

0

0-1=-

1

1-1=0 -6-6=-

12

-1-4=-

5

-2

-3-3=-

6

-4-5=-

9

9-9=0 4-4=0

1

4

3

8

3

0

0

0

-2

0

-1

0

-12

-5

-2

-6

-9

0

0

1

Wskaźniki optymalności

Wszystkie wskaźniki optymalności są niedodatnie
czyli dane rozwiązanie jest rozwiązaniem
optymalnym.

Koszt rozwiązania optymalnego to
492.