1

2

Analiza matematyczna

sem. II

rok akademicki 1999/2000

dr Mariusz J.Wasilewski

Wykład 7

3

7. Całka powierzchniowa

zorientowana

4

Rozważmy zagadnienie:

interesuje nas przepływ

pewnego medium z „jednej

strony powierzchni na drugą”.

Aby było to możliwe

powierzchnia musi mieć „dwie

strony”. Wydaje się to

oczywiste ponieważ nie

podejrzewamy, że istnieją

powierzchnie, które maja tylko

jedną stronę.

7.1. Wprowadzenie

5

Przykładem powierzchni, która ma

tylko jedną stronę jest wstęga

Möbiusa.

Dalej interesować nas będą

powierzchnie mające dwie strony.

6

Definicja 1.

Jeżeli funkcja

z = f(x,y)

, gdzie

(x,y)  D

spełnia warunki:

• pochodne cząstkowe

f’

x

(x,y)

i

f’

y

(x,y)

są ciągłe i

ograniczone w obszarze

D

• jest określona i ciągła

wewnątrz i na brzegu

C

obszaru regularnego

D

7

to, powierzchnię o równaniu

z =

f(x,y)

nazywamy

płatem

powierzchniowym regularnym

.

Podobnie określamy płaty

powierzchniowe regularne

określone równaniami

y = g(x,z)

i

x = h(y,z)

.

8

Definicja 2

. Wektorem normalnym

płata powierzchniowego

regularnego

]

1

),

y

,

x

(

'

f

),

y

,

x

(

'

f

[

n

0

0

y

0

0

x









(jest to wektor normalny

płaszczyzny stycznej do płata

S

w

punkcie

P

0

).

S = {(x,y,z)  R

3

: z = f(x,y) Ů

(x,y)  D}

w punkcie

P

0

(x

0

,y

0

,z

0

)  S

nazywamy wektor

9

Definicja 3

. Płat powierzchniowy

regularny

S = {(x,y,z)  R

3

: z = f(x,y) Ů

(x,y)  D},

nazywamy

płatem pow. zorientowanym

jeżeli jedną stronę płata nazwiemy

dodatnią,

a drugą

ujemną

.

Stroną dodatnią płata S

nazywać

będziemy tę stronę, po której

znajduje się wektor normalny

]

1

),

y

,

x

(

'

f

),

y

,

x

(

'

f

[

n

0

0

y

0

0

x









10

Podobnie definiuje się stronę

dodatnią płatów powierzchniowych

regularnych danych równaniami

)]

z

,

y

(

'

h

),

z

,

y

(

'

h

,

1

[

n

]

)

z

,

x

(

'

g

,

1

,

)

z

,

x

(

'

g

[

n

]

1

),

y

,

x

(

'

f

),

y

,

x

(

'

f

[

n

y

ln

norma

wektor

)

z

,

y

(

h

x

)

z

,

x

(

g

y

)

y

,

x

(

f

z

równanie

0

0

z

0

0

y

0

0

z

0

0

x

0

0

y

0

0

x































11

Definicja całki powierzchniowej

zorientowanej oparta będzie na

pojęciu całki powierzchniowej

niezorientowanej. Ponieważ

zagadnienie całki pow.

niezorientowanej należało

opracować samodzielnie

wprowadzimy najpierw kilka

ustaleń.

12

Dany jest płat powierzchniowy

regularny

}

D

)

y

,

x

(

)

y

,

x

(

f

z

:

R

)

z

,

y

,

x

{(

S

3











Na płacie tym jest określona i

ciągła funkcja skalarna

F(x,y,z)

.

13

W sposób konwencjonalny dzielimy

płat

S

na płaty częściowe o polach

s

. Na każdym z płatów częściowych

obliczamy wartość funkcji

F

i

tworzymy sumę całkową. Granicę tej

sumy nazywamy całką

powierzchniowa niezorientowaną i

oznaczamy symbolem



s

ds

)

z

,

y

,

x

(

F

14

Całkę tę oblicza się za pomocą

całki podwójnej według wzoru











S

D

2

y

2

x

.

dxdy

'

f

'

f

1

)]

y

,

x

(

f

,

y

,

x

[

F

ds

)

z

,

y

,

x

(

F

15

Przypomnienie !

Temat CAŁKA POWIERZCHNIOWA

ZORIENTOWANA

jest tematem do samodzielnego

opracowania

na podstawie lektury.

Przedstawione tu uwagi dotyczące

tej całki mają jedynie ułatwić

zrozumienie całki powierzchniowej

zorientowanej.

16

Definicja

4

. Niech funkcje

P(x,y,z),

Q(x,y,z)

i

R(x,y,z)

będą określone i

ciągłe na płacie powierzchniowym,

regularnym, zorientowanym

S = {(x,y,z)  R

3

: z = f(x,y) Ů (x,y)  D},

zaś

cos, cos, cos

oznaczają

kosinusy kierunkowe wektora

normalnego tego płata.

17

Całką powierzchniową zorientowaną

po płacie zorientowanym

S

nazywamy całkę postaci





.

ds

cos

)

z

,

y

,

x

(

R

cos

)

z

,

y

,

x

(

Q

cos

)

z

,

y

,

x

(

P

S













18

Ponieważ między polem

ds

dowolnie małego elementu płata

S

i polami

dydz, dxdz, dxdy

rzutu

tego elementu na płaszczyzny

Oyz,

Oxz

i

Oxy

odpowiednio, zachodzą

związki

ds

cos

dxdy

ds

cos

dxdz

ds

cos

dydz













19

zdefiniowaną całkę można zapisać

w równoważnej postaci







S

.

dxdy

)

z

,

y

,

x

(

R

dxdz

)

z

,

y

,

x

(

Q

dydz

)

z

,

y

,

x

(

P

20

7.2. Interpretacja fizyczna całki

powierzchniowej zorientowanej

Definicja 5

. Niech w pewnym obszarze

przestrzennym określone będzie pole

wektorowe

,

]

R

,

Q

,

P

[

F 



oraz zorientowany płat powierzchniowy

regularny

}.

D

)

y

,

x

(

)

y

,

x

(

f

z

:

R

)

z

,

y

,

x

{(

S

3











21

Przy tych oznaczeniach całkę

ds

}

cos

)

z

,

y

,

x

(

R

cos

)

z

,

y

,

x

(

Q

cos

)

z

,

y

,

x

(

P

[

S

















nazywamy strumieniem pola

,

]

R

,

Q

,

P

[

F 



przez powierzchnię zorientowaną

S

.

22

]

cos

R

,

cos

Q

,

cos

P

[

F

n











jest składową wektora

]

R

,

Q

,

P

[

F 



Wektor

wzdłuż normalnej wyznaczonej przez

wektor

n



23

W teorii pola wektorowego strumień

wektora pola

]

R

,

Q

,

P

[

F 



przez powierzchnię

S

w kierunku

wektora normalnego oznaczamy

,

s

d

F

S













.

]

dxdy

,

dxdz

,

dydz

[

s

d

gdzie 



24

7.3. Podstawowe twierdzenia

całkowe

Dla całki powierzchniowej

zorientowanej - podobnie jak dla

innych całek - zachodzą

podstawowe twierdzenia całkowe:

F



)

G

F

(







• o całkowalności funkcji ciągłej

• o całkowaniu sumy
(różnicy) funkcji

25

•o całkowaniu iloczynu funkcji przez
stałą

F

a















2

1

2

1

S

S

S

S

• o addytywności całki

(czyli o możliwości obliczania całki
po płatach
będących „składowymi” płata, po
którym
całkujemy)

26

Twierdzenia te należy sformułować

samodzielnie wzorując się na

podobnych twierdzeniach dla innych

całek.

27

7.4. Szczególne własności całki

powierzchniowej zorientowanej

1. Jeżeli przez

(-S)

oznaczymy ujemną

stronę płata

S

, to z definicji całki wynika

natychmiast, że





















S

S

.

Rdxdy

Qdxdz

Pdydz

Rdxdy

Qdxdz

Pdydz

28

Wynika to stąd, że zmiana strony płata

powoduje zmianę zwrotu wektora

orientującego płat, a tym samym

zmianę znaków jego kosinusów

kierunkowych.

29

2. Jeżeli funkcja

R(x,y,z)

jest ciągła na

płacie
powierzchniowym, regularnym,

}.

D

)

y

,

x

(

)

y

,

x

(

f

z

:

R

)

z

,

y

,

x

{(

S

3











zorientowanym dodatnio to







S

D

,

dxdy

)]

y

,

x

(

f

,

y

,

x

[

R

dxdy

)

z

,

y

,

x

(

R

gdzie

D

jest rzutem płata

S

na

płaszczyznę

Oxy

.

30

3. Podobne twierdzenia zachodzą w

przypadku

płatów danych równaniami

y =

g(x,z)

oraz

x = h(y,z)

.

Pozwala to, obliczyć całkę przez

całkowanie każdego jej członu osobno.

31

4. Całkę powierzchniową można
obliczyć całkując
każdy jej człon osobno





















S

S

S

S

.

Rdxdy

Qdxdz

Pdydz

Rdxdy

Qdxdz

Pdydz

32

7.5. Twierdzenie o zamianie całki

powierzchniowej zorientowanej

na całkę podwójną

Jeżeli funkcje

P(x,y,z)

,

Q(x,y,z)

i

R(x,y,z)

są ciągłe na dodatnio

zorientowanym płacie regularnym

}.

D

)

y

,

x

(

)

y

,

x

(

f

z

:

R

)

z

,

y

,

x

{(

S

3











33

to









S

dxdy

)

z

,

y

,

x

(

R

dxdz

)

z

,

y

,

x

(

Q

dydz

)

z

,

y

,

x

(

P





.

dxdy

)]

y

,

x

(

f

,

y

,

x

[

R

'

f

)]

y

,

x

(

f

,

y

,

x

[

Q

'

f

)]

y

,

x

(

f

,

y

,

x

[

P

D

y

x











34

Podobne twierdzenia zachodzą, gdy

płaty dane są równaniami

y =

g(x,z)

i

x = h(y,z)

.

Uwaga. W zadaniach oprócz

określeń „strona dodatnia”, „strona

ujemna”, będziemy używać

terminów „strona górna” lub

„strona dolna” płata

powierzchniowego, biorąc za

podstawę układ jak na rysunku.

35

36

Przykład 1

. Obliczyć całkę







S

zdxdy

xdxdz

ydydz

gdzie

S

jest górną stroną

powierzchni trójkąta

ABC

,

wyciętego z płaszczyzny

x - y + z =

1

płaszczyznami układu

współrzędnych.

37

Rozwiązanie

. Stosujemy twierdzenie o

zamianie całki powierzchniowej na

całkę podwójną. W tym celu z

równania płaszczyzny wyznaczamy

równanie płata

z = 1 - x + y

,

pochodne

z’

x

= -1

,

z’

y

= 1

.

Następnie należy wyznaczyć obszar

D

będący rzutem płata

S

na płaszczyznę

Oxy.

W tym celu wykonujemy rysunek.

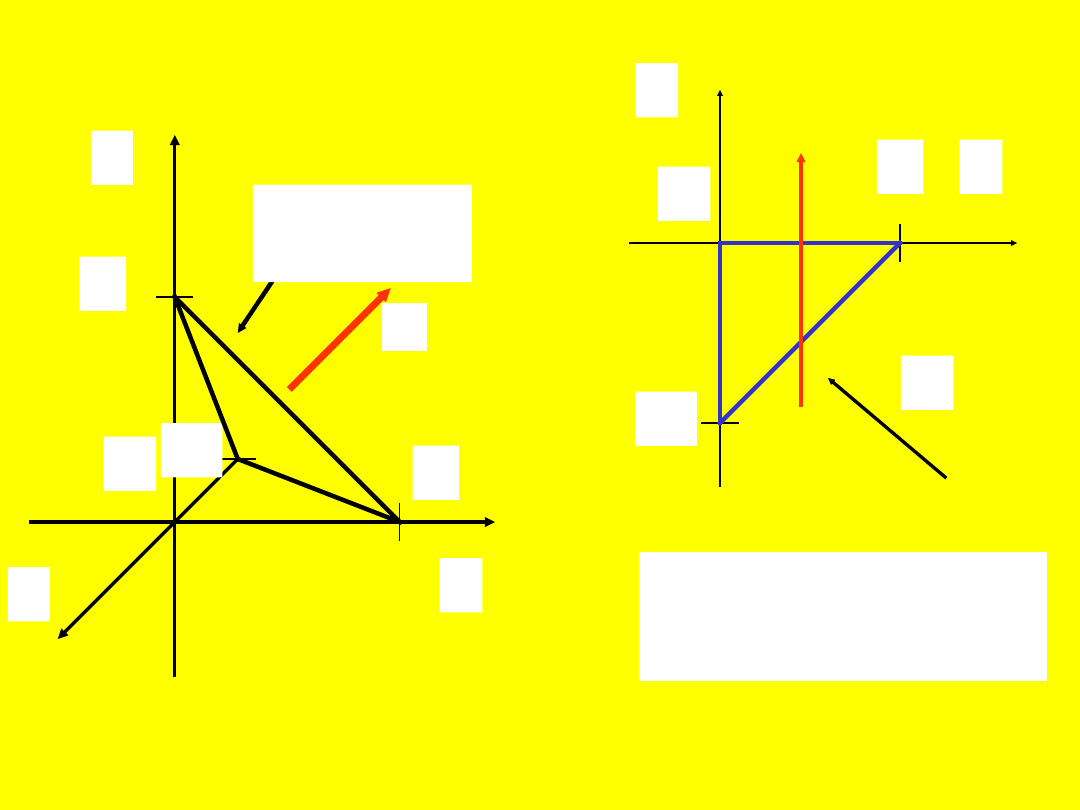
38

x

y

z

O

1

1

-1

z = 1 – x

+ y

n



x

y

O

1

-1

D

.

0

y

1

x

1

x

0

D

Ů

Ů

Ů













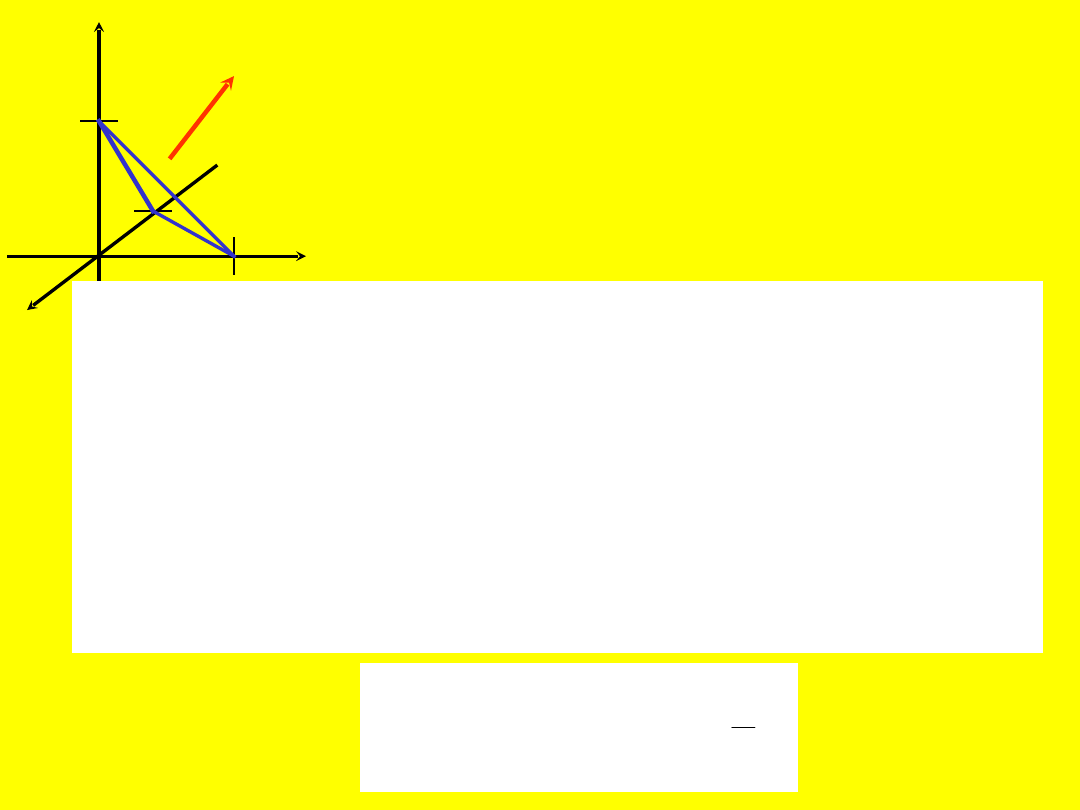
39

x

y

z

0

1

1

-1

Stwierdzamy, że strona

górna jest strona

dodatnią. Stosujemy

podane twierdzenie

 









ŮŮ

Ů

ŮŮ

Ů





































1

0

0

1

x

D

D

S

dx

dy

)

1

x

2

y

2

(

dx

)

1

x

2

y

2

(

dxdy

]

y

x

1

)

1

(

x

)

1

(

y

[

zdxdy

xdxdz

ydydz











1

0

2

.

6

1

dx

)

x

x

(

40

7.6. Zamiana całki

powierzchniowej zorientowanej

na całkę potrójną

Definicja 5

. Stroną dodatnią

powierzchni zamkniętej

nazywamy jej stronę zewnętrzną.

41

Twierdzenie Gaussa-

Ostrogradskiego

Jeżeli funkcje

P(x,y,z)

,

Q(x,y,z)

i

R(x,y,z)

są ciągłe wraz z

pochodnymi cząstkowymi

z

R

,

y

Q

,

x

P













wewnątrz i na brzegu

S

obszaru

przestrzennego

V

normalnego

względem wszystkich płaszczyzn

układu współrzędnych,

42

i jeżeli brzeg

S

obszaru

V

jest

powierzchnią regularną zamkniętą,

zorientowaną skierowaniem wektora

normalnego na zewnątrz obszaru

V

, to





Ů

Ů

Ů

Ů

Ů

Ů

























V

S

.

dxdydz

z

R

y

Q

x

P

Rdxdy

Qdxdz

Pdydz

43

Interpretacja twierdzenia G-O

w teorii pola

wektorowego

]

R

,

Q

,

P

[

F 



Strumień



wektora pola

przez powierzchnię zamkniętą

S

,

zorientowaną na zewnątrz, równy jest
całce potrójnej z dywergencji, po
obszarze

V

ograniczonym powierzchnią

S













S

V

.

dxdydz

F

div

s

d

F







44

Twierdzenie

G-O

wyjaśnia rolę

dywergencji jako charakterystyki pola

wektorowego

strumień domniemanie dotyczące źródeł
i upustów w
obszarze V

 < 0 suma wydajności źródeł mniejsza

od sumy

wydajności upustów

 > 0 suma wydajności źródeł mniejsza

od sumy

wydajności upustów

 = 0 pole bezźródłowe lub suma

wydajności

źródeł równa jest sumie

wydajności upustów

45

7.7. Zamiana całki

krzywoliniowej zorientowanej

na całkę powierzchniową

46

Twierdzenie Stokesa

Niech krzywa

k

będzie brzegiem płata

powierzchniowego

S

, zorientowanego

tak, by obieg dodatni na krzywej

k

wokół wektora normalnego do płata

S

był zgodny z obiegiem wokół osi

Oz

na krzywej

C

, która jest rzutem

krzywej

k

na płaszczyznę

Oxy

.

47

Jeżeli funkcje

P(x,y,z), Q(x,y,z),

R(x,y,z)

są ciągłe wraz z

pochodnymi cząstkowymi rzędu

pierwszego w obszarze

zawierającym powierzchnię

S

, to

.

dxdy

y

P

x

Q

dxdz

x

R

z

P

dydz

z

Q

y

R

Rdz

Qdy

Pdx

S

k





Ů

Ů

Ů

Ů

Ů

Ů













Ů

Ů

Ů

Ů

Ů

Ů













Ů

Ů

Ů

Ů

Ů

Ů



















48

Interpretacja twierdzenia Stokesa w

teorii pola wektorowego













S

k

.

s

d

F

rot

s

d

F

L









Cyrkulacja

L

wektora pola po krzywej

zamkniętej

k

, równa jest strumieniowi

rotacji wektora pola, przez

powierzchnię rozpiętą na krzywej

k

.

49

Koniec wykładu

50