Paweł Górczyński, Badania operacyjne, Slajd 1

Badania operacyjne, Solver

Paweł Górczyński

[e-mail]

Paweł Górczyński, Badania operacyjne, Slajd 2

Solver, podstawowe informacje



Dodatek Solver jest częścią zestawu

poleceń czasami zwaną narzędziami

analizy typu co-jeśli. Korzystając z dodatku

Solver, można znaleźć optymalną wartość

dla formuły w pojedynczej komórce —

zwanej komórką docelową — w arkuszu.



Dodatek Solver pracuje z grupą komórek

powiązanych, bezpośrednio lub pośrednio,

z formułą w komórce docelowej.



Dodatek Solver dostosowuje wartości w

zmieniających się komórkach określonych

przez użytkownika — zwanych komórkami

zmienianymi — w celu uzyskania wyniku

określonego przez użytkownika na

podstawie formuły w komórce docelowej.

Paweł Górczyński, Badania operacyjne, Slajd 3



Można zastosować ograniczenia, które

zmniejszają zakres wartości używanych

przez dodatek Solver w modelu i mogą

odwoływać się do innych komórek

wpływających na formułę w komórce

docelowej.



Dodatku Solver można używać do ustalenia

maksymalnej lub minimalnej wartości

określonej komórki przez zmianę innych

komórek, na przykład można zmienić

przewidywany budżet reklamowy i

zobaczyć wpływ tej zmiany na

przewidywany zysk.

Paweł Górczyński, Badania operacyjne, Slajd 4

Przykład

W pierwszej prezentacji poniższe zadanie zostało rozwiązane metodą

geometryczną.

Teraz zostanie przedstawione rozwiązanie z użyciem Solvera



Przedsiębiorstwo produkuje dwa wyroby W1 i W2.

W procesie produkcji tych wyrobów zużywa się

wiele środków, spośród których dwa są limitowane.

Limity te wynoszą: środek I – 96000 jedn.,

natomiast środek II – 80000 jedn.

Nakłady limitowanych środków na jednostkę

wyrobów W1 i W2 podano w tablicy 1.

Środki

produkcji

Jednostkowe nakłady

W1

W2

I

16

24

II

16

10

Paweł Górczyński, Badania operacyjne, Slajd 5

Przykład cd



Wiadomo, że zdolności produkcyjne

jednego z wydziałów, stanowiącego wąskie

gardło procesu produkcyjnego, nie

pozwalają produkować więcej niż 3000 szt.

wyrobów W1 oraz 4000 szt. wyrobów W2.



Optymalne proporcje produkcji kształtują

się odpowiednio jak 3:2. Cena sprzedaży (w

zł) jednostki wyrobu W1 wynosi 30, a

wyrobu W2 – 40.



Ustalić optymalne rozmiary produkcji

wyrobów gwarantujące maksymalizację

przychodu ze sprzedaży przy istniejących

ograniczeniach.

Paweł Górczyński, Badania operacyjne, Slajd 6

Rozwiązanie



Niezależnie od przyjętej metody zaczynamy

od zbudowania modelu matematycznego

opisującego przedstawioną powyżej sytuację.

Mamy dwa wyroby, więc będziemy mieli dwie

zmienne decyzyjne



Niech x1 oznacza ilość produkcji wyrobu W1,

a x2 – ilość produkcji wyrobu W2. Biorąc pod

uwagę limity środków produkcji I i II, mamy

dwa pierwsze ograniczenia.

96000

24

16

2

1



 x

x

80000

10

16

2

1



 x

x

Paweł Górczyński, Badania operacyjne, Slajd 7

Rozwiązanie cd



Trzeci warunek opisujący optymalne

proporcje przybierze postać:



Warunki brzegowe przybiorą postać:



Funkcja celu

1

2

3

2

)

3

(

x

x 

4000

0

)

5

(

3000

0

)

4

(

2

1









x

x

max

40

30

)

,

(

2

1

2

1







x

x

x

x

F

Wielkość produkcji nie może być
ujemna.
Z drugiej strony mamy ograniczenia
produkcji dla wyrobu I i II – „wąskie
gardła”

Paweł Górczyński, Badania operacyjne, Slajd 8



Podsumowując,

model

matematyczny dla

naszego problemu

wygląda następująco



Mając gotowy

model, możemy

przystąpić do

rozwiązania.



Zaczynamy od

przygotowania

wszystkich formuł w

arkuszu

kalkulacyjnym Excel

96000

24

16

)

1

(

2

1



 x

x

80000

10

16

)

2

(

2

1



 x

x

1

2

3

2

)

3

(

x

x 

3000

0

)

4

(

1



x

4000

0

)

5

(

2



x

max

40

30

)

,

(

2

1

2

1







x

x

x

x

F

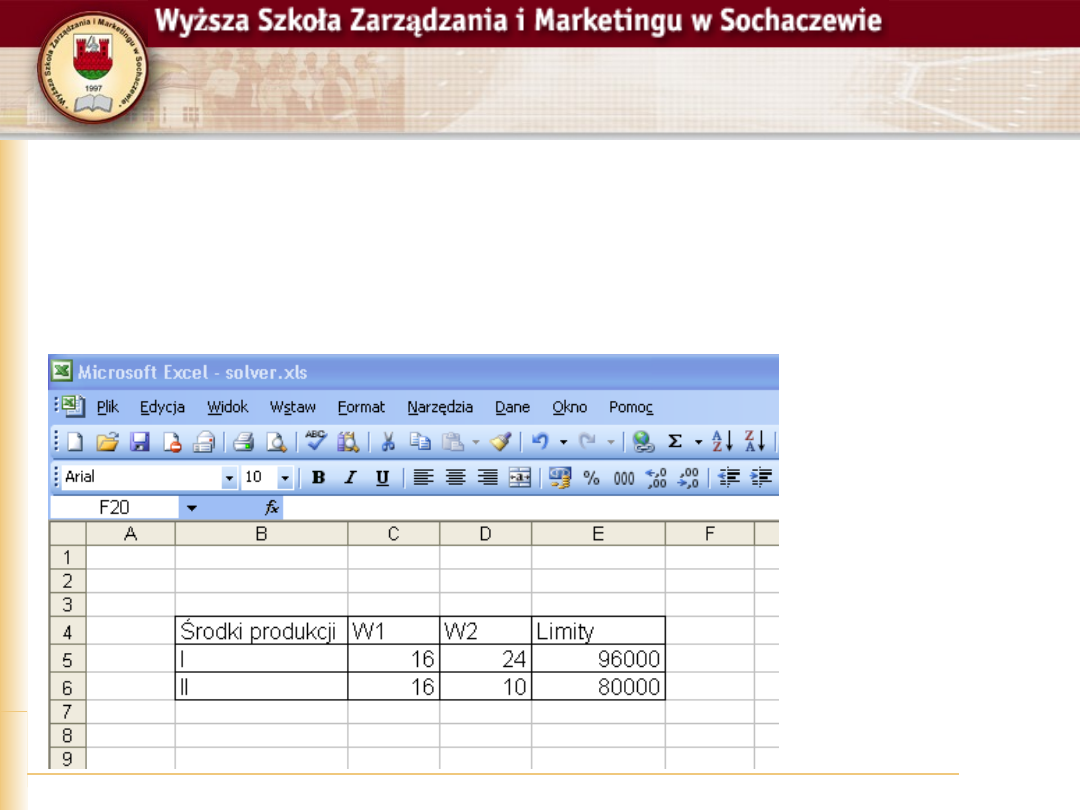
Paweł Górczyński, Badania operacyjne, Slajd 9

Rozwiązanie krok 1



Uruchamiamy Excela, pusty arkusz



Wprowadzamy lub kopiujemy

podstawową tablicę danych

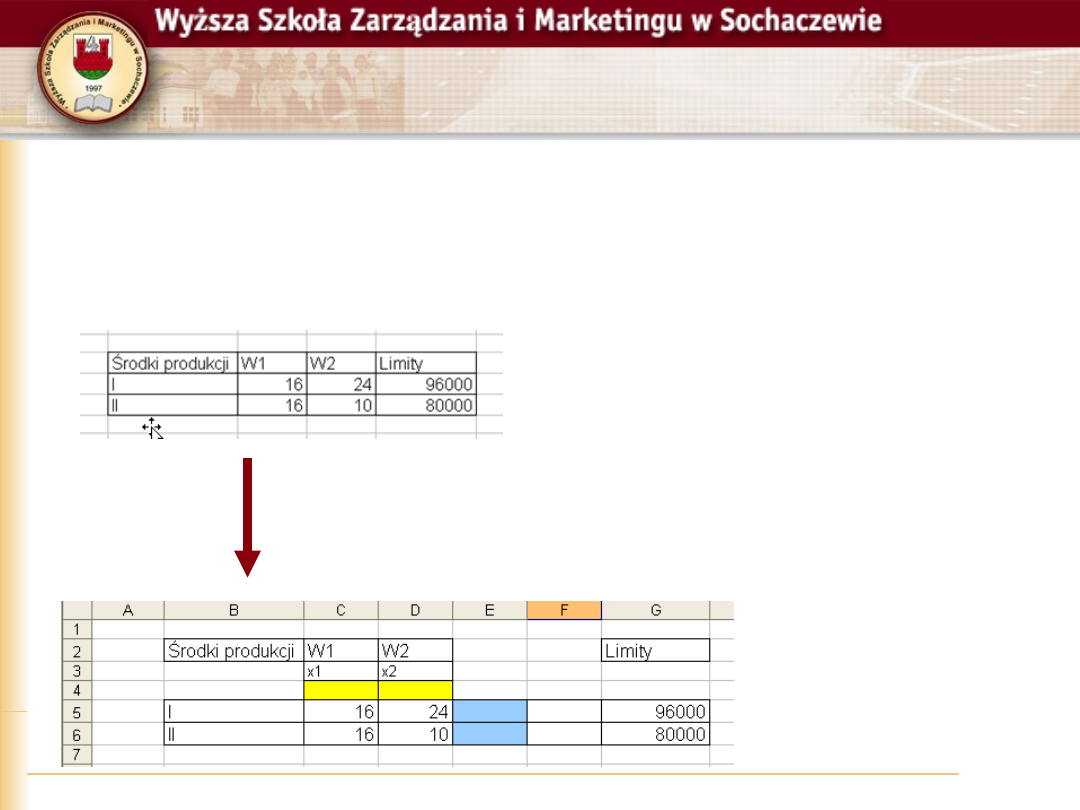
Paweł Górczyński, Badania operacyjne, Slajd 10

Krok 2



Modyfikujemy tablicę tak, aby

przygotować miejsce na formuły i

zmienne decyzyjne

W komórkach
oznaczonych na
żółto, będą zmienne
decyzyjne

W komórkach
oznaczonych na
niebiesko – formuły
warunków
ograniczających

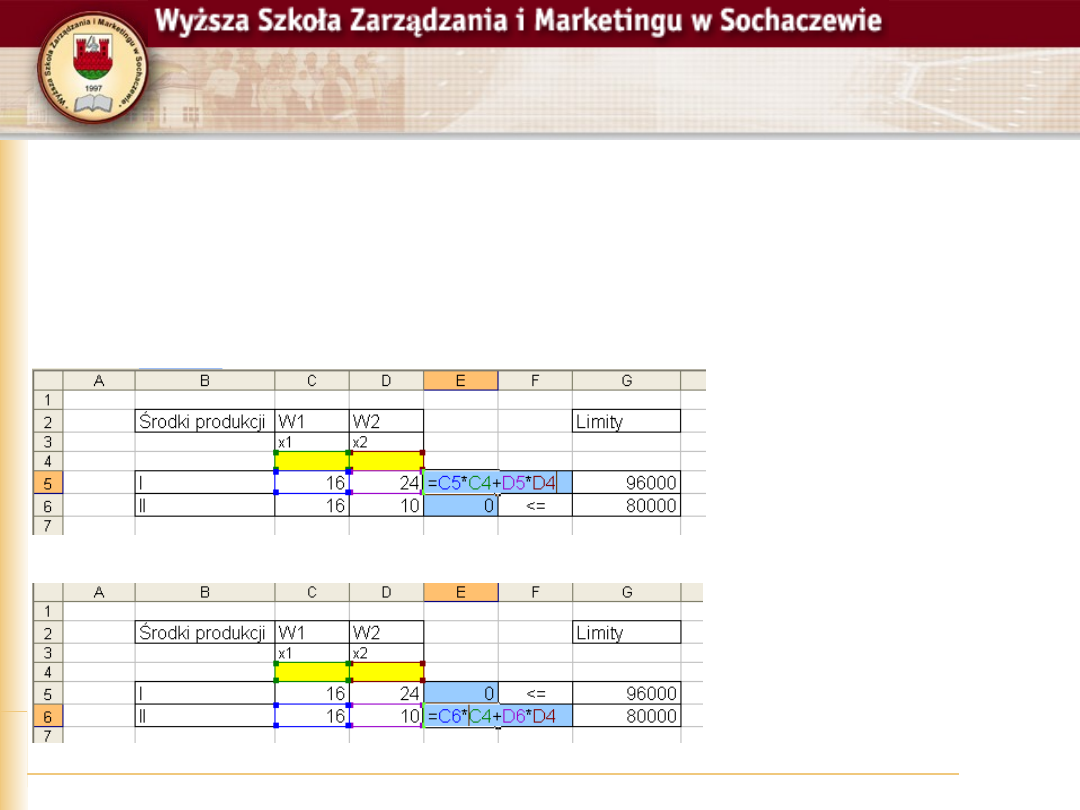
Paweł Górczyński, Badania operacyjne, Slajd 11

Krok 3



Wprowadzamy formuły dla

warunków ograniczających

96000

24

16

)

1

(

2

1



 x

x

80000

10

16

)

2

(

2

1



 x

x

Wprowadzamy lewe
strony warunków
ograniczających
Dla czytelności warto
też zapisać operator
porównania w
kolumnie „F”, tutaj
<=

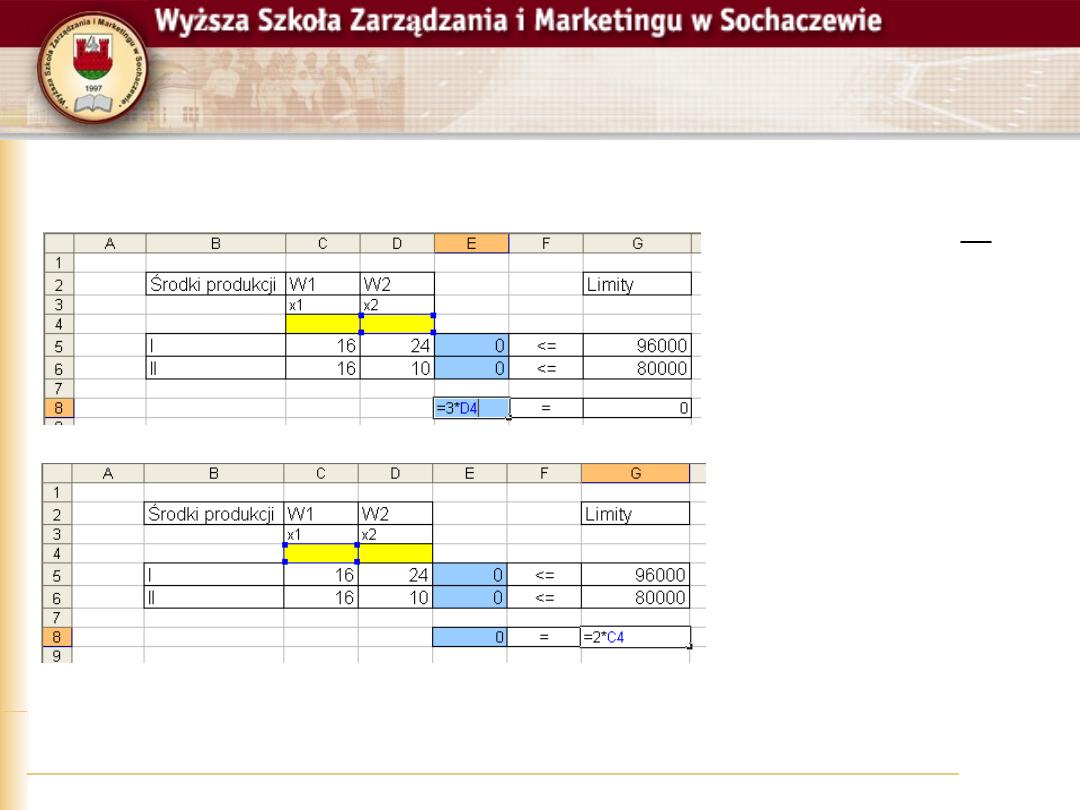
Paweł Górczyński, Badania operacyjne, Slajd 12

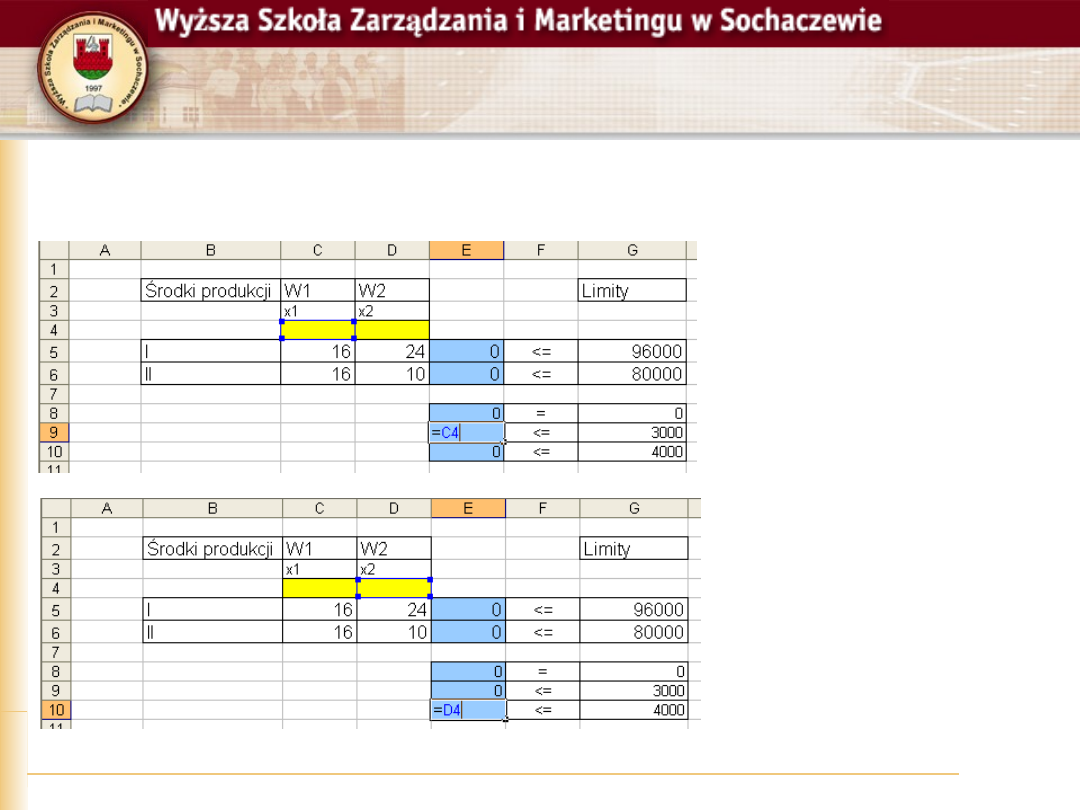
Krok 4



Zapisanie pozostałych warunków

1

2

3

2

)

3

(

x

x 

Paweł Górczyński, Badania operacyjne, Slajd 13

Krok 5

3000

0

)

4

(

1



x

4000

0

)

5

(

2



x

Dla ostatnich dwóch
warunków zostały
zapisane tylko
ograniczenia x1 <=
3000 i x2 <= 4000

Ograniczenie
brzegowe x1, x2 >=0
można ustawić
później w opcjach
SOLVERA

Paweł Górczyński, Badania operacyjne, Slajd 14

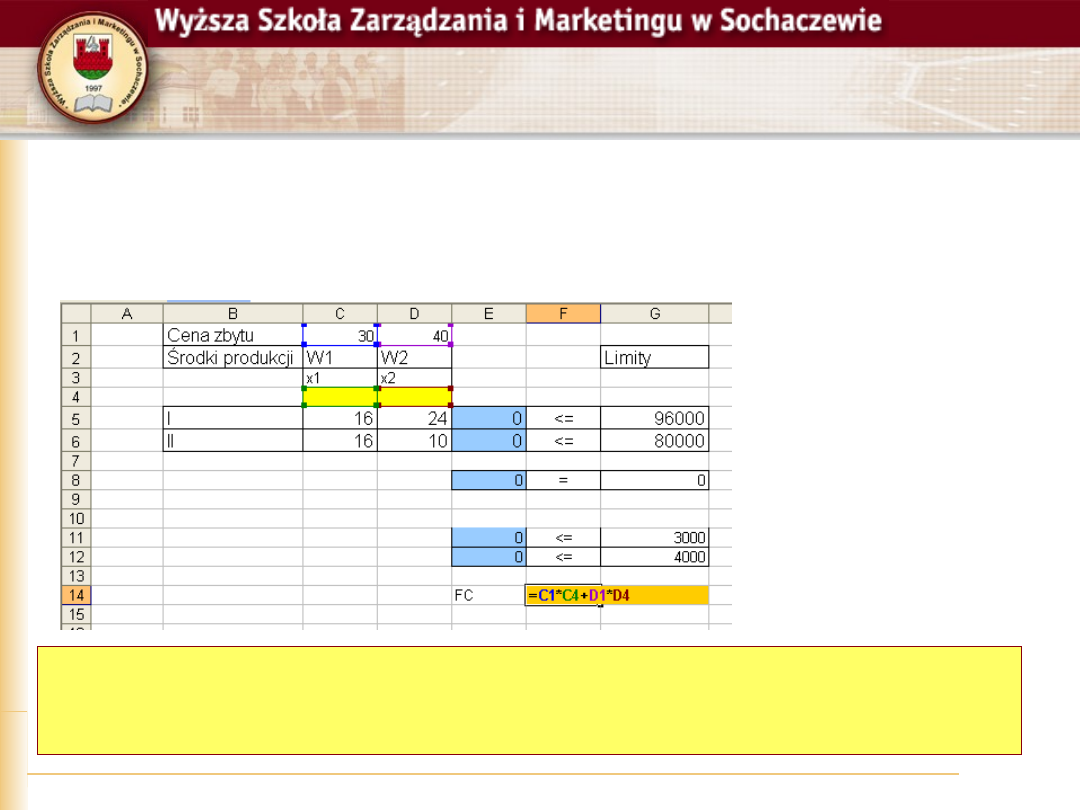
Krok 6



Zapisanie funkcji celu

max

40

30

)

,

(

2

1

2

1







x

x

x

x

F

Funkcję celu, jak i pozostałe warunki można zapisać efektywniej np.
blokując właściwe komórki i korzystając z funkcji suma iloczynów.
Jednak dla czytelności została tu użyta najprostsza postać

Paweł Górczyński, Badania operacyjne, Slajd 15

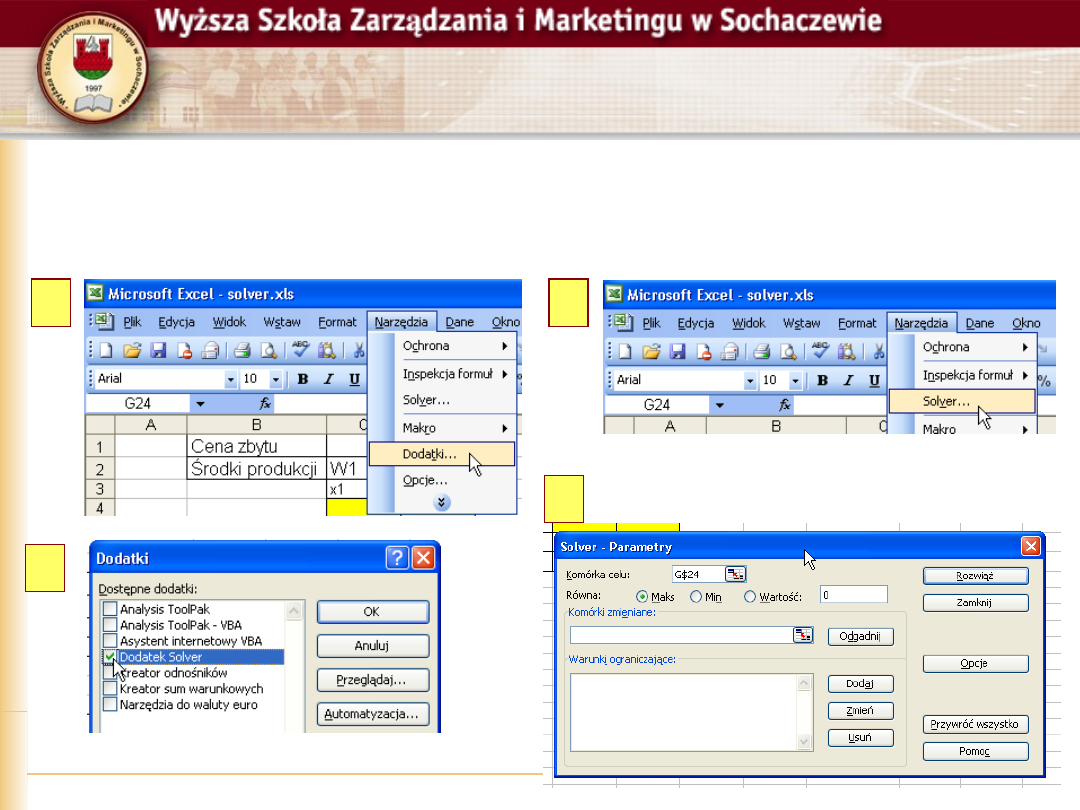
Krok 7, uruchomienie Solvera



Solver znajduje się w menu narzędzia



Jeśli nie jest widoczny na liście, należy go najpierw aktywować

1

2

3

4

Paweł Górczyński, Badania operacyjne, Slajd 16



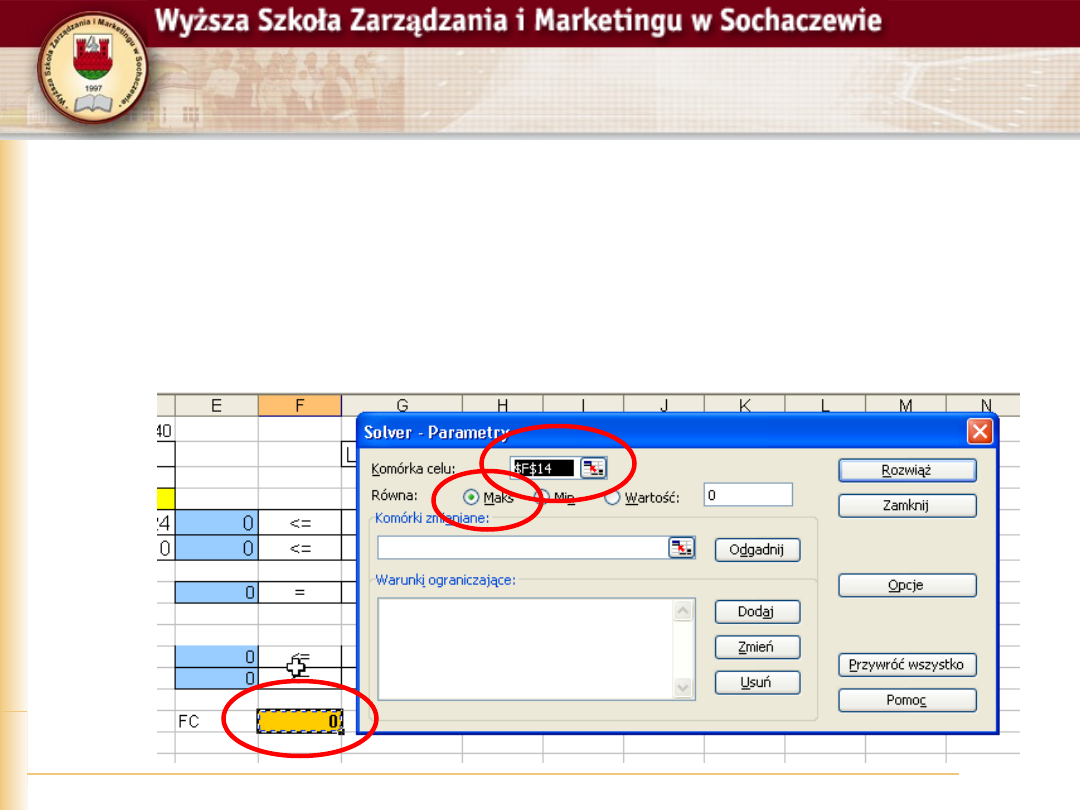
Po uruchomieniu Solvera, należy

uzupełnić właściwe parametry



Wskazać komórkę w której zapisaliśmy

funkcję celu



Określić czy szukamy wartości max czy min



Wskazać komórki zmieniane, ze zmiennymi

decyzyjnymi



Zdefiniować warunki ograniczające



Ustawić opcje



Model liniowy



Zmienne nieujemne

Paweł Górczyński, Badania operacyjne, Slajd 17

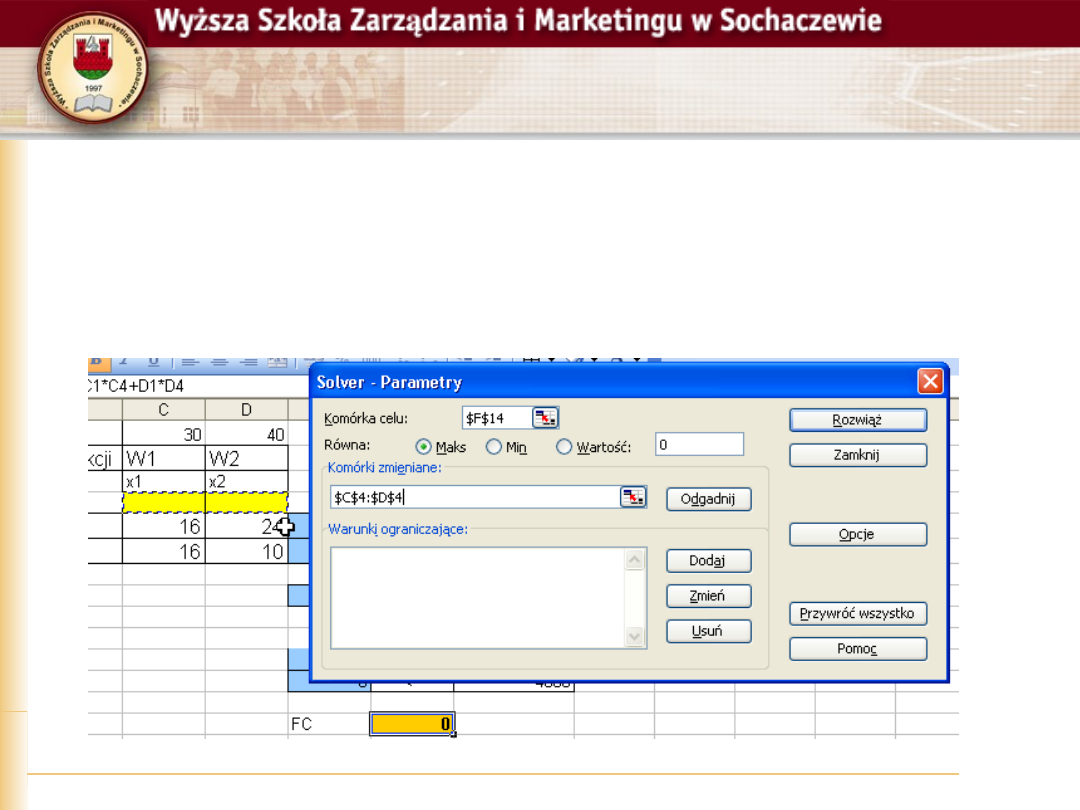
Solver, parametry



W pierwszym kroku wskazujemy komórkę w

której zapisaliśmy funkcję celu



Zaznaczamy także opcję Maks lub Min

Paweł Górczyński, Badania operacyjne, Slajd 18

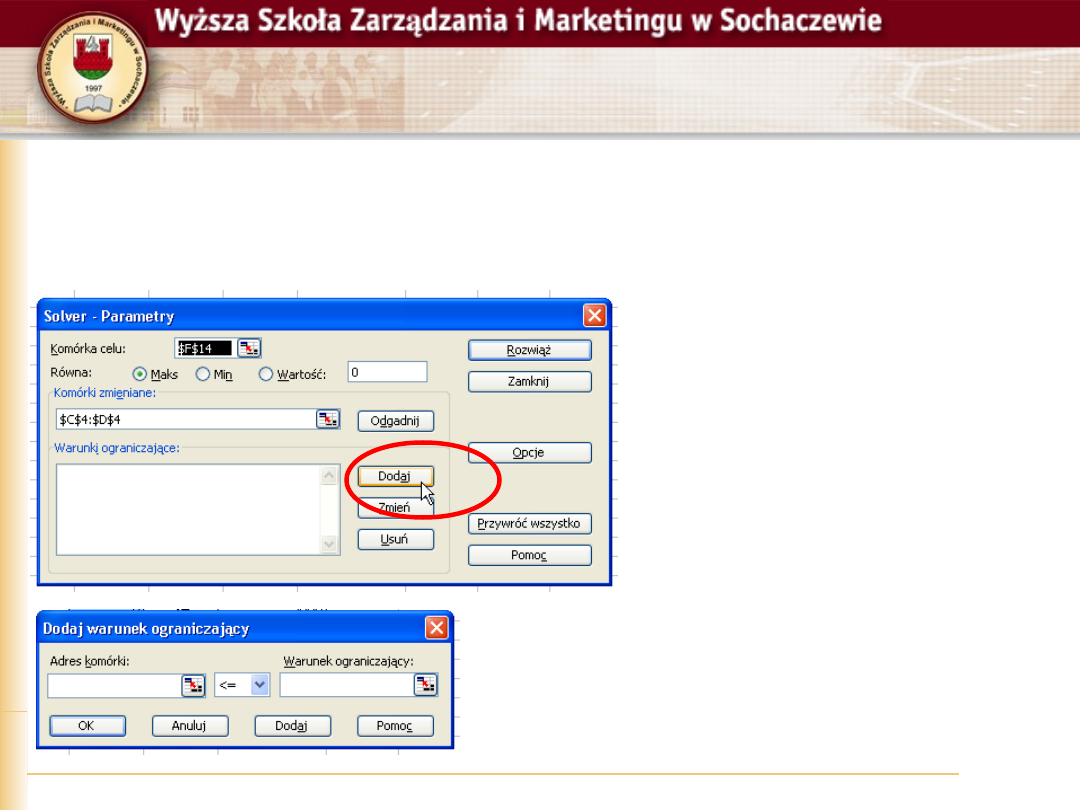
Solver, parametry



Kolejnym krokiem jest wskazanie

komórek zmienianych.

Paweł Górczyński, Badania operacyjne, Slajd 19

Solver, parametry



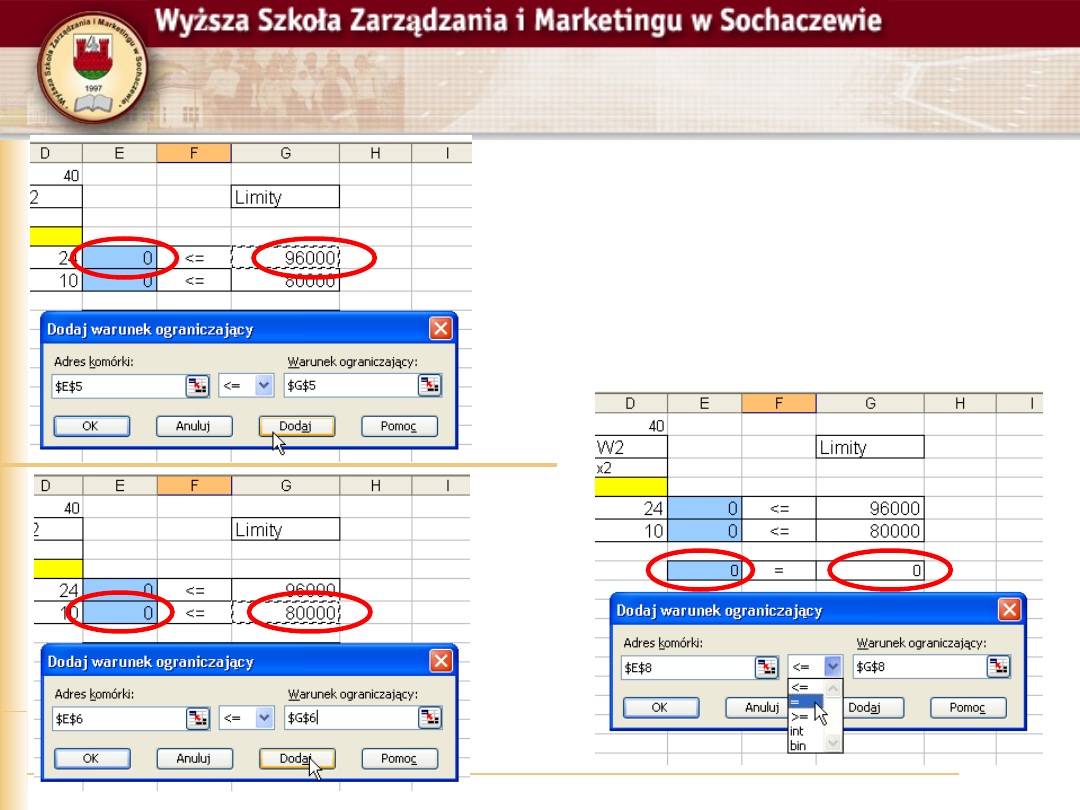
W kolejnym kroku definiujemy

warunki ograniczające



Okno dodawania

warunków składa się z

trzech elementów



Lewa strona warunku



Operator porównania



Prawa strona warunku



Definiowanie sprowadza

się do wskazań wcześniej

przygotowanych formuł



Po każdym warunku

klikamy przycisk Dodaj



Ostatni warunek

akceptujemy klawiszem

OK

Paweł Górczyński, Badania operacyjne, Slajd 20

Solver, parametry



Poniżej widać trzy

pierwsze warunki w

trakcie definiowania

Paweł Górczyński, Badania operacyjne, Slajd 21

Solver, parametry



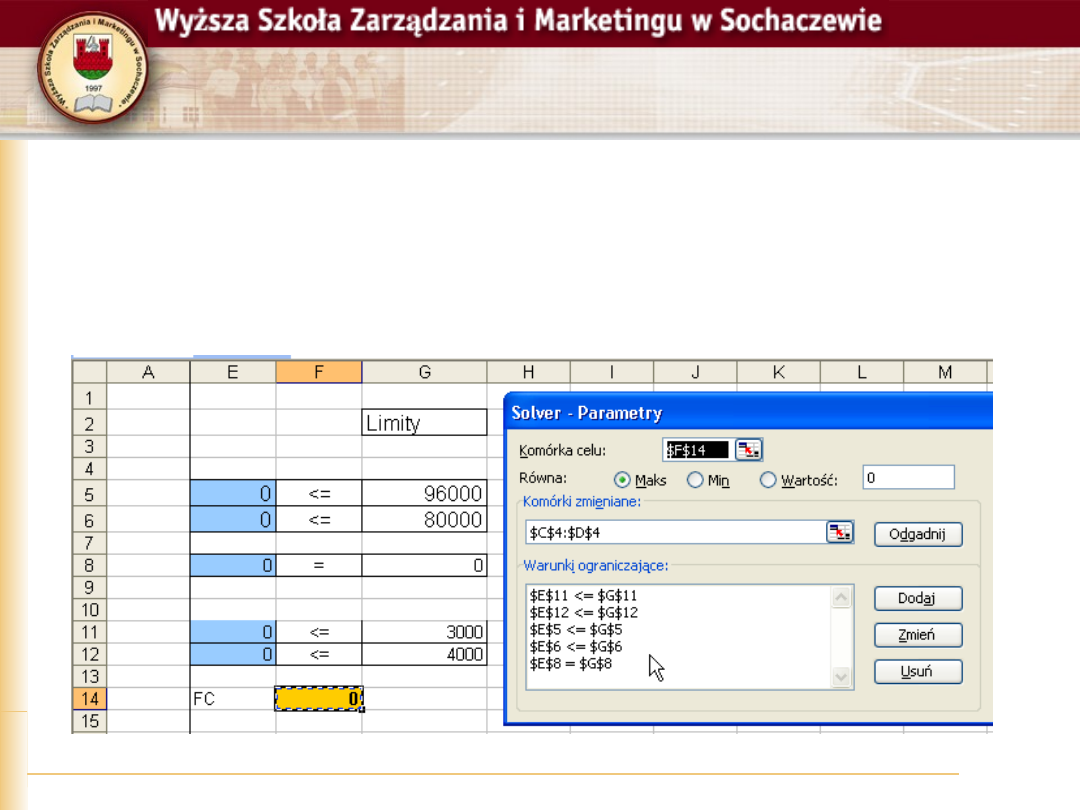
Po zdefiniowaniu wszystkich warunków w

oknie „Warunki ograniczające” możemy

podejrzeć i zweryfikować wszystkie

uprzednio zdefiniowane ograniczenia

Paweł Górczyński, Badania operacyjne, Slajd 22

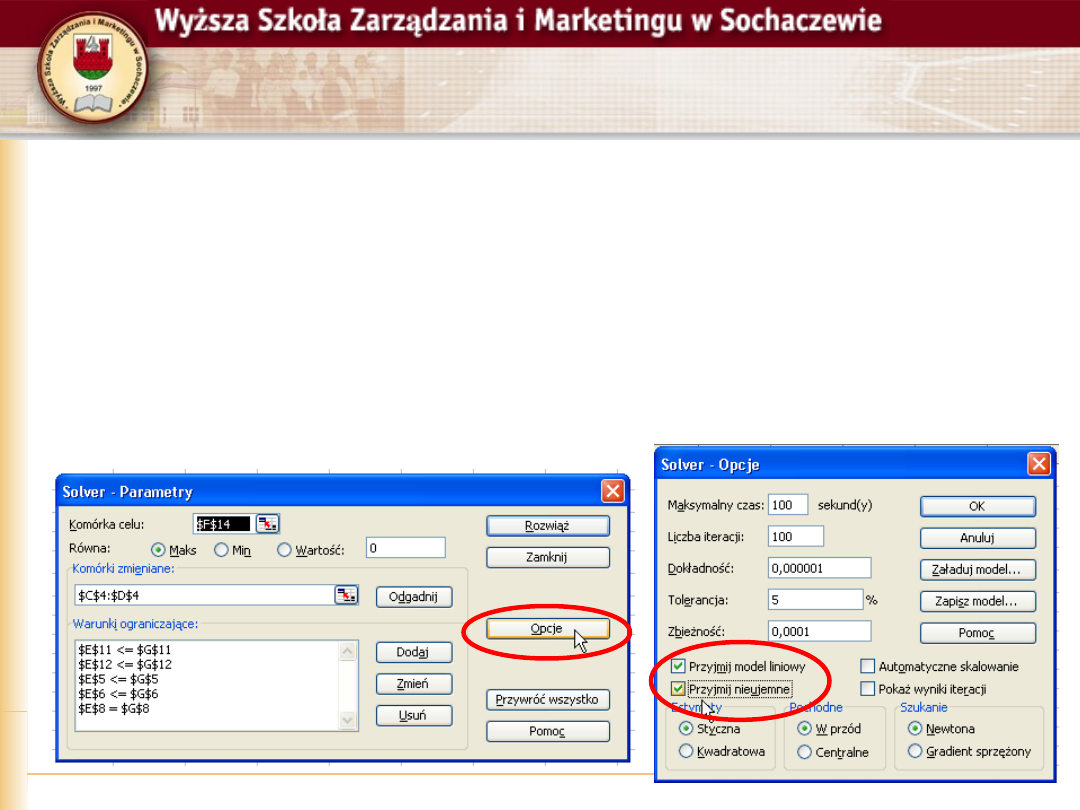
Solver opcje



Ostatnim krokiem, jest zdefiniowanie opcji



Z głównego okna wywołujemy okno

szczegółowe i aktywujemy dwa ustawienia



przyjmij model liniowy



przyjmij nieujemne

(to ograniczenie x1,x2 >= 0)

Paweł Górczyński, Badania operacyjne, Slajd 23

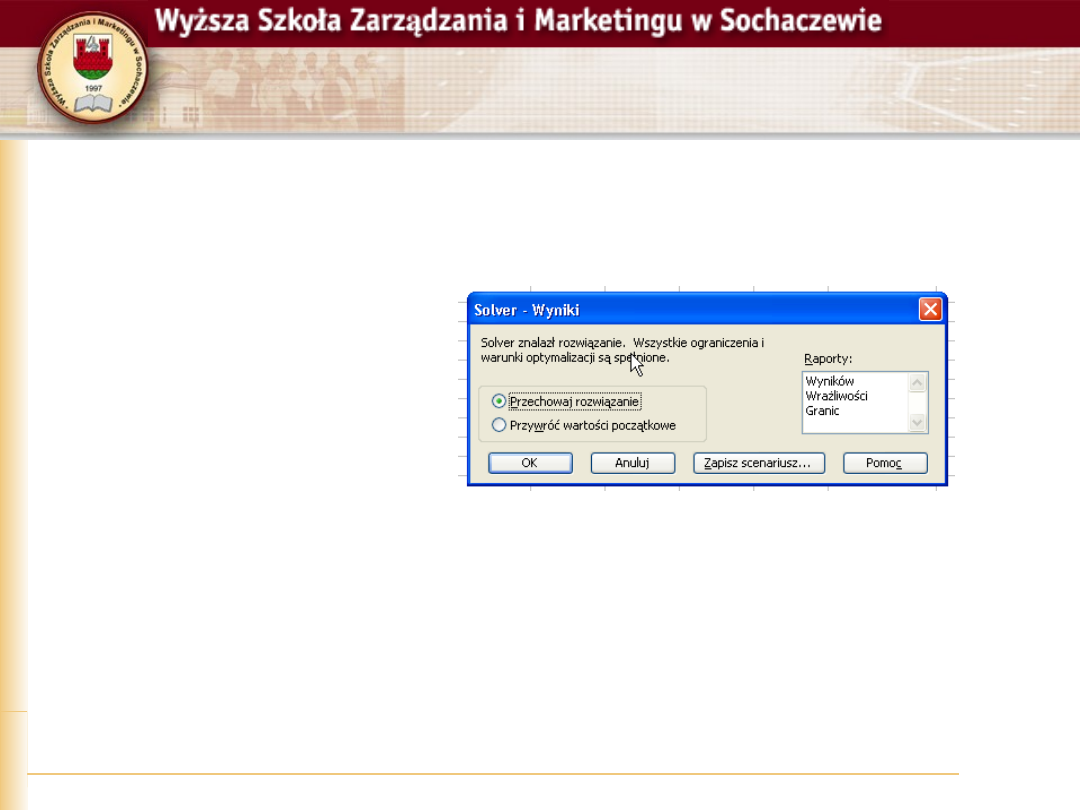
Solver rozwiązanie



Pozostało już tylko naciśnięcie przycisku

„Rozwiąż”



Jeśli wszystko zdefiniowaliśmy poprawnie

ujrzymy poniższy komunikat



Komunikaty należy czytać uważnie, ponieważ

komunikat informujący o braku rozwiązania

różni się tylko słowem „nie”



Możemy teraz nacisnąć klawisz OK. i przejść do

weryfikacji rozwiązania

Paweł Górczyński, Badania operacyjne, Slajd 24

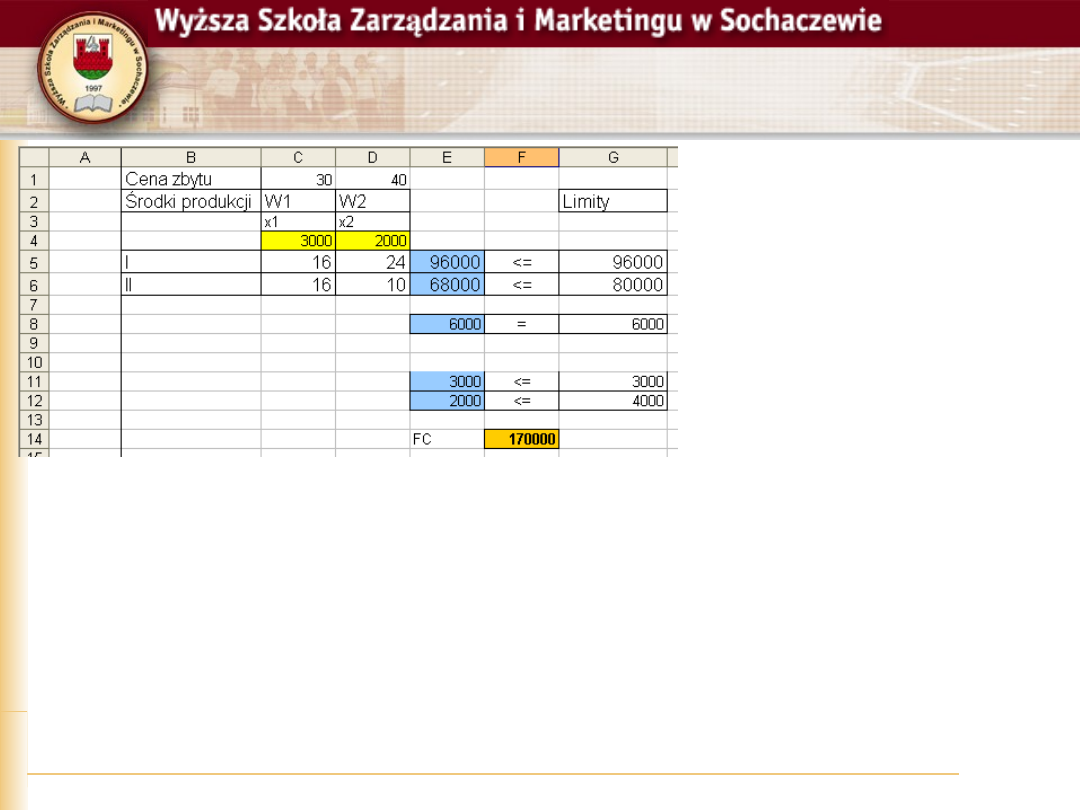
Solver, weryfikacja



Przede wszystkim

patrzymy na lewe

i prawe strony

warunków

ograniczających



Wszystkie warunki

są spełnione



Wartość funkcji celu to 170 000



Wartość x1 to 3000, wartość x2 to 2000

Paweł Górczyński, Badania operacyjne, Slajd 25

Odpowiedź do zadania



Ostatnim etapem rozwiązania jest

sformułowanie odpowiedzi



Na tym etapie nie mówimy już o x1 i x2



Przedsiębiorstwo powinno produkować 3000

jednostek Wyrobu W1 i 2000 jednostek wyrobu

W2



Maksymalna wartość przychodu wynosi 170 000

zł



Warto zastanowić się także, czy obydwa

surowce zostały w pełni wykorzystane a także

czy produkcja wykorzystuje w pełni dostępny

czas pracy oddziałów