22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Elementi di Astronomia e

Astrofisica per il Corso di

Ingegneria Aerospaziale

VI settimana

L'Atmosfera terrestre
Un esercizio di meccanica celeste

(in English)

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The terrestrial

atmosphere - 1

This chapter is devoted to the examination of the influence of
the Earth’s atmosphere on the apparent coordinates of the
stars and on the shape of their images; the discussion will be
limited essentially to the visual band. The discussion of the
effects

the

atmosphere

photometry

and

spectrophotometry are deferred to a later chapter.

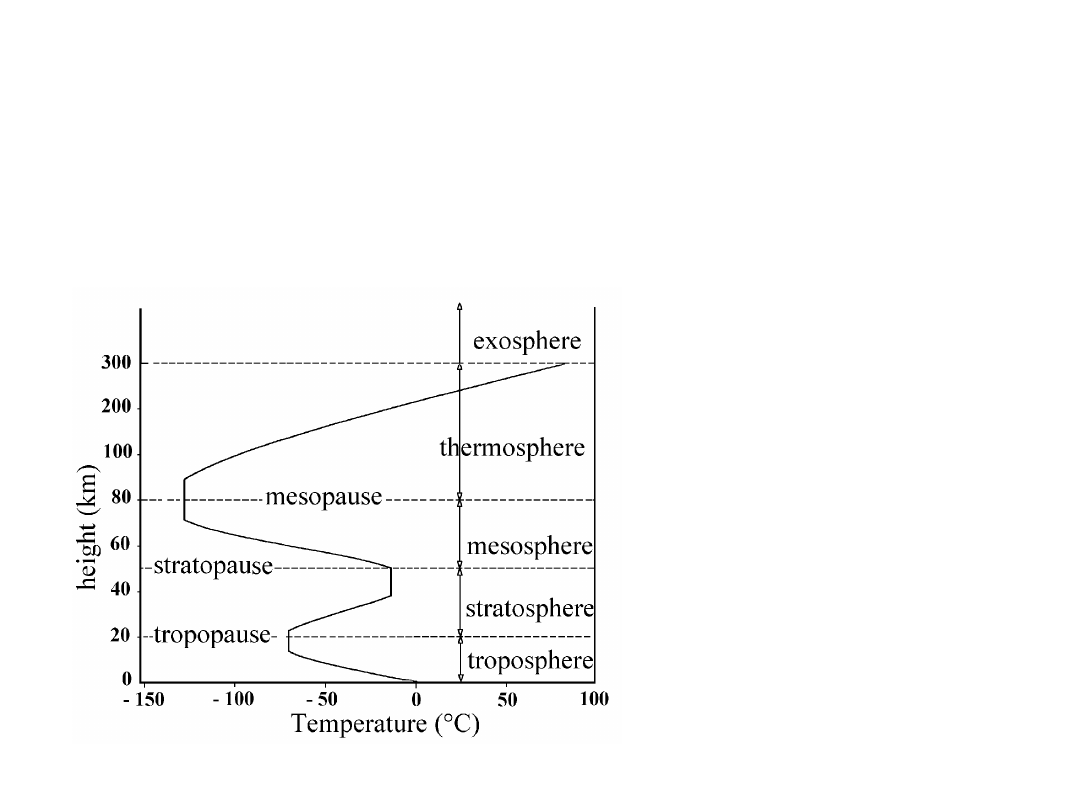
The figure gives a
schematic
representation

the

vertical

structure

the

atmosphere;

the

visual band is mostly
affected by what
happens

the

troposphere

namely in

the first

15 km or so of
height, where some
90% of the total
mass

the

atmosphere

contained.

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The terrestrial

atmosphere -2

Na Layer

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The terrestrial

atmosphere

- 3

The temperature profile in the troposphere is actually more
complicated than shown in the Figure. The height of the
tropopause (a layer of almost constant temperature) from the
ground ranges from 8 km at high latitudes to 18 km above the
equator; it is also highest in summer and lowest in winter. The
average temperature gradient is approximately –6 C/km, but
often, above a critical layer situated in the first few km,

the

temperature gradient is inverted

, with beneficial effects on

astronomical observations, thanks to the intrinsic stability of
all layers with temperature inversion (such as the
stratosphere and the thermosphere), essentially because
convection cannot develop. This is the case for instance of the
Observatory of the Roque de los Muchachos (Canary Islands,
height 2400 m a.s.l.), where the inversion layer is usually few
hundred meters below the telescopes at the top of the
mountain.

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Chemical composition and

structure

The chemical composition of the troposphere is mostly
molecular

Nitrogen

and

molecular

Oxygen

(approximately 3:4 and 1:4 respectively), with traces of the
noble gas

Argon

and of

water vapor

(the water vapor

concentration may be as high as 3% at the equator, and
decreases toward the poles).
Above the tropopause, at higher heights in the

stratosphere

the temperature raises considerably thanks to the solar UV
absorption by the Ozone (

) molecule with the process:

UV photon

+O+

heat

The

mesosphere

ranges from 50 to 80 km; in this region,

concentrations of

and

vapor

are negligible, hence the

temperature is lower than in the stratosphere. The chemical
composition of the air becomes strongly height-dependent, with
heavier gases stratified in the lower layers. In this region,
meteors and spacecraft entering the atmosphere start to warm
up.

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

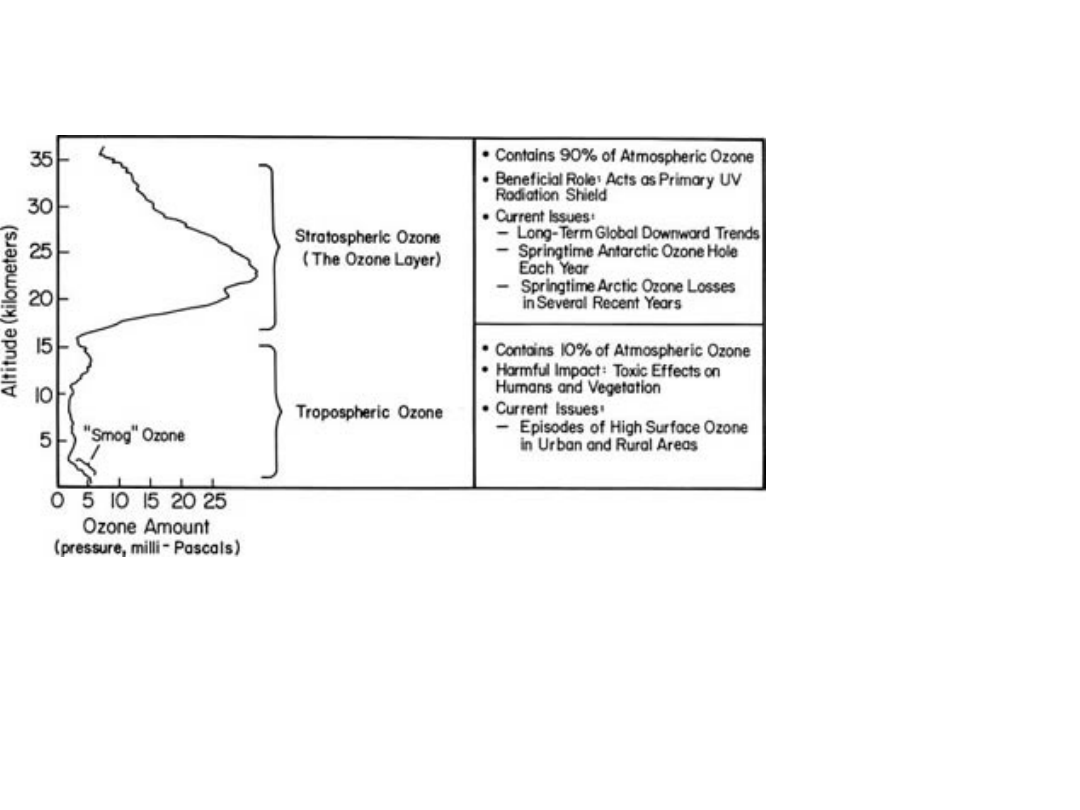
The ozone O

Most atmospheric ozone is concentrated in a layer in the
stratosphere, about 15-30 kilometers above the Earth's
surface. Even this small amount of ozone plays a key role in
the atmosphere, absorbing the

UVB

portion of the radiation

from the sun, preventing it from reaching the planet's surface.

is a molecule

containing 3 O
atoms.

It is blue

in color and has a
strong odor.

Normal molecular
O

, has 2 oxygen

atoms and is
colorless and
odorless. Ozone
is much less
common than
normal oxygen.
Out of each 10
million air
molecules, about
2 million are
normal oxygen,
but only 3 are
ozone.

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Water vapor nomenclature

- 1

Water vapor

is water in the gaseous phase.

The actual amount is the

concentration

of water vapor in the

air, the

relative concentration

is the ratio between the actual

amount to the amount that would saturate the air. Air is said
to be saturated when it contains the maximum possible
amount of water vapor without bringing on condensation. At
that point, the rate at which water molecules enter the air by
evaporation exactly balances the rate at which they leave by
condensation.
The partial pressure of a given sample of moist air that is
attributable to the water vapor is called the vapor pressure.
The vapor pressure necessary to saturate the air is the
saturation vapor pressure.

Its value depends only on the

temperature of the air

. (The Clausius-Clapeyron equation

gives the saturation vapor pressure over a flat surface of pure
water as a function of temperature.) Saturation vapor
pressure increases rapidly with temperature: the value at
32°C is about double the value at 21°C. The saturation vapor
pressure over a curved surface, such as a cloud droplet, is
greater than that over a flat surface, and the saturation vapor
pressure over pure water is greater than that over water with
a dissolved solute.

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Water vapor nomenclature

- 2

Relative humidity

is the ratio of the actual vapor pressure to

the saturation vapor pressure at the air temperature, expressed
as a percentage. Because of the temperature dependence of the
saturation vapor pressure, for a given value of relative humidity,
warm air has more water vapor than cooler air. The d

ew point

temperature

is the temperature the air would have if it were

cooled, at constant pressure and water vapor content, until
saturation (or condensation) occurred. The difference between
the actual temperature and the dew point is called the dew
point depression.
The wet-bulb temperature is the temperature an air parcel
would have if it were cooled to saturation at constant pressure
by evaporating water into the parcel. (The term comes from the
operation of a psychrometer, a widely used instrument for
measuring humidity, in which a pair of thermometers, one of
which has a wetted piece of cotton on the bulb, is ventilated. The
difference between the temperatures of the two thermometers is
a measure of the humidity.) The wet-bulb temperature is the
lowest air temperature that can be achieved by evaporation. At
saturation, the wet-bulb, dew point, and air temperatures are all
equal; otherwise the dew point temperature is less than the wet-
bulb temperature, which is less than the air temperature.

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

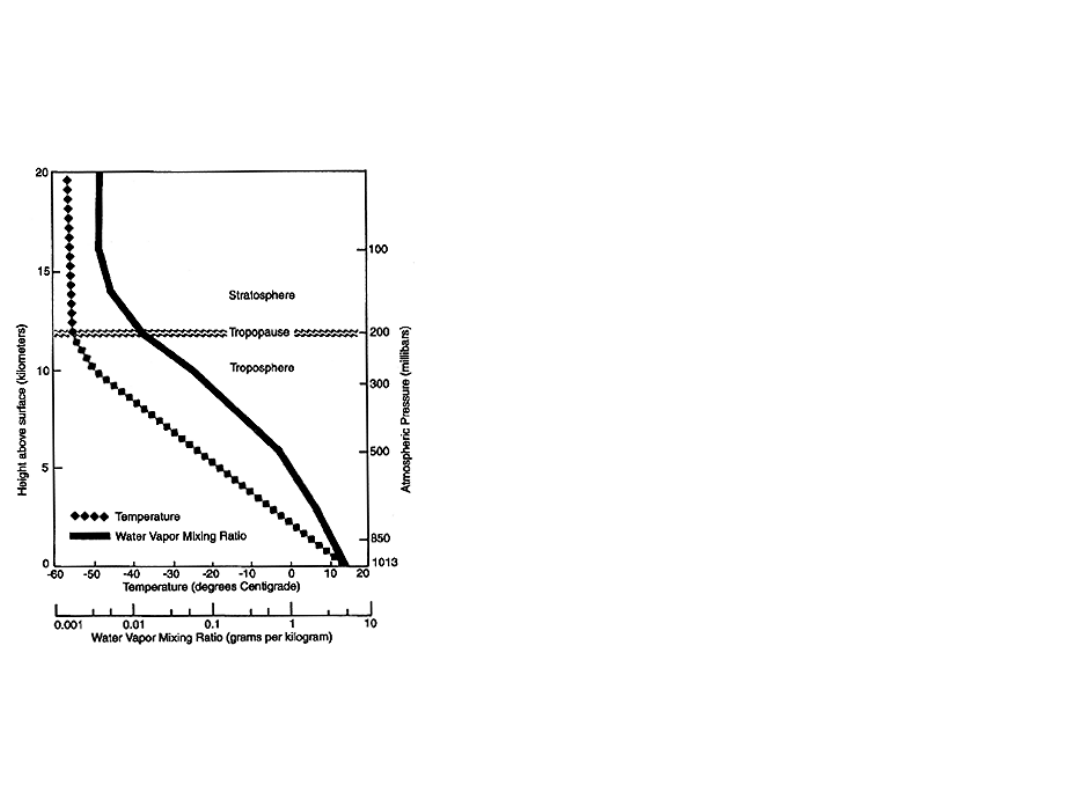
Water Vapor Mixing ratio

Specific humidity

is the ratio of the

mass of water vapor in a sample to the
total mass, including both the dry air
and the water vapor. The

mixing ratio

is the ratio of the mass of water vapor to
the mass of only the dry air in the
sample. As ratios of masses, both
specific humidity and mixing ratio are
dimensionless numbers. However,
because atmospheric concentrations of
water vapor tend to be

at most only a

few percent of the amount of air

(and

usually much lower), they are both often
expressed in units of grams of water
vapor per kilogram of (moist or dry) air.
Absolute humidity is the same as the
water vapor density, defined as the mass
of water vapor divided by the volume of
associated moist air and generally
expressed in grams per cubic meter. The
term is not much in use now.

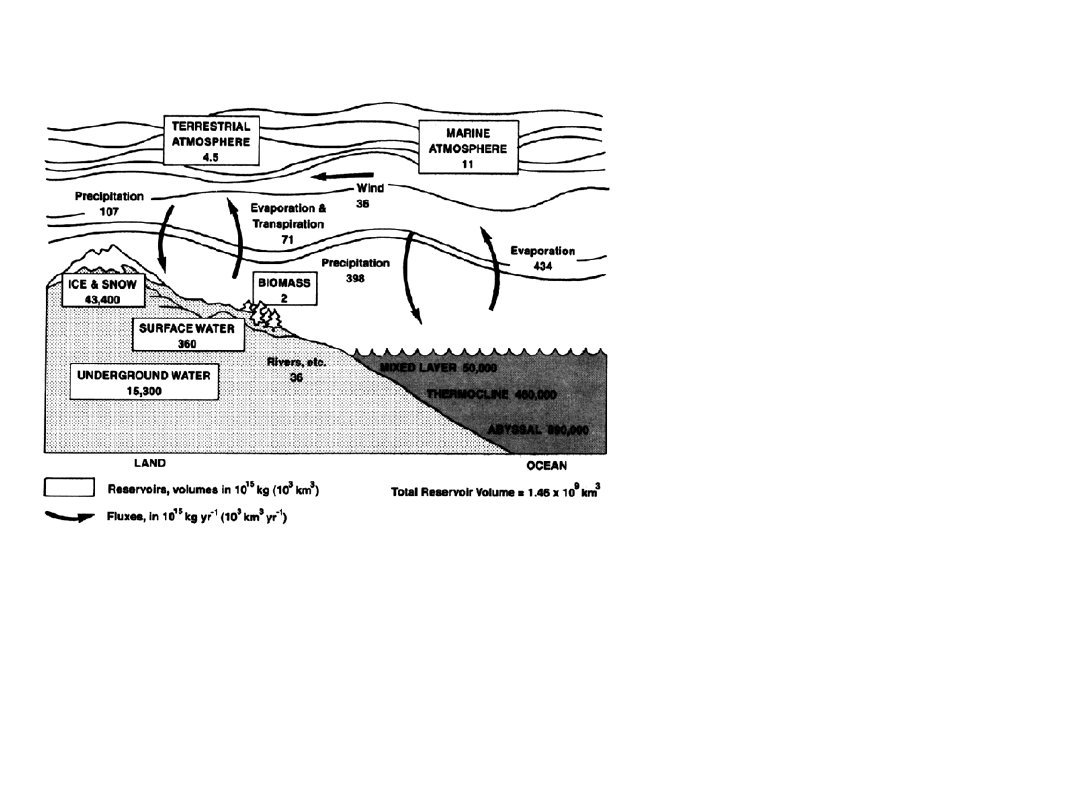
22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Water reservoir

Water

vapor

constantly

cycling

through

the

atmosphere,
evaporating from the
surface, condensing to
form clouds blown by
the

winds,

and

subsequently
returning to the Earth
as precipitation. Heat
from the Sun is used
to evaporate water,
and this heat is put
into the air when the
water condenses into
clouds

and

precipitates.

This

evaporation

condensation cycle is
an

important

mechanism

for

transferring

heat

energy

from

the

Earth's surface to its
atmosphere and in
moving heat around
the Earth.

Water vapor is the most abundant of the
greenhouse gases in the atmosphere and the
most important in establishing the Earth's
climate. Greenhouse gases allow much of the
Sun's shortwave radiation to pass through
them but absorb the infrared radiation
emitted by the Earth's surface. Without water
vapor and other greenhouse gases in the air,
surface air temperatures would be well below
freezing.

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Aerospace

devices

A multitude of
systems exist for
observing water
vapor on a global
scale and at high
altitudes,
supplementing the
instruments on the
ground, that measure
in special sites and at
ground level. Each
has different
characteristics and
advantages. To date,
most large-scale
water vapor
climatological studies
have relied on
analysis of
radiosonde data,
which have good
resolution in the
lower troposphere in
populated regions but
are of limited value at
high altitude and are
lacking over remote
oceanic regions.

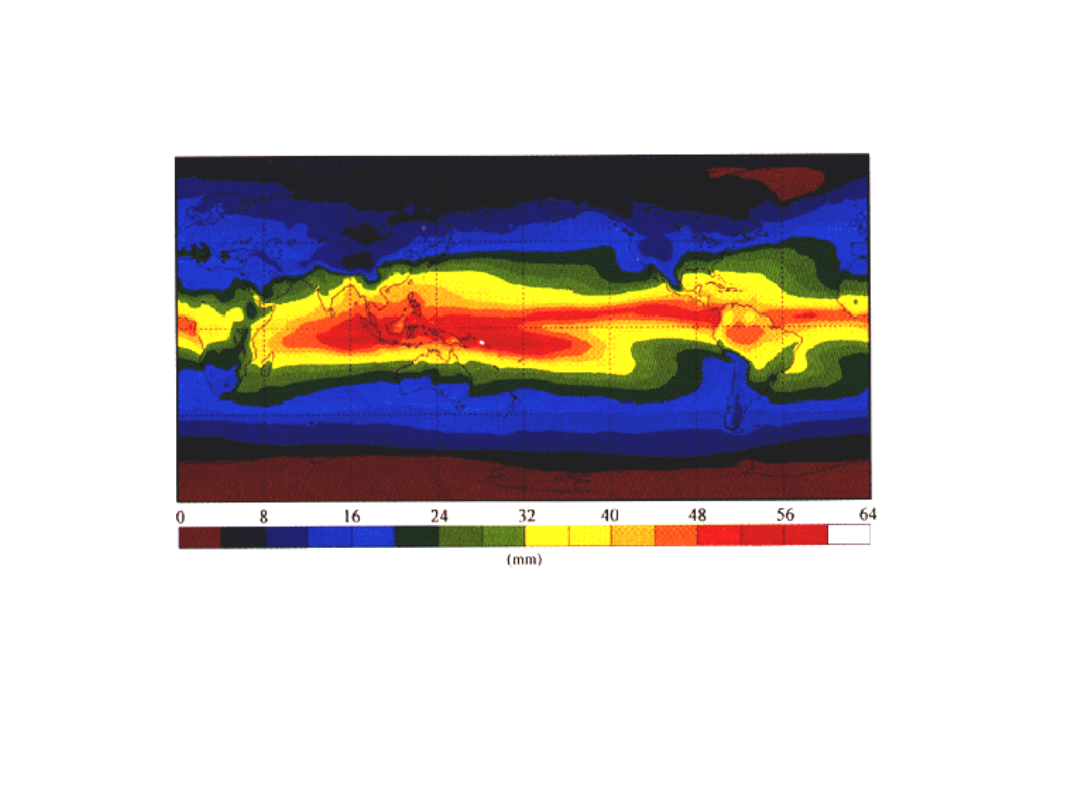
22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The Water Vapor content

in 1992

NASA Water Vapor Project (NVAP) Total Column Water

Vapor 1992

The mean distribution of precipitable water, or total atmospheric
water vapor above the Earth's surface, for 1992. This depiction
includes data from both satellite and radiosonde observations.

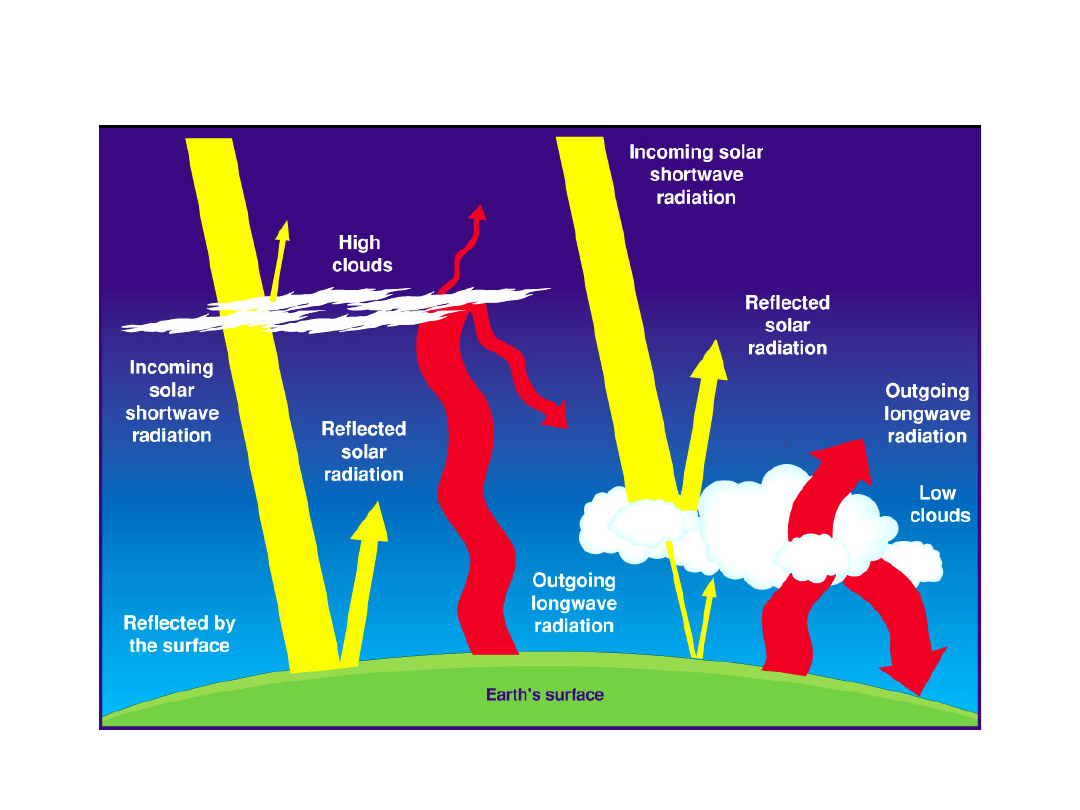
22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Cloud effects on Earth

Radiation

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The outer layers

Following the smooth decrease in the mesosphere, the
temperature raises again in the

thermosphere

, because the

solar UV and X-rays, and the energetic electrons from the
magnetosphere can partly ionize the very thin gases of the
thermosphere.
The weakly ionized region which conducts electricity, and
reflects radio frequencies below about 30 MHz is called

ionosphere

; it is divided into the regions

(60-90 km),

(90-140 km), and

(140-1000 km), based on features in the

electron density profile.
Finally, above 1000 km, the gas composition is dominated by
atomic Hydrogen escaping the Earth’s gravity, which is seen
by satellites as a bright

geocorona

in the resonance line

Ly-





= 1216 Å.

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Refraction Index

As is well known, the light propagates in a straight line in any
medium of constant refraction index

, with a phase velocity

given by

1/2

1/( )

c n

where



is the dielectric constant and



the magnetic

permeability of the medium. All these quantities are
wavelength dependent. The group velocity

is instead:

dv/d

= -

At the separation surface between two media of different
refraction index (say vacuum/air), the ray changes direction,
so that the observer immersed in the second medium sees the
light coming from an apparent direction different from the
‘true’ one (see Figure):

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The atmospheric

refraction - 1

Suppose that the atmosphere can be treated as a succession of
parallel planes (hypothesis of

plane-parallel stratification

by virtue of its small vertical extension with respect to the
Earth’s radius. According to

Snell’s laws

, when the ray

coming from the region of index of refraction

encounters the

separation surface with a medium of refraction index

part of the energy will be reflected to the left, on the same
hemi-space with the same angle

with respect to the normal.

This part will not be considered here, it only implies a dimming
of the source. The remaining fraction will be

refracted

, in the

same plane as the incident ray, to an angle

. Indeed, in a

clear atmosphere without clouds, no sharp air-vacuum
separation surface exists, the refraction index gradually
increases from 1 to a final value

near the ground, with

typical scale lengths much greater than the wavelength of light
(as already said, we limit our considerations to the visual
band), so that the continuously varying direction can be
considered as a series of finite steps in the plane passing
through the vertical and the direction to the star.

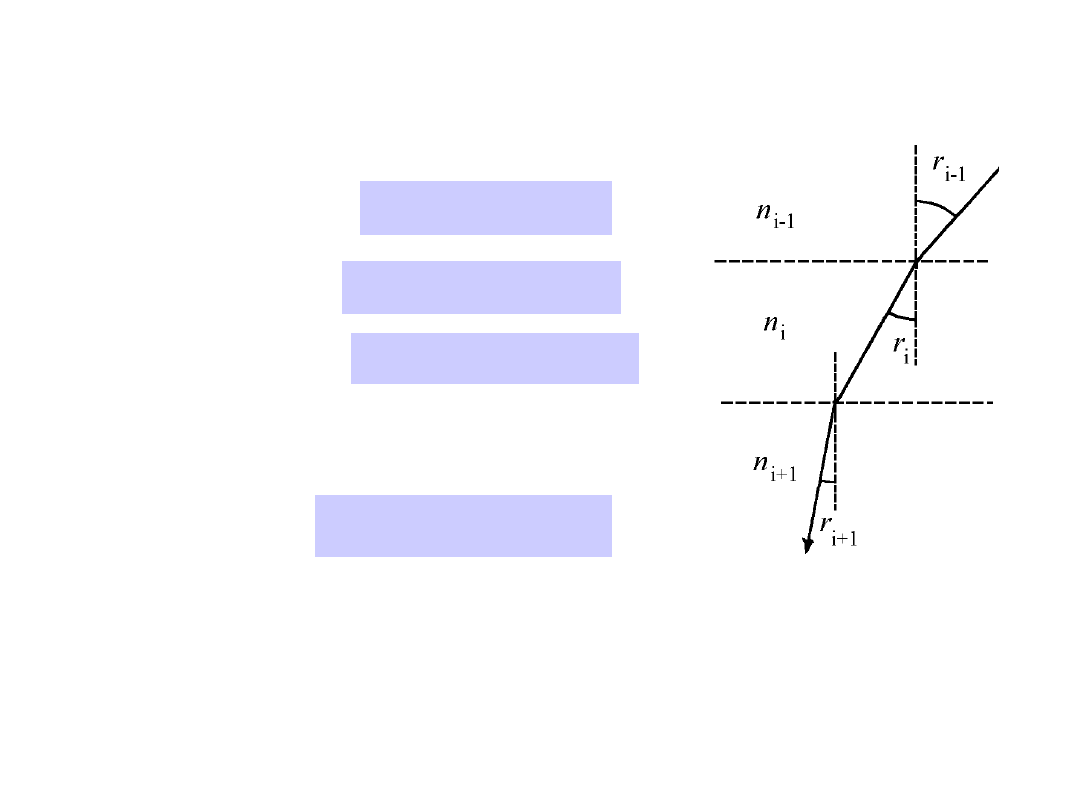
22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The atmospheric

refraction - 2

sin

1 1

sin

r n

sin

where

i+1

, and

i+1

. By equating each term:

sin

Therefore: in a plane-parallel atmosphere the total angular
deviation only depends on the refraction index close to the
ground, independent of the exact law with which it varies
along the path.

By following each refraction in cascade we have:

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The atmospheric

refraction - 3

By virtue
of

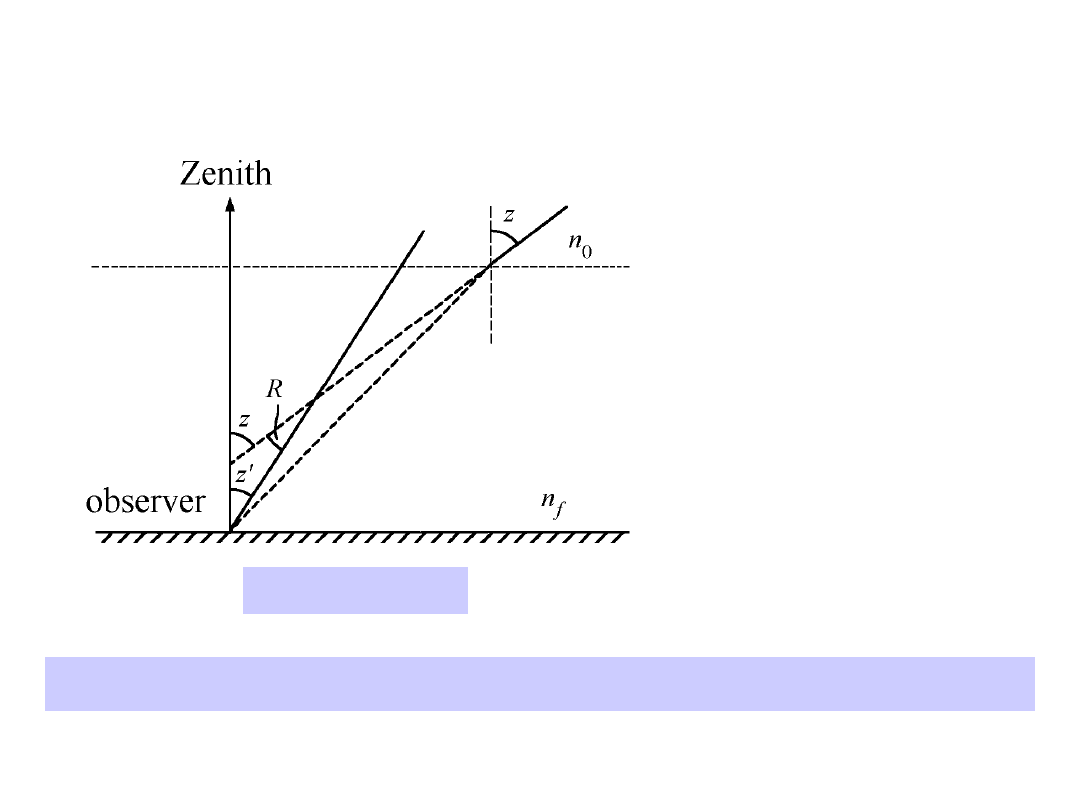
The net effect is as
shown in the figure:
the star is seen in
direction

z’

smaller

than the true direction

, namely closer to the

local Zenith, by an
amount

which is the

atmospheric
refraction:

z’

–

sin

and for small

’s (in practice, if

< 45°):

sin ' sin

sin( '

) sin 'cos

cos 'sin

sin '

cos '

z R

+ =

�

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The atmospheric

refraction - 4

(

1)tan '

In the visual band, for average values of temperature and
pressure (

= 273 K,

= 760 mm Hg),

 1.00029, so that

in round numbers

R(15°)  16”,

R(45°)  60”

Already for Zenith distances as small as 20°, the refraction is
larger than the annual aberration, and of any of the effects
discussed in previous chapters that alter the apparent
direction of a star.

and finally:

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The atmospheric

refraction - 5

For zenith distances larger than 45°, the path of the ray
inside the atmosphere is so long that the curvature of the
Earth cannot be ignored, and the mathematical treatment
becomes more intricate, even restricting it to successive
refraction in the same plane with

decreasing outwards

with continuity.

sin '

R a n

n d n

�

= �

� -

�

tan '

tan ' (

1) (1

)tan '

tan '

R A

z B

�

After

several

mathematical

steps:

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

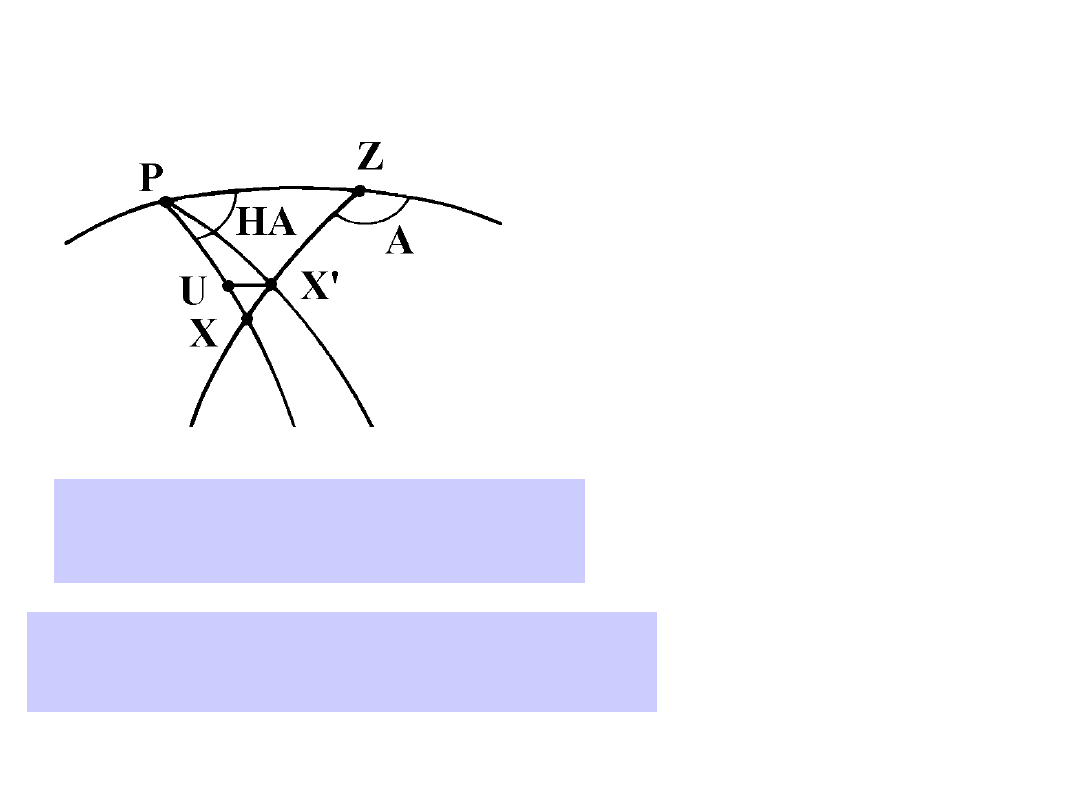
Effect of the refraction on the

coordinates

The main effect of refraction is
to move the star closer to the
Zenith in the vertical plane,
thus raising its elevation

but

leaving essentially unchanged
its azimuth

XX’ = R = h

PXX’ = PXZ = q

ZX = z, ZX’ = z’

PX = 90-



XU = 



cos

( '

)cos

sin

cos

a a

d d d

- D

�

D = -

�

cos cos

sin cos

cos sin cos

sin sin

cos

sin

cos sin

For an object in
meridian,

the

refraction is all in
declination, and in
particular this is
true for the Sun at
true noon.

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Approximate formulae for

refraction

For Zenith distance not greater than approximately 45°, after
several passages we finally get:

sec sin

(

cos

tan tan

tan

tan cos

(

cos

tan tan

�

D =

�

�D = -

�

by means of which formulae we can derive the true (or the
apparent, according to the sign)

topocentric

positions.

Obviously no such correction is necessary for a telescope in
outer Space.

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

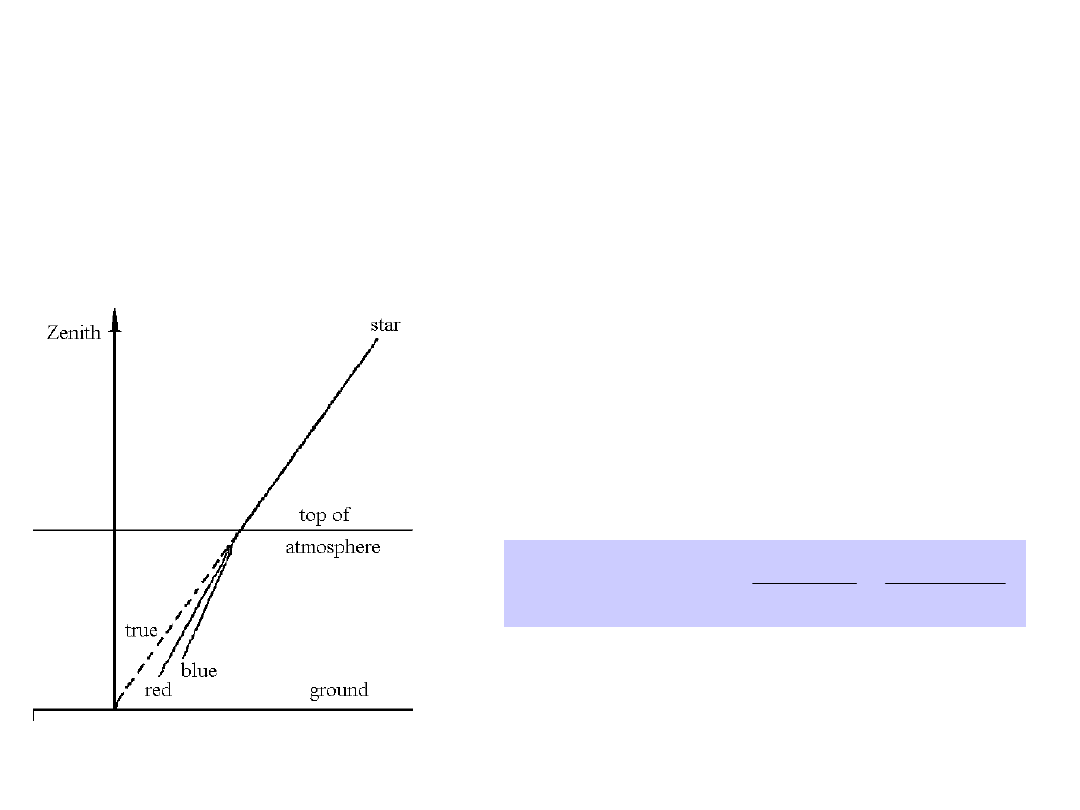
The chromatism of the

refraction

The refraction index

depends from the wavelength,

diminishing from the blue to the red, and the same will be true
for the refraction angle

: the image on the ground of the star

is therefore a succession of monochromatic points aligned
along the vertical circle; the blue ray will be below the red
one, and thus the blue star will appear to the eye above the
red one

The atmosphere behaves therefore
like a prism producing a

short

spectrum in the vertical plane

whose length increases with the
zenith distance, reaching several
arc seconds at low elevations. The
relationships



)

can

expressed

the

so-called

Cauchy’s formula:

0.00566 0.000047

( ) 0.00028 1

n l

�

(



in micrometers), corresponding to a

variation of about 2% over the visible
range, namely to about

1”.2 at 45°.

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Density - temperature

relationship

Once we have fixed



, the refraction index

depends from the

density



according to Gladstone-Dale’s law:

- =

and with the hypothesis of a perfect gas of pressure

temperature

and molecular weight



r =

(where

is now the gas universal

constant)

- =

P T

1 78.7 10

- �

�

( /760)

60".4

tan

( / 273)

�

(

in mm Hg,

in K)

22/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Vertical gradients of

temperature

Calling

the height over the ground,

we have:

n k

�

1 d

P T

P T P

T H T

P H

�

The variation of pressure with the height is equal to the weight
of the air in the elementary volume having unitary base and
height

g H

so
that:

�

where the constant

g/R

equals approximately 3.4 K/km, and is

called

adiabatic lapse

Hence the conclusion that the variations of the refraction index
depend from the vertical gradients of the temperature. A
practical consequence is that all effort must be made to control
and minimize those gradients over the accessible volume of the
telescope enclosure.

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Turbulence, Scintillation,

Seeing

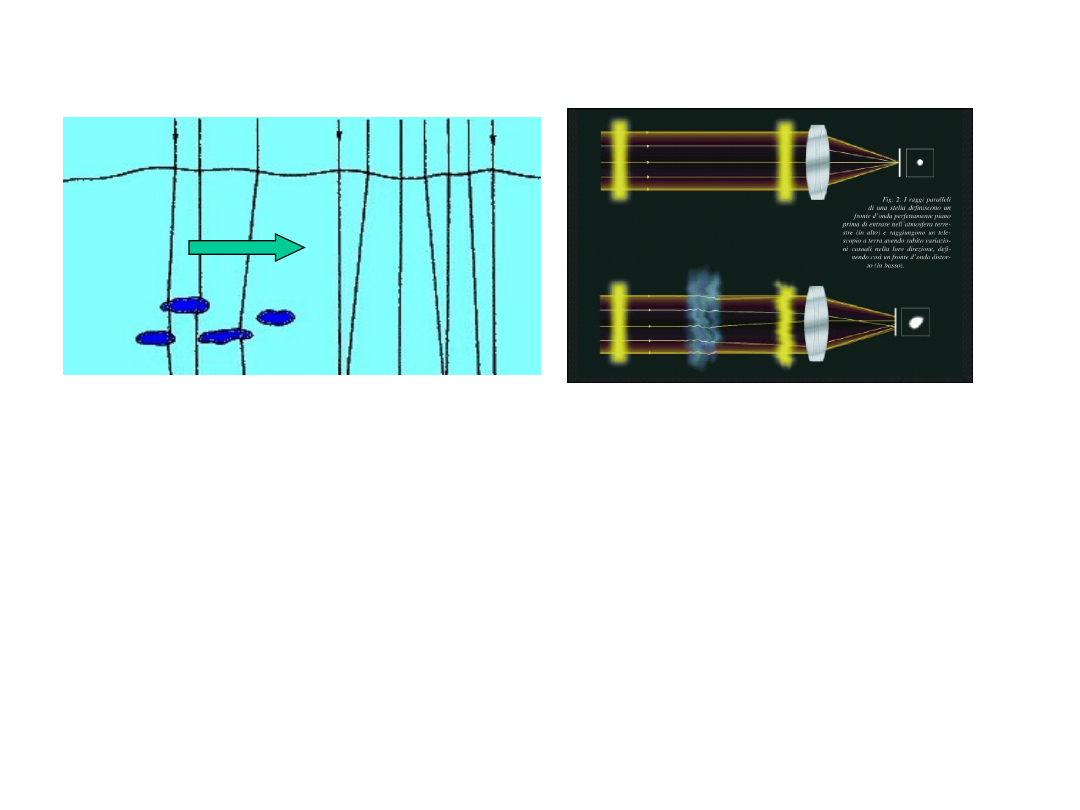
The Earth's atmosphere is turbulent and variations in the
index of refraction cause the plane wavefront from distant
objects to be

distorted

. This distortion introduces

amplitude

variations

positional shifts

and

image degradation

This causes two astronomical effects:

•scintillation

, which is amplitude variations, which typically

varies over scales of few cm: generally very small for large
aperture telescopes

•seeing

: positional changes and image quality changes. The

effect of seeing depends on aperture size: for small apertures,
one sees a diffraction pattern moving around, while for large
apertures, one sees

a set of diffraction patterns

(

speckles

)

moving around on scale of ~1 arcsec.
These observations imply:

• wavefronts are flat on scales of small apertures

• instantaneous slopes vary by ~ 1 arcsec.

The typical time scales are few

milliseconds

and up.

The effect of seeing can be derived from theories of
atmospheric turbulence, worked out originally by
Kolmogorov, Tatarski, Fried.

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Structure function

The structure of the refraction index

in a turbulent field can

be described statistically by a

structure function

( )

(

)

( )

D x

n r x n r

=� + -

�

where

is separation of points,

is position. Kolmogorov

turbulence gives:

2 2

( )

D x

C x

where

is the refractive index structure constan

t. From this,

one can derive the

phase structure function

at the

telescope aperture:

5/2

6.88

where the coherence length

(also known as the Fried

parameter) is:

3/5

6/5

3/5

0.185

cos

z C h

�

where

is zenith angle,



wavelength. Using optics theory,
one can convert D



into an

image shape.

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The Fried parameter

Notice that

increases with 



6/5





1. 2

Physically, the image size

from seeing is (roughly) inversely

proportional to

�

as compared with the image size from a diffraction-limited
telescope of aperture

�

Seeing dominates when

; a larger

means better

seeing. Seeing is more important than diffraction at shorter
wavelengths, diffraction more important at longer wavelengths;
effect of diffraction and seeing cross over in the IR (at  5

microns for 4m); the crossover falls at a shorter wavelength for
smaller telescope or better seeing. Fried’s parameter

varies

from site to site and also in time. At most sites, there seems to
be three regimes called:

surface layer

(wind-surface interactions and manmade seeing),

planetary boundary layer

( influenced by diurnal heating),

free atmosphere

(10 km is tropopause: high wind shears)

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

An example of

A typical
site has

 10

at 5000Å ,
namely a
seeing of
1". On
rare
occasions,
in the
best sites,
the seeing
can be as
low as
0".3.

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The isoplanatic angle

We also have to consider the coherence of the same
turbulence pattern over the sky: coherence angle call the

isoplanatic angle

0.314 /

r H

q �

where

is the average distance of the seeing layer:

For

 10 cm,

= 5000 m ,



 1.3 arcsec.

In the infrared

 70 cm,

= 5000 m ,



 9 arcsec.

Note however, that the ``isoplanatic patch for image motion"
(not wavefront) is  0.3

D/H

. For

= 4m,

= 5000 m,



kin



50 arcsec.

Another useful parameter is the correlation time



, which is approximately the dimension of the typical air

bubble divided by the velocity of the wind. As

also



increases with



6/5

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The seeing

Bubbles of air having slightly different temperatures, and
therefore slightly different refractive indexes, are carried by the
wind across the aperture of the telescope.
The Fried parameter

can be used to simplify the description

of a very complex rapidly varying medium, namely the typical
size of the bubble. Values vary from few centimeters (a poor site)
to some 30 cm (a very good site).

can be understood

also as

the effective

diameter

of the

diffraction limited telescope in that site (with respect to the
angular resolution).

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Representation of the

seeing

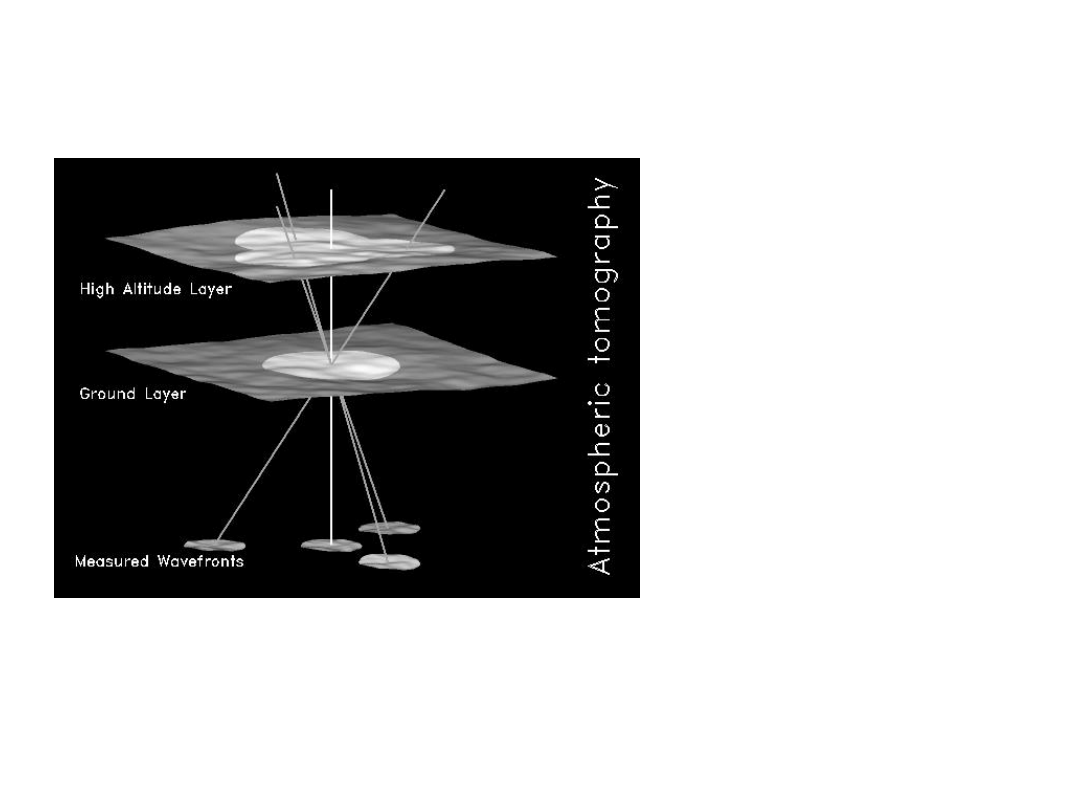
There are two main
components of the
seeing:
•one coming from high
altitudes (choice of
site)

•one due to ground

layers (it can be

actively controlled by

shape of dome and

proper thermalisation

of structure)

• The spectral power of

the air turbulence is

appreciable over a large

interval of frequencies ,

say 1 to 1000 Hz, with a

1/f distribution.

The angles are exaggerated, actually AdOpt correction can be
made over small fields of view. Another useful parameter is the
maximum angle over which fluctuations are coherent
(isoplanatic angle). Both Fried’s parameter and isoplanatic
angle improve with increasing wavelength, the correction is
better in the IR than in the Visible.

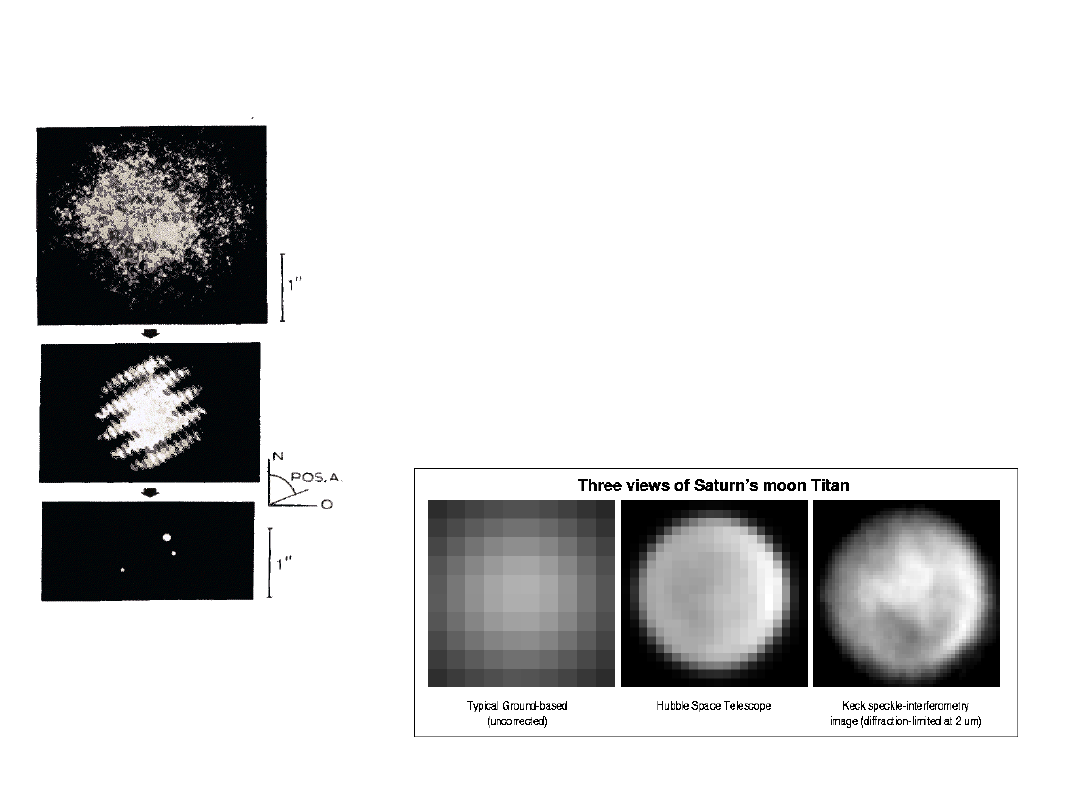
23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

A first remedy: Speckle

Interferometry

• a very large number of short duration

exposures are taken with very long focal length

(say 100m) and narrow bandwidth (say 1 nm);

in each exposure the seeing is frozen, each

speckle represents the diffraction figure of the

aperture

• Fourier Transforms allow the reconstruction of

the true image;

• The technique works well for simple structures

(e.g. double or multiple stars, disks).

Obtained
with the
Asiago 1.8
cm telescope

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

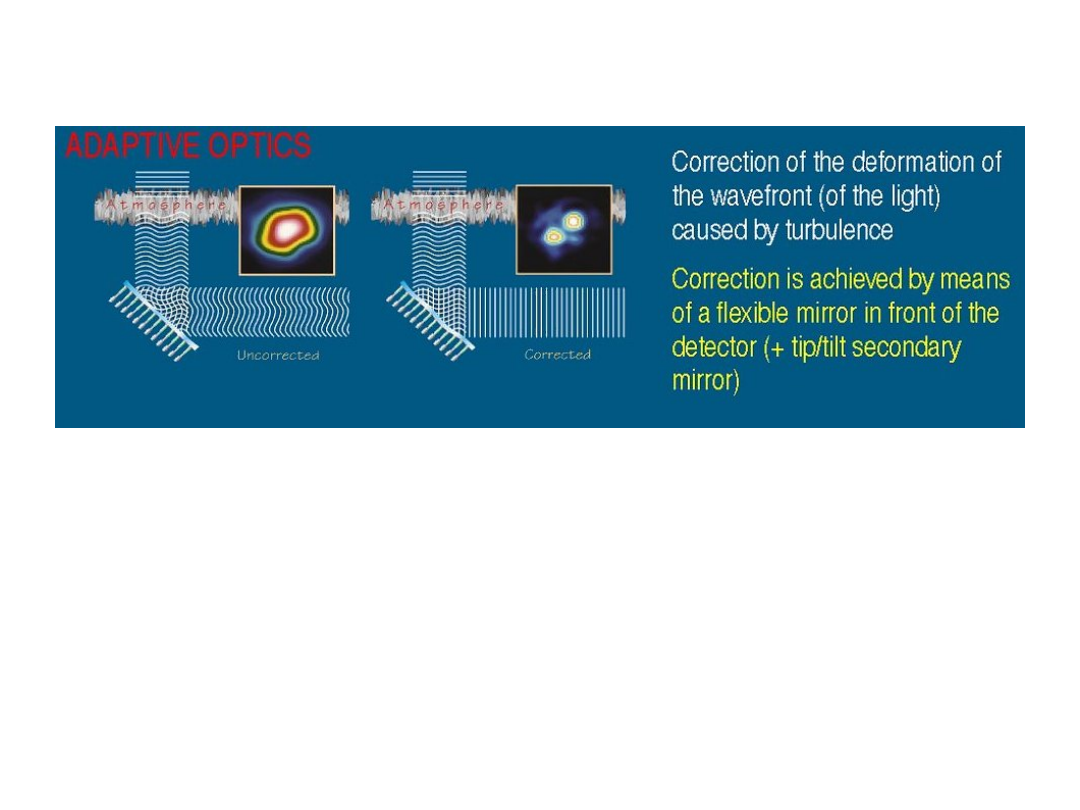
A better remedy: Adaptive

Optics

The fairly complex techniques that are nowadays
implemented on the largest telescopes to contrast the
seeing are known collectively as

Adaptive Optics

devices.
• A suitable reference wavefront is also necessary

Suitably bright stars are rare.

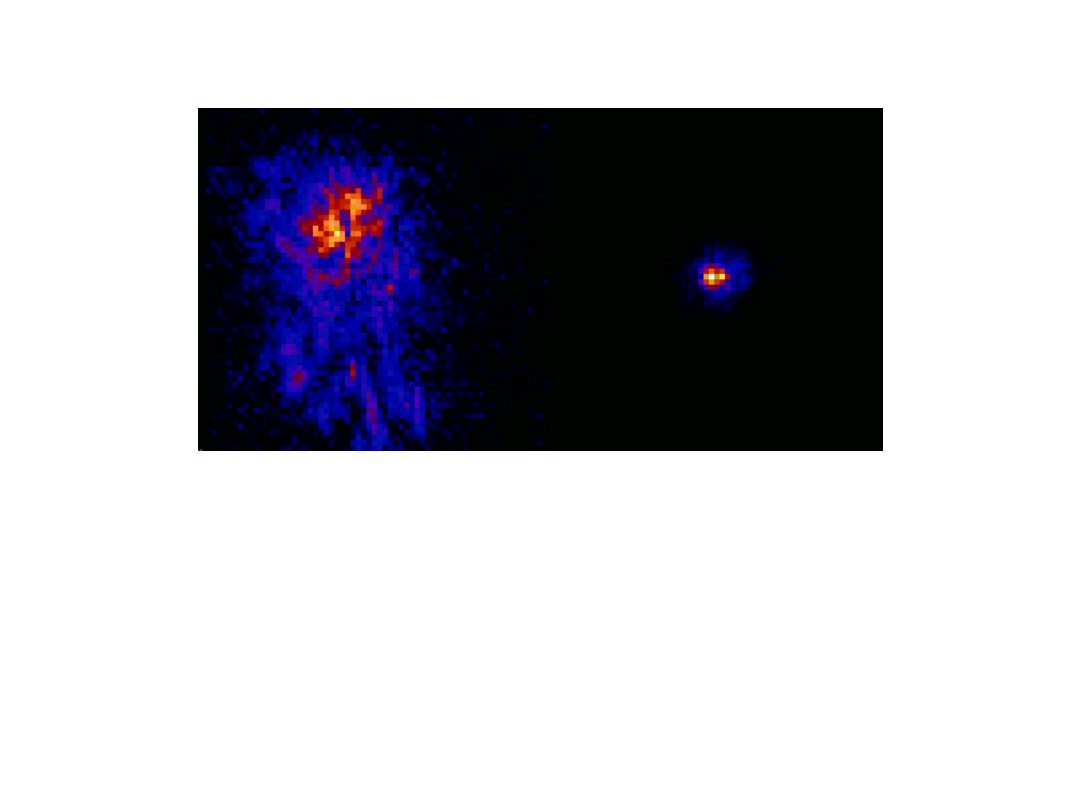
•An artificial

laser star

is a possible solution.

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The artificial laser star

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Before and after AdOpt

If one ‘freezes’ the image with short exposure times (say less
than 0.01 sec) and a narrow filter, the seeing image breaks up in
large number of ‘speckles’, each having dimension of the order
of the diffraction figure of the telescope.
The number of speckles is of the order of :

(seeing diameter/diffraction figure)

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

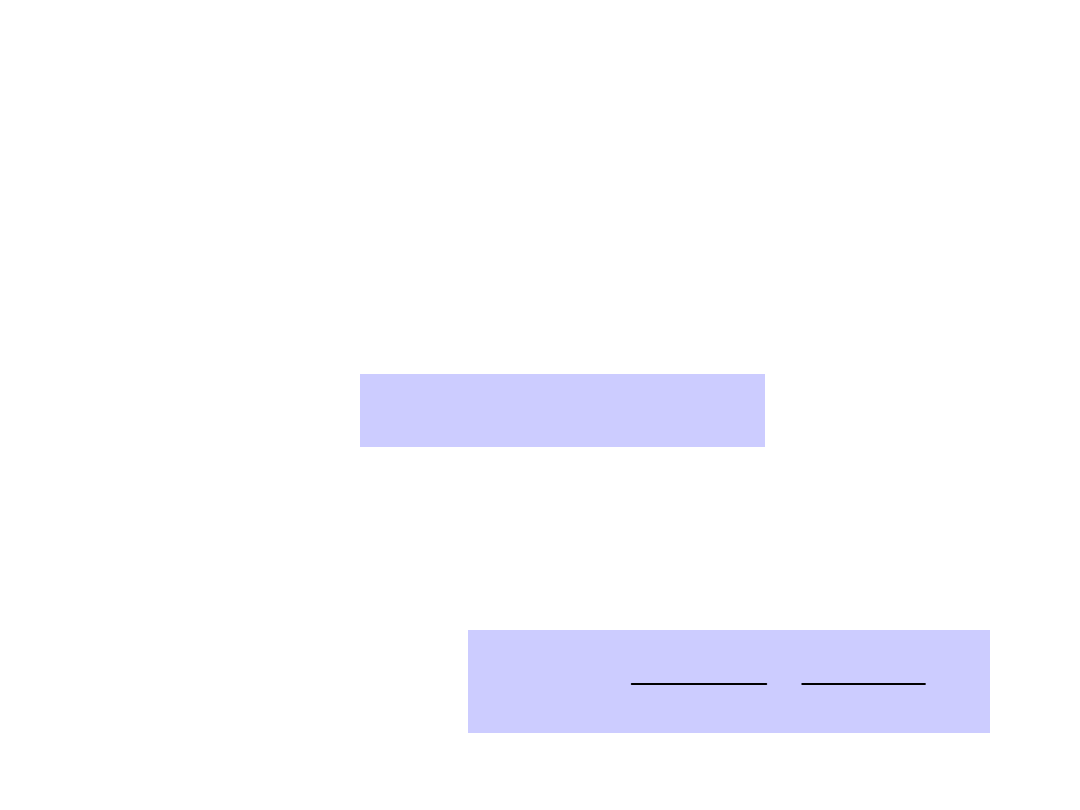
The Galactic Center with the

Keck AdOpt

Without AdOpt

With AdOpt

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Quality of the image -1

The quality of an image can be described in many different
ways. The overall shape of the distribution of light from a point
source is specified by the

point spread function (PSF)

Diffraction gives a basic limit to the quality of the PSF, but any
aberrations or image motion add to structure/broadening of
the PSF.
Another way of describing the quality of an image is to specify
it's modulation transfer function (MTF). The MTF and PSF are
a Fourier transform pair. Turbulence theory gives:

5/3

3.44( / )

MTF

where



is the spatial frequency. Note that a Gaussian goes as



, so this MTF is close to a Gaussian. The shape of seeing-limited

images is roughly Gaussian in core but has more extended
wings. This is relevant because the seeing is often described by
fitting a Gaussian to a stellar profile.

(

)

(

)

y p

x p

�

A potentially better
empirical fitting function is
a Moffat function:

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Quality of the image -2

Probably the most common way of describing the seeing is by
specifying the full-width-half-maximum (FWHM) of the image,
which may be estimated either by direct inspection or by fitting
a function (usually a Gaussian); note the correspondence of
FWHM to



of a Gaussian:

FWHM = 2.355



The FWHM doesn't fully specify a PSF, and one should always
consider how applicable the quantity is.
Another way of characterizing the PSF is by giving the

encircled energy

as a function of radius, or at some specified

radius.
A final way of characterizing the image quality, more commonly
used in adaptive optics applications, is the

Strehl ratio SR

. The

Strehl ratio is the ratio between the peak amplitude of the PSF
and the peak amplitude expected in the presence of diffraction
only. In practice, in the visible it is already very good reaching

0.1

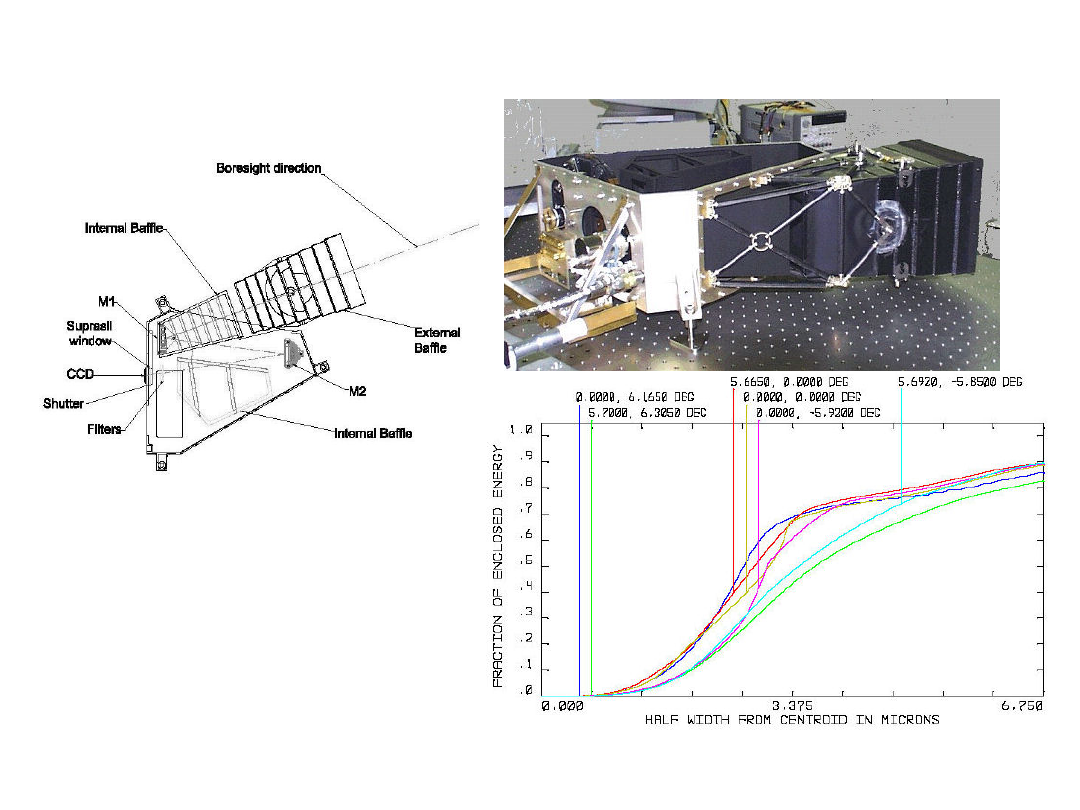
23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The EE of the Rosetta

WAC

The WAC is in space,
so there is no seeing
to worry about, only
the vibrations of the
spacecraft or thermal
distortions of the jitter
of the attitude.

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Effects of the atmosphere at

radiofrequencies - 1

The

ionosphere

will

introduce a delay on the
arrival time of the wave,
given by:

40.3

N s

D =

�

seconds, being

the path

along the line of sight and

the electron density

(cm

-3

). This density will

vary with the night and
day cycle, with the season
and also with the solar
cycle.

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Effects of the atmosphere at

radiofrequencies -2

The tropospheric delay can be resolved in two components, a
dry one and a wet one. The dry component amounts to about 7
ns at the Zenith, and varies with the ‘modified

cosec z

’ we

have discussed for the optical observations:

0.0014

7(cos

) ns

0.0445 cot

D �

The wet component depends on the amount of water
vapour, and amounts to about 10% of the dry one, but it
varies rapidly and in unpredictable way.

Finally, two other mediums affect the propagation

of the radio waves, namely the

solar corona

and the

ionized interstellar medium

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Extinction and

spontaneous emission by

the atmosphere

In addition to chaotic refraction effects, the atmosphere

absorbs

a fraction of the incident light, both in the

continuum and inside atomic and molecular lines and
bands.

Furthermore, the atmosphere spontaneously

emits

particular atomic and molecular bands (

this is in addition

to scattering of artificial lights

, see later).

The molecular oxygen

in particular is so effective at

blocking radiation around 6800A and 7600A that
Fraunhofer could detect by eye two dark absorption bands
in the far red of the solar spectrum, bands he called
respectively B and A (he examined the spectra from red to
blue, the current astronomical practice is from blue to
red).

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Extinction

Let us consider the absorption due to a thin layer of
atmosphere at height between

and

h+dh

in the usual

simple model of a plane-parallel atmosphere. The light beam
from the star makes an angle

with the Zenith, so that the

traversed path is

dh/cosz = seczdh



(h)

is the intensity at the top of the layer, at the exit it

will be reduced by the quantity:

( ) ( )sec d

I h k h

z h

In total, if



()

is the intensity outside the atmosphere, at

the elevation

of the Observatory the intensity will be

reduced to:

sec

( ) d

( ) sec

( )

z k h h

I h

�

��

�

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Optical Depth

where we have introduced the a-dimensional quantity





called

optical depth

( ) d

k h

t =

�

( ) d

k h

�

The variable



(dimensionally, cm

-1

) represents the

absorption per unit length of the atmosphere at that
wavelength.
Astronomers use a particular measure of the apparent
intensity, namely the magnitude, defined by

-2.5log

(see in a later lecture), so that:

ground

2.5 ( ) sec

outsi e

� �



is called the optical density of the atmosphere, while the

variable

X(z)

secz

is called

air-mass

. The minimum value of

the airmass is 1 at the Zenith, and 2 at

= 60° (the limit of

validity of the present approximate discussion).

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The Bouguer line

Suppose we start observing the star at its upper transit, and
then keep observing it while its Hour Angle (and therefore also
its Zenith distance) increases: we would notice a linear increase
of its magnitude in agreement with the previous equation,
namely

a straight line

with slope

2.5D



in a graph (

, sec

It is common practice to plot the

-axis pointing down. This

straight line is known as

Bouguer line

, from the name of the

XVIII century French astronomer who introduced it.
The extrapolation of this line to

= 0 (a mathematical

absurdity) gives the so-called

loss of magnitude at the Zenith

, or

else the magnitude outside atmosphere.
According to the formulae of the first lectures we have:

sec

( )

sin sin

cos cos cos

X z

where



is the latitude of the site,



and

the coordinates

of the star.

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The least continuous

extinction

The Table shows the continuous extinction of the
atmosphere above Mauna Kea, whose elevation above sea
level (4300 m) is higher than that of most observatories so
that the transparency of the sky is at its best, in the
extended visible region.

Wavelength (nm)

Extinction

(mag / air mass)

Wavelength

(nm)

Extinction

(mag / air mass)

310

1.37

500

0.13

320

0.82

550

0.12

340

0.51

600

0.11

360

0.37

650

0.11

380

0.30

700

0.10

400

0.25

800

0.07

450

0.17

900

0.05

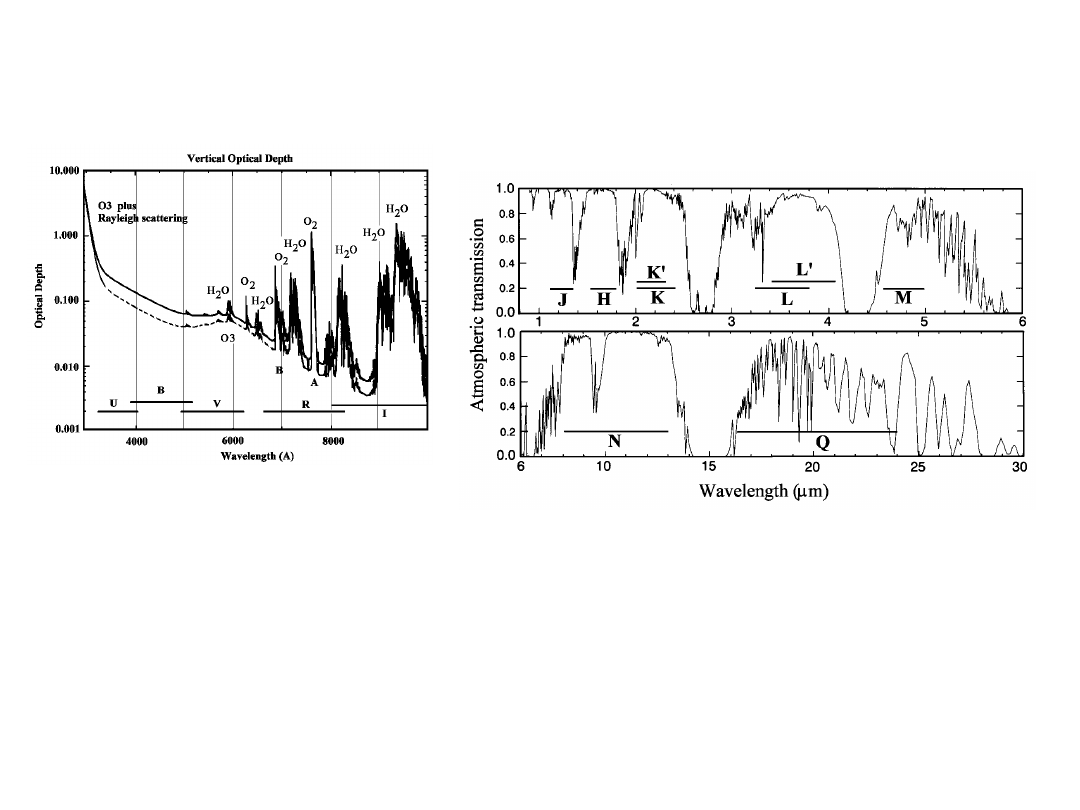
23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Figures of the extinction from the

visible to the near IR

The figure on the left gives the optical depth, the one on the
right the transmission (one is the reverse of the other). In the
violet region, the transparency quickly goes to zero, essentially
because of the ozone

molecular absorption; at the other end

of the spectrum the transparency is reasonably good until about
2.4 micrometers, when the

and

molecules heavily

absorb the light.

The astronomical photometric wide bands (U,B,V, R, I, J, H, …)
are indicated.

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Spontaneous and artificial

emissions

To complete these considerations about the influence of the
atmosphere on the photometry (and also on the spectroscopy)
of the celestial bodies, we must add that the atmosphere
contributes radiation, by spontaneous emission and by
scattering of natural and artificial lights. If the Observatory is
close to populated areas,

bright emission lines of Mercury and

Sodium

from street lamps are observed: Hg at



4046.6,

4358.3, 5461.0, 5769.5, 5790.7; Na at 5683.5, 5890/96 (the
yellow D-doublet), 6154.6; Ne at 6506, and so on.

Natural lines

come from the atomic Oxygen in forbidden

transitions (designated with [OI]) at



5577.4, 6300 and 6367,

and especially from the molecular radical

who provides a

wealth of spectral lines and bands filling the near-IR region
above 6800A.

The OH comes from the dissociation of the water

vapor molecule under the action of the solar UV radiation

Therefore, the atmosphere is a diffuse source of radiation,
whose intensity strongly depends on the Observatory site; to
set an indicative value in the visual band, a luminosity
equivalent to one star of 20

mag per square arcsec at the

Zenith can be assumed.

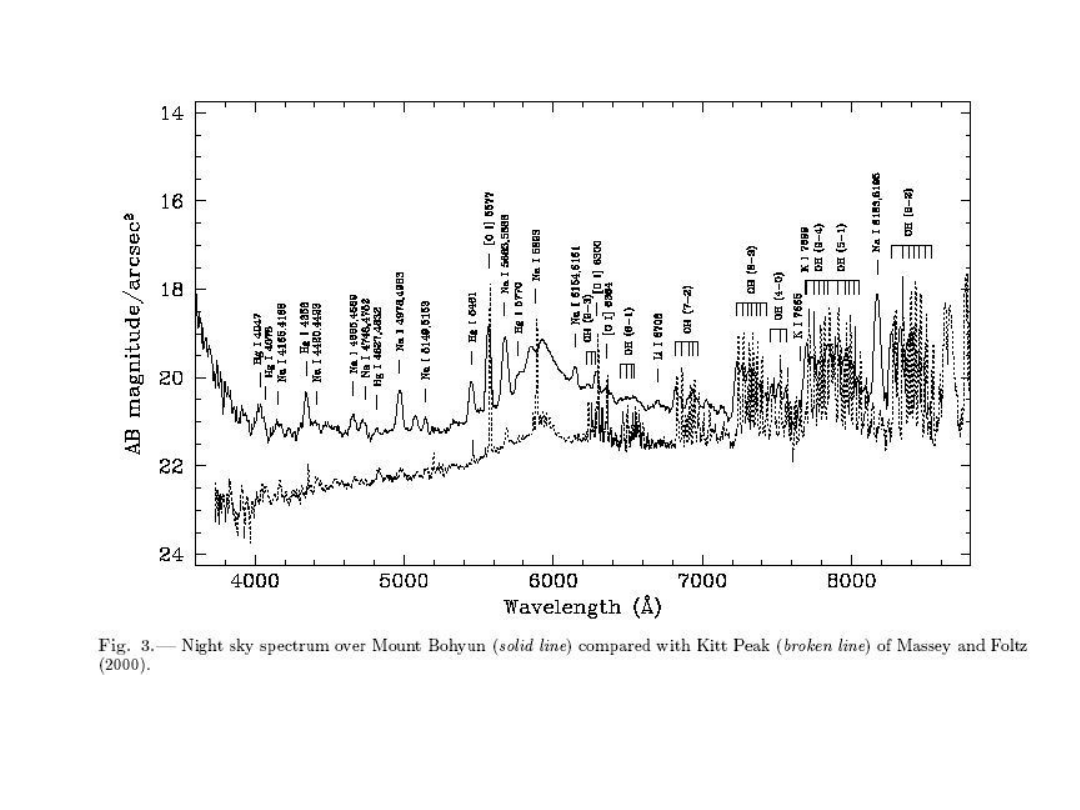
23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

The visible spectrum of the

night sky

The night sky is calibrated (see ordinate) in surface brightness, given
as mag/(arcsec)

. Mt. Boyun is in Korea.

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

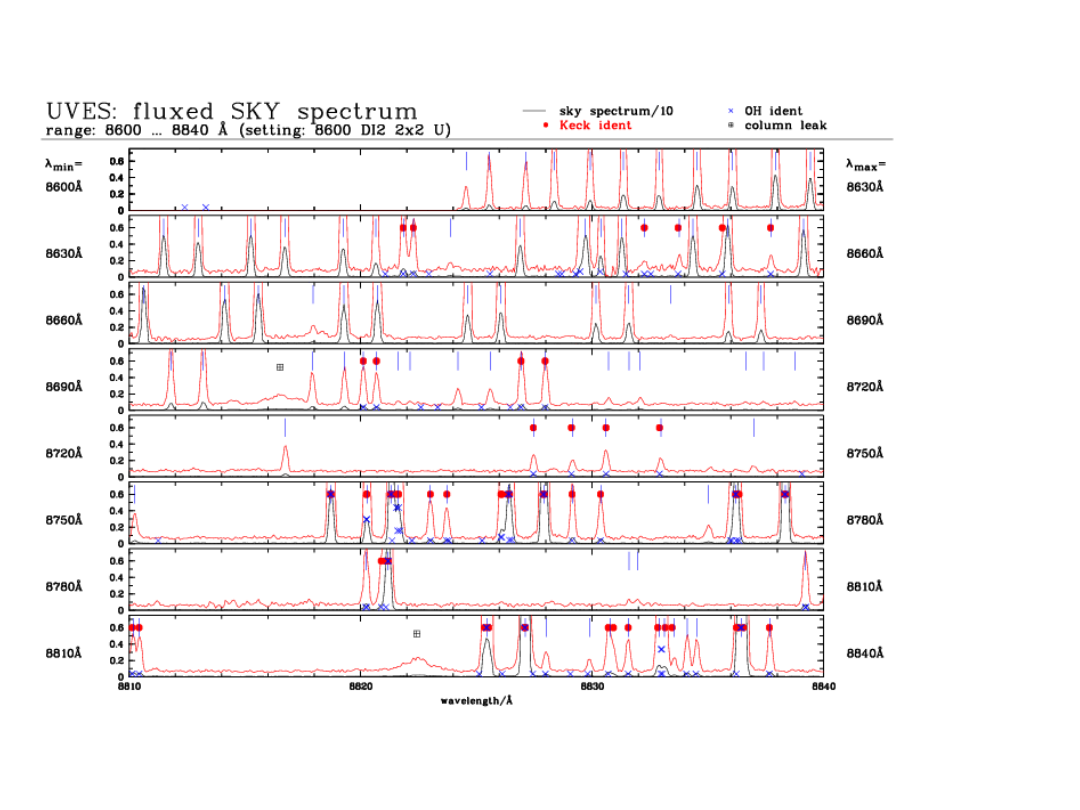
The Near-IR sky emission

- 2

A very
detaile
d
section
of the
near-IR
night
sky
OH-
emissio
n
obtaine
d at
ESO
Paranal
with
UVES.

http://www.eso.org/observing/dfo/quality/UVES/uvessky/sky_8600U_1.html

23/02/2005

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

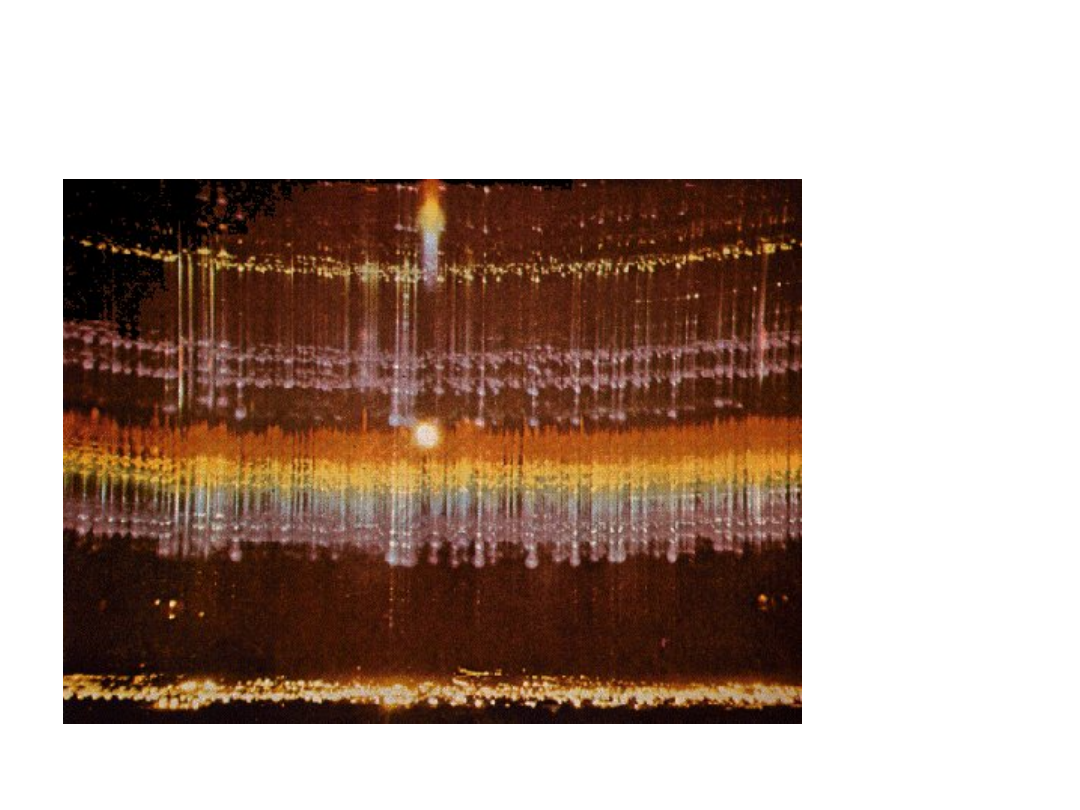
A second limit of the terrestrial

atmosphere: the artificial lights

The full
Moon has
difficulties
in
competing
with the
spectrum
of artificial
lights

23/02/2005

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

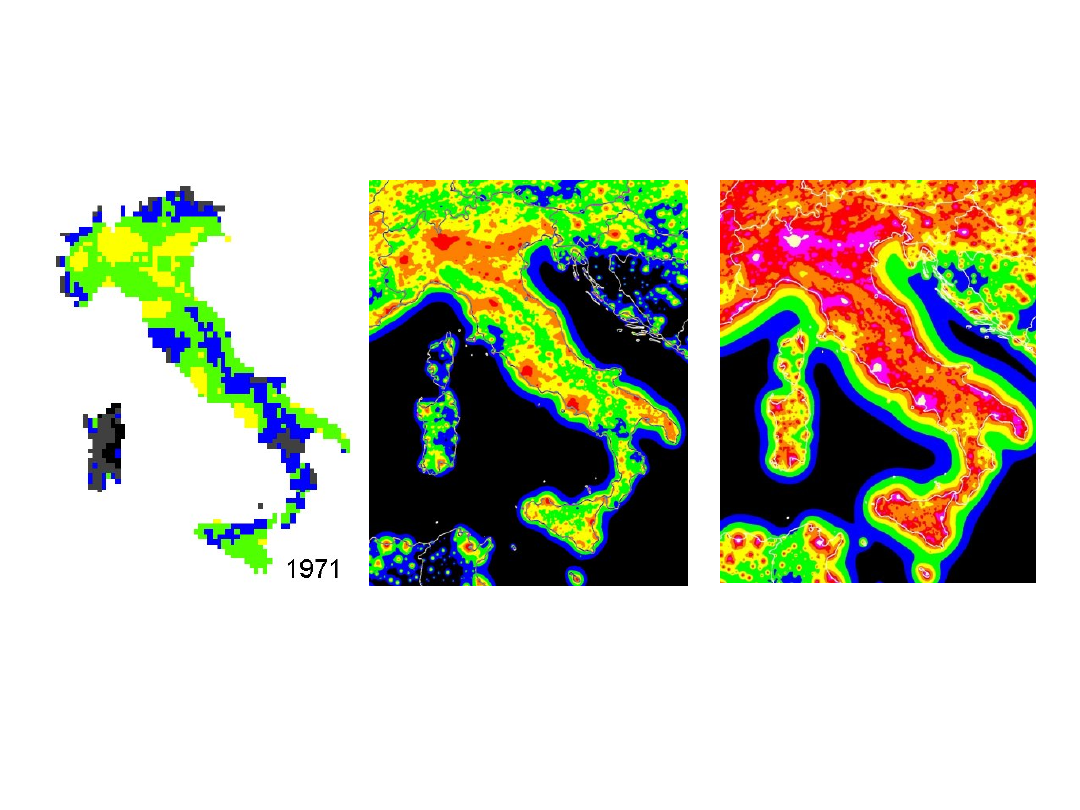
The situation in Italy

1998

2025

If the extrapolation is correct, in 2025 no Italian

will be able to see the Milky Way

23/02/2005

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

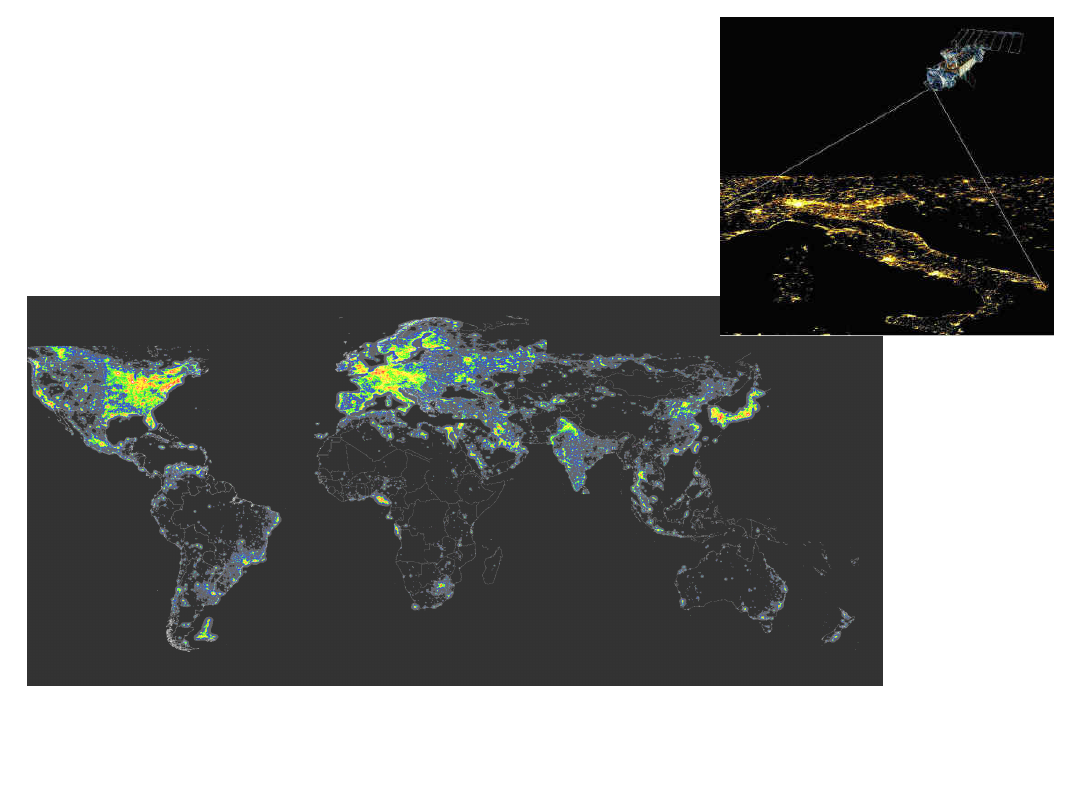
Planetary light

pollution

From a paper by Cinzano, Falchi e Elvidge (2001)

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

A first exercise of celestial

mechanics

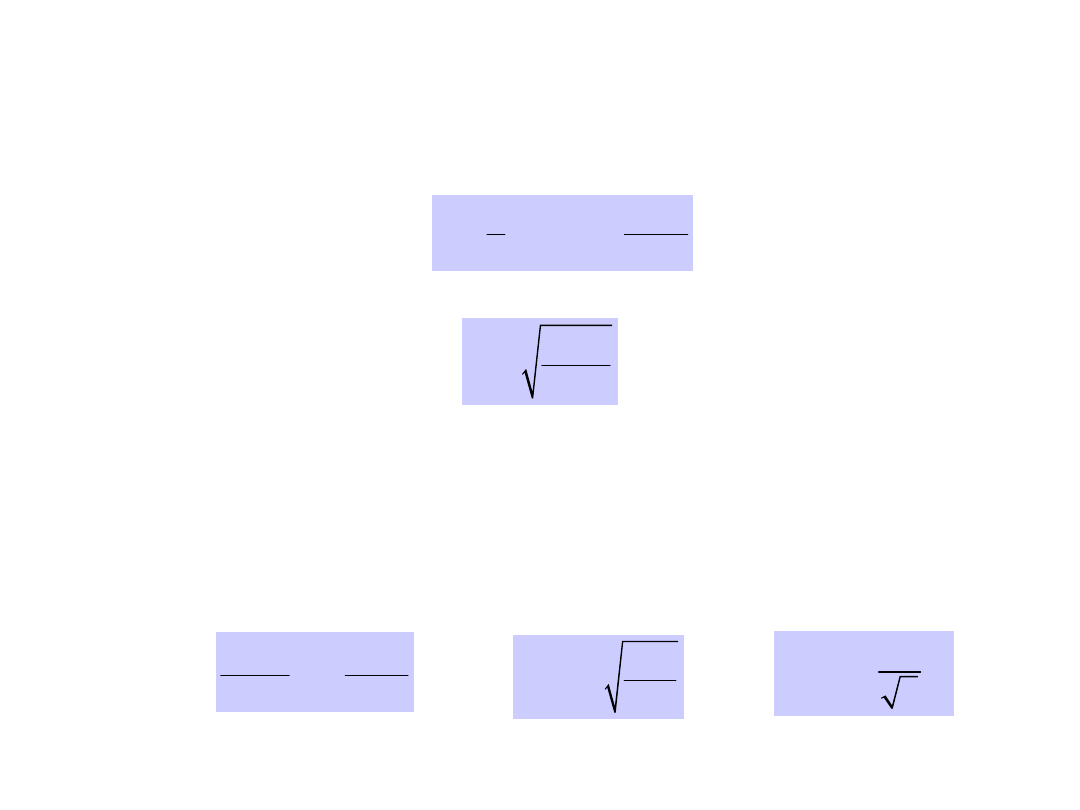
Consider the total energy

of a particle

of very small mass

at the surface of a non-rotating spherical body

of radius

and mass

1 2

The limiting velocity

2Gm

is said escape velocity from body

. If by some means we

impart to

a velocity V greater than

in any direction

will reach infinity with final velocity greater than zero.
Another useful critical velocity is that on the

circular orbit

distance

r>R

from the center of

; from the equilibrium

between centrifugal and gravitational forces we get:

1 2

( )

V r

( )

V R

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

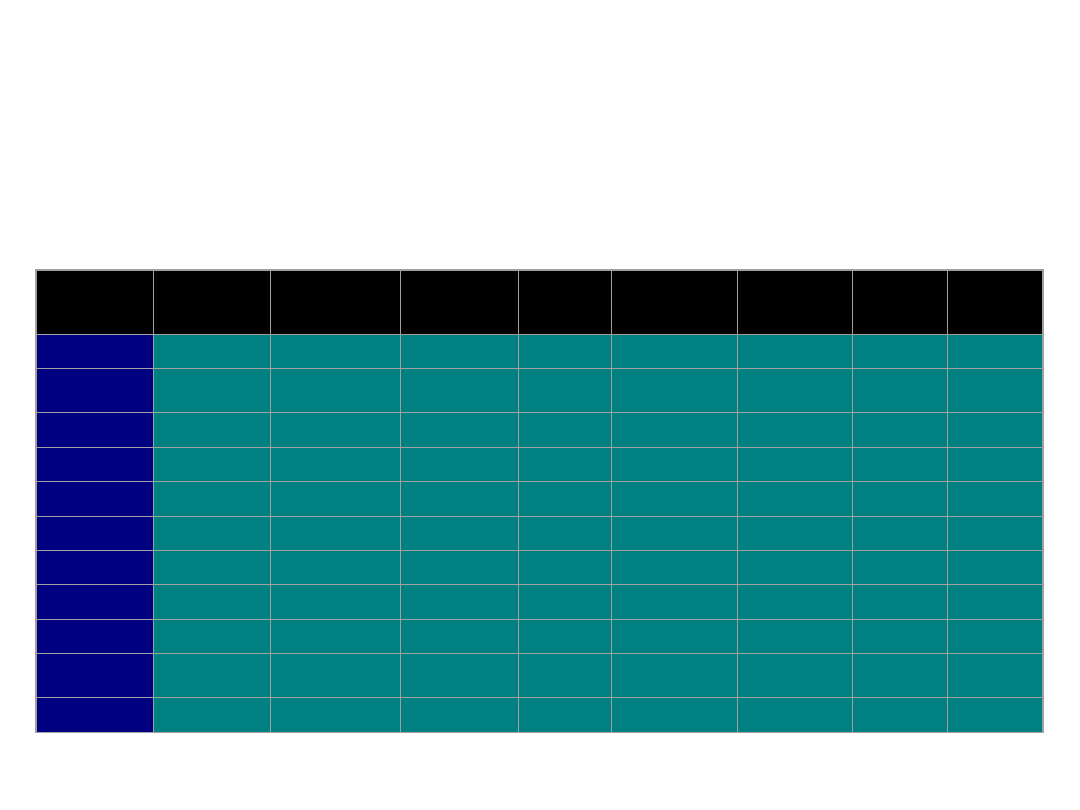
Escape velocities from the 9

planets

The table provides escape and circular velocities for the 9 planets,
neglecting their diurnal rotation. The 3

column gives the surface

gravity in comparison with that at the Earth’s surface (9.78 m/s

). The

first two velocities (4

and 5

column) pertain to the equator of each

body; the other two velocities (6

and 7

column) to the circular orbit at

the average distance of the body from the Sun.

Body

Distanc

(AU)

Mass

(g)

Radius

(km)

g/g



(km/s)

(⊙)

(km/s

)

(⊙)

(km/s

)

Sun

1.9910

6.9610

27.9

618

437

Mercur
y

0.387

3.310

2439

0.3

4.3

2.5

Venus

0.723

4.910

6051

0.9

10.4

7.3

Earth

1.000

6.010

6378

1.0

11.2

7.9

Moon

1.000

7.310

1738

0.2

2.4

1.6

Mars

1.524

6.410

3393

0.4

5.0

3.6

Jupiter

5.203

1.910

71492

2.3

59.6

42.5

Saturn

9.539

5.710

60268

0.9

35.5

25.0

Uranus

19.191

8.710

25559

0.8

21.1

15.5

Neptun
e

30.061

1.010

24764

1.1

23.6

16.0

Pluto

39.529

1.310

1150

0.04

1.1

0.8

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Escape velocities and

atmospheres - 1

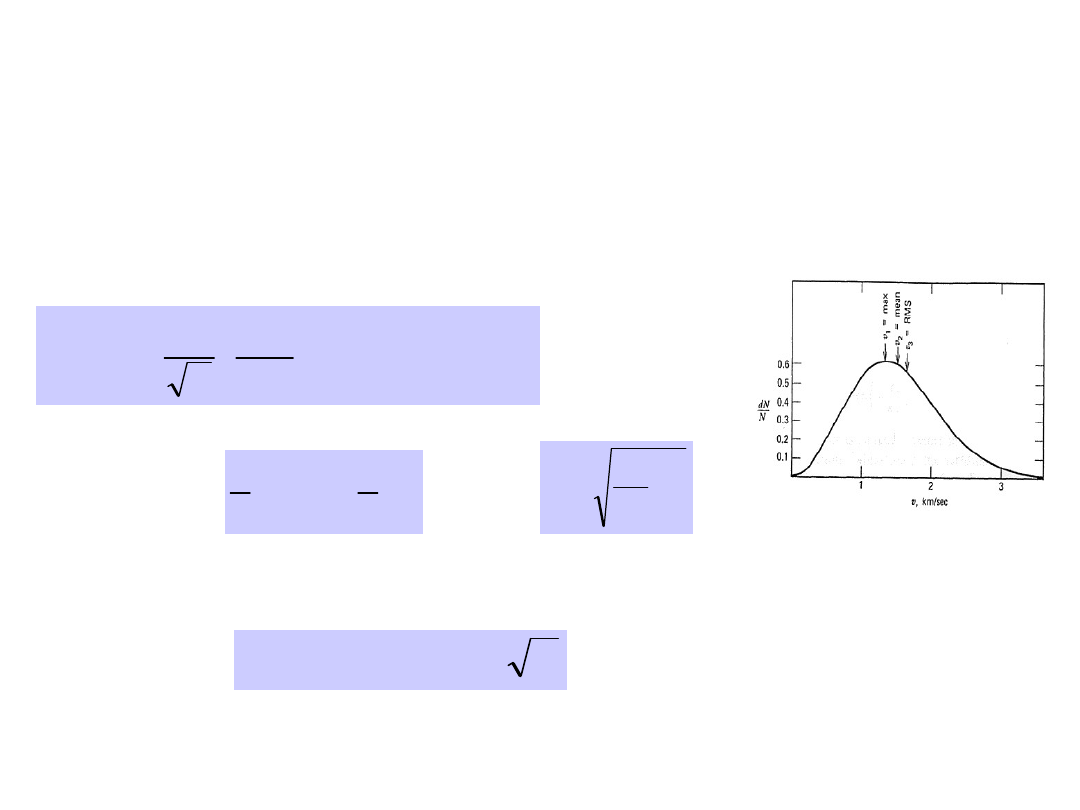
These considerations on escape velocities from the planetary
surfaces are useful not only for dynamical questions,

but also

for the understanding of their atmospheres

. Let

(in

Kelvin) be the temperature of such an atmosphere, supposed in
thermal equilibrium; the distribution function of molecules of
mass

among the velocities is given by Maxwell’s law:

dN V

N m

V e

( )



G IKJ



3 2



so that the mean square velocity of those
molecules will be:



where

= 1.3810

-16

erg/K is Boltzmann constant. For

instance, the mass of the Hydrogen atom H is

 1.610

-24

g, so that:

V T

( )

 



16 10

km/s (

in K)

At the surface of the Earth, assuming

 290 K we get

 2.7

km/s <<

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Escape velocities and

atmospheres - 2

All other molecules being heavier than the atom of H, we conclude
that the Earth

is well capable of retaining a substantial quasi-

stationary atmosphere

. However, Maxwell’s distribution has a

very long tail at high velocity, so that a fraction of the Earth’s
gases, and in particular of H, will continuously escape to the outer
space. The observational evidence of such loss is the so-call

geocorona

, well visible in the Ly- spectral line at



= 1216A.

Mercury and the Moon do not have such capability; their tenuous
atmospheres must be continuously lost by thermal escape and
replenished by phenomena such as UV solar photons and solar
particles impinging on the soil and extracting gases, or by
meteoroid bombardment.
In the case of the Sun, the surface gravity is 28 times that at the
surface of the Earth, and the photospheric temperature is
approximately 5800 K; higher up, in the cromosphere and in the
corona, the temperatures of the solar gases rise to tens, hundreds
and even millions of degrees, so that the thermal escape becomes
conspicuous. However, observations prove that the loss of
particles from the Sun (the so-called

solar wind)

is orders of

magnitude larger than that accounted for by thermal loss: other
more efficient mechanisms, whether magnetic or electric, must
act to accelerate the ionized (electrically charged) particles
escaping from the Sun.

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

A second exercise of celestial

mechanics

Let us launch from the surface of a spherical non-rotating
Earth of radius

⊕

a satellite of mass

with initial velocity

> V

. Its energy will be:

�

(

⊕

)

At an altitude

, the distance from the centre becomes

r = a

⊕

+ H

, and the energy:

�

or else, equating the two values for the conservation of the
energy:

�

1 1

�

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Delta V

At infinity:

(

)(

) 2

V V V V

V V

�

= -

� D

In conclusion, if we launch with V = + 1km/s, the satellite will

reach infinity with a velocity of approximately 4.7 km/s
(

ignoring the very small losses of energy due to the

atmospheric drag

). There are several practical consequences

of this ‘gain at infinity’, for instance one has to be careful not to
reach the final destination with too high a velocity.

We underline the convenience of using in space

applications the parameter V instead of the energy

The circular velocity at the surface of the Earth is

around 8 km/s, which will also be the velocity of low altitude
satellites (e.g. the International Space Station at 300 km).
Their period is then of approximately 90 minutes; suppose we
place such satellite in a polar orbit: it will go out of phase with
the Sun by about 30 min at each orbit, and for several orbits it
will see an almost constant illumination (day or night) of its
Nadir. The low polar orbit is therefore used for surveillance.

23/02/05

C.Barbieri Elementi_AA_2004
_05 Sesta settimana

Geostationary orbits

= 36.000 km the orbital period becomes of 24h, so

that a satellite placed on the equatorial plane at this
altitude in a circular orbit (e.g. the Meteosat) will be
practically stationary with respect to the ground observer.

Actually, several satellites have simply a

geosynchronous

orbit (that was the case of the International Ultraviolet
Explorer), slightly different from the rigorously defined
geostationary one.

At any rate, the two body condition is a

mathematical

abstraction

, several perturbing forces (like the Earth-

Moon and solar tides, the non-sphericity of the Earth
potential, the radiation pressure, etc.) will act to perturb
the orbit, and

appropriate corrections

must be performed

to keep the wanted position of the satellite, for instance by
occasional firings of small thrusters.

Document Outline

Slide 1
Slide 2
Slide 3
Slide 4
Slide 5
Slide 6
Slide 7
Slide 8
Slide 9
Slide 10
Slide 11
Slide 12
Slide 13
Slide 14
Slide 15
Slide 16
Slide 17
Slide 18
Slide 19
Slide 20
Slide 21
Slide 22
Slide 23
Slide 24
Slide 25
Slide 26
Slide 27
Slide 28
Slide 29
Slide 30
Slide 31
Slide 32
Slide 33
Slide 34
Slide 35
Slide 36
Slide 37
Slide 38
Slide 39
Slide 40
Slide 41
Slide 42
Slide 43
Slide 44
Slide 45
Slide 46
Slide 47
Slide 48
Slide 49
Slide 50
Slide 51
Slide 52
Slide 53
Slide 54
Slide 55
Slide 56
Slide 57
Slide 58
Slide 59
Slide 60
Slide 61

Wyszukiwarka

Podobne podstrony:
podrecznik 2 18 03 05
regul praw stan wyjątk 05
05 Badanie diagnostyczneid 5649 ppt
Podstawy zarządzania wykład rozdział 05
05 Odwzorowanie podstawowych obiektów rysunkowych
05 Instrukcje warunkoweid 5533 ppt
05 K5Z7
05 GEOLOGIA jezior iatr morza
05 IG 4id 5703 ppt
05 xml domid 5979 ppt
Świecie 14 05 2005
Wykł 05 Ruch drgający
TD 05
6 Zagrozenia biosfery 07 05 05

więcej podobnych podstron

LezioniAstroAstrofIng04 05 Sesta Settimana[1]

Document Outline