32 Crystallographic Point

Groups

Point Groups

The 32 crystallographic point groups (point groups
consistent with translational symmetry) can be
constructed in one of two ways:
1. From 11 initial pure rotational point groups,

inversion centers can be added to produce an
additional 11 centrosymmetric point groups. From
the centrosymmetric point groups an additional 10
symmetries can be discovered.

2. The Schoenflies approach is to start with the 5

cyclic groups and add or substitute symmetry
elements to produce new groups.

Cyclic Point Groups

5

 

1

1C

 

2

2 C

 

3

3C

 

4

4 C

 

6

6 C

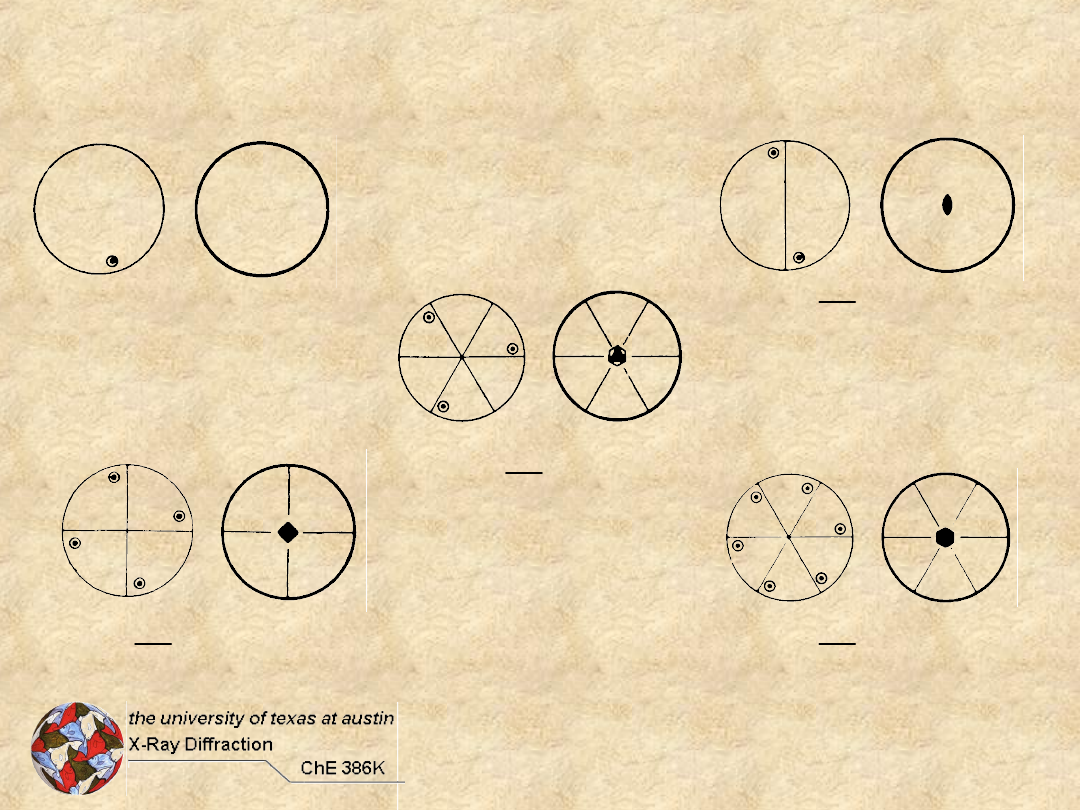
Cyclic + Horizontal Mirror

Groups

+5 = 10

 

h

C

m

1

 

h

C

m

2

2

 

h

C

m

3

3

 

h

C

m

4

4

 

h

C

m

6

6

Cyclic + Vertical Mirror Groups

+4 = 14

 

v

C

m

1

 

v

C

mm

2

2

 

v

C

m

3

3

 

v

C

mm

4

4

 

v

C

mm

6

6

 

h

C

m

1

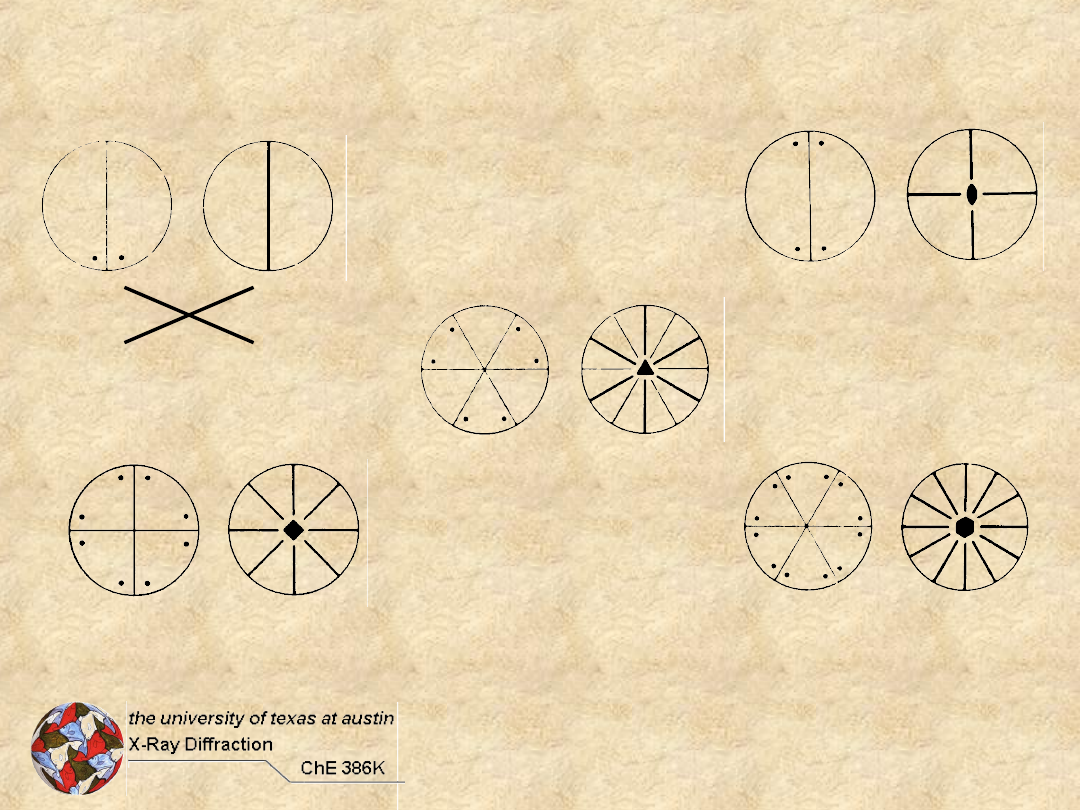
Rotoreflection Groups

 

1

2 S

 

2

1 S

 

3

6 S

 

4

4 S

 

6

3 S

 

h

C

m

1

 

h

C

m

3

3

+3 = 17

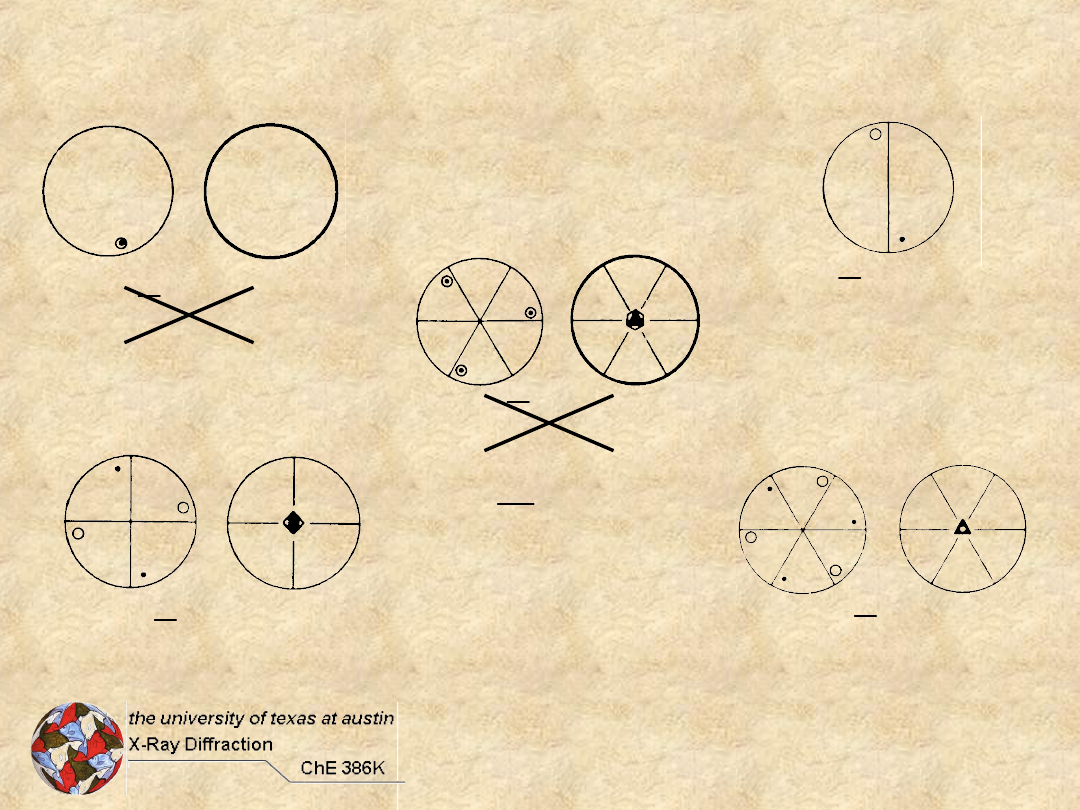
17 of 32?

Almost one-half of the 32 promised point groups
are missing. Where are they?

We have not considered the combination of
rotations with other rotations in other directions.
For instance can two 2-fold axes intersect at right
angles and still obey group laws?

The Missing 15

Combinations of Rotations

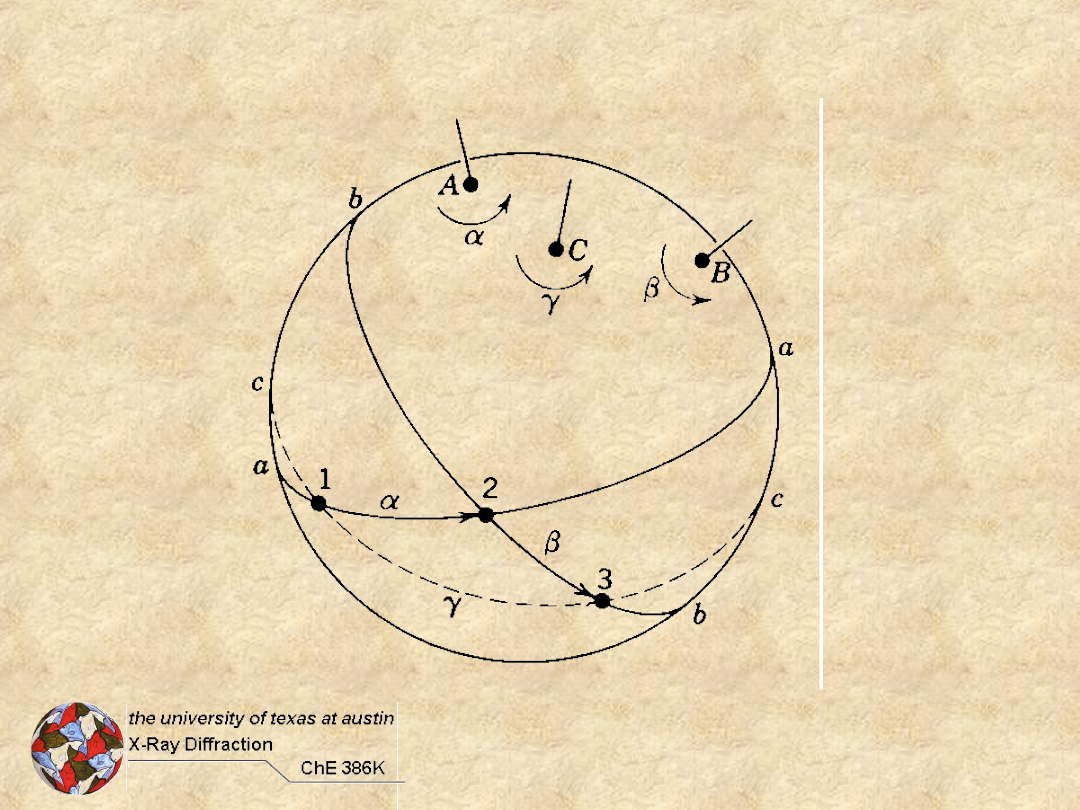
Moving Points on a Sphere

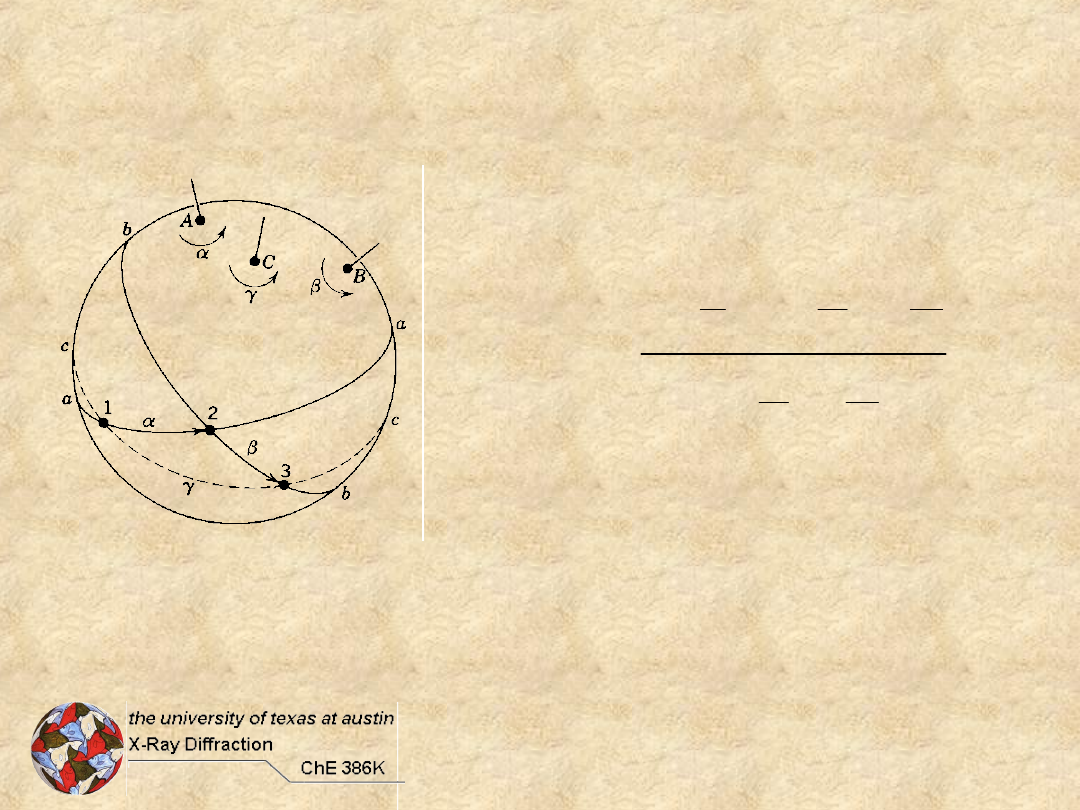
Moving Points on a Sphere

  =  "throw" of axis

i.e. 2-fold has 180° throw

Euler

2

sin

2

sin

2

cos

2

cos

2

cos

cos





























AB

Investigate: 180°, 120°, 90°, 60°

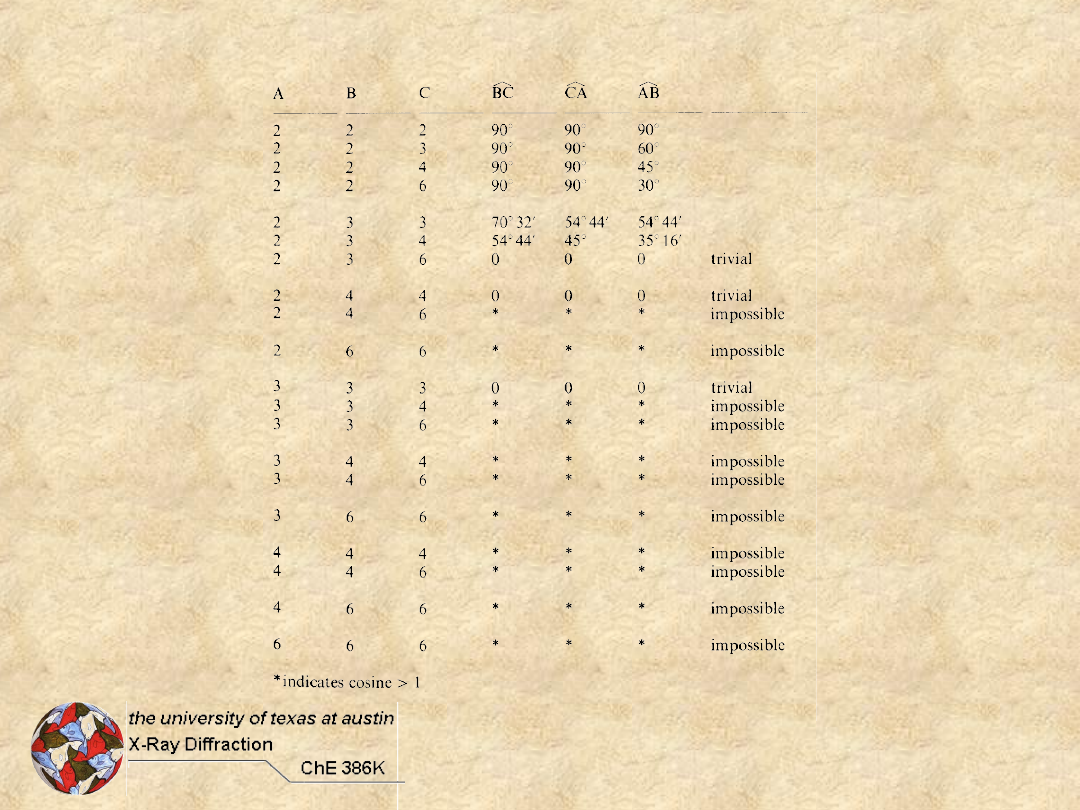
Possible Rotor Combinations

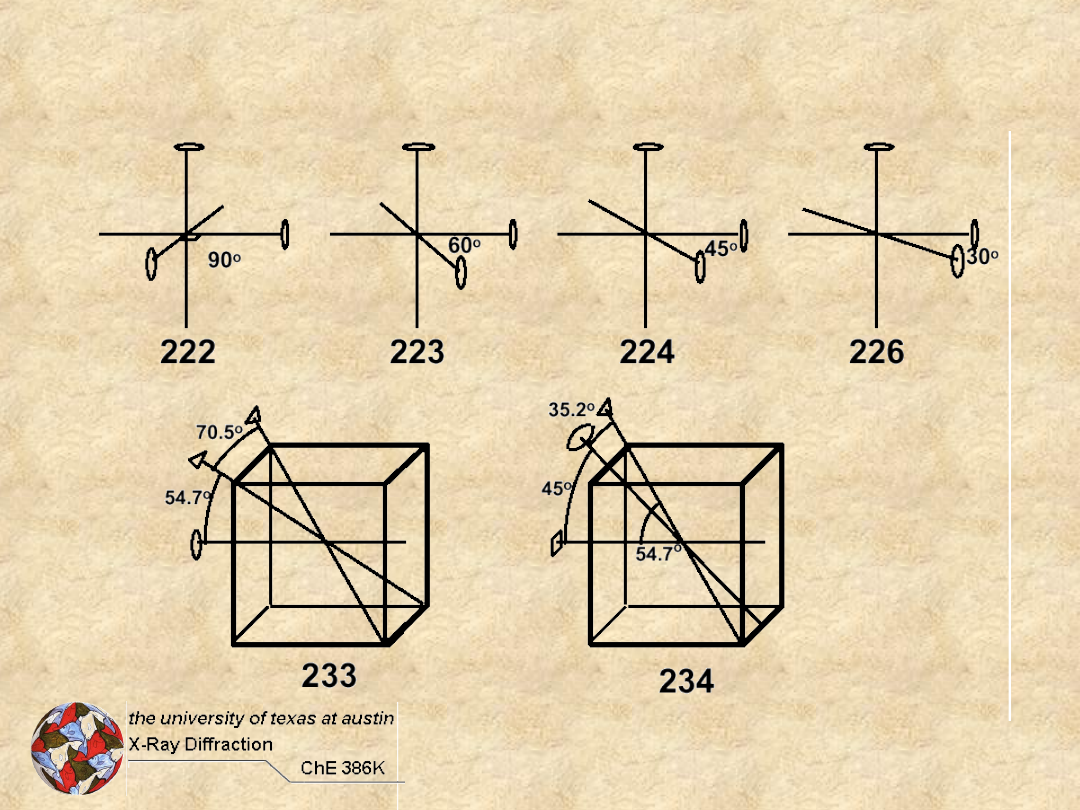
Allowed Combinations of Pure

Rotations

Rotations + Perpendicular 2-folds

Dihedral (D

n

) Groups

 

2

222D

 

3

32D

 

4

422D

 

6

622D

+4 = 21

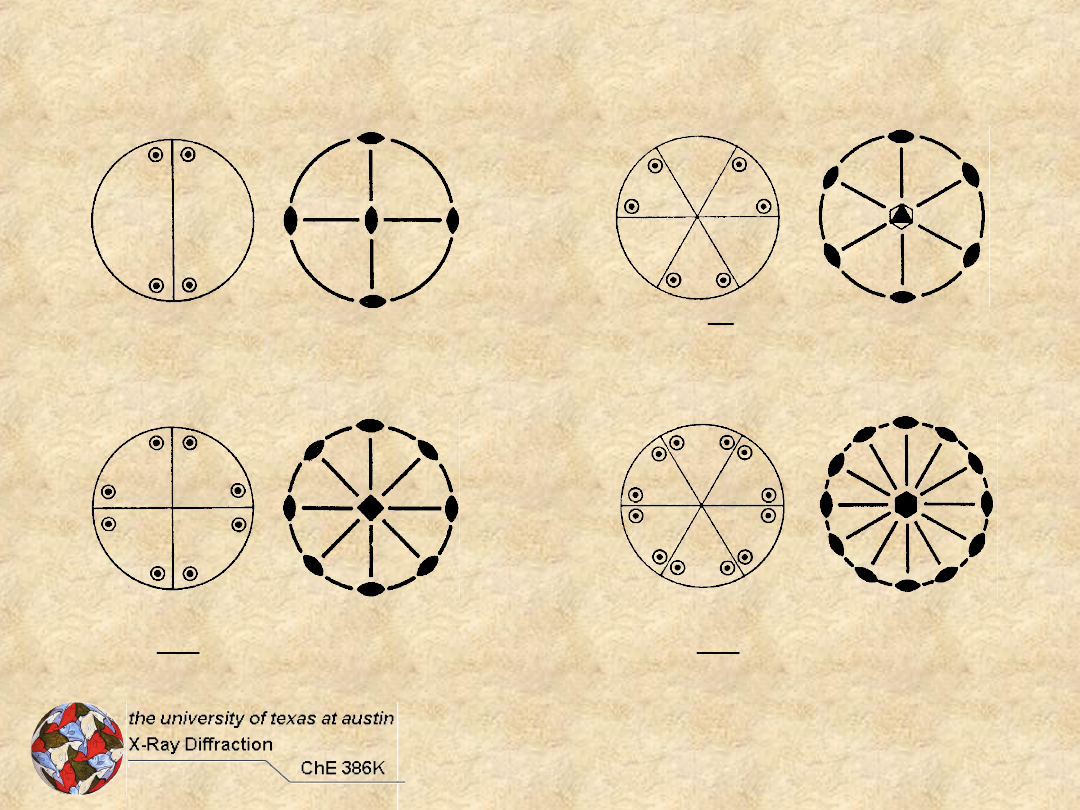
Dihedral Groups + 

h

 

h

D

mmm

2

 

h

D

m

3

2

6

 

h

D

mm

m

4

4

 

h

D

mm

m

6

6

+4 = 25

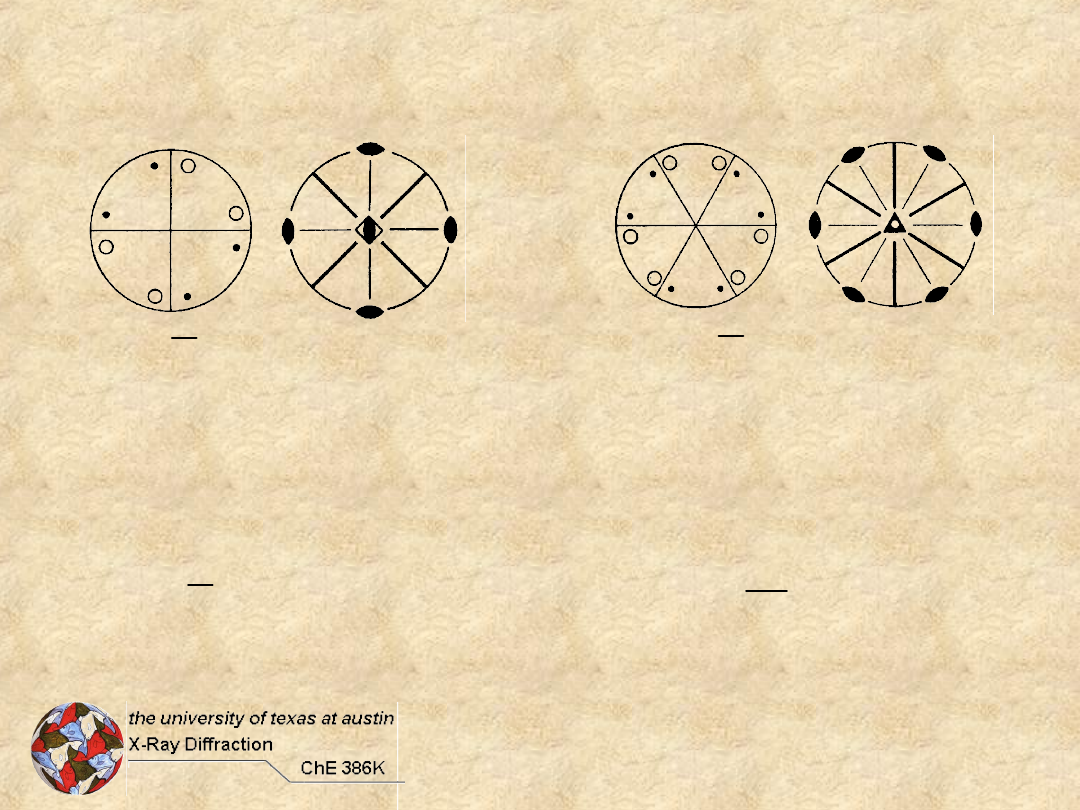
Dihedral Groups + 

d





d

D

m

2

2

4

 

d

D

m

3

3

?

4d

D

?

6d

D

m

2

8

m

2

12

+2 = 27

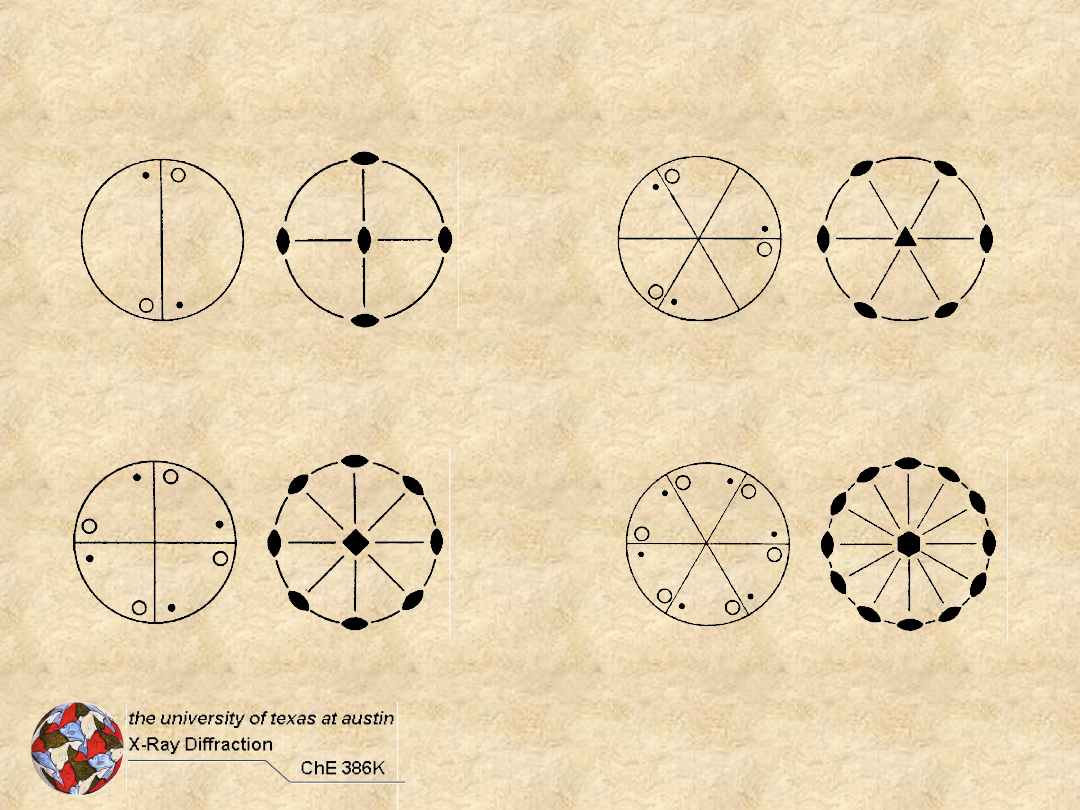
Isometric Groups

Roto-Combination with no Unique

Axis

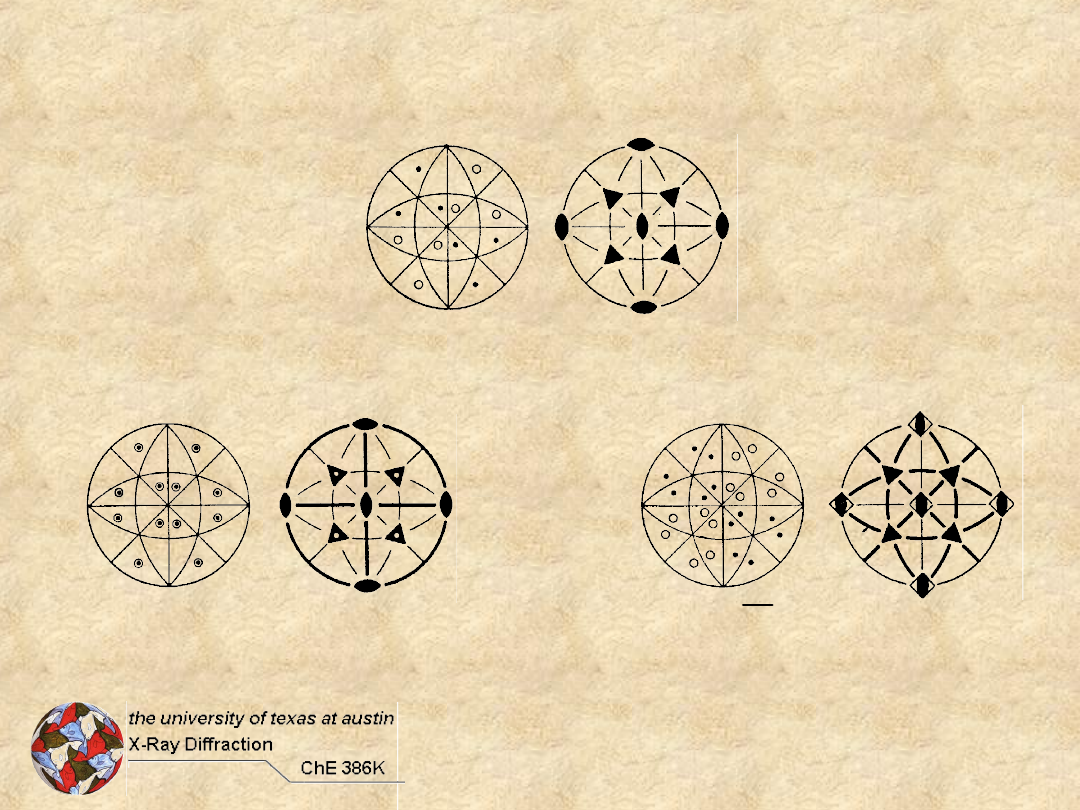
T Groups

 

T

23

 

h

T

m3

 

d

T

m

3

4

+3 = 30

T Groups

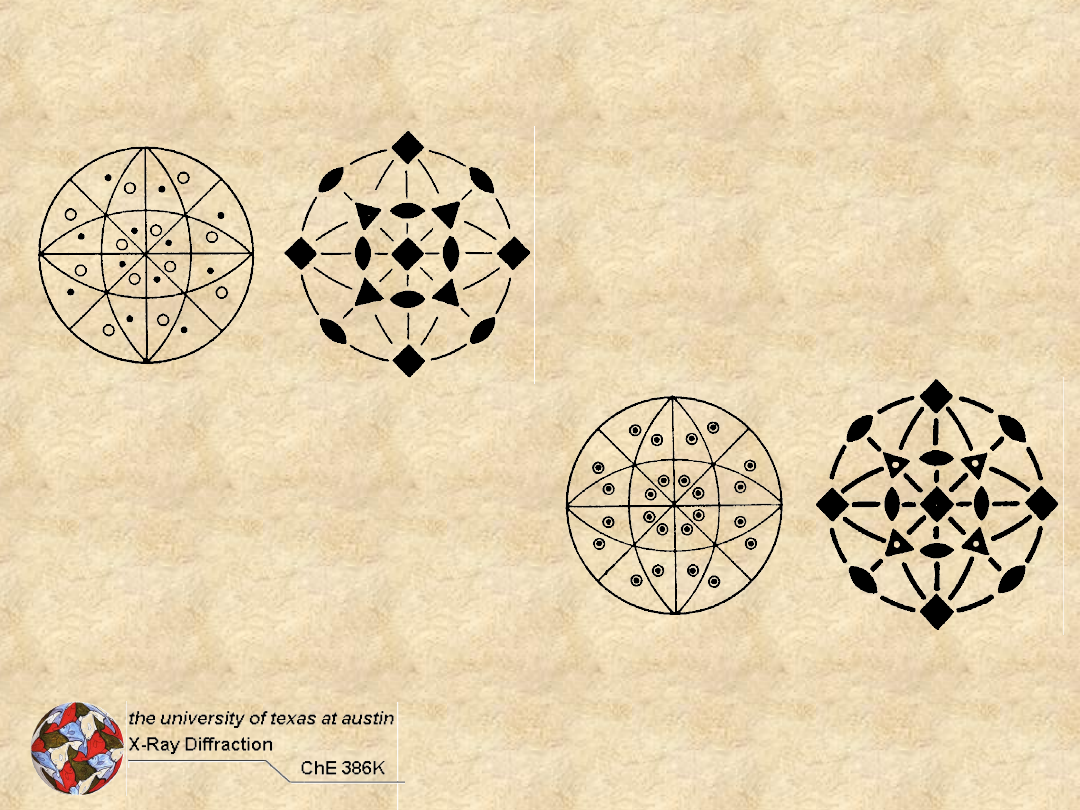
O Groups

 

O

432

 

h

O

m

m3

+2 = 32

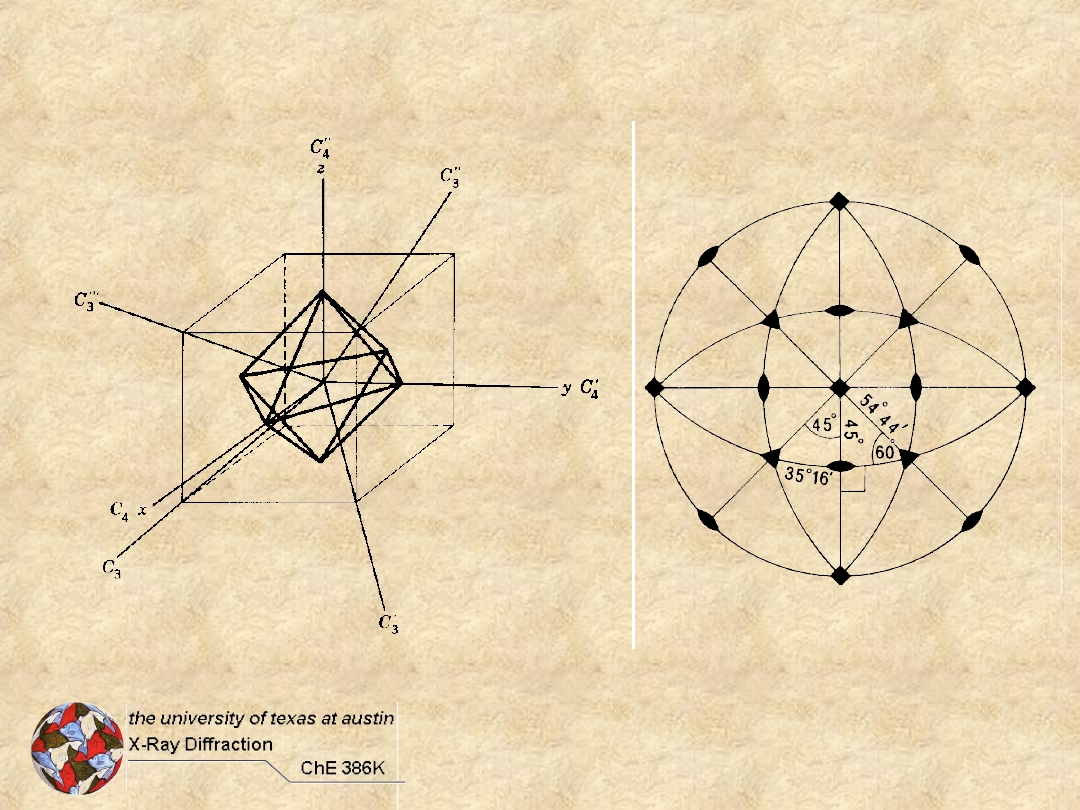
O Groups

Flowchart for Determining Significant

Point Group Symmetry