1
Dlaczego usuwamy wilgoć? Odpowiedź wydaje się oczywista,
jednak zaskakujące jest stwierdzenie jak często materiał jest suszony, a
następnie ponownie nawilżony w momencie jego użycia, lub w kolejnym
etapie procesu wytwórczego.
Można tu wymienić następujące powody:
1. Zmniejszenie masy – proces suszenia w znacznym stopniu obniża
koszty przechowywania i transportu. Jest to szczególnie istotne w
odniesieniu do poddanej dehydratacji żywności, której masa często
wynosi tylko 10% żywności świeżej.
2. Trwałość w przechowywaniu – reakcje utleniania, enzymatyczne i inne
powodujące pogorszenie zapachu, koloru oraz rozkład żywności i innych
produktów są w wyniku spadku zawartości wilgoci zwolnione lub
zminimalizowane.
3. Zmniejszenie objętości – niektóre materiały w czasie suszenia
znacznie się kurczą co prowadzi do udogodnień w magazynowaniu i
obniża koszty opakowań.
4. Łatwość przesyłania – materiały wilgotne z uwagi na ich lepkość i
tendencje do aglomeracji sprawiają problemy w transporcie. W stanie
suchym materiały te w większości są sypkie i nadają się do dalszej
obróbki czy przesyłania. Często materiał wilgotny musi być mieszany z
materiałem suchym dla polepszenia możliwości jego dalszej obróbki
(również suszenia).
2
5. Polepszenie jakości produktu – w wielu przypadkach proces usuwania
wilgoci odgrywa istotną rolę w rozwijaniu własności materiału.
Zagadnienie to nabrało ostatnio szczególnej aktualności z uwagi na
możliwość kształtowania jakości produktu. Jako przykład można tu podać
otrzymywanie katalizatorów i absorbentów ponieważ proces suszenia
wpływa na wewnętrzną strukturę porów. Dla niektórych materiałów
suszenie jest decydującym czynnikiem w uzyskaniu wysokiej
wytrzymałości materiału (np. ceramika). Wysoki stopień wysuszenia
materiału jest niekiedy podstawowym warunkiem poprawnej pracy
całego urządzenia, którego dany materiał jest częścią składową (np.
transformatory).
6. Trwałość bakteriologiczna – parametr ten jest istotny w odniesieniu do
naturalnych materiałów organicznych. Bakterie nie rozwijają się jeżeli
równowagowa wilgotność względna jest niższa niż 95%. Podobnie
drożdże i pleśnie nie rozwijają się przy wartości tej wilgotności poniżej
75%. Należy pamiętać, iż zazwyczaj taniej jest przechowywać materiały
w stanie suchym niż w lodówce.
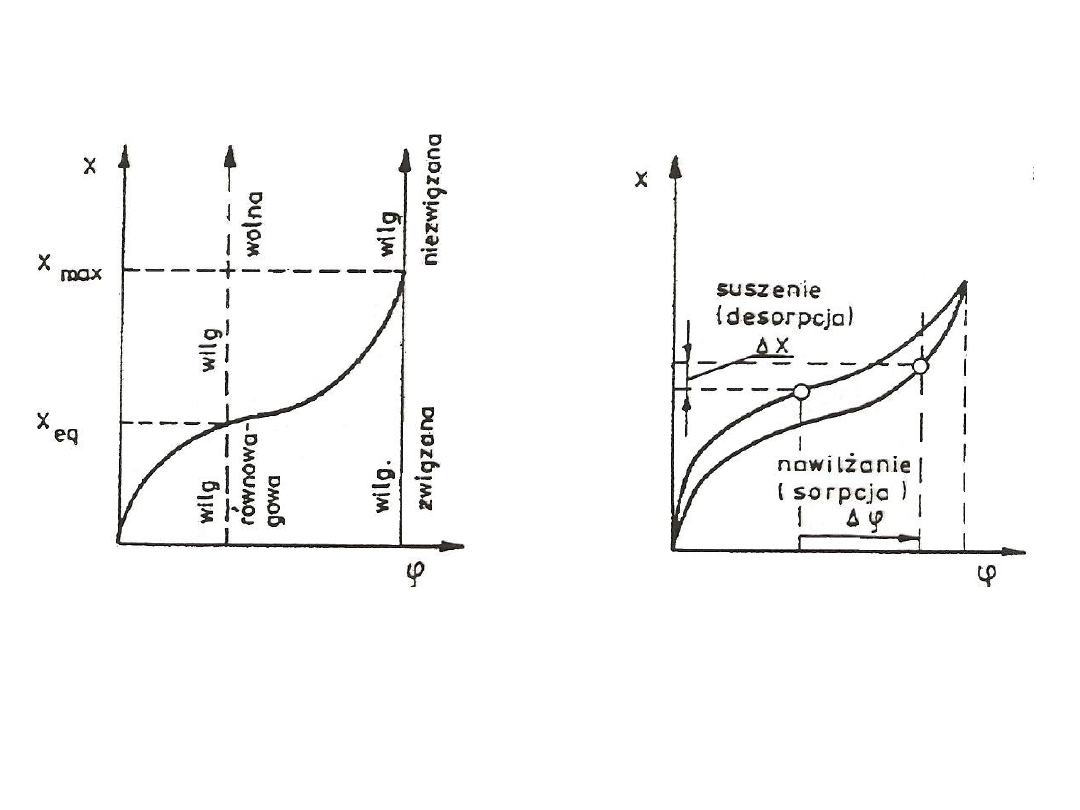
Charakter i energia wiązania substancji z cząsteczkami wilgoci
określają ogólną ilość wilgoci, która zdolne jest utrzymać dane ciało przy
jego równowadze fizykochemicznej (termodynamicznej) z otoczeniem.
3
Rys. 1. Schemat izotermy sorpcji (desorpcji)
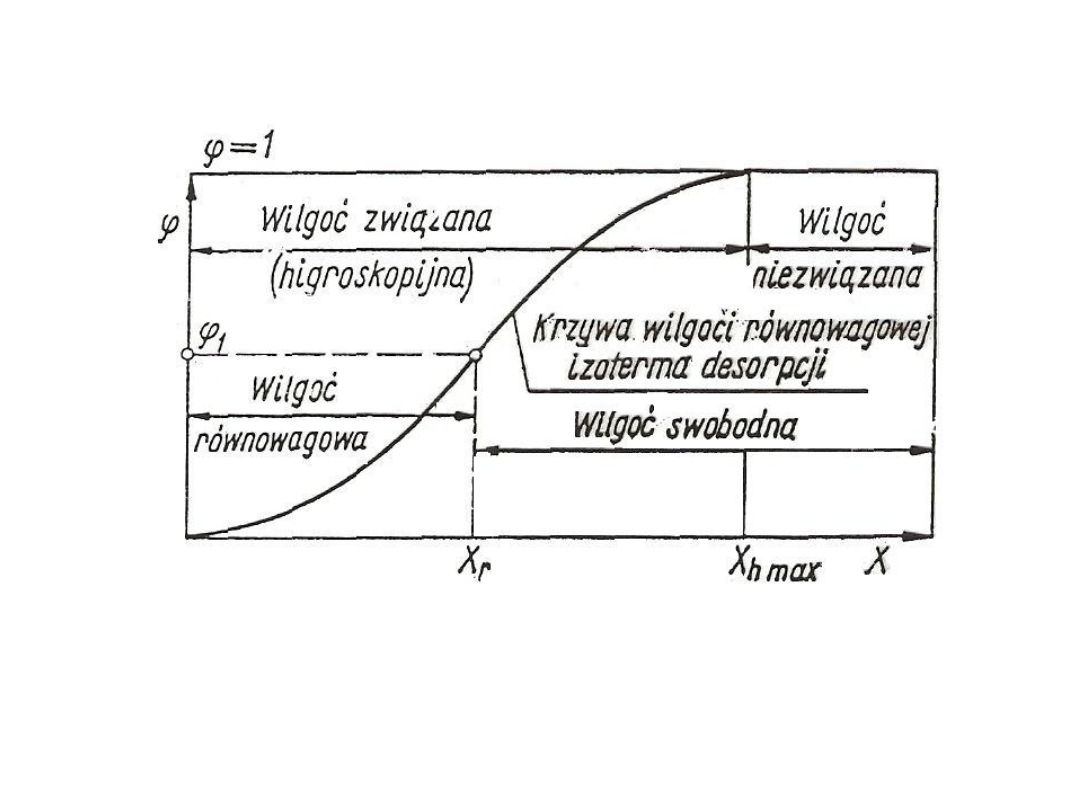
4
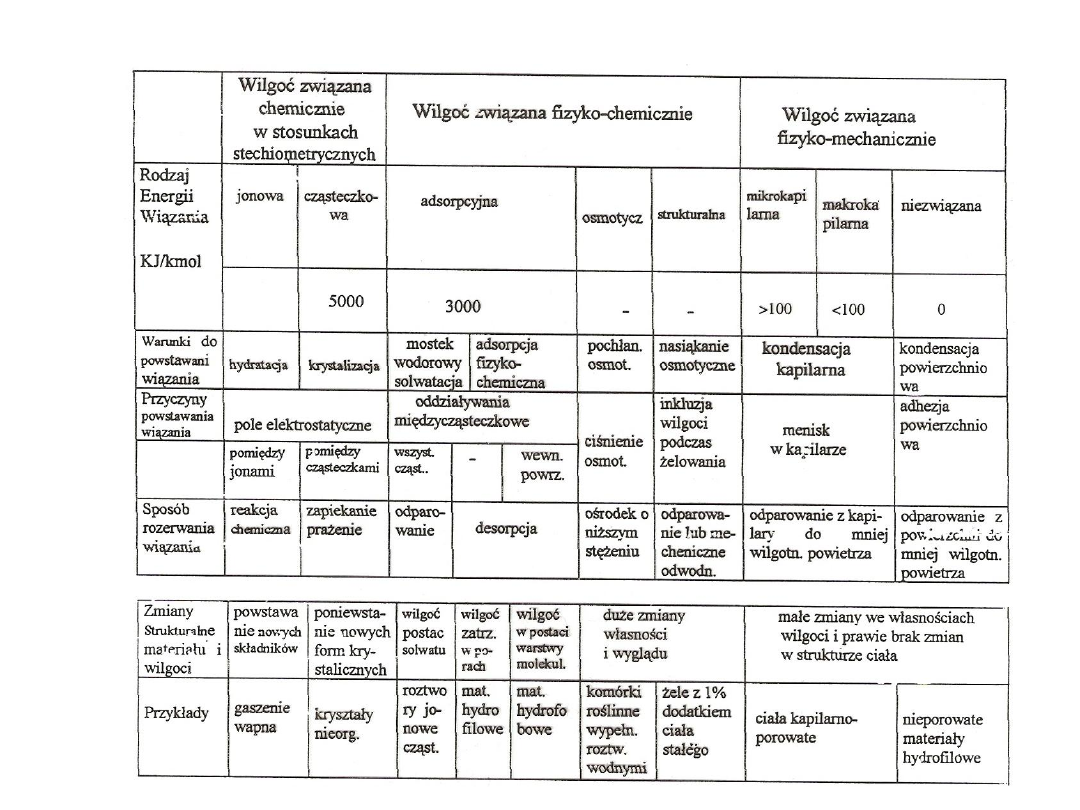
Rys. 2. Graficzna ilustracja rodzajów wilgoci
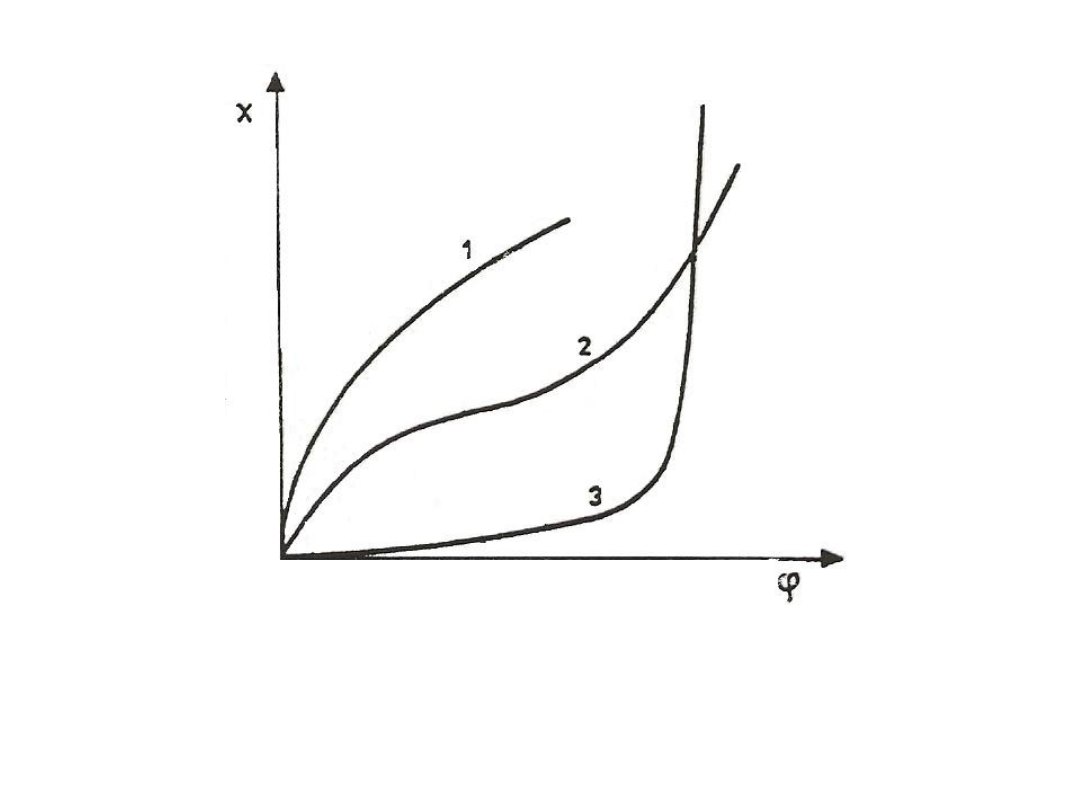
5
Rys. 3. Klasyfikacja izoterm sorpcji Heissa i Eichnera:
1 – materiał silnie higroskopijny; 2 – umiarkowanie higroskopijny; 3 –
niehigroskopijny
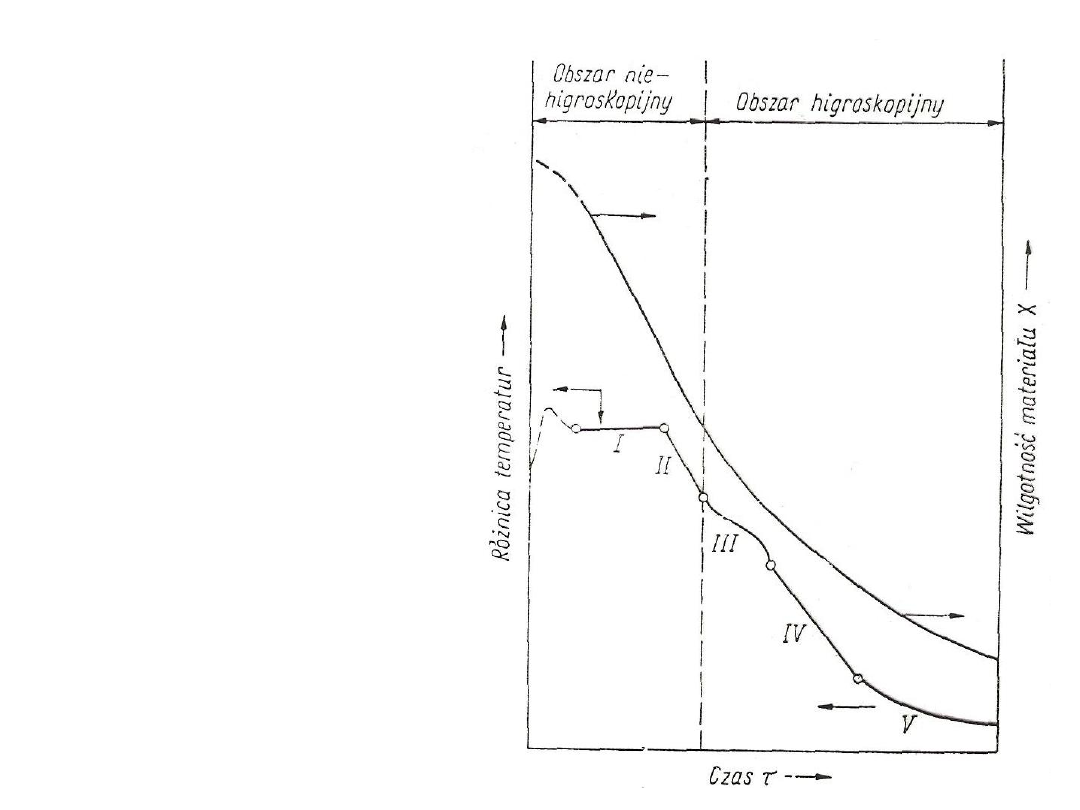
6
Rys. 4. Termogram procesu
suszenia:
I – wilgoć niezwiązana;
II – wilgoć w porach;
III – wilgoć kapilarna;
IV – wilgoć zaadsorbowana w
postaci warstw
polimolekularnych,
V – wilgoć zaadsorbowana w
postaci warstwy
monomolekularnej
7
Tab. 1. Rodzaje wilgoci z materiałem
8
Termodynamika gazu
wilgotnego
Układ:
(A) para cieczy – (B) gaz
(A) para wodna – (B) powietrze
Podstawowe parametry powietrza wilgotnego:
- wilgotność bezwzględna [masowa] (wilgotność absolutna, zawartość
wilgoci):
Y = m
A
/ m
B
[kg
pary wodnej
/ kg
suchego powietrza
]
- wilgotność bezwzględna objętościowa
A
= m
A
/ V
[kg
pary wodnej
/ m
3
wilg. pow.
]
- prężność cząstkowa p
A
:
p
A
V = n
A
RT
p
B
V = n
B
RT
P = p
A
+ p
B
n = m / M
9
Y = (M
A
/ M
B
) [p
A
/ (P – p
A
)]
gdzie: M
A
- masa cząsteczkowa pary wodnej = 18 kg/kmol
M
B
- zastępcza masa cząsteczkowa suchego powietrza = 29
kg/kmol
(M
A
/ M
B
) = 18/29 = 0,622
Y = 0,622 [p
A
/ (P – p
A
)]
p
A
= f(Y)
przy P = const
p
A
/ p
B
= n
A
/ n
B
- wilgotność bezwzględna molowa
Y
m
= p
A
/ p
B
= p
A
/ (P – p
A
)
Y = Y
m
(M
A
/ M
B
)
Y
n
= 0,622 [p
An
/ (P – p
An
)]
Y
mn
= p
An
/ (P – p
An
)
10
- wilgotność względna
= (
A
/
A
max
)
T
= (p
A
/ p
A
max
)
T, P
A
= (p
A
M
A
) / (RT)
A
max
= (p
A max
M
A
) / (RT)
gdy:
p
An
≤ P
to
p
A
max
= p
An
i
= (p
A
/ p
An
)
T
p
An
> P
to
p
A
max
= P
i
= (p
A
/ P)
T
p
A
= p
An
Y = 0,622 [ p
An
/ (P – p
An
)]
` = 100
- nasycenie procentowe
= (Y / Y
n
) 100
11
- objętość wilgotna:
= 22,42[(1/M
B
) + (Y/M
A
)] [(273 + t)/273] = 22,42[(1/29) + (Y/18)]
[T/273]
[]= [m
3
/kg
such pow
]
n
= 22,42[(1/29) + (Y
n
/18)] [T/273]
V = m
B
= (1 + Y) /
= [p
A
M
A
) / (RT)] + [p
B
M
B
) / (RT)] = (
A
)
T, pA
+ (
B
)
T, pB
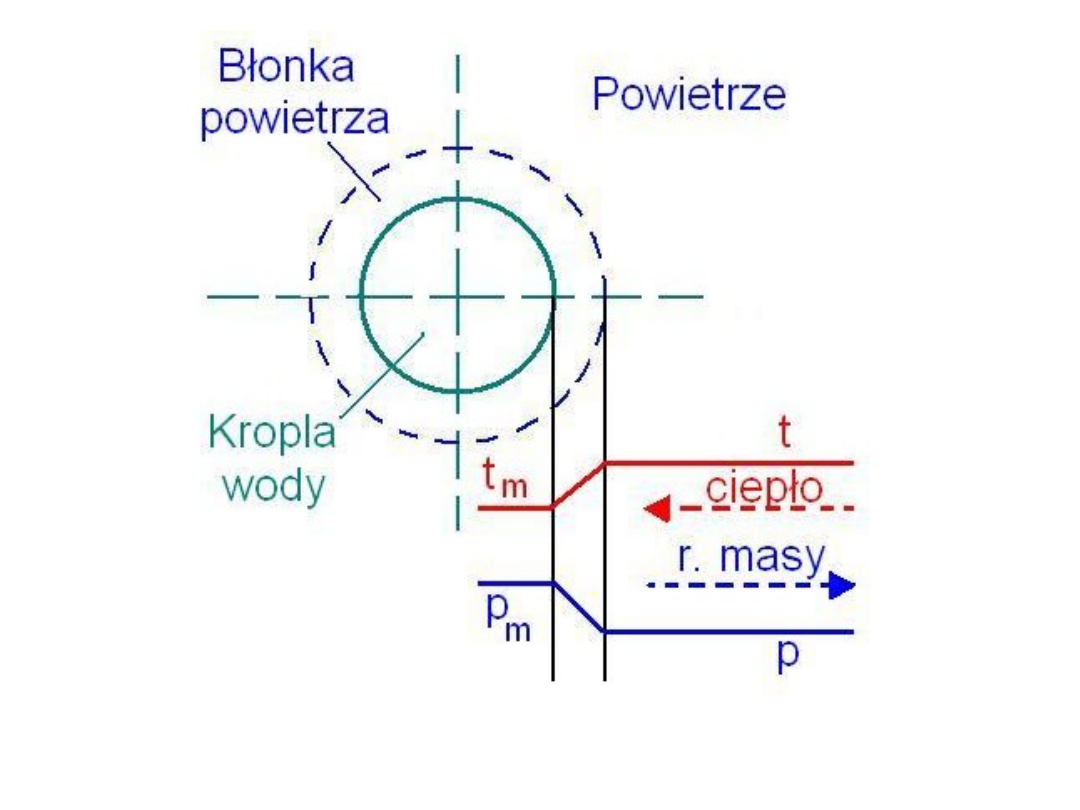
- temperatura suchego termometru t
- temperatura punktu rosy t
r
- temperatura wilgotnego (mokrego) termometru t
m
q = r
m
W
q = (t – t
m
) A
W = k
Y
(Y
m
– Y) A
q = W r
m
= k
Y
(Y
m
– Y) A r
m
t – t
m
= [r
m
(Y
m
– Y)] / ( / k
Y
)
12
c
H
= / k
Y
[(Y
m
– Y) / (t – t
m
)] = ( / k
Y
) (1 / r
m
) ≈ c
H
/ r
m
[(Y
m
– Y) / (t – t
m
)] = - { Le
-2/3
[(M
A
/ M
B
) / ((M
A
/ M
B
)+ Y)] (1 + Y
m
)} (r
m
/ c
H
)
Liczba Lewisa Le = Sc / Pr
(Y
m
– Y) / (t – t
m
) = - ( / k
Y
) (1 / r
m
) = - Le
2/3
(c
H
/ r
m
)
- temperatura adiabatycznego nasycenia t
an
(Y
2
– Y
1
) / (t
1
– t
an
) = c
H1
/ r
2
- entalpia gazu (powietrza) wilgotnego i
i = i
B
+ Y i
A
i
B
= c
B
t
i
A
= c
A
t + r
0
i = c
B
t + (c
A
t +r
0
)Y
i = (c
B
+ c
A
Y)t + r
0
Y
c
A
- średnie ciepło właściwe pary wodnej = 1,88 kJ/kgK
c
B
- średnie ciepło właściwe suchego powietrza = 1,01 kJ/kgK
r
0
- ciepło parowania wody w temperaturze 0 ºC = 2501 kJ/kg
13
Rys. 12. A [m
2
]; W [kg/s], t
m
, r
m
14
c
H
= c
B
+ c
A
Y
i = c
H
t + r
0
Y
- powietrze nasycone
i
n
= c
B
t
n
+ (c
A
t
n
+ r
0
) Y
n
- entalpia zamglonego powietrza
i
m
= c
w
t = 4,19 t
i
n
= i
B
+ i
A
Y
1
+ (Y – Y
n
)i
m
i
l
= -334,1 + 2,09 t
ciepło krzepnięcia wody = 334,1 kJ/kg
ciepło właściwe lodu = 2,09 kJ/kgK
15
Wykres gazu wilgotnego
Y = 0,622 [( p
An
) / (P - p
An
)]
i = c
B
t + (c
A
t + r
0
)
Y
i = (c
B
+ c
A
Y)t + r
0
Y
(di / dY)
T
= c
A
t + r
0
(di / dY)
T
= r
0
(di / dY) = 4,19 t dla wody
(di / dY) = -334,1 + 2,09 t dla lodu
P2
=
p1
(p
2
/ p
1
)
16
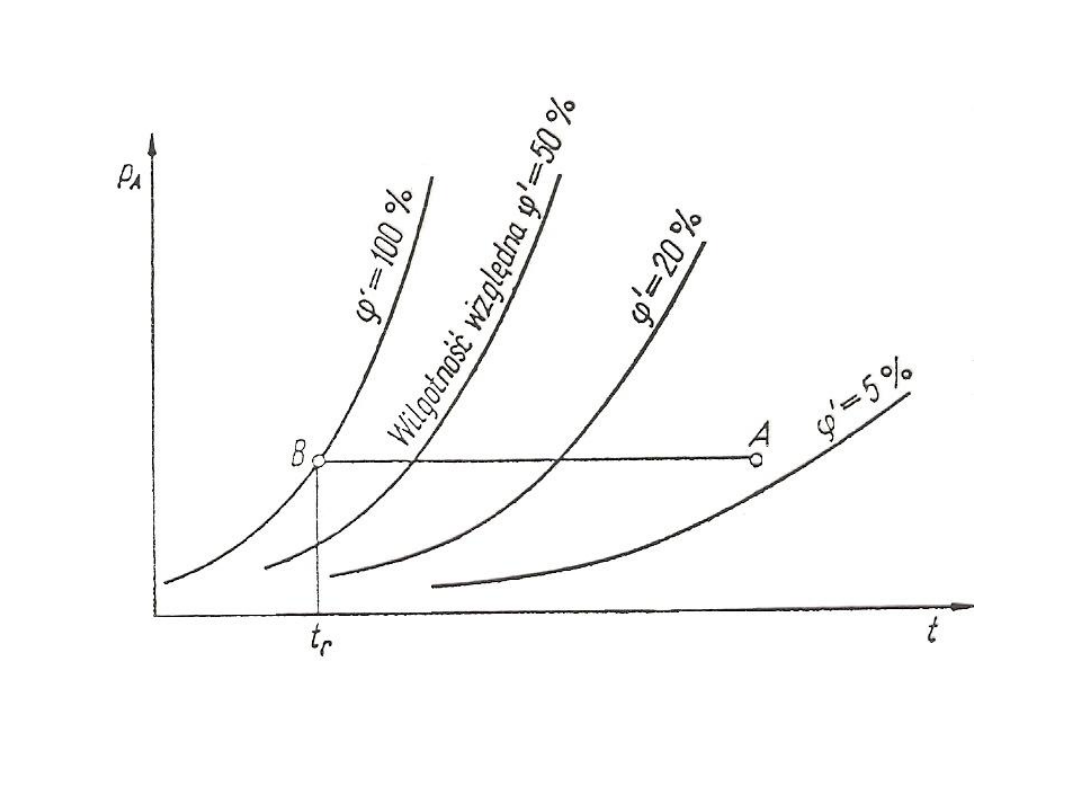
Rys. 13. Zależność prężności cząstkowej p pary wodnej od temperatury t
i wilgotności względnej powietrza `
17
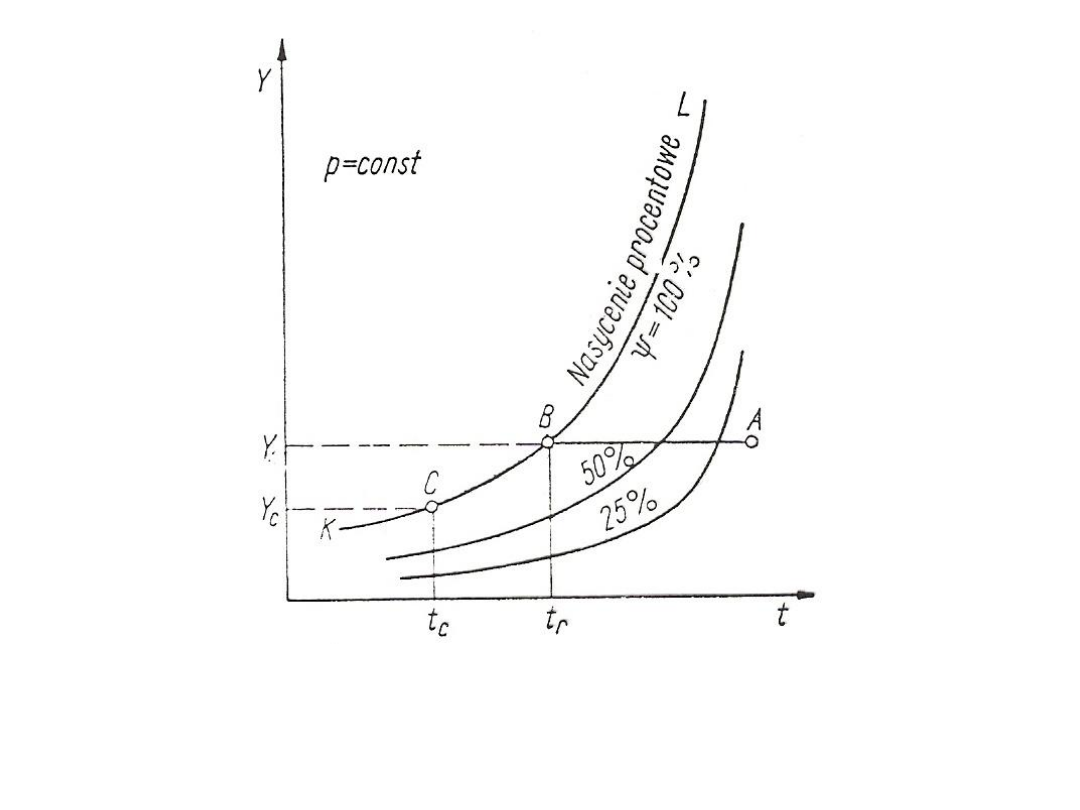
Rys. 14. Zależność wilgotności bezwzględnej Y od temperatury t
i nasycenia procentowego
18
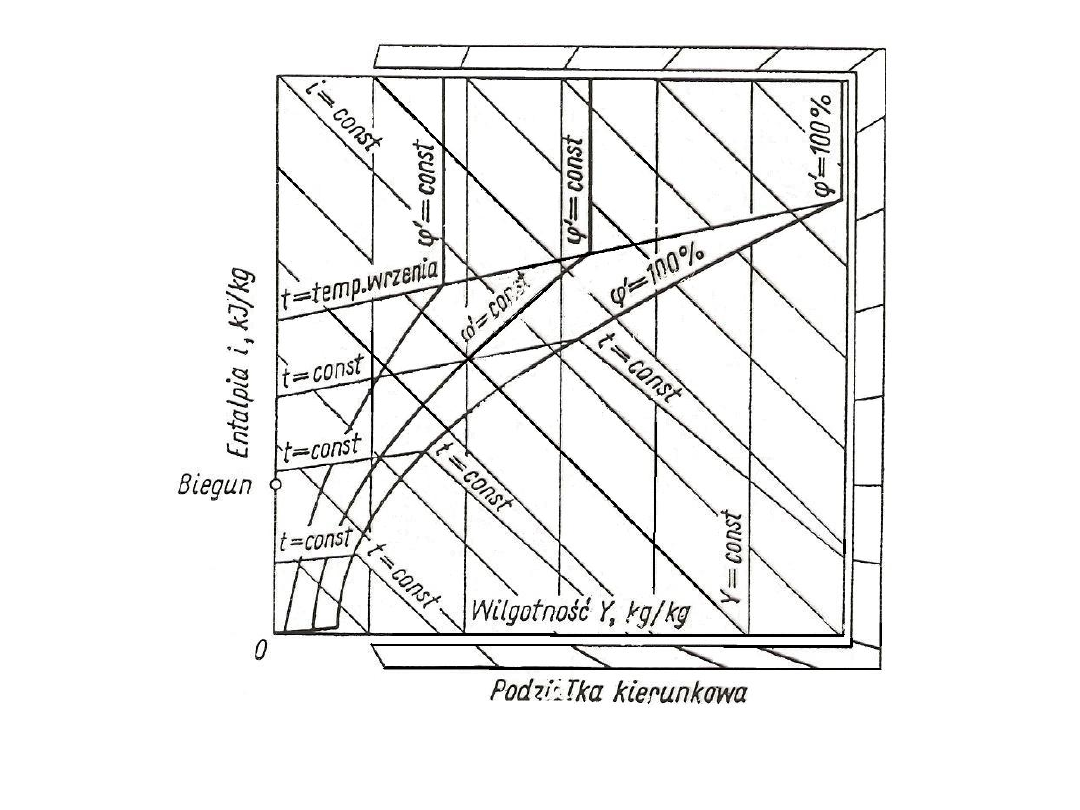
Rys. 15. Wykres Molliera – Ramzina w zakresie temperatur wyższych od 0 ºC
19
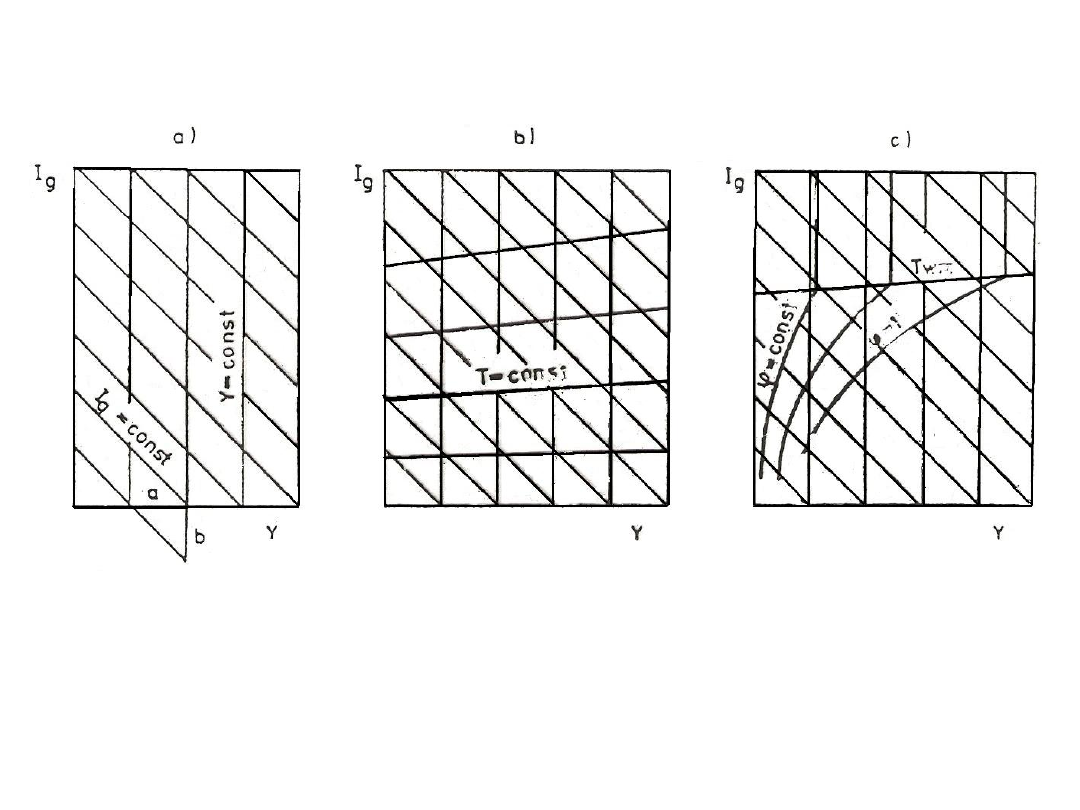
Rys. 16. Konstrukcja wykresu Molliera – Ramzina
20
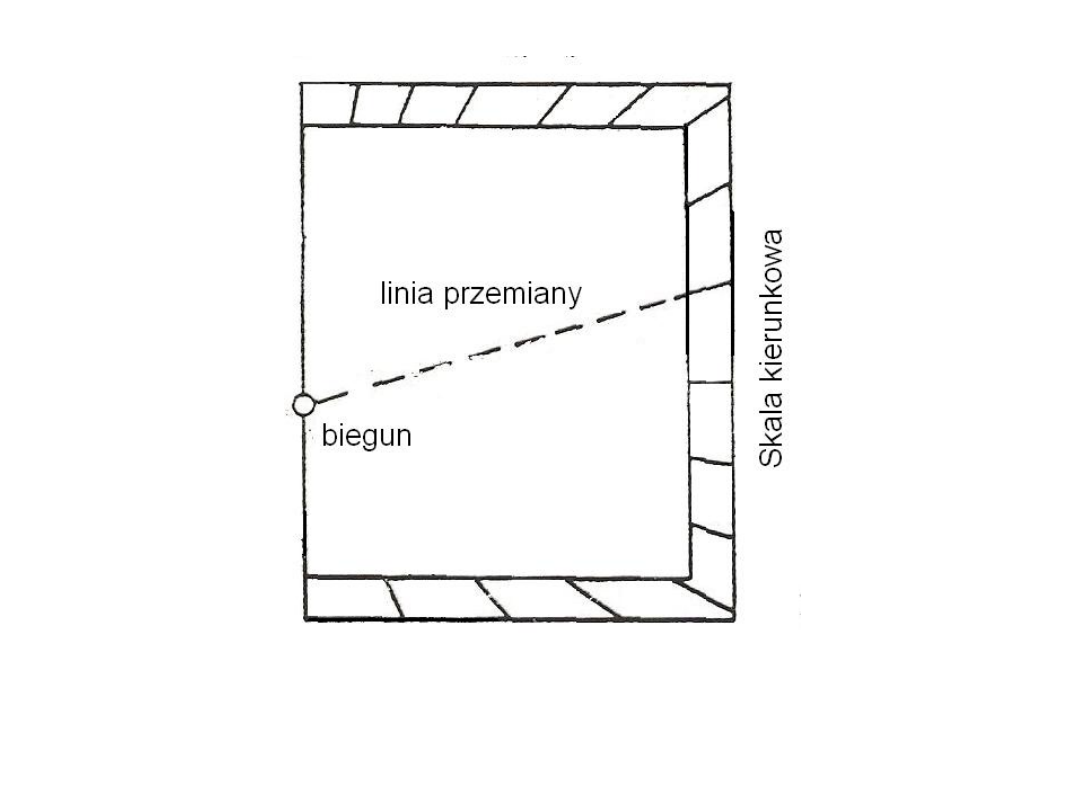
Rys. 17. Podziałka kierunkowa wykresu I
g
- Y
21
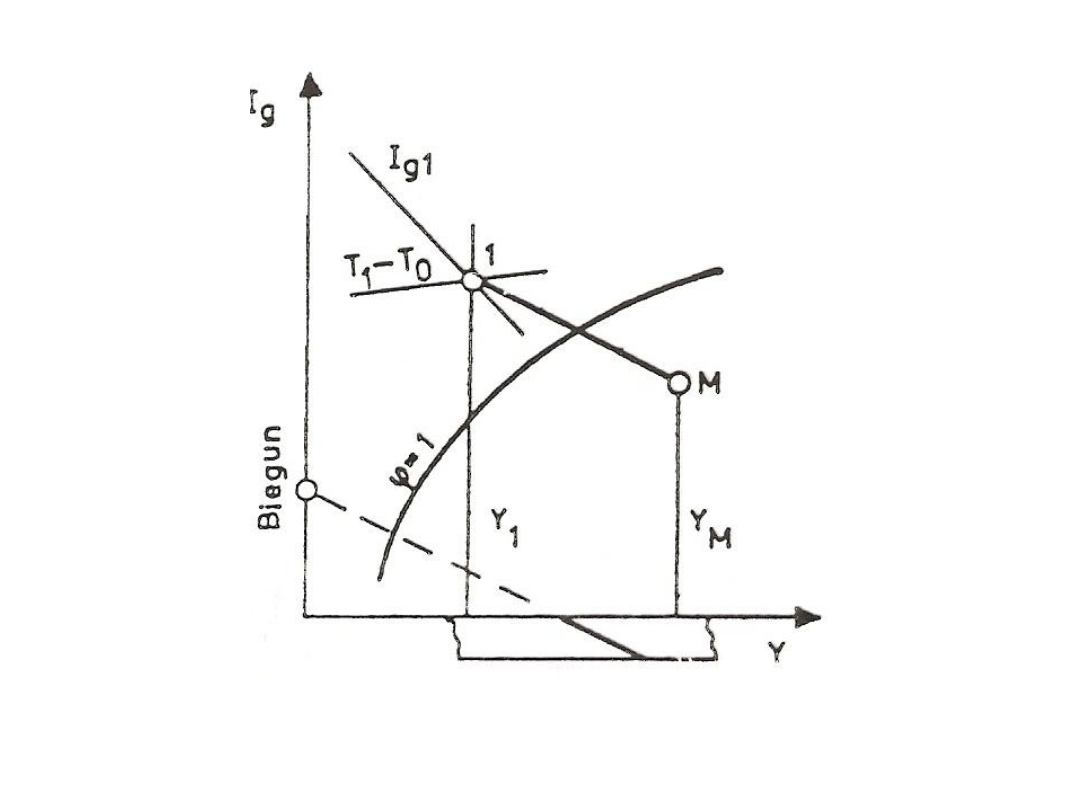
Rys. 18. Mieszanie gazu wilgotnego z cieczą lub parą
22
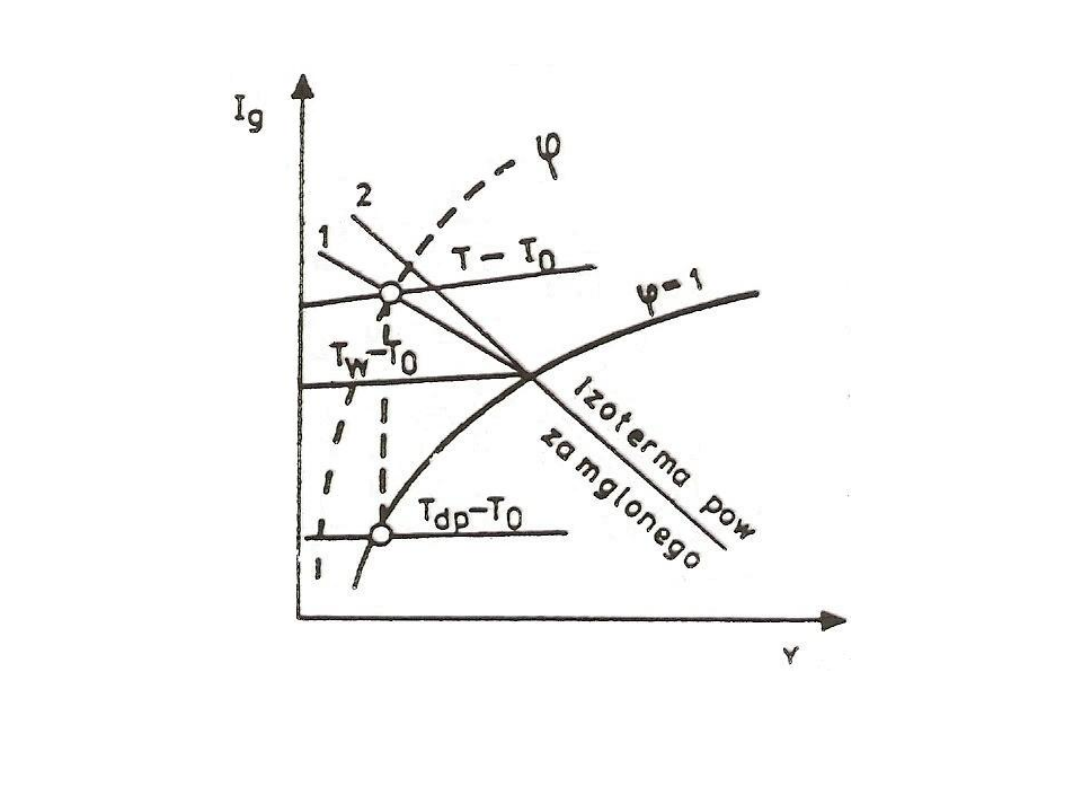
Rys. 19. Wyznaczanie wilgotności gazu za pomocą wykresu Ig – Y
1 – linia termometru wilgotnego; 2 – linia adiabatycznego nasycenia
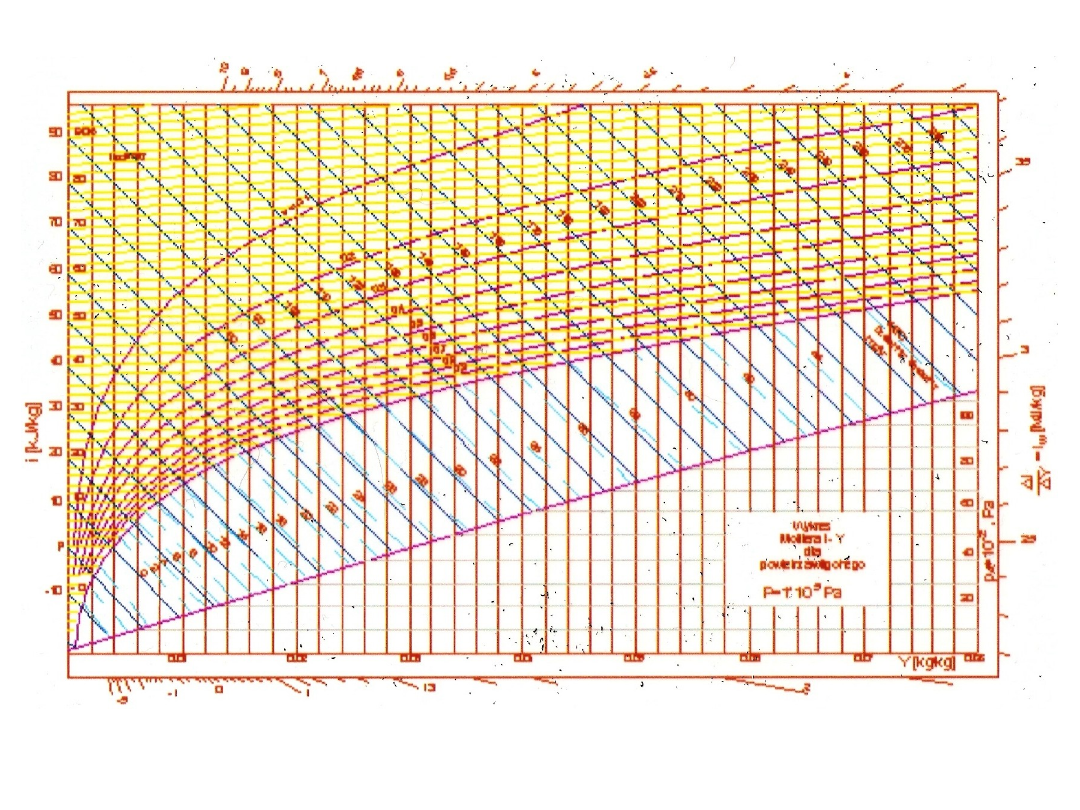
23
Rys. 20.
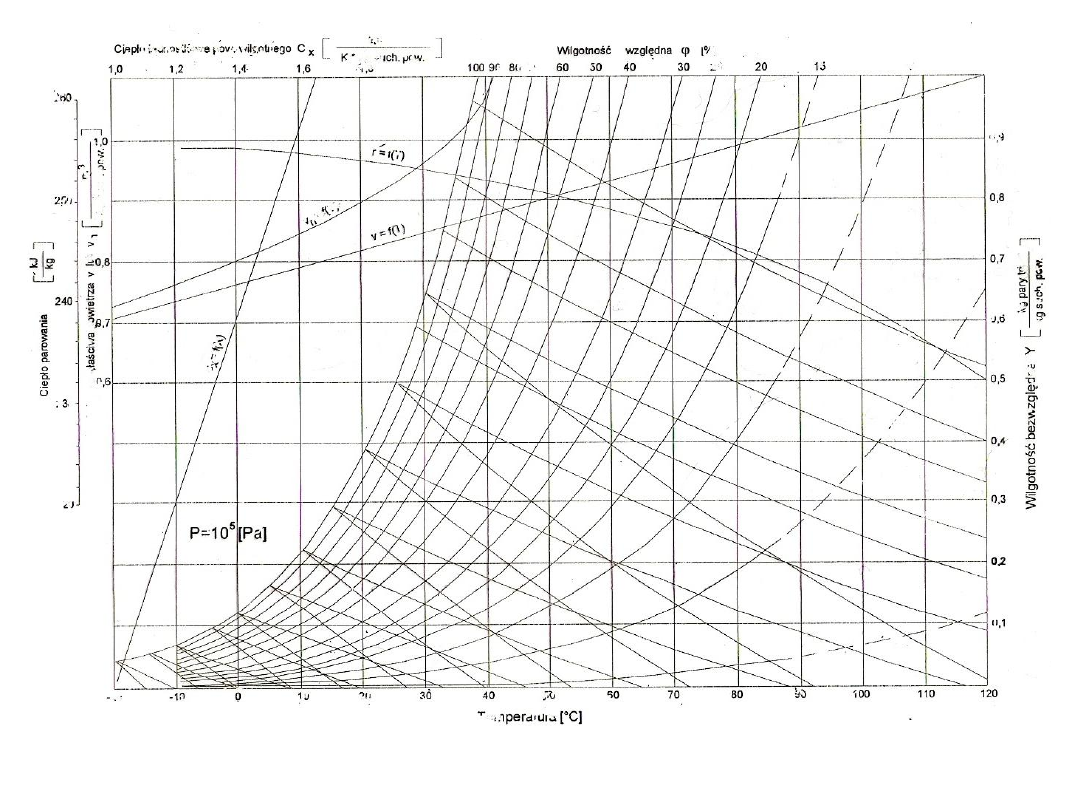
24
Rys. 21.
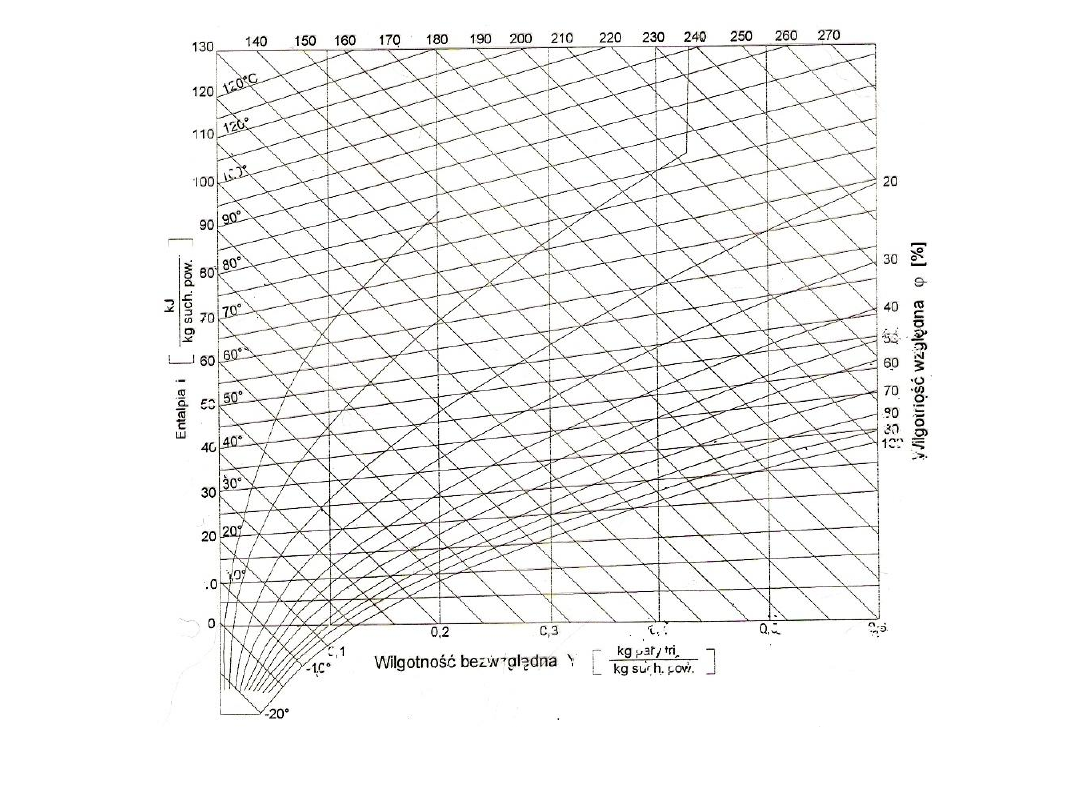
25
Rys. 22. Wykres i = f( ) dla układu powietrze – para trójch____cetylenu
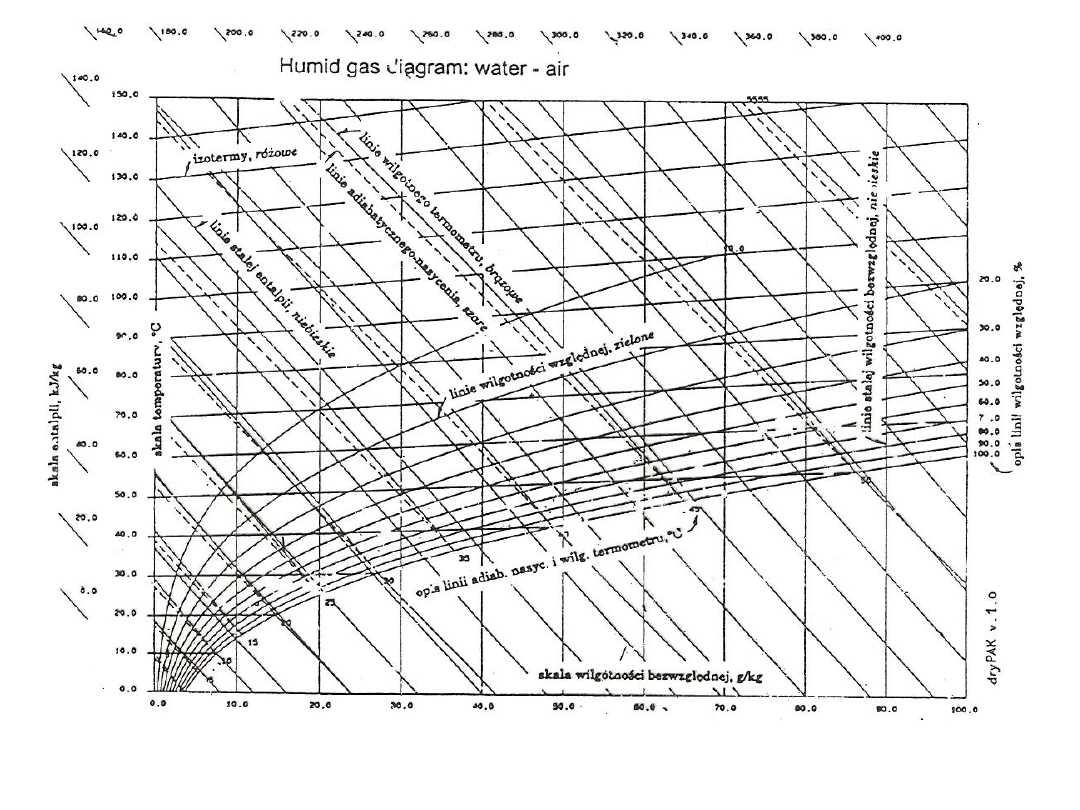
26
Rys. 23.
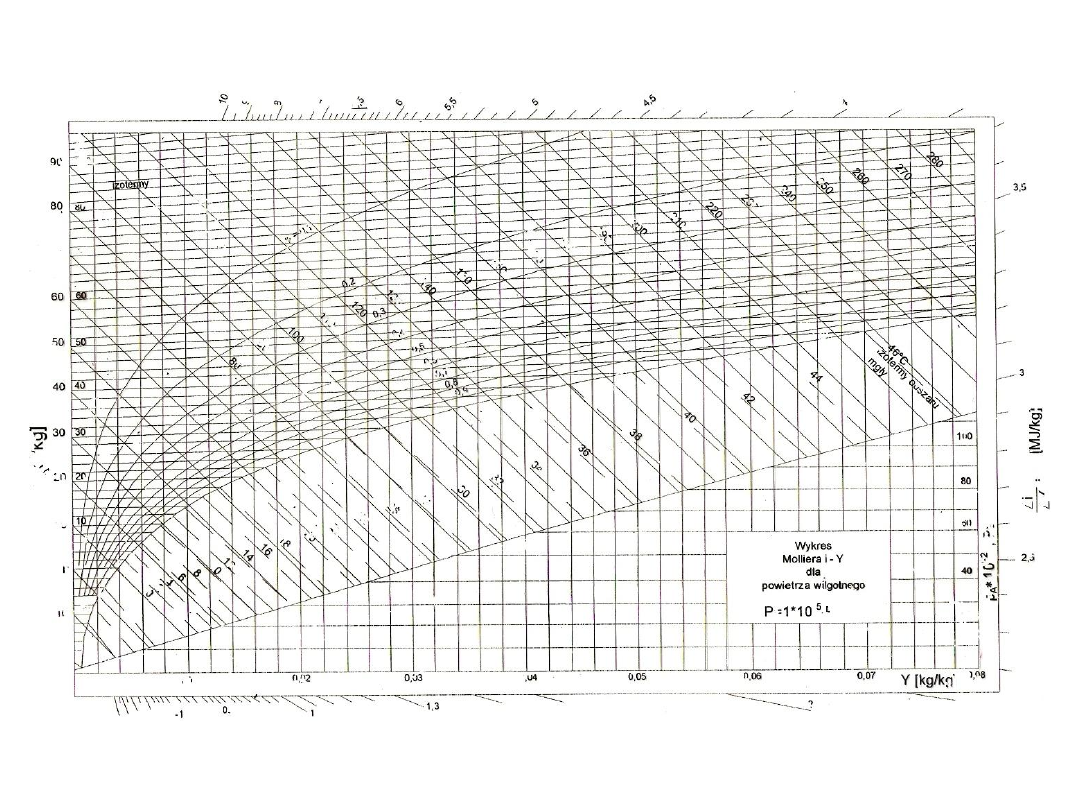
27
Rys. 24.
28
Mieszanie strumieni gazu
Strumień gazu
G
S1
+ G
S2
= G
SM
Strumień wilgoci
G
S1
Y
1
+ G
S2
Y
2
= G
SM
Y
M
Strumień energii
G
S1
i
1
+ G
S2
i
2
= G
SM
i
M
G
S1
/ G
S2
= (Y
2
- Y
M
) / (Y
M
- Y
1
) = (i
2
- i
M
) / (i
M
- i
1
)
G
S1
Y
1
+ W = G
S1
Y
M
G
S1
i
1
+ W i
L
= G
S1
i
M
(i
M
- i
1
) / (Y
M
- Y
1
) = i / Y= i
L
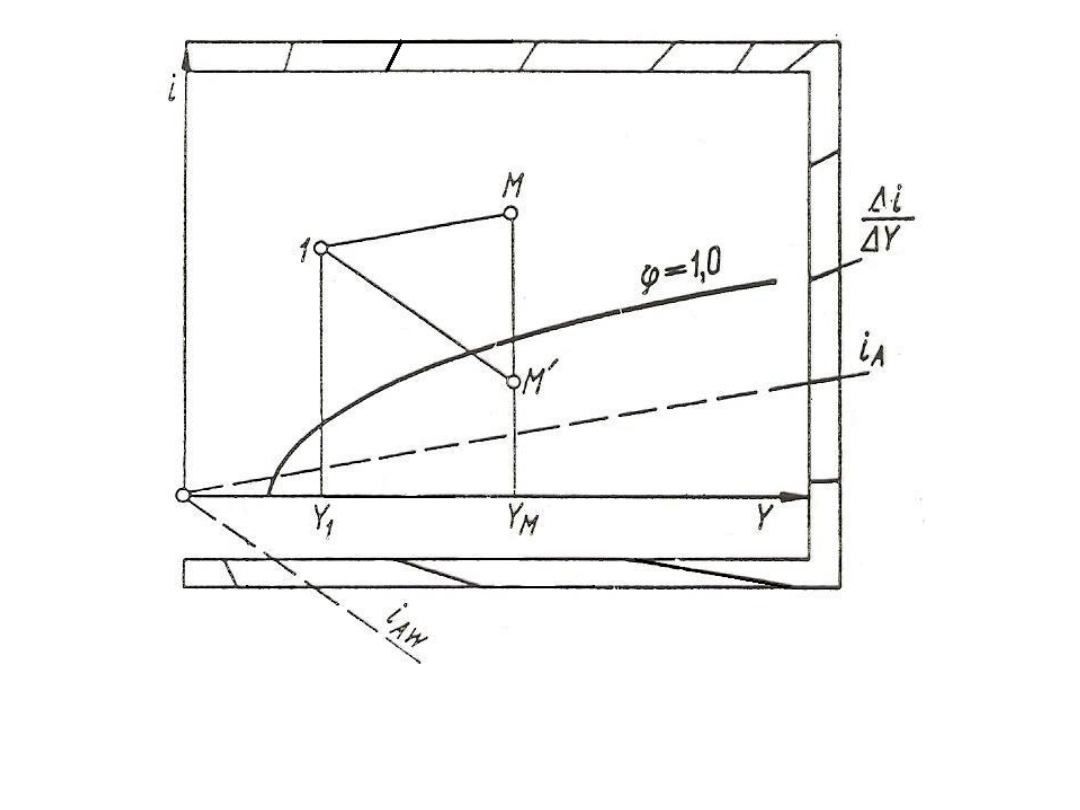
29
Rys. 25. Korzystanie ze skali kierunkowej na wykresie i – Y na przykładzie
dodawania do powietrza wody o entalpii i
AW
oraz pary wodnej o entalpii i
A
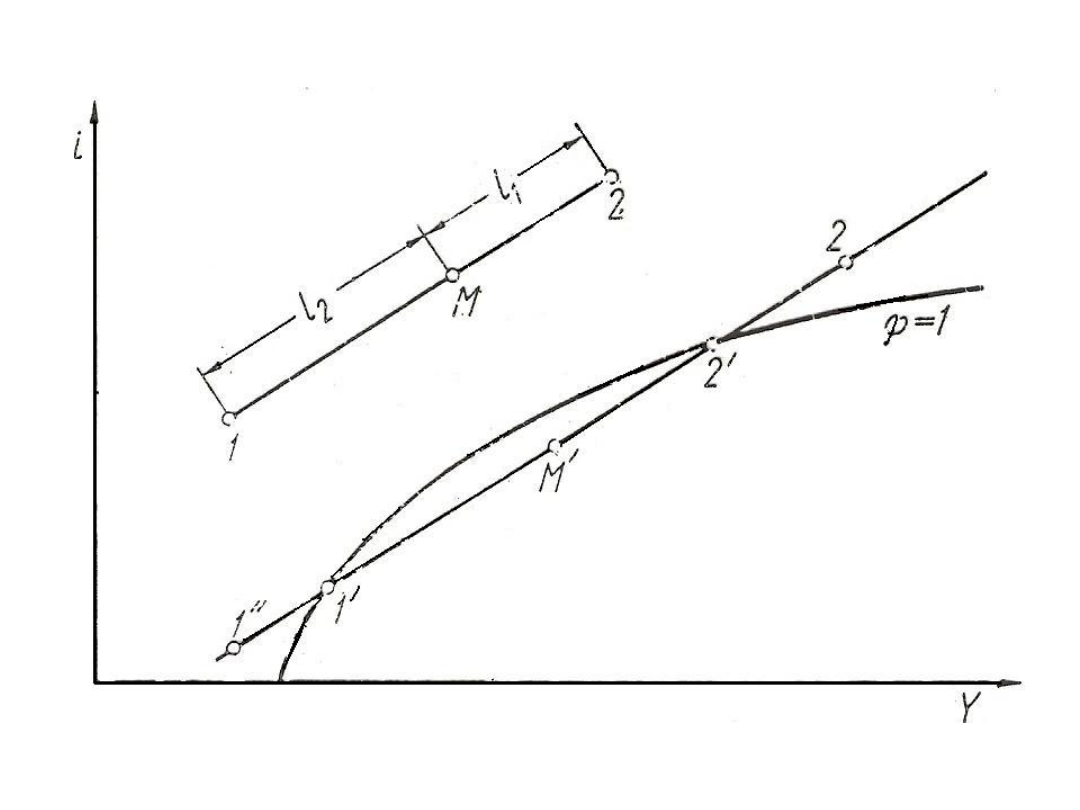
30
Rys. 26. Mieszanie strumieni powietrza na wykresie i – Y
31
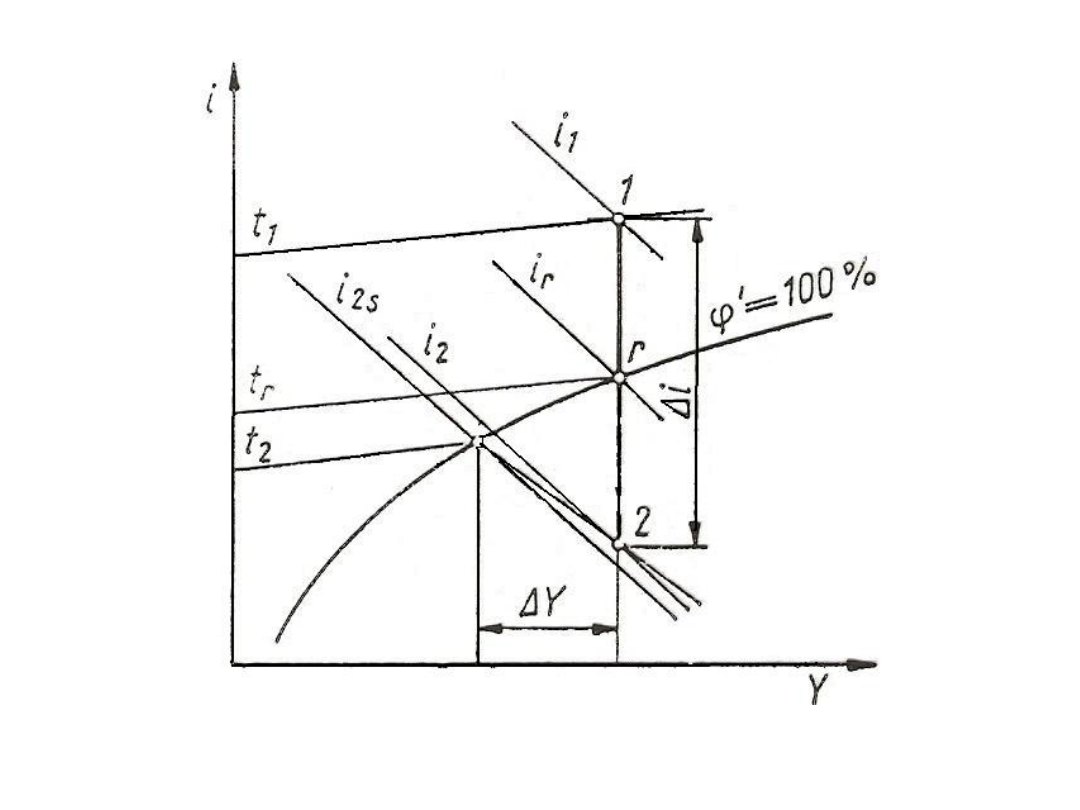
Rys. 27. Chłodzenie wilgotnego powietrza
32
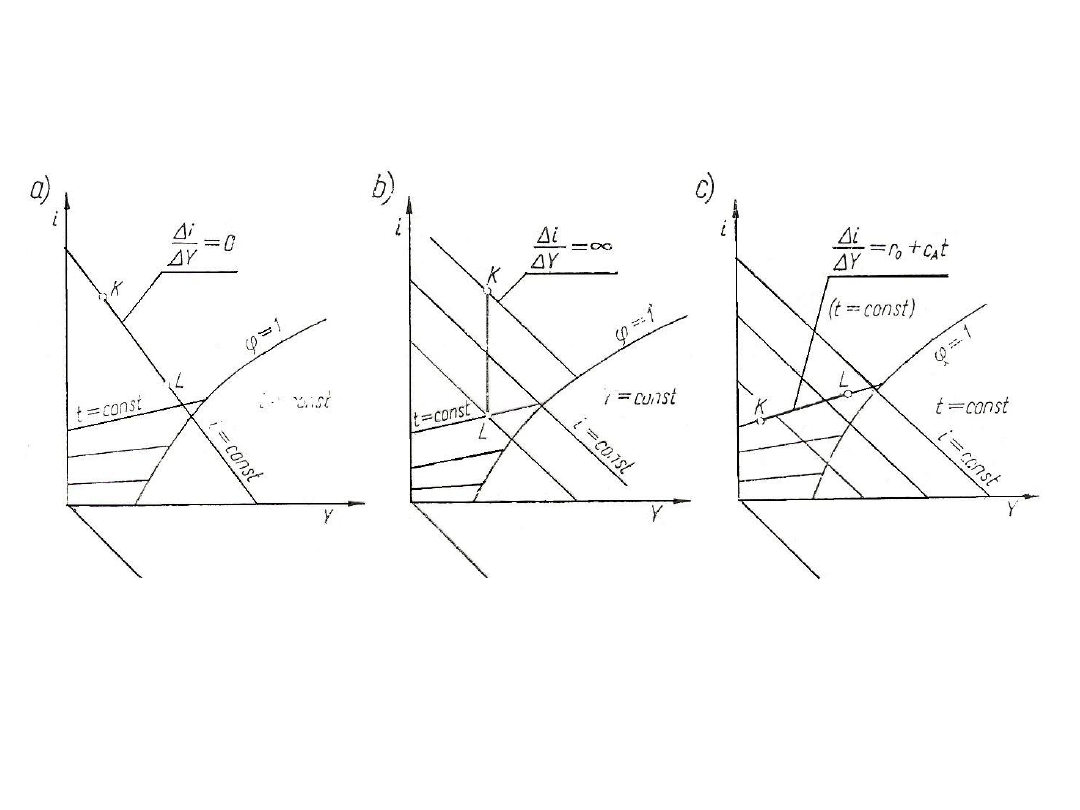
Rys. 28. Nawilżanie powietrza przez dodanie pary przypadki szczególne
33
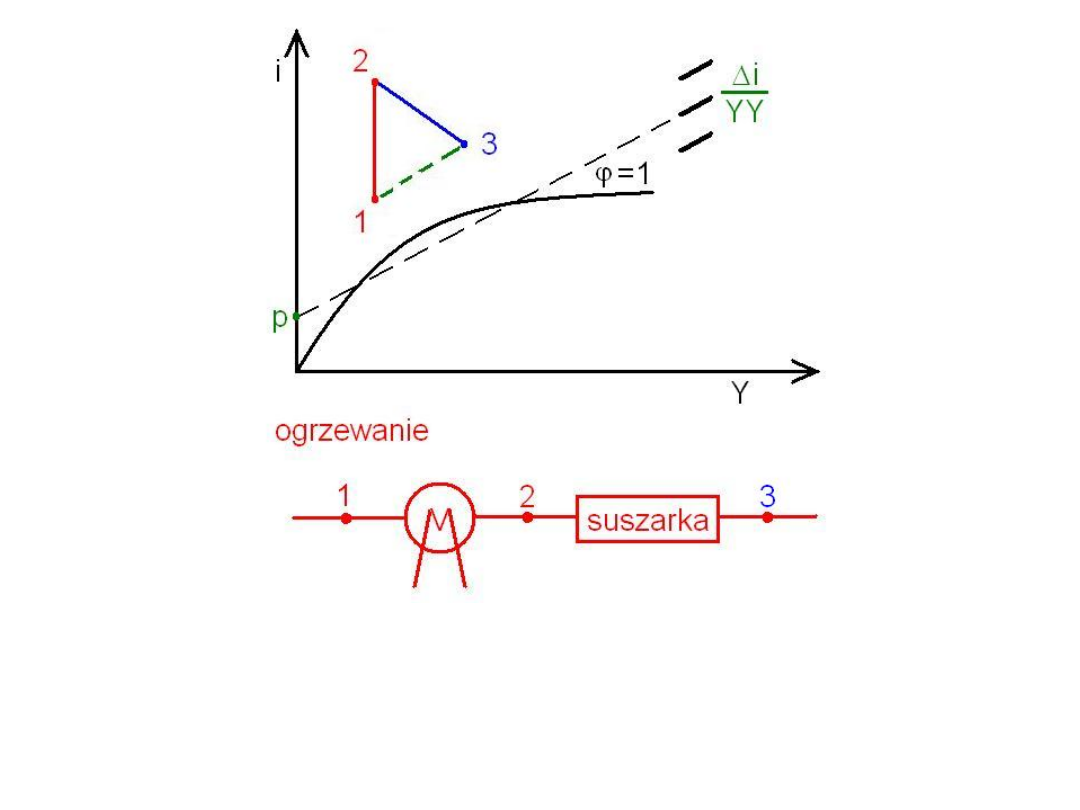
Rys. 29. 2 -3 mieszanie gazu z cieczą lub parą cieczy (dla uproszczenia
przyjmuje się, że ciecz posiada temp 0 ºC suszenie jest izentalpowe
1 – 3 nawilżanie gazu [jest ona (prosta) równoległa do prostej łączącej
biegun ze skalą kierunkową]
34
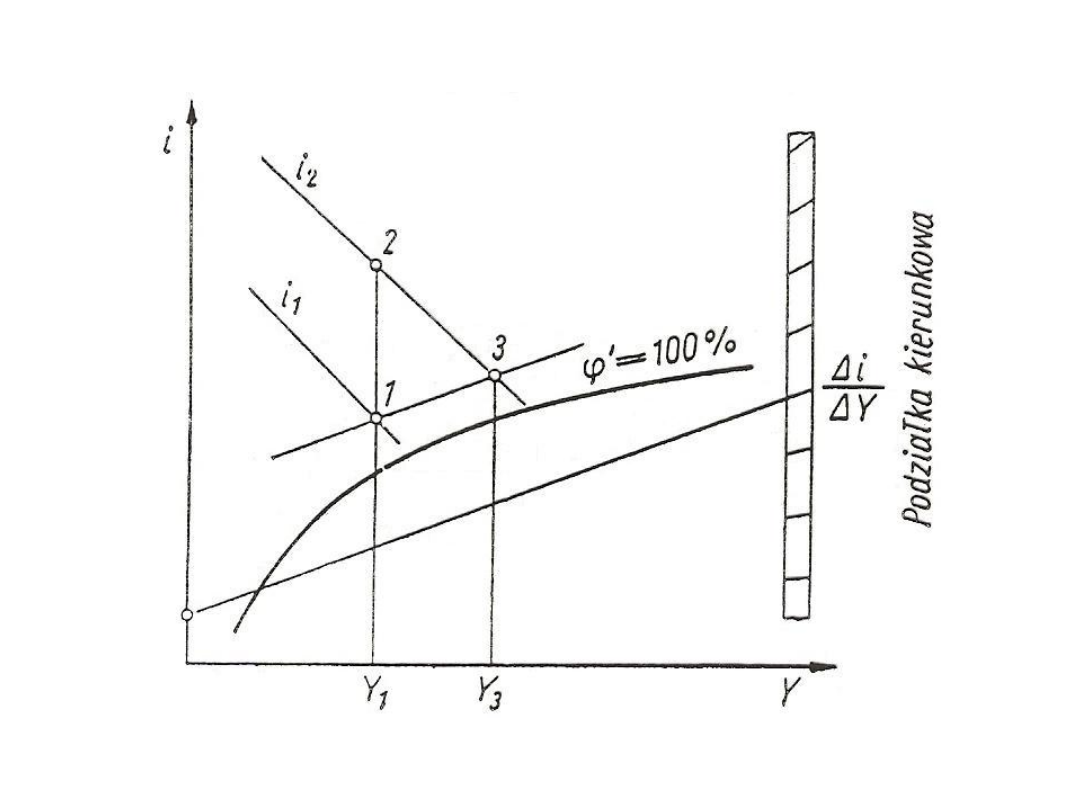
Rys. 30. Suszenie na wykresie i - Y
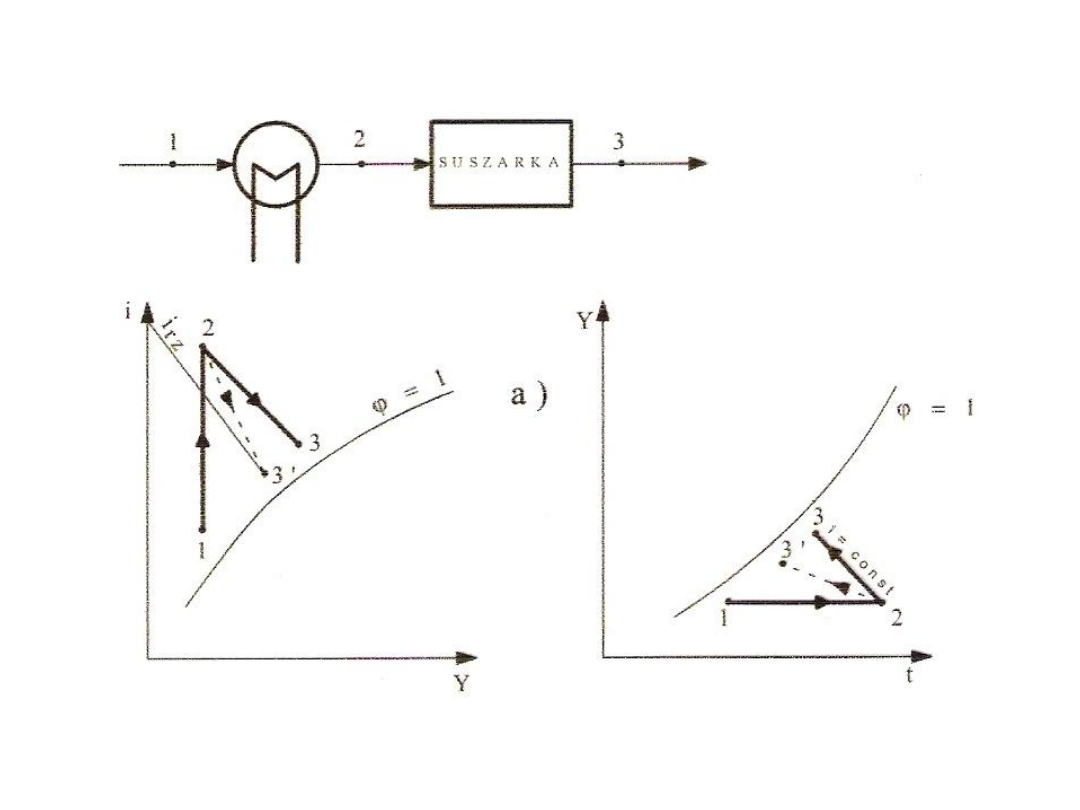
35
Rys. 31. Schemat instalacji suszarniczej - jednostopniowej
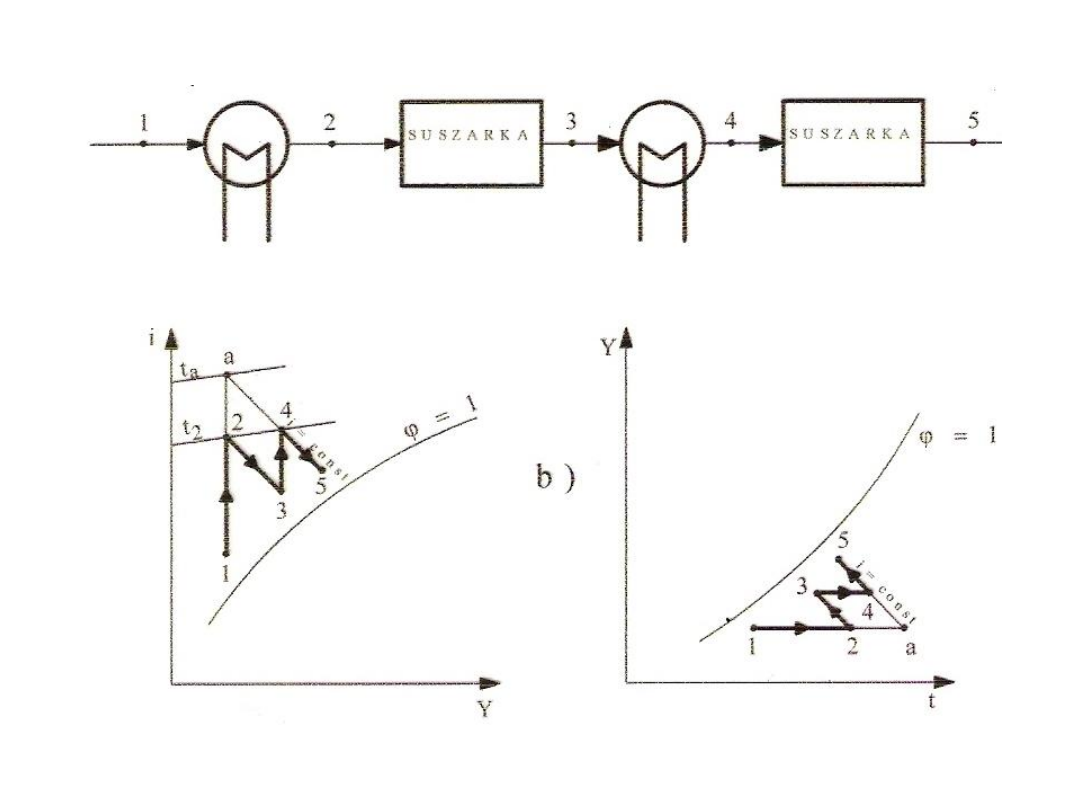
36
Rys. 32. Schemat instalacji suszarniczej - wielostopniowej
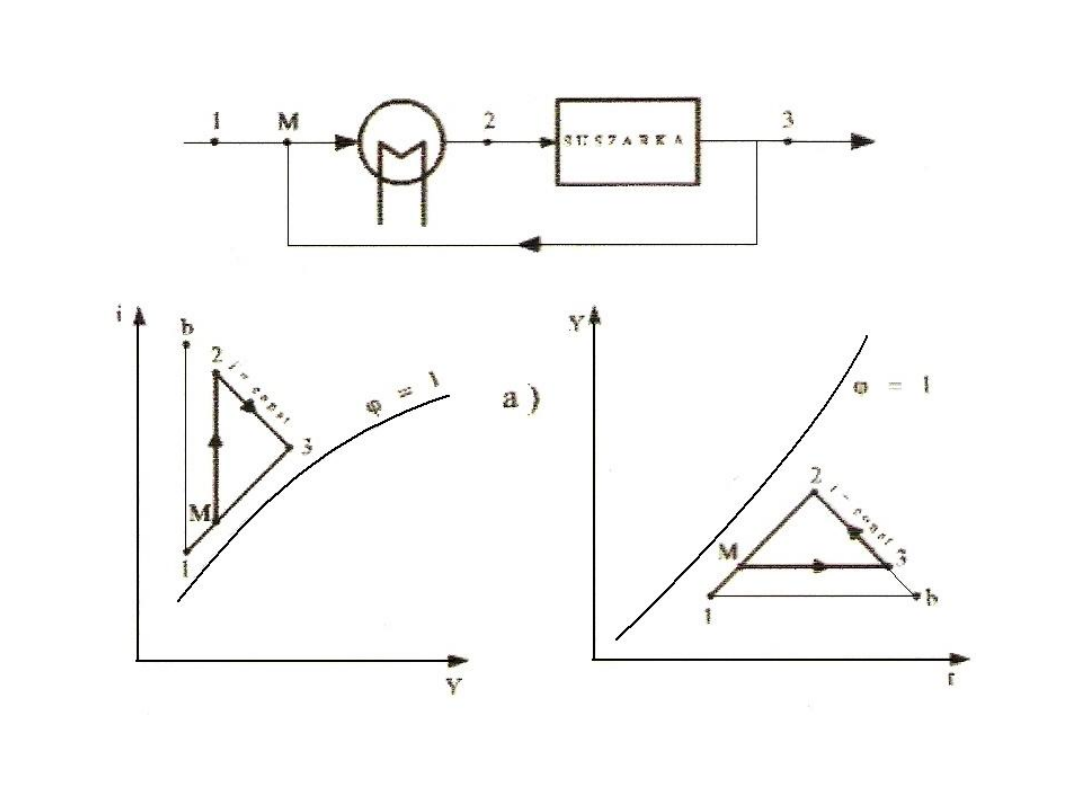
37
Rys. 33. Schemat instalacji suszarniczej – z recyrkulacją
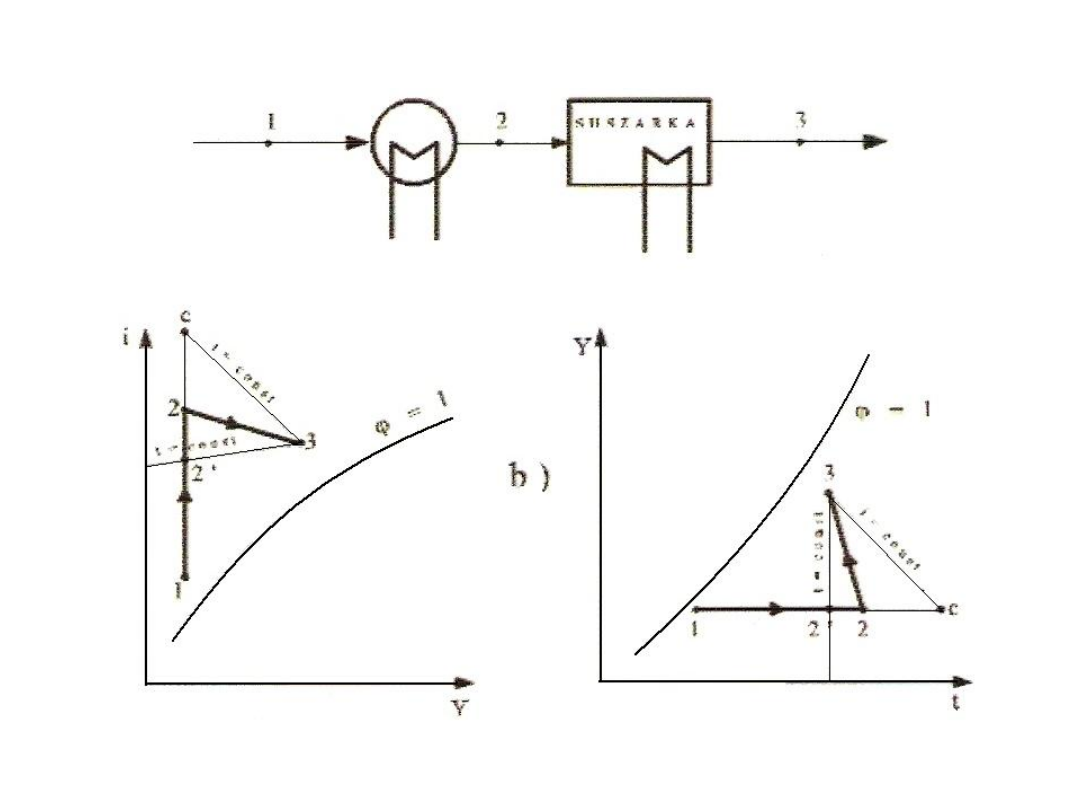
38
Rys. 34. Schemat instalacji suszarniczej – z podgrzewaczem
39
Charakterystyka materiału
wilgotnego
- wilgotność materiału u oznacza ilość kilogramów wilgotności W
przypadającej na jeden kilogram materiału wilgotnego S`:
u = W / S`
[kg
wilgoci
/ kg
ciała wilgotnego
]
- zawartość wilgoci z (wilgotność właściwa, wilgotność bezwzględna
materiału wilgotnego) wyraża ilość kilogramów wilgoci W przypadającej
na jeden kilogram materiału suchego S:
z = W / S
[kg
wilgoci
/ kg
ciała suchego
]
Wzajemne relacje między wielkościami u i z ujmują następujące
zależności:
u = W / S` = W / (S + W) = (W / S) / [1 + (W / S)] = z / (1 + z)
z = u / (1 – u)
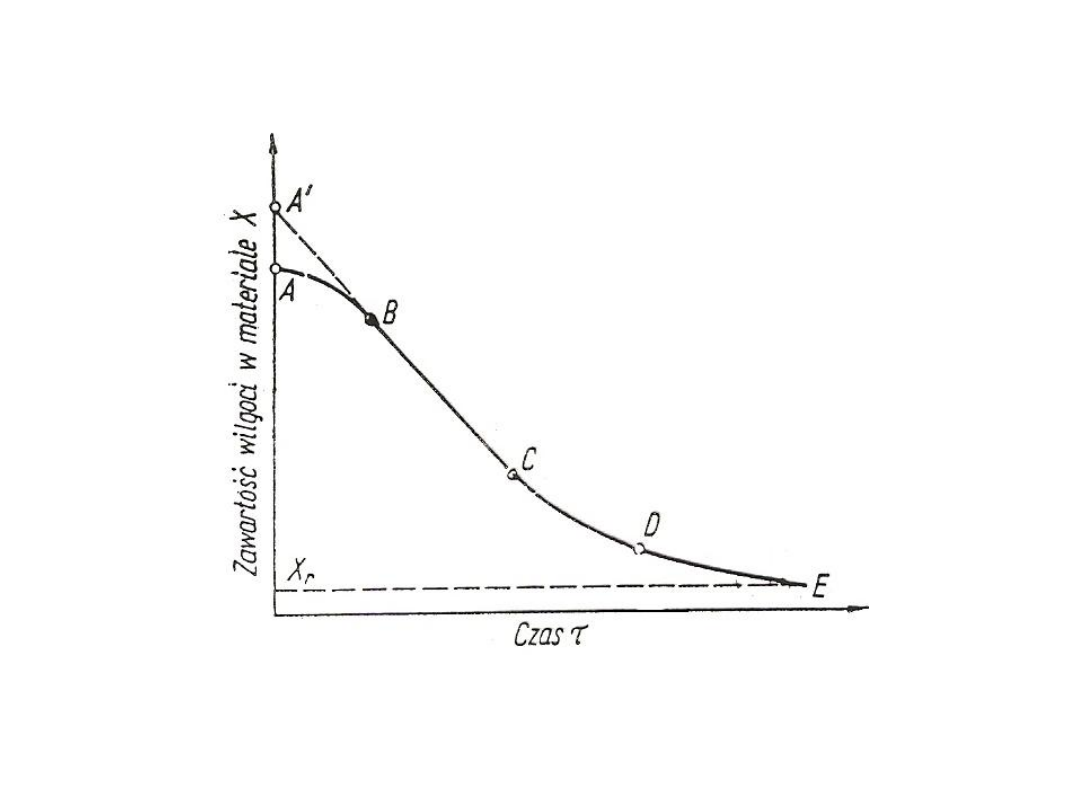
- zawartość wilgoci równowagowa
- zawartość wilgoci krytyczna
40
Rys. 35. Krzywa suszenia dla warunków ustalonych
41
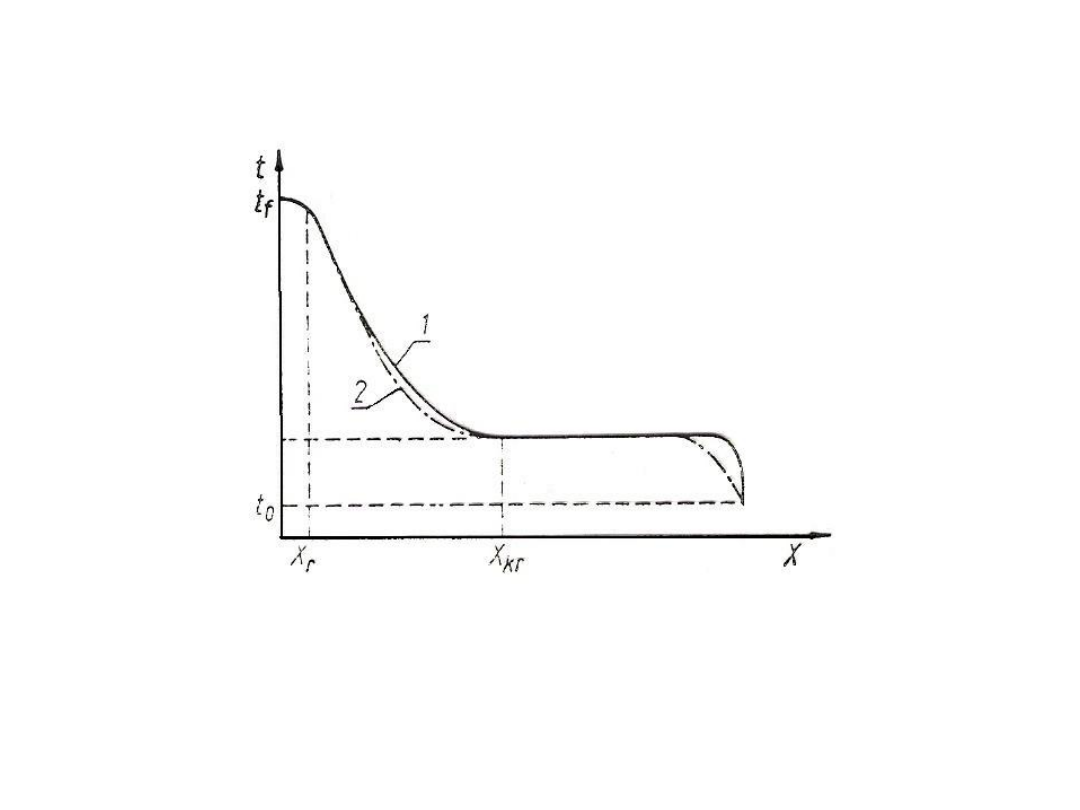
Rys. 36. Krzywe temperaturowe materiałów wilgotnych na powierzchni i w
środku materiału: 1 – temperatura powierzchni materiału [ºC]; 2 -
temperatura w środku materiału [ºC]; t
0
- temperatura początkowa [ºC]; t
t
-
temperatura otoczenia [ºC]
42
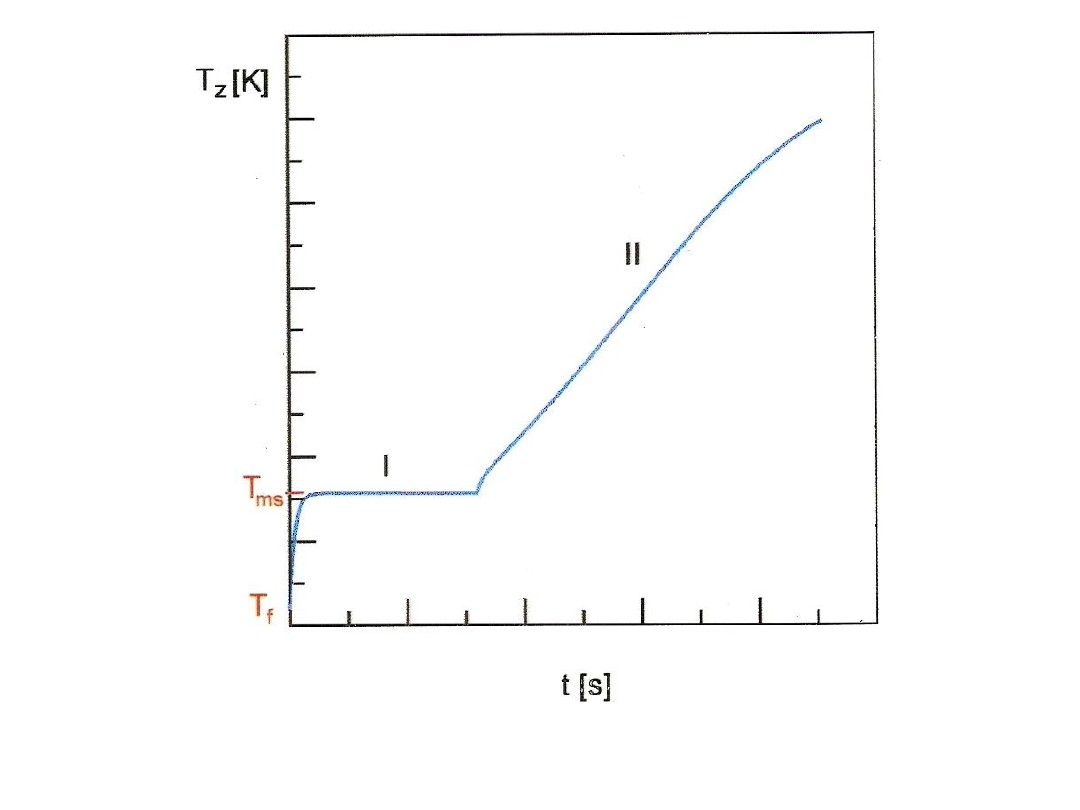
Rys. 37.
43
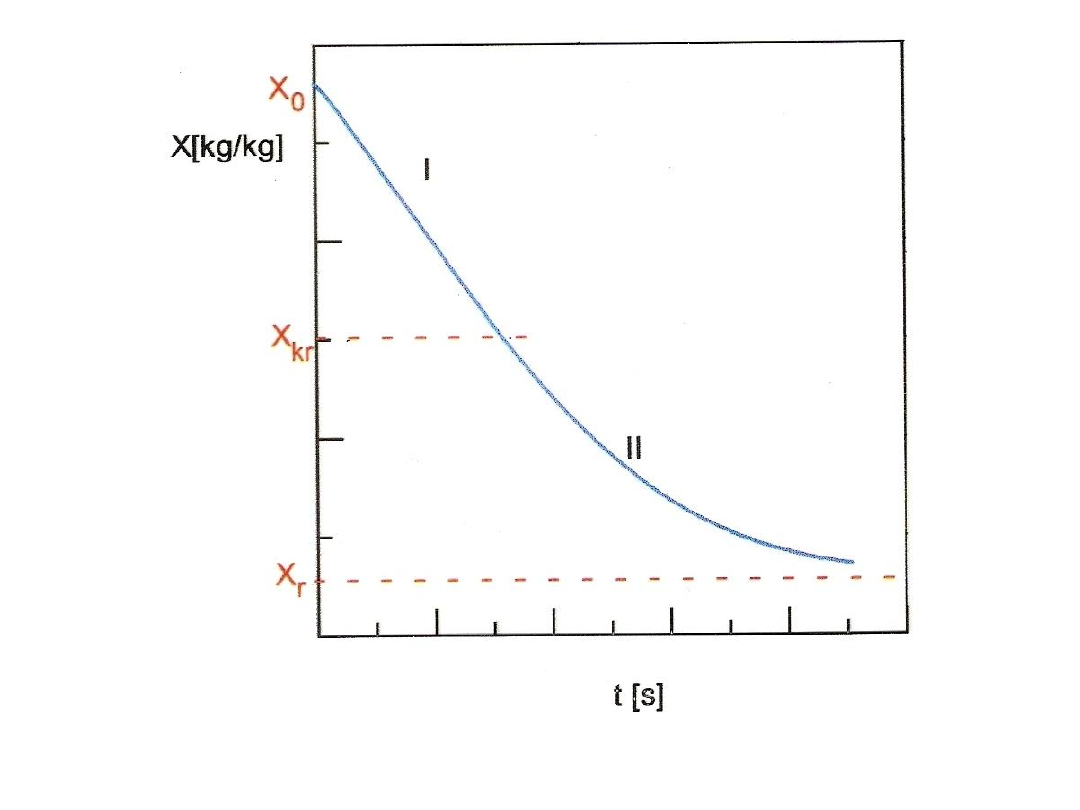
Rys. 38.
44
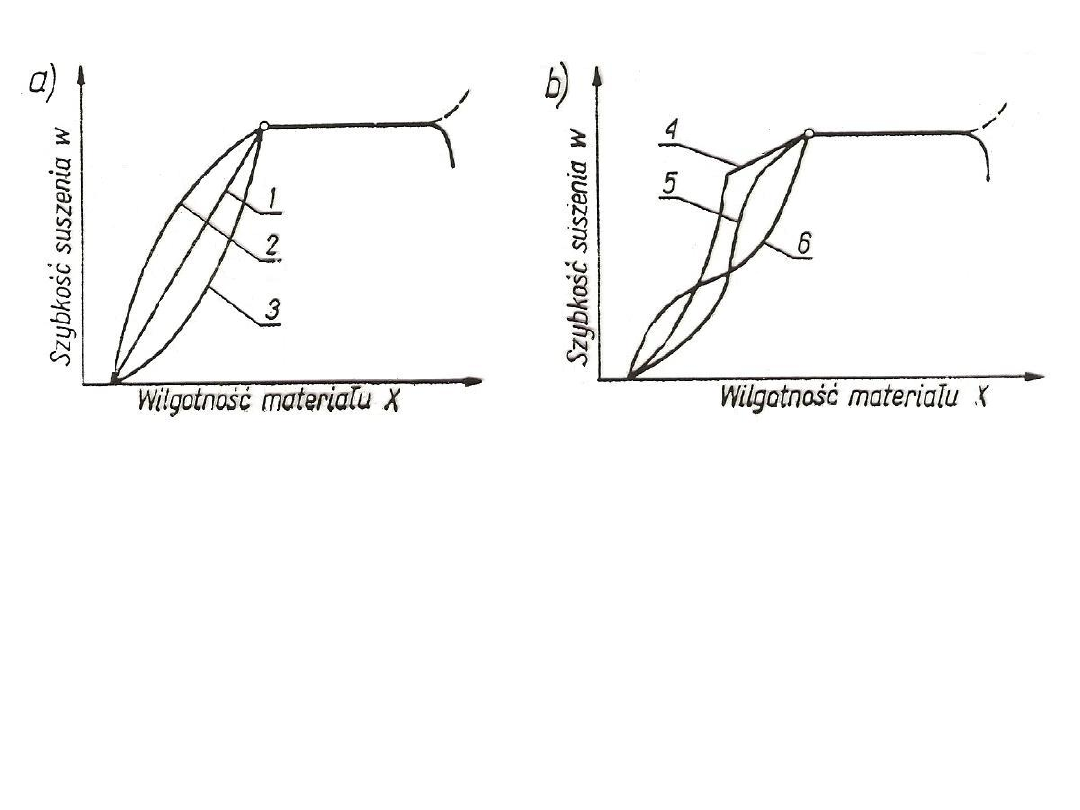
Rys. 39. Krzywe szybkości suszenia:
ciała kapilarno-porowate o dużej powierzchni właściwej odparowania: 1 -
papier, cienki karton; 2 - tkaniny, cienka skóra;
ciała kapilarno-porowate o małej powierzchni właściwej odparowania: 3 i 4 –
wyroby ceramiczne; 4 – piasek, glina;
ciała koloidalne: 2 – krochmal; układy złożone,
ciała kapilarno-porowate-koloidalne: 4, 5 i 6 – zboże, chleb, torf
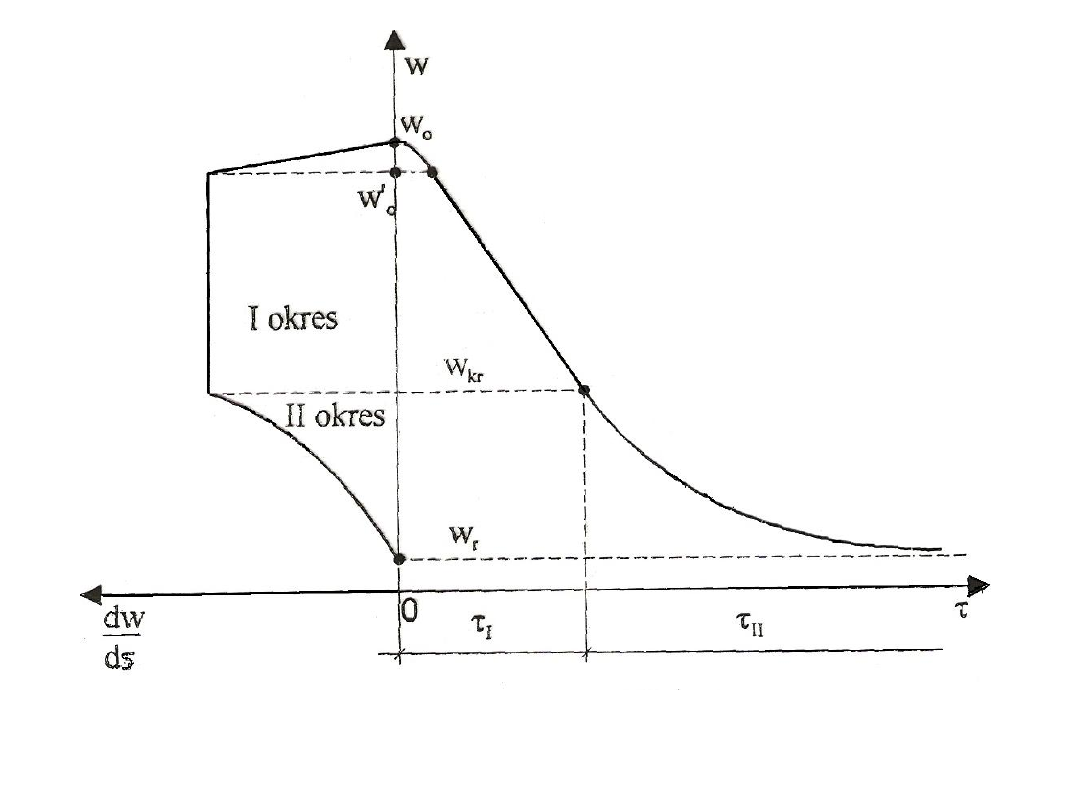
45
Rys. 40. Schemat zależności szybkości i czasu suszenia w I i II okresie
suszenia od zawartości wilgoci w ciele stałym
46
Bilans masowy suszarki
teoretycznej
Bilans masowy (wilgoci) suszenia doprowadza do zależności:
W = S`
p
[(u
p
– u
k
) / (1 – u
k
)] = S`
k
[(u
p
– u
k
) / (1 – u
p
)]
W = S`
p
- S`
k
W = S (z
p
– z
k
)
gdzie: indeks p – stan początkowy (wlot), k – stan końcowy (wylot)
S – masa lub masowe natężenie przepływu absolutnie suchego
materiału
[kg lub kg/s]
W - masa lub masowe natężenie przepływu wilgoci usuniętej w
trakcie
suszenia [kg lub kg/s]
S`
p
i S`
k
- masa lub masowe natężenie przepływu odpowiednio
surowca
wilgotnego wprowadzonego i
wyprowadzonego z suszarni
[kg lub kg/s]
47
Wskaźniki
Zużycie powietrza (w przeliczeniu na suche) do odparowania
kilograma wilgoci:
= G
S
/ W
Ogólne zużycie powietrza suchego niezbędnego do
odparowania wilgoci:
G
S
= W / (Y
2
– Y
1
)
G
S
– masa lub masowe natężenie przepływu powietrza suchego [kg
lub kg/s]
48
Bilans cieplny suszarki
teoretycznej
Dla suszarki teoretycznej, dla której Q
str
= 0, Q
dod
= 0, (
2
–
1
) =
0, zużycie ciepła w podgrzewaczu wyraża równanie:
Q = G
S
(i
2
– i
1
)
Dla suszarki rzeczywistej obowiązuje wyrażenie:
Q = G
S
(i
2
– i
0
) + S`
k
c
k
(
2
–
1
) + S`
tr
c
tr
(
2
–
1
) + Q
str
- Q
dod
– W c
w
1
gdzie: i
2
- entalpia powietrza na wylocie z suszarki [kJ/kg
suchego powietrza
];
i
0
- początkowa entalpia powietrza [kJ/kg
suchego powietrza
];
S`
k
- masa materiału wysuszonego, lub natężenie masowe
przepływu
[kg lub kg/s];
S`
tr
- masa urządzeń transportowych [kg/s];
c
w
, c
k
, c
tr
– odpowiednio ciepło właściwe wilgoci, materiału
wysuszonego
i urządzeń transportujących [kJ/kg·K];
Q
str
– straty ciepła do otoczenia [kJ lub kW];
Q
dod
– ilość ciepła doprowadzona dodatkowo do suszarki [kJ lub
kW];
1
– początkowa temperatura materiału [ºC];
2
– końcowa temperatura materiału [ºC].
49
Zużycie ciepła przypadające na 1 kg odparowanej wilgoci (tzw.
właściwe zużycie ciepła) dla suszarki teoretycznej oblicza się w oparciu o
równanie:
= Q / W = (G
S
/ W) (i
2
– i
0
)
zaś dla suszarki rzeczywistej z wyrażenia:
= Q / W = (G
S
/ W) (i
2
– i
0
) + [S`
k
c
w
(
2
–
1
)] / W + [S`
tr
c
tr
(
2
–
1
)] /
W +
+ (Q
str
/ W) – (Q
dod
/ W) – W c
w
1
) / W
lub
= (G
S
/ W) (i
2
– i
0
) + q
m
+ q
tr
+ q
str
- q
dod
-
1
c
w
Przy analizie procesu suszenia duże znaczenie ma wyrażenie
oznaczone symbolem :
=
1
c
w
+ q
dod
– (q
m
+ q
tr
+ q
str
)
Z czego wynika zależność między a :
= (G
S
/ W) (i
2
– i
0
) -
Uwzględniając, że Y
0
= Y
1
, można otrzymać wyrażenie:
= (i
2
– i
1
) / (Y
2
– Y
1
)
Dla > 0 entalpia powietrza wylotowego jest większa od entalpii
powietrza za podgrzewaczem zewnętrznym (i
2
> i
1
).
Dla < 0 zachodzi (i
2
< i
1
).
Jeżeli = 0 to (i
2
= i
1
). Oznacza to, że proces suszenia odbywa
się przy stałej entalpii powietrza.
50
Podstawy kinetyki suszenia
Kinetyka suszenia zajmuje się określeniem zmian wilgotności
materiału w czasie. Szybkość suszenia w
D
wyraża ilość wilgoci W
usuwanej w jednostce czasu z jednostki powierzchni suszonej A
[kg/m
2
·s]:
w
D
= dW / (A d) = - (S dz) / (A d)
Niekiedy szybkość suszenia wyraża zmianę zawartości wilgoci w czasie -
(dz/d).
Szybkość suszenia może być także wyrażona przez współczynnik
wnikania masy lub współczynnik wnikania ciepła w fazie gazowej:
w
D
= k
Y
(Y
m
– Y) = ( / r
m
) (t – t
m
)
gdzie: Y
m
, Y – odpowiednio wilgotność bezwzględna powietrza w
kontakcie z
powierzchnią siała stałego i w głębi fazy
gazowej;
T
m
, T – temperatura na powierzchni ciała stałego i w głębi fazy
gazowej;
– współczynnik wnikania ciepła;
k
Y
- współczynnik wnikania masy;
r
m
- ciepło parowania w temperaturze t
m
.
51
Czas suszenia przy stałych
parametrach powietrza
suszącego
Ze względu na odmienny charakter szybkości suszenia w różnych
okresach, czas suszenia oblicza się oddzielnie dla pierwszego i drugiego
okresu suszenia.
W pierwszym okresie suszenia (stałej szybkości suszenia) czas
suszenia można obliczyć z wyrażenia:
1
= [S / (A w
D1
)] (z
1
– z
kr
) = (z
1
– z
kr
) / [K
1
(z
kr
- z
r
)]
gdzie: w
D1
- szybkość suszenia w pierwszym okresie [kg/m
2
·s];
z
1
- początkowa zawartość wilgoci materiału suszonego;
z
kr
- krytyczna zawartość wilgoci (tj. zawartość wilgoci
charakterystyczna
dla przejścia z okresu stałej szybkości
suszenia do okresu
malejącej szybkości suszenia);
z
r
- równowagowa zawartość wilgoci (tj. zawartość wilgoci, która
znajduje
się w stanie równowagi z parą zawartą w
czynniku suszącym);
K
1
- stała suszenia [s
-1
]
52
W drugim okresie suszenia (malejącej szybkości suszenia) czas
suszenia obliczyć można z zależności:
2
= (S / A) ∫
2
zkr
dz / w
DII
gdzie: z
2
– końcowa zawartość wilgoci materiału suszonego.
W przypadku, gdy znana jest zależność w
DII
= f(z), jedną z
metod obliczenia całki w powyższym równaniu jest całkowanie graficzne.
przez sporządzenie pomocniczego wykresu w układzie współrzędnych [z,
1/w
DII
].
Krzywą szybkości suszenia w drugim okresie często przybliża się
linią prostą i wtedy:
w
DII
= [w
DI
/ (z
kr
– z
r
)] (z – z
r
)
Po podstawieniu i scałkowaniu:
2
= [S / (A w
DI
)] (z
kr
– z
r
) ln[(z
kr
– z
r
)/(z
2
– z
r
)] = 1/K
1
ln[(z
kr
– z
r
)/(z
2
– z
r
)]
Całkowity czas suszenia jest sumą czasu suszenia w pierwszym i
drugim okresie, co daje:
=
1
+
2
= 1/K
1
{[(z
1
– z
kr
)/(z
kr
– z
r
)] + ln[(z
kr
– z
r
)/(z
2
– z
r
)]}
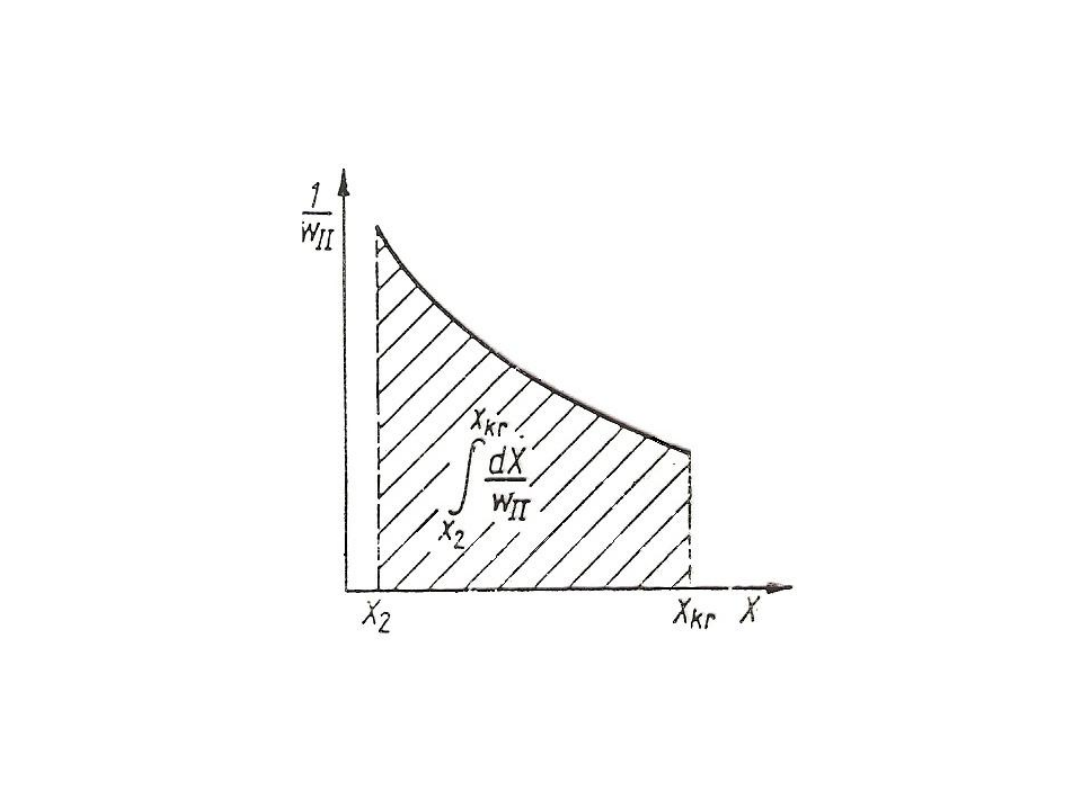
53
Rys. 41. Metoda graficzna obliczania czasu suszenia w drugim okresie
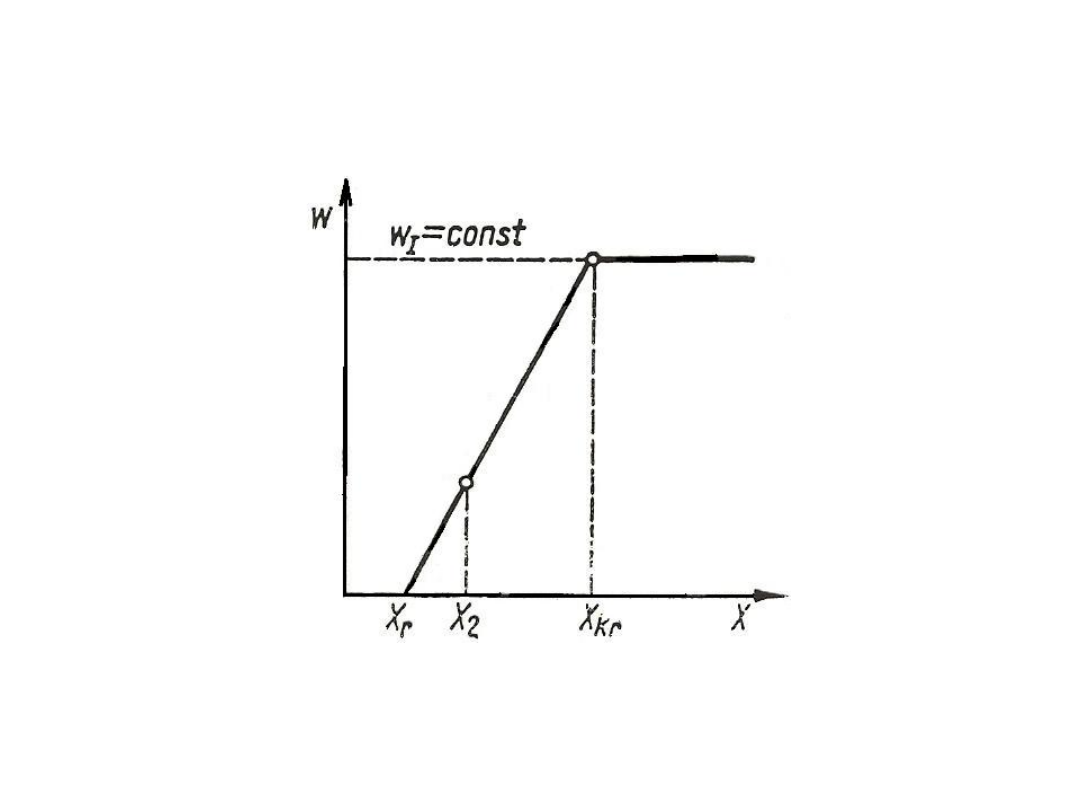
54
Rys. 42. Liniowy przebieg zależności w = f(X) dla drugiego okresu suszenia
55
Pytania na które musi odpowiedzieć projektujący instalację suszącą:
- Którą suszarkę wybrać?
- Jakiej wielkości?
- W co wyposażyć instalację?
Sposoby szukania odpowiedzi na powyższe pytania:
- Sięgnięcie do sprawdzonych rozwiązań.
- Budowa instalacji prototypowej.
- Współdziałanie w pracach wykonywanych w Centralnych Planach
Badawczo-Rozwojowych.
Podstawowym zagadnieniem przy doborze aparatury i technologii jest
ścisłe i wzajemne powiązanie technologii suszenia z konstrukcją
suszarki:
- Cel suszenia: uzyskanie produktu o określonych właściwościach.
- Często suszenie bywa łączone technologicznie z innymi operacjami
(aglomeracja, mieszanie kilku składników, apreturowanie, obróbka
termiczna).
- Wzajemne oddziaływanie różnych dziedzin techniki jest tak
intensywne, że w rezultacie za każdym razem dokonywania wyboru
instalacji należy poszukać rozwiązania optymalnego.
- Optymalną instalacją suszarniczą będzie taka instalacja, która
zapewnia uzyskanie produktu w określonej ilości i o wymaganych
właściwościach najmniejszym kosztem.
56
Przykład:
Suszenie krystalicznych surowców zawierających wodę, nie
stwarzających zagrożenia wybuchem:
- Suszarka musi być dostosowana do postaci surowca krystalicznego i
jego transportu w komorze suszenia (np. suszarka do tkanin nie będzie
odpowiednia w tym przypadku).
- Powinien zostać uwzględniony transport ciepła dostosowany do
konkretnych uwarunkowań.
- Dodatkowym utrudnieniem są zmiany własności transportowych
surowca (tj. sypkość, granulacja).
- Suszarki mogące znaleźć zastosowanie do tego procesu:
Konwekcyjne: - półkowe;
- tacowe;
- taśmowe;
- pneumatyczne;
- fluidyzacyjne;
- wibrofluidyzacyjne;
57
- fontannowe;
- wirowe;
- cyklonowe;
- bębnowe.
Kontaktowe:
- bębnowo-rurowe;
- obrotowe;
- mieszadłowe.
- O doborze suszarki decyduje koszt suszenia.
- Koszt suszenia kontaktowego jest wyższy niż suszenia konwekcyjnego.
- Wyższa intensywność suszenia zachodzi w warstwie zawieszonej niż w
warstwie nieruchomej.
- Wprowadźmy dodatkowy warunek unikania silnego tarcia kryształów o
ściany suszarki. Eliminuje to suszarki pneumatyczne, wirowe i
cyklonowe.
- W wyniku selekcji pozostały suszarki: bębnowe, wymagające więcej
stali do ich wykonania, często przegrywają w konkurencji, choć zużywają
mniej energii do przetłaczania powietrza.
- Mała masa suszarek wibrofluidyzacyjnych, także korzystnych pod
względem energii przetłaczania powietrza, powoduje, że mogą one mieć
największe szanse.
- Zazwyczaj jednak o przewadze instalacji nie decyduje suszarka, ale
system odzyskiwania ciepła oraz opinie o jej niezawodności i jakości.
58
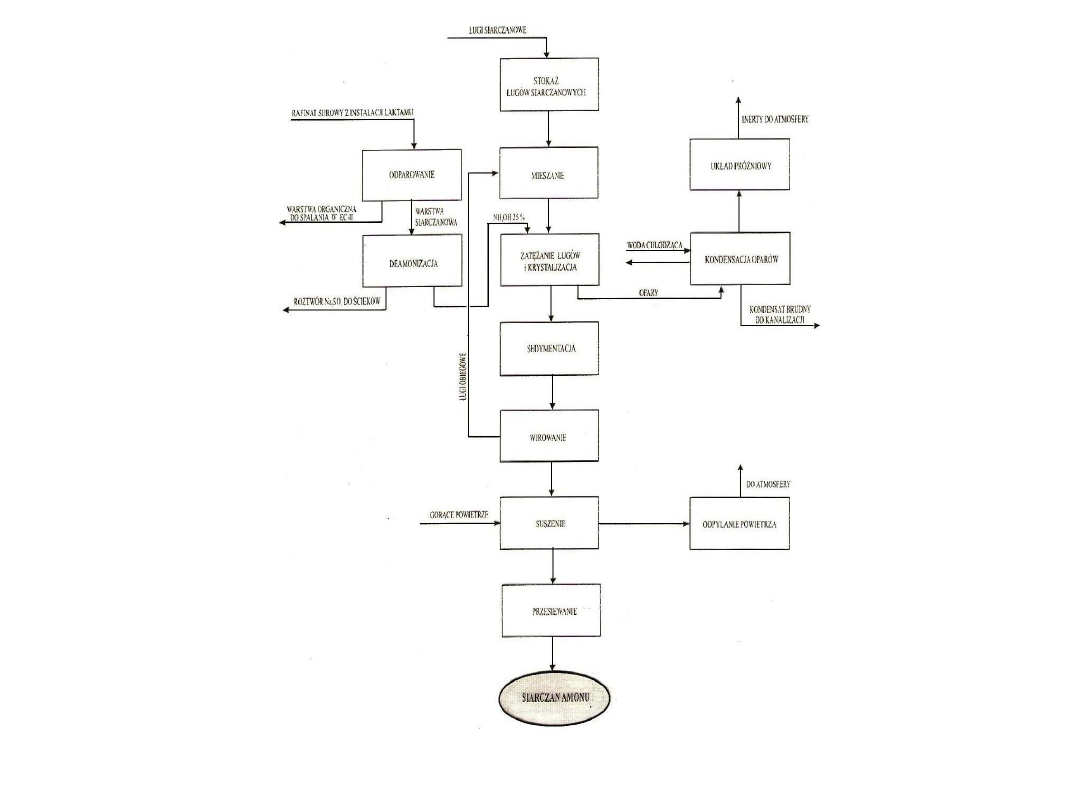
Rys. 43. Schemat ideowy procesu produkcji krystalicznego siarczanu amonu
59
Średni skład granulometryczny przedstawia się następująco:
ziarno >
3,15 mm
21 %
2,50 - 3,15 mm
15 %
1,00 - 2,50 mm
53 %
0,50 - 1,00 mm
8 %
poniżej 0,50 mm
3 %
Zgodnie z obowiązującą normą (PN – 85/C – 87002) produkt po
suszeniu powinien zawierać minimum 21 % azotu, maksymalna
zawartość wilgoci nie powinna przekraczać 0,3 %, zawartość wolnego
H
2
SO
4
nie więcej niż 0,05 %, a wielkość ziarn w 75 % powinna stanowić
frakcja powyżej 1 mm.
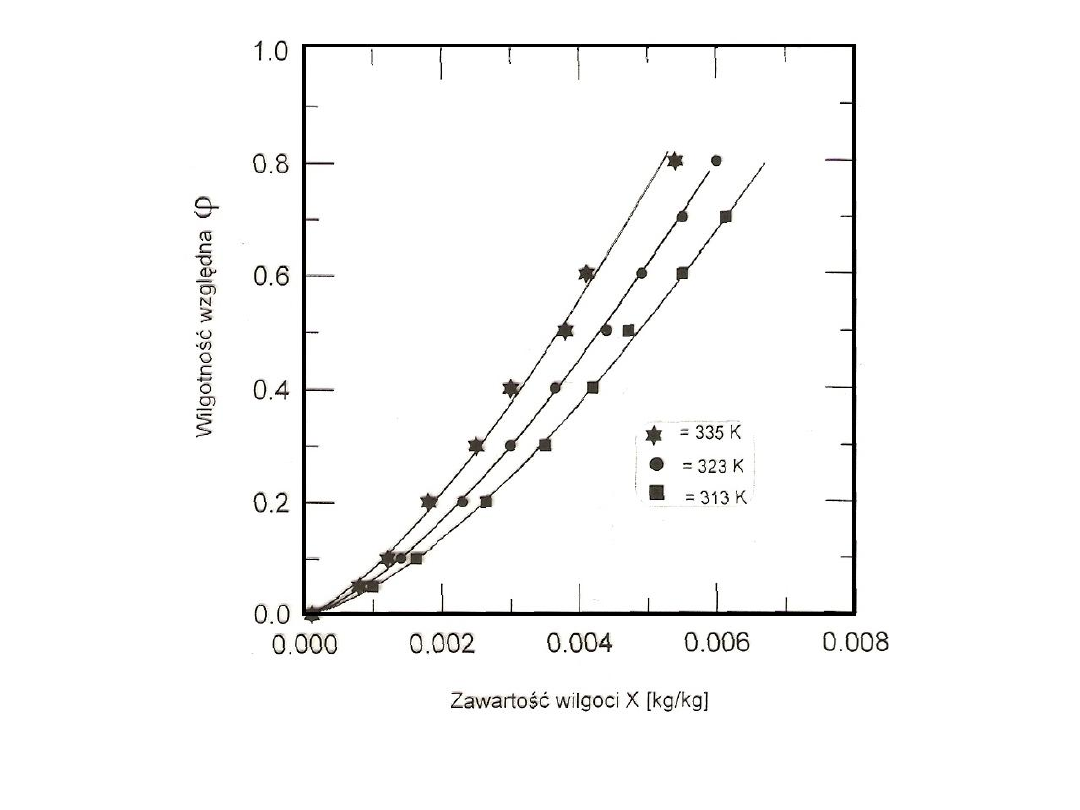
Izotermę desorpcji dla siarczanu amonu – wyznaczoną w ramach
kompleksowej analizy metod suszenia tej substancji przedstawia rys. 44.
Równanie równowagi desorpcji w postaci zależności wilgotności względnej
od zawartości wilgotności X i temperatury materiału T ma postać:
= 155,292 exp [(644,558 + 458,561 lnX) / T]
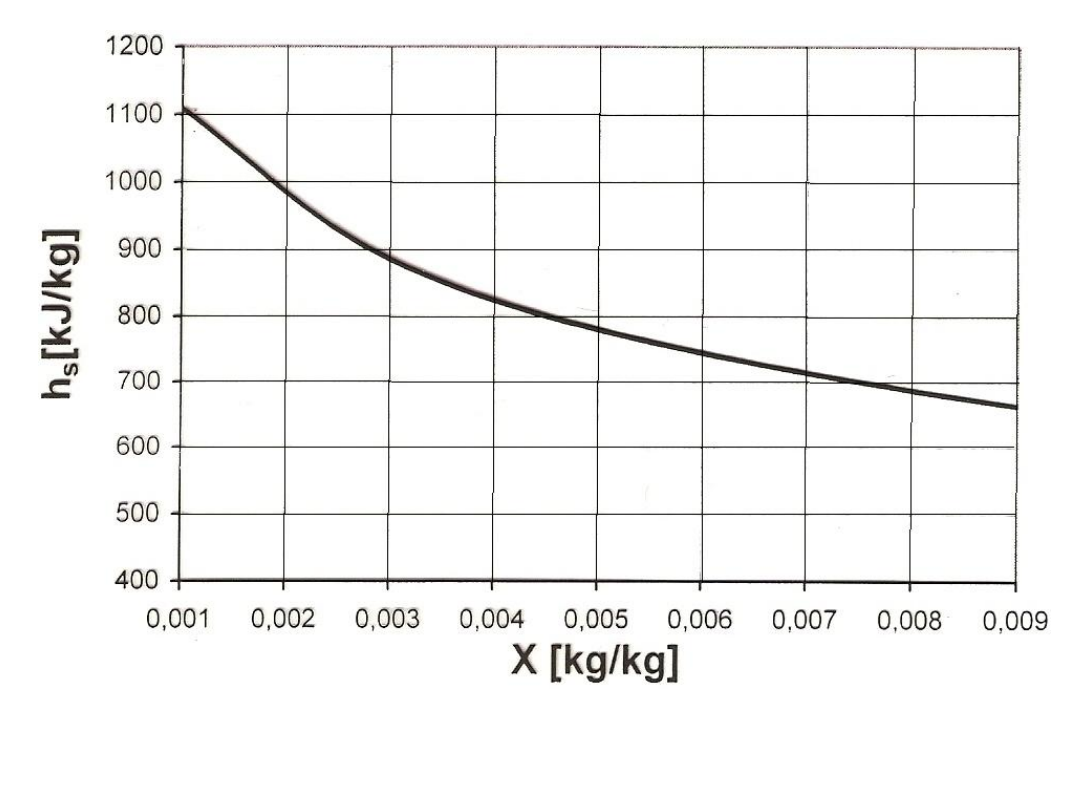
Dysponując tym wyrażeniem w oparciu o równanie Clausiusa-Clapeyrona
wyznaczono wartość ciepła sorpcji dla niskich zawartości wilgoci – rys. 45.
60
Rys. 44. Izotermy desorpcji siarczanu amonu
61
Rys. 45. Zależność ciepła sorpcji h
S
od zawartości wilgoci X dla siarczanu
amonu
62
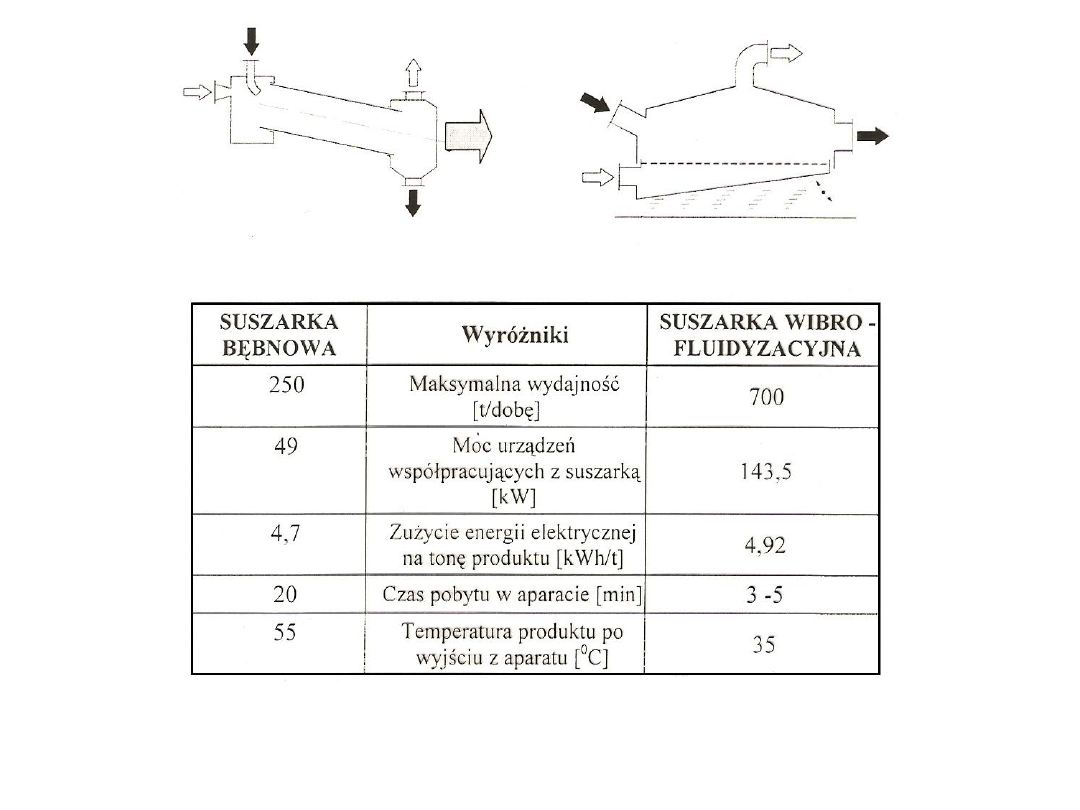
Rys. 46. Zestawienie wskaźników techniczno-ekonomicznych
analizowanych typów suszarek
63
Tab. 4. Porównanie warunków realizacji procesu suszenia
SUSZARKI BĘBNOWE
KONWENCJONALNE
SUSZARKI
WIBROFLUIDYZACYJN
E INNOWACYJNE
Spaliny metanu jako
czynnik suszący
Powietrze ogrzewane
parą wodną jako
czynnik suszący
Wyłącznie suszenie
Suszenie połączone z
chłodzeniem
Tendencja produktu do
zlepiania się
Praktyczna eliminacja
zlepiania się produktu
Maksymalnie 6
aparatów zajmujących
2800m
2
powierzchni
użytkowej
2 suszarki zajmują
700m
2
powierzchni
użytkowej
64
Sposoby zwiększenia sprawności energetycznej:
- stosowanie recyrkulacji czynnika suszonego;
- poprzez pobranie energii cieplnej z otaczającego powietrza;
- poprzez pompy ciepła.
Metody zmniejszenia energochłonności procesu:
- modyfikacja procesu suszenia;
- modyfikacja konstrukcji suszarek;
- stosowanie nowych rozwiązań suszarniczych;
- zastosowanie niekonwencjonalnych źródeł energii;
- stosowanie układów do odzysku ciepła.
Document Outline