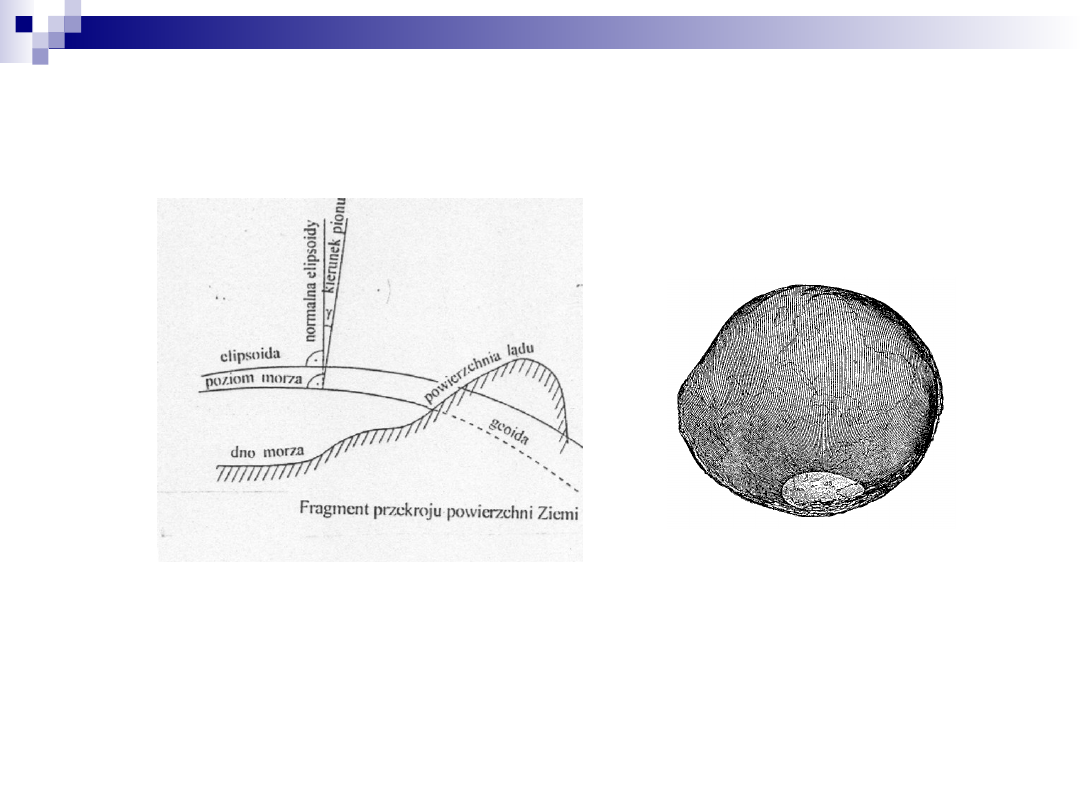
Kształt Ziemi.

Geoida

Powierzchnia geoidy charakteryzuje się

następującymi właściwościami:

•

prosta styczna do powierzchni geoidy w każdym jej

punkcie jest prostopadła do kierunku pionu,

• krzywizna powierzchni zmienia się w sposób ciągły,
• potencjał ziemskiego poła grawitacyjnego -

przyspieszenie ziemskie („g”), jest stałe w każdym
punkcie geoidy (powierzchnia ekwipotencjalna)

• jest to bryła niematematyczna, tzn. nie ma wzoru

matematycznego, który by określał jej kształt

.

Jedną z najczęstszych form opracowań pomiarów
geodezyjnych są mapy.

Mapa jest odtworzeniem w odpowiednim
zmniejszeniu trójwymiarowej przestrzeni całej
Ziemi lub jej mniejszych obszarów na
dwuwymiarowej płaszczyźnie przy zastosowaniu
odpowiednich reguł matematycznych oraz przy
wykorzystaniu umownych znaków graficznych.

Przekształcenie obszaru kulistego na obraz

płaski nazywa się odwzorowaniem

kartograficznym

.

Podstawowe wiadomości z kartografii

Ze względu na rodzaj zniekształceń dzieli się je na cztery

grupy:



równokątne (konforemne)



wiernopowierzchniowe



wiernoodległościowe



dowolne

Ogólnie można stwierdzić, że wielkość zniekształceń zależy:



od rodzaju zastosowanego odwzorowania,



od wielkości obszaru Ziemi przedstawianego w tym
odwzorowaniu



od odległości danego miejsca od środka rzutowania.

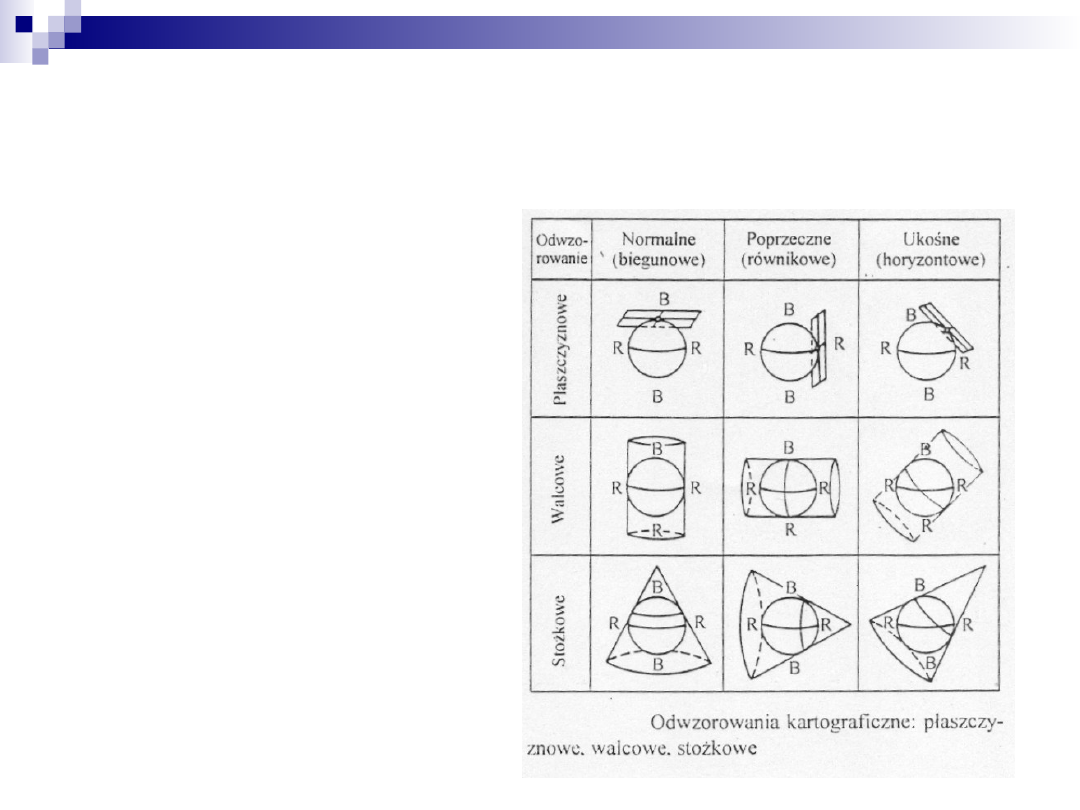
Ze względu na rodzaj powierzchni, na której odtwarza się

powierzchnię Ziemi jako oryginału, rozróżnia się następujące
odwzorowania:

1. płaszczyznowe,

2. walcowe,

3. stożkowe,

4. umowne,

Zależnie od położenia płaszczyzny,

walca albo stożka w stosunku do

osi obrotu elipsoidy ziemskiej

rozróżnia się odwzorowania normalne

lub biegunowe, poprzeczne

lub równikowe, ukośne

lub horyzontalne.

Rodzaje współrzędnych stosowanych w geodezji.

Współrzędnymi nazywamy wielkości kątowe lub liniowe,

wyznaczające położenie punktu na dowolnej powierzchni
lub w przestrzeni w sposób względny w stosunku do
przyjętych za początek układu płaszczyzn lub linii.

W geodezji stosuje się następujące układy współrzędnych:



geograficznych na powierzchni kuli lub elipsoidy,



prostokątnych płaskich



biegunowych płaskich.

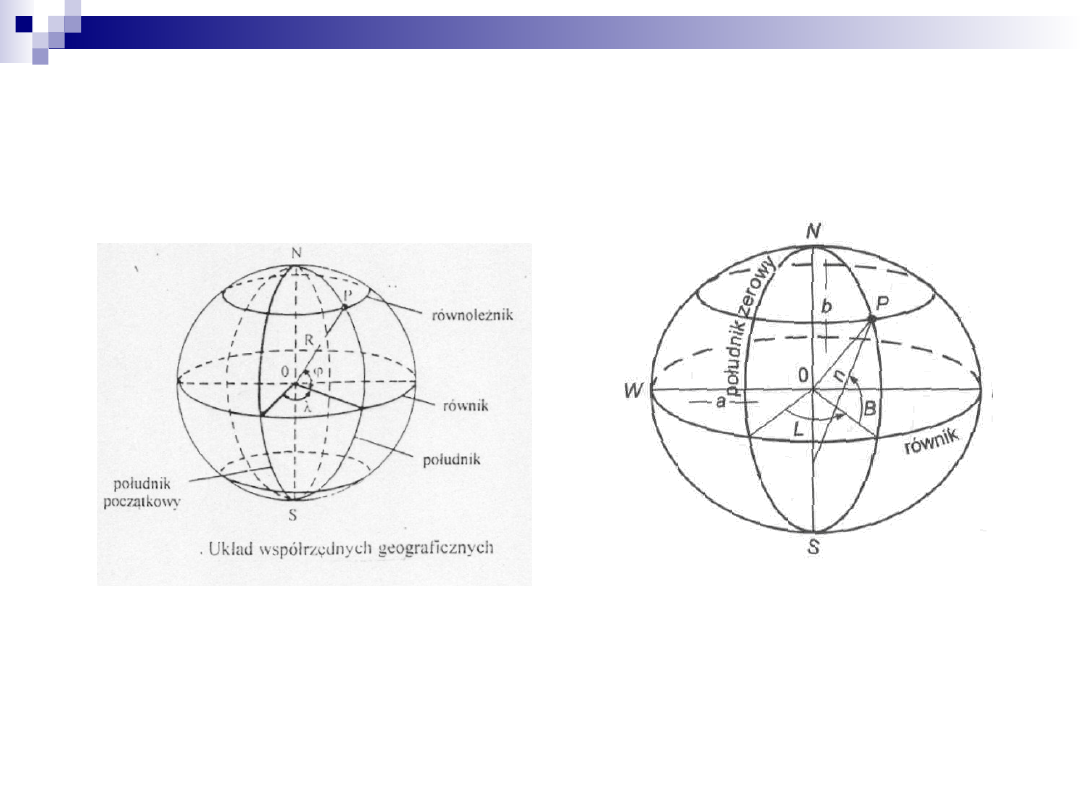
Układ współrzędnych na kuli i elipsoidzie.

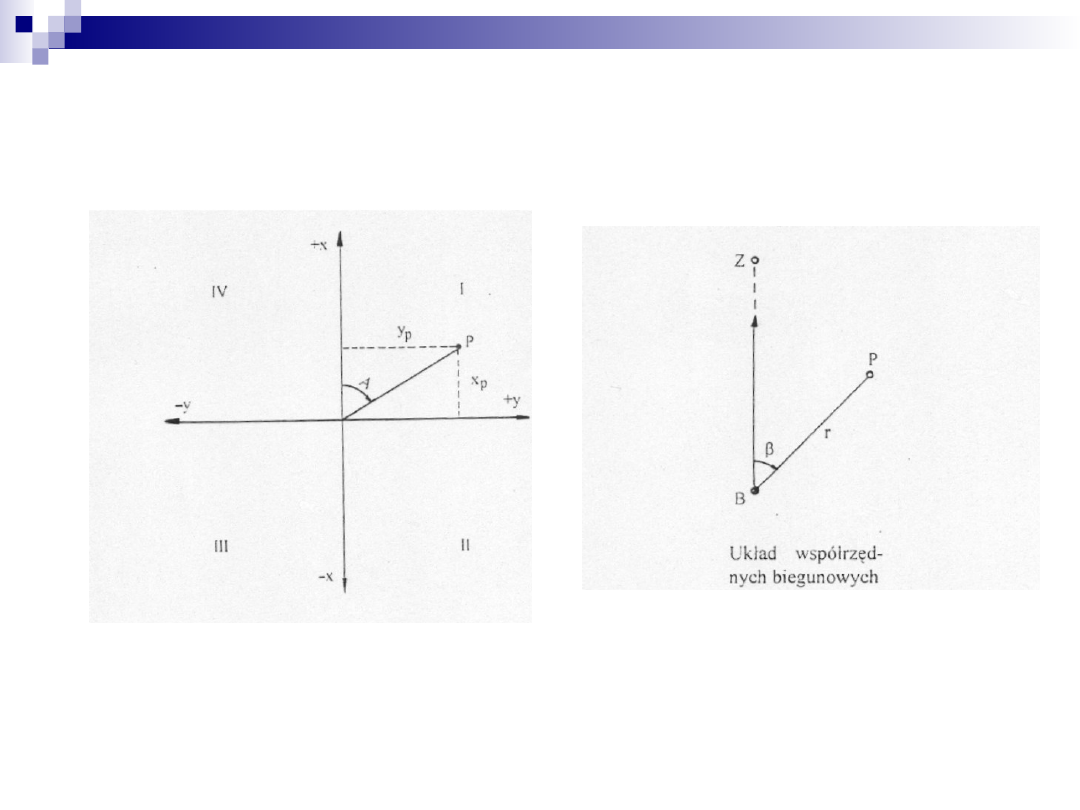
Układy współrzędnych płaskich.

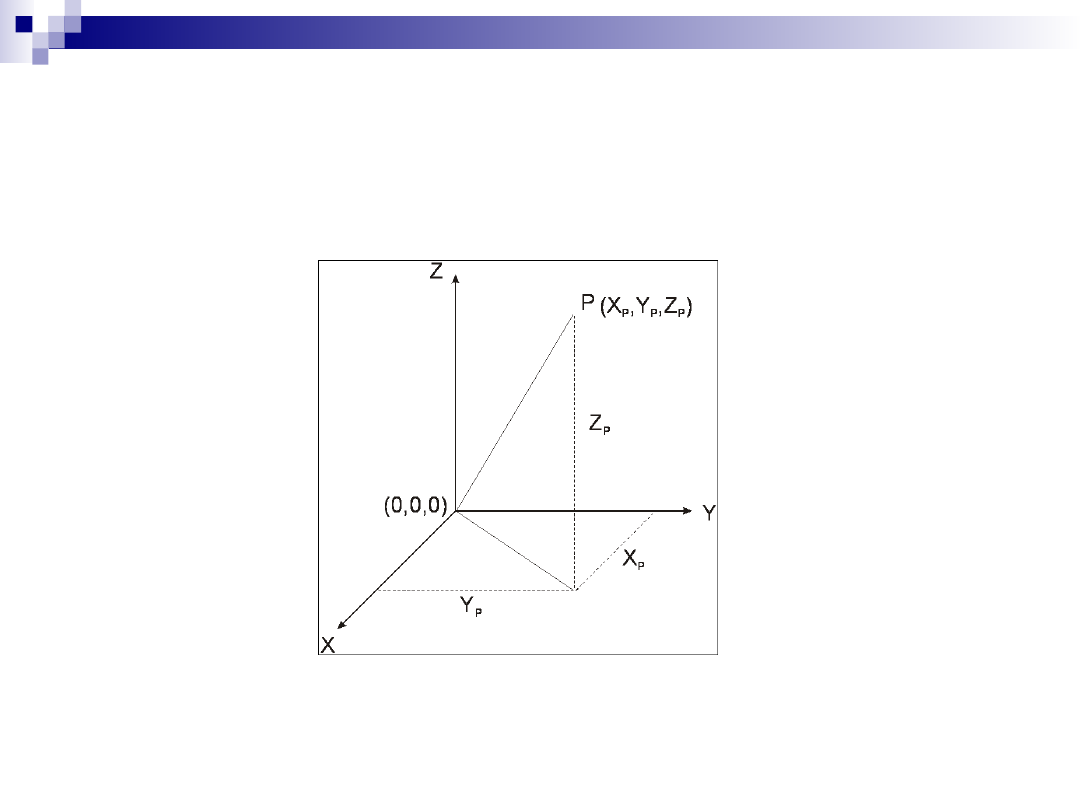
Kartezjański trójwymiarowy układ

współrzędnych













B

sin

h

a

Nb

z

L

sin

B

cos

h

N

y

L

cos

B

cos

h

N

x

2

2

















2

1

2

2

2

2

2

B

sin

b

B

cos

a

a

N







P

h

B

L

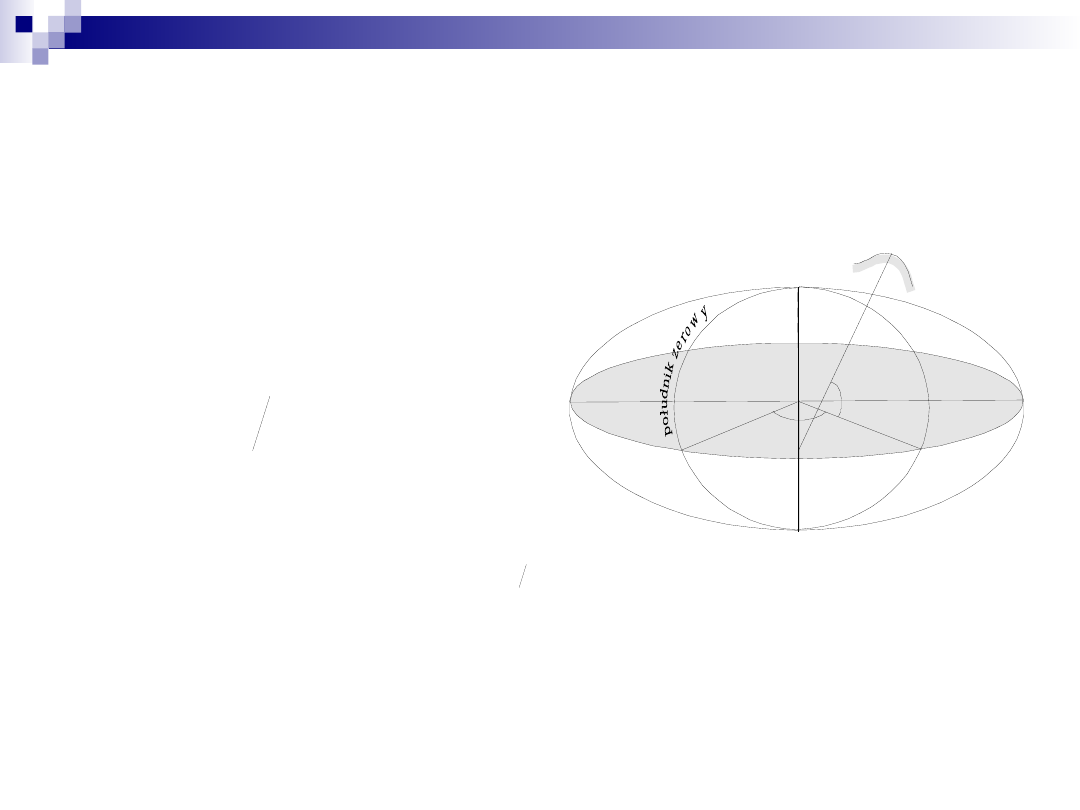
Zależność pomiędzy współrzędnymi

geodezyjnymi a kartezjańskimi.