1

1

ENERGETYCZNA METODA

ENERGETYCZNA METODA

MODELOWANIA

MODELOWANIA

MECHANICZNYCH WŁAŚCIWOŚCI

MECHANICZNYCH WŁAŚCIWOŚCI

MATERIAŁÓW

MATERIAŁÓW

TADEUSZ WEGNER

TADEUSZ WEGNER

Politechnika Poznańska

Politechnika Poznańska

Instytut Mechaniki Stosowanej

Instytut Mechaniki Stosowanej

Zakład Wytrzymałości Materiałów i Konstrukcji

Zakład Wytrzymałości Materiałów i Konstrukcji

2

2

3

3

Literatura

Literatura

1.

Wegner T., Metody energetyczne w wytrzymałości

materiałów,

Hipoteza

wytrzymałościowa

stateczności równowagi wewnętrznej. Wydawnictwo

Politechniki Poznańskiej, 81 stron, Poznań 1999.

2.

Wegner T., Surface of limit state in nonlinear

material and its relation with plasticity condition.

The Archive of Mechanical Engineering, Vol. XLVII,

Number 3, 2000, p. 205-223.

3.

Wegner T., A method of material modelling with the

use of strength hypothesis of inner equilibrium

stability. Mechanics and Mechanical Engineering, Vol.

4, No. 2, 2000, p. 139-147.

4.

Wegner T., Stability of the material under planar

state of stress. 3rd Conference Thin-Walled Vessels –

Karłów 2004, p. 271-276.

4

4

Maksymilian Tytus

Maksymilian Tytus

Huber

Huber

Sprawozdanie

Sprawozdanie

kwartalne nr 4

kwartalne nr 4

Instytutu Badań

Instytutu Badań

Lotnictwa,

Lotnictwa,

Warszawa 1930 rok

Warszawa 1930 rok



„

„

Chociaż więc podłoże teoretyczne naszej

Chociaż więc podłoże teoretyczne naszej

hipotezy nie może być uznane za ścisłe, to

hipotezy nie może być uznane za ścisłe, to

jednak oddaje ona i oddawać będzie doskonałe

jednak oddaje ona i oddawać będzie doskonałe

usługi przy budowie teoretycznych wzorów

usługi przy budowie teoretycznych wzorów

wytrzymałościowych (...).”

wytrzymałościowych (...).”



„

„

Miał przeto rację W. Voigt wypowiadając

Miał przeto rację W. Voigt wypowiadając

przypuszczenie, że zjawiska wytrzymałościowe

przypuszczenie, że zjawiska wytrzymałościowe

nie dają się w ogóle ująć ściśle w schemat

nie dają się w ogóle ująć ściśle w schemat

teoretyczny za pomocą stałych

teoretyczny za pomocą stałych

charakterystycznych dla materiału, jak to się

charakterystycznych dla materiału, jak to się

dzieje w teorii sprężystości.”

dzieje w teorii sprężystości.”



„

„

Z tego to powodu nie nazywam teoriami

Z tego to powodu nie nazywam teoriami

hypotez wytrzymałościowych stosowanych w

hypotez wytrzymałościowych stosowanych w

nauce o wytrzymałości.”

nauce o wytrzymałości.”

5

5

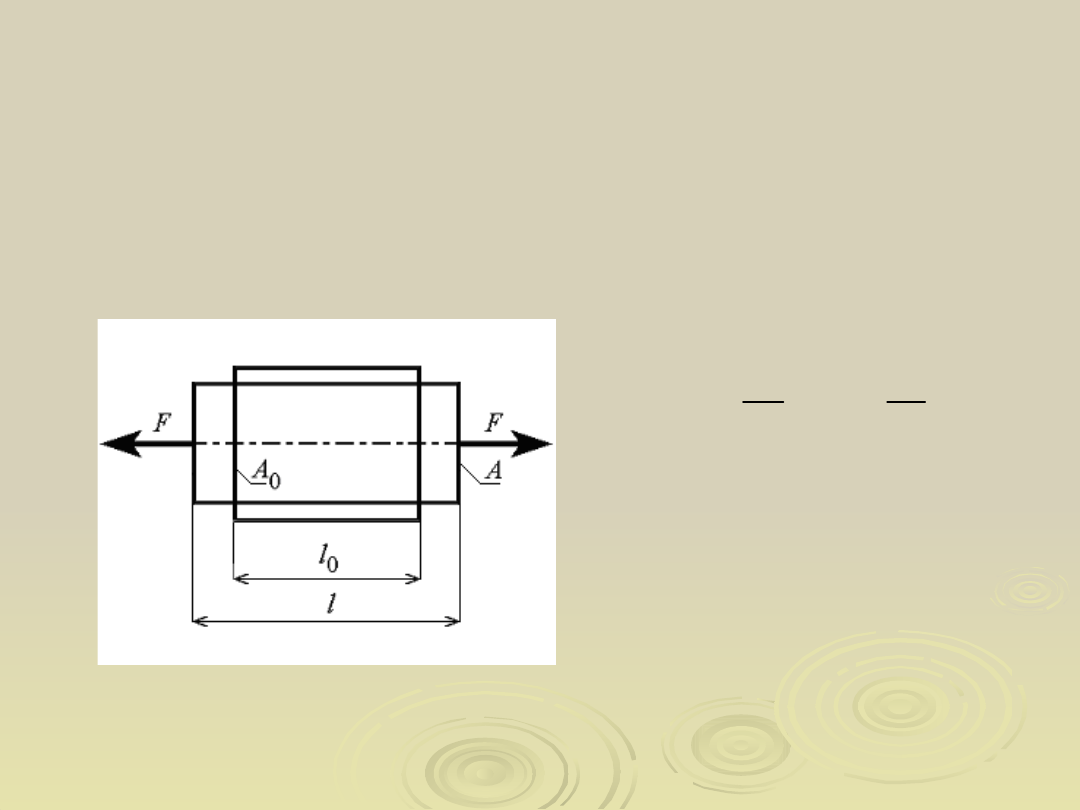
Energetyczna analiza procesu rozciągania

Energetyczna analiza procesu rozciągania

materiału w jednoosiowym stanie

materiału w jednoosiowym stanie

naprężenia

naprężenia

L

W 

0

0

,

l

l

A

F











Odkształcalny pręt

Odkształcalny pręt

w jednoosiowym stanie

w jednoosiowym stanie

naprężenia

naprężenia

W

W

- energia wewnętrzna

- energia wewnętrzna

odkształcenia

odkształcenia

L

L

- praca sił zewnętrznych

- praca sił zewnętrznych





- nominalne

- nominalne

naprężenie

naprężenie





- jednostkowe

- jednostkowe

wydłużenie

wydłużenie

6

6

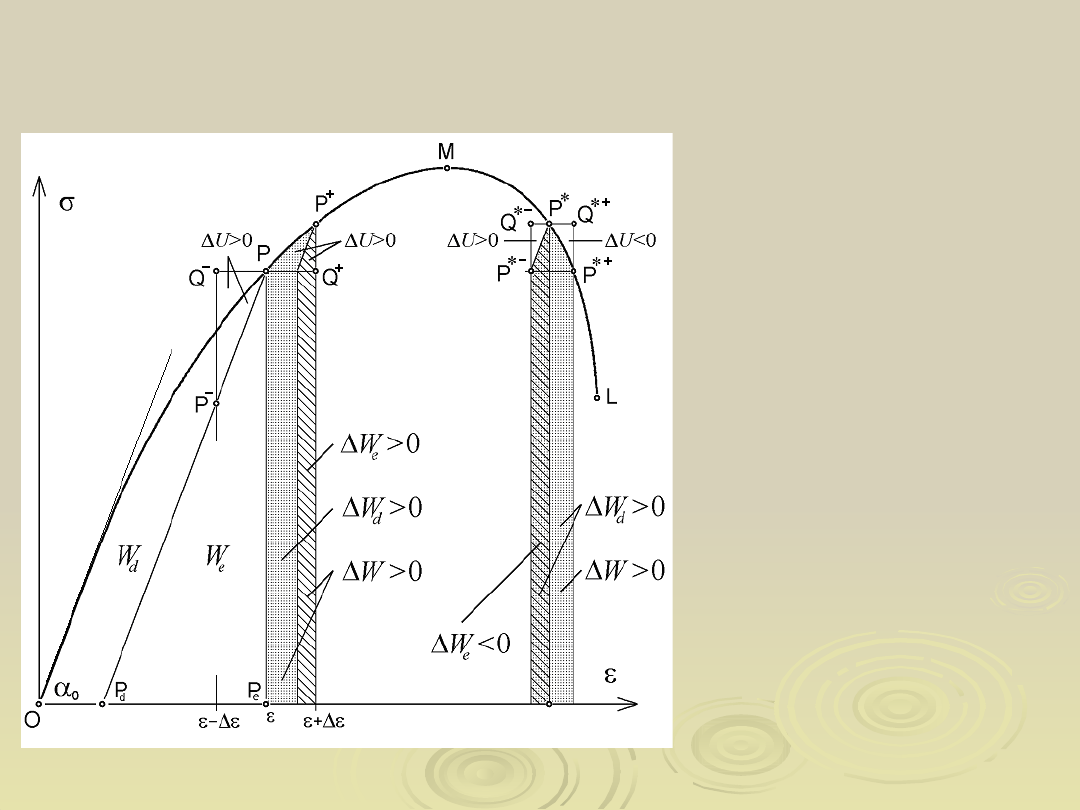
Stateczność stanów równowagi

Stateczność stanów równowagi

W

W

e

e

- energia potencjalna sił

- energia potencjalna sił

sprężystości materiału

sprężystości materiału

W

W

d

d

- energia dyssypowana

- energia dyssypowana

Wykres rozciągania

Wykres rozciągania

d

e

W

W

W



















W

U

U

U

-

-

energia całkowita

energia całkowita

L

W

U





7

7

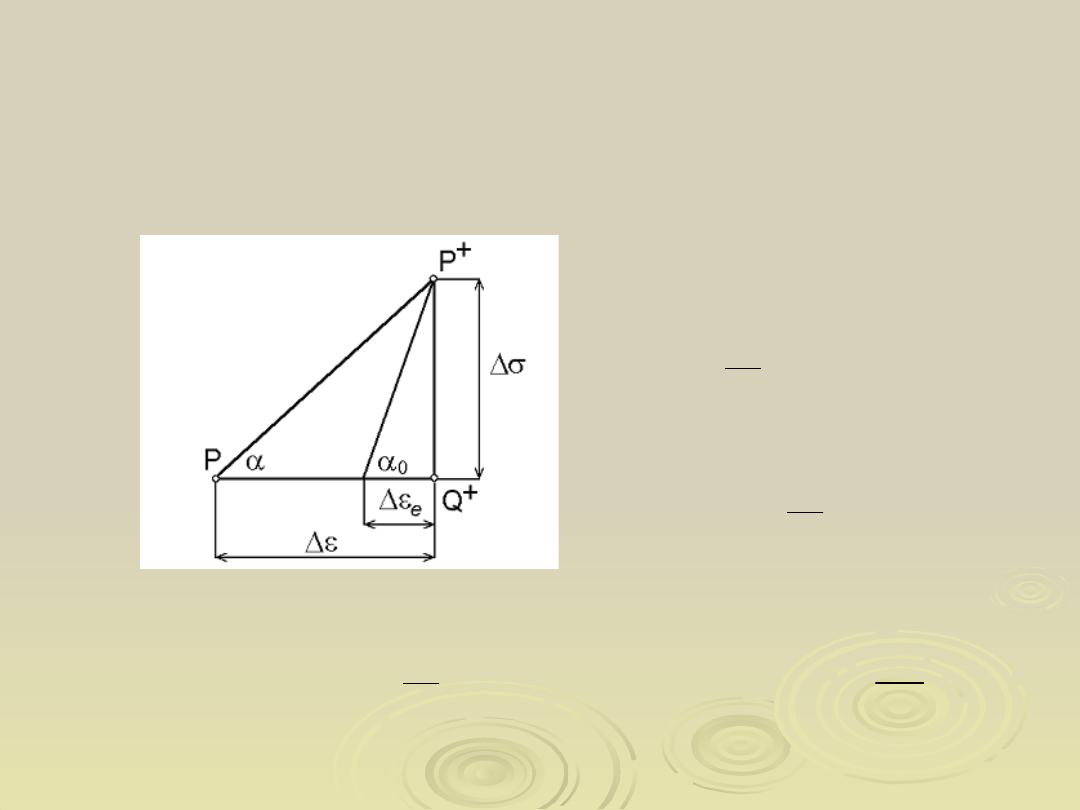
Zależności między przyrostami

Zależności między przyrostami

składowych odkształcenia

składowych odkształcenia



















0

)

1

(

)

(

d

E

W

d

E

d

W

d

2

)

(

2

0

























tg

d

tg

d

e



0







d

E

d

e





d

e

d

d

d

















d

E

d

d

)

1

(

























0

)

1

(

)

(

d

E

W

d

8

8

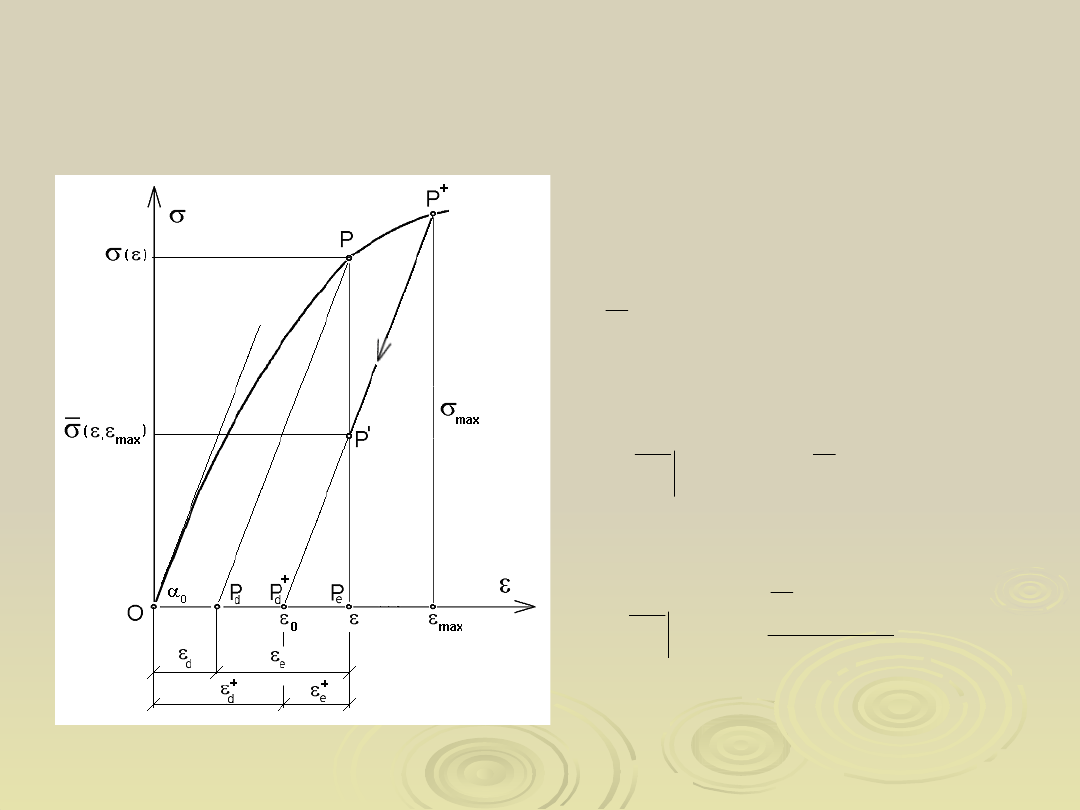
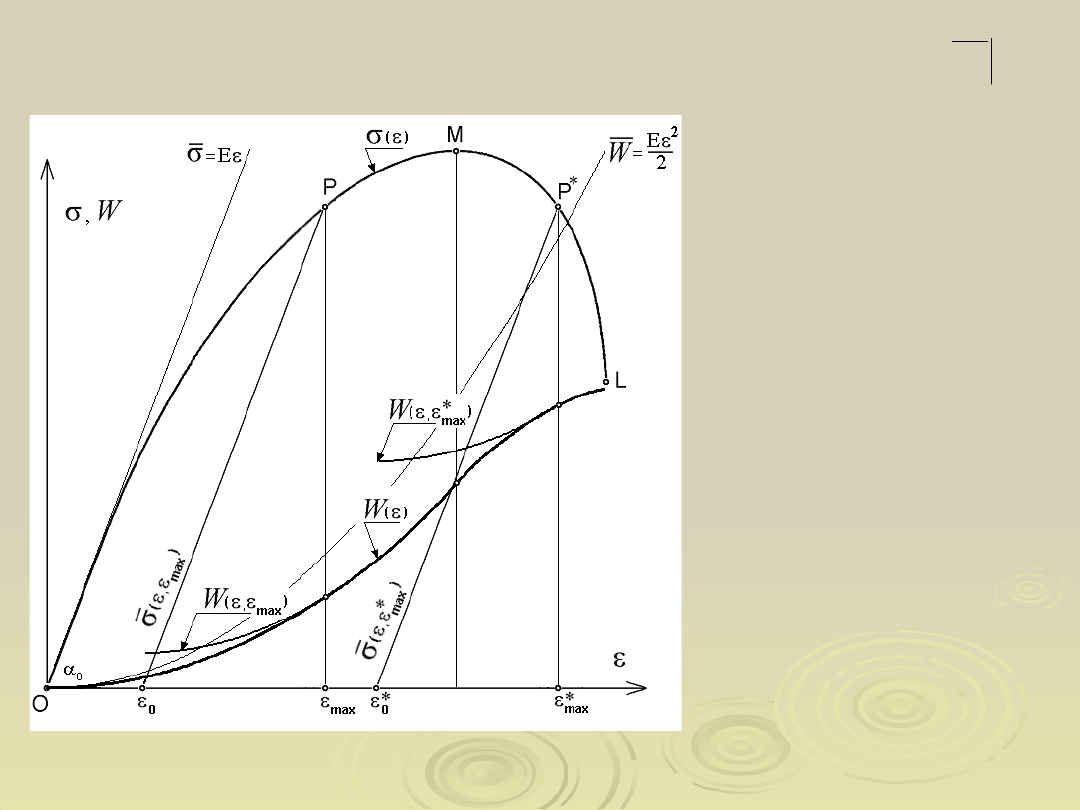
Proces jednoosiowego rozciągania z

Proces jednoosiowego rozciągania z

odciążaniem

odciążaniem

)}

(

max{

max

t







)

(

)

,

(

max

max

max



















E







max

max

max

)

,

(
















d

W

e

)

(

2

max

max

max




















e

W

9

9

Funkcje energii wewnętrznej odkształcenia

na tle wykresu rozciągania materiału

max

max

max

)

(

)

,

(










e

W

W

W







max

0











max







)

(

)

,

(

max







W

W

















0

)

(

)

(

d

W

10

10

Podsumowanie

Podsumowanie



Energia wewnętrzna odkształcenia materiału jest zawsze

Energia wewnętrzna odkształcenia materiału jest zawsze

jednoznacznie określona, ponieważ jest równa pracy włożonej w

jednoznacznie określona, ponieważ jest równa pracy włożonej w

odkształcenia materiału.

odkształcenia materiału.



W przypadku procesu, którego przebieg nie ma charakteru

W przypadku procesu, którego przebieg nie ma charakteru

monotonicznego, energia wewnętrzna odkształcenia materiału jest

monotonicznego, energia wewnętrzna odkształcenia materiału jest

funkcją dwu zmiennych: odkształcenia

funkcją dwu zmiennych: odkształcenia





oraz odkształcenia

oraz odkształcenia

maksymalnego, jakiemu materiał został poddany w całym procesie od

maksymalnego, jakiemu materiał został poddany w całym procesie od

początku do aktualnej chwili czasu

początku do aktualnej chwili czasu

t

t

.

.



W procesie jednoosiowego rozciągania, poszukując możliwości

W procesie jednoosiowego rozciągania, poszukując możliwości

wystąpienia w materiale niebezpiecznych ze względów

wystąpienia w materiale niebezpiecznych ze względów

wytrzymałościowych stanów, polegających na niestatecznej

wytrzymałościowych stanów, polegających na niestatecznej

równowadze wewnętrznej, możemy ograniczyć się do badania

równowadze wewnętrznej, możemy ograniczyć się do badania

procesu, w którym odkształcenia wzrastają monotonicznie, a energia

procesu, w którym odkształcenia wzrastają monotonicznie, a energia

wewnętrzna jest jednoznaczną funkcją odkształcenia materiału.

wewnętrzna jest jednoznaczną funkcją odkształcenia materiału.

11

11

Stateczność stanu równowagi wewnętrznej

Stateczność stanu równowagi wewnętrznej

w trójosiowym stanie naprężenia materiału

w trójosiowym stanie naprężenia materiału

Równowaga jest niestateczna, gdy istnieje taki ciąg
wartości przyrostów przemieszczeń uogólnionych

W e

e e

e

e

e

W e e

e

L

n

n

n

(

,

,...,

)

( , ,..., )

1

1

2

2

1

2



















(

,

,...,

)

 



e e

e

n

1

2

w którym przynajmniej jedna z nich jest różna od zera, że

zx

yz

xy

z

y

x













,

,

,

,

,

)

(

i

e

W

 funkcja gęstości energii wewnętrznej,

m

n

n

i





},

...,

,

2

,

1

{







W

W

L





1

2

2



2

0

W

m - liczba stopni swobody
układu

12

12

Równowaga jest stateczna, gdy dla każdego ciągu
wartości przyrostów przemieszczeń uogólnionych

(

,

,...,

)

 



e e

e

n

1

2

w którym przynajmniej jedna z nich jest różna
od zera



2

0

W

,

m

n

Przykład: stateczność odkształcenia materiału liniowo sprężystego

0

)

,

,

,

,

,

(

)

,

,

(

)

,

,

,

,

,

(

)

(

)

(







zx

yz

xy

z

y

x

s

z

y

x

v

zx

yz

xy

z

y

x

W

W

W































0

)

(

2

)

,

,

(

2

)

(









z

y

x

z

y

x

v

K

W













0

)]

(

2

3

)

(

)

(

)

[(

3

)

,

,

,

,

,

(

2

2

2

2

2

2

)

(





















zx

yz

xy

x

z

z

y

y

x

zx

yz

xy

z

y

x

s

G

W































)

1

(

2

,

)

2

1

(

3













E

G

E

K

0

)

,

,

,

,

,

(

)

,

,

,

,

,

(

2

1

2





zx

yz

xy

z

y

x

zx

yz

xy

z

y

x

W

W



























13

13

J

x

y

z

1

  







J

x y

y z

z x

xy

yz

zx

2

2

2

2

1

4













 

   







(

)

)

(

4

1

4

1

2

2

2

3

xy

z

zx

y

yz

x

zx

yz

xy

z

y

x

J



































2

1

)

(

2

J

K

W

v



)

3

(

3

2

2

2

1

)

(

J

J

G

W

s





J

1

1

2

3

  

 



J

2

1 2

2 3

3 1







 

 

 

J

3

1 2 3



  

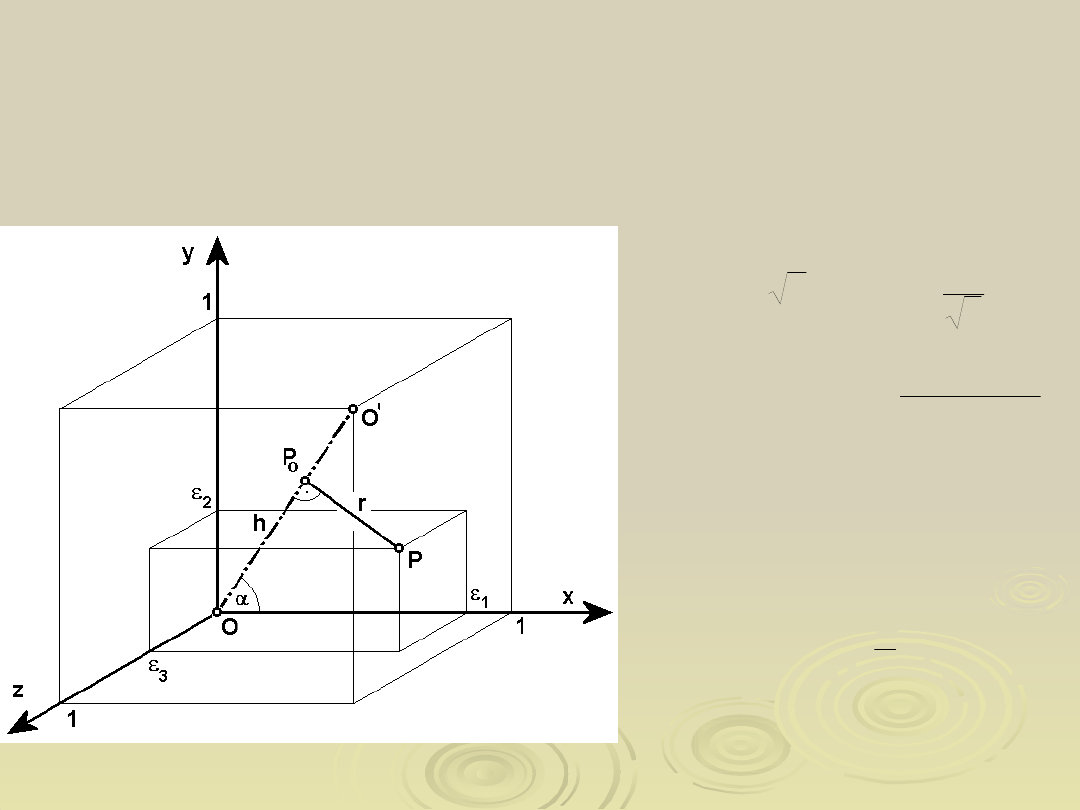
Energia odkształceń objętościowych i

Energia odkształceń objętościowych i

postaciowych

postaciowych

w zależności od niezmienników stanu

w zależności od niezmienników stanu

odkształcenia

odkształcenia

14

14

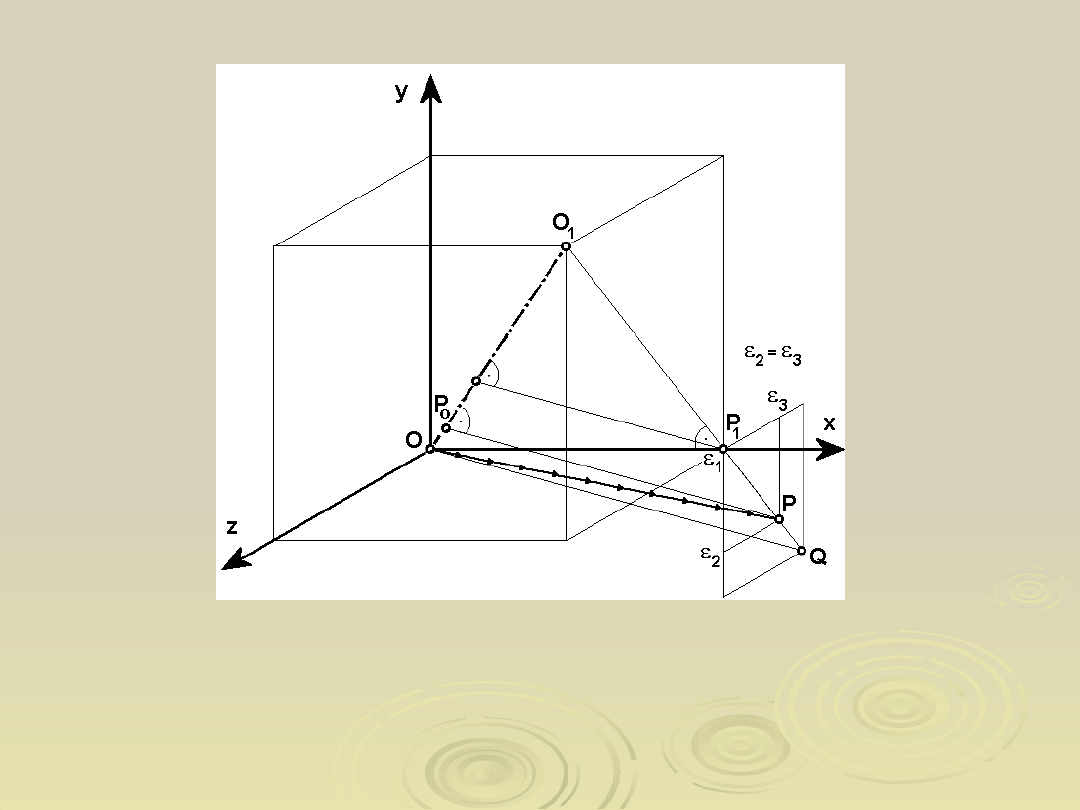
Energia odkształceń objętościowych i

Energia odkształceń objętościowych i

postaciowych w zależności od współrzędnych

postaciowych w zależności od współrzędnych

cylindrycznych

cylindrycznych

w przestrzeni głównych składowych

w przestrzeni głównych składowych

odkształcenia

odkształcenia

Przestrzeń głównych składowych
odkształcenia

)

,

,

(

P

3

2

1







)

,

,

(

P

0







3

3

2

1















2

2

3





h

2

3

2

2

2

1

2

)

(

)

(

)

(

























r

2

)

(

2

3

Kh

W

v



2

)

(

Gr

W

s



3

1

cos

,

2









tg



7

,

54





15

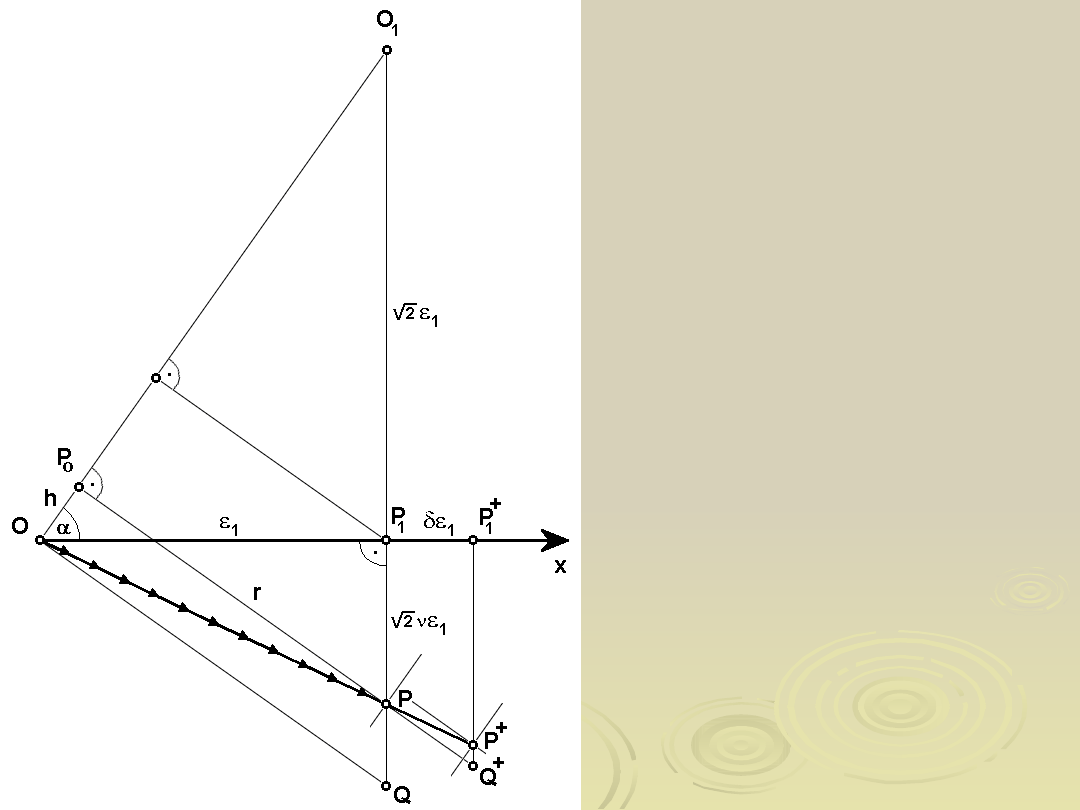
15

Proces jednoosiowego rozciągania materiału liniowo sprężystego

w przestrzeni głównych składowych odkształcenia

16

16

Przekrój przestrzeni

głównych składowych

odkształcenia

płaszczyzną symetrii o

równaniu



2

=



3

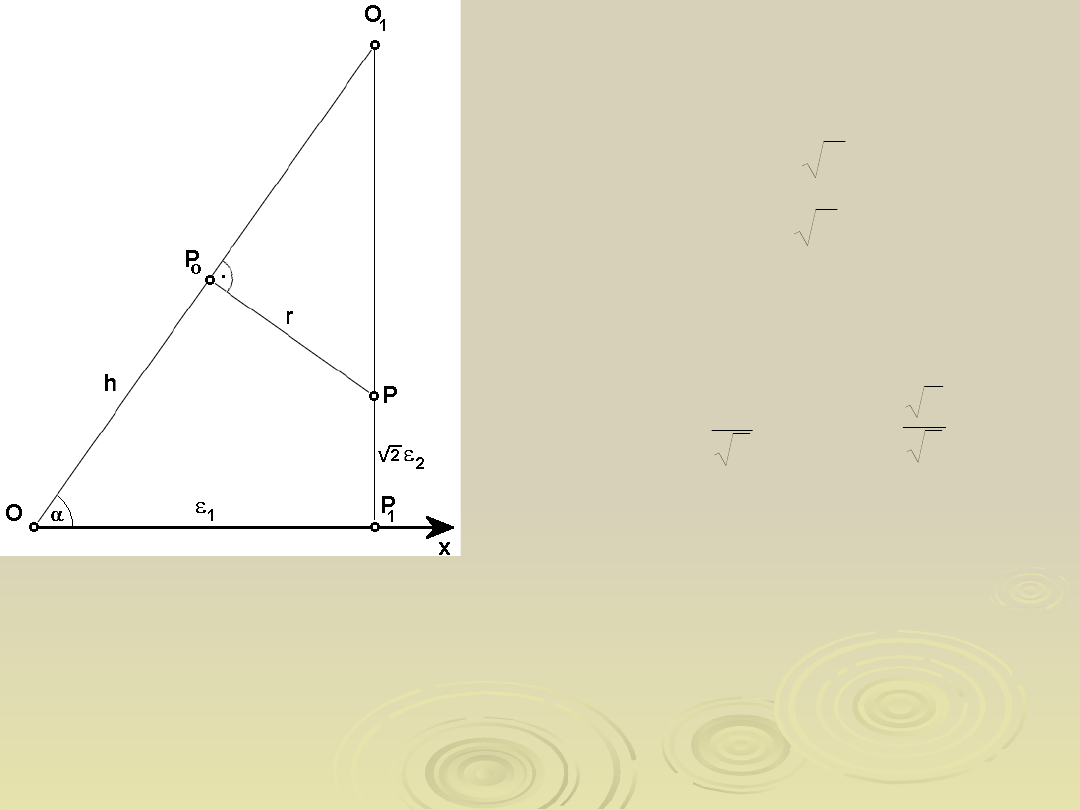
17

17

Zależności między
współrzędnymi
w płaszczyźnie symetrii
o równaniu



2

=



3









sin

2

cos

2

1





h









cos

2

sin

2

1





r

3

1

cos 



3

2

sin 



18

18

Uogólnione siły odkształcenia

Uogólnione siły odkształcenia

objętościowego i postaciowego

objętościowego i postaciowego

L

W

W

U

s

v







)

(

)

(





1

1

1

0







d

L

1

1

)

(

)

(

















r

F

h

F

U

r

h

Kh

F

h

3

)

(



Gr

F

r

2

)

(



0

2

)

cos

sin

(

)

sin

cos

(

2

)

(

)

(

1

1

)

(

)

(





























r

h

r

h

F

F

F

F

U

1

)

(

)

(

sin

cos











r

h

F

F

0

cos

sin

)

(

)

(









r

h

F

F





cos

1

)

(



h

F





sin

1

)

(



r

F

1

1





E



1

2









Założenie uogólnionych sił odkształcenia objętościowego i

postaciowego w postaci liniowych funkcji współrzędnych h

oraz r

prowadzi do liniowego modelu właściwości fizycznych

materiału.

19

19

Badanie stateczności równowagi

Badanie stateczności równowagi

wewnętrznej

wewnętrznej

w materiale o liniowych właściwościach

w materiale o liniowych właściwościach

fizycznych

fizycznych

)

(

)

(

s

W

W

W

v





r

F

h

F

W

r

h







)

(

)

(





2

2

2

)

(

)

(

r

dr

dF

h

dh

dF

W

r

h











0

2

3

2

2

2







r

G

h

K

W







Powyższa nierówność jest prawdziwa dla dowolnego przemieszczenia wirtualnego o

Powyższa nierówność jest prawdziwa dla dowolnego przemieszczenia wirtualnego o

składowych

składowych





h

h

,

,





r

r

z których przynajmniej jedna jest różna od zera.

z których przynajmniej jedna jest różna od zera.

Wynik ten jest oczywisty, ponieważ jak już wcześniej wykazaliśmy, stany równowagi

Wynik ten jest oczywisty, ponieważ jak już wcześniej wykazaliśmy, stany równowagi

wewnętrznej w materiale liniowo sprężystym są stateczne.

wewnętrznej w materiale liniowo sprężystym są stateczne.

20

20

Matematyczny model materiału

Matematyczny model materiału

o nieliniowych właściwościach

o nieliniowych właściwościach

fizycznych

fizycznych

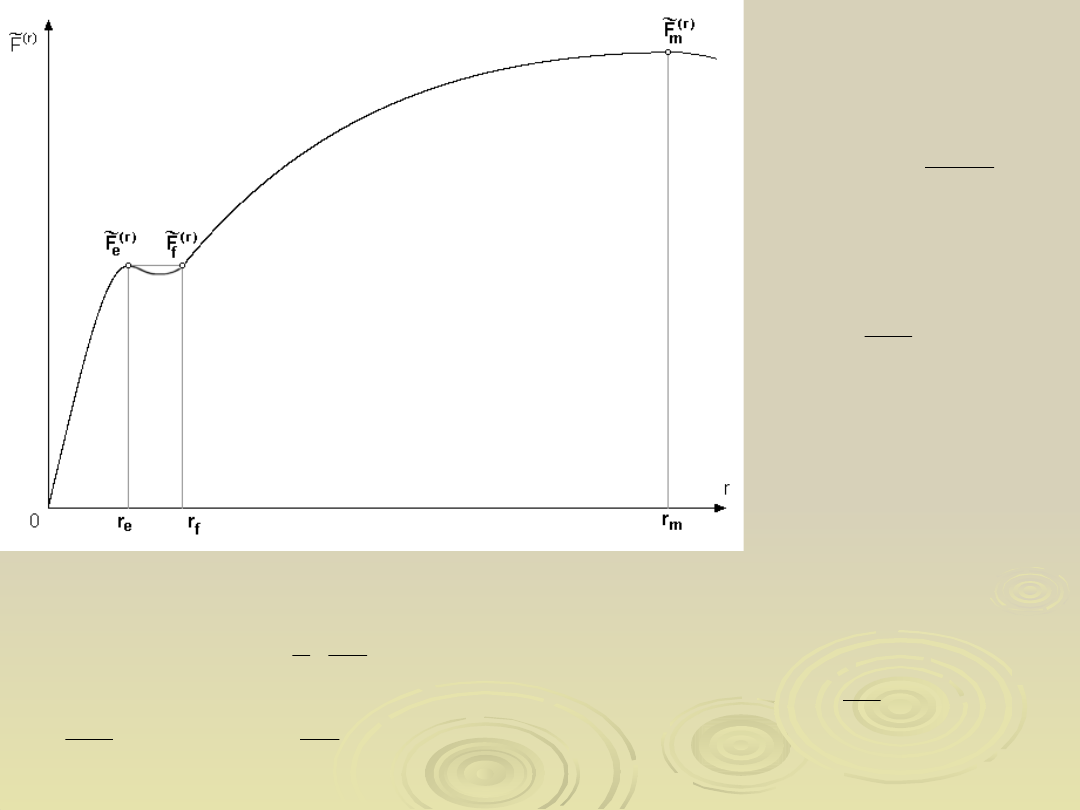
Dla stanów odkształcenia o współrzędnej

Dla stanów odkształcenia o współrzędnej

r = r

r = r

e

e

równowaga

równowaga

wewnętrzna jest niestateczna, co zgodnie z hipotezą

wewnętrzna jest niestateczna, co zgodnie z hipotezą

wytrzymałościową stateczności równowagi wewnętrznej oznacza

wytrzymałościową stateczności równowagi wewnętrznej oznacza

stan niebezpieczny ze względu na wytrzymałość materiału.

stan niebezpieczny ze względu na wytrzymałość materiału.

r

G

F

r

~

2

~

)

(



)

(

~

r

G

G 

G

G

r





~

lim

0

0

~

lim

0





dr

G

d

r

)

(

exp

~

b

r

a

G

G





]

exp[

~

)

(

1

b

e

b

r

r

G

G





]

)

(

1

[

~

2

~

)

(

b

e

r

r

G

dr

F

d

r









r

dr

F

W

r

s

0

)

(

)

(

~

~

)

(

~

)

(

s

W

W

W

v





r

F

h

F

W

r

h







)

(

)

(

~





2

)

(

2

)

(

2

~

r

dr

F

d

h

dh

dF

W

r

h











2

2

2

]

)

(

1

[

~

2

3

r

r

r

G

h

K

W

b

e













21

21

Uogólniona siła odkształcenia postaciowego

r

G

F

r

~

2

~

)

(



r

r

G

G

e

e

~

~

e

e

r

G

F

r

~

2

~

)

(



0

~

)

(



r

dr

F

d

2

2

3 h

K

W







]

)

(

exp[

~

1

c

m

r

r

c

H

G





]

)

(

1

[

~

2

~

)

(

c

m

r

r

G

dr

F

d

r





2

2

2

]

)

(

1

[

~

2

3

r

r

r

G

h

K

W

c

m













)

,

(

f

r

r

r

e









m

f

r

r

r

,

22

22

0

3

2









3

2







1

1

~







E

E

K

E

K

G

~

9

~

3

~





1

2

~











K

E

6

~

2

1

~







1

)

~

1

(

3

2









r

Dla

jednoosiowego

rozciągania

)

~

,

(

e

e

G

r

)

~

,

(

f

f

G

r

)

~

,

(

m

m

G

r

)

(

ln

~

1

e

G

G

b





0

1

)

(

ln

~

~







c

m

f

m

f

r

r

G

G

c

)

exp(

~

1

c

m

G

H 

23

23

Przykład

Przykład

liczbowy

liczbowy

węglowa stal konstrukcyjna

węglowa stal konstrukcyjna

zwykłej jakości

zwykłej jakości

St3S

St3S

3

.

0

,

MPa

10

05

.

2

5







v

E

MPa

10

788

.

0

,

MPa

10

708

.

1

5

5









G

K

MPa

237

,

10

50

.

2

,

10

55

.

1

3

3















e

f

e

R





MPa

445

,

10

3

.

11

3









m

m

R



granica plastyczności:

granica wytrzymałości:

24

24

MPa

10

394

.

0

~

,

MPa

10

948

.

0

~

,

MPa

10

529

.

1

~

5

5

5













m

f

e

E

E

E

MPa

10

135

.

0

~

MPa,

10

337

.

0

~

MPa,

10

566

.

0

~

5

5

5













m

f

e

G

G

G

462

.

0

~

,

407

.

0

~

,

351

.

0

~







m

f

e







3

3

3

10

49

.

13

,

10

87

.

2

,

10

71

.

1



















m

f

e

r

r

r

MPa

10

511

.

0

,

75147

.

0

,

02202

.

3

5









H

c

b

25

25

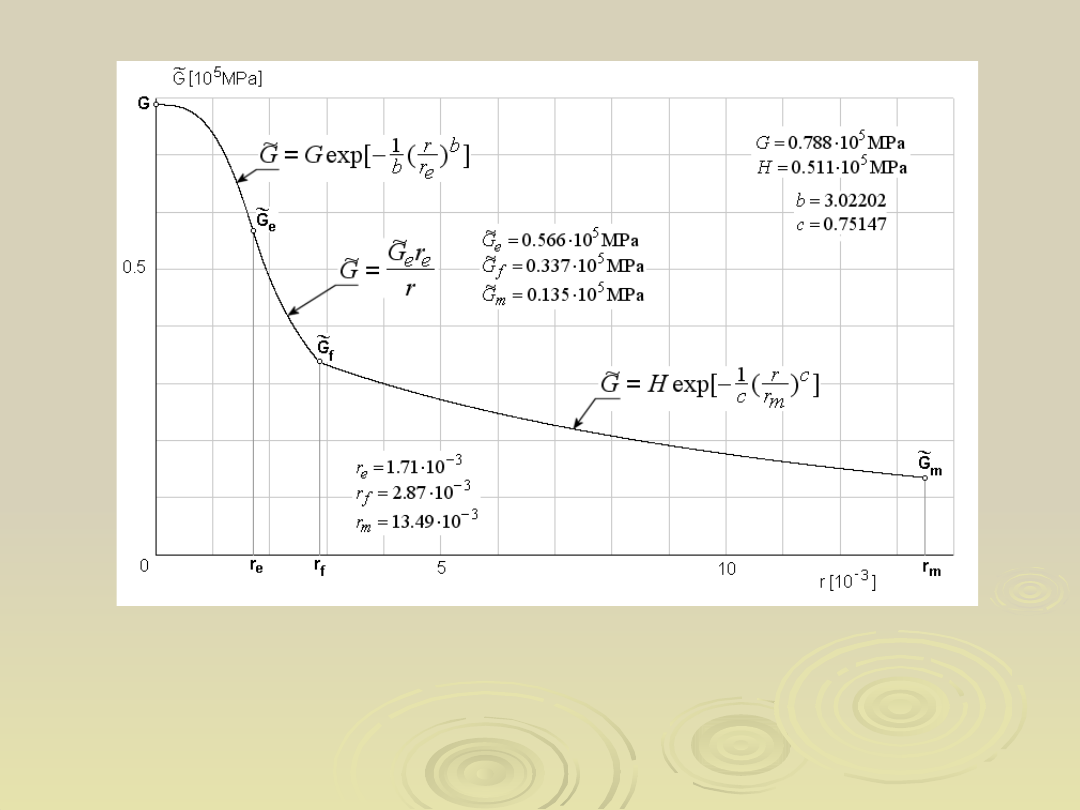
Zmienny moduł odkształcenia postaciowego

w funkcji współrzędnej odkształcenia

postaciowego r

26

26

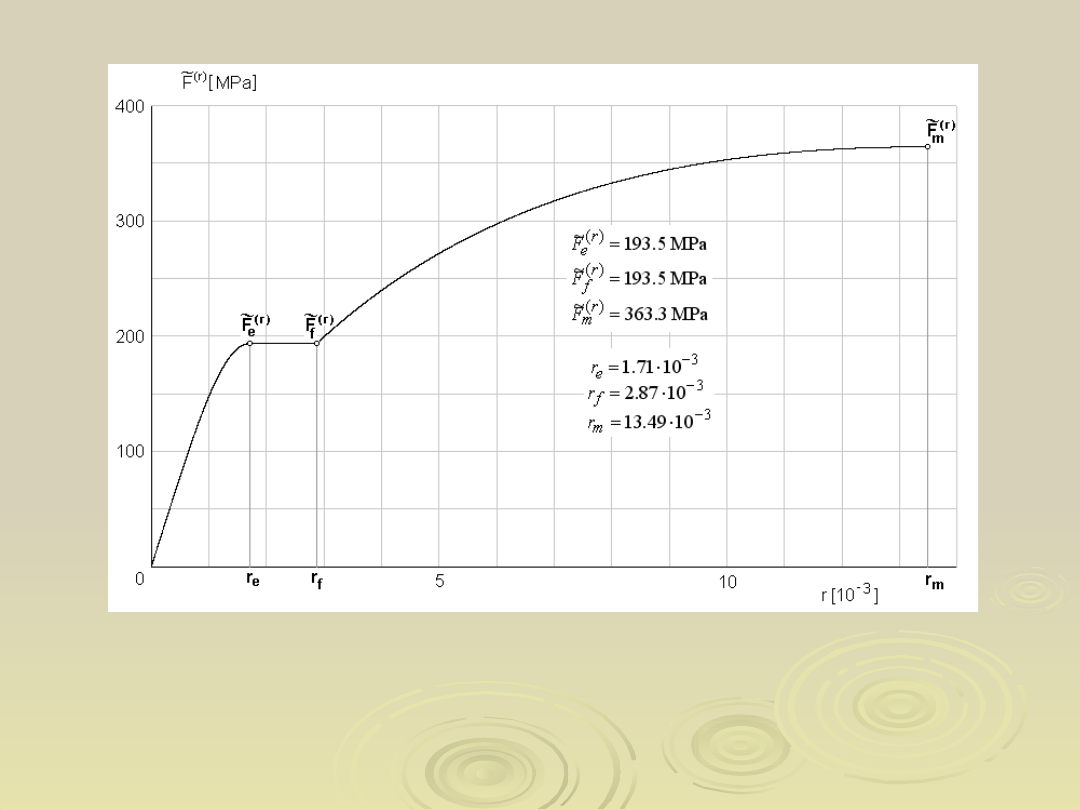
Nieliniowa uogólniona siła odkształcenia

postaciowego w funkcji współrzędnej

odkształcenia postaciowego r

27

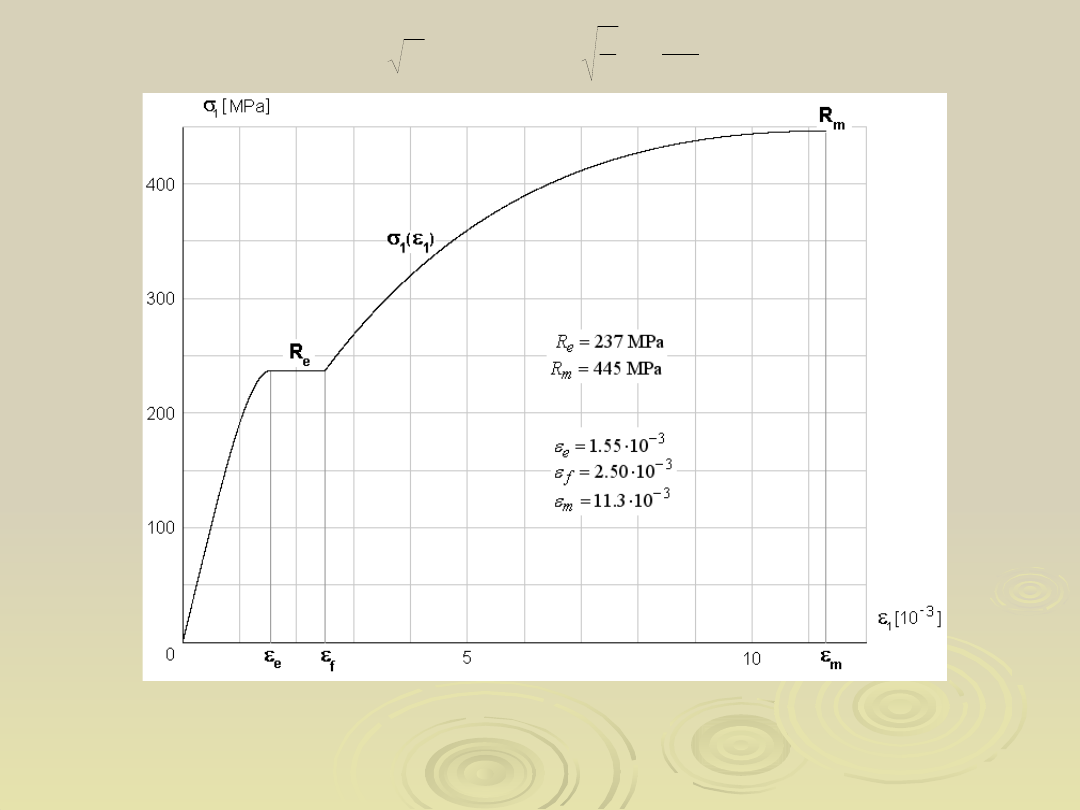
27

Krzywa jednoosiowego rozciągania uzyskana na podstawie

aproksymacji

mechanicznych właściwości materiału energetycznym modelem

r

K

G )

3

~

1

(

3

2

1







r

G

~

6

1





28

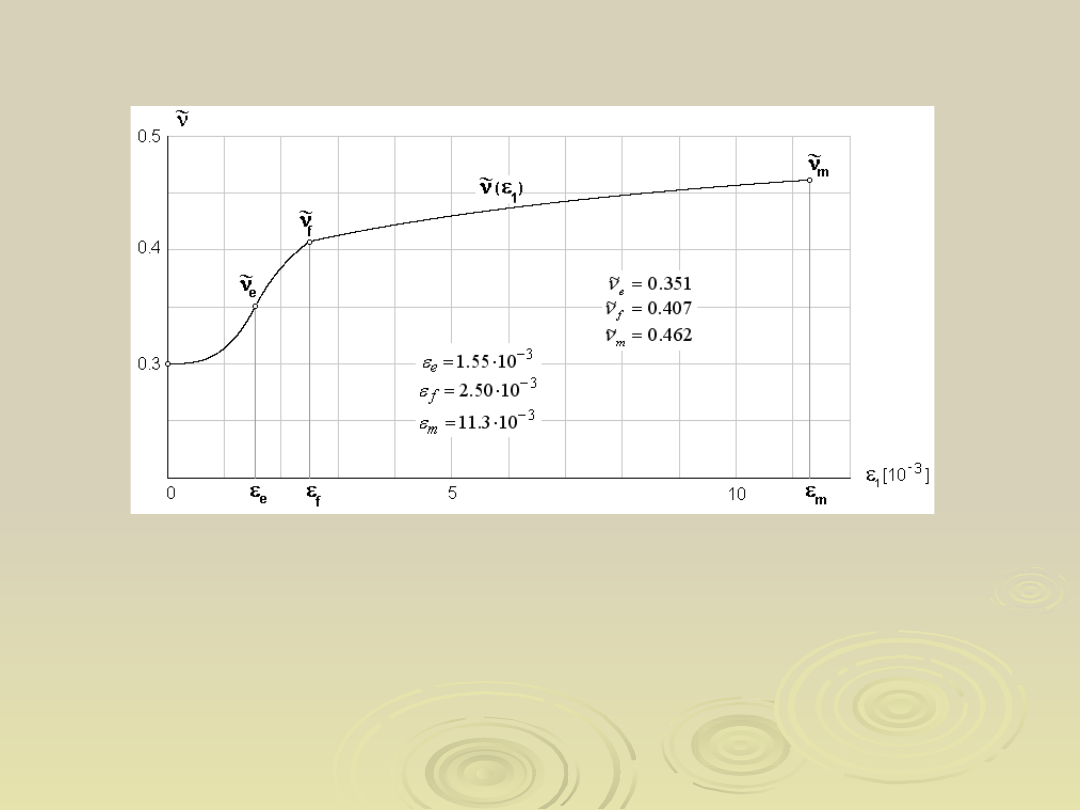
28

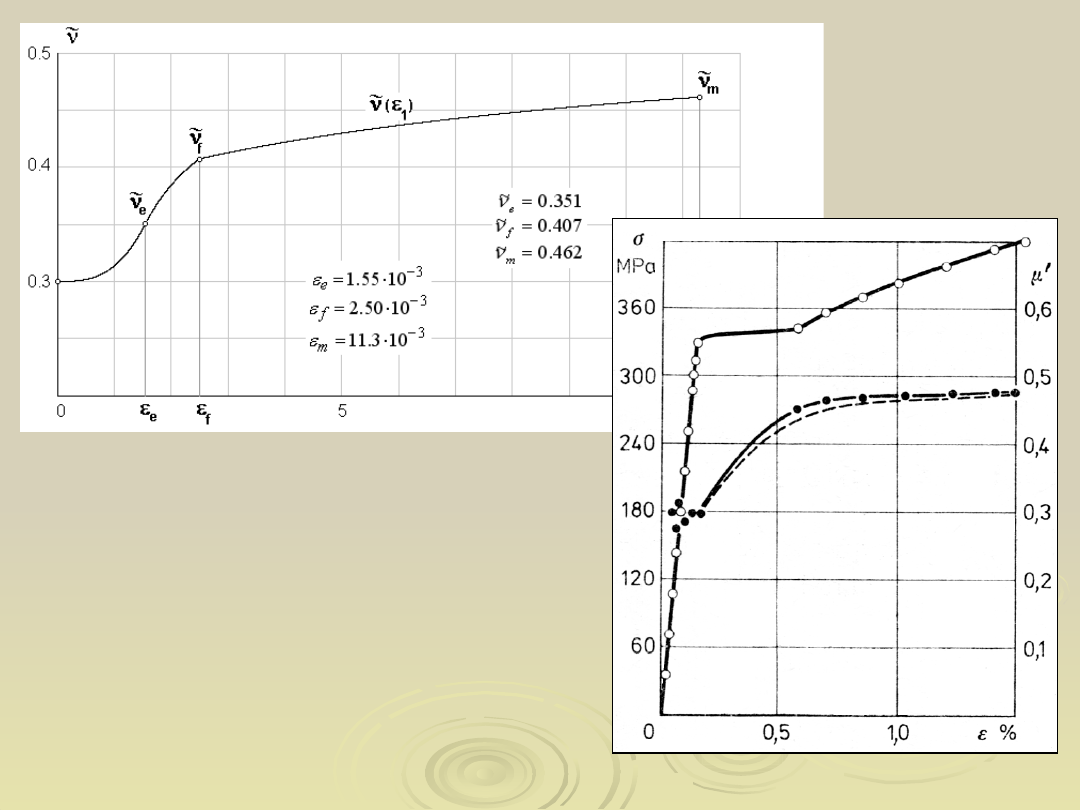
Wykres zmiennej liczby Poissona w funkcji jednostkowego

wydłużenia na podstawie energetycznego modelu

29

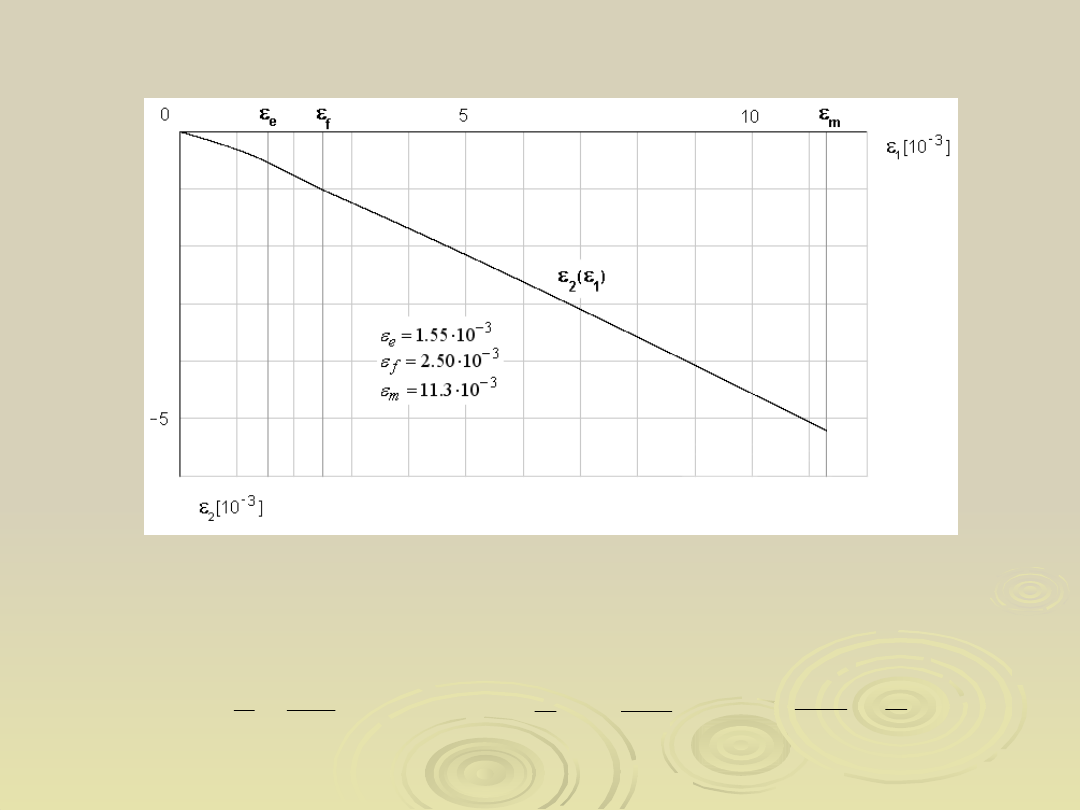
29

Wykres jednostkowego wydłużenia w kierunku poprzecznym do osi

rozciągania

w funkcji jednostkowego wydłużenia w jednoosiowym rozciąganiu

K

6

2

1

1

1

2













2

1

1

2









d

d

K

E

6

~

2

1

~







30

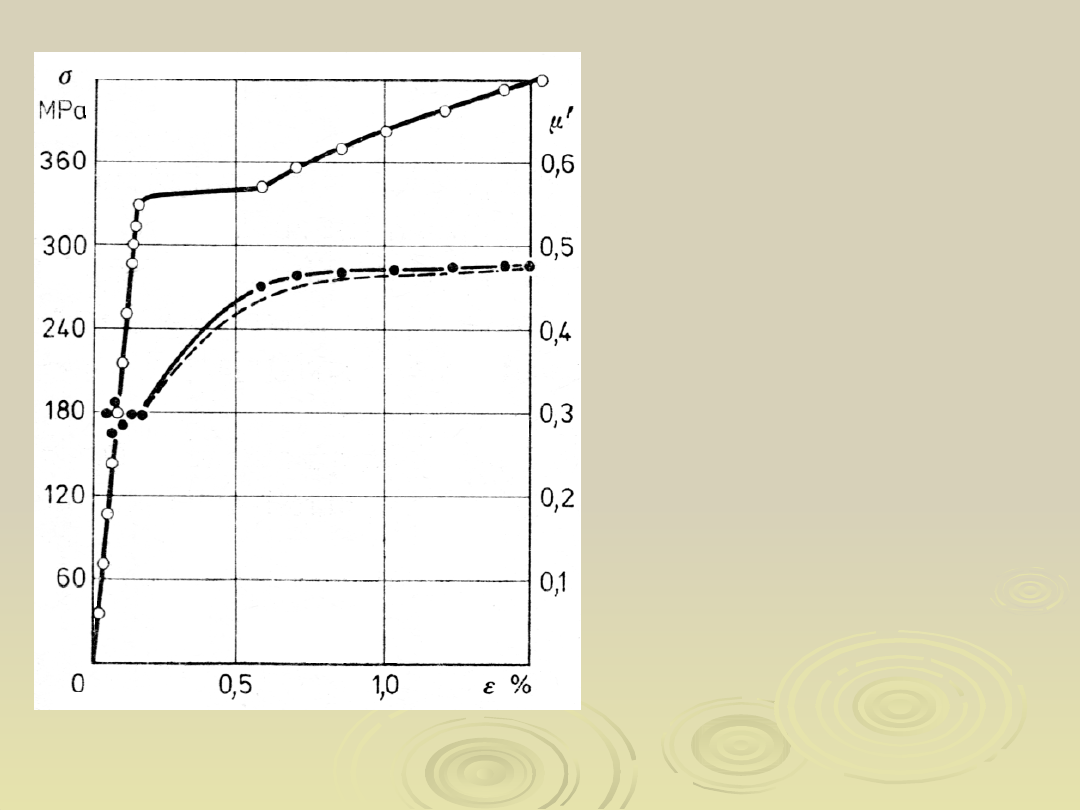
30

Wartości doświadczalne
współczynników
odkształcenia
poprzecznego otrzymane
przez A. M. Żukowa

Malinin M. N., Rżysko
J., Mechanika
materiałów. PWN,
Warszawa 1981,
str. 85

31

31

32

32

Wytrzymałościowa hipoteza

Wytrzymałościowa hipoteza

energii odkształcenia

energii odkształcenia

postaciowego

postaciowego

Jeżeli założymy, że w złożonym stanie naprężenia uogólniona siła

Jeżeli założymy, że w złożonym stanie naprężenia uogólniona siła

odkształcenia postaciowego przyjmuje podczas plastycznego płynięcia

odkształcenia postaciowego przyjmuje podczas plastycznego płynięcia

materiału taką samą wartość jak w jednoosiowym stanie naprężenia, to

materiału taką samą wartość jak w jednoosiowym stanie naprężenia, to

uzyskamy na tej podstawie warunek plastycznego płynięcia materiału

uzyskamy na tej podstawie warunek plastycznego płynięcia materiału





K

3



)

(

~

2

1

1















G

)

(

~

2

2

2















G

)

(

~

2

3

3















G

2

3

2

2

2

1

2

)

(

)

(

)

(

)

(

~

























r

F

]

)

(

)

(

)

(

[

3

1

~

2

1

3

2

3

2

2

2

1

2

)

(

























r

F

)

(

3

2

~

2

1

2

2

2

1

2

)

(















r

F

2

1

2

)

(

3

2

~





r

F

e

e

R

F

r

3

2

~

)

(



2

2

1

3

2

3

2

2

2

1

2

)

(

)

(

)

(

e

R

























2

2

1

2

2

2

1

e

R















2

3

2

2

2

1

2

)

(

)

(

)

(

























r

r

G

F

r

~

2

~

)

(



33

33

Stateczność odkształceń

Stateczność odkształceń

postaciowych

postaciowych

3

3

2

2

1

1





















W

0

3

2

1













3

3

2

2

1

1

)

(

)

(

)

(

































W

]

)

(

)

(

)

[(

~

2

3

3

2

2

1

1































 G

W

T

W

ε

B

ε









2

)

,

,

(

3

2

1











ε

}

3

,

2

,

1

{

,

],

)

)(

(

)

(

3

1

[

~

2

2













j

i

r

r

r

G

b

j

i

j

i

j

i

b

e











}

3

,

2

,

1

{

,

],

)

)(

(

)

~

ln(

3

1

[

~

2

2

)

(













j

i

F

G

G

b

G

b

r

j

i

j

i

j

i











34

34

Twierdzenie

Twierdzenie

Sylvestera

Sylvestera

Warunkiem koniecznym i dostatecznym na to, by forma kwadratowa o

Warunkiem koniecznym i dostatecznym na to, by forma kwadratowa o

symetrycznej macierzy

symetrycznej macierzy

B

B

była oznaczona dodatnio, jest przyjmowanie

była oznaczona dodatnio, jest przyjmowanie

dodatnich wartości przez wszystkie główne minory macierzy:

dodatnich wartości przez wszystkie główne minory macierzy:

0

det

)

(





k

k

B

Równowaga wewnętrzna w punkcie zdeformowanego materiału jest niestateczna, gdy

0

det

)

(





k

k

B

Warunki plastycznego płynięcia materiału:

.

0

det

,

0

det

,

0

33

23

13

23

22

12

13

12

11

22

12

12

11

11







































b

b

b

b

b

b

b

b

b

b

b

b

b

b

Badanie wypukłości funkcji energii odkształcenia na podstawie
powyższych warunków jest równoważne z poszukiwaniem takich
stanów naprężenia, dla których odkształcenia postaciowe nie są
stateczne.

35

35

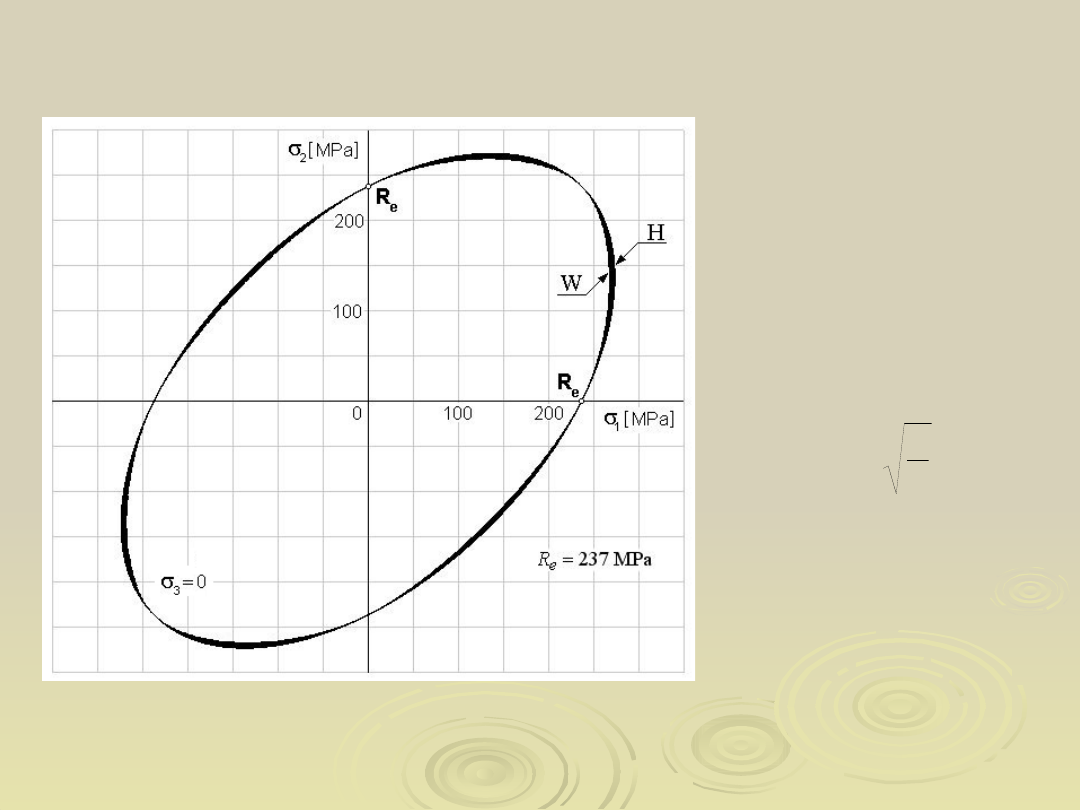
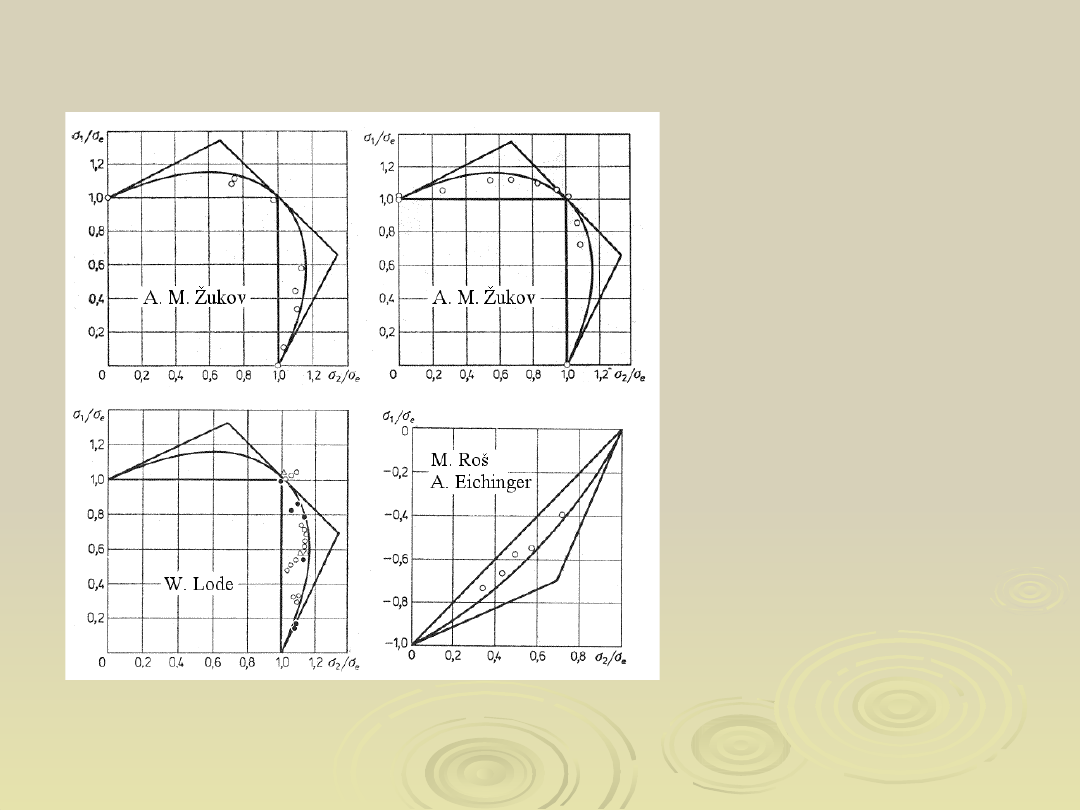
Porównanie wytrzymałościowej hipotezy energii

Porównanie wytrzymałościowej hipotezy energii

odkształcenia postaciowego z hipotezą stateczności

odkształcenia postaciowego z hipotezą stateczności

równowagi wewnętrznej

równowagi wewnętrznej

Obszar zawarty pomiędzy powierzchniami granicznymi

Obszar zawarty pomiędzy powierzchniami granicznymi

wynikającymi z warunków: Hubera (H) oraz nowego

wynikającymi z warunków: Hubera (H) oraz nowego

warunku (W) plastycznego płynięcia materiału

warunku (W) plastycznego płynięcia materiału

e

R

r

H

3

2



H

W

H

r

r

r





978

.

0

na podstawie
aproksymacji modelem
energetycznym
mechanicznych
właściwości stali St3S

36

36

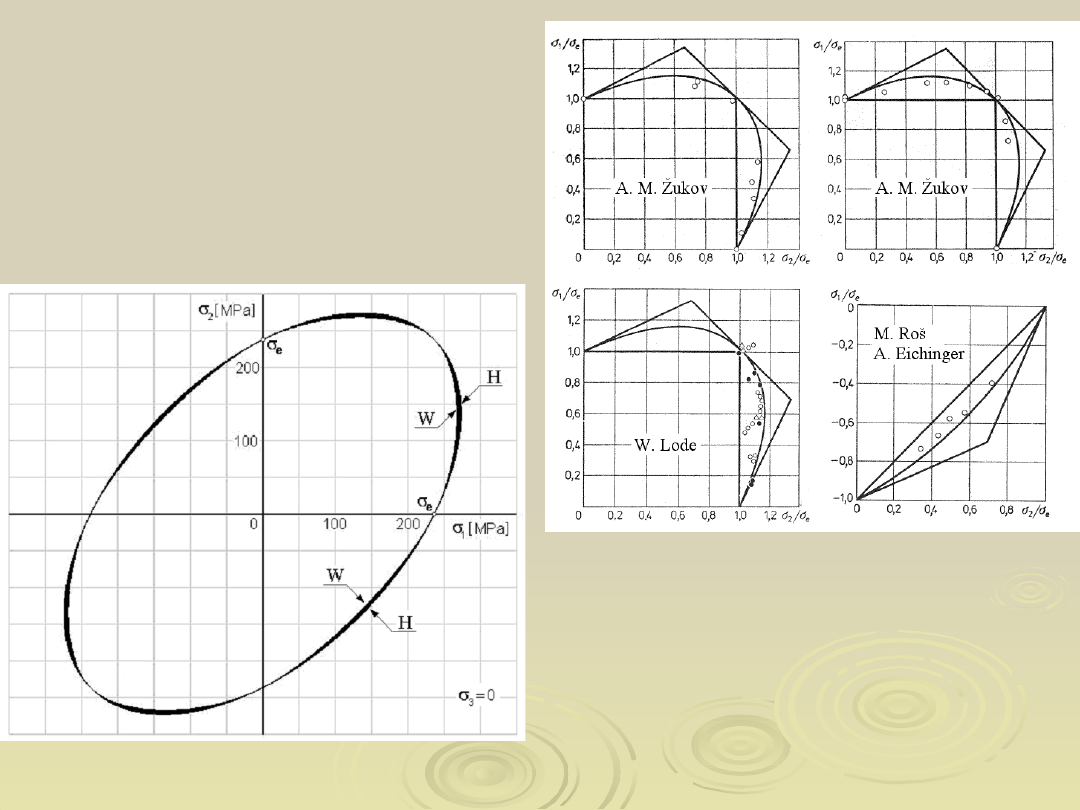
Porównanie wyników teoretycznych

Porównanie wyników teoretycznych

z badaniami eksperymentalnymi

z badaniami eksperymentalnymi

Wyniki eksperymentów A. M.

Żukowa,

W. Lode’a oraz M. Rosa i A.

Eichingera

Malinin M. N.,
Rżysko J., Mechanika
materiałów. PWN,
Warszawa 1981,
str. 47 i 48

37

37

38

38

Podsumowanie

Podsumowanie

1. Przedstawiona w pracy metoda modelowania mechanicznych

właściwości materiałów bazuje na wytrzymałościowej hipotezie
stateczności równowagi wewnętrznej.

2. W hipotezie tej przyjęto, że bezpośrednią przyczyną uszkodzenia lub

zniszczenia materiału jest utrata stateczności stanu równowagi
wewnętrznej w odkształconym materiale, a do badania stateczności
wykorzystano podstawową zasadę fizyczną – prawo zachowania
energii.

3. Hipoteza ta pozwala na nowe teoretyczne ujęcie podstawowego

problemu z dziedziny wytrzymałości materiałów – zagadnienia
zniszczenia materiałów.

4. Przedstawiona metoda stwarza duże możliwości rozwoju badań nad

mającą ogromne znaczenie techniczne problematyką wytrzymałości
materiałów w złożonym stanie naprężenia.

5. Jak pokazano w pracy, znajomość matematycznego modelu

mechanicznych właściwości materiału oraz jego stałych, jest
warunkiem wystarczającym do teoretycznego wyznaczenia stanów
deformacji powodujących plastyczne płynięcie lub utratę spójności
materiału.

39

39

6. W świetle uzyskanych wyników możemy stwierdzić, że hipoteza

stateczności stanu równowagi wewnętrznej potwierdza trafność
hipotezy Hubera w odniesieniu do materiałów charakteryzujących
się liniową zależnością sprężystości objętościowej i stanowi tym
samym jej merytoryczne uzasadnienie.

7. Poprawność dowolnej hipotezy wytrzymałościowej sformułowanej

dla określonego materiału można sprawdzić poprzez badanie
warunków stateczności stanów równowagi wewnętrznej w
matematycznym modelu materiału i porównanie uzyskanych w ten
sposób wyników z weryfikowaną hipotezą.

8. Zaprezentowana w pracy metoda modelowania matematycznego

może być zastosowana do materiałów o dowolnych nieliniowych
właściwościach fizycznych, w tym także do materiałów nie
wykazujących liniowej zależności sprężystości objętościowej.

9. Metoda ta pozwala na uzupełnienie procesu projektowania

elementów konstrukcyjnych z materiałów quasi-izotropowych o
dowolnych nieliniowych właściwościach fizycznych, o ocenę
wytrzymałościową wynikającą z teoretycznej analizy opartej na
prawie zachowania energii.

10.Zastosowanie w praktyce metody analizy proponowanej w

niniejszej pracy, wymaga opracowania matematycznych modeli
mechanicznych właściwości materiałów.

40

40

Deformacja ciał hipersprężystych

Deformacja ciał hipersprężystych

wykonanych z materiałów

wykonanych z materiałów

kauczukopodobnych

kauczukopodobnych

I

L

L

L

1

1

2

3

 



I

L L

L L

L L

2

2 3

3 1

1 2







I

L L L

3

1 2 3



L

i

i





2

i { , , }

1 2 3

L

L

L

L

1

2

3

  

I

L I

L

v

v

1

2

2

3

3

( )

( )

,





L I



3

1 3

/

I

I

I

i

s

i

i

v

( )

( )

 

}

2

,

1

{



i

I

I

L I

I

L L

L

L L L

s

1

1

1

3

3

1

2

3

1 2 3

3

3

3

3

0

( )

 

 

 







I

I

L

I

I

L L

L L

L L

L L L L L L

s

2

2

2

2

3

2

3

1 2

2 3

3 1

1 2

2 3

3 1

3

3

3

3

0

( )

(

)(

)(

)

 

 











41

41

Uogólnienie funkcji Mooneya

Uogólnienie funkcji Mooneya

U I

I

I

C I

C I

KU

I

s

s

s

s

m

(

,

, )

(

)

( )

( )

( )

( )

1

2

3

1 1

2 2

3







U

I

I

I

(

)

(

)

3

3

2

1

2

1





U

I

I

I

I

II

(

)

ln

3

3

3

3

1











U

I

I

I

III

(

)

[

(

)

]

/

3

3

1 3

3

3

4

4 3







U

I

I

I

IV

(

)

ln

3

3

3

1







U

I

I

I

V

(

)

(

)

3

3

2

3

1

2







I





K

I

(

)

3

1



II

K

I

ln

3



III





K

I

I

3

3

3

1



IV





K

I

I

3

3

1



V





K

I

I

3

3

1

2

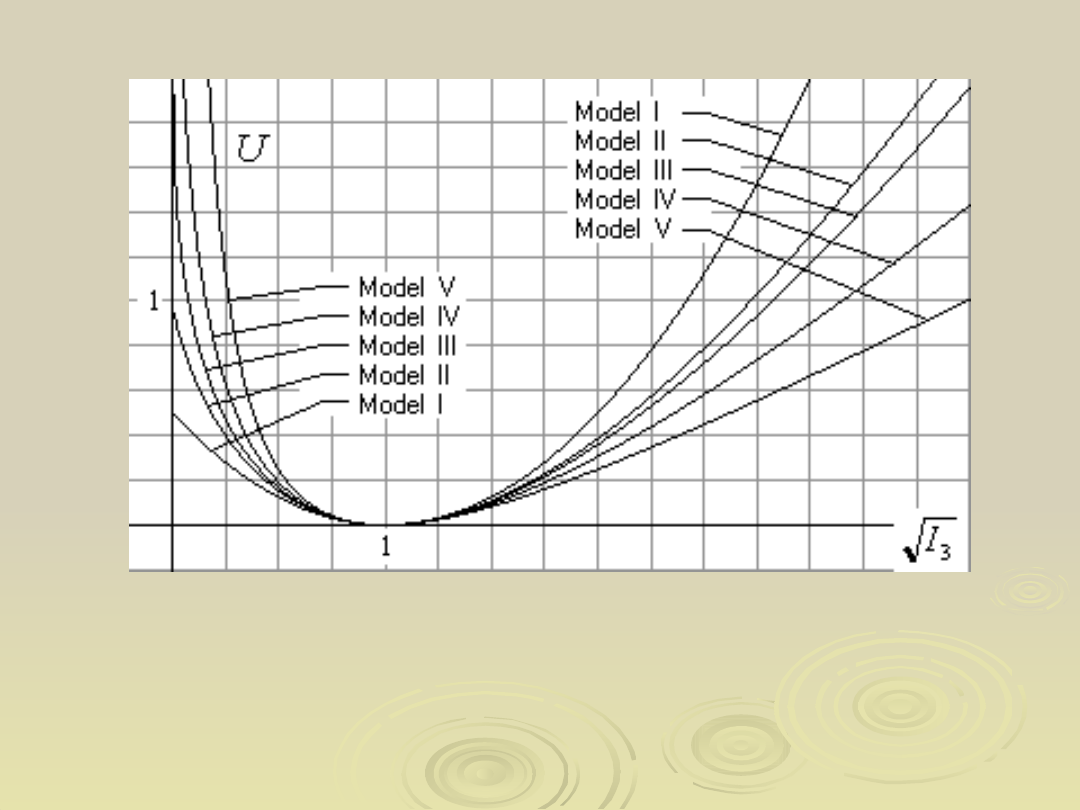
42

42

Energia właściwa odkształcenia

objętościowego

w zależności od względnej objętości ciała

dla różnych modeli ściśliwości materiału

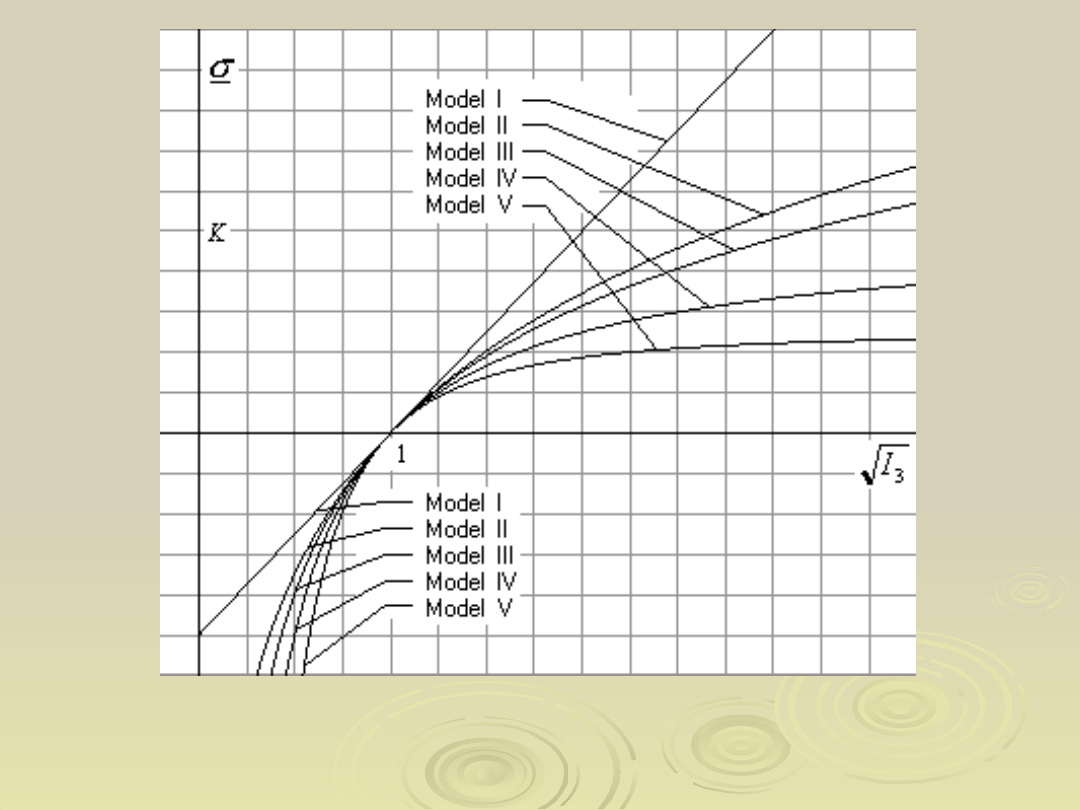
43

43

Rzeczywiste naprężenia w stanie równomiernego

wszechstronnego ściskania lub rozciągania w zależności od

względnej objętości ciała dla różnych modeli ściśliwości

materiału

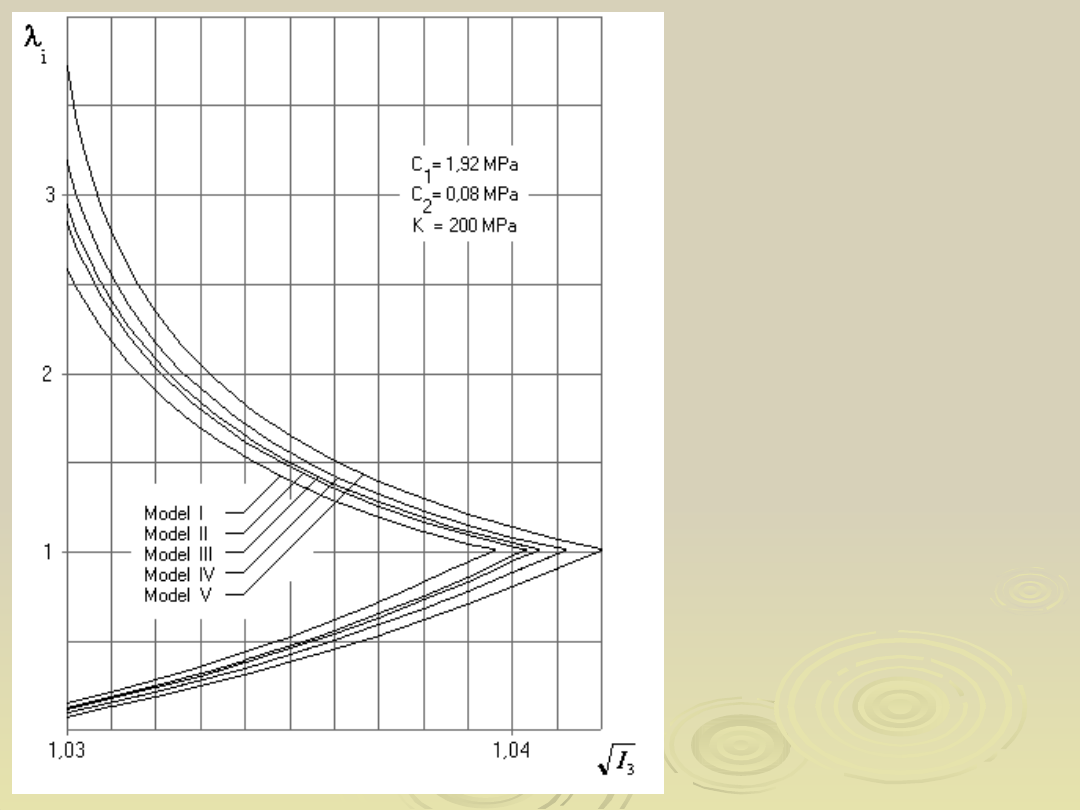
44

44

Górny i dolny brzeg
statecznego obszaru
składowych stanu
odkształcenia w funkcji
objętości względnej dla
różnych modeli materiałów
ściśliwych

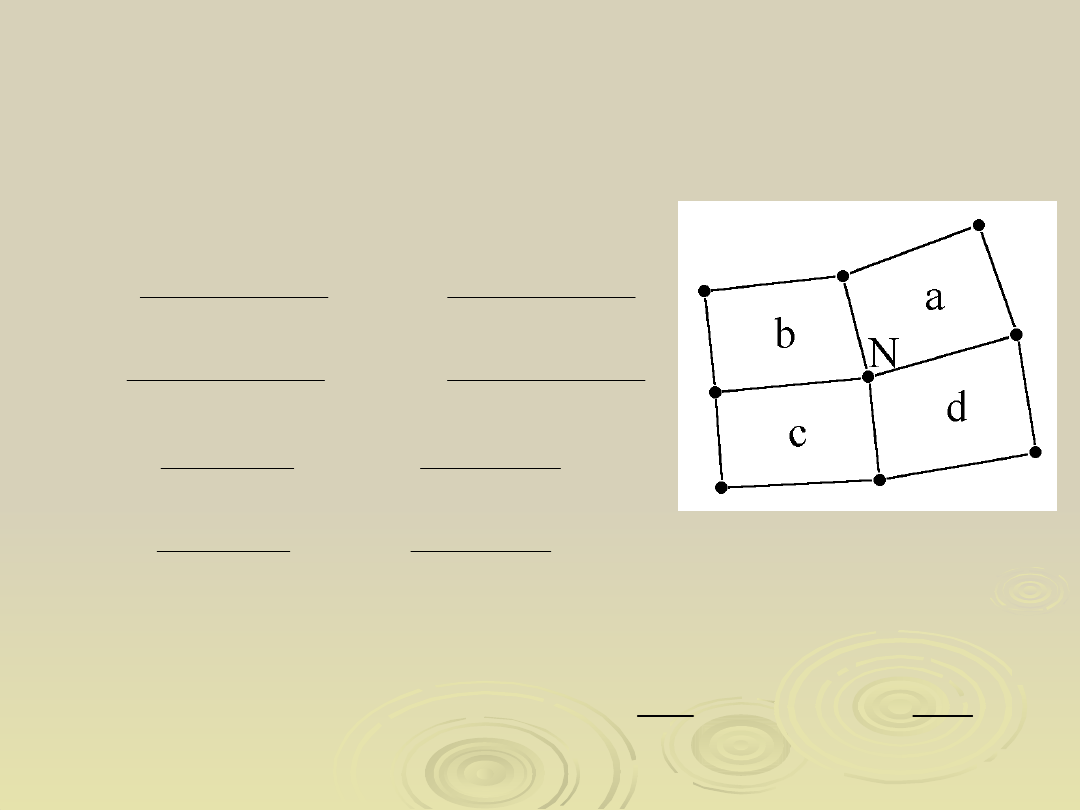
45

45

Metoda relaksacji lokalnej

Metoda relaksacji lokalnej

E

u w u w u w u w

e

a b c d

e

A

A

B

B

C

C

D

D

( )

( ,

, ,

, ,

,

,

) ,

{ , , , }



E

E

E

E

E

a

b

c

d

0









( )

( )

( )

( )

F

E u

u

E

u

F

E

E u

u

u

R

u

L

u

( )

( )

(

)

,

(

)













0

0

0

0









F

E w

w E

w

F

E

E w

w

w

R

w

L

w

( )

( )

(

)

,

(

)













0

0

0

0









F

F

F

F

F

F

u

R

u

L

u

w

R

w

L

w

( )

( )

( )

( )

( )

( )

,









2

2

k

F

F

u

k

F

F

w

u

R

u

L

u

w

R

w

L

w

( )

( )

( )

( )

( )

( )

,













R

S

F

R

S

F

u

u

u

w

w

w

( )

( )

( )

( )

( )

( )

,









u

u

R

k

w

w

R

k

i

i

u

u

i

i

w

w

( )

(

)

( )

( )

( )

(

)

( )

( )

,













1

1

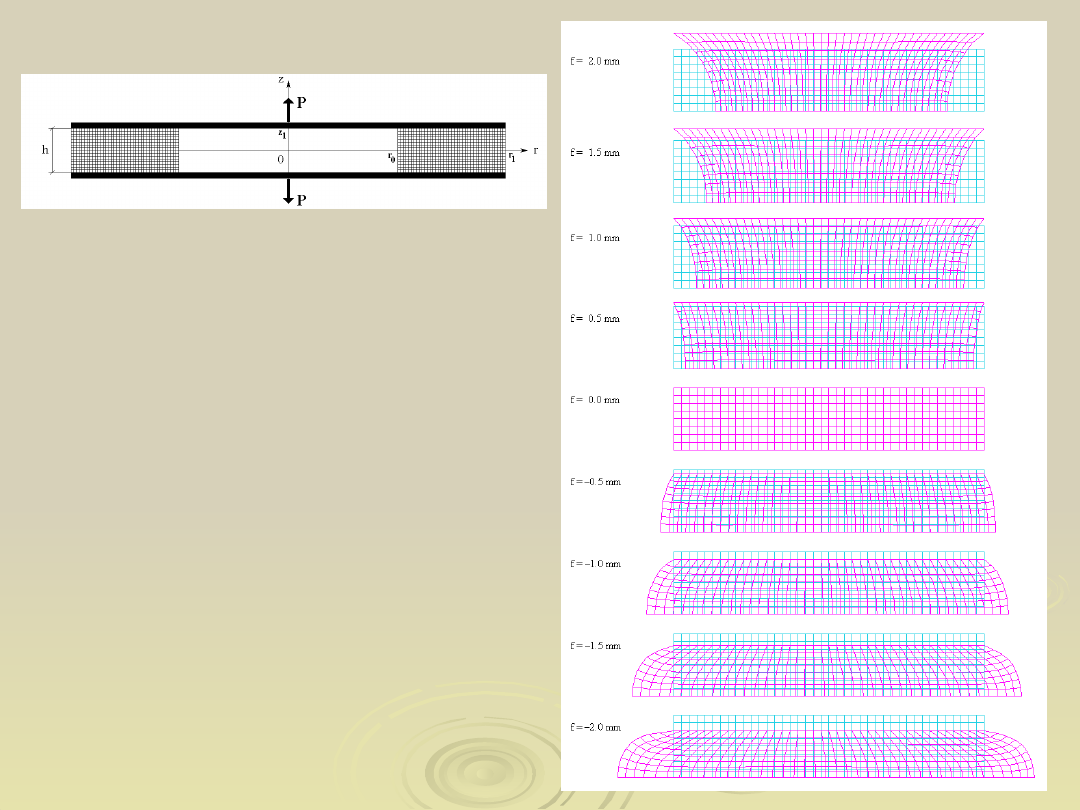
46

46

Stan przemieszczeń w

pierścieniu obciążanym

statycznie dla wybranych faz

procesu deformacji

47

47

Literatura cd.

Literatura cd.

5.

Wegner T., Metody energetyczne w wytrzymałości materiałów -
Hipoteza wytrzymałościowa stateczności równowagi wewnętrznej,
Seria Rozprawy Nr 323, Wydawnictwo Politechniki Poznańskiej,
Poznań 1999.

6.

Wegner T., Ograniczenia zakresu stosowalności uogólnionej funkcji
energii odkształcenia Mooneya wynikające z warunków Colemana-
Nolla oraz silnej eliptyczności, w: Materiały konferencyjne XXXVIII
Sympozjonu PTMTS „Modelowanie w Mechanice”, Wisła 1999,
Zeszyty Naukowe Katedry Mechaniki Stosowanej, zeszyt nr 10,
Wydawnictwo Katedry Mechaniki Stosowanej Politechniki Śląskiej,
Gliwice 1999, s. 327-332.

7.

Wegner T., Analiza porównawcza zakresu stosowalności
nieliniowych modeli materiałów ściśliwych, Studia i Materiały
XLVIII, seria Technika, zeszyt 1, Wydawnictwo Wyższej Szkoły
Pedagogicznej im. Tadeusza Kotarbińskiego, Zielona Góra 1999, s.
159-173.

8.

Wegner T., Zastosowanie metody relaksacji lokalnej do analizy
zagadnień uwzględniających zjawisko tarcia powierzchniowego,
Zeszyty Naukowe Politechniki Poznańskiej, seria Mechanika, nr 47,
Wydawnictwo Politechniki Poznańskiej, Poznań 2000, s. 73-87.