Obliczanie sił w

więzach podporowych

Zagadnienia statycznie

wyznaczalne

Zagadnieniami

statycznie

wyznaczalnymi

nazywamy takie zagadnienia, które dotyczą
równowagi układu sił działających w jednej
płaszczyźnie na jedno lub kilka ciał sztywnych
(układ mechaniczny), w których istnieje możliwość
wyznaczenia niewiadomych sił.

Niewiadome siły stanowią zwykle reakcje podpór
albo siły wzajemnego oddziaływania wewnątrz
rozważanego układu mechanicznego.

W przypadku układu statycznie wyznaczalnego
liczba reakcji zastępujących działanie więzów
jest równa liczbie równań równowagi.

Jeżeli więzów jest za mało, to dany układ
mechaniczny jest niesztywny.

Równowaga

takiego

układu

może

być

zapewniona

w

przypadku

spełnienia

dodatkowych

warunków,

które

zapewniają

układowi odpowiednią postać geometryczną.

Zagadnienia statycznie

wyznaczalne

Gdy

więzów

jest

więcej

niż

potrzeba

do

unieruchomienia danego układu mechanicznego,
dany układ jest przesztywniony.

Wówczas niewiadomych reakcji jest więcej niż mamy
równań równowagi i dlatego niektórych reakcji nie
można wyznaczyć metodami stosowanymi w statyce.

Zagadnienia

takie

nazywamy

zagadnieniami

statycznie niewyznaczalnymi.

Zagadnienia statycznie

wyznaczalne

Ustrój statycznie

wyznaczalny



0

X



0

Y



0

M

A

Belki swobodnie

podparte

Jest to belka jednoprzęsłowa, w której pod
działaniem sił zewnętrznych jeden jej koniec ma
możliwość obrotu oraz przesuwu w kierunku osi
belki, a drugi tylko możliwość obrotu.

Np. stalowe dźwigary mostowe, oparte jednym
końcem na tzw. łożysku przegubowym, a drugim
końcem na łożysku przegubowo-przesuwnym.

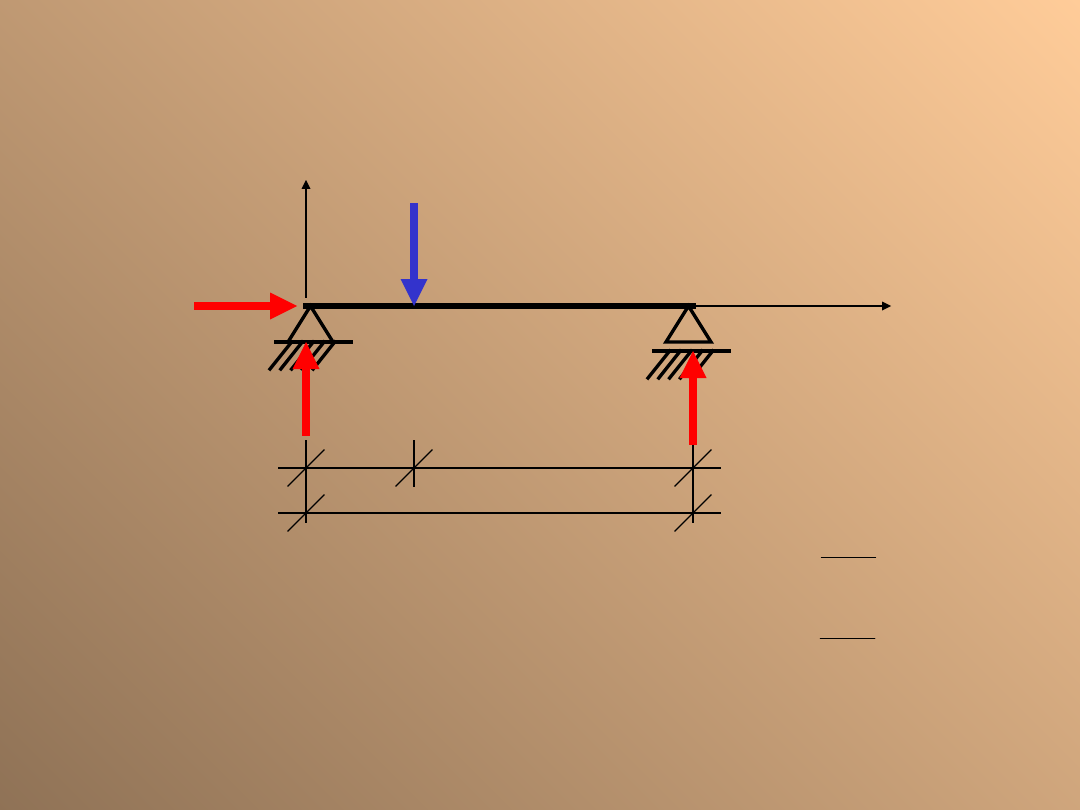
Belka swobodnie

podparta

y

x

B

A

P

a

b

l

H

A

V

A

R

B



0

X



0

Y



0

M

A

H

A

= 0

V

A

– P + R

B

= 0

– R

B

l + Pa = 0

l

a

P

R

B





l

b

P

V

A





H

A

= 0

Belka swobodnie

podparta

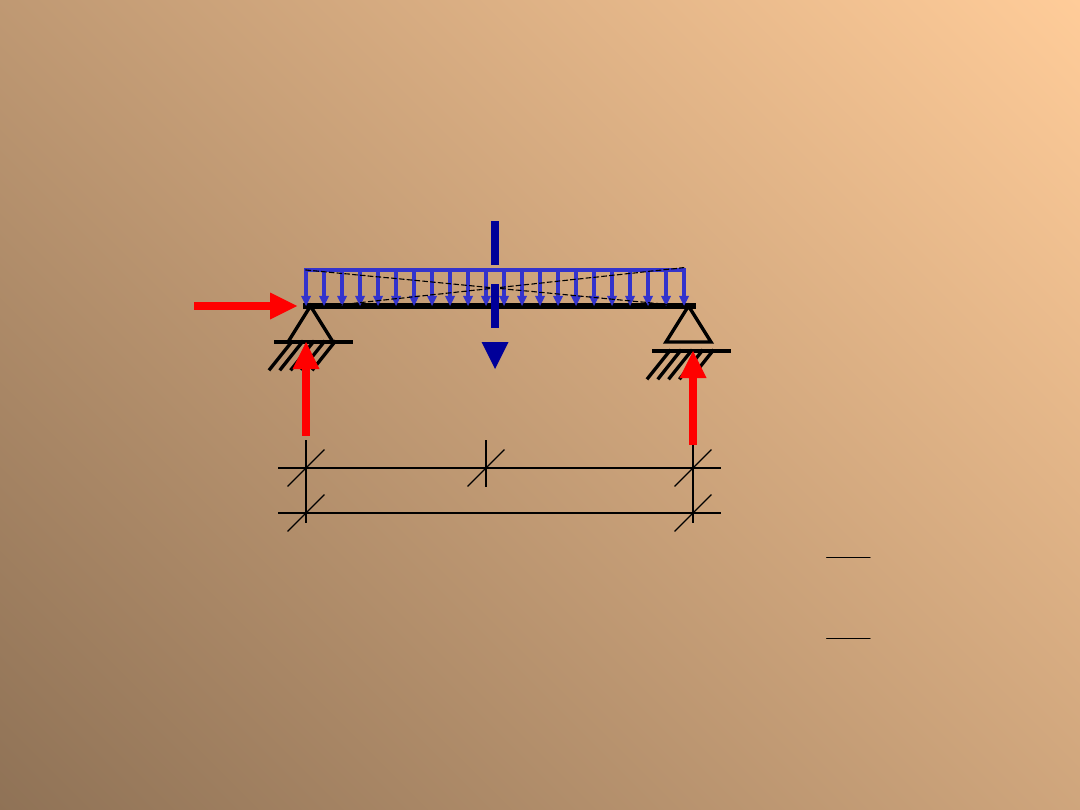
Belka swobodnie podparta

obciążona ciężarem równomiernie

rozłożonym

B

A

q

l/2

l

H

A

V

A

R

B



0

X



0

Y



0

M

A

H

A

= 0

V

A

– ql + R

B

= 0

– R

B

l + ql

2

/2 = 0

2

l

q

R

B





2

l

q

V

A





H

A

= 0

l/2

ql

Belka swobodnie

podparta

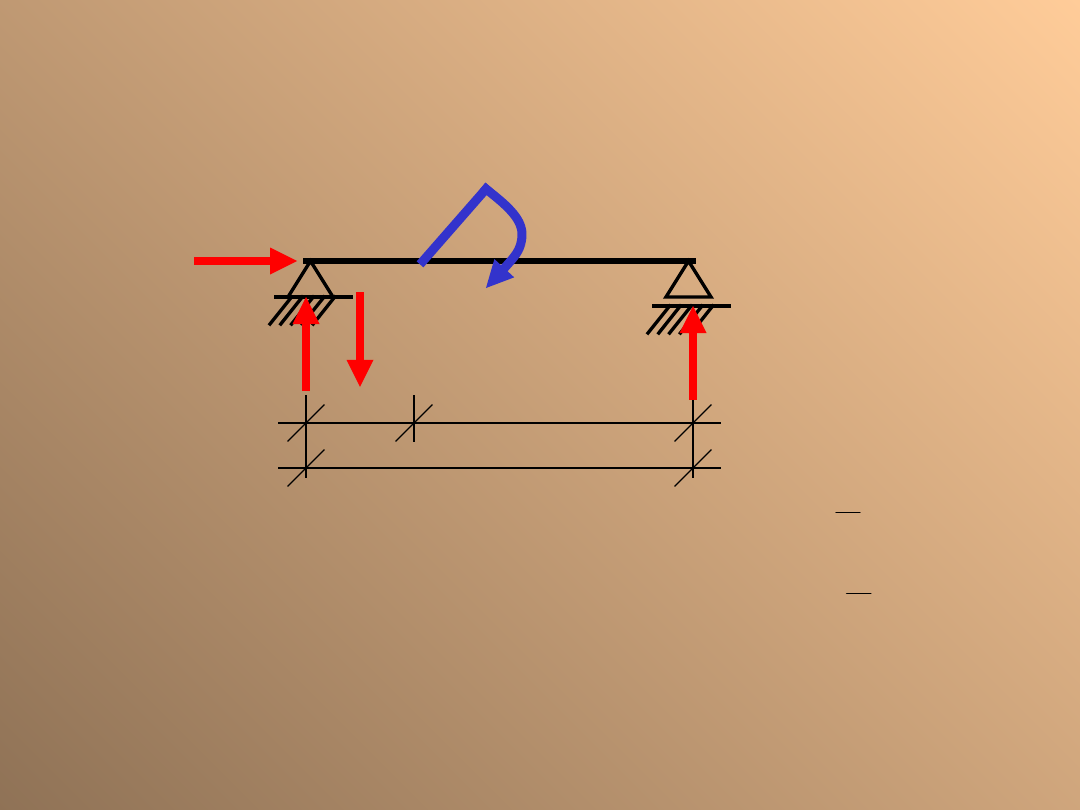
Belka swobodnie podparta

obciążona momentem

skupionym

B

A

a

b

l

H

A

V

A

R

B



0

X



0

Y



0

M

A

H

A

= 0

V

A

+ R

B

= 0

– R

B

l + M = 0

l

M

R

B



l

M

V

A





H

A

= 0

M

Znak minus oznacza, że zwrot V

A

należy zmienić na przeciwny.

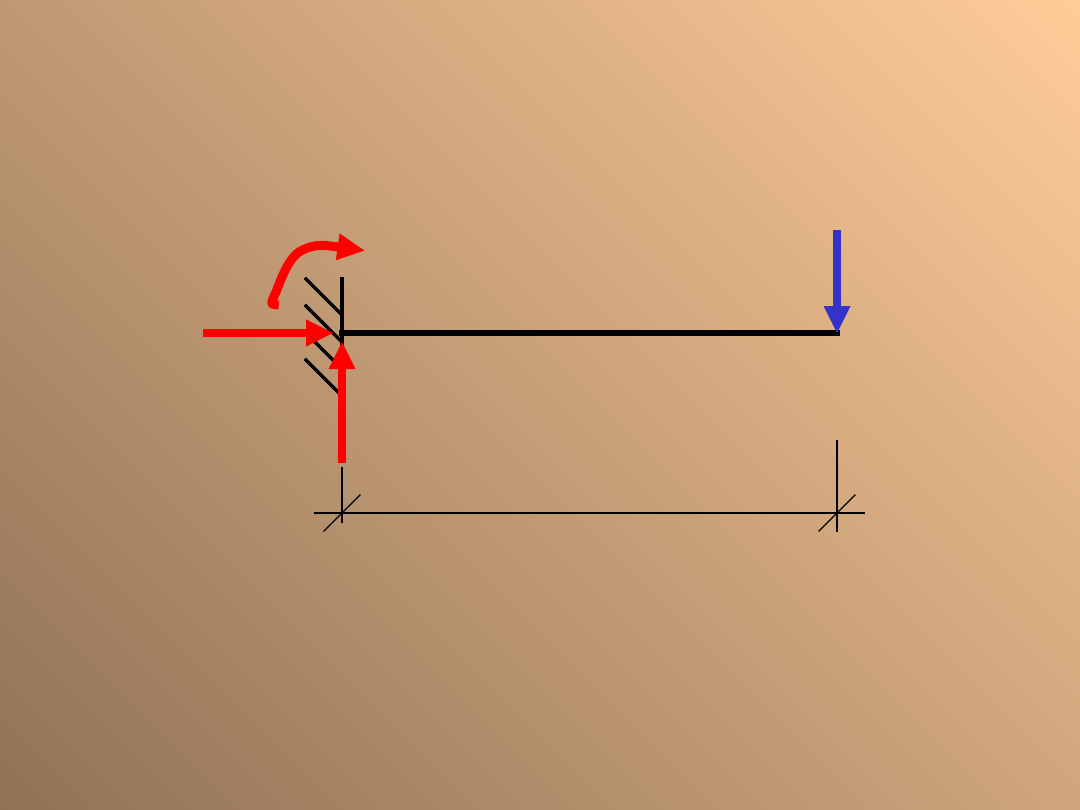
Belka sztywno

utwierdzona

P

V

A

H

A

M

A

A



0

X



0

Y



0

M

A

H

A

= 0

V

A

– P = 0

– M

A

+ Pl = 0

l

H

A

= 0

V

A

= P

M

A

= Pl

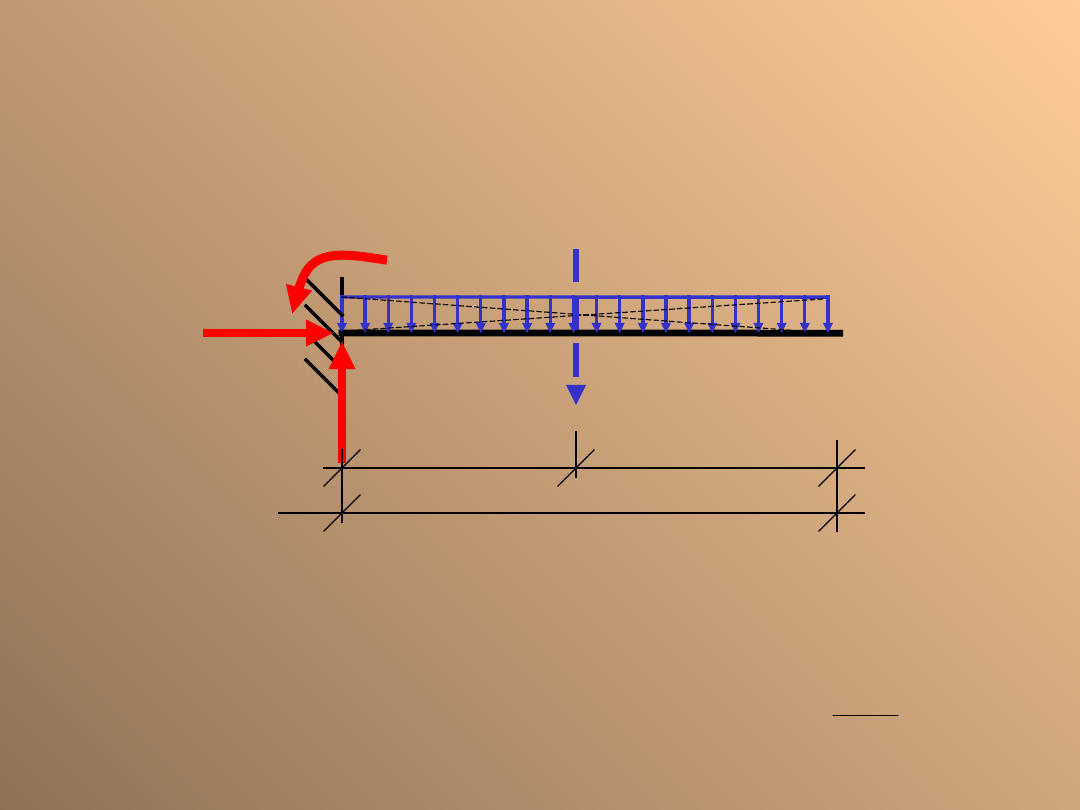
Belka sztywno utwierdzona

równomiernie obciążona

V

A

H

A

A

l

M

A

l/2

l/2

q

ql



0

X



0

Y



0

M

A

H

A

= 0

V

A

– ql = 0

– M

A

+ ql

2

/2 = 0

H

A

= 0

V

A

= ql

2

l

q

M

2

A





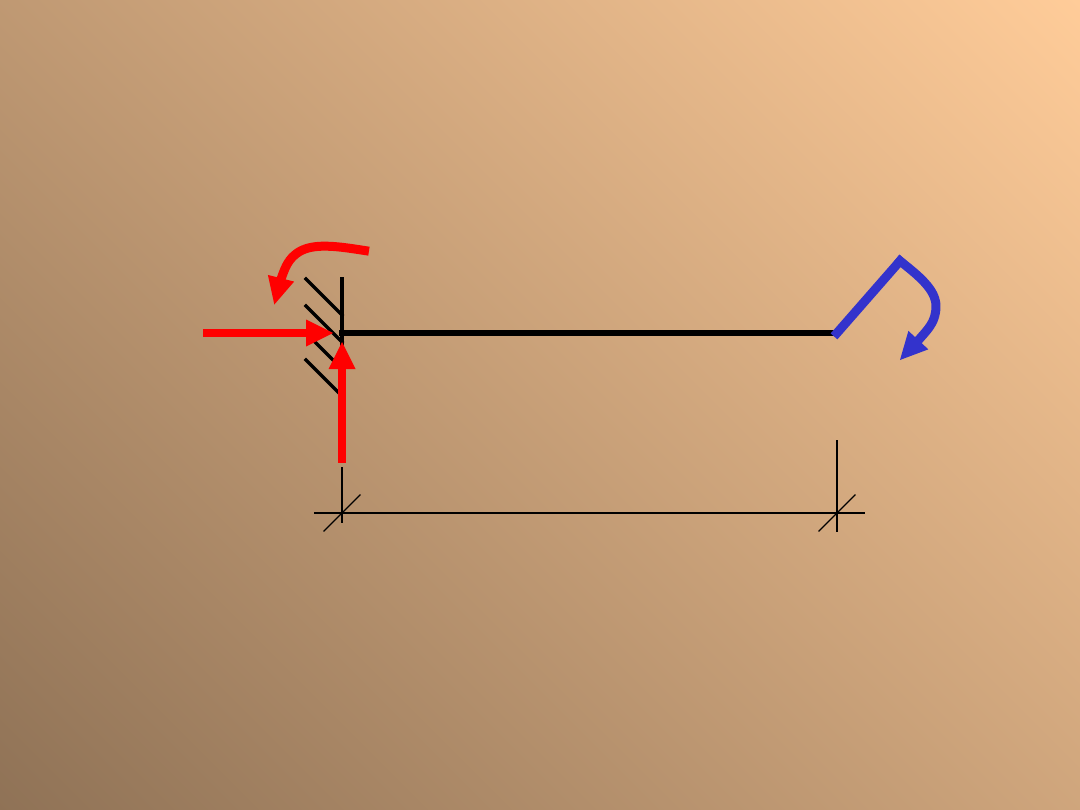
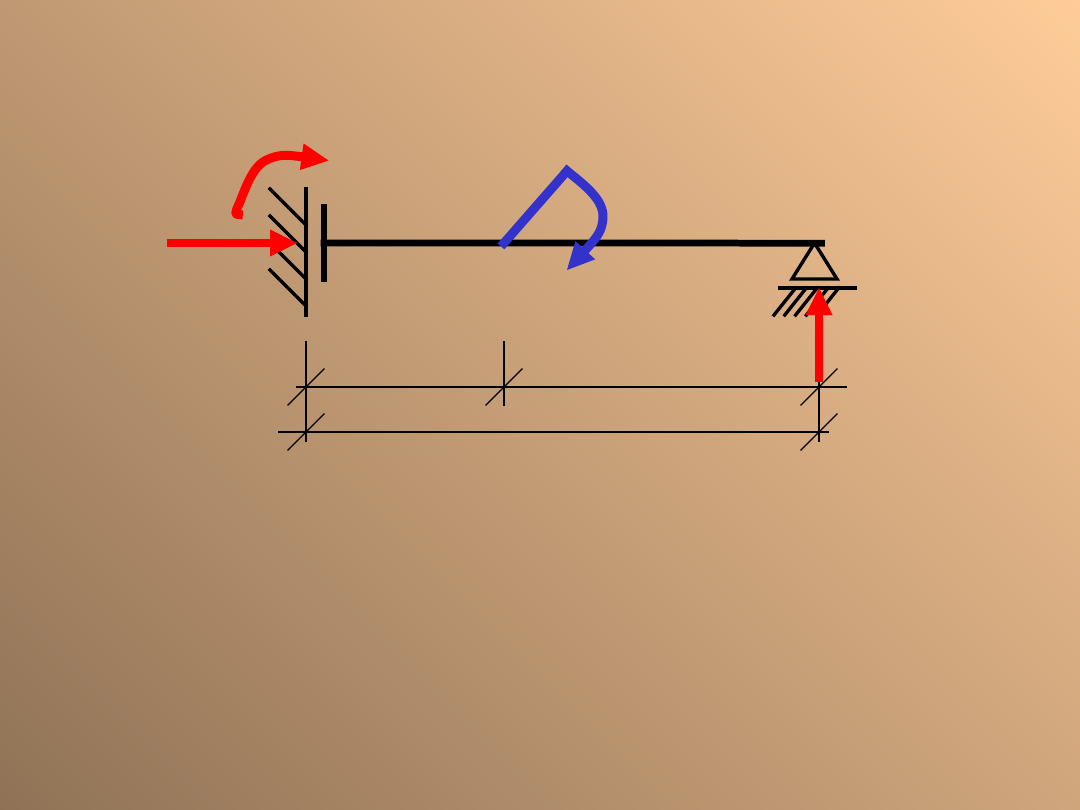
Belka sztywno utwierdzona

obciążona momentem

skupionym

V

A

H

A

M

A

A



0

X



0

Y



0

M

A

H

A

= 0

V

A

= 0

– M

A

+ M = 0

l

H

A

= 0

V

A

= 0

M

A

= M

M

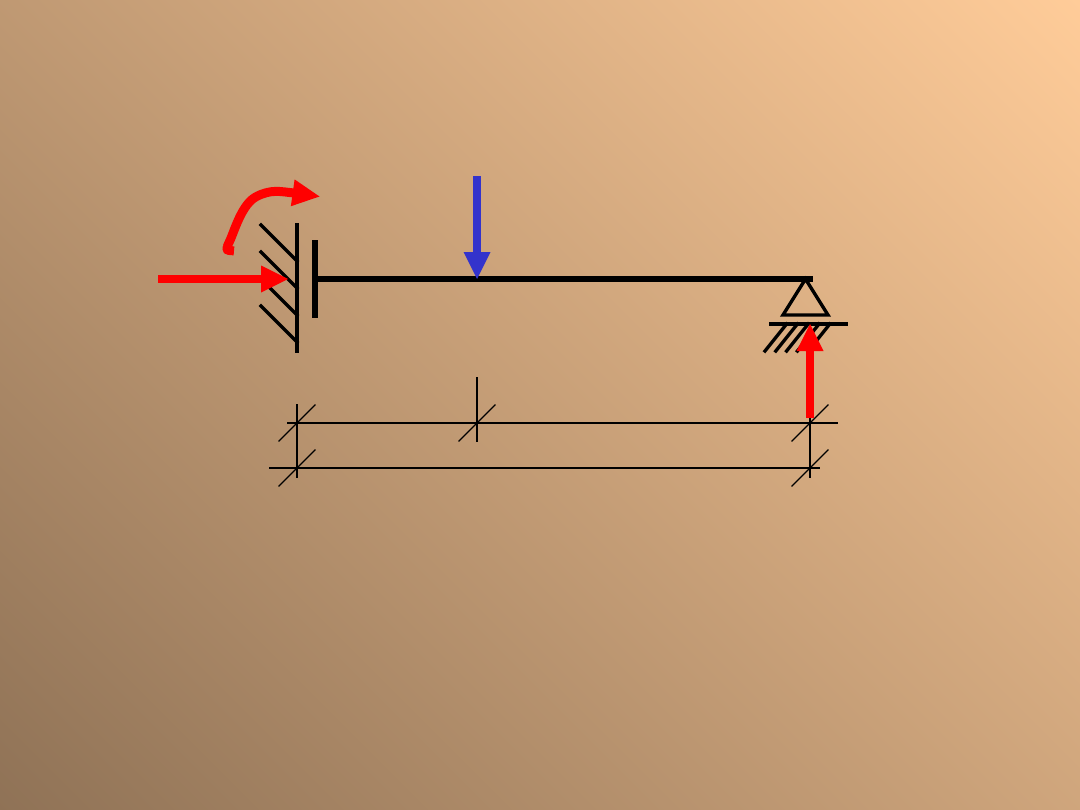
H

A

M

A

A



0

X



0

Y



0

M

A

H

A

= 0

R

B

– P = 0

M

A

+ Pa - R

B

l = 0

M

A

= P(l - a)

l

H

A

= 0

R

B

= P

M

A

= Pb

P

R

B

a

b

B

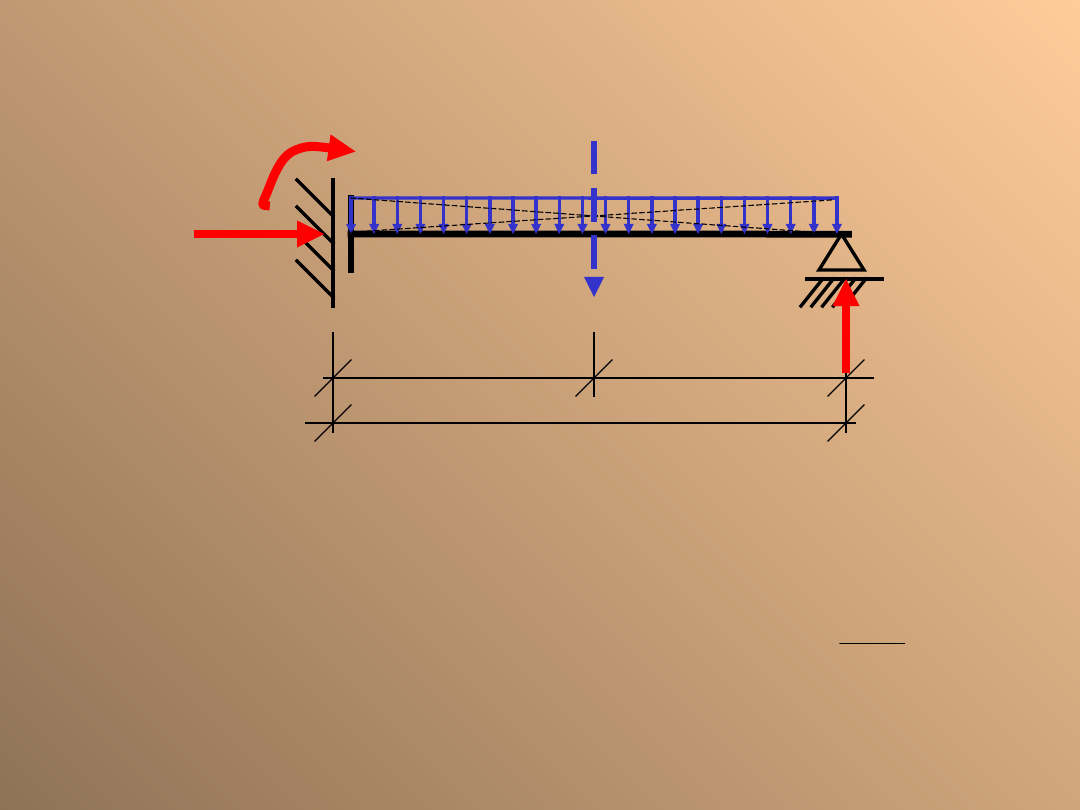
H

A

M

A

A

l

R

B

l/2

B

ql

l/2

q



0

X



0

Y



0

M

A

H

A

= 0

R

B

– ql = 0

M

A

+ ql

2

/2 - R

B

l = 0

H

A

= 0

V

A

= ql

2

l

q

M

2

A





H

A

M

A

A

l

R

B

a

B

b

M



0

X



0

Y



0

M

A

H

A

= 0

R

B

= 0

- M

A

+ M - R

B

l = 0

H

A

= 0

R

B

= 0

M

A

= M

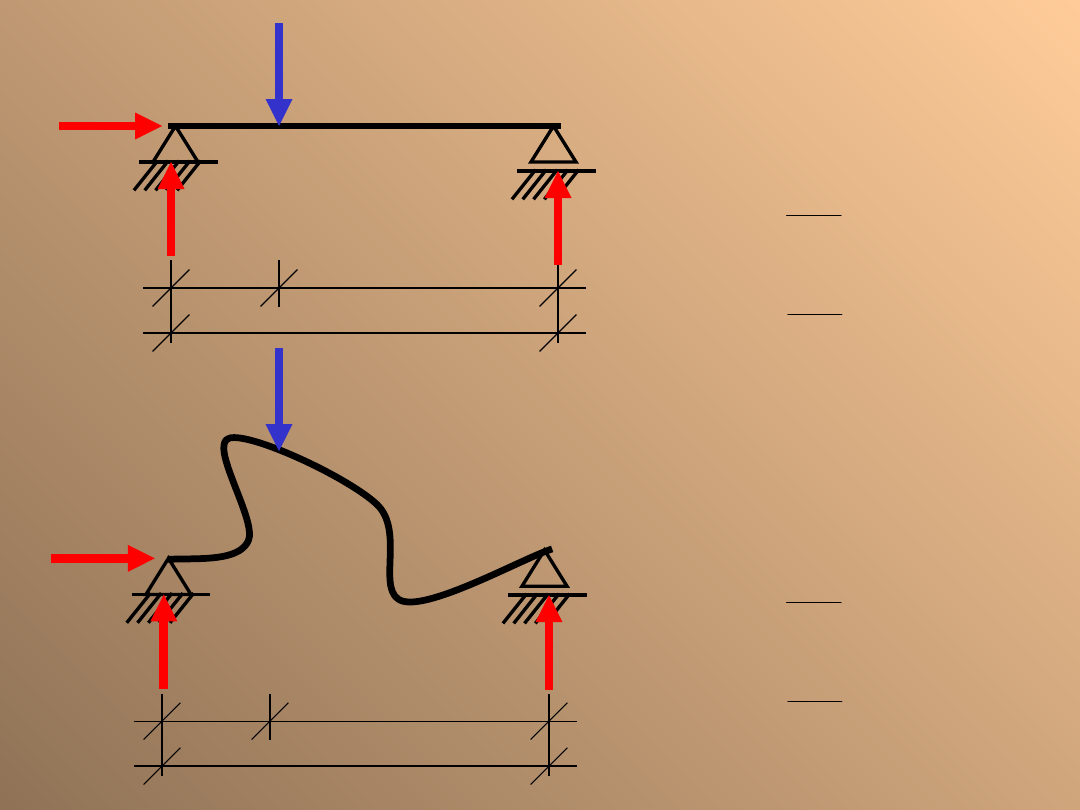
B

A

P

a

b

l

H

A

V

A

R

B

A

H

A

V

A

B

R

B

P

a

b

l

H

A

= 0

l

b

P

V

A





l

a

P

R

B





H

A

= 0

l

b

P

V

A





l

a

P

R

B





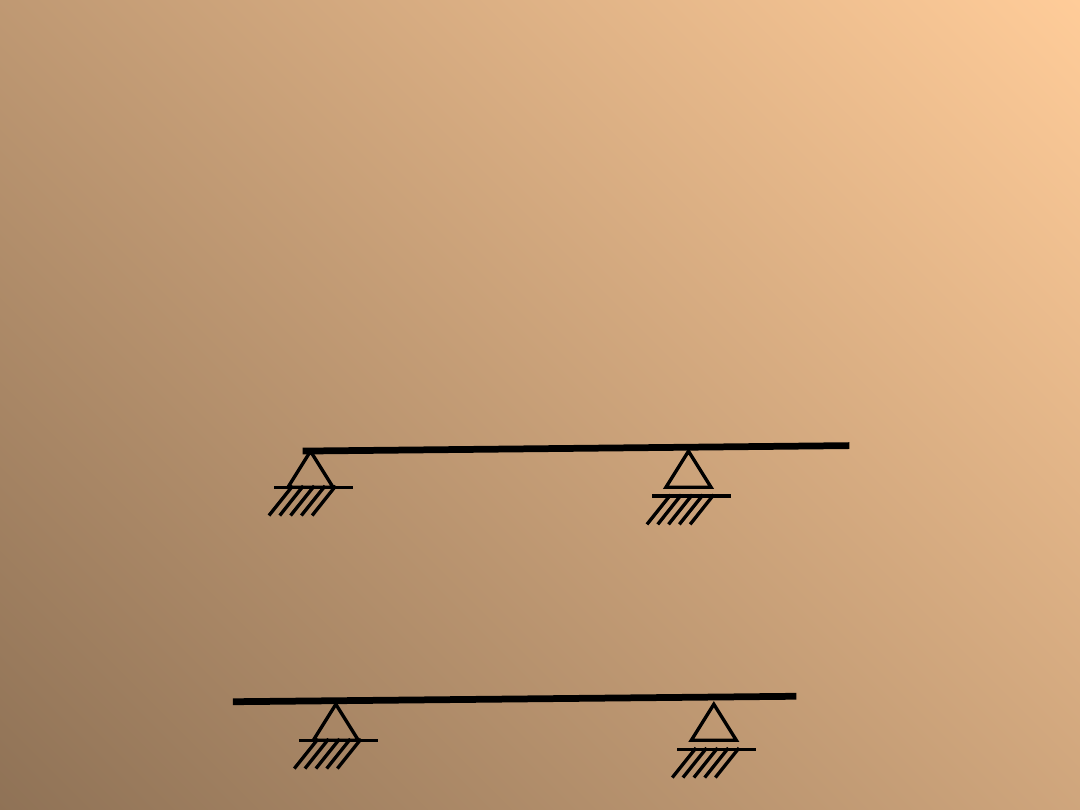
Belka wspornikowa

Jest to belka, która wystaje poza punkty podparcia A i B.

Jeżeli belka wystaje tylko poza jedną podporę,
nazywamy ją belką jednowspornikową,

a jeżeli belka wystaje poza obie podpory,
nazywamy ją belką dwuwspornikową.

B

A

B

A

Siły wewnętrzne w

płaskich statycznie

wyznaczalnych

utworach prętowych

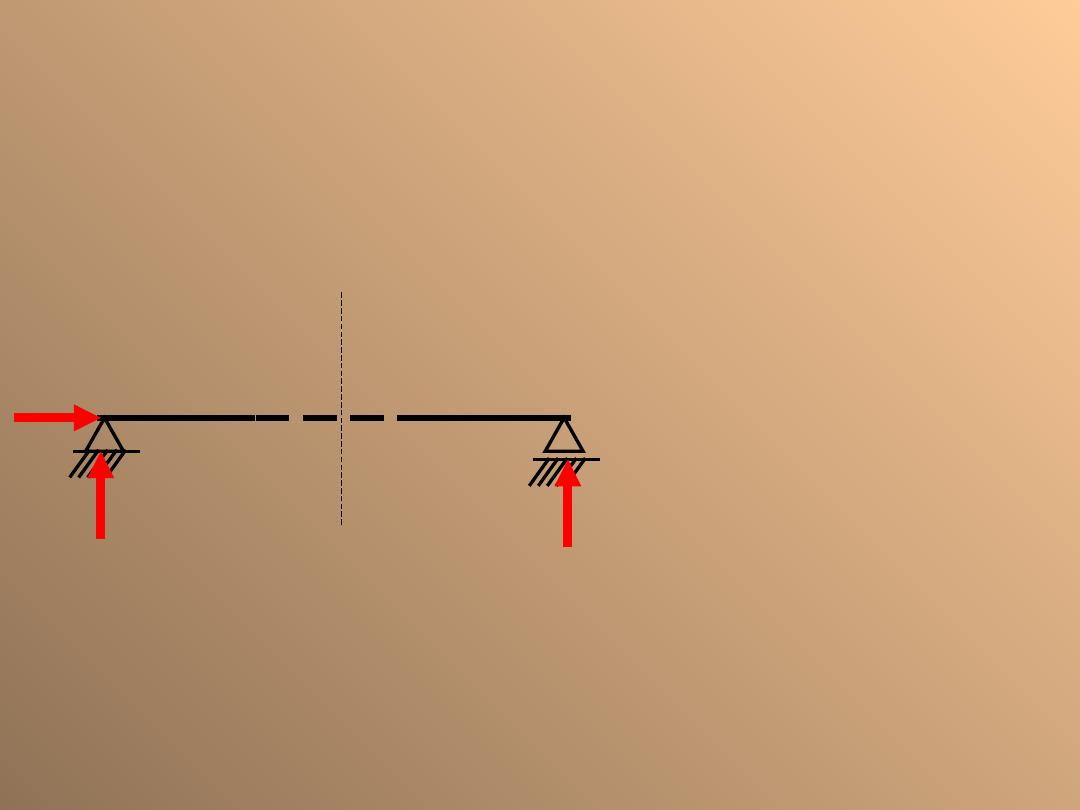
Równowaga ustroju

Aby pomimo przecięcia
ustrój

pozostał

w

równowadze należy:
-połączyć obydwie tarcze
trzema

elementarnymi

prętami nie przecinającymi
się w jednym punkcie;
-dobrać trzy siły M, T i N,
tak, aby tarcze znajdowały
się w równowadze.

V

A

A

H

A

R

B

I

II

1

1

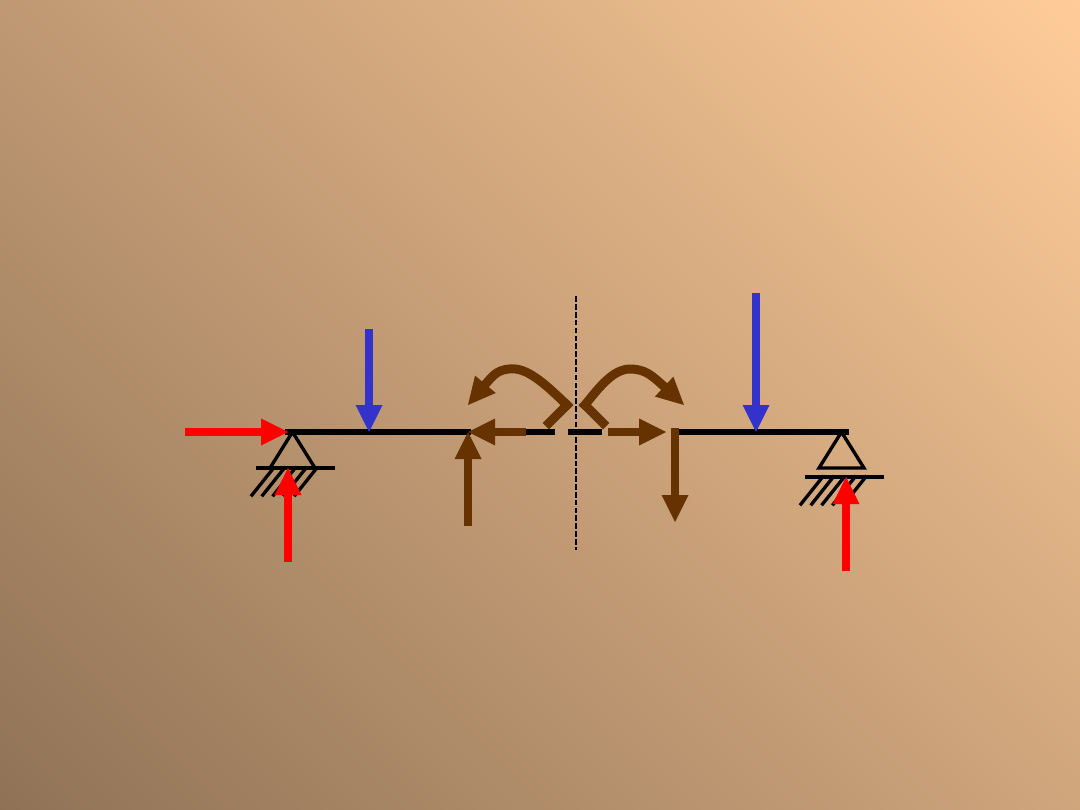
Moment gnący, siła tnąca

i siła osiowa

V

A

A

H

A

R

B

P1

P2

I

II

M

I

M

II

T

I

N

I

N

II

T

II

1

1

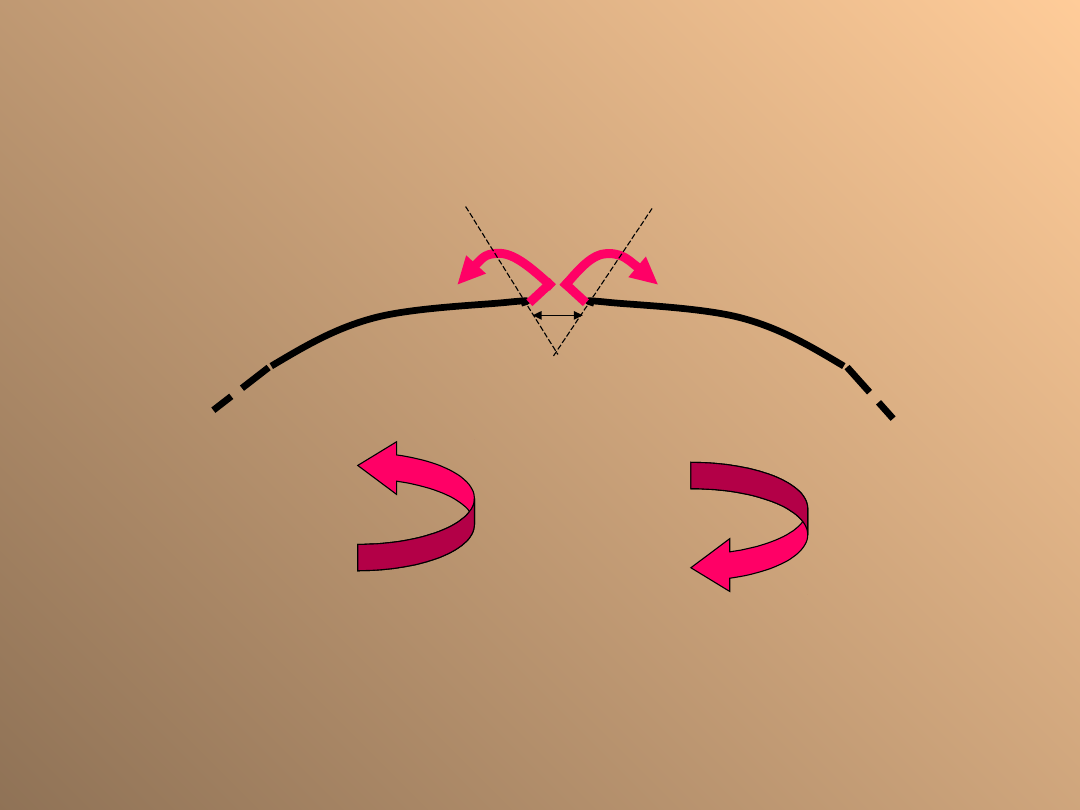
Moment gnący

M

I

M

I

I

-kąt zgięcia

-

+

MOMENT GNĄCY – jest to czynnik wywołujący zginanie, to

znaczy zmianę kąta położenia pomiędzy dwoma

sąsiadującymi przekrojami.

Moment gnący jest liczbowo równy sumie momentów
statycznych wszystkich sił położonych po jednej stronie
przekroju, względem środka masy tego przekroju.

Istnieją dwie umowy znakowania momentów gnących:
-wytrzymałościowa, według której za „+” uważa się
moment pochodzący od sił wyginających pręt wypukłością
do wnętrza;
-statyczna, gdzie moment gnący uważany za „+”
pochodzi od sił starających się obrócić rozpatrywany
przekrój zgodnie z ruchem wskazówek zegara.

Moment gnący

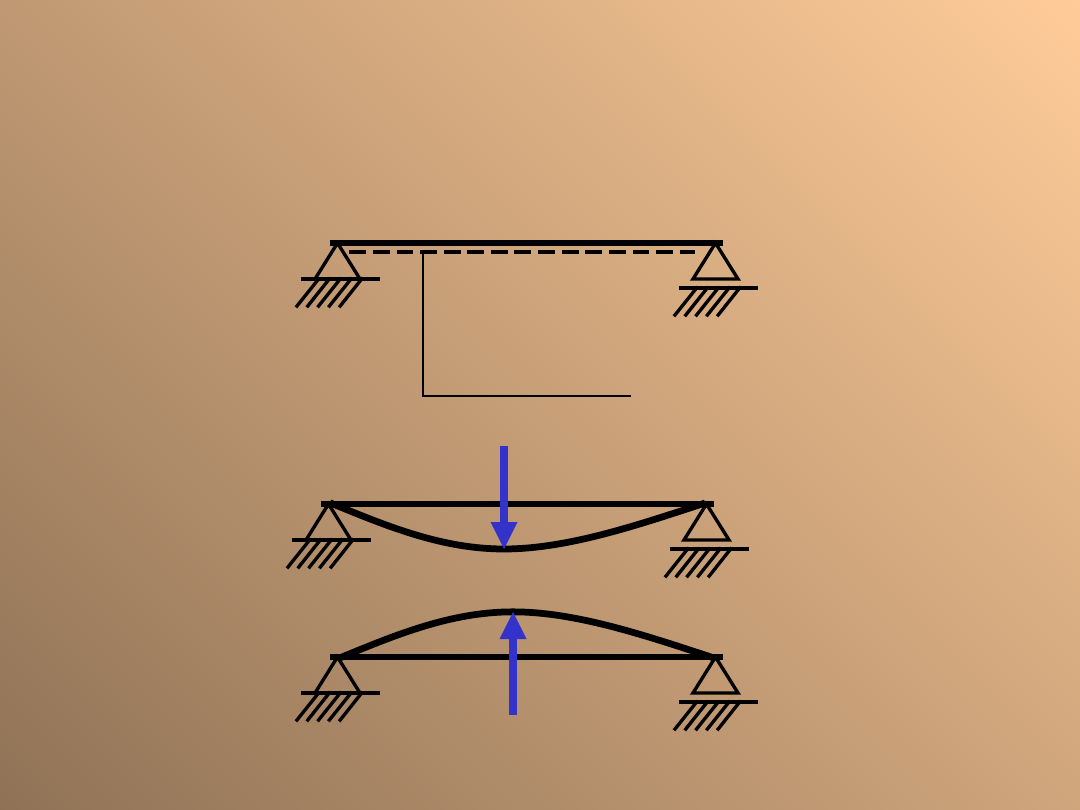
Moment gnący

WNĘTRZE

P

P

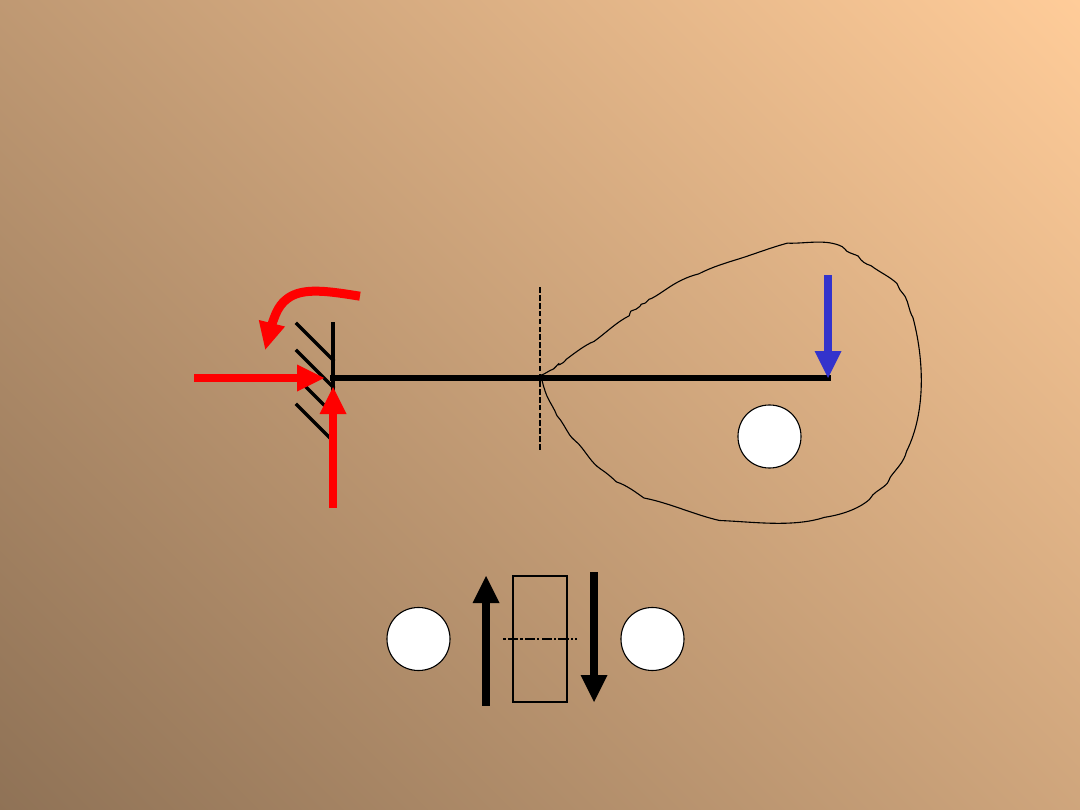
Siła tnąca

T

T

Siła tnąca jest to czynnik wywołujący ścinanie,
czyli

równoległe

przesunięcie

dwóch

sąsiadujących przekrojów.

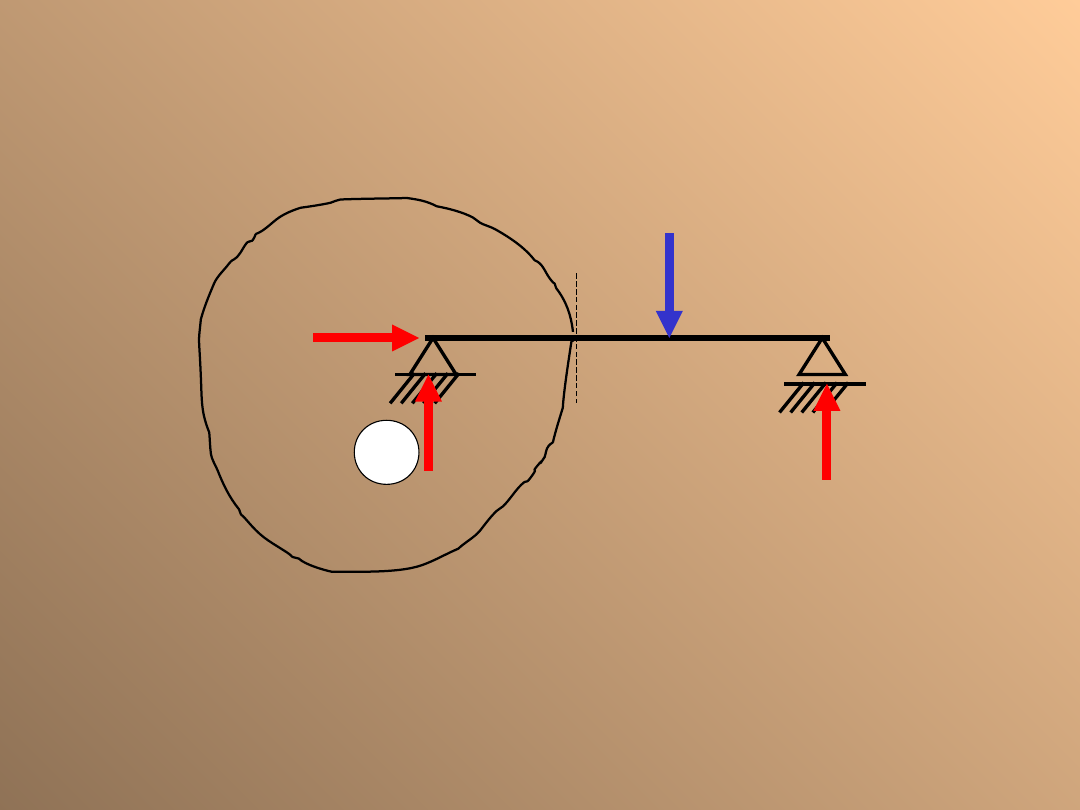
Siła tnąca

1

1

+T

Siła tnąca jest liczbowo równa sumie rzutów wszystkich sił

położonych po jednej stronie przekroju na kierunek

prostopadły do osi pręta.

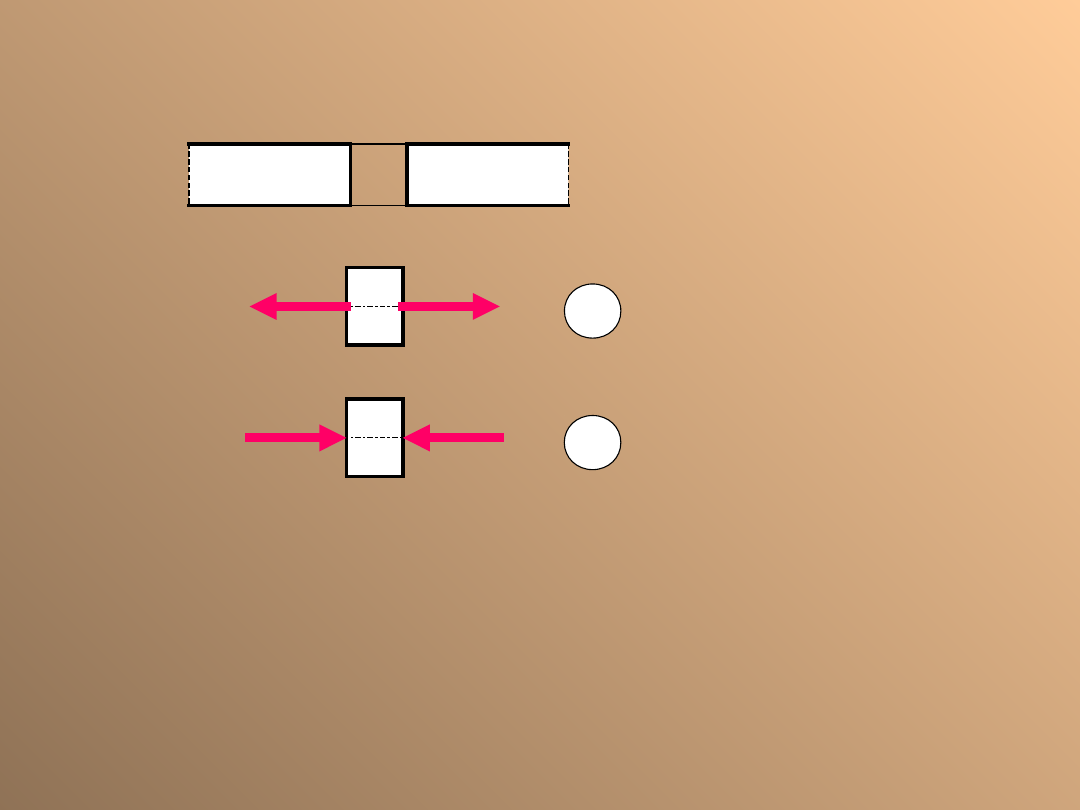
Siła tnąca

1

1

+T

+T

+T

Jest „+”, gdy licząc z
prawej

strony

przekroju

jest

skierowana

ku

dołowi

Jest „+”, gdy licząc
z

lewej

strony

przekroju

jest

skierowana

ku

górze

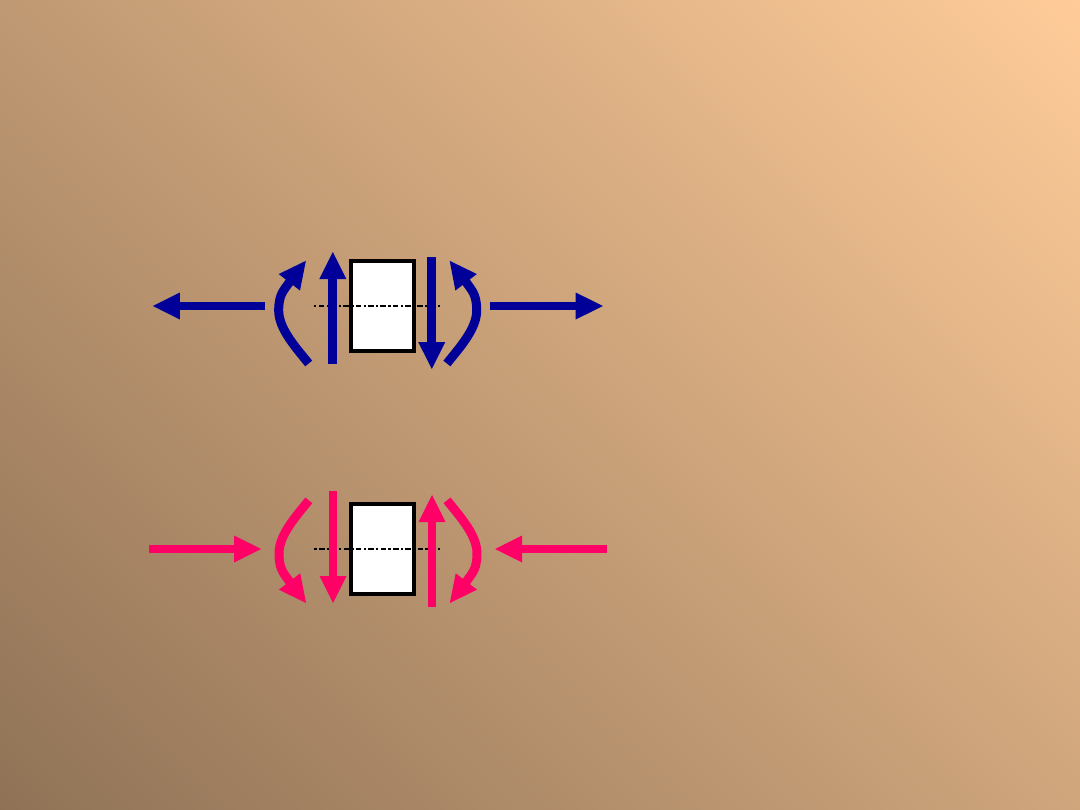
Siła osiowa

N

N

+N

rozciąganie

N

N

-N

ściskanie

Siła osiowa jest to czynnik powodujący ściskanie lub rozciąganie,

czyli zbliżenie lub oddalenie dwóch sąsiadujących ze sobą

przekrojów.

Siła osiowa jest liczbowo równa sumie rzutów wszystkich sił

położonych po jednej stronie przekroju na kierunek równoległy do

osi pręta.

Siły wewnętrzne

+N

+N

+T

+T

+M

+M

-N

-N

-T

-T

-M

-M

z prawej strony przekroju

z lewej strony przekroju

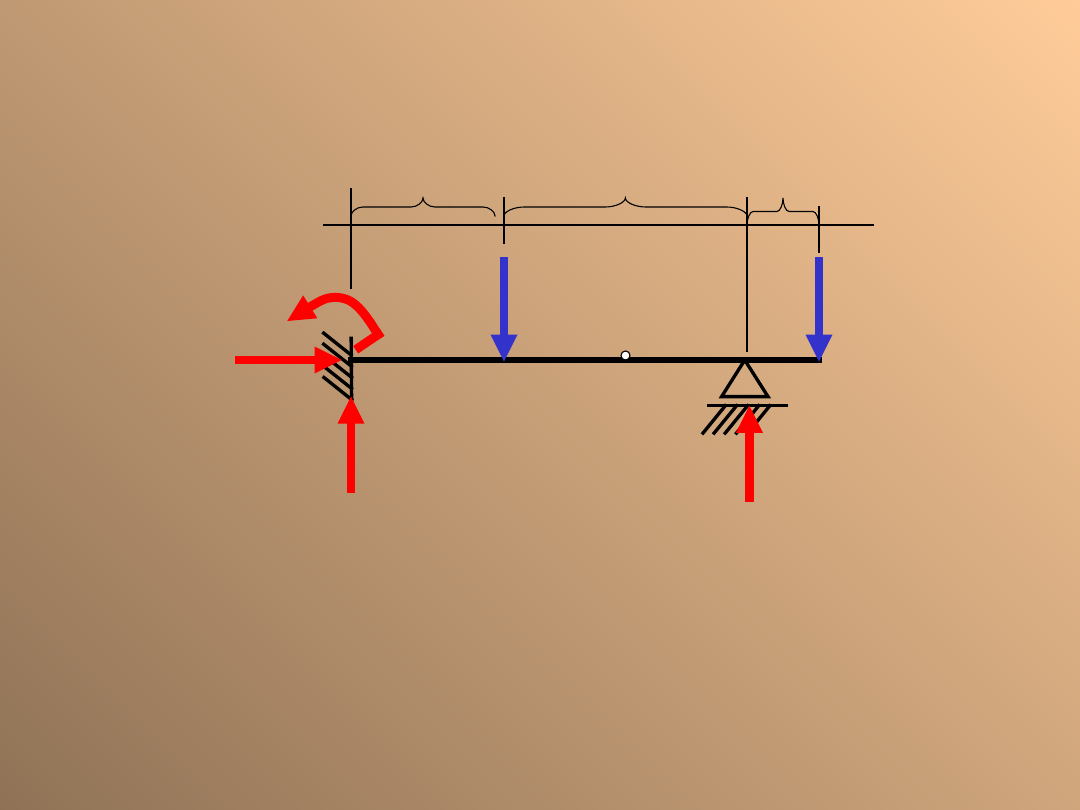
Przedział obciążenia

Przedziałem obciążenia nazywamy taką część ustroju,
mierzoną wzdłuż osi pręta, w której obowiązuje jedno
równanie momentów gnących, sił tnących i sił osiowych.

Przegub nie stanowi granicy przedziału obciążenia.

II

I

III

Dziękuję za uwagę