Eigenvalue Equations and
Operators

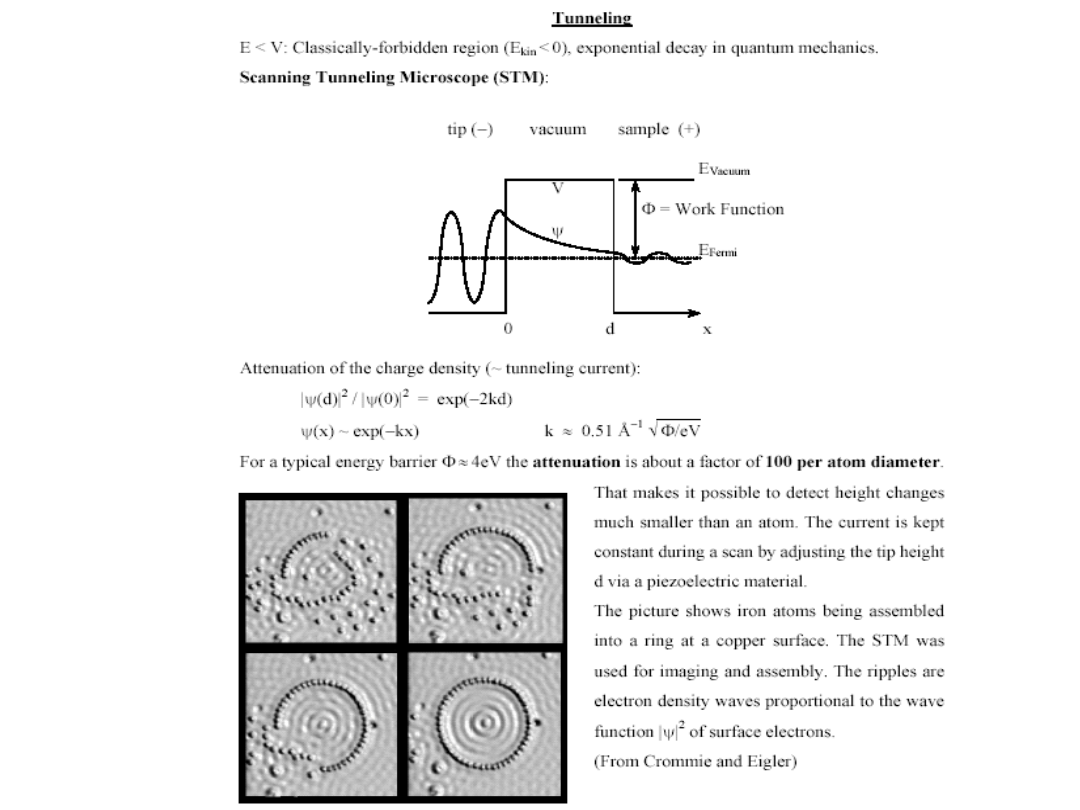
The Schrödinger equation

can be rewritten as

ˆ

H (x)E(x); ˆ

H =

h

2

2m



2



x

2

 V(x)

where ˆ

H is the quantum mechanical Hamiltonian







ˆ

(operator

)(function

) (constant)(samefunction

)

(operator)(eigenfunction)

=(eigenvalue)(eigenfunction)

cos;

:

 

2

Some non-linear operators

:

For linear operators the following identities apply

:

(ˆ

A +ˆ

B )ˆ

C = ˆ

A ˆ

C +ˆ

B ˜

C ; ˆ

A (ˆ

B + ˆ

C ) = ˆ

A ˆ

B + ˆ

A ˆ

C

ˆ

A {f(x) g(x)} ˆ

A f(x) ˆ

A g(x)

ˆ

A {kf(x)}k ˆ

A f(x)

Some linear operators

:

x;x

2

;

d

dx

;

d

2

dx

2

Multiplicative

Differential

Operator

ˆ

A Function f

ˆ

A f(x)

d

dx

f f'

(x)

3 f 3f
cos() x cosx

x

x

Rules for operators

:

( ˆ

A  ˆ

B )f(x)  ˆ

A f(x) ˆ

B f(x): Sum of operators

( ˆ

A  ˆ

B )f(x)  ˆ

A f(x) ˆ

B f(x):Dif. of operators

15

3

3

)

15

3

(

3

)

5

(

3

)

5

(

ˆ

)

5

)(

3

ˆ

ˆ

(

ˆ

3

2

3

2

3

3

3

























x

x

x

x

x

x

D

x

D

dx

d

=

D

Example

ˆ

A ˆ

B f(x)  ˆ

A [ ˆ

B f(x)]:product of operators

We first operate on f with the operator '

ˆ

B '

on the right of the operator product,

and

then take the resulting function (

ˆ

B f) and

operate on it with the operator

ˆ

A on the left

of the operator product.

)

(

'

))

(

ˆ

(

ˆ

)

(

ˆ

ˆ

)

(

'

)

(

))

(

(

ˆ

)

(

ˆ

ˆ

ˆ

;

ˆ

x

xf

x

f

D

x

x

f

D

x

x

xf

x

f

x

xf

D

x

f

x

D

x

x













dx

d

=

D

Example

Operators do not necessarily obey the commutative law

:

ˆ

A ˆ

B  ˆ

B ˆ

A 0: ˆ

A ˆ

B  ˆ

B ˆ

A [ ˆ

A , ˆ

B ]0

Cummutator

:

Example: ˆ

A = X

2

; ˆ

B =

d

dx

ˆ

A ˆ

B f x

2

df

dx

: ˆ

B ˆ

A f =

d(x

2

f)

dx

2xf x

2

df

dx

[ˆ

A ,ˆ

B ]f  2xf

The square of an operator is defined as the product of
the operator with itself

: ˆ

A

2

= ˆ

A ˆ

A

Examples : ˆ

D =

d

dx

ˆ

D ˆ

D f(x)= ˆ

D (ˆ

D f(x))= ˆ

D f'(x)f"(x)

ˆ

D

2



d

2

dx

2

apply

rules

follow

the

where

etc.

,

C

,

B

,

A

operators

linear

with

dealing

be

shall

We

ˆ

ˆ

ˆ

Hermetian Operators

Hermetian Operators

Consider a system described by the state function

 .

Let

F

^

be the operator representing the observable F

The average value of

F , or the expectation value is given by

<F>

= 



 

 

 

*

F

^

 d

A physical expectation value must be real
Thus :

<F> = <F>





 

 

  

*

F

^

 d



 

 

 

*

F

^

 d





=



 

 

  

(

F

^





d

An operator that satisfy this condition is

Hermitian

One Definition of

Hermitian operator

Funkcje własne odpowiadające tej samej wartości można ortogonalizować

(wartości własne zdegenerowane)

)

deg

(

,...,

2

,

1

ˆ

,

,

eneracji

krotno

śr

g

j

f

F

j

l

l

j

l









0

)

ˆ

(

,







j

l

l

f

F

j

i

j

l

i

l

l

l

l

l

l

l

l

l

l

l

i

l

l

g

j

j

l

j

l

i

l

d

itd

d

d

itd

x

x

N

x

N

)

-f

F

(

c

y

,

,

*

,

3

,

*

1

,

3,1

2

,

*

1

,

2,1

2

,

2

,

3

1

,

1

,

3

3

,

3

l,3

1

,

1

,

2

2

,

2

l,2

1

,

l,1

,

1

,

,

,

Wtedy

x

x

gdzie

.

)

(

)

(

wybierzmy

0

ˆ

wtedy

weźe

















































































n





n



n

For an observable

 with the corresponding

operator

ˆ

 we have the eigenvalue equation

:

(IIIa). The meassurement of the quantity represented by



has as the o n l y outcome one of the values



n

n=1,2,3 ....

(IIIb). If the system is in a state described by



n

a meassurement of

 will result in the

value



n

Examples of operators and their

eigenfunctions

Example Operator

Eigenfunction Eigenvalue

1





x

exp[ikx]

ik

2



2



x

exp[ikx]

 k

2

3



2



x

coskx

 k

2

4



2



x

sinkx

 k

2

with the eigenfunction f and the eigenvalue k

**

.

**

ˆ

A f kf

ˆ

A (cf) k(cf)

sh

ow

Mu

st

Demonstrate that cf also is an eigenfunction to

ˆ

A

with the same eigenvalue k if c is a constant

proof:

ˆ

A is a Linear operator

ˆ

A (cf)cˆ

A f

*

ˆ

A

(cf) cˆ

A

f

operator

linear

a

be

A

Let ˆ

c is a constant

f is a function

e.g. A =

d

dx

ckf

f is an eigenfunction of

ˆ

A

Rearrangement of constant

factors and QED

k(cf)

we can solve the eigenvalue problem

ˆ





n





n



n

For any such operator

ˆ



We obtain

eigenfunctions

and eigenvalues

The only possible values that can arise from measurements

of the physical observable

 are the eigenvalues



n

Postulate 3

A linear operator

ˆ

A will have a set of

eigenfunctions f

n

(x) {n=1,2,3..etc}

and associated eigenvalues k

n

such that

:

The set of eigenfunction {f

n

(x),n 1..}

is orthonormal

:

f

i

(x)

*

all space



f

j

(x)dx

ij

ˆ

A f

n

(x) k

n

f

n

(x)

o if ij

 1 if i=j

e

i

 e

j



ij

ei

ei

ei

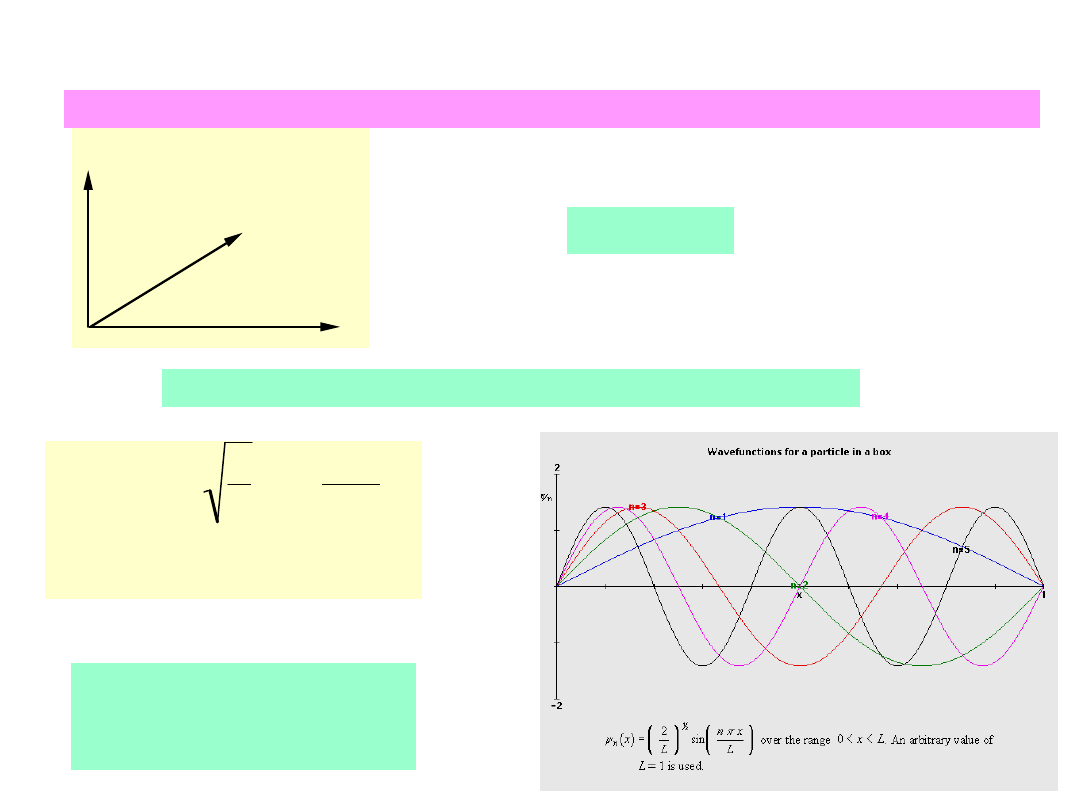
An example of an orthonormal set is the Cartesian unit vectors

An example of an orthonormal function set is



n

(x)=

1

L

sin

nx

L









n=1,2,3,4,5....



n

(x)

*

o

L





m

(x) 

nm

That is, any function g(x) that
depends on the same variables
as the eigenfunctions can be written

g(x)= a

n

f

n

(x)

i=1

all



where

a

n



f

n

(x)

*

g(x)dx

all space



The set of eigenfunction {f

n

(x),n 1..}

forms a complete set.

ei

ei

ei

r

e

i

; i=1,2,3 form a complete set

For any vector

r

v

v (

r

v 

r

e

1

)

r

e

1

 (

r

v 

r

e

2

)

r

e

2

 (

r

v 

r

e

3

)

r

e

3